Dynamic Adjustments of Attentional Control in Healthy Aging

Abstract

In standard attentional control tasks, interference effects are reduced following incongruent trials compared to following congruent trials, a phenomenon known as the congruency sequence effect (CSE). Typical explanations of this effect suggest the CSE is due to changes in levels of control across adjacent trials. This interpretation has been questioned by the finding that older adults, individuals with impaired attentional control systems, have been shown to produce larger CSEs in the Stroop task compared to younger adult controls. In two experiments, we investigate the generality of this finding by examining how the CSE changes in healthy aging in three standard attentional control tasks, Stroop, Simon and flanker, while controlling for additional confounds that have plagued some of the past literature. In both experiments, older adult participants exhibited a larger CSE in the Stroop task, replicating recent research, but smaller CSEs in both the Simon and flanker paradigms. These results are interpreted as reflecting a pathway priming mechanism in the Stroop task but a control adjustment process in Simon and flanker. Hence, there appears to be different mechanisms underlying the CSE which are engaged based on the type of attentional selection that is required by the task. More generally, these results question the use of the CSE in the Stroop task as a measure of dynamic adjustments in attentional control and highlight the importance of consideration of task-specific control systems underlying the CSE.

The ability to selectively attend to relevant aspects of the environment while ignoring highly salient, yet irrelevant, information is a critical component of goal-directed behavior. Attentional control is typically measured by using paradigms which place task-relevant information in conflict with task-irrelevant information. For example, the classic Stroop color naming task (Stroop, 1935) utilizes color words (e.g., “RED”) printed in colored ink (e.g., blue) and participants are asked to indicate the ink color while ignoring the word. Differences in response time (RT) between stimuli in which the two dimensions are aligned (“RED” in red ink, congruent trials) and when the dimensions are in competition (“RED” in blue ink, incongruent trials) serve as a measure for the efficiency of attentional control processes. Specifically, if attention is perfectly controlled such that only the color of the stimulus is processed, the difference in RT between congruent and incongruent trials (i.e., the interference effect) would be zero.

Deficits in attentional control over competing representations have long been proposed as a key mechanism underlying other cognitive deficits in healthy aging (Hasher & Zacks, 1988). To directly examine this hypothesis, numerous studies have been designed to examine age differences on classic attentional control tasks. In the case of the Stroop task, the magnitude of the interference effect does appear to increase with age (Aschenbrenner & Balota, 2015; Bugg, DeLosh, Davalos, & Davis, 2007; Jackson & Balota, 2013; Puccioni & Vallesi, 2012; Spieler, Balota, & Faust, 1996, but see Verhaeghen & De Meersman, 1998) and these age deficits are generally apparent across a number of tasks (Hasher, Zacks, & May, 1999; Jurado & Rosselli, 2007) supporting the notion of impaired attentional control in older adults.

Recently, researchers have attempted to further understand this general deficit by identifying specific components of attentional control that are most influenced by age in order to provide a better characterization of attentional changes across the lifespan. For example, researchers have examined age differences in sustained, top-down control over attention, (Bugg, 2014a; Mutter, Naylor, & Patterson, 2005; West & Baylis, 1998), as compared to a reactive control system by which levels of control are rapidly changed post-stimulus onset (Braver, Satpute, Rush, Racine, & Barch, 2005; Bugg, 2014b).

Another aspect of attentional control, and the focus of the present report, is the fluid adjustment of control across adjacent trials, independent of other item or list-wide constraints. Namely, how is control adjusted in response to previously encountered items within the list? Of course, standard implementations of attentional control tasks assume each trial is processed as a unique event and responses are typically collapsed across trials within a given condition when making inferences about underlying mechanisms. Such assumptions of independence can be problematic if the control system is consistently recovering from prior responses and / or preparing for future trials, based on past performance. Indeed, there is evidence to suggest that this is the case as the magnitude of interference on any given trial changes as a function of the congruency of the immediately preceding trial. The well-established pattern of results is that interference (both in RT and error rates) on Trial N is significantly reduced following an incongruent stimulus on Trial N-1 compared to following a congruent trial (Gratton, Coles, & Donchin, 1992; Schmidt, 2013a), known as the congruency sequence effect (CSE).

Although there are many explanations of this phenomenon, the most prominent account is the conflict monitoring hypothesis which ascribes the CSE to local adjustments of attentional control processes induced due to perceived conflict (Botvinick, Braver, Barch, Carter, & Cohen, 2001). Specifically, after having just responded to an incongruent stimulus, the conflict from that item signals the cognitive system to increase control for the following trial, which directly leads to the reduction in overall interference. Other accounts posit that participants track temporal information across stimuli and use that information on subsequent trials to adjust levels of response caution (Schmidt & De Houwer, 2011; Schmidt, 2013b), or that participants engage in a prediction strategy by which they change the focus of attention (e.g., from color to word) prospectively for the next trial (Gratton et al. 1992). As already mentioned, much research has been devoted to teasing apart these theoretical mechanisms (Duthoo, Abrahamse, Braem, Boehler, & Notebaert, 2014; Weissman, Egner, Hawks, & Link, 2015), but regardless of the exact account, larger CSEs are interpreted as indicating greater cross-trial adjustments in an ongoing response process.

Returning to the issue of healthy aging, because of more efficient control systems in younger adults as compared to older adults, one might expect that younger adults would also have a more flexible system, and thus be better able to modulate and adapt their levels of control in response to local context (i.e., the congruency of prior trials) relative to older adult participants. Recently, Aschenbrenner and Balota (2015) tested this hypothesis using a large dataset of 435 healthy older adults and found that, contrary to expectations, the CSE significantly increased with age, and this was particularly true for individuals who were relatively low in working memory capacity. However, other studies using the Stroop task have shown age equivalence in the CSE (Puccioni & Vallesi, 2012), as well as numerical, (but statistically non-significant) increases with age (West & Moore, 2005). Interestingly, other studies of the CSE using tasks other than Stroop have revealed mixed results with evidence for a reduction in the CSE with age in a Simon task (Aizenberg, Sapir, d’Avossa & Henik, 2014) and no age differences in a flanker task (Larson et al., 2016). However, because the task methodology and the degree to which stimuli repetition / contingency and other confounds were controlled varied across these studies (see further discussion below), it is difficult to make strong inferences about the underlying mechanisms producing the differences in previous literature.

At a theoretical level, intact or increasing CSEs with age appear inconsistent with the notion of the CSE reflecting an adjustment in control across trials. Specifically, according to the conflict monitoring account, age related increases in the CSE would suggest that older adults are better able to adjust control across adjacent stimuli. This is unexpected given that the prefrontal control regions posited to produce such changes preferentially decline with age (West, 1996). Similarly, if the CSE is produced by cross-trial changes in response caution, the age patterns would imply that older adults make larger adjustments to response thresholds on a trial by trial basis. Again, this is inconsistent with behavioral research that shows older adults are less willing to change their response thresholds even when explicitly instructed to do so (Starns & Ratcliff, 2010) and is related to reduced white matter integrity in the older adult brain (Forstmann et al., 2011).

In light of these findings, Aschenbrenner and Balota (2015) proposed that in the context of a Stroop task, the CSE might be the result of residual processing activity across trials based on the utility of a particular dimension on the previous trial, a mechanism they called pathway priming (see also Hubbard, Kuhns, Schäfer, & Mayr, 2016). Specifically, assume a typical model of Stroop performance in which there are two processing pathways, color and word, and an attentional system that biases the use of one pathway over the other. Activity accumulates along each pathway until sufficient evidence in favor of a particular response has been reached. If Trial N -1 was incongruent, trials on which only color processing yields a benefit, the color pathway is primed for use on the subsequent trial which speeds responses when the Trial N is also incongruent. In contrast, if Trial N – 1 was congruent, the word pathway is primed due to the relative utility of the word in making the correct response on those trials. If Trial N is subsequently congruent, responses will again be faster than otherwise due to greater activity along the (helpful) word pathway. However, if Trial N is incongruent, there is additional activation along the (now irrelevant) word pathway that must be controlled. If older adults are less able to control this cross trial pathway priming, they would be expected to show larger “adjustments” relative to younger adults. Importantly, pathway priming differs from the other accounts discussed above primarily in proposing a residual carry-over process rather than an explicit adjustment in response dynamics across trials. Hence, we will refer to this mechanism as a “priming” account to contrast against conflict monitoring and temporal learning as “adjustment” accounts whereby changes are made to decision or control processes. Of course, the priming account cannot accommodate significant reductions in the CSE across age which have also been shown in the literature at least in the Simon task (e.g., Aizenberg et al. 2014) suggesting that pathway priming may only be engaged under particular task constraints.

Motivated by these task differences in the magnitude of the CSE with age, the primary goal of the present report was to compare the direction of the CSE by age interaction across three attentional control tasks, Stroop, Simon and flanker. The hypotheses of this study are very straightforward. If a single mechanism underlies the CSE across tasks, we expect to observe consistent interactions with age, once relevant learning and stimuli confounds are appropriately controlled. Specifically, the adjustment accounts would predict decreases with age in the CSE and the priming account predicts an age-related increase. More interestingly, if different attentional selection tasks emphasize selection at different points within the processing stream (see for example, Pratte et al. 2010; Spieler et al. 2000), one might expect an age by CSE by task interaction whereby the CSE increases with age in certain tasks but decreases in others.

The three attentional tasks were chosen based on their popularity of use in testing the CSE as well as the apparent age differences in the CSE that each task produces as outlined above. Additionally, there are three important methodological issues to take into consideration when examining the CSE across different tasks. The first is the need to equate the types of stimuli that are used. Specifically, although Stroop tasks almost exclusively use color and word stimuli, Simon and flanker tasks could use words, arrows, letters or even shapes as their stimuli. It is possible that different stimuli (rather than different control tasks per se) drive the differential age patterns in the CSE. Thus, as outlined below, we developed versions of each task that used linguistic stimuli (words and letters) to better equate the tasks on that dimension. Second, response characteristics often differ across paradigms. Stroop tasks most often require a vocal response whereas flanker and Simon tasks almost always involve keypress responses. These response differences can make cross-task comparisons problematic, therefore in the present design, we used the same keypress response scheme in all three tasks. Third, and most importantly, the presentation of items was controlled in order to eliminate the cross trial repetition (Mayr, Awh, & Laurey, 2003) and contingency biases (Schmidt & De Houwer, 2011) that has confounded much of the past work in this area. Specifically, no aspect of the stimulus (in the case of Stroop, the color or the word) or the key press response was allowed to repeat across adjacent trials. Finally, we restricted the stimulus set such that no aspect of the stimulus was disproportionately predictive of a given response using a previously established method (Kim & Cho, 2014; Jimenez & Mendez, 2014; Weissman, Jiang, & Egner, 2014). Such controls are critical in constraining the interpretation of the CSE (see Duthoo et al. 2014b).

Experiment 1

Method

Participants

Forty young adults were recruited from the undergraduate research pool at Washington University in St. Louis who participated for course credit or for monetary reimbursement. Thirty-six older adults were recruited from a volunteer pool maintained by Volunteers for Health, a database of healthy, community dwelling seniors who are interested in participating in research studies. Older adults were given monetary reimbursement for their participation ($25). Demographic information collected on these individuals is provided in Table 1. Older adults had more years of education, t(74) = 5.35, p < .001 and lower working memory scores, t(68) = 2.47, p = .016 relative to younger participants.

Table 1.

Demographic characteristics of participants in Experiment 1.

	Younger		Older
	Mean	SD	Mean	SD
Age	20.3	2.2	72	4.5
Education	13.4	3.2	17.2	3
AD8	--	--	0.72	1.1
CompSpan	14.2	6.1	10.6	6.4

Note: A score of 2 or greater on the AD8 is suggestive of cognitive impairment. CompSpan = computation span task, higher scores = higher working memory

Procedure

Given the importance of controlling for the various confounds already identified in the literature, we first describe the general experimental procedure before discussing the materials and design of each specific task. First, to ensure that no aspect of a stimulus repeated across adjacent trials, we created four stimuli for each task (e.g., for Stroop we used four colors). These stimuli were placed into pairs such that only two stimuli appeared together on any given trial. The pairs then alternated across trials. For example, in the Stroop task, trial N-1 could consist of either Color 1 or Color 2 (either incongruent or congruent) and trial N could consist of either Color 3 or Color 4 (again either incongruent or congruent). Trial N + 1 would then sample from Color 1 / Color 2 again. Although the colors alternated in this pattern, the stimulus selected on a given trial was not contingent on the previously selected stimulus. Since only pairs of stimuli were used, all responses were 50% contingent, that is the irrelevant dimension predicted the correct response only 50% of the time. Additionally, in order to ensure that a response was not repeated across trials, participants used the numeric keypad on the right of the keyboard to input their choices. Specifically, the numbers 2, 4, 6 and 8 were assigned as responses and only two possible responses were available on a given trial. For example, on Trial N-1 the response options would be 2 and 8, then on Trial N the response options would be 4 and 6, etc.

On each trial of each task, the following events were identical: 1) a fixation cross was displayed for 500 ms, 2) a blank screen appeared for 200 ms, 3) the stimulus was shown for 5000 ms or until a response was made, 4) feedback was given for 1000 ms (“ERROR” for incorrect responses and “TOO SLOW” for a no response after 5000 ms, blank screen for correct responses), 5) a screen that said “Press 5 to continue” was displayed until the participant pressed the 5 key. This final step was done to insure the participant’s finger was equidistant from all responses for each trial. The average time to self-initiate the next trial was less than 1 second for each age group in each task. All study procedures were approved by the Washington University in St. Louis Institutional Review Board.

Materials

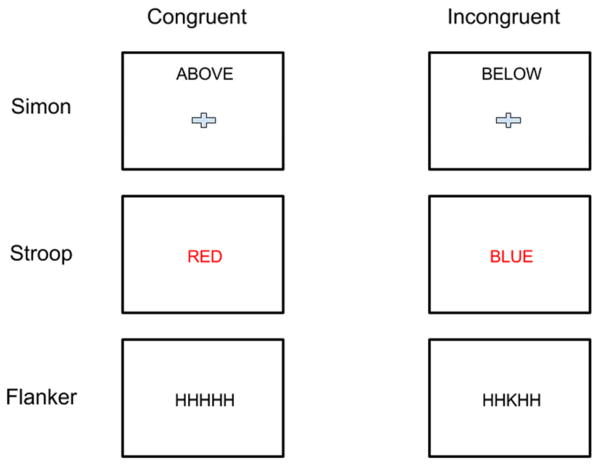
Examples of congruent and incongruent trials for each task are shown in Figure 1 and the frequency of their presentations are shown in Table 2. The Simon task consisted of spatial words (ABOVE, BELOW, LEFT, RIGHT) that were printed either at the top, bottom, left or right of the computer screen. Participants were asked to indicate the identity of the word and ignore the spatial location. Responses were indicated using the numeric keypad (response keys: 2, 4, 6, 8). The “2” key corresponded to “BELOW”, 4 to “LEFT”, 6 to “RIGHT” and 8 to “ABOVE”. Words and locations were placed into pairs (e.g., the word “LEFT” could appear on the left or the right side of the screen but never at the top or the bottom). Stimuli alternated between the top vs. bottom and the left vs. right so that no location, response or word was repeated across adjacent trials.

Figure 1.

Examples of each task used in Experiments 1 and 2.

Table 2.

Stimuli frequencies for each task in Experiment 1. The rows in each table are the irrelevant dimension and the columns contain the relevant dimension.

		Simon Task
		Word
		ABOVE	BELOW	LEFT	RIGHT
Location	ABOVE	48	48
	BELOW	48	48
	LEFT			48	48
	RIGHT			48	48

		Stroop Task
		Color
		RED	BLUE	GREEN	YELLOW
Word	RED	48	48
	BLUE	48	48
	GREEN			48	48
	YELLOW			48	48

		Flanker Task
		Central Letter
		C	S	H	K
Flanking Letters	C	48	48
	S	48	48
	H			48	48
	K			48	48

The Stroop task consisted of four color words (RED, BLUE, GREEN, YELLOW) which were printed either in the same color ink (congruent trials) or an incongruent color (e.g., RED printed in blue ink). Colors and words were split into pairs and counterbalanced and rotated across subjects, controlling for stimulus and response repetitions. For both the flanker and Stroop tasks, response keys (e.g., “4” = BLUE) were written on a “cue card” that was in full view of the participant to refer to at any time during the task.

The flanker task consisted of arrays of 5 letters (e.g., HHHHH) that were formed from a pool of 4 possible letters (C, S, H and K). Participants were instructed to indicate the central letter using the keypad. Stimuli were either congruent (the stimulus consisted of 5 identical letters) or incongruent (the central letter was different from the flanking 4 letters).

Each task was preceded by a practice block of 16 items. Additionally, the Stroop and flanker tasks included a 20 item “learning” phase, during which single letters (for flanker) or colored rectangles (for Stroop) were displayed and participants were instructed to press the corresponding button. This was intended to help map the response keys to the individual stimuli. The Simon task did not include a learning phase because the responses were already tied to a spatial location. There were 384 test trials in each task which were split into 3 blocks. Participants were instructed to take a break in between each block and also to take breaks within a block if necessitated by fatigue or other considerations (e.g., eye strain). Speed was encouraged throughout the task by instructing participants to respond as quickly as possible without sacrificing accuracy. After the administration of the three attention tasks, a computerized version of the computation span task was given as a measure of working memory capacity (McCabe, Roediger, McDaniel, Balota, & Hambrick, 2010).

Procedure

Participants first reviewed the informed consent document and clarifications about the procedures were provided by the experimenter if necessary. A series of demographic questions (including age and years of education) were answered. Older adults were also administered the AD8 (Galvin et al., 2005) which is a brief, 8 item questionnaire designed to detect early symptoms of dementia. The three attention tasks were then given in counterbalanced order followed by the computation span task. After the working memory assessment, participants were debriefed, compensated and dismissed. The entire set of tasks took approximately 1.5 hours for younger adults and 2 hours for the older group. There was variation in how quickly each individual proceeded through the tasks and because of the relatively lengthy sessions 4 younger adults and 2 older adults were unable to complete the working memory task and 1 older adult was unable to complete the flanker task.

Results

In both of the present experiments, behavioral results were analyzed with linear mixed effects (LME) models using the lme4 package in R (Bates, Maechler, Bolker, & Walker, 2015). Age group (young vs. old, coded as −0.5 / 0.5 contrasts), current trial congruency (congruent vs. incongruent, coded as −0.5 / 0.5 contrasts), previous trial congruency (congruent vs. incongruent, coded as −0.5 / 0.5 contrasts), and task (Stroop, Simon and flanker, dummy coded with Stroop as the reference group) and all the 2, 3 and 4-way interactions were specified as fixed effects. Given the length of the task, “trial number” (centered at trial number 192) and its interaction with group was included to control for age differences in fatigue or practice / learning. In addition, RT of the previous trial (log transformed to reduce the skew) was entered to control for the overall speed of the prior response as it has been shown that speed of responses on prior trials can change current response dynamics (Kinoshita, Mozer, & Forster, 2011). Omnibus tests for each effect are first provided using chi-square tests with Type III sums of squares using the Anova function in the car package (Fox & Weisberg, 2011). Follow-up contrasts of targeted effects (described below) were then conducted using t-tests of regression coefficients with degrees of freedom calculated using the Satterthwaite approximation in the lmerTest package (Kuznetsova, Brockhoff & Cristensen, 2015). This approximation has been shown to keep error rates at close to the nominal .05 level (Manor & Zucker, 2004). This complex analysis yielded a number of parameters and although significance tests are provided for all parameters, only the targeted effects will be highlighted which map onto the a priori hypotheses of interest.

In order to avoid the undue influence of outliers, response times were screened prior to analysis in the following manner. First, any RT faster than 200 ms was removed followed by any RT greater than 3 standard deviations above or below the individual participant mean. Following this, any trial that occurred immediately after a break or after an error was also removed. This procedure eliminated 4% of the total trials across tasks for older adults and 6% for younger adults, a difference that was statistically significant, F(1,73) = 14.89, p < .001. Although this trimming procedure was relatively conservative, it was necessary in order to eliminate other explanations of the CSE such as post-error slowing. The high proportion of trials removed is compensated for by the greater number of trials in these tasks overall. Finally, only correct RTs were examined so all error trials were also removed for analysis of the response time. In order to control for age-related reductions in general processing speed, all analyses were conducted on individual z-scored response latencies (Faust, Balota, Spieler, & Ferraro, 1999). These z-scores were calculated using each participant’s mean and standard deviation within a task but collapsed across conditions (i.e. congruency and previous congruency). Parallel analyses on raw response times were also performed and are reported in the Appendix for the interested reader.

Z-scored Response Time

Significance tests for each effect on z-scored RT are displayed in Table 3. As shown, the main effect of congruency was reliable, indicating slower responses to incongruent stimuli relative to congruent stimuli. This effect was modulated by the prior trial congruency as evidenced by the current by previous congruency interaction, i.e., a CSE. For each task interference was smaller following incongruent trials relative to congruent trials replicating prior findings (condition means shown in Table 4). There was a significant interaction between task and congruency, which indicated that interference was larger in the Simon task compared to the Stroop task, β = .15, t = 9.03, p < .001 as well as compared to the flanker task, β = −.30, t = −18.14, p < .001. Interference in the Stroop task was also significantly larger than the flanker task, β = −.15, t = −9.14, p < .001. The three-way age by task by congruency interaction was also reliable, indicating that age differences in the interference effect were larger in the Stroop task relative to both Simon, β = −.14, t = −4.20, p < .001, and flanker, β = −.21, t = −6.31, p < .001.

Table 3.

Significance tests of z-scored response time in Experiment 1.

Effect	Chi-Square	DF	p-value
Trial Number	466.53	1	< .0001
Age	87.72	1	< .0001
Congruency (C)	438.56	1	< .0001
Previous RT	488.36	1	< .0001
Previous Congruency (PC)	27.30	1	< .0001
Task * PC	67.86	2	< .0001
Trial * Age	296.70	1	< .0001
Age * Task	3.16	2	< .0001
Congruency * Task	328.97	2	< .0001
Task * PC	18.97	2	< .0001
Age * C	3.97	1	0.046
Age * PC	0.50	1	< .0001
Congruency * PC	15.88	1	< .0001
Age * Congruency * Task	41.29	2	< .0001
Age * Task * PC	5.51	2	0.064
Task * Congruency * PC	1.55	2	0.046
Age * Congruency * PC	3.27	1	0.071
Age * Task * Congruency * PC	10.15	2	0.006

Note: An asterisk (*) denotes an interaction among the factors. The C by PC interaction is the CSE.

Table 4.

Means (95% Confidence Intervals) of z-scored RTs for each task, condition and age group.

Young Adults			Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.260 (−0.309: −0.21)	−0.165 (−0.214: −0.116)	−0.358 (−0.41: −0.307)	−0.318 (−0.37: −0.265)
Incongruent	0.436 (0.385:0.486)	0.362 (0.312:0.412)	0.233 (0.182:0.285)	0.198 (0.145:0.251)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.121 (−0.173: −0.07)	−0.144 (−0.195: −0.093)	−0.300 (−0.353: −0.247)	−0.292 (−0.346: −0.237)
Incongruent	0.294 (0.242:0.346)	0.222 (0.171:0.274)	0.240 (0.187:0.294)	0.115 (0.06:0.17)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.141 (−0.181: −0.102)	−0.101 (−0.139: −0.062)	−0.177 (−0.218: −0.136)	−0.135 (−0.177: −0.094)
Incongruent	0.294 (0.254:0.333)	0.152 (0.112:0.191)	0.089 (0.048:0.13)	0.05 (0.009:0.091)

Note: The rows denote the current trial congruency and the columns contain previous trial congruency.

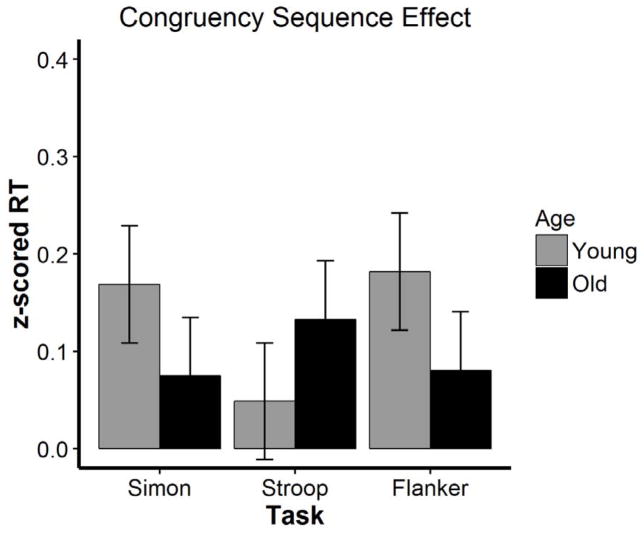
Most important for the present purposes, the four-way interaction among age, task, current and previous trial congruency was highly reliable indicating the magnitude of age differences in the CSE varied across the three tasks, χ²(2) = 10.15, p = .006. To simplify the presentation of this complex four-way interaction, Figure 2 plots the CSE (i.e., the difference in the interference effect as a function of the prior trial congruency) separately for each task and age group. As shown, the interaction is driven by a cross-over in the size of the CSE as a function of age across tasks. Specifically, the magnitude of the CSE decreased with age in the Simon, β = .09, t = 2.02, p = .04, and flanker, β = .10, t = 2.17, p = .03 tasks but marginally increased with age in the Stroop task, β = −.08, t = −1.80, p = .07.

Figure 2.

Congruency sequence effect as a function of age and task in Experiment 1. Errors bars are 95% confidence intervals of the interaction effect (i.e. the difference in interference as a function of the prior trial).

Accuracy

As mentioned in the introduction, a CSE is often found in accuracy rates as well as in response times. However, accuracy in each task for each age group was virtually at ceiling in the present design and thus these results will be discussed only briefly. Significance tests and condition means estimated from the generalized linear mixed effects model are presented in Table 5 and Table 6, respectively. Despite the high accuracy rates, our analyses revealed a reliable 4-way interaction among task, age, current and previous trial congruency, χ²(2) = 9.68, p = .008. Follow up tests showed this interaction was due to the Simon task which showed a marginally significant reduction in the CSE with age, β = −1.10, z = −1.90, p = .057, and the flanker task which showed the opposite effect, β = 1.47, z = 2.90, p = .003. Age differences in the CSE were not reliable for the Stroop task, β = .22, z = 0.61, p = .54. Again, it is important to note that these differences, while significant, are very small (on the order of 3 decimal places) and therefore should be interpreted with caution.

Table 5.

Significance tests of accuracy performance in Experiment 1.

Effect	Chi-Square	DF	p-value
Task	50.595	2	< .001
Age	10.773	1	< .001
Congruency (C)	44.403	1	< .001
Previous Congruency (PC)	0.693	1	< .001
Task * Age	42.867	2	< .001
Task * C	53.814	2	< .001
Age * C	2.272	1	0.132
Task * PC	2.420	2	0.298
Age * PC	0.039	1	0.844
C * PC	5.166	1	0.023
Task * Age * C	1.033	2	0.597
Task * Age * PC	2.452	2	0.293
Task * C * PC	1.375	2	0.503
Age * C * PC	0.350	1	0.554
Task * Age * C * PC	9.682	2	0.008

Note: An asterisk (*) denotes an interaction among the factors. The C by PC interaction is the CSE.

Table 6.

Means (95% Confidence Intervals) of estimated accuracy for each task, condition and age group in Experiment 1.

Young Adults			Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.994 (0.99–0.996)	0.990 (0.986–0.994)	0.998 (0.997–0.999)	0.999 (0.998–1)
Incongruent	0.956 (0.939–0.968)	0.970 (0.958–0.979)	0.991 (0.986–0.994)	0.994 (0.99–0.996)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.986 (0.98–0.991)	0.985 (0.978–0.99)	0.995 (0.991–0.997)	0.994 (0.989–0.996)
Incongruent	0.974 (0.962–0.982)	0.980 (0.97–0.986)	0.985 (0.978–0.99)	0.989 (0.983–0.993)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.98 (0.97–0.986)	0.984 (0.976–0.989)	0.998 (0.996–0.999)	0.997 (0.994–0.998)
Incongruent	0.976 (0.965–0.984)	0.981 (0.973–0.987)	0.995 (0.991–0.997)	0.998 (0.996–0.999)

Note: The rows denote the current trial congruency and the columns contain previous trial congruency.

Discussion

In each of the three tasks, we obtained evidence for a reliable CSE. This is noteworthy because all presently known confounds that have hindered cross-study interpretations of the CSE in past research (e.g., stimuli repetition, contingency confounds, response differences across tasks) were carefully controlled in the current design. However, the most striking finding is the clear cross-over interaction in the CSE as a function of age and task. Specifically, the CSE decreased in magnitude with age in the Simon and flanker tasks. This is consistent with the notion of a change in control induced by the congruency of preceding trials. If older adults are less able to increase control from trial to trial, as would be expected based on impaired attentional control systems, they should exhibit a smaller CSE which is precisely what was observed. In contrast, the Stroop task showed exactly the opposite pattern, namely that the CSE trended towards an increase with age, which is in accord with prior findings. As argued originally by Aschenbrenner and Balota (2015), this is consistent with a pathway priming mechanism by which processing activity remains in the system from the previous trial and that additional activity must be controlled when congruency alternates across trials.

Before speculating further on why these task differences in the CSE emerge, a few issues remain to be addressed. First, we felt it important to replicate these findings in a follow up experiment to ensure the stability of the complex 4-way interaction. Second, although accuracy rates were quite high for both age groups, we did detect a reliable age effect such that older adults were more accurate than the younger adult controls. This may in part reflect older adults’ cautiousness in responding and hence could compromise the interpretation of these data. Thus, in a second experiment, we implemented a response deadline procedure to attempt to equate the two groups on overall accuracy.

Experiment 2

Method

Participants

52 younger and 50 older adults were recruited from the same sources as Experiment 1. One older adult was removed from all analyses due to an error with the deadline procedure, leaving 49 older adults available for analysis. Demographic information on these participants is provided in Table 7.

Table 7.

Demographic characteristics in Experiment 2.

	Younger Adults		Older Adults
	Mean	SD	Mean	SD
Age	20	1.4	71.1	3.6
Education	14.1	1.5	17	2.7
CompSpan	12.4	6.4	9.1	6.1
Short Blessed	--	--	0.76	1.16
Flanker Deadline	823	132	1481	340
% Flanker Deadline	0.86	0.13	0.93	0.09
Simon Deadline	653	98	1206	335
% Simon Deadline	0.87	0.11	0.96	0.05
Stroop Deadline	690	110	1498	400
% Stroop Deadline	0.82	0.15	0.9	0.13
% Flanker Trimmed	0.15	0.07	0.08	0.02
% Simon Trimmed	0.14	0.06	0.08	0.02
% Stroop Trimmed	0.15	0.06	0.1	0.04

Note: CompSpan = computation span task, a measure of working memory capacity. Short Blessed scores range from 0–28 with a score of 5 or greater indicating questionable impairment. “Deadline” for each task reflects the average response deadline for the group. “% Deadline” refers to the average percentage of trials that was faster than the individual deadline. “% Trimmed” refers to the percentage of trials that were removed prior to analysis.

Materials and Procedure

The procedure was virtually identical to Experiment 1 with the exception of the response deadline. To implement the deadline, each participant was timed during the practice block and a deadline was set at their average response latency for the entire block. If the participant exhibited difficulty in understanding the instructions or made several errors during practice, the block was run a second time. Then during the test phase, on each trial, if a response was not initiated before the determined deadline was reached, a buzzing tone was played through the computer speakers. Participants were instructed that their goal was to respond at a fast enough rate that they did not receive the buzzing tone. However, if they did hear the tone they were to initiate a response immediately even if it required them to guess. The importance of speed was repeatedly emphasized.

Due to the anticipated increased cognitive effort required by maintaining a fast enough rate of responding such that the deadline was achieved, the number of trials in each task was reduced to 192 total trials (compared to 384 in Experiment 1). Hence, we also increased the total number of participants in this study. In addition, accuracy feedback was no longer provided after each trial and was replaced by a 1000 ms blank screen inter-trial interval. Again, the goal here was to lessen the focus on accuracy.

Results

Response time outliers were trimmed in the same manner as in Experiment 1. Due to the response deadline procedure, more errors were produced relative to Experiment 1 and because we removed post-error trials, relatively more trials were removed prior to analysis. Specifically, 14% in Simon, and 15% in Stroop and flanker for younger adults and 8%, 10% and 8% respectively for the older adults. The differences between age groups were highly reliable for each task (ps < .001). Again, although these trimming rates are high, it was necessary to remove post-error trials to avoid post-error slowing confounds which led to the high rate of trimming.

Influence of the Response Deadline

Before beginning an analysis of the CSE in this Experiment, we first examined overall accuracy and mean RTs across Experiments 1 and 2 to evaluate whether the implemented deadline was successful in prompting faster and consequently less accurate responses. To this end, data from both experiments (collapsed across congruency) were analyzed in a separate LME model for each task which incorporated age and experiment as fixed effects. As expected, RTs decreased across experiments for the flanker task, β = −134, t = −4.65, p < .001, for Simon, β = −118, t = −6.01, p < .001, and for Stroop, β = −166, t = −5.42, p < .001. Interestingly, although there was a trend for older adults to speed up more across experiments relative to the younger adults, the group by experiment interaction was not reliable for any of the tasks (ps = .12, .16 and .06 for flanker, Simon and Stroop respectively, condition means shown in Table 8).

Table 8.

Mean RT and accuracy (with 95% confidence intervals) for each Experiment as a function of age group.

Response Time			Accuracy
	Simon			Simon
	Younger	Older		Younger	Older
Exp 1	624 (584–664)	964 (922–1007)	Exp 1	0.98 (0.97–0.98)	0.93 (0.91–0.95)
Exp 2	533 (498–569)	818 (782–854)	Exp 2	1.00 (0.99–1.00)	0.99 (0.99–1.00)
	Stroop			Stroop
	Younger	Older		Younger	Older
Exp 1	675 (612–737)	1236 (1171–1302)	Exp 1	0.98 (0.97–0.99)	0.99 (0.99–0.99)
Exp 2	566 (511–621)	1013 (957–1070)	Exp 2	0.92 (0.90–0.94)	0.978 (0.97–0.98)
	Flanker			Flanker
	Younger	Older		Younger	Older
Exp 1	748 (690–806)	1192 (1129–1254)	Exp 1	0.98 (0.97–0.99)	1.00 (1.00–1.00)
Exp 2	659 (608–710)	1013 (960–1066)	Exp 2	0.92 (0.90–0.94)	0.984 (0.98–0.99)

Turning to the analysis of accuracy rates, there was evidence for decreased accuracy across the experiments for flanker, β = −1.46, z = −8.91, p < .001, for Simon, β = −.83, z = −5.01, p < .001, and for Stroop, β = −1.17, z = −7.63, p < .001. There was no evidence of a group by experiment interaction in the flanker task (β = −.16, z = −.50, p = .62), indicating that both groups equally dropped in accuracy across the experiments. In contrast, there was an age by experiment interaction for both the Simon (β = .70, z = 2.11, p =.03) and Stroop tasks (β = .62, z = .62, p = .05). These interactions indicate that the accuracy difference across experiments was smaller for the older adults relative to the younger.

Z-scored Response Time

Significance tests for the z-scored response time analysis are shown in Table 9. Replicating the first experiment, the main effect of congruency was highly reliable indicating slower responses to incongruent compared to congruent stimuli. The CSE was also significant indicating smaller interference effects following incongruent trials. The task by congruency interaction was significant indicating that interference effects were larger in the Stroop task relative to Simon, β = −.48, t = −22.77, p < .001, and relative to flanker, β = −.53, t = −25.12, p < .001. Interference effects by task varied by age reflected by the significant age by task by congruency interaction again indicating that age differences in overall interference were larger in the Stroop task relative to Simon, β = −.31, t = −7.42, p < .001 and relative to flanker, β = −.31, t = −7.25, p < .001.

Table 9.

Significance tests of z-scored response time in Experiment 2.

Effect	Chi-square	DF	p-value
Trial	270.72	1	< .0001
Age	25.02	1	< .0001
Congruency (C)	945.28	1	< .0001
Previous RT	104.87	1	< .0001
Task	46.65	2	< .0001
Previous Congruency (PC)	4.72	1	0.03
Trial * Age	359.08	1	< .0001
Age * Task	8.69	2	0.013
Task * Congruency	765.82	2	< .0001
Task * PC	1337.39	2	< .0001
Age * C	73.68	1	< .0001
Age * PC	2.01	1	0.156
C * PC	7.26	1	0.007
Age * Task * C	71.42	2	< .0001
Age * Task * PC	13.15	2	0.001
Task * C * PC	18.60	2	< .0001
Age * C * PC	2.42	1	0.12
Age * Task * C * PC	7.18	2	0.028

Note: An asterisk (*) denotes an interaction among the factors. The C by PC interaction is the CSE.

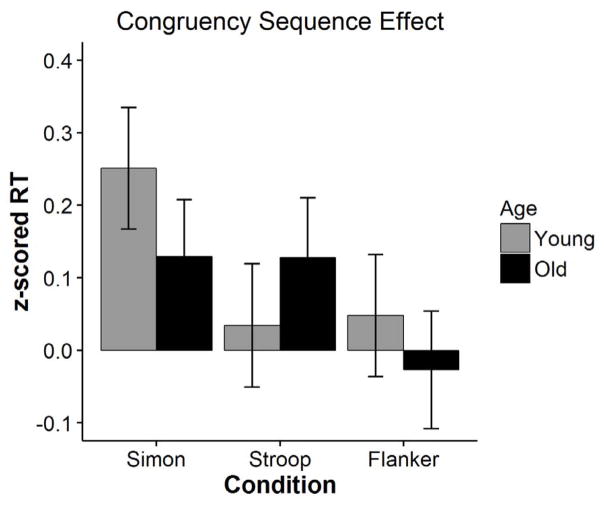
Clearly, the most important finding in Table 9 is that we replicated the 4-way interaction among task, age, previous and current trial congruency, χ²(2) = 7.18, p = .03. A plot of this interaction is shown in Figure 3. As before, age effects in the CSE were significantly different in the Stroop task relative to both Simon, β = .22, t = 2.55, p = .01, and flanker, β = .17, t = 1.99, p = .05, and the Simon and flanker tasks were not different from one another, β = −.04, t = −.56, p = .58. Although the age related increase in the CSE for the Stroop task was not reliable on its own, β = −.09, t = −1.56, p = .12, the age-related reductions in the Simon task were, β = .12, t = 2.06, p = .04. Of course, it is the difference between these differences (and hence the interaction) that is of critical importance. Namely the cross-over in the effect such that the CSE is becoming larger with age in the Stroop task but smaller in the Simon task.

Figure 3.

Congruency sequence effect as a function of age and task in Experiment 2. Errors bars are 95% confidence intervals of the interaction effect (i.e. the difference in interference as a function of the prior trial).

Accuracy

Significance tests for accuracy are shown in Table 11. As shown in Table 12, accuracy was no longer on ceiling for the younger adults due to the implementation of the speeded deadline. In contrast to Experiment 1, the highest order interaction among task, age, current and previous trial congruency was not reliable, χ²(2)= 0.98, p = .61, nor was there an interaction among age, previous and current trial congruency collapsed across task, χ²(1)= 3.11, p = .078. There was however, evidence of a CSE, χ²(1)= 4.97, p = .026 indicating slightly smaller interference effects following incongruent trials. This interacted with task, χ²(1)= 8.91, p = .012, which follow up comparisons revealed to be due to larger effects in the Simon task compared to both Stroop, β = .62, t = 1.98, p = .047, and flanker, β = −.93, t = −2.97, p = .002.

Table 11.

Significance tests of accuracy in Experiment 2.

Effect	Chi-Square	DF	p-value
Task	89.72	2	< .0001
Age	72.93	1	< .0001
Congruency (C)	136.25	1	< .0001
Previous Congruency (PC)	1.71	1	0.191
Task * Age	18.82	2	< .0001
Task * C	100.40	2	< .0001
Age * C	32.01	1	< .0001
Task * PC	95.95	2	< .0001
Age * PC	1.23	1	0.267
C * PC	4.97	1	0.026
Task * Age * C	26.61	2	< .0001
Task * Age * PC	5.07	2	0.079
Task * C * PC	8.91	2	0.012
Age * C * PC	3.11	1	0.078
Task * Age * C * PC	0.98	2	0.612

Note: An asterisk (*) denotes an interaction among the factors. The C by PC interaction is the CSE.

Table 12.

Means (95% Confidence Intervals) of accuracy for each task, condition and age group in Experiment 2.

Young Adults			Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.983 (0.975–0.988)	0.86 (0.822–0.89)	0.997 (0.994–0.998)	0.984 (0.976–0.989)
Incongruent	0.97 (0.958–0.979)	0.906 (0.877–0.928)	0.997 (0.994–0.998)	0.994 (0.99–0.996)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.935 (0.915–0.95)	0.944 (0.927–0.958)	0.993 (0.989–0.996)	0.99 (0.985–0.994)
Incongruent	0.89 (0.861–0.913)	0.911 (0.886–0.931)	0.956 (0.941–0.968)	0.968 (0.956–0.977)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	0.926 (0.906–0.942)	0.912 (0.89–0.931)	0.985 (0.979–0.99)	0.981 (0.973–0.987)
Incongruent	0.934 (0.915–0.948)	0.915 (0.893–0.933)	0.983 (0.976–0.988)	0.983 (0.975–0.988)

Note: The rows denote the current trial congruency and the columns contain previous trial congruency.

Combined Analyses

Although the response time results across the two experiments were quite similar in that the age by task by CSE interaction was consistently reliable, it is important to note that the age by CSE interaction in Stroop was marginal when tested alone. Of course, the numerical increases in the effect with age are consistent with the patterns identified in the extant literature, and given the small effect size, it is possible that both experiments were simply underpowered to statistically detect the age-related increase in the CSE in Stroop.

To address this issue, an analysis was conducted on the Stroop data combined across Experiments 1 and 2 using the same fixed effects as identified previously and “experiment” coded as an additional factor, effectively doubling our sample size. In this analysis, we now see a statistically reliable age by CSE interaction, β = −.08, t = −2.19, p = .029, and the higher order interaction with experiment was not significant, β = −.01, t = −0.14, p = .89. Thus, with sufficient increase in power, we were able to detect the predicted increase in the CSE with age in the present design.

Discussion

Overall, the effects from Experiment 1 were replicated in Experiment 2 even with faster, and presumably less cautious, responses induced by the inclusion of the response deadline. Indeed, the most important observation is that the age by CSE by task interaction in the z-scored RT analyses replicated. Specifically, we observed age-related reductions in the CSE for the Simon task but trends toward an increase in the effect in Stroop. These trends in the Stroop task were statistically significant in the combined, cross-experiment comparisons. Furthermore, although we did not completely equate the groups on overall accuracy, we found no evidence that the cross-task age differences in the CSE were driven by differences in accuracy as the 4-way interaction in error rates was not reliable. More important, the replication of the RT effects, even under speeded conditions, suggests that the age patterns are not entirely due to differences in cautiousness of responding.

General Discussion

The primary aim of this work was to understand whether and how the CSE changes with healthy aging across different attentional control tasks. Based on the extant literature, the CSE appears to vary as a function of task because studies using the Stroop task have found numerical trends or statistically significant increases in the CSE with age (Aschenbrenner & Balota, 2015; West & Moore, 2005) and at least one study showed a significant decrease with age in the Simon task (Aizenberg et al., 2014). Of course, as mentioned in the introduction, these tasks differ on a number of characteristics including the type of stimuli used, number of trials included, type of responses required, and the degree to which critical confounds were controlled. Across two experiments, we controlled these extraneous characteristics and showed that different patterns of the CSE as a function of age can be observed across three distinct attentional control paradigms. Most notably, the CSE was larger for the older adults relative to younger in the Stroop task but smaller than the younger adults in the Simon and flanker tasks in both experiments, under conditions in which cross-trial repetitions and contingencies were carefully controlled.

The CSE has often been used as an indicator of local or dynamic adjustments of attentional control and potentially provides a window for understanding how control is dynamically adjusted by the cognitive system. This is typically thought to take the form of a controlled and effortful process, possibly as an active recruitment of control mediated by prefrontal regions (e.g., Botvinick et al., 2001) or as trial level adjustments in response thresholds (e.g., Schmidt, 2013). Alternatively, as outlined in the introduction, it is also possible that the CSE results from a priming process by which relevant processing activity of a given dimension is maintained across trials based on the relative utility of that dimension. All of these explanations can accommodate the pattern of reduced interference following incongruent trials relative to following congruent trials.

How might these extant theories of the CSE accommodate the interaction with age? Arguably, the adjustments accounts would predict reductions in the CSE with age based on well-established declines in brain regions that underlie these processes (Forstmann et al. 2011; West, 1996). In contrast, the priming accounts would predict increases in the CSE with age in those same processes as individuals with impaired attentional control systems are less able to control residual activity from the prior trial. Critically, the cross-over interaction between the tasks with regards to the CSE and age makes it clear that a single mechanism cannot be producing cross-trial adjustments across the paradigms. Indeed, in the present series of studies younger adults did not produce a CSE in the Stroop task but did in the Simon task whereas older adults produced a reliable CSE in both tasks. Thus, within the current paradigm, the results support the original observations by Aschenbrenner and Balota of smaller CSEs in younger adults compared to older in the Stroop task. However, this differential age effect does not does not appear to extend to the Simon task. Importantly, this implies that any particular theory of the CSE would need to be modified to take into consideration these task specific effects or that different mechanisms are explicitly engaged depending on task constraints.

Indeed, based on the cross-over interactions with age, it would appear that adjustment accounts are operating in the Simon and flanker tasks whereas the Stroop data are more consistent with pathway priming. However, although independent evidence has been provided for the pathway priming account (Hubbard et al., 2016), the assumption that this is the mechanism operating in the Stroop task must remain speculative at this time. The more critical question is why Stroop alone seems to allow for the operation of different cross-trial mechanism (possibly priming), relative to the other attention tasks based on the differential age pattern. There are a number of possibilities, several of which were eliminated in the present design. For example, these paradigms differ with regards to the types of stimuli that are used with Stroop typically using words and colors while flanker and Simon paradigms often use arrows or shapes. Possibly, pathway priming phenomenon can only be observed when linguistic stimuli are used. However, given that we equated the stimuli as much as possible (i.e., used only letters and words), this factor is unlikely to be a major contributor to the present results. The second possibility concerns overall effect size. It is possible that certain CSE mechanisms are only engaged when interference reaches a certain magnitude. However, given that Simon produced greater overall interference than Stroop in Experiment 1, and the reverse in Experiment 2, and yet the CSE patterns were identical eliminates differential effect size as a confounding possibility as well. Furthermore, other researchers have shown that the CSE may not even be tied to overall interference effects at all (Weissman et al., 2015).

Thus, a more likely possibility is that the type of attentional selection required is different in each task and this differentially modulates the CSE. Evidence for different selection mechanisms can be found by the examination of characteristics of the response time distribution for congruent and incongruent items. For example, Spieler et al. (2000) fit an ex-Gaussian function to data from different interference paradigms. The ex-Gaussian is a convolution of two distributions, an exponential and a Gaussian, and has been shown to provide good fit to data from a variety of paradigms. There are three parameters to this function, Mu, Sigma and Tau. Condition differences that occur in Mu reflect a constant shift between the two distributions and differences in Tau indicate that effects become exaggerated at slower RTs (see Balota & Yap, 2011 for further discussion). Interestingly, Spieler et al. (2000) found that in the Stroop task, interference occurs in both Mu and Tau and in contrast, interference in both flanker and local/global tasks manifests only in Mu (indicating pure shifting), at least for younger adults. Spieler et al. interpreted these patterns as evidence for an attribute selection mechanism in the Stroop task when the conflicting elements are perceived as a single integrated unit, and a spatial selection mechanism in the flanker task in which a particular region of space must be attended. Indeed, Spieler et al. showed that when the color and word are spatially separated in a Stroop task, the distributional characteristics are quite similar to those in the flanker paradigm. Interestingly, the Simon task shows yet another distributional pattern, specifically, interference decreases as RTs become longer (Castel et al., 2007; Pratte et al. 2010), suggesting a third attentional selection mechanism. This pattern in the Simon task is often interpreted as indicating a rapid, automatic engagement of the ipsilateral motor response that is then continually inhibited over time. Regardless of the exact mechanism that is assumed, these different distributional characteristics clearly indicate differences in performance across the various paradigms. The patterns of the CSE across task and age provide further evidence of these processing differences which should be further explored in future research.

As already noted, the task designs of the current study were quite different from the extant literature and thus we checked that the same evidence for attentional selection mechanisms were also found in the present data. We examined the ex-Gaussian parameters for each task in Experiment 1, which was most similar to the experiments conducted by Spieler et al. (2000). Briefly, analysis of the interference effect in flanker revealed a significant condition effect in Mu (p = .031), but not in Tau, (p >.05). Similarly, the main effect of condition for Simon was significant in Mu (p < .001) but not in Tau (p = .44). In contrast, for Stroop, interference manifested in both Mu (p < .001) and Tau (p < .001). These analyses clearly indicate that our modified tasks are behaving in a fashion similar to Spieler et al., (2000).

Thus, a reasonable hypothesis is that the attribute selection required in the Stroop task, as opposed to spatial selection in the other tasks, allows for an age-sensitive engagement of pathway priming. For example, the integration of the conflicting dimensions might lead to greater carry-over of processing activity across abstract processing pathways. It is already known that older adults have particular difficulty in separating integrated features as in the current series of experiments, the age differences in overall interference were significantly larger in the Stroop task relative to the other two paradigms. Furthermore, West and Bell (1997) showed that when the color and word were spatially separated in a Stroop task, interference effects were comparable between younger and older adults. Clearly then, relatively more activation will persist across trials for the older adults leading to the increased CSE. However, such an account still does not adequately explain why irrelevant activation wouldn’t persist across trials in the other tasks. For example, why wouldn’t spatial location information in the Simon task maintain its activation into the subsequent trial?

We argue the reason is that attribute vs. spatial selection tasks differ in how information is accumulated towards a particular response. Specifically, Spieler et al. (2000) modeled performance in the Stroop and flanker tasks using two classes of sequential sampling models. The first, random walk models, posits that evidence accumulates towards one of two response boundaries in a single accumulator and evidence towards one response is necessarily evidence against the other. In the second class, accumulator models, evidence for each response accrues in separate, independent accumulators with activation in one accumulator being relatively neutral with respect to activity in the other. Spieler et al. (2000) determined that the fully interactive random walk models could accommodate the distributional effects in the integrated task (Stroop) and the accumulator model could account for the results from the spatially separate task (flanker). It is possible therefore, that pathway priming only occurs in situations in which evidence gathers in a single, interactive accumulator. Of course, only detailed computational modeling can truly answer this question but future research could also address this issue by measuring the CSE in a spatially separated Stroop task (i.e., separating the color and the word). If integration of stimuli is the key mechanism driving pathway priming, such a spatial manipulation should produce the reverse pattern with age (i.e., decreased CSEs in older adults).

More broadly, in addition to shedding light on changes in the control of attentional selection mechanisms across the lifespan, the current findings also warn against the use of the CSE as a measure of dynamic adjustments in control, at least in the Stroop task. Previous research has shown that low-level stimulus priming can confound interpretations of the CSE (Mayr, Awh, & Laurey, 2003) and here we show that such priming can extend to abstract processing pathways. This differential susceptibility to priming effects could be problematic for researchers wishing to use the CSE in Stroop as an individual differences marker of attentional processes.

Although there are strengths to the present study, there are a few limitations that should also be noted. First, the tasks we used were quite long, including almost 400 trials per task (in Experiment 1), and it is possible that these greater than usual trial numbers might be contributing to group differences in the CSE. However, the same pattern was also obtained in Experiment 2, which contained half the number of trials as Experiment 1. Additionally, we placed strong constraints on the order of stimuli in our design. Specifically, we precluded the presence of repetition trials by forcing pairs of stimuli to alternate between adjacent trials. Although this met our goal of eliminating a contingency bias, it also created an artificially constrained stimulus set than in standard versions of these attentional selection tasks. Similarly, in order to better equate the type of stimuli used across tasks, and control for extraneous variables often confounded in studies of the CSE, our Simon task differs from the original use of the task that mapped colors to responses and thus might be considered a relatively more pure stimulus-response task. Finally, although the patterns in the Stroop and Simon task was quite consistent across both experiments, it is important to note that the flanker task did not produce a CSE in our second experiment. It is unclear whether this elimination of the effect was due to simple variability of this phenomenon in the flanker task or if, for some reason, the response deadline procedure prevented the CSE from emerging.

In summary, the most noteworthy finding of the current series of experiments was the cross-over interaction with respect to the nature of the CSE as a function of age and task. This finding indicates that multiple mechanisms might underlie the CSE and are differentially brought online as a function of the particular task constraints. Although the selective engagement of a pathway priming mechanism can readily accommodate the present results, a few questions remain unanswered. For example, it is unknown to what extent the priming in the Stroop task is “automatic” in the sense that it occurs in a capacity free manner. Specifically, if attention was explicitly directed to the color dimension, would one expect greater cross-trial differences? Furthermore, it is unclear as to whether older adults have more activity carry over from trial to trial relative to younger adults or simply are less able to control the same amount of priming, or indeed both. Clearly, future research is necessary to tease apart these possibilities in order to provide a finer grained characterization of cross-trial response dynamics in healthy aging.

Table 10.

Means (95% Confidence Intervals) of z-scored RTs for each task, condition and age group in Experiment 2.

	Young Adults		Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.344 (−0.386: −0.302)	0.545 (0.5:0.59)	−0.431 (−0.471: −0.391)	0.351 (0.311:0.391)
Incongruent	−0.175 (−0.217: −0.133)	0.463 (0.419:0.506)	−0.346 (−0.388: −0.304)	0.305 (0.263:0.347)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.137 (−0.191: −0.082)	−0.134 (−0.188: −0.081)	−0.381 (−0.434: −0.329)	−0.374 (−0.429: −0.319)
Incongruent	0.256 (0.201:0.311)	0.23 (0.174:0.285)	0.346 (0.293:0.399)	0.225 (0.169:0.281)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	−0.169 (−0.215: −0.124)	0.270 (0.224:0.316)	−0.127 (−0.169: −0.084)	0.097 (0.054:0.141)
Incongruent	−0.148 (−0.193: −0.104)	0.241 (0.196:0.286)	−0.162 (−0.206: −0.118)	0.087 (0.044:0.131)

Note: The rows denote the current trial congruency and the columns contain previous trial congruency.

Appendix A

In this appendix, we report the results of the LME analyses on raw, as opposed to z-scored RTs. It is important to note that such an approach confounds general cognitive slowing that is well known to occur in older adults and we provide these data only for the interested reader.

Table 13.

Significance tests of the raw RTs in Experiment 1.

Effect	Chisq	Df	Pr(>Chisq)
Trial Number	375.24	1	< .0001
Age	182.46	1	< .0001
Congruency (C)	557.40	1	< .0001
Previous RT	3308.73	1	< .0001
Task * PC	5180.78	2	< .0001
Previous Congruency (PC)	113.73	1	< .0001
Trial * Age	335.88	1	< .0001
Age * Task	2033.50	2	< .0001
Congruency * Task	160.81	2	< .0001
Task * PC	17.18	2	< .0001
Age * C	81.07	1	< .0001
Age * PC	7.53	1	< .0001
C * PC	20.63	1	< .0001
Age * Congruency * Task	100.78	2	< .0001
Age * Task * PC	13.27	2	0.001
Task * Congruency * PC	1.99	2	0.371
Age * Congruency * PC	8.03	1	0.005
Age * Task * Congruency * PC	9.31	2	0.01

Table 14.

Means (95% confidence intervals) of raw RTs as a function of task, condition and age in Experiment 1.

Young Adults			Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	608 (564–652)	610 (567–654)	891 (844–937)	890 (843–936)
Incongruent	696 (652–740)	676 (633–720)	999 (953–1045)	986 (940–1032)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	676 (615–738)	667 (606–728)	1133 (1069–1198)	1133 (1068–1197)
Incongruent	746 (685–808)	727 (666–789)	1305 (1241–1370)	1254 (1190–1319)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	738 (675–802)	740 (677–803)	1140 (1072–1207)	1148 (1081–1216)
Incongruent	807 (744–870)	780 (716–843)	1206 (1138–1273)	1194 (1127–1262)

Table 15.

Significance tests for raw RTs in Experiment 2.

Effect	Chi-square	Df	p-value
Trial	155.91	1	< .0001
Age	252.30	1	< .0001
Congruency (C)	821.39	1	< .0001
Previous RT	2137.79	1	< .0001
Task	3899.91	2	< .0001
Previous Congruency (PC)	92.79	1	< .0001
Trial * Age	315.75	1	< .0001
Age * Task	1257.08	2	< .0001
Task * C	920.75	2	< .0001
Task * PC	743.96	2	< .0001
Age * C	219.50	1	< .0001
Age * PC	19.47	1	< .0001
C * PC	7.81	1	0.005
Age * Task * C	186.43	2	< .0001
Age * Task * PC	38.85	2	< .0001
Task * C * PC	7.75	2	0.02
Age * C * PC	2.57	1	0.109
Age * Task * C * PC	4.21	2	0.122

Table 16.

Means (95% confidence intervals) of raw RTs as a function of task, condition and age in Experiment 2.

Young Adults			Older Adults
	Simon Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	506 (479–533)	584 (557–611)	762 (735–790)	858 (830–885)
Incongruent	519 (492–546)	573 (547–600)	769 (742–797)	850 (822–877)
	Stroop Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	563 (511–615)	560 (508–612)	932 (879–986)	927 (873–980)
Incongruent	610 (558–662)	603 (551–655)	1088 (1035–1141)	1058 (1004–1111)
	Flanker Task
	Previous Congruent	Previous Incongruent	Previous Congruent	Previous Incongruent
Congruent	648 (606–689)	648 (607–690)	984 (941–1027)	976 (933–1019)
Incongruent	703 (661–744)	696 (654–738)	1024 (981–1067)	1020 (977–1062)