Mechanical sensitivity and the dynamics of evolutionary rate shifts in biomechanical systems

Abstract

The influence of biophysical relationships on rates of morphological evolution is a cornerstone of evolutionary theory. Mechanical sensitivity—the correlation strength between mechanical output and the system's underlying morphological components—is thought to impact the evolutionary dynamics of form–function relationships, yet has rarely been examined. Here, we compare the evolutionary rates of the mechanical components of the four-bar linkage system in the raptorial appendage of mantis shrimp (Order Stomatopoda). This system's mechanical output (kinematic transmission (KT)) is highly sensitive to variation in its output link, and less sensitive to its input and coupler links. We found that differential mechanical sensitivity is associated with variation in evolutionary rate: KT and the output link exhibit faster rates of evolution than the input and coupler links to which KT is less sensitive. Furthermore, for KT and, to a lesser extent, the output link, rates of evolution were faster in ‘spearing’ stomatopods than ‘smashers’, indicating that mechanical sensitivity may influence trait-dependent diversification. Our results suggest that mechanical sensitivity can impact morphological evolution and guide the process of phenotypic diversification. The connection between mechanical sensitivity and evolutionary rates provides a window into the interaction between physical rules and the evolutionary dynamics of morphological diversification.

1. Introduction

The pace of phenotypic diversification reflects a balance between constraint and release from constraint. Depending on the context, intrinsic factors (i.e. developmental, genetic, and mechanical) and extrinsic factors (i.e. ecological and environmental) can limit the variety of forms or serve to accelerate phenotypic evolution [1–4]. For example, the presence of strong genetic or performance trade-offs is usually considered a constraining influence on diversification, because multiple competing demands are expected to retard rates of evolution [3–5]. However, this is not always the case. Multifunctional genes do not necessarily evolve more slowly (e.g. [6,7]) and the morphological traits involved in stronger performance trade-offs can evolve faster than those exhibiting weaker trade-offs [8].

The dynamic connection between physics and evolutionary history determines the pace of phenotypic diversification, and is the cornerstone of the classic Seilacher's triangle of evolutionary theory [9,10]. Specifically, physical relationships and evolutionary history are expected to interact to determine the range and rate of morphological diversification [11–13]. Hence, evolutionary biomechanics provides a fertile testing ground for understanding the connection between form–function relationships and the pace of morphological diversification [14,15].

A well-studied form–function relationship is functional redundancy, which occurs when a common mechanical output is achieved through multiple configurations of the system's underlying morphology (i.e. ‘many-to-one mapping’, [16]). Many biomechanical systems exhibit functional redundancy, such as the four-bar linkage system enabling suction feeding in wrasses [17]. Similarly, anole lizards can exhibit similar sprint speeds through multiple configurations of limb bone lengths and corresponding muscle masses [18], and damselfly larvae can exhibit similar swimming speeds through various combinations of morphological, physiological, and behavioural features [19]. A weak relationship between functional and morphological variation has been posited as a potential source of morphological diversity, as morphological disparity can evolve with functional equivalence [16,17]. In wrasses, for example, equivalent jaw force transmissions can be achieved through multiple morphological combinations of the jaw's underlying four-bar linkage system, a feature that has been associated with the wrasse's high morphological diversity [20].

Comparisons between morphological and mechanical variation in systems exhibiting functional redundancy have typically combined all of the underlying morphological components into composite measures, such as principal components (e.g. [17,21,22]). However, the association between morphological and mechanical diversity may be unequal across the system's underlying morphological parts. For example, some morphological traits in mechanically redundant systems contribute disproportionately to mechanical output. That is, the mechanical sensitivity of output varies among the system's underlying features [22]. For example, in the case of sprinting speed in anoles described above [18], even though similar velocities could be achieved through the different overall combination of limb bone lengths, equivalent changes in the size of individual traits did not produce equivalent changes to sprint speed; rather, the functional impact of morphological variation varied across the femur, tibia, and metatarsus. Because the relationship between morphological variation and mechanical output can vary substantially among features of a functionally redundant mechanical system, we might expect corresponding differences in the evolutionary rate of morphological evolution, depending on the system's mechanical sensitivity to morphological variation. Testing this possibility can be accomplished by decomposing the mechanical system into its constituent parts, assessing each trait's relative contribution to mechanical output, and individually comparing rates of evolution between each morphological feature and mechanical output.

Here, we examine whether and how mechanical sensitivity influences the rate of morphological evolution within the functionally redundant system of the mantis shrimp four-bar linkage system. Mantis shrimp (Order: Stomatopoda) are a group of marine crustaceans that perform rapid, power-amplified strikes using raptorial appendages in which stored elastic energy is transferred through a four-bar mechanism to the swinging appendage segments (figure 1; [24–27]). Most mantis shrimp species either exhibit a ‘spearing’ raptorial morphology to harpoon elusive prey or a ‘smashing’ raptorial morphology that can crush hard-shelled prey [28,29]. To prepare for a strike, the spring mechanism is compressed and held in place by a latch in the merus segment of the raptorial appendage. During a strike, the input link (the meral-V) rotates distally and pushes against the output link, which is part of the combined spearing or smashing tool (carpus, propodus, and dactyl segments). The coupler link that completes the linkage system is the contracted extensor muscle running from the carpus to the merus. The amount of energy transmitted during the strike—kinematic transmission (KT)—is defined as the ratio of the rotation of the output link to that of the input link.

Figure 1.

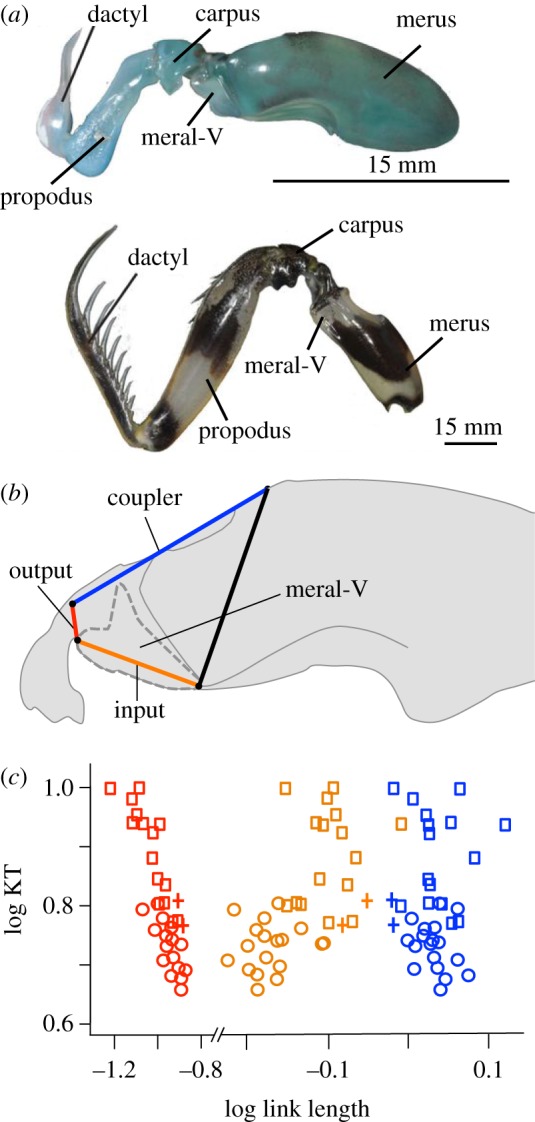
The mantis shrimp's four-bar linkage system exhibits functional redundancy at a composite level of analysis and mechanical sensitivity when analysed at the level of each component. (a) Mantis shrimp use their raptorial appendages to rapidly strike prey (lateral view, distal to left). Smashers (top, Gonodactylus smithii) use a club-like structure found at the proximal end of the dactyl to crush hard-shelled prey. Spearers (bottom, Lysiosquillina maculata) use an elongated, spiny dactyl to snag elusive prey such as fish. (b) The input, output, and coupler links connect to form the four-bar linkage system in mantis shrimp. The outline of the meral-V is indicated by thick grey dashed lines. Modified from McHenry et al. [23]. (c) The relationships between link size (x-axis) and kinematic transmission (KT, y-axis) demonstrate the greater mechanical sensitivity of the output link (red, left-most plot) compared with the input (orange, middle plot) and coupler (blue, right-most plot) links (see table 2 for phylogenetic generalized least squares analysis (PGLS) results). Squares denote spearers, circles denote smashers, and cross marks denote undifferentiated (Hemisquilla) species (see figure 2 and table 1 for species details). (Online version in colour.)

The four-bar linkage system exhibits functional redundancy across stomatopods, such that various morphological configurations of link sizes yield equivalent KT outputs [22]. Despite this functional redundancy, the relationships between KT and the components of the four-bar linkage system are unequal: KT is considerably more mechanically sensitive to variation in the output link than the input or coupler links [22,30]. Small changes in the output link yield disproportionately large mechanical effects on the output (KT) compared with an equivalent change in the other links. In other words, even in a system that, as a whole, is characterized by many-to-one mapping, KT and the output link exhibit a relationship that is closer to one-to-one mapping than the input and coupler links. The functional redundancy of the whole system coupled with differential mechanical sensitivity of its underlying components allows us to test whether mechanical sensitivity influences the rate of morphological evolution.

Here, we test the hypothesis that due to their tighter relationship, KT and the output link exhibit rates of evolution different from the input and coupler links. This hypothesis differs from the null expectation implicit to functional redundancy, which predicts that all components of a functionally redundant system should evolve at equal rates. In other words, we are testing whether the evolutionary rate (σ²) is similar between KT and the output link (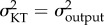), and different between KT and the input and coupler links. Previous research on the geometric morphometrics [31] and lever mechanics [30] of the raptorial appendage found that the evolutionary rate is faster in spearers than in smashers (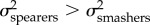). Based on their tight relationship, we predict that KT and the output link evolve faster in spearing mantis shrimp than smashers, with no expected rate differences between smashers and spearers for the input and coupler links.

2. Material and methods

(a). Morphology, biomechanics, and phylogeny

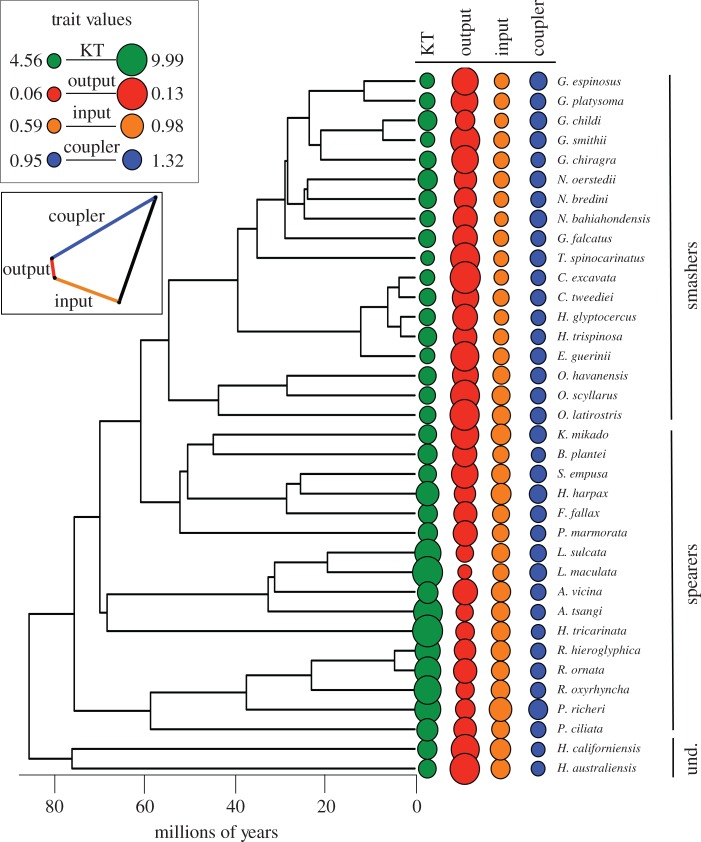
We gathered data on link length and KT from a previous study [22]. Briefly, morphological measurements were collected from 195 individual mantis shrimp from 36 species (electronic supplementary material, table S1). The dataset is comprised of 15 ‘spearing’ species, 18 ‘smashing’ species, and 2 ‘undifferentiated’ Hemisquilla species which possess a simple dactyl (neither hammer-shaped nor spear-shaped). The undifferentiated taxa are more similar to spearers than smashers, both in the morphological aspects of their raptorial appendage [30] and in the underlying muscle physiology [32].

The linkage system was measured using a series of landmarks placed on photographs of the lateral side of the raptorial appendage. Full details regarding the landmark analyses are available in Anderson & Patek [22]. Briefly, the landmarks encompassed the system's four rotation points, as well as the proximal and distal excursion points of the meral-V (figure 1). The kinematics, mechanics, and morphology of the mantis shrimp linkage system are well characterized [25,30]. Size-independent linkage measurements were gathered by dividing the output, input, and coupler links by the length of the fixed link, following well-established methods in mantis shrimp [25,30] and in other four-bar linkage systems [17,33–35].

 KT represents the ratio of output link rotation to input link rotation [36,37]. Briefly, higher KT values indicate more output rotation relative to input rotation, resulting in more displacement, but less force transmitted [34]. While it is often measured as a static metric, in this study KT was measured in a dynamic fashion (see [25] for methods and discussion). For analytical purposes, we focused on the minimum KT during a strike as it represents a conservative estimate of KT that can be consistently compared across individuals and species [22,25,30].

We used the time-calibrated molecular tree of Porter et al. [38], which we pruned from 49 species to the 36 analysed in this study. The tree was constructed from maximum-likelihood heuristic searches and is based on two nuclear (18S and 28S rDNA) and two mitochondrial (16S and COI) genes. The time calibration points used to create a chronogram were based on fossil data, using the relaxed clock method [39]. For a full description of calibration methods using stomatopod fossil data, see Claverie & Patek [31].

(b). Mechanical sensitivity

According to Anderson & Patek [22], the mechanical sensitivity of the output of a mechanical system with respect to its components is estimated as the coefficient of a phylogenetically corrected regression. Phylogenetic regression assumes that the residual error in the regression model is proportional to branch length [40,41]. We performed a phylogenetic generalized least-squares (PGLS) regression in which we simultaneously estimated the phylogenetic signal (λ, [42]) in the residual error with the regression parameters [41]. We estimated the contribution of each link (output, input, and coupler) to KT using PGLS regression with simultaneous maximum-likelihood estimation of λ as implemented with the pgls function in the caper package [43] in R [44]. We also performed a multiple regression analysis in which all links were considered predictors of KT: this model allowed us to estimate the proportion of total variation in KT explained by each variable. We used the stepAIC function in the R package MASS [45] to compare multiple regression models via stepwise addition and removal of predictors. Because significance tests based on stepwise methods can be subject to inflated type I error (e.g. [46]), we also performed model selection via direct comparison of AIC scores, with a ΔAIC > 4 considered to indicate strong support for an alternative model [46–48].

(c). Comparison of evolutionary rates

We addressed our first hypothesis—that the rates of output link and KT evolution should be more similar to each other than either is to input and coupler link evolution—using Adams' [49] likelihood ratio test (LRT) in R. Specifically, the test calculates the likelihood of a model in which the rates of evolution (σ²) are constrained to be the same (i.e. 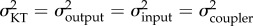) and the likelihood of an alternative model in which the rates of evolution are allowed to vary. We compared the fit of each model using an LRT [49]. We then performed pairwise comparisons among all four traits. As above, each test compared the likelihood of a model in which the rates were constrained to be the same (e.g. ) to a model in which the rates were allowed to vary (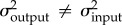). We log-transformed links for all statistical analyses to remove bias due to size differences among traits and to allow for rate comparisons among traits with different units [49–51]. We bounded each estimate of σ² using the 95% CI, which was derived from the standard errors of each evolutionary rate. To estimate the standard error, we obtained the Hessian matrix (comprised of the likelihood function's second-order partial derivatives; [52]). The standard errors of model parameters are the square root diagonals of the inverse Hessian matrix. The code to obtain standard errors was provided by D. Adams (personal communication, 2016).

To test our second hypothesis—that KT and the output link (but not the input and coupler links) exhibit faster rates of evolution in spearers than in smashers—we compared the evolutionary rate across smasher and spearer mantis shrimp species. We excluded the undifferentiated Hemisquilla species in this analysis due to their small sample size (n = 2) in our dataset. We first sampled potential histories of mantis shrimp raptorial appendage morphologies (spearers and smashers) in proportion to their posterior probability [53] by creating 500 stochastic character maps with the make.simmap function in phytools [54] in R, and then integrated each parameter estimate over the total sampled histories. We then estimated the evolutionary rate for each trait (KT, output, input, and coupler) using the OUwie function in the R package OUwie [55]. We fitted two different models: (i) a one-peak Ornstein–Uhlenbeck (OU) model, which is a Brownian motion (BM) model with pull towards a central trait optimum, and a common evolutionary rate (i.e. 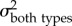) for both spearers and smashers [56–58], and (ii) a two-peak OU model, which allowed the evolutionary rate to differ between smashers and spearers (i.e. 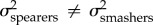) for each trait. We used AIC_C to assess the fit of both models. The model with the lowest AIC_C score indicated best fit and any models with ΔAIC_C ≤ 4 were considered to have equal support [47]. To account for uncertainty in model choice, we calculated the average rate parameters for each model using a model averaging approach [59] in which the evolutionary rate parameters of the two-peak model ( 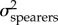and 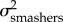) were weighted by the AIC_C weights of the one- and two-peak models.

3. Results

(a). Mechanical sensitivity

In order to validate and enhance the previous analysis of mechanical sensitivity [22] with these data, we performed a new analysis of mechanical sensitivity across mantis shrimp. We recovered a strong relationship between KT and the output link, but weak relationships between KT and the coupler and input links (table 1). Our phylogenetic multiple regression approach revealed that the model combining all three links—input, output, and coupler—best predicted KT, whether determined through stepwise procedures or comparison of AIC_C (electronic supplementary material, tables S2–S3). Although the output link exhibited the least range of variation relative to the input and coupler links (figures 1 and 2), it had the greatest contribution to KT (electronic supplementary material, table S3), and better predicted KT than a model combining both the input and coupler links (electronic supplementary material, table S2). These findings are consistent with the previously published results of Anderson & Patek [22].

Table 1.

PGLS models estimate the relationships between morphological links (input, output, and coupler) and kinematic transmission (KT) in the four-bar linkage system. For each regression, the maximum-likelihood (ML) estimate of phylogenetic signal (λ), the model coefficient (±1 s.e.), and the phylogenetic residual standard error (RSE) are presented.

predictor	ML estimate of λ	coeff. ± 1 s.e.	RSE	p-values
input	0.856	0.202 ± 0.316	0.009	0.527
output	0.912	−0.765 ± 0.079	0.005	2.24 × 10−11
coupler	0.878	0.025 ± 0.389	0.009	0.948

Figure 2.

The distribution of trait size across mantis shrimp species illustrates that relative output link size and KT exhibit greater variation than relative coupler and input link size. The phylogenetic tree depicts the evolutionary relationships of the 36 taxa examined in this study (18 smashers, 16 spearers, and 2 undifferentiated species). The smaller inset depicts the physical connections among the output, input, and coupler links in the four-bar linkage system (also see figure 1b). In the larger inset, the numbers indicate the size range for each trait (KT, output link, input link, and coupler link), showing how variation is much higher for the coupler and input link, but relative variation is much greater for the output link. The magnitude of each trait is depicted via relative circle diameter (see large inset) and is positioned next to the corresponding species. Colour denotes each trait as follows: KT (green), output link (red), input link (orange), and coupler link (blue). (Online version in colour.)

(b). Evolutionary rates

When all traits (KT, output, input, and coupler) were compared simultaneously, the model that allowed the evolutionary rate (σ²) to vary among traits fitted the data better than the model in which rates for all traits were constrained to be the same (LRT = 48.145, p = 1.98 × 10⁻¹⁰), indicating that rates vary among traits. Pairwise rate comparisons among traits revealed that the rate of output link and KT evolution were both three to seven times faster than the other links (figure 3 and table 2). Divergence rates did not differ between the coupler and input links, nor did they differ between KT and the output link (figure 3 and table 3). In other words, greater mechanical sensitivity of KT with respect to the output link is associated with accelerated rates of evolution in the output link.

Figure 3.

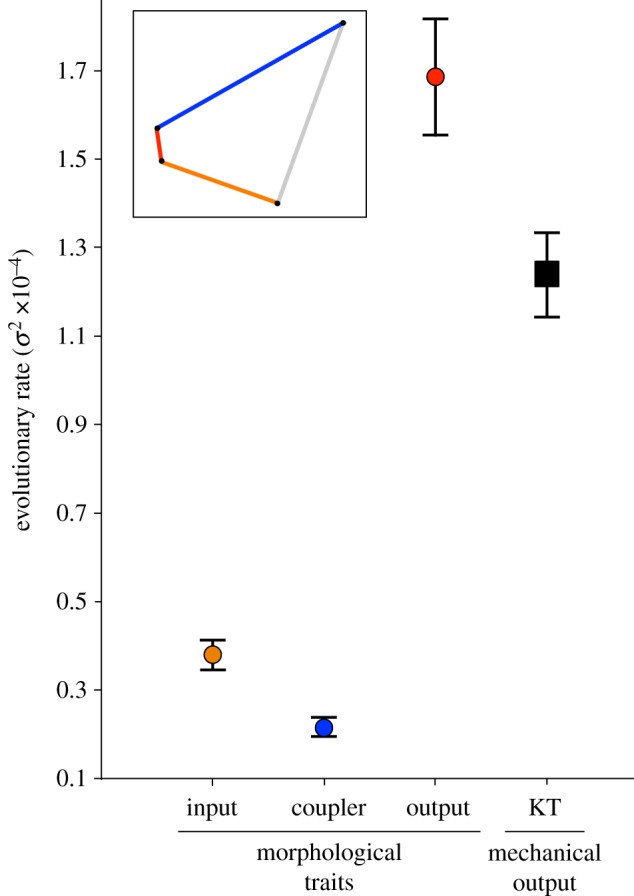
The evolutionary rates (σ²) for the output link and kinematic transmission (KT) are higher than the rates for the input and coupler links. Each rate is given with its 95% CI. Inset shows the configuration of the input (orange), output (red), and coupler (blue) links in the four-bar linkage system, and KT is denoted in the main panel in a black square. (Online version in colour.)

Table 2.

A comparison of evolutionary rates across all links and KT and pairwise comparisons of rates between each pair of traits. For each test, the AIC_C score for the model in which the rates are allowed to vary (AIC_C observed) and AIC_C score for a model in which the rates are constrained to be the same (AIC_C constrained) are presented. The test's likelihood ratio test (LRT) score and corresponding significance are also included. Significant results (highlighted in italics) indicate that the model allowing rates of evolution to vary provides a better explanation of the data than the model in which rates of evolution are constrained to be the same.

comparison	AICC (observed)	AICC (constrained)	LRT	p-values
all traits	813.188	855.333	48.145	1.98×10−10
input–output	456.917	473.842	18.925	1.36×10−5
output–coupler	436.120	467.948	33.827	6.02×10−9
input–coupler	383.040	383.936	2.897	0.089
KT–input	447.001	456.976	11.971	0.001
KT–output	452.134	453.314	3.180	0.075
KT–coupler	426.870	449.399	24.529	7.32×10−7

Table 3.

A comparison of model fits (ΔAIC_C and AIC_C weights within rows) and estimated evolutionary rates (σ²) from the trait-based diversification analyses comparing rates of evolution between spearers and smashers for each trait (KT, output link, input link, and coupler links). The two-rate Ornstein–Uhlenbeck (OU) model better fit the data than the one-peak OU model (high AIC_C weight difference between models) for kinematic transmission (KT) and the output link. The one-peak and two-peak OU had roughly equivalent support (similar AIC_C weights) for the input and coupler links. For the one-rate model, a single evolutionary rate (σ² both types) is given for both spearers and smashers. For the two-rate model, evolutionary rates for spearers and smashers are presented separately (σ²_spearer and σ²_smasher, respectively). Model-averaged evolutionary rate parameters (with 95% CI in parentheses) are calculated using the average OU rate parameter for smashers and spearers across both one- and two-rate models, weighted by their respective AIC_C scores.

	one-rate model			two-rate model				model averaged (95% CI)
trait		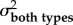ΔAICC	AICC weight		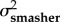	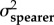ΔAICC	AICC weight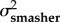
KT	1.47 × 10−4	8.74	0.01	9.65 × 10−4	3.84 × 10−3	0	0.99	9.57 × 10−4 (1.70 × 10−4–9.73 × 10−4)	3.80 × 10−3 (8.51 × 10−4–3.08 × 10−2)
output	3.15 × 10−4	5.55	0.06	1.47 × 10−3	3.59 × 10−3	0	0.94	1.40 × 10−3 (2.05 × 10−4–2.37 × 10−2)	3.40×10−3 (3.80 × 102–3.70 × 10−4)
input	5.60 × 10−5	1.82	0.29	8.28 × 10−5	9.22 × 10−5	0	0.71	7.50 × 10−5 (4.87 × 10−5–4.41 × 10−3)	8.17 × 10−5 (4.05 × 10−5–6.99 × 10−3)
coupler	6.44 × 10−5	0	0.61	5.43 × 10−5	1.57 × 10−4	0.93	0.38	5.99 × 10−5 (1.79 × 10−5–9.91 × 10−4)	9.90 × 10−5 (7.49 × 10−5–2.18 × 10−3)

We also found that the two-peak OU model allowing for different evolutionary rates between spearers and smashers was significantly better supported than the one-peak model for both KT and the output link (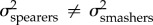; table 3). The model averaging approach revealed that the evolutionary rate for KT and the output link was two to three times faster in spearing mantis shrimp than in smashers (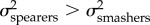). However, the confidence intervals bounding the evolutionary rate broadly overlap for the output link (table 3), limiting any hard conclusions on rate differences between spearers and smashers for this trait. By contrast, in the case of the coupler and input links, we found equivalent support for the one-peak and two-peak models (table 3). In other words, evolutionary rates were comparable between smashers and spearers for both the coupler and input links ().

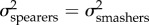4. Discussion

A hallmark of functionally redundant systems is that morphological and mechanical diversity are uncorrelated [17,35]. This pattern is robust at the whole-system level, given that composite measurements of morphology using principal component (PC) analysis indicate a weak relationship between PC score and KT [22]. Nonetheless, when decomposed into its individual parts, we find different relationships between morphology and mechanical output in the mantis shrimp four-bar linkage system. The output link is much more strongly correlated with KT and provides the strongest contribution to mechanical output, more so than the input and coupler link put together. Hence, a more accurate characterization of mechanical redundancy in this four-bar linkage system is that KT exhibits many-to-one mapping with respect to the input and coupler links, and a one-to-one relationship with the output link.

The differences in mechanical sensitivity among links correspond to dramatic differences in evolutionary rate. As expected, the disparity in evolutionary rate between the input and coupler links and KT reflects their weak relationship with respect to mechanical output. By contrast, the evolutionary rate of the output link reflects its stronger correlation with KT. Depending on the comparison, the rate of KT and output link evolution was three to seven times faster than that of the input or coupler link. The finding of variable evolutionary rates across linkages provides a new lens for understanding the diversification dynamics of many-to-one mapping. Specifically, the rate of morphological evolution can proceed unevenly across a functionally redundant system, a result that appears to reflect, at least in part, the mechanical sensitivity of KT to each underlying feature, and a result that would not have been predicted from composite measures of morphology.

As predicted, the evolutionary rate differs between spearing and smashing mantis shrimp for KT and, to a lesser extent, for the output link. Depending on the comparison, KT and the output link evolve two to three times faster in spearers than in smashers. By contrast, we did not detect rate differences between mantis shrimp types for the coupler and input links. Previous work by Claverie & Patek [31] examined rates of morphological disparity across mantis shrimp raptorial segments using composite, geometric morphometrics measurements that reflected the interdependence (modularity) of changes in size and shape across the segments (e.g. [60,61]). They found that disparity accumulated more quickly in spearers than in smashers. Even though the analysis by Claverie & Patek [31] examined shape and size across raptorial segments, in contrast with the present analysis that examined individual traits within a single mechanical system within one segment, the results echoed each other and exemplify the multi-level dynamics of form–function evolution.

Understanding the intersection between mechanical and evolutionary relationships is central to disentangling the processes that underlie phenotypic diversification [11,15]. In the case of the four-bar linkage system in mantis shrimp, greater mechanical sensitivity is associated with accelerated divergence rates, which might suggest that sensitivity enables, rather than constrains, morphological evolution. However, as is often the case with the challenging concept of constraints in biology, the same coin can be viewed from the opposite side [62]. The accelerated rate of change of the component to which the system is most sensitive can also be viewed as a constraint, because its variation is tightly tied to changes in the mechanical output of the system. In other words, the evolution of the output link could be constrained by the processes impacting KT evolution. Thus, we emphasize that the differences in evolutionary rate do not allow for hard conclusions on the selective pressures underlying link and KT evolution—indeed, making inferences of selection in functionally redundant systems is fraught with challenges (discussed in [19]). Rather, our results offer greater guidance to the evolutionary connections (or lack thereof) among the components of mechanical systems, and illustrate how mechanical sensitivity restricts the freedom of morphological evolution that has been implicit to the concept of functional redundancy.

Many key aspects of an organism's biology scale with size [63,64]. In mantis shrimp, the most likely biomechanical basis of mechanical sensitivity in the four-bar linkage system is size: the smallest link is the output link, such that smaller increments of link size change yield greater mechanical effects than they would in the other larger links [22]. On the one hand, one could predict that a small component such as the output link, to which small changes have disproportionately large effects on KT, is highly constrained to small changes given its large effects and, therefore, should have relatively slow evolutionary rates of change. Alternatively, one could argue that the smallest link should be released from constraints due to the ability to have great effects through small changes and, therefore, yield high evolutionary rates of change.

Observations of evolutionary rate can be influenced by size, with larger traits having greater variances and thus displaying greater changes per unit time [49,65]. Indeed, there is an order of magnitude more variance for the input and coupler links than for the output link. Log-transforming variables (as performed in our analyses) reduces the dependence of the variance on the mean, and inferred rates are described by the relative rate of change in proportion to the trait mean [40,49,50]. The evolutionary rates inferred from transformed traits reflect the greater rate of change in the small output link (relative to its mean) when compared with the larger-sized input and coupler links. Hence, the biomechanical relationship involving a small trait of large effect can involve pronounced differences in evolutionary patterns.

Mechanical sensitivity can play important roles at multiple levels of analysis. For example, differential mechanical sensitivity can be discovered based on comparative biomechanical analyses or predicted based on an equation in which one component disproportionately impacts mechanical output, such as the squared velocity term in calculations of drag [23,66]. Whether and how biomechanical sensitivity is associated with concomitant shifts in evolutionary rates needs to be tested across systems so that we can assess whether the dynamics observed in this study are specific to the level of analysis, the specific biomechanical system or can be understood as a fundamental dynamic of biophysical systems [11]. Moving forward, these approaches set the stage for analysing the evolutionary dynamics of the many diverse and well-studied biomechanical systems and establishing a quantitative framework for the dynamic interplay between evolutionary processes and physics.

Ethics

All measurements were performed on preserved specimens.

Data accessibility

Morphological and performance data: electronic supplementary material, table S1.

Authors' contributions

M.M.M. and S.N.P. conceived the study, M.M.M. performed the analyses, M.M.M., P.S.L.A., and S.N.P. interpreted the analyses and wrote the manuscript.

Competing interests

The authors declare no competing interests.

Funding

This research was supported by NSF (IOS-1149748) to S.N.P.