Guidelines for Finite Element Modeling of Acoustic Radiation Force-Induced Shear Wave Propagation in Tissue-Mimicking Media

Abstract

Ultrasound shear wave elastography is emerging as an important imaging modality for evaluating tissue material properties. In its practice, some systematic biases have been associated with ultrasound frequencies, focal depths and configuration, transducer types (linear versus curvilinear), along with displacement estimation and shear wave speed estimation algorithms. Added to that, soft tissues are not purely elastic, so shear waves will travel at different speeds depending on their spectral content, which can be modulated by the acoustic radiation force excitation focusing, duration and the frequency-dependent stiffness of the tissue. To understand how these different acquisition and material property parameters may affect measurements of shear wave velocity, simulations of the propagation of shear waves generated by acoustic radiation force excitations in viscoelastic media are a very important tool. This article serves to provide an in-depth description of how these simulations are performed. The general scheme is broken into three components: (1) simulation of the three-dimensional acoustic radiation force push beam, (2) applying that force distribution to a finite element model, and (3) extraction of the motion data for post-processing. All three components will be described in detail and combined to create a simulation platform that is powerful for developing and testing algorithms for academic and industrial researchers involved in making quantitative shear wave-based measurements of tissue material properties.

I. Introduction

Ultrasound shear wave elastography (SWE) is an imaging modality that utilizes acoustic radiation force to generate shear waves in soft tissues and ultrasound pulse-echo methods to measure the motion of the propagating waves [1]. The speed of the waves is directly related to the material properties of the medium, in particular, the elastic shear (or Young’s) modulus and the viscosity [1–4].

Shear wave elastography is being used in many different clinical applications, including staging of liver fibrosis and detection of tumors in the breast, thyroid, liver, and prostate [1, 5–8]. In addition, it is also being utilized for evaluating carotid atherosclerotic plaques, chronic kidney disease, the heart, and the musculoskeletal system [9–13].

In particular, SWE has been studied as a tool to noninvasively characterize liver fibrosis since the current clinical standard of liver needle biopsy is associated with risks for bleeding and infection, along with considerable patient discomfort [14, 15]; however, some clinical studies over the past few years have revealed SWE bias and variation across different manufacturer systems that could impede more widespread clinical adoption [16].

Given the differences observed between different SWE implementations, a standardizing approach for comparing across measurement platforms and patient cohorts is important. The Radiological Society of North America (RSNA) formed a Quantitative Imaging Biomarkers Alliance (QIBA) working group for ultrasonic shear wave speed measurements in 2012 to standardize shear wave speed measurements for liver fibrosis staging. This committee is using measurements in physical phantoms with different ultrasound scanners, simulations of shear wave propagation, digital phantoms, and measurements in patients with liver fibrosis to understand some of the sources of variation [17–19]. Studies associated with this standardization effort have demonstrated that different ultrasound frequencies, transducer types, and imaging depth contributing to biases of shear speed or shear modulus measurements. In phantom studies, it has been demonstrated that different machines and different transducer types (linear versus curved array) can introduced biases of 10–15% [18–21]. These biases can be explained by different acoustic radiation force distributions and by varying different aspects of the SWE implementations. Similar biases have also been observed in liver measurements [22–25]. An additional factor is the changes in liver viscoelasticity associated especially with patients with steatosis along with fibrosis [26–30].

Ideally, all shear wave speed reconstruction methods should obtain the same values for the material properties in a given phantom or patient. While it is important to identify that these biases exist, it is more important to understand their sources so that if possible protocols can be defined to reduce their effects or at the very least make clinicians aware that certain practices may be advised. The sources of variation amongst the different SWE implementations could be related to:

• The spatial and temporal characteristics of the acoustic radiation force (ARF),

• The material properties of the medium,

• The ultrasound-based motion tracking, and

• The algorithms used for processing and analyzing the motion data to extract the shear wave speed and material properties.

To understand some of the sources of variation, it is useful to have a validated simulation platform that allows researchers in academia and industry to generate three-dimensional (3D) propagating shear wave fields from realistic acoustic radiation force excitations in isotropic, homogeneous elastic and viscoelastic media. Elastic tissue mimicking phantoms have widely been used for elasticity imaging method development. However, soft tissues are inherently viscoelastic [28–36], so for elasticity imaging methods to be fully validated, viscoelastic phantoms are necessary. Temporally and spatially homogeneous viscoelastic phantoms with acoustic properties that mimic human tissue are notoriously difficult to fabricate in a reproducible manner, and it is equally difficult to characterize the viscoelastic properties of these phantoms in the spectral range associated with acoustic radiation force SWE methods (~100–2000 Hz), highlighting the value of having simulation tools for these studies. To maximize the utility of this simulation platform to be general enough for application across a variety of manufacturer systems, transducers and target tissue, it is necessary to simulate the acoustic radiation force push from the ultrasound array transducer, the motion related to the excitation in the tissue-mimicking material, and extract the motion for post-processing with the same signal processing methods used in clinical implementations.

The rest of the article is organized as follows. First, we will introduce the conceptual methodology employed by the simulation platform, and then provide detailed descriptions of the different steps involved in the simulation process. These steps include the ARF simulation, motion simulation with finite element models (FEMs), extraction of the motion and post-processing. As a demonstration of the type of results produced by this simulation platform, we will present results from simulations in elastic and viscoelastic tissue-mimicking media with a clinically relevant curved linear array transducer. Specifically, we will compare the results for two software FEM packages in a parametric study in elastic media. We will also show results with varying a more limited number of parameters in viscoelastic media. We will follow with discussion and conclusions.

II. Methods

A. Overview of Simulating Shear Wave Propagation with FEMs

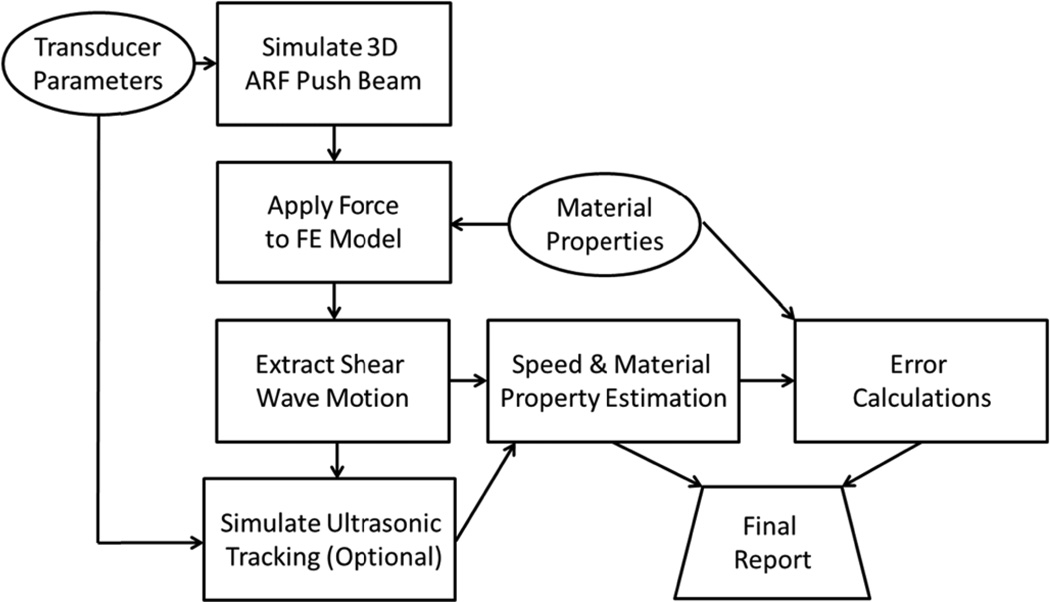
A block diagram of the simulation scheme is shown in Fig. 1. The input parameters for the simulation platform are the transducer characteristics and the mechanical properties. The ARF push beam distribution is simulated to obtain the input force for the finite element model. The material properties are input into FEM as well for calculation of the resulting motion after the force is applied. In this paper we only address the simulation of wave propagation in isotropic, homogenous, linear elastic and viscoelastic media. Some tissues, due to their structural architecture, are not properly modeled with these assumptions such as the kidney, artery, skeletal muscle, and myocardium where other considerations for anisotropy or thickness of the organ need to be addressed. The methods discussed in this paper can be extended to media with inhomogeneities with proper boundary condition considerations [37–39]. Anisotropic and nonlinear media can be modeled with appropriatematerial definitions or constitutive models [40, 41].

Fig. 1.

Simulation scheme for shear wave motion calculation. The transducer parameters are used to calculate the three-dimensional (3D) ARF push beam. The force is applied to the FE model and once completed, the motion is extracted. An optional step to simulate the ultrasonic tracking of the motion can be implemented. The motion is then used in post-processing algorithms to estimate the wave speeds and material properties. The original material property parameters can be used for error calculations and a final report is generated.

Once the motion is calculated, the particle displacement, particle velocity, or particle acceleration can be extracted from the mesh at each node or computational location at every sampled time point.

An optional step that has been incorporated in some reports is to model the ultrasound imaging of the medium after the ARF push. This is applied for simulating the motion detection in the SWE experiment. At each time point after the ARF push, the scatterer positions are moved according to the motion numerically evaluated in the FEM [42]. The ultrasound A-lines or B-mode image are simulated and the collection of ultrasound lines or frames are then processed either with normalized cross-correlation or autocorrelation to estimate the motion from the ultrasound radiofrequency (RF) or in-phase/quadrature (IQ) data.

After the motion is calculated either directly from the simulation method or estimated from the simulated ultrasound data, the shear wave velocity can be estimated. Different methods can be employed to evaluate the group velocity or the phase velocities over a specific bandwidth. From the group velocities, the shear elastic or Young’s modulus can be estimated. Alternatively, if the phase velocities are calculated, they can be fit to a viscoelastic model or a model-free approach to characterize the viscoelastic properties [32, 43]. The estimates of speeds and material properties can be compared to the input parameters of the model for error calculation and a final report can be generated.

B. Simulating Acoustic Radiation Force Distributions

We will briefly review previous efforts of simulating shear wave motion in tissue mimicking soft solids. The general approach is a two-step process: (1) to simulate the applied radiation force distribution, and (2) to simulate the wave propagation by solving the wave equation with the applied force. The array geometry, focusing characteristics, and ARF temporal duration are parameters that determine the spatial distribution of the acoustic pressure used for the push and the spectral features of the motion.

The length of typical ARF pushes is a few hundred microseconds, much longer than a typical B-mode pulse, so the full toneburst can be simulated or a continuous wave assumption can be reasonably made [31, 44, 45]. Software packages such as Field II, FOCUS, k-wave, and PZFlex have been used for simulation of the ultrasound pressure [46–50].

Many previous studies calculate the ARF body force using the following relationship

$$\overrightarrow{F}=\frac{2\alpha \overrightarrow{I}}{c_c},$$ (1)

where α is the ultrasound attenuation coefficient, I⃗ is the ultrasound intensity, and c_c is the compressional wave speed [44]. The ultrasound intensity is the square of the pulse average of the ultrasound pressure. The absolute value of I⃗ can be measured experimentally to scale simulated acoustic intensities to generate realistic force magnitudes for the simulations, or since these simulations are linear, the resultant displacement fields can be scaled to realistic values.

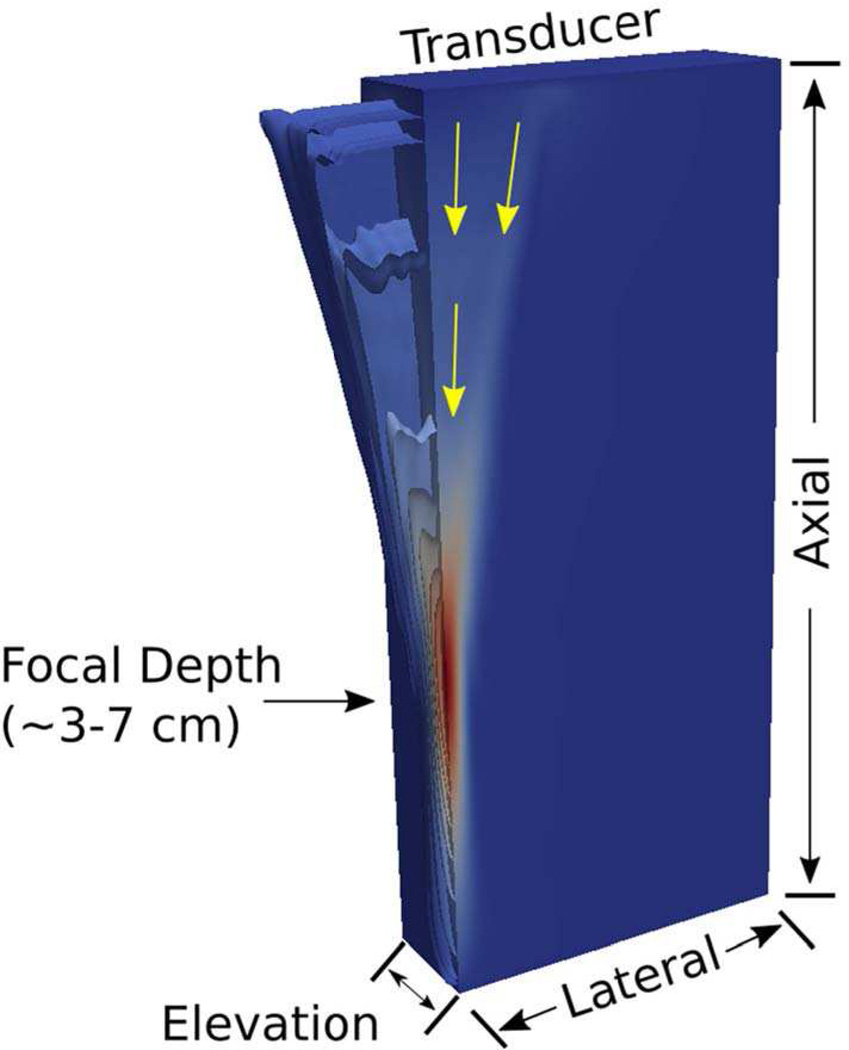
For simulation purposes, the force is applied only in the axial direction. There have been some efforts to incorporate the Poynting vector to determine the proper vectors for the applied force [51] instead of assuming that all of the force is directed purely in the axial direction, directly away from the transducer face While refining this specific net direction of the applied force can provide a more accurate representation of the displacement fields in the near field of aggressively-focused acoustic radiation force excitations (low f-number) (Figure 2), this is considered a minor contributor to the displacement response in less aggressive focal configurations (higher f-numbers) and down the center axis of the acoustic radiation force excitation, where orthogonal components of displacement do not exist due to symmetry in the excitation in the lateral and elevation dimensions. Since acoustic intensity is not readily calculated as a vector quantity by any of the acoustic simulation packages used in this work, we applied all the discrete acoustic radiation force loads in these models uniformly in the axial dimension.

Fig. 2.

Spatial distribution of a representative acoustic radiation force excitation intensity field, as simulated in 3D using Field II, shown in a quarter-symmetry volume as isosurfaces of relative intensity that peak in red at the focus. The yellow arrows show relative direction of the Poynting vector associated with the propagating acoustic waves generating this acoustic radiation force excitation. While the near-field of the excitation distribution has some lateral component to the force, the impact of this lateral force is minimal at the focal depth, and the symmetrically opposing lateral displacements related to these minor lateral forces in the near field cancel one another out along the axis of symmetry of the excitation. For these reasons, the acoustic radiation force vectors are applied in a purely axial orientation in these simulations.

Simulating the mechanical response of soft tissue to impulsive acoustic radiation force excitations occurs on a time scale of 10–20 ms after the ARF stimulation which is less than 1 ms, typically 0.1–0.4 ms. For that reason, simulating both the acoustic wave propagation and the resulting transient tissue deformation is too cumbersome to capture in a single numerical simulation framework. Instead the acoustic simulation can be decoupled from the mechanical simulation, and the acoustic radiation force distribution can be input as an initial forcing condition to the FEM model.

As previously mentioned, Field II, FOCUS, k-wave, and PZFlex are popular acoustic simulation packages to simulation the acoustic intensity. The ARF push in this report was modeled by Field II simulations and three different push beam profiles are tested. The following table (Table I) entails the physical dimensions of the simulated probe and the medium ultrasound attenuation. The focal number, F/N, is calculated as z_f/D where z_f is the focal depth and D is the aperture width.

TABLE I.

Curved array transducer parameters for simulations in elastic and viscoelastic media

Parameter	Value	Unit
Radius of Curvature	60	mm
Element Height	14	mm
Element Pitch	0.477	mm
Elevation Focus	50	mm
Center Frequency	3	MHz
Attenuation	0.45	dB/cm/MHz

Since we only consider linear models in this study, we can scale the ARF profile linearly to let the resulting wave motion close to the physical range. The body force is applied to each of the finite elements only in the axial direction, since, as discussion in relationship to Figure 2, the components of the Poynting vector that are orthogonal to the z-dimension tend to be at least an order of magnitude less than the axial components, and the orthogonal displacements that would result from such force components would cancel one another out across the symmetry planes of the acoustic radiation force excitation in the lateral and elevation dimensions. While we do apply the forces exclusively in the axial dimension, the finite element solvers completely solve for the resultant transient 3D displacement fields It should be noted that when using a uniform, rectilinear mesh that the orientation of the mesh is chosen such that one of the principle axes of the mesh aligns with the direction of the applied radiation force. Doing so ensures that (1) the acoustic radiation force can be directly applied using Eq. (1) without having to decompose it into vector components, and (2) it minimizes the chance of numerical dispersion since the shear wave propagation and primary displacement components align directly with the principle axes of the mesh.

There are several approaches to map the transmitted acoustic intensity distributions to the FEM mesh as an input loading condition:

1. Model the intensity over an adequately spatially sampled 3D grid that can be interpolated onto the FEM mesh, or

2. Solve for the intensity at the discrete spatial node/element locations based on the specific mesh being used for the finite element analysis.

Option 1 has the benefit of only needing to run the acoustic simulation once and applying that intensity field to multiple target FEM meshes with simply the 3D interpolation overhead, which can be advantageous when iterating over multiple meshes, especially when performing the mesh refinement studies. Option 2 can be favored when a limited number of meshes are being utilized for an analysis.

The acoustic radiation force (1) is a body force (force/volume) that can be applied in several ways to a FEM model:

1. The body force can be concentrated to a discrete point load by scaling the body force over a known element volume, where the point load is a force applied to a specific node, and the 3D spatial distribution of radiation force is captured by having loads over an appropriate cloud of nodes, or

2. Applying body forces to each appropriate element in the mesh.

If the mesh is adequately refined, then both methods should produce equivalent results. However, in the case where mesh density is limited by memory or run time, the point load approach allows for slightly coarser meshes to be used since a single, centered point load at the focal point can adequately capture the symmetry of the ARF excitation, whereas body forces applied to relatively larger elements will develop some artifacts related to the discretization of the input load function.

The final consideration in simulation of the ARF field is the temporal duration of the insonification. Unlike B-mode imaging transmit events, ARF excitations are typically applied for tens-to-hundreds of microseconds (hundreds of cycles), allowing the user to assume that the ultrasound excitation is operating in a quasi-continuous wave mode and ignoring the impact of the transients associated with turning the ARF on and off. The pulse-average intensity can be estimated at all the spatial locations described earlier, and the finite element model can prescribe when to apply these loads in time. The temporal loading curves, describing the “on time” of the acoustic radiation force loads, are typically applied as piecewise linear functions, with transitions from “on” to “off” being done as quickly as 1 µs without introducing any transient ringing or spurious high-frequency modes.

C. Mesh Definition

Once the force is calculated, it is used as an input for the simulation of the wave motion. Many different approaches have been utilized for computing the wave motion. Different approaches include finite element modeling (FEM), finite difference (FD), and Green’s function formulations [38, 41, 45, 50–57]. These studies involved validation of the methods with the prescribed mechanical properties. Many different FEM packages have been used in the literature, including LS-DYNA (Livermore Software Technology Corporation, Livermore, CA), Abaqus (Dassault Systems, Waltham, MA), COMSOL Multiphysics (Comsol Inc, Burlington, MA) and PZFlex (Weidlinger Associates, Inc, Mountain View, CA). The Green’s function approaches calculate the wave displacement from a convolution operation between the force and the Green’s function. The following sections describe the simulation of the shear wave motion using two different FEM packages, LS-DYNA and Abaqus. Considerable detail will be given for researchers to replicate this type of numerical simulations.

Finite element methods rely on discretizing the material being simulated into small subdomains where the material state—stress and strain—can be accurately represented by a linear or quadratic function (i.e., the shape functions of the elements). This approach allows for spatially complex distributions of force, such as a focused acoustic radiation force distribution from an ultrasound transducer, to be easily modeled. To accurately capture the acoustic radiation field and the resultant displacement and shear wave fields, this mesh needs to be spatially refined to adequately sample the highest spatial frequencies of the input source distribution. With increasing mesh size, however, comes longer computation runtimes, greater RAM requirements, and larger result file sizes.

The most common types of finite elements are tetrahedral elements (4 nodes) and hexahedral elements (8 nodes) [58]. Many automatic mesh generators, especially those dealing with complex mesh geometries, will use tetrahedral elements to accommodate the curvature of the structure being meshed. Unfortunately, tetrahedral elements can be ill-conditioned for modeling nearly incompressible media, as is done with soft tissue, sometimes demonstrating strong numerical dispersion (i.e., shear phase velocity gradients based on element shape and angle between adjacent faces) based on the size and aspect ratios of the tetrahedral [58]. In contrast, hexahedral elements do not suffer sharp interior angles and are resistant to these numerical dispersion artifacts. Hexahedral elements are most well-suited to meshes of regular geometries (e.g., rectangular solids) so that uniform element sizes can be used throughout the mesh to further minimize any numerical dispersion.

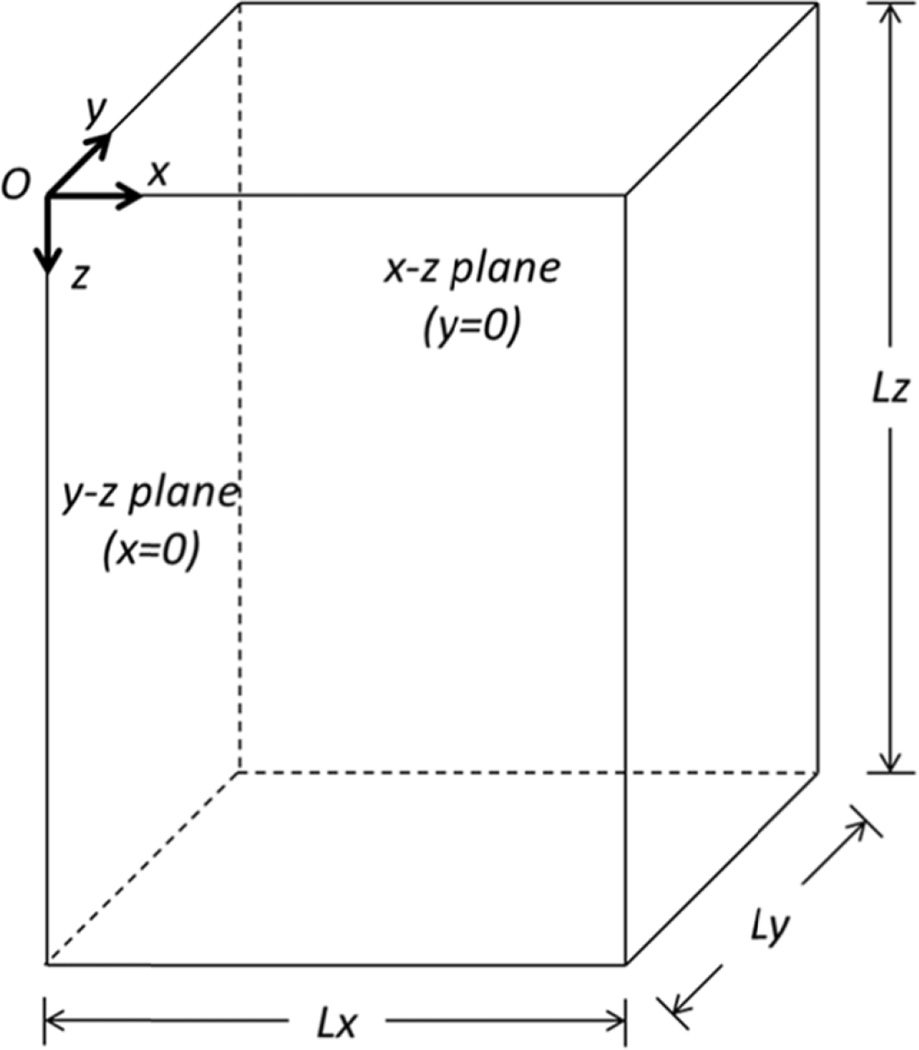
In this application we use the domain defined in Fig. 3 where the x-direction is the lateral or azimuthal direction, the z-direction is the depth direction, and the y-direction is the elevation direction and the transducer is situated in the at z = 0. The number of elements in the x-, y-, and z-directions are given by Lx, Ly, and Lz. Using conventional linear and curvilinear arrays to generate acoustic radiation force excitations tend to result in excitation spatial distributions that are symmetric across the center lateral and elevation planes. Overall mesh sizes can be reduced by a factor of 4 by implementing quarter-symmetry within the acoustic radiation force excitation when simulating isotropic, homogeneous viscoelastic media. This has been employed in the results shown in this article. This symmetry may be disrupted if phase aberration due to inhomogeneity in compressional wave speed is considered [59]. The compressional sound speed inhomogeneities produced by subcutaneous fat and muscle layers, which could induce changes in ultrasound propagation time-of-flight and cause errors in beam focusing, would not uniformly distributed, so a full 3D model would be necessary to account for these inhomogeneities. One assumption that could be made is that a phase screen, an adjustment of electronic focusing delays, could be applied across the elevation direction of the transducer [59].

Fig. 3.

Computational model domain of the FEM simulations. This assumes a quarter-symmetric simulation.

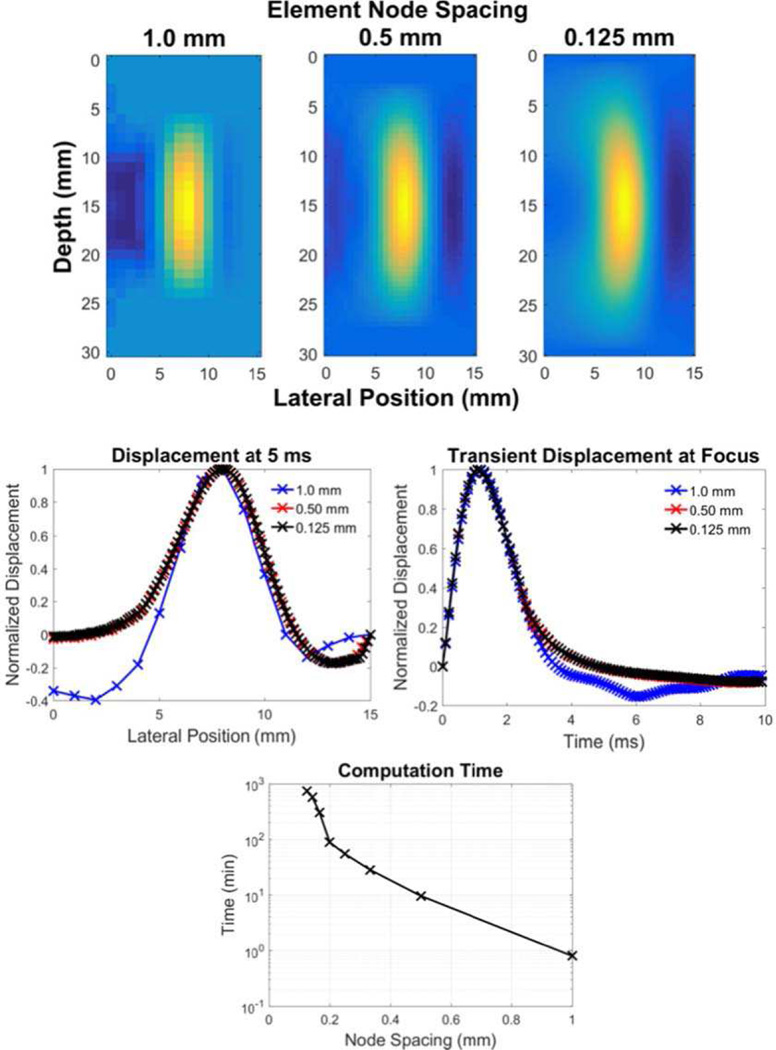
For focused acoustic radiation force applications, a general rule of thumb for choosing a node spacing that adequately samples the source distribution is to have at least 10 samples over the full-width half-maximum (FWHM) of the acoustic intensity distribution in the tightest spatial dimension at the focus [51]. When a sparser sampling of nodes is chosen, it is important to make sure that the mesh is centered about the acoustic radiation force field to ensure that the peak of the intensity is captured in the simulation. Confirmation of adequate mesh density can be achieved by refining the mesh for smaller node spacing and confirming that displacement responses in the regions of interest have converged to a response that is independent of mesh density (Fig. 4). At that point, the smallest element size that achieves this convergent behavior is the most efficient to use in parametric analyses.

Fig. 4.

An example of a mesh refinement analysis being performed on temporal and spatial response of a shear wave propagation model from a Gaussian ARF excitation source. The top row images show the qualitative representation of a propagating shear front for 1.00, 0.50, and 0.125 mm node spacing, 5 ms after the simulated acoustic radiation force excitation. The left middle row plot shows the displacement profile at 5 ms at the focal depth for each of these node spacings, and the right middle row plot shows the transient displacement response at the focus of the acoustic radiation force excitation for each node spacing. The bottom plot shows how the computation time increases as a function of finer node spacing for these models. Notice that too coarse of a mesh (1.0 mm node spacing) inadequately captures the acoustic radiation force distribution and resultant shear wave morphology, while there is no benefit to over-refining the mesh from an accuracy standpoint (equivalent displacement fields for 0.5 and 0.125 mm node spacing), while there is an appreciable runtime penalty for an overly-refined mesh.

The final consideration when developing the mesh for a finite element analysis is how boundary conditions are applied. For runtime considerations, symmetry in 3D models can be exploited to reduce the absolute mesh size, with quarter- and half-symmetry models being commonly utilized. Applying symmetry to a model requires that both the material and the ARF excitation can be properly represented with plane symmetry assumptions, where the planes of symmetry impose restrictions of the types of nodal displacements that are allowed. For example referring to Fig. 3, in a quarter-symmetry model, where the yz-plane and xz-plane are planes of symmetry, the nodes on that specific plane of symmetry are constrained such that displacement orthogonal to each symmetry face are not allowed, and rotations about the in-plane-axes are also not allowed (i.e., displacement are only allowed in-plane). In quarter-symmetry models, degrees of freedom of specified for each symmetry plane in addition to specification of the degrees of freedom on edge shared between the symmetry planes. On that edge, displacements are only allowed for translation in a single direction (along the axis of symmetry). Example syntax for both Abaqus and LS-DYNA models are available in the example files in the GitHub repository (Appendix A).

In addition to potential symmetry boundary conditions, the boundary planes at and opposing the simulated transducer need to be restricted. Typically, the boundary conditions are set to fully constrain all the degrees of freedom.

Finally, since many simulations are being done to represent semi-infinite media, but finite meshes are being used, the elements on the outer boundary planes in the lateral and elevation planes, along with the transducer and opposing-transducer planes, need to have boundaries that absorb both dilatational and transverse waves so that they do not reflect into the region of interest. In LS-DYNA, this can be accomplished with Perfect Matching Layers (PML) in elastic media, typically using 5–10 PML elements along each plane, and the outermost nodes are fully-constrained to all degrees of freedom. When modeling a viscoelastic medium, the elastic PML boundary condition cannot be reliably used, and instead a non-reflecting boundary can be assigned to element faces on the boundary planes of interest. Abaqus has infinite elements that behave similar to the LS-DYNA implementation of PMLs. Example syntax for Abaqus and LS-DYNA boundary conditions can be found in the annotated example scripts in the GitHub repository (Appendix A).

D. Material Property Definitions

Once the mesh is established, parameters for the material, such as the shear elasticity and the shear viscosity, or other viscoelastic formulations need to be defined. Additionally, the mass density (ρ) and Poisson’s ratio (υ) need to be defined. The Poisson’s ratio is typically assumed to be near 0.5 to model a nearly incompressible medium [51]. This assumption needs to be handled very carefully in numerical simulations. Compressional wave speeds in soft tissues are typically near 1500 m/s and shear wave speeds typically vary from 1–10 m/s [4]. However, in this simulation platform we are generally only interested in the shear wave propagation. Using a realistic Poisson’s ratio to obtain the realistic ranges of wave speeds in tissues would require a very fine spatial and temporal sampling to maintain numerical stability.

The transient displacement fields simulated in the presence of a finite bulk modulus (i.e., a small, but finite, amount of compressibility,) are a summation of dilatational and transverse fields, described by

$$\stackrel{\rightharpoonup }{u}=\nabla \mathrm{\Psi }+\nabla \stackrel{\rightharpoonup }{\times }\stackrel{\rightharpoonup }{w},$$ (2)

where ψ represents the dilatational component of the displacement field (strain associated with volume change in the material) and W represents the equivoluminal (shear) components of the displacement field that propagate transversely to the ARF-induced displacement and are the dominant component of displacement in these shear wave simulations [60]. Smaller bulk moduli will support more element volume change in the elements in response to the acoustic radiation force excitation, which is a deviation from our assumption that displacement fields are completely equivoluminal (pure shear). The compressional wave if not properly accounted for can produce artifacts in the shear wave motion. If the Poisson’s ratio is set too low, then compressional wave speeds start to approach shear wave speeds, which would complicate the analysis and post-processing of shear wave fields.. Increasing the Poisson’s ratio can cause exponential increases in simulation runtimes when using explicit solvers, so we will balance our need to have as close to an infinite bulk modulus as possible with achieving realistic model runtimes [58].

To address this issue we examine the relationship between the Poisson’s ratio and the two acoustic wave speeds. The compressional wave speed c_c and shear wave speed c_s for elastic media are related to the Young’s modulus, E, mass density and Poisson’s ratio as [4]

$$c_c=\sqrt{\frac{E(1-\nu )}{\rho (1+\nu )(1-2\nu )}},$$ (3)

$$c_s=\sqrt{\frac{E}{2\rho (1+\nu )}}.$$ (4)

Taking the ratio of the compressional and shear wave speeds gives a relationship that is only dependent on the Poisson’s ratio. Using this ratio, c_R, the impact of the choice of Poisson’s ratio can be evaluated.

$$c_R=\sqrt{\frac{2(1-\nu )}{(1-2\nu )}},$$ (5)

Table II shows the value of c_R for different values of υ. For at least an order of magnitude of difference in the compressional and shear wave speeds, the Poisson’s ratio must be greater than 0.495. Based on the authors’ experience, this is a minimally advised value of c_R taking into account the tradeoff between minimizing artifacts from compressional waves and computational expense.

TABLE II.

Values of c_R for varying Poisson’S ratio

Poisson’s ratio, v	cR
0.49	7.14
0.495	10.05
0.499	21.38
0.4995	31.64
0.4999	70.72
0.49995	100.05
0.49999	233.61

1) Elastic Model

The material of the digital phantom is defined as linear elastic. In Abaqus, such materials can be defined by specifying the Young’s Modulus and Poisson’s ratio. If the shear wave speed is c_s, then the Young’s Modulus in an infinite, isotropic, and homogeneous material is calculated by

$$E=2\rho c_s^2(1+\nu ),$$ (6)

where ρ is the mass density, which is typically set at 1000 kg/m³. In the results shown in this paper we varied E, and we set the Poisson’s ratio ν at 0.495. Specific input syntax for Abaqus and LS-DYNA can be found in the example scripts in the hosted GitHub repositories (Appendix A).

2) Viscoelastic Model

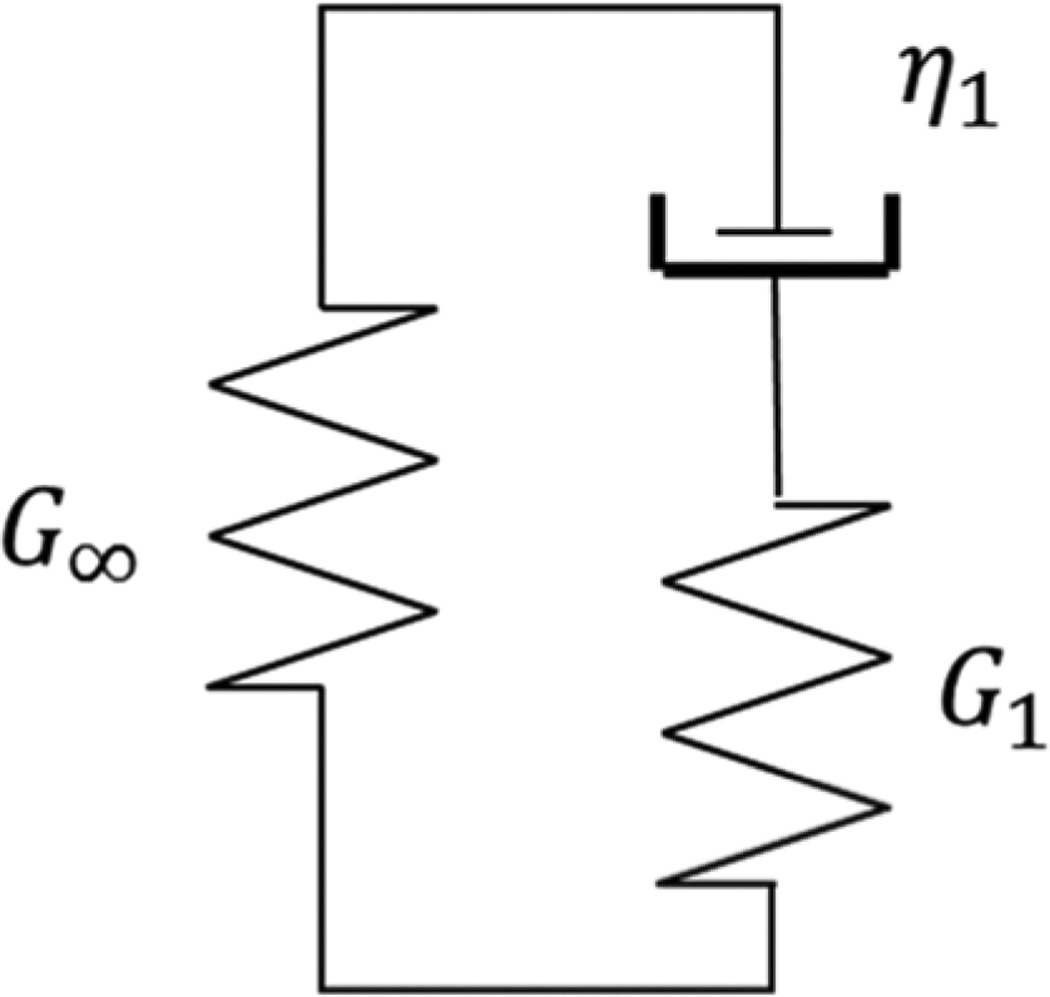
For implementing viscoelasticity in both LS-DYNA and Abaqus, we use a one-branch Generalized Maxwell model, as shown in Fig. 5 [29].

Fig. 5.

One-branch Generalized Maxwell Model with three parameters.

The relaxation shear modulus G_r of this model is

$$G_r(t)=G_{\infty }+G_1{e}^{-t/\tau },$$ (7)

where G_∞ is the long-term modulus, G₁ is the spring elasticity, and τ is the time constant of the relaxation modulus. The instantaneous shear modulus is

$$G_0=G_{\infty }+G_1.$$ (8)

The time constant is

$$\tau =\frac{1}{\beta }=\frac{{\eta }_1}{G_1},$$ (9)

where η₁ is the damper viscosity.

Because the infinite elements in Abaqus do not support viscoelastic material definition, only the elastic parameters (E and ν) are applied in those elements [57]. The probe dimensions and most ARF push parameters are the same as the elastic simulations. The same method was used to apply the ARF excitation as body forces. The same finite element input files and post-processing procedures are used as the elastic simulations, except for the material definition. Please see example syntax for viscoelastic media in the RSNA QIBA GitHub group (Appendix A).

E. Accelerating Model Runtime

Shear wave propagation models are transient in nature, and the most computationally efficient FEM solvers for these problems are explicit in nature. Explicit solvers reduce the forward problem into extremely small time steps (typically on the order of 10⁻¹² − 10⁻⁹ s) where the dynamic equations of state can be used to predict the next time state of the model. This solution time step is dictated by a combination of the element size and the bulk modulus of the material; smaller elements require smaller time steps since a mechanical perturbation can influence an adjacent node sooner, and higher bulk moduli result in faster compressional wave speeds, which are the first waves to also influence adjacent nodes. Overall, smaller, stiffer elements demand the greatest computation overhead, which then scales as a function of the total number of elements in the mesh. In the extreme case where the bulk modulus of the material approaches infinity (a perfectly incompressible material, ν = 0.5), the required numerical time step would approach 0, making the problem intractable. For this reason, explicit finite element solvers demand simulation of a material with a finite bulk modulus.

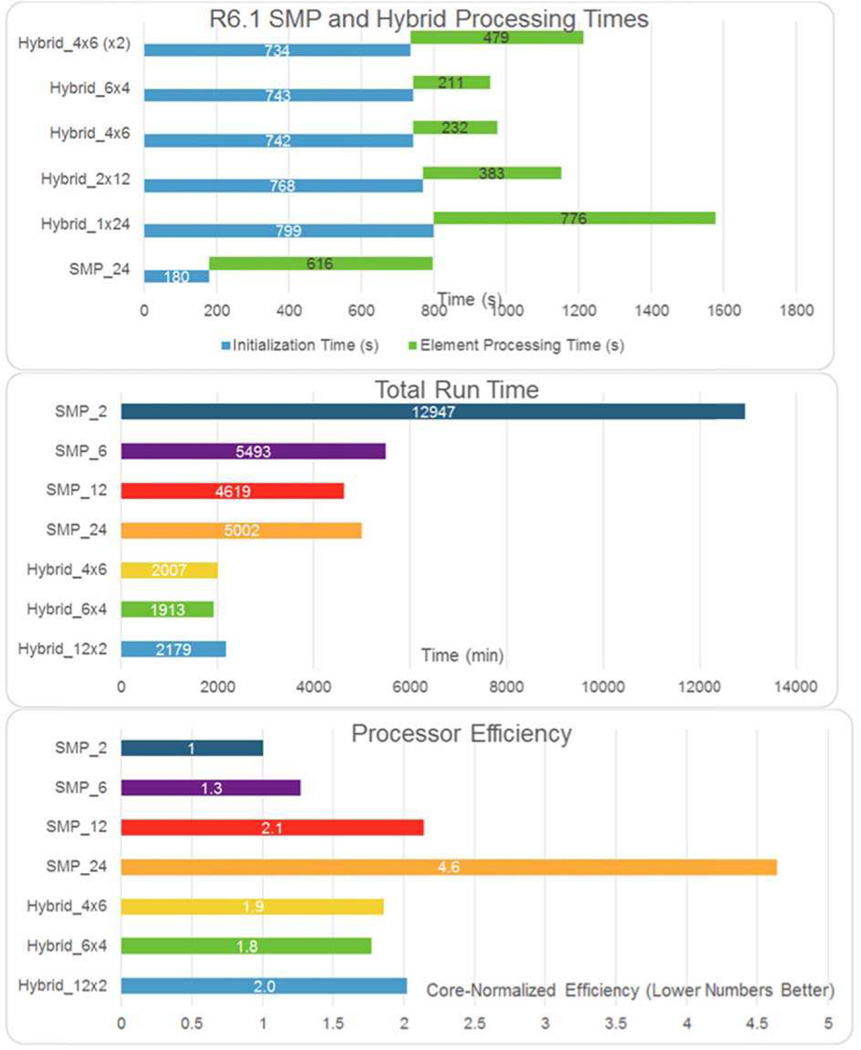
Both Abaqus and LS-DYNA offer explicit solvers with automatic time control to determine the necessary numerical time step for the forward solution based on element size and stiffness. To accelerate model runtime, explicit solutions can be decomposed into parallel solvers that run either through Symmetric Multiprocessing (SMP) or Message Passing Interface (MPI) schemes. The SMP approaches are amenable to multi-core solutions in a single computational node with a shared memory footprint, while an MPI solution can be distributed over multiple computations nodes, but at the expense of each MPI computation thread demanding its own memory footprint. Empirically, models run most efficiently when executed in an SMP environment, though MPI and hybrid SMP/MPI are possible. An example of runtimes associated with these approaches is presented in Fig. 6, with problem setup time (decomposition of the problem into parallel threads) also considered. It should be noted that while the relative performances shown in Fig. 6 are for an arbitrary SWE simulation, these trends can be generalized in that the overhead associated with generating multiple independent computation threads for parallel solution can impose an overall runtime penalty compared to reduced thread-count simulations. Additionally, MPI-based implementations incur a RAM penalty per thread that is not incurred with the SMP solver, which can also be a limited factor. Ultimately, any large-scale parametric finite element analyses should be internally benchmarked for a specific solver, model and hardware infrastructure.

Fig. 6.

A comparison of SMP and Hybrid (SMP/MPI) solver schemes for a single 24-core node, solving an arbitrary shear wave FEM model using LS-DYNA R6.1. The hybrid solution notation is given as the number of MPI threads x SMP threads in each MPI thread (e.g., 4 × 6 refers to 4 MPI threads, with each MPI thread containing a 6 thread SMP job). The top plot demonstrates how the SMP solution has much shorter initialization time compared to the hybrid solutions, while the hybrid solutions can have the shorter model solution time when using the higher degree of MPI parallelization. The middle plot shows a more complete comparison of SMP schemes for a varying number of computation cores, with the bottom plot showing the overall efficiency of core utilization for each solution scheme. Overall, the SMP solutions see diminishing returns for increasing degrees of parallelism, and even an overall computational penalty for too much parallelism (e.g., SMP_12 vs. SMP_24 in the middle and bottom plots). Abaqus data have not been presented, but similar trends are expected.

F. Extracting Raw Finite Element Data for Post-Processing

Large meshes with millions of elements containing many saved time steps of displacement data can create tens-to-hundreds of gigabytes of data to be post-processed, which can demand efficient schemes to handle plot and image generation, especially when generating 3D visualizations of data.

LS-DYNA natively saves a binary d3plot file that has a complex, dynamic header structure that can be difficult to export using non-proprietary tools. An alternative is to save an ASCII nodout file that makes the data accessible via standard text file reading schemes, but at the expense of a much greater transient disk storage need. These data can then be converted to compressed binary data, which can save considerable amounts of space under LZMA compression schemes given the amount of zero-displacement data over the mesh volume, especially at early time steps.

Abaqus simulations produce an ODB file, which is a binary file in a proprietary format. Abaqus provides a scripting interface protocol that allows nodal displacements and velocities to be extracted for saved results at different time steps.

Subsets of these data can then be either directly read into common post-processing environments, such as MATLAB®or Octave, or subsets of data can be saved along common imaging planes by exporting much smaller subsets of data to MATLAB or HDF5 format. The data from the finite element mesh can be interpolated to a finer 2D or 3D grid, and the temporal data can be saved at realistic pulse repetitions frequencies (typically 5–10 kHz) or even higher temporal sampling when demanded for spectral analysis or higher-order material reconstructions.

G. Post-Processing of Motion Data

The calculated motion needs to be processed to measure wave propagation velocities for estimating the material properties of the medium. Depending on the application and the occurrences of wave reflections from inclusions or organ boundaries can confound reconstruction algorithms that assume a wave propagating in a given direction. One preliminary pre-processing step may be to apply a directional filter to obtain waves that are traveling in one direction to make the 1D estimation more robust [39, 61–63]. Additionally, because some finite compressibility in these models due to the Poisson’s ratio being slightly < 0.5, the displacement fields can have some non-negligible dilatational component, Eq. (2), and not be pure shear displacement. This is typically a higher-order confounding factor, though it can influence the spectral analysis of shear waves when considering the lower-energy bands if the Poisson’s ratio is too low and the compressional strains start to approach the same order of magnitude as the shear strains.

The group velocity is the most common parameter that is measured. This involves tracking the energy of the propagating wave. Many one-dimensional (1D) estimators have been proposed in the literature. Typically, these estimators are applied on motion obtained near the focus of the ARF push beam. Some averaging over depth (1–3 mm centered about the nominal push depth) may be used to increase signal-to-noise ratio.

Most of these estimators are based on measuring the time-of-flight of the wave. The time-to-peak (TTP) algorithm finds the temporal peak in the particle displacement at each spatial location and fits a linear model to estimate the velocity of the wave [64]. Alternatively, the time-to-peak slope (TTPS) finds the maximum slope of the particle displacement or the peak of the particle velocity [38]. This method also uses a linear model, and is more robust to shear wave reflections. To improve the robustness or the conventional TTP, the RANSAC algorithm uses statistical methods to determine whether data points are inliers or outliers for a linear model describing the time delays associated with wave propagation measured at different spatial locations [65]. Another method that can be used to estimate the time delays of the wave is cross-correlation. Song, et al., used cross-correlation along with the Andersson-Hegland strategy to improve the robustness of the overall measurement [66]. This method can either be applied in a one-dimensional or two-dimensional manner. All of the estimators can be used for 2D SWV mapping but the choice of kernel size for the estimator needs to be determined. The SWV analysis can also be posed as an image processing problem. Methods based on Radon transform or Radon sum have been described [11, 67–69].

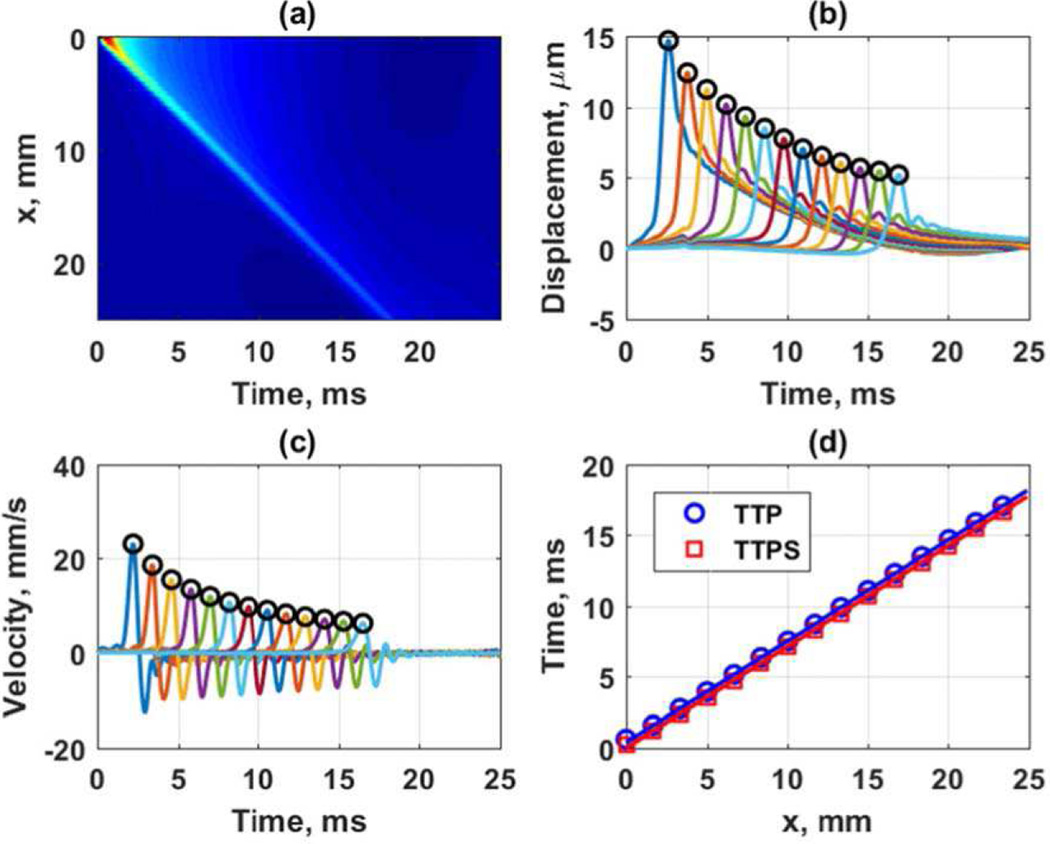
To demonstrate the TTP and TTPS algorithms with simulated data in an elastic medium we show an example. Figure 7 shows the results from a simulation from a curved array with a focal depth of 50 mm, F/N = 2, and an ARF push length of 167 µs (500 cycles at 3.0 MHz) in an elastic medium with shear modulus of 2 kPa performed in Abaqus. The data was originally sampled at 10 kHz and interpolated up to a sampling frequency of 50 kHz using spline interpolation. Figure 7(a) shows the spatiotemporal particle displacement, and Figs. 7(b) and 7(c) show the peaks identified in the TTP and TTPS algorithms (open circles) on the particle displacement and particle velocity, respectively. Figure 7(d) shows the regression of the peak times with distance for speed calculations of 1.40 and 1.40 m/s for the TTP and TTPS algorithms, respectively.

Fig. 7.

Estimation of group velocities with TTP and TTPS. Simulations were from a curved array with a focal depth of 50 mm, F/N = 2, and an ARF push length of 167 µs in an elastic medium with shear modulus of 2 kPa performed in Abaqus. (a) Spatiotemporal particle displacement, (b) TTP applied to particle displacement data separated by 1.5 mm with the open circles representing the detected peaks, (c) TTPS applied to particle velocity data separated by 1.5 mm with the open circles representing detected peaks, (d) regression of peak times with respect to distance for group velocity estimation.

To measure the phase velocity, there are two primary methods that have been used in the field, phase gradient, and the 2D Fourier transform (FT) [3, 70]. For a harmonic shear wave of frequency, f_υ, the phase of the wave can be measured at a minimum of two spatial locations separated by some distance Δr, and the phase difference, Δϕ, is used to calculate the wave speed at that frequency using [3]

$$c_s(f_{\nu })=\frac{2\pi f_{\nu }\mathrm{\Delta }r}{\mathrm{\Delta }\varphi }.$$ (10)

To improve robustness several locations can be used and a linear regression can be used to find the term Δr/Δϕ [32, 34].

An alternative method is to perform a 2D Fourier transform using the fast Fourier transform (FFT) on the spatiotemporal motion data, typically the particle velocity [70, 71]. The resulting Fourier distribution, or k-space, has one temporal frequency (f) axis and one spatial frequency (k) axis. For the harmonic wave case, a peak will occur at f_υ, and the coordinates where the peak occurs can be used to determine the phase velocity using c_s = f_p/k_p. For an impulsive wave that has multiple frequencies, the k-space will have a distribution that is spread across a frequency range. There are several ways to search for the peaks, but an intuitive one is to find the peak or peaks in the k-direction at a given temporal frequency and repeat for all the temporal frequencies of interest. The phase velocity curve from the phase gradient or 2D FT methods can be compared against the theoretical values to evaluate the error in the estimation.

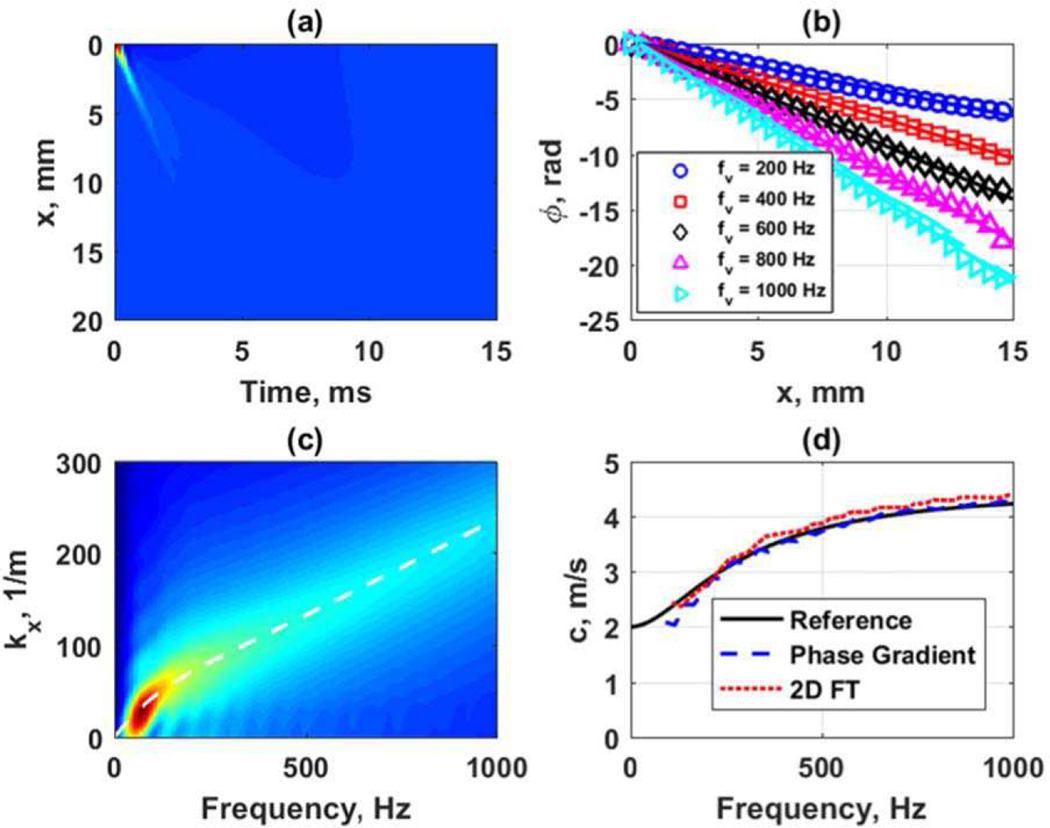
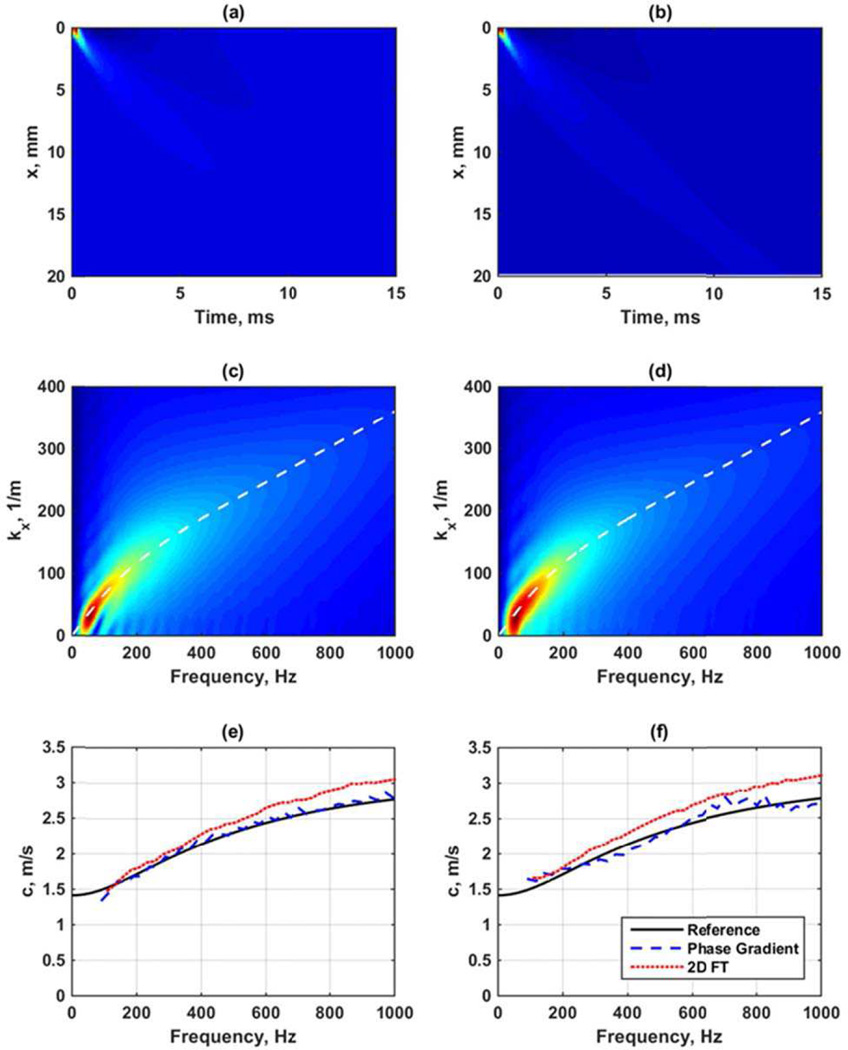
Figure 8 shows an example from a simulation in a viscoelastic medium modeled as a generalized Maxwell model with G₀ = 20 kPa, G_∞ = 4 kPa, β = 4000 s⁻¹ in LS-DYNA. The transducer simulated was a curved array with focal depth of 50 mm, F/N = 2 and an ARF push length of 167 µs. Figure 8(a) shows the spatiotemporal particle velocity. Figure 8(b) shows the phase gradient analysis at frequencies of 200, 400, 600, 800, and 1000 Hz. Figure 8(c) shows the k-space after the 2D FT and the white line is the reference curve for the velocity dispersion associated with the prescribed medium using the parameters noted above input into the generalized Maxwell model [29]. Figure 8(d) shows the phase velocity dispersion results from the phase gradient and k-space analysis compared to the reference values. The phase gradient method provides a closer match to the reference curve for this viscoelastic material. The k-space result is dependent on how the k-space is searched for peaks and windowing effects when performing the 2D FT. It is worth noting that all the motion data in Fig. 8(a) is used for generating the k-space in Fig. 8(c). It has been found by our groups that windowing or truncating the data either in time or space can affect the k-space and the resulting dispersion curves. In the examples throughout this manuscript the full spatial and temporal domains have been used for these calculations and as a result shown in their totality in subsequent figures.

Fig. 8.

Frequency domain analysis of data from viscoelastic medium with G₀ = 20 kPa, G_∞ = 4 kPa, β = 4000 s⁻¹ in LS-DYNA. The transducer simulated was a curved array with focal depth of 50 mm, F/N = 2 and an ARF push length of 167 µs. (a) Spatiotemporal particle velocity, (b) phase gradient data for 200, 400, 600, 800, and 1000 Hz, (c) k-space from 2D FT with white line depicting the phase velocity dispersion associated with the medium specifications, (d) phase velocity dispersion results for phase gradient and k-space analysis compared to the reference.

Additionally, the motion that is extracted for the analysis has laterally traveling waves from the focal position, but waves from the pre-focal and post-focal areas may cause some bias. Shear waves can be excited above (pre-focal) and below (post-focal) the focus. The ARF beam shape is typically shaped like an hourglass where the narrowest part of the hourglass is the focal region. The pre-focal and post-focal areas have an angled orientation that can give rise to shear waves traveling at an angle and not entirely laterally. As a result they may interact within the region lateral to the focal region and affect the wave motion. The algorithms employed to calculate the propagation velocities may be biased by these extra waves.

H. Digital Phantom Experiments

To demonstrate the uses of the simulation platform to create and evaluate digital phantoms we performed a comparison study with the results from elastic and viscoelastic simulations in LS-DYNA and Abaqus. The dimensions of the domain are x = ±25 mm in the azimuthal dimension, y = ±10 mm in the elevation direction, and z = 0–100 mm in the axial dimension. The mesh size is 0.167 mm in each direction. The mesh size is the same for all simulations in both LS-DYNA and Abaqus. The simulations were performed with quarter-symmetry so only the domain described by x = 0–25 mm, y = 0–10 mm, and z = 0–100 mm was evaluated. For the elastic phantoms, we used combinations of the parameters in Table I to generate four different focal configurations for each focal depth of 30, 50, and 70 mm and two values of F/N = 2.0, 3.5. We also varied the push duration to 167 and 334 µs (500 and 1000 cycles at 3.0 MHz, respectively). For elastic media, the Young’s moduli used were 3, 6, 15, and 30 kPa. The temporal sampling frequency was set to 10 kHz and the spatial mesh had a resolution of 0.167 mm in all directions. When comparing the results from the elastic models, motion profiles were compared. In addition, we calculated the group velocity with a TTP estimator and evaluated the percent difference from the value used in the model.

We also made comparisons with the viscoelastic digital phantom data. We compared the results from LS-DYNA and Abaqus for models with G₀ = 10 kPa, G_∞ = 2 kPa, β = 6667 s⁻¹ (Medium 1). The ARF configuration used a focal depth of 50 mm, F/N = 2 and push length of 167 µs. With this base model, we also evaluated changes made when increasing the F/N to 3.5, increasing the push length to 334 µs, and focusing the beam at 30 and 70 mm. We also changed the viscoelastic media with G₀ = 15 kPa, G_∞ = 4 kPa, β = 5500 s⁻¹ (Medium 2) and G₀ = 20 kPa, G_∞ = 4 kPa, β = 4000 s⁻¹ (Medium 3). The phase velocity curves were calculated with the phase gradient method in these cases.

III. Results

A. Comparison of LS-DYNA and Abaqus in an Elastic Medium

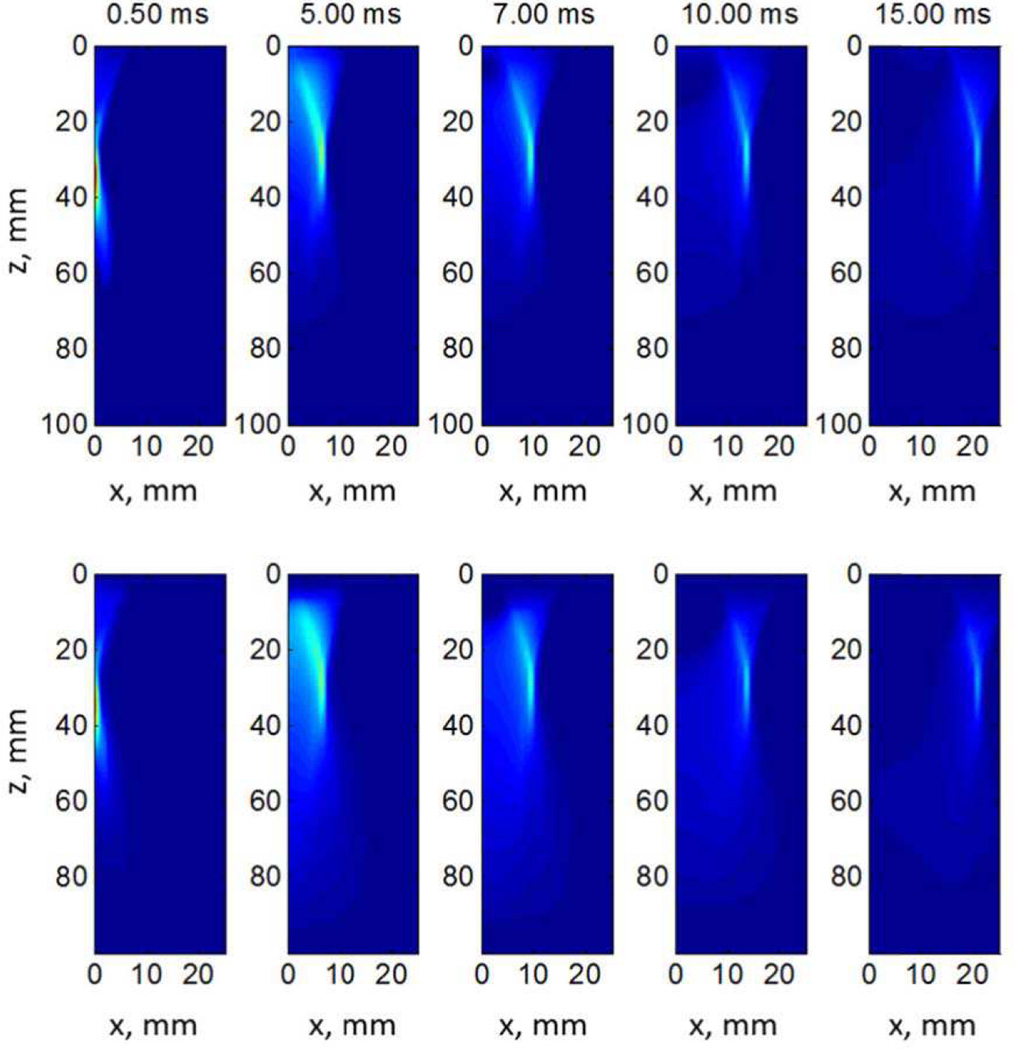
To demonstrate the utility of the simulation platform we demonstrate some qualitative and quantitative comparisons between LS DYNA and Abaqus in elastic media. Figure 9 shows a representative comparison between LS DYNA (top row) and Abaqus (bottom row) results. The material’s shear modulus is 2 kPa, ARF is focused at z = 30 mm, F/N is 2.0 and push duration is 167 µs. It shows the shear wave propagation at 0.5, 5, 7, 10 and 15 ms from the ARF push. We can see that the results from the two simulation platforms qualitatively compare well with each other.

Fig. 9.

Shear wave propagation of LS-DYNA (top row) and Abaqus (bottom row) at different time points in a quarter-symmetry mesh of an elastic µ = 2 kPa material. The color scale represents normalized displacement across each respective dataset. The isocontours of color in the 0.50 ms frames closely represent the half-plane of the acoustic radiation force excitation distribution use for the 30 mm focus in the digital phantoms accessible on the QIDW (Appendix A). Notice that the apparent skew in the shear wave displacement profile with propagation through time is expected as the recovery time from such an excitation is considerably slower than the initial time to achieve peak displacement (Figure 3, right middle row plot).

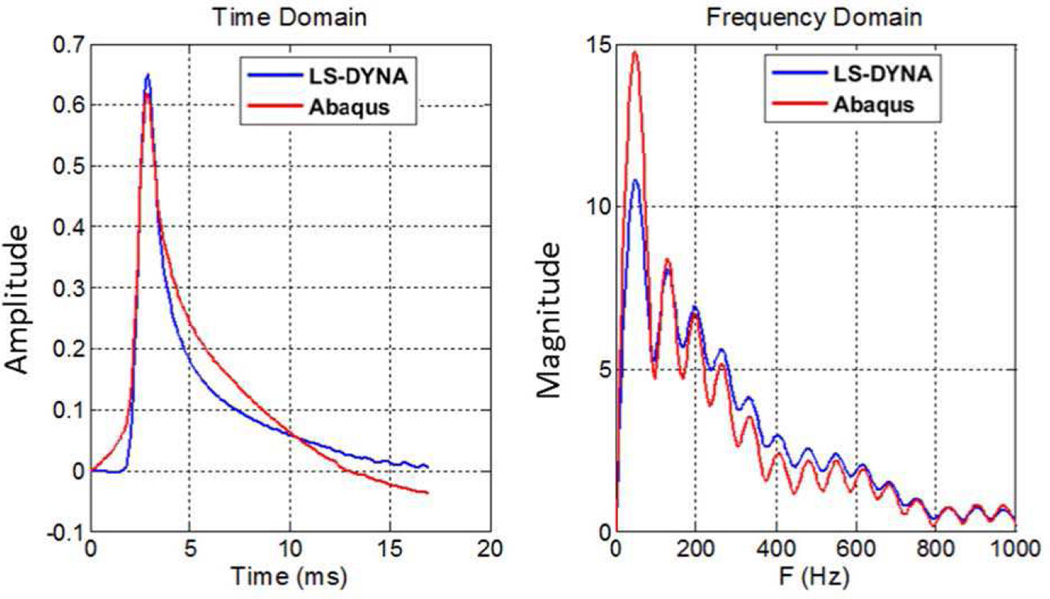
Figure 10 shows the normalized particle displacement at x = 10 mm along the focus depth (z = 30 mm). The shapes in the time-domain are somewhat different as the Abaqus response has a longer tail but the peaks are well-aligned from both software packages. Additionally, all the frequency-domain peaks are likewise in similar positions, but the magnitudes are slightly different.

Fig. 10.

Normalized particle displacement in both time- and frequency-domains at x = 10 mm. It should be noted that the strong ringing seen in the frequency domain plot (right) is primarily due to the effect of taking the Fourier transform of a finite temporal window of data that is only 17 ms long. While applying a Hann or Gaussian window to the temporal data, as is commonly done in a short-time Fourier transform, could reduce this ringing, such windows would also skew the time domain displacement profiles [55].

For a quantitative comparison, we conducted a parametric study in different elastic media and estimated the group velocity for comparison with reference values. Tables III–V provide values of group velocities estimated from simulations with LS-DYNA and Abaqus for the different parameter configurations outlined in Table II with mesh resolutions of 0.167 mm. These data are available at the QIDW website noted in Appendix A. The group velocities were estimated using a TTP estimator on the displacement data. The largest overall errors for LS-DYNA at 30, 50, and 70 mm focal depths were 1.130, −0.658, and 0.684%, respectively. The largest overall errors for Abaqus at 30, 50, and 70 mm focal depths were 0.978, −0.883, and 0.712%, respectively. In general the errors, albeit small increased with the material stiffness with a focal depth of 30 mm. There was generally not an appreciable difference when different F/Ns or push lengths were used. There was no consistent pattern in which the error was higher in LS-DYNA compared to Abaqus.

TABLE III.

Evaluation of group velocities obtained in elastic media with LS-DYNA and Abaqus with a focal depth of 30 mm.

E, kPa	F/N	T, µs	Reference cg, m/s	LS- DYNA cg, m/s	LS- DYNA Error, %	Abaqus cg, m/s	Abaqus Error, %
3	2.0	167	1.000	1.000	0.009	0.997	−0.349
3	2.0	334	1.000	1.000	−0.021	0.997	−0.291
6	2.0	167	1.414	1.417	0.182	1.412	−0.129
6	2.0	334	1.414	1.417	0.220	1.413	−0.112
15	2.0	167	2.236	2.242	0.272	2.237	0.049
15	2.0	334	2.236	2.247	0.504	2.234	−0.071
30	2.0	167	3.162	3.186	0.734	3.174	0.377
30	2.0	334	3.162	3.195	1.022	3.181	0.597
3	3.5	167	1.000	1.004	0.441	1.002	0.171
3	3.5	334	1.000	1.005	0.519	1.003	0.313
6	3.5	167	1.414	1.422	0.529	1.420	0.377
6	3.5	334	1.414	1.423	0.595	1.420	0.417
15	3.5	167	2.236	2.250	0.614	2.248	0.544
15	3.5	334	2.236	2.250	0.641	2.245	0.399
30	3.5	167	3.162	3.189	0.854	3.185	0.729
30	3.5	334	3.162	3.198	1.130	3.193	0.978

TABLE V.

Evaluation of group velocities obtained in elastic media with LS-DYNA and Abaqus with a focal depth of 70 mm

E, kPa	F/N	T, µs	Reference cg, m/s	LS- DYNA cg, m/s	LS- DYNA Error, %	Abaqus cg, m/s	Abaqus Error, %
3	2.0	167	1.000	0.997	−0.266	0.995	−0.512
3	2.0	334	1.000	0.998	−0.223	0.995	−0.507
6	2.0	167	1.414	1.411	−0.220	1.409	−0.385
6	2.0	334	1.414	1.412	−0.156	1.409	−0.393
15	2.0	167	2.236	2.234	−0.099	2.229	−0.304
15	2.0	334	2.236	2.237	0.036	2.228	−0.351
30	2.0	167	3.162	3.165	0.092	3.154	−0.256
30	2.0	334	3.162	3.174	0.364	3.160	−0.064
3	3.5	167	1.000	1.003	0.296	1.003	0.341
3	3.5	334	1.000	1.003	0.331	1.003	0.334
6	3.5	167	1.414	1.419	0.315	1.420	0.394
6	3.5	334	1.414	1.420	0.424	1.420	0.392
15	3.5	167	2.236	2.246	0.444	2.245	0.388
15	3.5	334	2.236	2.244	0.370	2.247	0.484
30	3.5	167	3.162	3.179	0.544	3.185	0.712
30	3.5	334	3.162	3.184	0.684	3.184	0.681

B. Viscoelastic Simulation Results

In addition to evaluating elastic media, we also performed simulations in viscoelastic media and compared the measured phase velocities with reference curves. A comparison of the LS-DYNA and Abaqus results for a viscoelastic medium are shown in Fig. 11 with G₀ = 10 kPa, G_∞ = 2 kPa, β = 6667 s⁻¹. The ARF configuration used a focal depth of 50 mm, F/N = 2 and push length of 167 µs. The spatiotemporal data (Figs. 11(a)–(b)) and the k-spaces (Figs. 11(c)–(d)) are very similar as are the estimated phase velocities which are close to the reference (Figs. 11(e)–(f)).

Fig. 11.

Comparison of viscoelastic data from LS-DYNA and Abaqus results. (a) Spatiotemporal data from LS-DYNA, (b) spatiotemporal data from Abaqus, (c) k-space from LS-DYNA with dashed line as reference for material, (d) k-space from Abaqus with dashed line as reference for material, (e) phase velocities from LS-DYNA results, (f) phase velocities from Abaqus results. The legend in (f) applies to (e) and (f).

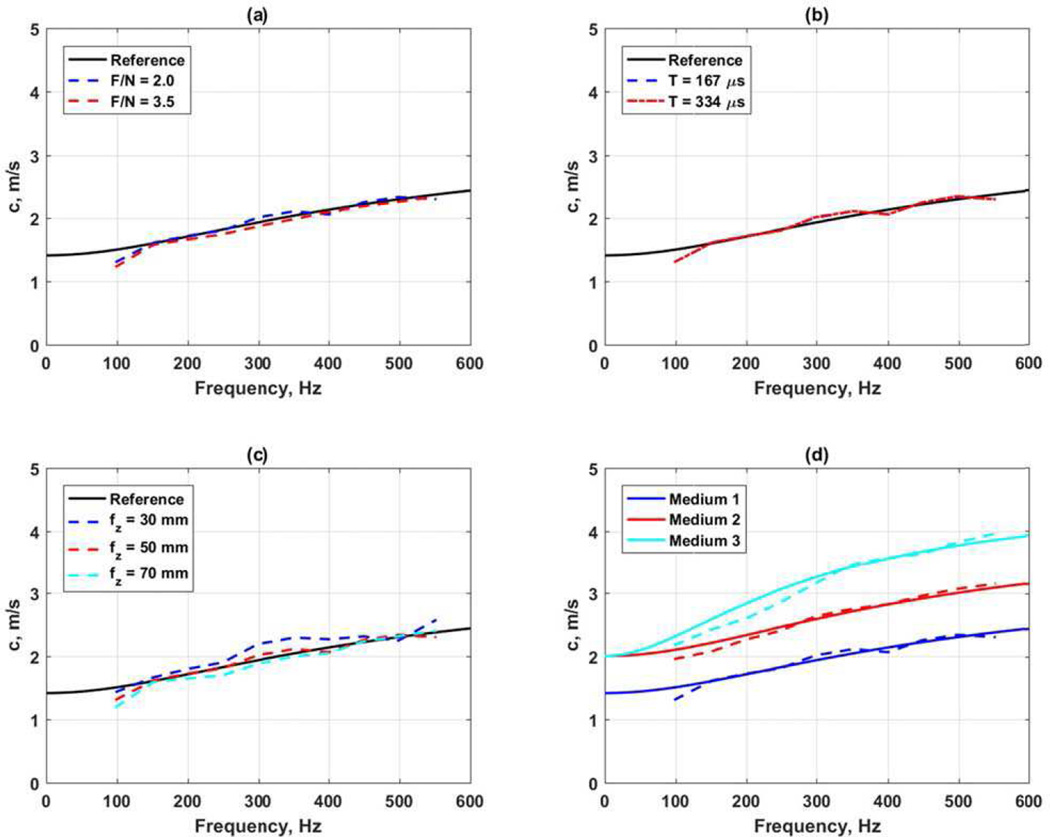
Figure 12 shows the results of several different comparisons from the LS-DYNA data sets. In all cases reference curves calculated from the viscoelastic parameters are plotted as solid lines [29]. For panels 12(a)–(c) G₀ = 10 kPa, G_∞ = 2 kPa, β = 6667 s⁻¹. The ARF configuration used a focal depth of 50 mm, F/N = 2 and push length of 167 µs unless otherwise noted. Figure 12(a) compares the differences between F/N = 2.0 and 3.5. There is very little difference in this case. Figure 12(b) shows the results using a push length of 167 and 334 µs. The results in this case appear almost identical. Figure 12(c) shows the variation with focal depth. The 30 mm focal depth results show the most deviation from the reference curve. This may be due the elevation focus of the transducer is near 50 mm. Figure 12(d) shows results from three different media where Medium 1: G₀ = 10 kPa, G^∞ = 2 kPa, β = 6667 s⁻¹, G₀ = 15 kPa, G_∞ = 4 kPa, β = 5500 s⁻¹, and Medium 3: G₀ = 20 kPa, G_∞ = 4 kPa, β = 4000 s⁻¹. The phase velocity curve for Medium 3 showed the most deviation from its reference curve.

Fig. 12.

Evaluation of viscoelastic phase velocity curves. (a) Comparison of F/N, (b) comparison of length of ARF push, (c) comparison of focal depth, (d) comparison of different viscoelastic materials. In all panels the solid lines are the reference curves calculated based on the viscoelastic model parameters.

IV. Discussion

Using numerical simulations for understanding the shear wave propagation in SWE imaging phantoms and soft tissues can be very valuable. Comparisons with data from experiments in phantoms or tissue can serve as a validation of the numerical methods to evaluate their realism [64, 72]. These simulations can also be used as a validation tool for researchers and device manufacturers to ensure that algorithms used in post-processing schemes come up with the same answer as the theoretical value.

The QIBA SWS committee is using this platform as a validation tool to examine differences between different commercial ultrasound scanners for standardizing the measurement of shear wave velocity in liver for fibrosis staging. A repository of digital phantoms with a variety of acoustic radiation force focal configurations applied to both elastic and viscoelastic media have been generated to provide researchers in academia and industry with ground truth datasets to evaluate the impact of acoustic radiation force focal geometries on shear wave speed reconstructions and to validate reconstruction algorithms in datasets with known material properties. These digital phantoms are available for public download at the RSNA Quantitative Imaging Data Warehouse (Appendix A). Experimental phantom and clinical scanning tests are also important but typically a reference value for comparison is not available or measurable, so this simulation platform fills that void. Ultimately, a combination of simulation, experimental and clinical data will be used to generate a QIBA profile recommending proper technical quality assurance protocols and clinical scanning protocols to reduce variability between different commercial SWE implementations. The latest QIBA activity and profile information can be found on the RSNA QIBA US SWS wiki (Appendix A).

These simulations can also provide a resource for changing the material properties, beam shapes, or other parameters that may be tedious or difficult to change experimentally. We demonstrated that different software packages, LS-DYNA and Abaqus, can provide similar results in elastic and viscoelastic media. Figs. 9 and 10 demonstrate qualitative similarities between the waves numerically calculated using the two packages. We evaluate the group velocity using the TTP estimator for several elastic moduli and focal configurations and found maximum errors of 1.130% and 0.978 for LS-DYNA and Abaqus, respectively. We also simulated shear wave propagation in viscoelastic media and showed good agreement from the measured phase velocity and the reference values. Data resulting from these simulations can also have noise added to evaluate different processing methods. This type of tool has important value for both academic and industrial researchers.

In this paper we have neglected the effects that ultrasound-based motion tracking may have on the estimation process. With the motion of the nodes, they could be translated to moving individual scatterers in the simulation domain [42]. Then, using Field II or FOCUS, images could be made at different time points using different beamforming approaches both on transmit and receive. The received RF or IQ data could then be used in conjunction with a myriad of motion estimation algorithms that may include autocorrelation [73, 74], normalized cross-correlation [75] or other similar methods.

From a FEM point-of-view, there are a few parameters that need to be considered when performing these simulations. The user must have a good understanding of the numerical methods being used in each FEM package or solver that is employed. We have detailed some of those for LS-DYNA and Abaqus, but other packages may have similar nuances that could affect the results. The mesh refinement is important for obtaining stable results, but also for achieving practical simulation times. An ultra-fine mesh may not be warranted and may be expensive computationally. The ideal mesh has uniform nodal spacing dense enough to adequately spatially sample the highest spatial frequencies of the excitation source (e.g., the narrowest region of the focused acoustic radiation force excitation). The sampling rate is another similar issue. Realistic sampling times need to be considered in relation to the expected frame rates that will be achieved experimentally. Stiffer materials may require higher frame rates to make accurate measurements. The incompressibility condition handled through the Poisson’s ratio should also be given special attention. Values for Poisson’s ratio have typically been set in the range of 0.49–0.499 [51, 56, 57]. The compressional waves need to be in a range of speeds where they will not adversely affect the shear wave velocity estimation, which for liver is in the range of 1–4 m/s so if the compressional waves are 1–2 orders of magnitude higher that is typically sufficient.

As mentioned above, one limitation is the requirement of some background in FEM, but the resources available in the Appendix are aimed at mitigating this requirement to get a user started without enduring a steep learning curve. Additionally, computational resources and commercial software packages available may vary by institution for conducting simulations of large-scale problems or parametric studies.

Using the presented standardized ARF-induced shear wave simulation platform, various aspects related to variations due to biological and disease dependent factors that influence the liver’s material properties could be investigated. While we have presented material models that are isotropic and homogeneously viscoelastic, these simulations can be further extended to capture other degrees of freedom in the biological characteristics of the tissue, including ultrasound attenuation, sound speed variation in different tissue layers that cause phase aberration, and differences in material properties related to specific diseases. Additionally, these models can be even further extended to address confounding factors associated with shear wave imaging structures that create shear wave reflections, along with more complex material models that include anisotropy and layered media [38, 40, 41]. More complicated structures require non-uniform meshes to be implemented to accommodate the shape and heterogeneous material properties of these structures.

V. Conclusions

We have presented an overview of a FEM-based approach to simulate shear wave propagation in an elastic and viscoelastic medium with ARF excitation. We compared and contrasted the implementations in two commercially available FEM packages, LS DYNA and Abaqus and have discussed nuances of each package. We have given an overview of the post-processing steps for estimating shear wave velocity both from time-of-flight methods and k-space methods. This simulation platform is a powerful tool for developing and testing algorithms for academic and industrial researchers involved in making quantitative shear wave-based measurements of tissue material properties.

TABLE IV.

Evaluation of group velocities obtained in elastic media with LS-DYNA and Abaqus with a focal depth of 50 mm

E, kPa	F/N	T, µs	Reference cg, m/s	LS- DYNA cg, m/s	LS- DYNA Error, %	Abaqus cg, m/s	Abaqus Error, %
3	2.0	167	1.000	0.993	−0.658	0.991	−0.883
3	2.0	334	1.000	0.994	−0.638	0.991	−0.872
6	2.0	167	1.414	1.406	−0.607	1.403	−0.818
6	2.0	334	1.414	1.406	−0.565	1.403	−0.776
15	2.0	167	2.236	2.226	−0.472	2.217	−0.844
15	2.0	334	2.236	2.229	−0.295	2.220	−0.724
30	2.0	167	3.162	3.146	−0.504	3.143	−0.620
30	2.0	334	3.162	3.162	−0.024	3.146	−0.502
3	3.5	167	1.000	0.995	−0.516	0.994	−0.499
3	3.5	334	1.000	0.995	−0.504	0.995	−0.478
6	3.5	167	1.414	1.407	−0.535	1.407	−0.517
6	3.5	334	1.414	1.406	−0.564	1.408	−0.473
15	3.5	167	2.236	2.224	−0.521	2.225	−0.491
15	3.5	334	2.236	2.224	−0.555	2.228	−0.383
30	3.5	167	3.162	3.146	−0.504	3.155	−0.216
30	3.5	334	3.162	3.150	−0.379	3.158	−0.133

Biographies

Mark L. Palmeri received his B.S. degree in Biomedical and Electrical Engineering from Duke University, Durham, NC, in 2000. He was a James B. Duke graduate fellow and received his Ph.D. degree in Biomedical Engineering from Duke University in 2005 and his M.D. degree from the Duke University School of Medicine in 2007. He is currently an Associate Professor of the Practice in Biomedical Engineering and Anesthesiology at Duke University. He is an Associate Editor for Ultrasound in Medicine and Biology and IEEE Transactions in Medical Imaging. He serves as a sub-committee co-chair for the RSNA Quantitative Imaging Biomarker Alliance (QIBA) ultrasound shear wave speed imaging committee. His research interests include acoustic radiation force, shear wave elasticity imaging, finite element analysis, medical image and signal processing, and medical device design.

Bo Qiang (IEEE/S’02, M ’12) is currently a data solution developer working for The Nielsen Company in Oldsmar, Florida. He is responsible for developing algorithms and software applications for media data analytics and visualization. Before joining Nielsen in April 2016, he worked for Mayo Clinic, Rochester MN, as a lead engineer. His projects involved developing better solutions for medical technologies such as ECG analysis and ultrasound imaging. Before joining Mayo in 2008, he worked for ASL Analytical in Oakdale IA and developed infrared spectrometers for biomedical applications. He holds a bachelor’s and a master’s degree, both in electrical engineering.

Shigao Chen (IEEE/M’02) received the B.S. and M.S. degrees in biomedical engineering from Tsinghua University, China, in 1995 and 1997, respectively, and the Ph.D. degree in biomedical imaging from the Mayo Graduate School, Rochester, MN, in 2002. He is currently an Associate Professor of the Mayo Clinic College of Medicine and Science. His research interest is noninvasive quantification of the viscoelastic properties of soft tissue using ultrasound.

Matthew W. Urban (IEEE/S’02, M ’07, SM ‘14) was born in Sioux Falls, SD on February 25, 1980. He received the B.S. degree in electrical engineering at South Dakota State University, Brookings, SD in 2002 and the Ph.D. in biomedical engineering at the Mayo Clinic College of Medicine in Rochester, MN in 2007. He is currently an Associate Professor in the Department of Radiology, Mayo Clinic College of Medicine and Science and Associate Consultant in the Department of Radiology, Mayo Clinic Rochester. His current research interests are shear wave-based elasticity measurement and imaging applications, applications of acoustic radiation force, vibro-acoustography, and ultrasonic signal and image processing. Dr. Urban is a member of Eta Kappa Nu, Tau Beta Pi, the American Institute of Ultrasound in Medicine, IEEE, and the Acoustical Society of America.

Appendix A: Online Resources

• RSNA QIBA US SWS Working Group Wiki: http://qibawiki.rsna.org/index.php/Ultrasound_SWS_Biomarker_Ctte

• RSNA QIBA GitHub Group: https://github.com/orgs/RSNA-QIBA-US-SWS/(http://doi.org/10.5281/zenodo.163866) This repository contains the code used to generating the digital phantoms in the QIDW-hosted database below, along with example templates for running elastic and viscoelastic models in Abaqus and LS-DYNA.

• Finite Element Modeling (FEM) Code: Python Tools, Field II Intensity Field Solution, LS-DYNA Pre/Post Processing: https://githublab.oit.duke.educom/mlp6/fem (http://doi.org/10.5281/zenodo.163864)

• RSNA Quantitative Imaging Data Warehouse (US-SWS-Digital-Phantoms): http://qidw.rsna.org/