Automatic detection of rapid eye movements (REMs): A machine learning approach

Abstract

Background

Rapid eye movements (REMs) are a defining feature of REM sleep. The number of discrete REMs over time, or REM density, has been investigated as a marker of clinical psychopathology and memory consolidation. However, human detection of REMs is a time-consuming and subjective process. Therefore, reliable, automated REM detection software is a valuable research tool.

New method

We developed an automatic REM detection algorithm combining a novel set of extracted features and the ‘AdaBoost’ classification algorithm to detect the presence of REMs in Electrooculogram data collected from the right and left outer canthi (ROC/LOC). Algorithm performance measures of Recall (percentage of REMs detected) and Precision (percentage of REMs detected that are true REMs) were calculated and compared to the gold standard of human detection by three expert sleep scorers. REM detection by four non-experts were also investigated and compared to expert raters and the algorithm.

Results

The algorithm performance (78.1% Recall, 82.6% Precision) surpassed that of the average (expert & non-expert) single human detection performance (76% Recall, 83% Precision). Agreement between non-experts (Cronbach Alpha = 0.65) is markedly lower than experts (Cronbach Alpha = 0.80).

Comparison with existing method(s)

By following reported methods, we implemented all previously published LOC and ROC based detection algorithms on our dataset. Our algorithm performance exceeded all others.

Conclusions

The automatic detection algorithm presented is a viable and efficient method of REM detection as it reliably matches the performance of human scorers and outperforms all other known LOC- and ROC-based detection algorithms.

1. Introduction

As first described by Aserinsky and Kleitman in 1953, Rapid Eye Movement (REM) Sleep is characterized by low muscle tone and rapid horizontal simultaneous movements of the eyes. REM sleep has been related to a range of biological and cognitive functions, including brain maturation (Marks et al., 1995), muscular efficiency (Cai, 2015), non-declarative memory consolidation (Stickgold, 2005; Mednick et al., 2003), rescuing memory from interference (McDevitt et al., 2015) and implicit cueing in a creativity task (Cai et al., 2009) among others. Yet despite over half a century of research, the specific cause and function of its defining feature, the rapid eye movements (REMs), is not understood. Ladd (1892) suggested that REMs represent saccadic shifts to visual elements of dreams. Consistent with this hypothesis, subjects woken from REM sleep, compared with other sleep stages, more frequently report vivid dreams (Hobson, 2009), and the same cortical areas involved in REMs are involved in waking eye movements (Hong et al., 1995; Hong et al., 2009). These findings suggest that similar neural activity occurs during REM sleep and waking. Furthermore, studies of lucid dreaming, in which a dreamer is purportedly cognizant and able to control the dream state, have shown deliberate eye movements in dreams that appear similar to waking REMs (LaBerge et al., 1981; LaBerge, 1990). However, it is unknown whether all REMs are caused by eye movements within dreams, or if this is an artifact of the atypical lucid dream state. Studies have also shown that clinical psychopathologies can be differentiated based on this sleep feature, with altered REMs patterns during sleep being related to depression (Gillin et al., 1981; Lahmeyer et al., 1983; Mellman et al., 1997), narcolepsy (Vanková et al., 2001), obsessive compulsive disorder (Insel et al., 1982), post-traumatic stress disorder (Ross et al., 1994; Mellman et al., 1997, 2002) and chronic sleep deprivation (Feinberg et al., 1987). Increased REM presence (measured as REM density, the number of REMs per minute of REM sleep) have been also associated with enhanced procedural (Fogel et al., 2007) and declarative (Schredl et al., 2001) memory and may be a marker of memory consolidation (Smith and Lapp, 1991).

Given that the average human spends approximately 5–6% of her life in REM sleep, it is surprising how little investigation has been done on this psychophysiological event. This is due, in part, to the difficulty, and time consuming task of manually counting REMs. Development of a computational algorithm to automatically detect these ocular events would provide a solution to this problem, and open a pathway to aid in the discovery of the nature and function of REMs. Here, we provide an automated approach to REM detection utilizing a learning algorithm designed to detect REMs from the Left Ocular Canthi (LOC) and Right Ocular Canthi (ROC) channels of EEG data. We compared our novel algorithm to several prior published algorithms (Minard and Krausman, 1971; McPartland et al., 1973; Ktonas and Smith, 1978; Hatzilabrou et al., 1994; Doman et al., 1995; Agarwal et al., 2005) and to expert and non-expert human scorers. Each algorithm detects a slightly different subset of REM, therefore we combine detections from each implemented detector to improve reliability and performance. Our best performing single algorithm integrates a novel set of features (Dynamic Time Warping and similarity features) and the powerful ‘AdaBoost’ classification algorithm to detect the presence of REMs.

For development and comparison of future algorithms, the MATLAB code from this investigation (both our detectors and our implementations of others) is available online through The Open Science Framework (https://osf.io/fd837/).

2. Materials and methods

2.1. Data Set

2.1.1. Participants

The data set consisted of 5 (3 Female) subjects polysomnography data (Astro-Med Grass Heritage model 15 amplifiers [Natus Neurology Incorporated, West Warwick, RI, USA]) taken from the control condition of a previous nap study (Mednick et al., 2013). Subjects gave informed consent and study protocol was reviewed by University Of California, San Diego Institutional Review Board. Participants were healthy (BMI = 23 ± 2.4 kg/m²), non-smokers aged 18 to 35 (22 ± 3 years) with no personal history of neurological, psychological, or other chronic illness and were normal sleepers, habitually obtaining approximately 8 h of sleep each night. Informed consent and original study was.

2.1.2. Sleep analysis

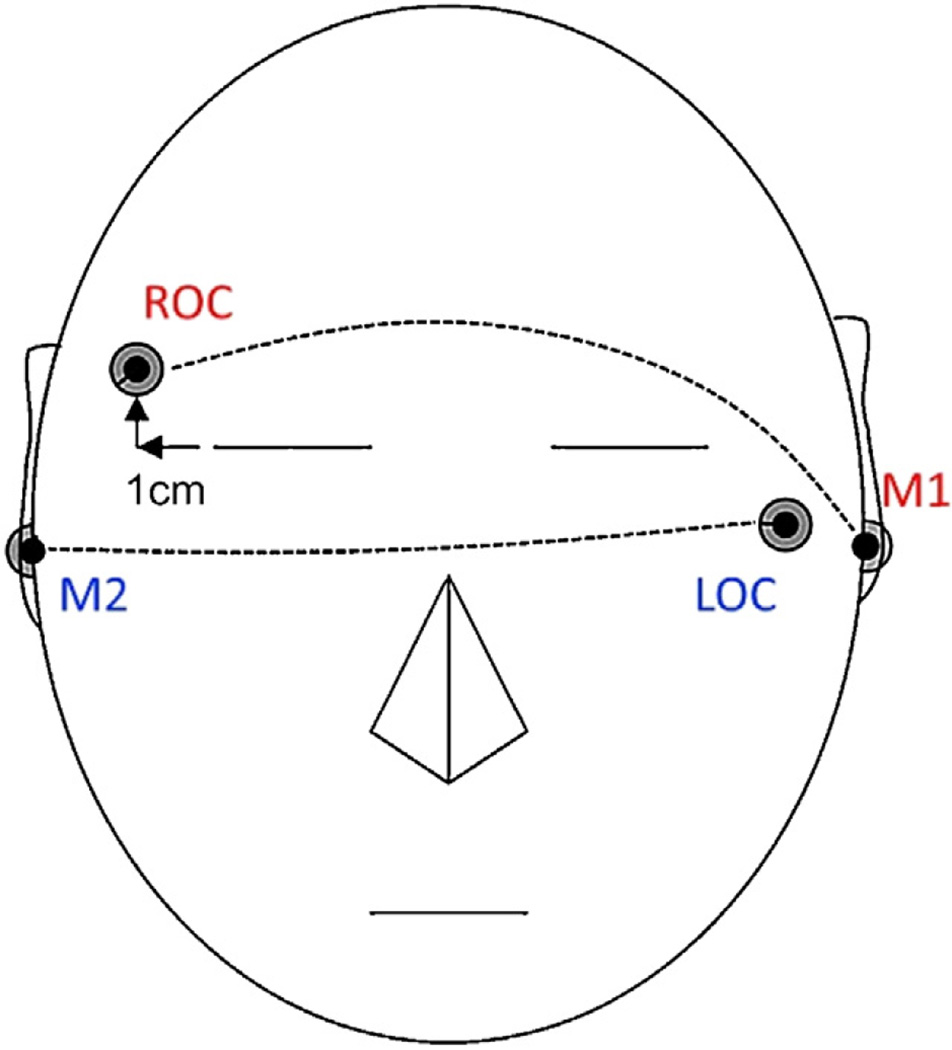
AASM (2007) guidelines recommend two channels of EOG, “recording from an electrode placed 1 cm above or below the outer canthus of the eye” (LOC and ROC). See Fig. 1 for approximate placements. Although the placement of these channels does not allow for the ability to detect differences between vertical and horizontal eye movements (Padovan and Pansini, 1972; Värri et al., 1996), they continue to remain the gold standard eye channels used in sleep labs. The goal of our algorithm is to generalize to the majority of sleep labs, hence LOC and ROC are used.

Fig. 1.

Left and Right Outer Canthi EEG placement, each eye channel referenced to opposite ear (LOC-M1/ROC-M2).

2.1.3. REMs scoring

Expert sleep scorers identified 110 min of REM stage sleep and this was used to train and test the algorithm. REM peaks in each subject’s PSG data were independently identified by an expert group (3 expert sleep scorers, each with 2 or more years of experience) and a non-expert group, (4 non-expert sleep scorers, familiar with PSG, and having undergone basic in lab training on identifying REMs) by marking REM movement peaks. Raters adhered to the AASM (2007) REM definition of ‘conjugate, irregular, sharply peaked eye movements with an initial deflection usually lasting less than 500 ms’. Horizontal lines at ± 37.5 µV (as suggested by Werth et al., 1996) were used as visual aids to alert raters to the possible presence of REM, although the EOG signal did not have to cross these lines to be considered as a REM. Slow Eye Movements (SEM) with sinusoidal peaks and longer deflection times (>500 ms) (AASM, 2007) were not considered by raters and are to be ignored by our the algorithm. Examples of REMs can be seen in Fig. 2, REM statistics for each subject in Table 1, and descriptive statistics of REMs can be found in the results.

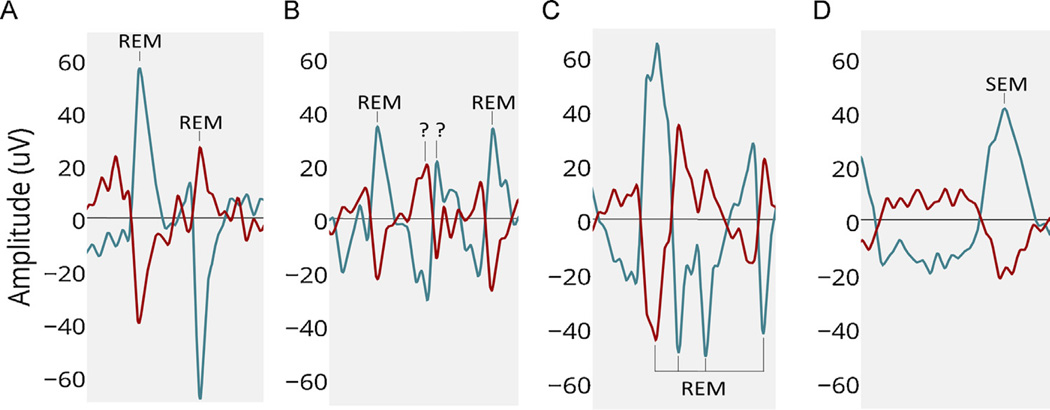
Fig. 2.

Examples of REM waveforms. Y axis represents 3 s (3 windows). LOC in blue, ROC in red: (A). An example of two ‘ideal REMs’ easily detected by simple thresholding (B). Example of REM like movements (?) to be ignored (C). Multiple REMs in close proximity with different amplitudes in channels, requiring a combination of features to detect (D). Slow Eye Movements (SEM) to be ignored.

Table 1.

Subject’s sleep parameters.

	Total sleep time(min)	Time in REM (min)	Rater 1 REM’s	Rater 2 REM’s	Rater 3 REM’s	Gold standard REM’s	REM density (events/min)	Mean REM amplitude of LOC/ROC (SD) (µV)
Subject 1	87	25.1	138	147	119	137	5.46	44(22)
Subject 2	96	27.6	201	198	183	192	6.96	58(37)
Subject 3	109.5	14.3	301	271	302	284	19.9	68(33)
Subject 4	106.5	28.3	166	172	158	157	5.55	81(54)
Subject 5	98	38.5	118	118	127	117	3.04	58(34)

2.2. Algorithm development

2.2.1. Overview

We employed two approaches: feature thresholding and machine learning. We obtained respectable results using a threshold-based approach with an intersection of Amplitude, Slope, Cross-Correlation, and Discrete Wavelet Transform (DWT) (e.g. if Amplitude > w AND slope > x AND Cross-Correlation > y AND DWT > z then label as a REM). By adding the features with high recall first and only adding precision in the later steps, we began with a high number of true and false positives and iteratively reduced false positives while controlling for false negatives.

A large set of features can be predictive, and this simple thresholding approach becomes intractable when REMs are best predicted from multiple feature interaction terms. In the second approach, we used an adaptive boosting (AdaBoost) classification algorithm (Freund and Schapire, 1997), which is able to automatically tune the thresholds and combinations of multiple features by learning the statistical regularities that predict REM from a training data set. It combines many simpler algorithms, each of which focuses on different examples of REM. This algorithm has been previously used on EEG signals to successfully classify epilepsy-related EEG signals (Niknazar et al., 2013b), sleep apnea (Xie and Minn, 2012), and schizophrenia (Boostani et al., 2009).

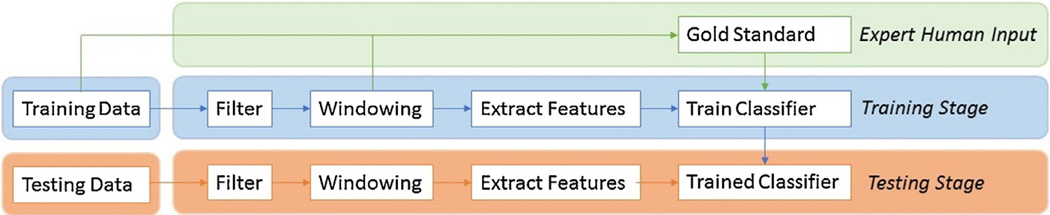
Our AdaBoost detection algorithm follows a 4-step process (Fig. 3). First, data is filtered, discretized (by splitting into consecutive windows) and a gold standard is created from human scorers (correct classification of each window). Next, features are extracted from each window. Third, a classifier algorithm trains a classifier to learn to distinguish between windows containing no REM, a single REM or two REMs in an iterative manner. Finally, the testing set is run through the now trained classifier, and classification performance is measured by comparing classifier output to the expert human gold standard (see Sections 2.2.3 and 2.3).

Fig. 3.

Algorithm Overview.

2.2.2. Filtering and windowing

The spectral power across all REMs peaks between 0.3 Hz and 5 Hz (Fig. 4). Frequency components higher or lower were considered as noise and removed with a zero phase digital bandpass filter [0.3 Hz–5 Hz, 40DB attenuation]. Other filter cutoff frequencies ranging from 0 Hz to 15 Hz were considered, but did not improve performance. Other than initial bandpass filtering, EOG signal artifacts were not removed from the dataset and did not affect results. The filtered LOC and ROC data across subjects were divided into 8022 consecutive 1 s windows, each of which undergoes feature extraction. This window size was chosen to capture the average time for a complete REM movement. Results of other window sizes (0.5, 0.7, 1.2, 1.4, 1.6 s among others) were investigated, but performance did not increase.

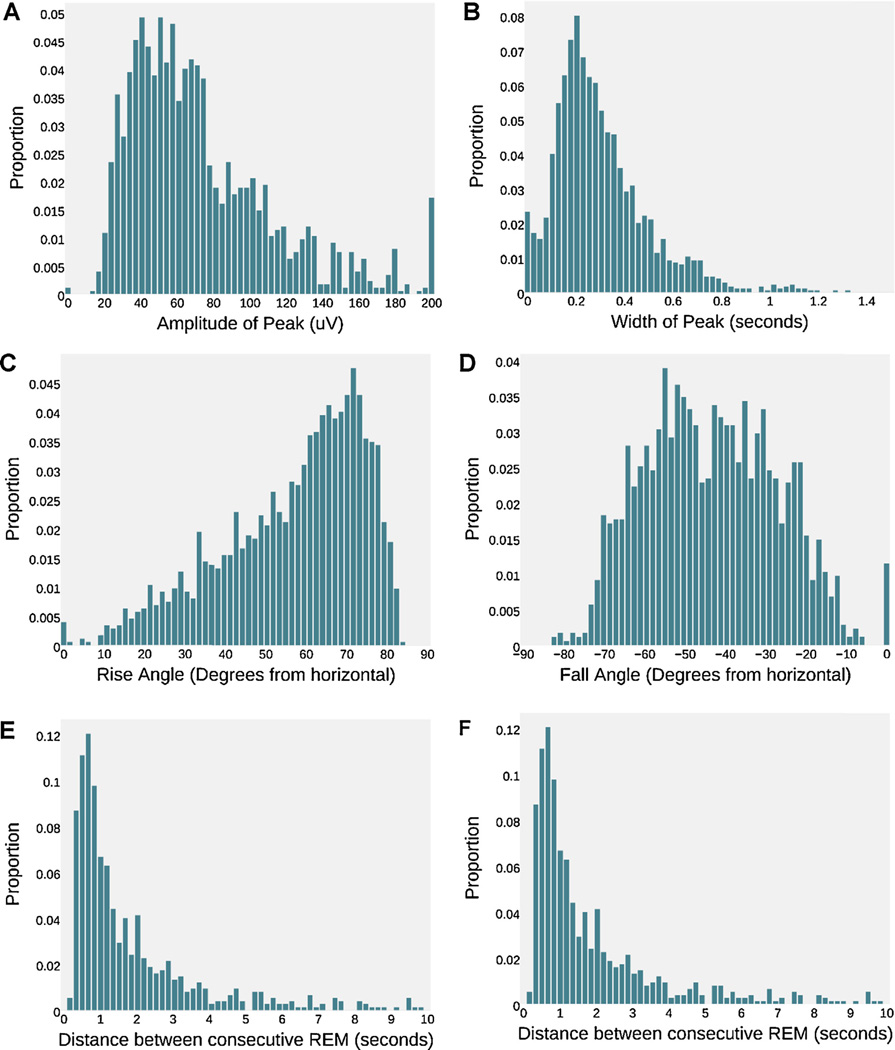
Fig. 4.

REM feature distributions. REM statistics are calculate from windows centered on GS REM peaks. (A) Amplitude of REM peaks. (B) Width of REM peaks, as measured in Section 2.2.4.1. (C) Rise slope, measured clockwise from the horizontal. (D) Fall slope, measured clockwise from the horizontal (note the negative sign). (C) The distance between consecutive REM movements. Distances greater than 10 s not shown. (F) Distribution of REM Spectral Power. Note that the zero width, rise and fall angle are artifacts of our rise and fall angle algorithm.

2.2.3. Gold standard

Raters were instructed to mark REM peaks by hand. A REM peak location ‘gold standard’ was created by combining the REM peaks scored by each rater. To avoid over counting the same REM as identified by different raters, MATLAB’s hierarchical clustering algorithm (MathWorks, 2015) was used. Effectively, REM peak marks closer than 120 ms across raters are merged into a single REM with the resulting peak at the maximum absolute value of the LOC or ROC signal. Only merged REM were considered as gold standard REM, in this way, at least 2 raters must agree on a REM movement before it is marked as such. Multi peaked waves (as marked by a single rater) closer than 120 ms did not occur, REMs further apart were always considered as separate movements.

2.2.4. Feature extraction

Features were extracted from each consecutive window of filtered LOC, ROC and the negative product of LOC and ROC (NEGP) (as proposed in Agarwal et al., 2005, this signal is maximal during REM movements). These features can be broken into 4 broad categories: time domain features, frequency domain features, time-frequency domain features and nonlinear features. This does not suggest that all time, frequency and time-frequency domain techniques are linear but rather they are not based on the theories of dynamical systems. Features were generally based on apriori theoretical intuition (e.g. REMs have higher amplitudes, thus amplitude is considered a good feature). However, human scoring is a subjective process that cannot be perfectly captured by a discrete set of rules, thus a range of features were implemented. Many features were trialed, however, only features used in the final algorithm are described.

2.2.4.1. Time domain features

Time domain features are continuous variables extracted from the filtered windows of voltage over time.

Amplitude (LOC, ROC, NEGP)

REMs are deflections from the voltage signal baseline; a simple index of this deflection is the maximum absolute amplitude of the voltage. This point is considered as the peak of the signal.

Peak prominence & peak width (LOC, ROC, NEGP)

For the maximum voltage peak in each window (positive or negative), a measure of how much it extends from the signals baseline (as opposed to the zero line for amplitude) was calculated (prominence) along with the width of the signal at half of the prominence (width).

Rise and fall slope at peak (LOC, ROC, NEGP)

REM movements deflect sharply (Rise) from the signal mean, then decay (Fall) at a slower rate back to baseline. The slope of the signal both before and after the max amplitude peak was calculated.

Cross-correlation

Cross-correlation is a measure of the similarity of two signals found by computing the correlation of their overlap as a function of the lag of one relative to the other. In a REM, both LOC and ROC simultaneously deflect from their signal baseline. The maximum cross-correlation of LOC and negative ROC provides a measure of this synchrony.

Local variance (LOC, ROC, NEGP)

The variance for each window was calculated.

Mobility (LOC, ROC, NEGP)

This is a measure of the variance of the sudden changes in a signal and is defined as the standard deviation of the first derivative of the signal to that of the original signal:

$$\text{mobility}=\frac{{\sigma }_{s\prime }}{{\sigma }_s}$$

where σ is standard deviation and s′(n) = s(n + 1) − s(n).

Complexity (LOC, ROC, NEGP)

Defined as the ratio of the mobility of the first derivative of the signal to the mobility of the signal:

$$\text{complexity}=\frac{{\sigma }_{s″}/{\sigma }_{s\prime }}{{\sigma }_{s\prime }/{\sigma }_s}$$

Coastline (LOC, ROC, NEGP)

Essentially, a sum of the derivative of the signal, this feature was chosen due to the relatively higher-amplitude and higher-frequency of REMs when compared to Non-REMs.

$$\text{coastline}=\sum _{n=2}^N|s(n)-s(n-1)|$$

where |.| represents the absolute value operator and N is the number of data points in the present window.

Nonlinear energy (LOC, ROC, NEGP)

This measure of signal energy is defined as follows:

$$NE=\frac{1}{N-2}\sum _{n=2}^{N-1}(s^2(n)-s(n-1)s(n+1))$$

where N is number of data points in the present window (Niknazar et al., 2013a).

Dynamic time warping (LOC, ROC, NEGP)

Dynamic Time Warping (DTW), commonly used in speech and handwriting recognition (e.g. Müller, 2007), is an algorithm for measuring similarity between two temporal signals that may vary in time or speed. The signals are “warped” iteratively in the time dimension to along an optimal ‘warp path’ to transform one signal into another. The length of the warp path gives a measure of signal similarity. Here, we compare the similarity of each time domain window to an ‘ideal’ REM created by averaging all gold standard REM windows centered on their peaks.

Many time domain features (peak amplitude, prominence, width, rise/fall angle) are calculated from the most prominent peak in a 1 s window. If two REMs are present, these features will be associated with the largest REM movement. Performance did not increase when features associated with the second largest peak were included.

2.2.4.2. Frequency domain features

Frequency domain windows for LOC and ROC were analyzed via Fourier transformation from the time domain.

Spectral skewness and kurtosis (LOC, ROC)

Skewness is a measure of the asymmetry of the probability distribution and can be defined as:

$$\text{Skewness}=\frac{E{(S-\eta )}^3}{{\sigma }^3}$$

where E(x) is the mathematic expectation of random variable x and S represents the amplitude of the fast Fourier transform (FFT) coefficient of an EEG signal in the present window. η and σ are the mean and standard deviation of S, respectively.

Kurtosis is a measure of the peakedness of the probability distribution of a real-valued random variable as is defined as:

$$\text{Kurtosis}=\frac{E{(S-\eta )}^4}{{\sigma }^4}$$

Higher kurtosis means that the variance is mostly the result of infrequent extreme deviations, as opposed to frequent modestly sized deviations. Both measures are common in descriptive statistics.

Shannon entropy (LOC, ROC)

In information theory, entropy is a measure of the uncertainty associated with a random variable. Spectral entropy can be calculated as the classical Shannon entropy (Shannon, 1948) after normalizing the frequency domain window:

$$\text{Entropy}=\sum _{i=1}^N|S(i)|o{g}_2|S(i)|$$

2.2.4.3. Time-frequency domain features. Discrete wavelet transform by Haar and DB2 (LOC, ROC, NEGP)

Discrete Wavelet Transforms (DWT) decomposes a discrete signal into a set of basis function (similar to Fourier transform, where the sine function is the basis). Here we use both the Haar wavelet and the Daubechies 2 (DB2) wavelet as basis function because they closely resemble REMs. For the Haar wavelet, we applied the DWT method on the approximate decomposition for 4 iterations (level −4, approximate signal) and used the maximum amplitude of the −4 level inverse DWT as our feature. The same method was applied for 6 iterations for the db2 wavelet. In this way, larger amplitude of the inverse DWT signal suggest the more the signal can be represented by a combination of these wavelets and the more likely that the window contains a REM (because wavelets resemble REM). Discrete wavelet transforms were successful in previous papers (Barschdorff et al., 1997; Tsuji et al., 2000).

2.2.4.4. Nonlinear features. Similarity features (LOC, ROC, NEGP)

These methods consist of the reconstruction and subsequent comparison of the EEG dynamics between each signal window and an ‘ideal REM’ reference window (created from the average of all REM movements). First we extracted the optimum embedding dimension (m) and delay (tau) from the complete LOC, ROC and NEGP signals using Cao’s algorithm (1997) and the mutual information (MI) function (Fraser and Swinney, 1986), respectively. From these parameters, each signal window, and the reference window, is transformed into a phase space of vectors. Next, a trajectory matrix is constructed from the vectors, thus describing the complete record of patterns that have occurred within a window. To reduce noise, the trajectory matrices of each signal window and the reference window are projected on the principal axes of the reference window by means of a singular value decomposition (SVD) (Feldwisch-Drentrup et al., 2010). The transformed data of each window is then compared to the transformed data of the ‘ideal’ REM reference window using similarity metrics of Dynamical Similarity Index (DSI) (Quyen et al., 2001), Fuzzy Similarity Index (FSI) (Ouyang et al., 2004) and Bhattacharyya based Dissimilarity Index (BBDI) (Niknazar et al., 2013a). Larger similarity means the current window is similar to an ideal REM and therefore has a higher probability that it contains a REM. Full descriptions and mathematical expression of each measure can be found in Niknazar et al. (2013a).

2.2.5. Feature reduction

A backward elimination stepwise algorithm was used to reduce the feature space. Here, the classifier starts with the set of all candidate features. We then remove each feature separately and measure algorithm performance (F1 Score, see Section 2.3). If removal of a feature corresponds to performance improvement, then that feature is eliminated from the set. This process was repeated until performance no longer increased.

2.2.6. Classifier methods and ECOC

With a window size of 1 s, and the high probably of short inter-REM intervals, 2 REMs were often present, therefore, a single Adaboost (binary) classifier, which could only label windows as containing no REM (0) or REM (1) would underestimate REMs. To limit classifier confusion to rare cases, windows containing 3 REMs in the gold standard were set to 2 REMs (<0.1% of windows), yielding 3 classes to distinguish between: windows containing No REM (90%), 1 REM (8%), 2 REM (2%).

Error-Correction Output Codes (ECOC) were used to overcome this 3-class problem. ECOCs were implemented as in Escalera et al. (2010), and provided a method of coding and decoding multiple one vs one binary classification decisions into multi-class decisions (Fig. 4). With three classes to classify, three separate dichotomous Adaboost classifiers are required, where each classifier learns to split a pair of classes (outputting a −1 or 1) while ignoring the third (classifier is not trained on the 3rd class and will output an erroneous −1 or 1). Each window’s three classifier outputs can be compared via a distance measurement (Laplacian distance gave the best results in our case), to the expected outcome for each class and the closest class is then selected for that window.

A worked example is provided for clarity:

If we have 3 classifiers (A, B and C) and 3 classes (0REM, 1REM, 2 REM) then we might expect the following results pattern:

Classifier	0REM	1REM	2REM
A	1	−1	? (−1 or 1)
B	? (−1 or 1)	1	−1
C	1	? (−1 or 1)	−1

We would expect a window containing 1 REM to give the following output pattern for each classifier:

A	−1
B	1
C	1 or −1

If we then compare the output pattern via the absolute difference (a form of distance measurement) to the expected pattern for each class, (where the unknown value is set at zero) then we see that indeed the output is closest to the true class of 1 REM:

	0REM		1REM		2REM
Actual output	Expected output	Distance	Expected output	Distance	Expected output	Distance
−1	1	2	−1	0	0	1
1	0	1	1	0	−1	2
1 or −1	1	2 or 0	0	1	−1	2 or 0
Total distance		3 or 5		1		3 or 5

As each subject’s REMs have unique eccentricities, the importance of algorithm generalizability to new data (other subjects) cannot be understated. Along with internal algorithm cross-validation, k-fold cross validation was used. Here, the algorithm is trained on 4 of the 5 subjects and then the remaining subject can be used to test algorithm performance. Performance statistics can then be averaged across all 5 different combinations of subjects, with each subject serving as the test subject one time. In this way, the algorithm is never trained on all types of REMs or all subjects, giving us greater confidence of generalizability. Within subject performance, where training and testing data (70:30 ratio) was taken from the same subject is also reported.

2.3. Performance statistics

Specificity and recall, (defined below) are common measures of quantifying algorithm performance. However, in our dataset the true percentage of windows containing REMs as scored by humans was 6%. With this relatively low ratio of true positives to true negatives, traditional measures of algorithm performance, such as specificity, are biased (even detecting no REMs give specificity greater than 90%). To overcome bias, we used precision, defined as the percentage of true positives (as determined by the gold-standard) detected by the algorithm. Recall is the number of true REMs correctly classified as such. We use F1 score as a single measure of performance useful in tuning and ranking algorithm performance:

$$\text{Precision}=\frac{TP}{TP+FP}\text{Recall}=\frac{TP}{TP+FN}F1=2\times \frac{\text{Recall}\times \text{Precision}}{\text{Recall}+\text{Precision}}$$

Our final algorithm makes decisions on the presence of REM in each 1 s window, but does not mark exact REM locations. Hence, for algorithm comparison, a windowed version of the gold standard is created by counting the number of gold standard REMs that fall in each consecutive window. Performance statistics are then based on the difference between the REMs per window as classified by our algorithm, and the windowed gold standard (“Win” statistics in Table 4). For example, if a window contains 2 gold standard REMs, and the algorithm detects 1 REM, then we have one True Positive and one False Negative. For algorithms that detect individual REM locations (such as our thresholding method), we create a windowed output in the same way as the gold standard.

Table 4.

Performance of our and previously published algorithms. Optimal thresholds found via k-fold cross validation when algorithms required tuning, or when exact thresholds were not reported. Precision and recall and F1 score from our dataset is shown, with previously reported precision and recall in parenthesis when applicable/available.

Algorithm	Brief Description of methods	Optimal thresholds	Win recall (%)	Win precision (%)	Win F1
Combinatory Algorithm   (F1 weighted)	The F1 weighted combinatory algorithm as described above	NA	81.3	80.2	0.807
Classification approach	Our classifier algorithm as described above	All threshold tuned via machine learning	78.1	82.6	0.803
Combinatory Algorithm   (unweighted)	The simple average combinatory algorithm as described above	NA	81.1	73.4	0.771
Hatzilabrou et al. (1994)	Bandpass filter (0.5–10 Hz), windowed and remove DC offset Compare each hamming smoothed window to a hamming smoothed template REM (template REM not described so we used our ‘ideal REM’) via Magnitude Squared Correlation FP removed via with monocular requirements (no method given so we thresholded amplitude in each channel)	Correlation threshold (0.0005) & Monocular Amplitude threshold (23 µV)	71.1	80.0	0.753
Doman et al. (1995)	Lowpass filter (8 Hz) Find points where slope changes 90 degrees in one channel Label these as REM if high amplitude, and there is a synchronous, high amplitude, opposite polarity signal in other channel	Synchrony threshold (62.5 ms)	64.9 (93)	86.6 (84)	0.742
Minard and Krausman (1971)	Rising slope threshold Out of phase requirement	Rising slope threshold (50 degrees)	74.2	68.5	0.712
Thresholding approach	Our feature thresholding algorithm as described above	Amplitude (21.2 µV), Cross Correlation (7000), Angle difference (76 degrees), DWT (2.2)	65.2	74.7	0.696
Best single feature	The single best feature thresholded (Peak amplitude)	Amplitude threshold (36 µV)	75.5	59.3	0.665
Agarwal et al., 2005	Bandpass filtering (1 Hz, 5 Hz) Amplitude threshold negative product of LOC and ROC False positive removed with slope and cross correlation requirements	Amplitude threshold (320 µV2) and cross correlation threshold (7200)	78.8 (67)	53.8 (75)	0.639
McPartland et al. (1973)	Lowpass filter of 15 Hz Synchrony (65 ms) Out of phase requirement Absolute amplitude requirement of at least 15 µV	NA	94.4	48.0	0.637
Ktonas and Smith (1978)	Bandpass LOC and ROC (0.3Hz–8 Hz) Out of phase absolute amplitude requirement of at least 50 µV in one channel, and 30 µV in the other This paper extends on two previous algorithms presented by the authors (Smith and Karacan, 1971; Degler et al., 1975)	Amplitude (26 µV) and synchrony threshold (49.2 ms)	44.8 (93)	89.8 (94)	0.597

Additionally, for location based algorithms, we compare results to the gold standard by marking true positives if a gold standard REM and an algorithm detected REM occur within 200 ms of each other (“Loc” statistics in Table 5) again using MATLABs clustering algorithm (MathWorks, 2015). Lone REM’s in gold standard are False Negatives, and lone REM’s in the algorithm output are False Positives.

Table 5.

Location based recall, precision and F1 and window based TP, FP, FN for each algorithm.

Algorithm	Loc recall	Loc precision	Loc F1	Win TP	Win FP	Win FN
Combinatory Algorithm (F1 weighted)	NA	NA	NA	721	178	166
Classification approach	NA	NA	NA	693	146	194
Combinatory Algorithm (unweighted)	NA	NA	NA	719	260	168
Hatzilabrou et al. (1994)	71%	79%	0.753	631	158	256
Doman et al. (1995)	66%	88%	0.742	576	89	311
Minard and Krausman (1971)	70%	63%	0.712	658	303	229
Thresholding approach	64%	75%	0.696	578	196	309
Best single feature	75%	62%	0.665	670	459	217
Agarwal et al. (2005)	76%	57%	0.639	699	601	188
McPartland et al. (1973)	94%	49%	0.637	837	906	50
Ktonas and Smith (1978)	44%	90%	0.597	397	45	490

To measure expert and non-expert rater reliability common methods of Cronbach alpha (α), and inter-rater-agreement are used (defined below). Also reported is the average precision and recall of each rater against the gold standard. This precision and recall will be artificially inflated when the gold standard contains that rater (similar to a correlation with itself), therefore we compare each rater to a gold standard created with that rater removed.

Note that inter-rater-agreement is biased by the high number of true negatives.

$$\alpha =\frac{K}{K-1}(1-\frac{{\sum }_{i=1}^K{\sigma }_{Y_i}^2}{{\sigma }_X^2})$$

where K is the number of consecutive windows, and Y a vector of the REM counts per rater for each window. ${\sigma }_{Y_i}^2$ is the variance of component i for the set of raters and ${\sigma }_X^2$ is the variance of the total REM scores of raters. Inter-rater-agreement is calculated as the average correlation between rater’s Y vectors.

2.4. Comparison to previous work

The finding that REMs may be linked to dreaming led to a flurry of rule-based classifiers implemented with analogue electronics (Minard and Krausman, 1971; McPartland et al., 1973; Ktonas and Smith, 1978). As computing power has improved, REM detectors using more complex combinations of features (Doman et al., 1995; Tsuji et al., 2000; Agarwal et al., 2005), matched filtering (Hatzilabrou et al., 1994), autoregressive modeling (Shokrollahi et al., 2009) and learning algorithms (Barschdorff et al., 1997) have emerged.

These algorithms have impressive performance, but comparison to own is biased by differing datasets (EEG channels used, subjects and numbers of human raters used to test performance) and further limited by different performance metrics. Therefore, along with developing our own algorithm, we implemented reported methods from all published LOC and ROC based detectors on our dataset. Note that our aim was to investigate the important features and principles of all successful published methodologies and provide fair comparison such that future sleep researchers may be better equipped in choosing the right detection algorithm. Detectors using channels other than LOC and ROC (such as vEOG/hEOG) have different signal characteristics and while their methods have been taken into consideration, were considered out of scope (e.g. Tsuji et al., 2000; Shokrollahi et al., 2009; Barschdorff et al., 1997; Gopal and Haddad, 1981; Takahashi and Atsumi, 1997; Ktonas et al., 2003; Tan et al., 2001). Table 4 outlines each method and its results, MATLAB code for all methods is open source and available at [PERM LINK TO BE INSERTED WHEN PAPER IN PRESS]. Training and testing with k-fold cross validation was used when algorithms required tuning, or when exact thresholds were not reported. Tuned parameters and their optimal threshold values are reported in Table 4

2.5. Combinatory algorithms

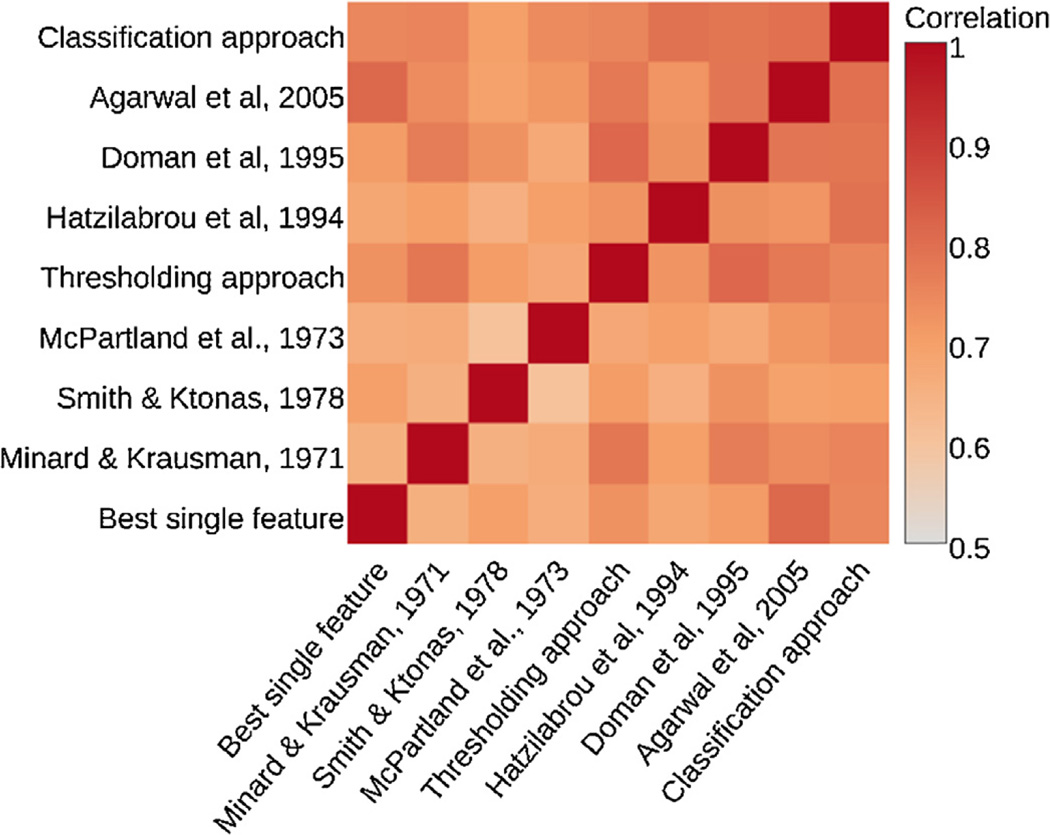
In 2007, Netflix [Netflix Inc, Los Gatos, CA, USA] held a 1 million dollar prize (Netflix, 2015) to create the best video recommendation algorithm. The eventual winning team (Bell et al., 2007), and runner up (Toscher et al., 2009), combined over 100 algorithms each. The combination of both teams’ algorithms again improved performance. Warby et al. (2014) found similar performance benefits when combining individual spindle detectors. However, improvement from combination algorithms only occurs if each detector finds a different subset of REM events. Correlating the REM counts per window for each detector (Fig. 5), does indeed show variability in REM events, highlighting a potential performance increase from combinatory algorithms. Two combination approaches were implemented:

• Simple average: Averaging the REM’s per consecutive 1 s window over all detectors.

• F1 weighted average: Weighting the algorithms by their F1 score before then averaging REM’s (again per consecutive 1 s window over all detectors).

Fig. 5.

Heatmap of correlations between each detector highlighting variability in REMs detected.

3. Results

3.1. REM statistics

Fig. 4 shows REM spectral power, intra-REM interval, amplitude, width, rise and fall angle distributions of our gold standard REMs. Ktonas and Smith (1978) note that many REM occur closer than 200 ms, with 4 REMs possible in less than 1 s. Aserinsky (1971) reports a peak in intra-REM intervals at 600 ms. Our REMs are similar, with intra-REM peak at approximately 0.7 s, but no more than 3 REMs appearing in a 1 s period.

A breakdown of REM count per window are reported in Table 2.

Table 2.

REM count per window.

0 REM	1 REM	2 REM	3 REM	Total
7271 (90%)	622 (8%)	122 (2%)	7 (<0.1%)	8022

3.2. Human scorer performance

As expected, the expert group raters had stronger agreement than that of non-experts (Inter-rater-agreement: Expert = 0.86, Non-Expert = 0.73). This is confirmed by Cronbach Alpha and Precision/Recall for a single rater vs each group (Table 3).

Table 3.

Agreement statistics between human raters in expert group, non-expert group, and combined.

Rater experience	Inter-rater-agreement	Cronbach alpha	Mean recall (SD) (%)	Mean precision (SD) (%)	F1	Windowed gold standard (GS) used to calculate precision and recall
Expert	0.86	0.80	79 (2)	91 (1)	0.846	Average of each expert compared to Expert GS (with compared expert removed)
Non-expert	0.73	0.65	68 (15)	77 (7)	0.722	Average of each non-expert compared to Expert GS
Combined raters	0.74	0.68	76 (13)	83 (9)	0.793	Average of each rater (non-expert and expert) compared to Expert GS (removing compared expert from GS)

3.3. Classification approach performance

The best algorithm performance averaged across subjects was 78.1% recall and 82.6% precision. The optimum feature set for the machine learning algorithm consisted of Amplitude, Width, Prominence, Rise and Fall Slope, Linear Variance, Cross Correlation, DWT, DTW, Coastline, Nonlinear Energy, Spectral Skew and Kurtosis, DSI, FSI and BBDI. Thresholds can be seen in Table 4. Average within subject performance was 74% recall (SD = 9%) and 80% precision (SD = 8%), with the best performance for a single subject at 78% recall and 90% precision. Algorithm performance is comparable to that of an expert human (79% Recall, 91% Precision), and surpasses average performance of our combined expert and non-expert set (76% Recall, 83% Precision). Considering the mixed experience of technicians in sleep research, the combined group is perhaps a more valid comparison.

3.4. Thresholding approach performance

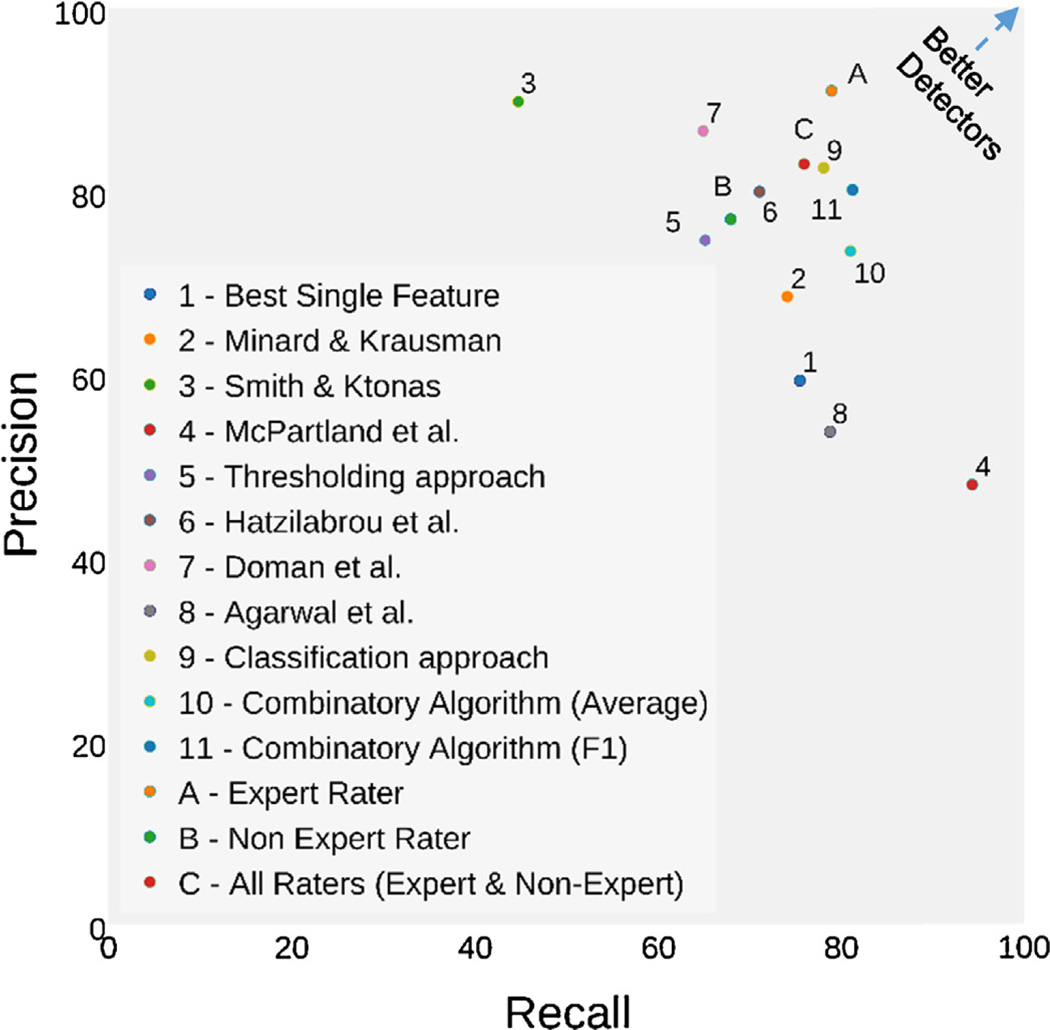
Using an intersection combination of extracted features (amplitude, slope, cross-correlation, and Discrete Wavelet Transform), a threshold algorithm reached a performance level of 65.2% Recall and 74.7% Precision. The single best feature of the thresholding approach was peak amplitude in at 75.5% Recall and 59.3% Precision (Table 4, Fig. 6).

Fig. 6.

Comparison of REM detector algorithms by Recall and Precision.

3.5. Comparison to existing REM detectors

Table 4, ranked by F1 score (i.e., the harmonic mean of recall and precision), a common single metric used to compare classifiers, shows our classifier based method outperforms all others on this dataset (see Fig. 6 for a graphical representation of this data). Haztilabrou et al. had the highest performance of the implemented methodologies of past literature (71.1% Recall, 80.0% Precision).

3.6. Combinatory algorithm performance

The simple average combination algorithm reaching 81.1% Recall and 73.4% Precision. The F1 weighted algorithm produced impressive performance of 81.3% Recall and 80.2% Precision (F1 = 0.807) making it the top performing algorithm overall (as measured by F1 Score).

4. Discussion and conclusion

Our top performing algorithm extracts over 25 features from bandpass filtered [0.3 Hz–5 Hz] LOC and ROC EEG data, and then uses ECOC classifier to train the algorithm to predict REMs from their statistical regularities. The optimum feature set consisted of Amplitude, Width, Prominence, Rise and Fall Slope, Linear Variance, Cross Correlation, DWT, DTW, Coastline, Nonlinear Energy, Spectral Skew and Kurtosis, DSI, FSI and BBDI. The automatic detection algorithm presented here is a viable and efficient method of REM detection as it reliably matches the performance of expert human sleep scorers.

By using the same features and algorithm parameters presented here, other researchers can be assured that their definition of a REM movement is consistent with our own. A major advantage of the learning algorithm used is its ability to learn. While our version was trained to match three trained sleep technicians, the learning aspect of the algorithm allows it to adapt to other expert gold standards. Thus, while performing well ‘out of the box’, the algorithm could also be automatically tuned to suit different detection needs. Furthermore, the algorithm could potentially be adapted to detect other features of sleep, such as sleep spindles. It is important to note that if researchers believe that REM movements in their population are significantly different to those presented here, or their own definition of REM is significantly different, feature sets and thresholds will no longer be optimal and performance will decrease. In this case, it is advised that algorithm retraining is undertaken. To quantify this difference researchers can mark REM movement peaks and then create statistical distributions as in Section 3.1 (MATLAB code provided).

We feel our dataset is of sufficient size for algorithm training, however, as with all machine learning algorithms, it is preferable to have more data to increase generalizability (Domingos, 2012). Current work by the authors includes creating a massive, open, online sleep dataset with expert annotations of REM, spindles and other sleep features to allow for better algorithm training and validation.

Importantly, any algorithm will only be as precise as its gold-standard. Our data show that the agreement between our experts is not unanimous and the disparity between experts and non-experts show some level of learning required for expertise. Since the classifier algorithm learns from humans, it is inherently limited by the agreement between observers. To achieve optimum performance, the validity of the gold-standard must increase. While adding more raters (and hence reliability) does not necessarily mean increased validity (Rosnow and Rosenthal, 1989), it does create a more reliable and generalizable standard. Since each sleep lab will have different criteria for scoring REM events, more algorithm generalizability is preferable. Gathering scored REM sleep data from expert sleep scorers across many different labs is possible, or potentially raters could be crowdsourced. Warby et al. (2014) used crowdsourcing technology to create a much larger pool of expert (24) and non-expert (114) raters for sleep spindle algorithm comparison (Each epoch was viewed approximately 5 times by experts and 10.7 times by non-experts). They also found that adding 3 confidence levels (1 = not a spindle, 2 = unsure, 3 = definitely a spindle) to spindle scoring lead to a better gold-standard and more agreement among raters. Similar methods would benefit future REM scoring.

A limiting factor of the current machine learning algorithm is its inability to directly pinpoint REM locations. The resolution is limited to a 1 s window. However, the current algorithm is suitable for investigation of REM density. If exact locations are required, then the thresholding algorithm or past algorithm implantations can be used. While each algorithm employed appropriate cross validation techniques to reduce overfitting, when selecting the best algorithm from a set of algorithms (we estimate approximately 100 variants tested), the choice is dependent on test data. This form of overfitting, common to algorithm development, where one algorithm may be chosen over another because it happened to perform well on this particular dataset, may affect our results and impact generalizability.

By reducing researcher time and effort, algorithms to detect NREM sleep spindles, have begun to give us insight into the role of sleep EEG features in cognition (Nishida and Walker, 2007; Wamsley et al., 2012; Mednick et al., 2013). Similarly, considering the strong link between REM sleep and memory (Genzel et al., 2015), the literature on the role of REMs in cognition is remarkably sparse (Smith et al., 1991, 2004; Schredl et al., 2001; Fogel et al., 2007). Thus, the use of an automatic, reliable and time-saving detector may increase the number of research studies addressing this issue. In this view, our versatile REM detector adds an additional piece to the sleep researcher’s toolbox and aids the quest to understand the role of rapid eye movements in biology and cognition.

For development and comparison of future algorithms, the MATLAB code from this investigation (both our detectors and our implementations of methods of others) is available online through The Open Science Framework (https://osf.io/fd837/).

HIGHLIGHTS.

• Application of previously published and novel extracted features to detect Rapid Eye Movements in Rapid Eye Movement Sleep.

• Novel application of powerful Adaptive Boosting classifier.

• Comparison of previously published and novel algorithms as well as expert and non-expert raters on the same REM dataset.

• Best performance of any algorithm published to date.

• A viable and efficient method of REM detection reliably matching the performance of human sleep scorers.