Incompressible fluid plays a mechanical role in the development of passive muscle tension

Abstract

Over short time scales, muscle fibres maintain a nearly constant volume of intracellular fluid. This fluid is essential to normal biochemical function, but its role in determining the mechanical properties of muscle has been considered in only a few theoretical analyses. Here we investigate the mechanical role of fluid in a fundamental property of muscle, its development of passive tension in response to stretch. We test a model of muscle structure in which incompressible fluid directly influences passive tension by constraining the geometry of intramuscular connective tissues. This interaction is demonstrated using a simple physical model of muscle morphology comprising a fluid-filled bladder wrapped by helical fibres. The behaviour of the model is compared with that of isolated bullfrog muscle subjected to an osmotic perturbation of intracellular fluid volume. Increasing muscle volume by 40% resulted in 69% increased passive tension, occurring in a manner consistent with the behaviour of the model. These observations support the notion that the interaction of connective tissues with the muscle fibres they surround influences the mechanical behaviour of whole muscles, and highlight the role of fluid as a mechanical component of muscle.

1. Introduction

Muscles maintain a nearly constant volume of intracellular fluid regardless of contraction state [1]. This fluid constitutes the bulk of each muscle fibre's mass and volume, and plays an important role in facilitating normal biochemical function. The roles of fluid in determining the biomechanical properties of muscle, however, remain largely unexplored. A recent model has predicted a significant mechanical role for pressurized fluid within muscle [2], but classic, well-accepted mechanical models of muscle physiology do not include terms for either cell volume or intracellular pressure [3]. The incompressible nature of intracellular fluid provides it with the potential to influence muscle during both passive and active force production by transmitting force within the tissue, by generating forces opposed to those produced within the sarcomere or by influencing the mobility of the extracellular connective tissues. Here we explore the potential role of fluid as a mechanical component of muscle by investigating its influence on one of muscle's most fundamental properties, its development of passive tension in response to stretch.

We focus on the interaction of incompressible fluid with the intramuscular connective tissues. These tissues wrap individual muscle fibres, fascicles and whole muscles, constituting the endomysium, perimysium and epimysium of muscle (reviewed in [4]). The helical, cross-plied arrangement of the collagen fibres composing these tissues allows their geometry to vary as a function of muscle length, and provides a means by which the tissues can extend longitudinally when stretched under low forces [5,6]. Mathematical models of intramuscular connective tissue assume that changes in collagen fibre geometry are largely constrained by the presence of a constant, incompressible volume of fluid present within muscle fibres [2,5,7], but a relationship between intracellular fluid volume, collagen geometry and passive muscle tension has not been shown empirically. Here we use a simple physical model of a fluid-filled bladder encompassed by a helically wound sleeve along with an osmotic perturbation of isolated bullfrog muscle to test the validity of this relationship, and to test the hypothesis that altering a muscle's internal fluid volume will alter the passive tension generated in response to stretch.

2. Material and methods

A simple physical model was built to explore the relationships between muscle length, fibre geometry, internal pressure and tension (figure 1). A fluid-filled bladder (Trojan ENZ non-lubricated, Church and Dwight Co.) represented a constant volume muscle fibre. A sleeve of helically wound fibres (Flexo PET, Techflex) surrounded the bladder and represented extracellular connective tissue. The model can be interpreted as representing either a muscle fibre wrapped in endomysial connective tissue or a muscle fascicle wrapped in perimysial connective tissue.

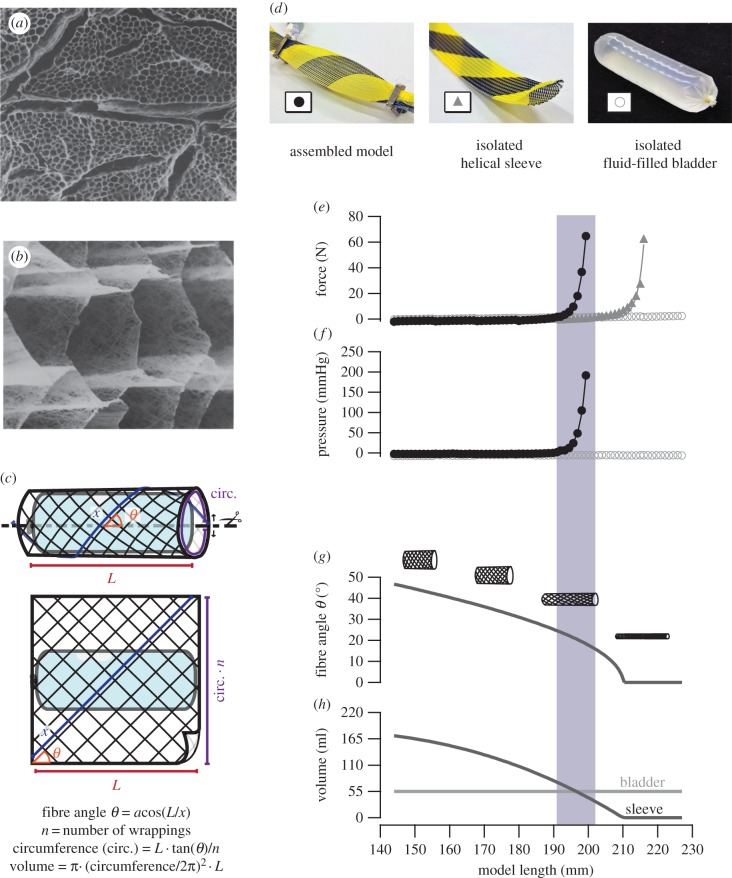
Figure 1.

The physical model and its mechanical behaviour. Scanning electron micrographs of chemically digested muscle show isolated intramuscular connective tissue at 100× (a) and 3200× (b) magnification, adapted from [6]. Collagen fibre geometry within these tissues is modelled mathematically (c) and physically (d) as a sleeve of helical fibres surrounding an incompressible volume of fluid. Mathematical modelling allowed for calculation of collagen fibre angle (θ) and sleeve internal volume as a function of length. Physical modelling allowed measurement of tension and pressure in response to stretch. When stretched, the physical model produced negligible force over a large strain, followed by a simultaneous increase in force (e) and pressure (f). Force development occurred when the internal volume of the helical sleeve approached the constant volume of the bladder (h). The isolated sleeve produced force only at long lengths, when calculated fibre angle (g) approached zero. Force and pressure data (e,f) are well fitted by the equation f(x) = e^{(a + bx)} which describes passive muscle tension as a function of length [8]. (Online version in colour.)

The angle (relative to the sleeve's long axis) at which individual fibres lie in a helically wound sleeve varies as a function of sleeve length, as does the maximum volume the sleeve can encompass [7]. The fibre angle and internal volume of the model's flexible sleeve were predicted across all lengths studied by assuming the sleeve to be a simple cylinder composed of helical fibres (figure 1c). Hydrostatic pressure inside the model was determined via a probe coupled to the bladder's interior (Mikro-tip SPC-340, Millar Instruments). The fluid volume of the bladder could be altered via an in-series syringe to compare mechanical properties at different internal volumes. The mechanical behaviours of the isolated fluid-filled bladder and isolated sleeve were also examined.

The mechanical behaviour of the physical model was compared with that of isolated bullfrog semimembranosus muscle. Passive length–tension curves were collected for four muscles before and after manipulating fluid volume via an osmotic perturbation. Curves were first collected in a standard, isotonic amphibian Ringer's solution (115 mmol l⁻¹ NaCl, 2.5 mmol l⁻¹ KCl, 1.0 mmol l⁻¹ MgSO₄, 20 mmol l⁻¹ imidazole, 1.8 mmol l⁻¹ CaCl₂, 11 mmol l⁻¹ glucose, pH 7.9). Curves were then remeasured following a 90 min soak in hypotonic Ringer's solution (20% concentration of all solutes). Bathing in hypotonic solution produces an osmotic gradient that favours movement of water into the muscle, leading to an increase in intracellular fluid volume [9]. The semimembranosus muscle from each study organism's opposite leg was also subjected to a 90 min hypotonic soak to quantify the effect on muscle weight (figure 2f). Tension in isolated muscles and the physical model was measured at a series of static lengths using a servomotor (310B-LR, Aurora Scientific). Models and muscles were attached at one end to a rigid post and at the other to the servomotor arm. The assembled model was held at both ends of the helical sleeve. Muscles were held by a fragment of hip bone at their proximal end and by a fragment of free tendon at their distal end. Attempts were made to measure intramuscular pressure via a small pressure transducing probe (Mikrotip SPR-320, Millar Instruments) embedded directly inside muscles, but consistent results could not be obtained. Prior to measurements of passive tension, nerve stimulation was used to generate an active length–tension curve for each muscle. All passive muscle lengths were normalized to the length at maximal active force (L₀), and all passive muscle forces were normalized to the passive force produced at 115% L₀ in the isotonic condition.

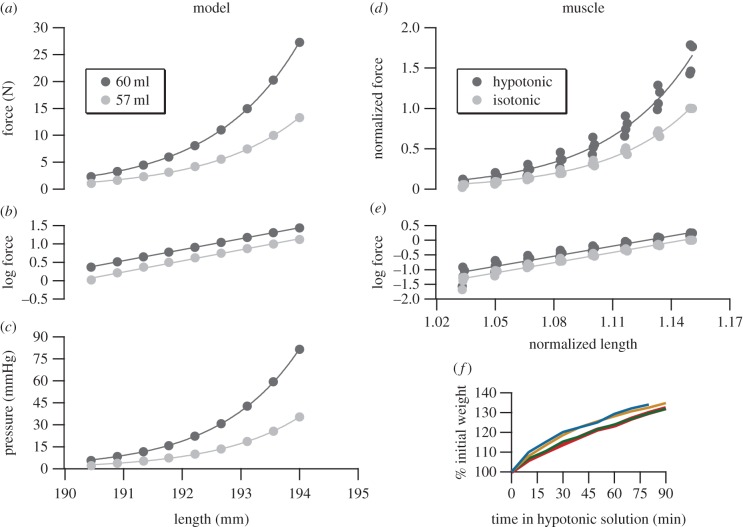
Figure 2.

Response of the physical model (a–c) and semimembranosus muscle (d–f) to increased internal volume. In both the model (a) and the muscle (d), force at a given length increased following an increase in internal fluid volume. Log-transformed passive tension data display consistent slopes before and after fluid volume increase in both the model and muscle, indicating that force increased in both via a change in zero-force length (b,e). In the model, higher fluid volumes and forces were associated with higher internal pressures (c). Measurements of mass for muscles soaked in hypotonic solution (N = 4) confirm the increase in fluid volume (f). (Online version in colour.)

3. Results

The mechanical behaviour of the physical model demonstrated the importance of the interaction of the helical sleeve and the constant volume bladder. When stretched, the model accommodated large displacements with negligible force development. Significant force developed only when the calculated volume of the sleeve approached the volume of the bladder (figure 1e–h, shaded region). Hydrostatic pressure within the model increased in parallel with force (figures 1e,f and 2a,c), indicating compression of the bladder by the sleeve. Isolated components of the model either produced negligible force (the bladder alone) or produced force at a longer length than did the intact model (the sleeve alone; figure 1e). Negligible pressure developed in the isolated bladder, regardless of length (figure 1f).

The model and isolated muscle showed similar exponential force–length relationships when stretched. In both, an increase in internal fluid volume resulted in a leftward shift of the force–length relationship to produce higher forces at a given length (figure 2a,d). In muscle, soaking in hypotonic solution resulted in an increase in tension of 69.1% (± 5.2%), regardless of length. Log-transformation linearized the exponential force–length curves, allowing their shapes to be characterized by slope (figure 2b,e). For both the model and muscle, slopes of linearized data did not change significantly after volume was increased (p = 0.711, 0.828, respectively), indicating that the forms of the exponential force–length curves were not altered by the perturbation. The statistical tool SMATR [10] was used to compare the slopes of log-transformed lines, and also to compare the elevations of lines along the y-axis. A significant vertical shift in the log-transformed length–tension relationship occurred following the volumetric perturbations (p < 0.0001 for both model and muscle), the equivalent of a significant leftward horizontal shift in the untransformed curves. These tests indicate that the observed increases in tension resulted from a change in the zero-load length, or resting length, of the model and muscles, rather than from a change in the form of their force–length curves.

4. Discussion

We find that increasing muscle fluid volume results in an increase in passive force, and that this same behaviour is observed in a simple model of a fluid-filled bladder wrapped by a helically wound sleeve. These results show fluid acting as a mechanical component of muscle, and provide empirical support for mathematical models in which muscle fibre incompressibility ultimately limits collagen fibre reorientation and influences force developed during stretch [2,5,7]. Interactions between helically wound connective tissue fibres and incompressible fluid have been identified in a variety of organisms in the form of hydrostatic skeletons [11]. The interaction of intramuscular connective tissues and muscle fibres discussed here appears to be an example of this broader biomechanical theme.

Regarding the perturbation used in this study, the possibility exists that a change in a muscle's osmotic environment might affect passive force through biochemical effects. For example, it has been suggested that changes in intracellular tonicity might result in cross-bridge binding in inactive muscle [12]. This is unlikely to play a major role in our results. Muscle force–length behaviour in the hypotonic condition was repeatable over several lengthen–shorten cycles which spanned large muscle strains (15%), well beyond the strain allowable by bound cross-bridges [13].

It is also possible that a perturbation to muscle biochemistry might alter titin's contribution to passive force, which increases under the influence of intracellular calcium [14]. ‘Activation’ of titin by calcium, however, is associated with an increase in stiffness, i.e. in the slope of titin's force–length curve [14]. In both the model and muscle, changes in fluid volume led to a change in zero-force length, but not in the shape of the force–length relationship, as evidenced by the insignificant differences in slopes of log-transformed data (figure 2b,e). Changes in the zero-force length of a muscle's force–length curve without an accompanying change in log-transformed slope have been observed immediately following exercise [15], and postmortem [16], and incorporating changes in cell volume into our understanding of passive tension has the potential to provide explanations for these phenomena.

Our physical model lacks many morphological and physiological complexities. Collagen fibre crimps [17], interconnections between collagen fibres and the cell membrane [18], and spring-like elements within the muscle fibre (e.g. titin) represent just some of the structural detail of muscle that might alter the mechanical behaviour of the model. Additionally, our models do not account for the interconnectedness of the intramuscular connective tissues, in which individual collagen fibres are shared across multiple helical sleeves, rather than contributing to only one [6]. These details are unlikely to prevent the eventual interaction of collagen fibres and incompressible fluid that is the model's central feature. The model in its current state behaves in a manner consistent with Gindre et al.'s detailed mathematical model [2], mimics the mechanical response of isolated muscle to increased internal volume, and is consistent with observations of collagen fibre reorientation [5,6] and increased internal pressure [19] in passively stretched muscle. This work provides one simple example of how intracellular fluid acts as a mechanical component of muscle. The study of how incompressible fluid influences other aspects of muscle physiology, especially those associated with active contraction, has great potential to increase our understanding of the tissue, and warrants further interest and research within the field of muscle mechanics.

Ethics

All procedures were approved by the Brown University IACUC no. 1602000189.

Data accessibility

Data are available on Dryad: http://dx.doi.org/10.5061/dryad.fb0f8 [20].

Authors' contributions

D.A.S. drafted the manuscript and collected and analysed data. D.A.S. and T.J.R. conceived the study and edited the manuscript. Both authors gave final approval for publication and agree to be held accountable for the content of this article.

Competing interests

We have no competing interests.

Funding

This work was supported by NIH grant no. AR055295.