Genome-wide association test of multiple continuous traits using imputed SNPs

Abstract

More and more large cohort studies have conducted or are conducting genome-wide association studies (GWAS) to reveal the genetic components of many complex human diseases. These large cohort studies often collected a broad array of correlated phenotypes that reflect common physiological processes. By jointly analyzing these correlated traits, we can gain more power by aggregating multiple weak effects and shed light on the mechanisms underlying complex human diseases. The majority of existing multi-trait association test methods are based on jointly modeling the multivariate traits conditional on the genotype as covariate, and can readily accommodate the imputed SNPs by using their imputed dosage as a covariate. An alternative class of multi-trait association tests is based on the inverted regression, which models the distribution of genotypes conditional on the covariate and multivariate traits, and has been shown to have competitive performance. To our knowledge, all existing inverted regression approaches have implicitly used the “best-guess” genotypes, which is not efficient and known to lead to dramatic power loss, and there have not been any proposed methods of incorporating imputation uncertainty into inverted regressions. In this work, we propose a general and efficient framework that can account for the imputation uncertainty to further improve the association test power of inverted regression models for imputed SNPs. We demonstrate through extensive numerical studies that the proposed method has competitive performance. We further illustrate its usefulness by application to association test of diabetes-related glycemic traits in the Atherosclerosis Risk in Communities (ARIC) Study.

1 Introduction

Genetic studies often collect multiple phenotypes, which could be analyzed jointly to increase power by aggregating multiple weak effects and provide additional insights into the etiology of complex human diseases (Solovieff et al., 2013). Existing multi-trait association test methods (see, e.g., Ferreira and Purcell, 2009; Liu et al., 2009; Yang et al., 2010; Rasmussen-Torvik et al., 2010; O’Reilly et al., 2012; Tang and Ferreira, 2012; van der Sluis et al., 2013; He et al., 2013; Schifano et al., 2013; Stephens, 2013; Seoane et al., 2014) can be broadly classified into two categories. The first one is based on jointly modeling the multiple correlated outcomes with some multivariate regression models. Another novel approach is based on the inverted regression model, where the genotypes are regressed on the covariates and multivariate outcomes to estimate and test the multi-trait associations and typically some ordinal multinomial regression model is used. For example, O’Reilly et al. (2012) adopted the proportional odds model (POM), and Wu and Pankow (2015) proposed the adjacent category logit (ACL) model. For the multivariate regression based approach, it is straightforward to accommodate the imputed SNPs by using their imputation dosages as the covariate. While for the inverted regression approach, to our knowledge, all existing methods have implicitly used the “best-guess” genotypes, which is not efficient and known to lead to dramatic power loss, and there have not been any proposed methods in the literature that can incorporate the imputation uncertainty into inverted regressions. We propose a general and efficient GEE modeling approach to extending the inverted regression model to multi-trait association test of imputed SNPs.

2 Materials and Methods

2.1 Genotype based multinomial regression model

Consider a collection of continuous traits Y = (y₁, … , y_m)^T, a p-vector of covariates X to be adjusted (which could contain both ancestry and non-ancestry covariates, e.g., ancestry principal components, age and gender), and a genotype score G (number of minor alleles). Assume the multivariate normal trait model, (Y |G,X) ~ N(γ₀ + γ_XX + γG, Σ), where γ₀ is a m-vector, γ_X is a m × p matrix, γ is a m-vector, and Σ is a m × m covariance matrix. The null hypothesis of multi-trait association is H₀ : γ = 0. When modeling the population genotype distribution Pr(G|X) with a logistic regression model (it holds when, e.g., the genotypes follow the Hardy-Weinberg equilibrium within each ancestry population), we can derive an adjacent-category logit model (ACL) (Wu and Pankow, 2015)

$$log\frac{{\varphi }_{g+1}}{{\varphi }_g}={\beta }_{0g}+X^T{\beta }_X+Y^T\beta ,g=0,1,$$ (1)

where ϕ_g = Pr(G = g|X, Y ) is the conditional genotype distribution probability, β_X is a p-vector, and β is a m-vector (specifically β = Σ⁻¹γ). The multi-trait association amounts to testing H₀ : β = 0. A closely related approach is the MultiPhen method (O’Reilly et al., 2012), which assumed the proportional odds model (POM) for analyzing the three genotypes

$$log\frac{{\sum }_{k=0}^g{\varphi }_k}{{\sum }_{k=g+1}^2{\varphi }_k}={\stackrel{\sim }{\beta }}_{0g}+X^T{\stackrel{\sim }{\beta }}_X+Y^T\stackrel{\sim }{\beta },g=0,1.$$ (2)

The multi-trait association amounts to testing H₀ : β̃ = 0. In general the POM provides a good approximation to the ACL, and two approaches have similar performance for directly genotyped/observed SNPs (Wu and Pankow, 2015). We want to remark that the inverted regression approach has assumed that the genotypes are directly observed, and all existing methods have implicitly used the “best-guess” genotypes for imputed SNPs. For both the inverted regression and multivariate regression models, the main parameters of interest are a vector of length m. The inverted regression model has smaller number of nuisance parameters, p+2, compared to the multivariate regression model, m+mp+m(m+1)/2.

2.2 Genotype imputation

To facilitate SNP association studies and across studies meta-analysis, many ungenotyped SNPs are typically imputed based on outside reference panel of existing samples, e.g., the HapMap and 1000 genome project (Browning and Browning, 2009; Howie et al., 2009; Li et al., 2010). These imputation approaches rely on the intuition that individuals can share short stretches of haplotypes inherited from distant common ancestors. Once these stretches are identified using those genotyped SNPs, alleles for intervening SNPs that are not genotyped in the individuals can then be imputed based on those individuals with measured SNPs (i.e., reference panel samples) (Li et al., 2009, 2010). The typical imputation takes as input those haplotypes for polymorphic markers in the reference panel (e.g., the phased HapMap or 1000 genome chromosomes), and those directly genotyped markers in the individuals to be imputed. The sequence of markers are modeled as a mosaic of the set of reference haplotypes based on a Hidden Markov Model (HMM) (Li and Stephens, 2003; Stephens and Scheet, 2005). In the HMM, the reference haplotypes are treated as the hidden states, and the genotyped markers are treated as the observed signals. The HMM parameters are estimated iteratively and missing genotypes are sampled at each iteration based on the current HMM estimates. The sampled genotype counts over all iterations are aggregated together to give an indication of the relative probability of observing each possible genotypes (Li et al., 2010). The relative fractions of three genotypes comprise the imputation scores for an imputed SNP.

In the following, we develop two modeling approaches to incorporating the imputation scores into the inverted regression. The first approach is rooted in the weighted multinomial regression approach with robust GEE covariance estimates (Lipsitz et al., 1994; Preisser et al., 2002). The second approach is based on the fractional multinomial regression modeling (Murteira and Ramalho, 2014), which is very suited to model the imputed genotype proportions. We will further show that these two modeling approaches are equivalent.

2.3 Association test of imputed SNPs: weighted multinomial regression

We develop a computationally fast weighted regression approach, where the imputation scores are treated as weights. Since the same sample will be used three times (for the three genotype scores), we need to take into account their dependence in the estimation of parameter covariance. The model-based covariance estimate from the independent weighted regression will under-estimate the variation. We propose to use the robust GEE sandwich covariance (Liang and Zeger, 1986). Specifically here we adopt the approach of Lipsitz et al. (1994) for modeling the multinomial outcomes, and the modeling framework of Preisser et al. (2002) for incorporating weights in the GEE.

For a collection of n unrelated individuals, denote X_i as the covariate, and Y_i as the m-vector of outcomes for sample i = 1, … , n. Consider testing association of an imputed SNP. For the i-th sample, denote (p_i0, p_i1, p_i2) as the imputation scores (posterior probabilities) of genotype 0, 1, 2. Denote Pr(G_i = k|X_i, Y_i) = ϕ_ik, i = 1, … , n,k = 0, 1, 2. We convert the genotype score into a bivariate indicator of being the first two genotypes: the genotype scores 0/1/2 are coded as (1,0), (0,1), (0,0) respectively. For the i-th sample, the three imputed genotypes (0,1,2) are represented by the working vector G_i = (1, 0, 0, 1, 0, 0)^T. We define a probability vector μ_i = (ϕ_i0, ϕ_i1, ϕ_i0, ϕ_i1, ϕ_i0, ϕ_i1)^T. Denote the imputation score matrix W_i = diag(p_i0, p_i0, p_i1, p_i1, p_i2, p_i2). Assume a block-diagonal working covariance matrix V_i with the 2×2 diagonal blocks equal to diag(ϕ_i0, ϕ_i1)–(ϕ_i0, ϕ_i1)^T (ϕ_i0, ϕ_i1), which is the multinomial covariance matrix. Denote θ as the collection of all model parameters. We use the following estimating equations for model estimation and inference

$$\sum _{i=1}^n{U}_i=0,U_i=D_i^T{V}_i^{-1}{W}_i({\mathit{G}}_i-{\mathit{\mu }}_i),D_i=\frac{\partial {\mathit{\mu }}_i}{\partial \mathit{\theta }}.$$ (3)

The robust sandwich covariance of θ̂ can then be computed as $B^{-1}\left({\sum }_{i=1}^n{U}_i{U}_i^T\right)B^{-1}$, where $B={\sum }_{i=1}^n{D}_i^T{V}_i^{-1}{W}_i{D}_i$ and we plugin the estimated θ̂.

Let θ̂₂ denote the m-vector of estimated regression parameters of main interest for the multivariate traits Y (i.e., β in the ACL and β̃ in the POM). Denote the corresponding covariance of θ̂₂ as V. The statistic $Q={\widehat{\theta }}_2^T{V}^{-1}{\widehat{\theta }}_2$, which asymptotically has a null m-DF chi-square distribution, can be used to test the multi-trait association. When genetic effects are similar across traits, we can further improve the multi-trait association test power using a 1-DF statistic to test linear combinations of θ₂ following the line of O’Brien (1984). To test the similar or similar scaled effects across different traits, we propose the test statistics: $T={\mathbf{1}}_m^T{\widehat{\mathrm{\sum }}}_0^{-1}{V}^{-1}{\widehat{\theta }}_2/{({\mathbf{1}}_m^T{\widehat{\mathrm{\sum }}}_0^{-1}{V}^{-1}{\widehat{\mathrm{\sum }}}_0^{-1}{\mathbf{1}}_m)}^{1/2},T^{\prime }=S^T{\widehat{\mathrm{\sum }}}_0^{-1}{V}^{-1}{\widehat{\theta }}_2/{(S^T{\widehat{\mathrm{\sum }}}_0^{-1}{V}^{-1}{\widehat{\mathrm{\sum }}}_0^{-1}S)}^{1/2}$, where 1_m is a column vector of m ones, S = [diag(Σ̂₀)]^½, and Σ̂₀ is computed as the sample covariance matrix of residual vector of regressing Y on X (see Appendix for details). Their significance p-values can be computed based on the standard normal distribution. This generic GEE modeling approach can be readily generalized to analyze imputed SNPs using any inverted regression methods.

In the following, we show that the proposed GEE modeling approach is equivalent to a fractional multinomial regression model, which provides more intuitive justifications to model the imputed genotype scores.

2.4 Genotype based fractional multinomial regression model

For the ith individual, note that its imputation scores (p_i0, p_i1, p_i2) tell the relative fractions of three genotypes under ideal repeated sampling: for N individuals with the same characteristics (including covariate values) as the ith individual, N(p_i0, p_i1, p_i2) will be the observed counts of three genotypes, and naturally we can model them with a three-category multinomial distribution. Thus we can model the imputation scores with a multinomial distribution based quasi-likelihood, ${\ell }_i={\sum }_{k=0}^2{p}_{ik}log({\varphi }_{ik})$, and study the following quasi-likelihood for parameter estimation, $L={\sum }_{i=1}^n{\ell }_i$. This model is also known as the fractional multinomial regression model (Murteira and Ramalho, 2014). We maximize L to obtain the quasi-maximum likelihood estimates (QMLE) for parameters, θ̃ = arg max_θ L, and compute its asymptotic covariance matrix based on the GEE as follows. Denote ${\stackrel{\sim }{U}}_i=\partial {\ell }_i/\partial \mathit{\theta }={\sum }_{k=0}^2\frac{p_{ik}}{{\varphi }_{ik}}\frac{\partial {\varphi }_{ik}}{\partial \mathit{\theta }}$. The estimator θ̃ is obtained by solving estimating equations ${\sum }_{i=1}^n{\stackrel{\sim }{U}}_i=0$, and its robust sandwich covariance matrix can then be computed as Ṽ = B̃⁻¹ΩB̃⁻¹, where $\mathrm{\Omega }={\sum }_{i=1}^n{\stackrel{\sim }{U}}_i{\stackrel{\sim }{U}}_i^T$, and $\stackrel{\sim }{B}={\sum }_{i=1}^n{\partial }^2{\ell }_i/(\partial \mathit{\theta }\partial {\mathit{\theta }}^T)$ and we plugin the estimated θ̃. We can show that this QMLE will lead to the same estimates as the previous weighted GEE approach. Specifically we can show that Ũ_i = U_i (see appendix for technical derivations). This QMLE can be cast into a weighted multinomial regression model and can be readily and quickly solved using existing software.

Previous derivations have assumed the additive genetic model, and they can be easily extended to recessive and dominant genetic models (see Supplementary materials).

In the following we conduct simulation studies to investigate the performance of the proposed methods for testing the multi-trait association of imputed SNPs.

3 Simulation study

We simulate a standard normal covariate X₁ and an ancestry Bernoulli covariate X₂ with probability of 0.5 (population indicator). The SNP genotype G is simulated from a Binomial distribution, Binom(2,f₀), where the minor allele frequency (MAF) f₀ = p₀ + p₁X₂. We conducted simulations for testing m related traits of 1,000 unrelated individuals. Each time we simulate the m traits from a multivariate normal distribution with a compound symmetry correlation matrix with correlation ρ. The first trait has a variance of 2 and all the other traits have unit variance, ${\sigma }_1^2=2,{\sigma }_{k>1}^2=1$. We set E(Y_k) = 1 + 0.5X₁ + 0.5X₂ + γ_kG for odd index k, and E(Y_k) = 1+X₁ + X₂ + γ_kG for even index k. For a given SNP G, we simulate its imputation probabilities from the Dirichlet distribution with parameters (α₀, α₁, α₂), where α_G = τ and α_g = (1 − τ )/2 for g ≠ G, with larger τ reflecting higher imputation accuracy. We used 10⁶ experiments to evaluate the type I error, and 10⁴ experiments to evaluate the power under various combinations of (γ₁, … , γ_m). We conducted simulations for various parameter settings. Here we reported the results for m = 4, p₀ = 0.3, p₁ = 0.1, ρ = 0.2, 0.5, and τ = 0.8, 0.95. The conclusions remain the same for other settings.

We studied the two inverted regression methods, the ACL and POM based GEE tests. For comparison we included the multiple linear regression model (MLM) based efficient GEE score tests (Avery et al., 2011; He et al., 2013), which have been shown to appropriately control the type I errors and have the overall best performance compared to the other methods (e.g., TATES of van der Sluis et al., 2013 and other univariate test based methods) in extensive numerical studies. All methods reported three p-values based on the m-DF omnibus test and two 1-DF tests assuming common or common scaled effects. Denote the respective three tests as (Q_a, T_a, $T_a^{\prime }$) for ACL GEE test, (Q_o, T_o, $T_o^{\prime }$) for POM GEE test, and (Q_s, T_s, $T_s^{\prime }$) for the MLM GEE test. We use the imputed dosage as a covariate in the MLM GEE tests. In the appendix, we technically show that the MLM GEE tests are essentially based on a joint model of the multivariate traits with the imputation dosage as a covariate. As a by-product, we derive very fast numerical algorithms for genome-wide association test. For illustration, we also include the naive approach of modeling the “best-guess” genotypes for the two inverted regression methods, denoted as (Q̃_a, T̃_a, ${\stackrel{\sim }{T}}_a^{\prime }$) for the ACL, and (Q̃_o, T̃_o, ${\stackrel{\sim }{T}}_o^{\prime }$) for the POM respectively.

Table 1 summarizes the estimated type I errors. Overall we can see that for the two inverted regression (ACL and POM) based tests, using the “best-guess” genotypes leads to slightly conservative type I errors compared to their corresponding GEE tests that properly account for the imputation uncertainty. The ACL “best-guess” tests are generally more conservative compared to the corresponding POM “best-guess” tests, which control the type I error rate reasonably well. All ACL based tests appropriately control the type I errors. The POM GEE tests have slightly inflated type I errors at small significance level. The MLM GEE tests have well-controlled type I errors.

Table 1.

Type I error of testing four continuous traits. The MAFs of SNP are 0.3 and 0.4 in the two populations. Q is the 4-DF omnibus test, T and T′ are the 1-DF tests assuming common or common scaled effect. (Q_a, T_a, $T_a^{\prime }$) are the ACL GEE tests. (Q_o, T_o, $T_o^{\prime }$) are the POM GEE tests. (Q_s, T_s, $T_s^{\prime }$) are the MLM GEE tests. (Q̃_a, T̃_a, ${\stackrel{\sim }{T}}_a^{\prime }$) are the ACL tests using the “best-guess” genotypes. (Q̃_o, T̃_o, ${\stackrel{\sim }{T}}_o^{\prime }$) are the POM tests using the “best-guess” genotypes. The type I errors have been scaled by the nominal significance level α.

ρ = 0.2, τ = 0.8
α	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
10−4	1.13	1.08	1.07	0.76	0.82	0.80	1.32	1.31	1.29	0.86	0.96	0.98	0.89	1.01	1.05
10−3	1.09	1.07	1.06	0.84	0.89	0.89	1.15	1.13	1.17	0.94	1.01	1.02	0.96	1.00	1.00
10−2	1.05	1.03	1.04	0.92	0.95	0.95	1.08	1.05	1.05	0.99	0.99	0.99	0.98	0.99	1.01
ρ = 0.5, τ = 0.8
α	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
10−4	1.03	0.94	1.09	0.65	0.69	0.74	1.26	1.18	1.22	0.76	0.79	0.89	0.81	0.84	0.96
10−3	1.10	1.03	1.02	0.80	0.88	0.88	1.15	1.11	1.11	0.94	0.96	0.96	0.92	0.95	0.96
10−2	1.06	1.02	1.03	0.92	0.94	0.94	1.09	1.06	1.04	0.99	0.98	0.99	0.98	0.98	0.99
ρ = 0.2, τ = 0.95
α	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
10−4	0.95	1.00	0.99	0.72	0.83	0.81	1.48	1.25	1.20	0.92	0.94	0.96	0.69	0.92	0.93
10−3	1.05	1.03	1.05	0.82	0.84	0.90	1.17	1.09	1.10	0.96	0.92	0.97	0.97	0.98	1.02
10−2	1.03	1.02	1.01	0.94	0.95	0.95	1.06	1.05	1.04	0.99	1.00	1.00	0.98	1.01	1.00
ρ = 0.5, τ = 0.95
α	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
10−4	1.04	0.97	0.96	0.76	0.73	0.71	1.51	1.27	1.25	0.96	0.87	0.84	0.94	0.94	0.88
10−3	1.02	0.99	1.00	0.82	0.88	0.88	1.16	1.10	1.04	0.96	0.95	0.96	0.93	0.95	0.96
10−2	0.99	1.01	1.01	0.90	0.94	0.95	1.05	1.02	1.04	0.97	0.99	0.99	0.96	0.99	1.00

Table 2 and 3 summarize the power under τ = 0.8 and τ = 0.95 respectively. The 1-DF tests are the most powerful when either γ_j or γ_j/σ_j are close to each other. Not surprisingly using the “best-guess” genotypes leads to power loss for the two inverted regression (ACL and POM) based tests especially under lower imputation accuracy. The ACL GEE tests have comparable performance as the MLM GEE tests under relatively high imputation accuracy (τ = 0.95). For imputed SNPs with less accuracy (τ = 0.8), the ACL GEE tests have improved power compared to the MLM GEE tests. Overall the POM GEE tests have the largest power among all methods, which need to be interpreted with caution since POM GEE tests have slightly inflated type I errors as we have shown in Table 1. Under the same imputation uncertainty, when multiple traits have similar genetic effects, all tests have larger power under ρ = 0.2 compared to ρ = 0.5; while when genetic effects are different across traits, all tests have larger power under ρ = 0.5 compared to ρ = 0.2. Here joint multi-trait association test works well when combining highly correlated traits with heterogeneous genetic effects or lowly correlated traits with similar genetic effects.

Table 2.

Power of testing four traits at significance level α = 10⁻⁵. The MAFs of SNP are 0.3 and 0.4 in the two populations. The SNP imputation uncertainty parameter τ = 0.8. γ_i is the SNP coefficient.

ρ = 0.2, τ = 0.8
(γ1, γ2, γ3, γ4)	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
(0.3,0,0,0)	0.066	0	0.001	0.031	0	0	0.078	0	0.002	0.041	0	0.001	0.057	0	0.001
(0.3,0.2,0.1,0)	0.274	0.051	0.111	0.152	0.026	0.059	0.307	0.063	0.130	0.183	0.034	0.074	0.248	0.047	0.102
(.25,.18,.18,.18)	0.293	0.496	0.528	0.168	0.335	0.367	0.325	0.531	0.563	0.202	0.380	0.413	0.268	0.480	0.509
(0.2,0.2,0.2,0.2)	0.379	0.623	0.591	0.226	0.452	0.422	0.415	0.659	0.626	0.267	0.500	0.472	0.351	0.606	0.573
ρ = 0.5, τ = 0.8
(γ1, γ2, γ3, γ4)	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
(0.3,0,0,0)	0.216	0	0.001	0.116	0	0	0.246	0	0.001	0.143	0	0.001	0.195	0	0.001
(0.3,0.2,0.1,0)	0.341	0.004	0.028	0.200	0.002	0.013	0.375	0.005	0.034	0.236	0.002	0.018	0.313	0.004	0.026
(.25,.18,.18,.18)	0.085	0.176	0.218	0.040	0.101	0.129	0.102	0.196	0.242	0.052	0.119	0.150	0.073	0.166	0.206
(0.2,0.2,0.2,0.2)	0.137	0.309	0.250	0.070	0.190	0.149	0.157	0.336	0.274	0.088	0.220	0.172	0.121	0.293	0.236

Table 3.

Power of testing four traits at significance level α = 10⁻⁵. The MAFs of SNP are 0.3 and 0.4 in the two populations. The SNP imputation uncertainty parameter τ = 0.95. γi is the SNP coefficient.

ρ = 0.2, τ = 0.95
(γ1, γ2, γ3, γ4)	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
(0.3,0,0,0)	0.242	0	0.003	0.206	0	0.002	0.256	0	0.004	0.222	0	0.002	0.229	0	0.003
(0.3,0.2,0.1,0)	0.658	0.140	0.286	0.601	0.108	0.245	0.674	0.157	0.309	0.622	0.131	0.272	0.643	0.148	0.291
(.25,.18,.18,.18)	0.684	0.850	0.872	0.634	0.819	0.843	0.699	0.859	0.879	0.657	0.832	0.852	0.672	0.848	0.870
(0.2,0.2,0.2,0.2)	0.781	0.924	0.906	0.732	0.904	0.879	0.793	0.928	0.913	0.752	0.911	0.890	0.768	0.922	0.903
ρ = 0.5, τ = 0.95
(γ1, γ2, γ3, γ4)	Qa	Ta	$T_a^{\prime }$	Q̃a	T̃a	${\stackrel{\sim }{T}}_a^{\prime }$	Qo	To	$T_o^{\prime }$	Q̃o	T̃o	${\stackrel{\sim }{T}}_o^{\prime }$	Qs	Ts	$T_s^{\prime }$
(0.3,0,0,0)	0.571	0	0.001	0.515	0	0	0.588	0	0.001	0.543	0	0.001	0.557	0	0.001
(0.3,0.2,0.1,0)	0.742	0.010	0.084	0.693	0.006	0.063	0.756	0.012	0.102	0.717	0.009	0.079	0.731	0.013	0.091
(.25,.18,.18,.18)	0.278	0.442	0.518	0.239	0.396	0.470	0.292	0.455	0.526	0.255	0.418	0.486	0.268	0.436	0.514
(0.2,0.2,0.2,0.2)	0.417	0.666	0.580	0.367	0.617	0.526	0.432	0.677	0.589	0.390	0.633	0.547	0.403	0.662	0.577

We also performed simulation studies for less frequent and rare MAF (0.1, 0.05, and 0.01). The complete results are available at the supplementary materials. The overall conclusions remain the same.

4 ARIC GWAS of diabetes-related glycemic traits

The Atherosclerosis Risk in Communities (ARIC) study (The ARIC Investigators, 1989) is a multi-center prospective investigation of atherosclerotic disease in men and women aged 45–64 years at baseline. They were recruited from four U.S. communities: Forsyth County, North Carolina; Jackson, Mississippi; suburban areas of Minneapolis, Minnesota; and Washington County, Maryland. A total of 15,792 individuals participated in the baseline examination in 1987–1989. The vast majority of ARIC participants are of European (73%) or African ancestry (26%). Among 15,792 ARIC participants, we jointly analyzed the four fasting glucose levels of 5947 genotyped ARIC white participants who were non-diabetic at four visits measured approximately three years apart. Excluded from the analysis are a total of 9845 participants due to the following reasons: (1) 4314 participants are non-white; (2) 2751 participants do not complete all four visits; (3) 1556 participants have diabetes diagnosis or unknown diabetes status at any of the four visits; (4) 373 participants have no fasting glucose measurements for at least one of the four visits; (5) 851 participants do not have GWAS data. All ARIC participants have complete information on age, gender, and study center. The ARIC Study design, plasma glucose measurement, genotyping and other covariates have been described previously (Rasmussen-Torvik et al., 2010). The glucose levels had an average correlation of 0.55 between visits. We applied an additive genetic model and adjusted for age, gender and study center (population indicators).

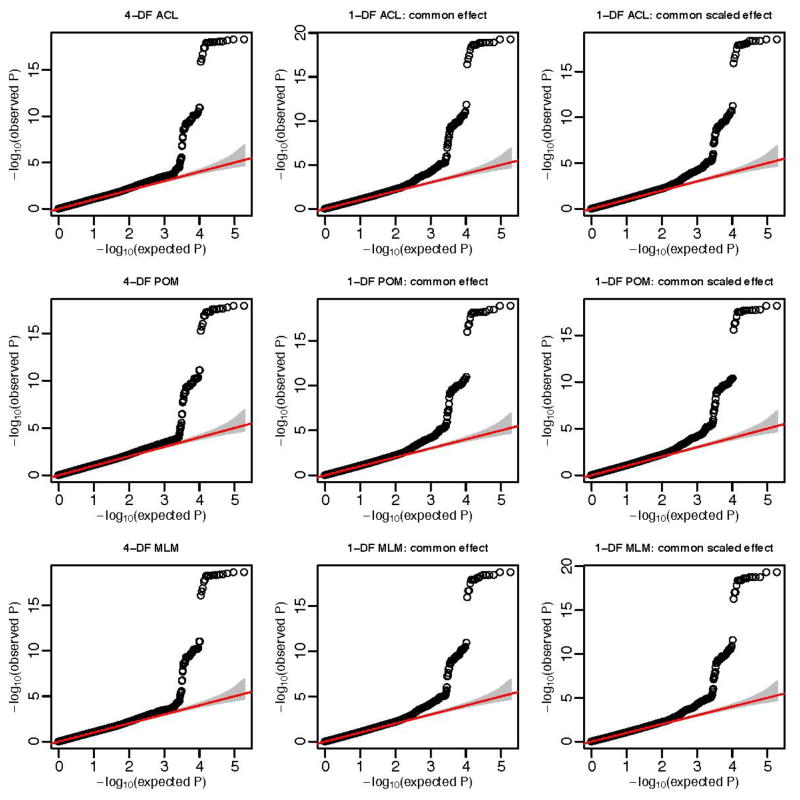
For illustration, we analyze those typed and imputed SNPs in chromosome 1 and 2. We test those common SNPs with MAF ≥ 0.05 and imputation R² ≥ 0.3, which leads to 163,048 and 189,023 SNPs in chromosome 1 and 2 respectively. There were no identified genome-wide significant SNPs (p-value ≤ 5 × 10⁻⁸) for chromosome 1, and multiple significant SNPs for chromosome 2. Specifically for the three tests: the m-DF omnibus test, and two 1-DF tests assuming common or common scaled effects, the ACL GEE tests (Q_a, T_a, $T_a^{\prime }$) identified 56, 60, and 60 significant SNPs, the POM GEE tests (Q_o, T_o, $T_o^{\prime }$) identified 56, 56, 59 SNPs, and the MLM GEE tests (Q_s, T_s, $T_s^{\prime }$) identified 56, 59, 60 SNPs. All the identified SNPs are genome-wide significant in a meta-analyses of 21 fasting glucose GWAS with around 46,186 non-diabetic participants conducted by the MAGIC Consortium (Dupuis et al., 2010). Compared to the MLM test $T_s^{\prime }$, the ACL test $T_a^{\prime }$ identified one additional genome-wide significant SNP, rs1260326, with p-value of 3.3 × 10⁻⁸. The p-value reported by the MAGIC meta-analysis of fasting glucose was 4.3 × 10⁻¹³. Compared to the POM test T_o, the ACL test T_a identified four additional genome-wide significant SNPs, rs1260326, rs574981, rs549410 and rs550151, with p-values of 3.3×10⁻⁸, 9.1×10⁻⁹, 9.1×10⁻⁹, and 7.5×10⁻⁹ respectively. Their respective p-values reported by the MAGIC meta-analysis of fasting glucose were 4.3 × 10⁻¹³, 8.6 × 10⁻¹⁴, 1.7 × 10⁻¹³, and 1.2 × 10⁻¹³.

All identified significant SNPs in chromosome 2 are imputed with imputation R² in the range of 0.90 to 0.9998. To our knowledge, all previous inverted regression approaches have implicitly used the “best-guess” genotypes. When using the “best-guess” genotypes, $T_a^{\prime }$ missed one significant SNP, rs1260326, $T_o^{\prime }$ missed three significant SNPs, rs574981, rs549410 and rs550151, and $T_s^{\prime }$ missed one SNP, rs1260326, at the genome-wide significance level, compared to their corresponding GEE tests using the imputation scores.

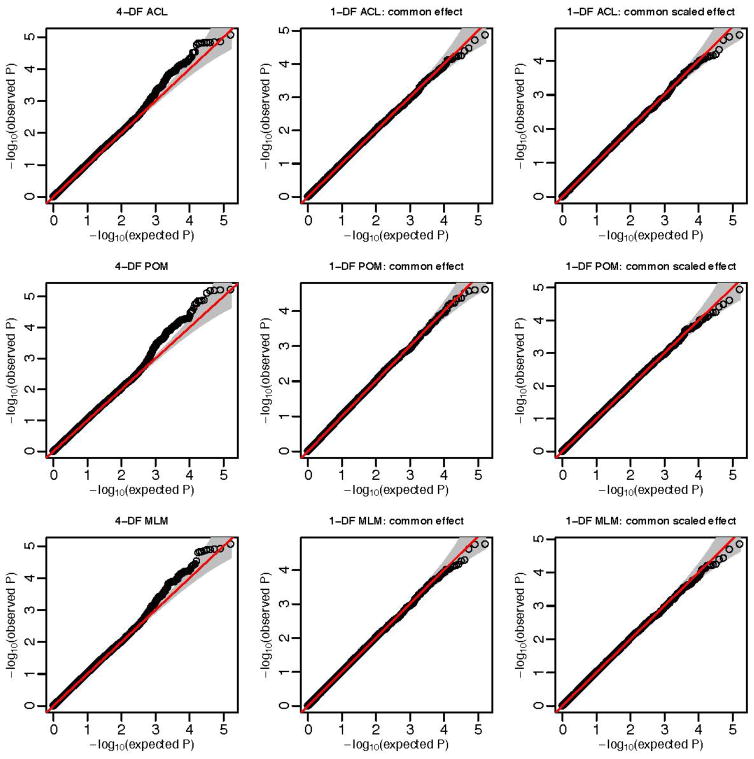
The QQ-plots of p-values for chromosome 1 and 2 SNPs are shown in figure 1 and 2 respectively. We also compute the genomic control (GC) parameters, which are the mean of the 1-DF chi-square test statistics, and the mean of the 4-DF chi-square test statistics scaled by four. The three methods have similar GC values: 1.01–1.02 for chromosome 1 and 1.04–1.10 for chromosome 2.

Figure 1.

QQ-plot for SNPs in chromosome 1.

Figure 2.

QQ-plot for SNPs in chromosome 2.

5 Discussion

Most existing GWAS have primarily focused on testing single trait associations, which have led to discovery of many genome-wide significant variants for many human diseases and traits. However for most complex human diseases and traits, the explained heritability or trait variance by these identified variants still remain very small, which indicates significant “missing heritability” and yet more variants with small or moderate effects to be discovered. Recently there have been many efforts of conducting joint association test of correlated traits that reflect common physiological processes to identify more interesting genetic variants and provide additional insights into the disease etiology. Testing multiple correlated traits can aggregate weak variant effects to improve the genetic association test power. Among the existing multi-trait association test methods, the inverted regression approach models the conditional distribution of genotypes on covariates and multivariate traits, and provides a convenient and powerful approach with competitive performance. However it is not straightforward to analyze imputed SNPs for the inverted regression models in contrast to the trait based regression modeling approach, which can readily use the imputed dosage as covariate. In this paper, we proposed a general GEE based inverted regression modeling method to appropriately and efficiently test the multi-trait association of imputed SNPs. We show that the naive approach of analyzing “best-guess” genotypes could lead to dramatic power loss, while the proposed GEE based modeling approach offers much improved power and has comparable or larger power compared to the dosage based trait regression modeling approach.

For genome-wide association analyses, speed and robustness are both key issues. The proposed GEE modeling approach is robust and computationally fast. It is worthwhile to explore the likelihood based approach (e.g., mixed effects modeling approach or more generally likelihood ratio test based approach), which could bring more power under correct model assumptions than the typically Wald test based GEE modeling approach.

In this paper, we have focused on the multiple continuous traits association test of single variants. It is worthwhile to extend the inverted regression methods to association test at the gene level (Guo et al., 2013; van der Sluis et al., 2015), and generally to joint association test of mixed outcomes.

Appendix

Equivalence of QMLE and weighted GEE estimates

In the weighted GEE approach, the three imputed genotypes (0,1,2) are represented by the working vector G_i = (1, 0, 0, 1, 0, 0)^T for the i-th sample. Denote a probability vector μ_i = (ϕ_i0, ϕ_i1, ϕ_i0, ϕ_i1, ϕ_i0, ϕ_i1)^T. Denote the imputation score matrix W_i = diag(p_i0, p_i0, p_i1, p_i1, p_i2, p_i2). Assume a block-diagonal working covariance matrix V_i with the 2 × 2 diagonal blocks equal to A_i = diag(ϕ_i0, ϕ_i1) − (ϕ_i0, ϕ_i1)^T (ϕ_i0, ϕ_i1), which is the multinomial covariance matrix. Denote θ as the collection of all model parameters. The weighted GEE for the i-th sample is defined as $U_i=D_i^T{V}_i^{-1}{W}_i({\mathit{G}}_i-{\mathit{\mu }}_i)$, where $D_i=\frac{\partial {\mathit{\mu }}_i}{\partial \mathit{\theta }}$. First note that

$$A_i^{-1}=\frac{1}{{\varphi }_{i0}{\varphi }_{i1}(1-{\varphi }_{i0}-{\varphi }_{i1})}\left[\begin{array}{cc}{\varphi }_{i1}(1-{\varphi }_{i1})& {\varphi }_{i0}{\varphi }_{i1}\\ {\varphi }_{i0}{\varphi }_{i1}& {\varphi }_{i0}(1-{\varphi }_{i0})\end{array}\right]$$

and we can check that $A_i^{-1}{(1-{\varphi }_{i0},-{\varphi }_{i1})}^T={({\varphi }_{i0}^{-1},0)}^T,A_i^{-1}{(-{\varphi }_{i0},1-{\varphi }_{i1})}^T={(0,{\varphi }_{i1}^{-1})}^T$, and $A_i^{-1}{(-{\varphi }_{i0},-{\varphi }_{i1})}^T={(-{\varphi }_{i2}^{-1},-{\varphi }_{i2}^{-1})}^T$. Therefore we have

$$U_i=\sum _{k=0}^1\frac{p_{ik}}{{\varphi }_{ik}}\frac{\partial {\varphi }_{ik}}{\partial \mathit{\theta }}-\frac{p_{i2}}{{\varphi }_{i2}}\left\{\sum _{k=0}^1\frac{\partial {\varphi }_{ik}}{\partial \mathit{\theta }}\right\}.$$

Note that ϕ_i2 = 1 − ϕ_i0 − ϕ_i1, and hence we have

$$U_i=\sum _{k=0}^2\frac{p_{ik}}{{\varphi }_{ik}}\frac{\partial {\varphi }_{ik}}{\partial \mathit{\theta }}={\stackrel{\sim }{U}}_i.$$

GEE score test of multiple continuous traits

Here we show that for multiple continuous traits, the MLM GEE test of He et al. (2013) is essentially based on a joint model of the multivariate traits with imputation dosage as a covariate. Given the observations, denote the n × p covariate matrix as X (intercept included), the genotype dosage vector as G, and the kth outcome vector as Y_k, k = 1, … , K. Consider the following joint multivariate linear regression model, Y_k = Xα_k + Gβ_k + E_k, where E_k = (ε_k1, … , ε_kn)^T. We model the error vector with a zero-mean multivariate normal distribution with $\mathit{Var}({\epsilon }_{ki})={\sigma }_k^2$ and Corr(ε_ki, ε_li) = ρ_kl. Denote the n × n projection matrix H = X(X^TX)⁻¹X^T. The scaled score statistic for testing β_k is u_k = (Y_k − HY_k)^TG/σ̂_k. Denote the score vector U = (u₁, … , u_K)^T. Note that we can equivalently write $u_k=Y_k^T(G-HG)/{\widehat{\sigma }}_k$. Hence we have asymptotically Var(u_k) = ||G−HG||², and Cov(u_k, u_l) = ||G−HG||²ρ_kl. The MLM GEE test is based on U and its estimated covariance, $U^T\widehat{\mathit{Cov}}{(U)}^{-1}U$, which asymptotically follows a K-DF chi-square distribution under null. He et al. (2013) consistently estimated $\widehat{\mathit{Cov}}(U)$ based on the efficient score vectors (Lin, 2005a,b). We can easily verify that the efficient score vectors are Z_k = (Y_k − HY_k) ∘ (G − HG)/σ̂_k, where ∘ is the Hadamard product (matrix element-wise product). Note that the residual vectors Y_k – HY_k and H can be pre-computed, and we just need to compute G – HG to test the genome-wide multi-trait associations.

1-DF multi-trait association test

Consider U = a^T θ̂₂. U asymptotically follows a normal distribution, U ~ N(a^T η, a^TV a), where η is the true value of θ₂. For the ACL (1), we have θ₂ = Σ⁻¹γ, where Σ is the covariance matrix of Y and γ is the corresponding marginal genetic effects. For the POM (2), we assume θ₂ ≈ Σ⁻¹γ since the POM approximates the ACL. Assuming a common genetic effect for all traits, we have η = νΣ⁻¹1_m. The effect size of U is then proportional to ν(a^TΣ⁻¹1_m)/(a^TV a)^½ = νb^TV ^−½Σ⁻¹1_m, where b = V ^½a/(a^TV a)^½ (note b^T b = 1). Taking b ∝ V ^−½Σ⁻¹1_m will maximize the effect size. Therefore we use the following statistic $T={\mathbf{1}}_m^T{\mathrm{\sum }}^{-1}{V}^{-1}{\widehat{\theta }}_2/{({\mathbf{1}}_m^T{\mathrm{\sum }}^{-1}{V}^{-1}{\mathrm{\sum }}^{-1}{\mathbf{1}}_m)}^{1/2}$. With a common scaled genotype effect for all traits, we have η = νΣ⁻¹S, where S = [diag(Σ)]^½. Similarly we can derive T′ = S^TΣ⁻¹V⁻¹θ̂₂/(S^TΣ⁻¹V⁻¹Σ⁻¹S)^½. In practice we estimate Σ by Σ̂₀, the sample covariance matrix of Ỹ, the residual vector of regressing Y on X.