3D-printed eagle eye: Compound microlens system for foveated imaging

A highly miniaturized vision system is realized by directly 3D-printing different multilens objectives onto a CMOS image sensor.

Abstract

We present a highly miniaturized camera, mimicking the natural vision of predators, by 3D-printing different multilens objectives directly onto a complementary metal-oxide semiconductor (CMOS) image sensor. Our system combines four printed doublet lenses with different focal lengths (equivalent to f = 31 to 123 mm for a 35-mm film) in a 2 × 2 arrangement to achieve a full field of view of 70° with an increasing angular resolution of up to 2 cycles/deg field of view in the center of the image. The footprint of the optics on the chip is below 300 μm × 300 μm, whereas their height is <200 μm. Because the four lenses are printed in one single step without the necessity for any further assembling or alignment, this approach allows for fast design iterations and can lead to a plethora of different miniaturized multiaperture imaging systems with applications in fields such as endoscopy, optical metrology, optical sensing, surveillance drones, or security.

INTRODUCTION

Direct three-dimensional (3D) printing of micro-optical and nano-optical components by femtosecond direct laser writing has recently revolutionized the field of micro-optics. While the first publications covered single optical components, such as microlenses (1), diffraction gratings (2), waveguides (3), free-form surfaces (4, 5), phase masks (6), or photonic crystals (7), the field has considerably developed in terms of complexity. Hybrid refractive-diffractive components (8), hybrid free-form lenses that are directly printed onto optical fibers (9), or even multicomponent optical systems (10, 11) exhibit a huge potential for many fields of application. The main advantages compared to traditional fabrication methods, such as microprecision machining (12), nanoimprint lithography, or traditional wafer-level approaches [such as liquid phase lens fabrication (13)], are an almost unrestricted design freedom, one-step fabrication without the necessity for subsequent assembly and alignment, and the flexibility to write on arbitrary substrates. Gissibl et al. (11) were the first to demonstrate multicomponent objective lenses directly printed onto a complementary metal-oxide semiconductor (CMOS) imaging sensor in a single step. The aim of this work is to further unleash the potential of this technology by creating a multiaperture foveated imaging system.

Foveated vision systems are very common in the animal world, especially among predators (14). Many tasks do not require an equal distribution of spatial resolution over the field of view (FOV). However, the central area near the optical axis should exhibit the highest resolution. This is the same in humans, where the cones in the eye are located at the so-called fovea, which gives the highest acuity in vision—thus the term “foveated imaging.” In eagles, this physiological effect is particularly pronounced, which is why foveated imaging is also sometimes called “eagle eye vision.” Similarly, technical applications, such as drone cameras, robotic vision, vision sensors for autonomous cars, or other movable systems, benefit from a higher resolution at the center of their FOV. Various publications present foveated imaging systems for different purposes (15–20).

Multiaperture miniaturized cameras are known for their flat design and usually use stitching of the FOV to combine the small subimages created by a specially designed microlens array into one larger image (21, 22). Foveated systems are of particular relevance if their bandwidth is limited by the size of detector pixels or by the readout time (23). In these cases, an optimum distribution of object space features on the limited spatial or temporal bandwidth becomes essential. Because of the high quality of our microimaging systems, optical performance and possible miniaturization are mainly limited by the size of the detector pixels. Therefore, we developed a multiaperture design that combines four aberration-corrected air-spaced doublet objectives with different focal lengths and a common focal plane that is situated on a CMOS image sensor. Particularly beneficial is the ability to create aspherical free-form surfaces, which are heavily used in the lens design.

Figure 1 shows a sketch of the setup and how the pixel data are subsequently fused to form the foveated image. Each objective lens creates an image of the same lateral size on the chip. However, because of the varying FOVs, the telephoto lens (20° FOV) magnifies a small central section of the object field of the 70° lens. Appropriate scaling and overlaying of the images thus lead to a foveated image with increasing object space resolution toward the center of the image. To resolve features with a certain spatial frequency in object space, the Nyquist limit requires at least twice the spatial frequency for the detector pixels in image space. In the case of the central telephoto lens, the same number of pixels covers only ~29% of the overall FOV. This means that the Nyquist frequency in the center is increased by a factor of ~3.5, allowing the resolution of significantly smaller features. This is indicated by the different pixel sizes in Fig. 1B.

Fig. 1. Working principle of the 3D-printed foveated imaging system.

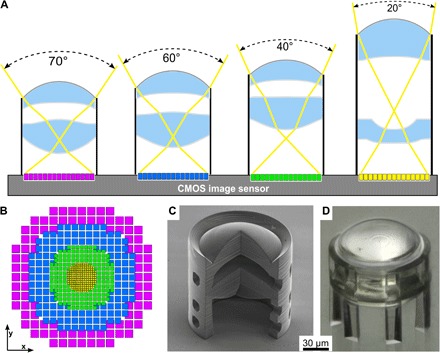
(A) System of four different compound lenses on the same CMOS image sensor, combining different FOVs in one single system. The lenses exhibit equivalent focal lengths for a 35-mm film from f = 31, 38, 60, and 123 mm. (B) Exemplary fusion of the pixelized object space content to create the foveated image. (C) SEM image of a 3D-printed doublet lens. The individual free-form surfaces with higher-order aspherical corrections are clearly visible. (D) Light microscope image of the 60° FOV compound lens.

RESULTS AND DISCUSSION

Figure 2 shows the image sensor after 3D-printing multiple groups of the foveated imaging systems directly on the chip. When compared to the scanning electron microscope (SEM) micrograph in Fig. 1C, the surfaces of the lenses appear less smooth and exhibit ridges on the surfaces. This can be partly explained by the depth of field stitching of the digital microscope, leading to artifacts. Furthermore, back reflections and interference fringes from inner surfaces become visible, which is not the case for SEM images. The ridges lead to an increased amount of stray light and reduce the overall contrast of the images. Further details about the surface quality can be found in Gissibl et al. (9, 11). To assess the optical performance without the influence of the chip, we characterized the lenses on a glass slide beforehand.

Fig. 2. 3D-printed four-lens systems on the chip.

(A) CMOS image sensor with compound lenses directly printed onto the chip. The change in color on the sensor surface results from scratching off functional layers, such as the lenslet array and the color filters. (B) Detail of one lens group with four different FOVs for foveated imaging forming one camera. The combined footprint is less than 300 μm × 300 μm.

Figure 3 compares the normalized on-axis modulation transfer function (MTF) contrast as a function of angular resolution in object space for the four different lenses after measurement with the knife edge method. As expected, systems with longer focal lengths and smaller FOVs exhibit higher object space contrast at higher resolutions because of their telephoto zoom factor. Compared to the design MTF, which is diffraction-limited or close to the diffraction limit, there is a significant loss in contrast, which can be explained by imperfect manufacturing. The dashed vertical lines indicate the theoretical resolution limit due to the pixel pitch of the imaging sensor. All systems deliver more than 10% of contrast at the physical limits of the sensor, which means that the resolution is limited by pixel pitch. More specifically, the pixel response function strongly suppresses all spatial frequencies above the ones indicated by the vertical lines. Because of the variation in magnification, the aliasing in the case of wide FOV systems is the limitation on angular resolution. Because the lenses for the outer zones of the foveated image are used off-axis, less MTF contrast has to be expected and imaging might not be pixel-limited in every case. However, some field-dependent aberrations, such as field curvature, can be minimized by readjusting the back focal distance for each of the doublet lenses individually. Off-axis MTF measurements of very similar lenses can be found in Gissibl et al. (11). MTF curves for the systems with FOVs of 40° to 70° show a similar optical performance in object space as a result of more similar f numbers (Table 1) and geometries. Nonetheless, using different lenses is still justified as long as the resolution is pixel-limited and a redistribution of sensor spatial bandwidth is desired.

Fig. 3. Design and measurement of normalized MTF contrast in object space as a function of angular resolution.

The data do not include the transfer function of the CMOS image sensor and are obtained by knife edge MTF measurements of the samples printed on a glass slide. The dashed vertical lines indicate the cutoff spatial frequency of the pixel response function above which the imaging resolution is strongly suppressed. The dashed horizontal line marks the 10% contrast limit, which was used as the criterion for resolvability in this work.

Table 1. Selected parameters of the designed lens systems.

	Lens 1	Lens 2	Lens 3	Lens 4
FOV (°)	70	60	40	20
Visible object diameter at a distance of 1 m (m)	2.75	1.73	0.84	0.36
Focal length (μm)	64.6	78.3	123.9	252.2
f Number	0.7	0.8	1.2	2.6
Hyperfocal distance (mm)	6.4	7.2	8.1	7.3
Fresnel number at λ = 550 nm	70	58	36.7	18
35-mm Equivalent focal length (mm)	31	38	60	123

Figure 4 shows the simulated and measured results for four cases. Figure 4A exhibits a comparison between measured and simulated imaging performance of lens 1 with a 70° FOV printed on a glass slide and imaged through a microscope. Because the simulated results do not include surface imperfections and scattering, a smaller overall contrast is the most striking difference. Figure 4B compares the foveated images of lenses 1 to 4. Both results exhibit visible improvement in resolved features for the central part. If the pixelation effects of the image sensor are taken into account, all images will lose resolution. Figure 4C shows the simulation results of lens 1 if a pixel size of 1.4 μm is assumed and compares it to the data attained on the chip. Because the chip does not perfectly record the image, there is a notable difference in quality if it is compared to the imaging on a glass slide. This effect can be explained by the chip plane being not perfectly aligned with the focal plane and by the fact that the microlens array on the chip, which is important for the imaging performance, was removed before 3D printing. After creating the foveated images (Fig. 4D), the imaging resolution is considerably increased toward the center of the images. Although the measured image does not completely achieve the quality of the simulated one, a significant improvement is visible. By using more advanced image fusion algorithms, it will be possible to further improve the image quality and increase the resolution toward the center in a smoothly varying fashion. However, the implementation of these approaches is beyond the scope of this paper.

Fig. 4. Comparison of simulation and measurement for the foveated imaging systems.

(A) Imaging through a single compound lens with a 70° FOV. (B) Foveated images for four different lenses with FOVs of 20°, 40°, 60°, and 70°. The measurement for (A) and (B) was carried out on a glass substrate. (C) Same as (A) but simulated and measured on the CMOS image sensor with a pixel size of 1.4 μm × 1.4 μm. (D) Foveated results from the CMOS image sensor. Comparison of the 70° FOV image with its foveated equivalents after 3D-printing on the chip. (E) Measured comparison of the test picture “Lena.” (F) Measured imaging performance for a Siemens star test target. (G) Simulated image for a single-lens reference with an image footprint comparable to the foveated system. (H and I) Geometry of reference lens and foveated system at the same scale.

To further demonstrate the potential of our approach, we used the test image “Lena” (24) and a Siemens star as targets (Fig. 4, E and F). In both examples, the center of the original images contains more details than the outer parts. Using our foveated approach, the totally available bandwidth is optimized such that the important parts (center) are transferred with a higher spatial bandwidth (resolution) compared to the less important outer areas in the pictures. The results confirm markedly that our multiaperture system delivers superior images. The advantages of a foveated system (Fig. 4I) are further shown in a simulated comparison of the four-lens system with a single-lens reference (Fig. 4H) having the same image footprint and FOV (70°). While the single-lens system is bulkier and requires more time for fabrication, its resolution in the center of the FOV is considerably lower than that for the foveated image (Fig. 4G). Although the numbers “2” and “3” are readable in the center of Fig. 4D, they are not resolvable in the nonfoveated case.

CONCLUSION

Our work demonstrates for the first time direct 3D printing of varying complex multicomponent imaging systems onto a chip to form a multiaperture camera. We combine four different air-spaced doublet lenses to obtain a foveated imaging system with an FOV of 70° and angular resolutions of >2 cycles/deg in the center of the image. At the moment, the chip dimensions and pixel size limit the overall systems dimensions and our optical performance, whereas future devices can become smaller than 300 μm × 300 μm × 200 μm in volume and, at the same time, transfer images with higher resolution. The method thus enables considerably smaller imaging systems as compared to the state of the art. To the best of our knowledge, there are no fabrication methods available that can beat this approach in terms of miniaturization, functionality, and imaging quality. Further improvements would include antireflection coatings on the lenses, either by coatings or by nanostructuring; the use of triplets or more lens elements for aberration correction; and the inclusion of absorbing aperture stops.

With fabrication times of 1 to 2 hours for one objective lens, cheap high-volume manufacturing is difficult at the moment. However, printing just the shell and a lamellar supporting frame and direct ultraviolet curing (8) can reduce the fabrication time. In addition, parallelization of the printing process can help to scale up the fabrication volumes. Finally, in some applications, such as endoscopy, high-throughput manufacturing is not desired as much as are functionality and optical performance. Another problem that is especially prevalent in multiaperture designs is the suppression of light from undesired angles, reducing overall contrast and potentially leading to ghost images. Within the all-transparent material system, special structures could be designed to guide light into uncritical directions by refraction or total internal reflection. However, it would be more favorable to use real absorptive structures. These could be created by filling predefined cavities with black ink or directly depositing black metal, among others.

As an example of how this kind of device can be used and outperform a conventional camera of similar size, we would see the usage in a small microdrone, which, similar to an insect, would be capable of transmitting a wide-field overview and, at the same time, offer detailed imaging of a certain region of interest as well. Similarly, an application in capsule endoscopy with directed vision or as a movable vision sensor on a robotic arm offers a broad range of opportunities.

MATERIALS AND METHODS

The 3D-printing technology used is almost unrestricted in terms of fabrication limitations. It offers high degrees of freedom and unique opportunities for the optical design. However, finding the optimum system can become more difficult because the parameter space is much less constrained as compared to many classical design problems. Because of the mature one-step fabrication process, the challenges of the development are—in comparison to competing manufacturing methods—thus shifted from technology toward the optical design.

To ensure an efficient use of the available space, we designed four different two-lens systems with full FOVs of 70°, 60°, 40°, and 20°. The numbers were chosen based on the achievable performance in previous experiments and such that each lens contributed to the foveated image with similarly sized sections of the object space. Table 1 shows an overview of the resulting parameters. Because the lens stacks and support materials were all fully transparent, it was important to keep the aperture stop on the front surface during design. Otherwise, light refracted and reflected by the support structures would negatively influence the imaging performance. Buried apertures inside the lenses were not possible until now because absorptive layers could not be implemented by femtosecond 3D printing. Because of the scaling laws of optical systems (25, 26), small f numbers could be easily achieved. The aperture diameter was 100 μm for all lenses. As a restriction, the image circle diameter was set to 90 μm.

Before simulation and optimization, it is important to determine the best-suited method. The Fresnel numbers of all systems indicate that diffraction does not significantly influence the simulation results (Table 1). Therefore, geometric optics and standard ray tracing can be used to design the different lenses. We used the commercial ray tracing software ZEMAX. Because the fabrication method posed no restrictions for the surface shape, the aspheric interfaces up to the 10th order were used. As a refractive medium, the photoresist IP-S of the company Nanoscribe GmbH was implemented based on previously measured dispersion data. After local and global optimization, the resulting designs revealed a diffraction-limited performance (Strehl ratio >0.8) for most of the lenses and field angles. The ray tracing design was finalized polychromatically with direct MTF optimization, which includes diffraction effects at the apertures. Compared to conventional single-interface microlenses, the close stacking of two elements offered significant advantages and was crucial for the imaging performance. On the one hand, pupil positions and focal lengths can be changed independently, which allows for real telephoto and retrofocus systems. On the other hand, aberrations such as field curvature, astigmatism, spherical aberration, and distortion can be corrected effectively.

After the optical design, the final results were transferred to computer-aided design software. In terms of support structure design, it was important to find a good trade-off between rigidity and later developability of the inner surfaces. To date, the best results had been achieved with open designs based on pillars, as shown in Fig. 1D. All of the lens fixtures had an outer diameter of 120 μm.

The fabrication process itself was described in detail by Gissibl et al. (9). Figure 5 shows the different stages of the development process. To measure the imaging performance, samples had been 3D-printed onto glass substrates as well as onto a CMOS imaging sensor (Omnivision 5647). This chip offers a pixel pitch of 1.4 μm, which resulted in single images with ~3240 pixels. Using a state-of-the-art sensor with a 1.12-μm pixel pitch would increase this number to ~5071 pixels. To improve the adhesion of the lenses, the color filter and microlens array on the sensor had to be removed before 3D-printing. Figure 2 shows the sensor with nine groups of the same four objectives. Each group forms its own foveated camera and occupies a surface area of less than 300 μm × 300 μm. The filling factor of ~0.5 still offers room for improvement, although, in principle, it is possible to design the system such that the four separate lenses are closely merged into one single object, which is then 3D-printed in one single step.

Fig. 5. Development cycle of different lens systems.

FOVs varying between 20° and 70°. The process chain can be separated into optical design, mechanical design, 3D printing, and measurement of the imaging performance using a USAF 1951 test target (top to bottom).

To characterize the optical performance without pixelation effects, we printed the four different compound lenses onto glass slides. Because the lenses were designed for imaging from infinity and their focal lengths were smaller than 260 μm, the hyperfocal distance was about 8 mm (Table 1) and objects from half this distance to infinity remained focused. To assess the imaging quality, we reimaged the intermediate image formed by the lenses with an aberration-corrected microscope. Measurements of the MTF based on imaging a knife edge were performed in the same way as previously described (11).

The foveated camera performance was evaluated after 3D-printing on the image chip. The sensor device was placed at a distance of 70 mm from a target, which consisted of different patterns printed onto white paper. The target was illuminated from the backside with an incoherent white light source. The image data from the chip were then read out directly. It has to be noted that the chip and the readout software automatically performed some operations with the images, such as color balance or base contrast adjustment. However, there was no edge enhancement algorithm used that would skew the displayed results. Because of their different f numbers, all lenses led to a different image brightness. To compensate for this effect, we adjusted the illumination lens such that approximately the same optical power was transferred to the image for all four lenses.

The images were then separated manually with external software. For proof-of-principle purposes, it was not necessary to fully automate the image fusion process and thus stitching of the partial pictures was performed manually.