Frontier Molecular Orbital Contributions to Chlorination versus Hydroxylation Selectivity in the Non-Heme Iron Halogenase SyrB2

Abstract

The ability of an Fe^IV=O intermediate in SyrB2 to perform chlorination vs. hydroxylation was computationally evaluated for different substrates that had been studied experimentally. The π-trajectory for H-atom abstraction (Fe^IV=O oriented perpendicular to the C—H bond of substrate) was found to lead to the S = 2 five-coordinate HO—Fe^III—Cl complex with the C^• of the substrate, π-oriented relative to both the Cl⁻ and OH⁻ ligands. From this ferric intermediate, hydroxylation is thermodynamically favored, but chlorination is intrinsically more reactive due to the energy splitting between two key redox-active dπ* frontier molecular orbitals (FMOs). The splitting is determined by the differential ligand field effect of Cl⁻ vs. OH⁻ on the Fe center. This makes chlorination effectively competitive with hydroxylation. Chlorination vs. hydroxylation selectivity is then determined by the orientation of the substrate with respect to the HO—Fe—Cl plane that controls either the Cl⁻ or OH⁻ to rebound depending on the relative π-overlap with the substrate C radical. The differential contribution of the two FMOs to chlorination vs. hydroxylation selectivity in SyrB2 is related to a reaction mechanism that involves two asynchronous transfers: electron transfer from the substrate radical to the iron center followed by late ligand (Cl⁻ or OH⁻) transfer to the substrate.

Graphical abstract

Introduction

Mononuclear non-heme iron (NHFe) enzymes are crucial catalysts in many vital biological processes.^1,2 Their high reactivity and selectivity towards chemical functionalization of unreactive C—H bonds have stimulated significant efforts from different fields of chemistry to elucidate their reaction mechanisms and the factors contributing to their enzymatic efficiency. One such NHFe enzyme is the chloride, O₂ and α-ketoglutarate dependent NHFe halogenase SyrB2.

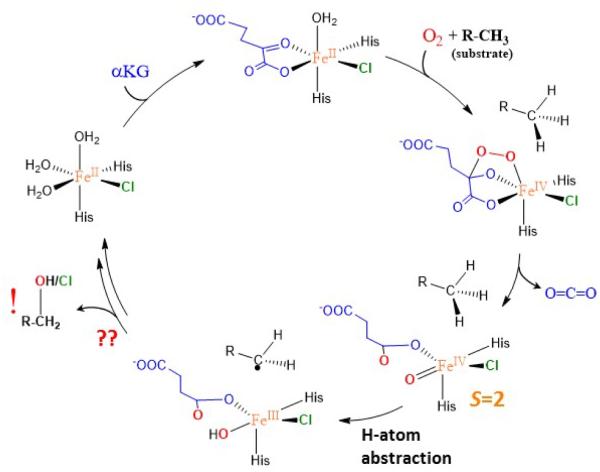
SyrB2 was discovered in the biosynthetic pathway of the phytotoxin syringomycin E (top of Scheme 1).^{3, 4} SyrB2 was found to catalyze chlorination of the native substrate L-threonine that is attached to a small acyl carrier protein (ACP) through its phosphopanteteine linker. As for other members of the NHFe family, SyrB2 activates dioxygen to generate a high-spin (S = 2) Fe^IV=O intermediate that further abstracts an H-atom from the C—H bond of the substrate for its subsequent functionalization (chlorination in SyrB2). The Fe^IV=O intermediate in SyrB2 was trapped and characterized using Mössbauer, Fe K-edge XAS and EXAFS spectroscopies.⁵ The geometric structure of this intermediate was later defined using nuclear vibrational resonance spectroscopy and density functional theory calculations. This study suggested a π-orientation of the oxo group relative to the native C—H bond (in this orientation, the oxo is oriented away from the substrate cavity as shown in Scheme 1 bottom right). ⁶ The π-orientation was proposed to be an important prerequisite for chlorination. More recently, this π-orientation of the Fe—oxo axis relative to the substrate was also implied in a related NHFe halogenase, WelO5. ⁷ Low temperature magnetic circular dichroism spectroscopy in combination with quantum chemical calculations were used to define the electronic structure properties associated with geometric structure of the (SyrB2)Fe^IV=O intermediate.⁸ The study revealed a π-anisotropy of the Fe^IV=O bond with the enhanced π-reactivity in the direction of the substrate cavity. Besides chlorination, SyrB2 was also demonstrated to catalyze hydroxylation depending on the substrate⁹ or azidation/nitration if the non-native (N₃⁻or NO₂⁻) anions were present in SyrB2 (instead of Cl⁻).¹⁰ The substrate-dependent selectivity was attributed to a substrate positioning with respect to the Fe center.^9,11 This was investigated by HYSCORE spectroscopy applied to the {FeNO}⁷ complex in SyrB2 with different deuteriated substrates.¹¹ The perpendicular orientation of the NO group relative to the substrate is consistent with the previously defined π-orientation of the oxo group with respect to the substrate C–H bond.

Scheme 1.

Proposed catalytic cycle of SyrB2.

Reactivity and selectivity of the halogenase SyrB2 have also captivated the attention of theoretical groups.^{12,13,14,15,16} These computational studies proposed various reaction mechanisms for chlorination vs. hydroxylation: (i) protonation of the Cl—Fe^III—OH intermediate to form Cl—Fe^III—OH₂; ¹² (ii) concomitant H-atom abstraction and radical chlorination; ¹³ (iii) propensity for hydroxylation vs. halogenation dependent on the delivery of the substrate into the cavity; ¹⁴ (iv) coordination isomerism of the Cl—Fe^IV=O intermediate;¹⁵ and (v) coordination isomerism of the Cl—Fe^IV—OH intermediate. ¹⁶ However, none of these calculations reflected the experimental data, in particular the NRVS-determined structure of (SyrB2)Fe^IV=O,⁶ the X-ray characterization of the related halogenase WelO5,⁷ or substrate dependent selectivity.⁹

In the present study we build on our previous combined experimental and theoretical investigations of the geometric and electronic structures of Fe^IV=O in SyrB2. The geometrical structural models of the active site of SyrB2 and DFT calculations calibrated to these results are employed to complete the catalytic cycle and provide insight into the key physicochemical factors contributing to chlorination vs. hydroxylation selectivity in SyrB2.

2. Computational Details

2.1 Structural Model of SyrB2

The cluster models of the active site of SyrB2 in the presence of a substrate consist of one Fe center, the Cl⁻/ OH⁻ ligands (for the intermediate resulting from H-atom abstraction by the Fe^IV=O), one crystal water molecule, truncated (His₁₁₆, His₂₃₅, succinate) ligands, truncated second-shell (Arg₂₅₄, Thr₁₄₃, Glu₁₀₂) residues, and a substrate radical fragment with the thiocarboxylic group (see Figure S1A in Supporting Information). The truncated models with the L-threonine/L-norvaline/L-aminobutyric substrates consist of 89/89/86 atoms. Starting Cl—Fe^III—OH structures for the chlorination and hydroxylation reactions were prepared from the O₂ activation and H-atom abstraction steps as described in refs 6 and 8 (see also Figure S1B).

2.2 Density Functional Theory Calculations

Unless indicated otherwise, all DFT calculations were performed using the G09 program.¹⁷ The hybrid three-parameter Becke’s (B3LYP)¹⁸ functional with the zero-damping empirical correction to dispersion (+D3)¹⁹ was used throughout. All of the geometry optimizations of the cluster models were carried out using the def2-SVP basis set, whereas the single-point energies were recomputed with the def2-TZVP basis set. In single-point calculations, to allow for solvation effects, the polarizable continuum model (PCM) was used with a dielectric constant reflecting the protein environment (ε_r=4.0). In this case, the PCM appears to be a plausible approach as judged from the comparison with QM/MM calculations from ref 16 that provide reaction energies for chlorination vs. hydroxylation that are comparable to results from this study. The smaller models used in section 3.3 were optimized in the gas phase at the B3LYP+D3/def2-TZVP level of theory. Reaction and activation Gibbs free energies were evaluated using vibrational analyses of systems with fixed atoms²⁰ according to the equation:

$$\Delta G^{(\ne )}=\Delta E_{el,solv}^{(\ne )}+\Delta E_{ZPE}^{(\ne )}-RT\Delta \text{ln}{q}_{vib}^{(\ne )}{q}_{rot}^{(\ne )}{q}_{trans}^{(\ne )}$$

where $\Delta E_{el,solv}^{(\ne )}$ is the reaction (or activation) energy of the solvated system (at the B3LYP+D3/def2-TZVP/PCM_(εr=4.0)//B3LYP+D3/def2-SVP level), $\Delta E_{ZPE}^{(\ne )}$ is the change in zero-point energy, and $-RT\Delta \text{ln}{q}_{vib}^{(\ne )}{q}_{rot}^{(\ne )}{q}_{trans}^{(\ne )}$ accounts for the change in the reaction (or activation) entropic terms and the thermal correction to the enthalpy as obtained from a frequency calculation (at 298 K, 1 atm; ideal-gas approximation) on top of optimized geometries.

Constrained density functional theory (cDFT) ²¹ was employed using the NWChem 6.1.1 program. ²² The single-point cDFT (and related) calculations were performed at the B3LYP/def2-TZVP/COSMO(ε=4.0) level of theory on top of B3LYP+D3/def2-SVP/PCM(ε=4.0) optimized geometries obtained from the G09 program. For the COSMO in the NWChem program, the atomic radii were set to 1.3 (H), 1.83 (N), 1.72 (O), 2.00 (C), 2.05 (Cl), 2.6 (S) and 2.223 Å (Fe), and the solvent accessible surface to 0.5 Å.

3. Results and Analysis

3.1. Chlorination vs. hydroxylation: the native L-threonine substrate

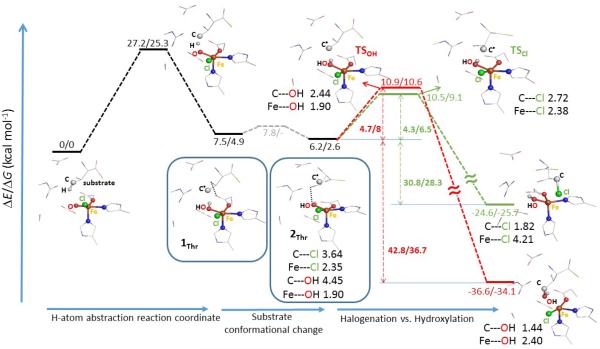
The Fe^IV=O intermediate with the oxo group oriented away from the substrate cavity was suggested in ref 6 to cleave the C—H bond of the native substrate via a π-attack (see Introduction). This would lead to an HO—Fe^III—Cl intermediate poised for chlorination due to the shorter distance between the substrate carbon radical and the Cl⁻ ligand relative to the OH⁻ ligand (by ~0.5 Å considering ionic radii). Alternatively, with the oxo group oriented toward the substrate cavity, H-atom abstraction (HAA) would proceed via a σ-attack to produce an HO—Fe^III—Cl intermediate poised for hydroxylation due to the favorable distance between C^• and OH⁻ relative to the Cl⁻ (by ~0.5 Å considering ionic radii).⁶ Indeed, for the σ-trajectory of the C—H bond activation, the Gibbs free energy barriers (ΔG^≠) for the chlorination vs. hydroxylation pathways were calculated to be 9.6 vs. 3.3 kcal mol⁻¹ (Figure S2 in Supporting Information - SI). Alternatively, starting from the product of the π pathway of ref 6 (1_Thr in Figure 1), chlorination vs. hydroxylation from the HO—FeIII—Cl intermediate have essentially the same ΔG^≠ (5.5 vs. 5.7 kcal mol⁻¹ from Figure S2B). However, a small conformational change in the substrate starting from 1_Thr gives the structure 2_Thr (Figure 1) that is more stable by 2.3 kcal mol⁻¹. 2_Thr maintains the π orientation and has a more pronounced asymmetry between the C^•---Cl⁻ and C^•---OH⁻ distances with Cl⁻ closer to the C^• relative to OH⁻ by ~1.3 Å (considering ionic radii; see Figure S3A). Starting from 2_Thr, chlorination was found to be lower in energy than hydroxylation by ΔΔG^≠ = 1.5 kcal mol⁻¹ (ΔΔE^≠/ΔΔH^≠ = 0.4/1.4 kcal mol⁻¹) despite the larger thermodynamic driving force for hydroxylation that is favored by ΔΔG₀ = 8.4 kcal mol⁻¹ (ΔΔE₀/ΔΔH₀ = 12/10 kcal mol⁻¹, at right in Figure 1). The fact that the product of hydroxylation is ~10 kcal mol⁻¹ more stable than the product of chlorination is attributed to the stronger C—OH bond (c.f., the experimental bond dissociation enthalpy of C—OH vs. C—Cl in C₂H₅OH vs. C₂H₅Cl is 94 vs. 84 kcal mol⁻¹)²³. These results are in contrast to the expectation based on the Bell-Evans-Polanyi principle that predicts a lower barrier for a more exergonic (exothermic) reaction.

Figure 1.

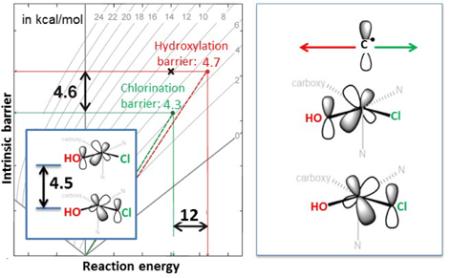
Chlorination vs. hydroxylation (in green vs. red) from the Cl—Fe^III(S=5/2)—OH product of the H-atom abstraction pathway (black), proceeding via the Cl—Fe^IV=O π-attack on the native substrate L-Thr. The relative potential energies and Gibbs free energies are in kcal mol⁻¹, the key geometric parameters are in Å. Note that the water molecule present in the cluster model (from Figure 9A in ref 8) is not depicted. The relative enthalpies are provided in Figure S2. For detailed comparison of two substrate-radical conformations 1_Thr vs. 2_Thr see Figure S3A. The dependence of equilibrium geometries on a basis set was tested by performing geometry optimizations for 2_Thr and the related transition states for chlorination and hydroxylation, using a combined basis set (def2-TZVP for Fe, ligating atoms and the terminal C atom of the substrate; def2-SVP for the rest). In comparison with the def2-SVP equilibrium geometries, the geometric changes are small, which translates into small changes of calculated reaction energies (c.f. 4.5 and 5.1 kcal mol⁻¹ for chlorination and hydroxylation using the hybrid basis set for geometry optimizations vs. 4.3 and 4.7 kcal mol⁻¹ with the def2-SVP equilibrium geometries).

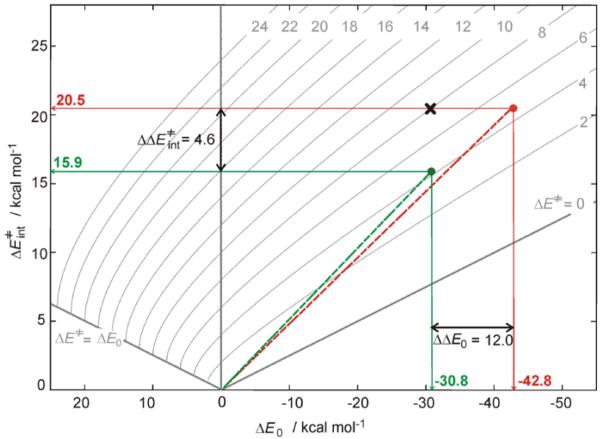
To evaluate the ‘net’ effect of non-thermodynamic contributions to the barriers of chlorination and hydroxylation from 2_Thr, Marcus theory ²⁴ was employed (Figure 2). Using this theory, the calculated activation energy ΔE^≠ is a function of the reaction energy and the intrinsic activation energy (ΔE₀ and ΔE^≠_int along the horizontal and vertical axes in Figure 2, respectively), the latter corresponding to the activation energy of a ‘thermo-neutralized’ reaction. Thus, from Figure 2 (and its correlation to the calculations in Figure 1, see caption), ‘thermo-neutralized’ chlorination (starting from 2_Thr) is favored over ‘thermo-neutralized’ hydroxylation by ΔΔE^≠_int = 4.6 kcal mol⁻¹ (ΔΔH^≠_int/ΔΔG^≠_int of 5.2/4.8 kcal mol⁻¹). Alternatively, as can be inferred from the plot in Figure 2 (point ×), hydroxylation would be favored over chlorination by ~4 kcal mol⁻¹ if chlorination had the same intrinsic barrier as hydroxylation of 20.5 kcal mol⁻¹ (i.e., for ΔΔE^≠_int = 0 kcal mol⁻¹, hydroxylation is favored by its thermodynamic contribution). Importantly, this analysis shows that chlorination, in comparison to hydroxylation, is intrinsically more accessible, which more than compensates for its lower exothermicity. Geometric and electronic factors that contribute in SyrB2 to halogenation over hydroxylation selectivity for the native substrate are analyzed below.

Figure 2.

The isocontour plots of the activation energy (ΔE^≠), which is, according to Marcus theory,²⁴ dependent on two variables: the reaction energy (ΔE₀ along the horizontal axis) and the intrinsic activation energy (ΔE^≠_int along the vertical axis) [ΔE^≠ = ΔE^≠_int + ΔE₀/2 + ΔE₀²/(16×ΔE^≠_int); for more details on the Marcus theory analysis see Figure S4A]. From the computational results for the native substrate L-Thr, from Figure 1, the green and red circles positioned at (ΔE₀, ΔE^≠) = (−30.8, 4.3) and (−42.8, 4.7) in the plot define the intrinsic activation energies of chlorination and hydroxylation of 15.9 and 20.5 kcal mol⁻¹, respectively. The point × with (ΔE₀, ΔE^≠_int) = (−30.8, 20.5) is associated with the activation barrier of 8 kcal mol⁻¹, and relates to chlorination if it had the same intrinsic barrier as hydroxylation. The analogous Gibbs free-energy plot is given in Figure S4B.

In considering the factors controlling selectivity, the geometric structures of 2_Thr (Figure 1) and the transition states of chlorination and hydroxylation (labelled TS_Cl and TS_OH in Figure 1) are evaluated first. In 2_Thr, the Fe^III ion is centered in the square pyramidal (SP) ligand field, with both the Cl⁻ and OH⁻ equatorial and cis to each other (the z-axis is the open position of the five-coordinate SP Fe^III center). The Fe—Cl and Fe—OH vectors are thus mutually perpendicular. As for the substrate location, the C radical is closer to Cl⁻ than to OH⁻ (as indicated earlier), above the Fe—Cl bond vector, perpendicular to the Cl—Fe—OH plane and trans to the axial histidine ligand. In going from 2_Thr to TS_Cl, there is no significant change in the SP arrangement around the Fe^III center. Notably the Fe—Cl bond elongates by only 0.03 Å (from 2.35 to 2.38 Å), while the C^• shifts from 3.64 to 2.72 Å with respect to the Cl⁻, remaining perpendicular to the Cl—Fe—OH plane. Similarly, the Fe^III in TS_OH maintains its SP ligand field with no change in the Fe—OH bond length relative to 2_Thr (1.90 Å), but the C^• shifts from 4.45 to 2.44 Å from the OH⁻ so that the C^•---OH vector becomes perpendicular to the Cl—Fe—OH plane with C^• located above OH⁻ (see Figure 1 and expanded structures are given in Figure S3B).

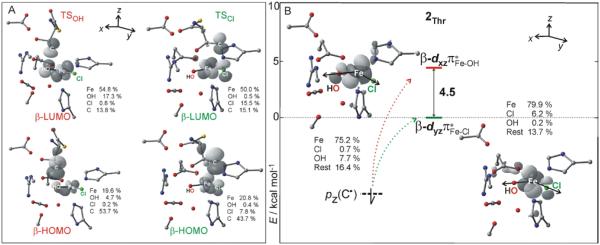
With respect to electronic structure contributions to the intrinsic barriers, the key FMOs are given in Figure 3. Given the C^• position with respect to the Cl⁻ or OH⁻ ligand at TS_Cl or TS_OH (desribed above) the respective β-HOMOs are identified as the β-p(C^•) orbital with admixture of β-dπ* along either the Fe—Cl or the Fe—OH bond (Figure 3A), while the respective β-LUMOs have the β-dπ*_Fe–Cl or β-dπ*_Fe–OH character mixed with the β-p(C•) (Figure 3A). From Figure 3, there are two different orthogonal, electron-accepting Fe-dπ* orbitals, one along the Fe—Cl axis and one along the Fe—OH axis both perpendicular to the Cl—Fe—OH plane. These are suggested to play key roles in the chlorination vs. hydroxylation selectivity of SyrB2. Indeed, as shown in Figure 3B, the energies of these β-dπ*_Fe–Cl and β-dπ*_Fe–OH orbitals at 2_Thr (in the absence of the substrate C^•) differ by 4.5 kcal mol⁻¹, with dπ*_Fe–Cl lying lower in energy. This energy difference between the two FMOs is similar to the difference between the intrinsic activation energies of chlorination and hydroxylation (i.e., 4.6 kcal mol⁻¹ in favor of chlorination, Figure 2). It is this energy difference between two crucial FMOs that makes chlorination kinetically competitive with hydroxylation; the hydroxylation would otherwise have an activation barrier lower by ~4 kcal mol⁻¹ due to the larger exothermicity of the hydroxylated product. Up to this point, the intrinsic selectivity vs. the energy splitting between two FMOs is an empirical correlation that is further evaluated in section 3.3 and is related to the mechanism of chlorination/hydroxylation that is analyzed in 3.4. Effects that destabilize Fe-dπ^* along the Fe—OH bond relative to the Fe-dπ^* along the Fe—Cl bond in SyrB2 are analyzed in section 3.3.

Figure 3.

A. Frontier molecular orbitals, β-HOMO and β-LUMO, and their atomic composition at the TS_Cl and TS_OH structures from Figure 1. B. The nature and relative energies of two frontier molecular orbitals calculated for the substrate-radical intermediate 2_Thr (in the absence of the substrate). The lower- and higher-energy FMOs, dπ*_Fe–Cl and dπ*_Fe–OH, are operative in chlorination and hydroxylation, respectively. The arrows indicate the interaction of the substrate orbital with FMOs, while in section 3.4 these are linked more specifically to electron transfer from the substrate to the Fe center.

3.2 Orientation dependence of chlorination vs. hydroxylation

From ref 6, the σ-pathway for H-atom abstraction by (SyrB2)Fe^IV=O, with the oxo oriented toward the substrate L-Thr, was proposed to result in substrate hydroxylation because of the favorable C^•---OH distance. This prediction was confirmed in section 3.1 (from Table 1, hydroxylation is favored by ΔΔG^≠ of −6.3 kcal mol⁻¹ for σ-Thr). In agreement with this, when the non-native substrate L-norvaline (Nva) was evaluated with a σ orientation for HAA (oxo toward the substrate cavity), both the terminal C₅ and the adjacent C₄ sites in Nva were found to result in a lower Gibbs free-energy barrier for hydroxylation relative to chlorination by ΔΔG^≠ = −2.3 kcal mol⁻¹ at C₅ and by −0.4 kcal mol⁻¹ at C₄ (σ-NvaC5/C4 in Table 1). These findings clearly demonstrate that the σ-trajectory for HAA performed by the oxo that is oriented towards the substrate leads to the C^•/HO—Fe^III—Cl intermediate, from which hydroxylation is favored. In contrast, from section 3.1 the π-trajectory for the native L-Thr leads to an intermediate with the OH⁻ oriented away from the substrate radical, favoring chlorination (2_Thr in Table 1). Here, we have also evaluated the π-orientation for the C₅ and C₄ sites of Nva. For this orientation, while chlorination does mostly occur on the C₄ site (ΔG^≠ = 7.0 vs. 5.9 kcal mol⁻¹ for hydroxylation vs. chlorination; NvaC4 in Table 1), Nva is in fact found to be preferably hydroxylated at C₅ (ΔG^≠ = 5.0 vs. 5.5 kcal mol⁻¹ for hydroxylation vs. chlorination; NvaC5 in Table 1). The energetics of the hydroxylation/chlorination pathways associated with the π-channel for HAA from Nva are in fact in better agreement with the experimental data than those associated with the σ-channel: experimentally the C₅ site is more hydroxylated (95% of the hydroxylated product)⁹, while the C₄ site is more chlorinated (65%)⁹. Another non-native substrate, L-aminobutyric acid that is experimentally known to be hydroxylated/chlorinated in a ratio of 69:31%,⁹ was also calculated. The π-trajectory has essentially equivalent barriers for hydroxylation and chlorination, while the σ-channel leads to hydroxylation (Aba vs. σ-Aba in Table 1). Thus, the π-channel for HAA, which is a required prerequisite for the less thermodynamically favorable chlorination (as analyzed in section 3.1) can also allow hydroxylation. Importantly, such a change in selectivity with the π-orientation does not reflect either a difference in the thermodynamics of hydroxylation vs. chlorination (ΔΔG₀), as these are approximately the same for all of the systems studied (see Figure S2), nor a difference in ligand field as this remains the same over the series (all having five-coordinate square-pyramidal Fe^III—hydroxy centers).

Table 1.

Gibbs free energy barriers for chlorination and hydroxylation of different substrate radicals that result from the H-atom abstraction (HAA) trajectory. For comparison, the experimental data from ref 9 are provided in the last column. All energies are in kcal mol⁻¹.

OH–FeIII–Cl intermediatea	HAA trajectory	Chlorination ΔG≠	Hydroxylation ΔG≠	Selectivityh ΔΔG≠	Experimental Product analysis:i OH vs. Cl product (%)
σ-Thrb	σ	9.6	3.3	−6.3	13 : 87
σ-NvaC5c	σ	3.1	0.8	−2.3	95 : 5j
σ-NvaC4c	σ	6.7	6.3	−0.4	35k : 65
σ-Abad	σ	10.8	7.0	−3.8	69 : 31
1Thre	π	5.5	5.7	+0.2	13 : 87
2Thre	π	6.5	8.0	+1.5	13 : 87
NvaC5f	π	5.5	5.0	−0.5	95 : 5j
NvaC4f	π	5.9	7.0	+1.1	35k : 65
Abag	π	5.4	5.3	−0.1	69 : 31

^aH-atom abstraction and hydroxylation/chlorination pathways with different substrates along with all relevant structures and their relative energies and geometric parameters are depicted in Figure S2.

^bThe C^•/ferric intermediate results from σ-HAA activation of L-threonine by Fe^IV=O, with the oxo oriented toward the substrate cavity.

^cThe C^•/ferric intermediate results from σ-HAA activation at the C₅ or C₄ site of L-norvaline by Fe^IV=O, with the oxo oriented toward the substrate cavity.

^dThe C^•/ferric intermediate results from σ-HAA activation of L-aminobutyric acid by Fe^IV=O, with the oxo oriented toward the substrate cavity.

^eThe 1_Thr and 2_Thr intermediates described in section 3.1.

^fThe C^•/ferric intermediate results from π-HAA activation at the C₅ or C₄ site of L-norvaline by Fe^IV=O, with the oxo oriented away from the substrate cavity.

^gThe C^•/ferric intermediate results from π-HAA activation at the terminal methyl group of L-aminobutyric acid by Fe^IV=O, with oxo oriented away from the substrate cavity.

^hChlorination (hydroxylation) is favored if ΔΔG^≠ > 0 (< 0).

ⁱTaken from ref 9.

^jThe substrate was deuteriated at the C₄ site; 5% of the product is chlorinated at C₄.

^kThe substrate was deuteriated at the C₅ site; 13% and 22% of the product is hydroxylated at C₄ and C₅, respectively.

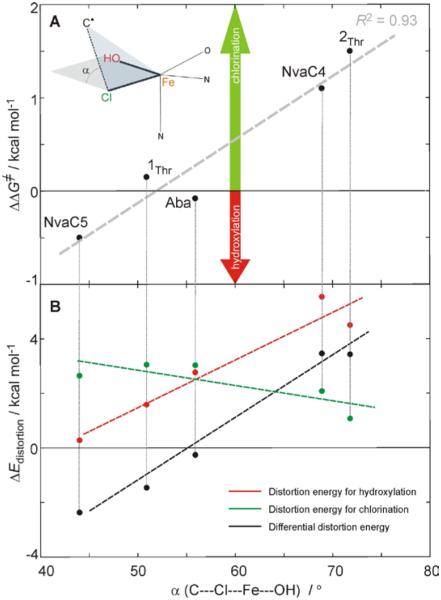
An effect, which tunes the reaction selectivity in these π-oriented systems enabling either chlorination or hydroxylation is the orientation of the substrate C^• with respect to the Cl—Fe—OH plane. Its orientation, defined by the dihedral angle α between the plane containing C^•---Cl vector and the Cl—Fe—OH plane, varies for the different C^•/HO—Fe^III—Cl π-oriented intermediates from 72° (2_Thr) through 69° (NvaC4), 56° (Aba), and 51° (1_Thr) to 41° (NvaC5). For chlorination (from the calculations given in SI in Figure S2), the C^• at TS_Cl maintains roughly the same orientation as in the associated intermediate (α = 79°, 62°, 51°, 50° and 44°). Alternatively, for hydroxylation, α is very similar at all of the TS_OH structures (falling in the range between 42° and 36°). Thus, the orientation dependence of ΔΔG^≠ is correlated with the angle α (essentially the same in the reactant and the TS_Cl) and reflects the amount the intermediate has to distort to reach the TS_OH structure (the larger the distortion, the more positive ΔΔG^≠). From the ΔΔG^≠ vs. α plot in Figure 4A, chlorination (green arrow) exhibits the largest preference for the most perpendicular orientation of the C^•---Cl vector relative to the Cl—Fe—OH plane (72° at 2_Thr), whereas hydroxylation is mostly preferred in the NvaC5 system, which has the most parallel orientation of C^•---Cl vector to the Cl—Fe—OH plane at the intermediate (44°). For the Aba system that has an intermediate orientation between those in NvaC5 and 2_Thr (56° in Figure 4A), chlorination and hydroxylation have comparable ΔG^≠ values. The fact that these correlations reflect the amount of reactant → TS_OH distortion is further supported by the analyses in Figure 4B. This gives the distortion energy (ΔE_distortion) for hydroxylation (red) and chlorination (green), which is defined as the energy required for distorting a substrate and the active site of SyrB2 to reach the transition state geometry, plotted against the angle α. For hydroxylation, the ΔE_distortion increases with α, while for chlorination it remains approximately the same (the green line). Thus, the differential distortion energy ΔΔE_distortion (black line in Figure 4B) exhibits a similar slope as ΔE_distortion for hydroxylation (red line in Figure 4B), with ΔΔE_distortion having a similar trend as ΔΔG^≠, i.e., both favoring hydroxylation in the NvaC5 system and chlorination in 2_Thr and NvaC4.

Figure 4.

A. Orientation dependence of chlorination versus hydroxylation selectivity in SyrB2 for the series of substrates studied experimentally in ref 9: the C₅ and C₄ sites of L-norvaline (NvaC5 and NvaC4), L-aminobutyric acid (Aba) and L-threonine with two different conformations (1_Thr and 2_Thr from Figures 1 and S3A), all activated through the π-channel for HAA. The positive value of ΔΔG^≠ (= ΔG^≠_{hydroxylation} − ΔG^≠_chlorination) reflects a lower barrier for chlorination, while hydroxylation is favored if ΔΔG^≠ < 0. The ΔΔG^≠ is plotted against the dihedral angle α (= C^•---Cl---Fe---OH) at Cl—Fe^III—OH intermediate geometries (α depicted in the inset). For each of the substrates, the TS_Cl and TS_OH structures are shown in Figure S2. B. The distortion energy (ΔE_distotion), defined as the energy required for distorting a substrate and the active site of SyrB2 to reach the transition state geometry of hydroxylation and chlorination along with the associated differential distortion energy (ΔΔE_distortion = ΔE_distortion[hydroxylation] − ΔE_distortion[chlorination]) as calculated for different substrates. Note that ΔE_distotion for hydroxylation starting from the substrate and the SyrB2 site of 2_Thr is corrected by +3 kcal mol⁻¹, which is due to the change in a number of H-bonds in going from 2_Thr to TS_OH. The energy cycle associated with the evaluation of distortion energies is shown in Figure S5.

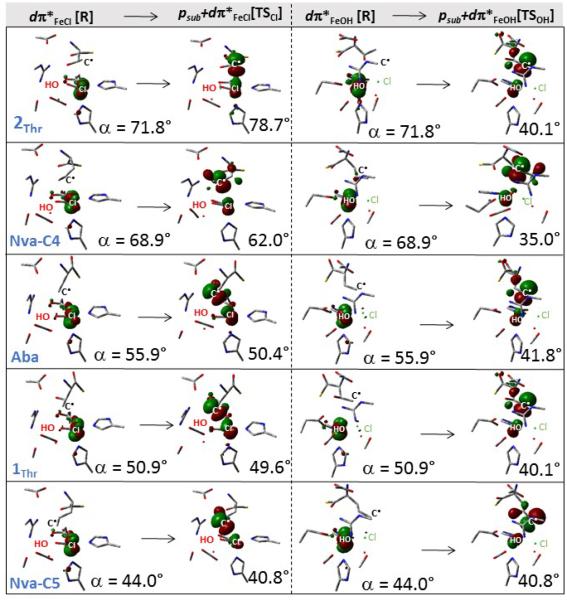
The difference in distortion energy required for reaching TS_OH vs. TS_Cl is linked to a difference in how much the dπ*_FeCl vs. dπ*_FeOH FMO distorts away from its perpendicular orientation relative to the HO—Fe—Cl plane upon the overlap with the substrate radical. In Figure 5, the two FMOs, dπ*_FeCl and dπ*_FeOH (the 1^st and 3^rd column) are displayed at the Cl—Fe^III—OH intermediate geometries in the presence of different substrates (each row for one substrate). Following the chlorination pathway (going from the 1^st to 2^nd column), the dπ*_FeCl π-overlaps with the substrate p orbital (the β-HOMO in the 2^nd column). From the comparison of all the β-HOMOs in the 2^nd column of Figure 5, the deviation of the p orbital from its perpendicular orientation relative to the HO—Fe—Cl plane increases with the decrease in the angle α. Consequently, the orientation of dπ*_FeCl follows the rotation of the C^• along the Fe—Cl bond to maximize its overlap with the p(C^•) orbital. This adaptability in the orientation of dπ*_FeCl is attributed to the p(C•)-mediated orbital mixing between dπ*_yz (from Figure 3) and the higher-energy dπ*_xy (axes defined in Figure 3B) that increases with the decrease in α (Table S2). For hydroxylation, where the dπ*_FeOH π-overlaps with the substrate p orbital at TS_OH, the dπ*_FeOH is also rotated to achieve good overlap with the substrate p(C^•) orbital (from the 3^rd to 4^th column in Figure 5). However, the dπ*_FeOH rotation is limited and approximately the same for all systems (see the β-HOMOs in the 4^nd column of Figure 5). This is rationalized by the limited flexibility in the OH ligand vector orientation, which is anchored by an H-bond to the neighboring monodentate carboxylate group and one from the nearby (crystallographic) water molecule (Table S3). This results in the similar angle α for all calculated TS_OH’s and the change in selectivity is therefore mostly given by how much the intermediate has to distort to reach TS_OH.

Figure 5.

Two dπ*_FeCl and dπ*_FeOH FMOs at the Cl—Fe^III—OH intermediate geometries (the 1^st and 3^rd column, respectively), as calculated for different substrates (rows) and their overlap with the substrate p orbital (β-HOMO) at the respective TS_Cl and TS_OH (the 2^nd and 4^th column). For chlorination and hydroxylation, structures are displayed with the Fe—Cl and Fe—OH bond axes pointing out of the plane of the paper, respectively. The magnitude of dihedral angle α (defined in Figure 4) is indicated for all structures.

3.3 Ligand field effects on FMOs and their contributions to selectivity

The difference between intrinsic activation barriers of chlorination and hydroxylation (starting from 2_Thr in Figure 1) was linked in section 3.1 to the energy difference between two FMOs: dπ*_Fe–OH and dπ*_Fe–Cl. In this section, this correlation is elaborated using small structural models to elucidate how ligand-field effects on the two FMOs correlate with intrinsic reactivity.

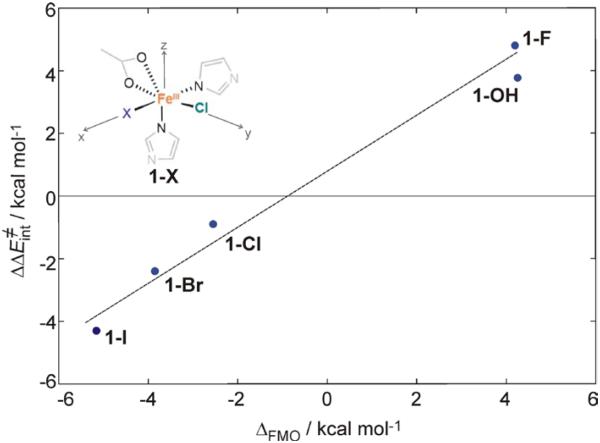
The trend in the intrinsic barrier favoring chlorination with the energy splitting of the dπ*^Fe–Cl / dπ*_Fe–OH FMOs was developed using a series of structures with two cis-positioned ligands, Cl⁻ and X = F⁻, OH⁻, Cl⁻, Br⁻, I⁻ (structures 1-X in Figure 6). For these structures, the intrinsic barriers for chlorination vs. halogenation (fluorination to iodination) were calculated as described in Figure S6 with a methyl radical positioned perpendicular to the transferring atom and correlated with the energy splitting of the dπ*_Fe–Cl / dπ*_Fe–X FMOs. This correlation is given in Figure 6. For I, the β-dπ*_Fe–I orbital is ~5 kcal mol⁻¹ lower in energy than β-dπ*_Fe–Cl (at 0 kcal mol⁻¹ on the abscisa), which directly correlates with the low intrinsic barrier for iodination vs. chlorination, favoring iodination by ~4 kcal mol⁻¹. In contrast, the β-dπ*_Fe–F orbital in 1-F is ~4 kcal mol⁻¹ higher in energy than β-dπ*_Fe–Cl and has the highest intrinsic barrier (for fluorination) as compared to chlorination by ~5 kcal mol⁻¹.

Figure 6.

The difference between chlorination and hydroxylation intrinsic activation energies ΔΔE^≠_int (= ΔE^≠_int[halogenation] − ΔE^≠_int[chlorination]) correlated with the FMO energy splitting Δ_FMO (= E[dπ*_xz,Fe–X] − E[dπ*_yz,Fe–Cl]), using five complexes with two cis-positioned ligands Cl⁻ and X = F⁻, OH⁻, Cl⁻, Br⁻ and I⁻ (structure defined in the inset). For clarity, H atoms in all of structures are not visualized. Reaction pathways were calculated as in Figure S6.

Thus, the Δ_FMO (= E[dπ*_xz,Fe–X] − E[dπ*_yz,Fe–Cl]) correlates with intrinsic reactivity and we can now consider the ligand field (LF) factors that influence Δ_FMO for a series of Fe^IIICl/X (=OH, F, Cl, Br, I) complexes. First, LF geometries were varied as shown in Figure S7, where calculations of the FMO energy splitting for octahedral (O) vs. square-pyramidal (SP) vs. trigonal-bipyramidal (TBP) structures show that there is no significant dependence on the structure (Δ_FMO = 4.2, 3.1, 4.1 kcal mol⁻¹ for O vs. SP vs. TBP). Next, for a group of five-coordinate square-pyramidal structures [(NH₃)₃(X)Fe^IIICl with X = OH⁻, F⁻, Cl⁻, Br⁻ and I⁻], we systematically varied the pair of Cl⁻/X⁻ cis-equatorial ligands as given in Figure 7. Within this series, the FMO energy splitting varies in a manner similar to that in Figure 6. This allows evaluation of the relative contributions of π donation and ligand electrostatics for X⁻ = OH⁻, F⁻, Cl⁻, Br⁻, I⁻ to the energy splitting of these FMOs. Note that the trend in the FMO splitting cannot be simply correlated with the trend observed in the spectrochemical series as this reflects both the π and σ donation ability of the ligand X rather than differences in π donation. The ability of the ligand X⁻ to impact the energy of the FMO by π-donation can be quantified by the ‘destabilization energy’ (E_π,Fe–X) that is estimated as the product of c_X² (the weighted admixture of ligand p_X character in the dπ*_Fe–X orbital) and Δ (the energy gap between the ‘non-interacting’ ligand p_X and d_Fe orbitals). While Δ can be evaluated directly and gives equivalent results (see SI Table S1), we employ here an approach (see SI) that estimates the π-donation contribution to a destabilization energy of a dπ*_Fe–X relative to the contribution of Cl π-donation to the dπ*_Fe–Cl energy:

$$E_{\pi ,Fe-X}-E_{\pi ,Fe-Cl}\cong c_X^2(I_X-I_{Cl})+E_{\pi ,Fe-Cl}\left(\frac{c_X^2}{c_{Cl}^2}-1\right)$$ eq. 1

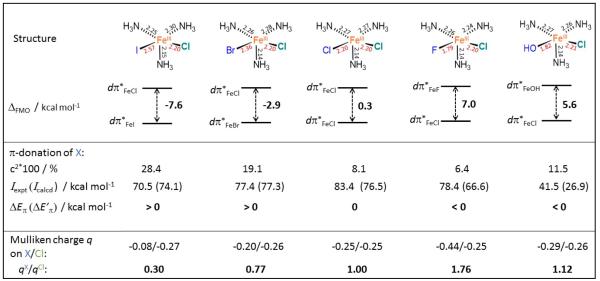
where I_X is the ionization potential of X, c_X² is defined above, and E_π,Fe–Cl is the π-donation contribution to the destabilization energy of the dπ*_Fe–Cl that is assumed to be positive for π-donation into a dπ* orbital. Importantly for a positive value of E_π,Fe–Cl (> ~2 kcal mol⁻¹), the E_π,Fe–I and E_π,Fe–Br are always larger than the E_π,Fe–Cl , while the opposite is true for the E_π,Fe–F and E_π,Fe–OH (see Figure S8). However, this is not the trend reflected in Δ_FMO, where dπ*_Fe–I and dπ*_Fe–Br are lower in energy than dπ*_Fe–Cl, while dπ*_Fe–OH and dπ*_Fe–F are higher (Figure 7). Considering the fact that X⁻ and Cl⁻ ligands in the complexes in Figure 7 are both trans to the σ-donating ligand NH₃, we can also exclude a trans effect contribution to Δ_FMO. The trend in Δ_FMO does however correlate with differences in the strength of the ligand field. This can be estimated from the relative partial Mulliken charges of the X⁻ vs. Cl⁻ ligand, as given by q^X/q^Cl quantity at the bottom row of Figure 7. These reflect the fact that lower electron donation leads to more negative charge on the ligand. From Figure 7, while OH⁻ is a weaker π-donor than Cl⁻, it is associated with a stronger LF, which leads to a higher-energy dπ*_Fe−OH as compared to the dπ*_Fe–Cl orbital.

Figure 7.

Series of five structures along with their geometric parameters, and the associated energy splittings between two FMOs: dπ*_Fe–X (X = I, Br, Cl, F and OH; atom label in blue) vs. dπ*_Fe–Cl (the Cl label in green). Weights of the ligand character in the dπ*_Fe–X (c_X²), experimental and calculated ionization potentials of X (I_expt and I_calcd), relative π-donation contributions to dπ*_Fe–X, as calculated using eq. 1 by employing I_expt or I_calcd (ΔE_π or ΔE’_π, where ΔE_π = E_π,Fe–X − E_π,Fe–Cl), and partial Mulliken charges are also provided. The experimental ionization potentials are taken from ref 23. For the dependence of ΔE_π or ΔE’_π on E_π,Fe–Cl see Figure S8. All of the structures were optimized with a geometric constraint to maintain the square-pyramidal ligand field (X, Cl and two N atoms were kept in one plane).

3.4 Possible mechanisms of chlorination and hydroxylation

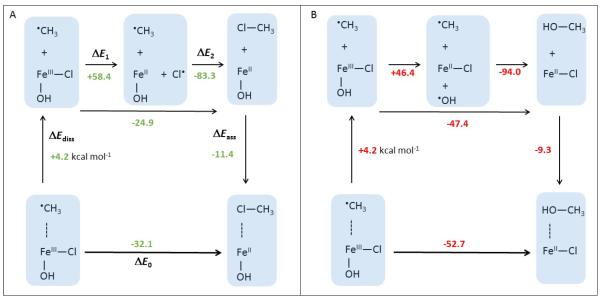
We first consider a ‘rebound’ mechanism. Within this process, the Fe^III—Cl (Fe^III—OH) bond would undergo homolytic cleavage, producing the Cl^• (OH^•) moiety that recombines with the substrate C^•. Figure 8 presents thermodynamic cycles for the chlorination and hydroxylation reactions in Figure S6A that include the two sequential steps – homolysis and recombination. From a comparison of the two cycles, homolysis of the Fe^III—Cl bond is 12 kcal mol⁻¹ less favorable than homolytic cleavage of the Fe^III—OH bond (c.f., ΔE₁ values in Figure 8A and B), which qualitatively parallels the experimental (and calculated) ionization potentials of Cl⁻ and OH⁻ (IP[Cl⁻→Cl^•)] = 3.6²³ (3.3) eV; IP[OH⁻→OH^•)]=1.8²³ (1.2) eV). Also, the recombination of the radicals (ΔE₂ in Figure 8) is calculated to favor hydroxylation by ~11 kcal mol⁻¹ (c.f., the experimental bond dissociation energy of CH₃—Cl vs. CH₃—OH is 92 vs. 83 kcal mol⁻¹)²³. From these numbers, chlorination would not compete with hydroxylation.

Figure 8.

A. The gas-phase thermodynamic cycle for chlorination of the CH₃^• substrate by complex 1-OH (depicted in Figure 6), where the reaction energy ΔE₀ is divided into the energy of dissociation of CH₃^• from 1 (ΔE_diss), homolytic cleavage of the Fe^III—Cl bond in 1 (ΔE₁), the formation of the H₃C—Cl bond (ΔE₂) and the energy of the association of H₃C—Cl with the Fe^II complex (ΔE_ass). B. The gas-phase thermodynamic cycle for hydroxylation of the CH₃^• substrate by complex 1, analogous to the cycle from panel A. The associated enthalpies and Gibbs free energies are provided in Figure S9.

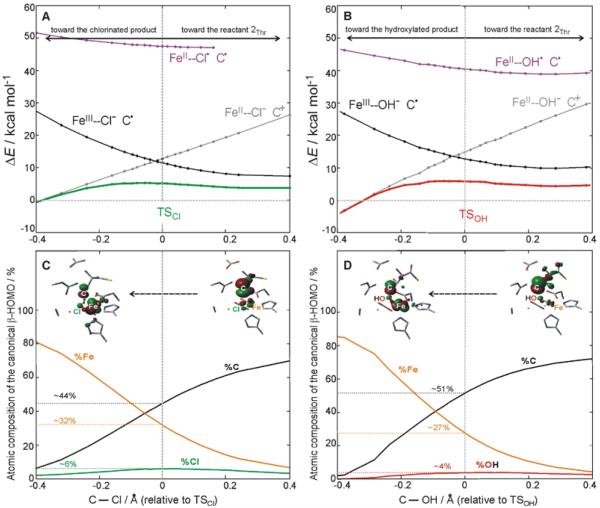
Another possible mechanism would correspond to a process, in which the Fe^III—Cl (Fe^III—OH) bond spin polarizes to Fe^II—Cl^• (Fe^II—OH^•) upon the attack of the substrate. Figure 9A presents the reaction coordinate for chlorination from 2_Thr from right to left that includes the DFT potential energy surface (PES) of the electronic ground state (green curve). The analogous PES for hydroxylation is shown in Figure 9B (red curve). Constrained density functional theory (cDFT) allows localization of the spin density along the reaction coordinate. Thus, cDFT is suitable for the evaluation of the energy required for Fe^III—X → Fe^II—X^• spin polarization along the reaction coordinate in Figure 9. Within the cDFT approach, an Fe^II—X^• state can be optimized by constraining one unpaired α electron on X (=Cl or OH), four unpaired α electrons on Fe and one unpaired β electron on the substrate. This constraint, maintained along the chlorination and hydroxylation reaction coordinates, allows for construction of ‘diabatic’ PESs of the spin-polarized Fe^II—Cl^• and Fe^II—OH^• states (mangenta curves in Figure 9A and B). From valence bond theory, a diabatic state preserves its character with a change in a molecular geometry. This differs from an adiabatic state that can be considered as a linear combination of diabatic states with weights that change with molecular geometry. Thus, the adiabatic ground-state PES (reaction barrier in green and red in Figure 9A and B) should result from a strong configuration mixing of two diabatic (‘reactant’ and ‘product’) states that cross each other at the transition state. The ‘reactant’ state is constrained to have the electronic structure of the 2_Thr intermediate, i.e., the HO—Fe^III—Cl/C^• state (the diabatic ‘reactant’ PES is plotted in black in Figure 9A and B). It is evident from Figure 9A and B that the Fe^II—Cl^•/C^• and Fe^II—OH^•/C^• states (in mangenta) do not cross with the ‘reactant’ state and are more than 40 kcal mol⁻¹ above the associated reaction barriers. Therefore, these states do not appear to participate in chlorination and hydroxylation. This conclusion is further supported by the results from section 3.1, which show no essential change in the Fe—Cl (Fe—OH) bond length in going from the reactant to the transition state, indicating little Fe^III—X → Fe^II—X^• polarization occurs upon substrate attack.

Figure 9.

A. Adiabatic S = 2 PES of chlorination (green) from 2_Thr and diabatic S = 2 PESs of three spin-density constrained states (black, grey and magenta), all calculated along the TS_Cl reaction coordinate (represented by the change in the C—Cl bond length relative to TS_Cl in going from right to left). B. Adiabatic S = 2 PES of hydroxylation (red) and diabatic S = 2 PESs of three spin-density constrained states (black, grey and magenta), all calculated along the TS_OH reaction coordinate (represented by the change in the C---OH bond length relative to TS_Cl in going from right to left). C. Evolution of the atomic composition of the β-HOMO along the chlorination reaction coordinate (the same coordinate as in A), including the contours of the β-HOMO before (right) and after (left) electron transfer from the substrate to the Fe center. D. Evolution of the atomic composition of the β-HOMO along the hydroxylation reaction coordinate (the same coordinate as in B), including the contours of the β-HOMO before (right) and after (left) electron transfer from the substrate to the Fe center.

Since the Fe^II—X^• state is predicted to be too high in energy to contribute to the chlorination/hydroxylation reactivity, there should be another lower-energy state that mixes with the ‘reactant’ HO—Fe^III—Cl/C^• state at the associated transition state. Indeed, cDFT calculations, imposing four unpaired α electrons on Fe and no unpaired electrons on the substrate and X (=Cl or OH), indicate that such an electron distribution (grey curves in Figures 9A and B) is almost isoenergetic with the ‘reactant’ HO—Fe^III—Cl/C^• electronic structure at the TS_Cl (Figure 9A) and TS_OH (Figure 9B). The ‘product’ state can be characterized as the HO—Fe^II—Cl/C⁺ state that differs from the ‘reactant’ state by one β-electron that is mostly transferred from the p orbital of the substrate to the redox-active dπ*_Fe–Cl (dπ*_Fe–OH) on the iron center (see FMOs from cDFT calculations in Figures S10). For both chlorination and hydroxylation starting from 2_Thr, the diabatic two-state crossing is located ~7 kcal mol⁻¹ above the top of the barrier of the adiabatic reaction coordinate. Note that the two diabatic PESs are related to the two parabolas used in the Marcus theory analysis in Figure 2 and S4 (this assumes that an electronic coupling between two parabolas is small, i.e., weaker than the couplings of ~ 7 kcal mol⁻¹ for chlorination/hydroxylation derived from Figure 9. However, the couplings for the two processes are equivalently large, which justifies the application of the Marcus analysis in Figure 2 for these two adiabatic reactions). These cDFT results indicate that both the chlorination and hydroxylation reactions are initiated by the electron transfer (ET) from the carbon radical to the Fe^III center, mediated by the Cl⁻ or OH⁻ ligand providing a superexchange pathway for ET. This would be followed by the ligand (Cl⁻ or OH⁻) transfer to the oxidized substrate.

This description of chloride and hydroxide transfer is supported by the evolution of the atomic composition of the β-HOMO from Figure 3A along the reaction coordinate for chlorination and hydroxylation as shown in Figures 9C and D. In both cases, when the substrate carbon approaches the Cl⁻ or OH⁻ ligand (going from right to left in Figure 9C and D), the weight of the C and Fe character decreases and increases, respectively, while the Cl or OH contributions to the respective β-HOMOs remain low and essentially constant along the coordinate, as would be expected for a superexchange-enabled ET. At both the TS_Cl and TS_OH, the β-HOMO has a significant radical character on the substrate, indicating that both transition states are early in the reaction coordinate. The fact that the superexchange controlled ET is followed by the ligand (Cl⁻ or OH⁻) transfer is further supported by the calculated C—Cl (C—OH) bond order at TS_Cl (TS_OH) that is only ~15% (~10%) of the final bond order of the product (see Figure S11). This superexchange mechanism for ET to the Fe is fully in line with the correlation of selectivity to the energy splitting between the two redox-active FMOs.

4. Discussion

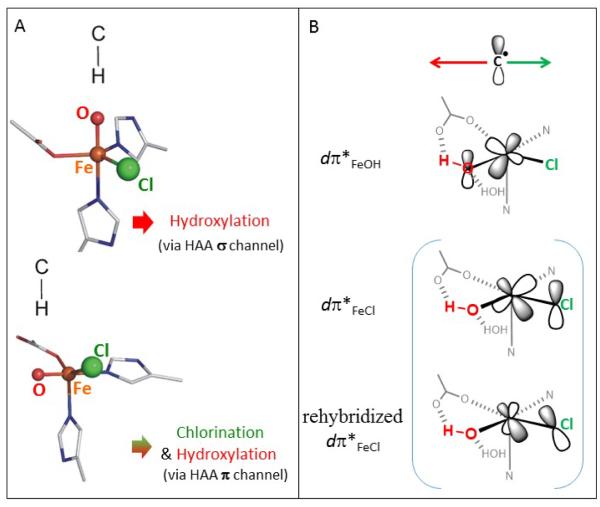
Considering a σ-trajectory for the H-atom abstraction reaction (with the oxo oriented toward the substrate cavity), hydroxylation is found to be favored over chlorination for all substrates investigated in this study (section 3.2; see also Scheme 2A). Thus, this σ-trajectory cannot be operative in SyrB2 in the presence of the native substrate L-Thr that is predominantly chlorinated. Instead, as already reported in refs 6 and 8, the HAA pathway with the L-Thr is suggested to follow the π-trajectory (with the oxo oriented perpendicular to the substrate cavity). Following the π-trajectory for HAA in SyrB2 with different substrates, the reaction barrier of chlorination is calculated to be comparable (and in some cases favored) to that of the more thermodynamically favored hydroxylation (Scheme 2A). This is associated with a higher intrinsic reactivity toward chlorination due to the lower intrinsic activation barrier (by 4-5 kcal mol⁻¹) as determined by a Marcus theory analysis (section 3.1). Thus, the intrinsic preference for chlorination compensates the thermodynamic propensity for hydroxylation. The difference between intrinsic activation barriers for the ‘thermo-neutralized’ chlorination and hydroxylation reactions correlates to the energy difference between two key frontier molecular orbitals (sections 3.1 and 3.3). One of these FMOs, which results from the antibonding π-interaction along the Fe—Cl bond axis (dπ*_Fe–Cl), is active in chlorination and is ~4-5 kcal mol⁻¹ lower in energy than the FMO active in hydroxylation, arising from the analogous antibonding interaction along the Fe—OH bond axis (dπ*_Fe–OH). These two FMOs are depicted in Figure 3. The FMO energy splitting Δ_FMO in the Cl—Fe^III—OH intermediate in SyrB2 is attributed to the differential effect of the ligand field that is larger for OH⁻ than for Cl⁻ (section 3.4).

Scheme 2.

A. The σ-channel for H-atom abstraction from a substrate by the Fe^IV=O intermediate leads to hydroxylation (top), while the π-channel can lead to either chlorination or hydroxylation (bottom). B. For the π-channel, the orientation of the substrate enables either the Cl⁻ or OH⁻ to rebound depending on the relative π-overlap with the substrate C radical (the red arrow indicates the region, where the π-overlap with OH⁻ favors hydroxylation and the analogous arrow in green indicates the region favoring chlorination). Note that the dπ*_FeCl FMO can rehybridize to maximize its overlap with the substrate C^• if this radical is not located above the Fe—Cl bond axis.

Calculations in this study reveal that the π-orientation can lead to chlorination or hydroxylation depending on the substrate orientation. The native L-threonine substrate and the C₄ site of L-norvaline are predicted to be chlorinated, the C₅ site of L-norvaline hydroxylated, and there is no calculated preference for hydroxylation relative to chlorination for the L-aminobutyric substrate. These results are in agreement with experimental observations of Bollinger and Krebs.⁹ Such a substrate-dependent selectivity derives from the orientation of the C radical with respect to the HO—Fe—Cl plane (Scheme 2B). The analysis from section 3.2 indicates that the orientation effect in SyrB2 is attributed to the distortion that needs to occur for the substrate C radical to achieve good π-overlap with the dπ*_Fe–OH FMO at the transition state of hydroxylation. It is this distortion that actually controls selectivity in SyrB2 (as the difference in the intrinsic barrier, related to the FMO energy difference favoring chlorination, is mostly compensated by the differential thermodynamic contribution to the rebound barriers that favors hydroxylation). The distortion to reach the transition state of hydroxylation is related to the fact that the dπ*_Fe–OH FMO has a fixed orientation (perpendicular to the Fe—O—H plane) due to the anchoring H-bond of the OH⁻ group with the coordinated carboxylate group. The analogous π-overlap with the dπ*_Fe–Cl FMO does not require such a substrate distortion due to rehybridization of the dπ*_Fe–Cl FMO toward the substrate radical. Thus, the orientation effect, which arises from the positioning of the substrate radical above the HO—Fe—Cl plane and the differential FMO orientation flexibility in overlapping with the substrate, corresponds to the differential overlap contribution to chlorination vs. hydroxylation selectivity as simplified in Scheme 2B.

The FMO control over selectivity is also consistent with reaction mechanism for chlorination and hydroxylation of the C radical by the HO—Fe^III—Cl intermediate. This would be initiated by β-electron transfer from the C^• to the S = 5/2 Fe^III center through the superexchange mediating Cl⁻ (OH⁻) ligand, which, after the transition state, is followed by the Cl⁻ (OH⁻) transfer (section 3.4). This mechanism is consistent with the correlation of the orbital energy splitting between two key dπ^* FMOs with differential intrinsic reactivity toward chlorination vs. hydroxylation.

Concerning oxidative ligand transfer (rebound) selectivity, it is worth noting that a synthetic high-spin (S=2) non-heme iron model of SyrB2 was demonstrated to halogenate with the unprecedented yield of 30-40%.²⁵ This work along with other studies^26,27 show that a rebound process in solution is somewhat slow, which allows the escape of a substrate radical from the solvent cage. This leaves an open question on a mechanism for halogenation/hydroxylation by biomimetic non-heme iron complexes in solution. However, radical substrates in solution are less restricted in their diffusive motion than radical substrates in a protein cavity, which would result in specific orientations of the substrate C^• relative to the HO—Fe—Cl plane of a reactive complex. We expect fast rebound to be favored over escape in SyrB2 due to interactions of the substrate radical with the protein cavity cage.

5. Conclusions

Chlorination vs. hydroxylation selectivity was computationally evaluated for different substrates and found to be in a good agreement with the experimental observations from ref 9. The π-trajectory for H-atom abstraction as defined in refs 6 and 8 was calculated to lead to the S = 2 5C HO—Fe^III—Cl intermediate with the C^• substrate, π-oriented relative to both of the Cl⁻ and OH⁻ ligands. Starting from this ferric intermediate, hydroxylation is thermodynamically favored, but chlorination is intrinsically more reactive. A higher intrinsic chlorination reactivity derives from the energy splitting between two key redox-active dπ* FMOs: the lower the FMO energy for chlorination relative to that for hydroxylation, the higher the intrinsic reactivity for chlorination. The orbital splitting arises from the differential ligand-field effect of Cl⁻ vs. OH⁻ on the Fe dπ* orbitals. This factor makes chlorination effectively competitive with hydroxylation. Chlorination vs. hydroxylation selectivity is then determined by the orientation of the substrate C^• with respect to the HO—Fe—Cl plane that is related to the differential overlap of the substrate p orbital with two dπ* FMOs. The differential contribution of the FMOs to chlorination vs. hydroxylation selectivity in SyrB2 is related to a reaction mechanism that employs two asynchronous transfers: electron transfer from the substrate radical to the iron center followed by late ligand (Cl⁻ or OH⁻) transfer to the substrate.