Abstract
We describe recent advances in quantifying the three-dimensional (3D) geometry and mechanics of whisking. Careful delineation of relevant 3D reference frames reveals important geometric and mechanical distinctions between the localization problem (‘where’ is an object) and the feature extraction problem (‘what’ is an object). Head-centered and resting-whisker reference frames lend themselves to quantifying temporal and kinematic cues used for object localization. The whisking-centered reference frame lends itself to quantifying the contact mechanics likely associated with feature extraction. We offer the ‘windowed sampling’ hypothesis for active sensing: that rats can estimate an object’s spatial features by integrating mechanical information across whiskers during brief (25–60 ms) windows of ‘haptic enclosure’ with the whiskers, a motion that resembles a hand grasp.
Introduction
The rodent vibrissal-trigeminal system is one of the oldest models for the study of active sensing in the field of neuroscience [1–5]. The past five years have seen several breakthroughs in the field of vibrissal research, including the discovery of the central pattern generating circuits responsible for rhythmic whisking [6] and their close association with sniffing behavior [6,7], as well as the elucidation of differential processing along parallel thalamocortical pathways [8,9]. However, we still do not fully understand how to interpret the signals in these central structures, in part because we do not yet fully understand the inputs: the tactile signals that drive the responses of primary sensory neurons in the trigeminal ganglion.
Recent advances in three-dimensional (3D) whisker mechanics [10,11••,12,13•] offer the opportunity to compute the complete set of tactile inputs transmitted by the vibrissae during active tactile exploration. The goal of the present paper is to review recent literature so as to establish a unified framework for describing the geometric and mechanical variables relevant to whisking behavior. Specifically, we develop formalisms for head-centered and whisker-centered reference frames, and compare them with the more traditional resting-whisker reference frame. The whisker-centered reference frame is well suited to describing mechanical information about the external world transmitted by the whisker, but it is geometrically unintuitive. The resting-whisker reference frame is well suited to describing the location of an object relative to a particular whisker, but is ill suited to describing mechanical variables and mechanoreceptor deformation.
By carefully distinguishing between these reference frames, we argue that a whisking rodent will face two separate problems during tactile exploration. The first is how to localize an object in head-centered coordinates based on tactile information that originates in whisker-centered coordinates (‘where’ is the object). The second is how to integrate information across multiple whiskers to estimate the object’s contour, independent of its location in head-centered coordinates (‘what’ is the object). In this review we focus on the rat whisker system, but the framework also applies to mice and other rodents.
The geometry of whisking
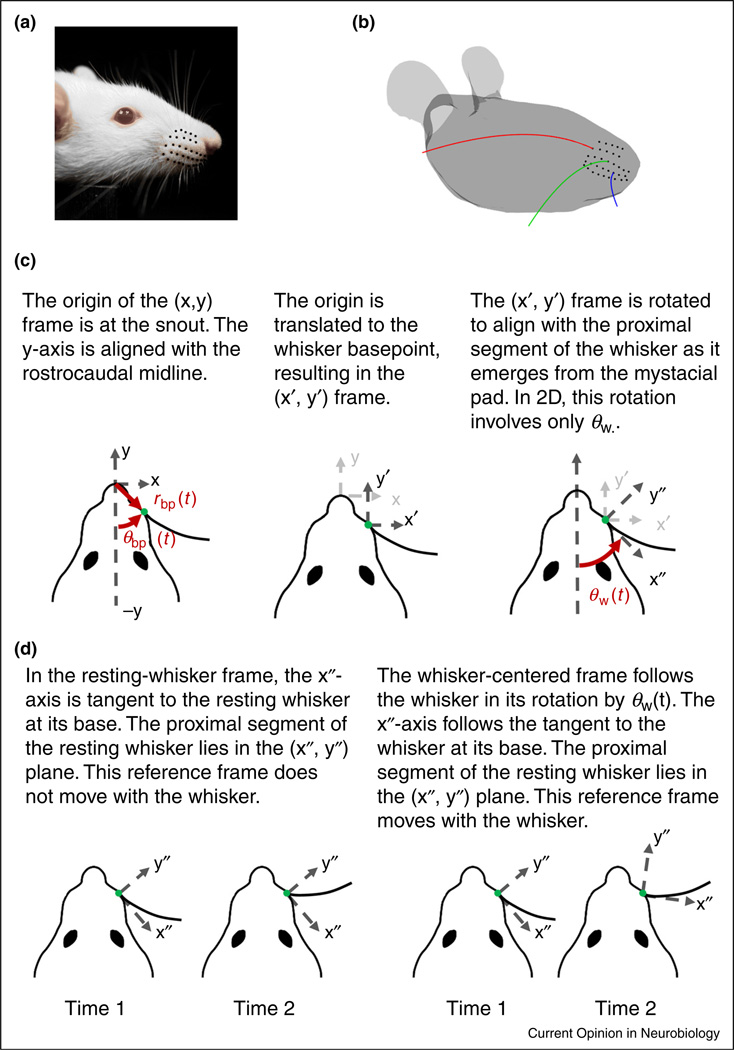
Whiskers are arranged in a regular array (rows and columns) on the rat’s face, and decrease in length from caudal to rostral (Figure 1a,b). Each whisker has an intrinsic curvature that follows from approximating its proximal shape by a parabola [12,14]. Intrinsic curvature varies systematically across the array (Figure 1b); shorter whiskers tend to have larger curvature than longer whiskers and also a more variable curvature [15].
Figure 1.
Arrangement of the whiskers on the mystacial pad and reference frames relevant to whisking mechanics. (a) The whiskers of the rat mystacial pad are organized in rows and columns. (b) Whisker length and curvature vary systematically across the array. (c) Panels illustrate a two-step process to transform between head-centered, resting-whisker, and whisker-centered reference frames. The translation moves the origin from the snout to a whisker basepoint with polar coordinates (rbp, θbp) in the head-centered reference frame; θbp is measured counterclockwise from the midline. The rotation results in a new reference frame in which the proximal segment of the whisker lies in the x″ –y″ plane and is tangent to the x″-axis at its base. The y″-axis is perpendicular to the x″-axis, with positive defined as the direction in which the tip curves concave. (d) The resting-whisker reference frame does not rotate with the whisker. In contrast, the whisker-centered reference frame rotates with θW(t).
Each whisker is held tightly within a follicle at its base [16,17]. Each follicle is packed with mechanoreceptors, and is actuated by both intrinsic and extrinsic muscles [18–23]. Whisking behavior allows rodents to move their whiskers independently of the head, and it is therefore important to distinguish between head-centered and whisker-centered reference frames.
Because each whisker is held tightly by its follicle [16], and because the base of a whisker is relatively stiff [15,24–28], the follicle and the proximal segment of the whisker move approximately as a single unit (a rigid body) relative to the head. Figure 1c describes the time-dependent position and orientation of this unit in a head-centered reference frame.
The two-step process depicted in Figure 1c — namely, a translation of the head-centered reference frame to the location of the whisker basepoint and a rotation that aligns the translated reference frame to the proximal segment of the whisker — describes the location and orientation of the whisker with respect to a head-centered reference frame. This process results in the two new reference frames shown in Figure 1d: a resting-whisker reference frame and a whisker-centered reference frame.
For the resting-whisker reference frame, the rotation considers the whisker at biomechanical rest and aligns the x″-axis with the proximal segment of the whisker at as it emerges from the mystacial pad. The y″-axis is perpendicular to the x″-axis, with positive defined as the direction in which the tip curves concave. This reference frame is now fixed. In contrast, the whisker-centered reference frame moves with the whisker. In this frame, the whisker always lies in the x″–y″ plane and is tangent to the x″-axis at its base.
This approach can be extended to the full three-dimensional (3D) case. In 3D, the base point coordinates (rbp, θbp, φbp) for the translation include an additional angle: the elevation angle φbp. In 3D, three angles (θw, φw, ζw) are needed to characterize the rotation, where θw is the horizontal angle, φw is the elevation angle, and ζw is the roll of the whisker around its own tangent at the base [12,14,29].
The angle θw is measured in a horizontal plane and the angle φw in an elevation plane, both oriented relative to the plane that defines the pitch of the rat’s head. In physiological experiments, zero head pitch is defined by aligning bregma with lambda. An alternative, appropriate in the context of some biomechanical and behavioral experiments, is to define zero pitch such that the basepoints of the whiskers lie in horizontal rows [14], or such that the two eyes and the nose lie in the horizontal plane [12]. Each choice offers distinct advantages and disadvantages, depending on the experimental questions asked. Once the zero head pitch plane, and thus the horizontal plane, has been identified, the elevation plane can be computed from the projection of the whisker onto the horizontal plane: the tangent to the real whisker at its base and the tangent to the projected whisker at its base define the elevation plane.
Finally, it is important to recall that all of these coordinates (rbp, θbp, φbp) and (θw, φw, ζw), are functions of time, as they describe the position and orientation of the whisker’s base in the head-centered reference frame.
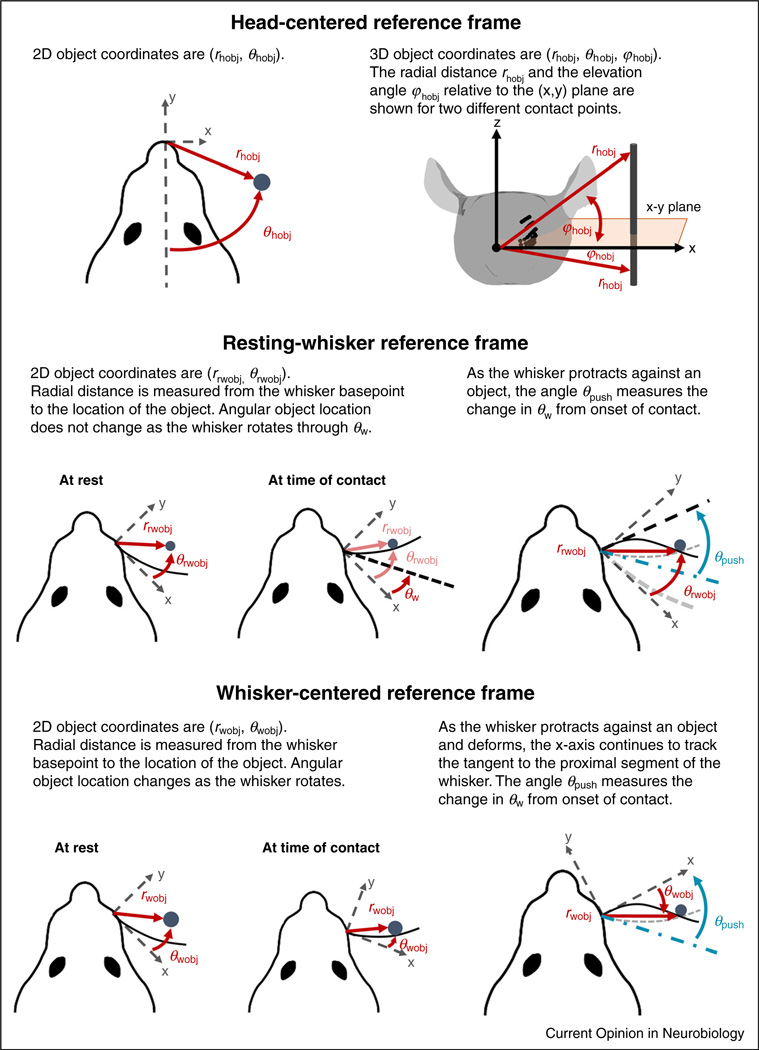
The position of an object relative to the rat can be described in any of the three coordinate systems of Figure 1c,d: the head-centered, the resting-whisker, or the whisker-centered reference frame. Throughout the present work, we assume the object to be a vertical peg, as is often used in behavioral experiments [30–33]. For simplicity, the peg is assumed to have infinitesimally small radius, as if it were a line segment.
Object coordinates in each of these three reference frames are illustrated in Figure 2. Object location in the head-centered reference frame is self-explanatory; the position of the object in this frame does not depend on how the whisker moves. The other two reference frames require a few additional notes.
Figure 2.
Object coordinates in the head-centered, resting-whisker, and whisker-centered reference frames. Here we drop the double prime notation used in Fig. 1 to refer to the axes in the resting-whisker and whisker-centered reference frames. Object location in the head-centered reference frame (h) does not depend on the motions of the whisker. The resting-whisker reference frame (rw) stays fixed as the whisker rotates; object coordinates do not change during whisker motion. The angle θpush measures the change in θw from the onset of contact. The whisker-centered reference frame (w) rotates with the whisker; the angular location of the object changes continuously, both before and during contact. As in the resting-whisker reference frame, θpush measures the change in θw from the onset of contact. In the resting-whisker reference frames, whisker position at rest is shown as a thick grey dashed line. In both resting-whisker and whisker-centered reference frames, whisker position at contact is shown as a thin grey dashed line, and whisker position when protracting against the object as a thin black line.
First, if the basepoint location (rbp, θbp, φbp) changed with time, the origin of these two reference frames and the object coordinates in these two reference frames would translate accordingly. For the pure rotational motion illustrated in the examples of Figure 2, basepoint translation is neglected; 2D object coordinates in the resting-whisker reference frame (rrwobj, θrwobj) thus remain constant during the whisk. In contrast, while rwobj also remains constant in the whisker-centered reference frame, θwobj changes continuously and becomes negative after significant deflection against an object. Note also that as the whisker makes contact with and deflects against the object, its 2D rotation from the onset of contact is measured by a new angle, θpush. If the whisker were perfectly straight, θpush would be equal and opposite to θwobj, but because the whisker has intrinsic curvature, the relationship between these two angles is more complicated and depends on the radial distance rwobj.
Finally, we note that the characterization of object location from any of the three reference frames is easily extended to the 3D case; this simply requires an additional angle for elevation relative to the corresponding horizontal plane, namely (rhobj, θhobj, φhobj), (rrwobj, θrwobj, φrwobj), or (rwobj, θwobj, φwobj). See ‘The location of whisker-object contact points from different reference frames’ section for a more detailed analysis of the unexpected subtleties of 3D object location.
The mechanics of quasi-static contact
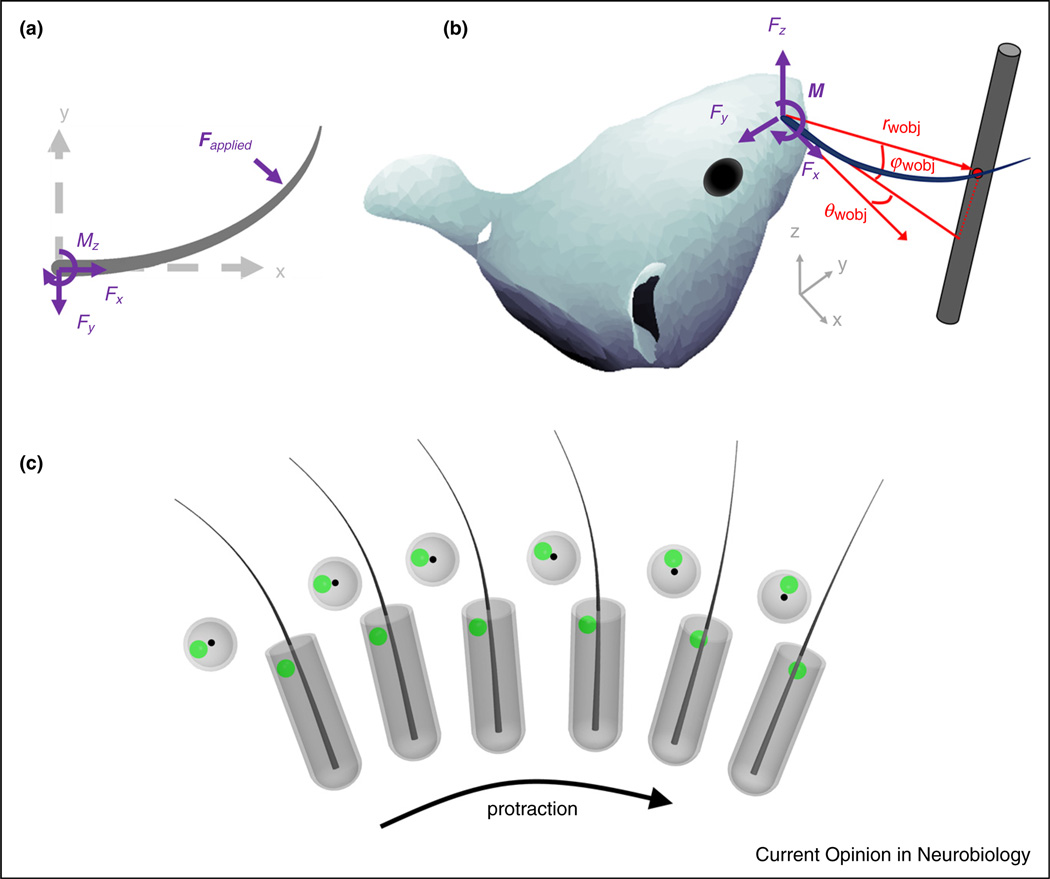
When the whisker makes contact with an object, a mechanical transient is generated (a dynamic effect), and the whisker begins to bend. The quasistatic forces associated with bending are slower, but generally larger in magnitude than the transient forces associated with the collision [34–36]. Figure 3a,b provides 2D and 3D illustrations, respectively, of the mechanical signals at the base of the whisker generated by contact [11••,24,33,37–41].
Figure 3.
Mechanical signals in the whisker-centered reference frame. (a) The 2D applied force F is decomposed into an axial component Fx along the whisker’s axis and a transverse component Fy. The bending moment at the whisker base is Mz. (b) The 3D applied force is F decomposed into an axial component Fx and two transverse components Fy and Fz. The bending moment M at the whisker base is M = rwobj × F. Contact point coordinates in the whisker-centered frame are (rwobj, θwobj, φwobj). (c) During a protraction, the follicle and the whisker base rotate and roll as a single unit. The deformations on a mechanoreceptor (green dot) within the follicle are computed in the reference frame of the whisker. Whisker-centered coordinates maintain the geometric relationship between the whisker base and any given mechanoreceptor within the follicle at all times during a protraction. Resting-whisker coordinates cannot achieve this invariance because they are fixed in a single angular location, corresponding to the start of protraction.
Mechanical signals at the whisker base cannot be directly measured, because placing a sensor at the whisker base would interfere with its mechanics. Quantifying these contact variables requires either mechanical modeling [10,15,28,33,37–39,42,43,44••] or the use of geometric proxies. For example, change in curvature near the whisker base during contact is sometimes an appropriate proxy for change in bending moment at the whisker base [45•,46].
The quality of the proxy will depend on the exact method by which changes in curvature are computed (e.g., computing a spline versus fitting a circle near the whisker base). Moreover, whenever the curvature is not computed precisely at the base, its actual value will depend on the somewhat subjective choice of a point ‘near the base’ at which the curvature is computed.
As noted, the diagrams in Figure 3a,b use the whisker-centered reference frame; it is in this coordinate system that mechanical signals are transmitted to the follicle. To clarify this point, consider the whisker’s location relative to mechanoreceptor endings within the follicle (Figure 3c). Mechanoreceptors respond to deformations caused by the motion of the whisker within the follicle.
These deformations activate Vg neurons, the ‘gatekeepers’ of all vibrissal-related information to the trigeminal pathway [44•,45•,47–55,56••]. A meaningful physical description of how mechanoreceptors will deform, and thus how Vg neurons will respond, requires a reference frame in which the location of the mechanoreceptor relative to the whisker does not change as the whisker moves. The Vg response to mechanical stimuli thus requires that these stimuli be characterized in the whisker-centered reference frame.
The location of whisker-object contact points from different reference frames
How might the rat localize an object in the context of the reference frames and variables described above?
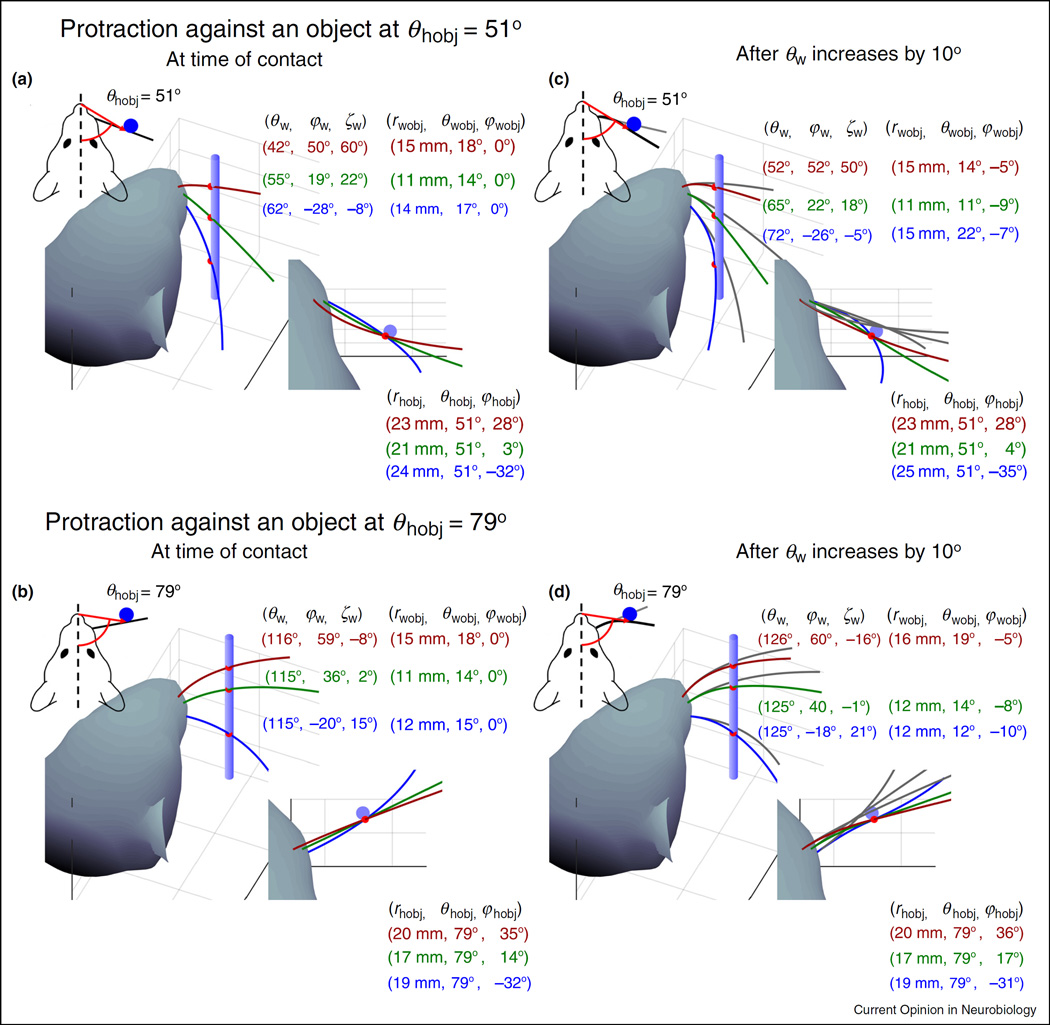
Consider a rat whisking against a peg situated at two different horizontal angles (θhobj = 51° and θhobj = 79°) relative to its snout at time of initial contact (Figure 4a,b). A 2D view from the top, further simplified by neglecting whisker curvature (see insets at top left), correctly indicates that all whiskers caudal to the peg will make contact with the peg at a single horizontal angular location in the head-centered reference frame (θhobj). However, the 2D view gives the misleading impression that there is a simple relationship between the angular location θhobj of the object in the head-centered reference frame and the angle θw through which the whisker must rotate in order to make contact with the object.
Figure 4.
The geometry of contact. (a) and (b) The figures depict a rat whisking against a peg situated at two different horizontal angles relative to its snout: θhobj = 51° and θhobj = 79°. Whisker angular coordinates in the head-centered reference frame, and contact point coordinates in both whisker-centered and head-centered reference frames, are shown for three different whiskers (red, green, and blue). (c) and (d) Whisker angular coordinates and contact point coordinates in the same reference frames and for the same three whiskers, after all three have protracted against the peg until θw has increased by 108. The changes in roll (ζw) and elevation (φw) with θw were simulated according to the kinematic equations for whisking motion developed by Knutsen et al. [12]. In all panels, variables in the head-centered reference frame (subscript hobj) describe the coordinates of the whisker-object contact points.
The 3D views reveal considerable more complexity. All three whiskers make initial contact with the object at different values of θw, φw, and ζw, because the orientations of each of the whiskers are different in the head-centered reference frame. Note that although θhobj differs by exactly 28° between Figure 4a,b, the θw values for the whiskers do not shift by 288. The complex relationship between θw and θhobj is due to the intrinsic curvature of the whiskers.
In whisker-centered coordinates, all whiskers have different values of rwobj and θwobj at the time of initial contact, while φwobj is identically zero because the whiskers have not deflected out of their individual x–y planes. Also note that in head-centered coordinates, the coordinates of the whisker-object contact point rhobj and φhobj are different for each whisker, while θhobj stays constant because the peg is assumed to have infinitesimally small radius. If the peg had finite radius, then θhobj would change as the whisker slips along its length; this type of motion is termed ‘longitudinal slip’ [22,37–39,41,42].
Figure 4c,d depicts the geometry of contact after all whiskers have protracted against the peg until θw has increased by 108. Roll (ζw) and elevation (φw) change with θw according to the kinematic equations for whisking motion developed by Knutsen et al. [12]. After this protraction, the coordinates (θw, φw, ζw) of whisker orientation relative to the head have changed, as have the coordinates (rwobj, θwobj, φwobj) of the object in the whisker-centered reference frame. The values of φwobj are no longer zero, because the whiskers have now deflected out of their initial elevation planes.
It is interesting to note that the location of the whisker-peg contact points have also changed in the head-centered reference frame, both from whisker to whisker and during the protraction. These changes may seem unintuitive, because the location of the peg does not change relative to the head. Nevertheless, the location of the whisker-peg contact points have changed because the whiskers slip against the peg, both vertically and along their length. In this example, the peg is assumed to have vanishingly small radius, so the value of θhobj does not change either with protraction or from whisker to whisker. In contrast, both rhobj and φhobj change considerably from whisker to whisker, but less so as a given whisker protracts against the peg. If the peg had finite radius, θhobj would also change during protraction and from whisker to whisker.
The panels of Figure 4 summarize the significant challenges of the 3D object localization problem for the rodent, and also implicitly reveal an important ‘where/what’ distinction in the vibrissal system. In panels 4a and 4b, the animal must localize the peg at two different angular positions. In panels 4c and 4d, as the whiskers deflect against the object the animal should have the same perception of the contour of the peg, regardless of whether the whiskers made contact with the peg at 51° or 79°.
Our approach to this problem is based on the observation that object location (‘where’ is the object) is most easily expressed in the head-centered or resting-whisker reference frames. In contrast, it is the whisker-centered reference frame that provides an optimal and most natural frame for the calculation of the contact forces and moments that lend themselves to a description of object contour (‘what’ is the object). In the next section, we examine the sources of information available to the animal for determining object location as well as object contour.
Where versus what: determining object location and contour
Consider first the problem of localizing the peg at either 51° or 79° (Figure 4a,b). Both the resting-whisker and the head-centered reference frames lend themselves to an intuitive description of object location [30–33,57–59]. To localize an object, the rat must detect the mechanical transients generated by collision with an object, determine the location of its whisker at the instant of contact, and determine the location along the whisker at which contact was made.
However, determining the whisker’s location at the instant of object contact is challenging because there are very few proprioceptors in the whisking muscles [9,17]. The rat has thus no direct access to (θw, φw, ζw), though some information may be available through the mesencephalic nuclei [60,61]. Recent studies have suggested that reafferent signals reporting whisking phase could be combined with an efferent copy of whisking midpoint and amplitude to estimate angular whisker position θw [62,63,64]. Given that the elevation and roll of the whisker are tied closely to protraction angle [12,29], the full 3D angular position of the whisker (θw, φw, ζw) at the time of contact could in principle be determined.
Several excellent review articles have recently surveyed the neurophysiological basis for the implementation of this type of localization scheme [57,58,65,66]. From a purely mechanical standpoint, this localization approach is plausible because the whisker has very little mass, and its proximal region behaves like a rigid body during non-contact whisking [12,29]. The rat would thus be able to monitor and control purely kinematic variables (i.e., phase, midpoint, amplitude) to obtain an estimate of whisker position during localization behaviors. However, this localization scheme requires precise timing information to allow the computation of θw at time of contact. Moreover, values of θw must be monitored separately for each whisker.
A complementary hypothesis emerges from considering 3D geometric and mechanical effects. Because the whisker rolls as it protracts, the orientation of the whisker varies systematically through the whisking cycle [12,29]. In turn, the whisker’s orientation at the time of object contact will determine the direction in which it is deflected by the object [10,11••,13•,41,42]. The direction of whisker bending could thus provide a mechanism for the rat to determine the horizontal angle at which the whisker has made contact with the object [12,13•].
Consider next the problem of extracting the contour of the peg. In principle, the rat could determine object contour by computing the location of each whisker-object contact point in head-centered coordinates; this would be done in the manner just described for object location (whisking phase, timing, etc). The contour of the object could then be determined by comparing these contact point locations — in head centered coordinates — across the array of whiskers. Although this scheme cannot be ruled out, it is computationally expensive and error prone, because the correct computation of object contour would depend on the correct computation of several object locations.
An alternative possibility is suggested by Figure 4c,d, which indicates that after object contact, a new source of information becomes available to the animal: the contact forces and moments at the base of each whisker. The signals associated with contact mechanics tend to be much larger than the signals present during non-contact whisking [34,35,45•,53,67–69]. Given the spatial invariance of a mechanoreceptor with respect to the follicle (Figure 3c), the deformation of mechanoreceptors associated with contact is optimally expressed in whisker-centered coordinates. Two recent studies indicate that this mechanical information is indeed encoded by primary sensory neurons of the trigeminal ganglion [44••,45•].
We therefore propose that — just as during human exploration with fingertips [70] — the rat exploits contact mechanics to determine object features such as contour. Although very few studies have examined whisker-object contact patterns, a few recent experiments provide clues as to how this computation is enabled by whisker motions.
First, several studies have indicated that as rats perform haptic exploration tasks, they gradually increase contact durations with the object [71–73]. Mechanically, this would have the effect of damping out vibrations associated with object collision and ensuring that the whisker enters a quasistatic regime in which bending is the dominant effect [28,34,35]. In 2D, the mechanical signals associated with bending have been shown to uniquely represent the whisker centered geometry (rwobj, θwobj) [43]. Moreover, recent work from our laboratory [13•] strongly indicates that a subset of forces and moments at the whisker base will also be sufficient to represent (rwobj, θwobj, φwobj).
Second, studies on orienting behavior have shown that rats tend to position their heads so as to maximize the number of whiskers in contact with a surface, given the expected orientation of the surface [74,75]. The tendency to maximize the number of whisker-object contacts suggests that the integration of information across multiple whiskers will play an important role during contour extraction.
Finally, a recent study employed a light sheet to directly visualize whisker-object contact patterns as naïve rats freely explored a flat, vertical surface [76•]. Results showed that every whisk exhibited brief windows during which many whiskers collectively made sustained (25–60 ms) contact with the surface. The number of whiskers in contact depended strongly on the pose of the head, but averaged around 15–20. Furthermore, during this contact window (termed the ‘sustained collective contact interval,’ or SCCI), all whiskers converged and moved more slowly on the surface.
Taken together, we interpret these studies to suggest that the rat employs a strategy of ‘windowed sampling’ during object exploration. As opposed to relying primarily on inter-vibrissal phase or timing cues to extract object spatial features (e.g., contour), the rat spatially integrates across whiskers the mechanical signals acquired during the SCCI. These mechanical signals can thus provide information about object identity through an integrative computation that does not depend on the object’s location in head-centered coordinates.
Conclusions
Three-dimensional investigation of vibrissotactile exploratory behavior is experimentally challenging, and simulations of 3D vibrissal geometry and mechanics are complex. Yet a 3D approach is critical if we are to begin understanding the input signals that drive activity at more central levels of the trigeminal system [10,11••,13•,51,54]. As the field progresses in its understanding of 3D mechanics, geometry, and vibrissal-object contact patterns, it will be essential to ensure a systematic notation for each of the reference frames relevant to quantifying input variables.
In particular, the head-centered and resting-whisker reference frames naturally lend themselves to a description of object location, while the whisker-centered reference frame provides a natural description of mechanics. We further suggest that by exploiting contact mechanics, the animal could obtain estimates of contact point location within the whisker-centered reference frame; object contours can then be determined by integrating mechanical information across vibrissae during a brief (25–60 ms) window of quasi-static deflection that lasts only a fraction of the whisk. We posit that rats perform a ‘haptic enclosure’ [77,78] with their whiskers, similar to a grasping motion of the human hand.
Although this article has implicitly raised a host of interesting questions about the neural representations of these coordinate systems, we can only offer speculative ideas as to how and where those neural representations would emerge. By analogy to reaching and grasping [79], we suggest that rodents may employ a variety of reference frames (head-centered, unilateral-array centered, whisker-centered) depending on their behavioral goals. Some evidence for task-specific coordination of head and whisker movements has recently emerged in freely behaving mice [80••]. We suggest that a careful consideration of whisking motions may make the rodent system an excellent model for the study of neural transformations between reference frames, a choice that would complement work in primates.
Acknowledgments
We thank Lucie A. Huet, Anne E. T. Yang, and Matthew M. Graff for useful discussions. This work was supported by National Science Foundation award IIS-1208118 to MJZH and National Institute of Health award R01-NS093585 to MJZH and SAS. NEB was supported in part by a National Institute of Health Ruth L. Kirschstein National Research Service Award, F31-NS092335.
References and recommended reading
Papers of particular interest, published within the period of review, have been highlighted as:
• of special interest
•• of outstanding interest
- 1.Richardson FE. A study of sensory control in the rat. Psychol Monogr. 1909;12:1–124. [Google Scholar]
- 2.Vincent SB. The functions of the vibrissae in the behavior of the white rat. Behav Monogr. 1912;1:1–81. [Google Scholar]
- 3.Welker WI. Analysis of sniffing of the albino rat. Behaviour. 1964;22:223–244. [Google Scholar]
- 4.Simons DJ. Response properties of vibrissa units in rat S1 somatosensory neocortex. J Neurophysiol. 1978;41:798–820. doi: 10.1152/jn.1978.41.3.798. [DOI] [PubMed] [Google Scholar]
- 5.Wineski LE. Facial morphology and vibrissal movement in the golden hamster. J Morphol. 1985;183:199–217. doi: 10.1002/jmor.1051830208. [DOI] [PubMed] [Google Scholar]
- 6.Moore JD, Deschenes M, Furuta T, Huber D, Smear MC, Demers M, Kleinfeld D. Hierarchy of orofacial rhythms revealed through whisking and breathing. Nature. 2013;497:205–212. doi: 10.1038/nature12076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ranade S, Hangya B, Kepecs A. Multiple modes of phase locking between sniffing and whisking during active exploration. J Neurosci. 2013;33:8250–8256. doi: 10.1523/JNEUROSCI.3874-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yu C, Derdikman D, Haidarliu S, Ahissar E. Parallel thalamic pathways for whisking and touch signals in the rat. PLoS Biol. 2006;4:e124. doi: 10.1371/journal.pbio.0040124. http://dx.doi.org/10.1371/journal.pbio.0040124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moore JD, Lindsay NM, Deschenes M, Kleinfeld D. Vibrissa self-motion and touch are reliably encoded along the same somatosensory pathway from brainstem through thalamus. PLoS Biol. 2015 doi: 10.1371/journal.pbio.1002253. http://dx.doi.org/10.1371/journal.pbio.1002253. [DOI] [PMC free article] [PubMed]
- 10.Huet LA, Hartmann MJZ. Simulations of a vibrissa slipping along a straight edge and an analysis of frictional effects during whisking. IEEE Trans Haptics. 2016;9:158–169. doi: 10.1109/TOH.2016.2522432. http://dx.doi.org/10.1109/TOH.2016.2522432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Huet LA, Schroeder CL, Hartmann MJZ. Tactile signals transmitted by the vibrissa during active whisking behavior. J Neurophysiol. 2015;113:3511–3518. doi: 10.1152/jn.00011.2015. This computational and behavioral study develops a quasistatic model of whisker bending that allows for the calculation of the three-dimensional mechanical signals at the vibrissal base. The model is used to compute all six components of force and moment at the whisker base as an awake rat whisks against a peg, even as the whisker slips significantly out of its plane of rotation.
- 12.Knutsen PM, Biess A, Ahissar E. Vibrissal kinematics in 3D: tight coupling of azimuth, elevation, and torsion across different whisking modes. Neuron. 2008;59:35–42. doi: 10.1016/j.neuron.2008.05.013. [DOI] [PubMed] [Google Scholar]
- 13. Yang A, Hartmann MJZ. Whisking kinematics enables object localization in head-centered coordinates based on tactile information from a single vibrissa. Front Behav Neurosci. 2016 doi: 10.3389/fnbeh.2016.00145. http://dx.doi.org/10.3389/fnbeh.2016.00145. This simulation study demonstrates that, for nearly all whiskers in the array, purely tactile signals at the whisker base — as would be measured by mechanoreceptors, in whisker-centered coordinates — could be used to determine the location of a vertical peg in head-centered coordinates.
- 14.Towal RB, Quist BW, Gopal V, Solomon JH, Hartmann MJZ. The morphology of the rat vibrissal array: a model for quantifying spatiotemporal patterns of whisker-object contact. PLoS Comput Biol. 2011;7:e1001120. doi: 10.1371/journal.pcbi.1001120. http://dx.doi.org/10.1371/journal.pcbi.1001120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Quist BW, Hartmann MJZ. Mechanical signals at the base of a rat vibrissa: the effect of intrinsic vibrissa curvature and implications for tactile exploration. J Neurophysiol. 2012;107:2298–2312. doi: 10.1152/jn.00372.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bagdasarian K, Szwed M, Knutsen PM, Deutsch D, Derdikman D, Pietr M, Simony E, Ahissar E. Pre-neuronal morphological processing of object location by individual whiskers. Nat Neurosci. 2013;16:622–631. doi: 10.1038/nn.3378. [DOI] [PubMed] [Google Scholar]
- 17.Ebara S, Kumamoto K, Matsuura T, Mazurkiewicz JE, Rice FL. Similarities and differences in the innervation of mystacial vibrissal follicle-sinus complexes in the rat and cat: a confocal microscopic study. J Comp Neurol. 2002;449:103–119. doi: 10.1002/cne.10277. [DOI] [PubMed] [Google Scholar]
- 18.Deschenes M, Haidarliu S, Demers M, Moore J, Kleinfeld D, Ahissar E. Muscles involved in naris dilation and nose motion in rat. Anat Rec Adv Integr Anat Evol Biol. 2015;298:546–553. doi: 10.1002/ar.23053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Haidarliu S, Golomb D, Kleinfeld D, Ahissar E. Dorsorostral snout muscles in the rat subserve coordinated movement for whisking and sniffing. Anat Rec Adv Integr Anat Evol Biol. 2012;295:1181–1191. doi: 10.1002/ar.22501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Haidarliu S, Kleinfeld D, Deschenes M, Ahissar E. The musculature that drives active touch by vibrissae and nose in mice. Anat Rec Adv Integr Anat Evol Biol. 2015;298:1347–1358. doi: 10.1002/ar.23102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Haidarliu S, Simony E, Golomb D, Ahissar E. Muscle architecture in the mystacial pad of the rat. Anat Rec Adv Integr Anat Evol Biol. 2010;293:1192–1206. doi: 10.1002/ar.21156. [DOI] [PubMed] [Google Scholar]
- 22.Kim J-N, Yoo J-Y, Lee J-Y, Koh K-S, Song W-C. A mechanism of rat vibrissal movement based on actual morphology of the intrinsic muscle using three-dimensional reconstruction. Cells Tissues Organs. 2012;196:565–569. doi: 10.1159/000338332. [DOI] [PubMed] [Google Scholar]
- 23.Simony E, Bagdasarian K, Herfst L, Brecht M, Ahissar E, Golomb D. Temporal and spatial characteristics of vibrissa responses to motor commands. J Neurosci. 2010;30:8935–8952. doi: 10.1523/JNEUROSCI.0172-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hires SA, Pammer L, Svoboda K, Golomb D. Tapered whiskers are required for active tactile sensation. eLife. 2013;2 doi: 10.7554/eLife.01350. http://dx.doi.org/10.7554/eLife.01350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Quist BW, Faruqi RA, Hartmann MJZ. Variation in Young’s modulus along the length of a rat vibrissa. J Biomech. 2011;44:2775–2781. doi: 10.1016/j.jbiomech.2011.08.027. [DOI] [PubMed] [Google Scholar]
- 26.Williams CM, Kramer EM. The advantages of a tapered whisker. PLoS ONE. 2010;5 doi: 10.1371/journal.pone.0008806. http://dx.doi.org/10.1371/journal.pone.0008806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Voges D, Carl K, Klauer GJ, Uhlig R, Schilling C, Behn C, Witte H. Structural characterization of the whisker system of the rat. IEEE Sens J. 2012;12:332–339. [Google Scholar]
- 28.Yan W, Kan Q, Kergrene K, Kang G, Feng X-Q, Rajan R. A truncated conical beam model for analysis of the vibration of rat whiskers. J Biomech. 2013;46:1987–1995. doi: 10.1016/j.jbiomech.2013.06.015. [DOI] [PubMed] [Google Scholar]
- 29.Knutsen PM. Whisking kinematics. Scholarpedia. 2015;10:7280. [Google Scholar]
- 30.Knutsen PM, Pietr M, Ahissar E. Haptic object localization in the vibrissal system: behavior and performance. J Neurosci. 2006;26:8451–8464. doi: 10.1523/JNEUROSCI.1516-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mehta SB, Whitmer D, Figueroa R, Williams BA, Kleinfeld D. Active spatial perception in the vibrissa scanning sensorimotor system. PLoS Biol. 2007;5:0309–0322. doi: 10.1371/journal.pbio.0050015. http://dx.doi.org/10.1371/journal.pbio.0050015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.O’Connor DH, Clack NG, Huber D, Komiyama T, Myers EW, Svoboda K. Vibrissa-based object localization in head-fixed mice. J Neurosci. 2010;30:1947–1967. doi: 10.1523/JNEUROSCI.3762-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pammer L, O’Connor DH, Hires SA, Clack NG, Huber D, Myers EW, Svoboda K. The mechanical variables underlying object localization along the axis of the whisker. J Neurosci. 2013;33:6726–6741. doi: 10.1523/JNEUROSCI.4316-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Quist BW, Seghete V, Huet LA, Murphey TD, Hartmann MJZ. Modeling forces and moments at the base of a rat vibrissa during noncontact whisking and whisking against an object. J Neurosci. 2014;34:9828–9844. doi: 10.1523/JNEUROSCI.1707-12.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boubenec Y, Shulz DE, Debregeas G. Whisker encoding of mechanical events during active tactile exploration. Front BehavNeurosci. 2012;6:74. doi: 10.3389/fnbeh.2012.00074. http://dx.doi.org/10.3389/fnbeh.2012.00074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hartmann MJZ. Vibrissal mechanical properties. Scholarpedia. 2015;10:6636. http://dx.doi.org/10.4249/scholarpedia.6636 [Google Scholar]
- 37.Clements TN, Rahn CD. Three-dimensional contact imaging with an actuated whisker. IEEE Trans Robot. 2006;22:844–848. [Google Scholar]
- 38.Kaneko M, Kanayama N, Tsuji T. Active antenna for contact sensing. IEEE Trans Robot Autom. 1998;14:278–291. [Google Scholar]
- 39.Scholz GR, Rahn CD. Profile sensing with an actuated whisker. IEEE Trans Robot Autom. 2004;20:124–127. [Google Scholar]
- 40.Solomon JH, Hartmann MJ. Robotic whiskers used to sense features. Nature. 2006;443:525. doi: 10.1038/443525a. [DOI] [PubMed] [Google Scholar]
- 41.Solomon JH, Hartmann MJZ. Extracting object contours with the sweep of a robotic whisker using torque information. Int J Robot Res. 2010;29:1233–1245. [Google Scholar]
- 42.Solomon JH, Hartmann MJZ. Artificial whiskers suitable for array implementation: accounting for lateral slip and surface friction. IEEE Trans Robot. 2008;24:1157–1167. [Google Scholar]
- 43.Solomon JH, Hartmann MJZ. Radial distance determination in the rat vibrissal system and the effects of Weber’s law. Philos Trans R Soc B Biol Sci. 2011;366:3049–3057. doi: 10.1098/rstb.2011.0166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Bush NE, Schroeder CL, Hobbs JA, Yang AET, Huet LA, Solla SA, Hartmann MJZ. Decoupling kinematics and mechanics reveals coding properties of trigeminal ganglion neurons in the rat vibrissal system. eLife. 2016;5:e13969. doi: 10.7554/eLife.13969. http://dx.doi.org/10.7554/ The authors record from primary sensory neurons of the trigeminal ganglion while using a novel manual stimulation technique to impose large angle deflections that decouple mechanics and kinematics. Data analysis based on Generalized Linear Models shows that when mechanics and kinematics are decoupled, mechanical information provided by forces and moments at the base of the whisker better predicts firing activity for a majority of Vg neurons.
- 45. Campagner D, Evans MH, Bale MR, Erskine A, Petersen RS. Prediction of primary somatosensory neuron activity during active tactile exploration. eLife. 2016;5:e10696. doi: 10.7554/eLife.10696. http://dx.doi.org/10.7554/eLife.10696. The authors use a combination of anesthetized and awake recordings analyzed within the framework of Generalized Linear Models to conclude that the activity of primary sensory neurons of the trigeminal ganglion (Vg) more directly represents mechanical (bending moment) than geometric (angular position) variables of contact.
- 46.Chen JL, Margolis DJ, Stankov A, Sumanovski LT, Schneider BL, Helmchen F. Pathway-specific reorganization of projection neurons in somatosensory cortex during learning. Nat Neurosci. 2015;18:1101–1108. doi: 10.1038/nn.4046. [DOI] [PubMed] [Google Scholar]
- 47.Arabzadeh E, Panzeri S, Diamond ME. Deciphering the spike train of a sensory neuron: counts and temporal patterns in the rat whisker pathway. J Neurosci. 2006;26:9216–9226. doi: 10.1523/JNEUROSCI.1491-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bale MR, Campagner D, Erskine A, Petersen RS. Microsecond-scale timing precision in rodent trigeminal primary afferents. J Neurosci. 2015;35:5935–5940. doi: 10.1523/JNEUROSCI.3876-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bale MR, Davies K, Freeman OJ, Ince RAA, Petersen RS. Low-dimensional sensory feature representation by trigeminal primary afferents. J Neurosci. 2013;33:12003–12012. doi: 10.1523/JNEUROSCI.0925-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jones LM, Depireux DA, Simons DJ, Keller A. Robust temporal coding in the trigeminal system. Science. 2004;304:1986–1989. doi: 10.1126/science.1097779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jones LM, Lee S, Trageser JC, Simons DJ, Keller A. Precise temporal responses in whisker trigeminal neurons. J Neurophysiol. 2004;92:665–668. doi: 10.1152/jn.00031.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Leiser SC, Moxon KA. Relationship between physiological response type (RA and SA) and vibrissal receptive field of neurons within the rat trigeminal ganglion. J Neurophysiol. 2006;95:3129–3145. doi: 10.1152/jn.00157.2005. [DOI] [PubMed] [Google Scholar]
- 53.Leiser SC, Moxon KA. Responses of trigeminal ganglion neurons during natural whisking behaviors in the awake rat. Neuron. 2007;53:117–133. doi: 10.1016/j.neuron.2006.10.036. [DOI] [PubMed] [Google Scholar]
- 54.Lichtenstein SH, Carvell GE, Simons DJ. Responses of rat trigeminal ganglion neurons to movements of vibrissae in different directions. Somatosens Mot Res. 1990;7:47–65. doi: 10.3109/08990229009144697. [DOI] [PubMed] [Google Scholar]
- 55.Lottem E, Azouz R. A unifying framework underlying mechanotransduction in the somatosensory system. J Neurosci. 2011;31:8520–8532. doi: 10.1523/JNEUROSCI.6695-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Whiteley SJ, Knutsen PM, Matthews DW, Kleinfeld D. Deflection of a vibrissa leads to a gradient of strain across mechanoreceptors in a mystacial follicle. J Neurophysiol. 2015;114:138–145. doi: 10.1152/jn.00179.2015. The authors used two-photon laser scanning microscopy in an ex vivo follicle preparation to visualize localized displacements of specific mechanoreceptor cells within the follicle during whisker deflection. These displacements were used to compute the strain field within the follicle in response to the whisker deflection.
- 57.Ahissar E, Knutsen PM. Vibrissal location coding. Scholarpedia. 2011;6:6639. [Google Scholar]
- 58.Knutsen PM, Ahissar E. Orthogonal coding of object location. Trends Neurosci. 2009;32:101–109. doi: 10.1016/j.tins.2008.10.002. [DOI] [PubMed] [Google Scholar]
- 59.Kleinfeld D, Deschenes M. Neuronal basis for object location in the vibrissa scanning sensorimotor system. Neuron. 2011;72:455–468. doi: 10.1016/j.neuron.2011.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Mameli O, Caria MA, Pellitteri R, Russo A, Saccone S, Stanzani S. Evidence for a trigeminal mesencephalic-hypoglossal nuclei loop involved in controlling vibrissae movements in the rat. Exp Brain Res. 2016;234:753–761. doi: 10.1007/s00221-015-4503-6. [DOI] [PubMed] [Google Scholar]
- 61.Mameli O, Stanzani S, Mulliri G, Pellitteri R, Caria MA, Russo A, De Riu P. Role of the trigeminal mesencephalic nucleus in rat whisker pad proprioception. Behav Brain Funct. 2010;6:69. doi: 10.1186/1744-9081-6-69. http://dx.doi.org/10.1186/1744-9081-6-69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Fee MS, Mitra PP, Kleinfeld D. Central versus peripheral determinants of patterned spike activity in rat vibrissa cortex during whisking. J Neurophysiol. 1997;78:1144–1149. doi: 10.1152/jn.1997.78.2.1144. [DOI] [PubMed] [Google Scholar]
- 63.Hill DN, Curtis JC, Moore JD, Kleinfeld D. Primary motor cortex reports efferent control of vibrissa motion on multiple timescales. Neuron. 2011;72:344–356. doi: 10.1016/j.neuron.2011.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Wallach A, Bagdasarian K, Ahissar E. On-going computation of whisking phase by mechanoreceptors. Nat Neurosci. 2016;19:487–493. doi: 10.1038/nn.4221. A clever, closed-loop modification to the ‘electrical whisking’ paradigm that generates naturalistic whisking in anesthetized rats allows the authors to demonstrate that primary vibrissal afferents and some regions of the trigeminal brainstem encode whisking phase, independent of the frequency and amplitude of the whisk.
- 65.Diamond ME, von Heimendahl M, Knutsen PM, Kleinfeld D, Ahissar E. ‘Where’ and ‘what’ in the whisker sensorimotor system. Nat Rev Neurosci. 2008;9:601–612. doi: 10.1038/nrn2411. [DOI] [PubMed] [Google Scholar]
- 66.Kleinfeld D, Ahissar E, Diamond ME. Active sensation: insights from the rodent vibrissa sensorimotor system. Curr Opin Neurobiol. 2006;16:435–444. doi: 10.1016/j.conb.2006.06.009. [DOI] [PubMed] [Google Scholar]
- 67.Khatri V, Bermejo R, Brumberg JC, Keller A, Zeigler HP. Whisking in air: encoding of kinematics by trigeminal ganglion neurons in awake rats. J Neurophysiol. 2009;101:1836–1846. doi: 10.1152/jn.90655.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Szwed M, Bagdasarian K, Ahissar E. Encoding of vibrissal active touch. Neuron. 2003;40:621–630. doi: 10.1016/s0896-6273(03)00671-8. [DOI] [PubMed] [Google Scholar]
- 69.Szwed M, Bagdasarian K, Blumenfeld B, Barak O, Derdikman D, Ahissar E. Responses of trigeminal ganglion neurons to the radial distance of contact during active vibrissal touch. J Neurophysiol. 2006;95:791–802. doi: 10.1152/jn.00571.2005. [DOI] [PubMed] [Google Scholar]
- 70.Tramper JJ, Flanders M. Predictive mechanisms in the control of contour following. Exp Brain Res. 2013;227:535–546. doi: 10.1007/s00221-013-3529-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Deutsch D, Pietr M, Knutsen PM, Ahissar E, Schneidman E. Fast feedback in active sensing: touch-induced changes to whisker-object interaction. PLoS ONE. 2012 doi: 10.1371/journal.pone.0044272. http://dx.doi.org/10.1371/journal.pone.0044272. [DOI] [PMC free article] [PubMed]
- 72.Grant RA, Mitchinson B, Fox CW, Prescott TJ. Active touch sensing in the rat: anticipatory and regulatory control of whisker movements during surface exploration. J Neurophysiol. 2009;101:862–874. doi: 10.1152/jn.90783.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Saraf-Sinik I, Assa E, Ahissar E. Motion makes sense: an adaptive motor-sensory strategy underlies the perception of object location in rats. J Neurosci. 2015;35:8777–8789. doi: 10.1523/JNEUROSCI.4149-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Hobbs JA, Towal RB, Hartmann MJZ. Probability distributions of whisker-surface contact: quantifying elements of the rat vibrissotactile natural scene. J Exp Biol. 2015;218:2551–2562. doi: 10.1242/jeb.116186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mitchinson B, Martin CJ, Grant RA, Prescott TJ. Feedback control in active sensing: rat exploratory whisking is modulated by environmental contact. Proc R Soc B Biol Sci. 2007;274:1035–1041. doi: 10.1098/rspb.2006.0347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Hobbs JA, Towal RB, Hartmann MJZ. Spatiotemporal patterns of contact across the rat vibrissal array during exploratory behavior. Front Behav Neurosci. 2016;9:356. doi: 10.3389/fnbeh.2015.00356. http://dx.doi.org/10.3389/fnbeh.2015.00356. The authors used a laser light sheet to quantify the spatiotemporal structure of whisker-surface contact as naïve rats freely explored a flat, vertical glass wall. Whiskers were found to sustain contact with the surface for extended durations (25–60 ms) before detaching. During this time window, the contact locations of the whiskers on the glass converged and moved more slowly on the glass sheet.
- 77.Klatzky RL, Lederman SJ. Identifying objects from a haptic glance. Percept Psychophys. 1995;57:1111–1123. doi: 10.3758/bf03208368. [DOI] [PubMed] [Google Scholar]
- 78.Lederman SJ, Klatzky RL. Haptic perception: a tutorial. Atten Percept Psychophys. 2009;71:1439–1459. doi: 10.3758/APP.71.7.1439. [DOI] [PubMed] [Google Scholar]
- 79.Graziano MSA. Is reaching eye-centered, body-centered, hand-centered, or a combination? Rev Neurosci. 2001;12:175–185. doi: 10.1515/revneuro.2001.12.2.175. [DOI] [PubMed] [Google Scholar]
- 80. Schroeder JB, Ritt JT. Selection of head and whisker coordination strategies during goal-oriented active touch. J Neurophysiol. 2016;115:1797–1809. doi: 10.1152/jn.00465.2015. The authors show that mice select from a diverse range of whisking and head-movement strategies when searching for a randomly-located reward aperture. These are some of the first experiments to demonstrate that rodents alter the coordination of head and whisker motions depending on behavioral task.