Revised RNA Dihedral Parameters for the Amber Force Field Improve RNA Molecular Dynamics

Abstract

The backbone dihedral parameters of the Amber RNA force field were improved by fitting using multiple linear regression to potential energies determined by quantum chemistry calculations. Five backbone and four glycosidic dihedral parameters were fit simultaneously to reproduce the potential energies determined by a high-level density functional theory calculation (B97D3 functional with the AUG-CC-PVTZ basis set). Umbrella sampling was used to determine conformational free energies along the dihedral angles, and these better agree with the population of conformations observed in the protein data bank for the new parameters than for the conventional parameters. Molecular dynamics simulations performed on a set of hairpin loops, duplexes and tetramers with the new parameter set show improved modeling for the structures of tetramers CCCC, CAAU, and GACC, and an RNA internal loop of noncanonical pairs, as compared to the conventional parameters. For the tetramers, the new parameters largely avoid the incorrect intercalated structures that dominate the conformational samples from the conventional parameters. For the internal loop, the major conformation solved by NMR is stable with the new parameters, but not with the conventional parameters. The new force field performs similarly to the conventional parameters for the UUCG and GCAA hairpin loops and the [U(UA)₆A]₂ duplex.

Introduction

As longer trajectories became possible with the availability of modern computers, limitations in the force fields for nucleic acids became apparent.^1,2 These limitations remain for simulations of RNA, where recent benchmarks of the Amber force field reveal serious flaws in its modeling of tetramers, noncanonical pairs in internal loops, and tetraloops. Tetramers were characterized by NMR, and simulations for those sequences do not match the experimental data.³⁻⁸ Moreover, free energy calculations on small systems involving noncanonical pairs do not match the conformational preferences demonstrated in solution structures.⁹⁻¹¹ Banáš et al. demonstrated signature interactions in tetraloops that are lost during state-of-the-art simulations.¹² Longer simulations using enhanced sampling show that problems simulating tetraloops persist, and that CHARMM36¹³ and an Amber force field with revised van der Waals parameters¹⁴ are also unable to correctly model the solution structures of tetramers and tetraloops.^4,15,16

To address the limitations of the Amber nucleic acids force field, work has largely focused on revising subsets of dihedral parameters by fitting a single dihedral at a time using model systems.^13,17−19 Development of protein force fields generally followed a similar approach,²⁰⁻²² although the simpler backbone has allowed for simultaneous fitting of both backbone dihedrals.²³ The version of the Amber force field for nucleic acids, distributed with Amber 14, was named ff10 (and was unchanged in the ff14SB force field).²⁴ This force field is a refinement of the ff94 force field of Cornell et al.²⁵ Initially, this force field was improved by changing the sugar pucker and glycosidic torsions in force fields ff98 and ff99.^26,27 Later, a new set of parameters called bsc0 was derived for α and γ dihedrals.¹⁷ The bsc0 force field was derived by fitting to quantum mechanical (QM) energies on an extended model of backbone atoms derived from RNA and DNA molecules based on B3LYP and LMP2 calculations.¹⁷ In 2010 and 2011, two new sets of glycosidic torsions were derived for each base, namely Chi_YIL¹⁹ and ChiOL3,¹⁸ respectively, with ChiOL3 being incorporated into ff10. Additionally, Chen & Garcia revised the van der Waals parameters in addition to the dihedrals,¹⁴ although that parameter set did not solve the problems with tetraloop or tetramer conformational preferences⁴ and introduced problems that can be observed in the loss of stacking in an HIV-1 kissing loop complex.²⁸

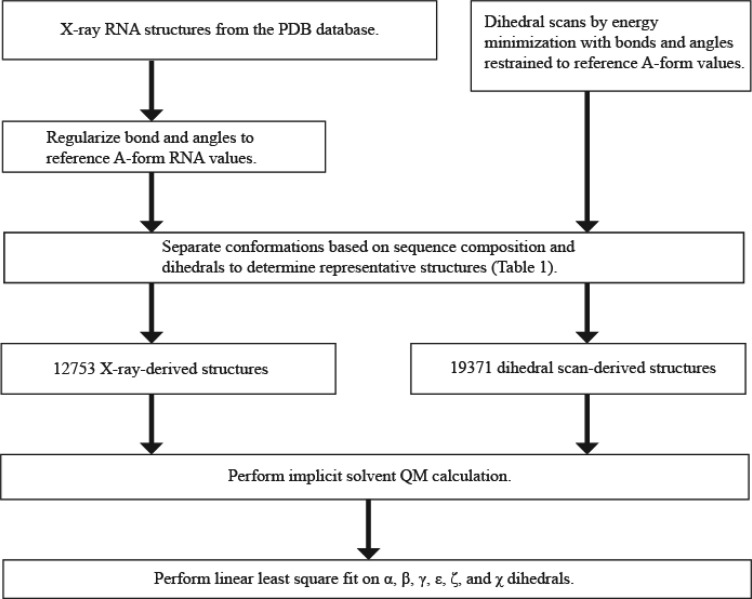
In this work, the Amber force field for RNA was improved by simultaneously refitting the α, β, γ, ε, ζ, and glycosidic dihedral (χ) parameters by linear regression to potentials determined by QM calculations. In place of the conventional scan of each individual dihedral, a diverse range of nucleotide and dinucleotide conformations were chosen, combining structures from the PDB with a set of dihedral scans to sample the high potential energy barriers. An overview of the procedure is shown in Figure 1.

Figure 1.

Procedure for fitting force field parameters. A diverse database of conformations was generated from X-ray structures and from dihedral scanning. For X-ray structures, bonds and angles were fixed to an A-form reference value using sander from the Amber software package.²⁴ The dihedral scan structures were generated by energy minimization with restraints on selected torsions. Additional restraints were applied on bond and angles to set them to the A-form reference value. The database was then reduced in size by considering sequence identity and dihedrals to remove redundancies. Structures generated by scanning and taken from the PDB were both used for the linear least-square fit.

The newly fitted parameters were tested in several ways. Free energy profiles for dihedral angles of mono- and dinucleotides were calculated using the new dihedral parameters with umbrella sampling. These profiles better resemble the population of conformations observed in the protein data bank than do conformational free energies using the conventional Amber force field. Additionally, molecular dynamics trajectories were calculated for tetramers, internal loops, and the UUCG tetraloop.^3,5,29 Improved agreement with solution structures was found for many systems, although the new parameters did not resolve all the anomalies.

Methods

Assembling a Database of Structures for Fitting

The first step was creating a database of diverse dinucleotide conformations. It was important that the database cover a variety of feasible conformations to ensure that the fitted dihedral parameters are transferable to diverse structures. The database was then subsequently reduced in size to remove redundant conformations (Figure 1). A database of 23 399 dinucleotide systems was generated by extracting all RNA dinucleotide fragments from a diverse set of X-ray structures with resolution of 4 Å or better from the Protein Data Bank (PDB).^30,31 All dinucleotides were terminated with OH groups at the 5′ and 3′ carbons. The list of structures is provided in Table S1. When the crystal structure contained alternative coordinates, only the primary structure was kept.

To expand the diversity of conformations beyond those found in crystal structures, an additional 16 499 dinucleotide and 2877 nucleoside conformations were generated using one-dimensional dihedral scans by energy minimization with the sander program from Amber.^24,32 The dihedral scans were performed in two ways. Both ways restrained the target dihedral angle with a force constant of 1000 kcal /(mol × rad²), while bonds and angles were kept close to those found in A-form RNA by applying restraints using a force constant of 500 kcal /(mol × Å ²) and 500 kcal /(mol × rad²), respectively. The structural parameters for A-form RNA were derived from the NAB module from Amber,³³ which determined them using fiber diffraction data.³⁴ The first set of scans additionally restrained the other dihedrals in the backbone to their starting configuration, with a force constant of 50 kcal /(mol × rad²). The second set of scans was performed without dihedral restraints other than the dihedral of the scan. This provided a diversity of conformations in addition to the diversity along the scanned dihedral. The starting structures for the dihedral scan were A-form helices built using NAB;³³ restraints for bonds and angles were generated using “rdparm” from Amber.²⁴ Backbone dihedral restraints for the first set were generated using cpptraj by calculating the dihedral angles of each X-ray structure from the database.^24,35 Each dihedral scan was done with 5° intervals between structures. Each structure was minimized for 2500 steps using the steepest descent algorithm, followed by 2500 steps of conjugate gradient minimization. During the scans, the solvent was represented using the Generalized Born implicit solvent model as implemented in the sander program.²⁴

Regularization of Bonds and Angles

The next step was to fix bonds and angles of all the X-ray-structure-derived configurations to those observed in reference A-form helices; for those structures generated above by scanning, the bonds and angles were regularized as part of the procedure for generating the coordinates.³⁴ This was done to ensure the bonded terms of the force field would have the same values in order to prevent excessive noise in the potential energies of the configurations being introduced by variations in these terms, and was accomplished using energy minimization with the GB implicit solvent³⁶⁻³⁸ model in sander.²⁴ Restraints for bonds and angles to the reference A-form helices were ramped slowly from an initial 100 kcal/(mol × Å²) and 100 kcal/(mol × rad²), respectively, to 500 kcal/(mol × Å²) and 500 kcal/(mol × rad²), respectively, over 1000 steps of steepest descent minimization and then kept at 500 kcal/(mol × rad²) for the rest of 1500 steps of steepest descent followed by a 2500 steps of conjugate gradient minimization. To keep the X-ray structure close to the original structure during bond and angle regularization, dihedral restraints with 30 kcal/(mol × rad²) were applied in one set of 10668 configurations. A second set of 2085 configurations were energy minimized without any dihedral restraint regularization.

Restraints for bonds and angles were generated using “rdparm” from AmberTools15.²⁴ “rdparm” prints all bonds, angles and dihedral angles in a file along with atom pair lists that form bonds, three atom pair lists that form angles and four atom pair lists that form dihedral angle. Sample output from “rdparm” is given in Tables S3–5. Restraints for the torsions were generated using cpptraj by calculating dihedral angle value of each X-ray structure from the database.^24,35

Next, clustering (in 5° wide bins on dihedral value as the selection criteria) was performed for systems of identical sequence. A set of diverse structures were generated (shown in Table 1), including 12 753 X-ray structure derived and 19 371 dihedral-scan derived structures, equally divided by configuration and sequence identity. Of the dihedral-scan derived structures, 2877 were nucleosides.

Table 1. Sequence Composition of All Dinucleotides and Nucleosides Used in Fitting.

sequence	no. conformations	sequence	no. conformations
AA	2198	CA	1913
AC	1832	CC	1756
AG	2152	CG	1782
AU	1903	CU	1610
GA	2048	UA	1737
GC	1714	UC	1700
GG	1753	UG	1728
GU	1785	UU	1636
A	717	G	724
C	718	U	718

Potential Energy Calculation

For each structure, the energy was calculated using dispersion corrected density functional B97 with dampening function D3(BJ) and the triple-ζ Dunning correlation consistent basis set with diffuse functions, AUG-CC-PVTZ.^39,40 This method was previously tested against a databases of high level QM calculations, the S66 database,⁴¹ which includes CCSD(T)/CBS energies of 66 complexes stabilized by hydrogen bonding and dispersion interactions. B97D3 produces results that are close to the reference values; the mean absolute deviation between B97D3/def2-QZVP calculated energies and the reference S66 energies is only 0.29 kcal/mol.⁴² A more recent benchmark with a database containing all possible RNA backbone conformations using various QM methods also found that similar functionals based on generalized gradient approximation (GGA) with dampening correction perform well in describing the RNA backbone.⁴³ B97D3 with this relatively large basis set was chosen as a balance between accuracy and computational efficiency, since it had to be run for a large number of conformations. These QM calculations were performed with Gaussian 09.⁴⁴ An implicit water model, solvation model based on density (SMD),⁴⁵ was used for the QM.

Regression Procedure

The next step was to perform a linear least-squares (LLS) fit of dihedral parameters so as to best reproduce the QM potential energies. The composition of the database, in terms of sequences, is shown in Table 1.⁴⁶ Because bond lengths and angles were regularized, relative energies exclude the undesired noisy contributions that would have resulted from changes in bond lengths and angles.

α, β, γ, ε, ζ, and four χ dihedrals (one for each base) were fit simultaneously. The delta torsion was excluded at this time because its energy is correlated with the other sugar ring torsions. To avoid conflict between the ε dihedral, defined by torsion angle C4_i^′–C3_i–O3_i^′–P_i+1, and the sugar ring torsion, defined by C2_i–C3_i^′–O3_i–P_i+1, the atom type of C4′ was changed from CT to CF; in Amber ff10, these chemically distinct dihedrals have the same definition. Details of all fit dihedrals are given in Table 2.

Table 2. Fitting Torsion Names, Atom Names, and Atom Types According to Amber Force Field Nomenclature^a.

		dihedral angle definition
	torsion name	atom name	atom type	alternative paths
1	α	O3i–1′–Pi–O5i–C5i′	OS/OH–P–OS–CI	OP1i–Pi–O5i′–C5i
				OP2i–Pi–O5i′–C5i
2	β	Pi–O5i′–C5i–C4i′	P–OS–CI–CF	Pi–O5i′–C5i–H5i′
				Pi–O5i′–C5i–H5i″
3	γ	O5i′–C5i–C4i′–C3i	OS/OH–CI–CF–CT	H5i′–C5i–C4i′–C3i
				H5i′–C5i–C4i′–H4i
				H5i′–C5i–C4i′–O4i
				H5i″–C5i–C4i′–C3i
				H5i″–C5i–C4i′–H4i
				H5i″–C5i–C4i′–O4i
				O5i′–C5i–C4i′–H4i
				O5i′–C5i–C4i′–O4i
4	ε	C4i′–C3i–O3i′–Pi+1	CF–CT–OS–P	H3i′–C3i–O3i′–Pi+1
				C2i′–C3i–O3i′–Pi+1
5	ζ	C3i′–O3i–Pi+1–O5i+1′	CT–OS–P–OS	C3i′–O3i–Pi+1–OP1i+1
				C3′i–O3i′–Pi+1–OP2i+1
6	χ adenine	O4′i–C1′i–N9i–C8i	OS–CT–N*–C5	O4i′–C1i–N9i–C4i
				C2i′–C1i–N9i–C8i
				C2i′–C1i–N9i–C4i
				H1i′–C1i–N9i–C8i
				H1i′–C1i–N9i–C4i
7	χ cytosine	O4i′–C1i–N1i–C6i	OS–CT–N*–C4	O4i′–C1i–N1i–C2i
				C2i′–C1i–N1i–C6i
				C2i′–C1i–N1i–C2i
				H1i′–C1i–N1i–C2i
				H1i′–C1i–N1i–C2i
8	χ guanine	O4i′–C1i–N9i–C8i	OS–CT–N*–CP	O4i′–C1i–N9i–C4i
				C2i′–C1i–N9i–C8i
				C2i′–C1i–N9i–C4i
				H1i′–C1i–N9i–C8i
				H1i′–C1i–N9i–C4i
9	χ uracil	O4i′–C1i–N1i–C6i	OS–CT–N*–CS	O4i′–C1i–N1i–C2i
				C2i′–C1i–N1i–C6i
				C2i′–C1i–N1i–C2i
				H1i′–C1i–N1i–C2i
				H1i′–C1i–N1i–C2i

^aThe atom type “OS/OH” is to include the atom type for terminal O3′ and internal O3′ atom type.

The equation used for the dihedral potential in Amber is

1

where φ is the dihedral angle, n is the multiplicity, γ_n is a phase offset, and v_n is a barrier height.²⁵ Although the energy is nonlinear in the phase, γ_n, a predetermined phase can be introduced, such that the cosine can be rewritten as eqs 2 and 3(46,47)

2

3

where the barrier height, v_n, and phase, γ_n, are

4

5

The linear function for each dihedral included four sine and cosine terms of differing multiplicity, which can be subsequently transformed to a sum of cosines (plus an arbitrary offset) as used in the Amber force field.^46,47Table S7 in the Supplement provides the values and standard errors for the fit parameters.

The total Amber energy, including the fitting part, is given by

6

where the total Amber potential energy (E_Amber), is the sum of terms for bond length (E_bonds), bond angles (E_angles), the dihedrals that are not being fit (E_dihed-const), the dihedrals being fit (E_dihed-fit), van der Waals (E_VDW), electrostatics (E_elect), and implicit solvation (E_solvation). All of these terms are constant except for the E_dihed-fit, and the goal of the fitting is to improve E_dihed-fit to best match the total potential energy calculated by QM, including implicit solvation (E_QM)

7

The potential energies calculated by Amber (in E_const) and in the QM as part of total potential energy (E_QM) both include implicit solvation to account for fact that most simulations are run in an aqueous environment. This is consistent with fitting done previously.⁴⁸ Only the electrostatic part of the solvation energy⁴⁸ was included.²⁴

Equation 7 reduces to the linear equation

8

where X is vector of fitting parameters v_i, B is a vector of energy differences between QM and MM, A is a p × n coefficient matrix with p being number of fitting parameters, and n is the number of structures. The derivation can be found in recent publications.^46,47 All constant terms are precalculated using the conventional Amber parameters before fitting.

The solvation free energy in eq 6 was estimated using the analytical linearized Poisson–Boltzmann^49,50 method from the Amber software package via sander with the effective atomic radii from Tsui and Case.^51,52 The solvent permittivity was set to 78.4 (water), ionic strength was set to 150 mM, and all other parameters were default.

Fitting Software

The potential energy, bond, angle, electrostatic, van der Waals, and the constant portion of dihedrals (E_const in eq 6), were computed using a custom FORTRAN code. Linear least square (LLS) fitting was by singular value decomposition (SVD) using the GELSS routine from the Intel FORTRAN 95 LAPACK library.⁵³

Umbrella Sampling Calculation to Validate Results

To test the new dihedral parameters, the free energy profiles along α, β, γ, ε, ζ, and the four χ dihedrals were determined using umbrella sampling on dinucleotides in TIP3P water. Free energies were determined using the conventional Amber parameters and using the new dihedral parameters. Sixteen RNA dinucleotide molecules (one molecule for each possible dinucleotide sequence) were used. For each dihedral, 1 ns of restrained molecular dynamics was performed for each of 72 windows at 5° increments. In total, per molecule, 1152 ns total sampling was performed. The initial conformation for each window was generated with a separate MD simulation prior to the sampling (see below). For each backbone torsion, the PMF was calculated by combining the sampled conformations of all 16 RNA molecules using WHAM.⁵⁴⁻⁵⁶ For the glycosidic dihedral, the umbrella sampling was performed for each base of the dinucleotide, one at a time. The χ PMF for each base type was determined by adding all sampling for that base type.

Each of the 16 RNA molecules was neutralized with a Na⁺ and then solvated with a cubic TIP3P water box. The box dimensions were set so that the RNA was at least 10 Å from the edge of the box. Finally, 0.1 M NaCl was added based on number of water molecules. Each starting structure was energy minimized for 2500 steps of steepest descent followed by 2500 steps of conjugate gradient minimization. The minimized structure was heated at constant volume from 0 to 300 K over 20 ps with a time step of 1 fs, then equilibrated at 300 K and 1 atm for 100 ps with a time step of 1 fs. Next, a series of 200 ns restrained MD simulations was performed using the previous restart file as a starting structure. The dihedral angle restraint had a force constant of 200 kcal/(mol × rad²), with a width of ±100°, where the potential was flat outside this width. Simulations were at constant temperature of 300 K and a pressure of 1 atm. For both the scanning and umbrella sampling simulations, SHAKE^57,58 was used to constrain bonds involving hydrogen atoms, allowing a 2 fs time step. All simulations were performed with periodic boundary conditions, using particle mesh Ewald^59,60 with an 8 Å direct space cutoff with the default grid spacing of 1 Å. The Langevin integrator was used with a collision frequency of 1 ps^–1.

Statistical Potential

The statistical potentials along each dihedral were generated by binning dihedrals observed in all crystal structures of 3 Å or better resolution from the PDB, which included 69 523 dinucleotides.³⁰ The statistical free energy profile was computed for dihedrals in 5° bins according to

9

where R is the gas constant, T = 300 K, bin(i) is number of structures found with torsions in bin i, and max(bin) is the value of the most populated bin for a given dihedral angle. Normalizing using max(bin) ensures that the largest bin value (the most probable/lowest free energy state) will have a free energy of 0 kcal/mol.

Estimating RMSD for Umbrella Sampling

The umbrella sampling PMF and statistical potential were compared using RMSD

10

where PMF(i) is umbrella sampling PMF value and P_stat(i) is the statistical potential. The sum is over all bins.

Force Fields and Simulation Software

All simulations were performed with the Amber 14 molecular dynamic simulation package.^24,32 All simulations used the TIP3P water model.⁶¹ Two sets of Amber force field parameters were used. The first set was with Amber ff10 (specified in the Amber leap programs using learpc.RNA.OL3).²⁵⁻²⁷ The second set of simulations was with the new backbone and glycosidic torsion dihedrals from this work.

Molecular Dynamics Setup

MD was performed on two duplexes, two hairpin loops, and five tetramers. For all MD simulations, four independent simulations were performed. All molecules were neutralized with Na⁺ ions and then solvated with a TIP3P water box of equal length sides. The box dimensions were set so that the RNA was no less than 10 Å from the edge of the box. Finally, 0.1 M NaCl was added based on number of water molecules. Starting structures for five tetramers (namely AAAA, CCCC, CAAU, GACC, and UUUU were built as starting structures using the NAB module of AmberTools.²⁴ In the case of NMR solution structures, the selected starting structures were the reported model found to have the lowest potential energy after energy minimization using ff10 with TIP3P water. Details are shown in Table 3.

Table 3. RNA Molecules Used for Molecular Dynamics Simulations.

sequence	source	model no.	PDB ID	no. NaCl
5′ GGUGAAGGC 3′	NMR	22	2DD2(71)	7
3′ CCGAAGCCG 5′
5′ GGCACUUCGGUGCC 3′	NMR	11	2KOC(29)	6
5′ U(UA)6A 3′	X-ray	1	1RNA(66)	11
3′ A(AU)6U 5′
5′ GCGCAAGC 3′a	NMR	6	1ZIH(77)	5
5′ AAAA 3′	single strand of A-form RNA built using NAB module of Amber24			3
5′ CAAU 3′
5′ CCCC 3′
5′ GACC 3′
5′ UUUU 3′
5′ CCCC 3′	C2′ endo anti	taken from the work of Condon et al.3,5
	C2′ endo syn
	C3′ endo syn

^aTwo base pairs were removed from the 1ZIH sequence for simulations relative to the solution structure.

Explicit Solvent Simulations

Tetramers, hairpins, and duplex RNA molecules were energy minimized, with the RNA atoms restrained with a force constant of 25 kcal/(mol × Å²) for 1000 steps of steepest descent, followed by a 1000 steps of conjugate gradient minimization. The final minimized structure was heated at constant volume from 0 K to a final of 150 K over 50 ps followed by a second heating at constant pressure from 150 to 300 K in another 50 ps. During the initial heating stage, the RNA was held fixed in space with a harmonic potential of 25 kcal/(mol × Å²); the spring constant was reduced to 5 kcal/(mol × Å²) for the second stage.

The final step before production was to equilibrate at constant temperature of 300 K and a pressure of 1 atm for 5 ns with a time step of 2 fs. During the equilibration, the RNA was held fixed in space with a harmonic potential of 0.5 kcal/(mol × Å²). For the simulations, SHAKE^57,58 was used to constrain bonds involving hydrogen atoms and the time step was 2 fs. Temperature was controlled with Langevin dynamics with a collision frequency of 2 ps^–1. All simulations were performed with periodic boundary conditions using Particle Mesh Ewald^59,60 and an 8 Å direct space cutoff.

Comparison to NMR Distance Measurements

To estimate how consistent the sampled structures are, compared to NMR estimates of proton distances from NOEs, the RMSD was calculated

11

where d is the number of distances estimated by NMR, D_iMD is the distance estimated by the simulation, and D_iNMR is the distance estimated by NMR. D_iMD is an average distance that is weighted by the negative sixth power of the distance to reflect that NMR NOEs decay by the sixth power of the nuclear distance

12

where r_i is the distance in a single snapshot of the trajectory and N is the number of snapshots.

Clustering of Tetramer Conformations

Conformations were sampled every 100 ps from the trajectories and clustered by RMSD. Dbscan clustering⁶² was used as implemented in the cpptraj³⁵ module of Amber. The minimum distance between points required for forming a cluster was 1.2 Å and the minimum number of points required for forming a cluster was 100.

Analysis of A-Form Helices

Calculation of structural parameters for the A-RNA double helix were performed using cpptraj module of AmberTools³⁵ and 3DNA software.⁶³ For exact definitions of structural parameters presented in Table 6, see Lu et al.⁶⁴

Table 6. Mean Structural Parameters for Watson–Crick Duplex [U(UA)₆A]₂^a.

	this work	ff10	X-ray
	local base-pair parameters
shear [Å]	0.02 (0.9)	0.0 (0.5)	–0.1 (0.4)
stretch [Å]	–0.05 (0.5)	0.01 (0.3)	–0.2 (0.1)
stagger [Å]	0.08 (0.5)	–0.04 (0.6)	–0.01 (0.2)
buckle [deg]	0.03 (13)	0.5 (15)	1.0 (5)
propeller [deg]	–12.2 (12)	–14.1 (14)	–18.8 (2)
opening [deg]	–0.3 (12)	1.9 (9)	0.1 (3)
	local base-pair step parameters
shift [Å]	0.0 (0.8)	–0.01 (0.7)	0.03 (0.4)
slide [Å]	–1.4 (0.7)	–1.2 (0.6)	–1.3 (0.1)
rise [Å]	3.1 (0.8)	3.1 (0.9)	3.3 (0.2)
tilt [deg]	0.0 (6)	0.07 (6)	–0.2 (3)
roll [deg]	8.5 (8)	12.2 (9)	10.7 (5)
twist [deg]	29.1 (10)	27.7 (8)	31.1 (5)
	local base-pair helical parameters
X-displacement [Å]	–3.7 (3)	–3.8 (2)	–4.1 (1)
Y-displacement [Å]	0.01 (2)	0.03 (2)	–0.1 (0.7)
helical rise [Å]	2.6 (1)	2.3 (1)	2.7 (0.3)
inclination [deg]	14.5 (14)	21.1 (15)	19.5 (10)
tip [deg]	–0.03 (11)	–0.1 (10)	0.02 (6)
helical twist [deg]	31.4 (12)	31.6 (10)	33.3 (4)

^aClosing base-pairs have been left out of analysis to avoid the noise from end fraying. Data presented is the average over all other nucleotides and over all four trajectories. The second column represents results using the revised force field from this work, and the third column represents the simulations with the conventional Amber force field. The last column contains the values from the starting X-ray structure (PDB 1RNA). The values in parentheses are standard deviations.

Results

Dihedral Energy Profiles

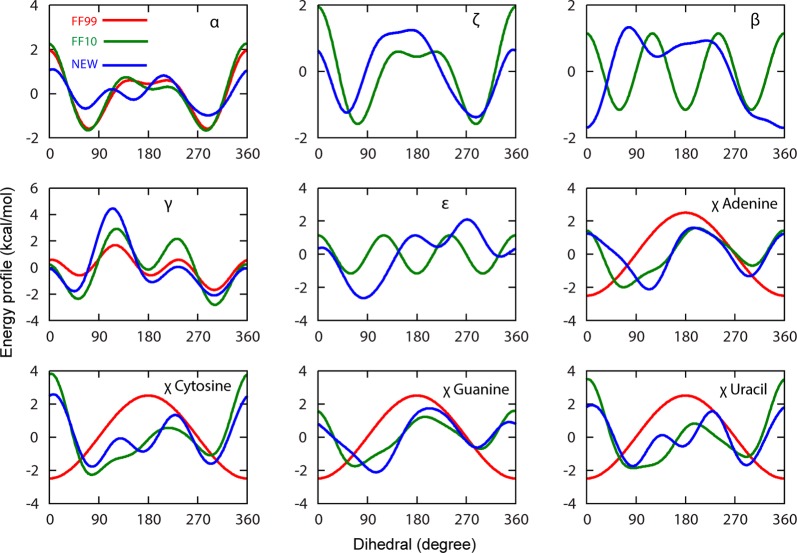
The dihedral potential energy for α, β, γ, ε, ζ, and χ of the four bases as a function of dihedral angle are shown in Figure 2. For comparison, Amber ff99, Amber ff10 (the conventional parameters), and this work are included in the plot. Each dihedral potential energy is sum of all paths for that particular torsion. The energy is offset such that the average energy of an individual energy profile is zero. Following the convention of Zgarbová et al.,¹⁸ the glyosidic dihedrals were defined with a phase difference of 180° as compared to the standard convention; to be compatible with standard definition of χ, all four glycosidic torsions were shifted back by 180°.²⁵

Figure 2.

Dihedral term potential energy (kcal/mol) as a function of dihedral angle for Amber99 (red),²⁵ Amber ff10 (Zgarbova et al. and α/γ bsc0; green),^17,18 χ, and this work (blue). For comparison, the average energy of each curve was set to zero.

Potentials of Mean Force Along Fitted Dihedrals

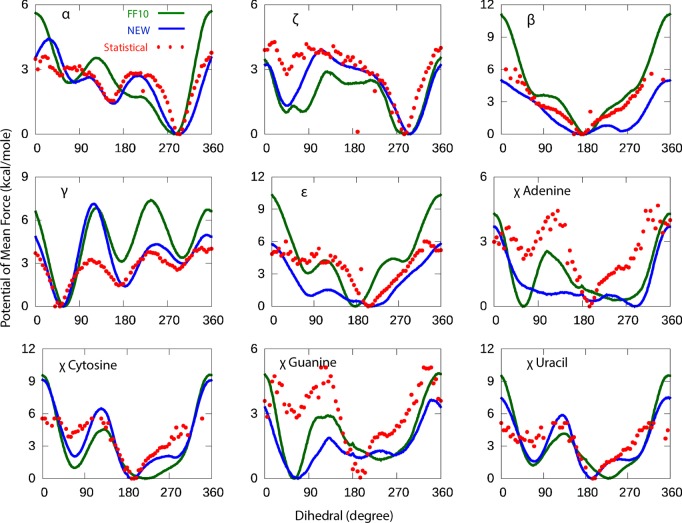
Umbrella sampling was performed in explicit solvent to calculate the potential of mean force (PMF) for each of the nine torsions with conventional Amber ff10 and the new parameters from this work. A statistical potential was also estimated from the population of torsions from the X-ray structures found in the PDB. The PMFs shown in Figure 3 are offset such that each has a minimum value of zero, and the glycosidic torsion PMF was shifted by 180° to be consistent with the Amber force field.²⁵

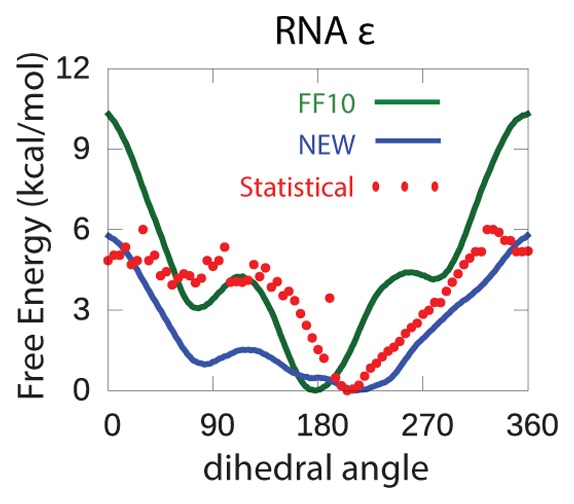
Figure 3.

Dihedral potentials of mean force (PMF) for nine torsions. Shown are the new dihedrals from this work (blue), Amber ff10^17,18 with χ and α/γ bsc0 correction (green), and a statistical potential derived from a set of crystal structures in the PDB (red). For bins of statistical data where there were no representatives in the pdb, the points are not plotted. The PMF is an average of 16 RNA dinucleotide molecules in explicit solvent (TIP3P) water model.

As shown in Figure 3, the PMFs calculated with the new parameters from this work are closer to the statistical potential than Amber ff10 (shown using with RMSD in Table 4), with the exception of the adenine and guanine χ dihedrals. The disagreement with the statistical potential is partly because adenine and guanine are known to not be at their global energy minima with respect to the χ in A-form helices; in other words, the population of χ values does not reflect the local energetics of this torsion, but rather frustration with other favorable interactions that stabilize A-form.¹⁸ The PMF calculated from the umbrella sampling is an average of all 16 RNA dinucleotide sequences. Overall, the results in this work show the same trends as the ff10²⁵⁻²⁷ parameters in terms of positions of minima and barrier heights in free energy, with a few exceptions. For example, the new α PMF has a similar overall shape and local minimum at about 130° as the statistical potential; by contrast, the PMF calculated with ff10 has a local maximum at 150° that is not reflected in the statistical potential (Figure 3). Moreover, the new γ PMF is similar to the statistical potential except around 120°, where the barrier height of the new dihedrals (and the conventional ff10 dihedrals) is higher than that suggested by the statistical potential.

Table 4. RMSD of Umbrella Sampling of Torsion Angles with Respect to Experimental Statistical Potential^a.

torsion	ff10	this work
α	1.12	0.60
β	1.36	1.41
γ	2.24	1.41
ε	2.31	1.86
ζ	1.37	0.92
χ adenine	1.54	1.95
χ guanine	1.56	2.02
χ cytosine	2.14	1.52
χ uracil	2.02	1.37

^aRMSD is calculated in 5° bin interval. Unit of RMSD is kcal/mol. Bins that were empty because there were no examples in the PDB were excluded from the RMSD calculation.

Testing the New Dihedral Parameters Using Single-Stranded Tetramers

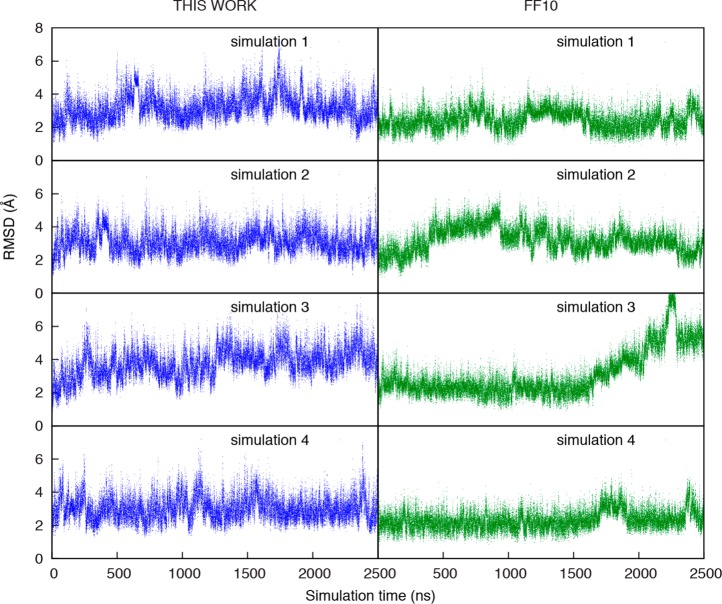
Tetramers are an excellent model to test an RNA force field, especially for backbone and glycosidic torsions, because their stability depends on the accuracy of the backbone parameters and water model. Moreover, their short length and fast dynamics in solution make adequate statistical sampling computationally tractable. A collection of five tetranucleotides r(GACC),⁶⁵ r(CCCC),⁵ r(UUUU),³ r(AAAA),³ and r(CAAU)³ were previously studied by NMR spectroscopy. Stacking, puckers, and backbone torsions for these sequences are generally consistent with A-form-like conformations but with some deviations. Spectra for r(GACC), r(AAAA), and r(CAAU) suggest minor conformations with C2′-endo 3′-end sugars.^3,65 r(GACC) and r(CCCC) have minor populations where the sugar in the C4 position is inverted.^5,65 r(UUUU) data indicates that all sugars are mostly in C2′-endo orientation and the nucleotides are dynamic.³ Sampling with the current ff10 RNA force field, using either conventional MD or replica exchange,^3,4,65 yields structures with the intercalated bases that are not observed in the NMR solution experiment.^3−5,65

In this work, four independent MD trajectories were run for each of AAAA, CAAU, CCCC, GACC, and UUUU, starting from A-form-like configurations. Additionally, three other starting structures for CCCC were used for 12 additional trajectories (4 for each starting structure) to test convergence. Table 3 details the simulations that were run. Simulations were run using both the force field from this work and the conventional Amber ff10.

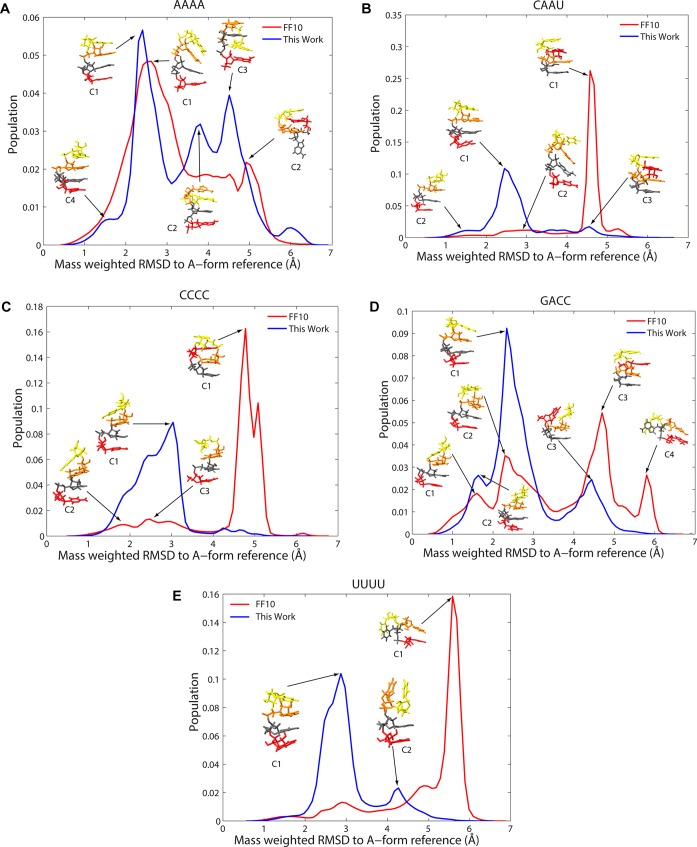
The tetramers sample a number of conformations in the simulations as they do in solution. Following prior practice,⁴ the trajectories were clustered and the dominant clusters compared to A-form-like structures and to the NMR data. Figure 4 shows histogram plots of RMSD to A-form-like structures, annotated with structures of cluster centroids, and Table 5 details each cluster.

Figure 4.

Histogram of mass-weighted RMSD to A-form-like reference. Histograms are provided for AAAA (panel A), CAAU (panel B), CCCC (panel C), GACC (panel D), and UUUU (panel E). Each histogram was generated by merging the conformations for four independent simulations. The bin widths are 0.01 Å. For major peaks in the histogram, corresponding centroid structures from clustering (Table 5) are labeled.

Table 5. Clustering Results from the Combined Trajectories of All Five Tetramers Run Using the Current Amber Force Field (ff10) and the Force Field Derived in This Work^a.

sequence	force field	% noise	cluster no.	% of frames	average distance within cluster (Å)	standard deviation within cluster (Å)	average distance between clusters (Å)	RMSD of centroid to A-form (Å)
AAAA	ff10	32.7	1	55.9	2.67	0.72	4.49	1.89
			2	4.2	1.08	0.38	4.02	5.27
			3	2.5	0.78	0.24	3.73	5.01
			4	2	1.39	0.35	4.33	4.42
	this work	39.7	1	28.1	1.67	0.54	3.89	2.42
			2	9.2	2.18	0.67	3.80	3.68
			3	5.5	1.53	0.40	3.63	4.74
			4	5.4	1.68	0.43	4.16	1.33
CAAU	ff10	13.3	1	73.3	0.97	0.48	4.57	4.60
			2	8.8	2.00	0.53	3.26	2.65
			3	3.5	1.94	0.65	3.79	1.00
			4	0.7	0.96	0.36	4.04	4.16
	this work	19.1	1	66.0	1.43	0.52	3.04	2.52
			2	10.0	1.42	0.45	3.47	1.46
			3	3.6	1.06	0.36	3.39	4.56
			4	1.0	0.88	0.28	3.13	4.00
CCCC	ff10	6.2	1	72.7	1.13	0.43	3.75	4.87
			2	11.4	1.76	0.76	4.02	1.91
			3	7.7	1.88	0.64	3.97	2.78
			4	0.8	0.99	0.42	3.81	4.40
	this work	3.3	1	93.9	1.71	0.64	4.11	2.25
			2	1.6	1.25	0.42	4.96	4.76
			3	1.1	0.83	0.27	5.21	4.40
GACC	ff10	20.0	1	21.3	1.66	0.77	3.93	1.46
			2	19.6	1.76	0.61	3.98	2.61
			3	7.7	1.34	0.48	3.85	4.83
			4	6.9	1.11	0.35	5.43	5.89
	this work	15.0	1	45.0	1.43	0.53	3.78	2.47
			2	28.0	1.18	0.41	3.78	1.74
			3	3.8	0.79	0.24	4.23	4.44
			4	2.6	0.92	0.30	4.38	4.75
UUUU	ff10	28.5	1	39.8	1.52	0.61	4.41	5.64
			2	9.9	1.27	0.40	4.43	5.79
			3	8.8	2.04	0.57	4.52	2.67
			4	4.7	1.27	0.40	4.29	5.04
	this work	18.5	1	72.8	1.43	0.60	3.06	2.78
			2	3.7	0.88	0.33	4.33	4.28
			3	3.3	1.41	0.43	3.23	1.53
			4	1.0	1.22	0.29	3.67	3.71

^aOnly the top 4 clusters are presented. The sizes of the remaining clusters (if they existed) were always less than 5% of total frames in trajectory. Starting from the left, columns denote molecule type, force field used, % of noise frames (those that did not get placed in a cluster), cluster number, % of frames within that cluster, average distance and standard deviation between elements of that cluster, average distance between that and all other clusters, and finally mass-weighted RMSD of the centroid of the cluster to the A-form conformation of the respective molecule.

A major finding of these simulations is that the intercalated structure, where a base intercalates between other bases in the sequence in an unexpected order in an A-form-like structure, is not found in the simulations using the newly fit parameters. This intercalated structure was observed in prior simulations of ff10, including the CCCC tetramer in 2013 by Tubbs et al.,⁵ dynamics of four RNA tetramers in 2015 by Condon et al.³ and the highly sampled replica exchange dynamics on GACC and CCCC by Bergonzo et al.⁴ There is no evidence for this intercalated structure in the NMR experiments, suggesting that this structure is at most a small component of the ensemble (if it is present at all). In the simulations here using ff10, intercalated structures were frequently observed. For example, the dominant clusters for ff10 for CAAU (Figure 4B), CCCC (Figure 4C), and GACC (Figure 4D) are intercalated structures.

Figure S1 shows RMSD to NMR distances, estimated from NOEs, as a function of time for ff10 (right panels) and the new parameters from this work (left panels) for the tetramers. Figure S3 compares the RMSD for NMR proton distances as a function of time for alternative starting structures for CCCC, and these confirm that the A-form-like structures are sampled when starting from alternative conformations. Because NOEs decay as a function of 1/r⁶, where r is atomic distance, Figure S4 compares the r^–6-weighted average of proton distances for protons with distances estimated from the NMR experiments. The figure shows the weighted average distance for the simulations using the new parameters, for simulations using the conventional ff10 parameters, and for the NMR experiments.

An additional set of four simulations was performed using CAAU to test convergence. Four snapshots of intercalated structures were manually chosen from the ff10 simulations, and these structures were used as starting conformations. Figure S2 shows the RMSD for the NMR proton distances, and the results confirm simulations with the new dihedral parameter are able to leave the intercalated state and return to the A-form-like conformation.

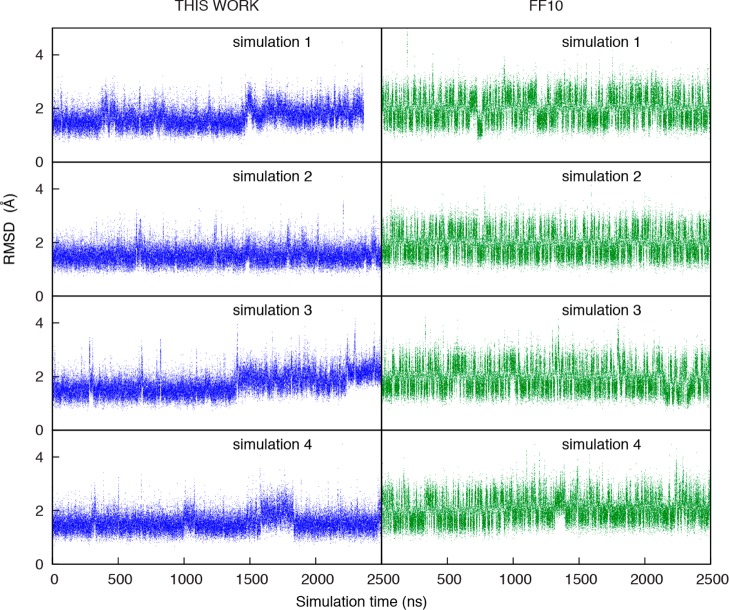
Simulations of Duplexes

To further test the revised dihedral parameters, long (>1 μs) simulations were run on RNA duplexes and hairpin loops, where solution structures are available for comparison. For example, the Watson–Crick duplex, [U(UA)₆A]₂,⁶⁶ was studied because of its tendency to form a “ladder-like” structure with the ff99 force field.^12,18,48,67 The atomic RMSD as compared to the starting structure was calculated for both the current Amber force field (ff10) and the parameters from this work (Figure 5); both force field parameters reproduced the structural well, and did not show any tendency to form the “ladder-like” structure. The third simulation of the Amber force field (ff10) has two terminal base pairs unpaired at one end of the helix and four terminal base pairs unpaired at the other end, as shown by high RMSD on Figure 5.

Figure 5.

Comparison of Amber ff10 (right panels, green) to the dihedral parameters fit in this work (left panels, blue) for dynamics of the Watson–Crick duplex, 5′ U(UA)₆A 3′.⁶⁶ Mass-weighted atomic RMSD to the solution structure is shown as a function of time for four independent simulations. The higher RMSD for ff10 of simulation 3 is an unfolding of four nucleotides of the 5′ terminal pairs. For comparison, these RMSDs as a function of time when excluding terminal base pairs are provided in Figure S5. The same trends are seen in both plots.

Additionally, the helical parameters were calculated across the trajectories of [U(UA)₆A]₂, and these are provided in Table 6 as mean values. The terminal base pairs were excluded from the analysis. Both the current Amber parameters and the parameters from this work show good agreement with the X-ray values, with the mean values falling between bounds set by standard deviations of values from the X-ray structure. The exceptions are the mean helical rise for simulations with the current Amber force field and the propeller twist calculated with both parameters sets. The propeller twists for both simulations with both force field parameters are outside X-ray bounds, but the distributions of observed conformations in the simulations are also broad.

Table 7 presents mean values of backbone and glycosidic dihedrals and sugar puckers from the simulations of [U(UA)₆A]₂. Again, the terminal base-pairs were not included to avoid noise because those pairs have a more conformational freedom than the base pairs on the interior of the helix. The sugar pucker values are the percentage of structures in C3′-endo conformation, where the remaining conformations are C2′-endo puckers. Using the dihedral parameters from this work, α and γ the distributions have two peaks. Approximately 15–20% of the population is in a trans position, of approximately 150° for γ and 180° degrees for α. This roughly matches the X-ray structure, as nucleotides 11 and 24 both have alpha and gamma in trans positions. In contrast, the conventional Amber force field includes α/γ parameters derived to prevent trans positions in B-form DNA,¹⁷ which completely prevent trans conformations. In view of the observation that α/γ trans/trans conformation is commonly seen in RNA structures,⁶⁸⁻⁷⁰ the ability of the force field derived in this work to visit these conformations is possibly an advantage. Figure S6 contains normalized populations of each dihedral for simulations with the force field from this work and also the conventional Amber force field.

Table 7. Mean Values of Backbone and Glycosidic Torsions, as Well as Sugar Puckers, from the Simulations of Watson–Crick Duplex [U(UA)₆A]₂^a.

	this work	ff10	X-ray	A-RNA PDB average
α [deg]	263 (66)b	277 (33)	287 (36)c	295 (8)
β [deg]	167 (32)	174 (11)	171 (14)	174 (8)
γ [deg]	86 (54)d	64 (16)	65 (31)e	54 (6)
δ [deg]	83 (15)	81 (13)	80 (5)	81 (3)
ε [deg]	217 (18)	203 (16)	213 (17)	212 (10)
ζ [deg]	268 (54)	284 (40)	280 (12)	289 (7)
χ [deg]	200 (20)	208 (17)	201 (9)	NA
pucker (% C3′-endo)	95.7	97.1	100	NA

^aClosing base-pairs have been left out to avoid noise from fraying of ends. The numbers are values in degrees averaged over all internal nucleotides and over all trajectories, except for pucker where % of C3′-endo conformation is indicated. The second column are the results using the parameters derived in this work, and the third column are the results from the conventional Amber current force field. The fourth column contains average values taken from the starting X-ray structure (PDB ID 1RNA). The fifth column contains averages from analysis of many structures with the A-RNA conformation taken from work of Richardson et al.⁵ The values in parentheses are standard deviations. The notes indicate angles were the average is affected by the presence of secondary peak. See Figure S6 for more details.

^b20% of population is in a trans conformation with a peak at 150°, 76.4% is in a gauche– population with a peak at 295°, and the remaining 3.6% is in gauche+ confirmation.

^cThe X-ray structure has 2 out of 24 nucleotides in trans position, that is, 8%; the rest is gauche–.

^d21.5% of population is in a trans conformation with a peak at 180°; the remaining 78.5% is in a gauche+ population with a peak at 58°.

^eThe X-ray structure has 2 out of 24 nucleotides in trans position, that is, 8%; the rest is gauche+.

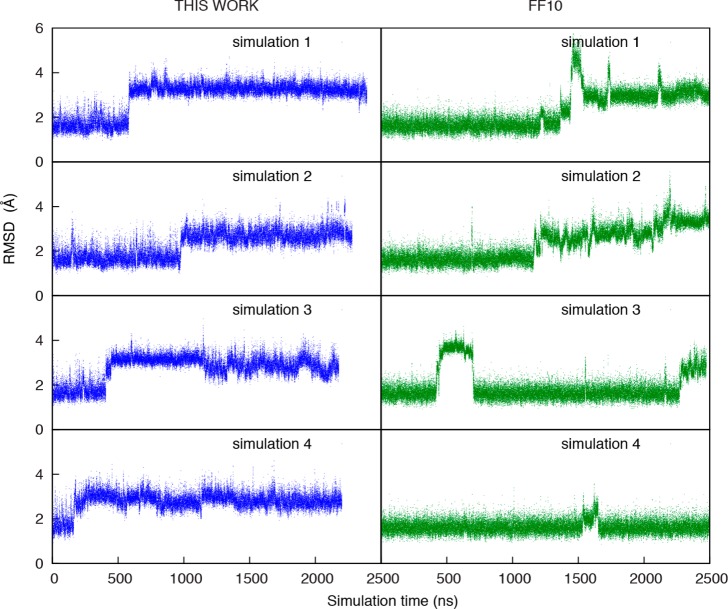
Another duplex with an internal loop (5′GGUGAAGGC3′/3′CCGAAGCCG5′), which is known by NMR to populate two conformations, was also studied.⁷¹ In prior work, it was shown¹¹ that ff99 + bsc0¹⁷ incorrectly stabilized the minor conformations over the major conformation.⁷¹ For this work, simulations were run starting from the major NMR conformation. Figure 6 shows RMSD as a function of time for four separate 2.5 μs simulations with ff10 (right panels) and the parameters fit in this work (left panels). The new parameters perform better than the conventional ff10 parameters. Using ff10, nucleotides U3 and C17 frequently leave their base-pairing partner to flip out into the solvent.

Figure 6.

Comparison of Amber ff10 (right panel, green) and the dihedral parameters fit in this work (left panels, blue) for dynamics of 5′GGUGAAGGC3′/3′CCGAAGCCG5′ (major conformation).⁷¹ Mass-weighted atomic RMSD to the solution structure is shown as a function of time for four independent simulations. The higher RMSD for ff10 is a result of of stem nucleotides U3 and C17 frequently moving from their base pairing partner and flipping out into solution.

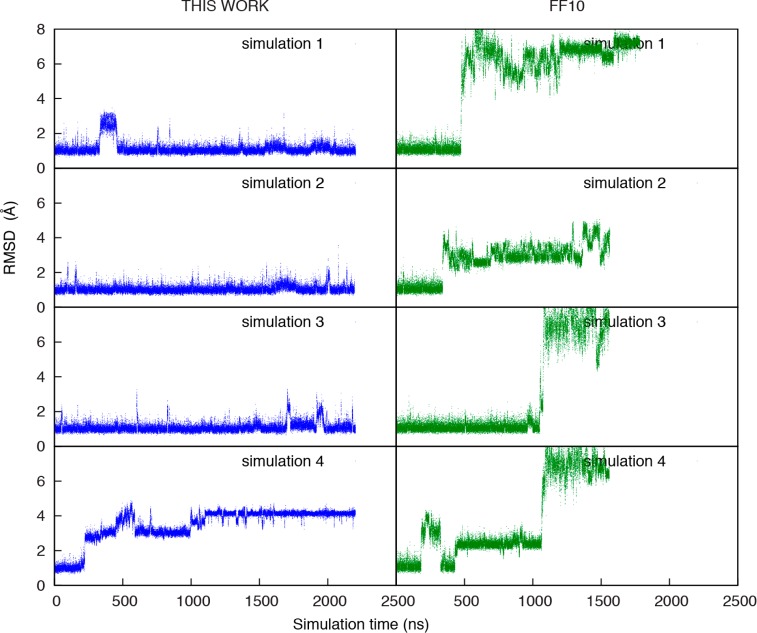
Simulations of Tetraloops

There are solution structures for a number of tetraloops, and prior work found that sets of signature interactions are lost in tetraloop simulations using ff99, ff10, CHARMM36, and f99 + Chen–Garcia.^{12−14,72−75} Even though the UUCG hairpin loop 2KOC (5′ GGCACUUCGGUGCC 3′)²⁹ is not stable for microsecond-time scale simulations, in this work a 2.5 μs simulation was used, as shown in Figure 7 to test the new parameters.^4,14,76 The result (Figure 7, left panel) was a higher RMSD compared to ff10 starting at 200–500 ns and remaining for the duration of the simulation. This is because U7 and C8 tend to be more dynamic with the new parameters, as compared to conventional ff10. On the other hand, the GCAA tetraloop with eight nucleotides, derived from 1ZIH (5′ GCGCAAGC 3′),⁷⁷ is more stable and stays close to the solution structure using the parameters from this work. In contrast, with ff10 the structure in the loop is unstable, and subsequently the whole structure denatures within 2.5 μs (Figure 8).

Figure 7.

Comparison of Amber ff10 (right panel; green) and the dihedral parameters fit in this work (left panel; blue) for dynamics of the UUCG tetraloop, 2KOC.²⁹ Mass-weighted atomic RMSD to the solution structure is shown as a function of time for four independent simulations. The higher RMSD for simulations with parameters derived in this work is a reflection of C8 (the loop C) leaves the conformation of the solution structure and becomes either exposed to solvent or extends into the helix major groove.

Figure 8.

Comparison of Amber ff10 (right panel; green) and the dihedral parameters fit in this work (left panel; blue) for dynamics of the GCAA tetraloop, 1ZIH.⁷⁷ Mass-weighted atomic RMSD to the solution structure is shown as a function of time for four independent simulations. The higher RMSD for both ff10 and this work is due to unfolding of the loop region away from the solution structure.

Discussion and Conclusion

In this work, the α, β, γ, ε, ζ, and χ dihedral parameters for the Amber RNA force field were reparametrized simultaneously using multiple linear regression on full nucleotide and dinucleotide models. This differs substantially from prior practice for nucleic acids, where the parameters were fit for one dihedral at a time for a scan around that dihedral.^17,18 Also, prior work for nucleic acids used simplified models for dihedral scans of sugar–phosphate backbones.¹⁷ The work of Vanommeslaeghe et al.⁴⁶ and Hopkins and Roitberg⁴⁷ showed an approach of force field fitting using linear least-squares fitting as a promising tool for generating dihedral parameters for molecular mechanics force fields. An advantage of this approach is that the optimal set of parameters, i.e. those that minimize the least squared deviation, is guaranteed from the fit. This work used the linear least squared approach to fit multiple dihedral parameters for RNA. Additionally, structures for fitting were generated with more diverse conformations than those from traditional potential energy scan-fits, sampling combinations of multiple dihedrals that would not be sampled with one-at-a-time fitting.²⁴ The diverse configurations here were obtained from X-ray and dihedral scans, without geometry optimization other than regularization of the bond lengths and angles. The improvement in RNA parameters was clearly seen by performance of simulations of tetramers that failed with the conventional Amber force field.³⁻⁵

An alternative approach for improving force field dihedral parameters also recently appeared.⁷⁸ In that work, the α, β, ε, and ζ dihedrals of Amber14 were revised using metadyanamics^79,80 for dinucleotides to match dihedral distributions derived from high-resolution crystal structures. Implicitly, this changes the parameters so that the simulation free energies match the statistical potentials for dihedrals. This work shares a similarity in that multiple dihedrals were revised simultaneously, without freezing all but one degree of freedom. In contrast, Gil-Ley et al. revise dihedrals to explicitly match the dihedrals observed in the database of crystal structures.⁷⁸ As they point out, there is likely a bias toward A-form helices in the database, which might prevent their parameters from being transferrable to all RNA systems. Tests using the AAAA, CCCC, and GACC tetramers did, however, show improved agreement with NMR data as compared to Amber14. In this work, improved agreement with quantum-calculated potential energies is the figure of merit for the fit. This should result in parameters that are transferable widely, given the Amber force field functional form.

The potential energy landscapes of the newly fitted dihedrals (Figure 2) show a large number of differences in barrier and minima positions as compared to the conventional Amber force field. In the conventional force field, β and ε are simple sinusoidal functions, but show a lot more structure in the newly fitted parameters. Interestingly, ε has much higher potential energy barriers, although the free energy barriers (Figure 3) are lower for the newly fitted parameters. This arises because the free energy surface is a function of the other force field potentials, and the high dimensional correlation with other dihedrals.⁸¹ This highlights the importance of calculating free energy surfaces for comparison of dihedrals, rather than simply comparing potential energy surfaces.

The potential of mean force (PMF) calculations showed good agreement with the positions of local minima as well as the global minimum as compared to the statistical potential for most of backbone dihedrals as shown in Figure 3. Because PMFs were calculated in explicit water using dinucleotides, the surfaces should be comparable with the statistical population in the PDB because it includes the influence of stacking, which should favor helix formation.

This work used the existing Amber force field functional form for dihedrals, which uses the same parameter values for terminal nucleotides as for nucleotides interior to a sequence. The QM potential energy calculations were performed on dinucleotides, and it was assumed that terminal nucleotides will have the same dihedral potential energies as interior nucleotides. It is possible this assumption is not correct; in particular, the terminal nucleotides have terminal OH groups on the 5′ and 3′ carbons instead of connections to phosphate groups. The good performance of the newly fitted parameters for simulations of duplexes supports the use of this assumption, but future work might test the assumption and improve the framework.

From the simulation benchmarks, the most striking improvement is in the simulations of tetramers. Prior work showed that the conventional ff10 tended to intercalate the fourth nucleotide between other nucleotides,^3−6,65 although NMR data suggested the major conformations are largely A-form-like.^3,5,65 These new parameters appear to correct this artifact. On the other hand, some problems persist. Most notably, the UUCG tetraloop solution structure²⁹ is not stable with these new torsions in ff10, conventional ff10, the Chen & Garcia force field, or CHARMM27.⁴ One promising direction for continued force field development is to continue the focus on optimizing van der Waals parameters,^13−15,82 as these affect base stacking, hydrogen bonding, and nucleotide-solvent interactions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00870.

• Summary of the revised parameters, plots of RMSD of NMR distance for trajectories of the five tetramers as a function of time, RMSD of NMR distances for the CAAU tetramer starting from an intercalated structure, RMSD of CCCC tetramer with three different starting structures, r^–6-weighted proton distances compared to NOE-estimated distances for all five tetramers, RMSD as a function of time for the A-form duplex, [U(UA)₆A]₂, histograms of dihedral populations from the simulations of [U(UA)₆A]₂, crystal structures used for generating the dinucleotide conformations for fitting, example output and restraint result from “rdparm” for the AA dinucleotide, restraint input for regularization, and values of the fitted dihedral parameters (PDF)

• Force field parameters and input files compatible with tleap (ZIP)

Author Contributions

^# A.H.A. and A.S. contributed equally to this work.

The authors declare no competing financial interest.