Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Dec 28;13(2):666–678. doi: 10.1021/acs.jctc.6b00918

Polarizable Multipole-Based Force Field for Aromatic Molecules and Nucleobases

Changsheng Zhang 1, David Bell 1, Matthew Harger 1, Pengyu Ren 1,*
PMCID: PMC5312700  PMID: 28030769

Abstract

graphic file with name ct-2016-009183_0013.jpg

Aromatic molecules with π electrons are commonly involved in chemical and biological recognitions. For example, nucleobases play central roles in DNA/RNA structure and their interactions with proteins. The delocalization of the π electrons is responsible for the high polarizability of aromatic molecules. In this work, the AMOEBA force field has been developed and applied to 5 regular nucleobases and 12 aromatic molecules. The permanent electrostatic energy is expressed as atomic multipole interactions between atom pairs, and many-body polarization is accounted for by mutually induced atomic dipoles. We have systematically investigated aromatic ring stacking and aromatic-water interactions for nucleobases and aromatic molecules, as well as base–base hydrogen-bonding pair interactions, all at various distances and orientations. van der Waals parameters were determined by comparison to the quantum mechanical interaction energy of these dimers and fine-tuned using condensed phase simulation. By comparing to quantum mechanical calculations, we show that the resulting classical potential is able to accurately describe molecular polarizability, molecular vibrational frequency, and dimer interaction energy of these aromatic systems. Condensed phase properties, including hydration free energy, liquid density, and heat of vaporization, are also in good overall agreement with experimental values. The structures of benzene liquid phase and benzene-water solution were also investigated by simulation and compared with experimental and PDB structure derived statistical results.

Introduction

Molecular mechanics (MM) modeling has become an important tool in the study of complex biological and chemical systems,1,2 including their structure, interaction, energy landscape, and dynamic behavior, often at time and physical scales difficult for experimental methods to access.3−6 The growth in application of molecular modeling demands more accurate force fields in order to obtain more reliable physical and chemical prediction.7,8 Currently, the commonly used MM force fields, AMBER,9 CHARMM,10 and OPLS,11 among others, all use fixed atomic charges to represent electrostatic potentials. In recent years, there have been increasing efforts to improve the modeling electrostatic potentials in general force fields. This has mainly been attempted via the introduction of explicit electronic polarization, either via Drude oscillator12−15 or induced dipole schemes.16−20 Recently, two comprehensive reviews on polarizable force field have been published.21,22 Polarizable force fields offer a practical and effective way of capturing the nonadditive effect in electrostatics, which can change significantly in different chemical environments, such as in gas vs liquid phase, or when surrounded by different solvents. The fixed charge force field, in which the influence of polarization is included in an average fashion, has limited transferability and is thus parametrized for specific environments or applications.8 In addition, adding additional off-atom-center charge sites23 or higher order atomic multipole moments are also found necessary to accurately describe the anisotropic electrostatic potential around molecules.24,25 Both atomic multipole moments and induced-dipole based polarization are employed in the AMOEBA force field,26 which has been developed and applied extensively to study water,17 various small molecules,27,28 ions,29 and proteins.30

Nucleobase stacking, hydrogen bond pairing,31 and the solvation effect (interaction with water) contribute to the specific nucleic acid structures.32 Besides the well-known Watson–Crick base pairs, hydrogen bonding base pairs using the Hoogsteen edge and the sugar edge are also observed in the DNA/RNA structure database.33 With recent advancements in computing power, high-level QM methods have been applied to the study of base stacking energy and the potential energy surface.34,35 Molecular dynamics simulations of nucleic acids show the limitations in accuracy of the recent force fields,36 with the lack of polarization specifically cited as one of the problems.37,38 For these nucleobases, especially the large adenine and guanine, the delocalization of the π electrons leads to a high molecular polarizability,39 which was found to be related to the thermal stability of the DNA duplex.40 Multipole electrostatic interactions are also important for anisotropic π-systems. With the fixed charge model, it is difficult to capture correct parallel stacking and T-shape stacking structures at the same time.41 Thus, the major goal of this work is to construct a polarizable multipole-based classical potential for heteroaromatic molecules using the AMOEBA framework, which is a necessary step to develop a general nucleic acid force field.

While nucleobase properties and interaction energies in gas phase are readily available from QM calculations, experimental data of nuleobases in condensed phase are lacking. Therefore, 12 aromatic molecules (Figure 1), for which experimental data of pure liquid and/or solution are available, have been included to systematically derive the force field for aromatics, especially shared valence and vdW parameters, and study the condensed phase properties for π-systems. Benzene is the aromatic molecule that has been most thoroughly studied by experimental, ab initio, and molecular simulation methods. Previous studies have investigated molecular properties in gas phase, π–π stacking energy,42 pure liquid structure43 and thermodynamic properties,44,45 and structures in water solutions.46−49 Pyrrole, pyridine, and aniline are three types of π-systems with one-heteronitrogen. 2-Aminopyridine, pyrimidine, 2-pyridone, 1-methyl-2-pyridone, 1-methylimidizole, and indole all share similar functional groups with nucleobases. Methylindole and methylpyridine are included because of the existence of experimental condensed phase data. Methylindole, benzene, and 1-methylimidizole are also found in the side chains of amino acids.50 These heteroaromatic molecules are also the core fragments of many drug-like molecules. Thus, this work will not only contribute to a new polarizable force field for nucleobases but will also be useful for modeling and understanding aromatic rings in general chemical and biological recognition.51

Figure 1.

Figure 1

Open in a new tab

Aromatic molecules studied in this work. Each molecule has a two-letter abbreviation (in the brackets).

For the five regular nucleobases (see structures in Figure S1) and these aromatic molecules, the molecular polarization, vibrational frequencies, electrostatic potentials, and conformational energies are investigated first by using QM methods. To accurately model the nonbonded interactions, a set of interacting pairs was designed, including aromatic-water pairs, stacking pairs, and hydration base pairs. We then proceeded to calculate the corresponding QM energies. Then, we present the parametrization and performance of the new AMOEBA force field for bases, including the comparison with all of the QM results, as well as experimental condensed phase properties such as liquid density, heat of vaporization, and hydration free energy. The pure benzene liquid and benzene-water solution structures were also analyzed and compared with previous experimental results.

Computational Methods

Gaussian 0952 was used for the ab initio QM calculations unless otherwise specified. Structure optimizations were performed using MP2/cc-pVQZ. Molecular polarization and molecular vibrational frequency were calculated with the wB97xD/aug-cc-pVTZ method. For computation of out-of-plane bending or rotational conformation energies MP2/aug-cc-pVTZ was used. The permanent atomic multipole moments were derived using the same procedure used in parametrization of small organic molecules28 and proteins.30 The atomic multipole moments were first assigned from QM electron density calculated at the MP2/6-311G** level and using Stone’s distributed multipole analysis (GDMA v2.2).53 The “Switch 0” and “Radius H 0.65” options were used with GDMA to access the “original” DMA procedure.54 The DMA charges were kept fixed, while the atomic dipole and quadrupole values were subsequently optimized against the QM electrostatic potentials computed using an MP2/aug-cc-pVTZ basis set.

QCHEM 4.255 was used to compute interaction energy for all dimers. The RIMP2 method, which provides accurate energy values and is computational efficient,56 was used with the dual basis set. For aromatic ring stacking energy calculation, cc-pVTZ and racc-pVTZ were used, and for other configurations and systems, aug-cc-pVTZ and racc-pVTZ were used.

All force field based calculations were performed using TINKER 7.57 The VALENCE program in TINKER was used to calculate molecular frequencies. The TINKER POLARIZE program was used to compute molecular polarizabilities based on atomic polarizability parameters. TINKER program POTENTIAL was used to obtain electrostatic potentials (ESP) around a molecule from Gaussian 09 cube files or based on AMOEBA atomic multipole parameters. POTENTIAL was also used to optimize the electrostatic parameters (permanent atomic dipole and quadrupole moments) against QM electrostatic potential grids (MP2/aug-cc-pVTZ). The AMOEBA force field parameters for water17 from previous studies were used here. The TINKER MINIMIZE program was used to optimize molecular structures using the AMOEBA force field, with the convergence criteria set to 0.0001 kcal/mol/Å. The TINKER ANALYZE program was used to calculate the total potential energy and the energy components, as well as the molecular multipole moments and induced dipole moments.

The nonlinear least-squares optimization method “lsqnonlin” in MATLAB58 was used to fit various parameters against QM values, including out-of-plane bending or rotational conformation energies and interaction energy between two monomers in a pair. The inputs of “lsqnonlin” program are the objective function, initial parameters, and the parameter limits. The objective function calculates the mean square of the difference between MM and QM values of all the structures. For more details, refer to the MATLAB program code in the Supporting Information.

Molecular dynamics (MD) simulations were carried out using TINKER 7.57 The Bussi-Parrinello thermostat59 and RESPA integration60 method were used in all the simulations, with a 2 fs time-step. Spherical energy cutoffs for van der Waals and Ewald direct-sum were 12.0 and 7.0 Å, respectively. Default PME cutoff and grid sizes were used in the reciprocal space.

For each of the aromatic neat liquids, simulations were performed at four temperatures, including the melting temperature, room temperature, and the boiling temperature. For each temperature, a cubic box containing 300 molecules was built using PACKMOL.61 The initial box sizes were set to match the density to the corresponding experimental value. All systems were relaxed via a 1 ns NVT simulation. Subsequently, NPT simulations, utilizing a Berendsen barostat62 and a target pressure of 1 atm, were performed for 2 ns at each of the four temperatures to evaluate the density and heat of vaporization of each liquid. In heat of vaporization calculations at boiling temperature, the gas-phase potential energy was calculated via stochastic simulation63 on a single molecule using the default (91.0 ps–1) friction coefficient and 0.1 fs time step.

The Bennett acceptance ratio (BAR) method was used for hydration free energy calculation, using protocol similar to previous studies.64 The aromatic molecule was solvated in a 40 × 40 × 40 Å3 cubic box containing 2138 water molecules. After system equilibration using NPT simulations at 298 K for 1 ns, the electrostatic interaction between aromatic molecule and water molecules was turned off with a scaling factor λ from 1.0 to 0.0 at a constant interval of 0.1. Here, 1.0 means 100% electrostatic interaction strength between the solute and water, while 0.0 means there is no electrostatic interaction. Subsequently, the soft-core van der Waals (vdW) interactions were scaled down in a series of steps: 1.0, 0.9, 0.8, 0.75, 0.7, 0.65, 0.6, 0.55, 0.5, 0.45, 0.4, 0.3, 0.2, 0.1, 0.0, which are scaling factors for the vdW interactions between the solute and environment. NVT simulation was carried out at each λ value for 2 ns. In the gas-phase recharging process (growing the solute electrostatics back to 100 in gas phase), the λ interval was set to 0.1, and the stochastic integrator was used with a 0.1 fs time-step, with a run time of 10 ns.

Atom Classes and Parametrization Process

The AMOEBA potential energy function comprises bonded (valence) and nonbonded interaction terms. Bond stretching, angle bending, out-of-plane bending, and torsional energy terms describe the valence potential in a molecule. van der Waals, permanent, and induced electrostatic interactions are the major factors for molecular interaction (see the functional forms in the SI or ref (26)). All the atoms in the studied molecules are reduced to 20 atomic classes (listed in Table 1) based on their chemical or environmental properties. The vdW and valence parameters in AMOEBA are determined according to atom “classes”, while electrostatic parameters are defined by more refined atom “types.” Different atom types can belong to the same atom class, which means atom classes are a super set of “atom types”. Carbon and nitrogen atoms on the 5-member ring, 6-member ring, and on the bridge of double-ring were put into different classes. Carboxyl carbon atoms were set to an individual class. Single rings were determined to hold both polar and nonpolar carbon types. Polar aromatic carbons on the single ring are defined as those linked with at least one nitrogen or carboxyl carbon on the ring. Carbons on the indole ring (except the bridge carbons) show similar properties with single-ring polar aromatic carbons, thus they were assigned to the same class. Nitrogen atoms on the aromatic ring with lone pair electron (pyridine nitrogen) and without lone pair (pyrrole nitrogen) belong to two different classes.

Table 1. AMOEBA Atom Classes, vdW Types, vdW Parameters, and Atomic Polarizability for Nucleobases and the 12 Aromatic Molecules.

atom class description vdW type D (Å) (reduction factor) ε (kcal/mol) polarizability (Å3)
101 methyl carbon 1 3.80 0.101 1.334
102 nonpolar 6-member ring carbon 2 3.79 0.106 1.750
103 nonpolar 5-member ring carbon 2 3.79 0.106 1.750
104 polar (or indole) 6-member ring carbon 3 3.74 0.106 1.750
105 polar (or indole) 5-member ring carbon 3 3.74 0.106 1.750
106 carboxyl carbon 4 3.72 0.095 1.750
107 bridge carbon of double ring 5 3.72 0.112 2.250
108 amino nitrogen 6 3.60 0.124 1.450
109 nitrogen with electron lone pair (6-member ring) 7 3.70 0.127 1.450
110 nitrogen with electron lone pair (5-member ring) 7 3.70 0.127 1.450
111 nitrogen without electron lone pair (6-member ring) 8 3.64 0.127 1.073
112 nitrogen without electron lone pair (5 member-ring) 8 3.64 0.127 1.073
113 carboxyl oxygen 9 3.35 0.129 1.300
114 methyl hydrogen 10 2.90 (0.91) 0.025 0.496
115 hydrogen linked with nonpolar carbon 11 3.05 (0.91) 0.029 0.696
116 hydrogen linked with polar carbon 12 3.08 (0.92) 0.029 0.696
117 amino hydrogen 13 2.65 (0.89) 0.020 0.696
118 hydrogen linked with nitrogen on ring 13 2.65 (0.89) 0.020 0.496
119 guanidine carbon 14 3.72 0.106 1.750
120 amino-pyridine carbon 14 3.72 0.106 1.750
Open in a new tab

As with previous force field development for small organic molecules,27 all the parameters, including atom polarizability, multipole moments, van der Waals, out-of-plane bending, torsion, and valence, were determined based on corresponding QM calculations of single molecules or dimers and subsequently fine-tuned by condensed phase simulations. AMOEBA electrostatic interactions comprise permanent and induced components. The permanent multipole moments were derived from Distributed Multipole Analysis (DMA)53 and then optimized to the QM electrostatic potential surface, a procedure described in detail previously.27 In the ESP fitting process for each base, in addition to the gas-phase monomer structure, the structure of the corresponding QM-optimized Watson–Crick base pair (AT, AU, and GC) was also used to ensure the transferability of multipole parameters among different molecular geometries. Atomic polarizabilities were adjusted from previous canonical values28,30 to match the QM-derived molecular polarizability tensor. Three important interacting dimer configurations, hydrogen-bonding pairs (if available), stacking, and aromatic-water, were constructed with different orientations and distances. The QM interaction energy for these dimers, after basis set superposition error correction, was utilized to optimize the van der Waals parameters. Next, a series of distorted conformations were generated with out-of-plane bending or rotation operation to fit the out-of-plane bending and torsion parameters. The bond and angle force constants were then determined by fitting to QM frequencies of all vibrational modes. It was necessary to re-examine the distorted conformational energy after valence parameters were finalized. Condensed phase properties, hydration free energy, liquid density, and heat of vaporization were used for fine-tuning the vdW and multipole parameters. The force field parameters of water for aromatic-water and hydration free energy calculation were from our previous work.17

Molecular Polarization for Aromatic Rings

Electronic polarization is described in our model via Thole’s damped induction approach.65 Besides the molecules listed in Figure 1, three other molecules are also included in this study, imidazole, phenol, and naphthalene. Excluding benzene, the molecular polarizability values determined by using the previous parameters28 are systematically lower than the QM value. Thus, we determined that the atomic polarizability parameters of nitrogen, oxygen, and the bridge carbon of the double-ring needed separate types, and their values were optimized to reproduce the three eigenvalues of the QM molecular polarizability tensors. We found that the polarizability of the following two types of nitrogen atoms should be increased by 35% (from 1.037 Å3 to 1.450 Å3): the N within the aromatic ring and with an electron lone pair (e.g., N of pyridine) and the N of the amino group connecting to the aromatic ring. The “H” atom of the amino group has the same polarizability as the “H” in benzene (0.696 Å3). The aromatic carboxyl “O” atom needs 55% greater atomic polarizability (from 1.037 Å3 to 1.450 Å3), and the bridge C needs 28% greater atomic polarizability (from 1.750 Å3 to 2.250 Å3). Table 2 lists the molecular polarizabilities calculated using the old and new AMOEBA parameters, compared with QM values. Using the new parameters, the correlation coefficient between QM and AMOEBA molecular polarizabilities was improved from R2 = 0.975 to R2 = 0.986, and the relative root-mean-square error was improved from 6.0% to 4.7%. The Thole damping coefficient for all atom types is fixed at 0.390 as in previous work.27

Table 2. Comparison of AMOEBA and QM (wB97xD/aug-cc-pVTZ) Molecular Polarizabilities (the Three Tensor Eigenvalues) of the 19 Aromatic Molecules.

molecule AMOEBA old (Å3) AMOEBA new (Å3) wB97xD/aug-cc-pVTZ (Å3)
PR 5.373 9.220 9.500 5.373 5.763 8.959 9.337 9.220 9.500
imidazole 4.885 7.797 8.727 5.015 5.029 8.068 8.478 8.084 8.929
MI 6.337 9.617 10.948 6.465 6.437 9.793 10.954 9.885 11.191
BE 6.619 12.201 12.201 6.619 6.625 11.921 11.925 12.201 12.201
phenol 6.907 12.508 13.566 6.907 6.925 12.323 13.634 12.508 13.566
AL 7.198 13.009 14.382 7.482 7.515 12.812 15.283 13.359 15.163
PD 6.159 10.642 11.492 6.275 6.028 10.721 11.333 10.928 11.699
PN 6.716 11.722 13.489 7.115 6.983 11.866 14.846 12.357 14.509
PO 6.462 11.589 12.125 6.702 6.350 11.248 13.714 11.850 12.702
MP 7.764 13.160 14.547 8.002 7.721 13.371 16.083 13.562 14.998
NM 7.840 13.287 14.642 8.052 7.726 13.699 15.381 13.751 15.001
PI 5.692 9.580 10.308 5.927 5.478 9.868 10.262 10.113 10.777
Cm 6.289 11.246 11.733 6.775 6.099 10.919 13.689 11.941 12.714
Tm 6.546 11.526 12.943 7.189 6.719 11.891 15.262 12.622 14.359
Um 7.587 12.426 14.531 8.052 7.412 12.658 16.282 13.181 15.459
IN 8.542 15.767 18.426 8.757 8.820 15.641 20.439 16.177 19.130
Am 7.678 14.135 16.060 8.541 7.942 15.961 18.263 16.159 17.831
Gm 7.994 14.099 17.905 8.998 8.260 16.458 20.053 16.031 20.139
naphthalene 9.724 18.434 21.827 9.914 9.749 18.219 24.716 18.864 22.578
Open in a new tab

Multipoles and Electrostatic Potentials

The permanent electrostatic energy is expressed as the sum of multipole-multipole interactions between atom pairs, excluding nearby through-bond pairs. For atomic dipole and quadrupole moments, a local frame is defined at each atom based upon the neighboring atoms. Most atoms follow the “Z-then-X” convention. The heaviest bonded atom is selected to define the Z-axis, and another neighboring atom defines the ZX-plane and the positive X-direction. If the linking of an atom has 2-fold symmetry, like the carbon of benzene, the “bisector” convention was used for this atom. For methyl carbons, the “Z only” convention is used, where the X-axis and Y-axis are on the plane perpendicular to the Z-axis.

The electron density matrix was computed at the MP2/6-311G** level, from which the initial atomic multipole moments were obtained using Stone’s distributed multipole analysis (DMA).53 The electrostatic potential on a grid of points around a molecule is constructed from MP2/aug-cc-pVTZ calculations. Grid points of four shells (0.35 Å apart) were generated around the molecule with an offset of 1 Å from the vdW surface. Then the multipole parameters for this molecule were determined by fitting to the electrostatic potential grids of one or two conformers using the TINKER POTENTIAL program. Only the atomic dipole and quadrupole moments were allowed to deviate from the DMA values during the ESP optimization, which stops when a gradient of 0.1 kcal/mol/electron2 is achieved. The root-mean-square of the grid potential between the QM and MM potential was smaller than 0.30 kcal/mol per unit charge (except for guanine, see Table S1).

Interaction Pair Design and the Interaction Energy

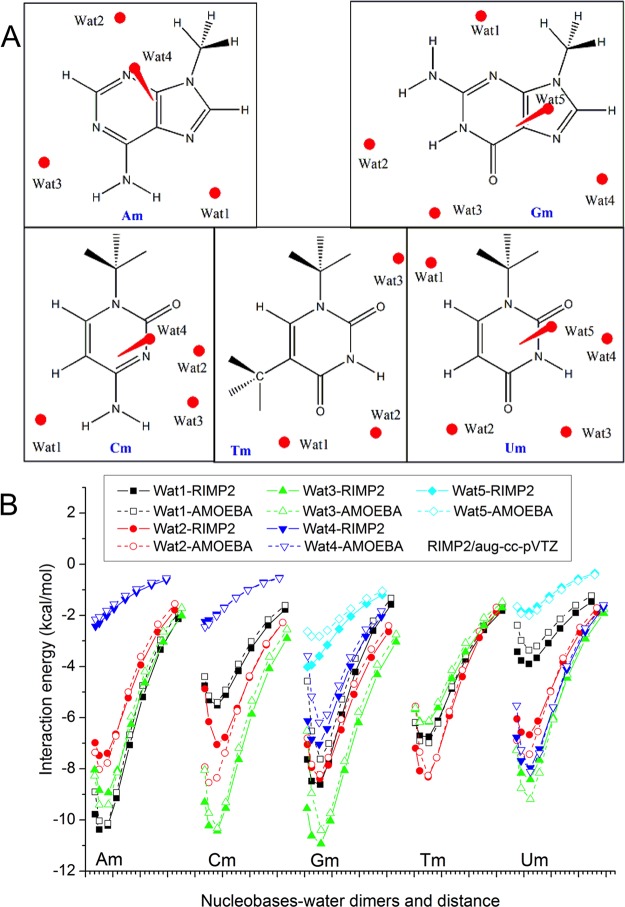
Water was used as a probe for the nonbonded interactions of a target molecule. Two kinds of base-water (Figure 2A) or aromatic-water (Figure S3) dimers were designed. In the first, a water molecule was put in the plane of the target molecule as a hydrogen bond donor, or acceptor, or both. Using HF/6-311G*, the dimer structure was optimized, and the distance between the two monomers was used as the equilibrium distance. The low level QM method was used here in order to broadly scan the potential energy surface at different distances and geometry, instead of finding the absolute minimum. In the second kind of dimer, the water molecule was positioned above or below the ring, forming a π-H hydrogen bond. After calculating the interaction energy at several discrete distances, the distance with minimum energy was assigned as the equilibrium distance.

Figure 2.

Figure 2

Open in a new tab

Nucleobases water interaction study. (A) Water molecule positions in the methylated nucleobases-water dimers. (B) Interaction energy calculated using AMOEBA and RIMP2/aug-cc-pVTZ.

Depending on the base edges participating in the interaction (Watson–Crick, Hoogsteen, or sugar edge) and the orientation of the glycosidic bonds relative to the hydrogen bonds (cis or trans), base pairs can be roughly divided into 12 classes (see UG pairs in Figure 3A).33 The regular Watson–Crick pair (for AU, AT, or GC) is a Watson–Crick edge–Watson–Crick edge pair in cis (WCcis for abbreviation). Hoogsteen pairs are mostly Watson–Crick edge–Hoogsteen edge pair (WCH for abbreviation). All of the 12 classes mentioned here are observed in RNA crystal structures and are important for the formation of different secondary and tertiary motifs of RNA and DNA. Among the pairs listed in Westhof lab’s work,35 all those with at least two hydrogen bonds and without protonation states were selected for studying base–base interaction and are shown in Figure S2. The hydrogen bonding pairs were also optimized using the simple HF/6-311G* method in Gaussian.

Figure 3.

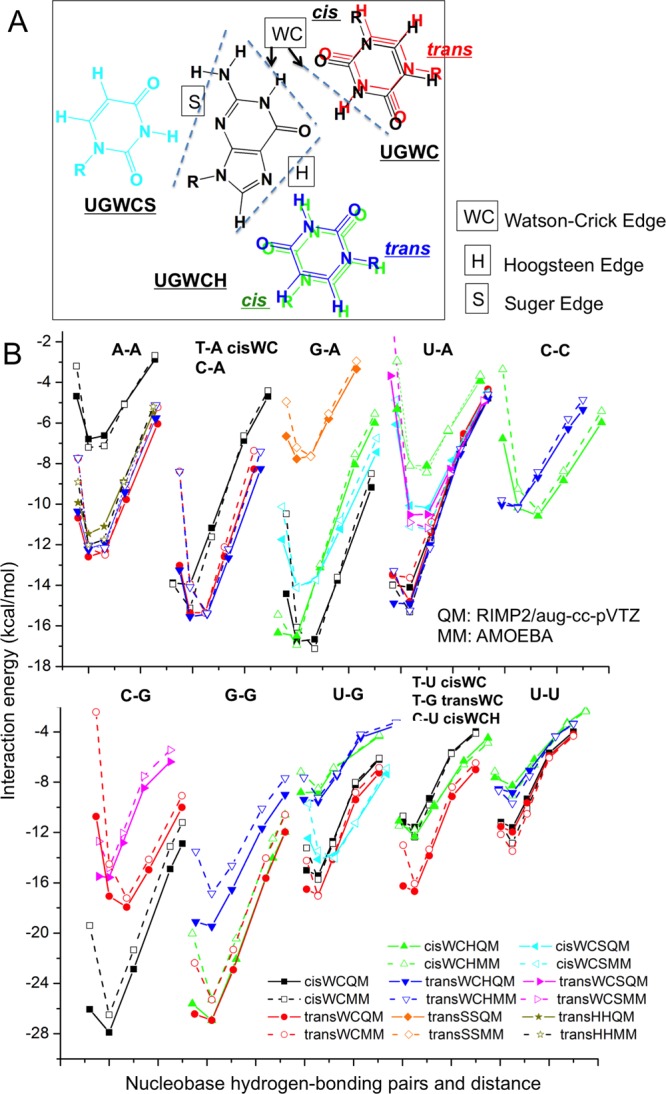
Figure 3

Open in a new tab

Nucleobases hydrogen bonding pairs study. (A) GU pairs forming hydrogen bonds using 3 edges and cis/trans configuration. (B) Interaction energy calculated using AMOEBA and RIMP2/aug-cc-pVTZ. See structures in Figure S2.

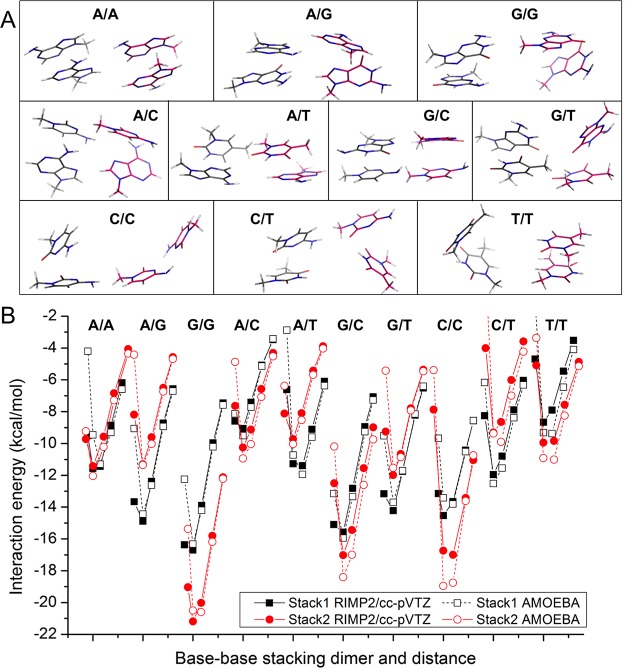
If two stacking bases are parallel, the angle of the two plane vector can be 0° (defined as cis) or 180° (defined as trans). Additional configurations occur through translation (rise, slide, and shift) and rotation (twist, roll, and tilt) as in nucleic acid helical stacking.35 We generated some configurations for vdW parameter fitting using the following process. For each of the 15 kinds of pairs (forming by any two of methylated A, C, G, T, and U), the initial conformation of cis or trans stacking was generated using a 3.3 Å rise. Then the dimer structure was optimized using HF/6-311G*. Since the potential surface of stacking is very flat, the optimization was stopped when the root-mean-square of force was smaller than 0.000300 au. This same stacking conformation generation method was used for all 11 aromatic rings (a-k in Figure 1). The stacking conformations for nucleobases and aromatic molecules are shown in Figure 4A and Figure S5, respectively.

Figure 4.

Figure 4

Open in a new tab

Nucleobase/nucleobase stacking study. (A) Stacking conformations. (B) Interaction energy calculated using AMOEBA and RIMP2/cc-pVTZ.

After preparing the above three types of dimers (aromatic-water, ring–ring stacking, and hydrogen bonding) at equilibrium distance of an orientation, 5 or 4 dimer structures with different distances were generated by translation from the equilibrium. Any atom of a molecule within 4.5 Å of the partner molecule is defined as an interface atom. The translation vector is defined as the direction of the two center points of the interface atoms.

Using the QM (RIMP2/cc-pVTZ or RIMP2/aug-cc-pVTZ) interaction energy of these designed pairs as the targets, the vdW parameters (atom diameter D, the potential well depth σ, and reduction factor17,66 for hydrogens I) for the 14 vdW types (Table 1) were optimized. The target vdW potential energy was the total QM interaction energy minus the AMOEBA electrostatic energy. Similar atoms, such as polar N on the 5-member and 6-member rings are assigned the same vdW type. The hydrogens linked with N atoms are also treated as the same type. Using the MATLAB nonlinear optimization program, the mean square of the difference between MM and QM values of all the weighted dimers was minimized. For every dimer orientation, the lowest target vdW energy was found from a set of distances. Then, the weight of a dimer in this series was assigned based on its relative vdW energy from the minimum. The initial values of the vdW parameters were picked from the original values of AMOEBA (amoebapro13.prm30). The three kinds of parameters D, σ, and I should have different parameter “stiffness”. For example, the relative change in σ could be greater than the molecular size D. The parameter deviation from the original value was added to the objective function using a harmonic function, and the stiffness was expressed as the force constant. See the program code for parameter optimization in the Supporting Information.

The potential well depth σ for almost all of the heavy aromatic atoms are ∼20% bigger than the initial values (Table 1). Smaller carbon and larger hydrogen radii seem to better reproduce the interaction of polar aromatic C–H. The RMSE for the three types of pairs are 0.69–1.64 kcal/mol (Tables S2–S4 and Tables S6–S7). The correlation coefficient between QM and AMOEBA interaction energies for a large number of molecular dimers is rather satisfactory. In general, for most cases, the AMOEBA dimer interaction energies with separation distance equal or greater than the equilibrium distance matched well with QM values, and those with shorter distance were somewhat more repulsive (Figures 2B, 3B, 4B, S4, and S6).

Distorted Ring Conformation Design and Energy

With thermal energy, atoms in the bases can bend out of the plane with different strength. This kind of distortion was described by three kinds of valence potential functions in AMOEBA: the out-of-plane bending, torsion, and π-orbital torsion. Only the 2-fold Fourier torsion terms, with 180° as the phase angle, were used for torsions angles formed by 4 linear arranged atoms on the plane of the aromatic ring. The 2-fold and 3-fold Fourier terms were used for the torsion of aromatic ring–methyl bond. A Wilson-Decius-Cross function is used at sp2-hybridized trigonal centers to restrain out-of-plane bending.67 π-orbital torsion describes the interaction of π-orbitals. Each sp2 carbon or nitrogen has a π-orbital which is perpendicular to the plane of the three linked atoms. The π-orbital torsion energy is a function of the torsion angle between the two adjacent π-orbitals.68

To investigate the bending energy of the out-of-plane distortion and the rotation energy of methyl and amino groups, different kinds of structures were generated from the most stable structure of an aromatic molecule (Figure 5). Out-of-plane distortion of one or a group of atoms are generated by rotating about a line (axis) defined by two atoms on the ring (see pyridine distortion in Figure 5C). The four types of distortion conformations are side atom/group out of plane, one ring atom out of plane, two ring atoms out of plane, and one ring out of plane in a double-ring molecule (the axes of these out-of-plane distortion conformations are shown in different colors in Figures 5B and 5E). The rotation angles were 7.5°, 10.6°, 13.0°, 15.0°, 16.8°, and 18.4°. Totally we got 1176 distorted structures across all 17 molecules. Then the QM energy for each generated structure was calculated using MP2/aug-cc-pVTZ. Six types of AMOEBA interactions contribute to the total deformation energy, including torsion, out-of-plane bending, π-orbital torsion, angle bending, the intramolecular vdW, and intramolecular electrostatic potential. All the π-orbital torsions were divided into 7 types, and the force constants (see Table S8) were slightly modified from the original values of AMOEBA.30 The total QM deformation energy minus the latter four terms is the target energy for torsion and out-of-plane bending force constant fitting. The force constants of 120 out-of-plane bending and parameters for 194 torsion angles (see these in the AMOEBA parameter file) were optimized together using MATLAB nonlinear optimization. The correlation coefficient square of the distorted conformational energy between QM and MM is 0.92 (Figure S7). The distorted conformational energy of QM and AMOEBA for pyridine (PD) and 9-methylguanine (Gm) are shown in Figures 5A and 5D, respectively.

Figure 5.

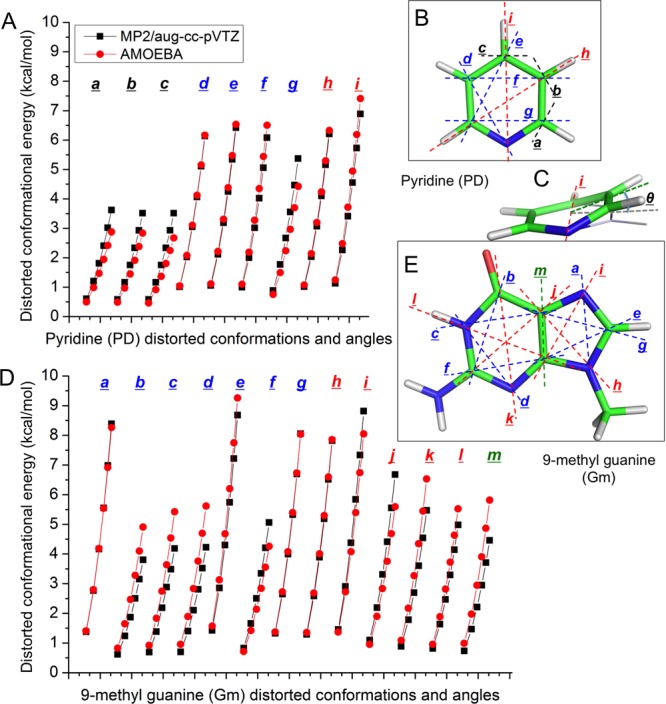
Figure 5

Open in a new tab

Distorted ring design and the conformational energy study. (B) and (E) show the axes (dashed lines) of out of plane for pyridine and 9-methylguanine. The axes of four types of distortion conformations are in different colors: side atom/group out of plane (black, only showed on pyridine), one ring atom out of plane (blue), two ring atoms out of plane (red), and one ring out of plane in a double-ring molecule (green). (C) Out-of-plane bending structure of pyridine about axis i. θ is the bending angle. (A) Distorted conformational energy of pyridine. (D) Distorted conformational energy of 9-methylguanine.

Valence Parameter and Molecular Vibrational Frequencies

The equilibrium bond lengths and bond angles were assigned as the average QM value in all molecules. The force constant parameters for bond stretching and angle bending were optimized, starting from typical values from prior AMOEBA force fields, to best match between the AMOEBA and QM vibrational frequencies. The frequencies were most strongly related to the force constants of hydrogen-containing bonds and angles. These parameters were optimized first. Then, these parameters were fixed, while the others were optimized. The bonds and angles were divided to several common types, with each type sharing the same force constant. A couple of iterations were needed to fully optimize all valence parameters. The average of unsigned error in vibrational frequencies for all these 16 molecules is 31.9 cm–1, about 1% error (see the comparison between AMOEBA and QM results in Figures 6 and S8).

Figure 6.

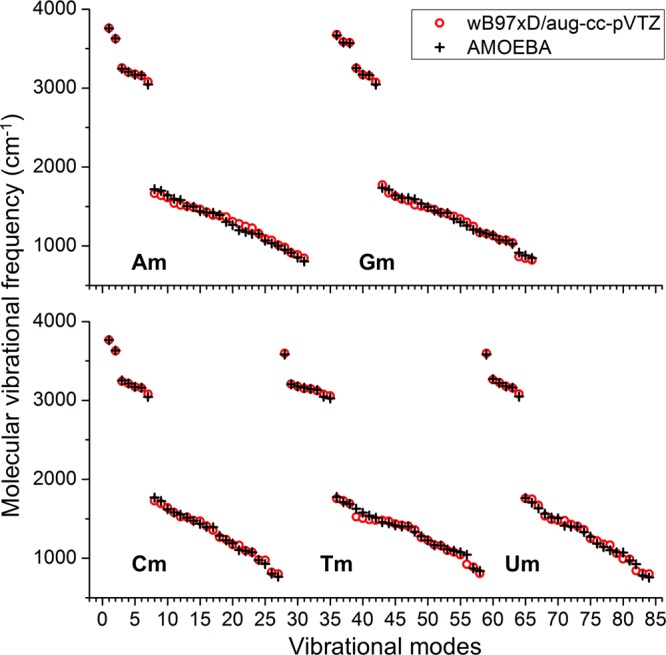
Figure 6

Open in a new tab

AMOEBA and QM values of vibrational frequencies of the five methyl-nucleobases.

Geometry of Nucleobase Pairs

The QM structures of 37 nucleobase pairs were optimized using the AMOEBA force field. The all-atom root-mean-square deviation (RMSD) between the QM structure and the AMOEBA structure is less than 0.3 Å, and the average of RMSD is only 0.11 Å (Table S9). The hydrogen bonding geometries of AU, GC Watson–Crick pairs, and AT Hoogsteen pairs reproduce the X-ray69 or neutron results70 (see Figure 7). The AMOEBA energy minima of these nucleobase pairs are also highly correlated with the QM values, and the correlation coefficient square is 0.972 (Table S9).

Figure 7.

Figure 7

Open in a new tab

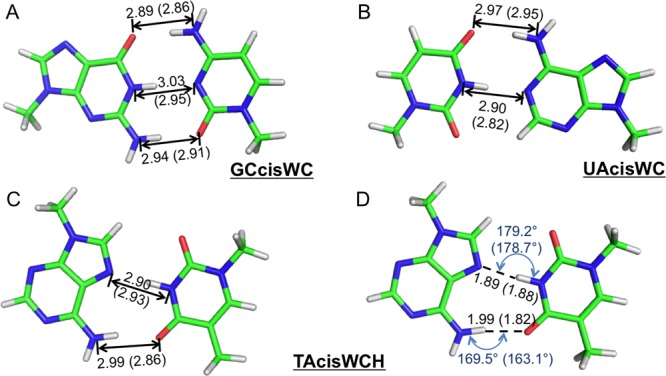
Optimized structures of Watson–Crick or Hoogsteen base pairs using the AMOEBA force field. (A) and (B) The heavy atom distance of hydrogen bonds in G-C and A-U Watson–Crick pairs (X-ray data69 are in parentheses). (C) and (D) The hydrogen bond length and angle in the A-T Hoogsteen pair (neutron data71 are in parentheses).

Condensed Phase Simulations

To fine-tune and validate the new AMOEBA force field parameters for nucleic acid bases and aromatic molecules, pure liquids and hydration have been simulated. The density of liquid at 4 temperatures, the heat of vaporization of liquid at the boiling, and the hydration free energy were calculated and compared to the experimental values. The experimental data of liquid density of 9 molecules and heat of vaporization of 8 liquids were obtained from the NIST/TRC Web Thermo Tables (WTT) database.71 Experimental hydration free energies are collected from the FreeSolv database72 (6 molecules) and other references.73−75 Vdw parameters were refined to better fit the experimental liquid density and heat of vaporization. For example, a size combination 3.74:3.08 Å of polar carbon and the linking hydrogen was better than the QM-fitted 3.70:3.14 Å for most related liquid densities. A smaller lone-pair nitrogen (from 3.69 to 3.64) also gave a better density for pyridine. For electrostatic parameters, only the point charge values of the carboxyl (C=O) with a methyl group were modified. The oxygen atomic charge becomes 5% more negative, and the positive charge on the carbon increased by the same amount. This change noticeably improves the liquid phase results for 1-methyl-2-pyridone (NM) in comparison with experiment (Table S11). With the final parameters, at room temperature, the errors of calculated densities are all within 2% of the experimental value (Figure 8 and Table S10). The differences of the calculated and experimental heat of vaporization for these 8 molecules were all within 1.20 kcal/mol, and the RMSE and correlation coefficient were 0.831 kcal/mol and R2 = 0.884, respectively (Table 3 and Figure 9A). The AMEOBA-calculated hydration free energies of the 10 molecules were also in good agreement with experimental measurements (Table 4 and Figure 9B).73 The RMSE between the calculated and experimental values was 0.907 kcal/mol, and the correlation coefficient was R2 = 0.950. The differences were all within 1.20 kcal/mol except methylindole (ML).

Figure 8.

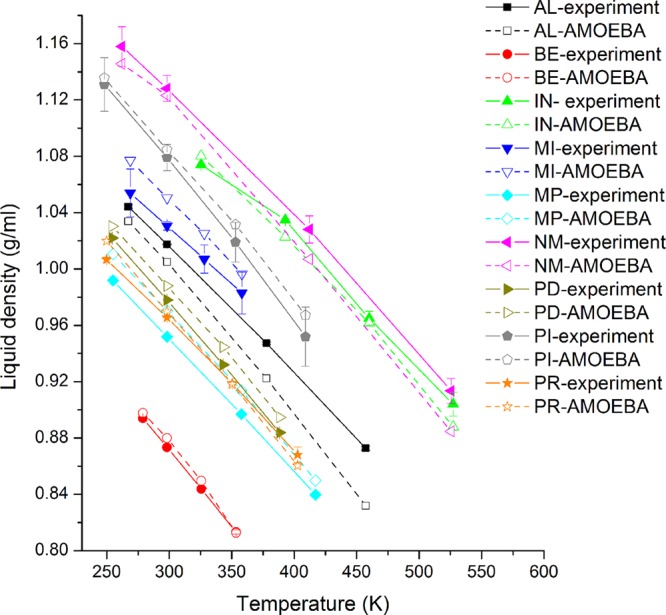
Figure 8

Open in a new tab

AMOEBA and experimental density of 9 liquids at different temperatures.

Table 3. Comparison Heat of Vaporization at Boiling Point between the Experimental and Calculated (Using the AMOEBA Force Field) Valuesa.

liquid temperature (boiling point) (K) experimental (kcal/mol) AMOEBA (kcal/mol) error (kcal/mol)
AL 457.2 10.301 ± 0.088 9.453 ± 0.024 –0.848
BE 353.4 7.347 ± 0.016 7.853 ± 0.014 0.506
IN 527.2 12.428 ± 0.621 11.407 ± 0.040 –1.021
MP 417.2 8.948 ± 0.057 9.815 ± 0.020 0.867
NM 525.6 13.002 ± 0.598 11.824 ± 0.037 –1.178
PD 388.4 8.337 ± 0.043 9.418 ± 0.024 1.081
PI 409.0 10.206 ± 0.526 9.752 ± 0.010 –0.454
PR 402.8 9.257 ± 0.038 9.230 ± 0.021 –0.027
Open in a new tab
a

Experimental values are from the NIST/TRC Web Thermo Tables (WTT) database.71

Figure 9.

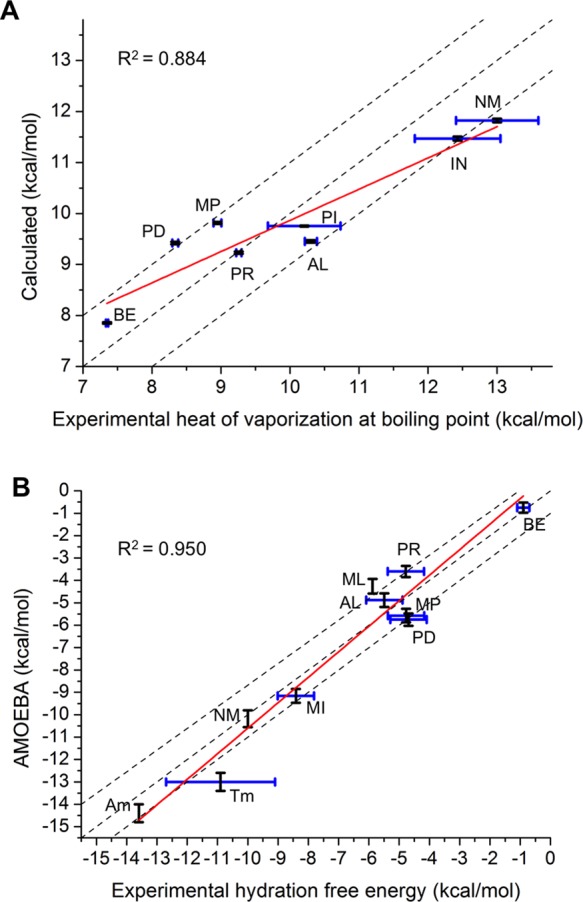
Figure 9

Open in a new tab

AMOEBA force field validation with condensed phase properties. (A) Heat of vaporization of pure liquid at boiling point. (B) Hydration free energy of dilute solution at room temperature. The dashed lines correspond to an exact prediction, plus and minus 1 kcal/mol. The linear fitting lines are in red. The correlation coefficient values between AMOEBA and experimental data are shown. [Tm] is not included in the correlation coefficient calculation.

Table 4. Comparison of the Hydration Free Energy at Room Temperature between the Experimental and Calculated (Using the AMOEBA Force Field) Valuesa.

solution experimental (kcal/mol) AMOEBA (kcal/mol) error (kcal/mol)
AL –5.49 ± 0.6 –4.88 ± 0.30 0.61
BE –0.90 ± 0.2 –0.75 ± 0.23 0.15
MI –8.41 ± 0.6 –9.16 ± 0.31 –0.75
ML –5.8875 –4.26 ± 0.33 1.62
MP –4.77 ± 0.6 –5.57 ± 0.30 –0.80
NM –10.00 –10.18 ± 0.38 –0.18
PD –4.69 ± 0.6 –5.75 ± 0.28 –1.06
PR –4.78 ± 0.6 –3.60 ± 0.25 1.18
Am –13.674 –14.4 ± 0.4 –0.8
Tm –(9.1–12.7)74 –13.0 ± 0.4  
Open in a new tab
a

Experimental values are from the SolvFree database,72 except for the three declared.

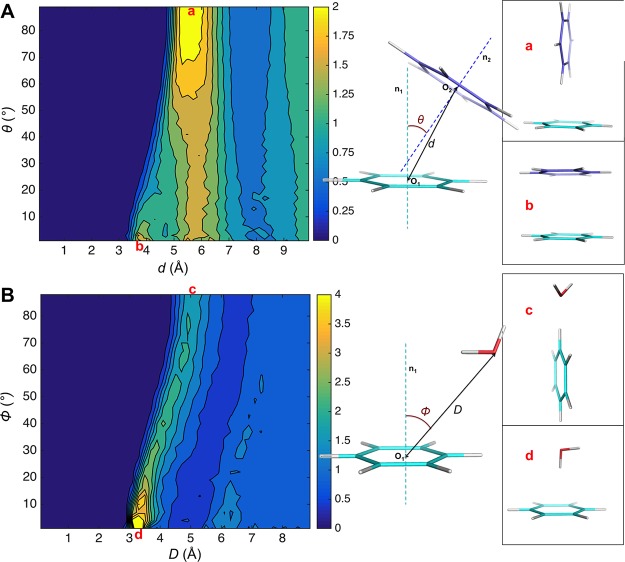
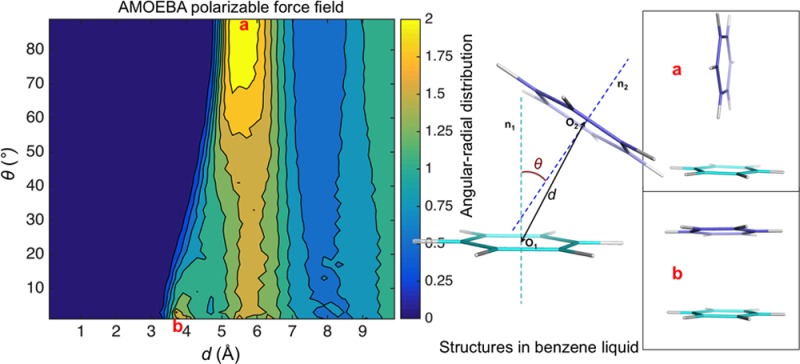
Structural features of pure liquid benzene and dilute benzene-water solution were obtained from 10 ns MD simulations and compared with experimental data or statistical results. Figure S9A shows the calculated ring-center—ring-center radial distribution functions in benzene liquid. Simulated benzene liquid shows a nearest neighbor coordination shell from approximately 4.0 to 7.5 Å, with a maxima at 5.65 Å. In the nearest neighbor shell, there are approximately 12 molecules. The orientational liquid structure was investigated using the radial distribution function of the angle between the normal to aromatic planes. Figure 10A shows the calculated 2D angular-radial distribution function from benzene liquid simulation. For parallel stacking, the main maximum is at 5.6 Å, with a shoulder at 4.0 Å. The perpendicular geometry shows a higher peak at about 5.7 Å. Figure S9B shows that molecular orientations of the first shell of benzene are nearly isotropic, and when the molecular separation is less than 5.0 Å, the parallel configuration is favored; and when it is between 5.0 and 6.0 Å, the perpendicular configuration is favored. All these results are in accordance with the high–resolution neutron diffraction data43 and are as good as the best recent popular force fields (in ref (76), the benzene liquid RDF and angular RDF performances of 8 force fields were reported).76 The distribution of water molecules around aromatic rings in solution was investigated from the simulation trajectories. A 2D angular-radial distribution function was also plotted (Figure 10B). The distance is defined as from the center of benzene to the oxygen of water, and the angle was defined as the angle between the benzene normal and the line of benzene-center—oxygen. The position at the normal line for water at 3.1–3.6 Å has the largest density. and the peak for the position on the plane was at about 5.0 Å. These features match well with the statistical results from protein structure database (PDB) and Cambridge Structural Database (CSD).47

Figure 10.

Figure 10

Open in a new tab

Benzene 2D angular-radial distribution in condensed phase calculated from MD simulation using the AMOEBA force field. (A) Benzene liquid. (B) Benzene water solution.

Discussion and Conclusions

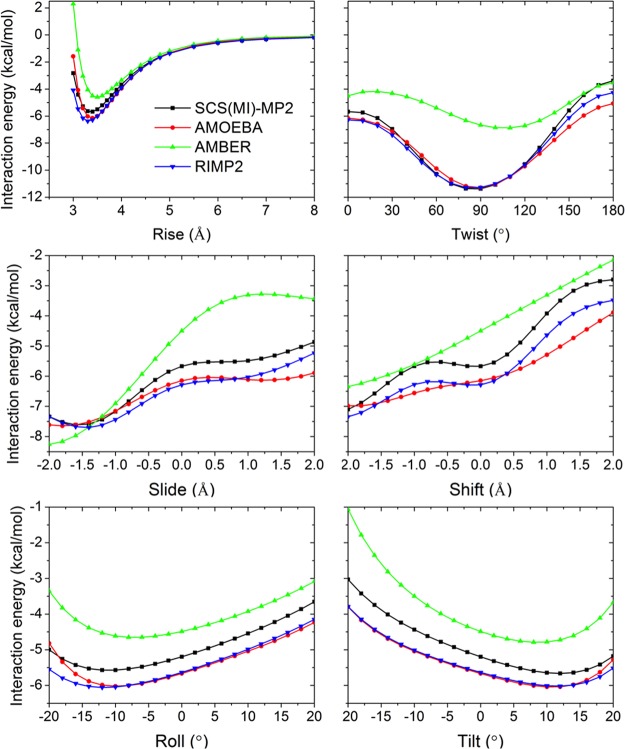
In this work, we constructed a classical polarizable multipole based force field for common nucleic acid bases and their analogs. QM methods were applied to provide target interaction energies for base-water, base pairing and stacking at various distances and orientations. Although the MP2 method overestimates the energy of stacking with the aug-cc-pVTZ basis set,77,78 the MP2/cc-pVTZ energy of the ten stacked nucleobase dimers agreed well (RMSE = 0.65 kcal/mol) with the reference energy79 using a complete basis set and CCSD(T) correction, namely the CBS(T) (Table S5). Energy computed using the new AMOEBA force field results in slightly better RMSE (RMSE = 0.48 kcal/mol) with the CBS(T) energy of these ten dimers. Sherrill’s base–base stacking database35 was also used to validate the new force field, in which the QM energy was calculated using SCS(MI)-MP2/cc-pVTZ. The correlation coefficient (R2) between AMOEBA and the SCS(MI)-MP2 energy for the three kinds of conformation in the database, rise-twist, slide-shift, and roll-tilt, were 0.932, 0.964, and 0.903, respectively (Figure S11). GU and AC stacking pairs were studied in detail (Figures 11 and S10, Table S12). For some cases, the RIMP2 and SCS(MI)-MP2 stacking energy did not agree, with RIMP2 predicting lower energy by up to 1 kcal/mol (using the same basis set, cc-pVTZ). Our model fits well with RIMP2 energies in all of the translation and rotation conformations. In some cases, AMBER greatly underestimated the stacking energy when compared to experiment, especially for the GU stacking pair.

Figure 11.

Figure 11

Open in a new tab

Comparison of stacking interaction energy computed for potential energy surfaces across rotations (Twist, Roll, Tilt) and translations (Rise, Slide, Shift) for the stacked guanine–uracil dimer. See details about the dimer conformation in Sherrill’s work. 35 QM results of SCS(MI)-MP2 and RIMP2 with the cc-pVTZ basis set and MM force field results of AMBER FF14 and the new AMOEBA are shown.

The interaction energies between nucleobases and three metal ions, Na+, K+, and Mg++ were also examined. Eight metal ion binding positions around four bases (A, C, G, and U) were selected: four ion positions around carboxyl groups and four ions positions around nitrogen groups with lone pairs (Figure S12). We found that the QM interaction energy of the bases with Na+ and K+ at the four ion positions near carboxyl groups are well reproduced using AMOEBA, while the interaction energy of Mg++ near carboxyl groups was too weak. The AMOEBA interaction energy for all the three ion types at the four ion positions around nitrogen groups was too strong. So special pairwise vdW parameters (Table S13) were used for metal ions-N and magnesium-O, and the results are also shown in Figure S12.

We investigated in detail the out-of-plane bending of aromatic rings. Multiple conformations with different bending axes and bending angles were designed, and the conformational energies were computed using QM. The new AMOEBA force field can reproduce the QM conformational energy with a 0.51 kcal/mol RMSE for all the distorted structures investigated here.

The AMOEBA polarization energies of dimers at equilibrium distance are highly correlated with the SAPT0 induction energy (Table S14). Water is a notably strong polar solvent; the induced dipoles on the aromatic molecules in water solution are much larger than those in pure liquid (Figure 12 and Table S15). Aromatic molecules adapt to different environments by changing the magnitude of their dipole moments, due to the high molecular polarizabilities of π-electron. Many drug molecules possess aromatic fragments, which play important roles in maintaining both desirable partition coefficients and binding affinity to the target biomolecules.80 The large polarization energy is likely important for such purposes. In DNA/RNA, the balance among base-water, base-pairing, and stacking interactions is the main driving force for forming biological structures such as duplexes and hairpins. In this study, we have successfully developed a new AMOEBA force field for nucleic acid bases and related aromatic analogs, based on comprehensive studies of molecular structures, energetics and liquid phase thermodynamic properties, and by systematic comparison with both QM calculations and experimental measurements.

Figure 12.

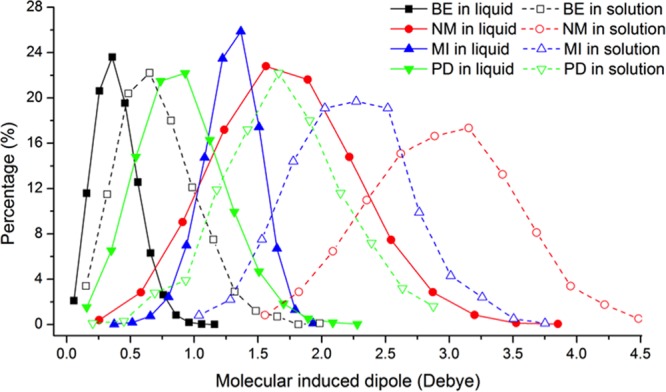
Figure 12

Open in a new tab

Molecular induced dipole in different environments (pure liquid and water solution).

Acknowledgments

The authors are grateful for support by the National Institutes of Health (R01GM106137 and R01GM114237 to J.W.P. and P.R.), the National Science Foundation (CHE 1152823 to J.W.P.), and the Robert A. Welch Foundation (F-1691 to P.R.). TACC and XSEDE (TG-MCB100057) provided high-performance computing resources.

Glossary

ABBREVIATIONS

QM

quantum mechanics

MM

molecular mechanics

AMOEBA

Atomic Multipole Optimized Energetics for Biomolecular Applications

WC

Watson–Crick

RMSD

root mean squared deviation

RMSE

root mean squared error

RDF

radial distribution function

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00918.

  • Supplementary figures and tables, MATLAB program code for vdW parameter optimization (PDF)

  • Force field functional forms and parameter file for the five regular nucleobases and the 12 aromatic molecules in AMOEBA format (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Funding was provided by the following: NIH R01GM106137 and R01GM114237; NSF CHE 1152823; and the Welch Foundation F-1691.

The authors declare no competing financial interest.

Supplementary Material

ct6b00918_si_001.pdf (4.4MB, pdf)
ct6b00918_si_002.pdf (183.3KB, pdf)

References

  1. Chessari G.; Hunter C. A.; Low C. M.; Packer M. J.; Vinter J. G.; Zonta C. Chem. - Eur. J. 2002, 8, 2860–2867. . [DOI] [PubMed] [Google Scholar]
  2. MacKerell A. D.; Nilsson L. Curr. Opin. Struct. Biol. 2008, 18, 194–199. 10.1016/j.sbi.2007.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Norberg J.; Nilsson L. Q. Rev. Biophys. 1999, 36, 257–306. 10.1017/S0033583503003895. [DOI] [PubMed] [Google Scholar]
  4. Hou T.; Wang J.; Li Y.; Wang W. J. Chem. Inf. Model. 2011, 51, 69–82. 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cruz J. A.; Blanchet M.-F.; Boniecki M.; Bujnicki J. M.; Chen S.-J.; Cao S.; Das R.; Ding F.; Dokholyan N. V.; Flores S. C. RNA 2012, 18, 610–625. 10.1261/rna.031054.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Schnieders M. J.; Baltrusaitis J.; Shi Y.; Chattree G.; Zheng L.; Yang W.; Ren P. J. Chem. Theory Comput. 2012, 8, 1721–1736. 10.1021/ct300035u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Tubbs J. D.; Condon D. E.; Kennedy S. D.; Hauser M.; Bevilacqua P. C.; Turner D. H. Biochemistry 2013, 52, 996–1010. 10.1021/bi3010347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Schmidt J. R.; Yu K.; McDaniel J. G. Acc. Chem. Res. 2015, 48, 548–556. 10.1021/ar500272n. [DOI] [PubMed] [Google Scholar]
  9. Foloppe N.; MacKerell A. D. Jr. J. Comput. Chem. 2000, 21, 86–104. . [DOI] [Google Scholar]
  10. MacKerell A. D.; Banavali N.; Foloppe N. Biopolymers 2000, 56, 257–265. . [DOI] [PubMed] [Google Scholar]
  11. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  12. Lopes P. E.; Roux B.; MacKerell A. D. Jr. Theor. Chem. Acc. 2009, 124, 11–28. 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Baker C. M.; Anisimov V. M.; MacKerell A. D. Jr. J. Phys. Chem. B 2011, 115, 580–596. 10.1021/jp1092338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lemkul J. A.; Huang J.; Roux B.; MacKerell A. D. Jr. Chem. Rev. 2016, 116, 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lopes P. E.; Huang J.; Shim J.; Luo Y.; Li H.; Roux B.; MacKerell A. D. Jr. J. Chem. Theory Comput. 2013, 9, 5430–5449. 10.1021/ct400781b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Cieplak P.; Caldwell J.; Kollman P. J. Comput. Chem. 2001, 22, 1048–1057. 10.1002/jcc.1065. [DOI] [Google Scholar]
  17. Ren P. Y.; Ponder J. W. J. Phys. Chem. B 2003, 107, 5933–5947. 10.1021/jp027815+. [DOI] [Google Scholar]
  18. Gresh N.; Cisneros G. A.; Darden T. A.; Piquemal J.-P. J. Chem. Theory Comput. 2007, 3, 1960–1986. 10.1021/ct700134r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Holt A.; Karlström G. Int. J. Quantum Chem. 2009, 109, 1255–1266. 10.1002/qua.21950. [DOI] [Google Scholar]
  20. Xie W.; Gao J. J. Chem. Theory Comput. 2007, 3, 1890–1900. 10.1021/ct700167b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Warshel A.; Kato M.; Pisliakov A. V. J. Chem. Theory Comput. 2007, 3, 2034–2045. 10.1021/ct700127w. [DOI] [PubMed] [Google Scholar]
  22. Shi Y.; Ren P.; Schnieders M. Rev. Comput. Chem. 2015, 28, 51–86. 10.1002/9781118889886.ch2. [DOI] [Google Scholar]
  23. Dixon R. W.; Kollman P. A. J. Comput. Chem. 1997, 18, 1632–1646. . [DOI] [Google Scholar]
  24. Williams D. E. J. Comput. Chem. 1988, 9, 745–763. 10.1002/jcc.540090705. [DOI] [Google Scholar]
  25. Kramer C.; Spinn A.; Liedl K. R. J. Chem. Theory Comput. 2014, 10, 4488–4496. 10.1021/ct5005565. [DOI] [PubMed] [Google Scholar]
  26. Ponder J. W.; Wu C.; Ren P.; Pande V. S.; Chodera J. D.; Schnieders M. J.; Haque I.; Mobley D. L.; Lambrecht D. S.; DiStasio R. A. Jr. J. Phys. Chem. B 2010, 114, 2549–2564. 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wu J. C.; Chattree G.; Ren P. Theor. Chem. Acc. 2012, 131, 1138. 10.1007/s00214-012-1138-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ren P.; Wu C.; Ponder J. W. J. Chem. Theory Comput. 2011, 7, 3143–3161. 10.1021/ct200304d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Piquemal J.-P.; Perera L.; Cisneros G. A.; Ren P.; Pedersen L. G.; Darden T. A. J. Chem. Phys. 2006, 125, 054511. 10.1063/1.2234774. [DOI] [PubMed] [Google Scholar]
  30. Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. J. Chem. Theory Comput. 2013, 9, 4046–4063. 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Da̧bkowska I.; Gonzalez H. V.; Jurečka P.; Hobza P. J. Phys. Chem. A 2005, 109, 1131–1136. 10.1021/jp046738a. [DOI] [PubMed] [Google Scholar]
  32. Kabeláč M.; Hobza P. Phys. Chem. Chem. Phys. 2007, 9, 903–917. 10.1039/B614420A. [DOI] [PubMed] [Google Scholar]
  33. Leontis N. B.; Stombaugh J.; Westhof E. Nucleic Acids Res. 2002, 30, 3497–3531. 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Šponer J.; Riley K. E.; Hobza P. Phys. Chem. Chem. Phys. 2008, 10, 2595–2610. 10.1039/b719370j. [DOI] [PubMed] [Google Scholar]
  35. Parker T. M.; Sherrill C. D. J. Chem. Theory Comput. 2015, 11, 4197–4204. 10.1021/acs.jctc.5b00588. [DOI] [PubMed] [Google Scholar]
  36. Šponer J. í.; Banáš P.; Jurečka P.; Zgarbová M.; Kührová P.; Havrila M.; Krepl M.; Stadlbauer P.; Otyepka M. J. Phys. Chem. Lett. 2014, 5, 1771–1782. 10.1021/jz500557y. [DOI] [PubMed] [Google Scholar]
  37. Gkionis K.; Kruse H.; Platts J. A.; Mladek A.; Koca J.; Sponer J. J. Chem. Theory Comput. 2014, 10, 1326–1340. 10.1021/ct4009969. [DOI] [PubMed] [Google Scholar]
  38. Gresh N.; Sponer J. E.; Devereux M.; Gkionis K.; de Courcy B.; Piquemal J.-P.; Sponer J. J. Phys. Chem. B 2015, 119, 9477–9495. 10.1021/acs.jpcb.5b01695. [DOI] [PubMed] [Google Scholar]
  39. Gowtham S.; Scheicher R. H.; Ahuja R.; Pandey R.; Karna S. P. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 033401. 10.1103/PhysRevB.76.033401. [DOI] [Google Scholar]
  40. Rosemeyer H.; Seela F. J. Chem. Soc., Perkin Trans. 2 2002, 4, 746–750. 10.1039/b200077f. [DOI] [Google Scholar]
  41. Cardamone S.; Hughes T. J.; Popelier P. L. A. Phys. Chem. Chem. Phys. 2014, 16, 10367–10387. 10.1039/c3cp54829e. [DOI] [PubMed] [Google Scholar]
  42. Tsuzuki S.; Honda K.; Uchimaru T.; Mikami M.; Tanabe K. J. Am. Chem. Soc. 2002, 124, 104–112. 10.1021/ja0105212. [DOI] [PubMed] [Google Scholar]
  43. Headen T. F.; Howard C. A.; Skipper N. T.; Wilkinson M. A.; Bowron D. T.; Soper A. K. J. Am. Chem. Soc. 2010, 132 (16), 5735–5742. 10.1021/ja909084e. [DOI] [PubMed] [Google Scholar]
  44. Gamieldien M. R.; Struempfer J.; Naidoo K. J. J. Phys. Chem. B 2012, 116, 324–331. 10.1021/jp2077159. [DOI] [PubMed] [Google Scholar]
  45. Fu C.-F.; Tian S. X. Phys. Chem. Chem. Phys. 2014, 16, 21957–21963. 10.1039/C4CP01537A. [DOI] [PubMed] [Google Scholar]
  46. Li S.; Cooper V. R.; Thonhauser T.; Puzder A.; Langreth D. C. J. Phys. Chem. A 2008, 112, 9031–9036. 10.1021/jp801693p. [DOI] [PubMed] [Google Scholar]
  47. Janjić G. V.; Malkov S. N.; Živković M. V.; Zarić S. D. Phys. Chem. Chem. Phys. 2014, 16, 23549–23553. 10.1039/C4CP00929K. [DOI] [PubMed] [Google Scholar]
  48. Villa A.; Peter C.; van der Vegt N. F. J. Chem. Theory Comput. 2010, 6, 2434–2444. 10.1021/ct100228t. [DOI] [PubMed] [Google Scholar]
  49. Albertí M.; Lago N. F.; Pirani F. Chem. Phys. 2012, 399, 232–239. 10.1016/j.chemphys.2011.08.009. [DOI] [Google Scholar]
  50. Gervasio F. L.; Chelli R.; Procacci P.; Schettino V. Proteins: Struct., Funct., Genet. 2002, 48, 117–125. 10.1002/prot.10116. [DOI] [PubMed] [Google Scholar]
  51. Meyer E. A.; Castellano R. K.; Diederich F. Angew. Chem., Int. Ed. 2003, 42, 1210–1250. 10.1002/anie.200390319. [DOI] [PubMed] [Google Scholar]
  52. Frisch M.; Trucks G.; Schlegel H. B.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Mennucci B.; Petersson H.. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009; p 200.
  53. Stone A. J. J. Chem. Theory Comput. 2005, 1, 1128–1132. 10.1021/ct050190+. [DOI] [PubMed] [Google Scholar]
  54. Stone A.University of Cambridge: Cambridge, UK, 1999.
  55. Shao Y.; Gan Z.; Epifanovsky E.; Gilbert A. T.; Wormit M.; Kussmann J.; Lange A. W.; Behn A.; Deng J.; Feng X. Mol. Phys. 2015, 113, 184–215. 10.1080/00268976.2014.952696. [DOI] [Google Scholar]
  56. Jurečka P.; Nachtigall P.; Hobza P. Phys. Chem. Chem. Phys. 2001, 3, 4578–4582. 10.1039/b105892b. [DOI] [Google Scholar]
  57. Ponder J.TINKER 7 Software Tools for Molecular Design; Washington University, St. Louis, MO, 2015.
  58. Guide, M. U. s. Inc, MATLAB; Natick, MA, 1998; p 5.
  59. Bussi G.; Donadio D.; Parrinello M. J. Chem. Phys. 2007, 126 (1), 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  60. Tuckerman M.; Berne B. J.; Martyna G. J. J. Chem. Phys. 1992, 97 (3), 1990–2001. 10.1063/1.463137. [DOI] [Google Scholar]
  61. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  62. Berendsen H. J.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  63. Gillespie D. T. J. Phys. Chem. 1977, 81, 2340–2361. 10.1021/j100540a008. [DOI] [Google Scholar]
  64. Shi Y.; Wu C.; Ponder J. W.; Ren P. J. Comput. Chem. 2011, 32, 967–977. 10.1002/jcc.21681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Thole B. T. Chem. Phys. 1981, 59, 341–350. 10.1016/0301-0104(81)85176-2. [DOI] [Google Scholar]
  66. Coppens P.; Guru Row T.; Leung P.; Stevens E.; Becker P. t.; Yang Y. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1979, 35, 63–72. 10.1107/S0567739479000127. [DOI] [Google Scholar]
  67. Wilson E. B.; Decius J.; Paul C.; McGraw-Hill: New York, 1955. [Google Scholar]
  68. Mannfors B.; Sundius T.; Palmo K.; Pietila L.-O.; Krimm S. J. Mol. Struct. 2000, 521, 49–75. 10.1016/S0022-2860(99)00425-1. [DOI] [Google Scholar]
  69. Neidle S.Principles of nucleic acid structure; Academic Press: London, UK, 2010. [Google Scholar]
  70. Frey M. N.; Koetzle T. F.; Lehmann M. S.; Hamilton W. C. J. Chem. Phys. 1973, 59, 915–924. 10.1063/1.1680114. [DOI] [Google Scholar]
  71. Kroenlein K.; Muzny C.; Kazakov A.; Diky V.; Chirico R.; Magee J.; Abdulagatov I.; Frenkel M.. NIST/TRC Web Thermo Tables (WTT) database, Version 2-2011-3-Pro; Thermodynamics Research Center (TRC), TP D, National Institute of Standards and Technology: Boulder, CO, 2011.
  72. Mobley D. L.; Guthrie J. P. J. Comput.-Aided Mol. Des. 2014, 28, 711–720. 10.1007/s10822-014-9747-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Wolf M. G.; Groenhof G. J. Comput. Chem. 2012, 33, 2225–2232. 10.1002/jcc.23055. [DOI] [PubMed] [Google Scholar]
  74. Ferguson D. M.; Pearlman D. A.; Swope W. C.; Kollman P. A. J. Comput. Chem. 1992, 13, 362–370. 10.1002/jcc.540130309. [DOI] [Google Scholar]
  75. Wolfenden R.; Andersson L.; Cullis P.; Southgate C. Biochemistry 1981, 20, 849–855. 10.1021/bi00507a030. [DOI] [PubMed] [Google Scholar]
  76. Fu C.-F.; Tian S. X. J. Chem. Theory Comput. 2011, 7, 2240–2252. 10.1021/ct2002122. [DOI] [PubMed] [Google Scholar]
  77. Sponer J.; Sponer J. E.; Mladek A.; Banas P.; Jurecka P.; Otyepka M. Methods 2013, 64, 3–11. 10.1016/j.ymeth.2013.05.025. [DOI] [PubMed] [Google Scholar]
  78. Sponer J.; Šponer J. E.; Petrov A. I.; Leontis N. B. J. Phys. Chem. B 2010, 114, 15723–15741. 10.1021/jp104361m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Sponer J.; Jurecka P.; Marchan I.; Luque F. J.; Orozco M.; Hobza P. Chem. - Eur. J. 2006, 12, 2854–2865. 10.1002/chem.200501239. [DOI] [PubMed] [Google Scholar]
  80. Ritchie T. J.; Macdonald S. J. F. Drug Discovery Today 2009, 14, 1011–1020. 10.1016/j.drudis.2009.07.014. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct6b00918_si_001.pdf (4.4MB, pdf)
ct6b00918_si_002.pdf (183.3KB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES