Refining Disordered Peptide Ensembles with Computational Amide I Spectroscopy: Application to Elastin-Like Peptides

Abstract

The characterization of intrinsically disordered protein (IDP) ensembles is complicated both by inherent heterogeneity and by the fact that many common experimental techniques function poorly when applied to IDPs. For this reason, the development of alternative structural tools for probing IDP ensembles has attracted considerable attention. Here we describe our recent work in developing experimental and computational tools for characterizing IDP ensembles using Amide I (backbone carbonyl stretch) vibrational spectroscopy. In this approach, the infrared (IR) absorption frequencies of isotope-labeled amide bonds probe their local electrostatic environments and structures. Empirical frequency maps allow us to use this spectroscopic data as a direct experimental test of atomistic structural models. We apply these methods to a family of short elastin-like peptides (ELPs), fragments of the elastin protein based around the Pro-Gly turn motif characteristic of the elastomeric segments of the full protein. Using a maximum entropy analysis of experimental spectra on the basis of predicted spectra from molecular dynamics (MD) ensembles, we find that peptides with Ala or Val sidechains preceding the Pro-Gly turn unit exhibit a stronger tendency toward extended structures than do Gly-Pro-Gly motifs, suggesting an important role for steric interactions in tuning the molecular properties of elastin.

Introduction

Over the last half-century, structural biology has played a pivotal role in our ability to understand and control biological systems at the molecular level. With the continued development of high-throughput structural methods like X-ray crystallography and nuclear magnetic resonance (NMR), the importance of these structural methods in biology and medicine is likely only to increase. Standard structural tools are often difficult to apply, however, when the function of the protein of interest depends explicitly on the absence of a unique native structure.^1–3 A prototypical example of such an intrinsically disordered protein (IDP) is the mammalian structural protein elastin that lends elasticity to skin, lungs, and other connective tissues.⁴ Although the molecular mechanisms of the process are not well understood, the presence of structural heterogeneity—that is, the availability of a large number of energetically similar structures at many different total protein extension lengths—appears to play a central role in the elastic function of the system.^4,5

The characterization of such a disordered conformational ensemble is difficult for two reasons. First, the problem is inherently complicated by the sheer number of distinct structures involved. Second, at a more technical level, many classic structure-determination methods are either inapplicable (e.g., X-ray crystallography) or more difficult to interpret (e.g., NMR) when applied to IDPs. ^6,7

Among the tools available to us, NMR spectroscopy provides by far the most comprehensive method for IDP ensemble characterization. Even for NMR, however, the interpretation of measured signals is complicated by motional narrowing when the intrinsic measurement time scale of the NMR experiment exceeds the conformational exchange time between IDP structures. In (¹³C) NMR spectroscopy, frequency differences between structures typically occur over a range of tens of kHz, giving rise to a peak coalescence time (or “shutter speed”) on the order of a microsecond.^7,8 For stably folded proteins, this microsecond cutoff presents no obstacle since large-scale structural rearrangements typically occur on a time scale of milliseconds or longer. The local conformational fluctuations so abundant in IDPs, however, occur on the much shorter scale of nanoseconds to microseconds, complicating the analysis of NMR data on disordered systems.^9–11

As a result of these technical complications, interest has increased in the development of new structural tools with faster intrinsic measurement time scales. One such technique is ultrafast vibrational spectroscopy, with a particular focus on the Amide I (backbone carbonyl stretch) vibration of peptides and proteins.^12,13 Experimentally, Amide I frequency differences Δν̄ are typically on the order of tens of cm⁻¹, corresponding to a coalescence time of a few ps, an increase in time resolution of nearly 6 orders of magnitude relative to ¹³C NMR chemical shift measurements.⁸

Conversely, however, the correspondingly short vibrational lifetime (~1.3 ps for Amide I vibrations¹⁴) produces significant peak broadening in IR absorption spectra, with severe spectral congestion often complicating the interpretation of experimental data. Experimentally, this congestion can be partially eliminated through isotope-labeling strategies.^15–22 A ¹³C or ¹³C¹⁸O isotope label introduced into an amide bond decreases the corresponding Amide I mode frequency by ~43 or ~65 cm⁻¹. This shift places the isotope-labeled absorption peak out of resonance with the main Amide I peak from the remainder of the peptide, allowing individual peptide groups to be monitored independently.^16,23,24

This spectroscopic data translates into structural information thanks to the acute sensitivity of Amide I vibrational frequencies to their local electrostatic environment. These Stark-like frequency shifts provide a quantifiable metric for local structural factors such as solvent exposure and hydrogen bond (HB) count.^15,25–27 As a rule of thumb, each HB donated to an amide carbonyl group reduces its vibrational frequency by roughly 16 cm⁻¹.

To facilitate a quantitative connection between experimental spectroscopy and protein structure, our group, along with many others, has been developing spectroscopic maps that translate structures from molecular dynamics (MD) simulations into predicted Amide I spectra.^{17,25,28–32} By parameterizing electrostatic frequency shift coefficients directly against experimental data, Amide I vibrational frequencies may be predicted within an accuracy of a few cm⁻¹ for both short dipeptide fragments²⁵ and isotope labels embedded within larger proteins^17,32. Although these models are expected to improve further, the predictability of Amide I spectra has reached a point where the method can be seriously evaluated as a tool to probe disordered peptide ensembles.

With these considerations in mind, we set out to apply Amide I spectroscopy to the structural analysis of a family of short (eight-residue) elastin-like peptides (ELPs), fragments of the disordered elastin protein introduced earlier. Although the full elastin protein contains a variety of different sequence motifs, it is believed that much of the protein’s bulk elasticity results from the reversible extensibility of the quasi-repeat motifs APGV and VPGV. These motifs occur approximately seven and thirteen times, respectively, in the ~786-residue human tropoelastin (precursor) sequence, along with numerous other variants of the XPGX motif.^33,34 Indeed, low-complexity synthetic polypeptides of the form GVG(VPGVG)_n have been found to reproduce many of the properties of wild-type elastin when n is on the order of 200.³⁵ Early studies suggested that the VPGV motif might be a nucleation point for ordered Type II β-turn structures³⁵, although subsequent study demonstrates that the long-range protein structure is disordered, regardless of conformational preferences at the local scale.³⁶ Our interest in these systems is in exploring the molecular origins of elastic function by characterizing the conformational ensembles occupied by short ELP fragments based on the VPGV sequence.

In an earlier study, some of us applied Amide I spectroscopy to three short ELPs with sequences GVGXPGVG with X = G, A, or V.³⁷ For brevity, we refer to these peptides here as GP, AP, and VP, respectively. In combination with spectroscopic modeling of structures from MD simulations using the most advanced spectral map available at that time, our experimental data for the VP peptide suggested a high population of a non-standard variant on the classic Type II β-turn in which two cross-turn HBs are formed between the X4 amide carbonyl and the V7 and G8 amide NH groups.³⁷ Since then, improvements have been made in the reliability of Amide I spectroscopic simulations.¹⁷ Furthermore, we have questioned whether harvesting structures by sampling from relatively short MD simulations could bias the assignment of conformers. In particular, our earlier work did not quantitatively account for computational uncertainty, either simulation error or inadequate sampling.

Our objective in the present study is to assess and develop isotope-edited Amide I spectroscopy as a quantitative tool for interpreting and refining ELP conformational ensembles. In this analysis, we aim both to investigate the influence of peptide sequence on ELP structure and to test the degree to which MD force fields (FFs) are able to predict these trends. Experimentally, we use peptides with a ¹³C-labeled X4P5 Amide I group, allowing full separation from the Amide I main band. In addition, we study a fourth peptide GVGVPVVG (designated simply “VPV”), intentionally designed to be unable to form compact turn structures due to steric interference between the V4 and V6 residues. At the computational level, we compare calculations from two different spectroscopic models, the Jansen/Roy (JR) map^30,38 adopted in our previous work and our new, empirically-parameterized single-point field (1F) map.^25,32 These simulations make use of extensively sampled MD ensembles from four different force fields (FFs) on each peptide. In order to place our structural assignments on a quantitative footing, we develop a maximum-entropy (ME) method for ensemble refinement.

Materials and Methods

FMOC Synthesis

¹³C-labeled peptides NH₂-GVGVPVVG-COOH, NH₂-GVGVPGVG-COOH, NH₂-GVGAPGVG-COOH, and NH₂-GVGGPGVG-COOH were synthesized at a 0.02 mM scale with 9-fluorenylmethyloxycarbonyl (FMOC) solid phase peptide synthesis. Isotope-labeling was achieved by incorporating 99% enriched 1-¹³C Gly, Ala, and Val FMOC-protected amino acids (Cambridge Isotopes Laboratories) at the X4 position. Synthesized peptides were purified using reverse phase chromatography and characterized by mass spectrometry, with an estimated purity of the target product greater than 90% for all peptides. See Supporting Information for further details.

FTIR Spectroscopy

Peptides were dissolved in D₂O/DCl at proton concentration of pD ≈ 1 and lyophilized overnight to remove residual hydrogen. Under these conditions, the peptides exist with protonated terminal groups ND₃⁺ and COOD, leaving a net charge of +1. For spectroscopy, the samples were again dissolved in D₂O/DCl at pD ≈ 1 and placed between two CaF₂ windows with a 50 μm spacer. FTIR spectra were recorded at room temperature using a Bruker Tensor 27 FTIR spectrometer at a resolution of 2 cm⁻¹. A background spectrum of D₂O/DCl at pD ≈ 1 was taken beforehand and subtracted from the peptide spectra to remove solvent bands. In addition, a linear baseline correction was applied to provide a flat baseline between 1545 and 1800 cm⁻¹. The OD of the main Amide I band was in the range of 0.05–0.15 for all peptides, while the OD of the isotopically labeled band was in the range of 0.01–0.04.

Isotope Label Absorption Profile

For ME calculations, we require the mean and variance of the IR line shape

$$\mu =\int s(\omega )\omega d\omega$$ (1)

and

$${\stackrel{\sim }{\sigma }}^2=\int s(\omega ){\left(\omega -{\mu }_{exp}\right)}^{2}d\omega$$ (2)

where s(ω) is the absorption profile of the isotope-labeled XP amide unit, normalized to unit area. The tilde in the definition of σ̃² highlights that the expectation is calculated with respect to the experimental mean frequency μ_exp for both experimental and simulated spectra. For experimental spectra σ̃² is simply the variance. For simulated spectra, the non-standard definition is adopted for consistency with ME reweighting. See Supporting Information for further details. In order to evaluate these integrals accurately for the experimental data, we first performed a (single) Gaussian fit to the red edge of the main band region (1620 cm⁻¹ to 1655 cm⁻¹) of the raw experimental spectrum; this main-band fit was then subtracted from the raw data to isolate the contribution of the isotope-labeled absorption peak. To avoid bias due to baseline drift over the experimental frequency window, we filtered the experimental isotope-labeled spectrum by a ~60 cm⁻¹ logistic function window before normalization. The width and steepness of this window were chosen to ensure a smooth decay of the spectrum to an accurately zeroed baseline outside of the region where the data provides meaningful signal. For consistency, we applied the same logistic function window to simulated spectra when evaluating Eqs. (1) and (2) so that any (weak) distortions induced by this window will be identical in simulated and experimental spectra. See Supporting Information for further details.

Molecular Dynamics Simulations

MD simulations were carried out in the GROMACS 4.6 simulation package³⁹ using the AMBER99sb-ildn,⁴⁰ GROMOS53a6,⁴¹ CHARMM27,^42,43 and OPLS-AA^44,45 FFs in explicit solvent boxes of ~4,000 water molecules (cubic box dimensions of ~5 nm). The choice of water model was tied to the corresponding FF: TIP4P-Ew⁴⁶ for AMBER99sb-ildn, SPC⁴⁷ for GROMOS53a6, SPC/E⁴⁸ for OPLS-AA, and TIP3P⁴⁹ for CHARMM27. Additional simulation details are provided in the Supporting Information. For spectroscopic calculations, we ran 400 ns of production data for each peptide/FF combination. In these trajectories, full structural coordinates were sampled at intervals of 20 fs to provide the finely-sampled structural trajectory required for spectroscopic simulations. In addition, we ran 1 μs production trajectories saving only peptide coordinates every 200 fs to better sample backbone conformations. For the CHARMM27 and OPLS-AA FFs, we also ran a third set of production runs of length 1 μs (CHARMM27) or 400 ns (OPLS-AA; 330 ns for the AP peptide). In total, we thus analyzed 1.4 μs of MD data for AMBER99sb-ildn and GROMOS53a6, 2.4 μs for CHARMM27, and ~1.8 μs for OPLS-AA.

Spectroscopic Simulations

Spectroscopic simulations were carried out using a mixed quantum/classical method described elsewhere.¹⁷ Briefly, beginning with our 400 ns MD structural trajectories, Amide I frequencies, couplings, and transition dipole moments were calculated frame-by-frame for each amide bond. The resulting excitonic Hamiltonian and dipole trajectory was converted to a simulated vibrational spectrum using either the dynamic wavefunction propagation method of Torii^50,51 (long trajectories) or the time-averaging approximation (TAA) of Auer and Skinner⁵² (10 ps trajectories, unsuitable for wavefunction propagation). For TAA spectra, we use a cosine averaging window (decaying to zero by 725 fs) whose width was set by comparison with numerically exact wavefunction propagation. In both cases, the Amide I lifetime was set to 1.3 ps.

Two different literature electrostatic maps were used to generate spectroscopic parameters (site energies, couplings, and dipoles). The JR map was employed in our previous study.^29,30,38 The 1F map is the newest generation of our single-point field models trained to a library of dipeptide fragments.^25,32 It differs from our previous 1F map (Ref.²⁵) in the use of modified Glycine charges and TIP3P water model charges (rather than SPC/E) as described in Ref.³² See Supporting Information for further details. Note that with the exception of the GROMOS53a6 calculations, CHARMM27 atomic charges were applied in all spectroscopic calculations (i.e. in post-processing after the MD run). This convention is based on our observation that CHARMM27 charges typically provide better spectroscopic predictions than other FF charges, even when applied to structures culled from other FFs.^25,32 Furthermore, this choice allows all three force fields (AMBER99sb-ildn, CHARMM27, and OPLS-AA) to be analyzed using the same spectroscopic map, minimizing bias due to different map parameterizations. (The GROMOS53a6 force field uses united-atom representation for some groups and so cannot be assigned CHARMM27 charges.)

Results

Amide I Absorption Spectroscopy

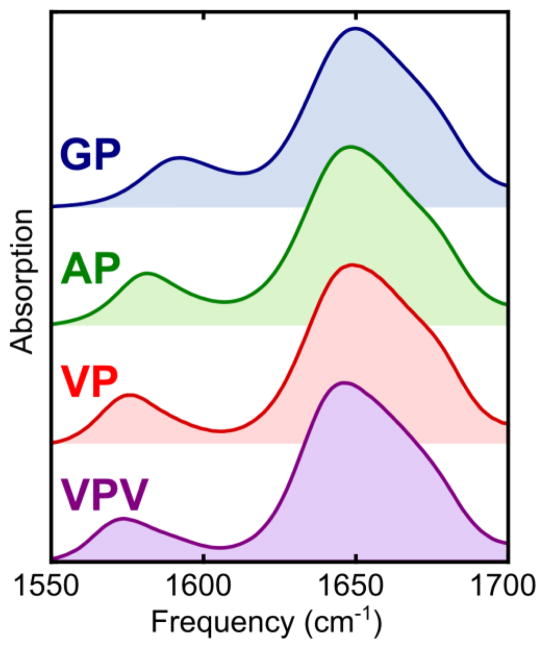
Our objective in this work is to extract conformational preferences for the GP, AP, VP, and VPV peptides from experimental, isotope-edited Amide I spectra. The starting point for this study is the set of experimental absorption spectra presented in Figure 1. In these spectra, the main band near 1650 cm⁻¹ corresponds to absorption from unlabeled peptide bonds, while the low-frequency peak between 1574 and 1592 cm⁻¹ corresponds absorption from the ¹³C-labeled X4P5 amide bond. The observed peak frequencies for the X4P5 bond are summarized in Table 1 and increase in the order VPV < VP < AP < GP, with a fairly small shift between the VPV (1573 cm⁻¹) and VP (1576 cm⁻¹) peptides and a large jump in frequency between the AP (1581 cm⁻¹) and GP (1592 cm⁻¹) peptides.

Figure 1.

Amide I absorption spectra for the four ¹³C-labeled ELPs studied in this work.

Table 1.

Peak frequencies for experimental and simulated ELP isotope-labeled peptides, quoted in cm⁻¹.

	GP	AP	VP	VPV
Experiment	1592	1581	1576	1574
1F	1586	1581	1580	1578
JR	1581	1581	1583	1583

Given the conclusion of our previous work that the VP peptide adopts a largely collapsed structure in solution,³⁷ the similarity between the VP and VPV peptide spectra is surprising. As noted above, steric clash between the V4 and V6/V7 sidechains is expected to restrict the VPV peptide to a largely extended ensemble in solution. In this light, the similarity of the VP and VPV spectra suggests an extended conformation for the VP peptide. This conclusion is consistent with other findings in which the absorption bands of isotope-labeled sites shift toward lower frequencies with increased solvent exposure.¹⁹ In our previous study, however, we were unable (using OPLS-AA FF simulations and the JR spectroscopic map) to account for the experimental trend for the GP, AP, and VP peptides without assuming a substantial population of two-HB β-turn structures for the VP peptide.³⁷ To investigate the source of this discrepancy, we turn to simulation data.

MD Simulations

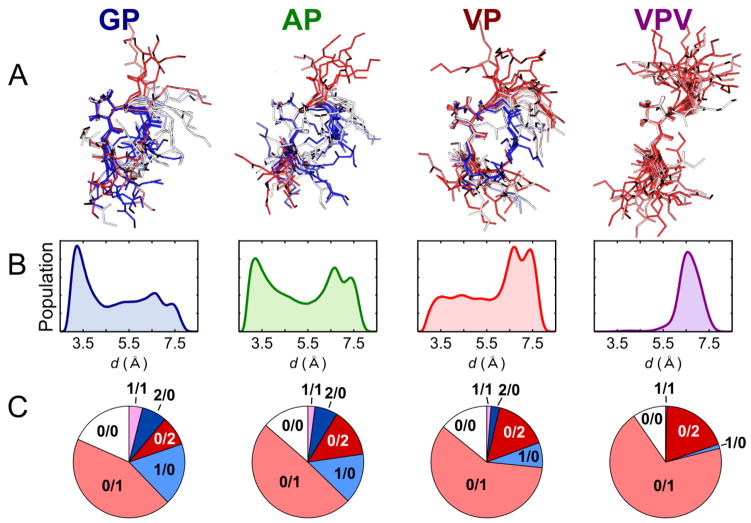
To explore these contrasting assignments from an MD perspective, we next carried out 400 ns MD simulations for each peptide in the NVT ensemble using the OPLS-AA FF with explicit SPC/E solvent. As illustrated in Figure 2A, the resulting structural ensembles show a distribution of conformations that shift on average from collapsed structures for the GP peptide toward extended structures for the VP and VPV peptides. A more quantitative view is provided in Figure 2B, where population histograms are presented for each peptide as a function of the cross-turn hydrogen-bonding distance

Figure 2.

Conformational ensembles predicted by 400 ns MD simulations. A: Uniformly sampled structural ensembles aligned around the central proline residue. Structures are colored from red to white to blue with decreasing turn extension distance d. B: Population histograms for the cross-turn distance d of Eq.(3). C. Conformational populations for different hydrogen-bonding configurations to the X4 carbonyl. Indices m/n indicate m peptide-to-peptide HBs and n peptide-to-solvent HBs.

$$d=\Vert {\mathbf{r}}_o^{x4}-{\mathbf{r}}_N^{V7}\Vert ,$$ (3)

where ${\mathbf{r}}_O^{X4}$ and ${\mathbf{r}}_N^{V7}$ are, respectively, the coordinates of the X4 oxygen atom and the V7 nitrogen (illustrated schematically in Figure 4 below). In a β-turn, these two atoms participate in a HB, as indicated by the histogram peak near d ≈ 3.5 Å for the GP peptide in Figure 2B. In the AP histogram, this 3.5 Å population occurs at nearly equal frequency with a fully-extended population near d ≈ 7 Å. The VP peptide, in contrast, shows a partial preference for the fully-extended 7 Å ensemble, while the VPV peptide adopts-fully extended conformations almost exclusively.

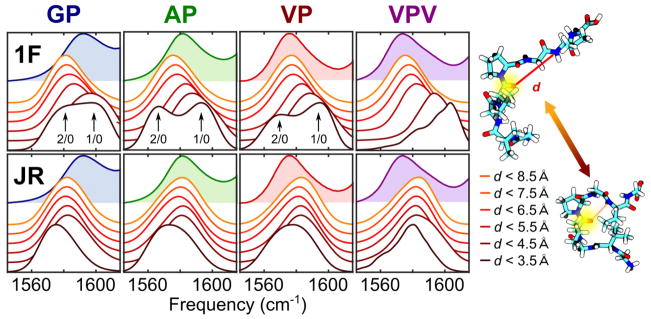
Figure 4.

Simulated isotope-label absorption spectra (white-filled spectra) as a function of turn distance d. Simulated spectra are calculated for 10 ps intervals from our 400 ns MD trajectory and are binned by the average turn distance d over the corresponding 10 ps interval. Structural bins are divided into 1 Å intervals with the darkest curve corresponding to collapsed structures with 2.5 Å < d < 3.5 Å, and the lightest corresponding to extended structures with 7.5 Å < d < 8.5 Å. All spectra are scaled to the same peak intensity. Experimental spectra (color-shaded curves) are shown in the background for reference. Top: Isotope-labeled spectra simulated using the 1F spectroscopic map. Bottom: Isotope-labeled spectra simulated using the JR spectroscopic map. Right: Graphical definition of the turn extension coordinate d used to define conformational bins.

These backbone conformational trends are mirrored in the local solvent exposure at the X4 carbonyl site, as illustrated in Figure 2C. Here pie charts for each peptide present the population of various HB configurations at the X4 site. The labels “m/n” indicate the number of HBs accepted by the X4 oxygen atom from peptide NH groups (m) and solvating water molecules (n). The extended VPV ensemble is composed almost entirely of conformations in which the V4 carbonyl forms one (0/1) or two (0/2) HBs to the surrounding solvent. In only ~1% of sampled conformations does the X4 carbonyl participate in intra-peptide HBs. In contrast, the VP, AP, and GP peptides show increasing populations of 1/0 and 2/0 conformations in which the X4 carbonyl accepts HBs from within the peptide itself, primarily from the V7 and G8 NH groups. Note, however, that the overall HB occupation number—the total number of HBs formed, on average, between the XP carbonyl group and either solvent or peptide—changes only quite modestly from peptide to peptide, increasing by ~10% from GP to VPV. As represented in the pie charts, HBs lost from solvent in the AP and GP peptides are largely replaced by those formed within the peptide itself. The trends observed thus represent a transition in the nature (i.e. peptide-solvent vs. peptide-peptide) rather than the number of XP carbonyl HBs.

Spectroscopic Simulations

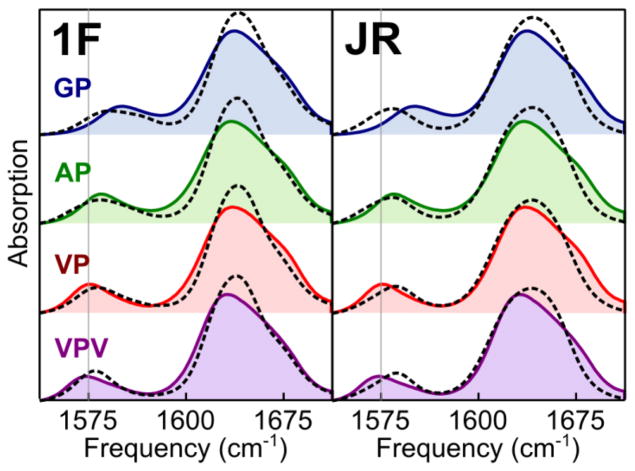
Any quantitative comparison between experiment and simulation must rely on the spectroscopic maps described in the introduction. To test our MD conformational ensembles against experimental data, we next performed simulations using the 1F and JR spectroscopic maps. The results are presented in Figure 3. For both maps, the line shape of the main-band region (1600 – 1700 cm⁻¹) is poorly captured by the simulation, likely a result of inaccuracies in our treatment of coupling interactions. As summarized in Table 1, however, the behavior in the isotope-label region (1550 – 1600 cm⁻¹) shows clear differences between the two maps. Although by no means in quantitative agreement with the experimental spectra, the 1F map does capture the correct qualitative trend, a steady decrease in isotope-label peak frequency from 1586 cm⁻¹ for the GP peptide to 1578 cm⁻¹ for the VPV peptide. In contrast, simulations using the JR map predict a slight increase in frequency from GP to VPV.

Figure 3.

Experimental (shaded) and simulated (open) spectra for GP, AP, VP, and VPV peptides. The left-hand panel shows results using the 1F spectroscopic map; the right-hand panel shows results for the JR map. For reference, thin, gray, vertical lines mark 1575 cm⁻¹ in each frame.

These trends are brought out more clearly by dividing the conformational ensemble into distinct structural bins based on the cross-turn distance d. To achieve this, we split up our 400 ns MD trajectory into 10 ps intervals I_n with n ranging from 1 to 40,000. On this time scale the turn distance d remains relatively static (fluctuations about the interval mean are approximately Gaussian with a standard deviation of ~0.3 Å). For each interval, we calculate an Amide I isotope-label spectrum using the TAA method. To emphasize the isotope-label absorption, in these calculations we set the oscillator strength of all sites other than the XP label to zero; in this way we treat all coupling interactions between sites correctly, while producing a simulated spectrum corresponding only to the absorption of the isotope-labeled unit. Finally, we bin each interval I_n based on average turn extension, combining their spectra to produce simulated spectra as a function of turn extension. For example, by averaging all spectra whose corresponding 10 ps interval shows an average turn distance between 2.5 Å and 3.5 Å, we obtain simulated spectra for tightly-collapsed, turn-like structures.

Figure 4 presents spectra binned by turn distance for each peptide using both the 1F and JR maps. Interestingly, the two maps display qualitatively different behavior as a function of turn extension. While the 1F map indicates a gradual blue shift of the absorption peak as turn extension decreases corresponding to the loss of the solvent-induced redshift, the JR map shows minimal variation with turn extension. Both maps show distinct behavior for the most tightly-collapsed structures (d < 3.5 Å). For this bin, the 1F map reveals two distinct subpopulations. The red-shifted peak corresponds to the sparsely populated 2/0 population identified earlier in which the NH groups of both V7 and G8 donate HBs to the X4 carbonyl (see Figure 2C). The blue-shifted peak corresponds to the 1/0 bin in which only the V7 NH group donates a HB. In the JR simulations, these bins are not distinguished clearly, with simulated spectra showing only a single broadened, red-shifted peak. Note that the 2/0 conformation is only accessible for extremely short turn distances; hence the absence of a red-shifted peak in bins with larger turn extensions. Likewise, the 0/1 and 0/2 bins fail to give rise to distinct spectral features due to strong solvent disorder; although spectra for 0/1 structures are, on average, blue-shifted from those for 0/2 structures, the spectra are sufficiently broadened by heterogeneity in the XP solvation shell that only a single broadened peak is observed in simulations using either spectroscopic map.

Taken together, these results highlight the critical role that the spectroscopic map plays in analyzing Amide I vibrational spectra. Indeed, the assignment in our previous study³⁷ of a high population of 2/0 turn structures appears to be due largely to the use of the JR map. For our present application, we believe that the 1F map provides a more accurate description of the experimental data. This assessment is based both on the favorable performance of the 1F map in recent isotope-labeling studies of protein standards¹⁷ and on the substantially better agreement in the isotope-labeled region displayed in Figure 3 and Figure 4. From this point we focus exclusively on 1F simulations.

Maximum Entropy Analysis

Our primary objective in this analysis is to test and refine predicted MD ensembles by comparison against experimental data. Qualitatively, the dependence of the 1F simulated spectra on turn distance supports the idea that the GP peptide adopts a predominantly collapsed conformational ensemble, while the VP peptide is biased toward more extended structures. To put such statements on a quantitative footing, however, we need an objective method for incorporating experimental constraints into our simulated structural ensemble. For this purpose, we turn to the Maximum Entropy (ME) method, a probability-reweighting scheme advanced by E. T. Jaynes as a means of incorporating external constraints into a probabilistic system with minimal bias.⁵³ In our context, we wish to reweight our MD conformational ensemble to produce a refined ensemble that is consistent with our experimental data. The ME method provides a rigorous means of identifying from all possible experimentally-consistent ensembles the one that deviates minimally from the initial MD ensemble. Given a set of initial (MD-based) estimates $p_n^o$ for the population of each structure n in a conformational ensemble, the ME principle states that the least-biased means of incorporating external constraints into the structural ensemble is to maximize the relative-entropy functional

$$\eta \left[\mathbf{p}\Vert {\mathbf{p}}^o\right]=-\sum _n{p}_{n}ln\frac{p_n}{p_n^o}$$ (4)

subject to the normalization constraint Σ_n p_n = 1 and any external constraints imposed by the user. In our analysis, the individual structures n that are to be reweighted according to Eq. (4) correspond to the “micro-ensemble” of structures sampled during the 10 ps intervals I_n rather than to the structure at any single frame in the MD trajectory. In the reweighting process, we constrain the ensemble to match the experiment in both mean frequency μ and variance σ̃² as defined by Eqs. (1) and (2). The ME reweighting procedure could be carried out with reference only to the 400 ns trajectory we used for spectroscopic simulations. In this case, the intervals I_n would be assigned equal starting probabilities $p_n^o$ since they are sampled uniformly in time across the simulation. To ensure that our starting ensemble accurately reflects FF predictions, however, we chose to run addition simulations (1.8 μs in total) for each peptide, adjusting the starting probabilities to more accurately reflect the better-sampled structural ensemble. Explicitly, to each interval I_n, we assign a probability

$$p_n^o=\sum _{i\in I_n}\frac{P_{\mathit{full}}\left(d_i\right)}{P_{400ns}\left(d_i\right)}\alpha (d_i)$$ (5)

where the sum extends over all structures i within the 10 ps interval I_n, the distance d_i is the cross-turn distance of structure i, and the probabilities P_400ns (d_i) and P_full (d_i) refer, respectively, to the ensemble frequency of structures with turn distance d_i in the 400 ns ensemble we used for spectroscopic simulations and in the longer (1.8 μs) reference ensemble. The scaling factor α(d_i) avoids numerical instability due to the finite sampling of P_400ns (d_i) as described in detail in the Supporting Information. Briefly, α(d_i) = 1 for those structures whose turn distance d_i falls into the upper 99.5% of all structures sampled in the 400 ns trajectory; for the 0.5% of structures whose turn distance is sampled less frequently, α(d_i) is a cosine window interpolating smoothly to P_400ns (d_i)/P_full (d_i), so that the weighting factor for these sparsely-sampled structures is unchanged by reference to the longer simulation ensemble. Our final structural ensemble corresponds to the sum of all micro-ensembles from each of the 10 ps intervals I_n weighted by the probabilities p_n. Further details on the numerical implementation of this procedure are provided in the Supporting Information.

The results of this ME refinement procedure are illustrated in Figure 5. On the whole, the changes induced by this ME refinement on our OPLS-AA ensemble are fairly mild. The primary trend is a uniform shift toward more pronounced structural trends, with the GP ensemble shifting toward more collapsed structures in the ME-refined ensemble and the VP ensemble shifting toward more extended structures. Only the VPV peptide shows no discernible shifts in overall turn extension, reflecting the close match between simulated and experimental spectra in the raw MD ensemble.

Figure 5.

ME-refinement results for the OPLS-AA FF. Left: Simulated spectra for each peptide before (dashed) and after (solid) ME refinement. Lightly shaded curves represent raw experimental absorption spectra; dark shaded curves are extracted spectra for the isotope-labeled site. Right: Raw (shaded) and ME-refined (solid black line) turn-distance histograms.

Force Field Dependence

To gain a sense for the reliability of these results, it is instructive to explore the sensitivity of these conclusions to both FF parameters and simulation error. To explore FF effects, we repeated our analysis using three additional FF/water model combinations: CHARMM27/TIP3P, AMBER99sb-ILDN/TIP4P-Ew, and GROMOS53a6/SPC, with total MD simulation times ranging from 1.4 μs (GROMOS53a6 and AMBER99sb-ildn) to 2.4 μs (CHARMM27). As a qualitative benchmark, we note that exchange times between extended and compact conformations typically occurred in our simulations on a time scale of a few tens of nanoseconds, so that a 1 μs trajectory can be expected to sample tens to hundreds of transitions. At a more quantitative level, we carried out a block-averaging analysis to test the adequacy of these trajectories for obtaining a reliable estimate of FF predictions. From this analysis, we estimate a standard error of approximately ±5% in the fraction of extended conformations in the starting MD ensemble (see Supporting Information for further details). To check the sensitivity of our ME analysis to spectroscopic errors, we repeated our analysis under the assumption of various systematic errors in Amide I frequency prediction. A reasonable range of errors for this purpose is ±4 cm⁻¹, the 2σ confidence interval for the 1F map against the original dipeptide data set for which it was parameterized.³²

The results of this analysis are summarized in Figure 6 and Table 2. Interestingly, while population predictions vary significantly from FF to FF in the raw MD data, the ME-refined ensembles show a consistent structural trend. The results for the CHARMM27 FF are particularly informative: the predictions of the ME-refined ensembles fairly closely resemble those of the remaining FFs, despite the fact that the raw MD data predicts essentially identical extended populations (45 – 47%) for all three XP ELPs. This increased uniformity in the ME-refined ensembles reflects the influence of the population restraints imposed by the experimental data on our MD ensembles. Significantly, only for the OPLS-AA FF do all raw MD values fall within the error bars of our ME analysis. The effects of the ME reweighting procedure are particularly pronounced for the GP peptide, with initial estimates of the extended population ranging from 44% for OPLS-AA to 63% for AMBER and ME-refined values ranging from 15% (GROMOS) to 33% (OPLS-AA). All four FFs thus appear to underestimate the propensity of this peptide to adopt collapsed turns in solution.

Figure 6.

ME analysis of the fraction of extended conformations in raw and ME-refined MD ensembles for the four force fields investigated. Extended conformations are defined by d > 5 Å. Raw MD fractions are represented by thick black lines. ME-refined values are represented by vertical bars. Error bars reflect uncertainty in spectroscopic predictions. The reported values correspond to the maximum and minimum populations obtained in repeated ME analyses for sys-tematic map errors of −4 cm 1, −3 cm 1, …, +4 cm 1.

Table 2.

ME-refined average turn distance d in Å. Raw force field estimates are in parentheses.

	GP	AP	VP	VPV
OPLS	4.6 (4.9)	5.2 (5.4)	5.8 (5.5)	6.6 (6.6)
CHARMM	4.1 (4.9)	4.8 (4.9)	5.1 (4.9)	6.1 (6.1)
AMBER	4.1 (5.4)	4.7 (5.7)	5.3 (5.9)	6.4 (6.4)
GROMOS	4.3 (5.3)	4.9 (5.5)	5.4 (5.6)	6.5 (6.5)

Discussion

The results presented above highlight both important strengths and limitations of isotope-edited Amide I spectroscopy as a tool for ensemble refinement. On the one hand, our experiments impose considerable restraints on the sampled conformational ensembles, drawing out a clear structural trend that would have been difficult to assign with confidence from the raw MD data alone. In this process, the ME method plays the critical role of providing a rigorous framework on which to base the ensemble refinement process.

On the other hand, our results also highlight that even modest spectroscopic simulation errors have a substantial impact on ensemble refinement. Taking the 2 (95%) confidence interval of our dipeptide 1F map as a reasonable measure of spectroscopic uncertainty, we expect our predicted frequencies to be within 4 cm⁻¹ of the experimental result for ~95% of structures. Even this modest error, however, results in variations in the estimated population of extended states as high as ±15% (AMBER FF). At first, this high population error might seem surprising. After all, a frequency prediction error of ±4 cm⁻¹ appears quite low in absolute terms (less than 1% error for a 1600 cm⁻¹ vibration). The significance of this error is more apparent, however, when one considers the limited range over which Amide I frequencies are distributed. Absorption frequencies for isotope-labeled sites typically span a range of around 30 cm⁻¹ in experimental data, from ~1570 cm⁻¹ for strongly hydrogen-bonded species to just above ~1600 cm⁻¹ for solvent-shielded sites. In comparison with this limited dynamic range, a frequency prediction error of ±4 cm⁻¹ appears quite significant, more than a quarter of the total dynamic range. In this light, our observed population assignment errors appear quite reasonable.

In large part, this spectroscopic error should be removable as advances in simulation methods improve our ability to accurately predict Amide I vibrational frequencies. A question of more fundamental interest involves the sensitivity of the ensemble refinement results to errors in the starting ensemble. In short, we wish to know how strong are the constraints that can be imposed by Amide I spectroscopic data. For example, can Amide I spectroscopic constraints “rescue” a bad FF prediction to produce an accurate conformational ensemble even given a poorly sampled or strongly biased starting point?

The FF comparison of Figure 6 provides at least a partial answer. Even in the absence of spectroscopic error, differences between the raw FF ensembles are large enough that the fraction of extended populations predicted for the GP peptide span a range of nearly 20%, from 15% for the GROMOS FF to 33% for OPLS-AA. In this sense, Amide I spectroscopy appears to serve as a relatively weak constraint on peptide structure: a wide range of structural ensembles can be made to reasonably fit the experimental data, leaving only a limited capacity for a priori structure prediction. At a physical level, this lack of discrimination stems from the fact that isotope-edited Amide I spectroscopy is primarily sensitive to short-range electrostatics, and reports only indirectly on larger-scale coordinates such as overall turn extension. Because solvent fluctuations give rise to significant variations in local electrostatic parameters at any given turn extension—and hence significant variation in the instantaneous Amide I frequency—Amide I spectroscopic data will rarely be capable of absolutely excluding any given conformation from a predicted ensemble.

Looking forward, it bears noting that such a weak-constraint situation is well-suited to the Bayesian ensemble refinement approaches.^54–56 These methods provide a concrete framework both for incorporating multiple weak constraints (e.g. spectroscopic data from multiple labeling sites) into a single structural ensemble and for testing the robustness of the result against experimental and simulation error. For Amide I spectroscopy in particular, multi-site labeling strategies should be particularly powerful once coupling models achieve sufficient accuracy that spectroscopic features like main band line shapes, energy transfer times, and (in multidimensional spectra) cross-peak intensity can be implemented as structural constraints. Multi-site labeling experiments will be particularly critical in the analysis of larger peptide or protein systems where larger-scale structural parameters are of interest (e.g. inter-strand distances or secondary structure content). Ultimately, of course, Amide I spectroscopy will be most effective when used together with other structural tools. In combination with ensemble-averaged constraints from NMR or electron paramagnetic resonance (EPR), Amide I spectroscopy should provide a useful tool for distinguishing between different conformational ensembles that yield identical ensemble averages but different degrees of disorder around the average structure.

Finally, with regard to the molecular properties of elastin, our results provide direct, experimental evidence that the conformational ensembles of ELPs in aqueous solution follow a bimodal distribution between extended and collapsed states. In particular, our finding of a ~40% population of collapsed structures for the VP peptide is in excellent agreement with the solid-state NMR findings of Ohgo et al. and Yao and Hong who assigned populations of 40% and 33%, respectively, to collapsed β-turn-like structures in related VPG-based ELPs.^57,58 Our results indicate that these low-temperature results are preserved in aqueous solution and that the AP peptide adopts a similar (but slightly more collapsed) ensemble.

At a mechanistic level, our results support the notion that the molecular properties of elastin are tuned to preserve local conformational disorder. In contrast to the preference of the GP and VPV peptides for collapsed and extended populations, respectively, the AP and VP peptides, which mimic the most common sequence motifs in native elastin, are more evenly split between collapsed and extended conformations. Recent global sequence analysis and mutational studies indicate that elastomeric function is, to a significant extent, a direct result of the periodic “kinking” of the protein chain conformation by PG units.^5,59 The conformational restrictions imposed by the proline residue thus disrupt the formation of long-range secondary structural motifs (α-helices or β-sheets), while the flexibility of the adjacent glycine facilitates the thermal accessibility of a large number of distinct conformation states at a wide range of overall extension lengths. Our analysis adds to this discussion the observation that the identity of the residue preceding the PG turn unit appears to tune (likely via steric effects) the average extension of each monomeric unit and thus the persistence length of the bulk polymer. In light of the measured persistence length of only 3.5 Å for native tropoelastin⁶⁰ (comparable to the turn length for a single XPGX unit), these observations are consistent with a molecular model for elastomeric function in which individual PG units switch independently between extended and turn-like structures, adding up collectively to yield bulk elasticity through an entropic chain mechanism.

In summary, we have explored here the utility of isotope-labeled Amide I spectroscopy as a quantitative tool for IDP conformational analysis. As a test case, we investigate the ensemble refinement of a family of short ELPs based on the elastin-like motifs APGVG and VPGVG. Experimental isotope-labeled data is compared with MD simulations and mixed quantum/classical spectroscopic simulations. We adopt a maximum entropy approach to provide an objective refinement of the conformational ensembles predicted by MD simulations against experimental data. The resulting conformational ensembles for the peptides tested reveal a distinct trend in overall peptide extension lengths in the order GP < AP< VP< VPV. The OPLS-AA FF is found to produce the best agreement with the experimentally-predicted trend, with populations of extended and compact structures falling within the error bars of our analysis. The GROMOS53a6 and AMBER99sb-ildn FFs capture the correct qualitative trend, although the assigned populations require substantial adjustments before reading agreement with experimental data. The raw CHARMM27 predictions differ most strongly from the refinement, assigning essentially identical populations for the GP, AP, and VP peptides. With regard to elastin structure, our findings suggest that steric effects imposed at the monomer level by the residue preceding proline in the characteristic elastin PG turn motif tune the persistence length of the bulk protein. In a broader sense, our results indicate that Amide I vibrational spectroscopy should serve as a valuable tool for ensemble refinement when used in conjunction with complementary methods such as NMR, EPR, and FRET spectroscopies.

Our results offer insight into the intertwined factors involving experimental data, spectroscopic models, and FFs that must be addressed in protein structural analysis. Experiment-based ensemble refinement requires, first of all, conformational sampling that is complete enough to visit all important energy basins. The populations predicted in those basins should be enough to bias against unphysically strained conformers. Maximum entropy or Bayesian refinement tools provide a critical framework incorporating experimental constraints into a refined ensemble. For Amide I, the accuracy of the spectroscopic model (particularly vibrational coupling) seems to be the leading factor to consider to improve confidence in these methods. As spectroscopic models improve, simulations can provide an active role not only in interpreting experimental data, but in guiding what experiments are performed. This feedback between simulation and experiment will be especially helpful in selecting isotope label sites to provide useful constraints for ensemble refinement. Already the current accuracy of our ensemble refinement indicates that these strategies for improving Amide I ensemble refinement will result in a useful tool for analysis of IDPs.

Abbreviations

IDP

intrinsically disordered protein

IR

infrared

ELP

elastin-like peptide

NMR

nuclear magnetic resonance

FF

force field

HB

hydrogen bond

ME

maximum entropy

EPR

electron paramagnetic resonance