Abstract
A fundamental feature of the temporal organization of neural activity is phase-amplitude coupling between brain rhythms at different frequencies, where the amplitude of a higher frequency varies according to the phase of a lower frequency. Here, we show that this rule extends to brain-organ interactions. We measured both the infra-slow (~0.05 Hz) rhythm intrinsically generated by the stomach – the gastric basal rhythm – using electrogastrography, and spontaneous brain dynamics with magnetoencephalography during resting-state with eyes open. We found significant phase-amplitude coupling between the infra-slow gastric phase and the amplitude of the cortical alpha rhythm (10–11 Hz), with gastric phase accounting for 8% of the variance of alpha rhythm amplitude fluctuations. Gastric-alpha coupling was localized to the right anterior insula, and bilaterally to occipito-parietal regions. Transfer entropy, a measure of directionality of information transfer, indicates that gastric-alpha coupling is due to an ascending influence from the stomach to both the right anterior insula and occipito-parietal regions. Our results show that phase-amplitude coupling so far only observed within the brain extends to brain-viscera interactions. They further reveal that the temporal structure of spontaneous brain activity depends not only on neuron and network properties endogenous to the brain, but also on the slow electrical rhythm generated by the stomach.
Keywords: Cross-frequency coupling, Phase-amplitude coupling, Resting-state dynamics, Alpha rhythm, Gastric rhythm, Brain-viscera interactions
Highlights
-
•
Spontaneous alpha rhythm fluctuations locked to gastric phase.
-
•
Gastric phase explains 8% of alpha variance.
-
•
Gastric-alpha coupling mostly to due to ascending influences from stomach to brain.
-
•
The stomach as an external oscillator constraining spontaneous brain activity.
Introduction
Phase-amplitude coupling (PAC) is a fundamental organizational rule where the amplitude of a high-frequency oscillation varies according to the phase of a lower frequency oscillation (Bragin et al., 1995, Canolty et al., 2006, Schroeder and Lakatos, 2009, Buzsaki, 2010). This rule has been recently shown to also govern the temporal organization of spontaneous large-scale brain activity in humans (Osipova et al., 2008, Roux et al., 2013, Florin and Baillet, 2015, Weaver et al., 2016). Here, we propose to extend the hierarchical organization of PAC to brain-viscera interactions. The brain at rest is not a closed system as it constantly receives information from visceral organs (Mayer, 2011, Critchley and Harrison, 2013, Furness et al., 2013). Some organs may provide an external source of slow frequency rhythms relayed to the brain and contributing to the temporal organization of resting-state brain dynamics. Specifically, we hypothesize that the gastric basal rhythm, an infra-slow electrical oscillation intrinsically and continuously generated by the stomach, may influence resting-state brain dynamics.
The stomach contains a specific cell type - the interstitial cells of Cajal (Sanders et al., 2006, Sanders et al., 2014) - at the interface between the enteric nervous system and gastric smooth muscles, that intrinsically generate an electrical slow wave at ~0.05 Hz (3 cycles per minute). During digestion, the gastric basal rhythm sets the pace of muscle contraction, but the rhythm is generated at all times, even in the absence of contraction (Bozler, 1945), or when the stomach is experimentally disconnected from the central nervous system (Suzuki et al., 1986). Gastric interstitial cells of Cajal form synapse-like connections with afferent sensory neurons (Powley and Phillips, 2011) that, via spinal and vagal nerve pathways and various subcortical relays, target a number of cortical structures comprising notably the insula, ventral anterior cingulate cortex and somatosensory cortex (Ito, 2002, Mayer, 2011, Critchley and Harrison, 2013, Furness et al., 2013). The stomach may thus be considered as an autonomous electrical pacemaker that may continuously feed the brain with a slow oscillatory input constraining resting-state brain dynamics.
We tested whether the phase of slow gastric oscillations is coupled to the amplitude of higher-frequency brain rhythms at rest in humans. We recorded brain activity with magneto-encephalography (MEG) along with gastric electrical activity measured from cutaneous electrodes placed on the abdomen (Fig. 1A), a technique called electrogastrography (EGG) (Koch and Stern, 2004), from 17 participants at rest with eyes open for 12 min.
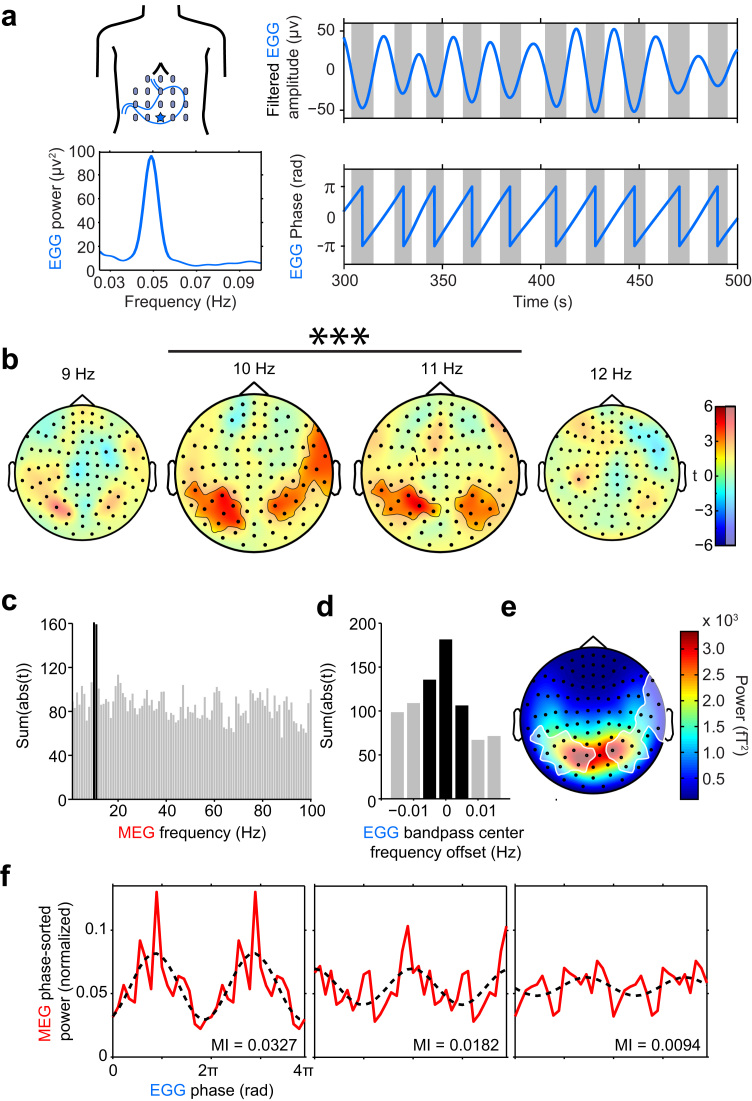
Fig. 1.
Gastric-alpha coupling. (a) Electrogastrogram (EGG) recording in a single participant. Left, electrode montage with the star indicating the electrode with the largest EGG amplitude and corresponding EGG power spectrum below. Right: 200 s filtered EGG signal and corresponding phase below. (b) Statistical maps of gastric phase - MEG power coupling at different frequencies. Significant gastric-MEG coupling occurred only at 10 and 11 Hz, in the two clusters indicated by black outlines and saturated colors (Monte-Carlo p=0.0008 for both clusters, corrected). (c) Summary statistics of gastric coupling strength across all sensors, for brain frequencies between 1 and 100 Hz, display a sharp peak at 10 and 11 Hz. (d) Coupling is specific to gastric frequency: summary statistics of EGG-alpha coupling strength across all sensors decreases when offsetting the filter above or below EGG peak frequency, that is presented at 0. Black bars in (c) and (d) indicate significant coupling. (e) Topographical map of 10–11 Hz power, grand average across participants. The clusters of significant gastric-alpha coupling at 10–11 Hz are overlaid in white. (f) Three examples of phase-amplitude coupling profiles, in the participant with the largest (left), median (middle) and smallest (right) MI. Profiles are presented over two gastric cycles (4π) for clarity. MEG average power in each bin was normalized by the sum of the average power across bins. The dashed black line is a cosine fit that emphasizes the 1:1 coupling between alpha power and gastric phase.
Material and methods
Participants
Seventeen right-handed adult participants (mean±sem age: 23.9±0.62, range 20–29; 8 males; mean body-mass index 22.02±0.62, range 17.5–26.1) with normal or corrected to normal vision took part in the study. None of the participants had any previous history of neurological, psychiatric or digestive disease. Participants had been fasting for at least 2 hours before the recordings. They signed a written informed consent and were paid for participation. All procedures were approved by the Ethics Committee CPP Ile de France III and were in accordance with the Helsinki declaration.
Procedure and recordings
Participants fixated a central black fixation mark (black dot, radius 0.13° of visual angle, surrounded by a black circle, radius 0.38° of visual angle) presented on a gray background at a viewing distance of 80 cm for 12 min. Participants were instructed to stay still, to fixate the central mark and to let their mind wander, avoiding any structured strategy such as counting or mentally reciting a text. Continuous magneto-encephalographic (MEG) signals were collected using a whole-head MEG system with 102 magnetometers and 204 planar gradiometers (Elekta Neuromag TRIUX MEG system) at a sampling rate of 1000 Hz and online low-pass filtered at 330 Hz. The electrogastrogram (EGG) was recorded via 19 disposable cutaneous electrodes (17 active, 1 reference and 1 ground) placed on the abdomen and acquired simultaneously with MEG data (DC recordings, low-pass filter at 330 Hz). In classical EGG montages, the reference electrode is located in the upper right part of the abdomen, and active electrodes are placed over the left part of the abdomen (Chen et al., 1999), where the stomach lays. We extended this montage to create a bilateral grid of EGG electrodes placed over four regularly spaced rows (Fig. 1a). In each participant, we first determined the midpoint between the xyphoid process and the umbilicus. The central electrode of the second row was located 2 cm above this midpoint (Chen et al., 1999). The vertical position of the top-row was then determined as the intersection of a 45° line originating from the central electrode of the second row, and the left mid-clavicular line. The horizontal positions of rows 3 and 4 were distributed such that the vertical spacing between each row was equal. The electrodes were horizontally centered on the midline and were evenly distributed between the left and right mid-clavicular lines. The first row consisted of 3 electrodes, with the rightmost electrode being used as a reference. The subsequent rows consisted of 5 electrodes. The ground electrode was located on the participant's left costal margin. An electrocardiogram (ECG) was simultaneously recorded. Eye position and pupil diameter were monitored with an EyeLink 1000 (SR Research) and simultaneously recorded with MEG, EGG and ECG data.
MEG data preprocessing
Signal Space Separation (tSSS) was performed using MaxFilter (Elekta Neuromag) to remove external noise. Subsequent analysis was conducted on magnetometer signals. The cardiac artifact was corrected using Independent Component Analysis (ICA), as implemented in the FieldTrip toolbox (Oostenveld et al., 2011). Briefly, the 12 min. resting period was divided into 5 s segments to compute ICA components. The number of independent components to be identified was the rank of the time x trial matrix. The continuous magnetometer data were then decomposed according to identified ICA components. The ICA-decomposed MEG signals and ECG data were epoched from 250 ms before to 400 ms after each R-peak and the pairwise phase-consistency (PPC) (Vinck et al., 2010) was computed between the ICA-decomposed signals and the ECG signal to isolate those components most reflective of ECG activity. Components with large PPC values and topographies matching the stereotypical ECG artifact were rejected from the continuous MEG data (mean 1.71±0.41 sem components rejected). Blink artifacts were defined as the blink intervals identified by the EyeLink eye-tracker system padded by ±100 ms. On average, 8.92%±2.19 sem of the total recording time was marked as contaminated by blink artifacts and was excluded from the analysis. ICA-corrected magnetometer data were then downsampled to 400 Hz and submitted to a Hann tapered 1 s window FFT, computed from 0 to 720 s at 0.050 s steps. The squared-magnitude of the resulting complex Fourier coefficients was used to generate the power envelope time series with a 20 Hz sampling rate for frequencies ranging from 1 to 100 Hz in 1 Hz steps.
EGG processing
EGG power at each abdominal electrode was computed via a Hann tapered FFT, using Welch's method with a 200 s window moving in 50 s steps. For each participant, the electrode exhibiting the largest spectral peak in the 0.05±0.01 Hz range, centered in the normogastric range (Riezzo et al., 2013), was selected for further analysis. To identify and mark EGG artifact periods, the raw signal was filtered between 0.01 and 0.5 Hz to isolate EGG related variance, and the standard deviation was computed over the trial. Segments of this filtered signal exceeding 4 standard deviations were marked as artifacts. These periods were padded by ± the filter order used to isolate the EGG peak frequency (±0.02 Hz of the peak frequency, see below) to compensate for temporal smearing of the artifact by the filter. On average 12.85%±2.71 sem of the total recording was discarded due to presence of artifacts in the EGG signal, mostly due to participant movement. The raw EGG was then downsampled to 20 Hz and filtered using a frequency sampling designed finite impulse response filter (Matlab: FIR2), with a bandwidth of ± 0.02 Hz of the peak EGG frequency, and a transition width between the passband and stopband of 15% of the upper and lower passband frequencies. The filter order was determined as the number of samples corresponding to 3 cycles of the lower passband frequency. Importantly, filter width was large enough to capture slower and faster gastric episodes. Filtered data thus retained all the frequency variability intrinsic to the gastric rhythm necessary for the statistical procedure we used (see below). The filter width was sufficiently narrow enough to exclude any contribution from respiration. The filtered EGG signal was then Hilbert transformed and the analytic phase was derived.
Phase-amplitude coupling (PAC)
As a result of the preprocessing steps, we obtained a pair (ϕgastric(t), PowMEG(t)), where ϕgastric is the phase of the gastric rhythm, and PowMEG the power of the MEG signal in a given frequency band at a given sensor, at each sample t of the artifact-free epochs. The EGG phases were sorted into 18 bins spanning the [–pi, pi] interval, and corresponding MEG power was averaged for each phase bin. MEG power sorted by EGG phase bin defined the PAC profile (Fig. 1f). To quantify the deviation of the PAC profile from a uniform distribution, we computed the modulation index (MI) (Tort et al., 2010). Briefly, when the MEG power shows no systematic relationship to the EGG phase, MEG power in each EGG phase bin will tend toward the overall average MEG power, resulting in a flat, or uniform, distribution. The MI of Tort et al. (2010) specifically measures deviation from a uniform distribution, and thus in this case a correspondingly low MI value will result. Alternatively, if the MEG signal power systematically differs across EGG phase bins, the PAC profile will deviate from a uniform distribution and MI will be larger. As shown by (Tort et al., 2010), MI is sensitive to 1:1 coupling but also to higher 1:m coupling modes (Palva et al., 2005).
Statistical determination of significant clusters of PAC
The statistical determination of significant clusters of phase-amplitude coupling was a two-step process. We first estimated, for each participant, chance-level PAC at each sensor and frequency. We then determined, at the group level, sensors and frequency where a significant difference between observed coupling and chance-level coupling differed. Those steps are detailed below.
We first estimated the level of PAC expected by chance and the corresponding chance-level MI for each participant, magnetometer and MEG frequency. We created surrogate data where the relationship between EGG and MEG signals was disrupted by shifting EGG phase and MEG power signals relative to one another by a random time interval exceeding ± 60 s, i.e. about 3 gastric cycles. Data at the end of the record were wrapped to the beginning, as in the cutting/swapping procedure proposed by Bahramisharif et al. (2013). This procedure best preserves phase autocorrelation and is much more conservative than the random shuffling of the full time series (Weaver et al., 2016). In other words, from the original pairs (ϕgastric(t), PowMEG(t)) we created surrogate pairs (ϕgastric(t), PowMEG(t+τ)) where τ is a value randomly chosen between 1 and 11 min. Because the filtered EGG signal, and MEG power envelope are not pure sine waves, but physiological signals that exhibits spontaneous increases and decreases in frequency, any link between gastric phase and brain rhythms is disrupted in the surrogate data. For each participant, MEG sensor and frequency, we obtained a distribution of surrogate MI values by creating 1000 surrogate data sets, corresponding to 1000 random τ, and computing the associated MIs. We defined the chance level, for each participant, sensor and MEG frequency, as the median of surrogate MI values.
We tested whether the empirical MI significantly differed from chance level MI at the group level using a cluster-based permutation procedure (Maris and Oostenveld, 2007), as implemented in FieldTrip (Oostenveld et al., 2011), that extracts significant differences between two conditions, across sensors and MEG frequencies, while intrinsically correcting for multiple comparisons. Briefly, this procedure entails comparing empirical MI with the corresponding chance level MI value across participants using a t test at each sensor and frequency. Candidate clusters are defined in space as sensors exceeding the first level t-threshold (p<0.05, two-sided) and that are connected to at least 2 neighboring sensors that also exceed this threshold, and across adjacent frequencies that exceeded the first level t-threshold. Each candidate cluster is characterized by a summary statistic corresponding to the sum of the t-values across the sensors and frequencies defining the cluster. The second-level statistic, i.e. whether a given sum of t-values in the candidate cluster could be obtained by chance, was determined by computing the distribution of cluster statistics under the null hypothesis. In practice, we randomly shuffled the labels 'empirical' and 'chance' 10,000 times, applied the clustering procedure and retained the largest positive and negative clusters from each permutation. Across the 10,000 permutations one can thus build the distribution of cluster statistics under the null hypothesis, which is then used to assess the empirical clusters for significance. Because the largest positive and negative clusters are retained at each permutation, this method intrinsically controls for multiple comparisons over sensors and frequencies (Maris and Oostenveld, 2007). The resulting clusters are described by their summary statistics, corresponding to the sum of t-values for each time sample and sensor belonging to the cluster, and by their MonteCarlo p-value describing significance at the cluster level corrected for multiple comparisons across sensors and frequencies.
Explained variance
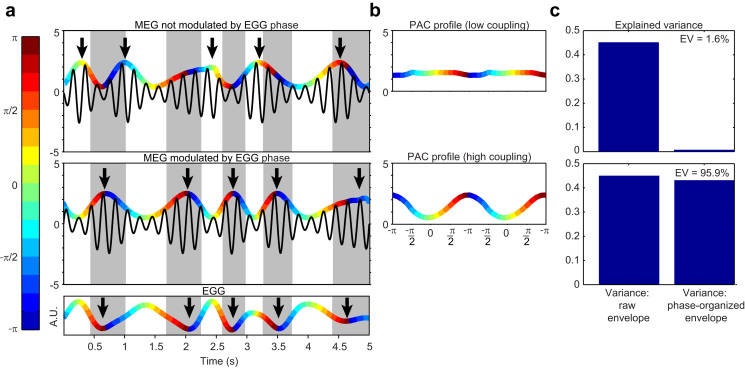
To determine the percentage of fluctuations of brain activity at a given frequency explained by the phase of the gastric rhythm, we computed the ratio between the variance of the original MEG amplitude envelope and the variance of the PAC profile, i.e. the MEG amplitude envelope sorted by gastric phase (Fig. 2). When MEG amplitude shows no systematic variation with EGG phase, then the distribution of phase-sorted amplitude will approach uniform, which will yield a low variance computed across the bins. Alternatively, when the MEG data is systematically modulated by EGG phase, the distribution of phase-sorted amplitude will be non-uniform giving rise to a larger variance across bins. The variance across bins of the phase-sorted amplitude is divided by the variance of the original non-phase organized signal, which gives the proportion of the MEG amplitude fluctuations in the original signal that is explained by EGG phase, or, in other words, the explained variance. In practice, we computed the ratio between the variance of the time-varying MEG 10–11 Hz amplitude envelope binned by EGG phase and the variance of the original MEG 10–11 Hz amplitude envelope smoothed in time-windows of a duration equal to the length of one phase bin, using a zero-phase moving average filter.
Fig. 2.
Rationale for the quantification of explained variance. (a) Bottom, simulated EGG signal, varying over time in amplitude (arbitrary units) and phase (color code). Arrows indicate EGG troughs. Middle, simulated rhythmic MEG activity with an amplitude envelope modulated by the phase of the EGG signal. Arrows indicate peaks in the MEG amplitude envelope. The color code in the amplitude envelope refers to EGG phase. Both arrows and color-coded phase reveal the systematic link between the MEG amplitude envelope and EGG phase. Top, simulated MEG signal with an amplitude envelope that varies over time but that is not coupled to EGG phase. Arrows indicate peaks in the MEG amplitude envelope. (b) Phase-amplitude profiles, i.e. MEG amplitude envelope sorted by EGG phase. When MEG amplitude has little relationship with EGG phase (top row), the phase-amplitude profile is flat. When alpha amplitude is tightly linked to gastric phase (bottom row), the phase-amplitude profile shows modulations as large as in the original non phase-sorted data. (c) Variance of the raw envelope as presented in (a) and variance of the phase-sorted envelope as presented in (b). Explained variance (EV) is the ratio between the variance of the phase-organized envelope and the variance of the raw envelope, expressed in percentage.
Source analysis
We used a beamformer-based source localization technique to obtain a time series of 10–11 Hz power per voxel, per participant. A 5 mm grid spanning the MNI ICBM 152 nonlinear high-resolution (0.5 mm) template brain was constructed. This grid was warped to the anatomy of each participant based on his or her individual MRI. The ICA corrected magnetometer signals were downsampled to 50 Hz, and zero-phase filtered between 10 and 11 Hz (FIR frequency sampling filter, transition band of 15% of the upper and lower passbands, order=200). A spatial filter was constructed using an LCMV beamformer and a single-shell head model, implemented in the FieldTrip toolbox (Oostenveld et al., 2011). Data containing blinks were excluded from spatial filter construction. Since resting-state data cannot be contrasted to another condition, the leadfields were normalized using the default parameter of 0.5 to reduce power bias towards the center of the head. Source time series of the 10–11 Hz data were constructed by projecting the 12 min 10–11 Hz filtered data segment through the spatial filter and taking the magnitude of each dipole along its principal axis. The power envelope was then determined as the squared-magnitude of the Hilbert transform. The resulting power envelope was downsampled to 20 Hz. These virtual source time series were used to determine PAC values using the same computation as at the sensor level. A one-tailed cluster statistic was then computed, using the same surrogate data sets and clustering procedure as described at the sensor level, to determine regions showing significant gastric-brain coupling at the source level. This test utilized a first level threshold corresponding to the 98.5 percentile of Student's t-distribution, and the default FieldTrip neighborhood definition and connectivity.
Transfer entropy
Transfer entropy (TE), a directional measure of information transfer sensitive to linear and non-linear coupling (Vicente et al., 2011), was used to determine the direction of interaction between the gastric slow-wave and the 10–11 Hz alpha power, at each of the source time series belonging to a significant PAC cluster. We computed TE between the alpha source power time series from the source-localized clusters and the EGG time series filtered ± 0.02 Hz of the EGG peak frequency using TRENTOOL (Lindner et al., 2011). The 12 min resting state data were segmented into 60 s segments for TE analysis, sampled at 20 Hz. The embedding delay and embedding dimension were estimated for each participant via Ragwitz’ criterion (Ragwitz and Kantz, 2002), with the maximal value of each measure taken across participants as the optimal parameters. The time series were embedded using these parameters, and the TE value was computed at each voxel between the alpha source power and EGG signal. Each TE value was tested for statistical significance via the non-parametric statistical test provided by TRENTOOL. The number of TE interactions exceeding an arbitrary threshold of p<0.05 uncorrected, either in the EGG→MEG, or MEG→EGG directions was tabulated for each participant, separately for the anterior and posterior significant PAC clusters. To test for an asymmetry of directional interactions, the number of pairs above this threshold was then compared between the two directions using a paired t-test, separately in the posterior and anterior clusters, with the results of both t-tests Bonferroni corrected for multiple comparisons.
Results
Existence of gastric-alpha coupling
For each participant, we determined gastric frequency at the EGG electrode showing the largest peak in the normal gastric range to take into account intersubject variability in stomach location and to maximize signal-to-noise ratio (Fig. 1a, mean EGG frequency 0.046 Hz±0.001 sem). We then computed coupling between the gastric phase and the amplitude of brain rhythms from 1 to 100 Hz using the modulation index (MI) (Tort et al., 2010). We compared the obtained MI values with estimated chance level (see Material and Methods) using a cluster-based procedure (Maris and Oostenveld, 2007) that intrinsically corrects at the group level for multiple comparisons across sensors, frequencies and time samples. Within the frequency range tested (1–100 Hz), significant gastric-brain coupling (Fig. 1b) occurred in the alpha range, at 10 and 11 Hz, in two bilateral parieto-occipital clusters with an extension over right fronto-temporal sensors (sum(t)=53.22, MonteCarlo p=0.0008, and sum(t)=52.57, Monte-Carlo p=0.0008, corrected for multiple comparisons). Summary statistics of gastric-brain coupling (Fig. 1c) show a distinct peak at 10 and 11 Hz, indicating that the effect is well localized to the alpha band. The topography of significant gastric-alpha coupling and alpha power overlap, but only partially (Fig. 1e).
Gastric-alpha coupling was highly specific to gastric frequency (Fig. 1d). We filtered the signal from the abdominal electrode with a center frequency slightly lower or higher than each participant's gastric frequency (±0.015 Hz, in steps of 0.005 Hz), and repeated the same PAC analysis. Clusters obtained with a slight offset from gastric frequency showed much smaller summary statistics, that decreased and became non-significant as the distance from the original EGG frequency increased. To determine if coupling between MEG power and EGG phase was sensitive to the individual alpha peaking frequency of each participant (10.35 Hz±0.13, range 9.6–11.6 Hz), we recomputed the sensor-level statistics after aligning to each participant's alpha peak. We found that this did not modify the results (two significant bilateral clusters, sum(t)=44.33, 34.16, MonteCarlo p=0.0020, 0.0064, with a similar topography). Individual phase-amplitude profiles of a subsample of participants (participants with largest, median and smallest MI) are plotted in Fig. 1f. Those profiles show that gastric-alpha coupling seem to involve both 1:1 and higher coupling modes since the PAC profile may show consistent deviations from a sinusoidal fit (Fig. 1f, left).
We then determined explained variance, i.e. the proportion of spontaneous alpha fluctuations explained by gastric phase. The rationale for determining explained variance is described in Fig. 2 (see also Material and methods). It relies on the comparison between the variance of the original alpha amplitude envelope and the variance of the alpha amplitude envelope sorted by gastric phase. We found that in the significant clusters gastric phase accounted for 8.0±0.5% (range across participants: 4.4–12.1%) of the variance of alpha amplitude.
Control analyses
MI is in principle independent from power (Tort et al., 2010), but we nevertheless verified that gastric-alpha coupling was not driven by EGG nor alpha power. There was no significant correlation across participants between MI and 10–11 Hz power averaged across the significant clusters (Spearman ρ=0.24, p=0.35). EGG power did not correlate with MI either (Spearman ρ=−0.34, p=0.178). We also estimated the false positives that our statistical approach might generate. We tested whether any of the 1000 surrogate data sets created to estimate chance level could give rise to cluster statistics as large as those produced by original data. We did not find any surrogate data set where two clusters were as large as the two empirical clusters, thereby showing that the Monte-Carlo probability of obtaining the two empirical clusters by chance was smaller than 0.001. The probability of obtaining by chance a single cluster larger than one of the two original clusters was p=0.0053.
Gastric-alpha coupling occurs in parieto-occipital regions and right anterior insula
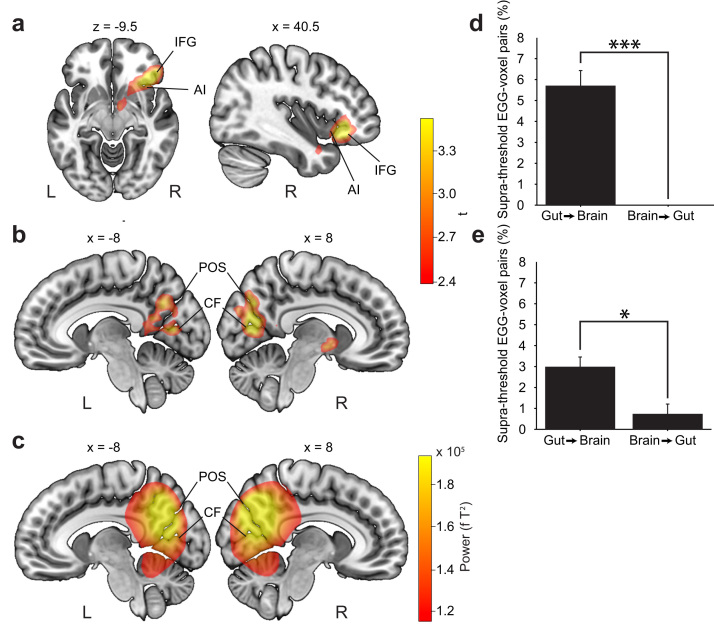
We then identified the cortical regions where significant gastric-alpha coupling takes place. We computed a time series of 10–11 Hz power per voxel per participant using a beamformer-based source localization, computed gastric-alpha coupling at each voxel using the MI and applied the same statistical approach as at the sensor level. Significant gastric-alpha coupling took place in two anatomical regions (Fig. 3 and Table 1). The posterior cluster (sum(t)=538.60, MonteCarlo p=0.014) comprised the parieto-occipital sulcus and calcarine fissure bilaterally. The anterior cluster (sum(t)=383.20, MonteCarlo p=0.044) was centered on the right anterior insula.
Fig. 3.
Localization and directionality of significant gastric-alpha coupling. (a) Anterior cluster, centered on the right anterior insula (AI) and inferior frontal gyrus (IFG). (b) Posterior cluster, encompassing the parieto-occipital sulcus (POS) and calcarine fissure (CF) bilaterally. (c) Source-localization of alpha power, centered on the parieto-occipital sulcus and calcarine fissure bilaterally. (d) Causal interaction between stomach and brain is greater in the stomach-to-brain direction (t(16)=7.98, p<10−5, corrected) in the right anterior insula. (e) Causal interaction between stomach and brain is greater in the stomach-to-brain direction (t(16)=3.07, p=0.015, corrected) in the posterior cluster.
Table 1.
Anatomical description of the regions involved in gastric-alpha coupling, based on Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002). Only areas with more than 1% of their volume involved are listed.
| Cluster / AAL region | Peak t | t/mm3 | mm3 | Percent activation | MNI |
||
|---|---|---|---|---|---|---|---|
| X | Y | Z | |||||
| Posterior | |||||||
| Right Calcarine | 5.21 | 3.59 | 3371 | 22.64 | 8 | −68 | 16 |
| Right Cuneus | 5.11 | 3.45 | 1396 | 12.25 | 12 | −68 | 20 |
| Right Precuneus | 4.91 | 3.26 | 1326 | 5.08 | 12 | −67 | 21 |
| Left Calcarine | 4.56 | 3.23 | 1854 | 10.26 | −8 | −72 | 20 |
| Left Cuneus | 4.41 | 3.13 | 1158 | 9.49 | −8 | −72 | 23 |
| Right Lingual Gyrus | 4.28 | 3.28 | 502 | 2.73 | 7 | −67 | 8 |
| Right Inferior Occipital Gyrus | 4.27 | 3.42 | 1528 | 19.31 | 44 | −76 | −4 |
| Right Middle Occipital Gyrus | 3.92 | 3.29 | 865 | 5.15 | 48 | −76 | 0 |
| Left Precuneus | 3.81 | 3.08 | 1825 | 6.47 | −4 | −67 | 28 |
| Left Superior Occipital Gyrus | 3.79 | 3.02 | 177 | 1.62 | −22 | −64 | 24 |
| Right Middle Temporal Gyrus | 3.77 | 3.13 | 401 | 1.14 | 44 | −73 | −3 |
| Anterior | |||||||
| Inferior Frontal Gyrus, Orbital part | 4.60 | 3.51 | 4423 | 32.39 | 36 | 28 | −8 |
| Right Insula | 4.55 | 3.23 | 1527 | 10.78 | 36 | 28 | −5 |
| Inferior Frontal Gyrus, Triangular part | 4.14 | 3.24 | 327 | 1.90 | 40 | 33 | −3 |
| Right Putamen | 3.52 | 2.99 | 372 | 4.37 | 25 | 22 | −8 |
| Temporal Pole, Superior Temporal Gyrus | 3.46 | 2.97 | 603 | 5.63 | 32 | 4 | −24 |
| Right Amygdala | 3.16 | 2.78 | 276 | 13.91 | 36 | 2 | −24 |
| Right Olfactory | 2.99 | 2.78 | 195 | 8.43 | 28 | 9 | −20 |
Directionality of interactions between stomach and brain
Lastly, we tested whether the stomach influenced the brain or vice-versa. Since the gastric rhythm is intrinsically generated in the stomach (Bozler, 1945, Suzuki et al., 1986, Sanders et al., 2014), we expected that the ascending direction, from stomach to brain, would predominate. We computed transfer entropy, a measure of directionality of information transfer, between the filtered EGG signal and amplitude envelope of the 10–11 Hz MEG signal, separately for the right anterior insula cluster and for the posterior parieto-occipital cluster. Information transfer was greatest from stomach to brain (Fig. 3) for both the parieto-occipital cluster (t(16)=3.07, p=0.015, Bonferroni corrected) and the anterior insula (t(16)=7.98, p<10−5, Bonferroni corrected).
Discussion
We show here that the temporal structure of large-scale spontaneous brain dynamics is coupled with gastric signals. Gastric-brain coupling was revealed by a modulation of the amplitude of the alpha rhythm by gastric phase, in the parieto-occipital sulcus and calcarine fissure bilaterally and in the right anterior insula. These results show that the basic rule linking the phase of slow rhythms with the amplitude of higher frequency rhythms, so far observed only within the brain (Bragin et al., 1995, Canolty et al., 2006, Schroeder and Lakatos, 2009, Buzsaki, 2010), can be extended to interactions between brain and viscera. 8% of spontaneous alpha fluctuations were explained by gastric phase, and gastric-alpha coupling appears to be driven by ascending signals from stomach to brain.
We found that the largest component of spontaneous brain activity, the alpha rhythm, is locked to gastric phase. The alpha rhythm is known to exert an inhibitory influence on spike-firing rate (Haegens et al., 2011) and has a versatile impact on perception, attention and memory (Palva and Palva, 2007, Jensen and Mazaheri, 2010, Klimesch, 2012). Given the wide range of perceptual and cognitive correlates of alpha oscillations, the gastric rhythm might impose a slow temporal constraint over a range of processes, including basic stimulus detection that displays slow fluctuations (Monto et al. 2008) in the gastric frequency range.
Interestingly, the parieto-occipital regions where we find gastric-alpha coupling are not only associated with alpha rhythm generation (Salmelin and Hari, 1994), but they are also deactivated in response to experimentally-induced mechanical distension of the stomach, which leads to conscious and sometimes painful stomach sensations (van Oudenhove et al., 2009). In addition, electrical intraperitoneal stimulation elicits a response in the monkey visual cortex during sleep (Pigarev, 1994, Pigarev et al., 2006). The right anterior insula is also activated during gastric distension (Mayer et al., 2009) and is linked to gastric frequency changes during disgust (Harrison et al., 2010). Those experiments, that involve active stimulation of the stomach or emotional challenges, reveal the existence of anatomical circuits relaying visceral information to cortical structures, including occipito-parietal regions and right anterior insula. Our results show that during resting-state, in the absence of active gastric stimulation but in the presence of the gastric basal rhythm that is continuously generated, this circuitry is functional: the alpha rhythm in parieto-occipital regions and right anterior insula is coupled to the stomach.
fMRI studies have underlined the importance of bodily signals such as cardiac activity, respiration and blood pressure fluctuations, during the resting-state. However in this literature bodily signals are most often considered as artifacts injecting non-neural influences on the BOLD signal (Glover et al., 2000, Birn et al., 2006, Shmueli et al., 2007, Murphy et al., 2013). Direct measures of cerebral electrical activity, such as MEG or EEG, although not immune to physiological artifacts (Dirlich et al., 1997, Kern et al., 2013) can better reveal the coupling between bodily signals and neural activity. For instance, the brain transiently responds to heartbeats (Schandry and Montoya, 1996, Kern et al., 2013, Park et al., 2014, Babo-Rebelo et al., 2016, Babo-Rebelo et al. in press). The link between those transient responses and the temporal structure of large-scale spontaneous brain activity is not yet known, although there are reported interactions between heart timing and stimulus processing (Birren et al., 1963, Elliott and Graf, 1972, Gray et al., 2009, Garfinkel et al., 2014).
Here, we show that gastric activity is directly coupled to spontaneous neural activity. The directionality analysis we performed indicates that the transfer of information is predominantly in the stomach-to-brain direction, congruent with the fact that the gastric basal rhythm is intrinsically generated in the stomach (Sanders et al., 2006). We thus propose that the stomach could be considered as an external oscillator constraining spontaneous fluctuations of brain activity. This implies that the temporal structure of spontaneous brain activity depends not only on neuron and network properties (Buzsaki and Draguhn, 2004, Deco et al., 2009, Petersen and Sporns, 2015), but also on a slow oscillator in the stomach wall. So-called "intrinsic" brain dynamics might thus be better understood, modeled and reproduced (Hyafil et al., 2015, Ponce-Alvarez et al., 2015) by including visceral generators of rhythmic activity acting as external oscillators coupled to the brain.
Author contributions
C.R., M.B.R. and C.T.B. designed the experiment; C.R. and M.B.R. acquired the data; C.R., D.S and C.T.B. analyzed the data; C.R., M.B.R., and C.T.B. wrote the paper.
Acknowledgments
We thank Patricia Wollstadt, Michael Wibral, Jan-Mathijs Schoffelen, Robert Oostenveld, and Adriano Tort for assistance with data analysis, Christophe Gitton and Antoine Ducorps for assistance with data acquisition and preprocessing. This work has received funding from Agence Nationale de la Recherche ANR-BLAN-BSH2-0002-01 and from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant agreement no 670325) to CTB, as well as from Agence Nationale de la Recherche ANR-10-LABX-0087 IEC and ANR-10-IDEX-0001-02 PSL.
Contributor Information
Craig G. Richter, Email: craiggrichter@gmail.com.
Catherine Tallon-Baudry, Email: catherine.tallon-baudry@ens.fr.
References
- Babo-Rebelo M., Richter C.G., Tallon-Baudry C. Neural responses to heartbeats in the default network encode the self in spontaneous thoughts. J. Neurosci. 2016;36:7829–7840. doi: 10.1523/JNEUROSCI.0262-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babo-Rebelo M., Wolpert N., Adam C., Hasboun D., Tallon-Baudry C., 2016. Is the cardiac monitoring function related to the self in both the default-network and right anterior insula? Phil. Trans. Roy. Soc. B. (in press). [DOI] [PMC free article] [PubMed]
- Bahramisharif A., van Gerven M.A., Aarnoutse E.J., Mercier M.R., Schwartz T.H., Foxe J.J., Ramsey N.F., Jensen O. Propagating neocortical gamma bursts are coordinated by traveling alpha waves. J. Neurosci. 2013;33:18849–18854. doi: 10.1523/JNEUROSCI.2455-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birren J.E., Phillips S.L., Cardon P.V. Reaction time as a function of cardiac cycle in young adults. Science. 1963;140:195–196. doi: 10.1126/science.140.3563.195-a. [DOI] [PubMed] [Google Scholar]
- Birn R.M., Diamond J.B., Smith M.A., Bandettini P.A. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage. 2006;31:1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Bozler E. The action potentials of the stomach. Am. J. Physiol. 1945;144:693–700. doi: 10.1152/ajplegacy.1955.182.1.92. [DOI] [PubMed] [Google Scholar]
- Bragin A., Jando G., Nadasdy Z., Hetke J., Wise K., Buzsaki G. Gamma (40–100 Hz) oscillation in the Hippocampus of the behaving Rat. J. Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G. Neural syntax: cell assemblies, synapsembles, and readers. Neuron. 2010;68:362–385. doi: 10.1016/j.neuron.2010.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G., Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Canolty R.T., Edwards E., Dalal S.S., Soltani M., Nagarajan S.S., Kirsch H.E., Berger M.S., Barbaro N.M., Knight R.T. High gamma power is phase-locked to theta oscillations in human neocortex. Science. 2006;313:1626–1628. doi: 10.1126/science.1128115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.D., Zou X., Lin X., Ouyang S., Liang J. Detection of gastric slow wave propagation from the cutaneous electrogastrogram. Am J Physiol. 1999;277:424–430. doi: 10.1152/ajpgi.1999.277.2.G424. [DOI] [PubMed] [Google Scholar]
- Critchley H.D., Harrison N.A. Visceral influences on brain and behavior. Neuron. 2013;77:624–638. doi: 10.1016/j.neuron.2013.02.008. [DOI] [PubMed] [Google Scholar]
- Deco G., Jirsa V., McIntosh A.R., Sporns O., Kotter R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. USA. 2009;106:10302–10307. doi: 10.1073/pnas.0901831106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dirlich G., Vogl L., Plaschke M., Strian F. Cardiac field effects on the EEG. Electroencephalogr. Clin. Neurophysiol. 1997;102:307–315. doi: 10.1016/s0013-4694(96)96506-2. [DOI] [PubMed] [Google Scholar]
- Elliott R., Graf V. Visual sensitivity as a function of phase of cardiac cycle. Psychophysiology. 1972;9:357–361. doi: 10.1111/j.1469-8986.1972.tb03219.x. [DOI] [PubMed] [Google Scholar]
- Florin E., Baillet S. The brain's resting-state activity is shaped by synchronized cross-frequency coupling of neural oscillations. Neuroimage. 2015;111:26–35. doi: 10.1016/j.neuroimage.2015.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furness J.B., Rivera L.R., Cho H.J., Bravo D.M., Callaghan B. The gut as a sensory organ. Nat. Rev. Gastroenterol. Hepatol. 2013;10:729–740. doi: 10.1038/nrgastro.2013.180. [DOI] [PubMed] [Google Scholar]
- Garfinkel S.N., Minatti L., Gray M.A., Seth A.K., Dolan R.J., Critchley H.D. Fear from the heart: sensitivity to fear stimuli depends on individual heartbeats. J. Neurosci. 2014;34:6573–6582. doi: 10.1523/JNEUROSCI.3507-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover G.H., Li T.Q., Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn. Reson. Med. 2000;44:162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Gray M.A., Rylander K., Harrison N.A., Wallin B.G., Critchley H.D. Following one's heart: cardiac rhythms gate central initiation of sympathetic reflexes. J. Neurosci. 2009;29:1817–1825. doi: 10.1523/JNEUROSCI.3363-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haegens S., Nacher V., Luna R., Romo R., Jensen O. alpha-Oscillations in the monkey sensorimotor network influence discrimination performance by rhythmical inhibition of neuronal spiking. Proc. Natl. Acad. Sci. USA. 2011;108:19377–19382. doi: 10.1073/pnas.1117190108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison N.A., Gray M.A., Gianaros P.J., Critchley H.D. The embodiment of emtional feelings in the brain. J. Neurosci. 2010;30:12878–12884. doi: 10.1523/JNEUROSCI.1725-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyafil A., Giraud A.L., Fontolan L., Gutkin B. Neural cross-frequency coupling: connecting architectures, mechanisms, and functions. Trends Neurosci. 2015;38:725–740. doi: 10.1016/j.tins.2015.09.001. [DOI] [PubMed] [Google Scholar]
- Ito S. Visceral region in the rat primary somatosensory cortex identified by vagal evoked potential. J. Comp. Neurol. 2002;444:10–24. doi: 10.1002/cne.10120. [DOI] [PubMed] [Google Scholar]
- Jensen O., Mazaheri A. Shaping functional architecture by oscillatory alpha activity: gating by inhibition. Front. Hum. Neurosci. 2010;4:186. doi: 10.3389/fnhum.2010.00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern M., Aertsen A., Schulze-Bonhage A., Ball T. Heart cycle-related effects on event-related potentials, spectral power changes, and connectivity patterns in the human ECoG. Neuroimage. 2013;81C:178–190. doi: 10.1016/j.neuroimage.2013.05.042. [DOI] [PubMed] [Google Scholar]
- Klimesch W. alpha-band oscillations, attention, and controlled access to stored information. Trends Cogn. Sci. 2012;16:606–617. doi: 10.1016/j.tics.2012.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch K.L., Stern R.M. Handbook of Electrogastrography. Oxford University Press; Oxford: 2004. [Google Scholar]
- Lindner M., Vicente R., Priesemann V., Wibral M. TRENTOOL: a Matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011;12:119. doi: 10.1186/1471-2202-12-119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maris E., Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J. Neurosci. Methods. 2007;164:177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- Mayer E.A. Gut feelings: the emerging biology of gut-brain communication. Nat. Rev. Neurosci. 2011;12:453–466. doi: 10.1038/nrn3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer E.A., Aziz Q., Coen S., Kern M., Labus J.S., Lane R., Kuo B., Naliboff B., Tracey I. Brain imaging approaches to the study of functional GI disorders: a Rome working team report. Neurogastroenterol. Motil. 2009;21:579–596. doi: 10.1111/j.1365-2982.2009.01304.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monto S., Palva S., Voipio J., Palva J.M. Very slow EEG fluctuations predict the dynamics of stimulus detection and oscillation amplitudes in humans. J. Neurosci. 2008;28:8268–8272. doi: 10.1523/JNEUROSCI.1910-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K., Birn R.M., Bandettini P.A. Resting-state fMRI confounds and cleanup. Neuroimage. 2013;80:349–359. doi: 10.1016/j.neuroimage.2013.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oostenveld R., Fries P., Maris E., Schoffelen J.M. FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011;2011:156869. doi: 10.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osipova D., Hermes D., Jensen O. Gamma power is phase-locked to posterior alpha activity. PLoS One. 2008;3:e3990. doi: 10.1371/journal.pone.0003990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palva J.M., Palva S., Kaila K. Phase synchrony among neuronal oscillations in the human cortex. J. Neurosci. 2005;25:3962–3972. doi: 10.1523/JNEUROSCI.4250-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palva S., Palva J.M. New vistas for alpha-frequency band oscillations. Trends Neurosci. 2007;30:150–158. doi: 10.1016/j.tins.2007.02.001. [DOI] [PubMed] [Google Scholar]
- Park H.D., Correia S., Ducorps A., Tallon-Baudry C. Spontaneous fluctuations in neural responses to heartbeats predict visual detection. Nat. Neurosci. 2014;17:612–618. doi: 10.1038/nn.3671. [DOI] [PubMed] [Google Scholar]
- Petersen C.C., Sporns O. Brain networks and cognitive architectures. Neuron. 2015;88:207–219. doi: 10.1016/j.neuron.2015.09.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigarev I., Almirall H., Pigareva M.L., Bautista V., Sanchez-Bahillo A., Barcia C., Herrero M.T. Visceral signals reach visual cortex during slow wave sleep: study in monkeys. Acta Neurobiol. Exp. 2006;66:69–73. doi: 10.55782/ane-2006-1588. [DOI] [PubMed] [Google Scholar]
- Pigarev I.N. Neurons of visual cortex respond to visceral stimulation during slow wave sleep. Neuroscience. 1994;62:1237–1243. doi: 10.1016/0306-4522(94)90355-7. [DOI] [PubMed] [Google Scholar]
- Ponce-Alvarez A., Deco G., Hagmann P., Romani G.L., Mantini D., Corbetta M. Resting-state temporal synchronization networks emerge from connectivity topology and heterogeneity. PLoS Comput. Biol. 2015;11:e1004100. doi: 10.1371/journal.pcbi.1004100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powley T.L., Phillips R.J. Vagal intramuscular array afferents form complexes with interstitial cells of Cajal in gastrointestinal smooth muscle: analogues of muscle spindle organs? Neuroscience. 2011;186:188–200. doi: 10.1016/j.neuroscience.2011.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragwitz M., Kantz H. Markov models from data by simple nonlinear time series predictors in delay embedding spaces. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:056201. doi: 10.1103/PhysRevE.65.056201. [DOI] [PubMed] [Google Scholar]
- Riezzo G., Russo F., Indrio F. Electrogastrography in adults and children: the strength, pitfalls, and clinical significance of the cutaneous recording of the gastric electrical activity. Biomed. Res. Int. 2013;2013:282757. doi: 10.1155/2013/282757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux F., Wibral M., Singer W., Aru J., Uhlhaas P.J. The phase of thalamic alpha activity modulates cortical gamma-band activity: evidence from resting-state MEG recordings. J. Neurosci. 2013;33:17827–17835. doi: 10.1523/JNEUROSCI.5778-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salmelin R., Hari R. Characterization of spontaneous MEG rhythms in healthy adults. Electroencephalogr. Clin. Neurophysiol. 1994;91:237–248. doi: 10.1016/0013-4694(94)90187-2. [DOI] [PubMed] [Google Scholar]
- Sanders K.M., Koh S.D., Ward S.M. Interstitial cells of Cajal as pacemakers in the gastrointestinal tract. Annu. Rev. Physiol. 2006;68:307–343. doi: 10.1146/annurev.physiol.68.040504.094718. [DOI] [PubMed] [Google Scholar]
- Sanders K.M., Ward S.M., Koh S.D. Interstitial cells: regulators of smooth muscle function. Physiol. Rev. 2014;94:859–907. doi: 10.1152/physrev.00037.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schandry R., Montoya P. Event-related brain potentials and the processing of cardiac activity. Biol. Psychol. 1996;42:75–85. doi: 10.1016/0301-0511(95)05147-3. [DOI] [PubMed] [Google Scholar]
- Schroeder C.E., Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K., van Gelderen P., de Zwart J.A., Horovitz S.G., Fukunaga M., Jansma J.M., Duyn J.H. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. Neuroimage. 2007;38:306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki N., Prosser C.L., Dahms V. Boundary cells between longitudinal and circular layers - essential for electrical slow waves in cat intestine. Am. J. Physiol. 1986;250:G287–G294. doi: 10.1152/ajpgi.1986.250.3.G287. [DOI] [PubMed] [Google Scholar]
- Tort A.B., Komorowski R., Eichenbaum H., Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J. Neurophysiol. 2010;104:1195–1210. doi: 10.1152/jn.00106.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- van Oudenhove L., Vandenberghe J., Dupont P., Geeraerts B., Vos R., Bormans G., van Laere K., Fischler B., Demyttenaere K., Janssens J., Tack J. Cortical deactivations during gastric fundus distension in health: visceral pain-specific response or attenuation of 'default mode' brain function? A H2 15O-PET study. Neurogastroenterol. Motil. 2009;21:259–271. doi: 10.1111/j.1365-2982.2008.01196.x. [DOI] [PubMed] [Google Scholar]
- Vicente R., Wibral M., Lindner M., Pipa G. Transfer entropy--a model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011;30:45–67. doi: 10.1007/s10827-010-0262-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinck M., van Wingerden M., Womelsdorf T., Fries P., Pennartz C.M. The pairwise phase consistency: a bias-free measure of rhythmic neuronal synchronization. Neuroimage. 2010;51:112–122. doi: 10.1016/j.neuroimage.2010.01.073. [DOI] [PubMed] [Google Scholar]
- Weaver K.E., Wander J.D., Ko A.L., Casimo K., Grabowski T.J., Ojemann J.G., Darvas F. Directional patterns of cross frequency phase and amplitude coupling within the resting state mimic patterns of fMRI functional connectivity. Neuroimage. 2016;128:238–251. doi: 10.1016/j.neuroimage.2015.12.043. [DOI] [PMC free article] [PubMed] [Google Scholar]