Is the Bifactor Model a Better Model or is it Just Better at Modeling Implausible Responses? Application of Iteratively Reweighted Least Squares to the Rosenberg Self-Esteem Scale

Abstract

Although the structure of the Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965) has been exhaustively evaluated, questions regarding dimensionality and direction of wording effects continue to be debated. To shed new light on these issues, we ask: (1) for what percentage of individuals is a unidimensional model adequate, (2) what additional percentage of individuals can be modeled with multidimensional specifications, and (3) what percentage of individuals respond so inconsistently that they cannot be well modeled? To estimate these percentages, we applied iteratively reweighted least squares (IRLS; Yuan & Bentler, 2000) to examine the structure of the RSES in a large, publicly available dataset. A distance measure, d_s, reflecting a distance between a response pattern and an estimated model, was used for case weighting. We found that a bifactor model provided the best overall model fit, with one general factor and two wording-related group factors. But, based on d_r values, a distance measure based on individual residuals, we concluded that approximately 86% of cases were adequately modeled through a unidimensional structure, and only an additional 3% required a bifactor model. Roughly 11% of cases were judged as “unmodelable” due to their significant residuals in all models considered. Finally, analysis of d_s revealed that some, but not all, of the superior fit of the bifactor model is owed to that model’s ability to better accommodate implausible and possibly invalid response patterns, and not necessarily because it better accounts for the effects of direction of wording.

Self-report personality and psychopathology measures designed to assess a single construct commonly include items that are written in both positive and negative directions. Among many possible examples, the Life Orientation Test Revised (LOT-R; Scheier, Carver, & Bridges, 1994) contains statements confirming optimism (“I'm always optimistic about my future”) and pessimism (“I hardly ever expect things to go my way”). The Penn State Worry Questionnaire (Meyer, Miller, Metzger, & Borkovec, 1990) includes items confirming anxious experiences (“My worries overwhelm me”) and denying such experiences (“I do not tend to worry about things”). Finally, the Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965), includes positive self-appraisals (“I feel that I have a number of good qualities”) and negative self-evaluations (“I certainly feely useless at times”). In such instruments, negatively-worded items are routinely reverse scored and summed with positively-worded items when computing scale scores.

Researchers commonly believe that, if all questions on a self-report measure are stated in the positive direction, response artifacts, such as response acquiescence, will occur and potentially invalidate test scores. Certainly, if only positively-worded items are included in a scale, trait-related and acquiescence-related variance cannot be distinguished. Having items that are both positively and negatively worded should at least partially mitigate the potentially invalidating effects of acquiescence (Hinz, Michalski, Schwarz, & Herzberg, 2007). The practice of routinely including items worded in a negative direction is not without controversy, however. Whereas some believe that including negatively-worded items can be important for construct validity (Kam & Meyer, 2015), others argue that it causes unwanted nuisance variance and thus detracts from construct validity (van Sonderen, Sanderman, & Coyne, 2013; Wong, Rindfleisch, & Burroughs, 2003; Woods, 2006; Zhang, Noor, & Savalei, 2016).

Given these opposing views, it is not surprising that, for instruments that include positively- and negatively-worded items, confirmatory factor analysis (CFA) has been used extensively to clarify the underlying factor structure and to ostensibly address the magnitude of direction of wording effects. In the following section, we briefly review the CFA literature for the RSES. We then outline the goals and motivations underlying the present study.

The Structure of the Rosenberg Self-Esteem Scale (RSES)

Item content for the RSES is shown in the top portion of Table 1. The RSES has five positively-worded items (items 1, 2, 4, 6, and 7), as well as five negatively-worded items (items 3, 5, 8, 9, and 10). A wealth of confirmatory factor analytic research has been conducted on the RSES in a variety of diverse samples. Much of this CFA model fit “beauty contest” literature is easy to summarize. Almost universally, researchers find that a multidimensional model with two correlated factors (representing direction of wording) fits better than a “straw man” one-factor (or unidimensional) model (see Huang & Dong, 2012, for meta-analytic review). Significant debate continues, however, on whether those two factors represent distinct but highly correlated substantive dimensions of positive and negative self-appraisal (Goldsmith, 1986; Horan, DiStefano, & Motl, 2003; Kaplan & Pokorny, 1969; Michaelides, Koutsogiorgi, & Panayiotou, 2016; Owens, 1993, 1994) or are merely a direction of wording method artifact (Marsh, 1996; Tomas & Oliver, 1999) that needs to be controlled for.

Table 1.

Item Content and Descriptive Statistics for the Rosenberg Self-Esteem Scale (N = 46,546)

I feel that I am a person of worth, at least on an equal plane with others. I feel that I have a number of good qualities. All in all, I am inclined to feel that I am a failure. (R) I am able to do things as well as most other people. I feel I do not have much to be proud of. (R) I take a positive attitude toward myself. On the whole, I am satisfied with myself. I wish I could have more respect for myself. (R) I certainly feel useless at times. (R) At times I think I am no good at all. (R)

				Response Option %
Item	r.drop	M	SD	1	2	3	4
1	.70	3.0	0.86	.06	.18	.44	.32
2	.67	3.1	0.79	.04	.13	.50	.33
4	.59	2.9	0.81	.05	.21	.50	.24
6	.75	2.6	0.92	.14	.33	.37	.17
7	.74	2.4	0.93	.18	.34	.35	.14
3(R)	.73	2.7	0.95	.13	.28	.37	.22
5(R)	.69	2.6	0.98	.14	.32	.32	.22
8(R)	.54	2.3	0.96	.21	.41	.24	.14
9(R)	.69	2.2	0.99	.27	.40	.20	.14
10(R)	.74	2.4	1.07	.24	.33	.22	.22

Note. (R) indicates reverse worded and scored. r.drop is the item-total correlation excluding the item. Coefficient alpha = .91. Total score mean = 26.30 (sd = 6.98). Mean for positive items = 14.05 (sd = 3.52). Mean for negative items = 12.24 (sd = 3.97). Correlation among positively worded items = .58; Correlation among negatively worded items = .55.

To further explore whether the RSES should be interpreted as two content factors, or two “direction of wording” factors, Greenberger, Chen, Dmitrieva, and Farruggia (2003) created two alternative versions of the RSES, one with all items written in a positive direction and one with all items written in the negative direction. Findings indicated that, for the original RSES, a two-factor model significantly improved chi-square as well as other practical fit indices relative to a one-factor model. In the “all positively worded” and “all negatively worded” alternative versions, chi-square did not significantly improve going from a one-factor to a two-factor model. Such results strongly suggest that the RSES is unidimensional, but direction of wording effects lead to or create multidimensionality. A critical question then becomes: To what degree does that multidimensionality in the original RSES interfere with our ability to score individuals on a single scale?

One approach to addressing that question is to use a bifactor structural representation where the general factor represents the substantive trait and the group factors represent method artifacts associated with item wording (see Hyland, Boduszek, Dhingra, Shevlin, & Egan, 2014; McKay, Boduszek, & Harvey, 2014; Sharratt, Boduszek, Jones, & Gallagher, 2014). These studies suggest that the RSES is essentially unidimensional once controlling for the effects of direction of wording (e.g., Donnellan, Ackerman, & Brecheen, 2016); moreover, problems appear localized to the negatively-worded items (Corwyn, 2000; Marsh, 1996). For example, based on longitudinal analysis, Marsh, Scalas, and Nagengast (2010) concluded that RSES responses reflect one single substantive trait and two response style or methodological factors.

Present Study: Goals and Motivations

Model comparison research is critically important, and its value will not be debated here. However, we do have concerns about the informativeness of model comparison research as currently conducted for applied researchers. Regardless of terminology used, a fit contest among plausible measurement models (e.g., unidimensional, correlated factors, second-order, bifactor) assumes that all persons belong to a homogeneous population for which a particular model applies¹ (i.e., is generating the data), and that some collection of fit indices can definitively adjudicate which is the “correct” model in the population based on sample data.

Our concerns with such SEM fit contests are several. One major concern is that, unless data are perfectly consistent with a model (i.e., no cross-loadings, correlated residuals, one indicator causing another indicator), fit indices will be biased toward the model with more parameters (i.e., the less constrained model). Murray and Johnson (2013), for example, provided a demonstration of why the bifactor model fits better than the second-order model if there are any so-called “unmodeled complexities” (i.e., cross-loadings, correlated residuals). We believe that a more complex model should only be “accepted” if it is needed to model plausible, interpretable, and scorable item response patterns that cannot otherwise be accounted for by a more constrained model; more complex models, such as the bifactor, should not be accepted merely because they have a high fitting propensity (Preacher, 2006), even to nonsensical response patterns.

Given this concern, we argue that a complimentary method of studying the relative viability of alternative measurement models, and to study direction of wording effects in particular, is to use a robust² factor analytic method, and to make better use of measures that index model fit at the individual level. Robust methods are needed to obtain more accurate estimates of population parameters; this is especially true in studies like the present investigation that are based on internet data, in which there is reason to suspect that there may be a sizable number of questionable response patterns. Individual-fit measures, we argue, are needed to better illuminate why more complex models are fitting better and for whom, questions that are seldom, if ever, asked in traditional fit contest research.

Thus, herein, we apply an iteratively reweighted least squares (IRLS; Yuan & Bentler, 2000) factor analytic methodology to study the latent structure and direction of wording effects in a large, publicly available set of responses to the Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965). One of the goals of this article is to introduce some key features of IRLS estimation to a broader audience. To our knowledge, IRLS has never been operationalized in any software or applied beyond the original Yuan and Bentler (2000) small sample examples and in Yuan and Zhong (2008).

This research is not a technical exposé or empirical exploration of IRLS however, a topic we are covering in depth elsewhere. Rather, the primary goal of this research is to use IRLS as a robust estimation tool, in particular as a tool for better understanding direction of wording effects on a popular assessment instrument. We argue that researchers testing whether an instrument such as the RSES is best represented with a one-factor, two-factor, or bifactor model are not necessarily asking the most useful questions. An alternative, perhaps more informative set of questions are: (1) for what percentage of individuals is a unidimensional model adequate, (2) what additional percentage of individuals can be modeled with multidimensional specifications, and (3) what percentage of individuals respond so inconsistently that they cannot be modeled well using any reasonable model? In what follows, we hope to demonstrate that techniques such as IRLS, combined with analyses of individual-level distance measures, allows researchers to study these latter, critical issues.

Present Data

The RSES data used in the present research were downloaded from the http://personality-testing.info/_rawdata/ webpage. According the website, “Users were informed at the beginning of the test that there [sic] answers would be used for research and were asked to confirm that their answers were accurate and suitable for research upon completion (those that did not have been removed from these datasets).” The original data contained 47,974 individual response vectors with three demographic variables: age, gender, and country of origin. Because of the large sample size, for ease of analysis we deleted 1,428 individuals with missing item response data. This left the analysis sample size at N = 46,546.

Descriptive statistics for the analysis sample are displayed in the bottom portion of Table 1. Item-test score correlations (corrected) were above .67, with the exceptions of Item 8 (.54) and Item 4 (.59); Item 4 is vague due to the use of the word “things”, and Item 8 is confusing for anyone who already has a sufficient amount of self-respect and doesn’t necessarily need or desire more. All reverse-worded items (3, 5, 8, 9, 10) had lower means and greater variance relative to the positively worded items (1, 2, 4, 6, 7). Interestingly, items 1 and 2 (two highly correlated positively-worded items) attracted few responses in categories 1 and 2. Just the opposite occurred for items 7 and 8 (two highly correlated negatively-worded items). The mean raw score was 26.29 (on a scale from 10 to 40) with standard deviation 6.98, skewness was < 0.01, and kurtosis 2.31. Coefficient alpha internal consistency was .91. Finally, considering just the five positively-worded items, the average item inter-correlation was .58 and alpha was .87; considering just the five negatively-worded items, the average item inter-correlation was .55 and alpha was .86.

ML and ADF Factor Analysis

To place the present data in the context of previous factor analytic work, our first step in exploring the structure of the RSES was to estimate confirmatory factor models using maximum likelihood (ML) and asymptotically distribution free (ADF; Browne, 1984) estimation methods. The following models were estimated: (a) a 1-factor (unidimensional) model with all items loading on a single factor; (b) a 2-factor model allowing the factors to correlate, and with each factor containing only the positively- and negatively-worded items, respectively; and (c) a bifactor model with all items loading on the general factor, and group factors corresponding to direction of wording. Models were evaluated through inspection of loadings and statistical indices of fit including: chi-square and chi-square difference tests, Tucker Lewis Index (TLI), root mean square error of approximation (RMSEA), standardized root mean residual (SRMR), and the Bayesian Information Criterion (BIC).

Although not technically appropriate for 4-option ordinal indicators³, ML estimation was applied because this method is by far the most commonly used in the RSES confirmatory factor analysis literature (typically with robust estimation of standard errors and adjusted fit indices). As is well known, ML estimation assumes multivariate normality in order to properly interpret fit indices. ADF was applied because it does not require any distributional assumptions, and it forms the mathematical basis and starting values for IRLS, to be described shortly.

A contentious issue in the RSES CFA literature is the inclusion of correlated errors in confirmatory models. Many researchers do not report or model correlated errors (without a substantive basis) and they justify this practice based on recommendations given by Bollen (1989) and Brown (2006). Bollen and Brown were concerned that researchers would haphazardly improve model fit through freeing up parameters (e.g., correlated residuals, cross-loadings) that, in turn, may not be replicable or theoretically meaningful.

On the other hand, it is well known that failure to model correlated residuals can lead to biased estimates of factor loadings and a distorted view of the factor structure (e.g., D. A. Cole, Ciesla, & Steiger, 2007). Correlated residuals are especially problematic in personality measures where the use of questions that are semantically similar is endemic. Such items tend to be correlated not only because they share a common latent variable, but also because they are asking essentially the same thing twice. We thus argue that in detailed model explorations such as the present research, identifying and modeling sizable correlated residuals is critically important. The main reasons are: (1) with the present large sample size, replication is not a concern, (2) estimation of major correlated residuals allows for the loadings to be more accurately estimated and ultimately a fairer test of competing models, and most importantly (3) accurate parameter estimates are paramount to the accuracy of the distance statistics we plan to compute.

Using a variety of methods including hierarchical clustering, fitting item response theory models and inspecting local independence violations, and using a variety of estimators for confirmatory models and subsequently inspecting modification indices, we concluded the following with respect to the RSES data. There are three item pairs that stand out in terms of correlated residuals, at least with respect to a unidimensional model. In order of magnitude, these are items 9 and 10, 1 and 2, and to a lesser degree, items 6 and 7. Inspection of content provides some clues as to what may be occurring. Items 9 and 10 are reverse worded, are the last two items responded to, and include the phrase “at times”. Items 1 and 2 are the first two items responded to, are both positively worded, and include the common phrase “I feel that”. Items 6 and 7 are positively worded and both refer to a positive overall evaluation of the self.

Results of the ML analyses are reported in the upper left hand panel of Table 2 with fit indices reported in Table 3. All fit indices suggest that, as expected, the two-factor model is superior to the one-factor model and the bifactor model is the best fitting of the three. In the unidimensional model, all items appear to have reasonable loadings, and the correlated residuals are small but significant. In the two-factor model, the correlation between the factors is .90, a value high enough to suggest at least “essential” unidimensionality to many researchers.

Table 2.

Standardized Loadings for Unidimensional, Correlated Factors, and Bifactor Models Under Maximum Likelihood (ML), Asymptotic Distribution Free (ADF), and Iteratively Reweighted Least Squares (IRLS) d_s

	ML						ADF
Item	1-Factor	2-Factor		Bifactor			1-Factor	2-Factor		Bifactor
	λ1	λ1	λ2	λGen	λGrp1	λGrp2	λ1	λ1	λ2	λGen	λGrp1	λGrp2
1	.72	.76		.71	.43		.75	.76		.72	.42
2	.68	.72		.67	.51		.72	.72		.68	.50
4	.62	.65		.59	.33		.64	.65		.60	.31
6	.78	.80		.86			.84	.85		.86
7	.76	.78		.84			.82	.83		.84
3 (R)	.78		.80	.71		.35	.80		.81	.72		.34
5 (R)	.74		.76	.67		.33	.76		.77	.68		.32
8 (R)	.57		.58	.53		.26	.61		.61	.53		.30
9 (R)	.70		.72	.62		.41	.73		.74	.62		.45
10 (R)	.75		.77	.68		.38	.78		.79	.68		.41
ϕ		.90						.89
θ9.10	.22	.18			.16		.17	.16			.13
θ1.2	.20	.15					.13	.13
θ6.7	.14	.11					−.02	−.02
ECV					.80						.80
ω					.93						.93
ωH					.84						.85
	IRLS ds
	1-Factor	2-Factor		Bifactor
	λ1	λ1	λ2	λGen	λGrp1	λGrp2
1	.77	.77		.74	.41
2	.73	.73		.70	.48
4	.67	.67		.62	.29
6	.86	.87		.87
7	.84	.85		.85
3 (R)	.82		.83	.78		.27
5 (R)	.79		.79	.75		.25
8 (R)	.63		.64	.58		.29
9 (R)	.74		.76	.68		.42
10 (R)	.79		.80	.73		.38
ϕ		.92
θ9.10	.17	.15			.11
θ1.2	.14	.13
θ6.7	−.02	−.02
ECV					.84
ω					.94
ωH					.88

Note. ECV is explained common variance, λ is factor loading on the first (1), second (2), general (Gen), or first or second group (Grp1, Grp2) factor, ϕ is factor correlation, θ_a.b is residual correlation between items a and b, d_s is implausibility” distance, ω is model-based composite reliabilty and ω_H is composite reliability based on general factor.

Table 3.

Model Fit Statistics Under Four Estimators: Maximum Likelihood (ML), Asymptotic Distribution Free (ADF), Iteratively Reweighted Least Squares (IRLS) d_s, and IRLS d_r

Model	χ2	df	${\chi }_{\mathit{\text{baseline}}}^2$	dfbaseline	TLI	RMSEA	SRMR	BIC	W-BIC
ML
1-Factor	9041	32	265659	45	.952	.078	.038	989686
2-Factors	5330	31	265659	45	.971	.061	.028	985986
Bifactor	3273	26	265659	45	.979	.052	.021	983981
ADF
1-Factor	5591	32	46850	45	.833	.061	.072	999890
2-Factors	4385	31	46850	45	.865	.055	.050	990522
Bifactor	2272	26	46850	45	.917	.043	.021	984677
IRLS ds
1-Factor	7120	32	49599	45	.799	.070	.039	1010039	849889
2-Factors	5352	31	50145	45	.846	.062	.035	999038	844502
Bifactor	3175	26	50529	45	.892	.052	.027	992076	839870

Note. W-LogL is the weighted log-likelihood, W-BIC is the weighted Bayesian information criterion, d_s is “implausibility” distance.

^*Indicates lowest value of BIC or W-BIC.

Finally, in the bifactor model, all items continue to have reasonable loadings on the general factor, but the loadings are reduced relative to the unidimensional model. We could not estimate a bifactor model in which items 6 and 7 loaded on a group factor (consistent with other studies, small negative loadings occurred indicating a poor solution), and thus group factor 1 is marked by only 3 items with modest loadings. We also could not estimate a bifactor model that included a correlated residual between items 1 and 2, and thus that was set to zero; the correlated residual between items 6 and 7 was very small and was subsequently eliminated from the model. The second group factor contains small loadings for items 3, 5, and 8, and modest loadings for items 9 and 10. The correlated residual between items 9 and 10 was .16.

Most importantly, the explained common variance (ECV) in the bifactor model was .80, indicating that 80% of the common variance is attributable to the general factor (20% of the common variance is due to group factors). Coefficient omega (ω; McDonald, 1999) was .93 suggesting that a unit-weighted multidimensional composite is very reliable, but coefficient omega hierarchical ω_h (Zinbarg, Revelle, Yovel, & Li, 2005) is .84. This indicates that 84% of the variance in unit-weighted RSES composite raw scores can be attributable to the general factor, and 84/93 = 90% of the reliable variance in RSES composite scores is attributable to the general factor.

Results for the ADF estimation are shown in the upper right panel of Table 2 and fit indices are shown in Table 3. As for the ML estimator, a two-factor model is superior to the one-factor model, and the bifactor model provides the best fit. Judging by the loadings, there do not appear to be any major differences of note between the ML and ADF solutions. If anything, the factor loadings are slightly higher in the ADF solution for most items, but on the other hand, the correlated residual estimates are lower in ADF than ML. Results in terms of ECV, ω and ω_H are also highly similar. At the very least, these results assure us that ADF, which is the basis of IRLS as implemented here, is leading to results highly consistent with the ML results, and thus our findings with ADF are comparable to the vast majority of the RSES literature which used ML.

Iteratively Reweighted Least Squares Factor Analysis

Iteratively reweighted least squares (IRLS; Yuan & Bentler, 2000) is a robust estimation algorithm comparable to the asymptotic distribution free (ADF; Browne, 1984) method. During IRLS estimation, each case is weighted according to its deviance from the estimated model, such that cases that deviate substantially from a model are down-weighted during estimation. In what follows, we borrow heavily from the notation and description provided in Yuan and Bentler (2000). We describe IRLS in terms of a unidimensional model fitted to the 10-item RSES which contains 4-point items. Although the data are ordinal, in ADF/IRLS the item response data must be considered continuous. We use the IRLS framework of Yuan and Bentler (2000), which was derived from ADF estimation, instead of the maximum likelihood procedures described in Yuan and Zhong (2008), to account for the non-normality in the ordinal item responses.

Define µ(θ) and Σ(θ) as model-implied mean vector and covariance matrix under the structured model, in this case the unidimensional model, then,

$${\zeta }_i=\left(\begin{array}{c}\mu (\theta )\\ \mathit{\text{vech}}[\mathrm{\Sigma }(\theta )+\mu (\theta ){\mu }^T(\theta )]\end{array}\right),\dot{\zeta }=\partial \zeta /\partial {\theta }^T,$$ (1)

$$Z_i={(X_i^T,{\mathit{\text{vech}}}^T(X_i{X}_i^T))}^T.$$ (2)

For p = 10, the number of items, the dimension of Z_i is p_z = p + p(p + 1)/2 = 65 (the number of means and unique elements in the variance-covariance matrix of X), and let q = 30 (the number of model parameters: 10 means, 10 loadings, and 10 uniquenesses).

One way to describe ADF/IRLS estimation is to say that the objective is to find a set of estimated model parameters that solve Equation 1.

$${\mathrm{\Sigma }}_i^n{\dot{\zeta }}^T(\theta )W_i(Z_i-\zeta (\theta ))=0.$$ (3)

where the matrix of partial derivatives ζ in Equation 3 is 65×30 and the weight matrix W used in estimation is 65×65. Because of the size of this latter matrix, and because it contains potentially inaccurate estimates of 4^th order sample moments, ADF/IRLS is generally not recommended in small samples. Finally, Equation 2 contains each person’s response pattern and the non-redundant cross-products of item scores which, in turn, represent an individual’s contribution to the (reproduced) mean vector and variance-covariance matrix.

In Equation 3, if the weight matrix is defined as the inverse of the sample variance-covariance matrix of Z $\left(W_i=S_z^{-1}\right)$, then Equation 3 is an ADF estimator. More precisely, an ADF estimator defines a weight matrix W that is constant for all individuals and, thus, does not weight W by a case’s distance between the individual’s Z_t and the estimated model ζ(θ) as done by IRLS.

In IRLS, the weight matrix, W (65×65 here), is defined to be a constant for all individuals which is to be weighted by a case weight

$$W_i={\omega }_{i}W.$$ (4)

In IRLS, individual weights (ω_i) are calculated as follows. Define the Mahalanobis squared distance of the case from the structured model as:

$$d_S^2={(Z_i-\zeta (\theta ))}^{T}W(Z_i-\zeta (\theta ))$$ (5)

With weight matrix defined as, W = Γ⁻¹

$$\mathrm{\Gamma }=\frac{{\mathrm{\Sigma }}_{i=1}^n{\omega }_i^2(Z_i-\zeta (\theta )){(Z_i-\zeta (\theta ))}^T}{{\mathrm{\Sigma }}_{i=1}^n{\omega }_i^2}.$$ (6)

Here, the matrix Γ is a blocked matrix, with the first p by p block containing the case-weighted variances and covariances of the observed variables, the second p(p+1)/2 by p(p+1)/2 block containing the case-weighted variances and covariances of the vectorized cross-products of the observed variables as in (3), and the off-diagonal blocks containing the case-weighted covariances of the observed variables with the vectorized cross-products. Finally, define a set of Huber-type weights ω with b₁ = 2, b₂ =∞, and let $d_0=\sqrt{p_z}+b_1/\sqrt{2}$. In the present case, d₀ = 9.48 which, when squared, approximately corresponds to the .025 critical value of a chi-square distribution with df = p_z.⁴ If d_s ≤ d₀ then ω_i, otherwise,

$${\omega }_i=(d_0\mathit{\text{exp}}[-.5{(d_S-d_0)}^2/b_2^2])/d_S$$ (7)

In words, a cut-point d₀ for the square-root distance in Equation 5 is defined for which an individual’s response is determined to be consistent with the estimated model parameters. Once this distance is larger than the cut-point, cases are down-weighted according to the degree of discrepancy between the cases and the structured model. Of course, researchers can define b₁ and b₂, as well as the cut-off, as they wish, but see Yuan and Bentler (2000) for the rational underlying this particular choice.

Again, if all ω_i = 1 and $W_i=S_z^{-1}$, then Equation 3 is the familiar ADF estimator. Equation 3 becomes IRLS by first starting with ADF estimates of model parameters and then alternating between two steps: (1) update the case weights, treating the model parameters as fixed; and (2) update the model parameters, treating the case weights as fixed and using weighted sample statistics for Z; and repeating until convergence.

Borrowing notation from Yuan and Zhong (2008), we refer to the above distances as $d_s^2$ in place of the $d_i^2$ notation used in Yuan and Bentler (2000). We will also refer to these distances are “implausibility” indices because the higher their value, the more unlikely or unusual the pattern is given an estimated model. Notice that to compute such distances, there is no need to estimate factor score(s), and the number of elements that go into the computation of $d_s^2$ stays constant regardless of the model. In the present study, the number of estimated means, variances, and unique covariances that constitute Z equals 65. The only way for $d_s^2$ distances to vary across models is for the models to yield drastically different reproduced variance-covariance matrices. When the reproduced variance/covariance matrices are similar across models, weights based on d_s will have similar values.

d_s is not the only distance measure that can be computed based on the IRLS (d_s) solution. A valuable additional index is a Mahalanobis distance in the residual space as described in Yuan and Hayashi (2010, Equations 3 through 8; see also Yuan & Zhong, 2008, Equations 9 and 10). Both d_s and d_r, to be defined shortly, can be calculated using model parameters from any estimation method, including ADF and ML.

Using Bartlett’s factor score estimates (Lawley and Maxwell, 1971, pp. 106-112), we can define a case residual

$$e_i=[I-\mathrm{\Lambda }{({\mathrm{\Lambda }}^T{\mathrm{\Theta }}^{-1}\mathrm{\Lambda })}^{-1}{\mathrm{\Lambda }}^T{\mathrm{\Theta }}^{-1}](X_i-\mu )$$ (8)

as a measure of the discrepancy between the predicted item responses based on the factor score estimates and the observed item responses. In the unidimensional model used here, Λ is a (10×1) matrix of factor loadings and Θ is a (10×10) matrix of residual variances and covariances. The residual vector e_i is of length p and its elements contain the residuals for the observed variables after controlling for the Bartlett factor score estimates. The covariance matrix of e_i is given by Bollen and Arminger (1991, eq. 21) as

$$\Omega =\mathrm{\Theta }-\Lambda {({\Lambda }^T{\mathrm{\Theta }}^{-1}\Lambda )}^{-1}{\Lambda }^T.$$

However, this covariance matrix is rank-deficient and cannot be inverted to calculate a Mahalanobis distance directly using e_i. Let A be a p by (p - q) matrix whose columns are orthogonal to Θ⁻¹; such a matrix can be defined using the eigenvectors of Ω corresponding to the (p – q) nonzero eigenvalues as columns. Then a residual-based M-distance using e_i can be calculated as (Yuan & Zhong, 2008)

$$d_r^2={(A^T{e}_i)}^T{(A^T\Omega A)}^{-1}(A^T{e}_i).$$ (9)

Again, borrowing notation from Yuan and Zhong (2008), we will call this index of the discrepancy between the estimated model and the individual response pattern d_r. $d_r^2$ values are distributed as chi-square with degrees of freedom equal to the number of items minus the number of factors. Here, the df is 9, 8, and 7 for the unidimensional, two-factor, and bifactor models, respectively. Substantively, we refer to this distance as an index of “unmodelability” because large residuals reflect individuals whose pattern of response cannot be adequately modeled by a given specification. The d_r distances are expected to meaningfully decrease as a function of model complexity, even if the model-implied covariance matrices are similar.

IRLS Results

IRLS results using d_s to determine case weights are shown in the bottom panel of Table 2. The appropriate comparison is between IRLS and ADF, since IRLS is the reweighted version of ADF. Clearly, the major difference between IRLS (d_s) and ADF is that all loadings are higher in the former, but not dramatically so; those differences reflect the difference between assuming sample homogeneity using ADF and modeling heterogeneity using IRLS. In addition, the correlation between the factors in the 2-factor model and the bifactor model indices (ECV, omega, and omega hierarchical) are all higher in IRLS (d_s), compared to ADF.

The fit indices shown in Table 3 require extended discussion. First, we recommend that chi-square values be used to compare models within estimator and not to answer “what estimator fits better, ADF or IRLS”? The reason is that there are two different data sets being analyzed here, one where all cases are weighted 1.0 and the other were a significant proportion are downweighted. Notice also that the baseline chi-squares for ADF and IRLS (d_s) differ as well, so it is not easy to directly compare the practical fit indices across estimators either.

Perhaps a more appropriate basis for evaluating the fit of the IRLS models relative to other models, such as ADF, is the weighted-BIC, which is a function of the case-weighted log-likelihoods. For IRLS (d_s), the weighted BIC indicates that the bifactor model has a lower value than the BIC in the ADF model. Ultimately, however, these fit index values are, arguably, not of tremendous value in terms of an applied researcher knowing what to do in practice. We suggest that inspection of distances used in IRLS may be more informative in terms of understanding what is actually occurring in the data as models of increasing complexity are fit, and why and how more complex models are fitting some individuals relatively better. We now turn to this topic.

A Closer Look at the Distances

The goal of this research is not only to provide a robust examination of the RSES structure. Rather, we hope to show that through IRLS one can explore structural issues in unique, informative ways. This process rests heavily on interpretation of distance measures, and in this section we will closely examine their functioning in the present data.

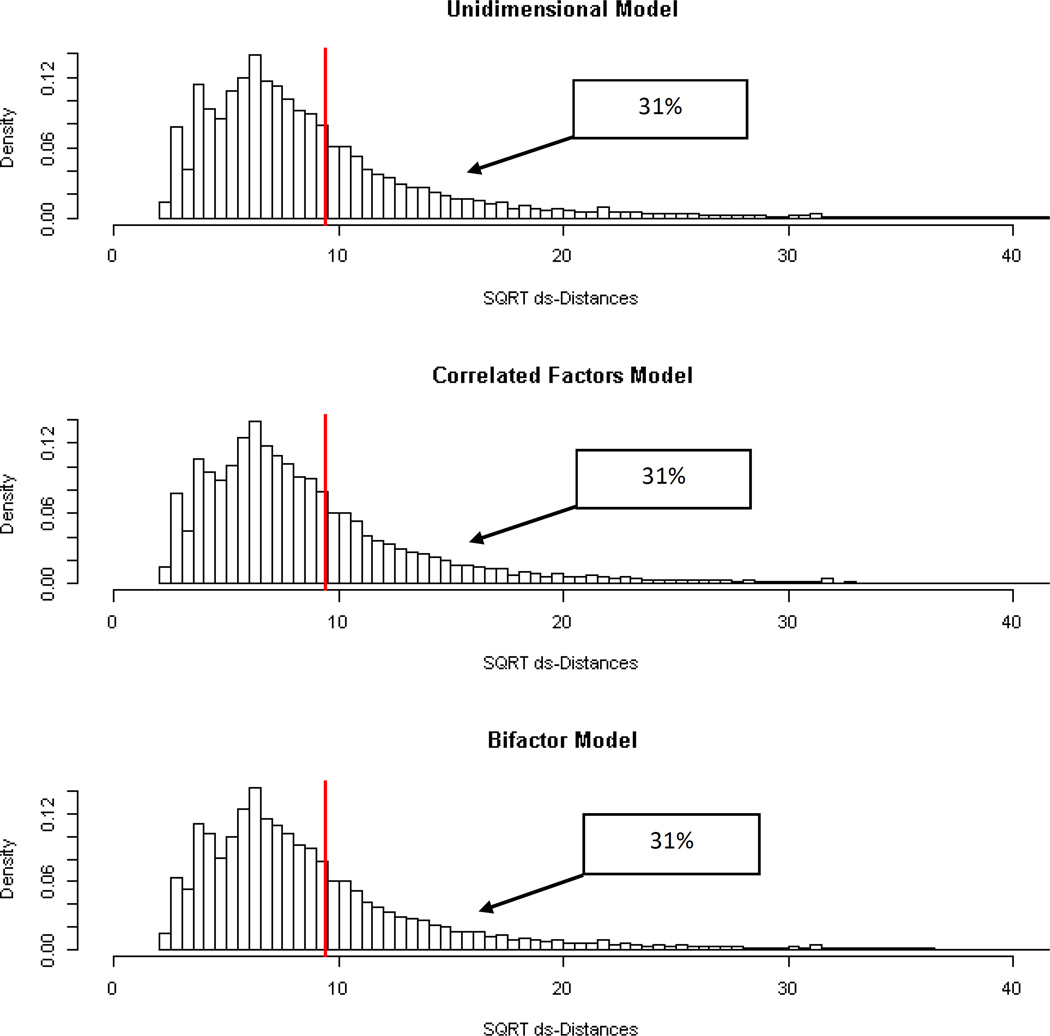
The first features to which we call attention are distributional issues and variation within individuals across models. Specifically, $d_s^2$ does not vary much across models, while $d_r^2$ displays meaningful variation. To illustrate, Figure 1 displays the distribution of d_s for the three models considered: unidimensional, correlated factors, and bifactor. Also shown in Figure 1 is the cut-off for d_s, 9.48. Recall that any individual with a d_s value above this critical value is down-weighted and any individual below the critical value is weighted 1.0. In the unidimensional model, for example, 69% were not down-weighted, 26% received weights of between .99 and .50, and 5% received weights of .50 and below. These values do not change appreciably in the other two models. The boxes represent the fact that around 31% of individuals were down-weighted within each model. One reason for this consistency in d_s across models is that the reproduced means and covariance matrices are very similar, and thus the individual’s distance stays about the same across models. In fact, the correlations among the d_s values in the three models are > .99, suggesting near perfect relative ordering across models.

Figure 1.

Distributions of the Square Root of ($d_s^2$) “Implausibility” Distances for the Unidimensional, Correlated-Factors, and Bifactor Models in the IRLS (d_s) Solutions

Because these indices reflect the likelihood of an item response pattern given an estimated model, and those likelihoods do not vary much across models, we suggest that d_s be interpreted as a general response inconsistency or “implausibility” index. Large values indicate a response pattern that is relatively unlikely given any measurement model that is consistent with the sample covariance matrix. Lower values of d_s reflect patterns that are potentially consistent with any model that fits the data well. Substantively, a pattern that is implausible under one model is likely to be implausible under the others as well.

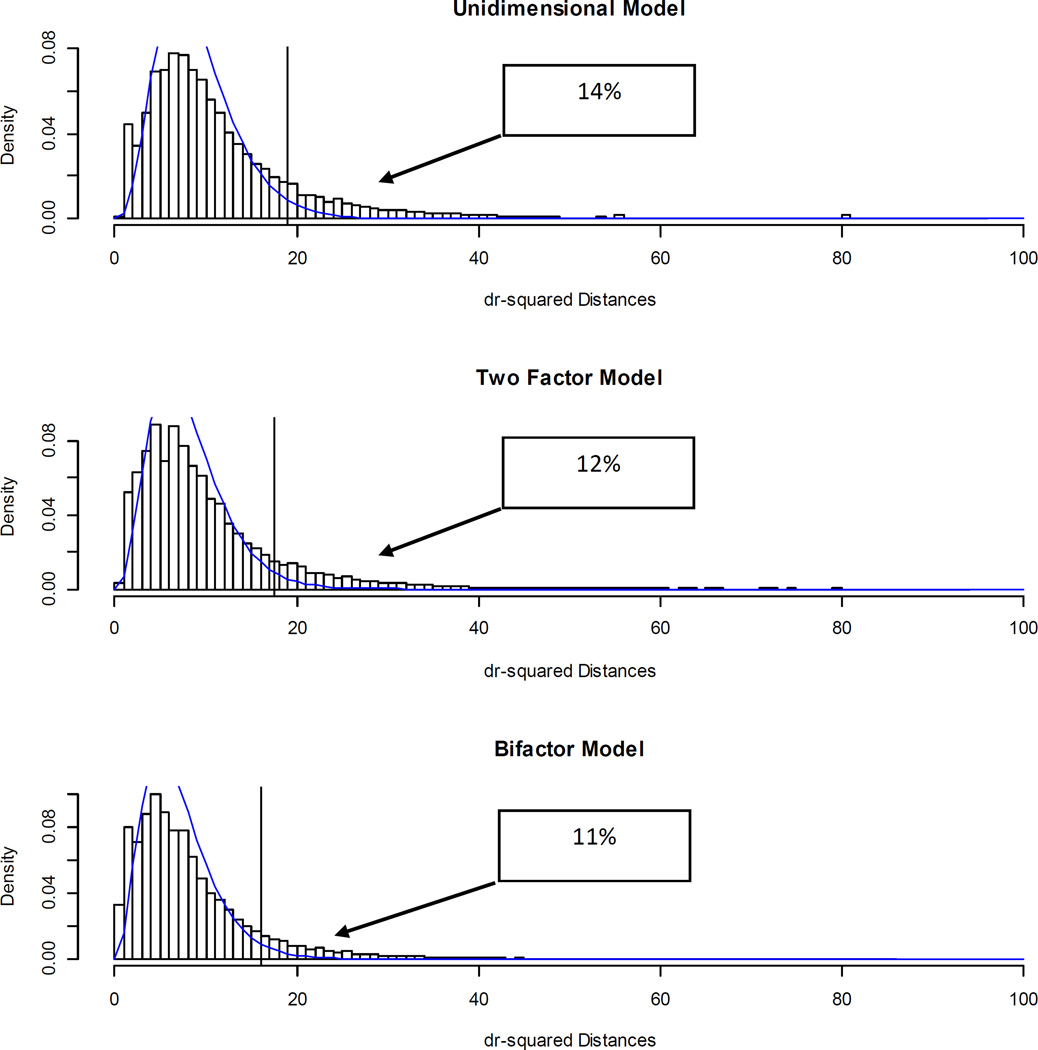
In Figure 2 are displayed the distribution of $d_r^2$ across the unidimensional, two-factor, and bifactor models, and the critical value (at alpha = .025) of chi-square on 9, 8, and 7 df, respectively; the superimposed curve is the expected distribution under the null hypothesis. Although highly correlated with d_s, the d_r values have a distinct interpretation. Specifically, d_r reflects the size of the model residual term for an individual, given an estimated model, or, how predictable an individual’s response pattern is given a model. Unsurprisingly, the distribution of d_r does change across models, with d_r values systematically becoming lower with more complex, highly parameterized models. One reason that more complex measurement models tend to produce smaller residuals is that they include more latent variables as predictors of the items, and a regression model with more predictors, especially optimal predictors such as factor score estimates, will usually yield smaller residuals.

Figure 2.

Distributions of $d_s^2$ “Unmodelability” Distances for the Unidimensional, Correlated-Factors, and Bifactor Models in the IRLS (d_s) Solutions

In the present research, d_r plays a critical role in defining what we term “unmodelability”. Precisely, we consider a response pattern to be “unmodelable” under a given specification if the d_r is statistically significant, here defined as having a p-value less than .025, one-tailed. Given this definition, one way to judge the value of increasingly complex models is to calculate the increasing percentage of modelable individuals as more complex models are applied. In Figure 2, the boxes display percentage of “unmodelable” individuals based on d_r for the unidimensional, two-factor, and bifactor models, respectively. In the unidimensional IRLS (d_r) model, 14% of participants had significant residuals and thus would be considered unmodelable; this is equivalent to saying that we have no statistical justification for rejecting the unidimensional model for 86% of the sample! An additional 2% were adequately modeled by the two-factor specification, and an additional 1% required a bifactor model to yield a non-significant d_r. We thus conclude that approximately 11% of the sample is not modelable even by the most complex model, the bifactor model.

To further understand the meaning of the weights, we conducted two additional analyses. First, as an intellectual exercise, we fit ADF models to three subsamples: (a) cases that were not downweighted (i.e., had weights of 1.0) as judged by the d_s in the unidimensional IRLS (d_s) model (N = 32,036, 69%); (b) cases that were moderately downweighted, receiving weights between .99 and .50 (N = 11,899, 26%); and (c) cases that were severely downweighted, receiving weights of .50 or less (N = 2,611, 5%). Results of these analyses are shown in Table 4. The message across the three models is clear: as weights decrease, the implausiblity of the response patterns increases, and the items become poorer indicators of a general self-esteem construct, especially for the negatively-worded items.

Table 4.

Unidimensional, Correlated Factors, and Bifactor Standardized Loadings for the RSE Data Under ADF Estimation For Subgroups Based on Weight in IRLS d_s in Unidimensional Model

Item	One factor	Two factor		Bifactor
	λ1	λ1	λ2	λGEN	λGRP1	λGRP2
Weight = 1 (N = 32,036)
1	.81	.81		.80	.39
2	.77	.77		.76	.45
4	.73	.73		.70	.26
6	.89	.90		.90
7	.88	.88		.89
3 (R)	.87		.88	.86		.17
5 (R)	.85		.85	.84		.16
8 (R)	.72		.72	.67		.28
9 (R)	.81		.82	.76		.40
10 (R)	.84		.85	.81		.36
ϕ		.95
θ9.10	.14	.13			.07
θ1.2	.13	.13
θ6.7	−.02	−.01
ECV					.88
ω					.96
ωH					.92
Weight = .99 - .50 (N = 11,899)
1	.67	.67		.62	.44
2	.63	.63		.57	.52
4	.52	.52		.43	.34
6	.77	.78		.79
7	.73	.74		.76
3 (R)	.70		.73	.64		.36
5 (R)	.60		.62	.54		.27
8 (R)	.36		.36	.35		.14
9 (R)	.56		.58	.50		.34
10 (R)	.64		.66	.59		.30
ϕ		.88
θ9.10	.24	.22			.21
θ1.2	.15	.14
θ6.7	−.04	−.03
ECV					.78
ω					.87
ωH					.78
Weight < .50 (N = 2,611)
1	.56	.58		.45	.53
2	.61	.64		.49	.62
4	.50	.58		.42	.40
6	.72	.71		.80
7	.58	.61		.64
3 (R)	.10		.34	−.06		.30
5 (R)	.15		.44	−.03		.42
8 (R)	.24		.38	.07		.40
9 (R)	.10		.45	−.07		.42
10 (R)	.21		.44	.03		.47
ϕ		−.04
θ9.10	.43	.32			.31
θ1.2	.17	.17
θ6.7	−.04	−.04
ECV					.50
ω					.68
ωH					.36

Note. (R) indicates a reverse worded item. ECV is the explained common variance, λ is factor loading on the first (1), second (2), general (Gen), or first or second group (Grp1, Grp2) factor ϕ is factor correlation, θ_a.b is residual correlation between items a and b, ω is model-based reliabilty and ω_H is reliability based on general factor.

For people who were not down-weighted and thus had weights of 1.0, the positively and negatively worded items appeared to conform well to a unidimensional model. All 10 items loaded highly on the single factor in the one-factor model. The two-factor solution had a very high correlation between the two factors (.95). Wording method effects were minimal, as judged by ω and ω_H values in the bifactor model, which showed that virtually all reliable variance in raw scores (.92/.96) was associated with the general factor. Thus for around 70% of the sample, there is little, if any, evidence of a “direction of wording” effect. However, we also note that even in this subsample with weights equal to 1.0, the bifactor model would still be considered an improvement over the unidimensional and correlated factors models in terms of fit (results not shown).

For individuals who were slightly down-weighted (i.e., with weights in the range from .99 to .50), the loadings in the unidimensional model were not as high, the factors were less highly correlated (.90) in the 2-factor solution, and the ω and ω_H were reduced, with less of the reliable variance associated with the general factor (.78/.87).

For people who were severely down-weighted (i.e., provided the most implausible response patterns), the positively-worded items continued to hold together well in the 1-factor solution, but the negatively-worded items failed to load on the single dimension. In the correlated factors model, the correlation between the factors was essentially zero. Finally, in the bifactor model, negatively-worded items failed to load on the general factor, instead loading only on their group factor. In turn, ω was a mediocre .68 and ω_H was only .36, suggesting that scores for these individuals do not primarily reflect a general factor.

Our final set of analyses was aimed at demonstrating that d_r and d_s can be used to better understand how and why models of varying complexity achieve a superior fit to data (or not). For clarity, we focus our attention solely on the distinction between the unidimensional and bifactor IRLS d_s models; as noted previously the difference between these models is highly significant, at least as judged by chi-square (Table 3). To efficiently illustrate our points, we will return to the ML solution (which is the most commonly used in the literature), and the associated chi-square test shown in Table 3. The virtue of a ML solution is that it is easy to partition the overall chi-square test into an individual’s contribution.

Thus, we begin by computing a log-likelihood for each individual under the unidimensional and bifactor ML models. The sum of these values yields the overall model log-likelihood (−494,719 in the unidimensional and −491,834 in the bifactor). Now we take −2 times the difference in these log-likelihoods and this yields each individual’s contribution to an overall likelihood ratio test of model differences (called INDCHI; Reise & Widaman, 1999; Sterba & Pek, 2012). High values of INDCHI reflect a case that contributes to the bifactor model being deemed as superior (a better fit) relative to the unidimensional model. Near zero values of INDCHI indicate that the models cannot be differentiated for a given response pattern. Negative values indicate that the response pattern is more likely under a unidimensional rather than bifactor model, and such cases decrease the overall chi-square difference test statistic.

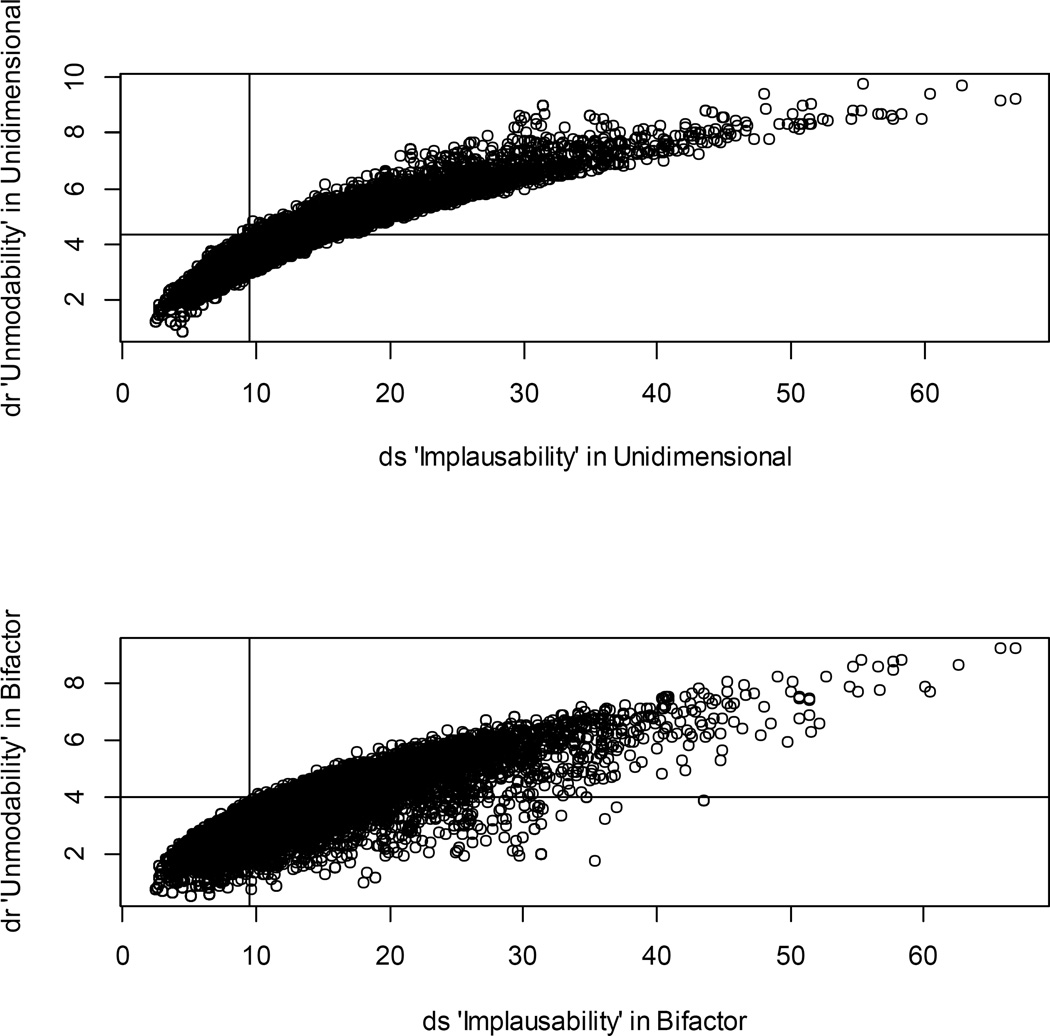
Before examining INDCHI more closely, first, in Figure 3 are displayed two panels that show the relation between d_s (implausibility) and d_r (unmodelability) within the unidimensional and bifactor models, respectively. In both models, as implausiblity goes up, so does unmodelability. Comparing the plots we see that for individuals receiving weights of 1, the decrease in residuals does not appear great, although there certainly is some. For individuals with modest levels of implausiblity (i.e., between 10 and 30) the decrease in unmodelability is rather striking; many individuals who were unmodelable under the unidimensional specification are now modelable under the bifactor. Finally, for individuals with very high values of implausiblity, residuals are also reduced in going from unidimensional to bifactor models, but in only a few cases do these patterns become “modelable” in the sense of having a non-significant residual. This suggests that some of the superiority in the fit of the bifactor may be a result of the bifactor being better able to model highly unlikely responses.

Figure 3.

Plots of “Implausibility” Distances (d_s) versus “Unmodelability” Distances (d_r) in the Unidimensional and Bifactor Models

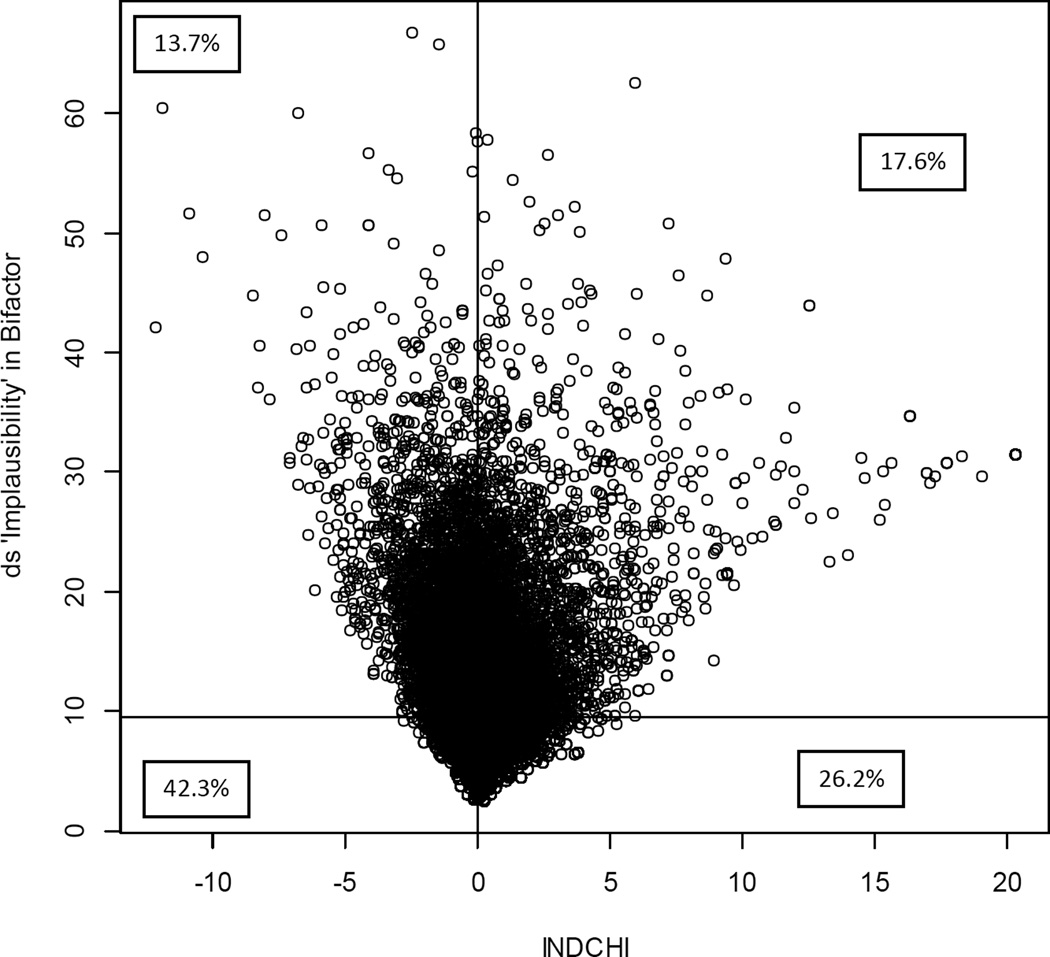
To address this issue, in Figure 4 is shown a plot of INDCHI versus d_s in the bifactor model (again recall that d_s values do not change appreciably across models and thus it does not matter which model is used for the y-axis). On the left hand side are the cases with negative INDCHI values and these are individuals who make the chi-square test favor the unidimensional model (by lowering the chi-square difference). The few cases in the far upper left are the most unusual or implausible response patterns, and clearly these cases are playing some role in making the difference between the unidimensional and bifactor models smaller. But also note that there are few of these cases and their INDCHI values do not go much below zero, thus their contribution to the overall chi-square difference test is relatively small.

Figure 4.

Plot of individual contribution to chi-square (INDCHI) versus “Implausibility” Distance (d_s) in the Bifactor Model

On the other hand, cases to the far right are contributing large positive INDCHI values to the overall chi-square. Moreover, these cases are almost universally implausible. Thus, the people who are contributing the most to making the bifactor look better than the unidimensional model (high positive INDCHI) are predominantly individuals with implausible response patterns, even when judged by the fitted bifactor model. These unusual and unlikely response patterns are possibly invalid response patterns, which are, for whatever reason, highly unlikely in the unidimensional, but less unlikely in the bifactor. This suggests that, while the bifactor is the better model in terms over overall fit to the data, it gains part of its superiority through being able to better assimilate unusual response patterns, and not necessarily by better accounting for the effects of reverse wording.

To further explore this and to make this phenomenon more concrete, Tables 5, 6, and 7 provide response patterns and a number of statistics. Table 5 displays patterns that are more likely under a unidimensional model, Table 6 displays patterns that are more likely under a bifactor model, and Table 7 displays patterns that are equally likely under each model. The first column is an item response pattern ordered as the five positively worded items (1, 2, 4, 5, 6), and the five negatively worded items (3, 5, 7, 9, 10). The remaining columns contain the following: the log-likelihood for the unidimensional and bifactor models, INDCHI, the $d_s^2$ values for the unidimensional and bifactor models, the corresponding weights used in IRLS (d_s) estimation, the $d_r^2$ values for unidimensional and bifactor models, and the probability of the $d_r^2$ residual under the unidimensional and bifactor models, respectively. The last column contains an index labeled PN, which is the difference in raw scores when computed for all the positive items, and when computed for all the negatively worded items. Values near zero indicate that people are scoring similarly for the positively and negatively worded items.

Table 5.

Examples of Response Patterns That Favor the Unidimensional over the Bifactor

df				65	65			9	7
Patterna	LogLU	LogLB	INDCHI	$d_{\mathit{\text{sU}}}^2$	$d_{\mathit{\text{sB}}}^2$	ωU	ωB	$d_{\mathit{\text{rU}}}^2$	$d_{\mathit{\text{rB}}}^2$	PU	PB	PN
11444 11211	−26.66	−32.73	−12.15	1774.96	1778.37	0.22	0.22	68.91	24.43	0	0	8
11444 11414	−36.91	−42.85	−11.88	3644.06	3658.99	0.16	0.16	88.16	59.23	0	0	3
11444 14423	−29.72	−35.17	−10.89	2648.96	2662.52	0.18	0.18	69.72	39.52	0	0	0
11344 11444	−32.35	−37.52	−10.34	2308.3	2305.34	0.2	0.2	78.57	50.98	0	0	−1
11444 34144	−26.33	−30.55	−8.45	1997.8	2009.76	0.21	0.21	58.71	27.68	0	0	−2
11433 14222	−22.08	−26.23	−8.3	1359.78	1371.94	0.26	0.26	46.9	31.42	0	0	1
11433 13344	−24.92	−29.04	−8.24	1631.59	1646	0.23	0.23	53.21	38.81	0	0	−3
11434 14444	−31.31	−35.33	−8.03	2640.6	2651.01	0.18	0.18	69.37	47.38	0	0	−4
11144 11111	−26.17	−30.08	−7.82	1287.47	1301.9	0.26	0.26	72.58	10.22	0	0.18	6
11344 14244	−29.33	−33.04	−7.4	2474.72	2475.69	0.19	0.19	68.9	35.34	0	0	−2
11343 31122	−20.64	−24.19	−7.1	944.23	946.37	0.31	0.31	46.2	16.56	0	0.02	3
12344 31111	−21.75	−25.28	−7.06	975.06	975.36	0.3	0.3	52.43	13.64	0	0.06	7
11444 34443	−25.64	−29.05	−6.81	1622.58	1626.69	0.24	0.23	55.7	22.95	0	0	−4
12244 11211	−21.97	−25.36	−6.78	829.58	835.17	0.33	0.33	57.48	14.07	0	0.05	7
11441 14411	−34.33	−37.71	−6.76	3573.61	3614.62	0.16	0.16	71.88	61.89	0	0	0
11422 12234	−20.85	−24.16	−6.63	1014.53	1030.97	0.3	0.3	40.04	34.05	0	0	−2
11344 42222	−22.25	−25.54	−6.56	1078.21	1078.63	0.29	0.29	51.57	10.92	0	0.14	1
44111 34132	−21.65	−24.86	−6.42	954.78	961.89	0.31	0.31	45.25	31.33	0	0	−2
11441 12112	−26.76	−29.96	−6.42	1850.86	1883.85	0.22	0.22	52.49	42.05	0	0	4
11422 21241	−24.88	−28.08	−6.42	1371.69	1378.43	0.26	0.26	47.14	44.47	0	0	0
44111 21221	−16.77	−19.95	−6.35	604.39	615.46	0.39	0.38	29.26	19.14	0	0.01	3
44121 41111	−21.82	−25	−6.35	1061.32	1071.79	0.29	0.29	41.81	38.84	0	0	4
11421 11141	−26.53	−29.7	−6.33	1631.72	1644.38	0.23	0.23	49.2	50.06	0	0	1
11243 12111	−20.26	−23.42	−6.32	819.29	818.55	0.33	0.33	48.91	6.74	0	0.46	5
11411 11244	−25.43	−28.5	−6.14	1386.98	1395.96	0.25	0.25	51.26	38.95	0	0	−4
11422 11211	−15.68	−18.73	−6.1	395.55	403.69	0.48	0.47	25.46	21.17	0	0	4
11342 21111	−20.18	−23.2	−6.03	824.14	828.3	0.33	0.33	41.83	16.53	0	0.02	5
11423 42122	−20.98	−23.96	−5.97	929.52	938.03	0.31	0.31	40.46	30.4	0	0	0
12244 22111	−19.73	−22.67	−5.89	685.77	688.89	0.36	0.36	48.96	5.67	0	0.58	6
11414 14111	−32.47	−35.4	−5.86	2557.28	2570.72	0.19	0.19	65.88	56.58	0	0	3

Note: df is degrees of freedom for distance measures; LogL_U is the log-likelihood under the unidimensional model; LogL_B is the log-likelihood under the bifactor model; INDCHI is individual contribution to chi-square; d_sU is “implausibility” distance in unidimensional model; d_sB is “implausibility” distance in bifactor model; ω_U is case weight based on d_sU in unidimensional model; ω_B is case weight based on d_sB in bifactor model; d_rU is “unmodelability” distance in unidimensional model; d_rB is “unmodelability” distance in bifactor model; P_U and P_B are significance levels of d_rU and d_rB respectively; PN is the difference between scores based on positively-worded items and negatively-worded items.

^aThe first five items (1, 2, 4, 6, 7) are positively worded, and the second five items (3, 5, 8, 9, 10) are the negatively worded.

Table 6.

Examples of Response Patterns That Favor the Bifactor over the Unidimensional

df				65	65			9	7
Patterna	LogLU	LogLB	INDCHI	$d_{\mathit{\text{sU}}}^2$	$d_{\mathit{\text{sB}}}^2$	ωU	ωB	$d_{\mathit{\text{rU}}}^2$	$d_{\mathit{\text{rB}}}^2$	PU	PB	PN
11111 44444	−34.63	−24.48	20.29	991.31	985.98	0.3	0.3	80.61	3.87	0	0.79	−15
11111 44344	−32.5	−22.98	19.04	883.97	877.6	0.32	0.32	74.68	4.38	0	0.73	−14
11111 44434	−33.07	−23.94	18.26	993.87	984.27	0.3	0.3	75.54	9.08	0	0.25	−14
11111 44244	−31.91	−23.05	17.72	958.7	949.88	0.31	0.31	72.47	8.35	0	0.3	−13
11111 34444	−31.71	−23.07	17.29	888.39	879.67	0.32	0.32	71.47	3.61	0	0.82	−14
11121 43444	−30.59	−22.05	17.08	861.13	849.99	0.32	0.33	67.05	4.47	0	0.72	−13
12111 44444	−31.77	−23.29	16.97	903.9	896.5	0.32	0.32	72.88	6.58	0	0.47	−14
11111 44144	−32.86	−24.7	16.32	1220.07	1207.85	0.27	0.27	73.98	15.78	0	0.03	−12
12111 44443	−30.94	−23.11	15.64	955.39	945.87	0.31	0.31	69.34	11.23	0	0.13	−13
11111 43343	−28.53	−20.85	15.37	746.36	740.02	0.35	0.35	62.45	5.88	0	0.55	−12
12112 44443	−29.94	−22.3	15.29	911.1	903.32	0.31	0.32	64.01	13.6	0	0.06	−12
11112 44333	−27.9	−20.3	15.21	679.5	675.22	0.36	0.36	58.97	10.45	0	0.16	−11
11212 44444	−30.02	−22.7	14.63	870.98	867.97	0.32	0.32	67.29	6.11	0	0.53	−13
21111 44244	−30.2	−22.95	14.5	976.3	968.74	0.3	0.3	68.02	13.31	0	0.06	−12
11122 44333	−25.23	−18.24	14	538.45	530.29	0.41	0.41	51.88	5.84	0	0.56	−10
11111 34234	−26.75	−20.02	13.44	721.64	709.17	0.35	0.36	56.65	9.05	0	0.25	−11
11111 34333	−24.98	−18.33	13.29	514.4	505.7	0.42	0.42	52.08	5.99	0	0.54	−11
12212 44444	−26.88	−20.59	12.58	689.12	685.18	0.36	0.36	58.51	7.27	0	0.4	−12
11111 44141	−36.13	−29.86	12.54	1940.75	1930.74	0.22	0.22	76.76	38.83	0	0	−9
11113 34333	−27.23	−21.09	12.3	820.4	814.27	0.33	0.33	53.98	14.72	0	0.04	−9
11112 34423	−26.61	−20.61	11.99	757.51	749.06	0.34	0.35	53.93	14.69	0	0.04	−10
11111 24244	−27.72	−21.73	11.99	926.32	906.78	0.31	0.31	58.67	10.56	0	0.16	−11
11144 44444	−32.07	−26.1	11.93	1249.39	1254.27	0.27	0.27	72.11	3.11	0	0.87	−9
11211 44144	−29.77	−23.95	11.64	1092.2	1084.47	0.29	0.29	67.59	16.43	0	0.02	−11
12113 33444	−28.01	−22.27	11.48	936.02	927.56	0.31	0.31	55.9	16.72	0	0.02	−10
11133 44333	−25.26	−19.61	11.3	661.09	655.29	0.37	0.37	52.62	3.76	0	0.81	−8
11111 44222	−25.9	−20.26	11.29	661.69	656.81	0.37	0.37	53.58	18.83	0	0.01	−9
12111 43144	−27.5	−21.86	11.28	901.57	890.64	0.32	0.32	59.13	15.79	0	0.03	−10
22111 44244	−26.01	−20.4	11.21	671.54	667.25	0.37	0.37	57.73	11.04	0	0.14	−11
12111 34234	−24.39	−19.01	10.75	614.85	607.27	0.38	0.38	50.22	11.78	0	0.11	−10

Note: df is degrees of freedom for distance measures; LogL_U is the log-likelihood under the unidimensional model; LogL_B is the log-likelihood under the bifactor model; INDCHI is individual contribution to chi-square; d_sU is “implausibility” distance in unidimensional model; d_sB is “implausibility” distance in bifactor model; ω_U is case weight based on d_sU in unidimensional model; ω_B is case weight based on d_sB in bifactor model; d_rU is “unmodelability” distance in unidimensional model; d_rB is “unmodelability” distance in bifactor model; P_U and P_B are significance levels of d_rU and d_rB respectively; PN is the difference between scores based on positively-worded items and negatively-worded items.

^aThe first five items (1, 2, 4, 6, 7) are positively worded, and the second five items (3, 5, 8, 9, 10) are the negatively worded.

Table 7.

Examples of Response Patterns That Favor Neither The Bifactor or Unidimensional Models

df				65	65			9	7
Patterna	LogLU	LogLB	INDCHI	$d_{\mathit{\text{sB}}}^2$	$d_{\mathit{\text{sB}}}^2$	ωU	ωB	$d_{\mathit{\text{rU}}}^2$	$d_{\mathit{\text{rB}}}^2$	PU	PB	PN
43332 34233	−9.91	−9.91	0	69.86	70.1	1	1	10.26	9.32	0.33	0.23	0
23231 12322	−13.88	−13.88	0	185.04	185.73	0.7	0.7	18.19	18.82	0.03	0.01	1
43321 21322	−12.81	−12.81	0	146.81	146.42	0.78	0.78	17.79	11.61	0.04	0.11	3
33224 21412	−18.6	−18.6	0	483.43	484.51	0.43	0.43	31.82	28.73	0	0	4
33232 22314	−16.14	−16.14	0	260.7	260.82	0.59	0.59	24.19	24.48	0	0	1
33221 21111	−9.51	−9.51	0	51.98	52.13	1	1	7.34	5.33	0.6	0.62	5
32233 32222	−9.99	−9.99	0	57.68	57.21	1	1	12.36	5.4	0.19	0.61	2
44333 33331	−12.29	−12.29	0	146.49	146.97	0.78	0.78	15.41	13.57	0.08	0.06	4
33322 33132	−9.21	−9.21	0	40.5	40.55	1	1	9.1	7.79	0.43	0.35	1
44433 33443	−10.3	−10.3	0	69.99	69.67	1	1	10.37	7.14	0.32	0.41	1
43333 33312	−9.61	−9.61	0	60.8	60.94	1	1	9.56	7.43	0.39	0.39	4
44334 34224	−12.08	−12.08	0	117.66	117.92	0.87	0.87	13.56	13.17	0.14	0.07	3
22321 23222	−9.41	−9.41	0	62.48	62.4	1	1	9.4	6.68	0.4	0.46	−1
33332 22332	−9.25	−9.25	0	44.18	44.44	1	1	8.47	8.72	0.49	0.27	2
23322 13121	−11.69	−11.69	0	117.78	117.57	0.87	0.87	14	13.12	0.12	0.07	4
32321 21311	−11.85	−11.85	0	112.26	112.64	0.89	0.89	13.29	13.2	0.15	0.07	3
23221 21112	−10.06	−10.06	0	68.31	68.58	1	1	8.06	8.35	0.53	0.3	3
13321 21111	−13.06	−13.06	0	147.07	147.97	0.78	0.78	14.65	14.81	0.1	0.04	4
34434 43233	−10.51	−10.51	0	85.3	85.75	1	1	10.18	10.15	0.34	0.18	3
33432 22422	−11.57	−11.57	0	117.19	117.48	0.88	0.87	14.31	14.06	0.11	0.05	3
43332 32224	−12.24	−12.24	0	118.63	118.91	0.87	0.87	15.21	15.28	0.09	0.03	2
43343 32433	−11.72	−11.72	0	101.73	101.8	0.94	0.94	14.42	13.42	0.11	0.06	2
14322 22312	−17.67	−17.67	0	391.62	392.11	0.48	0.48	27.42	27.82	0	0	2
33211 43133	−15.96	−15.96	0	288.96	288.7	0.56	0.56	31.24	14.33	0	0.05	−4
22211 21311	−9.84	−9.84	0	56.59	56.51	1	1	7.89	6.28	0.55	0.51	0
34334 34432	−12.86	−12.86	0	171.37	172	0.72	0.72	15.62	15.8	0.08	0.03	1
34433 44441	−20.6	−20.6	0	628.82	629.1	0.38	0.38	33.68	33.34	0	0	0
44444 41443	−17.76	−17.76	0	381.89	382.12	0.48	0.48	28.33	27.17	0	0	4
43344 43333	−9.57	−9.57	0	55.2	54.87	1	1	8.72	4.45	0.46	0.73	2
34333 33232	−8.71	−8.71	0	38.19	38.35	1	1	7.09	6.81	0.63	0.45	3

Note: df is degrees of freedom for distance measures; LogL_U is the log-likelihood under the unidimensional model; LogL_B is the log-likelihood under the bifactor model; INDCHI is individual contribution to chi-square; d_sU is “implausibility” distance in unidimensional model; d_sB is “implausibility” distance in bifactor model; ω_U is case weight based on d_sU in unidimensional model; ω_B is case weight based on d_sB in bifactor model; d_rU is “unmodelability” distance in unidimensional model; d_rB is “unmodelability” distance in bifactor model; P_U and P_B are significance levels of d_rU and d_rB respectively; PN is the difference between scores based on positively-worded items and negatively-worded items.

^aThe first five items (1, 2, 4, 6, 7) are positively worded, and the second five items (3, 5, 8, 9, 10) are the negatively worded.

We begin with Table 5, which shows the 30 individuals with the most negative INDCHI values (redundant patterns removed). Clearly the INDCHI values do not deviate much from zero. These appear to be individuals who are relatively consistent across positively and negatively worded items, as judged by PN values, but who clearly are inconsistent within item type. These individual all have implausible response patterns as judged by d_s, are severely down-weighted in estimation, and are judged as unmodelable by the d_r indices. Thus Table 5 contains the people with unusual, possibly invalid, response patterns that end up favoring the unidimensional model. What exactly to make of a response pattern of 11423 42111 as possibly reflecting a single “trait” of self-esteem is a mystery to us.

In Table 6 are shown example response patterns that are more likely under the bifactor and that make the bifactor statistically superior to the unidimensional model. Importantly, note that in Table 6, there were many response patterns such as 11111 44444, but we deleted redundant patterns. In contrast to Table 5, these individuals have very large PN values, indicating either invalid responding (e.g., not reading the items), yea or nay saying, misunderstanding how to use the response options, or they profess to have low self-esteem but will not endorse any negative self-evaluations or vice versa. Like the individuals in Table 5, these individuals also have very large d_s values and receive very low weights in estimation. Unlike the individuals in Table 5, these individuals are deemed not to fit the unidimensional model, but to have residuals that are small and not-significant in the bifactor.

This illustrates precisely our concern about the bifactor displaying superior fit, partly because it can accommodate a certain type of unlikely, possibly invalid response pattern, namely, a pattern that is inconsistent between item types, but consistent within. The pattern 12111 44444, for example, has a $d_r^2$ value of 69.34 in the unidimensional model, and 11.23 in the bifactor. In turn, this individual contributes 15.64 to the overall INDCHI; when there are many such individuals, as in this dataset, those sizable INDCHI can greatly impact model comparison.

Finally, for completeness, Table 7 shows individuals with response patterns about equally likely in the unidimensional and bifactor models. These are individuals who are consistent across item type as judged by the small PN values. Inspection of the response patterns reveals that they are fairly consistent within item type as well. Moreover, these individuals tend to be weighted at 1.0 during estimation (with exceptions) and have d_r residuals that are not statistically significant in either unidimensional or bifactor models (again with exceptions).

Discussion

We applied a robust IRLS estimation (Yuan & Bentler, 2000) to a large, publicly available, internet sample of responses to the RSES (Rosenberg, 1965). Two types of distance measures were used. The first, d_s called “implausibility”, reflects the discrepancy between an individual’s item response pattern and an estimated mean and covariance matrix. The second, d_r, called “unmodelability”, reflects the magnitude of an individual’s residual given a fitted model. In the following, our review of results is divided into three sections.

We begin by describing how robust estimation, joined with the interpretation of the two distance measures, contrasts with traditional model fitting. In this first section we also compare our findings with previous confirmatory factor analytic research on the RSES. In the second section, we describe some important technical issues that arise in IRLS in general and the computation and application of distance measures in particular. Finally, we conclude with some suggestions on how IRLS results can be used in practice.

Current Results

In this section, we highlight some critical differences between traditional model fit assessment and the IRLS approach taken here, as well as review current results. The first major point of departure is that, in traditional model fitting, it is assumed that all subjects are a random sample from the model population (i.e., sample homogeneity). This leads directly to implicitly weighting all subjects at 1.0 during estimation by applying standard ADF or ML estimation. IRLS, on the other hand, also assumes that there is a model in the population. However, it assumes the sample is heterogeneous, that is, not all members of the calibration sample are equally likely to be a random selection from the population. To the degree that the individual’s pattern of item responses is unlikely given, or inconsistent with, the estimated model parameters, that particular case is downweighted. In this sense, IRLS allows the estimated model to be a random effect with applicability varying across subjects.

Although both traditional modeling and IRLS allow researchers to pick “the best” model (through unweighted and weighted statistics, respectively), IRLS naturally provides additional information through the distance measures. In turn, the associated distance measures allow for consideration of model functioning at the level of the individual and how and why more complex models fit better.⁵ In the current research, for example, our IRLS (d_S) results are consistent with previous studies in several important ways, specifically: (1) a bifactor model with direction of wording group factors provided a superior overall fit, relative to unidimensional and correlated factors models, (2) analyses of bifactor-derived indices such as ECV, ω, and ω_H suggest that, despite multidimensionality, the RSES is “essentially” unidimensional – raw scores mostly reflect a single general factor, and (3) problems with the RSES appear isolated to the negatively-worded items; even in the 5% of the sample who were most down-weighted by d_S the five positively-worded items hung together to form a coherent factor.

However, inspection of d_S (implausibility) and d_r (unmodelability) led us to the following additional conclusions. First, judging by d_S, a significant proportion (about 30%) of the response patterns are highly unlikely (implausible) under any considered model. After ordering patterns by direction of wording (5 positive items and 5 negative items), patterns such as (11111 44444, $d_{s-uni}^2=991,d_{s-bif}^2=986$) and (44444 11111, $d_{s-uni}^2=463,d_{s-bif}^2=463$) appear easy to dismiss as faulty records. Implausible patterns such as (44314 11114, $d_{s-uni}^2=2098,d_{s-bif}^2=2100$) and (11133 44311, $d_{s-uni}^2=1121,d_{s-bif}^2=1117$) are all more likely under a bifactor model than a unidimensional, but are statistically aberrant under any model! Without further information we cannot even guess at the response process underlying these patterns. We would argue that these bifactor-model-favoring patterns do not appear to reflect anything resembling a “reverse wording” effect. For these individuals, one thus has to wonder what phenomena the bifactor model is “accounting for” better than the unidimensional.

Related to the above, inspection of the relation between $d_S^2$ values and INDCHI statistics taken from the ML solution (by far the most commonly used estimator in the applied literature), suggested that, although the bifactor model fits better than a unidimensional model, some of that advantage in fit is gained through being able to accommodate these highly unlikely, possibly invalid, patterns. One interpretation of this finding is to say that the bifactor model is “better” because it is better at modeling unusual response patterns, or, more cynically, it is better because it can more readily accommodate invalid patterns.

To understand this better, one way to think about the three models is as follows. The unidimensional model expects relative response consistency both between and within wording types. For this reason, patterns such as (22222 22222) are only slightly more likely under a bifactor than a unidimensional model, but that gain is solely due to the bifactor having more parameters. In turn, a correlated factors model expects relative response consistency within item wording type; inconsistency between is tolerable, but only to the extent that the factors are uncorrelated.

Finally, relative to the unidimensional model, the bifactor model is better able to accommodate both response variability within direction-of-wording item groups, and between direction-of-wording item group mean response differences. This can be good or bad. To the extent that patterns such as (44433 22211) reflect valid multidimensionality at the level of the individual (perhaps due to a direction of wording response scale shift), the bifactor is a superior representation and it is needed to make sense of this pattern. On the other hand, we do not want more complex models to fit better because they better accommodate invalid patterns, such as (44444 11111). To the extent that the bifactor model accomplishes this, it is an over-parameterization. We do not want to claim that the data are bifactor if, in fact, they are just odd or unusual.

The second index easily derivable from an IRLS solution is d_r (unmodelability) which reflects the magnitude of an individual’s residual. d_r and d_S values are highly correlated within models (r > .80), but they are not the same thing; d_r are typically smaller in more complex models while d_S values do not change much across models. Inspection of the d_r values within models led us to the following conclusions. Despite the bifactor model yielding the better overall fit: (1) the overwhelming majority of individuals (86%) have response patterns that are adequately modeled (i.e., have residuals that are not statistically significant) through a unidimensional model, (2) only an additional 3% of individuals have non-significant residuals when multidimensional models are applied, and (3) a substantial proportion (around 11%) have response patterns that are unmodelable under any model considered here – no model yielded an acceptably small, non-significant, residual.

The Two Distances and Technical Issues

The statistical theory behind, calculation of, and interpretation of distance measures has been discussed extensively by Yuan and colleagues (Yuan, Fung, & Reise, 2004; Yuan & Hayashi, 2010; Yuan & Zhong, 2008). This literature often describes distances in SEM by drawing analogies with regression diagnostics and robust estimation in regression (e.g., Yuan & Bentler, 2000). Our emphasis here was not on identifying individuals who are outliers in the predictor space (factor space) in order to identify good and bad leverage observations. Rather, here our interests center on using d_S and d_r as tools for understanding how models work at the level of the individual.

With this application in mind, it is obvious that much work is still needed to understand what d_S and d_r mean substantively, if anything, and how to optimally apply them in research. This is certainly true as we move into IRLS techniques based on ordinal estimation methods, and iteratively reweighted maximum likelihood estimation methods. For now, we focus on two obvious statistical concerns, namely, the distribution of the distances under the true model, and the Type I error rates inherent in using the distances as statistical tests at the individual level.

As for distributional properties, we noted earlier that d_s has no easily derivable sampling distribution, and thus it is not possible to perform statistical tests, per se. Although we used a chi-square .025 cut-off to decide who to down-weight and to what degree (following Yuan & Bentler, 2000), this simply acts as a tuning parameter determining the degree of robustification. Other researchers may make different choices leading to different results. This is not a unique problem to the present research; robust methods always require the researcher to select a degree of robustness.

On the other hand, when data are continuous and multivariate normal and generated from the population model, $d_r^2$ values are asymptotically distributed as chi-square with degrees of freedom equal to the number of items minus the number of latent factors. We make no claims about the precision of the assumed sampling distribution under all types of violations of the above conditions, especially in ordinal data. Clearly, additional research is needed. Researchers concerned about this issue are advised to conduct parametric or non-parametric bootstrapping (see Sinharay, 2016, for similar advice in the context of item response theory person fit measurement).

If the assumed sampling distributions are treated seriously as sampling distributions, rather than as rough guidelines for interpreting the distance measures, then what about the problems inherent in making, say, 49,000 “reject” versus “fail to reject” decisions based on d_r? We agree with Yuan and Zhong (2008) – there is nothing in the robustification of IRLS that mitigates Type I error rates. Those authors suggest that, for researchers desiring to use distances with strong statistical rigor, bootstrapping methods should be used. We also suggest that when Type I errors are a concern, being more stringent in the required p value may be useful. Ultimately, we prefer that the distances be used as indices or guidelines, and not be taken too seriously as test statistics. Perhaps taking the top 1% or 5% of values for further scrutiny is the wisest course of action at present. At the very least, however, the percentage of down-weighted cases and the distribution of d_r should be reported in any fit study, together with how these cases are affecting model comparisons described. To our knowledge these “inconvenient truths”, such as, in the present data, around 30% of individuals have implausbile response patterns under any model, have never been acknowledged in any CFA investigation.

Conclusion: Practical Implications

We believe there are three ways to frame the current research, one specific and two very general. Specifically, the research can be viewed as a warning against assuming the sample is homogeneous with respect to a model and, more importantly, consequently mindlessly concluding that the bifactor model is “better” for all subjects based on comparison of overall model fit indices alone. There are many reasons why a bifactor model may provide a better fit, one of the worrisome reasons is that it can better accommodate implausible, possibly invalid, response patterns. We warn readers that, even if such suspect patterns could be reliably identified with high precision, there is no “adjustment” to factor score estimates that can turn invalid responses into valid score estimates.

More generally, robust estimation through IRLS and interpretation of associated distance measures can be viewed either as complementary to existing measures of overall model fit to data or as a wholly different approach to CFA. As for the former, IRLS can be viewed much like robust adjustments to chi-square and standard errors – estimate models with and without robust adjustments, and see whether it matters as far as substantive conclusions. We note that in this regard, much of the CFA literature on the RSES used robust ML, but no study cited it as providing any different conclusions than ordinary ML.

To the extent that IRLS provides meaningfully different parameter estimates, and assuming sample size is sufficient to justify ADF, IRLS results are superior due to the fact that the unweighted ADF results violate the homogeneity of sample assumption. In comparing ADF with IRLS (d_s), we strongly suggest comparison of the size of loadings, and the percentage of implausible and unmodelable response patterns is what is critical. Judging these two estimators based on fit indices is not highly productive given one set is based on unweighted cases and the other is based on weighted data.

IRLS can be viewed as a different approach to CFA in the sense that the questions asked and answered are different. Traditional CFA is a competition among models where the goal is to find a substantively interpretable model that provides the best fit to the sample as a whole. In IRLS, as used here, we used d_r values to ask and answer, for what proportion of individuals is a unidimensional model (i.e., the most parsimonious model) adequate? Results indicated that using a p <= .025 criterion, the answer appears to be 86%. We then asked, for what additional percentage of individuals are a correlated factors or bifactor model needed to achieve a non-significant residual? The answer in this sample was an additional 3%. Finally, we observed that for around 11% of the sample no model considered could provide a non-significant residual – such patterns are simply unmodelable under the conditions considered here. It seems to us that this individual “unmodelability” problem should be a significant concern of applied researchers. Nevertheless, we know of no literature on this subject.

If traditional CFA and IRLS are viewed as alternative, competing approaches, a critical issue is whether the methods imply different advice for practitioners? We believe they do. The cumulative results with RSES can be interpreted in two ways. First, RSES responses appear to be multidimensional, mostly due to direction of wording factors, but there is very little evidence that the two factors are substantive rather than methodological. Moreover, despite the multidimensionality, the RSES can be safely considered as "essentially” unidimensional and scored or modeled as such. A second interpretation of the CFA literature is to argue that a bifactor model is needed to optimally account for the data, in particular to “control for” the reverse wording effect. Because there is no viable method of adjusting raw scores for reverse wording effects, this interpretation would call for the use of factor score estimates derived from a bifactor model be used in applied research⁶, or in SEM, a bifactor measurement model for the RSES be specified.

We argue that our results suggest a slightly different approach in practice. We believe that our results strongly support the use of a unidimensional scoring strategy for the overwhelming majority of individuals, which would include many cases that have somewhat implausible, but modelable, response patterns. This would avoid the knotty problems involved in estimating factor scores for orthogonal general and group factors, which is inherent in the bifactor model. It would also be more consistent with the vast majority of the data, wherein for the majority of individuals positively- and negatively-worded items appear to cohere strongly as indicators of a single latent variable. Analogously, we suggest that researchers specify the RSES using a unidimensional measurement model in SEM, perhaps making use of parceling for parsimony.

The obvious problem is what to do about the small percentage of remaining cases who can either be validly modeled through a bifactor (or correlated-factors), or who provided response patterns that are invalid and uninterpretable within the present modeling framework? We do not suggest that different models be used to score such individuals. That would be too unwieldy. We do suggest that, in applied research, scores for such individuals be weighted by either the weights derived from d_r or d_S, or both. A sensitivity analysis can then be performed – comparing results with and without using weights – as routinely performed in intervention research.

Contrasts With Mixture Modeling

In the preceding sections of this article, we considered IRLS in contrast to standard CFA practice. Here we briefly consider an alternative approach to modeling heterogeneity, called latent mixture modeling (Lubke & Muthén, 2005; Miettunen, Nordström, Kaakinen, & Ahmed, 2016). In a mixture model, two or more latent classes are specified, and then a measurement model is estimated within each latent class, typically by fixing factor loadings and allowing item intercepts to vary between classes. For each case, the relative likelihood of being a member of a latent class is calculated, and the consistency of an individual’s pattern of responses with an estimated mixture model can be estimated (Cole & Bauer, 2016).

Most relevant to the present research, mixture modeling has been used to study reverse wording effects. For example, Bandalos, Coleman, and Gerstner (2015) identified a three latent class solution in their two samples of RSES data, with one class (approximately 17% and 12% in each sample, respectively) responding differentially to the reverse worded items, in particular Item 5 (“I feel I do not have much to be proud of”). In turn, in one sample, membership in this class was associated with relatively low conscientiousness, while in a second sample, membership in this class was related to lower verbal ability. This study illustrates the use of mixture modeling to identify groups of individuals who are relatively more homogeneous with respect to their mean levels of item response. It does not reflect an application where different measurement models are estimated for different individuals.

As noted in Yuan and Bentler (2000), mixture modeling is best applied when one has an a priori theory about the population consisting of different “types” of people. In contrast, IRLS is best applied to measurement data when one believes there is a common quasi-nomothetic trait with a latent structure that applies to the majority of individuals, but for either substantive or response faultiness (Tellegen, 1988) reasons (e.g., carelessness, unique interpretation of item content), some percentage of response patterns is not reasonably generated under that model, and thus should be down-weighted in the estimation of parameters.

In the specific case of self-esteem, for example, there is no psychological or biological evidence in the literature that there are different latent “types” of persons with regard to self-esteem and that different nomological networks may apply to such types. In fact, there is some evidence that the construct of self-esteem is nomothetic (Yamaguchi et al., 2007). However, research also indicates that the psychometric functioning of self-reported self-esteem data may differ somewhat due to people from different cultural backgrounds interpreting items differentially (Schmitt & Allik, 2005), inattention to item content possibly due to low conscientiousness (Bandalos, Coleman, & Gerstner, 2015), or confusion when responding to reverse-worded items, possibly attributable to lower verbal ability (Marsh, 1996). Thus, because heterogeneity in RSES item response data is thought to arise due to response artifacts, and not because of latent taxons for whom different measurement models apply, IRLS is a quite appropriate choice. More generally speaking, IRLS methods are either complementary or competing with latent mixture modeling, depending on the particular application and one’s theoretical perspective on the nature of psychological traits.

Conclusion

Almost without exception, measures commonly used in psychological research, such as the RSES, have been extensively studied through confirmatory factor analysis, a process we label here as the “fit contest”. Such latent structure research can be important to the degree that it goes beyond declaring a “model champion” and truly informs: (1) on the quality of the items as indicators of latent variables (including full reporting of correlated errors), (2) on how an instrument is to be scored, or (3) on how best to represent the measurement model in structural equation models. We conclude that researchers testing whether an instrument such as the RSE is one-factor, two-factors, or bifactor are not making full use of CFA. When CFA results are looked at through the lens of individual response patterns, many instruments thought to be “bifactor”, like the RSES, may in fact be essentially unidimensional, a prospect we have faced in previous studies (Reise, Scheines, Widaman, & Haviland, 2013). Researchers should be especially cautious in concluding that the bifactor model is “controlling” for direction of wording effects solely on the bases of superior fit. To some degree the bifactor fits better because it better accommodates potentially invalid patterns of response by individuals.