Highly Coarse-Grained Representations of Transmembrane Proteins

Abstract

Numerous biomolecules and biomolecular complexes, including transmembrane proteins (TMPs), are symmetric or at least have approximate symmetries. Highly coarse-grained models of such biomolecules, aiming at capturing the essential structural and dynamical properties on resolution levels coarser than the residue scale, must preserve the underlying symmetry. However, making these models obey the correct physics is in general not straightforward, especially at the highly coarse-grained resolution where multiple (∼3–30 in the current study) amino acid residues are represented by a single coarse-grained site. In this paper, we propose a simple and fast method of coarse-graining TMPs obeying this condition. The procedure involves partitioning transmembrane domains into contiguous segments of equal length along the primary sequence. For the coarsest (lowest-resolution) mappings, it turns out to be most important to satisfy the symmetry in a coarse-grained model. As the resolution is increased to capture more detail, however, it becomes gradually more important to match modular repeats in the secondary structure (such as helix-loop repeats) instead. A set of eight TMPs of various complexity, functionality, structural topology, and internal symmetry, representing different classes of TMPs (ion channels, transporters, receptors, adhesion, and invasion proteins), has been examined. The present approach can be generalized to other systems possessing exact or approximate symmetry, allowing for reliable and fast creation of multiscale, highly coarse-grained mappings of large biomolecular assemblies.

I. Introduction

The symmetry of biomolecules originating from gene duplication and consolidated by evolution,¹⁻³ while often only approximate, is intimately linked to functionality.⁴ For transmembrane proteins (TMPs) in particular, symmetry is one of the common properties shared in their functional states,^5,6 and it has been related to dynamics,⁷ fast folding kinetics,⁸ high stability,² and allosteric regulation.⁹⁻¹¹ In addition, engineering of proteins with internal symmetry has become an emerging field with a growing body of reported success.¹²⁻¹⁴

TMPs, such as G protein-coupled receptors and ion channels, are crucial targets in drug discovery due to their physiological roles as direct rectors for drug-like solutes;^15,16 it has been suggested that for receptors of neurotransmitters, for instance,¹⁷⁻¹⁹ an indirect and less specific mechanism whereby solutes absorbed into the lipid bilayer²⁰⁻²⁴ can affect the receptor. With around half of current drug targets being these TMPs²⁵ and most of those drugs targeting only a few members,²⁶ it is hardly surprising that the study of TMPs has become an active field of research with an increasing amount of experimental and computational efforts for potential pharmaceutical applications.

Despite advances in both hardware and software for atomistic molecular simulations,²⁷⁻³⁰ there is still a large gap between the duration of all-atom molecular dynamics (MD) trajectories produced on a routine basis (typically, microseconds) and time scales of biologically relevant events observed in experiments involving TMPs (usually milliseconds to seconds^31,32). One fruitful strategy to overcome this gap and better bridge experiments and simulations is to apply a coarse-graining approach. The structure-based coarse-grained (CG) representation encompasses a reduced level of detail of the system, as atoms are grouped into “effective” particles also termed CG sites, and many of the biofunctionally irrelevant degrees of freedom are integrated out. One level of coarse-graining is the “high resolution” level in which each amino acid is represented by several CG sites or “beads”. Another level of coarse-graining is the “low resolution” highly CG level, where each CG site or bead represents some number of amino acids (e.g., tens or more). This paper concerns the latter limit of CG models.

A variety of modern coarse-graining approaches have been developed to define highly CG protein models, including essential dynamics coarse-graining,³³⁻³⁶ topology representing network,³⁷ and rigid unit recognition.³⁸ At the highly coarse-grained level, constructing CG models that satisfy the correct underlying physics is by no means a trivial task and often the resulting models are neither unique nor transferable.^39,40 To simulate TMPs at very large spatial and temporal scales relevant for most biological processes, it is both useful and necessary to resort to models of the lowest, such as ultracoarse-grained (UCG) models,^41,42 where one CG site represents many amino acid residues and may also have internal “states” to represent the various conformations, chemical forms, etc., of those eliminated amino acids from each CG site. The UCG methodology, often motivated in the context of modeling of the actin filament,⁴¹ has only recently been applied to other families of proteins⁴³ but not yet to TMPs.

This work therefore describes our most recent efforts to construct highly CG models for TMPs based on the essential dynamics coarse-graining (ED-CG) method.³³⁻³⁶ The ED-CG method (or a similar approach⁴⁴) is a systematic variational way of creating CG models that capture the most essential functional motions of biomolecules by a direct mapping of their atomistic motions. In this context, the essential dynamics⁴⁵ from the atomistic simulations is used as a proxy for the functionally relevant motions. The ED-CG method determines the assignment of atoms to CG sites (the CG mapping) such that the essential dynamics subspace is best preserved at a given resolution.³³ The ED-CG method has been applied to a variety of globular proteins and protein complexes, including a ribosome,⁴⁶ actin filaments,⁴⁷ and a hydrogenase.⁴⁸ However, two limitations of the ED-CG method should be taken into consideration. First, the ED-CG approach does not by itself automatically determine the optimal resolution level of a CG model. The total number of CG sites is an externally set parameter by the user. (We note that this issue has been partially resolved in our previous work where we developed a set of criteria to choose optimal numbers of CG sites in different parts of a large biomolecular complex in a self-consistent way.³⁵) Second, there is no guarantee that the ED-CG technique will create the same CG model for a protein in two or more discrete functional states. A previous study from our group shows that the ED-CG models of globular proteins like G-actin only share 60–80% of similarity between the ATP- and ADP-bound states.⁴⁷ This creates a difficulty in using a CG representation, especially when it is desirable to study effects of transitions between distinct topological conformations. In this work, we have focused on addressing these issues for an important class of proteins, namely, TMPs.

As pointed out in prior work,⁴¹ it is important to understand the biomolecular features and peculiarities of the systems in order to construct meaningful CG models. It is generally appreciated in the field of coarse-graining that even small “inadequacies” in the CG mapping can manifest as damage beyond repair when the usual pairwise interaction potentials are used; two-site methanol is a classic example of a problematic CG mapping for a molecular liquid.^49,50 For TMPs, the membrane environment imposes particular constraints onto the structure and dynamics of the transmembrane domains inserted into the lipid bilayer⁵¹ and differentiates them from extra- or intracellular domains of TMPs or their soluble counterparts. Such constraints give rise to many intriguing structural and dynamic properties of TMPs to account for their functions, such as symmetry. Although TMPs often exist in multimeric symmetric complexes of several repeating subunits with similar tertiary structures (even though the primary sequences of these subunits may be diverse),⁶ they also frequently possess approximate internal symmetry.

This work is primarily focused on TMPs with approximate internal symmetry, but the findings have the potential to be extended to cases with generalized symmetry; a comparison is made between CG models built using ED-CG methods and ones built on a simple and intuitive heuristic that exploits the molecular symmetry. It is shown that, by exploiting symmetry, we are able to construct CG mappings of TMPs for highly CG simulations consistent with the mappings resulting from the systematic “bottom-up” ED-CG method without the need for fine-grained MD trajectories and complex numerical optimization schemes.

II. Models, Theory, and Methods

In principle, the ED-CG method could be applied to all the atoms in a given protein structure. However, as a matter of practice, we use a residue-based strategy instead, wherein the position of each residue is represented solely by its C_α atom. Given a protein of N_res amino acid residues and N_CG CG sites to assign (N_res≫ N_CG), we can calculate the ED-CG variational residual χ² and use it as a measure of the accuracy of a CG mapping to an underlying atomistic MD trajectory with n_t frames. As defined in prior work,³³ the residual is given by

1

where Δr_i^ED(t) is the fluctuation of the C_α atom of residue i in the essential subspace at time t, calculated from principal component analysis⁵² of the atomistic MD simulation. If the C_α atom of another residue j exhibits motion (in the essential subspace) similar to that of the C_α atom of residue i, then it is reasonable to assign residues i and j to the same CG site I. This idea is mirrored in the definition of the χ² (a “cost function”) by summing terms of fluctuation differences |Δr_i(t) – Δr_j^ED(t)|² over pairs of atoms belonging to the same CG site. In this scheme, the ED-CG method samples a variety of possible ways to group atoms/residues and selects the one with the minimum residual χ² as the optimal CG model.³⁵

Sequence-Based and Space-Based ED-CG Methods

The ED-CG approach comes in two main variations, namely, sequence-based³³ and space-based³⁶ ED-CG. Both methods group the atoms into CG sites based on minimizing intrasite correlated fluctuations, but the different variants of the method applies different rules in sampling to locate the global minimum of χ². The sequence-based ED-CG method divides the primary sequence of the protein into contiguous CG domains, while the spaced-based ED-CG method favors CG site definitions with atoms/residues close in the three-dimensional space. Provided the contiguous sequence constraint, the sequence-based ED-CG method is less demanding in sampling, but it does not permit nonadjacent domains in the same CG site, even if they are correlated in fluctuation but separated in the sequence (for example, in the case of a disulfide bond). Because of the much greater number of CG mappings allowed by space-based ED-CG, a brute-force search for the global minimum of χ² would require looking through an exponentially greater number of combinations in comparison to sequence-based ED-CG. The use of simulated annealing and steepest descent techniques significantly decreases the number of combinations to be considered.³³ Nevertheless, the amount of computations required to achieve a reasonably low value of χ² is still greater in the case of the space-based ED-CG, and this gap increases with the number of atoms or residues in the biomolecule under investigation.

Power Law Scaling of the ED-CG Residual χ²

In our prior work,³⁵ it was demonstrated that the ED-CG residual χ² for the optimal CG map with a given number of CG sites can be approximated by a simple function of the protein size and the number of CG sites,

2

where the anomalous dimension γ is a protein-specific parameter, δ is a protein-independent coefficient, and C′(T) is a temperature-dependent prefactor. For a wide class of proteins, the value of γ was found³⁵ to range from 0.00 to 0.91 (however, TMPs were not included into the studied set of proteins), while δ ≈ 0.35.

Internal Symmetry, Protein Fluctuation, and Symmetric CG Models

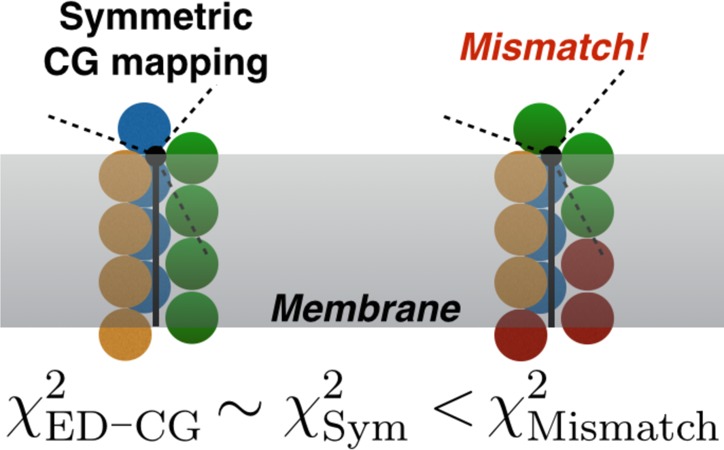
Internal symmetry will provide additional restraints in the coarse-graining of TMPs. In the context of biomolecules, we use the term internal symmetry for symmetry operations obeyed by the three-dimensional structure of the primary polypeptide chain sequence. On the basis of normal-mode analysis of MD simulations and group theory, Matsunaga and co-workers revealed that structural symmetry of homooligomers is a principal determinant of the entire protein complex’s symmetric fluctuation.⁷ In the same way, TMPs with internal symmetry should also have symmetric thermal fluctuation, which can be captured by ED-CG methods. Mapped onto the CG model, the symmetric domains of a TMP should result in identical CG domains. Directly, this suggests that the CG model should better describe symmetric fluctuation of the target TMP if it is consistent with the protein symmetry. In the simplest case of building a two-site CG model for a protein with perfect S-fold symmetry, we can always obtain the lowest ED-CG residual χ² when either CG site contains half of the residues.

Our direct method (without ED-CG) of systematically constructing directly comparable CG mappings (of adjustable resolution) that satisfy the three-dimensional structural symmetry of the molecule that it represents is as follows. The contiguous protein sequence is evenly divided into N_CG domains, which gives rise to a CG model that has an identical number of residues in each CG site (setting aside rounding errors); we shall refer to this construction as a symmetric model in this present work because these mappings satisfy a modular symmetry in the sense that each CG site is of equal size and separation in sequence space (N.B. only a subset of these mappings will be consistent with the structural symmetry of the molecule). We have collected a representative benchmark data set of eight important TMPs from Protein Data Bank (PDB)⁵³ (Table 1) that all exhibit approximate internal symmetry in order to compare the CG models built by the ED-CG method to these symmetric CG models and thereby elaborate on the necessity of preserving symmetries, exact or approximate, when constructing highly CG mappings for biomolecular systems.

Table 1. Transmembrane Proteins Analyzed in This Work Belong to Different Structural Types and Approximate Symmetry Groups.

protein	PDB ID code	residues	approximate symmetry point group	number of modular repeats	structure type
human integral membrane protein (hIMP) TMEM14A	2LOP(75)	25–99	C3	3	α-helical bundle
transmembrane domain of N-acetylcholine receptor (nAChR) β2 subunit	2KSR(76)	25–164	C4	4	α-helical bundle
human water channel aquaporin-1 (AQP1)	1H6I(77)	9–233	S2 (=Ci)	8	α-helical bundle
mitochondrial ADP/ATP carrier	1OKC(78)	2–293	C3	9	α-helical bundle
ammonia transporter (AMT1)	2B2F(79)	1–391	S2 (=Ci)	11	α-helical bundle
cytochrome c oxidase subunit 1 (COX1)-β	1QLE(80)	17–554	C3	12	α-helical bundle
outer membrane protein X (OmpX)	1Q9F(81)	1–148	C4	8	β-barrel
outer membrane protein A (OmpA)	2GE4(82)	0–176	C4	8	β-barrel

Modeling and Simulations of Transmembrane Proteins

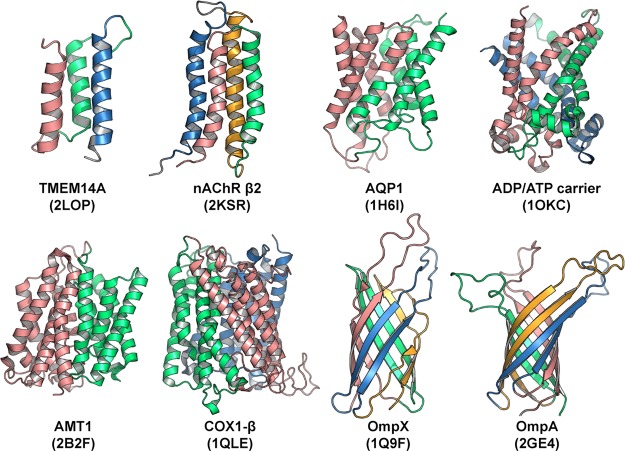
We selected a set of test cases by choosing TMPs with internal symmetry and no missing residues in the sequence. Our set of eight proteins represents TMPs of different size, structure, symmetry, function, and complexity and includes structures of either α-helical bundles or β-barrels (see Table 1 and Figure 1). We note that all of these proteins are folded and fluctuate around the stable equilibrium structure with no large-scale conformational rearrangements.

Figure 1.

Cartoon representations of eight transmembrane proteins studied in this work. Different colors are used to show symmetric units. PDB ID codes are indicated in parentheses.

These protein models were set up in a membrane-bound environment before performing the atomistic MD simulations. With Maestro (Schrödinger, Inc.), each PDB structure was prepared using Protein Preparation Wizard and embedded in a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) bilayer by the System Builder. The TMP-membrane assemblies were placed in the simulation boxes, which were filled with explicit water (TIP3P water model⁵⁴) and physiological salt (0.15 M NaCl) on both sides of the membrane. The distance between protein atoms and the box boundaries was at least 12 Å in all directions. CHARMM22/CMAP protein^55,56 and CHARMM36 lipid⁵⁷ force fields were used to assign parameters with the tool Viparr.⁵⁸ After a 9-step standard relaxation protocol, which has been successfully applied in previous studies,⁵⁹⁻⁶¹ each atomistic MD simulation was run for 30 ns in the isothermal–isobaric ensemble with constant temperature, T = 310 K, and constant pressure, P = 1 atm, using the Martyna-Tobias-Klein coupling scheme.⁶² Electrostatic forces were calculated using the particle mesh Ewald technique.^63,64 van der Waals and short-range electrostatics were cut off at 9 Å. Long-range electrostatics were updated every third time step. All MD simulations were performed in the Desmond 3.0 simulation package⁶⁵ with an integration time step of 2 fs. Hereafter, we applied the ED-CG method³³ to build the CG models from the simulated all-atom MD trajectories.

Data Analysis

Structure visualization was performed with VMD⁶⁶ and PyMOL.⁶⁷ Plots were prepared using Grace (xmgrace; http://plasma-gate.weizmann.ac.il/Grace) and NumPy⁶⁸/matplotlib.⁶⁹ For the different sets of CG models for each TMP with the same CG resolution level, we computed and analyzed the naïve model similarity defined as the fraction of residues assigned to the same CG sites in the two compared models,

where N_res is the number of residues and δ_M(i),N(i) is the Kronecker delta function adding to the similarity whenever residue i is mapped to the same CG site by the two mappings of equal resolution, M and N.

III. Results and Discussion

ED-CG and Symmetric Models of Transmembrane Proteins

Initial tests were performed to compare the CG models built with space- and sequence-based ED-CG methods. We decided to proceed with the sequence-based variant as a suitable representative approach; results were almost identical for the systems and resolutions studied in this paper (in general, though, they will not be), as the space-based method exhibited much slower convergence rates.

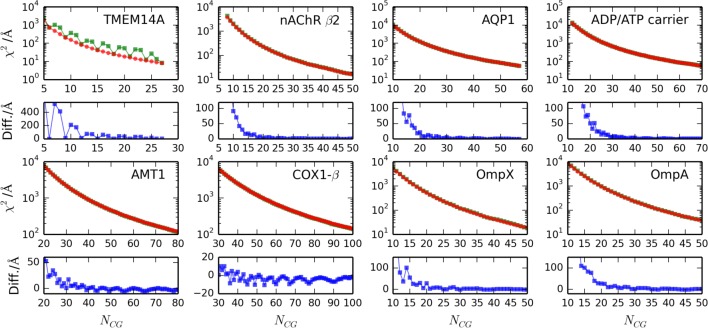
To compare the highly CG models built with the ED-CG method to the symmetric CG models, we calculated the value of the residual χ² (Figure 2) over a range of different numbers of CG sites (i.e., the CG resolution), corresponding to the highly CG mapping regime where multiple amino acid residues are represented by a single CG site. It is seen that the residuals for the symmetric models tend to exhibit an oscillatory behavior compared to ED-CG models and that the period of this oscillation depends on the CG resolution. These oscillatory “footprints” indicate that the collective dynamics, which encompasses symmetric modes for structurally symmetric molecules, is better captured by CG mappings that preserve the dominant symmetries. Since the calculated ED-CG χ² residuals are a good proxy for the lower bound of the residual χ² at a certain mapping resolution, we can identify a subset of the symmetric models that is optimal in the sense that the symmetric residual χ² is almost identical to its lower bound for these models. The error of the symmetric model can be estimated by comparing its residual χ² to the ED-CG χ²-residual-minimized mapping. While this error tends to be small, it increases systematically whenever the CG mapping does not preserve the structural symmetry of the TMPs, giving rise to what we shall call a symmetry mismatch that appears as an oscillatory difference in χ² between the symmetric model and the ED-CG model (Figure 2). It can therefore be eliminated to the point where the residual χ_Sym² ≅ χ_EDCG² by appropriately choosing the symmetric model that optimally aligns with the topological features of the TMP. The penalty for a symmetry mismatch follows the same power law relation as the ED-CG χ² residual, and the relative error is therefore strongly dampened as the resolution of the mapping is increased.

Figure 2.

Plots of the χ² residuals for the symmetric mappings (squares, green) and the ED-CG method resulting mappings (circles, red) for the eight transmembrane proteins plotted against numbers of CG sites (N_CG). The panel with blue dots below each major plot shows the difference in χ² between the symmetric model and the ED-CG model. Note the logarithmic scale for the y axis in the plotted χ² residuals.

Optimal Symmetric Models in the CG Regime with ∼10–20 Amino Acid Residues per CG Site Satisfy Symmetry

For all the test cases (Table 1 and Figure 1), it is observed that, for low values of N_CG (highly CG models), the optimal subset of symmetric models always contains models for which the number of CG sites complies with the symmetry point group in the sense that 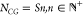for the TMP with approximate S-fold internal symmetry. When this rule is not obeyed, there will in general be a penalty in the χ² residual. Our results also show a number of differences between small and large TMPs. For small proteins, such as TMEM14A (75 residues), we observe excellent agreement between the two CG models when the N_CG is a multiple of 3, which can be visually understood looking at the CG map with 6 sites (Figure 3). The relatively large symmetry-mismatch penalty observed in the χ² residual for TMEM14A is attributed to two factors: (1) the small size of the protein and (2) the fact that the protein has three modular repeats (α-helices in this case), which coincides with the approximate 3-fold axis of symmetry (C₃). For the larger TMPs in our set of test cases, this effect is weaker (Figure 2). Model similarity between the ED-CG mapping and the symmetric mapping at this level of resolution was very high (∼80–90%) in all tested cases.

Figure 3.

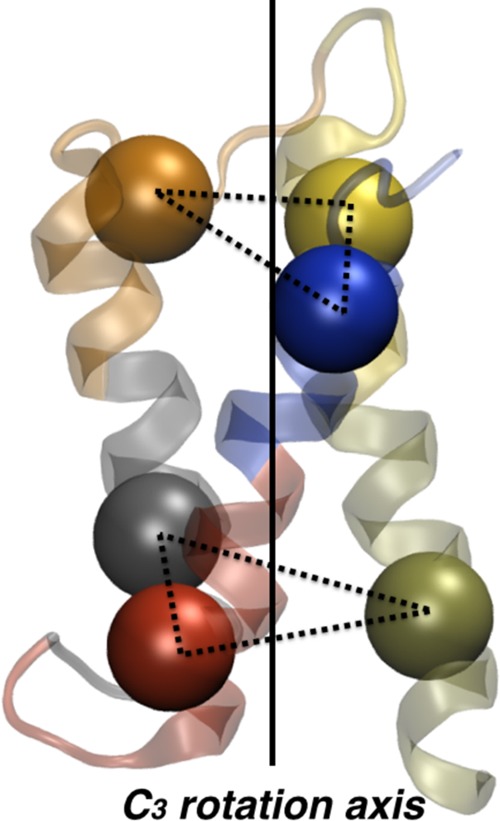
An example of a symmetric CG map for the protein TMEM14A. The backbone of the atomistic X-ray crystal structure is shown as translucent ribbons. The corresponding CG sites of the mapped structure are shown as solid spheres. The approximate C₃ symmetry axis is indicated by a vertical solid line. The geometric planes that flank the molecule in the long (transmembrane) dimension are indicated by dashed-line triangles.

Optimal Symmetric Models in the CG Regime with ∼5–10 Amino Acid Residues per CG Site Satisfy Modular Repeats in the Secondary Structure

The symmetry mismatch penalty for the higher resolution models is negligible. While model similarity between the ED-CG mapping and the symmetric mapping at this level of resolution for the tested cases varied somewhat (∼45–75%), the absolute difference in the values of the residual χ² is subtle (Figure 2, lower panels). This makes physical sense because, at a certain threshold resolution (here, ∼10 amino acids per CG site), there will be enough CG sites in the asymmetric subunit to adequately represent the dynamics of the unit in the essential subspace. However, it turns out that longer-period oscillations appear instead. These oscillations can be interpreted as mismatches (albeit numerically very small compared with the previously described symmetry mismatches) to the modular repeats in the secondary structure of the TMP. For α-helical bundles (β-barrels), the modular repeats are the individual helix-loop (strand-loop) motifs.

Physical Significance of the Anomalous Dimension γ

On the basis of the data plotted in Figure 2, we calculated the values of the anomalous dimension γ and the temperature-dependent prefactor C(T,N_res), as defined by eq 2. As shown in Table 2, γ falls in a small range around 1.0 for α-helical bundles and in another small range around 1.5 for β-barrels. These values are generally higher than the values previously reported for globular proteins like ubiquitin (γ = 0.50) or G-actin (γ = 0.33), implying that χ² decreases faster for TMPs than for other proteins when the resolution of the CG mapping is increased. Our results also show that the anomalous dimension γ falls within a very well-defined range for specific TMPs with similar topology. In addition, the similar γ values between the sequence-based ED-CG models and the symmetric CG models indicate good agreement with respect to scaling behavior through the whole range of mapping resolutions.

Table 2. Anomalous Dimensions γ of TMPs Are Close to 1, Unlike Those of Globular Proteins^a.

protein	Nres	ED-CG γ	sym. γ
human integral membrane protein (hIMP) TMEM14A	75	1.10 (0.02)	0.95 (0.04)
transmembrane domain of N-acetylcholine receptor (nAChR) β2 subunit	140	0.96 (0.01)	0.99 (0.03)
human water channel aquaporin-1 (AQP1)	225	0.96 (0.03)	0.98 (0.01)
mitochondrial ADP/ATP carrier	292	1.06 (0.04)	1.08 (0.05)
ammonia transporter (AMT1)	391	1.01 (0.01)	1.03 (0.02)
cytochrome c oxidase subunit 1 (COX1)-β	538	1.15 (0.02)	1.18 (0.03)
outer membrane protein X (OmpX)	148	1.54 (0.05)	1.57 (0.04)
outer membrane protein A (OmpA)	177	1.44 (0.05)	1.49 (0.03)

^aStandard deviations of our estimates of γ are shown in parentheses.

To explain why the values of γ in the case of TMPs are typically higher than in the case of globular proteins studied earlier, we studied two simplified models: one of a solid ball and the other of a straight rod. The anomalous dimensions for these two extreme case model systems are demonstrated to be 0 and 1, respectively (see Appendix A for details). Most proteins considered in the previous work³⁵ are globular; hence, it is reasonable that their anomalous dimensions are typically closer to 0. On the other hand, most TMPs considered in this work are formed by sets of transmembrane α-helices. A set of straight rods, in the approximation of weak interactions between the rods, has the same anomalous dimension as a single rod does (for details, see Appendix B). This analytical result explains why the anomalous dimensions of TMPs are closer to 1 and, therefore, greater than those for globular proteins.

The difference in the anomalous dimensions of the two groups of proteins (or, in general, any biomolecules) leads to an interesting consequence for a multimolecular complex formed by weakly interacting n_rod “rod-shaped” components (such as α-helices embedded into a lipid bilayer) and n_ball “ball-shaped” molecules (such as extra- or intracellular parts of membrane-associated proteins). In this case, an increase in the average resolution level of the CG model of the complex leads to a higher resolution representation of the “ball-shaped” parts in comparison to the “rod-shaped” parts or, in other words, the new CG sites added to the complex upon increasing resolution mainly end up in “ball-shaped” (e.g., extra- or intracellular) components of the complex. In mathematical terms, if the total number of CG sites in the multimolecular complex is denoted N_CG^total, then the ratio of the optimal number of CG sites per each “rod-shaped” component N_CG per rod to the optimal number of CG sites per each “ball-shaped” component N_{CG per ball} has the following asymptotic behavior as N_CG → ∞:

3

or, equivalently, the fraction of CG sites within “rod-shaped” components decreases with the increase of the resolution level of a CG model of the complex

4

Inversely, in coarser CG models, for example, UCG models,⁴¹ the optimal distribution of the CG sites implies a more detailed description of “rod-shaped” components (e.g., filamentous proteins or α-helices in a protein).

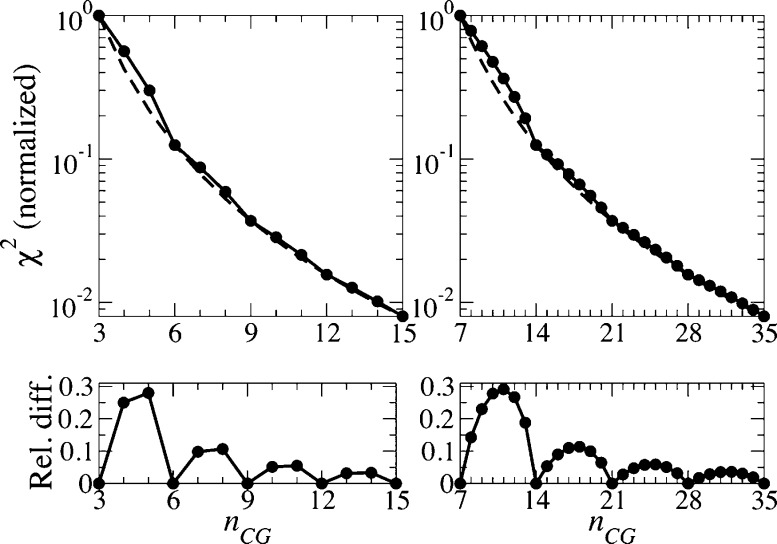
The oscillatory behavior of the χ²(N_CG) curves for TMPs with n_symm-fold rotational or rotoreflection symmetry can be explained on the basis of the universal scaling behavior for χ² provided by eq 2 and the fact that the anomalous dimension for straight rods equals 1 (see details in Appendix B). The dependence of χ² on N_CG predicted by this simple model is shown in Figure 4 in black solid lines. The behavior of these χ²(N_CG) curves is qualitatively similar to those in Figure 2 (especially, TMEM14A, AMT1, and COX1-β) despite the fact that the model of weakly interacting rods provides a simplified representation of dynamical behavior of TMPs.

Figure 4.

A model of n_symm = 3 (left panels) and n_symm = 7 (right panels) weakly interacting straight rods demonstrates an oscillatory behavior of the χ²(N_CG) curves (shown with solid lines and circles; the corresponding χ_lower²(N_CG) curves are shown with dashed lines). Therefore, the damped oscillatory behavior of the χ²(N_CG) curves for TMPs analyzed in this Article (see Figure 2) is qualitatively captured by the simple model approximating TMPs by several interaction rods. Note the logarithmic scale for the y axis in the top panels.

Connection to Information Content in the CG Model

Very recently, Foley et al.⁷⁰ investigated the connection between the entropic component of the potential of mean force (PMF) and the CG representation both in general terms and for concrete models, notably the Gaussian linear chain model where an exact explicit PMF could be derived. Their analysis suggests that there are bounds on the resolution range wherein information-efficient CG mappings can found. Our results presented herein add a new perspective by emphasizing that careful consideration of structural symmetries and local modularities in approximately symmetric transmembrane proteins may help to choose between CG mappings that preserve a comparable fraction of nontrivial information.

IV. Conclusions

In this work, we have demonstrated that accurate and precise CG mappings can be generated for a diverse class of TMPs without the use of computationally expensive MD simulations and subsequent global residual χ² minimization. To investigate the design principle in a general sense, we have studied CG mappings that partition transmembrane domains into contiguous segments of equal length along the primary sequence. The relative error in χ² resulting from the use of the proposed heuristic rule is oscillatory and strongly damped, which has two practical consequences. First, symmetry mismatch generally decreases for an increasing number of CG sites. Second, it is possible for the heuristic to produce CG mappings with negligible relative difference in χ² values to ED-CG methods even in the UCG regime, as long as the number of CG sites agrees with the overall symmetry group of the system (most important for low-resolution CG models) and conforms with the modular repeats (most important for medium-resolution CG models). It is likely that this heuristic will be especially useful when used in conjugation with other procedures to select optimal CG mappings on a case-by-case basis. Moreover, from the analysis of simple models, we predict that low resolution UCG models generated with the ED-CG approach should contain more CG sites in “rod-shaped” parts of proteins and protein complexes, such as α-helices immersed into a lipid bilayer, while higher-resolution CG models with more CG sites contain a larger fraction of CG sites in “ball-shaped” parts of the system, such as extra- or intracellular parts. In summary, our study provides new insight into highly CG modeling of TMPs and facilitates CG simulations by demonstrating that simple symmetry-preserving CG mappings are fast and reliable constructions, which have potential applications to future highly CG (or UCG) simulations of large TMPs and TMP assemblies on long time scales.

Appendix A

Two simple models are analyzed in this appendix: a solid ball and a straight rod. The solid ball was approximated by a set of N_res points (pseudoatoms) placed at random positions within a sphere of a constant radius with a uniform density distribution. The potential energy V of the system was approximated using an elastic network model (ENM),⁷¹⁻⁷³ namely,

5

where Δr_ij = r_ij – r_ij⁰ is the fluctuation of the distance between pseudoatoms i and j, r_ij is the equilibrium distance between these pseudoatoms, and the spring constants k_ij were chosen according to the following formula to make the model parameter-free:⁷⁴

6

where c is a constant. For various values of N_res, the Hessian matrix and the covariance matrix for the potential energy defined by eq 5 were computed as described by Zhang et al.,³⁴ followed by building CG models for various values of N_CG with the use of the space-based ED-CG method.^36,72 The space-based version of ED-CG was employed since the primary sequence of pseudoatoms is not defined in this model. The values of the anomalous dimension γ, as well as R² values characterizing the accuracy of eq 2, were computed by the method of least-squares for the resulting χ² (N_CG) dependencies in the log–log coordinates. Our numerical results indicate (see Table 3) that the value of the anomalous dimension monotonically decreases when the number of pseudoatoms N_res increases. The rate of the decrease in the anomalous dimension suggests that, in the limit of a continuous solid ball, γ = 0.

Table 3. Anomalous Dimensions γ of a Solid Ball and a Straight Rod Converge to 0 and 1, Respectively, in the Continuous Limit of the Number of Pseudo-Atoms N_res → ∞, Confirming the Validity of eq 2^a.

	Nres	500	1000	5000
solid ball	γ	0.063	0.041	0.020
	R2	0.99992	0.99998	0.99999
straight rod	γ	1.00005	1.00001	1.00000
	R2	1.00000	1.00000	1.00000

^aCalculations were performed using the χ²(N_CG) values at N_CG = 1, 2, ..., 9, 10. The coefficients of determination (R²) are very close to 1, showing the applicability of eq 2.

The second simple model is a straight rod formed by N_res pseudoatoms equidistantly positioned along the z-axis in three-dimensional space. The potential energy V of this system was defined in the following way:

7

where k is a constant, and the summation is performed only over all pairs of neighboring pseudoatoms. Expanding the right-hand side of eq 7 in a Taylor series in terms of the fluctuations in the Cartesian coordinates of each pseudoatom dx_i, dy_i, and dz_i and omitting the terms containing the third or higher powers of dx_i, dy_i, or dz_i, one arrives at the expression

8

suggesting that the problem of a straight rod in a three-dimensional space effectively reduces to the problem in a one-dimensional space. The Hessian matrix for the 1D problem is

9

(Note that omitting the third order terms in eq 8 does not affect the accuracy of eq 9, since these terms lead to zero contributions to the second derivatives at the reference geometry with zero displacements.) Using this Hessian, the covariance matrix and, subsequently, the χ²(N_CG) dependence can be obtained as described by Zhang et al.^34,36 The space-based and the sequence-based variants of the ED-CG method are effectively equivalent in the case of a straight rod, since sets of pseudoatoms located in space in the most compact way correspond to contiguous fragments of the sequence naturally defined in this model.

The values of the anomalous dimension, γ, as well as R² values, characterizing the goodness-of-fit of eq 2 for the model under consideration, are given in Table 3. They suggest that, in the limit of an infinitely large number of pseudoatoms N_res or, equivalently, for a continuous rod, the value of the anomalous dimension reaches γ = 1.

The two simple models analyzed here can be considered as two extreme cases of possible protein shapes. Globular proteins have shapes closer to a solid ball, and therefore, the values of the anomalous dimension γ are closer to 0, while rod-shaped proteins, as well as α-helices within a single protein in the approximation of weak interhelical interactions, are closer to the simple model of a straight rod, and therefore, their typical values of the anomalous dimension γ are closer to 1.

Appendix B

A symmetric TMP can be approximately represented as a set of n_symm weakly interacting straight rods. The term “weakly interacting” here implies the following. In the absence of interactions between the rods, the potential energy of the system is the sum of the potential energies of all rods, and the Hessian and covariance matrices acquire a block-diagonal form. Since each of these blocks is a positively defined matrix, the minimum of χ² defined by eq 1 is achieved for a CG mapping with atoms from different rods belonging to different CG domains. In other words, no CG domain in an optimal CG mapping includes atoms from different rods. Now, in the case of interacting rods, the lowest-order nontrivial terms in the expression for the potential energy are linear in terms of deviations of atoms from their reference positions. These terms, however, do not affect the Hessian since it is a matrix of the second order derivatives of the potential energy, and therefore, the linear terms accounting for inter-rod interactions do not change the values of the residual χ². In physical terms, this means that some attractive or repulsive forces may act between the rods and possibly distort their shapes, but these interactions between the rods and these distortions of the rods do not affect the stiffness of the rods. This approximation of “weak interactions” seems reasonable (at least some of TMPs), since it is well-known that the transmembrane α-helices and β-barrels in TMPs are structurally stable.

Due to the block-diagonal structure of the covariance matrix and therefore separability of the sum of squares of atomistic fluctuations into contributions from individual rods, the total residual χ² for the whole system of n_symm rods, according to eq 1, can be written as a function of the set of numbers of CG sites placed in the i-th rod N_CG,i in the following form:

10

where χ_i² (N_CG,i) is the value of the variational residue χ² for the i-th rod when the number of CG sites placed in that rod equals N_CG,i. Taking into consideration the universal scaling law for χ² provided by eq 2 and the fact that for straight rods the anomalous dimension is 1, eq 10 can be rewritten as

11

Minimization of χ²({N_CG,i}) under the constraints that the total number of CG sites in the system equals N_CG

12

and that each N_CG,i is an integer leads to the desired result for χ² of the system of n_symm rods as a function of the total number of CG sites N_CG:

13

We now define the function χ_lower²(N_CG) in the following way:

14

This definition differs from eq 13 in that N_CG,i^′ values are not limited to integers. Since the right-hand sides of both eqs 13 and 14 involve minimization but the latter case is less restricted, the following inequality must be satisfied:

15

The equality in this expression is achieved only when all N_CG,i^′ values from eq 14 are integers; otherwise, χ² > χ_lower². The values of N_CG,i and χ_lower² (N_CG) in eq 14 can be found using the technique of Lagrangian multipliers, leading to

16

Therefore, χ_lower² (as a function of N_CG) possesses the same power law behavior with γ = 1 as χ² for each rod. Note that {N_CG,i^′} values are integers if and only if the total number of CG sites N_CG is a multiple of the order of the symmetry axis n_symm. If this condition is not satisfied, then χ²(N_CG) > χ_lower²(N_CG). This explains why the χ²(N_CG) curve oscillates above χ_lower²(N_CG), only touching it when the CG mapping is consistent with the structural symmetry of the system (Figure 4). The χ_lower²(N_CG) curves in this figure were plotted using eq 16, while the χ²(N_CG) values were obtained by numerically solving the minimization problem in eq 13.

Author Present Address

^§ A.V.S.: Department of Chemistry, Stanford University, Stanford, CA 94305, United States.

Author Present Address

^# J.L.: Department of Chemistry, The University of Vermont, Burlington, VT 05405, United States.

Author Contributions

^‡ J.J.M., A.V.S., and J.L.: Authors contributed equally.

The authors declare no competing financial interest.