Rapid and Reliable Binding Affinity Prediction of Bromodomain Inhibitors: A Computational Study

Abstract

Binding free energies of bromodomain inhibitors are calculated with recently formulated approaches, namely ESMACS (enhanced sampling of molecular dynamics with approximation of continuum solvent) and TIES (thermodynamic integration with enhanced sampling). A set of compounds is provided by GlaxoSmithKline, which represents a range of chemical functionality and binding affinities. The predicted binding free energies exhibit a good Spearman correlation of 0.78 with the experimental data from the 3-trajectory ESMACS, and an excellent correlation of 0.92 from the TIES approach where applicable. Given access to suitable high end computing resources and a high degree of automation, we can compute individual binding affinities in a few hours with precisions no greater than 0.2 kcal/mol for TIES, and no larger than 0.34 and 1.71 kcal/mol for the 1- and 3-trajectory ESMACS approaches.

1. Introduction

Computational chemistry has been an established tool in drug discovery for a number of years. The number of crystal structures available in the public domain and within pharmaceutical companies on which to base computational studies continues to rise rapidly. Despite the increase in resources applied and in experimental data on which to base the studies, industrial structure-based design approaches have evolved very little in recent times.¹ In particular, the approaches are largely qualitative and largely dependent on the experience and knowledge of the practitioner.^2,3 Attempts to quantify protein–ligand binding affinities are rare. Expert practitioners have little confidence in existing tools to make robust predictions and certainly not to do so on a time scale that can substantially impact medicinal chemistry programmes.

Recently, there has been a renewed interest in the use of free energy calculations in drug discovery programmes. In particular, the FEP+ implementation of Free Energy Perturbation (FEP) has shown potential to improve the ability to predict protein–ligand binding affinities on an industrially relevant time scale.⁴ Research is ongoing to understand how broadly applicable the method is, and how accurate its predictions are when applied to active drug discovery programmes.

Although FEP+ applies replica exchange solute tempering (REST) in which exchange moves are made between different λ windows, its predictions, like those from many other approaches, are generated from a single output for each pair of mutations. Advances in high-end computing capabilities offer the opportunity to run vast numbers of calculations in parallel. The application of these computational capabilities to free energy calculations allows results to be returned quickly and multiple replicas of simulations⁵ to be run, leading to tighter control of standard errors. If such an approach could be validated and implemented in an industrial setting it would represent a major step forward in structure-based design capabilities. The first step in this process is to validate the performance on an industrially relevant data set.

Depending on the reliability, rapidity, and throughput of these calculations, they might find application at various stages of the drug discovery and development process across the wider pharmaceutical industry. As these methods require significant compute resources beyond existing in-house industrial capacity, assessment (and any subsequent adoption) of the methodology requires access to high performance computing resources.

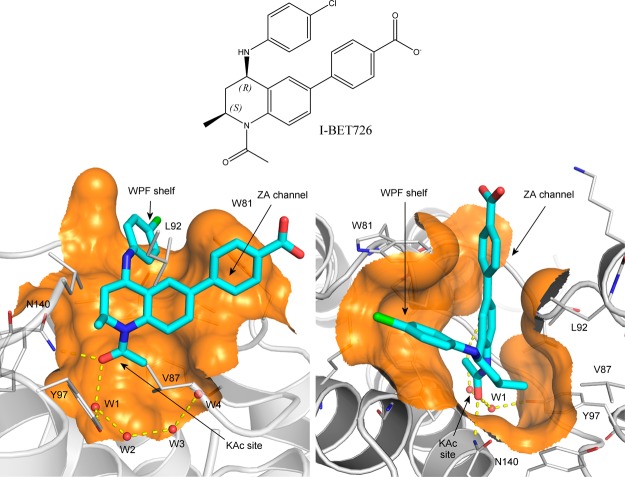
Research into epigenetic proteins is currently a major and rapidly evolving focus for the pharmaceutical industry.⁶⁻⁸ Bromodomain-containing proteins, and in particular the four members of the BET (bromodomain and extra terminal domain) family, each containing two bromodomains, have been widely studied. Small molecule inhibitors able to competitively antagonize the binding of acetylated histone tails to these modules have been shown to exert profound effects on gene expression and have shown promising preclinical efficacy in pathologies ranging from cancer to inflammation. Indeed, several compounds are progressing through early stage clinical trials and are showing exciting early results.⁹ Most inhibitors reported show similar binding potencies to all BET family bromodomains. A representative inhibitor-protein structure is given in Figure 1, showing the key elements for the inhibitor binding. This study will concentrate on the first bromodomain of bromodomain-containing protein 4 (BRD4-BD1) for which extensive crystallographic and ligand binding data are available.¹⁰⁻¹²

Figure 1.

Bromodomain inhibitor I-BET726 and its binding mode in BRD4-BD1. Two views are displayed for the binding mode (PDB ID: 4BJX(14)), in which I-BET726¹⁵ is represented as stick in cyan/blue/red/green, the protein is shown as cartoon in silver, the crystallographic water molecules are shown as red balls, and clipped protein surfaces are shown in orange.

The purpose of the present study is to assess the potential for rapid, accurate, precise, and reproducible binding affinity calculations based on the use of a Binding Affinity Calculator (BAC)¹³ software tool and associated services including a Python-based toolkit, FabSim,⁴¹ to automate data transfer and job submission. The approach is based on the use of high performance computing in an automated workflow which builds models, runs large numbers of replica calculations, and analyzes the output data in order to place reliable standard error bounds on predicted binding affinities.

2. Computational Section

Models

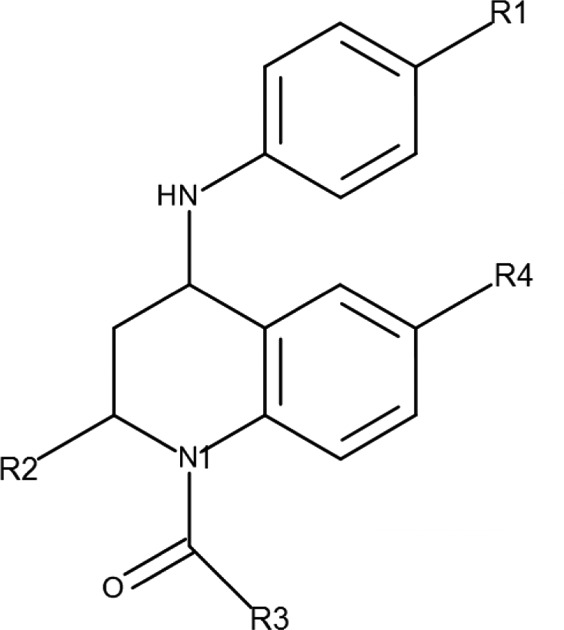
In this study, chemical structures of 16 BRD4-BD1 ligands based on a single tetrahydroquinoline (THQ) template¹⁵ were provided by GSK (Table 1). The compound set was designed to represent a range of chemical functionality and binding affinities, but also to contain sets of closely related compounds with key SAR trends. Specifically, there are two growth vectors which cause a drop off in potency, a growth vector where substantial structural variation is tolerated and an enantiomeric pair where one isomer is significantly more potent than the other. These will be described below. The calculations were then performed by the UCL group, initially blind, to investigate the ability of BAC to reproduce the SAR trends. The experimental binding affinities were not released to the UCL group until all of the computations had been completed and the estimation of binding free energies were reported (see Figure 3 below). These predictions were subsequently compared with the independently measured experimental free energies of binding (Table 1) as part of the assessment of the reliability of the method.

Table 1. Compounds Used in This Study, Ordered According to Their R4 Group, and Their Experimental IC₅₀s with Standard Deviations Converted into Binding Free Energies ΔG (kcal/mol).

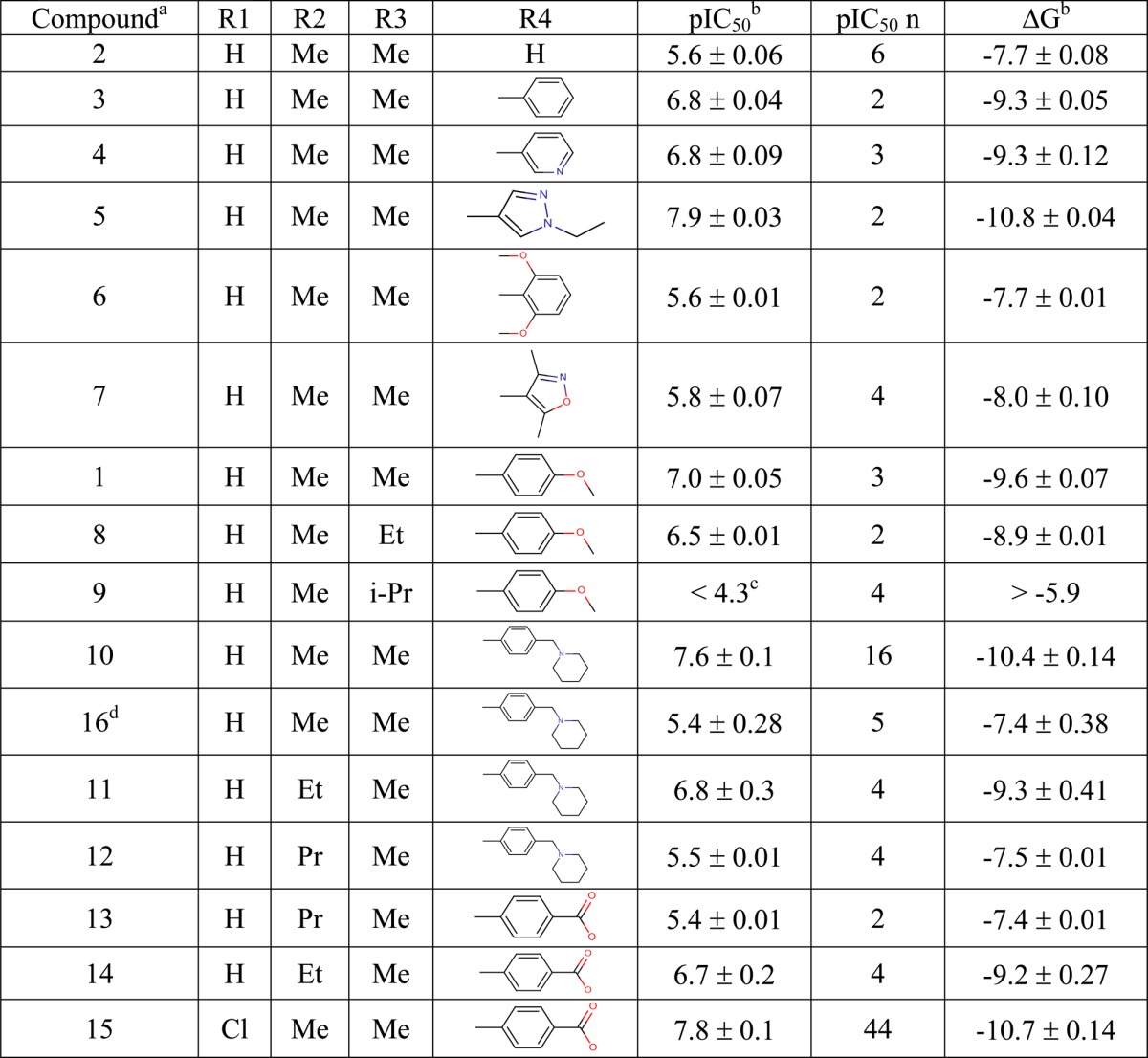
^aCompounds 1–9 are electrostatically neutral, compounds 10–12 and 16 are positively charged, and compounds 13–15 are negatively charged.

^bStatistical errors were calculated from repeated IC₅₀ measurements.

^cThere was no activity at the highest concentration (50 μM) tested.

^dAll compounds are the 2-(S) 4-(R) isomers (Figure 1) except compound 16 which is 2-(R) 4-(S).

Figure 3.

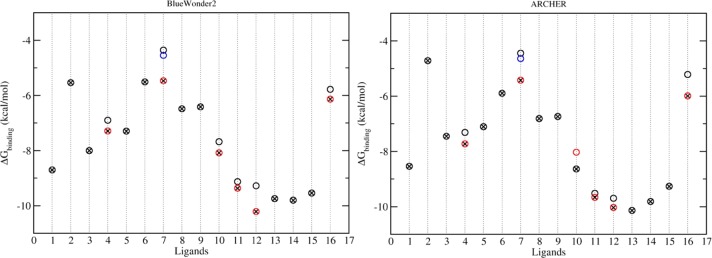
Calculated binding free energies from simulations on BlueWonder2 and ARCHER. The ligands are numbered as per Table 1. Circles with red/blue colors are the results based on studies with different rotamers. The circles with crosses are the final results with selected rotamers which are chosen on the basis of the sum of energies G_ligand and ΔG_binding (see eq 1). All of the calculated binding free energies are associated with standard errors of less than 1.7 kcal/mol, and are not shown in the figures for reasons of clarity.

The X-ray crystal structure used to represent BRD4-BD1 (published coordinates PDB ID: 4BJX(14)) is a complex with a THQ (I-BET726¹⁵) chosen in order to reproduce the likely conditions for which free-energy calculations might be used in a real drug discovery program. The binding mode of I-BET726 is shown in Figure 1. Both of the significant protein–ligand hydrogen-bonding interactions take place through the THQ N1-acetamide carbonyl group, which interacts directly with the Asn140 side chain of the acetyl-lysine binding site and also through the W1 water to the side chain of Tyr97. The W1 water forms part of a chain of water molecules buried within the site (W2–W4, Figure 1). Substituents larger than acetamide at the N1-position extend into the water-filled part of the site. Our ligand data set included a small series of increasing size at N1 (1, 8, and 9, see Table 1) to probe whether the computer methodology can accurately predict the outcome of growing into this region.

The THQ R2-position (S)-methyl group occupies a small lipophilic site between the side chains of three residues of the BRD4-BD1 ZA-loop (Val87, Leu92, and Tyr97). Carbon–carbon contacts for all three lie within 4.25 Å, apparently offering little room for extension of this group without some structural reorganization. Our ligand data set includes a small number of analogues exploring larger substituents at the R2-position (10–14) to see whether the simulation can accurately predict the consequences of pushing on these residues.

The THQ 6-phenyl substituent fills the narrow “ZA channel” between Trp81 and Leu92. This ring can be substituted at the R3- and R4-positions, but R2-substitution is detrimental because this causes an increase in the inter-ring torsion. The ZA channel does not seem to accommodate the resulting wider 6-substituents. The remainder of our data set includes a variety of substituents probing electrostatic and steric changes at this position.

The THQ 4-anilino substituent projects onto the “WPF-shelf” subsite outside the acetyl-lysine pocket, close to Trp81. SAR around this ring has been published previously,¹⁵ showing that substitution had small effects on potency, probably because one edge of the aniline ring is solvent-exposed. Therefore, we did not attempt to vary substituents at this position in our data set, preferring to keep it as constant as possible while exploring changes elsewhere.

In this series the 2-(S) 4-(R) isomers (see Figure 1) are significantly more potent than their alternative trans enantiomers. We included an enantiomeric pair of 2-(S) 4-(R) (compound 10) and 2-(R) 4-(S) (compound 16) isomers to explore whether the simulations were capable of distinguishing between them.

The ligand-protein complexes were constructed by replacing the ligand in the PDB file with the ligands of interest (see structures in Supporting Information). For the congeneric compounds studied here, it is plausible to assume that they bind in the same mode in which all key compound-protein interactions are preserved (Figure 1). For compounds with significant structural differences, computational docking may be required to generate reasonable complex structures.¹⁶ Preparation and setup of the simulations were implemented using BAC,¹³ including parametrization of the compounds, solvation of the complexes, electrostatic neutralization of the systems by adding counterions and generation of configurations files for the simulations. The AMBER ff99SB-ILDN¹⁷ force field was used for the protein, and TIP3P was used for water molecules. Standard protonation states were assigned to all titratable residues at pH 7, with histidines protonated on the ε position (HIE). Compound parameters were produced using the general AMBER force field (GAFF)¹⁸ with Gaussian 03¹⁹ to optimize compound geometries and to determine electrostatic potentials at the Hartree–Fock level with 6-31G** basis functions. The restrained electrostatic potential (RESP) module in the AMBER package²⁰ was used to calculate the partial atomic charges for the compounds. All systems were solvated in orthorhombic water boxes with a minimum extension from the protein of 14 Å.

Some of the ligands could adopt several rotamers for the R4 group (Table 1) in solution, which due to the constrained environment of the active site are unlikely to be sampled in a single bound simulation run with the protocol used (see Simulations subsection). To decide which rotamer(s) with which to start, metadynamics simulations²¹ were employed which used a history-dependent biasing potential to explore the conformational space of the chosen degrees of freedom, here the rotatable bond(s) involving groups R2 and R4 (see details in the Supporting Information). Five replicas were used for each metadynamics study to have a reasonable convergence of the potential profile of the chosen dihedral angle(s) of a ligand in complexed form. The calculated potential of mean force (PMF) was used to determine the most favorable rotamer(s) from which ESMACS simulations initiate. When unambiguous results ensued, the energetically most favorable rotamer was chosen. For some ligands, more than one rotamer showed similar free energies. In these cases, multiple initial structures were prepared using the rotamers suggested by the metadynamics study. The ligands with multiple rotamers were: 4, 7, 10, 11, 12, and 16. There are two rotamers for each of these, except for 7 for which there are three generated by the flip and twist between the two ring planes. This resulted in a total number of 23 complexes being simulated in the ESMACS study.

For each ligand with multiple rotamers, the energetic properties were analyzed and the most favorable rotamer was chosen as the final result of the ESMACS study (see Results section) and was used as the initial structure in the TIES study. For the latter, three subsets of the ligands were selected, within which relative binding free energies were calculated with the TIES approach. The subsets of the ligands were as follows: set 1 including ligands 1–9; set 2 including ligands 10, 11, and 12 which are positively charged; and set 3 including ligands 13, 14, and 15 which are negatively charged. The division of the full set of the cognate ligands into subsets is necessary because TIES, just as any other TI and FEP based method, encounters specific difficulties owing to major adjustments in long-range electrostatic interactions for the “congeners” where the net charges change.²² For each subset, ligands were paired based on their similarities, and TIES calculations were performed to alchemically mutate one ligand to another (see Theoretical Basis below).

Theoretical Basis

The UCL group have recently introduced new protocols for binding free energy calculations, termed “enhanced sampling of molecular dynamics with approximation of continuum solvent” (ESMACS)²⁴ and “thermodynamic integration with enhanced sampling” (TIES).²⁵ ESMACS is based on the molecular mechanics Poisson–Boltzmann surface area method (MMPBSA)²⁶ which makes a continuum approximation for the aqueous solvent, while TIES centers, as the abbreviation indicates, on thermodynamic integration (TI). Although the approaches are built around the standard MMPBSA and TI methodologies, our abbreviations are used to emphasize the central importance of the ensemble-based nature of the protocols employed as well as, in the case of ESMACS the wider generality and flexibility of the protocol.^5,24 The size of the statistical mechanical ensembles is determined systematically so that predictions are accurate, precise, and reliable.^24,27 Moreover, the term “MMPBSA” is used to mean very different things²⁸ in numerous journal articles and textbooks, including calculations based on single docked structures⁴ or on simulation trajectories, calculations with or without the inclusion of configurational entropies, and almost wholly using the so-called 1-trajectory approach. In the ESMACS protocol, we always mean a fully converged, ensemble-based determination of the free energy of binding from either a one-, two-, or three-trajectory method: this includes both the configurational entropy and the association free energy,^27,29 and (where appropriate) the relative or absolute adaptation energy.²⁴ Statistical analyses³⁰ were performed throughout the study for all of the quantities obtained. A Binding Affinity Calculator (BAC)¹³ was used to perform ESMACS and TIES studies. BAC constitutes a computational pipeline built from selected software tools and services (see Supporting Information), and relies on access to a range of computing resources. It automates much of the complexity of building, running, and marshalling the molecular dynamics simulations, as well as collecting and analyzing data. Integration and automation are central to the reliability of the method, ensuring that the results are reproducible and can be delivered rapidly.

In ESMACS, the free energy is evaluated approximately based on the extended MMPBSA method,^24,27 including configurational entropy, and the free energy of association.²⁹ Free energy changes (ΔG_binding) are determined for the molecules in their solvated states. The binding free energy change is then calculated as

1

where G_complex, G_receptor, and G_ligand are free energies of the complex, the receptor and the ligands, respectively. The Possion–Boltzmann calculation is performed here using the Amber built-in PBSA solver³¹ with radii taken from the parameter/topology files, and the configurational entropy is calculated by a normal mode (NMODE) method.

The three terms on the right-hand side of eq 1 can be generated from single simulations of the complexes or from separated simulations of complexes, receptor(s), and ligand(s). The former is the so-called 1-trajectory (1-traj) method of which the trajectories of the receptor(s) and the ligand(s) are extracted from those of the complexes. The latter is the so-called 3-trajectory (3-traj) method of which the trajectories are generated from separate simulations of the three components. In the drug development field, binding is usually investigated for a set of ligands bound to the same protein target. The free energy of the receptor G_receptor will then be the same for all ligands in the 3-traj method. In the current study, we employ three approaches to calculate the binding free energies ΔG_binding: (A) using single simulations of the complexes (1-traj); (B) same as (A) but using the average of the receptor free energies ⟨G_receptor⟩ from the 1-traj method (denoted as 2-traj); and (C) the same as (B) but invoking separated ligand simulations for the derivation of G_ligand (denoted as 3-traj).

In TIES, an alchemical transformation for the mutated entity, either the ligand or the protein, is used in both aqueous solution and within the ligand–protein complex. The free energy changes of the alchemical mutation processes, ΔG_aq^alch and ΔG_complex, are calculated by

2

and the binding free energy difference is calculated from

3

Here λ (0 ≤ λ ≤ 1) is a coupling parameter such that λ = 0 and λ = 1 correspond to the initial and final thermodynamic states, and V(λ) is the potential energy of an intermediate state λ. ⟨···⟩_λ denotes an ensemble average over configurations representative of the state λ. To avoid the well-known “end-point catastrophe”,³² a soft-core potential is used, along with an approach to decouple at different rates the electrostatic and van der Waals interactions of the perturbed atoms with their environment (for more details see the Supporting Information). The foregoing is a textbook account of thermodynamic integration; TIES differs by virtue of performing ensemble based calculations,^25,33 in the same manner as for ESMACS, thereby providing control of standard errors based on length of simulation and number of ensembles used. Indeed, it is important to note that the energy derivatives (eq 2) calculated for all λ windows are well described by Gaussian random processes, which makes it possible to draw on the theory of stochastic calculus to compute relevant properties reliably.⁵

Simulations

The ESMACS and TIES studies follow the protocol developed recently^24,25 (see Supporting Information). The Amber package²⁰ was used for the setup of the systems and analyses of the results, and the MD package NAMD2.9³⁴ was used throughout the equilibration and production runs of all simulations, including the metadynamics. An ensemble simulation was performed for each molecular system with identical atomic coordinates for all replicas. Energy minimizations were first performed with heavy protein atoms restrained at their initial positions. The initial velocities were then generated independently from a Maxwell–Boltzmann distribution at 50 K, and the systems were heated up to and kept at 300 K within 60 ps. A series of equilibration runs, totalling 2 ns, were conducted, while the restraints on heavy atoms were gradually reduced. Finally, 4 ns production simulations were run for each replica for all ESMACS and TIES simulations. In ESMACS, we used 25 replicas in an ensemble calculation for each ligand. In TIES, 5 replicas were used for each pair of the ligands. Simulation of each replica consists of 2 ns for equilibration and 4 ns for production run. Previous studies^24,27,30,35 have shown that the combination of the simulation length and the size of the ensemble provides a trade off between computational cost and precision.

Two independent ESMACS runs were performed to assess the reproducibility of the calculations. One was run on ARCHER, a Cray XC30 supercomputer (equipped with ca 118 000 cores), the UK’s National High Performance Computing Service located in Edinburgh; the other run on the BlueWonder2 supercomputer, an IBM NextScale Cluster (8640 cores) located in Science and Technology Facilities Council’s (STFC’s) Hartree Centre. A comparison between the two runs is very instructive, both in terms of performance and time to solution as well as providing an opportunity to conduct a valuable reproducibility study. Thanks to the large number of cores on ARCHER, we ran the entire set of ESMACS binding affinity calculations concurrently and had the findings available within 7 h. On BlueWonder2, we were hampered by a number of issues, resulting in the calculations taking significantly longer than on ARCHER. On BlueWonder2 and ARCHER, about 440 000 and 335 000 core hours were consumed in the course of this study, including 300 000 and 225 000 core hours for production molecular dynamics simulations and 140 000 and 110 000 core hours for free energy calculations, respectively.

The TIES study was performed entirely on ARCHER. TIES simulations of 7 out of 12 pairs were packed together (the currently enforced limit of maximum tasks for one job in ARCHER) and submitted as one single job, requiring 43 680 cores, which has high priority and executes rapidly on the machine (waiting time in the ARCHER queue was around 8 h). This made it possible to complete the entire TIES study of seven pairs within 1 day including queuing time. Further speed up is feasible on supercomputers with hybrid architectures which would permit for example GPU acceleration for some parts of these calculations.

3. Results

To assess the accuracy and precision of the method, we evaluated the binding affinities of the ligands (Table 1) to BRD4 and compared the computed results with experimental data. ESMACS was used for the full set of the ligands, including the stereoisomer which cannot be considered as a perturbation of any others. TIES was applied to three subsets of the ligands, of which each includes congeners with the same net charge.

Reproducibility

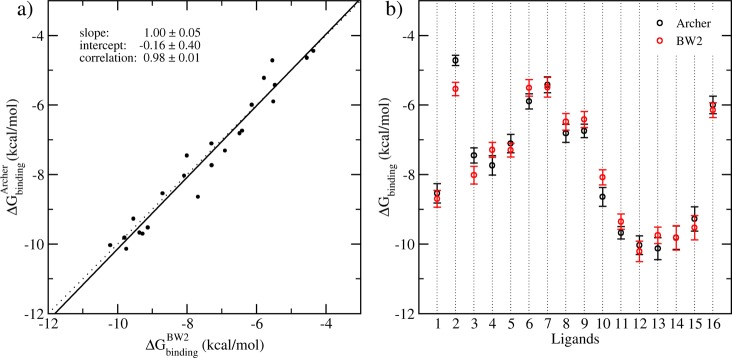
It is well-known that many complex systems exhibit sensitive dependence on initial conditions.^5,36 The differences of the initial velocities among individual simulations lead to rapid divergence of trajectories. The calculated thermodynamic properties from individual simulations will therefore inevitably differ. Two sets of ESMACS simulations were performed for the complexes independently on ARCHER and BlueWonder2 (see the Computational Section above). The results are compared by linear regression. Figure 2 shows the variances and correlation of the calculated binding free energies from the two sets of simulations. The correlation coefficient r is 0.98 ± 0.01, with no statistical differences between slopes and intercepts of the calculated regression line and the ideal line (x = y) (Figure 2a). The two studies produce consistent results, with an average difference of 0.07 ± 0.10 kcal/mol, and an average unsigned difference of 0.39 ± 0.06 kcal/mol. Only 3 out of 16 predictions do not overlap within their variances (Figure 2b). For the purpose of ranking compound selectivity, the Spearman correlation coefficient (r_S) is also calculated, which shows that the rankings from the two studies are very close to one another, with a highly significant Spearman correlation of 0.98 ± 0.02. In the following analyses, only the results from BlueWonder2 simulations are reported. The ARCHER-based calculations produced very similar results.

Figure 2.

Correlation and standard errors of the calculated binding free energies from two independent studies of the BRD4-ligand models performed on BlueWonder2 and ARCHER. (a) Correlation of the predictions, including all rotamers, from 1-traj calculations performed on BlueWonder2 (BW2, horizontal axis) and ARCHER (vertical axis). Solid line, regression of the data using means of the calculated free energies; dotted line, 1:1 ideal regression. (b) the averages and their standard errors from the two separate calculations. One rotamer is used for each ligand.

Choosing Rotamers

Some of the ligands (Table 1) would be able to adopt more than one rotamer in solution. When the ligands are complexed with the protein, they are usually trapped in a specific rotameric state. The energy barriers between rotamers are sufficiently high, especially for groups occupying the narrow ZA channel (Figure 1), that it is not feasible to achieve equilibrated populations of rotamers using the current protocol. We therefore initiated molecular dynamics simulations of complexes from all possible rotamers for six out of the 16 ligands. Simulations including different rotamers are only applied to the complexes, as the free ligands in water are able to fully sample all rotamers. The most favorable rotamer is selected (Figure 3) for each ligand in its complex form, based on the lowest ligand energy of the rotamer, which is approximated by (G_ligand + ΔG_binding).

Comparison between ESMACS Calculations and Experiments

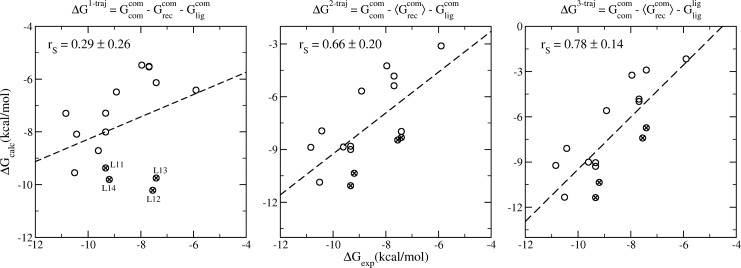
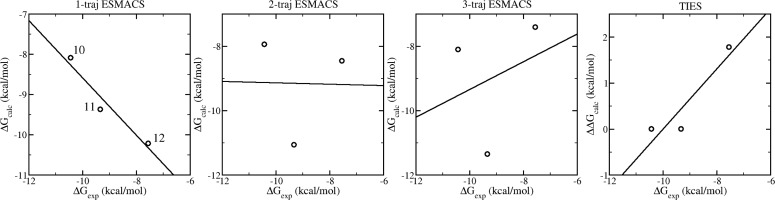
The predicted binding free energies from the 1-traj approach exhibit a weak Spearman correlation with the experimental data (Figure 4a). In the current study, as commonly employed in pharmaceutical drug development projects, a series of ligands are investigated for the same protein target. The energy of the protein therefore does not affect the ranking of the binding affinities (eq 1). Treating it as a constant, the 2-traj approach significantly improves the correlation between the predictions and experimental data (Figure 4b). Incorporating the free energies of the ligands from their individual simulations in free form, the 3-traj approach, further improves the correlation (Figure 4c). The most significant improvement appears in the compounds involving modifications at the R2 position of the tetrahydroquinoline (Table 1), for which the 1-traj approach predicts an increase (compound 11 to 12) or no change (compound 14 to 13) in the binding affinities when an ethyl is replaced by an n-propyl. The 2- and 3-traj approaches correctly rank the binding potencies of the two pairs, and indeed of these four compounds. Although the improvement is most evident for the listed four compounds, it is indeed applied to the overall correlation for the whole set (Figure 4). It should be noted, however, that although the 2- and 3-traj methods significantly improve the correlations between predictions and experimental data, relatively large standard deviations, up to 1.7 kcal/mol, are associated with the calculated free energies. This indicates that the binding free energies must differ by no less than 3.4 kcal/mol to be statistically significant to a 95% confidence level. With the experimental free energy differences ranging from 0.0 to 4.9 kcal/mol, a larger ensemble would be required to reduce the relatively large uncertainties in order to render all the predictions statistically significant. It is important to mention here that experimental binding affinities usually contain errors to a greater extent³⁷ than are implied by Table 1. Generating reproducible binding free energies from experiments is as important as that from simulations to make the comparisons statistically significant.

Figure 4.

Spearman ranking correlations of the calculated binding free energies and the experimental data from 1-traj (left panel), 2-traj (center), and 3-traj (right panel) ESMACS approaches. The equations on the subfigures indicate the calculations used in each case. The subscripts (com/rec/lig) and the superscripts (com/lig) in the equations indicate the components (complexes, receptor, and ligands) and the simulations (complexes and free ligands), respectively. The ligands with modifications at the R2-position of the tetrahydroquinoline are marked with crosses; they are all significantly improved in the 2- and 3-trajectory version. The standard errors, which are 0.19–0.34 kcal/mol for the 1-traj and 1.02–1.71 kcal/mol for the 2- and 3-traj approaches, are not shown for reasons of clarity. They are calculated using a bootstrapping method (see Supporting Information). The 2- and 3-traj approaches have similar errors because the energy of the receptor is treated as a constant and hence the uncertainties are dominated by the energies of the complexes.

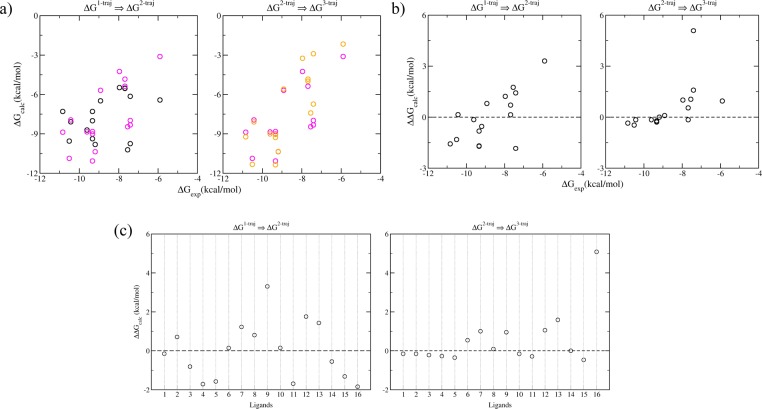
The improvements are achieved by including the adaptation energies of the receptor and the ligands (Figure 5). While the adaptation energies for the ligands are calculated as the differences between the free energies in their bound and free states, those for the receptor are calculated relative to the average of the receptor free energies in the bound states. The absolute adaptation energies of protein for each ligand binding would require a converged ensemble simulation of protein in solvent, preferably initiated from structures of the protein in its free state. As the ranking of the ligand binding is the main concern of the study, and the relative adaptation energies of the protein are energetically as informative as the absolute ones in the binding affinity comparison, no attempt has been made here to compute accurate absolute adaptation energies for the protein (all adaptation energies for the protein are relative ones in the current paper). Unfavorable adaptation energies are usually induced within the protein by the introduction of larger functional groups at R2 and R3 positions of the compounds (Figure 5c). It is interesting to note that, for the ligands with higher binding affinities (ΔG_binding < −8 kcal/mol), only small adaptation energies arise for both the receptor and the ligands, which makes the binding apparently closer to a “lock and key” recognition mechanism; while for the ligands with lower binding affinities, non-negligible adaptation energies are found for both the receptor and the ligands (Figure 5b). The one exception is the stereoisomer ligand 16 (Table 1) whose binding induces the smallest relative adaptation energy of the receptor but the largest adaptation energy for the ligand (Figure 5c). This compound was included in the set as a negative control to investigate the ability of the computational procedure to highlight the weak activity of the enantiomer of compound 10. Compound 16 has a very high ligand strain, suggesting that this isomer has the wrong shape for the binding site and must adopt a high energy conformation to interact with the protein.

Figure 5.

Improvement of the predictions by inclusion of the adaptation free energies of the receptor and the ligands: (a) the binding free energy changes between the 1-traj (black circles) and 2-traj (magenta circles) indicate the relative adaptation energies of the receptor; those between the 2-traj (magenta circles) and 3-traj (orange circles) show the adaptation energies of the ligands. The adaptation energies can be seen more clearly in panels b as a function of binding affinities, and in panels c for each ligand.

The ESMACS predictions are precise and accurate in terms of ranking the binding free energies, and are so in a reproducible way. However, ESMACS does not provide accurate absolute free energies. In our study, the 3-traj ESMACS protocol yields a much better correlation than the 1-traj ESMACS approach, while they have similar mean absolute deviations (1.97 ± 1.33 kcal/mol and 1.74 ± 0.29 kcal/mol, respectively). The mean absolute deviations can be significantly larger for more flexible ligands such as peptides binding to a major histocompatibility complex (MHC).²⁴ Some studies show that improved binding free energy prediction could be obtained by including important water molecules between ligands and protein.³⁸ Inclusion of the bridging water molecules (Figure 1) in the current ESMACS study, however, does not improve the correlation between the calculated binding free energies and the experimental measurements (see Figure S3 in the Supporting Information). Indeed, ours is a “generic” methodology which treats solvent implicitly and works well as such. Embarking on any approaches for treating water molecules explicitly would lead to a loss of simplicity in the method without conferring any benefit.

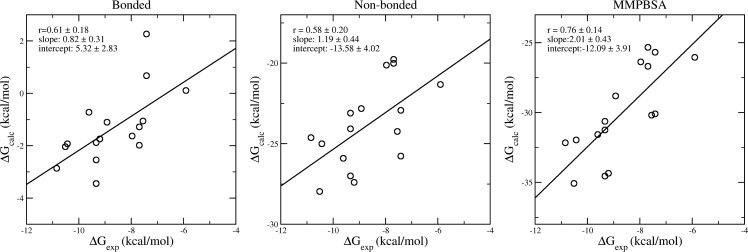
Component analyses of the binding free energies could provide insight into the mechanism of compound binding. In our study of peptide-MHC binding,²⁴ for example, the van der Waals interaction was shown to be the dominant component and to manifest a good correlation with the experimental binding free energies in the 3-trajectory ESMACS study. In the current molecular systems, however, there are no significant correlations between any energy component and the experimental data, except the bonded (including bond stretching, angle bending, torsions and improper torsions) and nonbonded (van der Waals, electrostatic and solvation) interactions as shown in Figure 6. The sum of the two interactions improves the correlation further, with a similar correlation coefficient as shown in Figure 4 for the 3-trajectory approach. It can therefore be deduced that the configurational entropy component does not contribute to the quality of the ranking prediction. As for the impact of the configurational entropy on the ranking of calculated binding affinities, different conclusions—improving,²⁷ worsening,³⁹ or having no effect²⁴—have been drawn for diverse protein–ligand complexes. The differences may indeed reflect the mechanism of protein–ligand binding which can be driven predominantly by enthalpy, by entropy, or by both.⁴⁰

Figure 6.

Correlations of free energy components and the experimental data from 3-traj approaches. Both bonded and nonbonded energy terms contribute to the ranking of binding affinities. Their combination (the MMPBSA energy) exhibits a better correlation with experimental data than the components themselves.

Comparison between TIES Calculations and Experiments

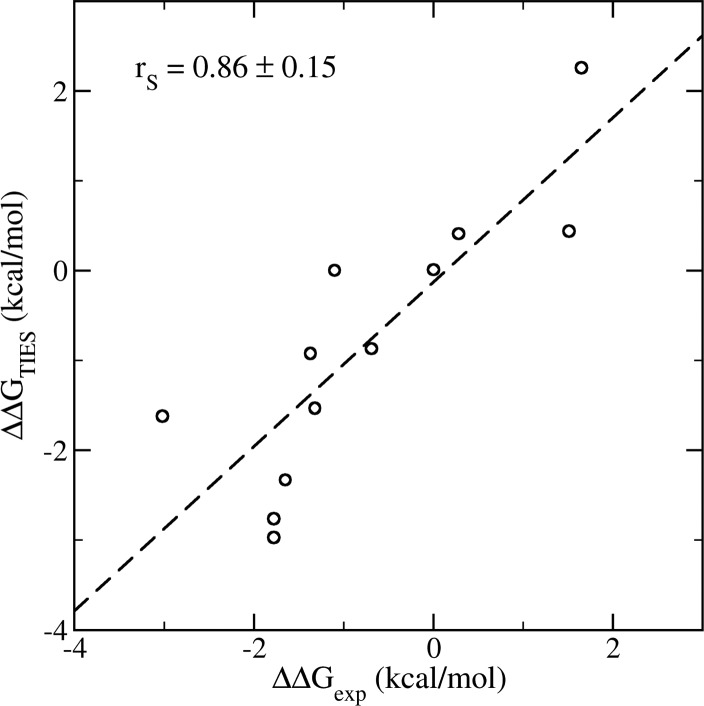
Good agreement is found for the binding free energy differences between the TIES calculations and the experimental measurements. The TIES approach is both accurate and precise, yielding a Spearman ranking coefficient of 0.92 for the means of calculated and experimental binding free energy differences. The bootstrap analyses give a Spearman coefficient of 0.86 ± 0.15, drawn from a non-normal distribution of resampling correlation coefficients (see Figure S4 in the Supporting Information). An average difference of 0.06 ± 0.26 kcal/mol, and an average unsigned difference of 0.75 ± 0.14 kcal/mol, are found between the predictions and experimental measurements (Figure 7). It should be noted that experimental binding affinities may have statistical errors of around 24% from isothermal titration calorimetry (ITC)³⁷ which is a more reliable method to measure binding affinities than the IC₅₀ measurements used in this study. The variances observed in the study can be partially attributed to these experimental errors. The regression line is close to an ideal 1:1 regression, with a slope of 0.93 ± 0.24 and an intercept of −0.10 ± 0.33 kcal/mol. A similar level of accuracy was recently reported¹⁶ in an absolute binding free energy calculation for a set of drug-like molecules binding to BRD4, albeit little attention was paid to reproducibility in that work.

Figure 7.

Correlations of the calculated binding free energy differences from the TIES study and from experimental measurement. The standard error bars from the TIES calculations are all no greater than 0.2 kcal/mol.

4. Discussion

To analyze the results it is necessary to consider the differences between the 1-, 2- and 3-trajectory methods. The 1-trajectory simulation calculates the ΔG_binding assuming there is no energetic penalty for the adaptation of the protein or ligand to the binding conformation, the 2-trajectory method takes the change in protein energy into consideration and the 3-trajectory method accounts for the changes in both protein and ligand energy.

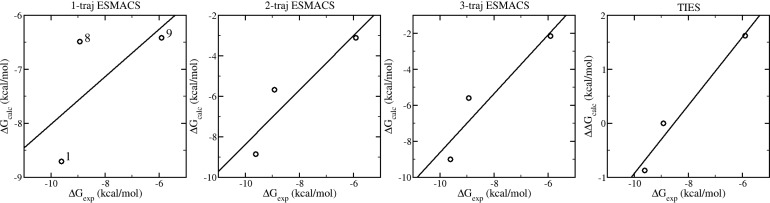
The test set for this evaluation was designed to investigate the ability of ESMACS to predict specific SAR trends. The first trend is the loss of potency observed as the hydrophobic part of the acetyl lysine mimetics is grown from methyl (1) to ethyl (8) to isopropyl (9). Figure 8 shows that, in the 1-traj simulation, compound 1 is predicted to be more potent than compounds 8 and 9, but no difference is predicted between 8 and 9. This is in contrast to the experimental results which show a modest loss of potency going from methyl to ethyl, but a substantial loss going from ethyl to isopropyl. On comparing the same three compounds in the 2-traj simulation, the predicted affinity of compound 9 is substantially reduced giving the correct ranking of the three compounds. The predictions for the three compounds are qualitatively the same for the 3-traj calculation. These results indicate that the low activity of compound 9 is the result of the increased bulk of the isopropyl group causing strain in the system, which is manifested in an increased internal energy of the protein. In fact, compound 9 has the highest protein internal energy of the whole data set (Figure 6c). The TIES study gives the same ranking for the binding affinities as those from the 2- and 3-traj ESMACS, but with an enhanced correlation coefficient compared to that of ESMACS. Structurally, this result makes sense because the isopropyl group is rigid and so the strain caused by the increased bulk cannot be accommodated by the ligand and hence is transmitted to the protein.

Figure 8.

Calculated vs experimental binding free energies for ligands 1, 8, and 9 which are labeled in the 1-traj subfigure.

The second SAR trend of interest is the effect of increasing bulk at the R2-position of the tetrahydroquinoline (THQ). Similar to the previous instance, increasing the size of the substituent at this position from methyl (10) to ethyl (11) to n-propyl (12) results in a sequential loss of activity. In this case the 1-traj method inverts the rank order of the three compounds (Figure 9), relative to experiment, predicting the n-propyl to be the tightest binder. The 2-traj calculation predicts a decrease of the potency of compound 12, consequently predicting it to be substantially weaker than compound 11, as observed experimentally. In the 3-traj method the potency of compound 12 drops further, relative to the other compounds. In all three ESMACS methods, the potency of compound 10 is under-predicted relative to the other compounds; the reason for this is unclear. The TIES study also predicts the binding of compound 12 to be the weakest in this subgroup, but could not distinguish the affinities of the compounds 10 and 11. A second pair of compounds also has the ethyl (14) to n-propyl (13) modification at the same position, and qualitatively the results parallel those described above. In this case, the n-propyl compound shows a correctly predicted loss of activity in both the TIES and 2- and 3-traj ESMACS methods, indicating the loss in potency for this bulky group is due to a combination of protein and ligand strain (Figure 6c). Again, this is consistent with the molecular structure of compound 12, because the n-propyl group is more flexible than the isopropyl group in the first example and consequently is more able to adopt a slightly strained ligand conformation.

Figure 9.

Calculated vs experimental binding free energies for ligands 10, 11, and 12 which are labeled in the 1-traj subfigure.

The carbonyl group in all compounds forms a hydrogen bond with a conserved asparagine Asn140 in the BRD4. This is a key interaction observed in bromodomain-ligand complexes as it mimics the interaction made by the carbonyl of the acetyl lysine of the substrate. The occupancies of this hydrogen bond in all of the compounds are very similar, and do not appear to correlate with their binding affinities. Hence, when bulk is increased adjacent to this key binding motif, as described in the previous cases, the loss of potency does not result from the disruption of this hydrogen bond. Conversely, the interaction is maintained at the expense of creating internal strain in the system. This is consistent with the observation that this is a ubiquitous interaction in this protein and a key binding pharmacophore.

For compounds 13, 14, and 15, there is an extra hydrogen bond formed between the carboxylate group of the ligands and the Lys 91 of the protein. The replacement of n-propyl (13) with ethyl (14) and methyl (15) slightly changes the orientations of the compounds, making the carboxylate group better aligned for the formation of hydrogen bonds. The occupancies of this hydrogen bond are 16.6%, 31.7%, and 33.3% for the compounds 13, 14, and 15, respectively (the cutoff values are 3 Å and 120° for the donor–acceptor distance and donor–hydrogen–acceptor angle). The occupancies of the hydrogen bonds for these 3 compounds appear to correlate with their binding affinities (−7.41, −9.20, and −10.51 kcal/mol). However, the energetic contribution of this solvent exposed interaction is difficult to quantify, and the energetic analysis elsewhere in this section suggests that differences in intermolecular interactions in the complex contribute modestly to the differences in binding free energy compared to differences in internal energies. Further evidence for this is seen in the pairs of compounds 11,14 and 12,13, which are identical except for a carboxylic acid to piperidine (base) modification in this region. These pairs of compounds have very similar binding affinities both in terms of experimental and predicted values.

These data suggest that the internal energy of the protein and ligand are major contributors to the relative binding affinities of this series of compounds. The internal energy contributions are exemplified by plotting the difference between the binding free energies predicted using the different ESMACS methods (Figure 10).

Figure 10.

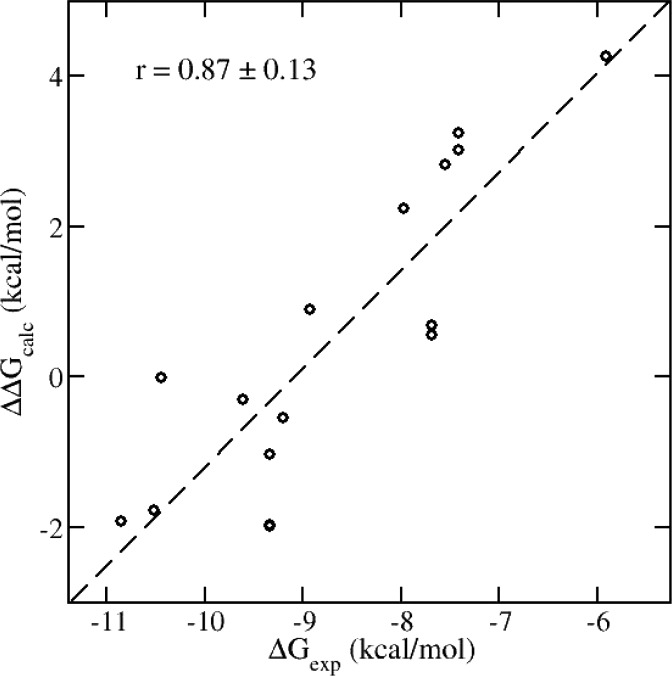
Correlations of the internal energy contributions to the calculated binding free energies and experimental measurement. The internal energy changes are calculated as the differences of the binding free energies between those from the 1-traj and 3-traj approaches: ΔΔG_calc = ΔG_binding^3-traj – ΔG_binding.

Figure 10 plots the difference between the ΔG_binding calculated by the 3-traj method and the 1-traj method against the experimental ΔG_binding. This is a plot of the internal energy of the protein and ligand against the experimental ΔG_binding; it shows a strong correlation (r = 0.87 ± 0.13). If this is contrasted with the 1 trajectory method—which essentially contains the intermolecular contributions to ΔG_binding, Figure 4a (r = 0.29 ± 0.26)—one can conclude that, for this protein and set of ligands, the internal energy of the ligand and the protein differentiate between the ligands to a far greater extent than protein–ligand interaction energies.

5. Conclusions

The Binding Affinity Calculator (BAC) software environment has been used to run ESMACS and TIES calculations against a series of inhibitors of BRD4 from the THQ chemical series. High performance computing was used in an automated workflow to build models, run multiple replicas of calculations and analyze the output, placing reliable standard error bounds on predicted binding affinities.

Despite the challenging data set used for this evaluation, good agreement is found for the binding free energy differences between the experimental measurements and the theoretical calculations, for both ESMACS and TIES. ESMACS is good as an “absolute” method for ranking an arbitrary set of ligands, which may be very diverse in terms of structures and electronic properties. To produce good rankings it is necessary in this case to use a 3-trajectory version, which has the further benefit of clearly distinguishing between ligands that adhere more closely to the “lock and key” or to the “induced fit” binding hypotheses. TIES performs well in determining relative binding free energies of congeners when there is no change of net charge, even when there are differences in structural features between pairs of compounds which one would not intuitively regard as minor.

Overall, ESMACS provides reliable binding affinity rankings and clear mechanistic insight into what factors drive binding processes in individual ligand–protein systems. TIES offers more quantitative accuracy in its predictions but, owing to its alchemical basis which necessarily keeps two congeneric ligands in play at all times, is less able to provide similar structural and mechanistic insights into binding. The standard errors in ESMACS and TIES are fully controlled through simulation length and number of replicas used in the ensembles chosen.^24,27

The results also offer insight into possible design strategies for BRD4 ligands. In particular it has been noted that, within a chemical series, differences in binding affinity do not seem to result from differences in protein–ligand interaction energies. On the contrary, to avoid unfavorable (in this case, mainly steric) interactions, both ligands and protein adopt strained states resulting in large adaptation energies. Hence, during the optimization of a chemical series for BRD4 it would be prudent to carefully consider the shape complementarity of the ligand and the active site cavity. It should be noted, however, that this study did not include molecules in which unfavorable electrostatic protein–ligand interactions were introduced.

The results offer encouragement that BAC, and its underlying approach of running multiple replicas of each simulation to improve predictive power,⁵ can accurately rank ligands by their binding free energy. Further evaluations are planned to confirm this potential. As large and secure computing resources become more routinely available, for example through cloud computing, it will become increasingly easy for industrial groups to access approaches like the one outlined in this study. Consequently, the robust prediction of protein–ligand binding affinities in an industrial setting should become more routine and offer a long awaited development in the field of structure-based design.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00794.

• Detailed description of the methods used, additional energetic analyses of the metadynamics, free energy calculation with inclusion of explicit water molecules, alongside the atomic coordinates of the compound-protein complexes and experimental data on compound binding (PDF)

• Structures of the studied compounds (ZIP)

The authors would like to acknowledge the support of EPSRC via the 2020 Science programme (http://www.2020science.net/, EP/I017909/1), the Qatar National Research Fund (7-1083-1-191), the MRC Medical Bioinformatics project (MR/L016311/1), the EU H2020 CompBioMed (675451) and ComPat (671564) projects, and funding from the UCL Provost. We acknowledge use of Hartree Centre computer BlueWonder2 in this work and assistance from its scientific support staff. The STFC Hartree Centre is a research collaboratory in association with IBM providing High Performance Computing platforms funded by the UK’s investment in e-Infrastructure. We made use of ARCHER, the UK’s national High Performance Computing Service, funded by the Office of Science and Technology through EPSRC’s High-End Computing Programme. Access to ARCHER was provided through the 2020 Science programme. This research was partially supported by the PLGrid Infrastructure through which access to Prometheus, the fastest Polish supercomputer run by ACK Cyfronet AGH in Krakow, was provided.

The authors declare no competing financial interest.