Abstract
OBJECTIVE
The objective of the present study is to develop and validate a fast, accurate, and reproducible method that will increase and improve institutional measurement of total kidney volume and thereby avoid the higher costs, increased operator processing time, and inherent subjectivity associated with manual contour tracing.
MATERIALS AND METHODS
We developed a semiautomated segmentation approach, known as the minimal interaction rapid organ segmentation (MIROS) method, which results in human interaction during measurement of total kidney volume on MR images being reduced to a few minutes. This software tool automatically steps through slices and requires rough definition of kidney boundaries supplied by the user. The approach was verified on T2-weighted MR images of 40 patients with autosomal dominant polycystic kidney disease of varying degrees of severity.
RESULTS
The MIROS approach required less than 5 minutes of user interaction in all cases. When compared with the ground-truth reference standard, MIROS showed no significant bias and had low variability (mean ± 2 SD, 0.19% ± 6.96%).
CONCLUSION
The MIROS method will greatly facilitate future research studies in which accurate and reproducible measurements of cystic organ volumes are needed.
Keywords: autosomal dominant polycystic kidney disease, geodesic active contour, planimetry, stereology, total kidney volume
For diseases such as autosomal dominant polycystic kidney disease (ADPKD) [1–3] and polycystic liver disease [4, 5], organ volume is used as a biomaker of disease severity. Organ volume has been shown to be both well correlated with clinical manifestations and an important factor in disease prognosis and therapy assessment [6–8].
The U.S. Food and Drug Administration recently issued a draft guidance on the use of total kidney volume (TKV), evaluated in combination with patient age and estimated glomerular filtration rate, as a qualified prognostic biomarker for use in clinical trials investigating treatments for ADPKD [9]. The Committee for Medicinal Products for Human Use, which is under the auspices of the European Medicines Agency, has also supported TKV, in combination with patient age and the estimated glomerular filtration rate, as a prognostic biomarker for identifying patients in whom a progressive decline in renal function, as characterized by a decline in the estimated glomerular filtration rate or progression to end-stage renal disease, is likely to develop [10].
Since 1981, investigators have worked to develop and refine techniques for efficiently measuring TKV [11–14]. The most widely used of these techniques are planimetry (tracing), stereology (i.e., defining grid points), and the ellipsoid method (i.e., assessment of width, depth, and sagittal length, coronal length, or both to obtain an estimate of TKV) [15–17]. Table 1 compares the findings of previously published studies that evaluated the use of one or more of these methods of measuring TKV.
TABLE 1.
Comparisons of Various Methods of Volume Measurement in Studies in the Literature
| First Author, Year of Publication [Reference] | Image Modality | Measurement Method | Processing Time | Reported Accuracy or Variability or Both |
|---|---|---|---|---|
|
| ||||
| Bae, 2000 [37] | MRI | Stereology | 30–60 s/slice | Interobserver right kidney volume variability, 1.3% |
| Chapman, 2003 [36] | MRI | Stereology | NA | Analyst reliability, 0.998 |
| O’Neill, 2005 [38] | Ultrasound and MRI | Ellipsoid method and stereology | NA | Coefficient of variation (for ultrasound), 21–35%; coefficient of variation (for MRI), 1.7%; mean (± SD) TKV measured on ultrasound by use of ellipsoid method, 11% ± 34%, compared with that measured on MRI by stereology |
| Kistler, 2009 [31] | MRI | Planimetry | 30–90 min | Intracorrelation coefficient, 1.00; intercorrelation coefficient, 0.996 |
| Cohen, 2012 [33] | MRI | Semiautomated method | 43 min (HASTE) 28 min (FISP) |
Median interobserver agreement > 95.2% and coefficient of variation < 7.1%; median intraobserver agreement > 98.1% and coefficient of variation < 2.4% |
| Warner, 2014 [27] | MRI | Planimetry | 45–90 min | Interobserver volume error range, ± 10%; intraobserver volume error range, ± 1–2% |
| Irazabal, 2015 [15] | MRI | Ellipsoid method | 7 min | Comparison between TKV measured by stereology vs TKV measured by ellipsoid method |
| Stereology | 45 min | Mean, 0.5% ± 10.1% | ||
| Kline, 2016 [30] | MRI | Planimetry | 45–90 min | Mean measurement variability, 0.77% ± 0.46% Mean measurement variability, 1.34% ± 0.70% |
| Stereology | 15–30 min | Mean 8.26% ± 0.99%, compared with that measured by MRI planimetry | ||
| Spithoven, 2015 [39] | MRI | Ellipsoid method | 5 min | Intravariation, 3.9%; intervariation, 6.3% |
| Middle slice | 15 min | Intravariation, 3.0%; intervariation, 3.4% | ||
| Planimetry | 55 min | Intravariation, 1.8%; intervariation, 2.3% | ||
Note—NA = not applicable, FISP = fast imaging with steady-state precession, TKV = total kidney volume.
Each technique involves trade-offs between accuracy and precision, mean measurement time, and ease of use. Although stereology is widely recognized as a way to measure organ volumes, grids overlaid on images can sometimes inhibit visibility or make it difficult to distinguish organ boundaries, especially if the image is noisy. The faster the analyst is able to navigate through the slices of an image, the easier it is to both determine the overall shape of the organ and identify the organ to which any exterior cysts may belong. For instance, cysts on the border between the kidney and the liver are often very difficult to attribute to one organ versus the other. An approach that addresses these challenges would greatly increase overall accuracy and reduce operator time. For example, manual planimetry requires spending a substantial amount of time on each slice to trace the irregularly shaped organ, which often includes large exophytic cysts. Similarly, stereology involves highlighting interior and exterior grid points on each slice of an MR or CT image, which, again, can be tedious and time-consuming. In contrast, the ellipsoid method requires minimal time (5–10 minutes) but is less accurate [15].
Fully automated segmentation of moderately to severely diseased organs has proven to be extremely difficult because the variability in and irregularity of shape precludes the use of anatomic models [6, 16–20]. Because of labor costs and the increasing demand for institutions to track TKV, the need exists to maximize the accuracy of planimetry tracing while minimizing user interaction and maintaining ease of use.
Toward this direction, we developed a program that measures cystic organ volumes, taking into account all of these characteristics. The program requires a user to create a crude polygon outline of the cystic organ(s) as it scrolls through slices, and it provides efficient editing tools to further refine segmentations if needed. This program significantly reduces processing time (to a duration of a few minutes), provides accuracy comparable to that of interobserver variation of manual planimetry, and is easier to use than manual planimetry.
Materials and Methods
MRI Data
The present study received approval from the institutional review board at Mayo Clinic. A total of 40 baseline MR images from 40 patients with ADPKD were obtained and used to verify our semiautomated segmentation approach, which is known as the minimal interaction rapid organ segmentation (MIROS) method. The MR images were coronal single-shot fast spin-echo T2-weighted sequences that were acquired using a 1.5-T scanner (Genesis Signa, GE Healthcare) with a reconstructed matrix size of 256 × 256 × z (with z large enough to cover the full extent of the kidneys within the imaged volume). The specific parameters for image acquisition were as follows: external magnetic field (B0), 1.5 T; TR/TE, minimum/190; acquisition matrix size, 256 × 128; pixel size, ≈ 1.5 mm; slice thickness, 3.0 mm; and slice spacing, 3.0 mm. The demographic and clinical characteristics of the patients are presented in Table 2.
TABLE 2.
Demographic and Clinical Characteristics of the 40 Patients Evaluated
| Characteristic | Value |
|---|---|
|
| |
| Sex, no. of patients | |
| Female | 25 |
| Male | 15 |
| Age (y) | |
| Mean ± SD | 36 ± 6 |
| Range | 19–46 |
| Height (m) | |
| Mean ± SD | 1.74 ± 9.88 |
| Range | 1.55–1.93 |
| Imaging classification, no. (%)of patients | |
| 1A | 0 (0) |
| 1B | 4 (10) |
| 1C | 16 (40) |
| 1D | 9 (22.5) |
| 1E | 11 (27.5) |
| Total kidney volume (mL) | |
| Mean ± SD | 1409 ± 629 |
| Range | 661–2837 |
| eGFR (mL/min) | |
| Mean ± SD | 75 ± 16 |
| Range | 48–121 |
Note—eGFR = estimated glomerular filtration rate.
Preprocessing
T2-weighted abdominal MR images often have motion and signal intensity nonuniformity, including both intra- [21] and interslice [22] components. Intraslice intensity artifacts can be produced by several sources (e.g., choice of radiofrequency coil, sample geometry, and other sources) that can degrade image quality and introduce low-frequency-intensity changes. These artifacts have been widely reported in the literature, and superior MRI performance has been noted when the publically available nonparametric nonuniform intensity normalization (N3) bias correction algorithm was used [23]. Building on this approach, we incorporated an improved version of this algorithm (known as “N4”) [24] into our preprocessing pipeline.
Because, in accordance with our protocol, the T2-weighted MR image is obtained in a slice-by-slice fashion, typically over several breath-holds, motion artifacts can be introduced. This type of acquisition causes positional shifting but little deformation of the shape of the kidneys [25]. To correct for this, we used a rigid registration approach to shift the slices individually. The similarity metric of mutual information was calculated between adjacent slices to determine the optimal translation.
Variations in interslice intensity are the result of gradient eddy currents and cross-talk between slices. These cause interleaving slices of high and low signal intensity, which can be drastically different. In contrast to intraslice intensity variations, interslice intensity variations have been given far less attention in the literature [22]. To correct for interslice intensity changes, we minimized the mean square error of a threshold-based segmentation (with the number of adjacent voxels greater than half-slice maximum value) by finding the best-fit linear multiplier to allow tissue signal homogeneity between slices. The entire T2 preprocessing pipeline resolves each issue sequentially, first correcting for motion, then for interslice intensity, and finally for intraslice intensity.
Planimetry Segmentation
All examinations were traced by two trained medical imaging analysts who had experience segmenting hundreds of kidneys with polycystic kidney disease within radiologic images. Both analysts used a software program (MRIcron, version 6 6 2013, Chris Rorden, www.mricro.com) that provides freehand drawing tools, to trace the kidney contours. Kidney segmentations were further reviewed by experienced radiologists. The analysts were instructed to trace both kidneys, including renal parenchyma and all cysts (including exophytic cysts). They were also instructed to exclude the renal pelvis and other hilar vascular structures. TKV was then calculated as the number of voxels contained within the segmentation multiplied by the voxel volume. Each analyst was blinded to the other’s planimetry segmentations (i.e., tracings).
Stereology Segmentation
An expert in stereology acquired stereology data for each examination with the use of an imaging software package (Analyze, version 12.0, Biomedical Imaging Resource, Mayo Clinic) [26]. The method used involved superimposing a grid over the image data. The stereology expert received the same instructions given for planimetry in terms of the grid points that should be included as part of the kidney structures for the measurement of TKV. The grid spacing was five voxels, and the grid points were highlighted on every coronal slice. In addition, because all images were reconstructed with a matrix size of 256 × 256 with a similar FOV (leading to resolutions varying by only a few tenths of a millimeter), variation in grid resolution was minimal. Next, the stereology grid was converted into segmentation with the use of an automated algorithmic approach [27]. The final segmentations were visually checked for accuracy. The TKVs were then calculated as the number of voxels contained within the segmentation multiplied by the voxel volume.
Ground-Truth Segmentation (Reference Standard)
We used the simultaneous truth and performance level estimation (STAPLE) [28] method to obtain a probabilistic estimate of the actual ground-truth segmentation incorporating the segmentation data from multiple observers. The STAPLE method assessed the two planimetry tracings as well as the stereology-converted segmentation to construct the ground-truth segmentation.
Ellipsoid Method
The TKV was estimated using the ellipsoid method, which uses measurements of the maximum length, width, and depth of the kidneys as measured on T2-weighted MR images. Maximum length was measured on both the coronal (Lc) and sagittal views (Ls), whereas the midkidney width (W) and depth (D) were measured on the axial view. The ellipsoid equation is as follows:
| (1) |
The equation was then applied to all four measurements in the right and left kidney to obtain the TKV.
Minimal Interaction Rapid Organ Segmentation
The MIROS software package has an interactive viewer that allows full exploration of the image data on coronal, sagittal, and axial views. Segmentations can be overlaid and edited using a range of interactive tools. The MIROS algorithm was implemented in a programming language (Python, version 2.7, Python Software Foundation) and has a push button that starts the interactive tool for defining the crude polygon contours of the cystic organ. This crude estimate of organ delineation can be defined for every slice, or it can be defined with a gap specified between slices. We tested the approach by obtaining user input for every third slice (approximately every 9 mm).
In response to user interaction, MIROS automatically performs a series of steps to refine the boundaries of the organ by first interpolating user-created contours for slices that were not defined by the user. Next, the contour is expanded or contracted to best match the intensity levels representing the kidney edge. A geodesic active contour (GAC) model was used to propagate the initial input toward the cystic organ boundary. For fast computation, the morphologic GAC was implemented, which consisted of approximating the typical partial differential equation for GACs with dilation, erosion, and curvature operators [29].
The normalized gray-scale image is used as the input to the GAC. In the GAC, the energy functional E(C), which depends on the image content, is assigned to a curve (C), and this energy is minimized until it reaches a steady state, as follows:
| (2) |
where ds is the Euclidean arc-length parametrization of the curve and g(I) selects the region of the image I to which the curve should be attracted. We also set g(I) to be low at the edges of the image and high in homogeneous regions, through use of the following relation:
| (3) |
where ∇Gσ is the first-order gaussian derivative filter with the SD σ and where α is a constant to adjust gradient strength. A steepest-descent approach was used to find the local minima, or steady state, as represented by the following equation:
| (4) |
where K is the Euclidean curvature of C and where N is the normal to the curve. Our GAC was run with σ = 3 and α = 1E5, which were found to be appropriate values on separate data [30].
Finally, a narrow band at the border defined by the GAC was constructed, and a watershed edge detection approach was performed on a Sobel-filtered version of the image to finalize the segmentation. Existing implementations of the watershed and Sobel filter was used (Scikit-image, Scikit-Image Development Team).
After segmentation of each kidney, the TKV was calculated by multiplying the number of organ voxels by the voxel volume (the same calculation was done for planimetry tracings). The resulting segmentations were then compared both visually and quantitatively with the use of more traditional TKV measurement methods. In addition, the amount of time each user took to perform the semiautomated routine was automatically recorded for each examination.
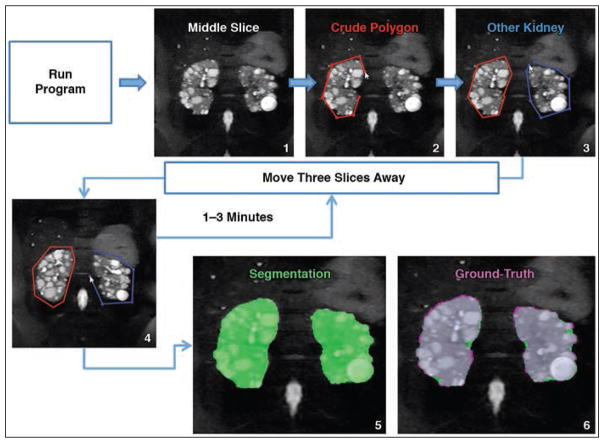
Figure 1 shows MR images obtained during the steps involved in the MIROS method. As shown in Figure 1, the algorithm begins with the user defining crude polygon contours around the right and left kidney on the middle slice. For example, with a slice thickness of 3 mm, the algorithm will move forward, prompting the user to define polygons on every third slice until the program has run through the entire image. Once this is complete, the final steps of refining the segmentation and finding the kidney border are completely automated, as previously described. Finally, the polygon and the final segmentation are automatically saved to the same location where the original image was saved. This entire process of user input and automatic refinement takes approximately 1–3 minutes.
Fig. 1.
Flow diagram with images that illustrates how user of minimal interaction rapid organ segmentation (MIROS) method is automatically guided to create contours. Only few control points on few slices are required to produce contour that is used to create final segmentation. Algorithm begins with operator using middle slice (step 1) to define crude polygon contours around right kidney (red line, step 2) and left kidney (blue line, step 3). With slice thickness of 3 mm, algorithm will move forward, prompting user to define polygons on every third slice (step 4) until program has run through entire image. Once this is complete, final steps of refining segmentation and finding kidney border are completely automated and semiautomated segmentation image (green area, step 5) is created. Ground-truth image (step 6) shows comparison of semiautomated segmentation (green area, step 5) with ground-truth (violet area, step 6), with gray areas in step 6 denoting regions of overlap between two segmentation images. Arrowheads denote mouse cursors.
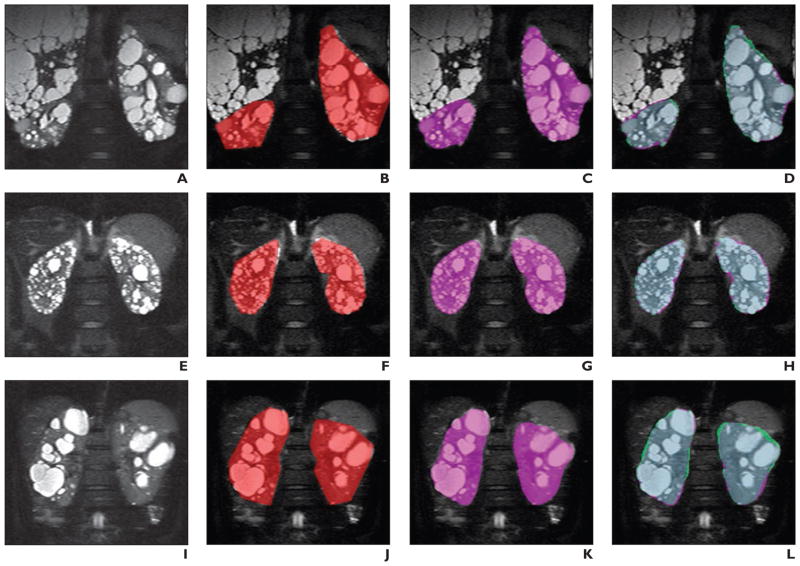
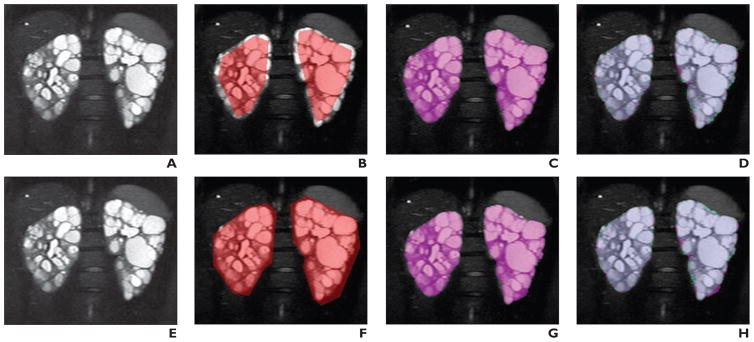
Figure 2 shows examples of images from three different patients (Figs. 2A, 2E, and 2I), the user-defined polygons (Figs. 2B, 2F, and 2J) and resulting MIROS segmentation (Figs. 2C, 2G, and 2K), and overlays showing agreement between the MIROS segmentation (shown as violet areas) and ground-truth (shown as green areas) (Figs. 2D, 2H, and 2L). In addition, Figure 3 shows how two significantly different polygon initializations will ultimately result in nearly identical final segmentations. The first polygon is purposely drawn to underrepresent the entire kidney volume, whereas the second polygon overrepresents the kidney volume (Figs. 3B and 3F). Both polygon definitions are run through the algorithm, and the resulting MIROS segmentations appear to be quite similar (Figs. 3C and 3G). Finally, the segmentations (shown as violet areas) are compared with the ground-truth segmentation (shown as green areas) to show the degree to which they match (Figs. 3D and 3H).
Fig. 2. Visual examples of results of minimal interaction rapid organ segmentation (MIROS) method used for T2-weighted MR images of three different patients with autosomal dominant polycystic kidney disease.
A–D, 46-year-old man. Images (left to right) show original T2-weighted MR image (A) in comparison with MR images showing polygon initialization made by one user (red area, B), resulting MIROS segmentation (violet area, C), and semiautomated segmentation (violet area, D) overlaid with ground-truth (green area, D).
E–H, 32-year-old man. Images (left to right) show original T2-weighted MR image (E) in comparison with MR images showing polygon initialization made by one user (red area, F), resulting MIROS segmentation (violet area, G), and semiautomated segmentation (violet area, H) overlaid with ground-truth (green area, H).
I–L, 38-year-old woman. Images (left to right) show original T2-weighted MR image (I) in comparison with MR images that show polygon initialization made by one user (red area, J), resulting MIROS segmentation (violet area, K), and semiautomated segmentation (violet area, L) overlaid with ground-truth (green area, L) to show agreement.
Fig. 3. Visual examples of different polygon initializations on original MR image and resulting minimal interaction rapid organ segmentation (MIROS) segmentation. 26-year-old woman with autosomal dominant polycystic kidney disease (ADPKD).
A–D, Original T2-weighted MR image (A) is shown for comparison with MR images showing polygon intentionally drawn to be inside true contours of kidneys (B), resulting in automatic segmentation for initialization (C), and areas for which these two images disagreed (D), with violet areas denoting areas included by automatic segmentation only and green areas denoting areas included in ground-truth segmentation only.
E–H, Original T2-weighted MR image (E) is shown for comparison with MR images on which polygon was intentionally drawn to be consistently outside true contour of kidney (F), resulting in automatic segmentation for initialization (G), and areas for which these two images disagreed (H), with violet areas denoting areas included by automatic segmentation only and green areas denoting areas included in ground-truth segmentation only.
Segmentation Accuracy Evaluation
Comparison statistics were generated to look at measurements made by planimetry, stereology, and the ellipsoid method versus MIROS performed by two different observers. Bland-Altman analysis was performed to compare the alternative TKV measurement methods to the ground-truth. To compare MIROS with the reference standard of manual tracing, a number of commonly used segmentation metrics were calculated. These included the Dice coefficient (i.e., the similarity index) and the Jaccard coefficient (i.e., the overlap ratio). Both of these metrics vary within the range of 0–1, with a value closer to 1 indicating closer similarity between the two segmentations. In addition, the percentage error in TKV, as measured using the different approaches, was calculated, and box-plot distributions were computed to compare the similarity statistics.
Results
Measurement of Total Kidney Volume
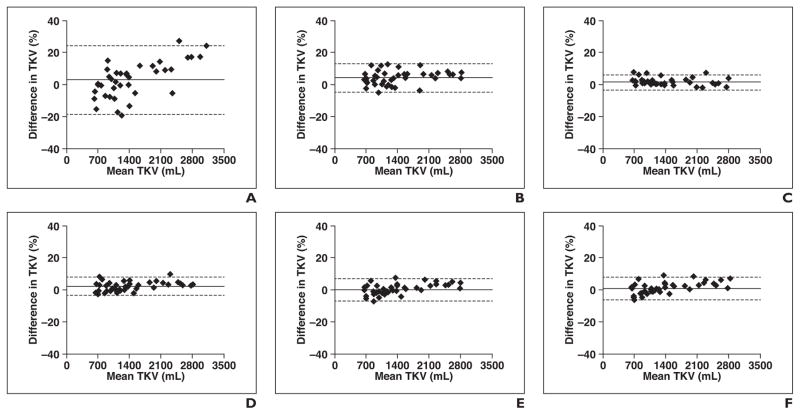
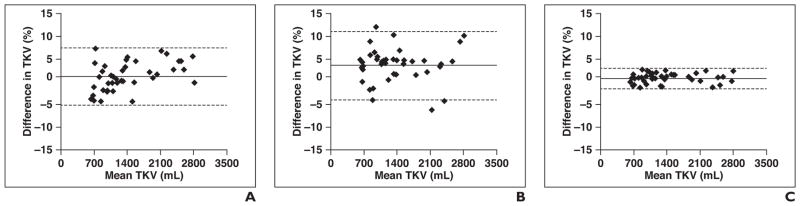
In all cases, MIROS-derived measurements of TKV had excellent agreement with the STAPLE-derived ground-truth measurement. Figure 4 shows the results of Bland-Altman analysis of TKV as measured by several currently used methods and the STAPLE ground-truth method. When compared with ground-truth segmentation, the ellipsoid method had a mean percentage difference of 2.64% and 95% CI of ± 21.34%. When stereology was compared with ground-truth, the mean percentage difference was 3.99% ± 8.82%. Tracings from two different operators were also compared with the ground-truth, and the mean percentage differences were comparable at 1.41% ± 4.78% and 2.56% ± 5.77%. Figure 5 shows the performance of MIROS through Bland-Altman analysis of the TKV. When two different observers performed manual tracings, the percentage difference in the TKV was 1.18% ± 6.33%, and the difference noted between the initial polygons drawn by the two different operators was 3.68% ± 7.56%. When the MIROS segmentation was compared with the ground-truth segmentation, the mean percentage difference in TKV was 0.19%± 6.96%, and when the MIROS approach as initialized by two different operators was compared, the mean difference was 0.75% ± 2.25%. Comparisons of all methods in relation to each other are shown in Table 3.
Fig. 4.
Bland-Altman analysis of all measurement methods compared with total kidney volume (TKV) measurement (measured in milliliters) derived from reference standard simultaneous truth and performance level (i.e., STAPLE) estimation. Bland-Altman plots show mean difference (solid line) and 95% CIs (dotted lines) (range, ± 5–20%) for each method versus reference standard. Diamonds denote data points. Ellipsoid method (A) had highest variance of four methods compared with ground-truth reference standard and was followed by stereology (B) and then by manual planimetry tracings (tracing 1 performed by user 1 [C] and tracing 2 performed by user 2 [D]). Data on minimal interaction rapid organ segmentation (MIROS) method performed by user 1 (E) and user 2 (F) are also shown.
Fig. 5.
Bland-Altman analysis of interobserver variability for manual tracing (i.e., tracing 1 by user 1 vs tracing 2 by user 2; A), initialized polygons (polygon initialized by user 1 vs polygon initialized by user 2; B), and total kidney volume (TKV) measurements derived using minimal interaction rapid organ segmentation (MIROS) method (as performed by user 1 vs user 2; C). Mean difference (solid line) and 95% CIs (dotted lines) for each method versus reference standard are shown. Diamonds denote data points. Polygons defined by two different users (B) had variance on order of interobserver variability of manual tracing (A), but this variance was significantly reduced on application of automatic approach (C). Use of MIROS approach compared with reference standard segmentation (C) is within expected variability seen by two different observers.
TABLE 3.
Comparisons of All Methods of Volumetric Measurement Evaluated
| Method | Tracing 1 by User 1 | Tracing 2 by User 2 | Stereology | Ellipsoid Method | MIROS Performed by User 1 | MIROS Performed by User 2 | Reference Standard |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Tracing 1 by user 1 | — | −1.07 ± 6.21 | −2.32 ± 9.12 | −0.09 ± 22.27 | 1.33 ± 8.60 | 0.59 ± 8.23 | 1.41 ± 4.78 |
| Tracing 2 by user 2 | 1.18 ± 6.33 | — | −1.21 ± 9.54 | 0.99 ± 21.78 | 2.43 ± 5.74 | 1.68 ± 6.06 | 2.56 ± 5.77 |
| Stereology | 2.59 ± 9.50 | 1.46 ± 9.76 | — | 2.37 ± 22.08 | 3.89 ± 10.20 | 3.13 ± 10.24 | 3.99 ± 8.82 |
| Ellipsoid method | 1.28 ± 21.62 | 0.10 ± 20.20 | −1.19 ± 21.12 | — | 2.40 ± 18.95 | 1.66 ± 19.39 | 2.64 ± 21.34 |
| MIROS performed by user 1 | −1.15 ± 7.84 | −1.15 ± 7.84 | −3.51 ± 9.73 | −1.46 ± 19.24 | — | −0.73 ± 2.23 | 0.19 ± 6.96 |
| MIROS performed by user 2 | −0.41 ± 8.19 | −2.29 ± 5.50 | −2.78 ± 10.01 | −0.71 ± 19.62 | 0.75 ± 2.25 | — | 0.94 ± 7.13 |
| Reference standard | −0.1.33 ± 4.55 | −2.42 ± 5.46 | −3.66 ± 8.23 | −1.49 ± 21.05 | −0.07 ± 6.98 | −0.81 ± 6.99 | — |
Note—Data are mean percentage difference ± 95% CI, where the columns are considered to show the true value and the rows are considered to show the experimental value. Dash (—) indicates not applicable. Reference standard = ground-truth simultaneous truth and performance level (i.e., STAPLE) estimation.
Analysis Times
For all examinations, MIROS-derived measurement of TKV required less than 5 minutes of user interaction for either user. User 1 made tracing 1 in a mean of 185 ± 42 seconds, and user 2 made tracing 2 in a mean of 105 ± 25 seconds. For each of the examinations, the range in analysis time was as follows: for planimetry measurements, 45–90 minutes; for stereology, 30–60 minutes; and for the ellipsoid method, 7–10 minutes.
Quantitative Segmentation Metrics
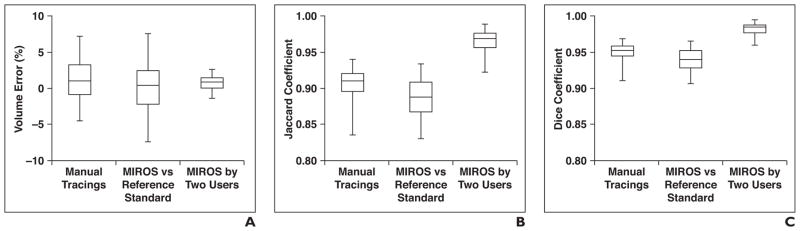
MIROS-derived segmentations closely correspond to the ground-truth segmentations and improve the interobserver variability of TKV measurements, as is shown in Figure 6. The mean percentage error shows no significant bias between methods, whereas the range in the percentage error is reduced in the MIROS-to-MIROS segmentation comparison for different users. Both the Jaccard and Dice similarity metrics are greatest in segmentations when MIROS was performed by two observers. The median Jaccard and Dice coefficients for the tracings, the stereology-to-segmentation algorithm, and the two MIROS outputs are all between 0.89 and 0.98. The percentage of volume error, when compared with the ground-truth, is lowest for both MIROS outputs, at 0.32% and 0.45%.
Fig. 6. Comparisons of three methods of total kidney volume measurement in relation to percentage of volume error and Jaccard and Dice similarity metrics.
A, Box-and-whisker plot shows percentage of volume error for three comparisons: interobserver manual tracings (i.e., tracing 1 by user 1 vs tracing 2 by user 2), minimal interaction rapid organ segmentation (MIROS) method performed by user 1 compared with ground-truth standard simultaneous truth and performance level (i.e., STAPLE) estimation (i.e., MIROS vs reference standard), and interobserver variability of MIROS (i.e., MIROS performed by user 1 vs MIROS performed by user 2). All measurement methods have low mean percentage of volume error, but range of volume error from comparison of MIROS performed by two users is reduced compared with manual tracings or MIROS versus reference standard. Horizontal lines within boxes denote mean values, vertical lines and whiskers denote 95% CIs.
B and C, Box-and-whisker plots show Jaccard (i.e., overlap ratio) coefficient (B) and Dice (i.e., similarity index) coefficient (C) for three comparisons: manual tracings, MIROS versus reference standard, and MIROS performed by two users. Both Jaccard and Dice coefficients were improved when segmentations from two different MIROS users are considered, compared with manual tracings and MIROS versus reference standard. Horizontal lines within boxes denote mean values, vertical lines and whiskers denote 95% CIs.
Discussion
To our knowledge, TKV currently is the best imaging biomarker with which to assess the therapeutic benefits of new drugs for patients with ADPKD. Mean percentage changes in TKV of 2.7% ± 4.8% occurring within 6 months of therapy initiation have been reported elsewhere [31]. In addition, a study of tolvaptan therapy showed a 2.7% reduction in TKV per year when control and treatment groups were compared [1]. These and other studies [3, 5] have suggested that measurement of TKV should be accurate and reproducible to within a few percentage points of the total volume, to ascertain treatment benefits and follow disease progression during relatively short intervals.
Other segmentation techniques have been introduced to increase institutional throughput of TKV measurements. Racimora et al. [32] tested both an active contour-based approach and a morphologic thresholding approach and found mean percentage volume errors of 22.0% ± 8.6% and 37.4% ± 8.7%, respectively. They suggested the use of a hybrid approach that combined these techniques with postprocess editing, which produced mean volume errors of 3.2% ± 0.8% for the morphologic thresholding approach and 3.2% ± 0.6% for the active contour-based approach. However, the mean postprocess editing time was 19± 11 minutes (± SD) for morphologic thinning and 15 ± 5 minutes (± SD) for the active contours-based approach, which is evidence of only minor improvements in the efficiency of a hybrid approach compared with complete manual tracing of the kidney borders. Cohen et al. [33] evaluated an interpolation approach that required less manual interaction (mean duration, 43 minutes for HASTE sequence and 28 minutes for true fast imaging with steady-state precession sequence) and observed minimal changes in the resultant measured volumes. Warner et al. [27] used routinely acquired stereology data as initialization for a semiautomated segmentation approach to kidneys with polycystic kidney disease on MR images.
In addition, our group recently developed an approach to automatically follow disease progression by using tracings from prior examinations as initializations to automatically follow kidney changes and measure TKV [30]. Sharma et al. [34] recently published a study on the use of a semiautomated segmentation approach to kidneys affected by AD-PKD, as seen on CT images and evaluated with the use of random forests. All of these methods require some level of user input, and it is likely that even the development of fully automated approaches will always necessitate quality assurance testing by a trained radiologist or technician to guarantee segmentation accuracy.
The present study showed that the method we developed (i.e., MIROS) is fast and accurate in generating segmentations of kidneys affected by polycystic kidney disease and that it provides a base for further image analysis. The similarity metrics for MIROS were quantitatively excellent. The variability of TKV, as assessed on the basis of findings of stereology, planimetry, and MIROS, was not significant compared with the accuracy required to characterize changes resulting from the disease process. When compared with the STAPLE-based ground-truth, MIROS had the lowest mean percentage difference in TKV, followed by manual tracings, the ellipsoid method, and then stereology. Although the ellipsoid method did not seem to have a significant over or under bias, its overall volume measurements varied the most, compared with ground-truth segmentation.
The time required to perform segmentation with MIROS is significantly shorter than that required by the other methods evaluated in the present study. Whereas MIROS required less than 5 minutes, the ellipsoid measurements required 7–10 minutes; stereology, 30–60 minutes; and manual segmentations, 45–90 minutes. Because MIROS can be performed in less than five minutes, approximately 9–18 measurements can now be performed in the time it takes to measure a single patient with the use of manual tracing. Although the ellipsoid method is comparable to MIROS in terms of the performance time required for analysis, the ellipsoid method varies the most from the ground-truth and, like stereology, estimates volume only. Without segmentation, further analysis of kidney tissue is not possible. Furthermore, automation allows robust study repeatability and removal of user subjectivity in generating segmentations. When two different operators performed manual tracings, the mean difference in bias was 1.18% ± 6.33%. However, when two different operators initialized polygons for MIROS, the mean percentage difference in polygon volume was 3.68% ± 7.56%, although the segmentations resulting from automation were reduced by a difference of 0.75% ± 2.25%. These results suggest that MIROS narrows the gap between volumes based on the tracings of two operators.
We see the possibility of this method being implemented during patient visits to the clinic. After a patient undergoes scanning, the physician or technician can quickly perform a crude tracing of the kidney contour; MIROS can then process the contour and output a volume that is valuable to both the patient and his or her physician. The ultimate goal is to minimize user interaction time without compromising the quality of the segmentation and the accuracy of TKV measurements, and this was accomplished by MIROS.
The renal pelvis traditionally is not included when performing kidney segmentations [27, 32]. However, the signal intensity and shape of the renal pelvis and other organs are often similar to those of simple cysts on T2-weighted MR images. Consequently, automated programs such as MIROS, let alone trained analysts, can have a difficult time distinguishing between the two. Similarly, after performing visual analysis, we found that the largest disagreement between MIROS and manual segmentation was noted for images with either minor inclusion of other organs containing fluid (e.g., liver, gallbladder, and intestines) or exclusion of kidney cysts that were thought to be liver cysts on the basis of the polygon initialized by the user or inclusion of the renal pelvis (i.e., user error). Nonetheless, these issues can be quickly corrected by performing a final quality check of the segmentations.
A limitation of the present study is that we performed the analysis for a single imaging modality (T2-weighted MRI). How use of this method could be extended to other imaging modalities (e.g., CT), other pulse sequences (e.g., T1-weighted sequences), or other organs (e.g., livers of patients with polycystic liver disease) needs to be explored. Another limitation is that the present study verified the approach but could not necessarily validate the approach against other, perhaps invasive, approaches. Fortunately, previous studies have shown strong agreement between volume measurements performed by MRI and those performed ex vivo (i.e., volume displacement of excised porcine kidneys [35]), as well as through comparison with experimental phantoms [36]. Formulating a ground-truth (reference standard) from multiple user segmentations through the use of the STAPLE algorithm allowed the current study to limit interrater variability of both the segmentations and the subsequent measurement of TKV.
In the present study, we proposed a new semiautomated technique known as MIROS for the robust and efficient segmentation of abdominal organs. The performance of this algorithm was compared with that of the following current methods of measuring TKV: planimetry, stereology, and the ellipsoid method. Quantitative outcomes were favorable in all areas tested, including accuracy and precision, and MIROS excelled at significantly reducing the amount of time required to perform segmentation, which allows further image analysis to be performed, if desired. Furthermore, the algorithm required minimal user input, resulting in lower costs and the possibility of the application being used in a clinical setting. In the present study, MIROS was used to assess the kidneys of patients with ADPKD, with the use of T2-weighted MRI. Future experiments should be performed on a variety of healthy and disease-affected organs and with the use of various imaging modalities, to test the generalizability of MIROS. We think that MIROS can be effectively implemented in a variety of areas to calculate organ volume and facilitate further image processing.
Acknowledgments
Supported by grant P30 DK090728 from the National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, to the Mayo Translational Polycystic Kidney Disease Center and by grant U01 CA160045 QIN from the National Cancer Institute.
We thank Mary E. Bennett for her help in preparing this manuscript.
Footnotes
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1.Torres VE, Chapman AB, Devuyst O, et al. Tolvaptan in patients with autosomal dominant polycystic kidney disease. N Engl J Med. 2012;367:2407–2418. doi: 10.1056/NEJMoa1205511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schrier RW, Abebe KZ, Perrone RD, et al. Blood pressure in early autosomal dominant polycystic kidney disease. N Engl J Med. 2014;371:2255–2266. doi: 10.1056/NEJMoa1402685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Caroli A, Perico N, Perna A, et al. Effect of longacting somatostatin analogue on kidney and cyst growth in autosomal dominant polycystic kidney disease (ALADIN): a randomised, placebo-controlled, multicentre trial. Lancet. 2013;382:1485–1495. doi: 10.1016/S0140-6736(13)61407-5. [DOI] [PubMed] [Google Scholar]
- 4.van Keimpema L, Nevens F, Vanslembrouck R, et al. Lanreotide reduces the volume of polycystic liver: a randomized, double-blind, placebo-controlled trial. Gastroenterology. 2009;137:1661–1668. doi: 10.1053/j.gastro.2009.07.052. [DOI] [PubMed] [Google Scholar]
- 5.Hogan MC, Masyuk TV, Page LJ, et al. Randomized clinical trial of long-acting somatostatin for autosomal dominant polycystic kidney and liver disease. J Am Soc Nephrol. 2010;21:1052–1061. doi: 10.1681/ASN.2009121291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.GranthAm JJ, Chapman AB, Torres VE. Volume progression in autosomal dominant polycystic kidney disease: the major factor determining clinical outcomes. Clin J Am Soc Nephrol. 2006;1:148–157. doi: 10.2215/CJN.00330705. [DOI] [PubMed] [Google Scholar]
- 7.GranthAm JJ, Torres VE, Chapman AB, et al. Volume progression in polycystic kidney disease. N Engl J Med. 2006;354:2122–2130. doi: 10.1056/NEJMoa054341. [DOI] [PubMed] [Google Scholar]
- 8.Chapman AB, Bost JE, Torres VE, et al. Kidney volume and functional outcomes in autosomal dominant polycystic kidney disease. Clin J Am Soc Nephrol. 2012;7:479–486. doi: 10.2215/CJN.09500911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.U.S. Food and Drug Administration (FDA) Draft guidance for industry: qualification of biomarker total kidney volume in studies for treatment of autosomal dominant polycystic kidney disease. [Accessed May 12, 2016];FDA website. www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/UCM458483.pdf. Published 2015.
- 10.European Medicines Agency (EMA) Draft qualification opinion: total kidney volume (TKV) as a prognostic biomarker for use in clinical trials evaluating patients with autosomal dominant polycystic kidney disease (ADPKD) [Accessed May 12, 2016];EMA website. www.ema.europa.eu/docs/en_GB/document_library/Regulatory_and_procedural_guideline/2015/11/WC500196569.pdf. Published 2015.
- 11.Thomsen HS, Madsen JK, Thaysen JH, Damgaardpetersen K. Volume of polycystic kidneys during reduction of renal function. Urol Radiol. 1981;3:85–89. doi: 10.1007/BF02927815. [DOI] [PubMed] [Google Scholar]
- 12.Gabow PA, Johnson AM, Kaehny WD, et al. Factors affecting the progression of renal disease in autosomal-dominant polycystic kidney disease. Kidney Int. 1992;41:1311–1319. doi: 10.1038/ki.1992.195. [DOI] [PubMed] [Google Scholar]
- 13.King BF, Reed JE, Bergstralh EJ, Sheedy PF, 2nd, Torres VE. Quantification and longitudinal trends of kidney, renal cyst, and renal parenchyma volumes in autosomal dominant polycystic kidney disease. J Am Soc Nephrol. 2000;11:1505–1511. doi: 10.1681/ASN.V1181505. [DOI] [PubMed] [Google Scholar]
- 14.Sise C, Kusaka M, Wetzel LH, et al. Volumetric determination of progression in autosomal dominant polycystic kidney disease by computed tomography. Kidney Int. 2000;58:2492–2501. doi: 10.1046/j.1523-1755.2000.00433.x. [DOI] [PubMed] [Google Scholar]
- 15.Irazabal MV, Rangel LJ, Bergstralh EJ, et al. Imaging classification of autosomal dominant polycystic kidney disease: a simple model for selecting patients for clinical trials. J Am Soc Nephrol. 2015;26:160–172. doi: 10.1681/ASN.2013101138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chapman AB, Wei W. Imaging approaches to patients with polycystic kidney disease. Semin Nephrol. 2011;31:237–244. doi: 10.1016/j.semnephrol.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bae KT, GranthAm JJ. Imaging for the prognosis of autosomal dominant polycystic kidney disease. Nat Rev Nephrol. 2010;6:96–106. doi: 10.1038/nrneph.2009.214. [DOI] [PubMed] [Google Scholar]
- 18.Liebau MC, Serra AL. Looking at the (w)hole: magnet resonance imaging in polycystic kidney disease. Pediatr Nephrol. 2013;28:1771–1783. doi: 10.1007/s00467-012-2370-y. [DOI] [PubMed] [Google Scholar]
- 19.Fick-Brosnahan GM, Belz MM, McFann KK, Johnson AM, Schrier RW. Relationship between renal volume growth and renal function in autosomal dominant polycystic kidney disease: a longitudinal study. Am J Kidney Dis. 2002;39:1127–1134. doi: 10.1053/ajkd.2002.33379. [DOI] [PubMed] [Google Scholar]
- 20.Clarke LP, Velthuizen RP, Camacho MA, et al. MRI segmentation: methods and applications. Magn Reson Imaging. 1995;13:343–368. doi: 10.1016/0730-725x(94)00124-l. [DOI] [PubMed] [Google Scholar]
- 21.Belaroussi B, Milles J, Carme S, Zhu YM, Benoit-Cattin H. Intensity non-uniformity correction in MRI: existing methods and their validation. Med Image Anal. 2006;10:234–246. doi: 10.1016/j.media.2005.09.004. [DOI] [PubMed] [Google Scholar]
- 22.Schmidt M. A method for standardizing MR intensities between slices and volumes. Edmonton, AB, Canada: Department of Computing Science, University of Alberta; 2005. [Google Scholar]
- 23.Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- 24.Tustison NJ, Avants BB, Gee JC. Directly manipulated free-form deformation image registration. IEEE Trans Image Process. 2009;18:624–635. doi: 10.1109/TIP.2008.2010072. [DOI] [PubMed] [Google Scholar]
- 25.Gardener AG, Francis ST. Multislice perfusion of the kidneys using parallel imaging: image acquisition and analysis strategies. Magn Reson Med. 2010;63:1627–1636. doi: 10.1002/mrm.22387. [DOI] [PubMed] [Google Scholar]
- 26.Robb RA, Hanson DP, Karwoski RA, Larson AG, Workman EL, Stacy MC. Analyze: a comprehensive, operator-interactive software package for multidimensional medical image display and analysis. Comput Med Imaging Graph. 1989;13:433–454. doi: 10.1016/0895-6111(89)90285-1. [DOI] [PubMed] [Google Scholar]
- 27.Warner JD, Irazabal MV, Krishnamurthi G, King BF, Torres VE, Erickson BJ. Supervised segmentation of polycystic kidneys: a new application for stereology data. J Digit Imaging. 2014;27:514–519. doi: 10.1007/s10278-014-9679-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;23:903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Marquez-Neila P, Baumela L, Alvarez L. A morphological approach to curvature-based evolution of curves and surfaces. IEEE Trans Pattern Anal Mach Intell. 2014;36:2–17. doi: 10.1109/TPAMI.2013.106. [DOI] [PubMed] [Google Scholar]
- 30.Kline TL, Korfiatis P, Edwards ME, et al. Automatic total kidney volume measurement on follow-up magnetic resonance images to facilitate monitoring of autosomal dominant polycystic kidney disease progression. Nephrol Dial Transplant. 2016;31:241–248. doi: 10.1093/ndt/gfv314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kistler AD, Poster D, Krauer F, et al. Increases in kidney volume in autosomal dominant polycystic kidney disease can be detected within 6 months. Kidney Int. 2009;75:235–241. doi: 10.1038/ki.2008.558. [DOI] [PubMed] [Google Scholar]
- 32.Racimora D, Vivier PH, Chandarana H, Rusinek H. Segmentation of polycystic kidneys from MR images. In: Karssemeijer N, Summers RM, editors. Medical imaging 2010: computer-aided diagnosis proceedings of SPIE. Vol. 7624. Bellingham, WA: SPIE; 2010. p. 76214W. [Google Scholar]
- 33.Cohen BA, Barash I, Kim DC, Sanger MD, Babb JS, Chandarana H. Intraobserver and interobserver variability of renal volume measurements in polycystic kidney disease using a semiautomated MR segmentation algorithm. AJR. 2012;199:387–393. doi: 10.2214/AJR.11.8043. [DOI] [PubMed] [Google Scholar]
- 34.Sharma K, Peter L, Rupprecht C, Caroli A, et al. [Accessed May 10, 2016];Semi-automatic segmentation of autosomal dominant polycystic kidneys using random forests. arXiv.org e-print archive website. arxiv.org/abs/1510.06915. Published October 23, 2015.
- 35.Bakker J, Olree M, Kaatee R, de Lange EE, Beek FJ. In vitro measurement of kidney size: comparison of ultrasonography and MRI. Ultrasound Med Biol. 1998;24:683–688. doi: 10.1016/s0301-5629(97)00212-3. [DOI] [PubMed] [Google Scholar]
- 36.Chapman AB, Guay-Woodford LM, GranthAm JJ, et al. Renal structure in early autosomal-dominant polycystic kidney disease (ADPKD): The Consortium for Radiologic Imaging Studies of Polycystic Kidney Disease (CRISP) cohort. Kidney Int. 2003;64:1035–1045. doi: 10.1046/j.1523-1755.2003.00185.x. [DOI] [PubMed] [Google Scholar]
- 37.Bae KT, Commean PK, Lee J. Volumetric measurement of renal cysts and parenchyma using MRI: phantoms and patients with polycystic kidney disease. J Comput Assist Tomogr. 2000;24:614–619. doi: 10.1097/00004728-200007000-00019. [DOI] [PubMed] [Google Scholar]
- 38.O’Neill WC, Robbin ML, Bae KT, et al. Sonographic assessment of the severity and progression of autosomal dominant polycystic kidney disease: the Consortium of Renal Imaging Studies in Polycystic Kidney Disease (CRISP) Am J Kidney Dis. 2005;46:1058–1064. doi: 10.1053/j.ajkd.2005.08.026. [DOI] [PubMed] [Google Scholar]
- 39.Spithoven EM, van Gastel MD, Messchendorp AL, et al. Estimation of total kidney volume in autosomal dominant polycystic kidney disease. Am J Kidney Dis. 2015;66:792–801. doi: 10.1053/j.ajkd.2015.06.017. [DOI] [PubMed] [Google Scholar]