Image-derived arterial input function for quantitative fluorescence imaging of receptor-drug binding in vivo

Abstract

Receptor concentration imaging (RCI) with targeted-untargeted optical dye pairs has enabled in vivo immunohistochemistry analysis in preclinical subcutaneous tumors. Successful application of RCI to fluorescence guided resection (FGR), so that quantitative molecular imaging of tumor-specific receptors could be performed in situ, would have a high impact. However, assumptions of pharmacokinetics, permeability and retention, as well as the lack of a suitable reference region limit the potential for RCI in human neurosurgery. In this study, an arterial input graphic analysis (AIGA) method is presented which is enabled by independent component analysis (ICA). The percent difference in arterial concentration between the image-derived arterial input function (AIF_ICA) and that obtained by an invasive method (ICA_CAR) was 2.0 ± 2.7% during the first hour of circulation of a targeted-untargeted dye pair in mice. Estimates of distribution volume and receptor concentration in tumor bearing mice (n = 5) recovered using the AIGA technique did not differ significantly from values obtained using invasive AIF measurements (p=0.12). The AIGA method, enabled by the subject-specific AIF_ICA, was also applied in a rat orthotopic model of U-251 glioblastoma to obtain the first reported receptor concentration and distribution volume maps during open craniotomy.

1. Introduction

In recent years, the concept of molecular-guided resection (MGR) (also called molecular-guided surgery or live-molecular navigation) has emerged as an alternative direction in fluorescence guided resection (FGR) that exploits an entirely different source of contrast—i.e., the molecular expression of transmembrane receptors[1] and intracellular peptides[2] that are preferentially upregulated in tumor cells. Guidance can be derived from endogenous signal—e.g., NADH fluorescence [3], hemoglobin absorption [4], or ultrastructure scatter differences [5]—or by the introduction of exogenous agents which are sensitive to molecular activity and binding. Optical contrast agents currently used in the clinic, including 5-aminolevulinic acid, fluorescein sodium and indocyanine green, are similar to CT and MRI agents in that they provide contrast which depends on the presence of the enhanced perfusion and retention (EPR) effect. However, EPR effect is not present in all tumors, and when present, can vary considerably across the tumor. As a result, EPR-based contrast provides partial tumor enhancement, but may not demarcate areas of vascular collapse or invasive margins where blood-brain barrier alterations are not yet substantial. Receptor concentration imaging (RCI) is an emerging technique that leverages tracer kinetic compartment models developed for PET imaging. Through dual-injection of a targeted-untargeted dye pair—in which the untargeted dye provides a control for non-specific uptake and accumulation—EPR-specific behavior is supressed in favor of binding-specific contrast. RCI has been validated against ex vivo and in vitro immunohistochemistry in subcutaneous glioma and gliosarcoma[6], pancreatic cancer[7], and squamous-cell carcinoma models.[8]

Despite being highly robust in preclinical subcutaneous models, the compartment models used in RCI thus far have several drawbacks that limit their use in clinical applications of glioma resection: they require two tracers with identical pharmacokinetics (i.e., distribution by, and clearance from the blood) and tissue kinetics (i.e., delivery and extraction to the tissue, and non-specific retention), or they require a reference region which can correct differences in pharmacokinetics but this approach is only accurate if tissue kinetics are approximately equal [9]. In the second case, the “reference tracer reference region” method presumes that an ideal reference region—i.e., a region with similar tissue kinetics but zero specific binding—can be interrogated within the imaging field-of-view. In particular, this assumption is unlikely to be achieved in neurosurgical applications for two reasons. First, in an open craniotomy, the area of skull removed is minimized while still allowing a surgical path to the tumor. Therefore, a region of brain that is absent of invading malignancy may not always be available in the cranial window. A more fundamental problem, however, is that no true “reference” for tumor exists. The significant vascular changes causing spatially varying areas of hypoperfusion and hyperperfusion are unlike normal parenchyma. For this reason, PET reference tissue models have mainly been applied to studying receptors involved in disorders with less-substantial vascular changes than tumor angiogenesis, e.g. Parkinson’s disease[10], Alzheimer’s disease [11], and drug addiction [12]. An alternative to these assumptions is using a compartment model with explicitly defined arterial input functions measured from the subject.

The motivation for this study is to enable non-invasive characterization of arterial input function to expand the utility of tracer kinetic compartment models for molecular imaging and MGR. As proof-of-principle, we describe use of an arterial input model to enable RCI in situ during glioma resection, where neither the previous deconvolution method [9], nor the direct carotid imaging approach [13] are feasible. The method proposed—termed arterial input graphical analysis (AIGA)—is also derived from established PET modeling approaches [14], and enables quantification of binding potential, which was defined by Mintun [15] as the capacity of a receptor to bind ligand. Unlike the previous RCI method, it also allows quantification of the volumes of distribution of both tracers. However, a significant challenge to applying AIGA is its requirement that the arterial input function—the time varying arterial concentration of dye—be measured along with the tissue uptake curves. While we have previously side-stepped this problem by direct imaging of the carotid arteries in mice, in the rat orthotopic model of glioma, the carotid arteries are inaccessible during imaging, being on the opposite side of the head from the craniotomy site. Furthermore, the clinical need to extract the AIF from the real-time surgical microscope imaging data, rather than using a specialized device, motivates development of a method to acquire image-derived arterial input functions (ID-AIFs). The goal of this study is to compare the ID-AIFs to the AIFs recovered by the carotid imaging technique in mice, and to demonstrate the potential of this technique to allow the AIGA method to be used in orthotopic glioma models.

2. Theory

2.1 Blind Separation of Arterial Input Function

Arterial input kinetic modeling requires the arterial input function, C_a(t), to be characterized. Accordingly, a blind-source separation scheme is used to extract C_a(t) from a time-series of fluorescence images acquired in situ, e.g., during surgery. Consider a zero-mean, M-dimensional random variable varying with time, r, s(r) = [S₁(r), …, s_M(r)]^T, whose elements are mutually independent each arising from unique kinetic elements within a tissue. In dynamic imaging, a mixed signal x(r) = [x₁(r),…,x_N(r)]^T is actually observed, where N represents spatially distinct sampling pixels or regions and the relationship between the mixed signal and the underlying independent components (ICs) is given by

$$\mathbf{x}=\mathbf{Ms}$$ (1)

where M is an N-by-M mixing matrix of unknown elements, causing the source signals to be mixed instantaneously and measured as x(r). The goal of ICA is to estimate the underlying ICs of the system, s, from the mixed signal x.

In dynamic imaging, each imaging element, x(r), can also be described as a sum of dynamic tissue elements [C₁(r),…,C_P(r)], which when imaged in a planar fluorescence configuration yields

$$\mathbf{x}=\mathbf{\eta }\mathbf{C}$$ (2)

where η is a scalar which represents the transfer function between the concentration of fluorophore and the signal detected by the CCD, and includes the quantum efficiency of the dye, the pixel-specific detector efficiency, the illumination field intensity, and the specific extinction coefficient within the pixel volume of interrogation. The individual dynamic elements can be defined in a variety of ways, depending on the compartment model applied. For example, in dynamic contrast-enhanced (DCE) MRI and DCE-CT the extended Tofts-Kety model is often used:

$$C(t)=V_b{C}_a(t)+K_1{e}^{-k_{2}t}\otimes C_a(t)$$ (3)

where V_b is the blood volume and K₁ and k₂ are rate constants describing the transfer of mass from the intravascular space (IVS) to the extravascular extracellular space (EES), and from the EES to the IVS, respectively. While K₁ and k₂ are spatially dependent, C_a(t) is assumed to be the same in all dynamic elements within a small region of interest. Therefore, the system is assumed to be given by the following matrix representation

$$\mathbf{x}=\mathbf{CW}=\left[\begin{array}{cccc}{C}_a(t=1)& C_1(t=1)& \cdots & C_k(t=1)\\ C_a(t=2)& C_1(t=2)& \cdots & C_k(t=2)\\ ⋮& ⋮& \ddots & ⋮\\ C_a(t=L)& C_1(t=L)& \cdots & C_k(t=L)\end{array}\right]\left[\begin{array}{cccc}{\eta }_1{V}_b& {\eta }_2{V}_b& \cdots & {\eta }_p{V}_b\\ {\eta }_1{V}_1& {\eta }_2{V}_1& \cdots & {\eta }_p{V}_1\\ ⋮& ⋮& \ddots & ⋮\\ {\eta }_1{V}_k& {\eta }_2{V}_k& \cdots & {\eta }_p{V}_k\end{array}\right]$$ (4)

where the [L x (K+1)] matrix C represents the ICs which include C_a(t) and k tissue-originating kinetic functions within the subject, which when combined with the [(K+1) x P] weighting matrix, W, specified for each pixel (or principle component) yield x, the [L x P] matrix of time-dependent concentration curves for each pixel (or principle component). V_k is the fractional volume that C_k contributes to the average. K is the number of non-arterial dynamic functions, and L is the number of time-points acquired for x. P is the number of pixels, or in the case where a dimension reduction has been applied to reduce the redundant information in x, P is the number of principle components. In reality the size of dimension, K, will depend on the size of the interrogation volume and heterogeneity of underlying tissue dynamics. Here, the signal-to-noise of the measurements is assumed to limit the number of separable elements in practice, such that the effective number of independent components will be much less than the actual number. The goal of the analysis is to separate the signal matrix, x, into the ICs representing dynamic curves and positively identify the IC corresponding to C_a while avoiding spillover or cross-contamination from other ICs.

2.2 Arterial input graphic analysis (AIGA) method

The graphic analysis approach to extracting volume of distribution was developed in PET imaging by Logan et al.[14], who generalized the earlier work of Patlak et al., which was developed to image irreversible PET tracers such as 14-fludeoxyglucose ([¹⁴F]-FDG) [16], which upon cellular uptake are enzymatically converted and trapped in the cytoplasm. Since this pioneering work first appeared, compartment models have been employed by many other researchers [17, 18] in PET imaging and more recently, optical imaging [6]. We defer to the consensus paper regarding nomenclature of constants [19], which include: delivery rate constant from the plasma to the first compartment, K₁ (ml/min/ml), also equal to the product of blood flow, F, and extraction fraction, E; the constant of return from compartment one to the plasma, k₂ (min⁻¹); rate constant from the first tissue compartment to the bound space, k₃ (min⁻¹); and finally, the rate constant from bound space back to the first tissue compartment, k₄ (min⁻¹). The two-tissue compartment model is governed by two differential equations describing the flow in and out of the free tissue compartment, C_F, and the specifically bound tissue compartment, C_S:

$$\frac{d{C}_F(t)}{dt}=K_1{C}_a(t)-\left(k_2+k_3\right)C_F(t)+k_4{C}_S(t),$$ (5)

$$\frac{d{C}_S(t)}{dt}=k_3{C}_F(t)-k_4{C}_S(t),$$ (6)

From this straight-forward definition, many different approximations and formulations have been developed to improve the condition of the inverse problem through simplified fitting, and avoid the need for sampling the plasma curve.[20] Of relevance to the techniques employed in this paper, Logan and colleagues provide the graphical method to solving Eq. (1) which involves rearranging the integral form of Eq. 5 to yield

$$\frac{\underset{0}{\overset{t}{\int }}{C}_{\mathit{ROI}}(u)du}{C_{\mathit{ROI}}(t)}=\left[\frac{K_1}{k_2}\left(1+B{P}_{ND}\right)+V_b\right]\frac{\underset{0}{\overset{t}{\int }}{C}_a(u)du}{C_{\mathit{ROI}}(t)}+I(t),$$ (7)

where C_ROI(t) is total concentration of tracer in the region of interrogation comprising C_F, C_S, and C_p, and BP_ND = k₃/k₄ is the non-displaceable binding potential. An important characteristic of this formulation is that the intercept term, I(t) is a constant when equilibrium between the compartments is reached; the slope term is also called the volume of distribution, V_D. In the same study, it demonstrated that BP_ND could be calculated from the ratio of V_D values (or distribution volume ratio, DVR) between receptor expressing and reference regions. Similarly, we take the ratio of the slope of a region of interest to the slope of a reference region without receptors:

$$\mathit{DVR}=\frac{\frac{K_1}{k_2}\left(1+B{P}_{ND}\right)+V_b}{\frac{K_1}{k_2}+V_b}$$ (8)

where DVR is the ratio of slopes from Eq. 3 applied to a volume of tissue with receptor binding, and no receptor binding, respectively. If the ratio k₁/k₂ also called the non-displaceable distribution volume, V_ND, is equal to k₁′/k₂′ and V_b is small compared to V_ND, then BP_ND = DVR−1 Rather than a physically distinct reference region, this study uses a “reference tracer”; therefore non-displaceable binding potential is given by:

$$B{P}_{ND}=\frac{V_{D,T}}{V_{D,U}}-1$$ (9)

where V_D,T is the distribution volume of the targeted tracer and V_D,U is the distribution volume of the untargeted tracer.

3. Materials and methods

3.1 Animal Preparation and Imaging Procedure

All animal experiments were performed in accordance with the guidelines approved by the Dartmouth Institutional Animal Care and Use Committee (IACUC) (Protocol ID: pogu.bw.2), under an Animal Welfare Assurance from the Office of Laboratory Animal Welfare (No. A3259-01) and conducted in compliance with the ARRIVE guidelines.[21] A total of 5 female athymic nude mice ((Crl:NU(NCr)-Foxn1^nu, Charles River, Wilmington, MA) were used. Subcutaneous implants of 1 x 10⁶ cells of U-251 MG glioma tumors (ATCC) were made on the right flank of the mouse using 50 μL of a 1:1 mixture of Matrigel (BD Biosciences) and complete cell culture media. After tumors had reached about 10 mm in diameter, mice were anesthetized and the carotid artery was exposed as previously described [22]. The skin superficial to the tumor was also removed to allow access to the mass. The animal was placed supine on the imaging tray of a planar fluorescence imaging system (Pearl Impulse, LI-COR Biosciences Inc., Lincoln, NE), and injected intravenously with 2 nmol each of IRDye800CW (LI-COR Biosciences Inc.) conjugated to anti-EGFR Affibody® molecules (Affibody AB, Solna, Sweeden) and IRDye680RD (LI-COR Biosciences Inc.) conjugated to negative control Affibody® molecules (Affibody AB). For short-hand, we refer to the targeted conjugate as “ABY-029” and the untargeted conjugate as “NEG-680” in this paper. A full set of three images (white-light, 700 nm emission and 800 nm emission) was acquired every minute for 60 minutes and then, animals were euthanized by overdose of anaesthetic followed by cervical dislocation, as outlined in the Guide for the Care and Use of Laboratory Animals.

As proof-of-principle that this approach enables AIGA imaging in the orthotopic model where the carotid is not accessible, a 10 week old, 200 g athymic rat (Crl:NIH-Foxn1^rnu, Charles River) was implanted with a U251 tumor by stereotactic intracerebral injection. After three weeks post-implantation confirmation of the tumor location and size was performed on a 3T MRI scanner (Koninklijke Philips N.V., Andover, MA) by gadolinium-enhanced T₂ MRI imaging (Fig. 5B). The fluorescence imaging began by inducing the animal with 4% isofluorane anesthetic nebulized and mixed with 1.5 L/min 100% O₂, and isofluorane anesthesia was maintained between 2–4% for the duration of the experiment. A subcutaneous injection of lidocaine (0.5 mL of 1% USP) was made superficially at the midpoint of the sagittal suture line, between the bregma and lambda, to reduce the extent of extracranial bleeding during surgery and imaging. Scalp tissue was removed and a high-speed dental drill was used to thin the skull in a circular path approximately 10 mm in diameter. Accidental trauma to the sagittal sinus or other vascular or cortical structures was avoided while drilling continued until the bone flap could be removed. The dura mater was pealed back exposing the cortex (Fig. 5A). Sterile gauze and absorbable hemostat cellulose (Surgicel®, Ethicon, Somerville, NJ) was used to pack the perimeter of the craniotomy and stop any minor bleeding. Lidocaine was applied pro re nata and the surgical area was irrigated frequently. Following injection of 2 nmol each of ABY-029 and NEG-680 (suspended in 0.5 mL PBS), a full set of images was acquired on the Pearl Impulse scanner every minute for 30 minutes. At the end of the experiment, euthanasia was performed by anaesthetic overdose and cervical dislocation.

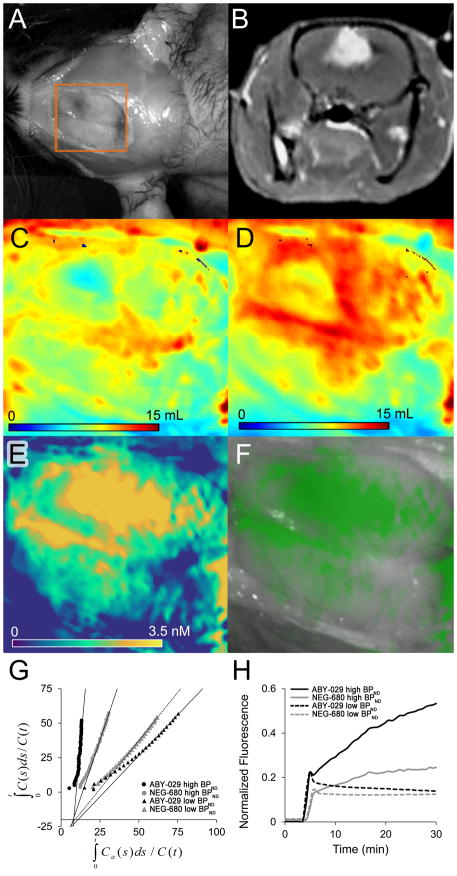
Figure 5.

(A) Open craniotomy of U251 human glioblastoma bearing rat and corresponding (B) Gadolinium-enhanced T2-weighted MRI image showing enhancing lesion in right hemisphere (C) NEG-680 distribution volume (mL), (D) ABY-029 distribution volume (mL) and (E) EGFR concentration map determined by AIGA. (F) Overlay of the [EGFR] map from E on the grayscale white-light image encoded by varying the transparency of a monochromatic green colormap according to a gamma function (A = 0.7, γ = 1.8) (G) The AIGA plots for high-binding (circles) and low-binding (triangles) region for NEG-680 (gray) and ABY-029 (black), (H) The tissue uptake curves for the high-binding (solid) and low-binding (dashed) regions for NEG-680 (gray) and ABY-029 (black). Spatial location of panels C–F are indicated by the orange box in panel A.

3.2 Imaging Data Analysis

Data acquired with the Pearl Impulse were saved to a local drive and imported into MATLAB 2013a (The MathWorks, Inc., Natick, MA) for processing with in-house and open-source algorithms. The white-light, 700-nm and 800-nm images from each time point were imported into the workspace using the bfopen function available under GNU public licence from the Open Microscopy Environment group, and stored as a datacube for AIF estimation and AIGA analysis.

To recover AIF_ICA, a linear transformation in Eq. 4, W, is sought for the measured imaging data x(r), which results in an estimate of the system sources, represented in the dynamic components, C, which are as independent as possible. FastICA was applied to imaging data after the following preprocessing steps: motion correction, negative curve concatenation, concatenation of 700 and 800 nm channels, and dimension reduction. First, a rigid image coregistration algorithm [23] was applied to each image in the series to mitigate motion with respect to the 10^th image in the set. The rigid transformation matrix determined from the white-light imaging data was applied to the 700 nm and 800 nm fluorescence images as well. Following motion correction, the ICA algorithm assumes a zero mean source signal [24], and therefore, the time-varying intensity signal of each pixel, x(r) with its negative, -x(r) was appended. The 700 and 800 nm channels are concatenated so that subsequent analysis is able to assume equal relative scaling is applied to the two channels. To stabilize the FastICA algorithm, a dimension reduction technique was applied to all pixels in the region-of-interest which reduced the number of components from about 1000 to exactly eight, yielding curves that represent concatenated 700 nm and 800 nm signals and their negative functions. The number eight was chosen based on a previous study which identified eight principle sources of time-dependent signal variance in regions outside of the head [25]. The FastICA algorithm, a fixed point routine seeking three independent components by projection pursuit, was applied to the reduced dimension data. Details of the algorithm have been published elsewhere;[26] random initial guesses for ICs were converged to a stopping criterion of ε = 0.0001 with a maximum of 1000 iterations. The scale of curves was adjusted by estimating the hypothetical concentration of dye in the blood from the known dose injected and assuming a total blood volume of 64 ml/kg for the rat. Variability in blood volume between animals has a negligible effect on the recovered value of [EGFR], since it influences both channels equally. This was confirmed by simulating a range of assumed blood volumes from 50 to 78 ml/kg and applying the resulting AIFs to recover [EGFR] from the forward-simulated data in Table 1. No effect on [EGFR] was observed, and the percent difference in [EGFR] was less than 0.5% in all cases. AIF_CAR data were estimated using the method described in a previous publication [13]. Briefly, the carotid arteries were exposed by blunt dissection, and imaged in front of a black piece of fabric to block fluorescence arising from non-vessel tissue below the area of interest. Vessels were segmented from the fluorescence images according to their similarity to the centroid pixel of a manually drawn contour, with a smoothness penalty enforced to expand the size of the ROI. Vessel diameter was estimated from the white-light images and average volume was calculated, and applied as a divisor to the time-dependent RFU curve extracted from the segmented region. Concentration curves were then estimated from these volume-normalized relative fluorescence unit (RFU) curves by means of a dye-specific calibration curve.

Table 1.

Parameters used to simulate untargeted and targeted tissue curves, which are based on typical parameters found in malignant tissue and healthy parenchyma.

Parameter	Untargeted Curve	Targeted Curve	Ref.
K1 (ml·min−1)	0.2	0.2	[28]
k2 (min−1)	0.05	0.05	[29]
k3 (min−1)	0.0	2.0	[30]
k4 (min−1)	0.0	1.0	[14]

Estimations of receptor concentration and volume distribution were calculated, either on a pixel-by-pixel basis (rat) or for an ROI drawn around the tumor (mice). Following calculation of the cumulative sums of C(t) and C_a(t), data were plotted according to Eq. 7 and the graphical approach of Logan and colleagues was applied to recover the V_D after equilibrium, which was determined by piecewise regression analysis of data points starting from the last data point and increasing the interval towards t = 0. The optimal interval was determined by a cost function which was the weighted sum of the r² goodness of fit and the relative length of the interval compared to the overall number of data points (the second term being given a relative weight of λ = 0.05). Binding potential (BP_ND) was determined by taking the ratio of the slopes from targeted and untargeted data, as in Eq. 8. Available receptor concentration, B_avail (also referred to as [EGFR] in this paper), was estimated as the product of BP_ND and K_D divided by the free tissue fraction, f. It was assumed that free tissue fraction, f, is approximately 1 since Affibody molecules have high specificity. The equilibrium dissociation constant, K_D was measured in vitro to be equal to 2.2 ± 0.3 nM [8]. Unless otherwise stated, all receptor concentration values represent available receptors, i.e., accessible for binding by the targeted dye.

3.3 Evaluation of Pharmacokinetic and Tissue Kinetic Equivalency

The hypothesis that the arterial input function (AIF) obtained from the independent component analysis approach (AIF_ICA) is equivalent to the AIF measured by direct carotid artery imaging (AIF_CAR) curves was tested in two different ways. First, a Kolmogorov-Smirnov test was performed [27] on the recovered AIF_CAR and AIF_ICA curves to determine whether these measurements represent the same distribution of continuous values, which is an accepted means of testing the equivalency of empirically characterized distribution functions.

Second, to determine whether the AIF_ICA curves led to tissue kinetic parameters identical to those obtained when using AIF_CAR curves, the full solution to the two-tissue compartment model [17] was used to generate uptake curves from the kinetic parameters summarized in Table 1. Then, the accuracy and precision of recovered values for [EGFR] as well as V_D for targeted and untargeted tracers were investigated.

3.4 Estimation of in vivo Receptor Concentration and Volume Distribution

Estimates of receptor concentration were obtained by applying the AIGA method to subject-specific AIF_ICA curves and C_ROI(t) curves acquired from subcutaneous tumors in mice bearing U251 gliomas and were compared with estimates obtained from the AIF_CAR curves. These estimates of EGFR concentration are also compared with values calculated by the previously validated deconvolution-corrected reference tracer method, which is accurate in this subcutaneous model when a muscle ROI is used as a reference tissue to correct for differences in pharmacokinetics.[9]

Finally, as proof-of-principle demonstrating the combined use of AIF_ICA data with AIGA in a case where, kinetic analysis has not been possible previously, receptor concentration and distribution volumes for ABY-029 and NEG-680 were estimated in a rat orthotopic glioma model following craniotomy and retraction of dura. Parametric maps were calculated from the motion-corrected planar fluorescence data by performing the AIGA method on a pixel-by-pixel basis, which uses least-squares fitting to recovering the slope, and then calculates the BP_ND indirectly from the DVR. Distribution volume and K₁ represent physical quantities which are defined per unit volume of tissue (1 cm³), however, conventionally this is not included in the unit.

3.5 Statistical Analysis

Statistical analysis was performed using SPSS 17.0 (SPSS Inc., Chicago, IL). Evaluation of AIF_ICA relative to AIF_CAR was performed in five mice. The recovered arterial input functions were compared using a Kolmogorov-Smirnov test for equivalency of the distribution of measured values, and the pharmacokinetic parameters (b and d) were compared by two-tailed t-test to confirm the agreement between constants extracted from the measured curves. To test the equivalency of the AIFs to extract tissue kinetic parameters, a two-tailed t-test was performed for each parameter. Unless otherwise indicated, values are presented as mean ± SEM.

4. Results

4.1 Representative example demonstrates blind separation of arterial input function from dynamic imaging data

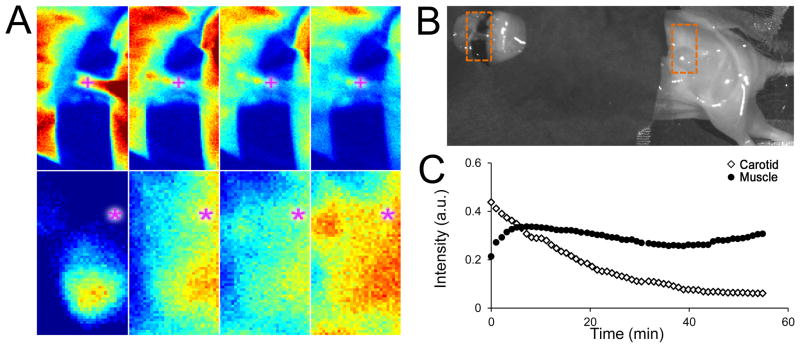
Figure 1 shows representative fluorescence intensity images acquired at post-injection time points of 1, 15, 30, and 45 min within a region-of-interest (ROI) centered on the exposed carotid artery (cross symbol) and an ROI centered on an area of leg muscle tissue in a mouse (asterisk symbol). The line plot depicts the average time-intensity curves corresponding to the locations at the two symbols demarcated in the intensity images (Fig 1A).

Figure 1.

(A) Fluorescence images acquired at 1, 20, 40, and 60 min post-injection for a region of interest centered on the carotid artery (top row) and leg muscle (bottom row). (B) White-light image of the animal draped in black cloth (to avoid light contamination from high-accumulation organs such as the liver and kidneys), with the two ROIs demarcated by rectangles. (C) Time-intensity curves following ABY-029 and NEG-680 dual-injection for a single pixel (indicated by + or * symbols) in each image-series show typical responses obtained at the carotid (white diamonds) and muscle (black circles) locations.

The time-series of fluorescence images corresponding to the bottom row of Figure 1A were processed according to the ID-AIF method described in the previous two sections, to characterize AIF_ICA. This multistep process, which involves taking the time-dependent curves from an ROI, appending them with their negative counterparts, performing a dimension reduction, and then independent component analysis is depicted in Figure 2, and leading to AIF_ICA for both NEG-680 and ABY-029 as shown in Figure 2D.

Figure 2.

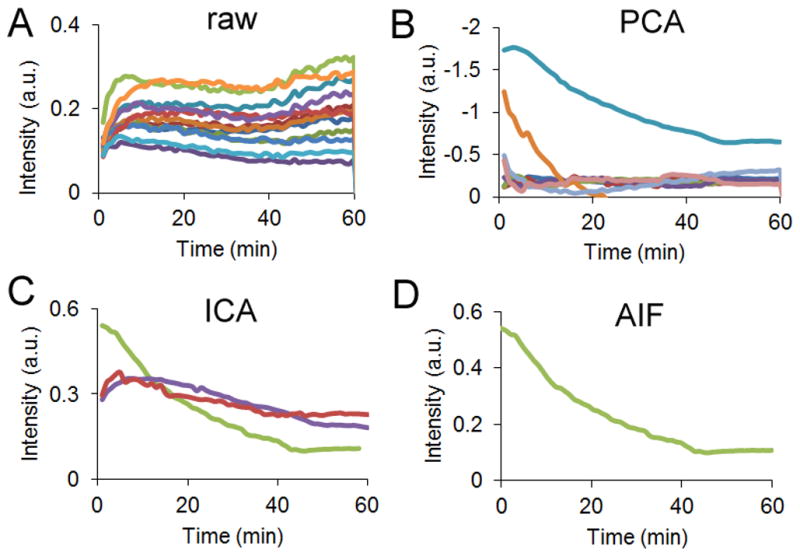
From a 1 cm x 1 cm region of interest, (A) the time-dependent curves from every 200th pixel (B) are reduced in dimension using principal component analysis. (C) An independent component analysis is performed on these curves, to recover 3 ICs. (D) The C_a(t) ICs are manually selected based on shape.

This procedure was repeated for all mice (n = 5) using ROIs of 91 ± 24 mm² taken from the thorax. The procedure required approximately 3 seconds on a PC with a 2.67 GHz Intel Core i5 CPU. Currently, manual selection of the C_a(t) IC from the three ICs was required, and selection was based on the assumption that the AIF is a biexponential function. In all cases, exactly one curve had this monotonically decreasing behavior.

4.2 Image-derived arterial input functions are equivalent to those obtained by direct carotid artery imaging

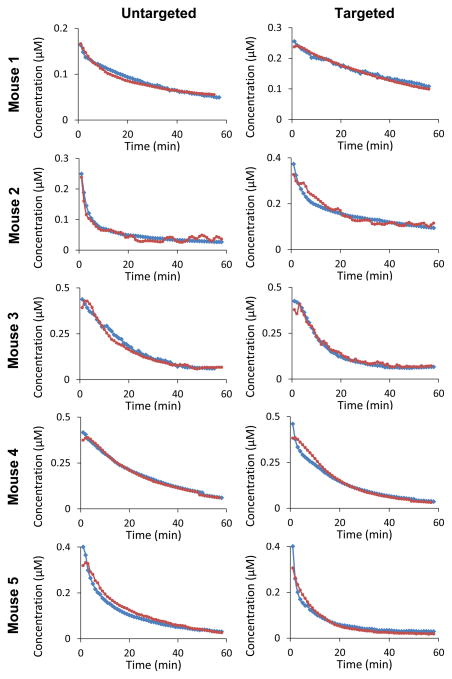
We investigated the accuracy and reproducibility of the AIF_ICA curves by focusing on two aspects of similarity: pharmacokinetic (PK) equivalence and tracer kinetic (TK) equivalence. Pharmacokinetic equivalence is considered on two levels: the equivalency of continuous distribution of values extracted by the two techniques as determined by the Kolmogorov-Smirnov test and the statistical equivalency of the extracted pharmacokinetic distribution and clearance rate constants as determined by a t-test. Here, the biexponential form, ae^bt + ce^dt (with the constraint that b ≤ d to ensure a unique solution), was fit to each curve to recover the distribution-phase rate constant, b, and elimination-phase rate constant, d. Fitting the AIF_CAR data resulted in recovered mean values for NEG-680 of −0.29 ± 0.12 min⁻¹ and −0.03 ± 0.005 min⁻¹, for b and d respectively, and for ABY-029 of −0.47 ± 0.19 min⁻¹ and −0.04 ± 0.01 min⁻¹, for b and d respectively. The mean values obtained for the two constants by fitting AIF_ICA were −0.13 ± 0.08 min⁻¹ and −0.05 ± 0.02 min⁻¹, respectively, for NEG-680 and −0.06 ± 0.02 min⁻¹ and −0.04 ± 0.01 min⁻¹, respectively, for ABY-029. None of these parameters was significantly different from each other when evaluated with a two-tailed, paired t-test (with a Bonferroni correction applied to avoid familywise type I error). Furthermore, the values obtained with the AIFCAR method and the values obtained with the AIFICA method belong to the same continuous distribution of variables as determined by Kolmogorov-Smirnov test, which was applied across all ABY-029 (p = 0.10, D = 0.11 ) and NEG-680 (p = 0.12, D = 0.10 ) curves. Qualitatively, this shape agreement is observed between the AIF_ICA and AIF_CAR data highlighted in Fig. 3. When deviations of AIF_ICA do arise, they typically appear at the early-time portions of the curves, as evidenced in mouse 4 where the maximum percent difference between the two ABY-029 curves approaches 24%. On average, the difference was 2.0% (s. d. 2.7%; min 0.0%; max 9.1%) across all animals.

Figure 3.

AIFs recovered from each animal using direct carotid imaging (blue circles) and the ID-AIF method (red squares) during dual injection of IRDye680 conjugated to negative control Affibody (untargeted; first column) and IRDye800CW conjugated to anti-EGFR Affibody molecules (targeted; second column).

Since this work is motivated by the goal of characterizing tissue distribution volume and receptor expression, a more important assessment of the equivalency of the two sets of AIFs is whether they lead to equivalent TK parameters—mainly [EGFR] and V_D for ABY-029 and NEG-680. As described in the Methods section, numerical simulations were performed by generating forward curves using AIF_CAR which were convolved with the full two-tissue compartment model according to Table 1, and then compared in terms of the values of V_d and BP_ND recovered with the AIGA method using either AIF_CAR or AIF_ICA. Table 2 summarizes the results of this evaluation. For all three parameters, no significant differences were observed in the values obtained when using either AIF_ICA or AIF_CAR.

Table 2.

Values and statistical difference of parameters recovered with the two different sets of AIF curves.

Parameter	Truth	Carotid	ICA	Difference (%)	p value
VD,U	4.0	3.8 ± 0.9	3.9 ± 0.9	2.6 ± 6.3	0.63
VD,T	12.0	12.1 ±1.1	12.7 ± 1.5	5.0 ± 7.9	0.24
[EGFR]	4.4	4.8 ± 0.4	5.0 ± 0.4	4.2 ± 9.5	0.90

The results of generating tissue uptake curves with AIF_CAR data, using a two-tissue compartment model and the parameters in Table 1, are summarized in Table 2. These entries represent the mean values obtained by performing the following simulation sequence: generate forward data, add Gaussian white noise to obtain a signal-to-noise ratio of 40 dB, and use AIGA method to recover the parameters of interest, which were then evaluated by between-model comparisons and comparison to the true parameters.

4.3 Estimates of receptor concentration in U251 tumor-bearing mice do not depend on which input function is used

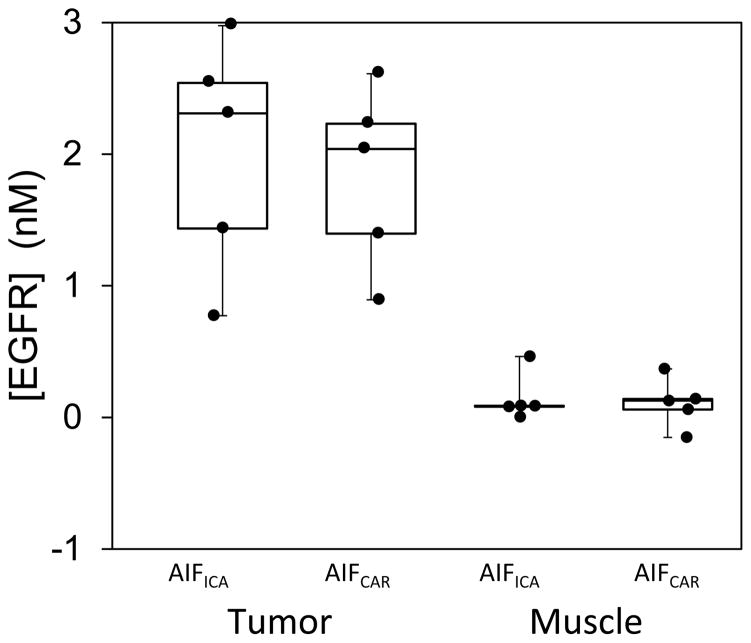
For the in vivo data, equivalency of the AIF_CAR and AIF_ICA groups was tested by estimating [EGFR] using the AIGA method in muscle and tumor ROIs in the same mice and comparing results obtained with the two sets of AIFs to the previously validated reference tracer model. Figure 4 presents box-and-whisker plots of the recovered values for the data groups. Using the AIF_ICA curves, the mean values of [EGFR] recovered from the tumor and muscle ROIs were 2.02 ± 0.40 nM and 0.14 ± 0.08 nM, respectively. Alternatively, when using the AIF_CAR curves, the mean values recovered were 1.84 ± 0.31 nM and 0.11 ± 0.08 nM for the same two tissue-types, respectively. These data agree with those calculated using the previously validated deconvolution-correction method, which recovered mean [EGFR] of 2.00 ± 0.46 nM for the tumor region. The recovered [EGFR] values using AIF_CAR and AIF_ICA were not significantly different as determined by a t-test (p = 0.12), and were not different than the deconvolution measured values (p = 0.98).

Figure 4.

Box-and-whisker plots of the [EGFR] values recovered from tumor and muscle ROIs in U-251 bearing mice (n=5) evaluated by the AIGA method using either carotid-artery derived (AIFCAR) or image-derived (AIFICA) arterial concentration curves.

4.4 Image-derived arterial input function combined with arterial input graphical analysis enables receptor concentration imaging in rat orthotopic glioblastoma

As proof-of-principle, we examined a scenario for which no AIF is available and for which the reference tissue model is likely to breakdown—a rat orthotopic U-251 tumor imaged during open craniotomy, which has been previously shown to overexpress EGFR when implanted intracranially [32, 33]. Figure 5 summarizes the results of this single preliminary case. A gadolinium-enhancing tumor was observed just under the cortical surface on the medial aspect of the right hemisphere (Fig. 5B). In a magnified region which is indicated by the orange box in Fig. 5A, parametric maps of V_D,U, V_D,T, and [EGFR] were calculated (panels C-E, respectively). Interestingly, substantial heterogeneity was observed in the V_D maps, with hypovolemic regions coinciding with the center of the tumor area. The [EGFR] map also shows heterogeneity, but with a more uniform distribution in the center of the tumor, which decreases outwardly from the suspected tumor mass. The color overlay (panel F) is the same [EGFR] map placed over the grayscale white-light image of the rat, with the alpha-value (transparency) set as a function of the [EGFR] magnitude. The graphical analysis plots are shown in panel G, for both NEG-680 (gray symbols) and ABY-029 (black symbols) from low-binding (triangles) and high-binding (circles) regions. Lines-of-best fit represent the linear region of the curves, which is the point at which equilibrium between the tissue compartments is reached. Panel H shows the time-concentration curves for the same low-binding (dashed lines) and high-binding (solid lines) regions for NEG-680 (gray lines) and ABY-029 (black lines).

5. Discussion

The inability to characterize the arterial input function has limited clinical use of optical tracer kinetic imaging and receptor concentration imaging in some situations. To overcome certain limitations, a reference tissue model approach that parallels those used in PET imaging has been introduced to the optical molecular imaging problem. These methods have the added benefit of encoding targeted and untargeted tissue curves spectrally using fluorophores with different emission wavelengths. This dual probe molecular imaging strategy was first applied in vivo using a ratiometric method to obtain EGFR binding potential in a mouse pancreatic cancer model [34]. A more robust and general model was established by Tichauer and colleagues which provided the basis for current receptor concentration imaging techniques that have been validated in several subcutaneous tumor lines, and more recently, has been applied to lymph node imaging [35] and ex vivo tissue analysis [36]. A growing body of work has appeared that suggests RCI is a very accurate technique for in vivo receptor quantification in preclinical models of cancer, and may even find new diagnostic applications. However, RCI is ultimately limited by two assumptions: (i) both tracers have identical pharmacokinetics (PK) and (ii) both tracers are extravasated from the blood to the extravascular space in a similar manner (i.e., they have identical tissue kinetics [TK]). Each assumption limits application of RCI in different ways. For example, clinical use of RCI in its current implementation would require FDA-approval for two agents, engineered to have identical pharmacokinetics but differing only in that one binds to EGFR (or another receptor of interest) and one does not. Attaining this equivalency is unlikely since the regulatory costs of approval of a single agent can be $100 million [37]. Recently, a correction method was reported to reduce the error caused by differences in PKs or TKs [9]. The technique requires a reference region, void of receptors-of-interest, and with similar TKs as the region of interest. No true “reference” for tumor exists, since tumors often have very different kinetics than surrounding tissue. In fact, the vascular organization, and therefore, flow and extraction fraction can be very different across tumor types, growth rates, and location [38]. The lack of a reference is one reason why the majority of PET receptor studies focus on neurochemical ligands which are expressed in different parts of the brain, but are not as structurally or dynamically different from the rest of the brain as tumors.

Despite the difficulties associated with characterizing the AIF, recent studies have used arterial-input methods to describe passive optical dye kinetics in rat tumors. One study exploited ICG and methylene blue (MB) using a single-tissue compartment model to estimate K₁ and k₂ values [39]. In this study, combined frequency-domain and steady-state broadband reflectance measurements was applied to extract blood volume independent of kinetics by means of the spectroscopic derivation of hemoglobin concentration, and enabled the plasma pharmacokinetic constants and the tissue kinetic constants to be fit in a single step. Future work might involve the use of a similar multifiber or imaging-based (i.e., structured light imaging) to perform optical blood volume characterization and ID-AIF might stabilize the inverse problem further. Another study evaluated the optimal kinetic model for first-pass passive tracer kinetics using ICG and untargeted IRDye800CW [40]. The AIF during first pass and recirculation contains high-frequency information that enables separation of blood flow, extraction fraction and permeability surface-area product when used in conjunction with the St. Lawrence-Lee model or more generally, the unified impulse model [41]. Several recent studies have highlighted the need for imaging methods that can separate leakage effects from blood flow,[42] since tumors show a high degree of heterogeneity in both parameters, and patient response to antiangiogenic treatment, photodynamic therapy, and radiation therapy might correlate with one parameter but not the other [42, 43]. The study by St. Lawrence and colleagues suggests this possibility in malignant tissue when using optical dyes and a robust arterial-input model, that allowed them to demonstrate increased extraction fraction of the smaller IRDye800CW molecule (1.17 kDa), compared with the larger albumin-ICG complex (67.3 kDa), while blood flow between the two agents remained constant. Despite the existence of studies showing the promise of applying models to determine tissue kinetics, the inability to reliably quantify the AIF—a precursor for these kinetic models—has slowed progress.

The methodology presented in this study extends work previously described for PET imaging to extract AIFs from the time-series of images [44–46]. Because of the diffuse nature of light signals in tissue, as well as the ability to image optically at high dynamic range with fast acquisition rates, each voxel contains a large amount of time-dependent information representing a linear combination of the AIF and other tissue curves. The AIFs presented in Fig. 3 from five mice show that for both the targeted and untargeted dyes, the ID-AIF is qualitatively similar to the AIF measured by carotid imaging. In animals 3 and 5, an inflection point is observed around 4 minutes post injection which is assumed to be an artifact from some spillover in the ICA algorithm; since the tissue uptake curves have a similar shape at this timeframe, it is more difficult to isolate the arterial component of the signal. However, this appears to only affect very early time-points and the overall impact on kinetic analysis is negligible. Despite some variability introduced to the distribution rate constant, b, by the spillover artifact, the values obtained from the two approaches represent the same distribution of continuous values, as evinced by the Kolmogorov-Smirnov test. Since our research team has been interested in the in vivo molecular imaging of EGFR-targeted agents, a natural application of the ID-AIF method occurs in conjunction with an arterial-input method to quantify binding potential and receptor concentration. Therefore, we investigated the equivalency of the ID-AIF method to recover [EGFR], and applied AIF_ICA in a case where we previously had no way to estimate AIF—a rat orthotopic model of glioma.

Two numerical simulations were performed to demonstrate the equivalency of ID-AIF in recovering TK parameters. First, an accuracy and precision analysis was executed in which no significant differences were observed in values extracted with ID-AIF compared with AIF measured by carotid imaging, and while both methods slightly overestimated binding potential—owing to the full two-tissue compartment model used to generate the forward data, which differs slightly from the simplified graphical analysis model—the difference between the two methods was less than 5%, and the reproducibility of the two methods was the same. Figure 4 compares the results of [EGFR] calculated using AIGA and either AIF_ICA or AIF_CAR from in vivo subcutaneous U-251 tumor uptake measured with a planar fluorescence imaging system in the same mice shown in Figure 4. Further indication of the equivalency of the two AIFs is supported by the results that the values obtained within the tumor ROI and within the muscle ROI, did not depend on which AIF was applied. Additionally, these data demonstrate the use of the AIGA method to quantify [EGFR] for the first time, showing strong agreement with [EGFR] calculated using the deconvolution-corrected reference tracer approach that has been validated previously [9].

Finally, as proof-of-principle of the potential for the ID-AIF method to provide new opportunities in optical kinetic modeling, Figure 5 presents the first receptor concentration image in an orthotopic rat model undergoing craniotomy. In addition, to the best of our knowledge, the same figure presents the first optically-derived distribution volume maps. As reflected in the uptake curves in panel H, the targeted ABY-029 tracer shows considerable uptake in the high-binding region when compared with a contralateral low-expression region. Interestingly, the negative control tracer also shows considerable uptake and retention in the high-expression region compared with the contralateral region. However, when these curves are compared with the AIFs obtained by graphical analysis, retention of the targeted ABY-029 is higher than that of NEG-680, presumably due to specific binding, and that the effect is partially obscured by an increased plasma clearance rate of ABY-029 compared with NEG-680 in this subject. When considering only the NEG-680 curves, the slope recovered from the high-expression tumor region was 2.4x greater than that of the contralateral “reference region”. While cautious not to over-interpret these preliminary findings, they highlight the interplay between tissue kinetics, binding kinetics, and pharmacokinetics, which is likely to be very complex, especially in the setting of orthotopic tumor models or in situ clinical imaging, and suggest that each of these kinetic “layers” must be carefully evaluated.

Limitations of this method stem primarily from how effective the measured untargeted dye controls for non-binding behaviours of the targeted dye. Since the [EGFR] measurements are based on ratiometry (Eq. 8), errors which differentially affect one channel are likely to increase measurement error. These include wavelength-specific absorption and scattering, quantum efficiency of the two dyes, differences in non-specific binding by blood proteins, and instrument response function effects. Many of these factors can be addressed by calibration of RFU images using equimolar dye-blood-intralipid phantoms; current development into a robust calibration procedure for dual-tracer imaging is underway. Future studies will focus on better understanding the influences of background uptake and non-specific binding on the [EGFR] measurements. However, it should be noted that these challenges are not limited to optical imaging, but are present in all medical imaging modalities and influence the accuracy and meaningfulness of derived kinetic parameters. For example, one of the major drawbacks to employing ICA in medical imaging is that it results in arbitrarily scaled source signals, relying on additional steps to restore quantitation. Since ICA is performed on both channels simultaneously, and therefore, both channels are scaled by the same mixing matrix, this problem is largely mitigated; however, unlike the [EGFR] which is derived from a ratio of data from the two channels, the volume of distribution measurements are influenced by absorption effects and errors in AIF quantification even when they affect both channels equally.

Orthotopic glioma models are incompatible with our previously developed invasive carotid imaging method of acquiring AIFs (the carotid arteries are located on the other side of the head from the imaging plane). Therefore, the ID-AIF method presents new opportunities for kinetic imaging of orthotopic tumor models. In parallel to these preclinical efforts, the ID-AIF method can be applied in current clinical scenarios—for example, during fluorescein sodium uptake for glioma resection [47], or during head and neck cancer guided by IRDye800CW labeled cetuximab (Erbitux®) [1]—and therefore, has the potential to provide new sources of contrast for intraoperative tumor margin assessments. Future work is needed to determine the accuracy and reproducibility of the AIGA method coupled with ID-AIF characterization in multiple rat orthotopic tumor lines. Careful comparison to other methods of FGR, such as intraoperative DCE-MRI, ALA-induced PpIX expression, and passive dye enhancement—with each in turn being coregistered to the gold standard, immunohistochemistry and histopathology—will provide insight into the incremental gains in tumor resection provided by this technique. Finally, strategies should be investigated to reduce the imaging times required for AIGA, since the clinical penetration of this technology will depend very strongly on minimizing disruption to current workflows. With the dye-pair used in the present study, imaging times could be reduced to 10 min using a delayed approach similar to that used by Tantawy and colleagues [48], although variability in [EGFR] would increase 4-fold. Further work is needed to reduce imaging times, through the use of delayed techniques, sequential injections, or selection of dyes with ideal kinetics, to provide acceptable imaging times for the intraoperative environment.

In conclusion, this study demonstrates that arterial input functions characterized using a blind separation method based on dimension reduction and independent component analysis are equivalent to those acquired by directly imaging the surgically exposed carotid artery, both pharmacokinetically, as well as in tissue kinetic analysis and in vivo receptor concentration measurement. As a corollary, a dual-tracer graphical analysis strategy—termed the arterial input graphical analysis method—was used in conjunction with ID-AIFs to recover [EGFR] in mice with U-251 subcutaneous tumors; values showed strong agreement with those obtained using a previously validated deconvolution-corrected reference tracer method. Finally, as proof-of-principle, we present the first orthotopic receptor concentration and distribution volume maps in a rat orthotopic glioma model, which were acquired in vivo during open craniotomy.