Human and Server Docking Prediction for CAPRI Round 30–35 Using LZerD with Combined Scoring Functions

Abstract

We report the performance of protein-protein docking predictions by our group for recent rounds of the Critical Assessment of Prediction of Interactions (CAPRI), a community-wide assessment of state-of-the-art docking methods. Our prediction procedure uses a protein-protein docking program named LZerD developed in our group. LZerD represents a protein surface with 3D Zernike descriptors (3DZD), which are based on a mathematical series expansion of a 3D function. The appropriate soft representation of protein surface with 3DZD makes the method more tolerant to conformational change of proteins upon docking, which adds an advantage for unbound docking. Docking was guided by interface residue prediction performed with BindML and cons-PPISP as well as literature information when available. The generated docking models were ranked by a combination of scoring functions, including PRESCO, which evaluates the native-likeness of residues’ spatial environments in structure models. First, we discuss the overall performance of our group in the CAPRI prediction rounds and investigate the reasons for unsuccessful cases. Then, we examine the performance of several knowledge-based scoring functions and their combinations for ranking docking models. It was found that the quality of a pool of docking models generated by LZerD, i.e. whether or not the pool includes near-native models, can be predicted by the correlation of multiple scores. Although the current analysis used docking models generated by LZerD, findings on scoring functions are expected to be universally applicable to other docking methods.

Introduction

Interactions between proteins are fundamental to many biological processes. Atomic-level detail of these interactions is important to understand the molecular mechanism of these processes. However, experimental techniques, including X-ray crystallography and cryo-electron microscopy, have often difficulty in determining the structure of a protein-protein complex and they are resource-intensive; thus, many biologically important protein complexes remain unsolved. To supplement the limited availability of experimentally determined complex structures, computational protein-protein docking methods can be used to provide structure models of complexes. Protein docking methods need the tertiary structure of single proteins to be docked. Compared to the number of complex structures, substantially more single protein structures are available and many more can be modeled by template-based structure modeling methods^1–3. Computational docking methods are also essential tools for artificial design of protein complexes^4;5.

Over the past two decades, many protein-protein docking methods have been developed^6;7. The methods are characterized by key algorithms and techniques used, including Fast Fourier transform^8–12, Monte Carlo search¹³, and local patch matching¹⁴ for docking conformational space search, energy funnel analysis for selecting docking models¹⁵, and the use of biochemical/biophysical data to guide docking¹⁶. Conformational changes of proteins upon docking are also addressed by various strategies^17–23.

Protein docking procedures can be roughly divided into four logical steps. The first step is preparation of the single protein structures. If the structure of the proteins are not available, it requires modeling of their structures. Then, protein docking is performed, which usually generates thousands of docking models (decoys). Subsequently, the most plausible decoys are selected by identifying frequently observed decoy structures with clustering analysis and ranking decoys using scoring functions. Finally, the selected models are refined, e.g. by relaxing structures and remodeling side-chains, to produce final models. Obviously, all these components need to work well in harmony for successful prediction. Among them, the scoring step is particularly crucial as it is still challenging to select near native models from thousands of alternatives. A straightforward approach for scoring is to combine physics-based terms, such as van der Waals forces, electrostatic potential, and a solvation term¹³. Many knowledge-based scoring functions, which are based on statistics of atom-atom^24;25 or residue-residue interactions^26;27 observed in known protein complexes, have been developed. At a more coarse-grained level, geometric shape complementarity has been considered^{28– 30}. Other interesting ideas for scoring decoys include consideration of energy funnels³¹, co-evolution of amino acids at the docking interface^32–36, and using dynamics simulation³⁷.

The Critical Assessment of Prediction of Interactions (CAPRI)³⁸ was established in 2001³⁹ to serve as an objective, community-wide assessment of the state of protein complex prediction methods. Since then, over 100 targets have been released for prediction and scoring. Our group have participated in CAPRI since 2009, participating in rounds 18–24 and 26–37. The core of the prediction pipeline is a protein-protein docking program named LZerD^40–44 developed in our group. LZerD represents protein surface with 3D Zernike descriptors (3DZD)^41;45;46, which are based on a mathematical series expansion of a 3D function. The 3DZD comprise a soft representation of the protein surface shape, making LZerD more tolerant to the conformational change that occurs on binding.

In this work, we summarize our group’s performance in the recent rounds of CAPRI, both human group and server predictions, and classified the reasons for cases that were not predicted successfully. We found that two major failures occurred in the prediction procedure. The first one is the low quality of single-chain models, which led to a sparseness of acceptable quality docking models. Another failure occurred at the decoy selection step, which used a two-step procedure of applying several scoring functions for the human group prediction. To improve decoy selection, we examined the performance of five scoring functions and their pairwise combinations and found that pairwise combinations provide more robust and accurate decoy selection results. Furthermore, we observed that the quality of a decoy pool, i.e. whether or not the pool contains acceptable quality models, can be predicted by the shape of the pairwise score distributions, and proposed an intuitive rule that predicts decoy pool quality.

Materials and Methods

Datasets

Two datasets were used in the current work. First, we discuss our performance on pairwise docking targets from CAPRI rounds 30–35. The targets included in the analysis are listed in Table 1. Targets were excluded if they were canceled or no group predicted any acceptable quality models. “Acceptable” and other model qualities have been defined according to the criteria used in previous CAPRI rounds⁴⁷. We also excluded multimeric complex targets from the current analysis because the multiple interfaces make it more difficult to determine the reason for failure and compare them with pairwise complex targets. Of the 27 targets from Round 30, 11 were excluded: T76 and T83 were canceled by the organizers; T68, T74, T77, T78, and T88 were not predicted with acceptable quality models by any group; and T70, T71, T73, T74, T78, and T81 were multimeric protein complexes. Of the 3 targets from Round 31, a multimeric complex target, T95, was excluded. All of Rounds 32, 33, and 35 were excluded due to no successful predictions by any group. Both of the targets from round 34 were included.

Table 1.

Summary of the performance of our group and other groups

Round	Target	LZerD hits	Kihara hits	Groups with hits	All group hits
30	T69	0	0	15	87/57**
	T72	0	0	3	3
	T75	0	1	15	65/47**
	T79	1	3	13	28/6**
	T80	0	0	21	105/71**
	T82	0	0	13	71/54**
	T84	0	4/1**	18	84/61**
	T85	0	0	13	83/55*
	T86	0	0	2	3
	T87	0	0	15	83/51**
	T89	0	0	15	87/26**
	T90	0	1	19	104/47**
	T91	2	8	17	109/40**
	T92	0	0	17	98/12**
	T93	0	9/2**	16	102/70**
	T94	0	0	12	58/1**
31	T96	0	0	5	5/2**
	T97	1	1	10	19/5**
34	T104 (wat)	10/10**	10/10**	27	224/204**/53***
		7+	9+	20	158+/75++/15+++
	T105 (wat)	10/10**	10/10**/1***	32	246/228**/42***
		10+/1++	10+/7++/2+++	25	197+/124++/64+++/1++++

“LZerD hits” and “Kihara hits” are the number of hits in the top 10 models we submitted to CAPRI. “Groups with hits” is the total number of CAPRI predictors with at least one hit and “All group hits” is the sum of all top 10 hits by all groups³⁸.

^**indicates medium quality models and

^***indicates high quality models. For example, “4/1**” means that in the top 10, 4 models were acceptable or higher quality and among them 1 was medium quality.

CAPRI model qualities defined previously⁴⁷. Rows marked (wat) indicate water prediction:

⁺fair;

⁺⁺good;

⁺⁺⁺excellent;

⁺⁺⁺⁺outstanding.

Second, using the 16 targets from round 30 in Table 1, we performed detailed analysis of scoring functions. We examined decoy selection performance of individual scores and their combinations as well as success/failure assessment of docking predictions from score distributions.

Docking prediction procedure

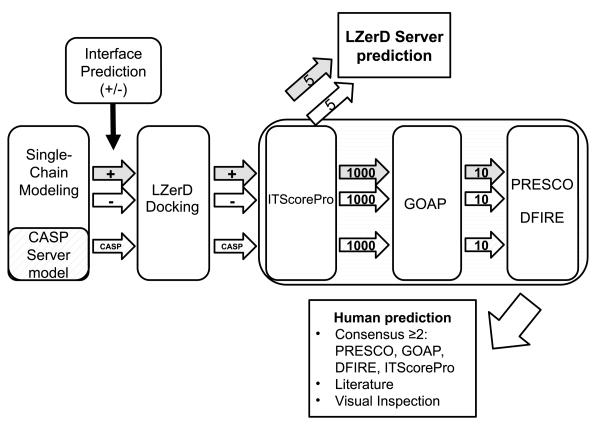
The Kihara lab submitted docking models to CAPRI under two groups, a human predictor group “Kihara” and server prediction “LZerD”. The predictions for the two groups shared a common primary procedure of running the LZerD docking program (with and without using interface prediction), followed by decoy selection with knowledge-based scoring functions and molecular dynamics (MD)-based refinement, but they differ in several ways. We first describe the common steps between the two submissions and later address how the two submissions differed. The prediction pipeline is illustrated in Figure 1. See the figure caption for an explanation of each step.

Figure 1.

Protein docking prediction pipeline used in our group. The tertiary structure of single proteins of a CAPRI target are modeled following the protocol described in Methods. For the human prediction of CAPRI Round 30, we also used structure models selected from CASP server models. Three parallel runs of LZerD protein docking are performed: two runs with(+)/without(−) binding residue constraints taken from prediction by BindML (the gray and white arrows in the diagram) and cons- PPISP using single chain models generated by our lab protocol, and the third LZerD run (only for human prediction, hashed arrows labeled as CASP) using single chain models selected from CASP server predictions. For each of the three tracks, decoys are ranked by ITScorePro, and top 1000 decoys are selected. For LZerD server prediction, top 5 models each from decoys with(+)/without(− ) binding residue constraints using our single chain models were submitted. 1000 models from each track are further reduced to top 10 models by GOAP, which are ranked by PRESCO and DFIRE, independently. Finally, out of the 30 models in total, models that are consistently ranked among the top by two or more scoring functions are chosen in principle for final submission. Usually such models do not fill the ten slots for submission, and rests are filled with models ranked high by either of the scores and visual inspection. Biological information from literature is also applied for final selection if available.

Protein-protein docking with LZerD

We used LZerD⁴⁰ (Local 3D Zernike Descriptor-based protein docking program) to generate docking decoys. 3D Zernike descriptors (3DZD) are the coefficients of a mathematical series expansion that describes the 3D surface shape of the protein. 3DZD are invariant to rotation and translation; thus, the similarity of two surfaces can be quantified by computing the Euclidean distance between two sets of 3DZD. LZerD spreads points across the protein surface and computes local 3DZD at each point. Decoys are ranked by a shape complementarity-based score, which evaluates the following four terms: buried surface area, excluded volume (e.g. clash), Euclidean distance between the 3DZD, and angle between the surface normal vector. The 20,000 decoys with the best shape complementarity scores were kept. Next, the decoys were clustered using an RMSD cutoff of 4.0 Å. The number of cluster centers was reduced to 9999 using the shape complementarity score and these cluster centers were scored using ITScorePro⁴⁸.

Docking interface prediction

We used interface residue predictions from BindML^49;50 and cons-PPISP^51;52. BindML uses the observed mutation patterns of docking interface residues and non-interface surface residues to predict whether residues are at the docking interface. The BindML score for a residue indicates the difference between the likelihood of the residue being non-protein binding and the likelihood of the residue being protein binding, with a negative score indicating that protein binding is more likely. Residues with a BindML score below −1.5 were chosen as interface residues. Cons-PPISP is a neural network classifier, which uses features of the sequence profile and solvent accessibility from neighboring residues. Residues predicted to be interface by either method (i.e. the union of the predictions) were used as an interface restriction for LZerD docking. We performed two independent runs of LZerD with and without using binding residue predictions (Figure 1).

Model refinement

After the decoys to be submitted are selected, the structures were relaxed using molecular dynamics (MD) simulation to reduce the number of atom clashes. CHARMM⁵³ was used for MD simulation with an implicit solvent model, SCPISM⁵⁴. For the entire simulation, all C_α atoms were restrained with a harmonic constraint of 100 kcal/mol/Ų. The complex was minimized with 500 steps of the steepest descent algorithm followed by 1000 steps of the adopted basis Newton-Raphson algorithm. Finally, the structure was equilibrated for 20 ps using a temperature of 100 K, 2 fs timestep and fixed covalent hydrogen bond lengths.

Human prediction and server prediction

Here we describe difference of prediction procedures between the human prediction “Kihara” and server prediction “LZerD”. First, the single chain models used were different in the CAPRI Round 30. For the “LZerD” server predictions, we created monomer models using our lab’s modeling protocol³⁸ (in the supplemental material of the paper³⁸). This protocol uses template based models generated by available modeling software including HHPred⁵⁵, SPARKS-X⁵⁶, and Modeller⁵⁷ version 9.11, followed by the CABS⁵⁸ coarse-grained protein simulation/modeling method for relaxation and refinement. The templates used are listed in Table S1. CAPRI 30 shared the same protein targets with the 12th Critical Assessment of Techniques for Protein Structure Prediction (CASP11)⁵⁹; thus, the automatic server models from CASP11 were available before the CAPRI human deadline. For human prediction, we used CASP stage 2 server models listed in Table S1 to generate a third independent decoy pool with LzerD (Figure 1).

The decoy selection procedure was substantially different between the Kihara human group and the LZerD server submissions. For LZerD group, the decoys were simply chosen using ITScorePro⁴⁸. In most cases, the top 5 decoys were chosen from each of the “interface” and “no interface” LZerD decoy sets. For the Kihara group submission, decoys from “interface”, “no interface”, and “stage 2 model” LZerD decoy sets were considered. Within each set, the decoys were pre-filtered using ITScorePro⁴⁸ and the top 1000 by ITScorePro were scored using GOAP⁶⁰. From each decoy set, the top 10 decoys by GOAP were scored using PRESCO⁶¹ (described later) and DFIRE⁶². Out of these 30, decoys that are consistently ranked high by any two or more scoring functions (PRESCO, ITScorePro, GOAP, and DFIRE) were chosen for final submission. In most cases, this did not fill the ten submission slots; thus, the rest of the ten were filled using decoys ranked high by PRESCO and visual inspection. Additionally, when available, literature information about interface residues or inter-chain residue-residue contacts was used to choose decoys.

Scoring functions used for decoy selection

Here we briefly describe six knowledge-based scoring functions used either for the decoy selection in CAPRI or benchmarked in this study. Three knowledge-based statistical scores, DFIRE⁶², ITScorePro⁴⁸, GOAP⁶⁰, as well as PRESCO⁶¹, were used in CAPRI (Figure 1). In addition, we benchmarked two more statistical scores, OPUS-PSP⁶³ and SOAP-PP⁶⁴, in the latter half of the current study.

The general approach of constructing a knowledge-based statistical scoring function is to determine the observed distribution of some feature (e.g. atom pair distance or angles) in a set of known protein structures and normalize the distribution by a reference state. Scoring functions typically differ in the choice of features and the method for determining the reference state.

DFIRE

DFIRE⁶² (Distance-scaled, Finite Ideal gas REference state) is a distance-dependent atom contact potential based on 167 atom types. It uses a reference state of an ideal gas atom distribution in a finite system.

GOAP

GOAP⁶⁰ (Generalized Orientation-dependent All-atom Potential), adds a orientation-dependent term to DFIRE to make it a distance- and orientation-dependent atom potential.

ITScorePro

ITScorePro⁴⁸ is a distance-dependent atom contact potential based on 20 atom types. It is originally intended for single-chain model evaluation. Instead of using a reference state, the pair potentials were iteratively refined to reduce error in protein model selection.

OPUS-PSP

OPUS-PSP⁶³ (Potential derived from Side-chain Packing), which considers orientation-specific packing interactions of side-chains that are classified into 19 rigid blocks. A repulsive energy term is added to prevent steric clash.

SOAP-PP

SOAP-PP⁶⁴ (Statistically Optimized Atomic Potential for Protein-Protein interactions) is a statistical potential for protein-protein interaction that considers atom pair distances based on 158 atom types, bond orientation, and relative solvent-accessible surface area. The atom pair distances and bond orientation also consider covalent separation, e.g. how many covalent bonds separate the atoms, how many residues separate the atoms, and whether the atoms are part of the same polypeptide chain.

PRESCO

For human group prediction we used PRESCO^61;65 (Protein Residue Environment SCOre), which was originally developed for single chain protein model selection. We modified it to improve protein-protein decoy ranking for CAPRI. In contrast to most of the existing pairwise knowledge-based statistical potentials that capture the preference of pairwise interactions between atoms or atom groups, PRESCO was designed to capture multi-body interactions of residue side-chains. PRESCO evaluates how much each residue in a decoy is native-like by comparing the neighboring residues of the target residue to those in a reference structure database by considering neighboring main-chain conformation, the number and the position of neighboring residues within a sphere of 8.0 and 6.0 Å radius. If the residue environment of a decoy matches with those from similar residue environments from reference proteins, the decoy is considered to be more likely to be near-native. Thus, the score of a decoy is the sum of the amino acid similarity score between residues in the decoy to residues in the reference structures that have the most similar environment. Multiple amino acid similarity matrices are combined including the CC80 matrix⁶⁶ and others taken from the AAIndex database^67;68. PRESCO performed very well in CASP11⁵⁹, leading our prediction group to the top rank in the free modeling category^59;65.

For CAPRI, we used 856 protein complexes in ITScore-PP training set⁶⁹ as the reference database. Also, to accommodate the conformational changes of side-chains at the docking interface upon binding, the C_α position and its corresponding side-chain centroid was paired and the vectorized pair-positions were used to describe residue locations, because the side-chain centroids that were used in original PRESCO are more sensitive to side-chain conformational change in amino acids.

Logistic Regression

In the latter half of the current study, we evaluated whether logistic regression could classify decoys as correct or incorrect. Binary classification was performed by grouping the quality labels acceptable, medium, and high into the positive class. A jackknife procedure was used where each target was used as the test set and the remaining targets were used as the training set. Logistic regression was performed with an L2 norm penalty, liblinear solver, and a regularization strength of 1.

Results

We start by discussing our prediction performance on pairwise docking targets from CAPRI rounds 30–35. Particularly, we classify the reasons for failed cases. Next, we test five scoring functions in decoy selection, both singly and in combination. Finally, we propose an evaluation metric for predicting whether or not a decoy pool contains acceptable models.

Overall performance for pairwise targets in recent CAPRI rounds

On the 18 pairwise docking targets listed in Table 1, our human group (Kihara) successfully submitted acceptable or better models according to the CAPRI criteria⁴⁷ for nine targets including four targets with medium quality models and one with high quality models. Our server prediction (LZerD) had a lower success rate than the human submission with acceptable or better models obtained for five targets.

For reference, there are two official evaluations by the CAPRI organizers covering targets in Table 1. Considering all 25 Round 30 targets for which the assessor’s evaluation paper is recently published³⁸ (Table 4 in the paper³⁸), our group’s performance was ranked 17th for the human submission among the 26 groups listed in the table (with 39 participants not listed) and 5th for the server submission. We did relatively well in the scoring category, where participants were asked to rank provided models: we were 5th (tied with Zou) out of 14 scoring groups listed in the table. In a more recent evaluation at the 6th CAPRI evaluation meeting at Tel Aviv in April 2016 (http://www.cs.tau.ac.il/conferences/CAPRI2016/), which covered targets from Rounds 28–35, our human prediction was ranked 18th among 42 groups, our LZerD server was ranked third among eleven servers, and 9th for both human and server in the scorer prediction among 32 groups. In our prediction, all the targets were modeled by running LZerD and no template-based modeling of complexes were performed. Thus, some targets might have been modeled better if template-based complex modeling were performed.

To understand our prediction performance, we analyzed the reasons for failure for the targets. For four targets (T69, T72, T94, and T96), none of the decoys generated by LZerD satisfied the acceptable quality. The number of hits in the decoy sets are shown in the first three columns of Table 2, decoys without using the binding residue prediction (No int.), decoys generated with restraints of the binding residue prediction (the Interf. column), and decoys using CASP models (CASP) (Fig. 1). The reason of obtaining no hit is due to a low quality of the single chain model used for docking. For both T69 and T72, the best decoys had values in the acceptable range for f_nat, but the single-chain model errors increased the L-RMSD to be incorrect. For T69, the single-chain RMSD was 7.9 Å and the best decoy had f_nat 0.14, I-RMSD 4.21 Å, and L-RMSD 17.29 Å. For T72, the single-chain RMSD was 5.8 Å and the best decoy had f_nat 0.18, I-RMSD 6.15 Å, and L-RMSD 18.89 Å. For T94, the N-terminus in the single chain model blocked the binding site, which made it impossible for docking to generate good quality complex models. When we repeated LZerD with the N-terminus truncated after we knew the reason of the failure, one acceptable model was produced. For T96, while the models had low single-chain RMSD (1.0 and 0.7 Å for the two chains), no acceptable models were produced. When we repeated LZerD with the bound subunits from PDB ID 4xl5, two acceptable models were produced. This suggests that the errors in the models, while small, prevented successful docking. Several residues at the interface have larger Cα shifts, such as 3.5 Å for Lys40 of chain A and 2.0 Å for His148 of chain B. In addition, the interface of chain A contains several aromatic rings and several have substantial χ₁ torsion angle error in the model, including Tyr33, Phe36, Tyr91, and Trp122. For the successful models (ones that have acceptable models), the RMSDs of single chain models were below 4.1 Å except for T89 and T92 (Tab. S1).

Table 2.

LZerD decoy pool hits and single score selection

	Hits in LZerD decoy pool			Top 10 selection by score
Target	No int.	Interf.	CASP	ITScorePro	GOAP	DFIR	E SOAP-PP	OPUS-PSP
T69	0	0	-	n/a	n/a	n/a	n/a	n/a
T72	0	0	-	n/a	n/a	n/a	n/a	n/a
T75	6	0	9	1	0	2	0	1
T79	81/1**	0	-	3	5	7	4	2
T80	1	0	8/2**	2/2**	3/1**	2/2**	4/2**	3/2**
T82	0	0	2	2	1	2	2	2
T84	3	6	7/3**	3/3**	3/3**	0	2/2**	3/3**
T85	0	0	1	1	1	1	1	1
T86	1	1	1	0	1	0	0	0
T87	0	0	1	1	0	1	1	1
T89	6	†	7	0	0	0	0	0
T90	0	0	6	4	5	4	5	3
T91	9	1	38/1**	5/1**	5	6/1**	2	3
T92	0	0	5	2	0	2	2	2
T93	0	0	10	7	6	7	5	6
T94	0	-	0	n/a	n/a	n/a	n/a	n/a
Hits	7/16	4/15	12/13	11/13	9/13	10/13	10/13	11/13

^**indicates medium quality models. For example, “4/2**” means that in the top 10, 4 models were acceptable quality or better, 2 out of the 4 models were medium quality, and 6 were incorrect.

The first 3 columns show the number of hits in each LZerD decoy pool. “No int.”: LZerD with no interface restriction; “Interf.”: LZerD with docking site restricted to the prediction by the union of cons-PPISP and BindML (score ≤ −1); “CASP”: LZerD with no interface restriction using a CASP server model (Table S1). The number of decoys in the pools are 9999 for No int. and CASP decoy sets, and a maximum of 9999 (i.e. could be less) for the interface-restricted runs.

- indicates that LZerD was not run for a strategy for a given target. n/a indicates that the decoy selection was not performed because the decoy pool did not have any hits.

^†indicates that the interface restricted LZerD run produced zero decoys because decoys that satisfied the interface restriction did not have sufficient shape complementarity scores.

The last five columns show the top 10 selection performance of five scoring functions on the thirteen targets with at least one hit. The selection was performed on the “CASP” decoy pool, except for T79. For T79, the “No int.” decoy pool was used because we did not run LZerD using CASP models during CAPRI.

Our CAPRI human group predictions failed on seven targets for which LZerD produced acceptable or better decoys in the decoy pool. Thus, these were failures in decoy selection. In four targets (T80, T82, T85, and T86), no hits were selected within the top 1000 decoys by ITScorePro, as done during the CAPRI experiment, although we found in this post-analysis that GOAP could find hits within the top 10 scoring decoys among all 9999 decoys. This demonstrates that the prefiltering by ITScorePro did not work for some cases. For another two targets (T87 and T92), although ITScorePro obtained acceptable models within the top 1000 or even in the top 10, GOAP, which was used to select the top 10 from the 1000 ITScorePro selected decoys, did not have any within the top 10, which caused no hits in the human submission. For one target (T89), there were seven acceptable decoys among the top 1000 selection by ITScorePro but neither ITScorePro nor GOAP had any within top 10 hits.

We also analyzed the LZerD server predictions, where decoys were simply selected with ITScore-Pro. While there were seven targets with hits in decoy pools (“No int.” and “Interf.” decoy sets in Table 2), ITScorePro selected hits for only two targets among them (T79 and T91, Table 1). But as we discuss later, ITScorePro performed fine when the decoy sets generated with CASP models were used, which include more hits (Table 2, right columns). Thus, the problem is convoluted between the problem of the scoring function and the quality of the decoy set.

Performance of docking interface prediction

In this section we examined the accuracy of binding residue prediction by BindML and cons-PPISP. The accuracy of the binding residue prediction impacts the docking prediction, since the docking conformational search was restricted by the predicted residues. In Table S2, the prediction accuracy of the two methods is summarized. Results are shown for the merged prediction of BindML with a −1.5 cutoff and cons-PPISP, which was used in CAPRI, and the predictions of the individual methods. For BindML, results using a more permissive cutoff (−0.5), leading to more predicted binding site residues, are also shown.

The merged prediction (columns on the left in Tab. S2) showed a reasonably high average precision of 0.53, considering the current status of binding site prediction methods⁴⁹. However, the recall was low for a number of cases, indicating that there were not sufficient numbers of predicted residues even after merging the two individual methods, which had even lower recall values. Comparing the two individual methods, cons-PPISP had better performance for the all three metrics, precision, recall, and F1-score. BindML could substantially improve recall and F1-score, to be better than the cons-PPISP results, if a relaxed cutoff of −0.5 was used instead of −1.5.

The effect of using interface residue prediction can be seen in the two left columns of Table 2, which report the number of hits in decoy pools using the merged binding residue prediction (the Interf. column) and results without using binding residue prediction (No int.). Without interface restriction, seven targets had hits; in comparison, interface restriction reduced the number of targets with hits to just three. T84 was the only target where using interface prediction increased the number of hits. Interface prediction accuracy for this target (Tab. S2) is relatively high, but the correlation to the docking outcome is not very clear, because a failed case, T80, had better binding site prediction in terms of recall and F1-score.

To conclude, using predicted interface information was not consistently effective in improving docking accuracy. Predicted interface residues were used as strict constraints such that the residues should locate at docking interface. Due to the limited binding site prediction accuracy (Tab. S2), the predicted binding site residues should be used as a more permissive constraint, as implemented in the PI-LZerD algorithm⁴². However, PI-LZerD was not used in these rounds of CAPRI due to its computational expense.

Decoy selection by individual scores

Next, we examined the performance of scoring functions for decoy selection, because as revealed in the previous section, many failures occurred at the decoy selection step. Note that this is a new experiment for this report seeking improvement in the decoy selection using the decoy pools generated during CAPRI but not to analyze our group’s performance in the CAPRI. The results are summarized in the right part of Table 2. We used five scoring functions, ITScorePro, GOAP, DFIRE, SOAP-PP, and OPUS-PSP to rank 9999 decoys generated with CASP server models (the “CASP” column in the table) except for T79, for which we used the decoy pool with no interface prediction (“No int.”). We did not perform this experiment for T69, T72 and T94, because their decoy sets did not have any hits (shown as n/a in the table).

Out of the 13 targets, in 12 cases at least one scoring function selected an acceptable or better decoy in the top 10. All scores selected at least one acceptable quality model within the top 10 selections for nine targets or more, with ITScorePro and OPUS-PSP the most successful, selecting acceptable models for 11 targets. To our surprise, these results are strikingly better the CAPRI results of our group (Table 1), which indicates that somewhat complicated process we employed (Figure 1) was not worthwhile for these targets, and a simple procedure of using just one scoring function on the decoy pool generated with CASP models would have yielded better prediction results.

For T89, there were seven acceptable decoys in the pool but none were ranked high by any scoring function. T89 is a heterodimer and the single-chain models of this complex had RMSDs of 8.9 and 8.7 Šfor the larger and smaller chains, respectively. By visual inspection, we found that the N-terminus of the smaller chain was modeled wrongly as a helix that partially occluded the interface in acceptable models. Thus, we repeated docking with a single chain model that has a different conformation for the N-terminus; however, the scores were still not effective (data not shown). The reason why the scores could not detect acceptable models was not entirely clear, but the interface area of this complex is relatively small at 873 Ų, which may be challenging for scoring functions.

Decoy selection by score combination

We further investigated if combinations of scoring functions showed improved ranking over a single scoring function. Scores were combined in three ways: all pairwise sums of scoring functions, the sum of all five scoring functions, and logistic regression using all five scoring functions. These combined scores were used to rank the decoys and the number of hits in the top 10 was evaluated. The left columns in Table 3 summarize the performance of the score pairs while the right columns show the performance of all five scores combined.

Table 3.

Decoy selection by score combinations

	Two scores										Five scores
Target	D+G	D+I	D+O	D+S	G+I	G+O	G+S	I+O	I+S	O+S	Sum	Log Reg
T75	1	2	3	1	2	2	1	3	1	1	3	2
T79	7	4	5	4	5	4	7/1**	4	4	4	5	9
T80	3/2**	2/2**	3/2**	3/2**	3/2**	5/2**	5/2**	3/2**	3/2**	5/2**	4/2**	5/2**
T82	2	2	2	2	2	1	2	2	2	2	2	2
T84	5/3**	3/3**	3/3**	3/3**	4/3**	3/3**	3/3**	3/3**	3/3**	3/3**	3/3**	1/1**
T85	1	1	1	1	1	1	1	1	1	1	1	1
T86	0	0	0	0	0	1	0	0	0	0	0	0
T87	1	1	1	1	1	1	1	1	1	1	1	1
T89	0	0	0	0	0	0	0	0	0	0	0	0
T90	5	4	5	5	5	4	5	5	6	6	5	5
T91	7/1**	6/1**	7/1**	5	7/1**	6	6	7/1**	4	4	7/1**	8/1**
T92	2	2	2	2	2	1	0	2	2	2	2	0
T93	7	6	6	6	7	6	5	5	6	5	6	8
Targets w/hits	11/13	11/13	11/13	11/13	11/13	12/13	10/13	11/13	11/13	11/13	11/13	10/13

“D+G”: the sum of the Z-scores of DFIRE and GOAP. Similarly, I, O, and S stand for ITScorePro, OPUS-PSP, and SOAP-PP, respectively. Sum: the sum of all five scores. Log Reg: logistic regression using all five scores; results from jackknife procedure. Trained weights for each subsample are shown in Table S3.

^**indicates medium quality models. For example, “3/2**” means that in the top 10, 3 models were acceptable quality or better, 2 were medium quality, and 7 were incorrect. CAPRI model qualities defined previously⁴⁷.

Compared to the single score results shown in Table 2, the score combinations improved in the number of targets for which at least one acceptable model is selected (Table 3). All combinations had ten or more successful targets, and the combination of GOAP and OPUS-PSP was successful for twelve targets, missing only one target (T89, which was missed by all scores). Interestingly, while the combination of GOAP and SOAP-PP was the only one to pick up a medium model for T79, it was also the only score pair to miss T92. The sum of five scores performed similarly to the score pairs. Logistic regression also performed similarly to the score pairs in terms of number of targets with hits, although it failed to pick up any hits for T92. Importantly, both five-score combinations picked up a medium model for T91, which half of the score pairs failed to do. Overall, while logistic regression did not perform the best, it did pick up the largest total number of hits. It was not possible to perform multi-class classification due to the limited number of medium hits, but the results suggest that with an adequate amount of training data, a logistic regression classifier could be trained to pick up the largest number of both medium and acceptable hits.

Prediction of decoy pool quality

While investigating the score combinations in the previous section, we noticed that score pairs correlate relatively well if a decoy set contains acceptable models (i.e. considered to be successful). The score correlation is usually particularly evident for a small subset of decoys with high ranks (i.e. low negative score values by both scoring functions), forming a “funnel”-like distribution. Assuming that two scores have a satisfactory capability of detecting near-native decoys, it is reasonable to speculate that acceptable models in a decoy pool form a funnel-shape score distribution because these good models will be identified consistently by the two scores. The funnel-like score distribution has been discussed as an indication of successful docking prediction by earlier papers^13;70.

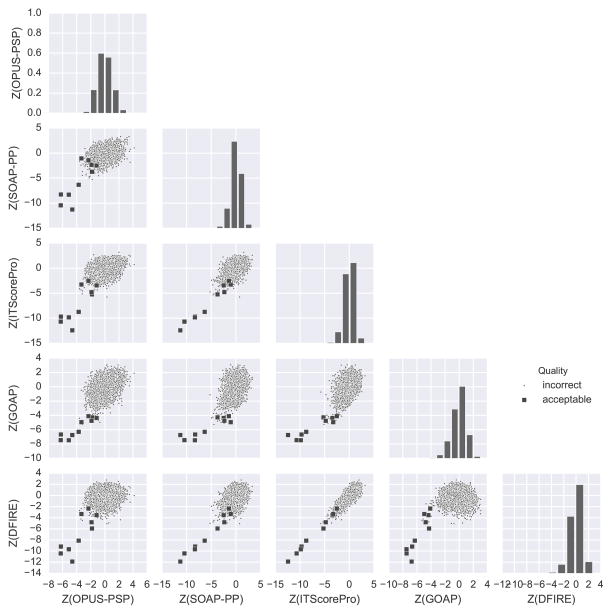
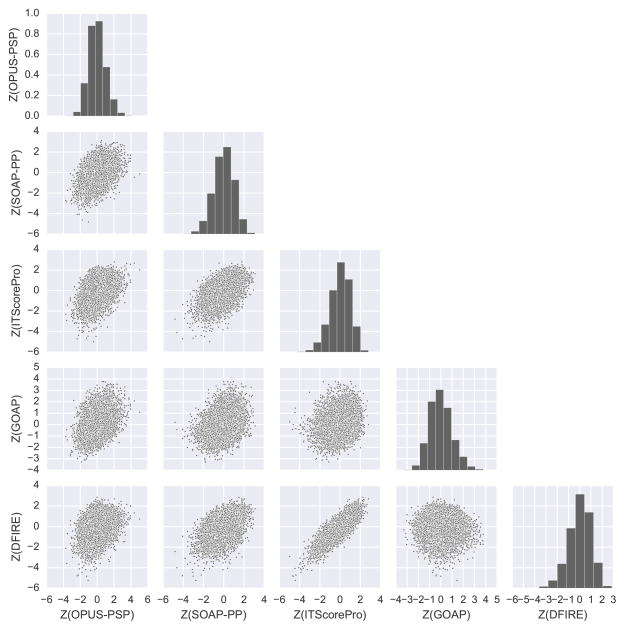
Figure 2 gives such an example of successful decoy pool from target T93. This decoy pool contains ten acceptable models out of 9999 total, which are indicated with squares in the score pair scatter plots. From the histograms of single scores, we can see that each score found low energy decoys that are seen as a tail at the left end of the histograms (negative skew). Furthermore, the ten panels of pairwise score scatter plots show that these decoys are forming a funnel-like distribution for all the score pairs. The observed funnel-like distributions are evident when compared with a negative example, T72 in Figure 3. The decoy set of T72 contains no acceptable decoys. It is apparent that the single score histograms for T93 are less skewed toward lower Z-scores than those for T72 and that the score pairs for T93 do not show a lower left tail.

Figure 2.

Single and pairwise score distributions for decoys of target T93. This decoy set is a successful example of docking, which contains ten acceptable decoys out of 9999 total. The scatter plots show pairwise score distributions. Acceptable models are shown in squares. Along the diagonal, histograms of the Z-scores of individual scores are shown.

Figure 3.

Single and pairwise score distributions for decoys of target T72. This is an unsuccessful decoy set example, which contains no acceptable decoys out of 9999 total.

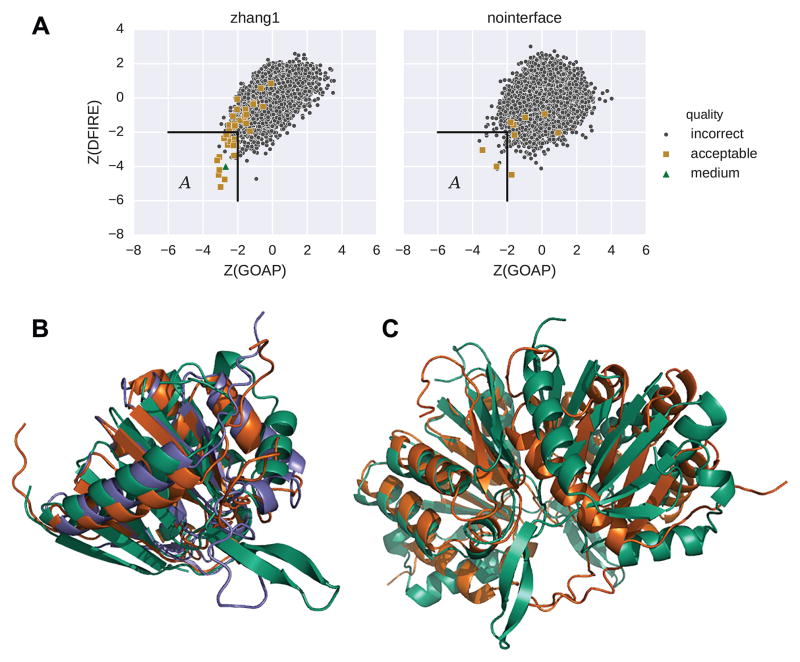
The score distribution is also affected by the quality of the single-chain model. For T91, using a single chain model selected from CASP stage 2 server models, which has RMSDs of 4.1 Å and 5.1 Å to the two chains of the native structure (Table S1), yielded many more acceptable models (37 models) including one medium model (Figure 4, left) in comparison with the case when our single chain model with RMSDs of 5.4 Å and 5.5 Å, respectively, was used (Figure 4, right) where only nine acceptable models and no medium models were obtained. Consistent with the observation in Figures 2 and 3, the score distribution of the former case (the left panel) shows a funnel-like tail that is not clearly observed in the latter case (the right panel).

Figure 4.

Score distribution of docking decoys of T91 computed using two single chain models of different quality. T91 is a homo-dimer, but the two subunits have slightly different conformations in the native structure, which resulted in different RMSD values for each model compared to the two subunits. The first model has RMSDs of 5.4/5.5 Å to the native structures of the two chains. Another model, a CASP server model (Zhang-Server_TS1), has RMSDs of 4.1/5.1 Å (Tab. S1). A, Distributions of Z-score of GOAP and DFIRE. Left, docking decoys from the Zhang-Server_TS1 single chain model. There are 37 acceptable decoys and one medium decoy out of 4793 total. Right, decoys from the former single chain model computed in our group. No interface prediction was applied. There are nine acceptable decoys out of 6168 total. Acceptable and medium quality models are shown in gold squares and green triangles, respectively. The left bottom corner (labeled A) are subsets of decoys that have Z-score below n = 2 for the two scores (Equation 1). The Spearman correlation coefficient for the decoys in A (Equation 2) is 0.56 (p = 0.0002) for the left distribution, and 0.17 (p = 0.5) for the right. B, Two single chain models superimposed to its native structure, T91, chain C. Green, native; blue, Zhang-Server_TS1; orange, our model. C, the best model from our submission (orange) superimposed to the native complex strucure (green). f_nat: 0.33, L-RMSD: 9.0 Å; I-RMSD 4.2 Å.

To quantify this observation, we devised a metric that describes whether the score pair distribution has a funnel-like tail. We consider the decoys that are nσ-outliers by both scoring functions:

$$A_{i,j,n}=\{(s_i,s_j):Z(s_i)<-n\wedge Z(s_j)<-n\}$$ (1)

where s_i and s_j are the values for scores i and i, respectively, n is a multiple of standard deviations, and ^ represents Boolean conjunction (AND). A is depicted visually in Figure 4A. If these double outlier decoys are showing a funnel-like shape, we expect them to be well-correlated. Thus, we compute the Spearman correlation coefficient (SCC) between the two scores for models that are double outliers:

$${\text{SCC}}_{i,j,n}=\text{SCC}(A_{i,j,n})$$ (2)

For example, in Figure 4A, the left panel has a double outlier SCC at n = 2 of 0.56 (p = 0.0002) while the right panel is only 0.17 (p = 0.5).

To summarize the correlation across all score pairs, we count the number with reasonable correlation across the score pairs and values of n from 2 to 5:

$$\text{Funnel}\text{score}=\sum _{(i,j)\in S}\sum _{n=2}^{n=5}\{\begin{array}{ll}n\hfill & {\text{SCC}}_{i,j,n}>0.4\text{and}{p}_{\mathrm{s}}<0.05\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (3)

where S is all pairwise combinations of scores except (DFIRE, ITScorePro) and p_s is the p-value of the SCC. The pair (DFIRE, ITScorePro) was excluded from the calculation of Equation 3 because the two scores showed high correlation even in negative cases (see Figure 3).

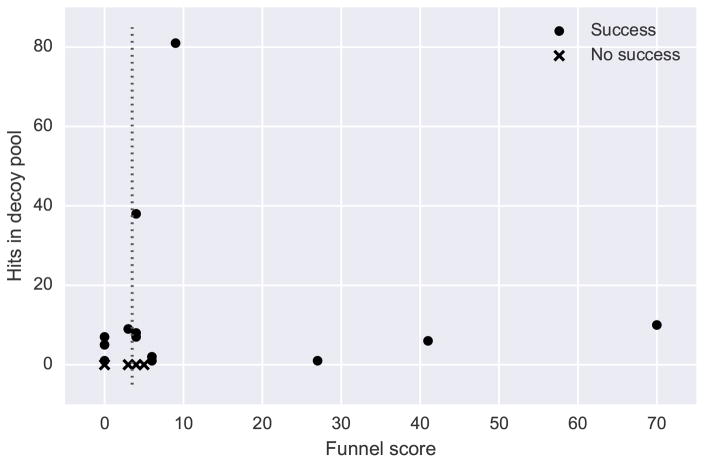
When applied to the decoy sets of the sixteen Round 30 targets in Table 1 as well as the three dimer targets with no hits by any group (T68, T77, and T88), four of six unsuccessful targets can be separated from the majority of the successful targets using a minimum funnel score of 3 (Figure 5). Specifically, there are nine true positives, four true negatives, two false positives (T77 and T88), and four false negatives (T75, T86, T89, and T92). Thus, on these targets, the classification has a positive class precision of 0.82, recall of 0.69, and F1-score of 0.75. The funnel score, which summarizes the shapes of multiple score pair distributions, is useful for predicting whether a decoy pool contains native-like models. If the funnel score is too low, different single-chain models could be used to lead to improved docking performance. It would be also interesting to combine this score with other features of a query decoy set, e.g. overall correlation of the scores or the score value itself, in a machine learning framework to develop a reliable evaluation metric for decoy quality.

Figure 5.

Prediction of decoy pool quality based on score pair distribution shape. “Funnel score” is the sum of n over all score pairs where the SCC for the nσ-outliers is significant (p < 0.05) and greater than 0.4 (Equation 3). The dotted line indicates a minimum Funnel score of 3, which classifies 9 true positives, 4 true negatives, 2 false positives (T77 and T88), and 4 false negatives (T75, T86, T89, and T92).

Decoy selection using PRESCO

In this section we examined the performance of PRESCO^61;65. Since PRESCO was developed in our group and has a different nature from the five scoring functions used above, we wanted to understand how PRESCO worked in decoy selection. Using the same decoy sets used in Tables 2 and 3, we first ran GOAP to choose top 200 scoring decoys, and then re-ranked the 200 decoys by PRESCO. Table 4 shows the results.

Table 4.

Decoy selection using PRESCO

Target	Top 200 hits by GOAP	PRESCO top 10 hits	PRESCO RFH
T75	2	0	11
T79	19/1**	0	12
T80	8/2**	0	12
T82	1	1	3
T84	7/3**	1/1**	1
T85	1	1	1
T86	1	0	39
T87	0	-	-
T89	0	-	-
T90	6	0	15
T91	26/1**	8/1**	1
T92	0	-	-
T93	10	3	1
Targets with hits	10/13	5/10	-

PRESCO was run on the top 200 decoys by GOAP; “Top 200 hits by GOAP” indicates the number of hits in that decoy pool; “RFH” is the numerical rank of the first hit.

^**indicates medium quality models. For example, 1/1** means that in the top 10, 1 model was acceptable or better, 1 model was medium, and the remaining 9 were incorrect. CAPRI model qualities defined previously⁴⁷.

Out of the ten targets that have at least one acceptable or better decoys selected by GOAP, PRESCO selected acceptable (or better) decoys within the top 10 for five targets. For the rest of the targets, although PRESCO missed ranking acceptable decoys within the top 10, the rank of such decoys were close to 10, between 11 and 15 for T75, T79, T80, and T90.

PRESCO performed well in ranking the decoys by quality. For T84, the top 200 decoys by GOAP contain three medium and four acceptable hits and PRESCO successfully picks out the medium hit at rank 1. For T91, the top 200 decoys by GOAP contain one medium and 25 acceptable hits. PRESCO successfully picks out the medium hit at rank 2 and the rank 8 decoy by PRESCO is the best quality acceptable model by f_nat, I-RMSD, and L-RMSD. For T93, the top 200 decoys by GOAP contain 10 acceptable hits. PRESCO successfully picked out three of ten acceptable hits in the top 10, including the rank 1 decoy, which has the best f_nat and I-RMSD out of all 10 acceptable models, and the fourth best L-RMSD. Thus, overall, although some further tuning of the PRESCO algorithm itself for docking decoy selection is needed, it will be an effective scoring function when put in an appropriate combination with other scores.

Discussion

In this work, we first examined our group’s docking prediction performance in the recent CAPRI rounds and investigated the reasons of failure for pairwise docking targets. We identified two major reasons: low quality single chain models and failure at ranking decoys by scoring functions. It is well known that errors in single chain models can significantly affect the protein docking outcome³⁸, which was also shown in Figure 4. Challenges in single chain modeling also include predicting the bound state structures by considering chain flexibility, which is still a very difficult problem^23;71. Without major modifications to the current protocol, small changes, such as using single chain models with the flexible terminus truncated (which was the problem for T94) as well as a full residue model, may occasionally improve prediction results.

The most problematic step in the CAPRI rounds was the scoring and selection process of docking decoys. It turned out the two-step procedure with a pre-screening by ITScorePro followed by GOAP and/or other scores, missed many acceptable decoys and employing simply a single score or a score pair can improve over the procedure we used. Based on the current study, we would use the pairwise combination of GOAP and OPUS-PSP as a single decoy selection step in the pipeline. We also learned that PRESCO, although it seems to have strength in selecting the best near-native decoy, needs some improvement or a better arrangement specifically for docking decoy selection.

It was also found that the interface residue prediction was not effective for guiding docking. Particularly, considering the low recall of predictions by the two methods used, docking should not have been guided too strictly by the predicted binding residues; rather, a larger conformational space should be explored.

Overall, the prediction pipeline (Figure 1) was unnecessarily complex and could be simplified. The pipeline was designed based on several small benchmarks done at that time, but based on the current analysis, we will redesign decoy selection by scoring functions and reconsider integration of the interface residue prediction step. More fundamentally, we have not attempted template-based docking modeling, which was fairly successful by other CAPRI participants³⁸. It is reasonable to add template-based complex modeling as the foremost step in the prediction pipeline.

Apart from the post-analysis of our CAPRI results, the current study showed that a rather simple Z-score-based pairwise score combination gives robust, improved decoy selection. Moreover, we showed an interesting observation for quality assessment of docking decoy sets using the funnel score. Quality assessment of docking models is an important, but understudied topic in protein docking⁷². It will be an interesting direction to explore further along this line to develop a prediction method for docking quality. We believe the results obtained from the decoy selection using combined scores and the funnel score are general enough and applicable for other decoy sets generated by different docking methods because the scoring functions used in this study were developed for selecting protein models of various quality but not specific for docking models computed by LZerD.