Accuracy comparison of several common implicit solvent models and their implementations in the context of protein-ligand binding

Abstract

In this study several commonly used implicit solvent models are compared with respect to their accuracy of estimating solvation energies of small molecules and proteins, as well as desolvation penalty in protein-ligand binding. The test set consists of 19 small proteins, 104 small molecules, and 15 protein-ligand complexes. We compared predicted hydration energies of small molecules with their experimental values; the results of the solvation and desolvation energy calculations for small molecules, proteins and protein-ligand complexes in water were also compared with Thermodynamic Integration calculations based on TIP3P water model and Amber12 force field. The following implicit solvent (water) models considered here are: PCM (Polarized Continuum Model implemented in DISOLV and MCBHSOLV programs), GB (Generalized Born method implemented in DISOLV program, S-GB, and GBNSR6 stand-alone version), COSMO (COnductor-like Screening Model implemented in the DISOLV program and the MOPAC package) and the Poisson-Boltzmann model (implemented in the APBS program). Different parameterizations of the molecules were examined: we compared MMFF94 force field, Amber12 force field and the quantum-chemical semi-empirical PM7 method implemented in the MOPAC package. For small molecules, all of the implicit solvent models tested here yield high correlation coefficients (0.87–0.93) between the calculated solvation energies and the experimental values of hydration energies. For small molecules high correlation (0.82–0.97) with the explicit solvent energies is seen as well. On the other hand, estimated protein solvation energies and protein-ligand binding desolvation energies show substantial discrepancy (up to 10 kcal/mol) with the explicit solvent reference. The correlation of polar protein solvation energies and protein-ligand desolvation energies with the corresponding explicit solvent results is 0.65–0.99 and 0.76–0.96 respectively, though this difference in correlations is caused more by different parameterization and less by methods and indicates the need for further improvement of implicit solvent models parameterization. Within the same parameterization, various implicit methods give practically the same correlation with results obtained in explicit solvent model for ligands and proteins: e.g. correlation values of polar ligand solvation energies and the corresponding energies in the frame of explicit solvent were 0.953–0.966 for the APBS program, the GBNSR6 program and all models used in the DISOLV program. The DISOLV program proved to be on a par with the other used programs in the case of proteins and ligands solvation energy calculation. However, the solution of the Poisson-Boltzmann equation (APBS program) and Generalized Born method (implemented in the GBNSR6 program) proved to be the most accurate in calculating the desolvation energies of complexes.

Graphical Abstract

1. Introduction

1.1 The role of solvent in drug development efforts

Small-molecule inhibitors represent the basis for new drugs: their effect usually is to block the active site of the target protein associated with a disease. The initial stage of new drug development is to find such molecules which are inhibitors of the given target-protein; this task may involve analysis of many thousands of small molecule candidates. Quick and effective solution of this problem decreases considerably material costs and duration of subsequent stages of the drug development. Nowadays, this task can be addressed effectively with the help of computer simulations [1,2]. High accuracy of the protein-ligand binding energy calculations is the key problem to be solved to increase considerably the effectiveness of computer simulation in the new inhibitors development. Sufficiently reliable prediction of the inhibition activity can be achieved if the error of the calculation of the protein–inhibitor binding energy does not exceed 1 kcal/mol [2]. So, the accuracy of the calculation of various contributions to the protein–ligand binding energy should be better 1 kcal/mol.

The desolvation energy (the difference between the complex solvation energy and the sum of the protein and ligand solvation energies) gives a significant contribution to the free energy of protein-ligand binding in the protein-ligand binding process, and its calculation accuracy directly determines the calculation accuracy of the ligand binding constant [3–10]. In this paper we focus on calculations of the contribution due to the interaction of molecules with solvent (solvation and desolvation energies). In human or animal organisms as well as in experiments in vitro and in vivo the protein-ligand binding occurs in solvent (in the aqueous solution). So, the presence of solvent (water) must be taken into account in the calculation of protein-ligand binding energy. Upon protein-ligand binding, solvent is displaced partly from the active site of the target protein, and some of ligand and protein atoms cease to interact with solvent.

There are two commonly used approaches to calculate solvation energy: those based on the explicit solvent model, and those that utilize the implicit (or continuum) one. Of the two models the former is considered be more accurate but at the same time much more expensive computationally – the solvent is described as an ensemble of larger number of discrete water molecules. In contrast, the orders of magnitude less time-consuming implicit solvent model [11–24] is represented by the homogeneous continuum with the dielectric constant ε (for water ε = 80 at 300 K) filling the space around the solute molecule. In this model the dominant contribution to the solvation energy is its electrostatic part: Coulomb interaction of solute atoms charges with the polarization charges induced on the dielectric boundary. Within the basic continuum solvent framework, this interaction can be estimated through numerical solution of the three-dimensional Poisson–Boltzmann (PB) equation by using freely available software such as APBS [25]. In addition, there are several algorithms (models) for the calculation of the polar component of the solvation energy of molecules focused on solving the relevant equations on the dielectric boundary.

Since numerical solutions of the PB equation are also relatively time-consuming, a variety of fast approximations to these solutions for biomolecules has been developed. Three different algorithms of the solvation energy polar component calculation are implemented in the DISOLV program [26, 27]: PCM (Polarized Continuum Model), S-GB (Surface Generalized Born method proposed in [28]) and COSMO (COnductor-like Screening Model) [19]. All these three implementations demonstrate high numerical accuracy for the sufficiently small triangulation network step size on the same solvent boundary, and the PCM method demonstrates highest accuracy, but it needs more computing time. The faster algorithm of the same PCM method has been recently implemented in the MCBHSOLV program [27, 29] using a novel multicharge approximation for large dense matrices.

The performance of this algorithm can be up to two orders of acceleration (for the triangulation step size of 0.1 Å and for solute molecules of 2000 – 4000 atoms) as compared to the PCM implementation in the DISOLV program without loss of accuracy [27, 29]. Smaller acceleration is obtained for the greater step size of the triangulation network and for smaller molecules.

Methods implemented in DISOLV and MCBHSOLV for the same smooth solvent boundary surface [26, 27, 30] have been parameterized [26] in the frame of the MMFF94 force field [31] and they demonstrate high numerical accuracy as well as good parameterization, i.e. good correspondence of the calculated hydration energies to experimentally measured ones for a set of more than 400 small molecules [26]. Taking into account that DISOLV and MCBHSOLV programs are used successfully for new inhibitors development [32–34] at the post-processing stage [10] and in the gridless docking procedure [35] in the frame of the MMFF94 force field [31] there is a need to compare results of DISOLV and MCBHSOLV calculations with ones performed with other implicit solvent programs and parameterization methods [14, 20–22, 25] for same sets of molecules. Here we will also examine a relatively recent addition to the family of GB models, GBNSR6, which has already demonstrated high accuracy in estimates of hydration free energies of small molecules [14].

Accuracy of solvent representation is just one variable that affects the over-all accuracy of solvation energy predictions: the underlying gas-phase force-filed, including the choice of partial charges, affect the accuracy significantly [36]. Thus in D. Mobley’s recent study [36] various approaches for obtaining partial charges for computing hydration free energies of small molecules have been tested to examine the influence of charge model on agreement with experiment. Also, other studies [37, 38] demonstrated that calculation of small molecules solvation energies allows one to test whether the given parameterization is adequate, and to improve the underlying methods and force fields. In this respect, the novel quantum-chemical semi-empirical PM7 method [39] included in the MOPAC package [40] is becoming popular recently for new inhibitors development at the postprocessing stage [32, 33, 41]. Due to the unprecedentedly wide range of molecules used for the parameterization of the PM7 method and due to including corrections on dispersion interactions as well as ones for hydrogen and halogen bonds PM7 is significantly superior to previous semi-empirical methods in respect of calculation accuracy, especially for intermolecular interactions [39], including those semi-empirical methods used for the atomic charge calculations in some force fields, e.g. the Amber force field.

In this work we compare not only the different methods of solvation energy calculation, such as in [21, 23], but also several different implicit solvent models in their various software implementations. Among these implementations DISOLV and MCBHSOLV programs are interesting due to high and controlled numerical accuracy of realization of three implicit models PCM, COSMO and SGB for the one and the same smooth SES surface constructed by primary and secondary rolling procedures [26, 27, 30]: it was shown that for sufficiently small triangulation network step size (0.1 – 0.3 Å) variations of the solvation energy due to variations of the triangulation network position on SES are less than 1 kcal/mol [26, 27]. However, there is no detailed comparison of the DISOLV program with other independent programs, which realize the solvation energy calculations. The other reason is that the algorithms used in DISOLV and MCBHSOLV programs are also implemented in the FLM docking program [35] and they directly influence the docking accuracy.

Thus, we compare the above methods and their implementations with one another, with experimental data for small molecules, and with the results of the much more computationally expensive reference calculations using the explicit water model for the same sets of small and large molecules including protein-ligand complexes. To the best of our knowledge, no comprehensive accuracy comparison of all of the above methods on the same footing is available. In addition, we perform the COSMO calculations implemented in MOPAC using parameterizations (atoms charges and radii) of the new semiempirical quantum-chemical PM7 method.

2. Materials and methods

2.1 Solvent models. Non-polar component of the solvation energy

In the process of dissolution the molecule passes from vacuum into the solvent. The corresponding change of the Gibbs free energy ΔG_s is mainly due to change of the solute-solvent interaction (e.g. air vs. water), and, secondly, due to formation of the cavity in the solvent where the solute molecule is located:

$$\mathrm{\Delta }{G}_s=\mathrm{\Delta }{G}_{\mathit{\text{pol}}}+\mathrm{\Delta }{G}_{\mathit{\text{np}}}+\mathrm{\Delta }{G}_{\mathit{\text{cav}}},$$

where ΔG_pol is the polar component of the solute-solvent interaction, ΔG_np is the van der Waals solute-solvent interaction, and ΔG_cav is the cavitation component of solvation free energy due to the cavity formation in the solvent. The latter two terms are the non-polar part of the solvation free energy ΔG_np + ΔG_cav. This part can be calculated in the explicit and implicit water models, however, its contribution to the total solvation energy is relatively small compared with the polar component for most systems. The simplest empirical formula for calculation of the non-polar component of the solvation energy is as follows [42]:

$$\mathrm{\Delta }{G}_{\mathit{\text{np}}}+\mathrm{\Delta }{G}_{\mathit{\text{cav}}}=\sigma S_{SAS}+b,$$

where S_SAS is the SAS surface area (Solvent Accessible Surface), b and σ are fitting parameters whose values may depend on the solvent and the types of atoms composing the solute molecule, e.g. σ = 0.00387 kcal/(mol*Ų), b = 0.698 kcal/mol [42] for water in the non-polar calculations included in DISOLV [26] and MCBHSOLV [27] programs. A more accurate approach described in [43], represents the non-polar part of the solvation energy depending not only on S_SAS, but also on the energy of van der Waals interactions of individual atoms of the solute molecule with the solvent. This approach is implemented in the GBNSR6 [14] program. In the MOPAC [40] program non-polar components were not calculated.

2.2 Solvation models. Polar component of the solvation energy

2.2.1 Explicit solvent model

In the framework of the explicit solvent model, the aqueous environment of the solute molecule is represented in the form of a set of individual water molecules constituting the hydration shell. This model allows an atomic level description of the interactions between the solute and water. One of the most popular models of explicit water molecules is the rigid three-point TIP3P model developed by Jorgensen et al. [44]. In this model the charge of the oxygen atom equals to q(O) = −0.834e and each of the two hydrogen atoms has the charge of q(H) = 0.417e. Length of O-H chemical bonds equals to r = 0.957 Å, the value of the valence angle is θ = 104.52°. While some modern water models [45] surpass TIP3P with respect to accuracy of hydration energy estimates, these estimates are, in general, computationally very demanding. Therefore, here we use results from a previous comprehensive estimates of hydration free energy in the explicit water for small molecules from Ref. [38]. In the case of proteins and protein-ligand complexes the explicit water model was used as described in [22] to perform calculations with the Amber package [46] by the thermodynamic integration (TI) method implemented in the sander program (the Amber package). Obtained values of the solvation energy are used as reference data to evaluate the quality of implicit solvent models.

Convergence of the TI protocol and its sensitivity to the initial conditions were checked for two randomly selected complexes as it is described in [22]. For these complexes the calculations were repeated using the different random seeds, and it was notices that the obtained received differences didn't exceed a standard deviation for the calculated solvation energy values, which is of ±0.7 kcal/mol [22] for complexes and proteins. To confirm the convergence of the TI results the simulation time was extended from 2 to 5 nanoseconds, and it was observed that the resulting values of the solvation energies didn't exceed a standard deviation.

2.2.2 Implicit solvent models

Implicit (or continuum) models consider solvent as a continuous homogeneous medium describing electrostatic interactions of a solute molecule with solvent. This medium has predetermined electrostatic properties including a specified dielectric constant; the solute is separated from the solvent by a dielectric boundary (DB), the results of practical calculations are very sensitive to the choice of DB [47], with several possible, generally non-equivalent, choices [20]. In this study the PCM, S-GB and COSMO models implemented in the DISOLV program and the PCM model in the MCBHSOLV program employ the same DB (the Solvent Excluded Surface or SES) constructed as follows [10, 26, 27, 30]. The molecule is represented as an ensemble of hard spheres centered at the nucleus of atoms; radii of these spheres are different for different atom types and they are parameters of the continuum solvent model; the construction of SES involves two main steps: the primary and the secondary probe rolling [48, 49] steps. The primary rolling step is the construction of the molecular surface by rolling of the probe sphere over the solute molecule, which simulates the solvent molecule. All possible points of contact of primary rolling sphere and atoms' spheres determine points of SES. The primary rolling procedure may sometimes result in undesirable self-intersections of the surface and fractures; the secondary rolling procedure is applied for SES smoothing [49]. The essence of the secondary rolling method is to replace the surface fragments close to self-penetrations and fractures by other smooth fragments defined by the rolling of SES near to fractures with the small sphere (called the secondary rolling sphere). The TAGSS program [26, 27, 30] is the program building the surface with application of primary and secondary rolling. It should be noted that the GBNSR6 program [14] uses other method relies on MSMS-based solvent excluded surface [50] to represent the dielectric boundary.

Within the framework of the continuum (implicit) solvent model the polar part of the solvation energy is the energy of electrostatic interaction between the atoms charges of the molecule located in the cavity of the dielectric continuum and the polarization charges induced on SES. Implicit solvent models are currently included in many software packages for molecular modeling: quantum chemical packages Gaussian [51], Gamess [52], MolPro [53], MOPAC [40], and molecular dynamics packages such as Charmm [54] and Amber [46]. In addition there are independent software implementations for finding the polar part of the solvation energy, for example, DelPhi [15], APBS [25], DISOLV [26, 29], MCBHSOLV [27, 29].

The popular approach to estimate the solvation free energy is the Generalized Born model (GB) [16], in which the Green function of the Poisson equation is approximated by a simple closed form expression, see e.g. Ref. [13] for a review. The GB implementation in DISOLV program calculates the electrostatic part of the solvation free energy as follows [26, 28]:

$$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=-\frac{1}{2}(1-\frac{1}{\epsilon })\sum _{i,j}\frac{Q_i\times Q_j}{\sqrt{{\left|{\overrightarrow{R}}_{i,j}\right|}^2+a_i\times a_j\times \text{exp }(-\frac{{\left|{\overrightarrow{R}}_{i,j}\right|}^2}{c\times a_i\times a_j})}},$$ (1)

where R⃗_i,j = R⃗_i − R⃗_j, R⃗_i is the radius-vector that defines the position of the charge Q_i of i-th atom of the solute molecule, c is an empirical constant (c=8 in the DISOLV program), summation is over all atoms of the solute molecule, and the Born radii a_i can be calculated by different ways: by the volumetric method [16] as the integrals over the cavity volume and the surface method (S-GB) [28], in which the integrals are calculated over SES. The Born radii in SGB are calculated as follows [28]:

$$a_i=\frac{1}{2(\sum _{n=4}^7{A}_n·I_n^i-A_0)}.$$ (2)

Here A_n are empirical constants, $I_n^i$ are the integrals over SES:

$$I_n^i={[\oint \frac{({\overrightarrow{n}}_s·({\overrightarrow{r}}_s-{\overrightarrow{R}}_i))dS}{{|{\overrightarrow{r}}_s-{\overrightarrow{R}}_i|}^n}]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n-3$}\right.},7\ge n\ge 4,$$ (3)

where n⃗_s is the normal to SES, r⃗_s is the radius-vector of the point at SES.

The GB polar component of the solvation energy calculated by the GBNSR6 program is realized as follows [14]:

$$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=-\frac{1}{2}(\frac{1}{{\epsilon }_{\mathit{\text{in}}}}-\frac{1}{{\epsilon }_{\mathit{\text{out}}}})\frac{1}{1+\beta \alpha }\sum _{i,j}{Q}_i\times Q_j(\frac{1}{\sqrt{{\left|{\overrightarrow{R}}_{i,j}\right|}^2+a_i\times a_j\times \text{exp }(-\frac{{\left|{\overrightarrow{R}}_{i,j}\right|}^2}{4\times a_i\times a_j})}}+\frac{\alpha \beta }{A}),$$ (4)

where ε_in and ε_out are the dielectric constants of the solute and the solvent respectively, β= ε_in/ε_out, α = 0.571412, and A is the electrostatic size [55] of the molecule. The extra terms in the Green function, Eq 4, compared to the original one due to Still et al (Eq. 1) ensure physically correct dependence on the dielectric constants [55, 56].

Here the effective Born radii a_i is calculated by the following equation [14]:

$$a_i=\frac{1}{{(-\frac{1}{4\pi }{\oint }_{\partial V}\frac{\overrightarrow{r}-{\overrightarrow{R}}_i}{{|\overrightarrow{r}-{\overrightarrow{R}}_i|}^6}d\overrightarrow{S})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}},$$ (5)

where ∂V represents the molecular surface of the molecule, and dS is the infinitesimal surface vector.

Further, in the work we will perform the calculations using the GB method implemented in the GBNSR6 program described in [14], as well as the GB-calculations using the S-GB method implemented in the DISOLV program.

The PCM (Polarized Continuum Model) [12, 17, 18, 26, 27] method is the reduction of the three-dimension Poisson equation to the integral equation at SES (see below). It is assumed in the DISOLV program that the dielectric constant inside the surface equals to 1 and the outside dielectric constant equals to ε. The density of the polarization charges induced on SES can be determined from the integral equation:

$$\sigma (\overrightarrow{r})=\frac{1-\epsilon }{2\pi (1+\epsilon )}\left(\sum _i\frac{Q_i((\overrightarrow{r}-{\overrightarrow{R}}_i)·\overrightarrow{n})}{{|\overrightarrow{r}-{\overrightarrow{R}}_i|}^3}\right)+\underset{SES}{\int }\frac{\sigma (\overrightarrow{r}\prime )((\overrightarrow{r}-\overrightarrow{r}\prime )·\overrightarrow{n})}{{|\overrightarrow{r}-\overrightarrow{r}\prime |}^3}dS\prime ,$$ (6)

where σ(r) is the surface density of charge induced on SES at point with radius-vector r⃗, r⃗' is the radius-vector of the surface element, R⃗_i is the point that defines the position of the atomic charge Q_i of each atom of the solute molecule, n⃗ is the normal to the cavity surface directed into the solvent; ε is the dielectric constant of the solvent. The electrostatic component of the interaction energy with the solvent equals to:

$$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=\frac{1}{2}\sum _i{Q}_i\underset{SES}{\int }\frac{\sigma (\overrightarrow{r})}{|{\overrightarrow{R}}_i-\overrightarrow{r}|}dS.$$ (7)

To solve the resulting integral equations the DB surface SES is divided into the small elements, i.e. it is triangulated, and the equation is converted to the matrix representation:

$$Aq=BQ,$$ (8)

where q is the column vector of the polarization charges σ_i of discrete surface elements S_i, Q – is the column vector of the solute molecule atoms' charges.

This matrix equation is solved by the one-step iterative method procedure proposed in [18] with a carefully chosen initial solution and a set of specially chosen parameters [26, 27, 29]. This method is implemented in the DISOLV program [26, 27, 29]. However, the solution of this matrix equation using the iteration procedure requires O(N²) operations (where N is the matrix size) since a standard matrix-by-vector multiplication has this complexity. Since the matrix size N is large (N ≈ 10⁵) for the calculations with high accuracy [26, 27, 29] the time of getting the solution of the matrix equation becomes very large.

The recently developed multicharge method [57] works if the matrix A in equation (8) has a certain structure – the so-called H²-structure [58]. This structure implies that the matrix has a mosaic partitioning, i.e. it can be represented in the form of a set of sub-matrices so that each element of the matrix belongs to exactly one sub-matrix from this set. So in this problem the matrix A can be approximated by this H²-matrix with a high degree of reliability. It requires O(N) operations to build the H²-decomposition of matrix A and to get the matrix-by-vector product in the format of H²-decomposition, so it can accelerate significantly the solution of equation (8). The PCM method for finding the polar component of solvation energy using multicharge approximation was implemented in the MCBHSOLV program [27, 29], and it was shown that this program can run faster than the DISOLV program [27, 29], based on the classical algorithm for solving the PCM equations without loss of high numerical accuracy of the calculations – better than 1 kcal/mol [27, 29]. In this work we used both methods of solving the PCM equations: the classical method implemented in the DISOLV program [26, 27], and the method using multicharge decomposition implemented in the MCBHSOLV program [27, 29]. Both cases use the same program TAGSS [26, 27, 30] for constructing the triangulation grid on SES.

Another method COSMO (COnductor-like Screening MOdel) [19] is applied to solvents with large dielectric constants (e.g. for water, ε = 80). In this model dielectric continuum surrounding the solute molecule is replaced by metal (ε = ∞) continuum. The polar part of the solvation energy in this case is calculated as follows:

$$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=\frac{1}{2}{C}_f\sum _i{Q}_i\underset{SES}{\int }\frac{\sigma (\overrightarrow{r})}{|{\overrightarrow{R}}_i-\overrightarrow{r}|}dS,$$ (9)

Where C_f is the corrective coefficient due to the finite dielectric constant:

$$C_f=\frac{\epsilon -1}{\epsilon +1/2}$$ (10)

Based on the vanishing potential on the surface of a conductor, the COSMO integral equation for the polarization charges is written as follows:

$$\underset{SES}{\int }\frac{\sigma (\overrightarrow{r}\text{'})}{|\overrightarrow{r}-\overrightarrow{r}\text{'}|}dS\text{'}+\sum _{i=1}^N\frac{Q_i}{|\overrightarrow{r}-{\overrightarrow{R}}_i|}=0,$$ (11)

Where r⃗ is the radius-vector of any point on the surface or out of the surface, R⃗_i is the point that defines the position of the atomic charge Q_i of each atom of the solute molecule.

In the present work calculations have been made also by the COSMO method implemented in the DISOLV program, as well as COSMO implemented in the quantum-chemical package MOPAC [40]. All methods listed above (PCM, S-GB, COSMO – program DISOLV; PCM - program MCBHSOLV) use the TAGSS program [26, 27, 30] to construct the triangulated SES surface. When the non-polar component is calculated with the DISOLV program, SAS is built from SES by the similarity transformation: each triangular element on SAS is obtained by shifting of the three vertices of the corresponding triangle on SES by the value of the radius of the primary rolling sphere along normal to the SES surface in these vertices [26, 27, 30].

In addition to the methods listed above, in this work we carried out calculations using the APBS program [25] solving the Poisson-Boltzmann equation for calculation of the polar part of solvation energy.

For the methods mentioned above and implemented in the DISOLV program (S-GB, PCM, COSMO), MCBHSOLV program (PCM), GBNSR6 program, and the APBS program the following parameters were selected: the radius of the primary rolling sphere was selected R_pr = 1.4 Å, the dielectric constant of solvent (water at room temperature) was ε = 80, and the step of triangulation grid on the SES surface was set to 0.3 Å. (except for the GBNSR6 program where the default value of 6 triangles per 1 Ų was used). For the MOPAC program the dielectric constant of water was the same and the effective radius of the solvent molecule equals to 1 Å.

2.2.3 Polar component of the complex desolvation energy

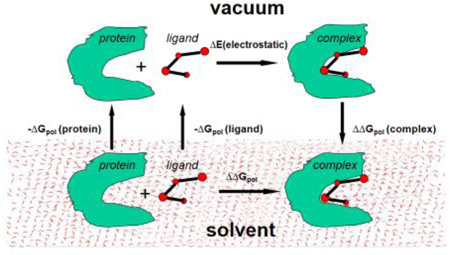
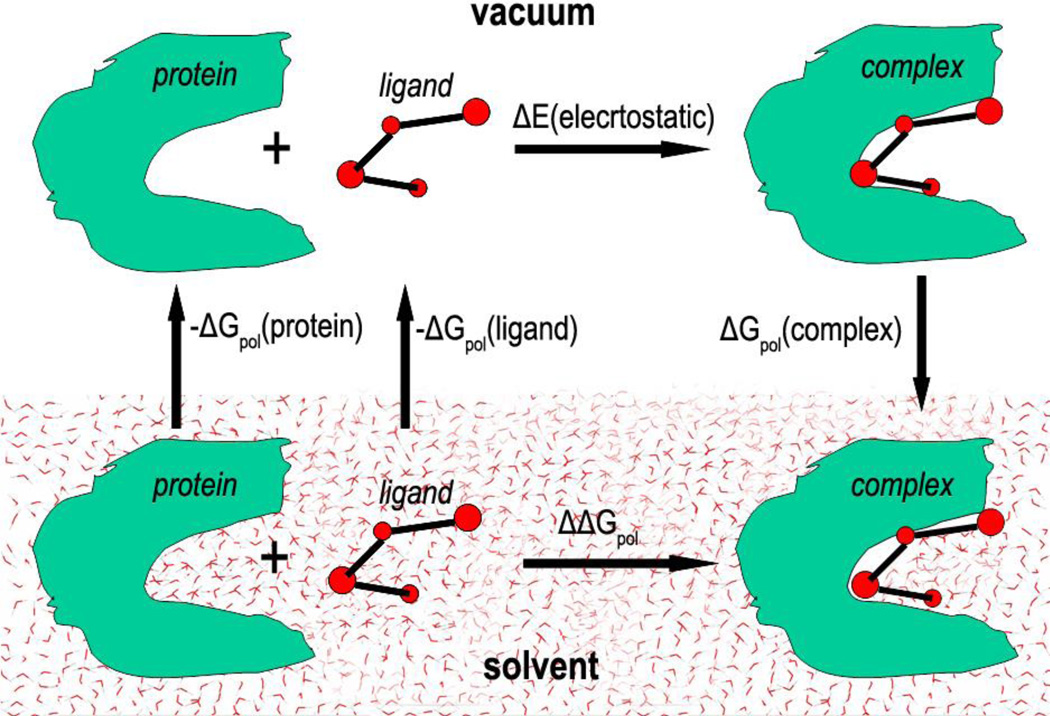
Figure 1 illustrates the thermodynamic cycle of binding of the protein and the ligand in the solvent and in vacuum. The solvation energies of the protein, the ligand and the complex are designated as ΔGpol(protein), ΔGpol(ligand) and ΔGpol(complex) respectively, the polar component of binding energy in vacuum designated as ΔE(electrostatic). Here we consider only the polar components of the Gibbs free energy, and do not consider the components associated with the cavity formation and non-polar components of solvation energy. The change of the polar component of the free energy upon binding of the protein and the ligand in the solvent will be the same independently of the path in the thermodynamic cycle, therefore we can calculate the energy ΔΔG_pol as follows: the protein and the ligand are transferred from solvent into vacuum, then form the complex in vacuum, and then the complex is transferred from vacuum into the solvent:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{pol}}}=\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{complex}})-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{protein}})-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{ligand}})+\mathrm{\Delta }E(\mathit{\text{electrostatic}})$$ (12)

Since in vacuum the polar component of the binding energy equals

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{vacuum}}}=\mathrm{\Delta }E(\mathit{\text{electrostatic}}),$$ (13)

we compute the desolvation energy (influence of the solvent on the protein-binding energy in the solvent) as:

$$\mathrm{\Delta }{G}_{\mathit{\text{pol}}}^{\mathit{\text{desolv}}}=\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{complex}})-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{protein}})-\mathrm{\Delta }{G}_{\mathit{\text{pol}}}(\mathit{\text{ligand}})$$ (14)

This formula will be used for calculating the desolvation energy of protein-ligand complexes.

Figure 1.

Thermodynamic cycle for the binding of the protein and the ligand in solvent and in vacuum.

2.3 Test structures

Three test sets were collected for this work: a set of small molecules, a set of proteins and a set of protein-ligand complexes. 104 structures of small molecules were previously used by Aguilar et al. in [14]; these structures were randomly selected from the original David Mobley database [38]. The experimental hydration energies were also known for these molecules and the values are given in [38] and in the respective Supplementary materials. The second set consists of 19 small charge neutral proteins with no more than 500 atoms per structure: [20] (PDB IDs: 1az6, 1bh4, 1bku, 1brv, 1byy, 1cmr, 1dfs, 1dmc, 1eds, 1fct, 1fmh, 1fwo, 1g26, 1ha9, 1hzn, 1paa, 1qfd, 1qk7, 1scy), which were selected from the larger set [21]. The third set used here for the desolvation energy calculations, consists of 15 protein-ligand complexes (PDB IDs: 1b11, 1bkf, 1f40, 1fb7, 1fkb, 1fkf, 1fkg, 1fkh, 1fkj, 1fkl, 1pbk, 1zp8, 2fke, 2hah, 3kfp) [22]. The following criteria were used for choosing them from the PDB [59]: the total number of atoms was no more than 2000, there were no missed atoms in the structures other than hydrogens, and the ligands are neutral at pH = 7 and have known binding constants.

Configurations of molecules for calculations in the implicit solvent models were the same, which were used in the explicit solvent calculations.

Different parameterizations are used in some cases due to following reasons. The parameters included the atom charges, for which we calculate the interaction with the charges induced on the solvent boundary surface, and the atom radii, on which the solvent boundary surface (SES) is built. These parameters are external parameters for the implicit solvent model and may influent the accuracy of the solvation energy calculations. The main parameters set (parameter set 1) uses the radii ZAP9 [60, 61] and the charges am1-bcc [62, 63] for small molecules, and also the atomic radii mbondi2 and the charges of the ff14SB force field [64] on atoms for proteins and complexes (in this case proteins and complexes are prepared with the help of H++ webserver (http://biophysics.cs.vt.edu/) [65]), so far as this parameterization is used in the TI calculations in the explicit model (using Amber package for protein and complexes and taking results from [38] for small molecules). Therefore, this parameter set 1 is used in all implicit models and programs which allow it: GBNSR6, DISOLV and APBS programs. The choice of the ZAP9 [60, 61] radii set for small molecules is based on the results presented in [14], where it has been shown that radii set ZAP9 more precisely reproduce experimental values of solvation energies for small molecules. In case of proteins and complexes we have taken the radii set mbondi2 because it has also provided good results [20].

As it was mentioned in the Introduction, DISOLV and MCBHSOLV programs initially have been parameterized [26] in the frame of the MMFF94 force field. Therefore, we performed the solvation energy calculations for all methods of these two programs with the parameter set 2 using the atomic charges of MMFF94 force field [31] and the corresponding atomic radii for building SES [26].

Finally, the quantum-chemical program MOPAC uses its own parameterization in the PM7 method (parameter set 3).

Table 1 contains all calculation methods and defined parameters (charges and radii of atoms) used for each of these methods.

Table 1.

Solvent models and sets of parameters (atomic radii and charges) used for each implicit method.

	Method	Charges (proteins / small molecules)	Radii (proteins / small molecules)
1	GB (GBNSR6) (parameter set 1)	ff14SB / am1-bcc	mbondi2 /ZAP9
2	GB (DISOLV) (parameter set 1)	ff14SB / am1-bcc	mbondi2 /ZAP9
3	GB (DISOLV) (parameter set 2)	Mmff94	Disolv
4	COSMO (DISOLV) (parameter set 1)	ff14SB / am1-bcc	mbondi2 /ZAP9
5	COSMO (DISOLV) (parameter set 2)	Mmff94	Disolv
6	COSMO (MOPAC) (parameter set 3)	Mopac	Mopac
7	PCM (DISOLV) (parameter set 1)	ff14SB / am1-bcc	mbondi2 /ZAP9
8	PCM (DISOLV) (parameter set 2)	Mmff94	Disolv
9	PCM (MCBHSOLV) (parameter set 2)	Mmff94	Disolv
10	PB (APBS) (parameter set 1)	ff14SB / am1-bcc	mbondi2 /ZAP9
11	Explicit solvent model (Amber)	ff14SB / am1-bcc

The calculations of the non-polar component of the solvation energy using the DISOLV program (see paragraph 2) have been performed for two sets of parameters: DISOLV with parameter set 1 (atomic charges and radii are ff14SB / am1-bcc and mbondi2 /ZAP9) and DISOLV with parameter set 2 (atomic charges and radii are mmff94 and Disolv).

3. Results

In order to evaluate the quality of different calculation methods the following criteria were used: the root mean square deviation (RMSD) and the Pearson correlation coefficient (R²) between the calculated and reference values with averaging over the corresponding set of molecules. As the reference data we used either experimentally determined solvation energies (only for small molecules set) or calculated using explicit water model (for all test sets).

Experimental hydration energies for small molecules are considered as the total solvation energies including the polar and non-polar part. Both polar and non-polar components of the solvation energy are also calculated for the small molecules using the explicit solvent. Similarly, polar and non-polar parts of solvation energies (as well as total solvation energies) are obtained for small molecules using GBNSR6, DISOLV and MCBHSOLV. The programs MOPAC and APBS carry out the calculations of only the electrostatic (polar) component of solvation energies, so for these programs we do not compare the calculated total solvation energies with the experimental data. The correlation coefficients and values of RMSD for small molecules are given in tables 2–5. Table 2 shows that root mean square deviations of the polar components calculated by different implicit models from the results of calculations in explicit solvent are 0.9 – 1.9 kcal/mol; the range of absolute values of the polar component is about 16 kcal/mol (from −14 kcal/mol to 2 kcal/mol), consequently errors of polar component of solvation energy calculations (compared with the calculations in explicit solvent) by implicit solvent models are 6 – 12% for low molecular weight molecules. The corresponding correlation coefficients are quite high and are 0.82 – 0.97, and the correlation is slightly higher if the implicit models (models 1, 2, 4, 7 and 10 – see table 1) use the same radii and charges as the explicit solvent model uses (method 11 – see table 1).

Table 2.

Comparison of the polar part of the solvation energy calculated by different implicit solvent models with the respective values calculated in explicit solvent for small molecules. RMSD is the root mean square deviation between the polar components of the solvation energy calculated using respective implicit solvent models and explicit solvent model. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and ones calculated in explicit solvent.

Method	PCM (DISOLV) param. set 1	COSMO (DISOLV) param. set 1	S-GB (DISOLV) param. set 1	GB (GBNSR6) param. set 1	APBS param. set 1
RMSD, kcal/mol	1.634	1.642	1.782	0.930	1.911
R2	0.966	0.965	0.953	0.954	0.966
Method	PCM (DISOLV) param. set 2	COSMO (DISOLV) param. set 2	S-GB (DISOLV) param. set 2	PCM (MCBHSOLV) param. set 2	COSMO (MOPAC) param. set 3
RMSD, kcal/mol	1.464	1.473	1.475	1.664	3.577
R2	0.877	0.876	0.854	0.822	0.843

Table 5.

Comparison of the total solvation energy calculated by different implicit solvent models with the respective values obtained from the experimental data for small molecules. RMSD is the root mean square deviation between the total solvation energy calculated by respective implicit solvent models and experimental hydration energies. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and experimental hydration energies.

Method	PCM (DISOLV) param. set 1	COSMO (DISOLV) param. set 1	S-GB (DISOLV) param. set 1	GB (GBNSR6) param. set 1
RMSD, kcal/mol	1.431	1.436	1.667	1.277
R2	0.929	0.929	0.906	0.923
Method	PCM (DISOLV) param. set 2	COSMO (DISOLV) param. set 2	GB (DISOLV) param. set 2	PCM (MCBHSOLV) param. set 2
RMSD, kcal/mol	1.195	1.196	1.290	1.493
R2	0.920	0.919	0.916	0.874

An exception is the COSMO method implemented in the MOPAC package where the deviation from the explicit solvent reference is substantially larger (RMSD = 3.577 kcal/mol), possibly due to the insufficient selection of atomic radii used for the construction of the surface separating solvent from the solute molecule. We should note also that MOPAC uses the SAS surface instead of the SES surface, as it is usually accepted – see, e.g., [26, 27, 29, 30].

Two methods were used for the calculations of the non-polar component of the solvation energy (table 3): the method based on a linear dependence of non-polar component of the solvation energy on SAS area (DISOLV – param. set 1 or DISOLV – param. set 2 in table 3, depending on the selected options: am1-bcc - ZAP9 or mmff94 - disolv) and the method [43] taking into account the individual contributions of separate atoms and implemented in the GBNSR6 program (see above, section 2). Values of the non-polar part of the solvation energy were in the range from −0.18 kcal/mol to 3.31 kcal/mol for small molecules. Non-polar component of solvation energies demonstrates (see table 3) a poor correlation with explicit model results for the calculation method used in the DISOLV program (non-polar component is a linear form of SAS area), and it shows significantly better correlation with explicit model results for the GBNSR6 program, which takes into account Van der Waals contributions from individual solute atoms.

Table 3.

Comparison of the non-polar part of the solvation energy calculated by different implicit solvent models with the respective values calculated in explicit solvent for small molecules. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and ones calculated in explicit solvent.

Method	DISOLV param. set 1	DISOLV param. set 2	GB (GBNSR6) param. set 1
RMSD, kcal/mol	0.661	0.696	0.696
R2	0.184	0.043	0.745

However, the total solvation energy (which is the sum of polar and non-polar parts) continue to have a high correlation with the total solvation energies obtained by calculations in explicit solvent (table 4) and with the experimental hydration energies (table 5).

Table 4.

Comparison of total solvation energies calculated by different implicit solvent models with the respective values calculated by in explicit solvent for small molecules. RMSD is the root mean square deviation between the total solvation energy calculated by respective implicit solvent models and explicit solvent model. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and ones calculated in explicit solvent.

Method	PCM (DISOLV) param. set 1	COSMO (DISOLV) param. set 1	S-GB (DISOLV) param. set 1	GB (GBNSR6) param. set 1
RMSD, kcal/mol	1.560	1.567	1.669	1.292
R2	0.966	0.9655	0.955	0.957
Method	PCM (DISOLV) param. set 2	COSMO (DISOLV) param. set 2	S-GB (DISOLV) param. set 2	PCM (MCBHSOLV) param. set 2
RMSD, kcal/mol	1.604	1.611	1.639	1.787
R2	0.872	0.872	0.860	0.820

The total solvation energy of small molecules for different methods includes the polar solvation energy, calculated by different implicit methods, and the non-polar solvation energy, calculated by the DISOLV program (for methods 2,3,4,5,7,8,9 – see table 1) or the GBNSR6 program (for method 1 - see table 1). Importantly, when comparing the solvation energies (polar part) with the results obtained using explicit water model (Amber12 force field) influence of the radii and atoms charges is observed (for example, the correlation is 0.97 for the PCM calculations in the DISOLV program with the same parameters as calculations in explicit solvent, and it is 0.88 for the calculations with the parameters of MMFF94 force fields), but when comparing the total solvation energies of small molecules with the experimental hydration energies, the correlation coefficients between the calculated solvation energies and experimental hydration energies for different choices of radii and charges of atoms were close (for different methods implemented in DISOLV and GBNSR6 correlation coefficients equal to 0.90–0.93). RMSD also decreases when the comparison with the results in explicit solvent is changed to the comparison with the experimental hydration energies, and in this case the standard deviation is smaller for sets of parameters DISOLV (param. set 2), but not DISOLV (param. set 1).

Comparison of polar parts of the protein solvation energy was made between the explicit solvent reference and the following methods: PCM (implemented in the DISOLV program), COSMO (implemented in the DISOLV program), S-GB (implemented in the DISOLV program), Poisson-Boltzmann method (implemented in the APBS program) and COSMO (implemented in the MOPAC program) – see table 6. The polar component of proteins solvation energies are in the range from −250 kcal/mol to −750 kcal/mol. The corresponding root mean square deviations between the polar components of the solvation energies calculated using the respective implicit solvent models and the polar components of the solvation energies calculated in explicit solvent are shown in table 6, and the errors for the different methods range from 2% (GBNSR6) to 30% (S-GB method implemented in the DISOLV program and using the atomic radii and charges, different from that used in the calculations in explicit solvent).

Table 6.

Comparison of the polar part of the proteins solvation energy calculated by different implicit solvent models relative to the values calculated in explicit solvent. RMSD is the root mean square deviation between the polar components of the solvation energy calculated using respective implicit solvent models and explicit solvent model. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and ones calculated in explicit solvent.

Method	PCM (DISOLV) param. set 1	COSMO (DISOLV) param. set 1	S-GB (DISOLV) param. set 1	GB (GBNSR6) param. set 1	APBS param. set 1
RMSD, kcal/mol	12.303	12.452	28.994	11.699	13.037
R2	0.998	0.998	0.997	0.998	0.998
Method	PCM (DISOLV) param. set 2	COSMO (DISOLV) param. set 2	S-GB (DISOLV) param. set 2	PCM (MCBHSOLV) param. set 2	COSMO) (MOPAC) param. set 3
RMSD, kcal/mol	130.781	137.216	148.417	131.202	99.155
R2	0.683	0.652	0.668	0.683	0.769

As in the case of small molecules there is significant dependence of the results on the selected parameters (radii and charges of atoms), and weak dependence on a specific method of the calculation when comparing the solvation energies calculated using implicit solvent models and ones calculated in explicit solvent. Here all the methods using the same parameters also give approximately equal accuracy of the calculations.

A similar situation is observed for the polar parts of the desolvation energy of protein-ligand complexes (table 7). Different models calculating the polar component of the solvation energy give close results to those in explicit solvent if the parameters are the same as ones used in the explicit solvent calculations. For the same parameters set two methods (the GB (GBNSR6) method and the Poisson-Boltzmann (APBS) method) show the better values of correlation coefficients and the lower RMSD with the results of calculations in explicit solvent. If another parameters are used the correlation coefficient noticeably decreases (except is the COSMO method implemented in the MOPAC package). The absolute values of the polar parts of the desolvation energies for complexes ranged from 25 kcal/mol to 85 kcal/mol (the range is 60 kcal/mol), and thus for the methods that use the same parameterization as in the calculations in explicit solvent the error is 8% – 21%, and for methods that use the different parameterization (3, 5, 8 methods in table 1) this error is significantly larger – 32 – 38%. The exception here is also the COSMO method implemented in MOPAC which gives small root mean square deviation from the results of the explicit solvent reference (RMSD equals 8.2 kcal/mol).

Table 7.

Comparison of the polar part of the desolvation energy of protein-ligand complexes calculated by different implicit solvent models with the respective values calculated in explicit solvent. RMSD is the root mean square deviation between the polar components of the desolvation energy calculated using the respective implicit solvent models and explicit solvent model. R² is Pearson correlation coefficient between the values calculated using implicit solvent models and ones calculated in explicit solvent.

Method	PCM (DISOLV) param. set 1	COSMO (DISOLV) param. set 1	S-GB (DISOLV) param. set 1	GB(GBNSR6) param. set 1	APBS param. set 1
RMSD, kcal/mol	12.915	12.465	11.439	7.042	5.138
R2	0.886	0.886	0.909	0.956	0.963
Method	PCM (DISOLV) param. set 2	COSMO (DISOLV) param. set 2	S-GB (DISOLV) param. set 2	PCM (MCBHSOLV) param. set 2	COSMO (MOPAC) param. set 3
RMSD, kcal/mol	20.240	20.477	23.163	19.697	8.251
R2	0.794	0.790	0.828	0.758	0.899

It was shown in [27, 29] that the numerical accuracy of the PCM method implemented in DISOLV and MCBHSOLV programs are the same when the same model parameters (atoms charges and radii for the dielectric boundary construction) were used. So, we should expect the same RMSD and correlation values between results of PCM MCBHSOLV program solvation energy calculations and ones obtained by the explicit solvent model as it is demonstrated for PCM DISOLV program calculations for the parameters set 1 (see respective cells in tables 6 and 7). The possibility of higher computation speed for large solute structures is the main advantage of PCM MCBHSOLV program over PCM DISOLV one, and the advantage is growing with decrease of the triangulation network step size and with increase of the solute molecule size [27, 29].

Calculations of solvation energy (polar component) of the small molecules take a few seconds for all methods. Computational times of solvation energy calculations benchmarked for the different methods for the proteins and complexes are shown in table 8.

Table 8.

Computational times of solvation energy calculations for the proteins and complexes, for the methods described in the article. The COSMO method implemented in MOPAC is not presented in this table because MOPAC calculations include not only the calculations of the solvation energy. Except where noted, the calculations are performed on a single CPU.

Method	PCM (DISOLV)	COSMO (DISOLV)	S-GB (DISOLV)	GBNSR6	APBS	TI in explicit solvent	PCM (MCBHSOLV)
Proteins calculatio n time	2 – 15 seconds	1 – 5 seconds	0.5 – 1 seconds	~ 5 seconds	2 – 5 minutes	12 hours on 12 processores	15 – 40 seconds
Complex es calculatio n time	~ 35 – 125 seconds	20 – 45 seconds	3 – 6 seconds	~ 7 – 10 seconds	~ 15 minutes	12 hours on 12 processores	50 – 120 seconds

As expected, the different implementations of the Generalized Born method are the fastest among all methods under consideration. The MCBHSOLV realization of PCM slower than the DISOLV one for small proteins (no more than 500 atoms), but demonstrates the same calculation speed for complexes with no more than 2000 atoms.

4. Conclusions

Need to increase considerably effectiveness of computer assisted drug design demands high accuracy of the protein-ligand binding energy calculations – better than 1 kcal/mol. This demand results in necessity to shed light on the accuracy of desolvation energy calculations with different implicit solvent models and their different realizations due to the desolvation energy is the important contribution to the protein-ligand binding energy. In this paper we have considered different implementations of several popular implicit solvation models: PCM (Polarized Continuum Model), GBNSR6 (a recent “R6” version of the generalized Born model), S-GB (Surface version of the generalized Born model), COSMO (COnductor-like Screening MOdel) and the standard numerical solution of the Poisson-Boltzmann equation (APBS program). For models without recommended default parameters we use either MMFF94 or Amber12 force fields for the charges and radii. For the COSMO model implemented in the MOPAC package we use PM7 quantum-chemical semiempirical method. The models are tested for small molecules, proteins and protein-ligand complexes. For small molecules the comparison between calculated total solvation energies and experimental hydration energies is performed, as well as between polar parts of solvation energies calculated with implicit solvation models and with explicit solvent. For proteins and complexes polar parts of solvation energies calculated with implicit solvation models are compared with the corresponding explicit solvent results, which are obtained by TI using rigid three-point TIP3P water model.

In terms of correlation coefficients between the results obtained using implicit models and the results of calculations in explicit solvent model (or experimental data for small molecules set), most of the tested models show similar results when the same parameters (radii and charges of atoms) are chosen. As expected [36] the choice of these parameters influences on the solvation energies: this can be seen from the comparison of the calculated solvation energies with the explicit solvent reference. However, in the case of small molecules it is also possible to notice that different model parameter sets lead to similar values of the correlation coefficients when comparing calculated total energies of solvation with the experimental hydration energies.

At the same time, despite the high correlation coefficients with results obtained in explicit solvent model (and experimental data), the desired “chemical accuracy” of solvation/desolvation energies (not exceeding 1 kcal/mol from the experimental values) has not yet been achieved by the methods and programs tested here. Even for small molecules the standard deviation (RMSD) of the solvation energies of small molecules computed by implicit solvent models from the experimental hydration energies have a range 1.2 – 1.7 kcal/mol for different implicit models. Similar standard deviation (1.2 kcal/mol) can be obtained comparing total solvation energies computed in the explicit solvent with experimental hydration energies of small molecules. The standard deviation of the desolvation energies calculated using the implicit models from the desolvation energies obtained using explicit solvent model are higher and equals to 5–20 kcal/mol with the range of desolvation energies of the complexes of about 60 kcal/mol (the difference between the maximum and minimum values of the desolvation energies, selected from the whole set of molecules). Since in this case (when comparing with the results of the calculations in explicit solvent model) the choice of atomic radii and charges has strong influence on the results, perhaps a more detail parameterization could reduce RMSD values.

It is difficult to anticipate that more accurate parameterization of implicit models is able to decrease significantly these discrepancies because the desolvation energy is a small difference between two large values and is subjected to large errors. However, for accuracy of docking positioning [35] we do not need to calculate the desolvation energy. The target function of the global minimization in the docking procedure is the energy of the protein-ligand complex [35] and only the complex interaction with water solvent has to be considered and the desolvation energy calculation is avoided.

In the present work, DISOLV and MCBHSOLV programs proved to be on par with the other used programs in the case of proteins and ligands solvation energy calculation. Also the numerical Poisson-Boltzmann (APBS program) and GBNSR6 methods proved to be the most accurate in calculating the desolvation energies, with GBNSR6 being much faster. The methods implemented in the DISOLV program allow getting almost the same results as the GBNSR6 and Poisson-Boltzmann methods in the case of the same parameterization. The S-GB method demonstrates the high speed of calculations as the GBNSR6 method. However it is also shown that the parameterization which uses mmff94 charges and DISOLV radii is need to be improved.

All models listed above have already been used in molecular modeling packages, for example: in quantum-chemical packages [51–53], in molecular dynamics packages [46, 54], in the MOPAC package (COSMO) [40]. Regarding docking programs, implicit solvent models are generally not used at all in most docking programs. Sometimes implicit models are used after the docking procedure calculating the scoring function for a given ligand pose, as it is implemented in the DOCK program [66]. The only exception is the SOL program [10] where the simplified GB model is used for the generation of the grid of potentials for probe ligand atoms (module SOL_GRID). The S-GB method and the PCM method using the multicharge approximations were recently used in the direct (gridless) docking program FLM [35], and it has been shown that the inclusion of the implicit solvent models into the calculation of the protein-ligand binding energies in the docking procedure, firstly, allowed to improve the quality of docking positioning and, secondly, brought the calculated protein-ligand binding energies much closer to the binding energies derived from the experimental data. The application of implicit models to estimation of the free energy of protein-ligand complexes formation, e.g. in the frame of the docking procedure, imposes certain restrictions on the calculation times, and in this case the methods using the GB model have a significant advantage.

It should be noted that the more accurate binding energy calculations should take into account polar and non-polar components of solvation energy both. In the present study the non-polar component calculation is discussed only briefly, and in calculations of protein solvation and protein-ligand desolvation energies only the polar component is considered. Though the non-polar component gives rather small contribution into the total solvation energy of large molecules, e.g. protein-ligand complexes, the lack of the non-polar component can lead to noticeable errors in accurate binding energy calculations. It was shown that the more sophisticated method of the non-polar component calculation considering individual contributions of solute atoms, demonstrates better correlation with the explicit solvent calculations: R² values of DISOLV and GBNSR6 in Table 3 have to be compared. But this sophisticated method uses some model parameters (in GBNSR6), which have been optimized only for small molecules [14]. Therefore it is impossible to tell definitely that these parameters will be suitable for calculations of the proteins and complexes. In the present work non-polar components have been calculated only for small molecules. Further improving of implicit solvent models should be directed to self-consistent optimization of non-polar individual solute atoms contributions and polar model parameters for proteins as well as for small molecules.

Due to the vital necessity to improve accuracy of protein-ligand binding energy in docking calculations the fast and accurate implicit solvent models are urgently needed and the conclusions of the present work are extremely demanded. The main conclusion is that implicit models: GB (realized in GBNSR6 program [22]) and S-GB (realized in DISOLV program [26, 28]) have sufficient accuracy and computing speed to be used in docking programs. PCM and COSMO models implemented in DISOLV and MCBHSOLV programs are one order of magnitude slower than GB but they also can be used in docking [35] for higher computational accuracy.

On the other hand, it is revealed that further improvement of the implicit models parameterization polar and non-polar components both is needed to increase the accuracy of solvation energy calculations and as a result to improve docking accuracy.

Highlights.

• Implicit solvent models are compared with each other and with the explicit solvent

  Choice of solvation model parameters has strong influence on the results

  For small molecules solvent models yield high correlation with experimental values

  Generalized Born model demonstrates best combination of accuracy and computing speed