Machine-learned cluster identification in high-dimensional data

Graphical abstract

3-D representation of high dimensional data following ESOM projection and visualization of group (cluster) structures using the U-matrix, which employs a geographical map analogy of valleys where members of the same cluster are located, separated by mountain ranges marking cluster borders.

Highlights

• •High-dimensional biomedical data are commonly searched for structures.
• •Common cluster algorithms may impose non-existent clusters or assign data to the wrong clusters.
• •We highlight accepted proposals of using emergent self-organizing maps for clustering.
• •The addition of the U-matrix provides a visually controllable representation of cluster structure.

Abstract

Background

High-dimensional biomedical data are frequently clustered to identify subgroup structures pointing at distinct disease subtypes. It is crucial that the used cluster algorithm works correctly. However, by imposing a predefined shape on the clusters, classical algorithms occasionally suggest a cluster structure in homogenously distributed data or assign data points to incorrect clusters. We analyzed whether this can be avoided by using emergent self-organizing feature maps (ESOM).

Methods

Data sets with different degrees of complexity were submitted to ESOM analysis with large numbers of neurons, using an interactive R-based bioinformatics tool. On top of the trained ESOM the distance structure in the high dimensional feature space was visualized in the form of a so-called U-matrix. Clustering results were compared with those provided by classical common cluster algorithms including single linkage, Ward and k-means.

Results

Ward clustering imposed cluster structures on cluster-less “golf ball”, “cuboid” and “S-shaped” data sets that contained no structure at all (random data). Ward clustering also imposed structures on permuted real world data sets. By contrast, the ESOM/U-matrix approach correctly found that these data contain no cluster structure. However, ESOM/U-matrix was correct in identifying clusters in biomedical data truly containing subgroups. It was always correct in cluster structure identification in further canonical artificial data. Using intentionally simple data sets, it is shown that popular clustering algorithms typically used for biomedical data sets may fail to cluster data correctly, suggesting that they are also likely to perform erroneously on high dimensional biomedical data.

Conclusions

The present analyses emphasized that generally established classical hierarchical clustering algorithms carry a considerable tendency to produce erroneous results. By contrast, unsupervised machine-learned analysis of cluster structures, applied using the ESOM/U-matrix method, is a viable, unbiased method to identify true clusters in the high-dimensional space of complex data.

1. Introduction

High-dimensional data is increasingly generated in biomedical research. An intuitive approach at utilizing these data is the search for structures such as the organization into distinct clusters. For example, gene expression profiling by grouping genes and samples simultaneously is a widespread practice used to identify distinct subtypes of diseases [1], [2], [3]. Usually, disease-specific expression-patterns are displayed on a clustered heatmap [4] as the most popular graphical representation of high dimensional genomic data [5]. Such plots show the cluster, respectively distance, structure at the margin of the heatmap as a dendrogram. A typical example result of this approach is shown in Fig. 1 that resembles results of genetic profiling analyses where several subgroups were suggested [2], [3], [6], [7].

Fig. 1.

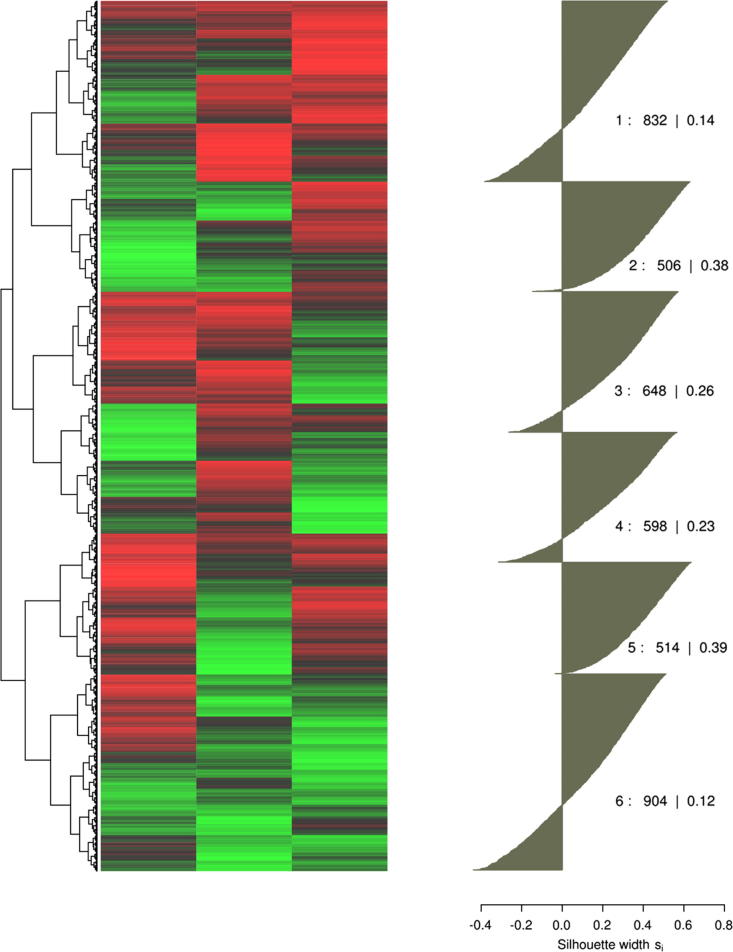
Visualization of high dimensional data. Left panel: data presented in the form of a clustered heatmap as commonly used to identify groups of subjects (rows) sharing a similar gene expression profile. Data is presented color coded with smaller values in red and larger values in green. The dendrogram at the left margin of the matrixplot shows the hierarchical cluster structure. This suggests several distinct clusters up to possibly 4–11 subgroups, for which the right panel shows a silhouette plot for a six cluster solution. The silhouette coefficients for the six clusters indicate how near each sample is to its own relative to neighboring clusters. Values near +1 indicate that the sample is far away from the neighboring clusters while negative values indicate that those samples might have been assigned to the wrong cluster. The average silhouette coefficient is positive. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

However, the data underlying the heatmap in Fig. 1 is displayed in Fig. 2. It consists of an artificial data set with 4002 points, in a 3D view resembling a golf ball [8], that with its equidistant distance distribution lacks any cluster structure. The apparent structure seen in the heatmap of Fig. 1 (left panel) is a direct result from a weakness of most clustering algorithms. That is, these methods impose a structure onto the data instead of identifying structure in the data. The majority of clustering algorithms use an implicit or explicit shape model for the structure of a cluster, such as a sphere in k-means or a hyperellipsoid in Ward clustering. This means, given a predefined number of clusters k, a clustering algorithm calculates the coverage of the data with k of these geometric shapes, independently of whether or not this fits the structure of the data. This can result in erroneous cluster associations of samples or in the imposing of cluster structures non-existent in the data.

Fig. 2.

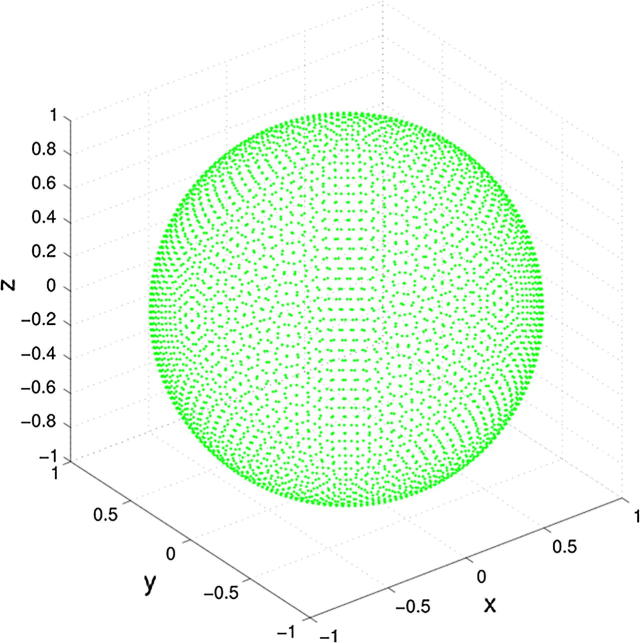
Golf ball data set (data set #1) from the Fundamental Clustering Data Suite (FCPS) [8]. This is the data on which the clustering shown in Fig. 1 was based. This data set contains 4002 points on a sphere with equal distances of each point to its six nearest neighbors.

The example (Figs. 1 and 2) shows how cluster algorithms may suggest a more complex data structure than truly present. Clustering algorithms such as those mentioned above are implemented in standard data analysis software packed with laboratory equipment or in widely used statistical data analysis software packages. However, it is imperative that the quality of the algorithm for biomedical data structure analysis correctly reflects the truly included clusters. Toward this end, emergent self-organizing feature maps (ESOM) are proposed as a viable, unbiased alternative method to identify true clusters in the high-dimensional data space produced in biomedical research [9], [10], or, as a comparable method the vector-filed representation of high-dimensional structures [11]. ESOM/U-matrix overcomes imposing of clusters by addressing the structures in the high dimensional data without assuming a specific cluster form in which the clusters need to be squeezed. Moreover, ESOM/U-matrix rate is an intuitive, haptically interpretable representation with a sound basis in bioinformatics [12].

Therefore, the present work aimed at analyzing whether erroneous cluster identification can be avoided by the application of ESOM [13] with the use of the U-matrix [14]. As a start point, when applying this method to the same data shown in Fig. 2, no cluster structure was suggested (Fig. 3). Hence, the present paper will point at research pitfalls of clustering analysis and proposes an approach that circumvents major errors of other algorithms, that unfortunately are the standard in this field and therefore often routinely chosen by data scientists involved in biomedical research.

Fig. 3.

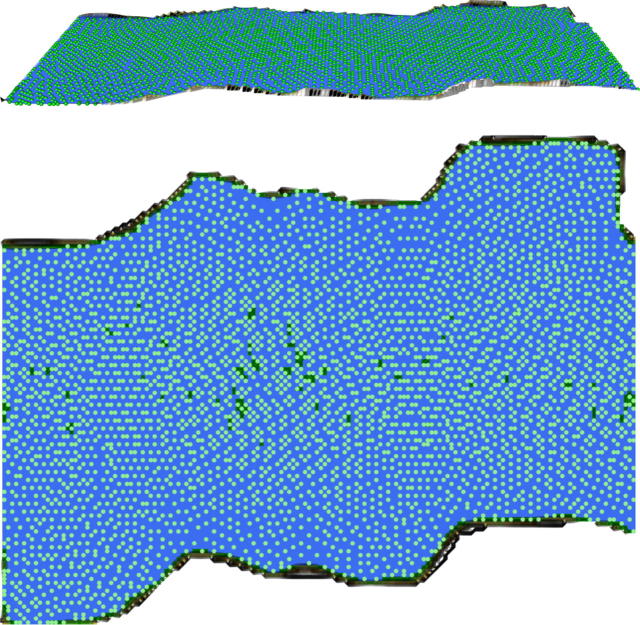
U-matrix representation of the golf ball data set (data set #1, see Fig. 2) showing the result of a projection of the 4002 points evenly spaced on a sphere onto a toroid grid of 82 × 100 neurons where opposite edges are connected. The dots indicate the so-called “best matching units” (BMUs) of the self-organizing map (SOM), which are those neurons whose weight vector is most similar to the input. The U-matrix is flat and structures as evident in the 3D view (top) and in the top view (bottom). This indicates that the gold ball data contains no cluster structure at all, which is correct. Compare the imposture of a structure by classical clustering algorithms in Fig. 1.

2. Methods

2.1. Data sets

The first data set consisted of the above-mentioned “golf ball” data composed of 4002 data points. The points are located on the surface of a sphere at equal distances from each of the six nearest neighbors. This data set was taken from the “Fundamental Clustering Problems Suite (FCPS)” freely available at https://www.uni-marburg.de/fb12/datenbionik/data [8]. This repository comprises a collection of intentionally simple data sets with known classifications offering a variety of problems at which the performance of clustering algorithms can be tested. The data sets in FCPS are especially designed to test the performance of clustering algorithms on particular challenges, for example, outliers or density versus distance defined clusters can be tested on the algorithms.

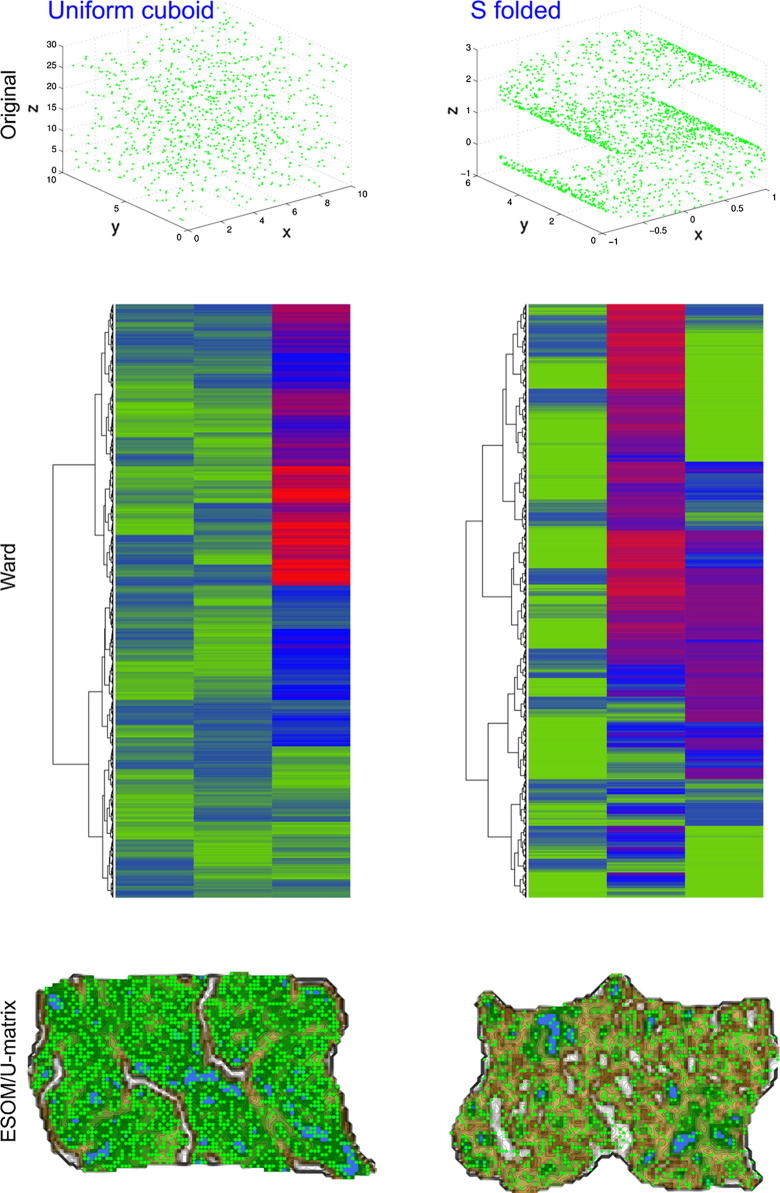
The second and third data sets present data sets akin to set #1, i.e., also of structure-less data. Specifically, the second data set, called “uniform cuboid” was constructed by filling a cuboid with uniformly distributed random numbers in x, y and z directions. The third data set, called “S folded” consisted of uniformly distributed random data on a two dimensional plain that was subsequently folded to form the letter “S” in the third dimension. In both data sets, a group structure was clearly absent by construction, similarly to the first data set.

A fourth and fifth data sets originated from the biomedical literature. Specifically, a classical data set that had been assembled to demonstrate the feasibility of cancer classification based solely on gene expression monitoring was chosen [15]. The data was available at https://bioconductor.org/packages/release/data/experiment/html/golubEsets.html. In brief, this data set comprised microarray analyses of 72 bone marrow samples (47 acute lymphoblastic leukemia, ALL, 25 acute myeloid leukemia, AML) that had been obtained from acute leukemia patients at the time of diagnosis. Following preparation and hybridization of RNA from bone marrow mononuclear cells, high-density oligonucleotide microarrays analyses had been performed for 6817 human genes [16]. The original analyses had identified roughly 1100 genes regulated in the leukemia samples to a higher extent than expected by chance. This gene set was available for identifying cluster structures in a typical biological data set (data set #4). The expectation at the clustering algorithm was to reproduce the original data set composition of ALL versus AML [15]. Subsequently, the cluster structure was destroyed by permutation, i.e., patients were randomly assigned to a gene expression vector without regard of the original association respectively clinical diagnosis (data set #5).

In a sixth data set, the complexity of the second data set was further increased. A set of microarray data comprising differentially expressed genes was available from a previous publication [2]. The data consisted of whole-genome expression profiles from patients with leukemia or controls, specifically, from 266 patients with acute myeloid leukemia, 15 patients with acute promyelocytic leukemia, 163 patients with chronic lymphocytic leukemia, and 108 healthy matched controls [2]. The expectation at the ESOM/U-matrix algorithm was to reproduce the composition of this data set.

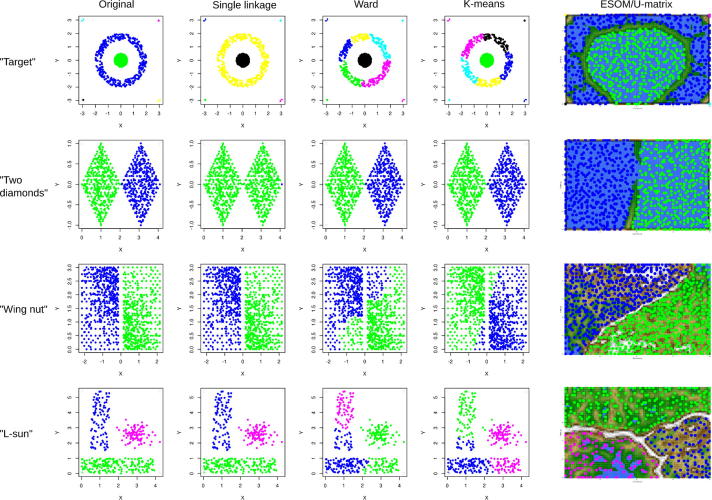
The seventh to tenth data sets were again, as data sets #1–#3, artificial data sets created for testing clustering algorithms taken from the FCPS. The selection comprised the “target”, “two diamonds”, “wing nut” and “L-sun” data sets, named according to their visual appearance (Fig. 8 left column). These data sets pose different degrees of challenge on the clustering algorithm. That is, in the “target” data set there are distinct outliers, in the two “two diamonds” data set the clusters almost touch at one corner. The “wing nut” data set contains two clearly separated clusters with different densities just at the touching borders of the clusters. Finally, “L-sun” is a simple data set with three clearly distinct clusters of different shapes that can be used to identify the borders of the geometrical model for a cluster shape that is often implicitly imposed onto the data structure by the cluster algorithm.

Fig. 8.

Comparative performance of the ESOM/U-matrix (right column) versus classical clustering algorithm in identifying groups in pre-structured data sets (#7–#10) where clusters can be easily spotted visually (left column). Each data set represents a certain problem that is solved by clustering algorithms with varying success. While the standard clustering methods, e.g. single-linkage, Ward und k-means, are not able to solve all problems satisfactorily, the ESOM/U-matrix method provides always the correct cluster structure. In the latter, the cluster structure emerges from visualization of the distances between neurons in the high-dimensional space by means of a U-matrix [36]. The U-matrix was colored as a geographical map with brown or snow-covered heights and green valleys. Thus, valleys indicate clusters and watersheds indicate borderlines between different clusters. For further examples, see the “Fundamental Clustering Problems Suite (FCPS)” freely available at [8]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Analysis of the data cluster structures

Data were analyzed using the R software package (version 3.3.1 for Linux; http://CRAN.R-project.org/ [17]). The main analytical methods made use of unsupervised machine learning to identify structures within the data space [18]. This was obtained by the application of emergent self-organizing feature maps (ESOM) that are based on a topology-preserving artificial neuronal network (Kohonen SOM [13], [19]) used to project high-dimensional data points x_i ∈ R^D onto a two dimensional self-organizing network consisting of a grid of neurons. There are two different prototypical usages of SOM, those where the neurons represent clusters, and those where the neurons represent a projection of the high dimensional data space. In SOMs where the neurons are identified with clusters in the data space, typically a small number of neurons is used. It can be shown that this type of SOM usage is identical to a k-means type of clustering algorithm [20]. The second prototype are SOMs where the map space is regarded as a tool for the characterization of the otherwise inaccessible high dimensional data space. A characteristic of this SOM usage is the large number of neurons. Thousands or tens of thousands neurons are used. Such SOMs allow the emergence of intrinsic structural features of the data space (ESOM). Emergence in this regard is a precisely defined phenomenon of multi agent systems [21].

The central formula for SOM learning is $\mathrm{\Delta }{w}_i=\eta (t)h({\mathit{bmu}}_{i\text{,}}\text{,}r\text{,}t)(x_i-w_i)$ where x_i is a data point, bmu_i the closest neuron for x_i in the SOM (best matching unit, BMU), w_i the weight vector of neuron n_i, h(…) the neighborhood and $\eta (t)\in [0\text{,}1]$ the learning rate. Learning rate and neighborhood are decreased during learning [15]. Let U_i be the set of neurons in the immediate neighborhood of a neuron n_i in the map space. The U-height of a neuron uh(n_i) is the sum of all data distances d(…) from the weight of n_i to the weight vectors of the neurons in U_i: $\mathit{uh}(n_i)={\sum }_{n\in U_i}d(w(n_i)\text{,}w(n))$. A visualization of all U-heights at the neuron’s coordinates in an appropriate way gives the U-matrix [10].

The U-matrix is the canonical tool for the display of the distance structures of the input data on ESOM [14]. Specifically, the U-matrix is based on a planar topology of the neuron space. Embedding the neuron space in a finite but borderless space such as a torus avoids the problems of borderline neurons [14]. High dimensional datasets are usually projected by ESOM onto a finite but borderless output space. The typical space is a grid of neurons on a torus (toroid). This avoids the problem of neurons on borders and subsequently boundary effects [14]. For toroid ESOM neuron grids four adjoining instances of the same U-matrix are used in order to visualize all the ridges and mountains of the borderless U-matrix. This is called a tiled display [14]. The tiled display has, however, the disadvantage, that each input data point is represented on four locations. Therefore, the tiled U-matrix is trimmed at cluster borders such that only one representation of each data point remains. This leads to U-matrix landscapes with curved boundaries [10].

Thus, the D dimensional feature space was projected onto a two dimensional toroid grid [14] of so-called neurons. The size of the grid was chosen to meet the following three main criteria. Firstly, it should not be too small as it has been shown that in that case SOMs degenerate to a k-means like clustering algorithm with no potential to show emergent structures on a U-matrix [20]. Secondly, it should not be too large to avoid that each input data point can be represented on the map on a separate neuron with a surrounding area of other neurons interpolating the data space. This would have the effect that the cluster borders, i.e., their visualization as “mountains” in the U-matrix (see next paragraph) will be broadened and flattened. Thirdly, edge ratios between 1.2 and the golden ratio of 1.6 should be applied as it has been observed that SOMs perform better if the edge lengths of the map are not equal [23]. Combining the requirements for size and form of the SOM, as a starting point for the exploration of structures in a data set a SOM with 4000 (80 × 50) neurons has been successful in many applications and was approximately applied to the present data sets #4–#6. The size can be increased in larger data sets to provide two or more neurons to each data point, such as for the present data set #1 with n = 4002 points that were projected on a grid with 82 rows and 100 columns. For small data sets of, e.g., less than 200 points, the number of neurons provided for each point can be further increased from two to approximately six to obtain a better resolution of the projection.

On the SOMs with sizes as determined according to the heuristics described above, each neuron held the input vector from the high-dimensional space and a further vector carrying “weights” of the same dimensions. The weights were initially randomly drawn from the range of the data variables and subsequently adapted to the data during the learning phase that used 25 epochs. A trained emergent self-organizing map (ESOM) is obtained that represents the data points on a two-dimensional toroid map as the localizations of their respective “best matching units” (BMU), i.e., neurons on the grid that after ESOM learning carried the vector that was most similar to a subjects’ data vector. On top of the trained ESOM the distance structure in the high dimensional feature space was visualized in the form of a so-called U-matrix [12], [24]. This facilitated drug classification by displaying the distances between the BMUs in the high-dimensional space in a color-coding that employed a geographical map analogy where large “heights” represent large distances in the feature space while low “valleys” represented data subsets which are similar. “Mountain ranges” with “snow-covered” heights visually separate the clusters in the data [25]. These procedures were performed using our interactive R-based bioinformatics tool available as R library “Umatrix” (M. Thrun, F. Lerch, Marburg, Germany, http://www.uni-marburg.de/fb12/datenbionik/software [22]; file http://www.uni-marburg.de/fb12/datenbionik/umatrix.tar.gz; publication and CRAN upload of the R library under the same name pending). Results of ESOM/U-matrix based clustering were compared with the cluster structure identified by using classical clustering algorithms including single-linkage, Ward and k-means clustering [26].

3. Results

Applying Ward hierarchical clustering to the cluster-less “golf ball” data set (data set #1) resulted in the suggestion of a cluster structure (Fig. 1 left). According to the visual inspection of the dendrogram at the left margin of the matrix plot, Ward clustering hinted at least two very distinct clusters up to possibly 10–11 subgroups. In sharp contrast with this result was the interpretation of the structure analysis by applying the ESOM and U-matrix approach to the cluster-less golf ball data set. A flat U-matrix resulted (Fig. 3), which correctly indicated the absence of any meaningful cluster structure. Similar results were obtained with the cluster-less “uniform cuboid” (data set #2) and the also cluster-less “S folded” (data set #3) examples. That is, while ward clustering again found clearly separated groups (Fig. 4 middle panels), the ESOM/U-matrix method produced no meaningful cluster structure as indicated by the impossibility to observe a clear separation of data by ridges in the geographical landscape analogy of the U-matrix representation (Fig. 4 bottom panels).

Fig. 4.

Cluster analyses of two cluster-less data sets, i.e., the “uniform cuboid” (left) and the “S folded” (right) data sets (#2 and #3, respectively. Top panels: 3D display of the original data sets. Middle panels: Data presented in the form of a clustered heatmap as commonly used to identify groups of subjects (rows). Data is presented color coded with smaller values in red and larger values in green. The dendrogram at the left margin of the matrixplot shows the hierarchical cluster structure identified by the ward algorithm suggesting the existence of several subgroups in the cluster-less data. Bottom panels. U-matrix representation of data sets #2 and #3 showing the result of a projection of the data points onto a toroid grid of 82 × 100 neurons where opposite edges are connected. The dots indicate the so-called “best matching units” (BMUs) of the self-organizing map (SOM), which are those neurons whose weight vector is most similar to the input. The U-matrix fails to display valleys clearly separated by ridges. Hence, a clustering attempt fails with this method, which is the correct result for the present data sets. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

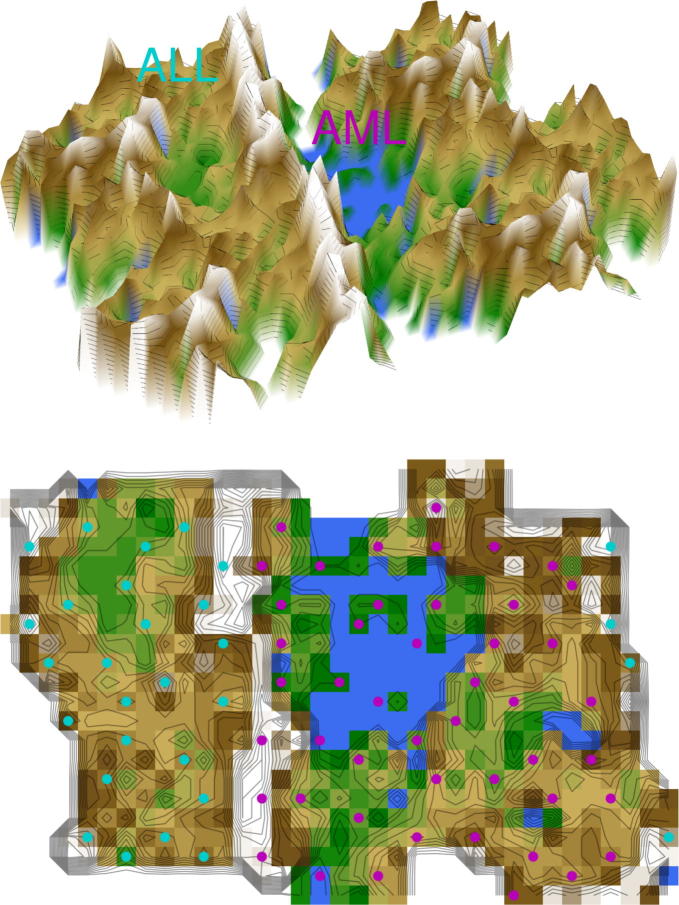
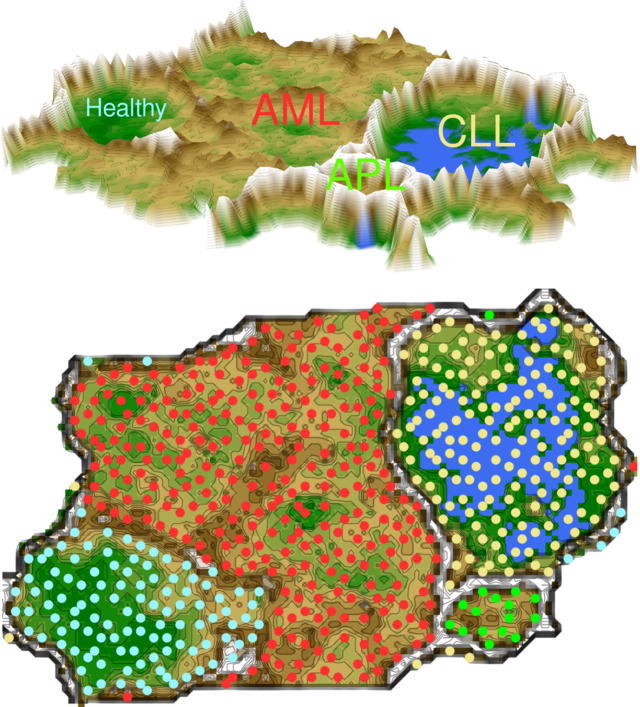
While the ESOM/U-matrix method did not impose a cluster structure where none was in the data, it was able to identify a cluster structure in biomedical data previously assembled to demonstrate the feasibility of cancer classification based solely on gene expression monitoring [15]. The U-matrix resulting from that data set correctly indicated the original clustering into acute myeloid leukemia and acute lymphoblastic leukemia (data set #4), which was evident as a large mountain range or watershed between the two types of leukemia (Fig. 5). By contrast, when destroying the cluster structure of data set #4 by permutation, the results of applying the ward algorithm could still be interpreted as suggesting two clustersin data set #5 whereas the ESOM/U-matrix clearly indicated no coherent cluster structure (Fig. 6). A successful clustering of biomedical data was again obtained in the more complex leukemia data set (#6) where the ESOM/U-matrix method indicated four different clusters that could be clearly seen as valleys surrounded by “snow-covered” mountain ranges (Fig. 7). Hence, the ESOM/U-matrix method correctly identified groups in microarray data with a clear cluster structure.

Fig. 5.

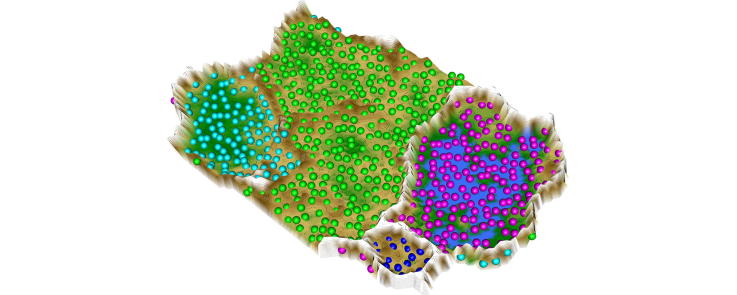
U-matrix representation of a classical dataset composed of microarray data of acute myeloid or lymphoblastic leukemia first used to propose the use of clustering algorithms to automatically discover distinctions between genetic profiles without previous knowledge of these classes [15] (data set #4). The figure shows the result of a projection of the data points onto a toroid grid 4000 neurons where opposite edges are connected. The cluster structure emerges from visualization of the distances between neurons in the high-dimensional space by means of a U-matrix [36]. The U-matrix was colored as a geographical map with brown or snow-covered heights and green valleys. Thus, valleys indicate clusters and watersheds indicate borderlines between different clusters. On the 3D-display (top) of the U-matrix, the valleys, ridges and basins can be seen. Valleys indicate clusters of similar drugs. The mountain range with “snow-covered” heights separates main clusters of leukemia. On the top view (bottom), the dots indicate the so-called “best matching units” (BMUs) of the self-organizing map (SOM), which are those neurons whose weight vector is most similar to the input. The BMUs are colored according to the obtained clustering of the data space, i.e., in magenta for acute myeloid leukemia (AML) and in light blue for acute lymphoblastic leukemia (ALL). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Analysis of permutated microarray data (data set #5) obtained from data set #4 with the two-cluster structure destroyed by permutation of the data. Left: Ward clustering of the data, indicated by the dendrogram above the matrixplot of the permutated microarray data of acute myeloid or lymphoblastic leukemia [15]. Observation of the dendrogram would suggest, as expected, a two-cluster structure. Right: U-matrix display of the data. A cluster structure was clearly absent.

Fig. 7.

U-matrix representation of a microarray analyses derived data set comprising blood gene expression data in healthy subjects and in patients with acute myeloid leukemia, acute promyelocytic leukemia or chronic lymphocytic leukemia [2] (data set #6). The figure shows the result of a projection of the data points onto a toroid grid 4000 neurons where opposite edges are connected. The cluster structure emerges from visualization of the distances between neurons in the high-dimensional space by means of a U-matrix [36]. The U-matrix was colored as a geographical map with brown or snow-covered heights and green valleys. Thus, valleys indicate clusters and watersheds indicate borderlines between different clusters. On the 3D-display (top) of the U-matrix, the valleys, ridges and basins can be seen. Valleys indicate clusters of similar drugs. The mountain range with “snow-covered” heights separates main clusters. On the top view (bottom), the dots indicate the so-called “best matching units” (BMUs) of the self-organizing map (SOM), which are those neurons whose weight vector is most similar to the input. The BMUs are colored according to the obtained clustering of the data space, i.e., light blue for healthy subjects, red for acute myeloid leukemia (AML), green for acute promyelocytic leukemia (APL) and yellow for chronic lymphocytic leukemia (CLL). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The superior performance of the ESOM/U-matrix approach to classical clustering algorithms prevailed in further data sets (#7–10) assembled with known a priori classifications [8]. Specifically, data sets from the FCPS provided similar evidence for consistently correct cluster identification when using the ESOM/U-matrix (Fig. 8), whereas other methods such as single linkage, Ward or k-means occasionally failed in correct cluster assignment of the data points.

4. Discussion

In the analysis of multivariate biomedical data, the identification of clusters respectively subgroups is a task of central interest. Interpretations of data, the planning of subsequent experiments or the establishment of stratified therapy approaches may depend upon a valid cluster structure found in a biomedical data set. The present analysis emphasized that classical hierarchical clustering algorithms carry a considerable tendency to produce erroneous results. This can lead to wrong cluster associations of samples or to the imposing of cluster structures that are non-existent in the data. Both types of error will skew the data interpretation. This is a known phenomenon in clustering [27], [28]. To ameliorate it, independent methods to (in)validate the cluster structures such as silhouette plots [29] have been recommended to be added to the cluster analysis of biomedical data [30]. However, these plots can also be misleading. The silhouette plot in Fig. 1 (top right panel) shows the results obtained for “golf ball” data set with six clusters obtained using the Ward algorithm. The average silhouette value of 0.22 apparently confirmed the clustering. This value is considerably higher than the average silhouette value of 0.09 elsewhere presented to support a cluster structure spotted in the gene expression profiles from 21 breast cancer data sets (Fig. 2 in [31]).

The use of ESOM [13] and the U-matrix [14] provides obvious advantages to classical clustering algorithms and their combination with supporting assessments. ESOM are based on the topology-preserving projection of high-dimensional data points onto a two dimensional self-organizing network. The U-matrix allows to visually (in)validate cluster structures in the data directly, without the help of additional analyses of plots. If a high dimensional data set contains distance and/or density based clusters, the resulting U-matrix landscape possesses a clear valley - mountain ridge - valley structure as in the present AML/ALL data set (Fig. 4). Importantly, the ESOM/U-matrix does not impose cluster structures onto a data set. For data without any cluster structure, such as the “golf ball”, “uniform cuboid” and “S folded” data sets, the resulting U-matrix landscapes were a conglomerate of humps and dips without letting any consistent structure to be observed. This allows visually assessing the quality of a clustering as an implicit analytical step during clustering [13], [14].

Unsupervised machine-learned analysis of cluster structures provides a valid method for subgroup identification in high-dimensional biomedical data. However, as already mentioned in the methods section of this paper, it has to be noted that a previous contemplation of Kohonen-type neuronal networks for analyzing high-dimensional biomedical data, in particular microarray data [32], [33], provided a reluctant judgment of their utility in this field. This owes to an unfortunate selection of only 30 or less neurons for the output grid in these attempts. It has been shown that with such small numbers of neurons, SOM are equivalent to a k-means clustering and lose their superior clustering performance [20]. By contrast, the presently proposed ESOM/U-matrix uses 4000 or more neurons, which ameliorates the problems with representing a high dimensional space in a lower space without losing distance relations and is therefore suitable to obtain the correct cluster structure of microarray and other biomedical data.

Cluster identification is a central target in the analysis of high-dimensional biomedical data as a general strategy for discovering and predicting classes independently of previous biological knowledge [15]. The analytical method is, however, crucial to avoid non-reproducible pattern recognition due to an exaggeration of accidental outliers from otherwise homogenous data sets. Considering the present demonstration with the golf ball data, previous findings focused on the identification of an increasing number of subgroups in, e.g., cancer data might merit reconsideration. It is imperative, that the quality of the algorithm for data analysis correctly reflects cluster structures which are really in the data. Toward this end, we have proposed ESOM/U-matrix method as a viable, unbiased alternative method to identify true clusters. If a high dimensional data set contains distance and/or density based clusters, the resulting U-matrix landscape possesses a clear valley-mountain ridge-valley structure. In biomedical informatics, the method has been already successfully applied to pain-related [34] and pharmacological [35] data sets. Apart from the presently used R implementation, the method is also implemented available in Matlab or JAVA (http://www.uni-marburg.de/fb12/datenbionik/software). In addition, the 3D structure of the U-matrix allows intuitive cluster recognition and can provide a haptic access to the data space by means of 3D-printing [22], [25].

Funding

This work has been funded by the Landesoffensive zur Entwicklung wissenschaftlich - ökonomischer Exzellenz (LOEWE), Hessen, Germany, Schwerpunkt: Anwendungsorientierte Arzneimittelforschung (JL) with the specific project funding under the name “Process pharmacology: A data science based approach to drug repurposing”. In addition, the work received support within the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 602919 (JL, GLORIA). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Conflict of interest

The authors have declared that no conflicts of interest exist.

Author contributions

Conceived and designed the analysis: AU, JL. Analyzed the data: AU, JL. Wrote the paper: JL, AU. Prepared the figures: JL, AU. All authors reviewed the manuscript.