The effects of cracks on the quantification of the cancellous bone fabric tensor in fossil and archaeological specimens: a simulation study

Abstract

Cancellous bone is very sensitive to its prevailing mechanical environment, and study of its architecture has previously aided interpretations of locomotor biomechanics in extinct animals or archaeological populations. However, quantification of architectural features may be compromised by poor preservation in fossil and archaeological specimens, such as post mortem cracking or fracturing. In this study, the effects of post mortem cracks on the quantification of cancellous bone fabric were investigated through the simulation of cracks in otherwise undamaged modern bone samples. The effect on both scalar (degree of fabric anisotropy, fabric elongation index) and vector (principal fabric directions) variables was assessed through comparing the results of architectural analyses of cracked vs. non‐cracked samples. Error was found to decrease as the relative size of the crack decreased, and as the orientation of the crack approached the orientation of the primary fabric direction. However, even in the best‐case scenario simulated, error remained substantial, with at least 18% of simulations showing a > 10% error when scalar variables were considered, and at least 6.7% of simulations showing a > 10° error when vector variables were considered. As a 10% (scalar) or 10° (vector) difference is probably too large for reliable interpretation of a fossil or archaeological specimen, these results suggest that cracks should be avoided if possible when analysing cancellous bone architecture in such specimens.

Introduction

Cancellous bone is a highly complex tissue found throughout the vertebrate skeleton. It is remarkable in its ability to adapt its structure to suit the prevailing mechanical environment, as demonstrated by in vivo experiments (Radin et al. 1982; Goldstein et al. 1991; Biewener et al. 1996; van der Meulen et al. 2006; Pontzer et al. 2006; Polk et al. 2008; Volpato et al. 2008; Barak et al. 2011) and computer simulations (Mullender & Huiskes, 1995; Huiskes et al. 2000; Adachi et al. 2001; Ruimerman et al. 2005; Wang et al. 2012). Further, studies of extant animal species have demonstrated that differences in locomotor behaviour often lead to differences in cancellous bone architecture (Fajardo & Müller, 2001; Ryan & Ketcham, 2002b, 2005; Maga et al. 2006; Hébert et al. 2012; Ryan & Shaw, 2012; Barak et al. 2013; Su et al. 2013; Tsegai et al. 2013; Matarazzo, 2015).

Given the sensitivity of cancellous bone to its mechanical environment, researchers have sometimes used cancellous bone architecture to help interpret locomotor biomechanics in extinct animals, or recently extinct human populations (Thomason, 1985; Macchiarelli et al. 1999; Ryan & Ketcham, 2002a; Ryan & Krovitz, 2006; Moreno et al. 2007; Gosman & Ketcham, 2009; DeSilva & Devlin, 2012; Barak et al. 2013; Su et al. 2013; Bishop et al. 2015; Chirchir et al. 2015; Ryan & Shaw, 2015; Skinner et al. 2015). Underpinning these studies is the quantification of various micro‐structural characteristics of cancellous bone, such as bone volume fraction (a measure of porosity), trabecular thickness and spacing, and fabric direction or anisotropy (Odgaard & Gundersen, 1993; Odgaard, 1997, 2001; Ketcham & Ryan, 2004; Doube et al. 2010). These measures are typically made at fine spatial scales in the specimens, often approaching the continuum‐scale (the scale at which the mechanical behaviour of a volume of cancellous bone can be replaced by a set of material properties that are averaged across the same volume). Each of the aforementioned studies has provided new insight that otherwise could not be obtained from the fossil or archaeological record. However, fossil and archaeological specimens may not be well preserved, on account of their age and the many environmental factors they can be subject to. A particularly common form of post mortem, taphonomic degradation is brittle deformation – cracking or fracturing – which can occur both before and after burial of the specimen (Behrensmeyer & Hill, 1980).

Macroscopic cracks that run through a fossil or archaeological specimen may potentially influence the results of a quantitative analysis of cancellous bone architecture, because they are features that are present in the specimen but were not there in the original, living bone. For instance, cracking of a fossil or archaeological specimen may sever trabecular connections, displace trabeculae relative to each other or introduce a void into the specimen (i.e. obliteration of actual bone structure). The presence of cracks could therefore confound interpretation, yet what influence they might have remains unknown. Further, if the presence of cracks does indeed influence the results of architectural analyses, it remains unknown as to whether this is true of all cracks, or only those of a certain size or shape. This is a potentially important problem, because essentially all fossil and archaeological specimens will have suffered macroscopic cracking to some degree, and the extent of cracking may not be able to be fully appreciated from visual examination of the specimen in hand sample. In previous studies of cancellous bone architecture in fossil or archaeological specimens, it is often unclear if the potential problems posed by cracks were addressed, perhaps because the studies’ specimens (usually being of recent geological age) were indeed well preserved. One exception is the study of Ryan & Ketcham (2002a), who explicitly noted the presence of cracks in one specimen and moved their region of analysis away from the cracked region of bone. By and large, however, this approach of active identification and avoidance of cracks does not appear to have been followed in palaeontological and archaeological studies. It therefore remains that cracking in a fossil or archaeological specimen could present an impediment to the analysis and interpretation of cancellous bone architecture, especially in older fossil material that has the potential for greater taphonomic deformation.

The purpose of this study was to use computer simulations to elucidate the effects of crack size and orientation on the quantification of cancellous bone architecture in fossil and archaeological specimens. The approach was to analyse a variety of ‘pristine’ (undamaged) samples of modern cancellous bone, simulate the presence of cracks in those specimens and re‐run the analyses, and compare the results for pristine vs. cracked specimens. The focus here is directed towards measures that describe the cancellous bone fabric tensor, because this strongly relates to the direction and stereotypy of in vivo loading (Fyhrie & Carter, 1987; Goldstein et al. 1991; Ryan & Ketcham, 2005; Pontzer et al. 2006; Barak et al. 2011).

Materials and methods

Image acquisition and processing

Ten samples of cancellous bone, derived from X‐ray computed tomography (CT) scans of the limb bones of various modern avian and reptilian species, were studied (Table 1). The CT scans were acquired using either a Siemens Inveon (Siemens AG, Germany) or a GE BrightSpeed (GE Healthcare, UK); scan settings are detailed in Table 1. The scans were processed in the open‐source software ImageJ 1.47 (http://imagej.nih.gov/ij/), and segmented using the local thresholding algorithm of Bernsen (1986), as implemented in ImageJ (Landini, 2008; Landini et al. 2016; see also Appendix). For the large bird bones scanned using the GE Brightspeed, the scans were resampled to isotropic voxels and at triple the original resolution using a bicubic interpolation algorithm; this did not alter the underlying structure in the scan data, but did facilitate a more effective segmentation of the cancellous bone. The samples for analysis were extracted as large cubes from the proximal and distal ends of the bones in the CT scans, and displayed a wide variety of structures.

Table 1.

Samples of cancellous bone investigated in this study.

Sample	Collection numbera	Description	Sample dimensions (mm)	Mean trabecular spacing (mm)	CT scan settings
					Peak tube voltage (kV)	Tube current (mA)	Exposure time (ms)	Voxel resolution (mm)a
1	QMJ 48127	Saltwater crocodile (Crocodylus porosus) femoral head	10.653	0.399	80	0.45	1000	0.053
2	QMJ 48127	Crocodylus porosus medial femoral condyle	10.653	0.491	80	0.45	1000	0.053
3	PJB	Domestic chicken (Gallus gallus) femoral head	4.611	0.351	80	0.45	1000	0.053
4	QMJ 84416	Spencer's goanna (Varanus spenceri) proximal femur	7.473	0.694	80	0.5	900	0.053
5	AM R.106933	Komodo dragon (Varanus komodoensis) proximal tibia	7.473	0.590	80	0.45	1000	0.053
6	QMJ 47916	Australian freshwater crocodile (Crocodylus johnstoni) proximal tibia	5.247	0.505	80	0.5	900	0.053
7	QMO 30105	Southern cassowary (Casuarius casuarius) proximal tibiotarsus	14.673	0.811	120	55	1681	0.073 (0.219 × 0.3)
8	QMO 30105	Casuarius casuarius distal tibiotarsus	11.023	1.011	120	55	1681	0.073 (0.219 × 0.3)
9	MV R.2385	Ostrich (Struthio camelus) femoral head	24.613	1.482	120	55	1681	0.163 (0.488 × 0.3)
10	MV R.2385	Struthio camelus medial femoral condyle	18.093	1.949	120	55	1681	0.163 (0.488 × 0.3)

Samples 1–6 were CT scanned using a Siemens Inveon, and samples 7–10 were scanned using a GE BrightSpeed. Crack thicknesses were one‐half, one, two and three times trabecular spacing; VOI diameter was five, nine and 13 times trabecular spacing (the last only possible for specimens 1, 2, 3, 7 and 9).

Museum collection number abbreviations: QMJ, QMO, Queensland Museum Biodiversity Collections; AM R., Australian Museum Herpetology Collections, MV R., Museum Victoria Ornithology Collections; PJB, P.J.B. personal collection.

^aSamples 7–10 were scanned with an anisotropic voxel resolution (original resolution in parentheses), and were resampled to an isotropic resolution.

Crack simulation

Cracks were simulated as planar prisms running through the middle of each sample at one of nine orientations (Fig. 1). These orientations were fixed relative to the orientation of the pre‐determined fabric tensor for each specimen, such that four cracks were parallel to the primary fabric direction, one was perpendicular to the primary fabric direction, and four were at a 45° angle to the primary fabric direction (Fig. 1b). Although cracks can often assume a complex shape throughout a fossil or archaeological specimen, at the fine spatial scale at which cancellous bone architectural analyses are typically performed they can be reasonably approximated as planes. Moreover, the effect of cracks as simulated in this study was one of occlusion only: the cracks occluded the original cancellous bone structure in the CT scans, but did not introduce any new structure of their own (as might occur if high‐density minerals precipitated along the internal surfaces of the crack). Crack geometry was initially defined in Rhinoceros 4.0 (McNeel, USA), and converted to voxels in an image stack using Mimics 17.0 (Materialize NV, Belgium). The voxels representing the crack were then subtracted from the CT scan image stack of the bone sample to simulate the obliteration of cancellous bone by the crack (Fig. 1e).

Figure 1.

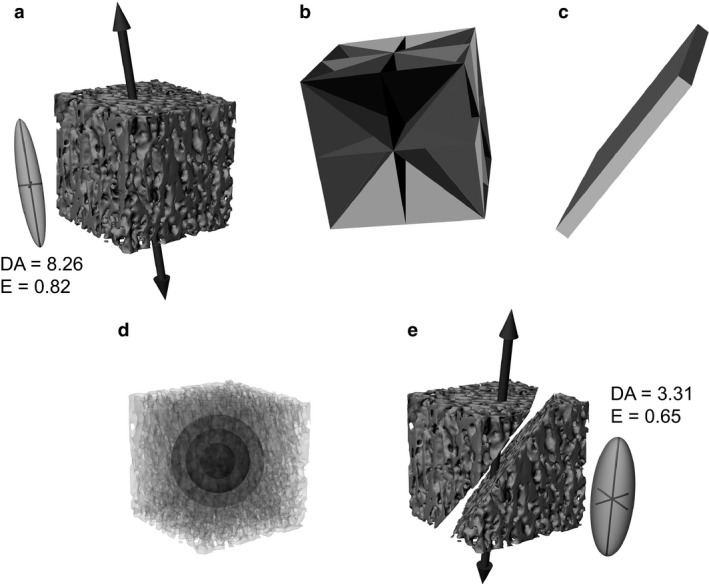
The simulation of cracked specimens in this study. (a) A pristine sample of cancellous bone, from the proximal tibiotarsus of a cassowary, Casuarius casuarius (side length of cube = 14.673 mm). The large vector indicates the orientation of the primary fabric direction calculated for the whole sample, and the inset is the three‐dimensional fabric ellipsoid (geometric expression of the fabric tensor) with associated measures (see text for explanation). (b) Nine standard orientations for the simulated cracks in this particular sample; all pass through the centre of the cube. Four planes are parallel to the primary fabric direction, one plane is perpendicular to it, and four planes are at a 45° angle to it. (c) One particular crack, simulated as a planar prism, here with thickness equal to twice the mean trabecular spacing of the sample. (d) Three spherical VOIs were used in the simulations, of diameter five, nine and 13 times the mean trabecular spacing. (e) The simulated cracked sample, where the cancellous bone in the volume of the crack in (c) has been removed, to simulate how a crack obliterates the structure. The resulting effect on the primary fabric orientation and nature of the fabric ellipsoid (and associated measures) is also illustrated.

To investigate the effect of crack size on the results of an architectural analysis, a variety of crack thicknesses were simulated across the 10 samples. In absolute terms, these thicknesses ranged from 0.18 to 5.8 mm, which encompasses much of the range of macroscopic crack sizes that would be encountered in fossil or archaeological specimens. The thickness of the cracks was scaled to the mean trabecular spacing for each specimen, calculated using the method of Hildebrand & Rüegsegger (1997), as implemented in the BoneJ 1.3.11 plugin for ImageJ (Doube et al. 2010). Four thicknesses were tested, one‐half, one, two and three times mean trabecular spacing. Only that part of the cancellous bone sample within a specified volume of interest (VOI) was included in an analysis; the VOIs were defined as spheres centred at the centre of the cube, to avoid corner effects (Fig. 1d). Three VOI sizes were tested for both pristine and cracked samples, five, nine and 13 times mean trabecular spacing (the last only possible for five of the 10 specimens), each of which is sufficiently large for continuum‐level analysis of cancellous bone architecture (Harrigan et al. 1988; Cowin, 2001). By scaling both crack thickness and VOI size to the intrinsic dimensions of each individual sample, this meant that constant ratios of crack thickness to VOI size were attained across the samples. Moreover, as the orientation of cracks was set up to be consistent with the intrinsic fabric of each individual sample, this also allowed for the effect of crack orientation to be investigated.

Architectural analyses

Analyses of cancellous bone architecture in pristine and cracked samples were conducted using the software Quant3D (Ryan & Ketcham, 2002a,b; Ketcham & Ryan, 2004). Two techniques that determine the fabric tensor (Cowin, 1986) were tested, the star volume distribution (SVD) and mean intercept length (MIL) methods; the MIL method in Quant3D was set to be the ellipsoid‐based material tensor formulation. These are the two most widely used approaches in three‐dimensional architectural analyses of cancellous bone, and the results of both have been demonstrated to show strong correlation with cancellous bone mechanical properties (Turner et al. 1990; Odgaard et al. 1997; Kabel et al. 1999; Ulrich et al. 1999). The SVD method essentially measures the spatial distribution (and in turn alignment) of bone material in a given volume, whereas the MIL method focuses on the distribution (and in turn alignment) of interfaces between the bone and non‐bone phases in a given volume (Odgaard, 1997, 2001). For both methods, measurements were made for 2049 uniformly distributed orientations at 4000 points within the bone phase, with random rotation and dense vector sampling. (For the determination of the whole‐sample fabric tensor, to guide the set‐up of crack orientations, the SVD method was used with the same parameters, on a sphere centred in the middle of the sample and occupying as large a volume as possible.) Upon calculation of the fabric tensor, the following variables were derived: the orientations of the primary, secondary and tertiary fabric directions (eigenvectors: u ₁, u ₂ and u ₃, respectively), the corresponding primary, secondary and tertiary fabric eigenvalues (e ₁, e ₂ and e ₃, respectively), degree of fabric anisotropy (DA, calculated as e ₁/e ₃) and fabric elongation index (E, calculated as 1 – e ₂/e ₁).

Comparing pristine and cracked samples

The effect of cracks was assessed by determining the mean (± 1 SD) difference from the pristine sample, as a percentage for the scalar variables and as an angular deviation for the vector variables. This was computed for each combination of crack thickness and VOI size, and for each type of crack orientation (parallel, perpendicular or 45° to the orientation of u ₁). Angular deviation between the orientation of vectors in a cracked and pristine sample was calculated using the dot product of the two vectors:

$${\mathit{\theta }}_{\mathrm{cracked}-\mathrm{pristine}}=\text{arccos}\left(\frac{{\mathbf{v}}_{\mathrm{cracked}}\bullet {\mathbf{v}}_{\mathrm{pristine}}}{|{\mathbf{v}}_{\mathrm{cracked}}|\times |{\mathbf{v}}_{\mathrm{pristine}}|}\right)$$

Additionally, the frequency of unacceptably large differences was investigated. An unacceptably large difference is one where an error of that magnitude in the real world would confound interpretation of a fossil or archaeological specimen. Thus, an a priori maximum acceptable difference was set for each scalar and vector variable examined, and the proportion of instances in which the difference between cracked and pristine samples exceeded that limit, P(Δ_max), was determined for each combination of VOI size and crack thickness and for each type of crack orientation. For scalar variables, this limit was ± 10% of the value determined for the pristine sample. For vector variables, the limit was a 10° cone around the vector determined for the pristine sample. These limits were chosen based on the results of previous studies, which have shown that distinct locomotor differences in species can manifest themselves as architectural differences of these magnitudes, or even less (Ryan & Ketcham, 2002b; Maga et al. 2006; Pontzer et al. 2006; Polk et al. 2008; Griffin et al. 2010; Barak et al. 2013; Su et al. 2013; Tsegai et al. 2013). Hence, errors in measurement of 10% (for scalar variables) or 10° (for vector variables) could be large enough to preclude reliable and in‐depth interpretation of a fossil or archaeological specimen.

Results

Scalar variables – DA and E

Attention is only given to the degree of anisotropy (DA) and elongation index (E) here, because the individual eigenvalues of a fabric tensor are not meaningful in their own right; it is only when expressed relative to each other (in measures such as DA and E) that they are informative (Ryan & Ketcham, 2002b; Maga et al. 2006; Hébert et al. 2012; Matarazzo, 2015). In both the SVD and MIL analyses, both the mean positive differences (where the cracked value was greater than the pristine value) and mean negative differences (where the cracked value was less than the pristine value) tended to decrease as the ratio of crack thickness to VOI size decreased (Fig. 2a). The margin of error about these means also tended to decrease as the ratio of crack thickness to VOI size decreased, although it is important to note that even at the lowest ratio tested (1/26 or 3.8%) the margin of error often remained considerable, with a standard deviation usually in excess of 10%. The proportion of instances in which the maximum acceptable difference for both DA and E was exceeded, P(Δ_max), generally decreased as the ratio of crack thickness to VOI size decreased, for both SVD and MIL analyses (Fig. 2b). Even at the lowest ratio tested, however, P(Δ_max) was at least 0.18; that is, there was essentially a one‐in‐six chance or greater that a measurement for a cracked sample was more than 10% in error of that calculated for the pristine sample.

Figure 2.

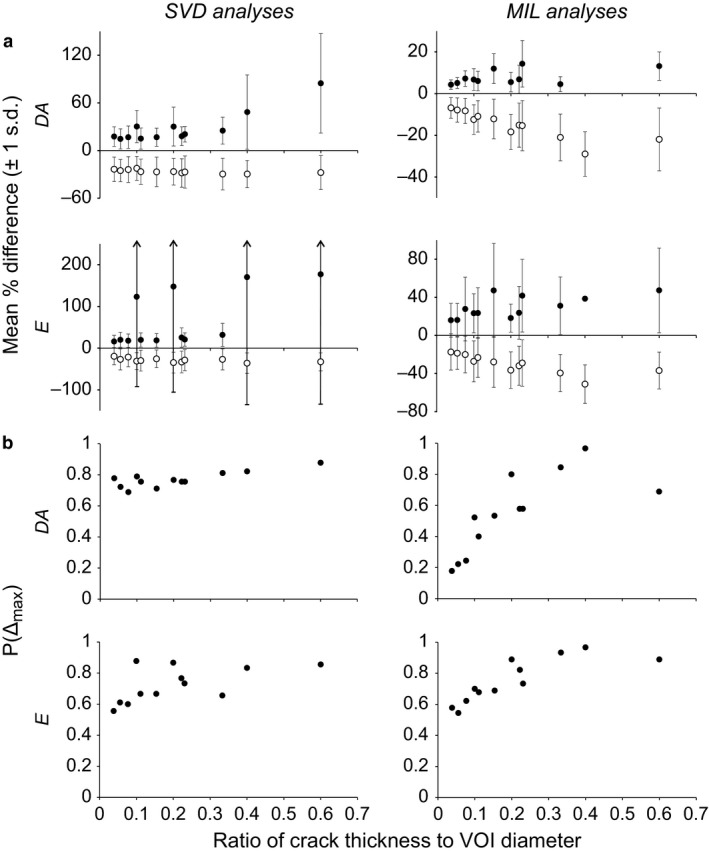
The effect of cracks on scalar variables describing the cancellous bone fabric tensor. (a) In terms of the mean percentage difference from the pristine sample. (b) In terms of P(Δ_max), the proportion of instances where the maximum acceptable difference was exceeded. For the mean difference plots, filled circles denote positive differences from the values for the pristine sample, and hollow circles denote negative differences from the values for the pristine sample.

Vector variables – principal fabric directions

The mean angular difference between the vector orientations of cracked and pristine samples tended to decrease as the ratio of crack thickness to VOI size decreased, for all three fabric directions and for both SVD and MIL methods (Fig. 3a). The margin of error about the mean also tended to decrease as the ratio of crack thickness to VOI size decreased, although again it remained considerable even for the lowest ratio tested, with the standard deviation being at least 6°, and often in excess of 10°. As with the scalar variables, P(Δ_max) generally decreased as the ratio of crack thickness to VOI size decreased (Fig. 3b). However, P(Δ_max) remained above 0.16 in all SVD analyses, and in the MIL analyses it typically remained above 0.11; only at the lowest ratio of crack thickness to VOI size was a lower value observed (0.067), and this was only in regards to the orientation of u ₁. Thus, for the SVD analyses, there was essentially a one‐in‐six chance or greater that a vector orientation calculated for a cracked sample was more than 10° off that calculated for the pristine sample. Furthermore, for the MIL analyses, there was essentially a one‐in‐10 chance or greater that a vector orientation calculated for a cracked sample was in error of 10° or more, except at the lowest ratio of crack thickness to VOI size.

Figure 3.

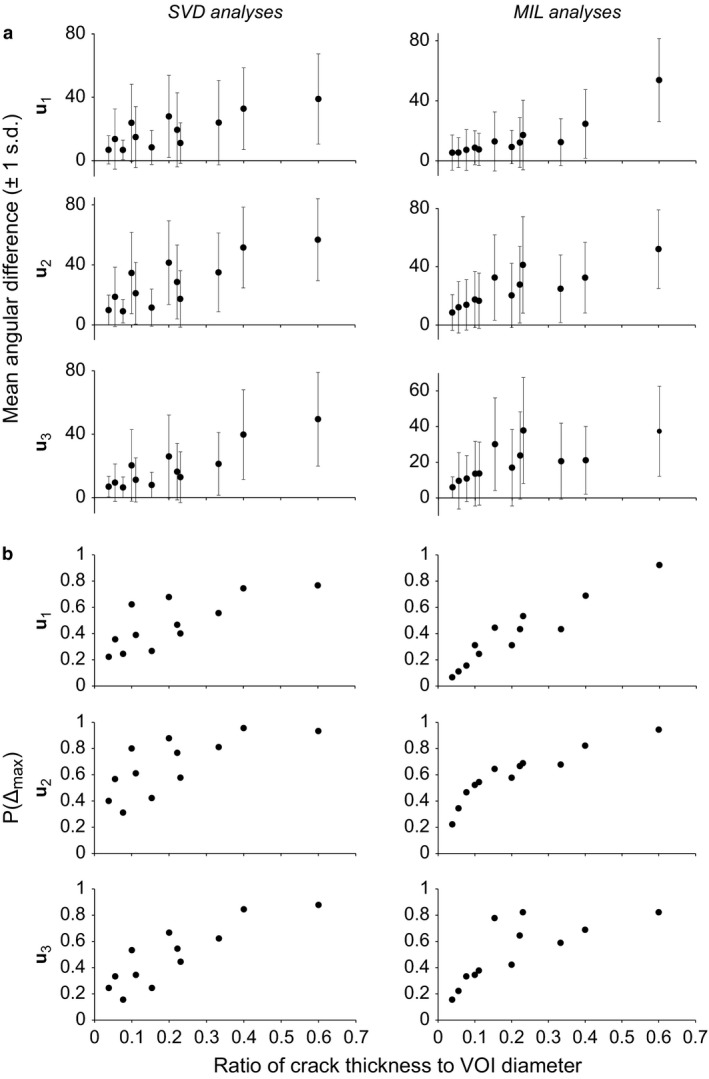
The effect of cracks on vector variables describing the cancellous bone fabric tensor. (a) In terms of the angular differences from the pristine sample. (b) In terms of P(Δ_max), the proportion of instances where the maximum acceptable difference was exceeded.

The effect of crack orientation

Crack orientation had a largely consistent effect on the results for both scalar and vector variables, calculated with both SVD and MIL methods (Fig. 4a,b). Overall, the error decreased as the crack orientation became more parallel to the orientation of the primary fabric direction, u ₁. There were a few exceptions to this general pattern (two of which are illustrated in Fig. 4c,d); in these cases, error tended to increase as the crack approached being parallel to u ₁, although this was typically only slight.

Figure 4.

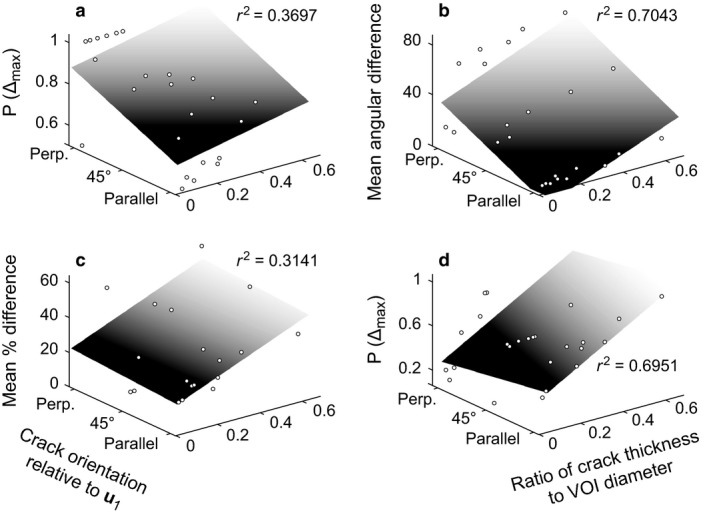
The effect of crack orientation on the quantification of the cancellous bone fabric tensor, as illustrated with several exemplar cases. These three‐dimensional plots tease apart the general patterns shown in Figs 2 and 3, to illustrate how crack orientation (relative to the primary fabric direction) also influences the results of quantitative analysis. (a) Proportion of excessively erroneous instances for degree of anisotropy in SVD analyses. (b) Mean angular difference for the orientation of the primary fabric direction in SVD analyses. (c) Mean percentage difference for positive error in elongation index in MIL analyses. (d) Proportion of excessively erroneous instances for the orientation of the secondary fabric direction in MIL analyses. By and large, the general pattern was that demonstrated in (a) and (b), where error markedly decreases as the crack becomes more parallel to the orientation of the primary fabric direction, although exceptions did exist, as illustrated in (c) (little decrease with more parallel orientation) and (d) (slight increase with more parallel orientation). For illustrative purposes, planes were fitted to the data (and associated r ² values calculated) assuming a coding of parallel orientation = 1, 45° orientation = 2, perpendicular orientation = 3, using the Curve Fitting Toolbox in MATLAB (version 8.0, MathWorks, Natick, MA, USA).

Discussion

The simulations performed in this study sought to examine the effect of including cracks in a VOI on the quantitative analysis of cancellous bone architecture. It was found that, in general, as the size (thickness) of the crack relative to the size of the VOI decreased, so too did the mean difference between pristine and cracked samples, in terms of both scalar (fabric anisotropy and elongation index) and vector (principal fabric directions) variables. The margin of error about the mean also tended to decrease as relative crack size decreased. As a consequence, the proportion of instances in which the maximum acceptable difference was exceeded, P(Δ_max), also tended to decrease as relative crack size decreased, although the decrease for the scalar variables tended to be only slight. This result was expected, as the crack is occupying a smaller proportion of the total volume of cancellous bone being analysed, and thus obscuring less of the actual structure. The orientation of a crack relative to the underlying cancellous bone fabric was also shown to have an influence on the magnitude of error encountered; in general, as the crack became more parallel to the primary fabric direction (u ₁), the error decreased.

Despite these trends, even at the smallest relative size of crack tested (crack thickness = 3.8% of VOI diameter, and VOI diameter many times greater than trabecular spacing), the magnitude of error often remained substantial, when both mean difference and error about the mean are taken into consideration. Furthermore, P(Δ_max) was still considerable, at least 18% for scalar variables and at least 11% for the orientation of principal fabric directions (with the exception of the direction of u ₁ in MIL analyses, for which it was 6.7%). That is, there was still a considerable probability that calculated scalar parameters were more than 10% off their true value, and calculated vectors were more than 10° off their true orientation. This sizeable degree of uncertainty and error involved would hence effectively preclude meaningful interpretation of the specimen. Although the present study did not simulate cracks finer than 0.18 mm across (or finer than one‐half mean trabecular spacing), the trends observed in Figs 2 and 3 suggest that even at smaller crack thicknesses, there may still be significant potential for error.

Before drawing any conclusions, it is important to bear in mind the limitations of the current study. For the sake of simplicity, cracks were simulated under a particular set of assumptions regarding shape (planar geometry), extent (extending the whole way through a VOI) and number (only a single crack in a given VOI), and their effect was assumed to be of occlusion only. More complex crack manifestations were not investigated. Moreover, all analyses were made at fine to medium spatial scales; the effect of cracks on the analysis of large VOIs that occupy a large portion of an articular condyle, for example (as in the studies of Ryan & Walker, 2010; Scherf et al. 2013), remains untested. It is conceivable that variations in the above parameters could have different effects on the results of quantitative analysis, but this would need to be the subject of further, more detailed study. An additional complexity is the possibility of differential displacement of otherwise well‐preserved portions of cancellous bone on either side of a crack.

Notwithstanding these factors, the results of this study do suggest that caution should be exercised when quantitatively analysing cancellous bone architecture in fossil or archaeological specimens. When selecting specimens for cancellous bone architectural analysis, the best approach would be to carefully inspect potential specimens for cracking (using a magnifying glass or microscope if necessary), and select the specimen or specimens that have suffered the least amount of taphonomic degradation. In some situations, it may be possible for a researcher to visually identify cracks from even the finer end of the thickness spectrum investigated in the present study, and thus immediately reject a specimen from consideration. However, a number of complicating factors can exist. Most importantly, cracks may be present within the specimen that have not yet reached the surface: these cracks are invisible to the researcher until the bone is actually CT scanned. Secondly, fine hairline cracks at the surface, which may be able to be easily seen in relatively young specimens, may be less easily discerned in older fossils, especially if they are obscured by matrix, consolidant or other material. Thirdly, the researcher may not always have multiple specimens among which to choose the best specimen for study; for example, if there is only one femur specimen known for a given extinct species, then that specimen would have to be studied if anything is to be learnt at all for that species. It is therefore of great importance to not only visually inspect a potential specimen for cracking in hand sample, but to also inspect the resulting CT scans before attempting a quantitative analysis. Ideally, even if cracks are found to be present, they should be avoided in a VOI for analysis, regardless of their size or the method used to quantify the cancellous architecture. If this is not feasible, for instance for the purposes of achieving a consistently positioned VOI in comparative studies (Fajardo & Müller, 2001; Kivell et al. 2011), then the VOI used should be as large as possible, although this may in turn introduce bias through inconsistent VOI sizes used across samples (Kivell et al. 2011; Lazenby et al. 2011).

Author contributions

P.J.B., R.S.B. and D.G.L. conceived the study design. P.J.B., C.J.C. and S.A.H. collected CT scan data. All authors contributed to data analysis, interpretation and drafting of the manuscript. All authors approved the final draft.

In this study, the CT scans were segmented using the algorithm of Bernsen (1986), as implemented in ImageJ (Landini, 2008; Landini et al. 2016; note that the implementation operates on 8‐bit images only). This algorithm is a binary pixel classifier, identifying whether a given pixel in an image belongs to the foreground (bone tissue, assigned a value of 1) or background (intertrabecular spaces, assigned a value of 0). Moreover, it takes into consideration only pixels within the focal pixel's local neighbourhood (a ‘window of interest’), the size of which is given by a pre‐specified radius. By considering an image in terms of local regions, and moving the window of interest from pixel to pixel, this approach can overcome variations in brightness or contrast across an image, which can present difficulties to global thresholding approaches that consider an entire image simultaneously. The steps used by the algorithm for each pixel are as follows.

1. Calculate the local contrast (C _local) of the pixels within the local neighbourhood of the focal pixel, equal to the difference between maximum and minimum grey values in the neighbourhood: C _local = value_max − value_min.

2. If C _local equals or exceeds a pre‐specified contrast threshold (C _thresh), then the segmenting threshold is set as the mid‐grey value of the pixels within the local neighbourhood, which is the average of the maximum and minimum grey values in the neighbourhood: M = ½(value_max + value_min). This is then used to classify the focal pixel as either belonging to the foreground (value_focal ≥ M) or background (value_focal < M).

3. If C _local is less than C _thresh, then the focal pixel is classified according to whether the mid‐grey value of the pixels in the local neighbourhood is brighter or darker than the mid‐point of the 8‐bit spectrum: if M ≥ 128, it belongs to the foreground, if M < 128, it belongs to the background.

The exact values for the window radius and contrast threshold used to segment the scans in the present study varied from specimen to specimen, and were chosen based on visual comparison of the original vs. segmented scans.