A multilevel framework to reconstruct anatomical 3D models of the hepatic vasculature in rat livers

Abstract

The intricate (micro)vascular architecture of the liver has not yet been fully unravelled. Although current models are often idealized simplifications of the complex anatomical reality, correct morphological information is instrumental for scientific and clinical purposes. Previously, both vascular corrosion casting (VCC) and immunohistochemistry (IHC) have been separately used to study the hepatic vasculature. Nevertheless, these techniques still face a number of challenges such as dual casting in VCC and limited imaging depths for IHC. We have optimized both techniques and combined their complementary strengths to develop a framework for multilevel reconstruction of the hepatic circulation in the rat. The VCC and micro‐CT scanning protocol was improved by enabling dual casting, optimizing the contrast agent concentration, and adjusting the viscosity of the resin (PU4ii). IHC was improved with an optimized clearing technique (CUBIC) that extended the imaging depth for confocal microscopy more than five‐fold. Using in‐house developed software (DeLiver), the vascular network – in both VCC and IHC datasets – was automatically segmented and/or morphologically analysed. Our methodological framework allows 3D reconstruction and quantification of the hepatic circulation, ranging from the major blood vessels down to the intertwined and interconnected sinusoids. We believe that the presented framework will have value beyond studies of the liver, and will facilitate a better understanding of various parenchymal organs in general, in physiological and pathological circumstances.

Introduction

The liver is the largest internal organ of the human body (Mitra & Metcalf, 2012). It has a unique macro‐ and microvascular system, profoundly determining blood flow distribution and regulation. In contrast to other organs, it comprises two afferent vessels, namely the hepatic artery (HA) and the valveless portal vein (PV). This dual blood supply ramifies throughout the liver into consecutive blood vessel generations and finally merges into sinusoids, the liver‐specific fenestrated capillaries. After passing this capillary bed, blood drains into the systemic circulation via the hepatic venous (HV) tree (Braet & Wisse, 2002; Roskams et al. 2007; Abdel‐Misih & Bloomston, 2010; Debbaut et al. 2012a).

At the macrolevel, previous research on liver angioarchitecture focused on automated segmentation, branching pattern analysis and visualization of the hepatic vascular trees. This resulted in a number of novel algorithms with various applications, ranging from extracting and representing the 3D branching morphology (Wan et al. 2000; Op Den Buijs et al. 2006; Debbaut et al. 2014; Morales‐Navarrete et al. 2015), the algorithmic generation of realistic hepatic vascular systems (Schwen & Preusser, 2012), preoperative liver surgery planning (Soler et al. 2001; Selle et al. 2002) to modeling the impact of partial hepatectomy (Debbaut et al. 2012b). Segmentation algorithms were typically optimized for the venous systems, as the hepatic artery required higher imaging resolutions (Soler et al. 2001; Selle et al. 2002; Op Den Buijs et al. 2006; Schwen & Preusser, 2012). However, in the case of impaired blood flow conditions (e.g. cirrhosis), it is also vital to segment the hepatic arterial network to gain more insight in the pathogenesis. Furthermore, ramification patterns were usually assumed to consist merely of bifurcations (Op Den Buijs et al. 2006; Schwen & Preusser, 2012). This assumption is rather imprecise in the case of rats, whose portal vein has been shown to trifurcate (Martins & Neuhaus, 2007).

At the microanatomical level, the prevailing theory concerning the hepatic substructure is the classic hexagonal lobule, established by Kiernan (1833). This model describes hexagonally shaped lobules which are presumed to be organized in a tessellated pattern. The central vein (CV), a terminal tributary of the hepatic vein, constitutes the central axis of the lobule. The portal triads (PTs) are situated at the periphery, between the corners of adjacent liver lobules. Each triad contains a bile ductule, a portal venule and hepatic arteriole. The blood flow through the lobule is thus oriented centripetally (Debbaut et al. 2012a). However, this blood flow cascade remains a simplification of the complex reality (McCuskey, 2000; Kan & Madoff, 2008; Debbaut et al. 2012c).

In addition to the hexagonal lobule model, several other functional liver units have been published in the literature [e.g. the primary and secondary lobule of Matsumoto et al. 1979 and the hepatic acinus of Rappaport et al. (Rappaport et al. 1954; Rappaport, 1958)]. Characteristic for all these models is that they represent a simplification of the true complexity of the three‐dimensional (3D) structure of the liver microcirculation as demonstrated by Debbaut et al. (2012a).

More detailed 3D anatomical knowledge of the entire liver vasculature across different length scales is therefore essential to understand its function, its hemodynamics, and its role in various liver pathologies (e.g. liver cirrhosis).

Previously, vascular corrosion casting (VCC) in combination with high‐resolution micro‐CT (μCT) scanning provided unique insight into the hepatic vasculature, covering both macro‐ and microcirculation. Detailed 3D reconstructions of human and rat livers allowed accurate morphological and geometrical analysis down to a resolution of 1–2 μm (Van Steenkiste et al. 2010; Debbaut et al. 2011, 2012b, 2014; Peeters et al. 2015). Current limitations of the casting technique include perfusion difficulties, especially for microcirculatory perfusion, and the reactivity of casting resins with other chemical compounds and surrounding tissue (Krucker et al. 2006; Verli et al. 2007). Also, Debbaut et al. (2012b) experienced technical difficulties while dual casting rat livers, and geometrical data on all vascular trees (HA, PV, and HV) could only be gathered by splitting the protocol over two rat livers (one to obtain the PV and HV systems, and one to retrieve the HA system). In addition, Kline et al. (2014) noted functional evidence of the existence of shunts between the HA and PV in rats in normal and various pathological conditions. It was hypothesized that these arteriolo‐portal venular shunts (occurring between branches of approximately 50 μm diameter) function as a one‐way valve‐like mechanism, i.e. allowing flow only from the HA to the PV and not vice versa. Due to these shunts, dual liver casting of rodents (i.e. simultaneous casting of HA and PV) may be problematic when contrast‐based differentiation between the supplying blood vessels is desired. Confocal microscopy of immunostained liver tissue has proven to be applicable for imaging 3D geometries at the microlevel down to a resolution of 0.2 μm (White et al. 1987; Dickie et al. 2006; Hoehme et al. 2010). This method can also provide information about structures other than the microvascular network, such as connective tissue and the biliary network (Hammad et al. 2014). 3D reconstructions of microvascular hepatic networks using IHC in mice have shown that anatomical geometries with a height up to 100 μm can be achieved (Hoehme et al. 2010). A bottleneck of conventional immunohistochemistry and confocal microscopy, however, is the limited penetration depth of antibodies and photons. With the advent of chemical clearing technologies and advanced 3D immunohistochemistry, various methods emerged to overcome both limits (Richardson & Lichtman, 2015).

As both VCC (with μCT scanning) and IHC (with confocal imaging) still face a number of challenges and more detailed morphological data on the liver vasculature is needed, the aim of this study was to optimize and combine the VCC and IHC protocols in a rat liver model. The VCC protocols were revised to allow dual casting of rodents, thereby retrieving all the required geometrical data from a single rat liver. Differences with previous work (Debbaut et al. 2012b) included usage of another casting resin (PU4ii) and contrast agent (Lipiodol), adapting the casting sequence (sequentially), and increasing the reproducibility of the VCC protocol. IHC methods, on the other hand, were tailored specifically to the rat vascular system and supplemented with a chemical clearing technology to increase the visualization depth. Combining the complementarity of both techniques enabled us to set up multilevel models, which allow the macro‐ as well as the microvasculature of the rat liver to be examined accurately in 3D. Such detailed 3D models are fundamental to a better understanding of the angioarchitecture in normal liver conditions, but they can also be extended to study liver diseases (cirrhosis, hepatocellular carcinoma, etc.).

In addition, we implemented an alternative 3D ordering algorithm, based on the diameter‐defined Strahler system of Jiang et al. (1994), to present and quantify the branching topology in a logical manner.

Materials and methods

Animals

Male Wistar rats (n = 5) with a body weight ranging between 250 and 400 g were kept in cages at a constant temperature and humidity in a 12‐h controlled light/dark cycle, with food and water provided ad libitum. All the procedures were approved by the Ethical Committee of the University Hospitals Gent and Leuven (Belgium).

Vascular corrosion casting

Animals (n = 2) were anesthetized by intraperitoneal injection of 130 μL 100 g⁻¹ pentobarbital (Nembutal, Ceva Sante Animale, Brussels, Belgium). Next, the upper thorax and abdomen were shaved, and a combined midline thoracotomy and laparotomy was performed to expose the liver. Heparin (0.3 mL; 5000 U mL⁻¹) (Heparine Leo, Leo Pharma, Lier, Belgium) was injected intrasplenically with a 26‐gauge (G) needle (Terumo, Leuven, Belgium) to prevent clotting. The PV and abdominal aorta (AA) were cannulated with a 14‐G and a 22‐G catheter (Terumo, Leuven, Belgium), respectively. Additional measures to support precise catheterization included ligatures, tissue glue and clamping of the PV proximal to the inserted catheter. After cannulation, the thoracic aorta (TA) and renal arteries (RA) were clamped to force the arterially injected resin to flow into the HA. Several interventions were made to the procedure to reduce the amount of air bubbles in the vascular replicas, including the introduction of a three‐way stopcock (Discofix; B. Braun, Melsungen, Germany), vacuuming the resin solution before injection (4 min), and priming the syringe with resin solution. The casting resin was prepared just before injection. It consisted of PU4ii and Hardener (VasQtec, Zurich, Switzerland), 27% ethyl methyl ketone (EMK; Merckx, Darmstadt, Germany), color dyes (yellow and blue for the HA and PV system, respectively), and 15% Lipiodol (Guerbet, Roissy‐CdG, France). The contrast agent Lipiodol was only added to the HA casting resin to enhance the contrast between the HA system and the venous systems on the μCT images.

The AA and PV were injected sequentially (AA followed by PV) and manually with approximately 20 and 30 mL of the HA and PV resin mixtures, respectively. To avoid bloating of the microcirculation, a probe (portex polythene tubing, internal diameter 1.67 mm and outer diameter 2.42 mm; Fisher Scientific, Loughborough, UK) was inserted into the caudal vena cava via the right atrium to facilitate outflow drainage. Following the injection, the thoracic caudal vena cava (CVC), AA and PV were clamped to prevent resin leakage during polymerization. In addition, special attention was paid to avoid manipulation of the specimen during polymerization.

The specimen was left undisturbed for approximately 72 h to allow polymerization at room temperature (RT). Subsequently, the casted liver was macerated using a 25% potassium hydroxide (KOH) bath for about 5 days. After maceration, the vascular replica was flushed with distilled water and laid to dry under a vented hood during 5 days.

X‐ray imaging was performed using a high‐resolution μCT scanner developed in‐house (HECTOR) (Center for X‐Ray Tomography (UGCT), Ghent University, Belgium) (Masschaele et al. 2013).

The resulting μCT dataset (resolution of 40 μm) was processed using mimics software (Materialise, Leuven, Belgium) to obtain segmentations and 3D reconstructions of the macrocirculation (Debbaut et al. 2014). Algorithms including dynamic region growing and smart expand were supplemented with morphological (closing, opening) operations to obtain the vascular systems. Several manual adjustments (e.g. multislice editing) were additionally carried out to optimize the segmentations and calculate the 3D reconstructions (Fig. 1A). A geometrical analysis was performed to quantify the branching topology (see Morphological analysis of the macrocirculation ).

Figure 1.

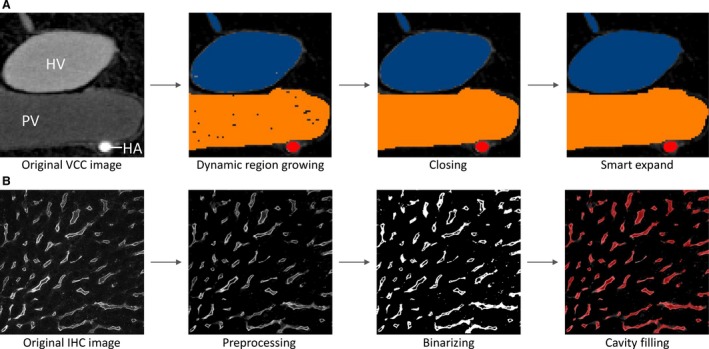
(A) Segmentation pipeline of the macrocirculation obtained by vascular corrosion casting (VCC) and μCT scanning: (i) original image with three different gray values for hepatic artery (HA), portal vein (PV), and hepatic vein (HV) is exposed to (ii) a dynamic region growing; (iii) subsequently a closing operation is performed; (iv) which is then followed by smart expansion (of the borders) and slight manual operations. (B) Segmentation pipeline of the microcirculation obtained by immunohistochemistry (IHC) and confocal laser scanning: (i) original image is (ii) preprocessed; (iii) thereafter binarized and despeckled, and finally (iv) a morphological cavity‐filling algorithm and several morphological operations (opening, closing, remove small objects) are executed.

Afterwards, a smaller sample (approximate dimensions 2.5 × 2.5 × 2.5 mm³) was dissected from the right medial lobe of the cast to investigate the microcirculation. Scanning electron microscopy (SEM; JEOL JSM‐5600LV, Jeol, Zaventem, Belgium) and microscope imaging (Olympus SZ Stereo microscope with Colorview 1 camera and cell^d software, Olympus, Hamburg, Germany) were performed to assess the filling of the microcirculation. Subsequently, the microcirculation sample was re‐scanned at a resolution of 1.89 μm. Thresholding of the μCT datasets – using mimics – enabled accurate 3D reconstructions of the microvascular network. To quantify the microcirculation (see Morphological analysis of the microcirculation ), an even smaller sample with the dimensions 350 × 350 × 200 μm³ was virtually dissected in‐between portal triads. Special care was taken to exclude blood vessels other than sinusoids.

Immunohistochemistry

Animals (n = 3) were anesthetized by intraperitoneal injection of 130 μL 100 g⁻¹ pentobarbital (Nembutal®, Ceva Sante Animale, Brussels, Belgium). The chest and abdomen were shaved, and a combined midline thoracotomy and laparotomy were performed. The pericardium was incised and the heart was exposed. Central arterial access was obtained by inserting a flushed 22‐G butterfly needle (Medicare, Ghent, Belgium) in the apex of the left ventricle. To allow exsanguination of the animal, the right atrium was opened by a small incision in the right auricle. To avoid occlusion of the vasculature by clots or vasospasm, the animal was first perfused with the physiological saline Krebs (37 °C) at 100 mmHg. After 10 min, the perfusate was switched to 4% phosphate‐buffered paraformaldehyde for 20 min.

After perfusion fixation, a hepatectomy was performed. The lobes of the excised liver were separated and immersed in the same fixative for 2 h on an orbital shaker (100 rpm) at room temperature (RT). Subsequently, the liver lobes were washed in phosphate‐buffered saline (PBS; 0.01 m, pH 7.4) and stored in PBS with 0.01% sodium azide (NaN₃).

The right medial lobe was cut with a vibratome (Microm HM650V; Thermo Scientific, Waltham, MA, USA) to 350‐μm slices. The other dimensions were adjusted by means of a razorblade to create slices of approximately 5 × 5 × 0.35 mm³. The samples were washed in PBS/0.2% Triton X‐100 (3 × 10 min) and permeabilized in PBS/0.2% Triton X‐100/20% dimethylsulfoxide (DMSO) at 37 °C for 2 h, following a protocol adapted from Renier et al. (2014). Thereafter, the samples were washed in PBS/0.2% Tween‐20 with 10 μg mL⁻¹ heparin (PTwH) (3 × 10 min), and incubated in a blocking buffer, containing bovine serum albumin (Sigma‐Aldrich, St. Louis, MO, USA) and normal horse serum (Nodia, Boom, Belgium) at 37 °C for 3 h. Following a sample wash in PTwH (3 × 10 min), immunostaining was initiated by incubating with primary antibody to stain viable endothelial cells (1/40 RECA‐1; Serotec, Kidlington, UK) for 24 h at 37 °C. The samples were then washed in PTwH (4 × 15 min and 2 × 30 min) and incubated with secondary antibody (1/150 Donkey anti‐mouse CY3; West Grove, PA, USA) at 37 °C for another 24 h. Thereafter, the samples were washed in PTwH (4 × 15 min and 2 × 30 min).

To resolve the limited imaging depth of the samples encountered with traditional IHC, part of the CUBIC clearing method (Susaki et al. 2014, 2015) was adapted to optimize IHC of rat liver samples. The samples were incubated overnight in ScaleCUBIC‐2 at RT, which is a mixture of sucrose, urea, water, 2,2,2‐triethanolamine, and Triton X‐100. ScaleCUBIC‐2 increases the transparency of the tissue and minimizes light scattering by matching the refracting index, while preserving fluorescent signals. Control samples were not cleared using CUBIC and were stored in PBS + NaN₃ after IHC.

After the IHC protocol, the samples were imaged using a Nikon A1R confocal laser scanning microscope (Nikon; Tokyo, Japan) at a voxel resolution of 0.63 × 0.63 × 1.4 μm³ with a 40× Plan Fluor air lens with extra‐long working distance [numerical aperture (NA) 0.6; Working distance (WD) 3.6–2.8 mm; Nikon Instruments, Paris, France] or a resolution of 1.28 × 1.28 × 1.3 μm³ using a 20× Plan Apo air lens (NA 0.75; WD 1 mm; Nikon Instruments). During acquisition, a linear Z intensity correction was applied to adjust the laser intensity with increasing imaging depth. Preprocessing of the image datasets included correcting the intensity decay due to photo‐bleaching with histogram matching (Bleach correction; Fiji), denoising the images for Poisson and Gaussian noise (PureDenoise, Luisier et al. 2011); Fiji plugin), executing a blind 3D deconvolution (PSF generator, Kirshner et al. 2013), 3D iterative deconvolution; Fiji plugins), and enhancing local contrast by applying the 3D contrast limited adaptive histogram equalization (CLAHE) algorithm.

Automated segmentation of the vascular network was achieved with the software DeLiver developed in‐house, which is linked to the open‐source libraries VTK and ITK. The software builds on the principles used by the tiquant Software (Hammad et al. 2014; Friebel et al. 2015), but was expanded to detect and remove background noise more accurately to cope with the variable quality of our confocal images, to improve the automated segmentation pipeline (especially near imaging borders), and to adjust and tune graph settings for better visualization and statistical interpretation.

Basically, segmentation entailed binarizing the images using adaptive Otsu thresholding, filtering noise, and executing a morphological cavity‐filling algorithm to segment the lumens of the sinusoids. Additional morphological operations (opening and closing) were performed to smooth structures and remove small disconnected objects (Fig. 1B). A geometrical analysis was carried out to quantify the morphological parameters (see Morphological analysis of the microcirculation ). The 3D reconstruction of the segmented datasets was performed using the commercial software package mimics.

Morphological analysis of the macrocirculation

The morphological analysis of the macrocirculation (VCC datasets) was performed in DeLiver by applying graph theory. By means of a 3D thinning algorithm, the skeleton of the segmented vasculature tree (HA, PV and HV) was acquired and converted to a graph structure. Such a graph is composed of intersection nodes and branches (Fig. 2A). A branch consists of multiple nodes and edges connecting adjacent nodes. For each node of the graph, the radius was measured using a best‐fit diameter approach. This was implemented by calculating the normal plane for every node and subsequently measuring the radius in this plane in eight radially evenly distributed directions. The best‐fit radius was then obtained by averaging over the eight radii.

Figure 2.

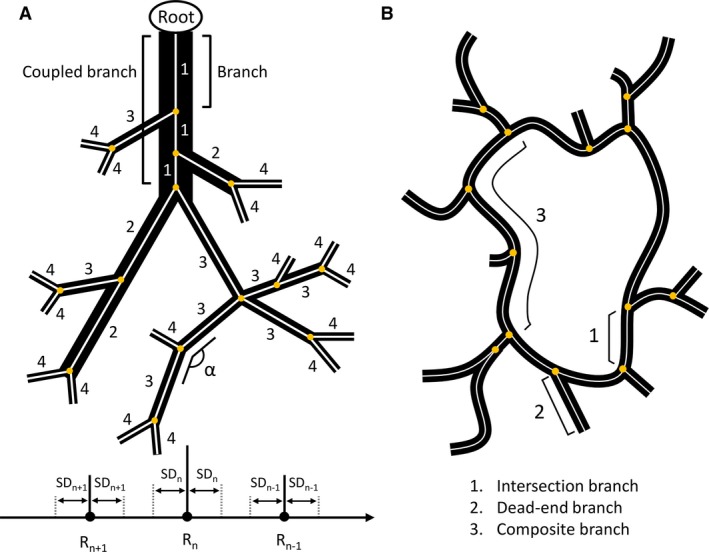
Schematic illustration of the morphological analysis approach. (A) Example of a converged diameter‐defined top‐down ordering method for the macrocirculation (black structures). The analysis is applied to the skeleton of the macrocirculation (white), whereby intersection nodes are indicated as yellow circles. Branches are connected to at least one intersection node. For the ordering method, branches (e.g. three branches belonging to the inlet) are first combined into one coupled branch if the tapering of the radius is higher than 0.7 and the angle (α) between the last segment (last five nodes) of the parent branch and the first segment (first five nodes) of the daughter branch is greater than 160°. The generation numbers are then iteratively reordered based on the mean radius of the coupled branches compared with the mean radii (R _n) and standard deviations (SD _n) of the generations. (B) Simplified 2D sinusoidal network (black) with its skeleton (white). Intersection branches (1) are found in‐between adjacent intersection nodes (yellow circles). Dead‐end branches (2) are only connected to one intersection node. Composite branches (3) are located between two intersection nodes, which are not part of a dead‐end branch and usually comprise several intersection branches. Image is based on Hammad et al. (2014).

The resulting graph allowed the mean radius for each branch to be extracted. We implemented a diameter‐defined top‐down ordering method to assign generation numbers to the branches, partially based on the method used by Jiang et al. (1994). First, the inlet (= root) was selected and branches were combined into coupled branches based on radius tapering and angle deviations. Branches (starting at the root) were linkable if two conditions were met: (i) the ratio of the mean radius of the daughter branch to the mean radius of the branches belonging to the parent branch was larger than 0.7; and (ii) the angle between the last segment (last five nodes) of the parent branch and the first segment (first five nodes) of the daughter branch (α; Fig. 2A) was larger than 160°. At each intersection node, only the most suitable daughter branch (least tapering and largest angle) was coupled to the parent branch, from which point on, it was considered part of the parent branch. The tapering ratio and branching angle were manually calibrated based on the 3D branching topology of the largest vessels. Secondly, generation numbers (n) were assigned to the coupled branches, starting with generation 1 at the inlet (= root), whereby coupled parent branches always have generation numbers lower than their corresponding daughter branches. Thirdly, the assigned generation numbers were iteratively reordered based on the mean radius of the branches. For each iteration, the mean radius (R _n) and standard deviation (SD_n) were calculated for every generation (n). One iteration entailed comparing the mean radius of a branch, initially belonging to generation n, with the range [R _n − SD_n; R _n + SD_n]. If its value did not lie within that range, but instead was lower than (R _n+1 + SD_n+1) or higher than (R _n−1 − SD_n−1), its generation number was increased to n + 1 or decreased to n−1, respectively. This process was repeated – always starting at the inlet (= generation number 1) – until the generation numbers of the branches converged and remained unchanged.

Morphological analysis of the microcirculation

The morphological analysis of the microcirculation (VCC and IHC datasets) was performed using DeLiver. Similar to the macrocirculation analysis, a 3D thinning algorithm was used to obtain the skeleton of the segmented microvasculature, which was converted to a graph structure (Fig. 2B). The resulting graph allowed several morphological parameters of the microcirculation to be extracted, including the average radius of the sinusoidal vessels, branch lengths, the tortuosity, and the porosity of the vascular network. The radius was measured using the best‐fit diameter approach. Branch lengths were measured as the cumulative Euclidian distance between successive nodes belonging to the branch. The tortuosity of a branch was defined as the ratio of the total branch length to the Euclidian distance between the first and last node of the branch. The 3D porosity of the vascular network was calculated as the total sinusoidal volume divided by the volume of its envelope. To limit the impact of outliers, dead‐end branches and branches within a 5‐μm range of the imaging borders were automatically excluded from the morphological analysis.

Results

Vascular corrosion casting reveals the hepatic angioarchitecture at different scales

The resulting vascular replicas, including all seven rat liver lobes, were densely filled (Fig. 3). A smaller sample was dissected from the right medial lobe to visualize the branching topology at the microlevel (Fig. 3C). Near the liver surface, hepatic lobules could be visualized using stereomicroscopy (1.25×; Fig. 3D), and sinusoids using SEM (Fig. 3E), indicating complete filling of the microcirculation.

Figure 3.

Vascular corrosion cast of a rat liver, showing the liver lobes. The medial lobe is formed by the right medial lobe (RML) and left medial lobe (LML). The right liver lobe is formed by the superior right lateral lobe (SRL) and the inferior right lateral lobe (IRL). The left liver lobe is formed by the left lateral lobe (LLL). The caudate lobe (CL) is formed by the anterior caudate lobe (ACL), posterior caudate lobe (PCL) and caudate process (CP). (A) The portal venous (and part of the hepatic venous) system is colored blue, whereas the hepatic arterial (and part of the hepatic venous) system is pigmented with a yellow dye. A smaller sample was dissected from the right medial lobe (RML) to study the microcirculation. (B) Yellow‐colored parts of the intestines' arterial system are also included (see black arrow) as well as the portal venous catheter (see dashed arrow). (C) Dissected microvascular sample of a rat liver. (D) Microscope image of the cast surface, illustrating the liver lobules (i.e. cloud‐like structures in the image; black contour). (E) SEM‐image of the sinusoids.

As a result of the arterially added contrast agent (Lipiodol), segmentations and 3D reconstructions of the different hepatic trees (HA, PV and HV) based on the μCT‐images could be carried out semi‐automatically. Sequential casting – HA followed by PV – was of great importance to achieve this, as the contrast agent that entered the PV through the arteriolo‐portal shunts was flushed afterwards. Hence, the contrast agent not only allowed the PV to be distinguished from the HA system, but additionally assigned a different gray value range to the HV system due to mixing of the injected AA (with contrast agent) and PV resin. Because the gray value ranges of the hepatic trees did not overlap, all morphological data could be gathered from a single rat liver (Fig. 4).

Figure 4.

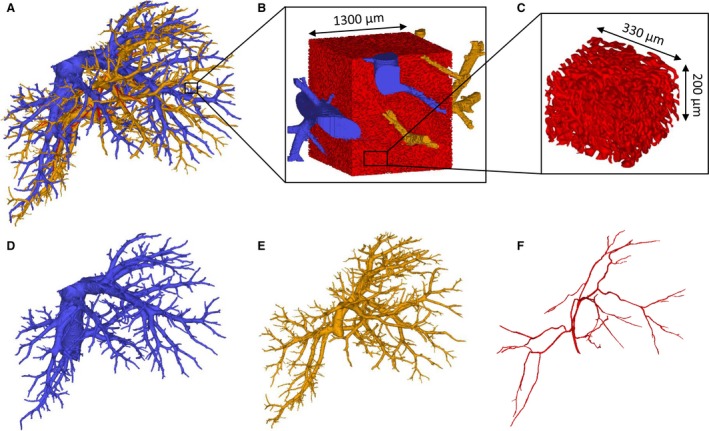
3D reconstructions of a rat liver. (A) The three vascular trees. (B) 3D reconstruction of the microcirculation containing sinusoids (red), afferent and efferent microvessels. (C) A virtually dissected and reconstructed 3D cube containing only sinusoids with the dimensions 350 × 350 × 200 μm³. (D) Hepatic venous system. (E) Portal venous system. (F) Hepatic arterial system.

Each of the vascular trees was classified according to its diameter‐defined branching topology (Fig. 5), resulting in six, eight and nine generations for the HA, PV and HV tree (including CVC), respectively. In contrast to the HV and PV system, fewer blood vessel generations could be segmented for the HA system because of the limited μCT scanning resolution and the fact that HA vessels typically have smaller diameters than PV and HV vessels. The HV mean radii decreased from 2.73 (CVC) to 9.61 × 10⁻² mm, the PV radii from 1.18 to 9.84 × 10⁻² mm, and the HA radii from 1.80 × 10⁻¹ to 4.36 × 10⁻² mm.

Figure 5.

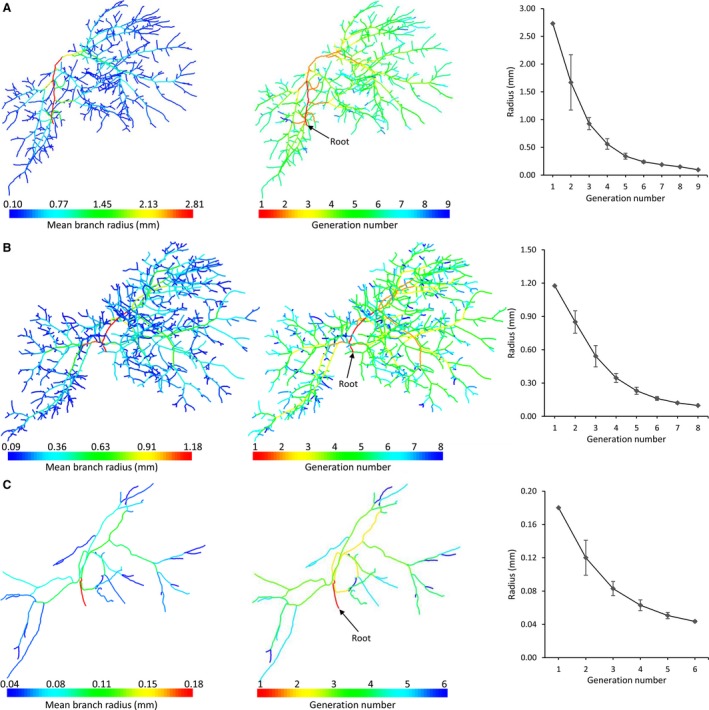
Diameter‐defined top‐down ordering method for the vascular trees, resulting in nine, eight and six generations for the (A) hepatic vein [HV; including caudal vena cava (CVC)], (B) portal vein (PV), and (C) hepatic artery (HA), respectively. The HV mean radii decreased from 2.73  (CVC) to 9.61 × 10⁻² mm, the PV radii from 1.18 to 9.84 × 10⁻² mm, and the HA radii from 1.80 × 10⁻¹ to 4.36 × 10⁻² mm.

Following 3D reconstruction of the high resolution μCT images of the microvascular sample, 3D cubes with the dimensions 350 × 350 × 200 μm³ were virtually dissected (Fig. 4C), and only contained sinusoids. The afferent and efferent microvessels were omitted from the morphological analysis. According to the VCC data (n = 3), the mean radius measured 7.3 ± 0.93 μm, the mean branch length was 27.3 ± 2.7 μm, and the mean tortuosity was 1.2 ± 0.01 for 6603 composite branches. The porosity of the sinusoidal network in the virtually dissected samples was 31.9 ± 6.7%.

Immunohistochemistry reveals the hepatic micro‐angioarchitecture

When imaging 350‐μm‐thick non‐cleared liver slices using confocal microscopy (with air lenses), the imaging depth is typically limited to a maximum of 50–60 μm (Fig. 6A). By clearing the tissue using the CUBIC protocol, the imaging depth was increased by approximately a factor of 5 (300–350 μm). However, at imaging depths of 150–200 μm, the desired stained blood vessels were no longer unambiguously identifiable on the recorded confocal images of the cleared tissue (later referred to as the information retrieval depth; Fig. 6B). Furthermore, uniform image intensity can be maintained over the entire information retrieval depth (about 150 μm) in cleared liver tissue, whereas the intensity decay is already noticeable at about 40–50 μm in non‐cleared liver slices.

Figure 6.

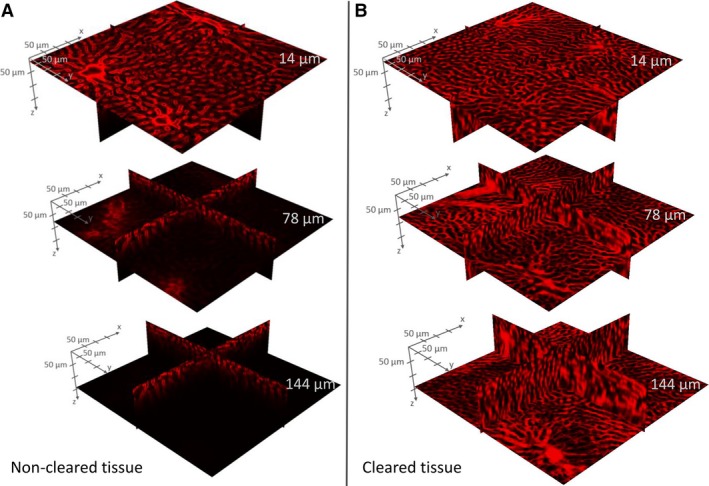
Example of intensity decay in Z stacks acquired through confocal microscopy. Non‐cleared sample (A) versus cleared liver tissue sample (B) at imaging depths z = 14, 78 and 144 μm. For cleared liver tissue, a uniform image intensity can be maintained over the entire information retrieval depth, whereas the intensity decay is clearly noticeable for non‐cleared liver samples.

Automated segmentation of the sinusoidal network was executed for the cleared datasets (Fig. 7A). A 3D reconstruction of the segmented microcirculation is depicted in Fig. 7B. By means of graph theory (Fig. 7C–F), a morphological analysis – similar to the segmented μCT dataset – was carried out to quantify the microcirculation in the case of non‐cleared (NC; n = 3) and cleared (C; n = 3) liver samples. The mean radius measured 3.9 ± 0.3 μm (NC) and 4.6 ± 0.2 μm (C), the mean branch length was 20.2 ± 0.4 μm (NC) and 20.1 ± 1.4 μm (C), and the mean tortuosity was 1.3 ± 0.1 (NC) and 1.3 ± 0.02 (C) for 1183 (NC) and 8436 (C) composite branches, respectively. The porosity of the sinusoidal network in the virtually dissected samples equaled 21.2 ± 0.7% (NC) and 21.2 ± 0.6% (C).

Figure 7.

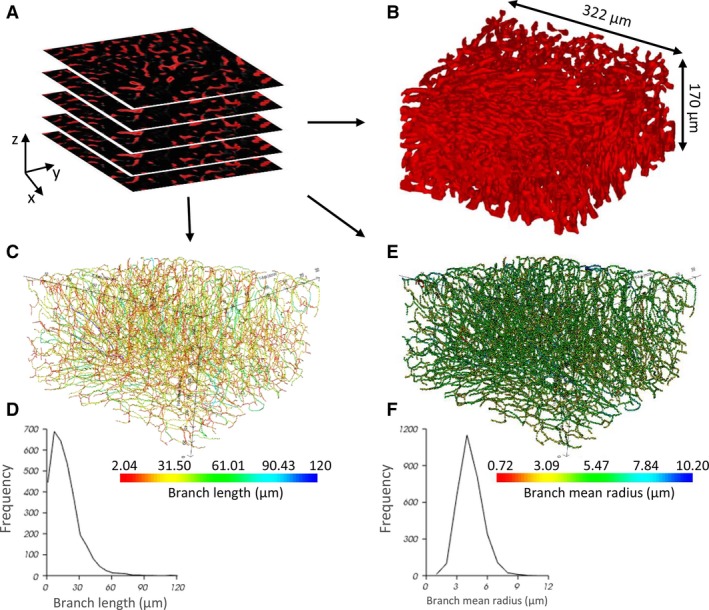
The morphological graph analysis pipeline for microsamples obtained by immunohistochemistry (IHC) and vascular corrosion casting (VCC). (A) Segmented 2D image stack of a IHC cleared sample (B) 3D reconstruction of the segmented structures (dimensions 322 × 322 × 170 μm³). (C) Visualization of the network graph, where the edges are colored according to their branch length. (D) Histogram of the branch length. (E) Visualization of the network graph, where the nodes are colored according to their branch mean radius. (F) Histogram of the branch mean radius.

An overview of the geometrical parameters of the sinusoidal network, obtained by IHC and VCC, is depicted in Fig. 8.

Figure 8.

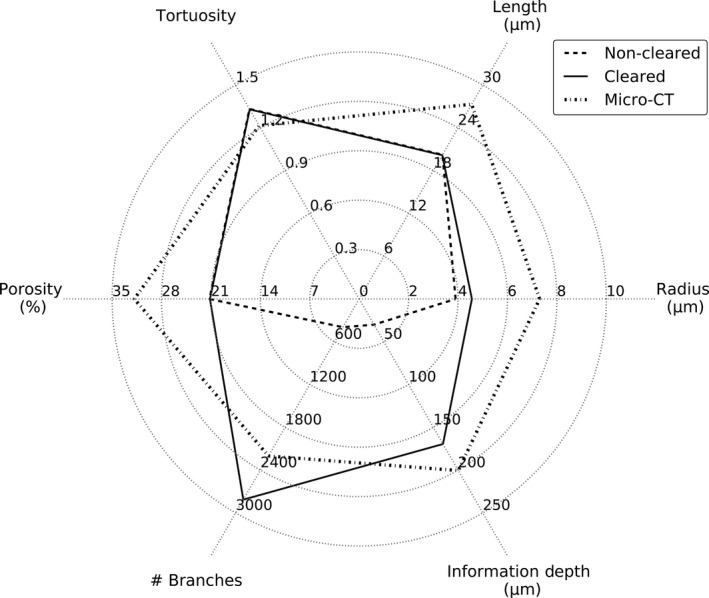
Overview of the measured morphological parameters in case of non‐cleared (n = 3), cleared (n = 3) and μCT (n = 3) samples. Calculated parameters include (i) the mean composite branch radius; (ii) mean composite branch length; (iii) mean composite branch tortuosity; (iv) number of composite branches for each sample; (v) mean sinusoidal porosity; and (vi) the maximal information retrieval depth.

Discussion

In this study, a multilevel framework was presented to study the hepatic vasculature in rats. We optimized the VCC protocol and IHC technique to setup detailed multilevel models. With dual VCC, we were able to semi‐automatically obtain accurate 3D macrocirculatory models of all vascular trees (HA, PV and HV) from a single rat liver. This was accomplished by sequential casting (PV followed by HA) with arterially added contrast agent, allowing the three vascular trees to be distinguished from another on the μCT images. By implementation of a novel 3D ordering algorithm, which is partially based on the diameter‐defined Strahler system of Jiang et al. (1994), we were able to classify these vascular trees according to their diameter‐defined branching topology. Furthermore, it was shown that reconstructing 3D geometries of the microvasculature is feasible using both VCC and IHC. To enhance the limited imaging depth of conventional IHC (< 50–100 μm), we adapted the CUBIC clearing protocol, thereby reaching unprecedented information retrieval depths of 150–200 μm in (rat) liver tissue.

Our data clearly highlight the strengths, weaknesses and complementarity of both techniques. Submicron resolution can be achieved with IHC, thereby allowing visualization of smaller vessels which are harder to detect with VCC. However, the information retrieval depth (150–200 μm) – even after clearing – remains restricted to the microvasculature level. VCC, on the other hand, is not limited in depth resolution, and scales from the macro‐ down to the microlevel.

A quantitative comparison of relevant morphological parameters of the microcirculatory data obtained from rats and mice is provided in Table 1. Most data are available on radii. Our values are within the same range but at the higher end for rats. This is most likely due to the applied imaging technique (3D confocal microscopy), as our values are in excellent agreement with recent data imaged using the same technique in mice. This suggests that quantitative analyses of the microcirculation can be carried out by combining IHC and CUBIC.

Table 1.

Comparison of microcirculatory morphological parameters with available and relevant data obtained from rats and mice

Microcirculation
Species	Imaging technique	Radius (μm)	Length (μm)	Tortuosity	Porosity (%)	Reference
Rat	3D confocal microscopy	4.6 ± 0.2	20.1 ± 1.4	1.3 ± 0.02	21.2 ± 0.6	Peeters et al. (2016)
Rat	Intravital fluorescence microscopy	3.9 ± 1.4				Li et al. (2010)
Rat	Intravital fluorescence microscopy	4.25 ± 0.05				Vollmar et al. (1998)
Rat	In vivo fluorescence microscopy	3.2 ± 0.05 – 4.15 ± 0.1				Komatsu et al. (1990)
Rat	Scanning electron microscopy	2.95 ± 0.09 – 3.55 ± 0.15				Wisse et al. (1985)
Rat	Serial photomicrography	3.15 ± 0.06				Koo et al. (1975)
Mouse	3D confocal microscopy	4.8 ± 2.25	23.93 ± 5.9		15.3 ± 3.9	Hammad et al. (2014)
Mouse	3D confocal microscopy	4.75 ± 2.25	16.45 ± 4.22			Hoehme et al. (2010)
Mouse	High‐resolution in vivo microscopy	2.95 ± 0.05 – 3.65 ± 0.05				MacPhee et al. (1995)

The slight variation between the mean radius of the cleared and not‐cleared IHC samples can be attributed to tissue heterogeneity or the reported marginal expansion of tissue due to the CUBIC protocol (Susaki et al. 2014, 2015; Richardson & Lichtman, 2015).

Comparing the mean radii of the IHC and VCC morphological analyses of the microcirculation (Fig. 8), on the other hand, suggests bloating of the rat liver capillaries in the case of VCC. Even though special care was taken to avoid this phenomenon, manually injecting the resin always resulted in a minor expansion of the sinusoids. Absolute quantitative measurements of the microcirculation are thus recommended with IHC, while VCC can be used for relative measurements. The VCC samples may still provide valuable information on the branching topology as larger samples of the microcirculation – compared with IHC – can be examined. Especially in the case of liver pathologies, this VCC feature may be relevant for example for recognizing shunting vessels at both the macro‐ and the micro‐level.

The radii of the macrocirculation, which were reported in this paper as a function of their generation number, were compared with the literature and appeared to be in agreement (Martins & Neuhaus, 2007; Debbaut et al. 2012b; Peeters et al. 2016). A strict one‐on‐one comparison between the radii of the generation numbers and literature values was impossible due to our novel classification system and the lack of anatomical knowledge about the ramifying hepatic vasculature in rats. Therefore, we chose to compare the diameters of the 1st generation with the available literature (see Table 2).

Table 2.

Comparison of macrocirculatory morphological parameters with available and relevant data obtained from rats

Macrocirculation
Species	Diameter HA (mm)	Diameter PV (mm)	Diameter HV (CVC) (mm)	Reference
Rat	0.36	2.36	5.46	Peeters et al. (2016)
Rat	0.27	2.2	5.3	Debbaut et al. (2012b)
Rat	0.29 ± 0.11	2.54 ± 0.62	5.33 ± 0.49	Martins & Neuhaus (2007)

We measured the radii using the best‐fit diameter approach. Generally, radii are estimated using the largest inscribed sphere principle. However, venous blood vessels and sinusoids may have an ellipsoidal shape. Measuring the radius using the largest inscribed sphere principle would – in that case – result in an underestimation. Our best‐fit calculation tries to take into account this ellipsoidal character, as radii are measured by averaging over eight uniformly spaced directions.

A number of noteworthy pitfalls were encountered when optimizing the techniques.

For VCC, removal of air bubbles in the resin and setting up the dual casting sequence appeared the most troublesome. The former was resolved by subjecting the final mixture to vacuum for at least 4 min and using an air buffer in the injecting syringe. Optimizing the dual casting sequence was hampered by the apparent existence of arteriolo‐portal venular shunts with a one‐way valve mechanism between the rat HA and PV (Kline et al. 2014). We believe that the presence of these shunts – which are extensively described by Kline et al. (2014) – prevented us from simultaneous casting of the PV and HA. When casting simultaneously, contrast agent (injected in the HA) always ended up in the PV, thereby preventing a contrast‐based differentiation between the supplying blood vessels. We hypothesize that the contrast agent from the HA was able to flow through arteriolo‐portal shunts to the PV. However, our analysis did not allow these shunts to be identified, possibly due to low imaging resolutions of the macrocirculation. Sequential casting – HA followed by PV – resolved this issue, as contrast agent entering the PV during the HA injection was flushed out by the subsequent PV injection.

For IHC, next to CUBIC, two other clearing methods were found potentially eligible during a feasibility study: CLARITY (Tomer et al. 2014) and iDISCO (Renier et al. 2014). However, we found that passive CLARITY had limited compatibility with immunostaining due to impairment of epitope recognition, as the clearing step inherently precedes the immunostaining process. The long time required to complete the clearing process (2 weeks) is another disadvantage. The iDISCO protocol proved to be a very potent clearing method, enabling deep antibody visualization (200–300 μm); however, the main impediment was considerable tissue shrinkage and deformation (approximately 80% shrinkage for a normal hepatic lobe). The tissue deformation resulted in severe undulation of the tissue slices, severely hampering confocal microscopy.

Several challenges were identified while setting up the presented framework. Regarding the IHC technique, one major difficulty remains the limited diffusion of (primary) antibody penetration. Using CUBIC, we reached unprecedented imaging depths of about 300–350 μm of a nuclear counterstain (TO‐PRO3; Thermo Fisher Scientific). The information retrieval depth (depth at which the antibody staining could be visualized) was, however, restricted to 150–200 μm. It is hypothesized that the high extracellular matrix content, which is on the whole not affected by clearing, is responsible for this impediment of the free diffusion of macromolecules. This is particularly present in hepatic tissue, as opposed to other organs such as the brain or spleen (Lee et al. 2016), despite prolonged incubation times and high antibody concentrations. The explanation for the discrepancy between imaging and information retrieval depths is that antibodies can use the lumen of the large vessels to penetrate more deeply into the tissue. We hypothesize that even greater information retrieval depths may be attained by either actively injecting antibodies or using electro‐induced antibody diffusion systems (Kim et al. 2015; Li et al. 2015; Lee et al. 2016). Additionally, we estimate that – with readjustments to the applied settings and even to the hardware (the use of more high‐end confocal microscopes, e.g. two‐photon excitation microscopy) – an even higher imaging and information depth (> 500 μm) might be achievable in liver tissue.

Concerning VCC, the hypothesis that the casting resins caused significant tissue shrinkage, was refuted (Kratky & Roach, 1984; Krucker et al. 2006; Debbaut et al. 2014). We hypothesize that the known shrinkage of the cast resin was compensated for by the pressure exerted during the injection of the polymer. However, at the microlevel, bloating of the sinusoids was observed due to the injection pressure, even though resin outflow was ensured. Pressure‐regulated resin injection, particularly in the PV, may help resolve this issue.

Conclusions

Two complementary protocols were presented, optimized for application to the rat liver. Hereby, we were able to reconstruct detailed 3D geometries of the hepatic circulation, allowing the quantification of the entire length scale of the vasculature, which is essential for modeling of vascular trees for hemodynamic analysis. We applied these protocols to the liver, an organ that is unique in many respects and thus posed organ‐specific challenges (e.g. dual blood supply), but we are convinced that the presented protocols will have value beyond the study of the liver (and its pathology) and will impact the study of parenchymal organs in general in both physiologic and pathologic circumstances.