Measuring Residential Segregation With the ACS: How the Margin of Error Affects the Dissimilarity Index

Abstract

The American Community Survey (ACS) provides valuable, timely population estimates but with increased levels of sampling error. Although the margin of error is included with aggregate estimates, it has not been incorporated into segregation indexes. With the increasing levels of diversity in small and large places throughout the United States comes a need to track accurately and study changes in racial and ethnic segregation between censuses. The 2005–2009 ACS is used to calculate three dissimilarity indexes (D) for all core-based statistical areas (CBSAs) in the United States. We introduce a simulation method for computing segregation indexes and examine them with particular regard to the size of the CBSAs. Additionally, a subset of CBSAs is used to explore how ACS indexes differ from those computed using the 2000 and 2010 censuses. Findings suggest that the precision and accuracy of D from the ACS is influenced by a number of factors, including the number of tracts and minority population size. For smaller areas, point estimates systematically overstate actual levels of segregation, and large confidence intervals lead to limited statistical power.

Introduction

With little doubt, the replacement of the census long form with the American Community Survey (ACS) has led to many advantages for researchers, policy makers, and community leaders. In particular, the increased number of data releases has opened up a variety of new applications that were formerly contingent on the more timely and detailed data that the ACS provides. However, the complex design of the ACS creates greater demands on the user, who may falsely assume that ACS data can be used and interpreted in the same manner as decennial census data. One of the more difficult aspects that users must address is the presence of sampling error across all ACS data products.

To aid data users, the U.S. Census Bureau produces a measure of sampling error—the margin of error (MOE)—and includes it with all tabulations to allow users to quickly compute confidence intervals (CIs) for ACS estimates. Although MOEs are new, sampling error is not. The census long-form estimates, which the ACS replaced, were also based on samples and hence were subject to sampling error, albeit to a lesser extent. With those data, if CIs were needed, they had to be calculated from a set of instructions and tables located at the end of each volume (e.g., U.S. Census Bureau 2002). Many users never looked at them, perhaps because the 10-year intervals between censuses made it more plausible that changes—even to small groups or in small places—reflected reality rather than sampling error.

Given the growing ethnic and racial diversity in places throughout the United States, questions about small populations and small places have become increasingly important. The so-called third demographic transition is projected to have wide-ranging effects on American society as large numbers of younger and less-affluent minorities replace older, more-affluent non-Hispanic whites (Lichter 2013). These changes are occurring, or have already occurred, in large, historically diverse metropolitan areas (see Frey 2011). Minorities are also moving to smaller urban and rural areas (Lee et al. 2012), some of which have had historically little experience with diversity (Massey 2008; Zúñiga and Hernández-León 2005).

Although a vast array of outcomes will be affected by increasing diversity, one source of concern is the growth or development of racially homogenous, segregated residential areas. Segregation has been associated with a wide range of negative outcomes that are difficult to escape, such as limited mobility and poverty, even after generations have passed (e.g., Massey and Denton 1993). A large proportion of the growing nonwhite population can be attributed to Latino immigrants, who have experienced less segregation than the most segregated minority— specifically, blacks (Logan and Stults 2011)—although Latinos are subject to limited residential mobility and poor neighborhood environments in areas of high immigrant concentrations (Alba et al. 2014). Also of concern is that, in general, places with more recent experiences with diversity or immigration tend to have higher levels of segregation (Hall 2013; Lichter et al. 2010), although for Latinos, micropolitan areas have lower segregation than metropolitan areas (Wahl et al. 2007).

This study focuses on the complexities the ACS introduces for measuring segregation. Existing studies using five-year ACS data files have largely neglected sampling error. Other issues with the ACS also may affect hypothesis testing and the comparability of ACS data with decennial census products (e.g. Frey 2010; Iceland et al. 2013; Kershaw and Albrecht 2014; Lichter et al. 2012; Reardon and Bischoff 2011). Of particular concern are smaller places, which are most likely to be adversely affected by sampling error yet stand to benefit most from the more frequent data releases through ACS. As the minority population continues to gravitate toward new areas of the country, researchers will increasingly need to broaden their inquiries to encompass a more diverse set of areas. An important but unanswered question is, How useful can ACS data be for measuring segregation in such areas, particularly after sampling error has been taken into account?

Sampling Error and the MOE

The MOE, a measure of statistical error due to sampling that arises from using a subset of a population to generalize to the entire population, is calculated for each ACS estimate using the successive differences replication method,¹ which is used to compute variance estimates for systematic samples of finite populations (Fay and Train 1995; Wolter 1984). This simulation method is useful for complex applications, such as the ACS and the Current Population Survey (CPS), because variances “can be computed without consideration of the form of the statistics or the complexity of the sampling or weighting procedures” (U.S. Census Bureau 2009a:12-1).

The effort to provide more accurate measures of sampling error is related to its increased presence in the ACS. Coefficients of variation, which measure reliability by taking the ratio of the standard error (of an estimate) to the estimate. For the ACS, they are estimated to be 1.41 times larger, on average, than for the 2000 long form for larger units (like counties) but are as much as two times larger for tracts (Starsinic 2005). The lower ACS reliability is directly related to the smaller sample size of the five-year ACS. For example, the 2005–2009 ACS contains 15 million cases, but 19.4 million would be needed to reach the average sampling rate of the 2000 census long form (Metropolitan Philadelphia Indicators Project 2012). Apparently, the original conception of the five-year estimates was to replicate the sample sizes and accuracy of the census long form, but budget constraints have limited the implemented sample sizes (Williams 2013). Although yearly sample sizes were increased starting in 2011, from 2.9 million to 3.54 million households (U.S. Census Bureau 2011a), these increases were needed partly to offset the growing U.S. population. Nevertheless, even the larger sample is too small to closely replicate standard errors of the long form.

Some issues with the ACS result from the lack of current, highly accurate population controls. Because the long-form was collected simultaneously with the short form, 100 % population counts are available to adjust the sample data at a very low level of geography: contiguous block groups with as few as 400 sample persons (Schindler 2005; U.S. Census Bureau 2002). However, the ACS uses population controls from the Population Estimates Program (PEP), resulting in lower-quality estimates. Although PEP uses the decennial census counts as a baseline, it must rely on other sources of data, such as birth and death records, in an attempt to bring estimates up to date. Consequently, PEP estimates are much less accurate than a full census. They are also not available at finer units of analysis: estimates are produced for counties or groups of small-population counties and for subcounty areas, such as minor civil divisions (MCDs) and incorporated places. As a result, adjustments are made using a two-step process with these much larger units (see U.S. Census Bureau 2009a,b).² Although the process increases the reliability of ACS population estimates (Starsinic 2005), the result is a less-refined product than comparable long-form data.

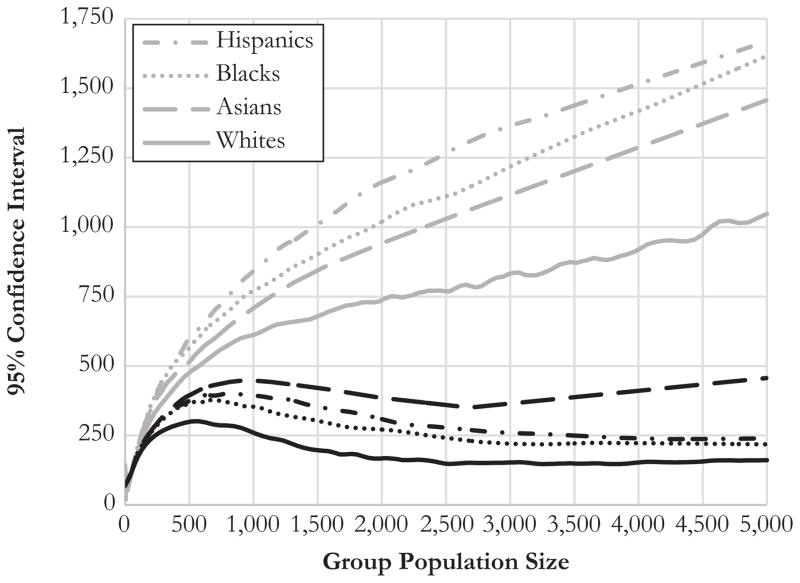
To illustrate the effects of sampling error on the precision of ACS population estimates, Fig. 1 displays LOESS curves fitted to 95 % confidence intervals (CIs)³ by tract population. Two sets of CIs are displayed. The first is computed using the MOEs and population estimates from the 2005–2009 ACS. The second is calculated using the same ACS population estimates but with the techniques designed for the 2000 Summary File 3 (SF3) tabulations (see U.S. Census Bureau 2002).⁴ The intent is to provide a comparison of the two data sets that is direct as possible. All CBSA tracts in the 2005–2009 ACS are used, and separate curves are fit for non-Hispanic blacks, non-Hispanic whites, non-Hispanic Asians, and Hispanics.⁵

Fig. 1.

LOESS curves for the tract 95 % CIs by group population size using the 2005–2009 ACS population estimates with CIs computed using ACS MOEs (gray lines) and Census 2000 SF3 instructions (black lines). Groups are plotted with the same type of line (e.g., unbroken, long dash, and so on) for both data sets

This comparison illustrates a few important points. First, the SF3 CIs (graphed using black lines) are much smaller than are those from the ACS (gray lines). Starting at a population of 0, the average CI is 144 for the ACS, whereas it is 68.5 when the SF3 method is used (U.S. Census Bureau 2002). ACS estimates are smaller for only those tracts with very small group populations—between 3 and 50 people. The ACS CIs drop rapidly after 0 but then increase, whereas the SF3 CIs begin to increase directly after 0, albeit at a slightly lower rate than the ACS CIs. At roughly 500–750 people, the two sets of estimates begin to trend in different directions: the ACS CIs continue to increase, while the SF3 CIs begin to decrease and eventually stabilize. Consequently, the difference between the two estimates grows larger as the size of the groups’ populations grows. At 3,000 population, for example, the Hispanic SF3 CI spans 259 people, whereas the ACS CI is 1,365 people—a difference of 427 %. Overall, the ACS estimates are much less precise, especially for tracts with zero population and large minority populations.

Among the CIs for the specific racial/ethnic groups, whites have the smallest CIs using both methods, except at very low populations. The ranking of the minority groups differs using the two approaches: for the SF3, the next-smallest CIs belong to blacks, followed by Hispanics and then Asians; for the ACS, the next-smallest intervals generally belong to Asians, then blacks and Hispanics.

However, when the groups’ population sizes are not taken into account, a different story emerges. Whites, on average, have the largest CIs from the ACS (at a width of 789 people) and the smallest CIs from the SF3 (with 181 people). In the ACS, Asians have the smallest average CIs (253), followed by blacks (429) and then Hispanics (512). Using the SF3 method, Asians have the second-smallest CIs (183), followed by blacks (213) and then Hispanics (243). The variation in the size of the CIs is due to the unequal overall sizes of the groups, their distribution across tracts, and the strong relationship between the size of the CI and the size of the group population.

Although many data users ignore sampling error for long-form tabulations, there is a greater need to incorporate sampling error into analyses using ACS data. More sampling error occurs in ACS, which translates into increased levels of uncertainty in measures of segregation.

Nonsampling Error in the ACS

Additionally, we find the potential for increased amounts of nonsampling error in ACS estimates. The aforementioned use of population controls is designed to minimize error by keeping the ACS aligned with the most accurate intercensal estimates available (through the PEP). However, using these estimates rather than full counts from a census can lead to random and systemic errors, particularly for smaller areas and some ethnic/racial groups (Breidt 2006; Citro and Kalton 2007; U.S. Census Bureau 2011b; see also Passel and Cohn 2012). In addition, because the PEP’s population estimates are calibrated using decennial census data, the potential for error is greater—particularly, systematic error—as the length of time since the previous census increases.

However, compared with the 2000 long form, the ACS has less nonsampling error because of lower nonresponse and similar completeness rates. Using preliminary ACS data collected between 1999 and 2001, Bench (2003) found that although the ACS has lower self-response rates—that is, fewer people fill out and return the mailed form—the follow-up efforts are highly successful and have resulted in lower unit and item nonresponse rates. The ACS, though, follows up with nonresponders via telephone interviews and then, if needed, personal interviews for only 33 % to 66 % of the existing nonresponders (U.S. Census Bureau 2009a:4–10). By comparison, all nonresponding households were followed up with personal interviews in the 2000 census. Nevertheless, completeness ratios (which measure how well samples represent their target populations by accounting for both nonresponse and survey under/overcoverage) are similar to those from the long form (Griffin et al. 2003). The success of ACS data collection efforts are thought to be the product of a permanent and more highly skilled staff, a more manageable sample size, and improvements in data collection procedures, such as follow-up interviews for item nonresponse in returned surveys (Bench 2003). Since these initial studies, ACS response rates have increased, ranging from 97 % to 98 % between 2005 and 2012 (U.S. Census Bureau n.d.b), which likely reflects further advancements in data collection techniques.

An additional source of uncertainty in the ACS is created by its long data collection periods, which are required in order to accumulate enough cases to protect the confidentiality of respondents and obtain reliable estimates in small geographic units. The long data collection periods affect the interpretation of the estimates, which represent the average characteristics across the range of years surveyed instead of a snapshot of characteristics in time, as with the decennial census data. Accordingly, measuring changes within the time span covered by the pooled year estimates or identifying the characteristics of a place at any single point in time, is not possible. The long interval also creates a mismatch with the PEP data, which is used as a population control given that the PEP estimates correspond to the population snapshot on July 1 annually.

Differences in data collection methods and survey instruments between the decennial censuses and the ACS result in systematic differences between estimates. First, as noted earlier, the reference periods are not the same. Second, residence rules differ: the ACS uses each respondent’s current residence at the time of the survey, whereas the decennial census uses their usual residence (e.g., Cresce 2012; Griffin 2011). Third, although both sources rely on the master address file (MAF), the ACS uses additional filters, which are not needed for the decennial census, to both add and remove various sets of questionable cases. Note that the ACS draws its primary sample from the MAF in the summer preceding the year of data collection; consequently, because of additional lags in processing and data collection, the results of the 2010 census were not fully integrated into the ACS until the 2012 sample (Bates 2012; Cresce 2012). As a result, the 2010 ACS sample frame omitted 5.8 million housing units and falsely excluded another 6.4 million through its filtering process, while erroneously including 17.3 million units (Bates 2012). Much of the improvement in the 2010 census sample frame is due to the extensive fieldwork both before and after the census, which is prohibitively expensive to conduct regularly alongside ACS data collection efforts. Consequently, years further removed from decennial census MAF updates are likely to have additional nonsampling error.

Specifically regarding the measurement of race and ethnicity, evidence suggests that systematic differences exist between ACS and the 2000 census. Hispanics were much more likely to respond as “Some other race” in the 2000 census instead of “White” (Bennett and Griffin 2002). Both the Hispanic Origin and Race questions experienced revisions in 2008, which had small effects on both variables: in 2009, more Hispanic/Latino respondents reported a specific origin and, as with the comparison of the 2000 census with the ACS, were more likely to identify as white alone instead of some other race (U.S. Census Bureau 2009c). These differences may account for small changes over time.

In general, nonsampling error in the ACS can have effects on measuring segregation that are difficult to predict because they cannot be precisely measured. Although some sources of nonsampling error, such as sample completeness, do not appear to differ significantly from the census long form, other sources introduced using population controls and coverage error through outdated MAF files could have effects such as increased bias on ACS data.

The Index of Dissimilarity

Because of its prevalence in segregation research, segregation is measured with D, which is interpretable as the percentage of the minority group that would need to change neighborhoods (without replacement) in order for the two groups to be distributed evenly throughout the area as a whole. As Duncan and Duncan (1955) illustrated, D also can be interpreted as the maximum vertical difference between the Lorenz curve and a horizontal line of evenness. The formula for the D—in this case, for whites and blacks⁶—is as follows:

$${{}_{w}D}_b=100\times \frac{1}{2}\sum \left|\frac{w_i}{W}-\frac{b_i}{B}\right|.$$

In the preceding equation, i indexes tracts up to the total number in the CBSA, where b_i is the tract population count of blacks and w_i is the tract population count of whites; B and W are the total CBSA counts of blacks and whites, respectively. The final score is multiplied by 100 to convert it from a proportion to a percentage. To compute D for whites and Hispanics, or whites and Asians, the population counts of these subgroups are substituted in the formula, and the notation is changed accordingly (_wD_h and _wD_a, respectively).

Despite its popularity, a number of issues can hinder the capability of D to measure segregation. Conceptually, it is unclear whether complete evenness—a D score of 0—is the appropriate concept to use when measuring the complete lack of segregation (e.g., Cortese et al. 1976). More specifically, Winship (1977) argued that D is a mixture of random and systematic segregation. Random segregation is created through random allocation of individuals across areal units, and systematic segregation is essentially the remainder. Random segregation is problematic because it often creates an upward bias in D when the index is near its lower bound. (The opposite occurs when D is near the upper bound—producing a downward bias—although this has been studied far less.) For example, when segregation, as measured by D, is exactly 0, sampling variation will cause random deviations in w_i/w and b_i/B in the preceding equation. Because of the use of an absolute value in the formula, the index will increase. Bias is more likely to happen when D is computed from units with small sample sizes or with small minority shares (Carrington and Troske 1997; Farley and Johnson 1985; Ransom 2000).

A number of solutions have been proposed to circumvent problems stemming from random allocation. One is to adjust D in reference to a random, theoretical distribution of the two populations instead of a completely even distribution (a D score of 0). Some, mostly early studies adjusted or rescaled D to remove the random segregation component or provided a statistic to test whether D came from randomly allocated populations (Cortese et al. 1976; Winship 1977; see also Carrington and Troske 1997). Although these statistics have experienced little to no usage in the mainstream segregation literature, they are theoretically useful for studying the causes of segregation (as opposed to its effects) given that random variation in standard indices could include substantial amounts of unexplainable (random) variation (see Winship 1977).

Others have developed methods that generate the distribution of D using numerical methods, which can then be used to conduct hypothesis tests (Carrington and Troske 1997; Farley and Johnson 1985; Ransom 2000). Some studies have used simulation or resampling methods, such as jackknifing and bootstrapping (e.g., Farley and Johnson 1985; Massey 1978; see also Boisso et al. 1994); Ransom (2000) developed an asymptotic sampling distribution, which he found to closely mimic the distribution of D generated using a simulation. However, these methods are not applicable to the ACS because they do not incorporate the error terms.

Overall, this study addresses three limitations of the current segregation literature. The first concerns the accuracy and precision of ACS data for measuring segregation. In general, the quality of ACS data appears to be high. However, the ACS has a greater potential for nonsampling error, especially in years furthest from updates to the PEP and the MAF that occur with the decennial censuses. Nonsampling error will create biases in estimates, whereas the smaller sample sizes will increase the statistical noise around the estimates. Indexes computed using small numbers of sample observations or very small minority groups (or both) will also result in an upward bias to segregation estimates. The second limitation is the lack of a simple, flexible method to compute CIs and standard errors for segregation indexes from sampled data, such as ACS summary files. The third is a lack of a detailed discussion of how the precision and accuracy of D varies among areas of different sizes.

Data

The data come primarily from the 2005–2009 ACS and the 2000 and 2010 census summary files. The 2005–2009 ACS data are particularly useful because a substantial amount of time had elapsed since the full 2000 census was conducted, which made the ACS data particularly valuable. Also noteworthy is that when the 2010 census data were released, it was the most recent five-year ACS available that contained population estimates for small geographic units. Consequently, researchers wishing immediately to use 2010 census data often combined them with the 2005–2009 file for information unavailable on the short form. Data users will likely be in a similar situation with the 2015–2019 ACS and the 2020 decennial census. The 2005–2009 ACS is also valuable because it does not overlap with the 2010 census, which allows for a clear test of segregation indexes between the data sets.

The calculations of the indexes use persons in metro- and micropolitan areas or CBSAs. Two sets of CBSAs are used: (1) for broader statistical issues, all U.S. CBSAs are used to increase the scope of our arguments; (2) to provide more detailed analyses, a much smaller and more manageable set of CBSAs from New York state is used. New York state works well for this purpose because it has a wide range of CBSAs of different sizes, including 12 metropolitan areas and 15 micropolitan areas, with varying levels of diversity (see Table 1).⁷

Table 1.

Descriptive statistics and _wD_b indexes computed using two methods for CBSAsa in New York, 2005–2009 ACS, and wDb indexes from the 2000 and 2010 census

CBSA Name	Tracts	Population Point Estimates			Zero-PopulationTracts (%)	ACS, Numerical Method				Standard Calculation
		Total	Black	% Black		Lower	Median	Upper	Range	2000	ACS	2010
Metropolitan Areas
Albany-Schenectady-Troy	214	852,162	55,591	7.7	18	60.8	62.9	65.0	4.2	62.4	63.7	61.3
Binghamton	65	245,576	8,104	3.7	22	50.3	55.1	59.8	9.5	51.0	56.9	51.8
Buffalo-Niagara Falls	302	1,128,813	132,826	14.5	25	72.5	73.7	75.0	2.6	78.0	74.5	73.2
Elmira	23	88,161	4,919	6.3	9	43.8	50.4	57.2	13.5	52.6	50.9	50.1
Glens Falls	33	128,229	2,287	1.9	33	57.4	64.8	72.2	14.8	69.0	71.2	58.1
Ithaca	23	100,583	3,244	4.0	4	39.7	47.1	54.4	14.7	33.9	45.6	30.1
Kingston	49	181,510	9,761	6.4	10	47.7	52.5	57.3	9.6	43.8	52.1	41.3
New York-Northern NJ-Long Island	4,505	18,912,644	3,124,875	32.1	16	78.5	78.7	79.0	0.5	80.2	79.1	78.0
Poughkeepsie-Newburgh-Middletown	133	668,735	60,743	12.4	2	48.0	50.3	52.7	4.7	52.7	49.1	47.7
Rochester	253	1,033,026	110,767	13.4	9	65.1	66.6	68.1	3.0	67.9	66.5	65.3
Syracuse	189	645,302	46,082	8.3	21	67.2	69.1	71.1	3.9	71.4	70.5	67.8
Utica-Rome	92	293,468	12,799	4.9	25	64.4	68.2	71.9	7.5	65.4	71.2	64.7
Average	490	2,023,184	297,667	9.6	16	57.9	61.6	65.3	7.4	60.7	62.6	57.5
Micropolitan Areas
Amsterdam	16	48,632	600	1.4	25	39.7	52.1	64.9	25.3	33.7	54.7	40.0
Auburn	20	79,994	2,866	3.9	15	61.8	69.6	77.1	15.3	63.9	70.5	59.4
Batavia	15	58,208	1,231	2.3	0	30.4	42.8	55.3	24.9	44.4	36.8	41.8
Corning	30	96,674	1,418	1.5	27	37.4	46.0	54.7	17.3	36.5	46.1	38.3
Cortland	12	48,207	740	1.6	33	34.0	49.1	64.2	30.2	31.7	55.7	34.7
Gloversville	15	55,031	886	1.7	33	32.9	44.7	56.8	24.0	42.6	49.6	37.0
Hudson	20	62,217	3,052	5.5	15	52.5	63.0	73.1	20.6	59.7	63.6	56.9
Jamestown-Dunkirk-Fredonia	34	134,078	2,455	2.0	21	41.2	48.9	56.7	15.5	54.9	48.3	47.1
Malone	13	50,374	3,458	8.4	38	64.0	71.0	78.0	14.0	71.1	73.7	77.3
Ogdensburg-Massena	28	109,742	3,039	3.0	14	59.9	66.4	72.3	12.4	67.1	69.1	62.7
Olean	21	80,349	954	1.3	33	44.7	55.4	66.2	21.5	42.5	61.1	39.7
Oneonta	16	62,086	1,162	2.0	13	36.5	45.8	55.3	18.7	47.5	43.2	45.6
Plattsburgh	19	81,755	2,567	3.4	26	56.7	64.4	72.1	15.4	57.1	67.6	52.4
Seneca Falls	10	34,181	1,512	4.9	20	52.3	61.8	70.7	18.3	51.5	64.4	67.2
Watertown-Fort Drum	23	117,595	5,420	5.3	4	42.7	47.8	53.5	10.8	46.7	45.6	37.6
Average	19	74,608	2,091	3.2	21	45.8	55.3	64.7	18.9	50.1	56.7	49.2
Average of All Areas	229	940,642	133,458	6.1	19	51.2	58.1	65.0	13.8	54.8	59.3	52.9

^aCore-cased statistical areas

As commonly done in segregation research, tracts are viewed as proxies for neighborhoods (e.g., Iceland and Nelson 2008; Logan et al. 2004; Massey and Denton 1993). Metro- and micropolitan areas are viewed as independent housing markets, and a consistent set of counties is used to define the CBSAs across the three data sets. The definitions are from the December 2009 Office of Management and Budget Classification, which yields 940 CBSAs, 366 of which are classified as metropolitan.

Plan of Analysis

We use a numerical approach to compute the standard error. We directly incorporate the MOEs provided by the Census Bureau into the index by repetitively sampling from the simulated distribution of tract populations formed using the MOEs and population estimates. Thus, each sample is a possible arrangement of the population in the CBSA. D is then calculated for each arrangement. After many samples, the D scores converge on the sampling distribution of D. Consequently, this method does not involve assumptions about the shape and size of the sampling error of D or any of its components beyond those existing in Census Bureau calculations.⁸

In more specific terms, the distribution of each group’s population in each tract is normally distributed with the mean equal to the population estimate from the ACS and the standard deviation set to the estimate’s MOE/1.645. A population value is then randomly drawn (with replacement) from each tract’s distribution, and D is computed. As an extension of the standard D formula, this method computes the distribution of D, where b_i ~N(E(b_i),SE(b_i)), w_i ~ N(E(w_i),SE(w_i)), b_i ≥ 0, and w_i ≥ 0.⁹ Also, B = Σb_i, and W = Σw_i instead of the point estimates of B and W. We provide the SAS software programming code for these calculations in the appendix.¹⁰

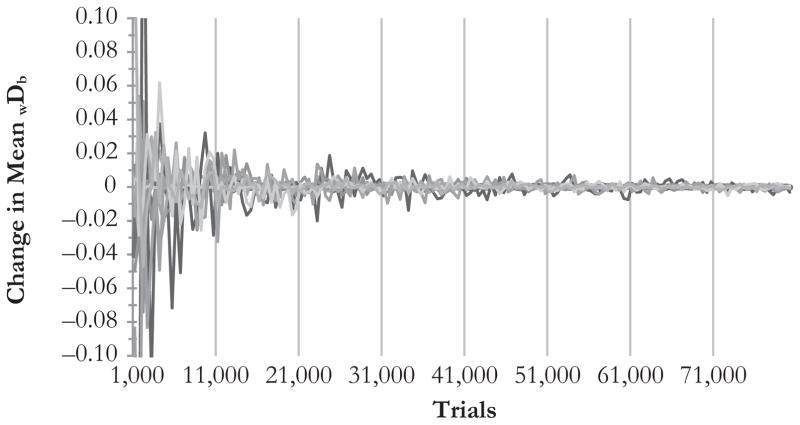
It is unclear exactly how many samples are required to obtain the most precise results using this method, but a reasonable approximation can be found. From looking at a subset of CBSAs in New York, the simulated distributions of _wD_b become stable for many areas after a few hundred trials. However, CBSAs with few tracts may not converge even after thousands of trials. Figure 2 illustrates this by plotting the change in the average¹¹ of simulated _wD_b scores after every 500 trials. Here, it can be seen that after approximately 30,000 trials, most CBSAs are not fluctuating more than +/−0.01 from the previous average, indicating a stable distribution. After approximately 50,000 trials—and much sooner for many of the larger areas—there is little change in the distribution of _wD_b. Given the degree of stability at this point, the distributions for all CBSAs and D indexes are computed using 50,000 trials.¹²

Fig. 2.

The change in mean _wD_b by trial for selected CBSAs in New York: 2005–2009 ACS

To provide an overview of the simulated distributions of D, we examine two key measures using graphical displays and regression models. The first measure is the difference between the standard D score and the median D score generated using the simulated distributions. This measure determines how much the simulated point estimates differ from those produced using the standard calculation currently used by researchers. Differences may exist due to skewness in the distribution of D as a result of the upper and lower bounds of D (Ransom 2000) but also due to nonrandom variation in tract-level error variances, as noted earlier, regarding minority population sizes (see Fig. 1). The second measure is the width of the 95 % CI of D. Although it is clear that the precision of D will be positively related to the sizes of the CBSAs, the strength and functional form of the relationship is not clear. The focal explanatory variables for both measures are the number of tracts and the size of the minority population. These are chosen because they are common attributes considered when selecting the universes for segregation studies; they are also both strongly related to the measures. Ordinary least squares (OLS) regressions are undertaken on the two measures to analyze the amount of variance in D explained by a variety of predictors. This procedure is used as a means to investigate the relative importance of factors contributing to the variation in D. Finally, D indexes computed using the 2000 and 2010 censuses are presented alongside those from the ACS for a subsample¹³ of CBSAs using _wD_b to provide a comparison of ACS indexes with those from higher-quality data sources.

The Simulated Distribution of D

Examining the results from the simulations makes clear that the distributions of D appear normal for all but the smallest CBSAs. More specifically, only those with fewer than 15 tracts are likely to have modest departures from normality, particularly those with low D scores or, to a lesser extent, high D scores. The presence of small numbers of minorities also tends to result in nonnormality. Consequently, statistics that are robust to departures from normality are used. The median of the simulated distribution is used as the measure of central tendency, and 95 % CIs are constructed by dropping 2.5 % of observations from both tails.

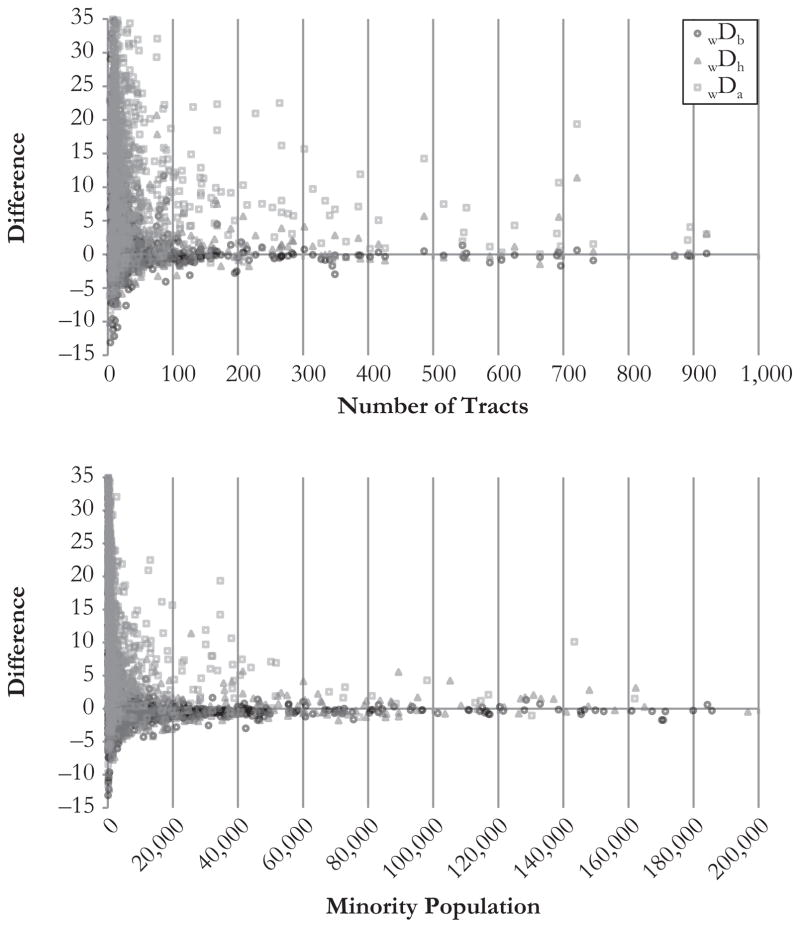
Differences between the simulated point estimate and standard D indexes can be expected given that the standard D index ignores sampling error. Figure 3 plots the difference between nonsimulated and simulated Ds for both the number of tracts and the size of the minority population. _wD_b differences tend to be tightly clustered around 0 for CBSAs with more than 100 tracts; however, for _wD_h and especially for _wD_a, more variation exists for larger CBSAs (top panel of Fig. 3). This is less true for the size of the minority population (bottom panel of Fig. 3): _wD_a still stands out in terms of some large discrepancies for CBSAs with less than 40,000 Asians; the other two indexes rarely have differences greater than +/–5 until minority populations drop below 5,000.

Fig. 3.

The difference between the standard calculation and the median of simulated scores of _wD_b, _wD_h, and _wD_a by (top) the number of tracts and (bottom) the size of the minority population for all CBSAs in the United States: 2005–2009 ACS. Both axes are limited to increase the detail for lower values

A few CBSAs have very large differences between the standard and simulated D indexes. The Pittsburgh (Pennsylvania) metropolitan area is one that stands out: it has much higher standard _wD_h and _wD_a scores but with a large population and modest numbers of Asians and Hispanics.¹⁴ What is different about Pittsburgh, however, is that it has a high percentage of zero-population estimates for minorities—in this case, 48 % for Asians and 34 % for Hispanics, compared with 26 % and 7 % for all other tracts in CBSAs. In Pittsburgh, and other areas with many zero estimates, segregation is lower using the simulated D because introducing small numbers of minorities (due to nonzero MOEs) in zero-population areas equalizes the distribution across all tracts.

Regression models are used to give further insight into the difference¹⁵ between the standard and simulated D values. R² coefficients¹⁶ are used to measure how well six factors¹⁷ affect the differences for the three D scores: the number of tracts, the total population, the size of the minority group population (corresponding to the minority group in the index), the percentage of minority group population, and the number and percentage of tracts with zero minority population estimates. Each variable is entered into the model both alone and in various combinations with other variables to facilitate a more complete discussion of the shared and independent effects of the factors.

Overall, the percentage of tracts with zero minority populations has a strongest overall effect on the difference between the two D indexes. This is particularly true for _wD_a, for which it alone explains 67 % of the variation in the difference. When comparing the full model (predictors 1, 2, 3 or 4, and 6) with one that excludes the 0 % population tracts variable, the difference in the R² coefficients shows that it independently explains 25 % (0.69 – 0.44 = 0.25) of the total variation. This is true, but to a much lesser degree, for _wD_b (52 % alone; 4 % independent) and _wD_h (34 % alone; 8 % independent). The percentage minority variable—and to a lesser extent, the size of the minority population—are also strongly related to the difference in scores, especially for _wD_h and _wD_b. The number of tracts and the total population are also related to the difference, although to a lesser degree. A simple count of the number of tracts with zero minority population has little to no effect, which is noteworthy given that the rate (of zero-population tracts) has the largest effect, and a much larger independent effect. A plausible explanation is that the effect of zero-population tracts interacts with the total number of tracts in affecting the difference in the D scores; increases in the number of zero-population tracts has larger effects as the overall number of tracts decreases.

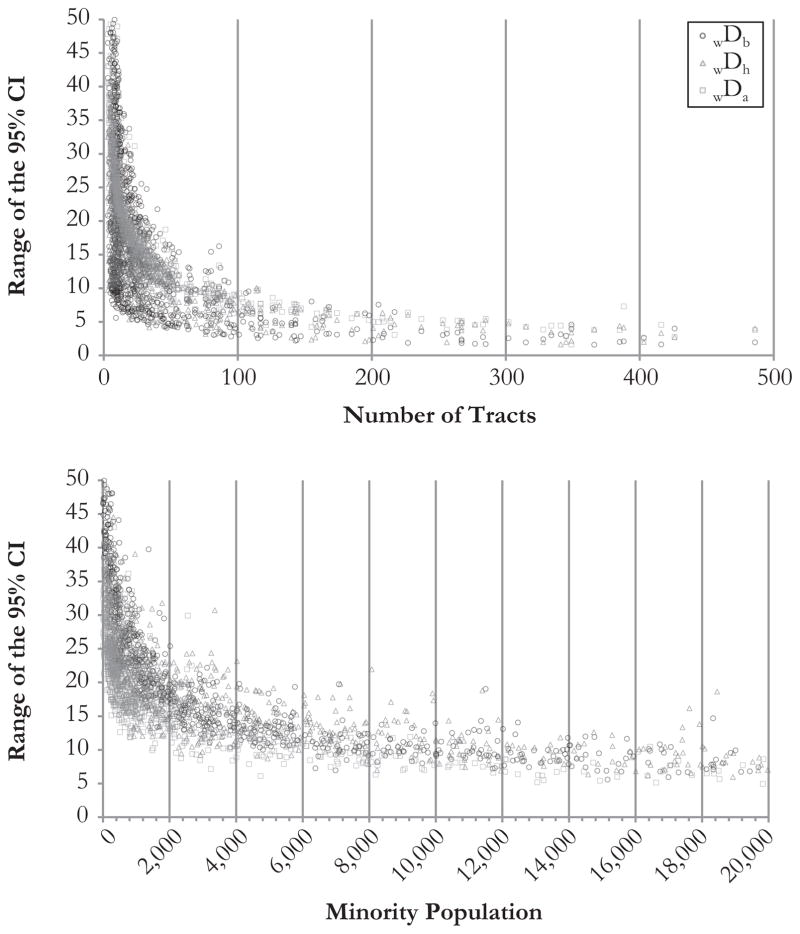
The width of the 95 % CI of D is influenced by many of the same factors as the difference between the D indexes. The number of tracts and the size of the minority population have particularly strong relationships. As seen in the top panel of Fig. 4, the size of the CIs decreases rapidly as the number of tracts increases until 50–100 tracts. After this point, the decrease tapers off until roughly 300–400 tracts, when the width of the CI remains relatively constant. A similar nonlinear relationship is evident in the bottom panel of Fig. 4 for the size of the minority group population. In this case, the slope changes most rapidly between 2,500 and 6,000 population and approaches equilibrium between 50,000 and 100,000. In this plot, the clustering of the CBSAs is more pronounced, although a few distinct outliers are also evident, especially for _wD_h. These outliers represent micropolitan areas in Texas (Rio Grande City–Roma and Eagle Pass), which have small numbers of whites and large numbers of Hispanics; because D is symmetric in regard to the order of the comparison of the groups, the numerical minority at the CBSA level is actually the best indicator of variance in D.

Fig. 4.

The range of the simulated 95 % CI for _wD_b, _wD_h, and _wD_a by (top) the number of tracts and (bottom) the minority group population for all CBSAs in the United States: 2005–2009 ACS. Both axes are limited to increase the detail for lower values

Regression models in Table 2 further explore the predictors of the 95 % CI. The minority population is most closely related to its width for two of the three indexes and accounts for 86 % to 96 % of the total variance. Its independent influence, however, is much lower (net of the number of tracts and total population), from 2 % for _wD_a to almost 30 % for _wD_b. The number of tracts and the total population are strongly related to the CIs and explain between 67 % and 93 % of the total variation. The proportion of zero-population tracts is much less related to the CI compared with the difference between the D indexes, and in this case, its effect is almost completely shared with the minority population size variables. As with the difference between D indexes, additional covariates were tested in models, all of which had small effects.

Table 2.

R² statistics from unweighted regression models^a predicting the absolute difference between the standard D index and the simulated median D index, and the simulated 95 % CI of D

Predictor(s)	Absolute Difference in D			Range of the 95 % CI of D
	wDb	wDa	wDh	wDb	wDa	wDh
(1) Number of Tracts	.10	.10	.02	.66	.93	.75
(2) Total Population	.11	.14	.03	.67	.91	.77
(1) and (2)	.11	.20	.06	.67	.93	.77
(3) Minority Population	.45	.30	.25	.93	.86	.86
(4) Percentage Minority	.49	.40	.36	.57	.44	.30
(1), (2), and (3) or (4)	.51	.44	.36	.96	.95	.93
(5) Number of Zero-Population Tracts	.01	.00	.02	.20	.47	.17
(6) Percentage Zero-Population Tracts	.50	.67	.34	.42	.15	.10
(1), (2), (3), and (5)	.51	.46	.37	.96	.95	.93
(1), (2), (3), and (6)	.56	.69	.44	.97	.96	.93
N	938	936	940	938	936	940

Note: Because the percentage minority population variable is a linear combination of the minority population and total population variables, all three variables cannot be included in the same model.

^aVariables were logged as needed to achieve normality.

These results suggest that researchers should carefully consider how to address sampling errors in D. The simulated distributions of D are largely normal. However, the point estimates of D are affected by sampling error, particularly when the size of the minority population is small and/or many tracts have an estimated zero minority population; these areas also have larger CIs. As a result, care should be taken with interpreting results for small CBSAs because they are likely to have large CIs and potentially biased scores when using the conventional formula.

Segregation in New York CBSAs and Beyond

This section focuses on New York state CBSAs and detailed comparisons between _wD_b indexes from the ACS and the 2000 and 2010 decennial censuses. Based solely on chronology, the general expectation is that D computed from the 2005–2009 ACS will fall between those from the 2000 and 2010 censuses—most likely, closer to the 2010 value—because segregation does not change rapidly enough to rise or fall substantially above or below both scores.¹⁸ It is also expected that the simulated scores will (correctly) be able to detect sizable differences with the 2000 scores because much of the value of ACS is related to its ability to detect change. Based on the previous discussion, one can also expect that smaller CBSAs with fewer minorities and more zero-population tracts will have the largest CIs.

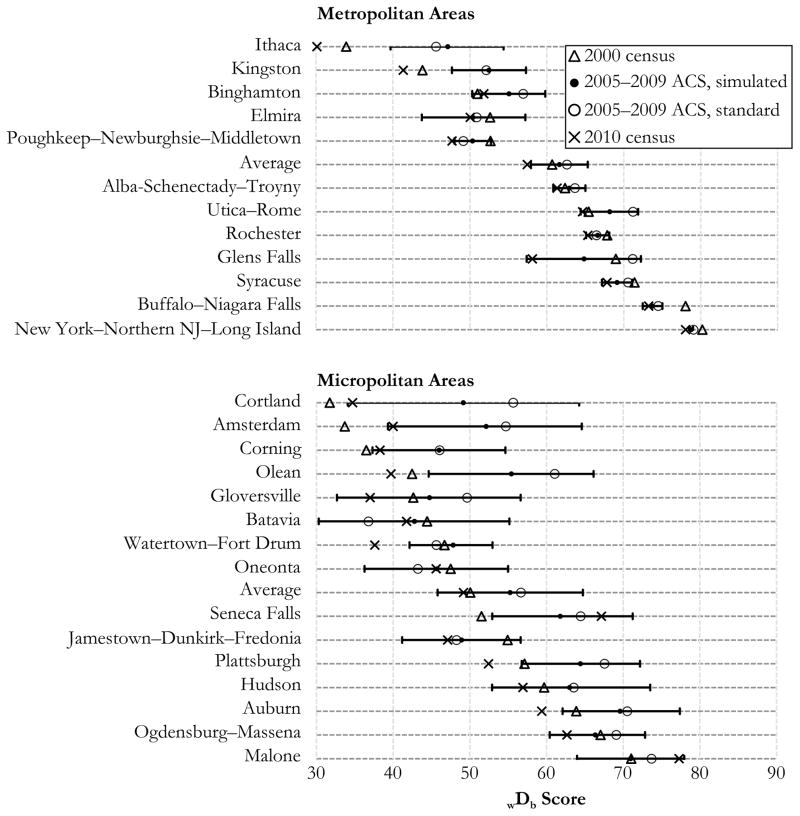
Figure 5 plots all the D indexes, including the simulated 95 % CIs. Indexes from larger New York state metropolitan areas (such as New York City, Buffalo, Syracuse, Rochester, and Albany) fit with expectations and generally have small CIs. However, in smaller metro- and micropolitan areas, ACS scores tend to perform poorly. First, the scores from the ACS tend to be higher than both of the decennial census scores. The simulated scores for micropolitan areas are, on average, 5.2 points higher than the 2000 census and 6.1 points higher than the 2010 census (vs. 0.9 and 4.1 points, respectively, for metros). When the standard calculation is used, the ACS is even further from expectations: the difference is larger by 1.4 points in both 2000 and 2010 (1.0 point for metros) in contrast to an overall decline in segregation over the 10 years, as measured by the decennial census scores (−3.2 points for micros and −0.9 points for metros). However, when using the simulated scores with CIs, some of these differences are not statistically significant, and the scores are plausible given that the CIs often overlap with one or both decennial census scores. Some exceptions are the Ithaca and Kingston metropolitan areas and the Olean micropolitan area, which have ACS scores that are larger than both 2000 and 2010 scores, even when the CIs are included.

Fig. 5.

_wD_b indexes for New York state metropolitan areas and micropolitan areas: 2000 census, 2005–2009 ACS, and 2010 census

We find a limited number of statistically significant differences between the 2000 census and ACS scores. Although the aforementioned Ithaca, Kingston, and Olean scores achieve significance, they incorrectly suggest that segregation increased when it actually decreased. This result is problematic because statistically significant change will be viewed as sufficient evidence that actual change has occurred. It is difficult to point to a specific cause for this irregularity, but one characteristic all instances of it have in common is small black populations. Only in some of the largest, most segregated metros (New York City, Buffalo, and Syracuse) is the ACS statistically significant from the 2000 census, of a realistic magnitude, and in the same direction as the change between the censuses. In four micropolitan areas (Cortland, Amsterdam, Corning, and Seneca Falls), the ACS scores were so large relative to the 2000 census scores that significance was achieved in the correct direction, although the magnitude of the increases (compared with the difference between the 2010 and 2000 censuses) was vastly overstated. A few statistically significant differences between the ACS and 2010 census exist, although with the exception to the New York metro, these are due to ACS scores that are much larger than either of the census estimates.

Also of issue is the ranking and comparing metros with scores computed using the ACS. Because D is not independent of population composition (Carrington and Troske 1997; Cortese et al. 1976), comparisons should be made with caution using any data source. Nevertheless, when examining differences across CBSAs using CIs, the overall picture of segregation in New York state becomes more complex and uncertain. For the largest metros, some distinctions are still possible, although often not between metros with similar levels of segregation. For example, New York City is more segregated than Albany, which in turn is more segregated than Poughkeepsie; however, Poughkeepsie is not statistically distinguishable from four other metros with lower levels of segregation. Note that these comparisons are made without consideration to the increased probability of rejecting the null when multiple comparisons are made. Nevertheless, among micropolitan areas, far fewer statistically significant differences exist because of large CIs. The two most extreme examples—which are the two micropolitan areas with the smallest share of blacks—are Cortland and Amsterdam, with CIs more than 25 points wide. Other small micropolitan areas with relatively large minority populations, such as Hudson (3,052, or 5.5 %, with 15 % of tracts having zero black population) and Malone (3,458, or 8.4 % with 38 % of tracts with a black population of 0), also have large CIs of 20.6 and 14 points, respectively.

When this analysis is broadened to include all CBSAs in the United States, similar conclusions are reached. Differences between ACS and decennial census indexes are actually larger in the CBSA population, increasing to 7.2 (from 5.2 for New York state) for the 2010 census and 5.3 (from 3.3 for New York state) for the 2000 data. Just as before, these differences are exacerbated if nonsimulated scores are used: they increase 2.1 points for both 2010 and 2000, compared with just 1.2 and 1.0, respectively, in New York state. Regarding statistical significance, 37.7 % of all CBSAs exhibit statistically significant change from the 2000 census (compared with 37.0 % from New York state). However, as with the New York state data, some of these differences are likely due to abnormally large ACS scores. In fact, 19.3 % of all CBSAs (11.1 % in New York state) have 2005–2009 ACS scores that are significantly larger than both the 2000 and 2010 scores. Although this result is possible because of nonlinear changes in segregation, many of these differences imply the unlikely: rapid fluctuations over a short period. For example, for these 181 CBSAs, if the total (absolute) change in segregation is computed using the three point estimates, only five would experience less than a 10-point change, and 33 would experience less than a 20-point change (meaning that 81.8 % experienced more than a 20-point change). To put this in context, the absolute change between the decennial census scores for 95 % of all CBSAs is less than 13; for 99 %, it is less than 22.

If a similar analysis is conducted for the more recent 2008–2012 ACS, many of same abnormalities persist, suggesting that the findings presented earlier are not specific to the 2005–2009 data. For the 2008–2012 ACS, perhaps the most telling comparison is with the 2010 census because the ACS is centered on the year it was conducted. The average ACS CBSA has a _wD_b score that is 8.8 points higher than the 2010 score, further illustrating the upward bias of ACS scores. As might be expected, the greatest differences are observed for smaller places, particularly those with very few blacks. Except for three outliers, CBSAs with more than 4,000 blacks remain within +6.0 to −2.5 points of the 2010 score. Moving on to other comparisons, one of the few discrepancies between the two ACS data sets is the difference between the simulated and nonsimulated (standard) scores. Here, the simulated scores are 1.3 points lower, and the variance in differences between the two types of scores is much smaller. This result is at least partly due to the reduced size of MOEs as a result of sample size increases for more recent years—and perhaps most importantly, decreases in MOEs for zero-population tracts (U.S. Census Bureau n.d.d). However, approximately 50 % of 2010 census scores still fall outside the 95 % CI for the 2008–2012 ACS scores, and of those that do, 97.8 % are (significantly) larger than 2010 scores. Although it is tempting to view the 2008–2012 data as benefiting from the improvements from the 2010 census, the majority of the data in the file were produced before improvements were made to the MAF. And although it is tempting to assume that the data from revised intercensal population estimates were used to recompute estimates from previously released years of data, it is unclear whether this was the case. Consequently, many of the problems seen with the earlier data carry over to this more recent file and future releases as well. It is not until late 2018, when the 2012–2017 data are released, that the full benefit of the 2010 decennial census will be present in five-year data.

In general, the ACS estimates are useful only in some of the largest metros for consistently and accurately detecting changes in segregation. In other places, CIs are too large to facilitate useful comparisons. Moreover, the point estimates are regularly much higher than either of the decennial census scores. Further analysis confirms that these are systematic problems in the ACS data.

Given the results presented earlier, a few factors likely play important roles in the high D scores. First is the upward bias in D scores due to sampling variation: because the absolute value is used in the formula for D, sampling error of any amount will result in higher D scores. Second, although the rapid increases in diversity through the 2000s were likely correctly incorporated into the population controls, they may have not been correctly distributed across the relatively small tract units due to limited sample sizes, outdated MAF files, and the lack of detailed population controls. It seems plausible that the methodology in place would allocate new diversity to neighborhoods that already contained minorities, which in turn resulted in an increased D score.

Conclusion and Discussion

The ACS offers researchers more frequent data releases compared with the decennial censuses. However, greater care must be taken when using and interpreting the data, particularly with segregation indexes such as D, because of the design of the ACS, which is motivated by a need for more regular data releases but is limited by budgetary constraints. Consequently, the ACS cannot achieve the same accuracy of the long-form census data it replaces. In particular sampling error is increased because of a smaller sample size and because of different sources of nonsampling error.

As diversity has spread throughout the country, ACS data have allowed users to track and monitor changes in a timely fashion. However, we must be sensitive to differences between the ACS and the decennial census data it is designed to replace, particularly the increased levels of sampling error. To address this issue, we introduced a new simulation method for calculating segregation indexes, which uses the MOEs released with ACS data. Using the 2005–2009 ACS, we computed D indexes using both the standard technique and the simulation method and then compared them. We conducted a more detailed analysis using a subsample of CBSAs on _wD_b, which included comparisons with D from the 2000 and 2010 censuses and a brief discussion of 2008–2012 ACS data.

The results suggest that the simulation method should be used for medium and small places, which are most affected by sampling error. Differences between the simulated D point estimates and standard D indexes were most apparent for places with fewer minorities and a large percentage of tracts with zero minorities. The range of the 95 % CI of D was greatly affected by both the size of the minority population and the size (measured by total population or number of tracts) of the CBSAs. The more detailed analysis of _wD_b and comparison with the 2000 and 2010 censuses raises three important points. First, D indexes for the ACS tend to be higher than plausible, especially for smaller places with fewer minorities. This is the case for 2005–2009 and 2008–2012 ACS data, which suggests that the issue is not resolved through updated population estimates (and controls) after the 2010 census. The lag in incorporating improvements in the MAF from the 2010 census into the ACS sampling frame is likely to play a role in the disparities as well. Second, CIs are also very large for smaller places—in some cases, so much so that it will be difficult or impossible to detect change both over time and between places, even when differences in the point estimates are large. Although not attempted here, more difficulties will arise if comparisons are made between two (nonoverlapping) ACS five-year periods—as is necessary for non-short-form variables—because each index would be subject to independent sources of error. Third, we detect significance for some places but in the incorrect direction. These cases, unfortunately, undermine much of the usefulness of the ACS for small places.

Researchers can take steps to improve the quality of their results when using ACS data. They should use the simulation method to minimize the effects of bias and to account for substantial amounts of sampling error in places that are smaller, have few minorities, or have many zero-population tracts. The existing method for dealing with various statistical issues related to D is to exclude places with small numbers of minorities. However, depending on the type of analysis, the common threshold of 1,000 (e.g., Cutler et al. 2008; Hall 2013; Iceland and Scopilliti 2008; Park and Iceland 2011) or even 2,500 (e.g., Logan et al. 2004), when applied to ACS data, will retain a large number of CBSAs with extremely imprecise D scores. Findings presented here show that the size of CIs decreases rapidly until a minority population of roughly 4,000 is reached. Using this threshold, for example, the difference in _wD_b scores for all CBSAs between the 2008–2012 ACS and the 2010 census drops from 7.5 to 3.1 points. However, if the results are weighted by the minority population (e.g., Cutler et al. 2008; Logan et. al 2004; Massey and Denton 1988), a lower threshold may be acceptable because weighting will reduce the influence of imprecise scores through the relationship between minority population size and precision (and accuracy) of D. In any case, when using ACS data, researchers should conduct analyses with sensitivity to the potential for imprecision and inaccuracy.

This study did not address three related issues. First, the application of the simulation method can be used with other segregation indexes and data sets. This method may even have its most useful applications with complex indexes that involve comparisons among multiple groups, like the entropy index, or involve numerous variables in their calculation, such as some spatial segregation measures. Second, different units of analysis will produce results that differ from those presented here. Using smaller areal units, which have larger MOEs compared with their population estimates, will increase the CIs of D along with the potential for upward bias for the standard D index formula. Finally, we have not examined in detail the computation of indexes for more recent periods. The 2005–2009 ACS provides for a clean test between the 2000 and 2010 censuses, but also potentially represents a near worst-case scenario. As the ACS program progresses, further improvements to its design and implementation are likely. However, additional analyses with 2008–2012 data make clear that these issues are not unique to the 2005–2009 data, and more improvement is needed: 2008–2012 ACS D indexes are still much larger than those from the 2010 census and have large CIs. Future research examining the ACS data should be sensitive to the issues raised here; the ACS is much different from the traditional long-form samples, particularly in regard to segregation.

Appendix: Sample SAS Code for Simulating D

/*
Program: Simulation Code for D
(1) Paste code into a SAS program.
(2) Modify the libname statement before the macro to match the directory where your data is
stored.
(3) Modify the output location of the printto procedure near the bottom to where you want the
output saved.
(3) Modify the line of code to invoke the macro at the very bottom of the program to match your
variables names.
*/
libname ssd ‘C:\Data\’; *change the directory here;
%macro stderrD(cbsa, dataset, mean_x1, marginoferror_x1, mean_x2, marginoferror_x2,
iterations, title);
libname ssd ‘C:\Data\’; *change the directory here;
           proc sort
                      data=&dataset(keep = &cbsa &mean_x1 &mean_x2 &marginoferror_x1
&marginoferror_x2)
                      out = maindata;
                      by &cbsa;
           %do i = 1 %to &iterations; * start iteration loop;
                      data temp;
                                  set maindata;
                                  if &cbsa ne.; * drop any cbsas that are not needed in this datastep;
                                  x1 = &mean_x1 + normal(0) * (&marginoferror_x1/1.645); * get tract
pop.;
                                  if x1 < 0 then x1 = 0; * set pop. counts less than 0 to 0;
                                  x2 = &mean_x2 + normal(0) * (&marginoferror_x2/1.645);
                                  if x2 < 0 then x2 = 0;
                                  keep x1 x2 &cbsa; * these are the only variables needed;
                      proc means data=temp sum noprint;
                                  by &cbsa;
                                  var x1 x2;
                                  output out=sum(keep = &cbsa sum_x1 sum_x2) sum = sum_x1 sum_x2;
                      data temp_sum;
                                  merge temp sum;
                                  by &cbsa;
                                  diff = abs((x1/sum_x1) – (x2/sum_x2));
                      proc means data=temp_sum sum noprint;
                                  by &cbsa;
                                  var diff;
                                  output out=newrate(keep = &cbsa sum_diff) sum = sum_diff;
                      data newrate;
                                  set newrate;
                                  rate = .5 * sum_diff;
                                  interation = &i;
                                  keep &cbsa rate interation;
                      data rates;
                                  set %if (&i ne 1) %then %do;
                                              rates
                                  %end;
                                              newrate;
           %end; *end of iterations loop;
           proc sort data=rates;
                      by &cbsa;
           proc univariate data=rates noprint;
                      by &cbsa;
                      var rate;
                                  pctlpts = 2.5 50 97.5 mean = mean std = stddev KURTOSIS = kurt
                                  SKEWNESS = skew pctlpre = p;
           proc print data=out noobs;
                      title “&title”; * this will output the final results;
           run;
%mend stderrD; * end of the macro;
data yourdata;
           set ssd.acs20095yrcbsatract; * put in your dataset here;
* the following procedure will write the excessive log output to a separate file;
proc printto log = ‘C:\ Sim.log’ new; * change directory here;
run;
*change parameters below to fit your data. See the instructions above the macro for details;
%stderrD(cbsa, yourdata, enhispwh, mnhispwh, enhispbk, mnhispbk, 50000, wDb Index);
proc printto; * reset logging to the default source;
run;