Association mapping for phenology and plant architecture in maize shows higher power for developmental traits compared with growth influenced traits

Abstract

Plant architecture, phenology and yield components of cultivated plants have repeatedly been shaped by selection to meet human needs and adaptation to different environments. Here we assessed the genetic architecture of 24 correlated maize traits that interact during plant cycle. Overall, 336 lines were phenotyped in a network of 9 trials and genotyped with 50K single-nucleotide polymorphisms. Phenology was the main factor of differentiation between genetic groups. Then yield components distinguished dents from lower yielding genetic groups. However, most of trait variation occurred within group and we observed similar overall and within group correlations, suggesting a major effect of pleiotropy and/or linkage. We found 34 quantitative trait loci (QTLs) for individual traits and six for trait combinations corresponding to PCA coordinates. Among them, only five were pleiotropic. We found a cluster of QTLs in a 5 Mb region around Tb1 associated with tiller number, ear row number and the first PCA axis, the latter being positively correlated to flowering time and negatively correlated to yield. Kn1 and ZmNIP1 were candidate genes for tillering, ZCN8 for leaf number and Rubisco Activase 1 for kernel weight. Experimental repeatabilities, numbers of QTLs and proportion of explained variation were higher for traits related to plant development such as tillering, leaf number and flowering time, than for traits affected by growth such as yield components. This suggests a simpler genetic determinism with larger individual QTL effects for the first category.

Introduction

Plant architecture, phenology, productivity and quality of cultivated plants have been repeatedly shaped by selection to meet human needs. Although technology to support this process has dramatically evolved, especially in recent decades, breeders' objectives have not fundamentally changed over the last 10 000 years. They still have to overcome the difficulty of conducting multiple trait selection in different and variable environments and their choices are often trade-offs between an ideal plant architecture, product quality, yield and adaptation to targeted environments. Low cost genotyping can accelerate the selection of large effect beneficial alleles and high throughput genotyping can improve the accuracy of breeding value predictions for multi-traits controlled by small effect quantitative trait loci (QTLs).

In cereals, yield remains the main objective even though it may be negatively correlated with some quality traits. Yield is a complex trait to predict as it is the result of many trait interactions during plant development and growth. The objective is to combine plant architecture that maximizes light interception, phenology that synchronizes reproduction stage with optimal environmental conditions to minimize abortion, inflorescence architecture for optimal seed set, and numerous factors contributing to environmental adaptation and grain filling.

Some plant architecture traits such as leaf number are controlled by developmental genes that express in meristems and their genetic architecture may be relatively simple. Other traits such as plant height or yield are the result of both developmental and growth related factors, likely leading to a more complex genetic architecture. Plant architecture, phenology and growth traits have been constrained to evolve and to be selected together and are consequently often correlated. The challenge is to determine whether these correlations are due to pleiotropic or linked QTLs, to target some useful recombination between beneficial alleles that are in repulsion. It is essential to consider genetic complexity and pleiotropy in maize where breeding is based on the exploitation of hybrid vigor by crossing parents from highly differentiated heterotic groups with possibly different trait variation and correlation patterns.

Considering only main races from American temperate regions, flints and floury open pollinated varieties from the northern USA and the plains region are adapted to low temperatures thanks to a short plant cycle. They generally bear two ears with 8–10 kernel rows, many tillers, long and thin leaves, and ears prolonged with long husk leaves. These features yield a ‘bushy' architecture (short and high number of leaves) that maximizes light interception early in the plant cycle. The Southern Dents adapted to the Southern US are tall plants with a short node interval at the base of stems, some with 8–10 kernel rows, and others with more than 24. The corn belt dent (CBD) open pollinated varieties were produced intentionally by crossing Northern Flints and Southern Dents ~200 years ago. They were adapted to the temperate Midwestern United States region and were widely cultivated for most of the 19th century and part of the 20th. They have cylindrical ears with 14–22 kernel rows and no tillers (Doebley et al., 1988). Diffusion of maize outside America led to additional races like European Flints that recombine genomes from Northern America and tropical origins (Rebourg et al., 2003).

Modern breeding methods based on the hybrid concept succeeded the open pollinated variety selection era in the U.S. Corn Belt in the early 1930s. Along with mechanized agriculture, it led to major yield increase. Over the years, there have been noteworthy gains in growth, development and resource partitioning efficiency, accompanied by a number of correlated responses of diverse traits, as fully documented in Duvick (2005). Adaptation to diverse environments increased whereas the harvest index and flowering time remained stable. The anthesis to silking interval (ASI) was reduced, especially under stress conditions. Seedling emergence was accelerated to reduce the risk of exposure to soil microorganisms or cool temperatures. Tillering was reduced. As yield increased, plant height and ear height were reduced to prevent lodging (Johnson et al., 1986). As plant density increased (Andrade et al., 1993), light penetration into the canopy was maximized by optimizing leaf angle, leaf size, tassel size and angle (Fischer et al., 1987). Since the 1970s, leaves became more upright above the ear (Russell, 1991) to minimize shading of lower leaves. Plant yield components like the number of ears per plant, kernel number and to a lesser extent kernel weight (KW) improved. Note that these trends may differ in breeding programs, depending on the germplasm, the grain or biomass nature of the variety, the targeted environment and the use as male or female genetic materials in hybrid seed production. Male parents with relatively large tassels that shed copious amounts of pollen over a long period of time may be preferred, whereas female parents with large ears and relatively small tassels may be preferred (Lambert and Johnson, 1978).

Despite these major trends, little is known about the genetics of plant architecture related traits in maize. Only domestication genes, flowering time and plant height have been fully documented. Most of major developmental genes that have been cloned are fixed in elite germplasm, such as the Tb1 allele that suppresses tillering (Doebley et al., 1997), the Tga allele that confers naked grains (Wang et al., 2005) and the Br2 allele that reduces plant height (Multani et al., 2003). However, substantial variation remains to be explained and exploited for most traits. QTL mapping experiments revealed that plant total height (PTHT) and flowering time are highly heritable polygenic traits and that their variation is controlled by many unlinked genes, each contributing a small additive effect (Buckler et al., 2009; Romay et al., 2013; Bouchet et al., 2013; Peiffer et al., 2014). Many QTL experiments for inflorescence traits showed that they are less heritable (Brown et al., 2011).

Association studies on diversity panels are effective for identifying genetic variants associated with phenological and morphological traits in maize (Thornsberry et al., 2001; Flint-Garcia et al., 2005; Camus-Kulandaivelu et al., 2006; Ducrocq et al., 2008, 2009; Durand et al., 2012; Romay et al., 2013; Bouchet et al., 2013). In the current study, 375 lines of maize originating from the tropics, USA and Europe were successfully phenotyped for 24 ecologically and agronomically important traits related to (i) phenology, (ii) plant architecture, (iii) ear and yield components and (iv) tassel architecture. The evaluation was conducted under natural growing conditions in 4 environments (9 trials in total). Variation and co-variation among traits were examined in the light of population structure. The correlations and their relative complexity in terms of genetic architecture were described through a genome-wide association study based on 43K single-nucleotide polymorphisms (SNPs) across the genome. The power of QTL detection was compared between developmental traits and traits influenced by growth.

Materials and methods

Genetic material and genotyping

We considered for this study the set of 375 lines previously described by Camus-Kulandaivelu et al. (2006). They were genotyped for 94 simple sequence repeat (SSR) markers and with the 50K Illumina Golden Gate beadchip leading to 43 224 polymorphic SNPs. Conformity check and heterozygosity rate led to a set of 336 maize inbred lines used for association studies (Bouchet et al., 2013). The structure of this panel was analyzed with STRUCTURE software (Pritchard et al, 2001) using 55 tri-nucleotidic SSRs, leading to 5 main genetic groups (Camus-Kulandaivelu et al., 2006). The size of a given group was calculated as the sum of quantitative assignments of all lines to this group (Q_55SSRs matrix below), which led to 57 for Northern Flints (NF), 62 for European Flints (EF), 26 for Stiff Stalks (SS), 115 for other CBD and 76 for tropical lines (Trop).

Field experiments

The diversity panel was evaluated for 24 traits. The whole panel was tested at three different locations (Einbeck, Germany: 52° N, 10° E, Gif-sur-Yvette, France: 49° N, 2° E, Saint-Martin-de-Hinx, France: 43° N, 1.3° W). The lines from the two latest flowering groups (see details below) were also evaluated at Mauguio, Southern France (44° N, 4° E) but not in Northern locations where they would have not flowered in time to produce harvestable ears before winter. The French locations were evaluated for 2 or 3 years (2002–2004) and the German location for 1 year (2005), yielding a total of 9 trials (Supplementary Table S1).

Each trial was organized into two blocks situated side by side. All lines were observed in each block. Each block was organized into four sub-blocks. To limit competition effects between lines having different sizes, lines were ranked according to their a priori earliness and classified into four sub-groups. To prevent confusion due to fertility gradient that would affect yield and other traits, assignation of sub-groups to sub-blocks was done according to increasing average expected flowering time in block 1 and according to decreasing average flowering time in block 2. Each sub-block included all lines from a given sub-group plus additional lines selected at random in adjacent expected flowering time sub-groups. Overall, 16 lines were repeated twice in each block to adjust for putative confounding environmental effects associated with sub-blocks. Lines were randomized within each sub-block. Each individual plot consisted of a row of 15 plants sown at a density of approximately six plants per square meter. Depending on the trait, they were measured as a whole for each plot or as an average of five measurements on different individual plants. Most of phenology, plant architecture, yield components and tassel architecture traits were assessed at 3–4 different sites with two trials conducted in different years (Supplementary Table S1).

The plant germination dynamics were measured by counting the number of visible plants after seeding every 2 days until 50% of plants were visible (days to emergence: Em). At this date, emergence vigor was qualitatively assessed based on leaf color and size of the plant. Emergence (Em), days to third leaf, days to anthesis for male flowering (MFLW), days to silking for female flowering (FFLW) and anthesis to silking interval (ASI) were measured in days and in thermal time (growing degree days) according to Ritchie and NeSmith (1991) with parameter values (Tb=8° and To=30 °C) that maximized correlations between trials. They are referred to as Em8, S3LF8, MFLW8, FFLW8, ASI8 and correspond to Em, S3LF, MFLW, FFLW, ASI, respectively.

Plant architecture traits were measured either for the whole plot (tiller number for the whole plot divided by the number of plants: tiller number (TINB)) or as an average of 5 plants (husk leaf length: HL, plant height: PTHT, ear insertion height: EARHT, leaf number: LFNB, leaf number above top ear: LFNBa, leaf number below top ear: LFNBb) at least 5 days after flowering. To be able to score leaf number accurately, the first five leaves were marked early during the cycle before senescence.

For yield components, we harvested separately (i) top ears and (ii) all other ears from all plants of the plot. One hundred random grains from all top ears of the plot were weighed to estimate the thousand KW (TKW) after 48 h drying at 120 °C. The number of ears (EARNB) per plant including secondary ears was counted. Yield was estimated as the total KW divided by the number of harvested plants. The kernel row number (ROWNB) and the number of kernels per row (KERROWNB) were evaluated as the average of observations on the top ears of five random plants.

Tassel architecture was described for the whole plot for tassel standing (TaSt) as 3 classes (1: erect, 2: horizontal and 3: falling), and averaged over five plants, for tassel secondary branch angle (TaAk) as 3 classes (1: <30°, 2: 30° < angle <60°, 3: >60°), tassel length (TL), tassel spike length (SL), tassel branch zone length (BZL) and number of branches (BRNB) as 4 classes (1: 0–3, 2: 4–10, 3: 11–15, 4: >15).

Statistical analyses

The variance components of the 24 traits were assessed with ASReml-R using the following model:

y_ijkl is the phenotype of genotype i, in field trial j, in block k and sub-block l. μ is the grand mean, G_i is the effect of genotype i, E_j is the effect of trial j (combination of year and site), B_k(j) is the effect of block k in trial j, S_l(k) is the effect of sub-block l in block k, GE_ij is the effect of the interaction between genotype i and environment j, R_ijkl is the residual error. All effects were considered as random.

Significance of G and GE variance components was tested with likelihood ratio tests as recommended by ASReml documentation (Welham et al., 2013). Significance of G component was tested as:

where l2 is the REML-likelihood of the general model (including G) and l1 the REML-likelihood of the restricted model (excluding G). Note that, as variances are estimated under the constraint of being positive, this test procedure is conservative (Stram and Lee, 1994; Welham et al., 2013). Significance of GE was tested similarly considering the REML-likelihoods of models with and without the GE interaction term.

Repeatability was estimated at the plot and design levels as:

Where 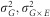and 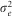are the genotype, genotype x environment and residual variances respectively, nb trials and nb reps are the average number of trials and replicates per inbred line respectively.

Considering that genotype x environment interaction variances were low compared with genotype effects, we estimated adjusted means using model:

Where all terms stand as described above, considering now inbred lines as fixed effects (α_i), trials, blocks and sub-blocks as random effects.

Principal component analysis

To get a global picture of trait correlations and characterize the lines by synthetic variables that summarize these trends, we performed a principal component analysis (PCA) of standardized adjusted means of all traits with the R package FactoMiner. To avoid discarding lines with missing phenotypes in this analysis, we imputed missing data using the R package missMDA. The number of PCA dimensions to consider for imputation was determined by cross-validation (Lê et al., 2008).

Differentiation among groups, within and among group trait variation and correlations

To investigate the effect of population structure in trait differentiation, we estimated the proportion of phenotypic variation explained by the first four columns of the matrix of assignment of each line to each of the five genetic groups (Q_55SSRs matrix), using a linear model. We estimated the five group adjusted means as the predicted values of hypothetical pure lines from each group.

We also used the matrix of population structure described above to calculate phenotypic variation and correlation within and among genetic groups.

The phenotypic covariance of traits a and b within each group q was calculated as the weighted sum of product:

With δ_q(i) the assignment proportion of line i to group q, X_a(i) the value of line i for trait a, μ_a(q) the adjusted mean of trait a within group q.

The global within-group covariance of traits a and b (residual covariance) was calculated as:

With 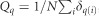, the proportion of lines in group q, N the total number of lines.

The global among-group covariance of traits a and b was calculated as the weighted sum of product:

With q the genetic group, Q_q the proportion of lines in group q, μ_a(q) the adjusted mean of trait a within-group q, μ_a the general mean for trait a. Note that this estimation has four degrees of freedom and is specific to the population structure of our panel.

The within (among) group correlations between traits a and b were calculated as:

where variances were estimated following the same procedure as for covariances. We then calculated the correlation between pairwise correlations within and among groups and those observed for adjusted means.

Whole-genome association genetics

To test the association of the 43 224 SNPs with the 24 traits and the first 5 PCA axes, we considered the association model described in Yu et al. (2006):

where y is the trait adjusted mean, μ the intercept, S individual genotypes, α the SNP fixed effect, Q the matrix of assignment of each line to each of the first n−1 (4) genetic groups, v the genetic groups fixed effects, Z the matrix of line occurrences, u the vector of polygene background effects and e is the vector of residuals. Var(u)=2KVg, where Vg is the genetic variance and K is a matrix of similarity between lines.

In order not to use candidate SNPs for population structure and kinship estimations, we used STRUCTURE vectors calculated with 55 SSRs (Q_55SSRs) and 10 identity by state kinship matrices calculated with ~30 K Panzea (http://www.panzea.org/) SNPs (Bouchet et al., 2013). To test SNPs located on one chromosome, we used a kinship calculated with SNPs belonging to all chromosomes but that one (Rincent et al., 2014). Single locus associations were run with FaST-LMM (Listgarten et al., 2013) for the 24 traits and the 5 PCA axes described above.

We compared the number of overall QTLs and shared QTLs between traits using one common threshold. The number of independent tests estimated according to Li and Ji (2005) was 4740. The corresponding 5% Bonferroni threshold was E-05.

Finally, to estimate the proportion of variation accounted by the QTL(s) that were detected, we used a fixed multi-locus linear model including population structure. In order not to eliminate an increasing number of lines during the procedure, we imputed the 2.2% missing data with FastPHASE (Scheet and Stephens, 2006). We chose the number of hypothetical ancestors (5) that minimized imputation errors using cross-validation. Imputation error was <0.5%. For each trait, a forward–backward variable selection based on AIC criterion was applied to (i) the markers with P-value < E-05 and (ii) the markers with P-value <E-04, using a linear model that included four structure vectors. Analysis was performed using the stepAIC function of the MASS-R package. Coefficient of determination (R²_m) of the model with selected marker(s) was compared to that of the model including only population structure (R²_s). The variation explained by marker(s) was estimated as R²_m–R²_s.

Genes located in the vicinity of QTLs were identified according to maize annotation version 2 (maizegenome.org).

Results

Trait variation within the entire diversity panel

All traits but Em had highly significant genetic effects (Table 1). All traits showed significant genetic by environment (G × E) interaction. G × E variance was generally low compared with genetic variance, except for S3LF8, ASI8, TINB, EARNB and KW for which the two components had a similar magnitude. Repeatability ranged from 0.31 for Em8 to 0.97 for MFLW8. Entry-mean repeatability level ranged from 0.57 to 1 for these two same traits. Adjusted means of genotypes estimated with the total network of trials were used for association analyses.

Table 1. Variance components of the 24 traits.

Abbreviation	Name	G/Da	Mean valueb	Varianceb	Gc	G × Ec	Errorc	Plot repd	Design repe
Phenology
EmVIG	Emergence vigor (qualitative)	G	5.74	0.82	0.00**	1.06***	0.6	0.00	0.00
Em8	Emergence (GDDf)	G	94.75	115.67	43.82***	56.78***	554.69	0.31	0.57
S3LF8	3rd leaf stage (GDDf)	G	120.02	84.89	45.48***	44.89***	328.76	0.40	0.77
MFLW8	Male flowering (GDDf)	D/G	879.16	26076.80	25382.50***	453.90***	1904.7	0.97	1.00
FFLW8	Female flowering (GDDf)	D/G	912.35	28152.08	27293.18***	746.07***	4388.2	0.96	1.00
ASI8	Anthesis silking interval (GDDf)	G	35.62	676.30	3.31***	2.66***	2.2	0.45	0.89
Plant architecture
PTHT	Plant height (cm)	G/D	170.75	1045.27	893.38***	126.57***	434.03	0.81	0.98
EARHT	Ear insertion height (cm)	G	66.48	702.13	601.31***	46.46***	62.95	0.89	0.99
LFNB	Leaf number	D	17.97	13.74	5.74***	0.93***	0	0.95	0.99
LFNBa	Leaf number above top ear	D	5.11	0.94	0.71***	0.09**	0.06	0.82	0.97
LFNBb	Leaf number below top ear	D	12.84	9.06	5.53***	0.24***	0	0.94	0.98
TINB	Tiller number per plant	D	0.11	0.04	0.03***	0.03***	0.01	0.42	0.87
HL	Ear husk leaf length (cm)	G/D	3.55	19.69	12.75***	66.29***	107.15	0.66	0.92
Ear and yield components
EARNB	Ears per plant	G/D	1.23	0.08	0.06***	0.05***	0.07	0.45	0.78
ROWNB	Kernel row number	D	13.07	5.41	4.91***	0.81***	0.15	0.82	0.97
KERROWNB	Kernels per row	G	22.05	20.55	16.89***	6.93***	6.44	0.53	0.88
TKW	Thousand kernel weight (g)	D/G	194.45	1761.81	1461.94***	522.76***	443.67	0.60	0.91
KW	Kernel weight per plant (g)	G	37.05	287.79	17756.21***	9602.84***	14549	0.41	0.85
Tassel architecture
TL	Tassel length (cm)	G	29.94	17.07	15.03***	3.16***	3.46	0.73	0.95
SL	Tassel length above top secondary branch (cm)	G	20.45	11.35	10.58***	2.54***	1.02	0.70	0.94
BZL	Length from the first branch to the top branch of the tassel (cm)	G/D	9.48	7.25	5.64***	1.27***	1.15	0.69	0.95
BRNB	Tassel branch number (qualitative)	D	2.79	0.44	0.36***	0.10***	0.06	0.65	0.93
TaAk	Tassel secondary branches angle (qualitative)	_	1.96	0.36	0.32***	0.08***	0	0.62	0.92
TaSt	Tassel floppiness (qualitative)	_	1.59	0.33	0.29***	0.11***	0.05	0.52	0.89

Abbreviations: ASI, anthesis to silking interval; BRNB, tassel branch number; BZL, branch zone length; EARHT, ear insertion height; EARNB, number of ears; Em, emergence; EmVIG, emergence vigor; FFLW, female flowering; GDD, growing degree days; HL, husk leaf length; KERROWNB, number of kernels per row; KW, kernel weight; LFNB, leaf number; MFLW, male flowering; PTHT, plant total height; ROWNB, kernel row number; SL, spike length; S3LF, 3rd leaf stage; TL, tassel length; TaST, tassel standing; TKW, thousand kernel weight, TINB, tiller number.

^aEmpirical classification from mostly affected by development (D) to mostly affected by growth (G).

^bMean and variance of phenotypic adjusted means.

^cVariance components estimated with r-ASREML; G, genetic; G × E, genetic-environment interaction; error, residuals. Genotypes, trials (combination of year and site), blocks and sub-blocks were considered as random effects. P-values of G × E were calculated with a log-ratio test between models with and without interaction between lines and sites. G × E P-values were all inferior to E-16, except for LFNBa. G P-values were all inferior to E-16 except for EmVIG.

^dPlot repeatability=varG/(varG+varGxE+vare).

^eDesign repeatability=varG/(varG + varGxE/nb_trial + vare/nb_rep).

^fGDDs, thermal time following Ritchie and NeSmith (1991), Tb=8 °C, To=30 °C. ‘**' and ‘***' indicate significancy at 0.01 and 0.001 risk levels, respectively.

Phenology traits (Em8, S3LF8, MFLW8, FFLW8 and ASI8) were highly positively correlated with most plant architecture traits (PTHT, EARHT and LFNB), but not TINB nor HL. They were also positively correlated with some tassel architecture traits (TL, SL, BZL and BRNB) and negatively correlated with yield components (EARNB, ROWNB, KERROWNB, KW and TKW), as well as some tassel architecture traits (TaAk and TaSt). Note that yield (KW) was positively correlated with KERROWNB (0.70) and ROWNB (0.29) and negatively correlated with ASI8 (−0.31), FFLW8 (−0.27), MFLW8 (−0.25), S3FL8 (−0.35), Em8 (−0.31) and LFNB (−0.17). TINB was positively correlated with the length of husk leaves (HL; 0.38; Supplementary Table S2).

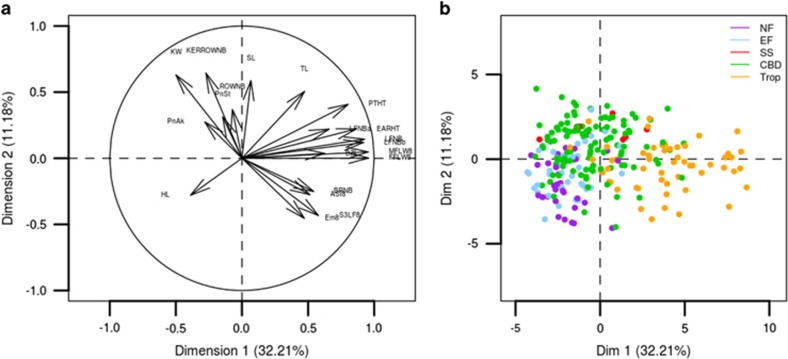
The traits were summarized into 8 principal components (Figure 1,Supplementary Figure S1), accounting for 79% of the global phenotypic variation. The first PCA axis (Dim1) explained 32% of the total variation (Supplementary Table S3) and was positively correlated with male (MFLW8) and female (FFLW8) flowering (0.96), other traits related to phenology (Em8, ASI8, PTHT, EARHT and LFNB) and tassel architecture (BZL and BRNB; Supplementary Table S4). Dim1 was negatively correlated with yield (KW), HL and TaAk to a lesser extent. It separated Tropicals that flower late and have a typically tall stature from temperate lines that all displayed highly negative values on Dim1 (Figure 1).

Figure 1.

Projection of traits (a) and inbred lines (b) on the two first PCA axes built with the 24 traits. Colors on the right hand plot indicate genetic groups.

The second axis (Dim2, r²=11%) was correlated positively with yield (KW) and its components, KERROWNB in particular, and also tassel architecture (SL). It separated flints (Northern Flints and European Flints) from dents (CBD and Stiff Stalks), the latter characterized by higher yield. The third axis (Dim3, r²=9%) was positively correlated with tassel architecture traits (TaSt, TaAk, BZL, TL and BRNB) and plant architecture traits (TINB and HL). It also separated dent versus flint groups, with the highest values contributed by Northern Flint individuals. PCA axes beyond axis 3 had no clear link with the diversity panel structure. Dim4 was positively correlated with ROWNB and negatively with TKW. Note that TKW was negatively correlated with ROWNB and KERROWNB. Dim5 was correlated with EARNB. TINB was correlated with axes 3–5.

Comparison of trait variation between and within groups

According to Supplementary Table S5, the five-group population structure explained from 2% (SL) to 54% (MFLW8) of trait variation. Structure had a high contribution to variation of flowering time related traits (LFNB: 0.53 and EARHT: 0.37) and growth affected traits to a lesser extent (KW: 0.29, PTHT: 0.30 and HL: 0.40). Tropicals differentiated from the other groups according to phenology. They showed later Em8, S3LF8, ASI8 and flowering time (MFLW8 and FFLW8). They typically had higher PTHT, and more LFNB. Dents differentiated from flints according to yield components, with higher ROWNB, KERROWNB and KW. Stiff Stalks differentiated from CBD with high TKW. Northern Flints was particularly differentiated from the other groups regarding numerous traits including early flowering time. Those lines had higher TaAk and floppiness (TaSt), more TINB, longer HL, lower PTHT and fewer LFNB resulting in a ‘bushy' architecture.

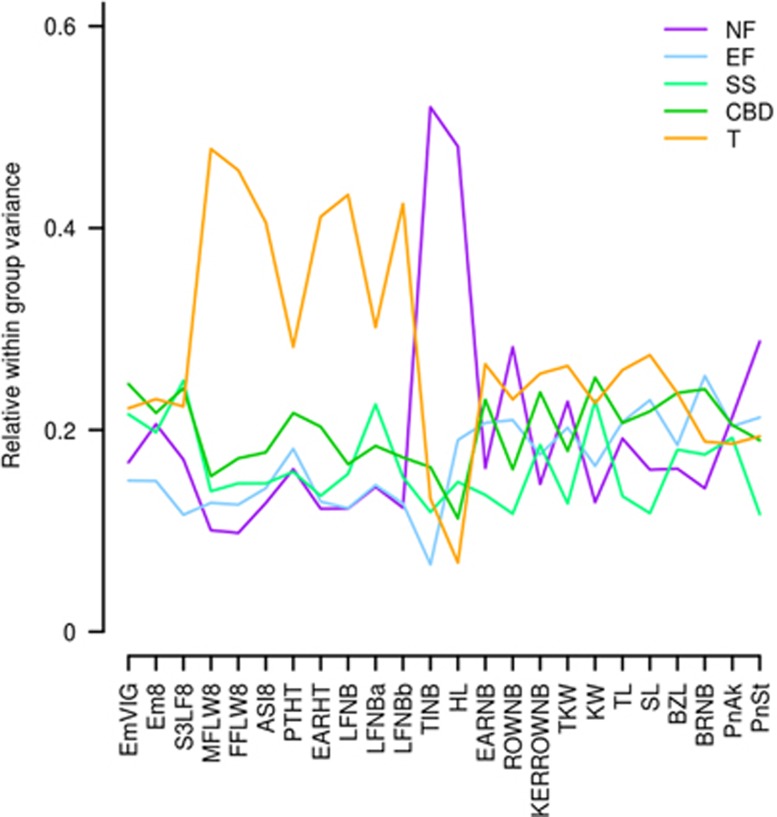
Relative within group phenotypic variation was homogeneous among groups for yield component and inflorescence traits. It was higher for (i) flowering time and correlated traits in tropicals and (ii) TINB and HL in Northern Flints. Within group variation represented approximately 50% of the total variation in these two cases (Figure 2).

Figure 2.

Within genetic group variance of the 24 traits. For each trait on the x-axis, the relative within group variance on the y-axis corresponds to the variance within each group divided by the overall variance.

Within-group trait correlations were similar to overall trait correlations (r²=0.98 among all pairs of traits, Supplementary Table S2,Supplementary Figure S2). The relation between among groups and overall trait correlations was looser (r²=0.64) and presented a sigmoid shape (Supplementary Figure S2). Traits with a high positive overall correlation all displayed a high among group correlation. Traits with a moderate overall correlation displayed a wider range of correlations among groups, sometimes with opposite signs. TKW and KERROWNB for instance were negatively correlated within groups (r=−0.37) and positively correlated among groups (r=0.45). TKW and KW were slightly correlated within groups (r=0.21) and not correlated among groups (r=0.01).

Whole-genome phenotype–genotype associations

The estimated number of independent tests (Li and Ji, 2005) in association studies was 4740. The corresponding 5% Bonferroni threshold was E-05. According to the QQ-plot representation of observed P-values (Supplementary Figure S3), the E-05 P-value threshold corresponded to a break on the P-value distribution for most traits. Results for single locus association analyses conducted for each trait and combination of traits (PCA coordinates) are described in Supplementary Table S6,Supplementary Figure S3 and summarized in Table 2.

Table 2. Number of QTLs using a single or a multi-locus model.

Trait	G/Da	R2.strb	#QTL5c	R2.5d	#QTL.model.5e	prop.QTL5f	#QTL4g	R2.4h	#QTL.model.4i	prop.QTL4j	R2.5-R2.strk
Phenology
EmVIG	G	0.06	1	0.11	1	1.00	5.00	0.20	4.00	0.80	0.05
Em8	G	0.13	0	0.13	0	NA	4.00	0.29	4.00	1.00	0.00
S3LF8	G	0.18	0	0.18	0	NA	4.00	0.33	4.00	1.00	0.00
MFLW8	D/G	0.55	3	0.68	3	0.75	14.00	0.77	11.00	0.79	0.13
FFLW8	D/G	0.53	3	0.65	3	0.75	16.00	0.75	11.00	0.69	0.13
ASI8	G	0.13	1	0.21	1	1.00	13.00	0.44	12.00	0.92	0.08
Plant architecture
PTHT	G/D	0.30	1	0.38	1	1.00	11.00	0.57	8.00	0.73	0.07
EARHT	G	0.38	0	0.38	0	NA	21.00	0.65	13.00	0.62	0.00
LFNB	D	0.53	3	0.66	2	0.67	22.00	0.81	15.00	0.68	0.13
LFNBa	D	0.26	0	0.26	0	NA	7.00	0.45	6.00	0.86	0.00
LFNBb	D	0.53	4	0.68	3	0.75	14.00	0.75	9.00	0.64	0.14
TINB	D	0.10	19	0.58	13	0.68	64.00	0.71	30.00	0.47	0.48
HL	G/D	0.36	2	0.44	2	1.00	11.00	0.60	10.00	0.91	0.08
Ear and yield components
EARNB	G/D	0.02	0	0.02	0	NA	5.00	0.21	4.00	0.80	0.00
ROWNB	D	0.11	5	0.37	5	1.00	8.00	0.41	8.00	1.00	0.26
KERROWNB	G	0.21	0	0.21	0	NA	15.00	0.41	8.00	0.53	0.00
TKW	D/G	0.05	1	0.14	1	1.00	5.00	0.26	5.00	1.00	0.08
KW	G	0.33	1	0.39	1	1.00	16.00	0.57	12.00	0.75	0.06
Tassel architecture
TaSt	G	0.05	1	0.07	1	1.00	10.00	0.34	9.00	0.90	0.02
TaAk	G	0.08	0	0.08	0	NA	7.00	0.33	6.00	0.86	0.00
TL	G/D	0.11	3	0.19	3	1.00	9.00	0.26	6.00	0.67	0.08
SL	D	0.03	0	0.03	0	NA	7.00	0.25	6.00	0.86	0.00
BZL	—	0.11	1	0.17	1	1.00	8.00	0.37	8.00	1.00	0.06
BRNB	—	0.15	2	0.21	2	0.67	13.00	0.35	7.00	0.54	0.06

Abbreviations: ASI, anthesis to silking interval; BRNB, tassel branch number; BZL, branch zone length; EARHT, ear insertion height; EARNB, number of ears; Em, emergence; EmVIG, emergence vigor; FFLW, female flowering; HL, husk leaf length; KERROWNB, number of kernels per row; KW, kernel weight; LFNB, leaf number; MFLW, male flowering; NA, not applicable; PTHT, plant total height; ROWNB, kernel row number; QTL, quantitative trait loci; SL, spike length; S3LF, 3rd leaf stage; TL, tassel length; TaST, tassel standing; TKW, thousand kernel weight, TINB, tiller number.

^aEmpirical classification from mostly affected by development (D) to mostly affected by growth (G).

^bVariance explained by the four first vectors of STRUCTURE.

^cNumber of QTLs detected with P-value < E-05.

^dVariance explained by a forward–backward linear model testing markers with P-value < E-05.

^eNumber of QTLs with P-value < E-05 included in the model.

^fProportion of QTLs with P-value < E-05 included in the model.

^gNumber of QTLs detected with P-value < E-04.

^hVariance explained by a forward–backward linear model testing markers with P-value < E-04.

ⁱNumber of QTLs with P-value < E-04 included in the model.

^jProportion of QTLs with P-value < E-04 included in the model.

^kVariance explained by markers selected in the muli-locus model : difference between the variances ^d and ^b.

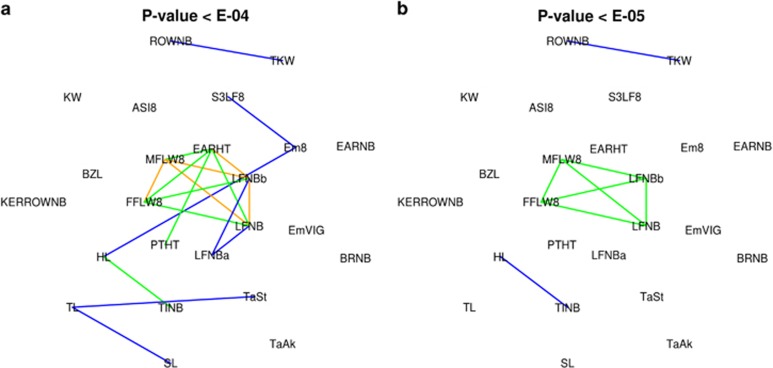
Overall, 57 markers corresponding to 40 genomic regions, defined as 1 Mb windows, passed the E-05 threshold for at least one trait or PCA component. The number of QTLs per trait (evaluated by the number of markers included in the multi-locus model) ranged from 0 for several traits (Em8, SL, TaAk, S3LF8, EARHT, LFNBa, EARNB and KERROWNB) to 13 for TINB leading to 48% of the variation explained in addition to population structure. Five QTLs had an effect on more than one trait. The number of associations shared between two traits increased with trait correlation (Figure 3, Supplementary Figure S4).

Figure 3.

Pleiotropic effects of detected QTL. Lines in orange, green and blue correspond to more than 5, 1 and 0 markers with associations for both traits, respectively. Traits were positioned empirically to minimize the number of crossing links in Supplementary Figure S6C. (a) Associations were accounted for P-values <E-04. (b) Associations were accounted for P-values <E-05.

Phenology

For FFLW8 and MFLW8, three loci were significant with P-value < E-05. Two were shared by the two traits: one at ZCN8 (Chr 8: 123506141; P-value < E-06) and one on chromosome 3 (Chr3: 168961638; P-value < E-05). Additional ones were located on chromosome 9 for FFLW8 (Chr 9: 57186011; P-value < E-05) and on chromosome 8 for MFLW8 (Chr 8: 162507079; P-value < E-05). The three markers detected for each trait were selected by a forward–backward selection linear model, explaining 13% of the variation of both FFLW8 and MFLW8. Two additional phenology related QTLs were detected, one for ASI8 (Chr2: 210854720; P-value < E-07) that explained 8% of the variation and one for emergence vigor (Chr3: 93414822; P-value < E-06) that explained 5% of the variation.

Plant architecture

Most of plant architecture related QTLs were distinct from phenology QTLs. For PTHT, a single region was significant at the P-value < E-05 threshold (Chr7: 120203200, P-value < E-06) and explained 8% of the variation. Two QTLs were detected for LFNB. The most significant one (Chr 8: 123506141; P-value < E-06) corresponded to ZCN8, which also had a major effect on FFLW8 (P-value < E-07) and MFLW8 (P-value < E-07). The second one (Chr1: 228051413; P-value < E-07) was not detected for phenology. An additional locus was associated with LFNBb on this chromosome (Chr1: 191 585 492; P-value < E-05). Those 3 markers were included when using a forward–backward selection linear model, explaining 14% of the variation. Note that no QTL was detected for LFNBa.

TINB was distinguished by the highest number of associated markers (19) corresponding to 13 QTL regions passing the E-05 P-value threshold. The greatest effects for TINB were found on chromosome 1 (Chr1: 271 334 672, P-value < E-12), chromosome 3 (Chr3: 40 524 625, P-value < E-07) and chromosome 6 (Chr6: 100 670 572, P-value < E-07). A group of 6 markers were associated between positions 53 260 938 and 54 552 245 (P-value < E-05) on chromosome 4, 10 Mb away from Tga1 (GRMZM2G101511, Chr4: 44508235), a region involved in maize domestication. Out of the 19 markers, 13 markers corresponding each to a genomic region were selected in the multi-locus linear model by the forward–backward procedure. These markers explained 48% of the variation (Table 2).

Two QTLs passed the E-05 P-value threshold for HL. The first was on chromosome 1 (Chr1: 167 864 888, P-value <E-05) and was among the most important loci for TINB. The second was on chromosome 4 (Ch4: 136 690 013, P-value < E-05). Both markers were included using a forward–backward selection linear model, explaining 8% of the variation.

Ear architecture and kernel traits

No QTL passed the E-05 threshold for KERROWNB but 5 were detected for ROWNB. The most significant one (Chr10: 15 004 433, P-value < E-06) was also associated with TKW (P-value < E-05). All 5 markers were included using a forward–backward selection linear model, explaining 26% of the variation. The locus associated with TKW explained 8% of its variation. The only QTL that passed the E-05 threshold for KW was on a different chromosome (Chr4: 695,932, P-value < E-05) and explained 6% of variation.

Tassel traits

A total of seven QTLs were associated with tassel traits. Note that no QTL was observed for TaAk and SL at the E-05 P-value threshold. For BRNB, two QTLs were significant (Chr3: 62 260 589 and Chr5: 204 590 439; P-value < E-05). Both markers were included using a forward–backward selection linear model, explaining 6% of the variation. For TL, three different QTLs passed the E-05 P-value threshold (Chr1: 55 083 883 and 55 386 821; Chr4: 26 888 62; P-value < E-05). All 3 markers were included using a forward–backward selection linear model, explaining 8% of the variation. One QTL was detected for TaSt (Chr5: 160 165 587; P-value < E-05) and one for BZL (Chr3: 191 612 805; P-value < E-05). They explained, respectively, 2% and 6% of trait variation.

Pleitropy and QTL for PCA axes

At E-05 P-value threshold, pleiotropy was found for one QTL between TKW and KW, one QTL between TINB and HL and two QTLs at ZCN8 for LFNB, FFLW8 and MFLW8 (Figure 3).

Three QTLs were associated with the first dimension of PCA (Chr8: 123 506 141; P-value < E-06, Chr2: 78 699 684; P-value < E-05 and Chr1: 264 954 421; P-value < E-05). The first QTL was ZCN8, which was also associated with LFNB, MFLW8 and FFLW8 (see above). The second was the centromere of chromosome 2, which displayed no close association significant at E-05 for any individual trait in this study. The third was the closest marker from Tb1. Note that the closest individual trait association was found more than 5 Mb apart for TINB. Two QTLs were associated with the second dimension of PCA (Chr2: 163 318 812; P-value < E-05; and Chr4: 28 836 464; P-value < E-05). The first QTL was at 3 Mb from a QTL associated with TINB. The second QTL was at 2 Mb from a QTL associated with TL. No QTL was associated with the third dimension of PCA but three were detected for the fourth dimension (Chr6: 102 399 359; P-value < E-05; Chr8: 15 109 180; P-value < E-05; and Chr10: 15 004 433; P-value < E-05). The first QTL was at 2 Mb from a QTL associated with TINB and the third one was also associated with ROWNB and TKW. Note that no individual trait was associated with the second QTL. Only one QTL was associated with the fifth dimension of PCA (Chr9: 102 399 359; P-value < E-05). It also affected TINB.

Discussion

The panel investigated here included American material used in the first maize association study (Thornsberry et al., 2001) supplemented with original European material presenting high diversity and limited relatedness (Camus-Kulandaivelu et al., 2006). It displayed marked variation in flowering time, from extremely early materials to photoperiod sensitive tropical materials. These features have contributed to the discovery of interesting associations based on candidate gene approaches such as Vgt1 (Ducrocq et al., 2008), ZmCCT (Ducrocq et al., 2009) and Opaque2 (Manicacci et al., 2009), with a first genome-wide scan in this panel revealing ZCN8 as a major gene corresponding to Vgt2, 8Mb from Vgt1, as well as other QTLs involved in flowering time (Bouchet et al., 2013). Our study highlighted the high variation in this panel regarding plant architecture and grain yield related traits, and contrasted genetic architectures for these traits.

Phenotypic variation

The morphological evaluation in a network of 9 trials (2 or 3 years at 3 French sites, 1 year at 1 German site) highlighted a strong variation, with most traits presenting a high repeatability. Repeatability for plant height (0.87), ear height (0.86) and flowering time (0.92) were in the same range as in the US NCRPIS panel (Peiffer et al., 2014), and the Chinese panel (Yang et al., 2014). ASI8 repeatability (0.45) was in the same range as in the European panels (Rincent et al., 2014). Yield component repeatabilities were within the same range as in the Chinese panel (TKW=0.60 and KW=0.40) and comparable to the dry matter yield in European panels (~0.70 for tassel architecture traits, 0.50 for EARNB and KERROWNB, 0.82 for ROWNB).

All traits showed genotype by environment interactions. Traits that showed the highest interactions were sometimes among the most heritable traits, such as flowering time (MFLW8 and FFLW8), PTHT and EARHT, and sometimes among the least heritable traits such as yield components. Among plant architecture traits, TINB showed a high interaction with the environment, whereas tassel traits were among those with the lowest interaction with the environment. Genetic variance was, however, generally much more significant than G × E and here we focus on the main genetic effects.

Trait correlation and differentiation among genetic groups

The range of correlations between flowering time and stature related traits was similar in our panel and in the US NCRPIS panel, that is, 0.78 (NCRPIS) and 0.76 (this study) for plant height, 0.77 (NCRPIS) and 0.83 (this study) for ear height. The correlation between plant height and ear height was stronger in this study (0.86) than in NCRPIS (0.59). The estimated average within group trait correlations and the global trait correlations showed similar trends, suggesting that pleiotropy or linkage were to a large extent responsible for the observed correlations (Supplementary Figure S2,Supplementary Table S2). The relationship between among groups and overall trait correlations was looser (r²=0.64) and presented a sigmoid shape (Supplementary Figure S2). Absolute correlation values were systematically higher among groups compared to within groups, highlighting that differential selection among groups targeted specific combination of traits that were not necessarily highly correlated originally. This suggests that more recombination/dissociation occurred between moderately correlated traits compared with highly correlated traits such as FFLW8 and LFNB or PTHT, allowing selection in different directions, on purpose or because of drift.

Phenology was the main factor of phenotypic differentiation, as illustrated by the first dimension of PCA which was highly correlated with FT and explained 32% of the total phenotypic variation. This first axis was also highly correlated with the total number of leaves, especially those below the ear. This was consistent with the fact that leaves and flowers are both produced by apical meristems, with flowers only being produced after the switch between vegetative and reproductive stages, and leaf primordia then turning to male inflorescence primordia (Kwiatkowska, 2008). Yield was negatively correlated with FT, which could be explained by the poor adaptation of late photoperiod sensitive materials to temperate environments. Because of this confounding effect between precocity and yield, interpretation of yield QTLs detected in our study should be taken with caution. The PCA nevertheless revealed a second trend in yield independent of phenology. The second PCA axis highlights that yield related to the variation in the number of kernels per row (KERROWNB). Dent material of American origin (Stiff Stalks and CBD) had a clear advantage in that sense, consistent with its well-established contribution to high yielding material in various regions worldwide, crossed with other American dents or with locally adapted material. Tillering (TINB), mostly related to axes 3–5, was another feature that appeared to be orthogonal to flowering time, along with the length of husk leaves (HL, related to axes 3–5) and to some extent the number of kernels per row (KERROWNB, related to axes 2 and 4). These traits distinguished Northern Flints, which showed high TINB and long HL compared with other genetic groups. This ‘bushy architecture' maximizes light interception at sparse densities, which is consistent with the limited light radiation conditions under which this material was cultivated by semi-nomadic Iroquoian people.

Associations, pleiotropic effects and candidate genes

It was recently shown that including candidate SNPs in kinship calculation causes ‘proximal contamination' and decreases the power of linear mixed models. To circumvent this problem, we used in Bouchet et al. (2013) SSR markers to estimate the kinship. Although this method always proved to be much superior to a naive model, the P-value distribution suggested incomplete control of false positives for some traits in the present study (results not shown). We therefore decided to use a kinship calculated with SNP markers that were not on the chromosome carrying the candidate SNP (Rincent et al., 2014).

As discussed in Bouchet et al. (2013), the 43 224 markers that were used here do not represent a sufficient density to comprehensively assess the genetic architecture of complex traits. This could be illustrated, for instance, by the discovery by Romay et al. (2013) of a single SNP within the ZmCCT region highly associated with the flowering time gene among 680 000 SNPs. Increasing the number of markers would be of great value for a more in-depth analysis of this data set but the density that was used in this study nevertheless gave some general and specific information about the genetic architecture of most traits.

Overall, 71 associations were detected in our study at P-value E-05, corresponding to 40 genomic regions of 1 Mb affecting at least one individual trait or a principal component. The traits were highly contrasted in terms of number of QTLs detected and the phenotypic variation explained by these QTLs (Table 2). No association was found for Em8, SL, TaAk, S3LF8, EARHT, LFNBa, EARNB or KERROWNB. A single QTL was detected for ASI8, emergence vigor, TKW, KW, TL, BZL, TaSt and PTHT. The maximum variation explained by markers in the multi-locus model was 48% with 13 QTLs for TINB. Number of associations common to two traits increased with window size and lower P-values (< E-04; Figure 3, Supplementary Table S7). Main pleiotropic effects were observed between phenology related traits (MFLW8, FFLW8, LFNB and PTHT), TINB and HL, and ROWNB and TKW (Figure 3, Supplementary Figure S5, Supplementary Figure S6). Note that QTL effect directions were consistent with trait correlations. We comment below on main associations for development traits (TINB, HL, LFNB, MFLW8, FFLW8 and ROWNB) for which the highest number of associations was found.

TINB was associated with 13 QTLs that jointly explained 48% of the trait variation. These QTLs displayed no pleiotropic effects with other traits in our study, except with HL (Chr 1: 167 864 888), suggesting that TINB was mostly under a specific genetic control. Five QTLs displayed candidate genes. The most significant association (Chr1: 271,334,672, P-value < E-12) was observed for the transcription factor Knotted-1 (Kn1, GRMZM2G017087, (Vollbrecht et al., 2000). Knotted1-like homeobox (KNOX) proteins accumulate in cells of the shoot apex and maintain the meristematic properties of the cells. This gene may contribute to the differentiation of axillary meristems controlling tiller number and would deserve further investigation. Note that in this same region of chromosome 1, we found no association between TINB and Tb1 itself (Chr1: 265 745 979), although the latter would have been a logical candidate. Interestingly, we found an association for the first PCA axis close to GRMZM2G346263 (Chr1: 264 953 283) at 700 kb from Tb1, and a locus associated with ROWNB (Chr1: 273 450 920). This confirms that many genes affecting plant architecture cluster in this region, consistent with findings of Studer and Doebley (2011) who highlighted that this region fractionates in several QTLs involved in plant and ear architecture. Another candidate gene in another region on chromosome 5 was the aquaporin ZmNIP1-1 (GRMZM2G041980).

LFNB and LFNBb were associated with two and three QTLs respectively. The QTL located at ZCN8 (GRMZM2G179264; Chr8: 123 501 085) was detected by Bouchet et al. (2013) for flowering time using the same panel but a different model. Its effect on both FFLW8 and MFLW8 was confirmed in the present study with a more stringent model (see below). Note that ZCN8 was associated with the first PCA axis, confirming a major role in the overall phenotypic variation observed in our panel. Its effect on LFNB was also found by Peiffer et al. (2014), in the US diversity panel and in the US NAM (P-value < E-76). It corresponds to the Vgt2 QTL found in numerous studies (Romay et al., 2013; Bouchet et al., 2013). Danilevskaya et al. (2011) suggested that ZCN8 plays a pleiotropic role in the regulation of generalized growth of vegetative and reproductive tissues, controlling leaf and stem growth as well as tassel branch number. It was consequently associated with flowering time and to a much lower extent with correlated traits such as the tassel branch number in our study. Note that the second QTL with a large effect on LFNB (Chr1: 228 051 413) had a milder effect on flowering time (P-value < E-03).

Four QTLs were detected for flowering time (FFLW8 and/or MFLW8). The three QTLs detected in addition to the ZCN8 region had lower significance levels.

ROWNB was associated with 5 QTLs. The strongest association was observed on chromosome 10 (15 004 433) at 300 kb from the exopolygalacturonase1 (PGL1; GRMZM2G418644; Chr10: 14 690 751). This QTL also affected TKW and the opposite direction of effects on both traits was consistent with the global negative correlation that was observed between those traits. The candidate genes for other QTLs were a glucose-1-phosphate adenylyltransferase (GRMZM2G391936; Chr1: 273,447,466), zma-MIR393b (Chr3: 18 638 816) and a protein at 800 kb from GOS1 (GRMZM2G113414; Chr3: 189 347 802). One QTL was found for KW in a gene that could be a good candidate for selection, RUBISCO activase1 (Rca1; GRMZM2G162200).

Note that association analyses with PCA axes identified 3 associations that were shared by individual trait analyses (PCA1 and LFNB at ZCN8 on chromosome 8, PCA5 and TINB on chromosome 9, and PCA4 and ROWNB on chromosome 10) and also 6 new associations.

As discussed above, one new association detected with the first PCA axis was close to GRMZM2G346263 (Chr1: 264 953 283) at 700 kb from Tb1 (Chr1; 265 745 979) and 400 kb from the transcription factor sigma-like factor2B (Sig2B, GRMZM2G164084; Chr1: 264 461 820). A second new association detected with the first PCA axis was a serine/threonine protein at 3 Mb from a protein (Chr2: 78 698 293; GRMZM2G474153) involved in carbohydrate metabolism and remobilization (ACC1; GRMZM5G858094; Chr2: 82 394 515) on the centromere of chromosome 2. Note that this region was reported as associated with flowering time using a less stringent model (Bouchet et al., 2013).

One new association detected with PCA axis 2 was a cyclin delta-3 (GRMZM2G161382; Chr2: 163 317 827) involved in germination process and plantlet establishment controlled by growth regulators (Quiroz-Figueroa and Vázquez-Ramos, 2006). A second was a protein with transporter activity (GRMZM2G431314; Chr4: 28 833 860) at 100 kb from the phytohormone outer cell layer 5a involved in kernel size (OCL5a; GRMZM2G130442; Chr4: 28 979 897; Khaled et al., 2005).

Finally, two new associations were detected with the fourth PCA axis.

Exhaustive information about QTL positions and candidate genes are in Supplementary Table S6.

As the traits discussed above are being documented to an increasing extent in the literature and are less subject to G × E interactions than yield, a formal meta-analysis of all QTL investigations projected on the same version of the maize genome would be highly beneficial to gain a deeper understanding of pleiotropy and gene networks.

Differences in genetic architecture among traits

Overall, numbers of detected QTLs and the proportion of variation explained by detected QTLs appeared to be higher for traits related to development (D, D/G in Table 2, typically TINB, LFNB below the ear, FFLW8, MFLW8 and ROWNB) than for traits affected by growth (G, G/D in Table 2, typically PTHT and yield components). This suggests that these last traits were either more subject to environmental effects or displayed a more complex genetic determinism which diminished the power of detection. As an example, less QTLs were found for PTHT than LFNB. Note that the fact that no QTL was found for EARNB and EARHT may seem to contradict this trend but it is well known that the development of ears results from complex trophic factors that control the fate of pre-established primordia, which is very different from the differentiation of the apex from the vegetative to reproductive stage (Kwiatkowska, 2008). This trend may nevertheless be confounded with other factors, like the type of selection that traits are/have been experiencing. One may expect that traits for which more QTLs were detected were not subject to directional selection but displayed an optimum in a given environment, which is typically the case for flowering time and LFNB. This stabilizing selection is known to maintain diversity and consequently the overall power of QTL detection. This phenomenon is less likely to occur for ROWNB and TINB, selection being expected to be generally positive for the first one and directional conditionally to environmental conditions and agricultural practices for the second one (for example, selection against tillers in modern selection of varieties adapted to high planting densities). This supports the hypothesis of a simpler genetic determinism for developmental traits that would be controlled by small to medium effect QTLs acting additively whereas growth affected traits would be putatively controlled by more pleiotropic or even epistatic QTLs.

Conclusion

As discussed in the introduction, different periods of maize selection that succeeded each other since domestication have led to contrasted plant architectures, mostly as an indirect consequence of yield maximization given specific environmental constraints and agricultural practices. Some attempts have been made to select for new variety types with different plant architecture such as leafy types, by monitoring known developmental genes (Modarres et al., 1997), but this has remained limited so far to our knowledge. Our results suggest that association genetics is particularly adapted to the discovery of QTLs for developmental traits and the evaluation of their possible pleiotropic effects. This may help the breeder to counter select genes with unfavorable effects with respect to classical ideotypes, or positively select new plant ideotypes, leading to a more efficient utilization of genetic resources.

Data Archiving

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.13074.