Discrimination thresholds of normal and anomalous trichromats: Model of senescent changes in ocular media density on the Cambridge Colour Test

Abstract

Age-related changes in chromatic discrimination along dichromatic confusion lines were measured with the Cambridge Colour Test (CCT). One hundred and sixty-two individuals (16 to 88 years old) with normal Rayleigh matches were the major focus of this paper. An additional 32 anomalous trichromats classified by their Rayleigh matches were also tested. All subjects were screened to rule out abnormalities of the anterior and posterior segments. Thresholds on all three chromatic vectors measured with the CCT showed age-related increases. Protan and deutan vector thresholds increased linearly with age while the tritan vector threshold was described with a bilinear model. Analysis and modeling demonstrated that the nominal vectors of the CCT are shifted by senescent changes in ocular media density, and a method for correcting the CCT vectors is demonstrated. A correction for these shifts indicates that classification among individuals of different ages is unaffected. New vector thresholds for elderly observers and for all age groups are suggested based on calculated tolerance limits.

1. INTRODUCTION

Trichromatic discrimination relies on signals originating in three classes of cone photoreceptors that are combined by postreceptoral opponent mechanisms. Color discrimination in the Rayleigh region of the spectrum (λ ≥ 540 nm) is affected by many factors, the dominant one being sex-linked polymorphisms of the photopigments. About 8% of Caucasian males and 0.5% of Caucasian females have some sort of congenital color vision deficiency resulting from either the absence (in the case of dichromats and monochromats) or a slight shift (in the case of anomalous trichromats) in the spectral sensitivity of the middle- and/or long-wavelength cone photopigments. The consequences for color mixture equations or color discrimination form the basis of classification of congenital color vision deficiencies. Tests that screen for color vision deficiency are standardized using results from a large group of observers whose color vision is classified by other tests. Known effects of age-related changes in color vision are, however, seldom part of the norms.

Numerous senescent changes take place in the optics and visual pathways that may contribute to color vision changes across the life span. Separating the consequences of these factors has been a major challenge [1]. With age, sensitivity of cone mechanisms is reduced, and there are anatomical changes affecting mechanisms of transduction and adaptation [2,3]. Between the ages of 20 and 80 years, approximately 25% of retinal ganglion cell axons are lost [4,5], and there is about a 50% decrease in neuronal packing in the area of visual cortex subserving the macula [6,7]. In addition, there are age-related reductions in pupil size and age-related increases in ocular media density [8]. Quantitative analyses of changes in visual performance with age, and individual variation at each age, benefit from controlling or measuring these optical effects for each subject [9,10]. Often, however, this is not possible, so data from the literature may be used to estimate them. Age-related changes in the ocular media have been described by linear [11,12] and nonlinear functions of age [13]. Pokorny, Smith, and Lutze [14] reported a bilinear increase in lens optical density with age, with a first slow phase until the age of ~60 years and a faster second phase for ages above 60 years. van de Kraats and van Norren [13] proposed a nonlinear model of the optical density by incorporating a set of “age-related density coefficients” that change as a function of squared age. As shown in this paper, these changes have consequences for assessment of color vision using standardized parameters for all ages.

The Rayleigh match is considered definitive in classifying M- and L-cone deficiencies, while pseudo-isochromatic plates (e.g., Ishihara, HRR) and arrangement tests (e.g., the Farnsworth and Lanthony D15) are more broadly available. Modern graphics cards for control of computer-based color vision tests have become popular because of their ease of use, ability to test simultaneously different directions in color space, and incorporation of rigorous psychophysical procedures {e.g., Cambridge Color Test (CCT) [15,16] and Color Assessment and Diagnosis (CAD) test [17]}. All of these tests are designed based on congenital color vision deficiencies, but they also have proven valuable for detecting acquired deficiencies of color vision [18–22].

Lakowski [23] found that red/green color matching, as assessed with an anomaloscope, remains stable up to the age of 55 years while discrimination along a blue–yellow axis changes significantly after the age of 35 years. He identified a class of observers as “pseudo-anomalous,” which referred to mild tritan deficiency. Verriest, van Laethem, and Uvijls [24] concluded that the error score of the Farnsworth–Munsell 100-hue discrimination test is smallest in the twenties and increases with age. Later studies showed that, following adolescence, there is a decline in sensitivity of all three cone types [3,10] and a decrease in chromatic discrimination along all the three cone axes (protan, deutan, and tritan) with age [25]. These changes are due, in part, to changes in receptoral and postreceptoral mechanisms [9,10,26]. More recently, Paramei [27] reported that chromatic discrimination along a deutan line deteriorates significantly after the age of 40 years and that there is a significant decline in chromatic sensitivity for all three axes after the age of 50 years. This study did not, however, screen participants for physiological abnormalities that are known to be more frequent with increasing age [1] and which result in acquired deficiencies of color vision.

The focus of this report is on the use of the CCT, a computer-controlled test designed to minimize brightness cues using the principle of pseudoisochromaticity with the rigors of four alternative forced choice and adaptive staircases. The task for participants was to detect the orientation of a Landolt C [16]. As luminance cues are negligible, the gap must be detected based on chromatic contrast along protan, deutan, or tritan confusion lines. This is known as the tri-vector test, but other vectors can be measured with the CCT to define discrimination ellipses. The developers of the test determined performance standards for the tri-vector test, which may be used for classification of color vision deficiency, based on young adult observers. Several previous studies [27–29] have already demonstrated age-related changes in performance on the CCT but have not evaluated the consequences for changes in the white point and vector directions due to change in the density of the ocular media. This is the purpose of this study while also presenting new threshold data for the CCT tri-vector mode across an extensive age range (from 16 to 88 years old) with inclusion only of individuals whose performance is uncomplicated by abnormalities of optical or retinal/optic nerve disorders that are common among the elderly.

2. METHODS

A. Subjects

Two hundred subjects (16 to 88 years old, 112 males and 88 females) performed the CCT monocularly in its tri-vector mode. Participants in this study were recruited for a number of different studies over the past 10 years in our laboratory. One study explicitly recruited participants with congenital color vision deficiencies [30], hence the high percentage of color vision deficient observers in this paper. A certified ophthalmic technician excluded participants with best-corrected visual acuity (BCVA) worse than 20/25, intraocular pressure >22 mm Hg, abnormal pupil exam, abnormal ocular motility, and abnormal visual fields (assessed with a confrontational visual field test). An ophthalmologist or optometrist from the UC Davis Eye Center performed a slit lamp exam and dilated fundoscopy to exclude participants with abnormalities of the anterior or posterior segment. Digital fundus photographs (TRC.501X Mydriatic Retinal Camera; Topcon Medical Systems, Inc.) were reviewed by a retinal specialist to exclude individuals with retinal or optic nerve abnormalities. Lens classification was not available; however, significant lens opacity (or cataract) would be detected in clinical examination. Note also that clinically significant opacity of the lens would be inconsistent with the inclusion criterion of 20/25 visual acuity or better. Among the participants, 162 subjects (74 male and 88 female) were classified with the Neitz OT anomaloscope (Model: OT [one lamp model], Neitz co. Ltd.) as normal trichromats. Another six subjects were excluded because they were statistical outliers.

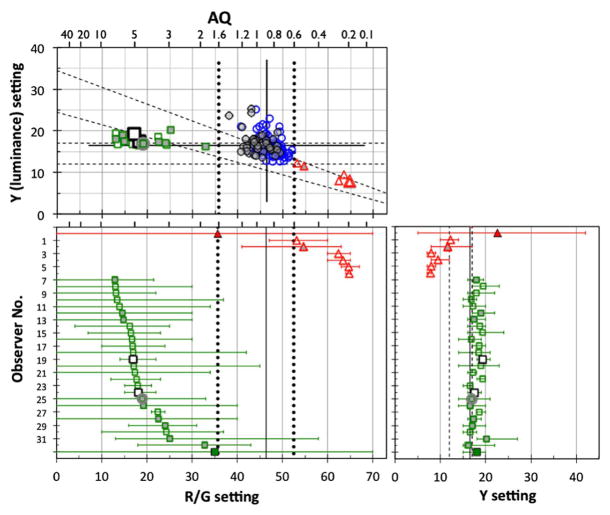
Color normal observers, denoted by circles in Fig. 1, were so classified as they had a narrow range of mixtures (R/G setting) in free-matching and anomalous quotients (AQ) from 0.6 to 1.6 (52.5 > R/G > 35.7). Because of the wide age range of our observers, we used a slightly wider AQ range than usual, 0.7 to 1.4 (50.1 > R/G > 38.2) [31]. The manufacturer’s nominal value of R/G is 44.2 in the AQ equation for an observer with normal color vision. The mean R/G and AQ for all color normal observers in this study were 46.4 ± 2.5 and 0.89 ± 0.13, respectively. The mean of the Y for all color normal observers was 16.5 ± 2.2.

Fig. 1.

R/G and Y settings of Rayleigh matches on the anomaloscope based on the mean of three to five free-matching trials for 194 subjects. (Top panel) R/G versus Y settings. (Bottom left) Mean of R/G setting with the range between maximum and minimum matches for observers who were not classified as normal trichromats. (Bottom right) Mean of Y setting with range. Protanomalous (triangles) and deuteranomalous (squares) subjects were differentiated from color normals (circles). Bottom panels also show data of one protanopic (filled triangles) and one deuteranopic (filled squares) subject in this study. Open and gray symbols denote the data of observers younger and older than 60 years, respectively. R/G and Y settings were the means of all satisfied matches for each observer. Two larger open squares (observer #19 and #24) denote “mild anomalous subjects” as classified by the CCT (as explained elsewhere). The square with gray circle (#25) denotes “the subject showing high thresholds” on the CCT (see Fig. 6 and text for details). Diagonal and horizontal dashed lines in the top panel denote auxiliary lines by the anomaloscope manufacturer for separating protanopes (protanomaly) and deuteranopes (deuteranomaly), respectively. Solid vertical and horizontal lines denote the mean of all normal observers. Vertical dotted lines denote R/G settings corresponding to anomalous quotients (AQ) of 1.6 and 0.6. Vertical dashed lines in the bottom right panel denote the manufacturer’s deuteranomaly line. Numbers at the top of the panels denote AQs.

We also identified 6 protan and 26 deutan subjects. The anomalous trichromats were classified by the results of free-matching trials for R/G and Y adjustments and fixed-matching trials at R/G settings in steps of 10 units from 0 to 70. Range bars in the bottom panels of Fig. 1 show the maximum and minimum matches and indicate that variation of anomalous trichromats’ R/G and Y settings in the top panel of Fig. 1 were not caused by inclusion of matching in free trials nor by taking the match average. Instead, the range of matching had variation as R/G setting shift between the anomalous trichromats.

Protanomaly was classified by choosing matched values of R/G and Y settings over a much wider range than the color normal and arrayed along lines parallel to the protan range, which is between the lines from (0, 34.5) (R/G, Y) to (73, 5) and from (0, 24.5) to (73, 2.5) with this anomaloscope, as shown in the top panel of Fig. 1. To classify deuteranomaly, we identified matched values arranged along horizontal lines parallel to the deutan range, which is between the lines from (0, 17) to (73, 17) and from (0, 12) to (73, 12). Protanopes and deuteranopes were classified by their acceptance of all matches in fixed R/G steps from 0 to 70. If the protanomalous or deuteranomalous observers were unable to match at least one of the fixed R/G settings, their mean points were averaged from all accepted matches both in free matching and fixed matching. From traditional anomaloscope classifications [31], the protanomalous should have anomalous quotients (AQ) <0.6 and the deuteranomalous >1.6. Two mild anomalous subjects, denoted by larger open squares in Fig. 1, were classified as deuteranomalous by their Rayleigh matches but classified differently by the CCT (details explained in Results). One deuteranomalous observer, denoted by the square with gray circle, denotes “the subject showing high thresholds” on the CCT (detailed in Results).

Subjects were also tested with the Panel D-15 arrangement test as well as the F2 and HRR plates under an illuminant with a correlated color temperature of 6280 K. These latter tests provided additional confirmation of color vision classifications, but they are not presented here primarily because they are dichotomous tests.

The procedures and experiments conformed to the principles expressed in the Declaration of Helsinki and were approved by the UC Davis Medical Center’s Institutional Review Board. Written informed consent was obtained from each subject prior to testing.

B. Cambridge Colour Test

The CCT was used in its tri-vector mode with the background and stimulus generated by a VSG 2/3 graphics card (Cambridge Research Systems) installed on a PC and presented on a CRT monitor (Eizo FlexScan T566). The 5.3° diameter background, (u′, v′) = (0.198, 0.469) in CIE LUV color space, consisted of many circular disks of varying size and luminance (2–16 cd/m²; mean = 9 cd/m²). A subset of pseudoisochromatic disks varied in chromaticity to form a Landolt C having inner and outer diameters of 2.2° and 4.3°, respectively, with a gap size of 1° at a viewing distance of 247 cm. The chromaticity of the Landolt C changed in three directions in color space coinciding with protan, deutan, and tritan confusion lines; co-punctual points are (u′, v′) = (0.658, 0.501), (u′, v′) = (−1.217, 0.783), and (u′, v′) = (0.257, 0), respectively. Subjects were provided 5 s to respond, 2 s longer than recommended by the test developers because some older observers had difficulty responding in shorter times. The test was performed monocularly with the eye found to have better BCVA. The presentation of the three chromatic directions was interleaved, and each vector’s threshold was obtained with a separate staircase after 11 reversals. The reported threshold is the average vector length of the last six reversals in CIE u′v′ color space multiplied by 10⁴.

We performed the CCT in a darkened room where the only illumination originated from the CRT monitor used for CCT measurement. The monitor was calibrated using a luminance and color meter (CS-100, Konica-Minolta) and custom-made software with the gamma calibration system provided by the manufacturer of the VSG card (OptiCal and control software, Cambridge Research Systems).

C. Model for Fitting Threshold Changes with Age

We initially evaluated five models with least-squares regression to describe CCT vector lengths as a function of age: three functions using the raw vector lengths without any transformation (linear, bilinear, quadratic) and two functions with the data transformed to a decadic logarithm scale (log-linear and log-quadratic). The linear model was selected for its simplicity and ease of use as a test standard. The bilinear model was selected because of evidence that the optical density of the ocular media [14] follows a bilinear function. The quadratic model was selected because of evidence that color discrimination can be described with a U-shape function having a minimum around the second decade of life [24,25]. The log-transformed models were selected so as to minimize the variance in the data.

These analyses were performed on unbinned CCT data. The linear model [Eq. (1)] proved adequate for describing the protan and deutan vector changes with age; the tritan vector was best fitted with the bilinear function [Eq. (2)]. Quadratic and log models did not improve the prediction to the data of this study: for quadratic and log-quadratic models, reductions of errors by their quadratic terms were not statistically significant by the likelihood ratio test [32] except for the quadratic model used to fit the tritan data. The log-linear model was slightly worse than the linear model for protan and deutan data fits and much worse than the bilinear model for tritan data fit:

$$y=a+bx,$$ (1)

$$y=m(x-a)+b(m=c(x\le a),d(x>a)).$$ (2)

D. Implications of Changes in Retinal Stimulation with Age

Interpreting age-related changes in visual performance requires taking into account the change in intensity and spectral composition of the retinal stimulus with age, owing to the increase in ocular media density and reduction in pupillary diameter, as previously described [13,14]. One of the safest ways to control this change is to use stimuli comprised of monochromatic lights, combined with individual measurement of heterochromatic flicker photometry (HFP) as in previous color discrimination studies [9,10]. However, even when using a CRT monitor for stimulus presentation, the effect of the ocular media density change can be compensated by individual HFP measurements using the same CRT monitor [33,34].

To control the effect of age-related change in pupil size, either a Maxwellian-view optical system or an artificial pupil may be used. However, we used natural viewing for the CCT in this study, which means that pupil size was not equated across observers. Individual differences in pupil size thus result in individual variations of cone stimulation at the retina, which can affect the analysis of mechanisms and quantitative models of color discrimination measured with the CCT, unless only contrasts of cone stimulation between background and stimuli determine color discrimination. Our previous research [10] suggests that chromatic discrimination thresholds mediated by red–green chromatic-opponent mechanisms (L-M cone signals), but not a blue–yellow chromatic-opponent mechanism (S-cone versus L- and M-cones), can be predicted without individual corrections for ocular media density. The CCT is administered in Newtonian view and the software does not use HFP measurement to control for individual differences in retinal illumination but instead exploits the pseudoisochromatic test principle of jittering luminance. Nevertheless, the chromatic coordinates of the stimuli may be shifted because of the increased ocular media density with age. In this study, we used two kinds of ocular media density models with the measured spectral radiance distribution of the RGB phosphors to calculate actual chromatic coordinates of stimuli as presented for a 20-year-old observer’s stimulation shown in Fig. 2. In the bilinear model, the lens optical density (T_L) of an average observer is described by Eq. (3) as a function of wavelength (λ) and age (A) in years [14]:

$$T_{L,BL}(\lambda ,A)=\{\begin{array}{ll}{T}_{L1}(\lambda )[1+0.02(A-32)]+T_{L2}(\lambda )\hfill & A<60,\hfill \\ T_{L1}(\lambda )[1.56+0.0667(A-60)]+T_{L2}(\lambda )\hfill & A>60,\hfill \end{array}$$ (3)

where T_L1 and T_L2 are wavelength-dependent coefficients from Pokorny et al. [14]. In addition, a nonlinear model from van de Kraats and van Norren [13] was tested in a form modified by the CIE Technical Committee 6–15, 2012 [35]. This model is not described further because it produced fits comparable to the less complex Eq. (3).

Fig. 2.

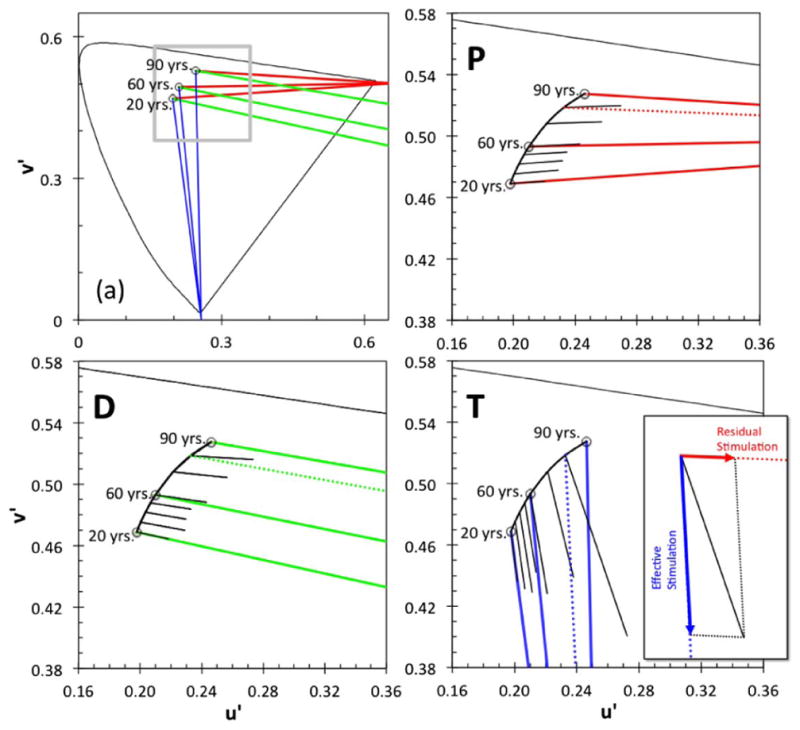
(a) Protan (red), deutan (green), and tritan (blue) vector directions for 20-, 60-, and 90-year-old “standard observers” in u′v′ chromaticity coordinates, starting from the shifted white background, calculated on the basis of age-related changes in the ocular media. The gray inset denotes the portion of the chromaticity diagram shown in panels P, D, and T depicting magnified color confusion lines (colored lines) and the average of measured vector lengths (black lines) of protan (P), deutan (D), and tritan (T) vectors for each decade (±5 years, but the 80-year-old group includes one 88-year-old observer), multiplied by a factor of 5 for clarity. Dotted lines denote confusion lines starting at white for an 80-year-old standard observer (not shown in Fig. 2(a)). These age-dependent vectors originate from different backgrounds and have a different slope than the nominal CCT color confusion lines because chromaticities of the white background and the targets are shifted by age-related changes in the ocular media, calculated from the bilinear model. The inset in panel T shows an example of effective stimulation (tritan vector) and residual stimulation (in the case of protan vector) caused by the original (uncorrected) tritan test.

Following Eq. (3), we calculated the retinal stimulation induced by each phosphor using the ratio of the lens optical density, T_L between an individual at a given age and the 20-year-old standard observer. This permitted the neutral constant value in the optical density to be ignored. The spectral radiance distribution of each phosphor, LE_i, was reduced with the T_L ratio for each wavelength and the X, Y, Z tri-stimulus values were given by

$$\begin{array}{l}{X}_i(A)=k\sum _{\lambda }\left\{{LE}_i(\lambda )·I_i·\overline{x}(\lambda )·{10}^{\{T_L(\lambda ,20)-T_L(\lambda ,A)\}}\right\}\hfill \\ Y_i(A)=k\sum _{\lambda }\left\{{LE}_i(\lambda )·I_i·\overline{y}(\lambda )·{10}^{\{T_L(\lambda ,20)-T_L(\lambda ,A)\}}\right\}\hfill \\ Z_i(A)=k\sum _{\lambda }\left\{{LE}_i(\lambda )·I_i·\overline{z}(\lambda )·{10}^{\{T_L(\lambda ,20)-T_L(\lambda ,A)\}}\right\}\hfill \end{array}\}(i=R,G,B),$$ (4)

where k is a constant such that Y_i(A) matches the luminance unit (cd/m²) and I_i is the intensity of each phosphor in arbitrary units defined by k. x̄(λ), ȳ(λ), and z̄(λ) are the color-matching functions [36]. From the stimulus chromaticity coordinates (x_sc, y_sc, L_sc), the tri-stimulus values of each phosphor were calculated for the 20-year-old standard observer with each phosphor’s chromaticity coordinates (x_i, y_i) given by Eq. (5), and each kI_i was obtained from the tri-stimulus values given by Eq. (4):

$$\begin{array}{c}{X}_{sc}=\frac{x_{sc}}{y_{sc}}{L}_{sc}=\sum _i\{X_i(20)\}=\sum _i\left\{\frac{x_i}{y_i}{Y}_i(20)\right\}\\ Y_{sc}=L_{sc}=\sum _i\left\{Y_i(20)\right\}\\ Z_{sc}=\frac{1-x_{sc}-y_{sc}}{y_{sc}}{L}_{sc}=\sum _i\{Z_i(20)\}=\sum _i\left\{\frac{(1-x_i-y_i)}{y_i}{Y}_i(20)\right\}\end{array}\}(i=R,G,B).$$ (5)

Using the kI_i, reduced tri-stimulus values for each observer [from Eq. (4)], the lens-corrected L-, M-, S-cone stimulation and chromaticity coordinates were calculated. Because the graphic card’s RGB values remain the same for all subjects, the greater attenuation of shorter wavelengths at the retina of older observers implies that the chromaticity coordinates of the stimuli, as defined for the 20-year-old standard observer, are shifted toward middle wavelengths.

With this analysis, we can estimate the age-dependent cone stimulation for each observer. L-, M-, and S-cone luminance-based excitations for an observer (of age A) can be estimated by the cone fundamental matrix of Smith and Pokorny [37] and the X_i(A), Y_i(A), and Z_i(A) from Eq. (4). We may next consider the extent to which the protan, deutan, and tritan confusion lines used by the CCT will be shifted because of ocular media density changes with age. Figure 2(a) shows the theoretical protan, deutan, and tritan confusion lines for different origins under the bilinear model. These origins are the calculated background chromaticities for different ages, as they are shifted by the change in the optical density of the ocular media. Panels P, D, and T show the averaged measured vector lengths for each age group (steps of one decade) of normal trichromats in this study for the protan, deutan, and tritan vectors (denoted by black lines) starting from the shifted background white. For clarity, only the portion of the chromaticity diagram denoted by the gray square in Fig. 2(a) is shown. From panels P, D, and T, the shift in direction can be seen between the theoretical confusion lines (red, green, and blue lines for protan, deutan, and tritan confusion lines, respectively) and the vector used during the experiment (black lines). This shift in vector direction represents the error in stimulation vectors due to intrusion of other cone types, which we call “misdirection” of the original (uncorrected) stimulation vector. The misdirection is relatively small for the protan and deutan vectors but larger for the tritan vector.

3. RESULTS

A. Normal Trichromats

Figure 3 shows the CCT data for protan, deutan, and tritan vectors of 162 color normal observers. The linear model provides an adequate fit to the protan and deutan CCT vector data. As can be seen in panels P and D, the protan and deutan thresholds are positively and significantly correlated with age (r = 0.379, p < 0.001 and r = 0.431, p < 0.001, respectively). For the tritan vector (panel T), the bilinear model describes the data best. The intersection of the two linear functions is at the age of 67.7 years. Both linear regressions are positively and significantly correlated with age; the first branch describes the data for the younger population (r = 0.356, p < 0.001), and the second branch fits the data of the older population (r = 0.452, p < 0.01). The coefficient of determination (proportion of variance explained), r², for the tritan model fit is higher than protan and deutan vectors, as shown in Table 1.

Fig. 3.

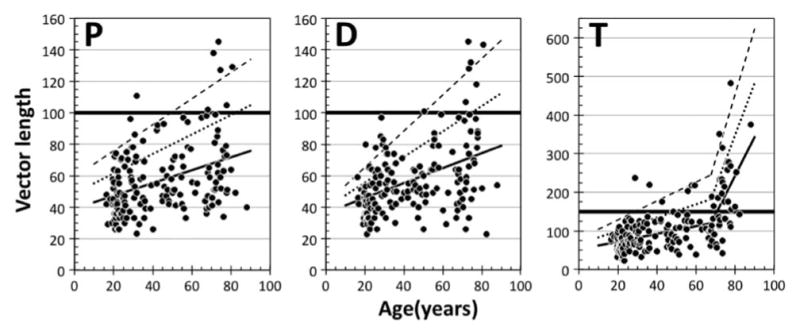
Protan (P), deutan (D), and tritan (T) CCT vector threshold data plotted in separate panels as a function of age. The solid lines were fitted by linear regressions. Note that the tritan data were fitted with two linear regressions as suggested by modeling. In each panel, dotted and dashed lines represent the mean +1 SD and +2 SD, respectively (see text for details). The thick solid horizontal line represents the maximum threshold for each vector expected for a normal trichromat, as given by the developers of the CCT (100 for protan and deutan vectors and 150 for the tritan vector). Note the different y-axis range on the tritan plot.

Table 1.

Vector Length for Three Ages with Linear and Bilinear Models^a

Vector	Line	Slope (1st)	Slope (2nd)	V.L. at 20	V. L. at 67.7	V. L. at 80	r2
Protan	Mean	0.409	–	47.0	(66.5)	71.6	0.144
	Mean + ISD	0.619	–	61.4	(90.9)	98.5	–
	Mean + 2 SD	0.829	–	75.7	(115.3)	125.5	–
Deutan	Mean	0.468	–	45.6	(67.9)	73.7	0.185
	Mean + ISD	0.812	–	55.6	(94.3)	104.3	–
	Mean + 2 SD	1.149		65.4	(120.2)	134.4	–
Tritan	Mean	0.992	10.02	72.4	119.7	243.0	0.449
	Mean + ISD	1.723	13.45	100.7	182.8	348.5	–
	Mean + 2 SD	2.454	16.89	128.9	246.0	453.9	–

^aV.L. refers to vector length; slope (2nd) denotes the slope of the second linear function in the bilinear model fitted to the tritan vectors.

To describe age-related variation in CCT thresholds, we calculated standard deviations (SDs) separately for age groups using 10-year bins (e.g., 15–24.9, 25–34.9, and so forth, but one 88-year-old observer was included in the 80-year [75–84.9] bin). Numbers of observers in each bin are 42, 33, 13, 20, 11, 30, and 13 from 20- to 80-year bins. All mean +1 SD and mean +2 SD points were fitted with linear regressions to yield the dotted and dashed lines shown in Fig. 3. Because the tritan data were fitted with the bilinear function, two sets of +1 and +2 SD linear functions were calculated. These +1 SD and +2 SD limits are not parallel to the regression line but rather diverge, indicating that the variation increases with age. In the deutan and tritan vector data, the correlation of the standard deviations of thresholds with age is statistically significant (deutan, r = 0.880, p < 0.01 and tritan, r = 0.886, p < 0.01 for all tritan data) but not significant in the protan vector data (protan, r = 0.719, p = 0.069). Although the increase of the standard deviation with age is characteristic of prior aging studies (e.g., [38]), it may simply reflect the higher thresholds with age. Thus, we also calculated the standard deviation in the natural logarithmic scale. The correlation of the standard deviations of thresholds with age is, however, statistically significant only for the deutan data (r = 0.834, p < 0.05). Because the size of the standard deviation in the logarithmic scale reflects the ratio, instead of the difference, with the (geometric) mean, it is consistent with the interpretation that the accuracy of color discrimination does not change significantly with age. Rather, the increase of the standard deviation can be explained by variation of ocular media density in older individuals (e.g., [38]) as suggested by no significance in the protan vector data, as the chromaticities of this vector correspond to longer dominant wavelengths. Table 1 summarizes parameters and numeric values at specific ages of the linear and bilinear fitting functions.

In Fig. 3, there are four (out of 162) color normal observers (ages: 23.8, 28.3, 30.9, and 71.9 years old) for whom all three vector lengths exceed the mean +1 SD and three observers (ages: 23.3, 70.5, and 73.5 years old) having all three vector lengths less than the mean −1 SD. These individual differences cannot be explained by clinical abnormalities, as all observers were carefully screened by experienced clinicians and measures described in Methods.

Using the transformations described in Methods (Section 2.D), we estimated the age-dependent coefficients that should be used to correct for possible discrepancies between the theoretical confusion lines and the vectors used in the CCT, although note that these coefficients are specific to the spectral radiance of our monitor. Increased ocular media density in the elderly observers has a significant effect on the direction and length of the CCT vectors for the different cone types. As shown in Fig 2, panel T, a change in the vector direction reduces the stimulation of cones on the selected vector and increases the stimulation of other cone types. It is, thus, important to calculate coefficients that correct the vector lengths for this age-related change. Figure 4(a) shows these coefficients. Each CCT P, D, and T vector can be considered part of a discrimination ellipse along each color confusion axis. Ocular media density changes cause minimal change in the direction of protan and deutan color confusion lines (as seen in Fig. 2 and as shown by the coefficients in Fig. 4); therefore, the color discrimination ellipses along these two axes should not change significantly with age for normal trichromats. Thus, we employed the simplest treatment of the underlying color discrimination mechanisms in which detection by L- and M-cone stimulation differences can be considered independent of each other. Therefore, effective L-cone (or M-cone) stimulation by the chromatic change of protan (or deutan) vector stimuli in the CCT measurement could be calculated as the “true” length of the protan (or deutan) vector, which is the length of the projection from the corrected vector (as shown by black lines in Fig. 2) on the protan (or deutan) confusion line (colored lines in Fig. 2). Note that if this effect is not negligible, it also may affect the “true” tritan vector (projected on the tritan confusion line). For the protan and deutan vectors of the CCT, the lengths of the “true” protan and deutan vectors are almost the same as the nominal vector lengths (the maximum error is less than 0.18% and 1.19%, respectively), as shown in Fig. 4. Any bias (unintended stimulation of other cone types) introduced by the “true” tritan vectors can be ignored (see Fig. 5(a) and the next paragraph).

Fig. 4.

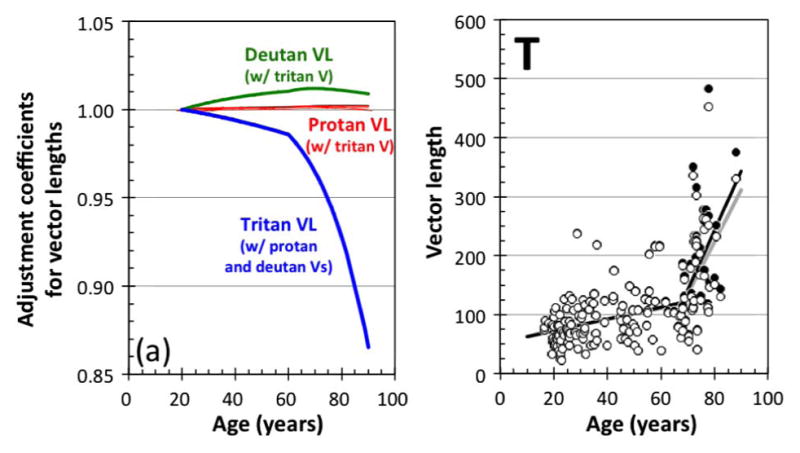
(a) Correction coefficients plotted as a function of age to calculate the effective vector lengths (VLs) of the protan (red curves), deutan (green curves), and tritan (blue curves) vectors (Vs) on the protan, deutan, and tritan confusion lines. Lines denote coefficients calculated from the linear and bilinear model. The coefficients for the tritan vector length are the mean of two coefficients each associated with the protan or deutan vectors. (Panel T) Original tritan vector length data (filled circles) and corrected tritan vector length data (open circles) modified by the coefficients shown in Fig. 4(a). Black and gray solid lines denote the best bilinear fits of the original and corrected tritan vector lengths, respectively.

Fig. 5.

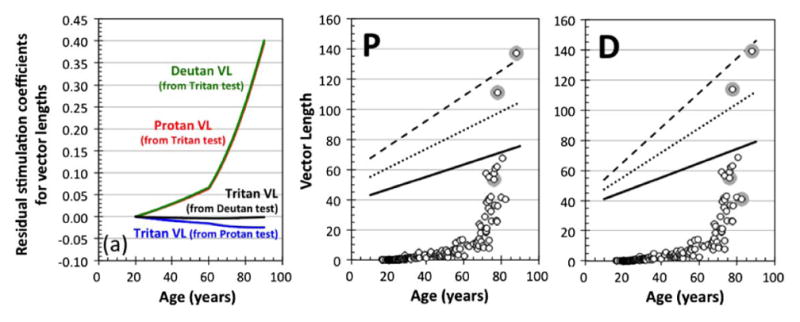
(a) “Residual” stimulation coefficients as a function of age to calculate the effective vector lengths (VLs) of the protan (red curves), deutan (green curves) and tritan (blue and black curves) vectors on the protan, deutan, and tritan confusion lines. These “residual” stimulations represent excitation of untargeted cone types caused by vector direction errors in the CCT. Functions denote coefficients calculated by the bilinear model of the ocular media density. (Panels P and D) Comparison of protan vector length (panel P) and deutan vector length (panel D) between the mean, +1 and +2 SDs of original protan and deutan vector lengths, as shown in Fig. 3, and the “residual” protan and deutan vector lengths (open symbols) calculated by uncorrected (misdirection) tritan vector length with the bi-linear model (see text for details). Gray circles denote the “residual” vector length data that are longer than the original protan and deutan vector length data for each individual observer.

In contrast, the relatively large change of the tritan vector direction could introduce errors in the estimation of tritan vector lengths with age. Figure 4 (panel T) shows the original (filled circles) and the corrected tritan vector lengths (open circles). For most of the tritan data, the lens density change has little to no effect, although the older observers’ data show a slight reduction in the tritan vector length. Overall, the age-related changes measured for the confusion lines on the CCT on a CRT monitor do not cause significant shifts in vector lengths except for ages above 75 years in which they are overestimated by at least 5%. This overestimation does not cause a significant change in the best fit of our data using a bilinear model. The new first slope is 0.953 instead of 0.992, and the new second slope is 8.60 instead of 10.02. The crossing point of the two linear functions is at the age of 67.6 years instead of 67.7 years [the black and gray solid lines in Fig. 4 (panel T)].

From these analyses, we conclude that the discrepancy between the nominal and the “true” vectors does not cause any misclassifications. However, it has to be noted that the amount of misdirection of the tritan vector for observers above the age of 80 is large, as shown in Fig. 2 (panel T). The misdirection of the tritan vector here not only causes a reduction of the tritan vector length projected on the tritan confusion line, as shown in Fig. 4(a), but also causes significant L- and M-cone stimulation. As shown below, the tritan (T) vector threshold can be determined by L- and/or M-cones, not by S-cones in some elderly observers. This could be a problem, especially in the screening of patients with acquired deficiencies of color. Thus, we have to estimate the extent of the residual stimulation on vector thresholds, especially on the tritan vector. Figure 5(a) shows coefficients indicating these “residual” stimulations caused by the misdirection of protan, deutan, and tritan tests in the CCT. Such “residual” stimulation coefficients allow us to calculate the “possible” (effective) vector lengths of the protan (red curves), deutan (green curves), and tritan (blue and black curves) vectors on the “true” protan, deutan, and tritan confusion lines. At the age of 75 years, the residual stimulations of L- and M-cones, which are indicated as effective protan and deutan vector lengths, are 19.6% and 20.1% of the uncorrected tritan vector length. With such strong stimulation to L- and M-cones, the measured threshold (vector length) could be affected. Figure 5 (panels P and D) shows the comparisons between the mean, +1 and +2 SDs of originally measured protan and deutan vector lengths (as in Fig. 3) and the calculated protan and deutan vector lengths of “residual” stimulations from the tritan test data. In the 80-year-old observer group, three to four of 13 observers demonstrate longer protan and deutan vector lengths calculated as “residual” stimulations than the original protan and deutan test data (in Fig. 3, panels P and D), respectively. This result suggests that, for observers older than 75 years, there is a slight risk that the tritan vector length from the CCT could be affected by stimulation of the L- and/or M-cones.

B. Color Vision Deficiency

Figure 6 shows the protan, deutan, and tritan CCT vector data for the protanomalous and deuteranomalous subjects plotted as a function of age and compared with the best-fitting functions derived from normal trichromats. Note again that classification of color vision deficiency was based on Rayleigh matches. For the case in which the protan or deutan vector measurement was not possible, the vector length was set arbitrarily to 1100 (outside the range of the test). Two deuteranomalous subjects (aged 28 and 50 years) shown as “mild anomalous observers” in Fig. 1 with AQs 4.98 and 4.49, however, failed to be classified as deuteranomalous with CCT deutan thresholds of 78 and 81, respectively. They are shown in Fig. 6 (panel D) by the two points under the thick horizontal line representing the thresholds for the deutan vector test given by the test developers of the CCT. Except for these two observers, the CCT classified all color deficiencies in a manner that was consistent with the anomaloscope. Both protan and deutan tests indicated that anomalous observers exceeded the maximum threshold for each vector expected for normal trichromats, owing to the close correlation of these two vectors in color space. The test protocol relies on the longer vector for classification. In protan tests, protanomalous observers tend to have longer vector lengths than the deuteranomalous as expected. In deutan tests, however, deuteranomalous observers did not necessarily have longer vector lengths than the protanomalous observers. These facts are not surprising because color discrimination ellipsoids for dichromats and anomalous trichromats have much longer axes than color normals in the direction of their individual confusion lines. As shown in Fig. 2, the direction of protan and deutan confusion lines differs by only 16.5 and 6.3 deg for 20- and 80-year-old standard observers in u′v′ coordinates, respectively. Also, the CCT is affected by the bandwidth of the monitor phosphors, and the “true” confusion lines for individuals with cone polymorphisms [39] may differ from the nominal CCT vectors that are appropriate for a standard observer.

Fig. 6.

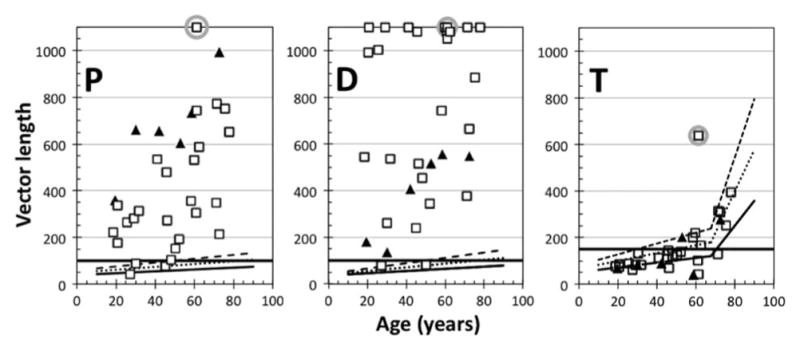
Protan (P), deutan (D), and tritan (T) vector lengths for protanomalous and deuteranomalous subjects as a function of age. The filled triangles and open squares represent the protanomalous and deuteranomalous subjects, respectively. The solid lines are the normal mean, with dotted and dashed functions representing +1 and +2 SDs (as in Fig. 3). The thick solid horizontal lines represent the thresholds for each vector, as given by the developers of the CCT. For cases in which the protan or deutan vector measurement was not possible, the vector length was set as 1100 (four deuteranomalous subjects’ data points were plotted at 1080 or 1050 for clarity in the plot). Data points enclosed by a gray circle denote the deuteranomalous observer (discussed in the text).

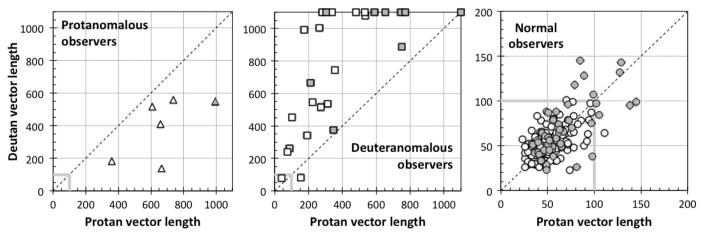
For the classification of anomalous trichromats by the CCT, the protan and deutan data for each observer were compared in Fig. 7. This comparison demonstrates that the classifications agree with Rayleigh matches of all protanomalous and deuteranomalous observers except for the two aforementioned mild anomalous trichromats. With respect to the classification of color deficiency, ratios of protan- and deutan-vector length were higher in the protanomalous than the deuteranomalous (p = 1.96e – 6 <0.001; Mann–Whitney U-test). All protanopes and deuteranopes had vector lengths at the test maximum of 1000 for their missing cone type. However, it is impossible to separate the deuteranopes from the extreme deuteranomalous observers confidently with the CCT data, partly because, among anomalous trichromats, 11 of 26 deuteranomalous observers had vector lengths that reached the measurement ceiling of the CCT (plotted as the length of 1100).

Fig. 7.

Comparison between protan and deutan vector lengths for protanomalous (triangles; left panel), deuteranomalous (squares; middle panel), and normal subjects (circles; right panel) classified by Rayleigh matches. Open and gray symbols denote the data of observers younger and older than 60 years, respectively. The vector length of 1100 means that the protan or deutan measurement was not possible (one deuteranomalous subject’s data points were plotted at 1080 for clarity).

For normal trichromats, the protan- and deutan-vector lengths are strongly correlated (r = 0.632; p < 0.001), as shown in Fig. 7. The mean ratio of protan-to-deutan-vector length is 1.06, and there is no statistically significant difference in ratios between age groups of less than or over 60 years. These facts suggest that sensitivities of color discrimination on these two color confusion lines are almost the same for color normal observers regardless of the absolute value of these vector lengths.

As shown in Fig. 6, the majority of tritan thresholds of color deficient subjects fall within the limits for color normals with the exception of one deuteranomalous observer. This means that “residual” stimulations caused by the misdirection of tritan tests, as described previously, did not influence the protan and deutan test data over 150. The observer denoted by a square with gray circle in Fig. 6 was classified as a deuteranomalous observer by the Rayleigh match (see Fig. 1), but he showed unusually high thresholds on all three color confusion lines. Overall, the results indicate that correct classification of anomalous trichromats by the CCT is not dependent on age.

4. DISCUSSION

Data from the tri-vector mode of the CCT are presented for observers from 16- to-88 years of age. The protan and deutan threshold data were best described with a linear function, while the tritan vector data were best described with a bilinear function. The effects of age-related change in the optical density of the ocular media on the tritan vector’s origin and length were calculated, and it was found that the modeled shifts are not critical for classification of protanomalous and deuteranomalous observers, although the tritan data for observers above age 70 can be affected modestly by L- and M-cone intrusion. The advantage of this study is the classification of subjects by their Rayleigh match with careful screening of subjects’ eye health.

The CCT is commonly used to screen color deficient observers and the maximum vector lengths, as given by the test developers, for a normal trichromat are 100 for protan and deutan vectors and 150 for the tritan vector. As shown in Fig. 3 and Table 2 for the protan and deutan vectors, these values seem to accurately classify red–green color vision for all ages. Intersections of the +1 SD lines (mean +1 SD) to the maximum thresholds for the protan and deutan vectors were at 82.4 and 74.8 years, respectively. As expected, the protan and deutan tests for the four protanopes and two deuteranopes, respectively, were not possible, and thresholds reached the ceiling of 1000. For anomalous observers, vector lengths were much longer than normal observers and, except for two mild deuteranomalous observers, the classification of protanomaly and deuteranomaly could be made by the CCT, regardless of age. In contrast, on the tritan vector test, many older observers had thresholds above 150, and the intersection of the +1 SD fit was at 48.6 years. It should be pointed out, however, that, while the Rayleigh matches provide external validation for protan and deutan classifications, we have no external validation that our subjects were free of congenital S-cone abnormalities. The incidence of congenital tritan deficiency is, however, low [40,41], and it is unlikely that any observers had congenital tritan defects. Furthermore, tritan scores of the elderly did not indicate tritanopia, at least when compared with the tritan vector length (at the limit of 1000) observed for one congenital tritanope, not included in this study, with a confirmed P264S mutation of the S-cone opsin gene on chromosome 7 [42,43]. For other older subjects with high tritan vectors, we cannot exclude the possibility of incomplete penetrance of an S-cone mutation that could result in milder tritan deficiencies [44,45], although this is unlikely in view of the low prevalence. Older observers often have acquired deficiency of color vision secondary to retinal or optic nerve disease affecting tritan discrimination [46,47]; however, retinal diseases were exclusion criteria for participation in this study. Thus, tritan vector lengths above 150, while indicating poor discrimination, are not abnormal among individuals even close to 50–55 years of age.

Table 2.

Tolerance Limits of Vector Length of Thresholds^a

Age (yrs.)	16–30	31–60	61–88	16–50	51–88	All Ages
N	62	55	45	101	61	162
Protan	78.3	95.8	124.9	83.8	117.5	97.6
Deutan	79.3	88.8	131.7	78.3	123.9	98.8
Tritan	138.1	190.5	356.4	149.5	326.5	237.9

^aTolerance limits are for 90% of the population with 95% probability.

To estimate the maximum CCT thresholds for classification of an individual as having normal color vision, we summarize the tolerance limits of protan, deutan, and tritan vector tests (for 90% of the population with 95% probability [48] for younger (16 to 30 years), middle-aged (31 to 60 years), and older (>60 years) observers in Table 2. Tolerance limits of protan and deutan vector tests for all observers irrespective of age are 97.6 and 98.8, respectively. The maximum protan and deutan threshold for observers younger than 50 years is approximately 90 and for observers older than 50 years is approximately 130, meaning that the maximum threshold of 100, given by the test developers of the CCT, is too low for all ages. In contrast, the results of this study indicate that the maximum threshold for normals on the tritan vector (150) is valid only until ~50 years of age; therefore, this threshold is too low for observers over that age, under our testing conditions. The maximum tritan threshold for observers older than 50 years is approximately 350. Additionally, we suggest using a 5 s stimulus presentation instead of 3 s as the default, in which the vector lengths can be much longer than these values.

We have already proposed a model of red–green and blue–yellow chromatic-opponent mechanisms to predict age-related change in color discrimination [9,10]. However, it is difficult to apply this model to the results here because we cannot derive the Weber fraction and noise constant for our model based on the lengths of only three vectors (directions in color space), and there was no direct compensation for age-related changes of ocular media optical density and pupil size. Thus, we simply calculated the threshold elevations in terms of the vector length change due to age-related changes in ocular media density. We specified thresholds for each cone type at the retina, as described in Eq. (6), with age, A:

$$\begin{array}{ll}\hfill \mathrm{\Delta }{P}_{m,\text{Cornea}}(A)& ={10}^{[T_{L,m}(A)]}·\mathrm{\Delta }{P}_{m,\text{Retina}}(A)(m=1,2,3)\hfill \\ \hfill [(P_1,P_2,P_3)]& =(L,M,S),(T_{L,1},T_{L,2},T_{L,3})\hfill \\ \hfill & =(T_{L,\text{Lcone}},T_{L,\text{Mcone}},T_{L,\text{Scone}})].\hfill \end{array}$$ (6)

The ratio of measured thresholds at age A and age 20 years is expressed as the multiple of the lens density ratio and the ratio of threshold at retina as in Eq. (7):

$$(\mathrm{\Delta }{P}_{m,\text{cornea}}(A)/\mathrm{\Delta }{P}_{m,\text{Cornea}}(20))=(10[T_{L,m}(A)/10[T_{L,m}(20)])·(\mathrm{\Delta }{P}_{m,\text{Retina}}(A)/\mathrm{\Delta }{P}_{m,\text{Retina}}(20)).$$ (7)

Figure 8 shows the ratio of measured thresholds calculated from tolerance limits in Table 2 (the unit value was the data of the 16–30 observer group, denoted by points) and the ratio of lens density for each cone type calculated with the bilinear model (denoted by solid lines). These two ratios are close at least in deutan and tritan tests, meaning that the ratios of the thresholds at the retina, (ΔP_m,Retina(A)/ΔP_m,Retina(20)), are about one, and the age-related change of the lens density influences deutan and tritan discriminations. As we described in our previous work [9,10], even by exclusion of the age-related changes of ocular media optical density and pupil size, impairment of the S- and L-cone pathways is partly due to losses in sensitivity at a neural level, mainly caused by the reduction of cone signals with a stable noise level [9,49]. The impairment of S-cone pathways, however, appears mostly at relatively low S-cone stimulation levels (i.e., color discrimination in yellowish colors), and the thresholds of tritan vector test, measured with bluish colors against neutral colors, would be less influenced. In contrast, the color discrimination depending on L-cone stimulation difference became worse with age, as demonstrated by an increment of Weber fraction with age [9]. Overall, it is clear that the age-related changes in cone sensitivities and discrimination are dependent on reduced cone stimulation due to ocular media and neural changes that effectively reduce photon capture [9,10,50]. Thus, a critical consideration for future development of screening tests for color deficiency is their dependence on light level that especially affects tritan discriminations in the elderly.

Fig. 8.

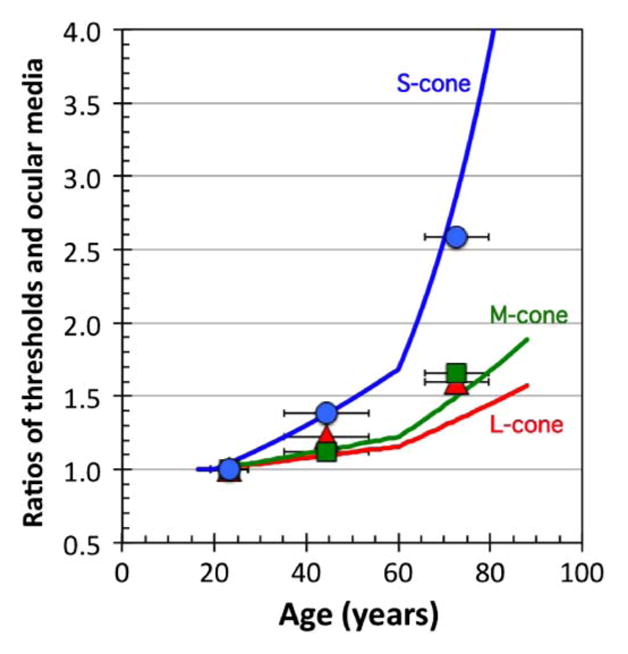
Ratio of measured thresholds (vector lengths) calculated from tolerance limits (as in Table 2) for protan (red triangles), deutan (green squares), and tritan (blue circles) tests and ratio of ocular media density for L- (red curve), M- (green curve), and S- (blue curve) cones calculated with the bilinear model. These ratios are based on the youngest age group (16–30 observer group) and 20-year-old standard observer (see text for details). Horizontal error bars denote standard deviations of age in each observer group of tolerance limits.

Several previous reports have described normative data for the CCT with observers of different ages. Ventura et al. [28] presented data for a limited age range (18–30 years). For this age range, our data and their data agree well, and with the original norms for the CCT. Ventura et al. found that limits of normal threshold (tolerance limits for 90% of the population with 95% probability) for the protan, deutan, and tritan vectors are 69.3, 82.4, and 113.4, respectively (in u′v′ × 10⁻⁴ units), while the limits from the data in this study for the same age range are 79.5, 80.1, and 139.6 for the protan, deutan, and tritan axes, respectively. The Ventura et al. [28] study, however, had a large number of subjects (75 subjects) for this restricted age range, resulting in smaller standard deviations from the mean (11.4, 15.0, and 19.6 for protan, deutan, and tritan, respectively) while corresponding standard deviations from our 59 subjects in the same age range are 15.8, 16.5, and 33.5. This might explain the difference in the tritan vector results, although in the Ventura et al. [28] study, tritan vector lengths over 150 were not included. If we were to eliminate subjects with vector lengths over 150, our limits of threshold would be 121.9 for the tritan axis with a standard deviation of 25.9.

Paramei [27] reported data from 160 subjects whose age varied from 20 to almost 60 years. The thresholds (upper tolerance limit) for the decade from 50 to 59 years were 82, 127, and 159 for the protan, deutan, and tritan axes. The biggest difference between Paramei’s [27] data and this study is on the tritan axis where we found for the same decade a normal limit of 245.8. However, she used a stimulus presentation time of 8 s while we used 5 s. The longer stimulus duration might facilitate S-cone discrimination and, hence, reduce the CCT thresholds. The other difference of experimental conditions is that she used a luminance range of 8–18 cd/m², while we used a range of 2–16 cd/m². The maximum luminance contrasts in the circular disks of the CCT stimuli were 2.25 and 8.0, respectively. Because dithering of luminance contrast is reduced, discrimination would be enhanced. In a subsequent study, Paramei and Oakley [29] described results from the same subjects but added additional younger and older observers for a total sample of 291 normal trichromats from 10 to 88 years of age. Using Tables 1 and 2 of that paper, we recalculated the upper tolerance limits of her 91 subjects 60–88 years of age and found that the protan, deutan, and tritan axes for 90% of the population with 95% probability were 127, 128, and 323, respectively. Thus, their data for protan and deutan thresholds generally agree with this study (61–88 years of age: 124.9, 131.7, and 356.4 as in Table 2); however, there is a large difference on the tritan thresholds for the older subjects.

Another difference between the study by Paramei and Oakley [29] and this one is the model used for fitting the discrimination data to age. The authors found that all three axes show a U-shaped trend with a minimum discrimination around the third decade of life (20–30 years of age) when the vector lengths were plotted in a natural logarithmic scale. Other studies also demonstrated a similar U-shaped discrimination function [24,25] with a minimum around the second decade of life. The major parameter that might account for the difference of the function shape in fits is the inclusion of younger observers. We did not include any observers younger than 16 years of age; thus, more complex models of discrimination performance with age were not required to describe our data. Additionally, our middle-age observers tended to show higher thresholds than their data.

5. CONCLUSION

The CCT tri-vector test reliably identified and classified individuals with congenital red–green color vision defects. However, our data suggest that, to classify an individual as normal, there must be different CCT vector thresholds for older age groups. The developers’ guidelines can be applied confidently for ages up to ~50 years. Above this age, the thresholds of color normal observers for all three axes are greater than the normal limits specified by the test developers. Finally, our data suggest that age-related changes in thresholds, especially the tritan thresholds, are due to reduced cone excitation resulting, in part, from increases in optical density of the ocular media as well as neural losses.