Renal plasma flow (RPF) measured with multiple-inversion-time arterial spin labeling (ASL) and tracer kinetic analysis: Validation against a dynamic contrast-enhancement method

Abstract

Purpose

To propose and validate a method for accurately quantifying renal plasma flow (RPF) with arterial spin labeling (ASL).

Materials and methods

The proposed method employs a tracer–kinetic approach and derives perfusion from the slope of the ASL difference signal sampled at multiple inversion-times (TIs). To validate the method's accuracy, we performed a HIPAA-compliant and IRB-approved study with 15 subjects (9 male, 6 female; age range 24– 73) to compare RPF estimates obtained from ASL to those from a more established dynamic contrast-enhanced (DCE) MRI method. We also investigated the impact of TI-sampling density on the accuracy of estimated RPF.

Results

Good agreement was found between ASL- and DCE-measured RPF, with a mean difference of 9 ± 30 ml/min and a correlation coefficient R = 0.92 when ASL signals were acquired at 16 TIs and a mean difference of 9 ± 57 ml/min and R = 0.81 when ASL signals were acquired at 5 TIs. RPF estimated from ASL signals acquired at only 2 TIs (400 and 1200 ms) showed a low correlation with DCE-measured values (R = 0.30).

Conclusion

The proposed ASL method is capable of measuring RPF with an accuracy that is comparable to DCE MRI. At least 5 TIs are recommended for the ASL acquisition to ensure reliability of RPF measurements.

1. Introduction

Renal perfusion, often reported as renal plasma flow (RPF), has been shown to be a valuable parameter for assessing renal diseases including chronic kidney disease [1], renal artery stenosis [2], and diabetic nephropathy [3,4]. Para-aminohippurate (PAH) clearance methods for measuring RPF [5,6] involve complicated procedures requiring urine collection and blood sampling [7], and do not measure RPF separately for the individual kidneys. Dynamic contrast-enhanced (DCE) techniques record tracer enhancement in the renal tissues using either computed tomography (CT) [8] or magnetic resonance imaging (MRI) [9–11], and quantify tissue perfusion from the dynamic images with tracer kinetic modeling. Despite the reliability of DCE techniques, they require the injection of contrast agents that are either radioactive or have been linked to the development of nephrogenic systemic fibrosis (NSF) [12].

Arterial spin labeling (ASL) MRI was proposed to measure tissue perfusion without the use of any exogenous contrast agents [4,13,14]. In ASL, the magnetization of blood flowing into the tissue is modified, thereby acting as an endogenous contrast agent. A number of different ASL schemes have been proposed, such as the pulsed ASL technique called flow-sensitive alternating inversion recovery (FAIR) [15,16]. In FAIR, two otherwise identical images are acquired following different inversion pulses; one after a spatially non-selective (NS) inversion, and the other after the inversion of a slab slightly thicker than and centered on the imaging slice (referred to as the slice-selective or SS inversion). The time delay between inversion and image readout is called the inversion time (TI). Subtraction of the two images (SS – NS) nullifies signal from static tissue, leaving only signal from inflowing blood. Essentially, the difference between the SS and NS images is a perfusion-weighted image analogous to the contrast-enhanced images from DCE MRI.

However, quantification of tissue perfusion from ASL data is more challenging than from DCE MRI data. First, the ASL difference signal is weak [17,18] and decays within 3–5 s due to T₁ relaxation [19]. With such low and decaying signal intensity, artifacts from respiratory motion or unequal NS and SS inversion-efficiencies can introduce large errors into ASL perfusion estimates. Furthermore, the signal difference depends heavily on the time interval between labeling and imaging, i.e., the inversion time (TI) [19,20]. These challenges prompt us to follow the approach taken by Buxton et al. [19] and acquire ASL data at multiple TI values. Similar to the idea of dynamic imaging, ASL data acquired at multiple time points can be analyzed using a tracer kinetic approach so that the above confounding factors can be properly considered based on their temporal characteristics, thereby enabling the accurate quantification of tissue perfusion.

In this study, we propose to quantify renal perfusion from multiple-TI ASL data using a tracer kinetic approach. For a group of human subjects, renal perfusion estimates from ASL were compared to those from DCE MRI. Using the same data, we also investigated the impact of TI sampling density on the accuracy of perfusion estimation.

2. Materials and methods

2.1. MRI data acquisition

This HIPAA-compliant study was approved by the local institutional review board. Fifteensubjects(9male,6 female; age range 24–73) were recruited: 7 were healthy volunteers without a history of chronic illness while the other 8 had suspected liver cirrhosis (with glomerular filtration rate estimates from the serum-creatinine MDRD formula ranging from46to93ml/min). After giving written informed consent, each subject underwent renal ASL and DCE MRI scans in a 3T scanner (TimTrio; Siemens Medical Solutions, Erlangen, Germany).

For ASL imaging, we used a FAIR tagging scheme with balanced steady-state free precession (bSSFP) readout [21] with the following imaging parameter values: repetition time (TR) 3.68 ms, echo time (TE) 1.84 ms, field of view (FOV) 380 × 380 mm, matrix 256 × 256, slice thickness 8 mm, and GRAPPA acceleration factor of 2. Before recording the bSSFP signals, an alpha/2 pre-pulse and 10 dummy pulses were applied to establish a steady state. To allow for magnetization recovery after image acquisition, an idle period was appended so that the total time for each acquisition was 6 s. During a 24-s breath-hold, we were able to acquire two pairs of SS and NS images from an oblique-coronal slice through the long axis of both kidneys. For the 7 healthy volunteers, the acquisition was repeated using 16 different TIs (requiring 16 breath-holds): 150 ms, then 200 to 1600 ms at 100-ms intervals. Our preliminary study indicated that this protocol of sixteen 24-s breath-holds was challenging for diseased patients. Therefore, for the 8 cirrhosis patients included in our study, we only acquired ASL data at 5 TIs: 150, 500, 800, 1000 and 1500 ms.

Following the ASL examination, DCE MRI was performed using a previously published protocol [9,22] to obtain reference measurements of renal perfusion. Briefly, dynamic images of 2D slices through the abdominal aorta and the kidneys were acquired using a saturation-recovery-prepared FLASH sequence after the injection of 4 ml gadoteridol (500 mmol/l). The imaging slice though the kidneys was positioned to match the slice from the ASL acquisitions. This 2D sequence allowed for a high temporal resolution of 1.5 s which was important for tracking rapid tracer kinetics during the dynamic scan. Dynamic MR signals were sampled from manually drawn ROIs covering the renal cortex and medulla [23] and were then converted to the concentration of contrast material [9,24]. The volumes of the renal cortex and medulla were obtained from 3D-VIBE measurements. Using the renal volumes and an arterial input function (AIF) sampled from the abdominal aorta at the level of the renal arteries, contrast enhancement in the renal cortex and medulla was analyzed using a 3-compartment tracer kinetic model to extract renal cortical and medullary RPF. More details can be found in the published studies [9,22].

2.2. Quantifying renal perfusion from ASL images

The ASL images with different TIs were acquired during separate breath-holds, so there was typically some relative displacement between image sets. Therefore, the first processing step was image registration using a previously validated technique [23,25] that uses the generalized Hough transform to align all image frames with a common user-defined template. On the registered images, ROIs were defined to include all cortical regions and all medullary regions for each kidney. When defining each ROI, the renal hilum was avoided in order to exclude the segmental arteries. From the cortical and medullary ROIs for each kidney, we obtained averaged NS and SS signal values at the different TIs.

Cortical and medullary RPF was estimated from the ASL signal vs. TI curves using a tracer kinetic approach (presented in the Appendix). Briefly, we reconstructed the NS curve to correct for differences in inversion efficiency between the NS and SS inversions. A piecewise linear formula was derived to quantify the relationship between tissue perfusion and the ASL difference signals, and by fitting the formula to the signals, renal perfusion was estimated. Multiplying perfusion estimates by the cortical and medullary volumes obtained from the VIBE data yielded cortical and medullary RPF.

2.3. Comparing RPF between ASL and DCE MRI

The agreement between RPF measured from ASL and that from DCE MRI was evaluated by computing the mean and standard deviation of the absolute difference between the two groups of RPF values. We also computed Pearson's correlation coefficient (R) between the two groups of measurements.

Using the acquired data, we also investigated the impact of TI sampling density (analogous to temporal resolution in DCE MRI) on the accuracy of the perfusion estimates. Specifically, we down-sampled the signal vs. TI curves from the 16-TI acquisition group (Table 1). At each down-sampling step, we dropped the signals from two TI values such that the remaining TI values were as evenly distributed as possible. Perfusion values were estimated from all down-sampledsignal vs.TIcurves using the proposed method, and were compared to the reference values measured from DCE MRI.

Table 1.

TI sampling of the ASL signal and its impact on the accuracy of perfusion estimation.

Number of TIs	TI values (ms)	Mb0∙(1+fss) factor	R	RPFASL–RPFDCE (ml/min)
16	150, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600	13.0 ± 3.9	0.92	−9 ±30
14	150, 200, 300, 400, 500, 700, 800, 900, 1000, 1100, 1300, 1400, 1500, 1600	13.2 ± 4.1	0.91	−9 ±31
12	150, 200, 300, 500, 600, 700, 900, 1000, 1100, 1300, 1400, 1500	14.1 ± 5.8	0.85	−9 ± 44
10	150, 300, 500, 600, 800, 1000, 1100, 1300, 1400, 1600	12.9 ± 4.6	0.86	−8 ±45
8	150, 300, 500, 700, 900, 1100, 1300, 1500	13.0 ± 5.6	0.84	−8 ±42
6	150, 400, 700, 1000, 1300, 1600	13.3 ± 3.8	0.86	−12 ± 37
5	150, 500, 800, 1000, 1500	12.2 ± 5.5	0.84	−5 ±51
4	150, 600, 1100, 1600	11.9 ± 6.2	0.80	−12 ± 52
2	400, 1200	19.2 ± 20.3	0.30	16 ± 243

3. Results

ASL images were acquired from all subjects without noticeable artifacts. Representative NS and SS images are shown in Fig. 1. Fig. 2 demonstrates how the proposed method was implemented for quantifying renal perfusion. In Fig. 2a, a large difference between representative NS and SS signals from the renal cortex can be observed, likely due to different NS and SS inversion efficiencies. After correcting for this discrepancy, the ASL difference signal exhibits a linear increase from which tissue perfusion can be extracted (Fig. 2b).

Fig 1.

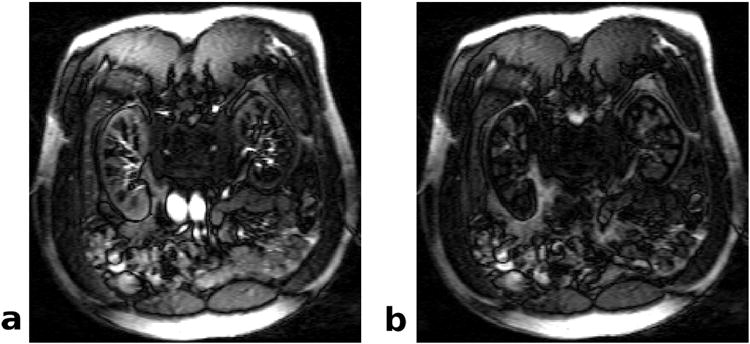
FAIR-bSSFP images of human kidneys. These coronal images were acquired at a TI of 1000 ms after (a) slice-selective and (b) nonselective inversion pulses.

Fig 2.

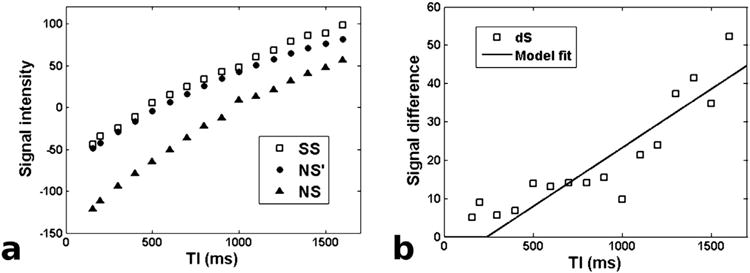
Demonstration of the proposed method for extracting perfusion from multi-TI ASL data. a) Example SS and NS signals from the renal cortex. The black circles (NS') mark the NS signals that were reconstructed to correct for the imperfect-inversion artifact. b) The multi-TI difference signal dS_n is the difference between the SS and NS' signal curves normalized by T₁ relaxation. The solid line is the fit of our proposed model to the data.

For the seven subjects with ASL data acquired at 16 TIs, the measured RPF was 151 ± 37 ml/min in the cortex and 25 ± 22 ml/min in the medulla. These values differ from the DCE-measured values (cortex: 152 ± 41; medulla: 43 ± 12) by 9 ± 30 ml/min. The correlation coefficient between the two groups was 0.92. For the eight subjects with ASL data acquired at 5 TIs, ASL-measured RPF was 158 ± 103 ml/min in the cortex and 36 ± 31 ml/min in the medulla, differing from the DCE-measured values (cortex: 180 ± 70; medulla: 33 ± 10) by 9 ± 57 ml/min. The correlation coefficient between the two groups was 0.81. Correlation plots for these comparisons are shown in Fig. 3.

Fig 3.

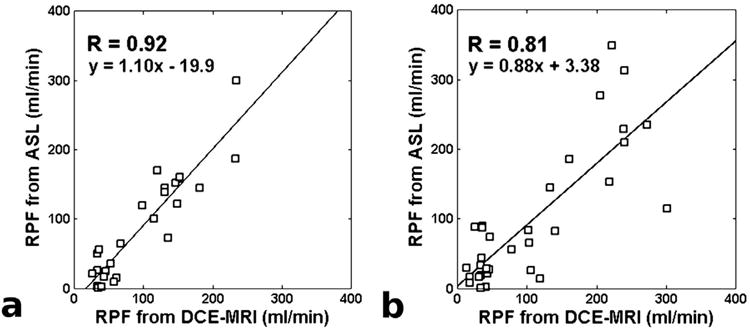
Correlation between RPF estimates from ASL and DCE MRI in the subject groups with 16-TI (a) and 5-TI (b) acquisitions.

The ASL signal vs. TI curves with 16 TIs were down-sampled, and the estimated RPF values were compared to those from DCE MRI (Table 1). As a general pattern, correlation between ASL- and DCE-measured RPF values decreased with TI-sampling density, from R = 0.92 with 16 TIs to R = 0.80 with 4 TIs. The 5-TI dataset had a correlation coefficient of R = 0.84, comparable to the 5-TI data from the other subject group (R = 0.81, Fig. 3b). When data from only two TIs were used for model fitting, the resulting perfusion estimates showed low correlation with DCE MRI (R = 0.30). A similar trend was observed in the difference between ASL and DCE-measured RPF values. With 16-TI data, the difference between ASL and DCE-measured RPF was −9 ± 30 ml/min, but when down-sampled to only 2 TIs, the difference increased to 16 ± 243 ml/min. Note that as long as the ASL data was sampled at more than two TIs, the average difference between RPF estimates from ASL and DCE MRI was relatively constant (less than 13 ml/min), suggesting that decreasing the TI-sampling density did not introduce significant systematic bias into the perfusion estimation.

In Table 1, we also list the factor M_b0∙(1+f_ss) (see Eq. (A.4) in the Appendix) estimated for the subjects. This factor was relatively constant across the different TI sampling sets (around 12–14; variability of ∼30%), except when only 2 TIs were used (19.2 ± 20.3). This finding confirms that the M_b0 and f_ss parameters are relatively constant between MR examinations as long as the experimental setup is the same.

4. Discussion

In this study, we proposed a method for accurately quantifying renal perfusion from ASL data acquired at multiple TIs. In a group of human subjects with a wide range of renal perfusion, the measurements from our technique were in good agreement with those from a more established DCE MRI method. Results from this study also suggest the acquisition of ASL data at a minimum of 5 different TI values to ensure the reliability of renal perfusion measurements.

Despite the potential of ASL as a non-invasive tool for measuring tissue perfusion, a number of challenges have limited its clinical application. These include low SNR, complicated tracer kinetics, and variability of the transit-delay from the labeling region to the imaging slice [18,20,26]. We recommend the acquisition of ASL data at multiple different TIs, which will naturally consider the effect of the variable transit delay. With data from multiple-TIs, we also have the opportunity to estimate and therefore reduce the difference in inversion efficiency between SS and NS acquisitions which would otherwise result in an overestimation of perfusion [27,28]. In analyzing the multiple-TI data, we chose to use a simple and therefore presumably robust fitting approach to estimate the slope of the ASL difference signal. This idea is similar to the Patlak-Rutland plot [29] for estimating glomerular filtration rate (GFR).

A popular method for estimating tissueperfusion from dynamic data is Miles' maximum-slope method [30], which computes perfusion from tissue and arterial signals at the time of maximal upslope in the tissue enhancement curve. It was speculated that this method may underestimate perfusion due to venous washout [31]. Our method, however, estimates the slope from all data points between the transit delay t₀ and the maximalTI (1600 ms in our case), instead of only computing perfusion from one single point as in the maximum-slope technique. Furthermore, venous washout is unlikely to occur before such an early maximal TI [9,32].

In designing an acquisition protocol for renal ASL, we hope to acquire enough data to achieve highly accurate perfusion estimates but are often limited by scan time and/or a patient's breath-hold ability. In this study, we acquired ASL data at a large number of TI values for a group of subjects and evaluated the potential decrease in perfusion-estimation accuracy when fewer of the ASL signals were used in the estimation. We found that as long as more than two TIs were used, reducing the number of TIs did not introduce significant bias into the perfusion estimates. The precision of perfusion estimates, however, did decrease with fewer TIs. This decreased precision likely resulted from the increased difficulty in fitting our ASL signal model to fewer data points. In this study, we only investigated how the density of TI sampling (i.e. the number of evenly distributed TIs) impacts the perfusion estimation. A more thorough optimization would involve the selection of TI values when the number of TIs is fixed, which can be achieved by an error propagation analysis and is beyond the scope of this study.

This study has a number of limitations. First, by using the slope approach, we assume that no labeled blood exits the imaging slice before the end of imaging, which worked for our ASL protocol with a maximal TI of 1.6 s. Acquisitions at longer TIs are not recommended due to the increasing signal decay from T₁ relaxation. Second, we did not measure the M_b0 ∙(1+f_ss) factor for each subject, instead using its average value across a group of subjects. However, we found that the factor was relatively constant for specific data-acquisition settings (Table 1). Third, our perfusion quantification technique was only applied to data acquired with pulsed ASL (FAIR) labeling. For ASL data acquired with continuous labeling, we expect some adjustment to the AIF and T₁-relaxation terms in Eq. (A.2) (Appendix) to account for the different labeling scheme. Fourth, we used an ROI-based analysis to quantify renal perfusion instead of a voxel-wise analysis due to the low SNR of the ASL signals. We are currently designing customized RF coils to improve SNR and thus achieve reliable voxel-wise mapping of renal perfusion.

In conclusion, our proposed method is shown to be accurate and robust in quantifying renal perfusion from multi-TI ASL data. To ensure a reliable implementation, 5 or more acquisitions at different TIs are recommended, although optimization of the TI values warrants further study.

Appendix A

A. 1.A tracer kinetic approach for analyzing multi-TIASL data

ASL signals, more specifically the difference between SS and NS signals, are relatively weak and decay due to T1 relaxation. Even with acquisitions at different TIs, it is difficult to reliably extract fine tracer-kinetic features from ASL data. Below, we simplify a complex tracer kinetic model to a linear form and estimate perfusion from the slope of the regression line.

The first step of the proposed method is to properly quantify the NS and SS signals. Conventionally, SS and NS signals are subtracted directly to obtain a perfusion-weighted signal difference. However, in reality the NS and SS signals are acquired independently and may differ due to factors other than perfusion. Unequal inversion efficiency, for example, can create a net difference between NS and SS signals that is much higher than the true perfusion effect. We propose the following method to eliminate such a non-perfusion signal difference. Based on the Bloch equation, the NS signal at some TI can be expressed as:

$$\mathit{\text{NS}}(\mathit{\text{TI}})=M_0-[M_0-\mathit{\text{NS}}(0)]·exp(-\mathit{\text{TI}}/T_1)$$ (A.1)

where M₀ is the equilibrium magnetization and NS(0) is the magnetization immediately after inversion. Note that NS signals do not depend on perfusion. By fitting Eq. (A1) to the acquired NS signals, we can estimate the unknowns: M₀, T1, and NS(0). Because of unequal inversion efficiencies between NS and SS inversions, NS(0) would be different from SS(0), which can be fitted from the initial segment of the SS signal vs. TI curve [20]. Using SS(0) as the new initial magnetization, we can regenerate NS signals with Eq. (A1) and refer to the regenerated signals as NS' (“NS prime”). Subtraction of NS' from SS results in a signal difference (dS) that is free of unequal-inversion artifacts.

The signal difference dS is generated by the tagged blood which is inverted by the NS inversion but not the SS inversion, and is related to perfusion (F) by the following convolution:

$$\mathit{\text{dS}}(t)=exp(-t/T_1)·{\int }_0^{\mathrm{t}}F·\mathit{\text{AIF}}(\tau )·\mathit{\text{IRF}}(t-\tau )·d\tau$$ (A.2)

In Eq. (A.2), F denotes tissue perfusion, AIF denotes the arterial input function, which is the magnetization difference of the inflowing blood between NS and SS acquisitions, and IRF denotes the impulse retention function that characterizes the passage of tracer through renal tissue. T₁ relaxation of the inverted signals is expressed by the exponential term in Eq. (A.2).

We re-write Eq. (A.2) with the following considerations. First, the AIF can be expressed as:

$$\mathit{\text{AIF}}(t)=\{\begin{array}{cc}0& t<t_0\\ M_{b0}·(1+f_{\mathit{\text{ss}}})·u(t-t_0)& t\ge t_0\end{array}$$ (A.3)

where t₀ is the transit delay required for tagged blood to reach the imaging slice, M_b0 is the equilibrium magnetization of blood, and u(t) is the Heaviside step function. The factor f_ss equals SS(0)/(−M₀), where M₀ is the equilibrium magnetization of the tissue. Here we use SS(0) because both SS and NS' start from SS(0). Second, TI values are typically restricted to less than 2 s due to T₁ relaxation, which is too short of a time for tagged blood to exit the tissue [33]. For this reason, the IRF can be set to unity. With these considerations, Eq. (A.2) can be rearranged as follows:

$$\mathit{\text{dS}}(t)/exp(-\mathrm{t}/T_1)=\{\begin{array}{cc}0& t<t_0\\ M_{b0}·(1+f_{\mathit{\text{ss}}})·F·(t-t_0)& t\ge t_0\end{array}$$ (A.4)

Eq. (A.4) indicates that the difference signal normalized by T₁ relaxation stays zero prior to the transit delay t₀ and increases linearly afterwards, and that the slope of this increase is proportional to tissue perfusion. By fitting Eq. (A.4) to the ASL difference signals, we can determine the value of M_b0∙(1+f_ss)∙F. To determine the value of F, one can choose to measure M_b0 and f_SS or, if a consistent data-acquisition setting is used, assume the factor M_b0∙(1+f_ss) to be constant across different subjects. In this study, we estimated the factor M_b0∙(1+f_ss) from a group of subjects by computing the average ratio of ASL-measured M_b0∙(1+f_ss)∙F to perfusion (F) measured from DCE MRI. This averaged factor was then used to derive the ASL-based perfusion measurement from Eq. (A.4).