A Novel Maturation Index Based on Neonatal Diffusion Tensor Imaging Reflects Typical Perinatal White Matter Development in Humans

Abstract

Human birth presents an abrupt transition from intrauterine to extrauterine life. Here we introduce a novel Maturation Index (MI) that considers the relative importance of gestational age at birth and postnatal age at scan in a General Linear Model. The MI is then applied to Diffusion Tensor Imaging (DTI) in newborns for characterizing typical white matter development in neonates. DTI was performed cross-sectionally in 47 neonates (gestational age at birth=39.1±1.6 weeks [GA], postnatal age at scan=25.5±12.2 days [SA]). Radial diffusivity (RD), axial diffusivity (AD) and fractional anisotropy (FA) along 27 white matter fiber tracts were considered. The MI was used to characterize inflection in maturation at the time of birth using GLM estimated rates of change before and after birth. It is proposed that the sign (positive versus negative) of MI reflects the period of greatest maturation rate. Two general patterns emerged from the MI analysis. First, RD and AD (but not FA) had positive MI on average across the whole brain (average MI_AD=0.31+/−.42, average MI_RD=0.22+/−.34). Second, significant regions of negative MI in RD and FA (but not AD) were observed in the inferior corticospinal regions, areas known to myelinate early. Observations using the proposed method are consistent with proposed models of the white matter maturation process in which pre-myelination is described by changes in AD and RD due to oligodendrocyte proliferation while true myelination is characterized by changes in RD and FA due to myelin formation.

Graphical abstract

1 Introduction

Human birth presents an abrupt transition from intrauterine to extrauterine life. Profound physiological changes occur with the cessation of maternal provision, including the re-organization of the neonate's cardiovascular system and the onset of pulmonary function. Within 8 minutes of delivery, oxygen saturation levels increase from roughly 60% to over 85% (Rabi et al., 2006). From the perspective of a single cell in the neonatal brain, these are dramatic changes that, based on in vitro work, may represent a shift from a local environment that promotes oligodendrocyte proliferation to one that drives oligodendrocyte maturation (Pistollato et al., 2007). Higher oxygen tension is thought to be a regulator of white matter maturation through down regulation of hypoxia-inducible factor (Yuen et al. 2014), with oxygen saturation potentially playing an important role in cystic and diffuse white matter diseases (Wellman et al. 2015). Furthermore, Toda et al. (2013) have demonstrated the initiation of barrel formation in the somatosensory cortex of mice through a reduction in serotonin signaling at birth. Birth also presents an abrupt increase in external sensory stimuli that may promote maturation through axonal signaling (Coman et al., 2005). In addition, recent work has highlighted perinatal changes in physiological dehydration, skull contraction and cerebrospinal fluid reductions as possible mediators of increased gyrification in pre-term versus fetal brains matched for postmenstrual age (Lefèvre et al., 2015). Based on these dramatic changes at the time of birth, the transition from intrauterine to extrauterine life is likely to present a significant inflection point in brain maturation, including the maturation of white matter fiber tracts. While we cannot test these mechanisms directly in this work, here, we aim to identify white matter regions with significant inflection points in maturation near the time of birth and establish a metric for characterizing the relative average rates of maturation before and after birth in a healthy population of near term born neonates.

Cross-sectional Diffusion Tensor Imaging (DTI) studies aimed at describing perinatal brain maturation trajectories typically apply univariate analyses using postmenstrual age as a predictor of microstructural maturity (Hüppi et al., 1998; Oishi et al., 2011; Ou et al., 2015; Provenzale et al., 2012; Qiu et al., 2013) or using postmenstrual age while correcting for age at scan (or gestational age) (Van Kooij et al., 2012) in a linear model. In the former case, the assumption is made that growth is linear with time from conception, despite the environmental shift that occurs when the developing brain is first exposed to the postnatal environment. Using postmenstrual age as the predictor but correcting for age at scan (or gestational age) adequately adjusts for inter-individual variation in time spent in utero. Although this may often be an appropriate choice, this approach neglects potentially interesting information about prenatal versus postnatal developmental changes when the rate of maturation may not follow a linear trajectory from conception.

Previous work describing white matter maturation has been instrumental in describing the formation, organization and maturation of white matter in early life, yet lacks a quantitative description of maturational trajectories surrounding birth. By first separating postmenstrual age (PM) into gestational age at birth (GA) and postnatal age (chronological age) at scan (SA) for regression analysis, we examine and demonstrate the ability to describe inflection points in developmental trajectories near the time of birth. Second, using tract-based statistics we propose that the newly described Maturation Index (MI) is potentially indicative of spatially asynchronous perinatal maturation in white matter microstructure.

2 Methods and Materials

2.1 Linear Regression Models, Model Comparison and the Maturation Index (MI) Defined

2.1.1 Linear Regression Models

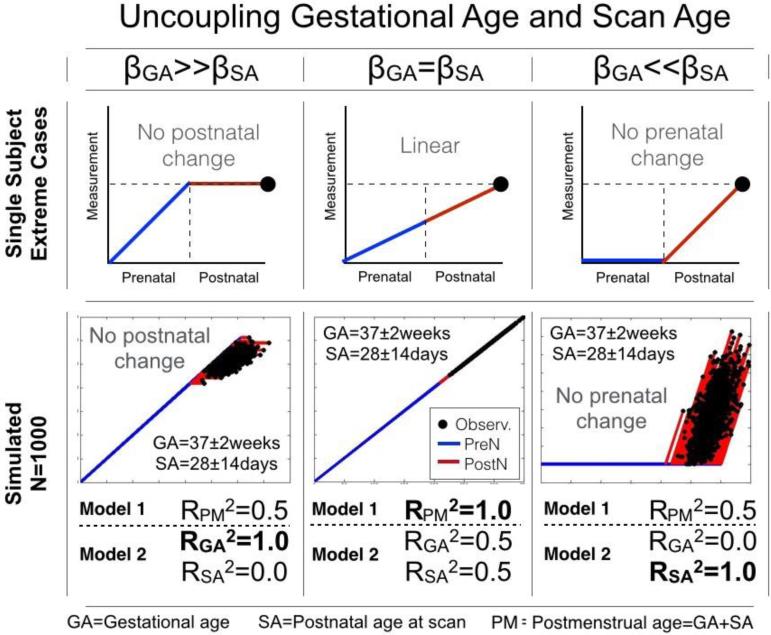
Linear regression models were implemented using Matlab (www.mathworks.com) for the examination of predictive power using two separate models. Model 1 used PM as the only indicator of participant age at the time of the MRI scan and as the predictor of diffusion measures. Model 2 used GA and SA as separate independent variables representative of age at the MRI scan and as predictors of diffusion measures. Both model 1 and model 2 included intracranial volume (ICV) as a continuous covariate and sex as a binary covariate. For this study the dependent variables were Fractional Anisotropy (FA), Radial Diffusivity (RD) or Axial Diffusivity (AD) (Y in below equations). This is shown below for the ith position along a fiber tract (models 1 and 2). In the case of linear maturation, growth rates before and after birth are equal (β_i,GA = β_i,SA). In this special linear case, model 2 is reduced to model 1, as PM is the sum of GA and SA (Figure 1), by definition. For this reason, the greater the difference between β_i,GA and β_i,SA, the greater the inflection in growth rates at the time of birth.

$$Model1:Y_i={\beta }_{i,PM}\cdot PC+{\beta }_{i,BV}\cdot ICV+{\beta }_{i,Sex}\cdot Sex+\epsilon$$ Equation 1

$$Model2:Y_i={\beta }_{i,GA}\cdot GA+{\beta }_{i,SA}\cdot SA+{\beta }_{i,BV}\cdot ICV+{\beta }_{i,Sex}\cdot Sex+\epsilon$$ Equation 2

Figure 1. Schematic of post-conceptional age (PM), gestational age (GA) and age at scan definitions (SA).

PM is shown as the sum of GA and SA.

2.1.2 Model Comparison

The gain in predictive power moving from model 1 to model 2 is descriptive of the divergence of β_i,GA from β_i,SA and therefore reflective of whether major maturational changes occur before or after birth. In order to justify the use of model 2, the gains from using the unrestricted model (model 2) were statistically characterized using an F-distribution. Here, RSS_j is the residual sum-of-squares from the respective model j, n the number of observations and p_j the number of model parameters. A p-value was then calculated along the tract using an F-test, F(p₂-p₁,n-p₂). Because model 2 always has the potential to reduce to model 1 (when β_i,GA = β_i,SA), RSS₁ will always be larger than or equal to RSS₂. A large F-statistic is driven by a difference in the residual errors between the two models and is therefore indicative of an increase in the asymmetry of maturation (β_i,GA ≠ β_i,SA) about the time of birth.

$$F=\frac{(RS{S}_1-RS{S}_2)∕(p_2-p_1)}{RS{S}_2∕(n-p_2)}$$ Equation 3

2.1.3 Simulated Data Sets

Three basic data sets were simulated to demonstrate the advantages of using the unrestricted second model. The three sets each consisted of 1,000 simulated observations, Y_i = β_i,GA · GA + β_i,SA · SA, with GA and SA randomized to a normal distribution and variance matched to our neonatal sample (GA_SIM=259+/−14 days; SA_SIM=28+/−14 days) whose dependent variable increased with GA only (set 1, in utero maturation only), GA and SA equally (set 2, linear maturation from the time of conception), or SA only (set 3, postnatal maturation only). Each set was then examined for correlations between the simulated dependent value and each of the three age variables individually: 1) GA, 2) SA and 3) PM. Explained variance of 1.0 (or 100%) occurs when the simulated data can be fully explained. The total variance explained by model 2 is given by the sum of R_GA² and R_SA².

2.1.4 Maturation Index Definition

MI values were defined using output from model 2. Specifically, MI is defined as the ratio of the difference in the squared slopes (beta value) of GA and SA, to the sum of squared slopes of GA and SA (Equation 4). The square of the slope was used to remove the sign dependence of the slope in the calculation. MI will tend towards +1 when the absolute rate of change during prenatal development is large relative to postnatal development, zero when the rates of change during pre- and postnatal development are equal and −1 when the postnatal rate of change is large relative to the rate of change during prenatal development.

$$MI=\frac{{{\beta }_{GA}}^2-{{\beta }_{SA}}^2}{{{\beta }_{GA}}^2+{{\beta }_{SA}}^2}$$ Equation 4

MI was plotted against the increase in explanatory power from model 2 compared to model 1 (Equations 1 and 2). A large F-Ratio coupled with a large (non-zero) MI suggests a meaningful increase in power due to accounting for the non-linearity of developmental trajectories (using GA and SA, model 2) having an inflection point at the time of birth. The MI has two principal benefits over examining the slopes individually: 1) the dimensionality of the rates of change are reduced to a single number (an index), and 2) the magnitude of the slopes are effectively normalized so that the magnitude of the inflection becomes a dimensionless parameter, facilitating whole-brain characterization.

2.2 Sample, Image Acquisition and Analysis

Infant neuroimaging was approved by the Institutional Review Board of the University of California at Irvine, and all parents provided informed, written consent. All of the 47 infants evaluated in this study were from healthy pregnancies with no major obstetric, birth or current health complications. Mother-child pairs were recruited for a research study of normative development.Sample demographics are provided in Table 1. Gestational age was determined by best obstetric estimate with a combination of last menstrual period and early uterine size, and was confirmed by obstetric ultrasonographic biometry before 15 weeks using standard clinical criteria(O'Brien et al., 1981). The mean gestational age at birth was 39.1 ± 1.6 (±SD) weeks and ranged from 34.4 to 41.9 weeks. The mean postnatal infant age at assessment was 25.5 ± 12.2 (±SD) days and ranged from 5 to 56 days. Gestational age at birth and postnatal infant age at assessment were not correlated with one another (R²=−2.8%,p=0.25).

Table 1.

Sample Demographics.

Gestational Age at Birth (weeks)
Mean (S.D.)	39.1 (1.6)
Postnatal Age at Scan (days)
Mean (S.D.)	25.5 (12.2)
GA, SA Distribution
N (%), GA>mean(GA) & SA>mean(SA)	12 (26%)
N (%), GA>mean(GA) & SA<mean(SA)	13 (28%)
N (%), GA<mean(GA) & SA>mean(SA)	8 (17%)
N (%), GA<mean(GA) & SA<mean(SA)	14 (29%)
Sex
Male, N (%)	19 (40%)
Birthweight (kg)
Mean (S.D.)	3.35 (0.49)
Birthweight for GA (percentile)
Median (IQR)	74.2 (39.5-96.1)
Race/Ethnicity
Hispanic White N (%)	14 (36%)
Hispanic of Other Race N (%)	11 (23%)
Non-Hispanic White N (%)	17 (30%)
Non-Hispanic of Other Race N (%)	5 (11%)
Cesarean Section Deliveries
Yes, N (%)	8 (17%)

Summary statistics are provided for the infant sample. GA=Gestational Age, SA=Postnatal Age at Scan (Chronological Age).

MRI scans were acquired during natural sleep using a 12-channel head receive coil at 3T field strength. High-resolution anatomical scans including T1-weighted (MPRAGE, TR/TE/TI=2400/3.16/1200ms, Flip Angle=8 degrees, Matrix=256×256×160, Resolution=1×1×1mm, 6m18s) and T2-weighted (TSE, TR/TE=3200/255ms, Matrix=256×256×160, Resolution=1×1×1mm, 4m18s) images were acquired. The 49-direction diffusion weighted protocol (EPI, TR/TE=8900/83ms, Matrix=256×256×75, Resolution=2×2×2mm, 42 unique directions at b=1000s/mm², 7 at b=0) was 7 minutes and 43 seconds in duration. After feeding and soothing to the point of sleep, neonates were placed in a CIVCO beaded pillow (www.civco.com). The pillow covered the neonates’ body and head, became rigid under vacuum, and provided a comforting swaddle, motion prevention and hearing protection when used in conjunction with standard foam earplugs. A pediatric specialist observed the neonates throughout the duration of scans, monitoring for heart rate and oxygen saturation via a pulse-oximeter attached to the foot. The entire protocol included T1-weighted, T2-weighted, diffusion tensor and functional imaging of the brain.

Diffusion profile measurements were generated via the NA-MIC atlas based fiber analysis toolkit (Verde, 2014). In brief, diffusion datasets were first rigorously checked for appropriate quality. This was followed by weighted least square tensor estimation, skull stripping via prior brain mask from co-registered structural T2 weighted images, and unbiased study specific DTI atlas building. Fiber tract streamline DTI tractography (Fillard et.al. 2003) was performed via 3D Slicer (version 4.3.0) (http://www.slicer.org) in the DTI atlas space followed by fiber cleaning with FiberViewerLight (www.nitric.org/projects/fwlight). Tractography was performed for major fiber bundles: corpus callosum (genu, rostrum, tapetum, occipital, parietal), Left(L)/Right(R) cingulum, L/R fornix, L/R inferior fronto-occipital fasciculus (IFOF), L/R inferior longitudinal fasciculus (ILF), L/R superior longitudinal fasciculus (SLF), L/R uncinate fasciculus (UF), L/R motor, L/R pre-motor, L/R cortico-fugal parietal and L/R thalamo-cortical parietal and L/R optic tracts. The main body (central portion) of the corpus callosum was not analyzed as part of this study. Fiber profiles of FA, MD, AD, RD were extracted after fiber parameterization for profile analysis. For more detail please refer to Verde (2014). DTI data was visually evaluated for appropriate mapping into the DTI atlas space via slice overlay. Visual inspection and quantitative quality assessment of the extracted fiber profiles were additionally performed by computing the cross-correlation coefficient between the FA tract profiles of the DTI atlas and of each subject case (minimal r > 0.75). For most tracts, all subjects passed quantitative profile QC. Few subjects were excluded for cingulum L (5), cingulum R (7), CST L (1), fornix L (2), and uncinate R (1). Brain tissue volumes were determined for gray matter, unmyelinated white matter, myelinated white matter, and cerebral spinal fluid using an automatic, atlas-moderated expectation maximization segmentation tool as previously described(Gilmore et al., 2007; Prastawa et al., 2005). Intracranial volume defined here is the sum of the four preceding tissue classes.

2.3 MI Analyses

2.3.1 Whole Brain Analyses

A unique MI value for FA, RD and AD was calculated as described above for each point along the defined white matter fiber tracts. For the remainder of this work, each of these values will be denoted respectively as MI_FA, MI_RD, and MI_AD. MI_FA, MI_RD, and MI_AD values were evaluated globally to test three basic hypotheses related to the developmental timeline of white matter microstructure: 1) the rate of change of AD is greatest during pre-myelination (see discussion), a process occurring prenatally before true-myelination, therefore average MI_AD is expected to be greater than MI_FA and MI_RD, 2) the rate of change of RD is more linear than those of AD and FA as it changes with both pre- and true-myelination (see discussion), therefore MI_RD should have a mean between those of AD and FA, 3) FA changes are greatest after birth when true-myelination (see discussion) begins to increase globally and MI_FA should, therefore, skew towards −1. Two-way paired t-tests between diffusion parameter MIs were used to test the above order in MI_FA<MI_RD, and MI_RD<MI_AD.

MI values along the fiber tracts used in this study were visualized in four groups: association (anterior-posterior connection), commissural (left-right connection), projection (superior-inferior connection) and limbic (those connecting limbic structures connection). Despite their anterior to posterior orientation, the cingulum and ILF (Latini 2015) were assigned to the limbic group together with the UF and fornix. The fiber groups were compared for differences within the group (paired t-tests between diffusion parameter MIs within group) and MI_FA, MI_RD, and MI_AD were compared across groups using independent two sample t-tests. The location, size and significance of the clusters with the largest magnitude MI are reported with a focus on MI_RD as justified further below.

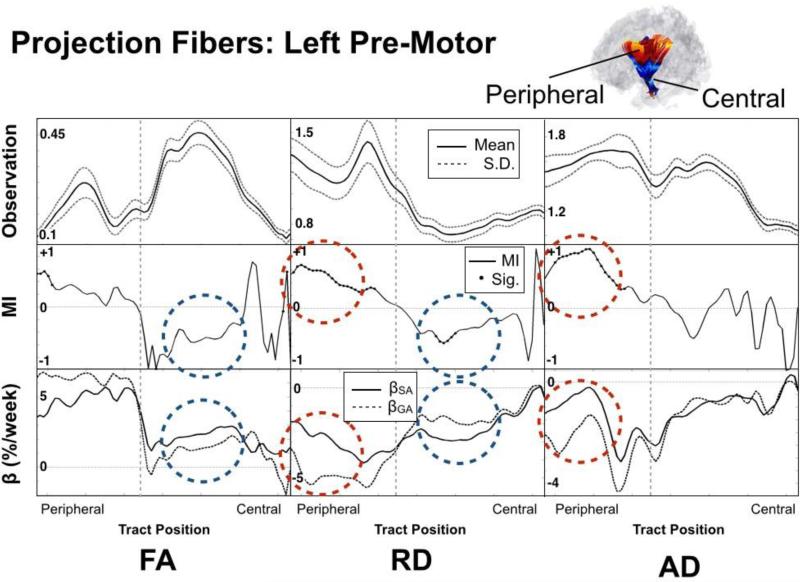
2.3.2 Post-hoc Analyses of Projection Fibers

A post-hoc examination within a selected fiber tract was conducted in order to further elucidate the descriptive relationship between MI_FA, MI_RD, and MI_AD. The left pre-motor tract was chosen based on two criteria: 1) the projection fibers collectively showed the greatest amount of variability, each bisected by a region of large positive MI and large negative MI, and 2) the left sided projection fibers had the most negative MI values and have been shown to myelinate before right sided fibers(Dubois et al., 2009). ROIs were defined post-hoc as having a significant F-ratio between model 2 and model 1 (Equation 3) and were applied as a mask to the tract-based data extracting a mean slope for GA and SA from the model for comparison.

A post-hoc exploration of the relationship between MI_RD, MI_AD, and MI_FA was made using a simple colored scatter plot depicting the three metrics together.

Results

3.1 Simulated Data Sets in Support of Model 2

Three sets of simulated data were evaluated for illustrative purposes (Figure 2). The two non-linear sets (prenatal-only or postnatal-only change) had predictably marked increases in explained variance (R_PM²=0.50; R_GA²+R_SA²=1.0) when acknowledging the separate contribution of GA and SA to PM, while the linear set (equal increase in prenatal and postnatal periods) was fully predicted (R_PM²=1.0; R_GA²+R_SA²=1.0) by both model 1 and model 2.

Figure 2. Splitting post-conceptional age (PM) into gestational age (GA) and age at scan (SA).

Top row: Cartoon depicting three distinct paths to the same outcome. Bottom row: Three sets (β_GA>>β_SA; β_GA=β_SA; β_GA<<β_SA) of outcomes (N=1,000) were generated using the model Y=β_GA*GA+β_SA*SA with normally randomized GA (259+/−14 days) and SA (28+/−14 days). The PM age dependence (model 1) is significant in all three sets, however only the use of model 2 (GA and SA) is able to explain 100% of the variance in all three sets.

3.2 MI Analyses

3.2.1 Whole Brain Analyses

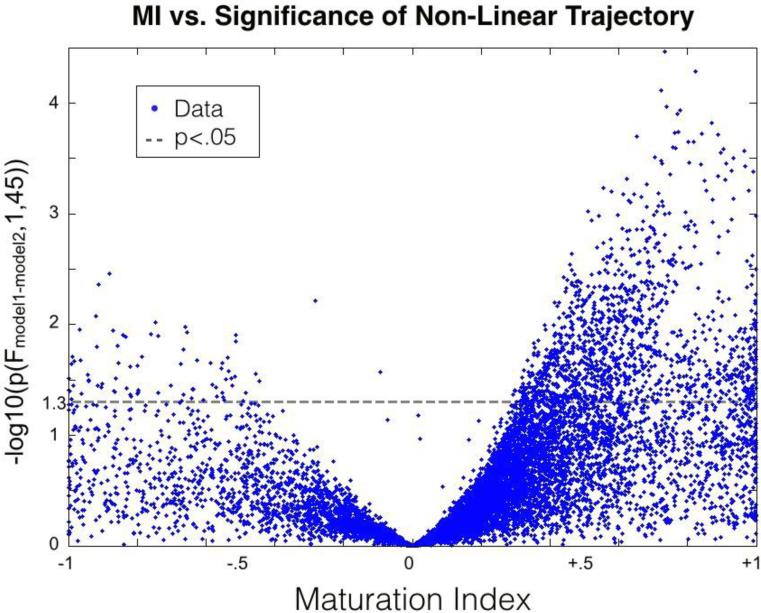
MI plotted against the F-Ratio comparing models 1 and 2 demonstrated increasing significance, and variability in significance, with increasing MI magnitude. Observations with large MI magnitude and high significance are driven by a sizeable relative difference between β_i,GA and β_i,SA that results in a significant increase in explanatory power. A parabolic upper limit was observed centered around an MI value of zero (the point at which β_i,GA = β_i,SA and model 2 reduces to model 1, hence a null increase in power) (Figure 3). The values contradicting this upper limit represent the points at which separating β_i,GA and β_i,SA allowed one of the other covariates (intracranial volume and/or sex) to significantly increase the explanatory power of model 2. These outlying points were limited to less than 0.1% of total observations. Points with large MI magnitude, but small F-Ratio, suggest observations that had an optimized model with β_i,GA unequal to β_i,SA . However, in these points, separating GA and SA resulted in little increase in explanatory power, likely due to the over-fitting of noise by the unrestricted variables GA and SA.

Figure 3. Explanatory Power Increase as a Function of Maturation Index.

The increase in explanatory power when separating PM into GA and SA is plotted against MI. MI reflects the change in estimated rates of change after birth relative to the estimated rate before birth. A large difference in slopes before and after birth results in a large magnitude MI and large increase in explanatory power when considering GA and SA as independent variables.

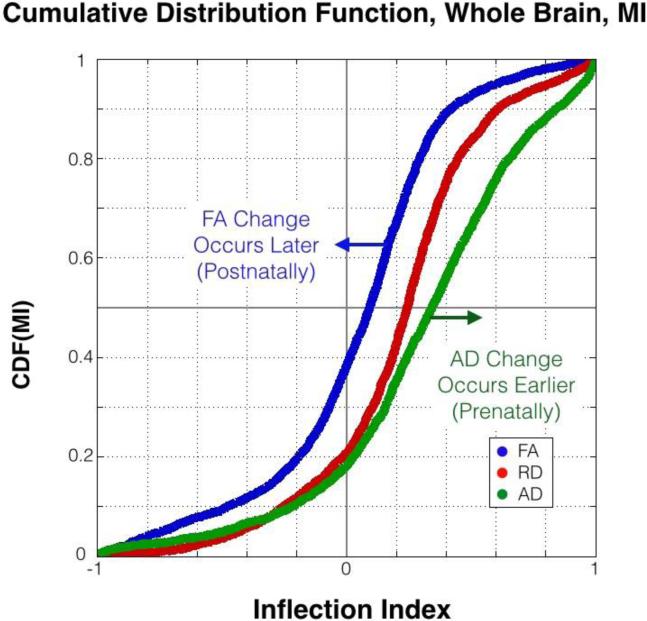
The MI across all fiber tracts revealed global differences in diffusion metrics (interquartile range, Q1/Q2/Q3: MI_FA=−.12/.09/.26, MI_RD=.05/.25/.40, MI_AD=.09/.34/.59, Figure 4). All MI measurement distributions were skewed with long tails in the negative MI region, a region indicating more rapid post-natal compared to prenatal fiber maturation. MI_AD had the most skewed distribution of the three (skew[MI_FA]=−0.03, skew[MI_RD]=.09, skew[MI_AD]=−0.25), reflective of relatively early change in AD. The hypothesized order of MI values (MI_AD>MI_RD>MI_FA) was confirmed (MI_RD>MI_FA, Δ_RD-FA=.17, 95% CI [.154 .195], p_RD-FA<10⁻¹⁰; MI_AD>MI_RD, Δ_AD-RD=.10, 95% CI [.074 0.112], p_AD-RD<10⁻¹⁰).

Figure 4. Cumulative Distribution Function of MI_FA, MI_RD, and MI_AD.

MI_FA was significantly greater than MI_RD (p_paired<10⁻¹⁰) and MI_RD was significantly greater than MI_AD (p_paired<10⁻¹⁰) across the whole brain. Large MI results from a greater estimated rate of change prenatally relative to postnatally.

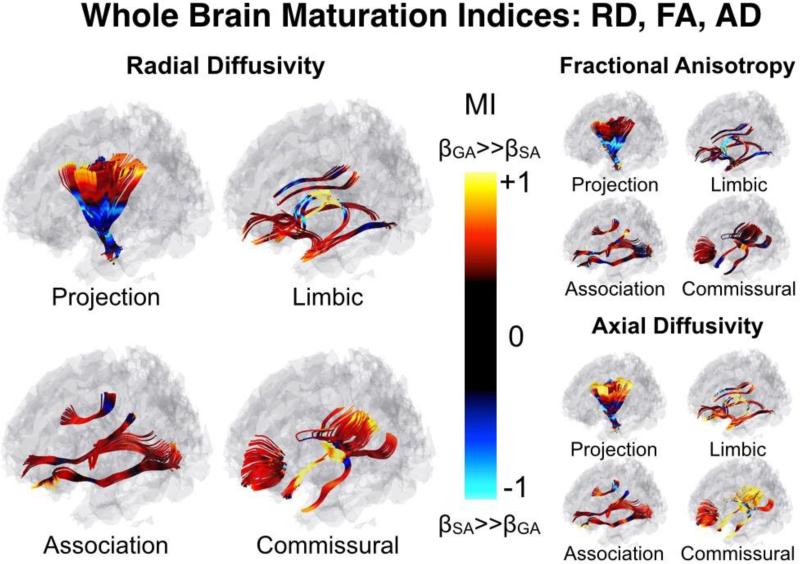
A quantitative map of MI across the brain's white matter tracts can be seen in Figure 5. In addition to the global differences in MI_FA, MI_RD and MI_AD, there are apparent differences between fiber groups. Specifically, MI_FA, MI_RD and MI_AD were greatest in commissural fibers, lowest in projection fibers, and with moderate values in association and limbic fibers (Table 2). While this is discussed in more detail below, these findings are reflective of large regions of negative MI bilaterally in the projection fibers, and large regions of positive MI bilaterally in the fornix and the tapetum of the corpus callosum.

Figure 5. Whole Brain Maturation Index Map.

White matter tracts are separated by group: Projection (Inferior-Superior), limbic (limbic connections), association (anterior-posterior), and commissural (left-right). Note the large negative MI_RD in the inferior projection fibers (internal capsule), and large positive MI_RD in the more peripheral ends of the tract. MI_RD is emphasized, here, as it is predictive of both MI_FA and MI_RD (see figures 6 and 7). One-dimensional tract-based statistics are projected onto the three-dimensional streamlines for visualization purposes.

Table 2.

Interquartile values of MI_FA, MI_RD and MI_AD by fiber group.

Fiber Group	MIFA	MIRD	MIAD
Commissural**	.01/.18/.32†	.20/.34/.49	.23/.49/.73†
Association*	−.04/.14/.28†	.11/.21/.33†	.11/.23/.41
Limbic**	−.15/.04/.19	.10/.25/.44†	.17/.39/.60†
Projection**	−.42/−.03/.20	−.26/.03/.27	−.18/.16/.47

The statistics for MI are shown using the interquartile range, 25/50/75. Commissural fibers had the largest MI and projection fibers had the lowest, with association and limbic fibers in the middle. The order of microstructural MI is retained in all fiber groups. *, ** denote fiber group retained MI_FA<MI_RD<MI_AD within the fiber group at a minimum pairwise significance of p<.005, or p<10⁻¹⁰, respectively. Each microstructure MI had a pair of fiber groups that were not significantly different (two sample t-test, p>.05), these pairs are denoted with a †. All other pairs were significant at p<.05.

All 27 tracts assessed in this study had at least one cluster with significantly (p<.05, Equation 3) positive MI_RD. The top ten (by significance) positive MI_RD clusters are shown below (Table 3). Only 4 of the 27 tracts assessed had significant clusters of negative MI_RD. All 4 of the significant clusters were located in the left sided projection fibers. At the trend level (p<.1), three of the four right sided projection fibers and the left optic tract were also significant (Table 4) suggesting left-right asymmetric development.

Table 3.

Estimated rates of change for, and coordinates of, significant clusters of positive MI_RD.

Tract	Cluster Extent (%)	Loc.	Coord. MNI	βRD,GA (%/week)	βRD,SA (%/week)	ΔβRD (%)	MIRD	p(F)min
L Par. Post. CF	10	SPG	−16,−55,56	−5.4	−2.5	+54	0.65	<.001
CC Parietal	8	SPG	13,−62,49	−5.3	−2.6	+51	0.62	0.002
R Premotor CT	6	SFG	11,6,59	−5.3	−1.9	+64	0.77	<.001
R Par. Post. CF	5	SPG	17,−37,56	−5.1	−2.8	+44	0.53	<.001
CC Occipital	4	SOG	23,−86,31	−5.1	−2.4	+53	0.64	0.002
L SLF	3	SPG	−28,−44,61	−4.4	−1.5	+67	0.80	<.001
R Cingulum	3	SPG	12,−53,48	−5.6	−3.0	+46	0.54	0.003
R Fornix	3	ITG	35,2,−35	−5.0	−2.0	+60	0.78	0.003
R ILF	2	STG	49,8,−17	−4.4	−1.9	+58	0.69	0.002
R IFOF	1	MOG	18,−101,−5	−4.8	−2.5	+47	0.55	0.004

Top ten clusters identified as having a significant (p<.05) increase in explained variance when splitting up post-conceptional age into gestational age and age at scan. All metrics are averaged across clusters unless otherwise specified. Cluster extent is expressed in percentage of length relative to the tract. TC=Thalamocortical, CF=Corticofugal, CT=Corticothalamic, SLF=Superior Longitudinal Fasciculus, ILF=Inferior Longitudinal Fasciculus, IFOF=Inferior Fronto-Occipital Fasciculus, SPG=Superior Parietal Gyrus, SFG=Superior Frontal Gyrus, SOG=Superior Occipital Gyrus, MOG=Medial Occipital Gyrus, STG=Superior Temporal Gyrus, MTG=Medial Temporal Gyrus, ITG=Inferior Temporal Gyrus.

Table 4.

Estimated rates of change for, and coordinates of, significant clusters of negative MI_RD.

Tract	Cluster Extent (%)	Loc.	Coord. MNI	βRD,GA (%/week)	βRD,SA (%/week)	ΔβRD (%)	MIRD	p(F)min
L Motor CT	13	PLIC	−25,−15,23	−1.6	−2.9	−84	−.54	.02
L Par. Post. TC	11	PLIC	−25,−21,21	−1.1	−2.4	−127	−.68	<.01
L Par. Post. CF	10	CP	−15,−22,−12	−1.1	−2.7	−142	−.68	.01
L Premotor CT	9	PLIC	−22,−7,17	−1.6	−2.9	−81	−.53	.02
R Par. Post. TC	9	PLIC	24,−20,17	−1.3	−2.0	−62	−.45	.05
R Motor CT	9	PLIC	24,−15,17	−1.0	−2.0	−102	−.58	.06
L Optic	3	ST	−29,−25,−2	−1.2	−2.3	−89	−.55	.08
R Premotor CT	3	PLIC	21,−6,15	−1.0	−2.1	−104	−.61	.09

Four clusters were identified as having a significant (p<.05) increase in explained variance when splitting up post-conceptional age into gestational age and age at scan. Four additional clusters are listed at the trend level (p<.1). All metrics are averaged across clusters unless otherwise specified. Cluster extent is expressed in percentage of length relative to the tract. TC=Thalamocortical, CF=Corticofugal, CT=Corticothalamic, PLIC=Posterior Limb Internal Capsule, ST=Stria Terminalis, CP=Cerebral Peduncle.

3.2.2 Post-hoc Examination of Projection Fibers

Diffusivity measures, MI and fitted slope values are shown for the left premotor corticothalamic tract in Figure 6. As seen in the figure, the tract can be considered as two distinct regions (peripheral and central) bisected by the switch in sign of MI and changing microstructural properties (FA, RD, AD), reflective of the anatomical transition into the internal capsule. The peripheral portion can be described as having: 1) small FA, large RD and moderate to high AD, 2) large positive MI_AD and MI_RD, and 3) large differences in AD and RD beta values with β_GA>β_SA. Conversely, the central portion can be qualitatively described as having: 1) large FA, small RD and moderate to low AD, 2) large negative MI_FA and MI_RD, and 3) large differences in beta values with β_SA>β_GA. Percent differences in rates of change before and after birth for FA, RD and AD in the peripheral portion were +32%, +62% and +107%, respectively. For the central portion the same changes in FA, RD and AD were −43%, −41% and −27%.

Figure 6. Detailed Features Along the Left Premotor Tract.

Top row: microstructural value (FA, RD, AD); Middle row: Maturation index; Bottom row: estimated rate of change (GA dashed line, SA solid line). Note the clear delineation between inferior and superior regions (marked by vertical dashed lines) reflected in the anatomy, MI and rate of change. Red dashed circles highlight a peripheral region with large positive MI_RD and MI_AD, reflective of premyelination and blue dashed circles highlight a central region with large negative MI_RD and large negative MI_FA reflective of true myelination. Observation axes units of measurement are relative (FA) and 10⁻³mm²/s (AD, RD).

Discussion

By devising a model of development that considers the rates of perinatal maturational change of white matter fiber tracts, this work has demonstrated three principal findings: 1) group level information about pre- versus post-natal developmental changes of white matter fiber tracts can be retrieved based on a cross-sectional sample of healthy newborns with similarly varying gestational age at birth and postnatal age at scan; 2) when evaluating imaging associations with age in neonates, separating postmenstrual age into gestational age and age at scan (postnatal age) results in a significantly more powerful model, as compared to using postmenstrual age as a predictor, because it accounts for an inflection in maturational changes at the time of birth; 3) the prenatal and postnatal rates of change can be cast as a unit-less index (MI), the value of which is reflective of relatively increasing or decreasing maturational processes after birth.

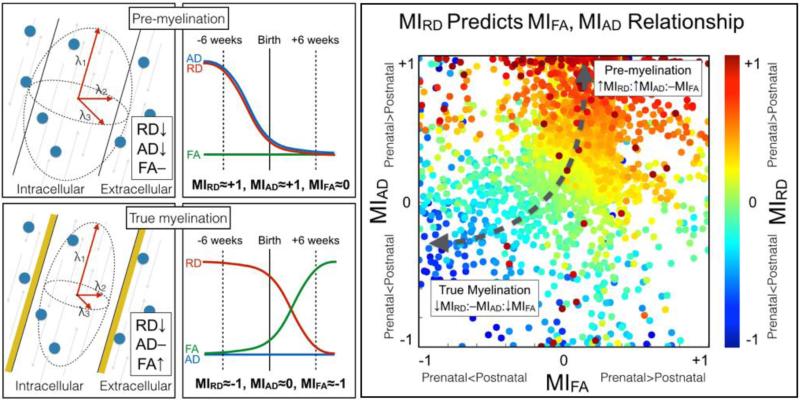
Two additional postulations based on adopted (Dubois et al. 2008) DTI models of myelination, the application of the proposed MI and deductive reasoning are made below: 1) shortly before birth, the developing brain is primarily in a state of pre-myelination which appears to slow at birth; and 2) more mature central regions are increasing the process of true myelination near the time of birth.

Neonatal white matter microstructural development across the brain has been characterized indirectly via DTI (Dubois et al., 2014; Dietrich et. al., 1988; Yoshida et al., 2013) measures of diffusivity (FA, AD, and RD). We are here adopting the model used by Dubois et al. (2008; Beaulieu, 2002) for inferences on myelin development based on observed DTI properties. RD measures diffusivity perpendicular to the axon and monotonically decreases during the three identified stages of axonal development: axonal organization, oligodendrocyte proliferation (premyelination) and myelin deposition (true myelination). AD measures water diffusion along the axis of the axon and increases during axonal organization as the axons become more coherently arranged along the main axis, decreases along with RD during premyelination due to isotropic reduction in water content and, unlike RD, is largely stable during true myelination as the hydrophobic myelin sheathing restricts diffusion in the perpendicular direction. FA is a relative measure of AD and RD and is therefore reflective of the difference between the two. Axonal organization is characterized by an increase in AD and decrease in RD resulting in increased FA. Premyelination has a concomitant decrease in AD and RD and therefore results in no change in FA. FA increases during true myelination are driven by a decrease in RD. While axonal organization, or fascicle coherence, will be discussed further below, it is thought that the majority of fascicles are already organized by the late prenatal stages due to an abundance of extracellular matrix and guidance molecules (Kostović and Jovanov-Milošević, 2006). Consequently, the primary mechanisms discussed here are restricted to pre-myelination (RD decrease, AD decrease, FA no change) and true myelination (RD decrease, AD no change, FA increase), the major maturational processes that occur around the time of birth.

Signs of rapid in utero premyelination (based on adopted models) followed by a decreasing rate of premyelination after birth were present throughout a relatively large percentage of the observed white matter fiber tracts (16% at p(F(_+MI,RD))<.05, 25% at p<.1). All 27 of the tracts included in the analyses had at least one significant cluster suggestive of slowing premyelination at birth. Among those, commissural tracts showed the greatest propensity towards this pattern as manifested by large positive MI_RD and MI_AD, on average. Because the premyelination process is observed to be slowing at birth (positive MI), it is reasonable to assume it is largely being completed near term. Certainly, oligodendrocyte proliferation continues through childhood, yet this finding is consistent with typical oligodendrocyte lineage (Barateiro and Fernandes, 2014) and the window of vulnerability (23-32 postmenstrual weeks) for perinatal white matter injury (Back et al., 2001).

As expected, only a small percentage of fiber tracts in the neonatal brain suggested signs of true myelination (1% at p(F(_−MI,RD))<.05, 2% at p<.1). These observations are consistent with the adopted model of true myelination (FA, RD changes) occurring postnatally (negative MI) within tightly bound regions of the tract (internal capsule). The tracts that did show evidence of true myelination at the time of birth were those that based on postmortem studies are known to be myelinated early (around the time of birth) (Kinney 2014). Specifically, the portion of corticospinal tracts running through the posterior limb of the internal capsule (PLIC) extending down into the cerebral peduncle as well as a portion of the left optic tract showed significant signs of true myelination (large negative MI_RD and MI_FA). Postmortem analysis in 40 postmenstrual week old infants has detected microscopic traces of myelin at birth in these regions (Kinney 2014). In addition, these sites have been identified in utero (Zanin et al., 2012) and in preterm cohorts (Kersbergen et al., 2010; Partridge et al., 2004) as early myelination sites and in in vivo neonates as being one of the earliest maturing tracts when using adults as normative measures (Dubois et. al., 2008). Finally, PLIC is the first region detectable by myelin water fraction (MWF) mapping as early as 107 postnatal days (Deoni et al., 2011).

The concept that large positive MI_RD is associated with large magnitude MI_AD and, conversely, large negative MI_RD is associated with large magnitude MI_FA is introduced using a simple scatter plot. In order to further emphasize the relationship between MI_FA, MI_RD, and MI_AD, the three metrics are shown together alongside a cartoon depiction of the hypothesized mechanisms (Figure 7, left panels) leading to the observed relationship between MI_RD and the magnitude of MI_AD or MI_FA (Figure 7, right panels). A larger positive MI_RD resulted in a large positive MI_AD and null MI_FA. These findings are consistent with the adopted (Dubois et al. 2008) model of pre-myelination occurring more rapidly prior to birth. Alternatively, a larger negative MI_RD indicated a large negative MI_FA and relatively null MI_AD. These data points are consistent with the adopted model of true myelination occurring more rapidly after birth. Using this framework, MI_RD is the most informative measure of diffusivity as its sign appears to be reflective of simple models of either pre-myelination or true myelination.

Figure 7. The inter-relationship bewteen MI_RD, MI_AD and MI_FA.

Left panel set: DTI model of pre- and true myelination (far left panels) and a cartoon depiction of pre-myelination occurring before birth and true myelination occurring after birth (middle two panels). Note the process-dependence of FA, RD and AD (far left) as well as the hypothesized values for MI_FA, MI_RD, and MI_AD (middle). Far right panel: MI_RD predicts the relationship between MI_FA and MI_AD. As expected, the majority of data points are found to have a large positive MI_RD, large positive MI_AD and null MI_FA. A large cluster of data points with large negative MI_RD, large negative MI_FA and roughly null MI_AD, were found in regions known to show early signs of myelin.

One common criticism of the conventional DTI techniques applied here is the lack of specificity. Indeed, all common measures of diffusion (RD, AD, FA) may be confounded by a number of concomitant attributes including axonal diameter, compaction, water content and fiber coherence (Jones et al., 2013). While these confounds cannot and should not be dismissed in whole, we believe that because the calculation of MI is relative (comparison of rates of change before and after birth), all static confounds will be controlled for. As such, many of the inherent weaknesses of using absolute measures of FA, RD and AD are uniquely avoided using this technique. It should also be noted that alternatives to conventional diffusion imaging, while considered at the onset of the current study, were deemed to be either too long of an acquisition time (High Angular Resolution Diffusion Imaging) (Zhan et al., 2012) with the available hardware or potentially not sensitive enough to myelin (MWF) at less than 48 postmenstrual weeks (Deoni et al., 2011).

This study focused on two primary stages of axonal development: premyelination and true myelination. A third developmental stage often considered in neonates is axonal organization. During this stage, one would expect FA and AD to increase with a concomitant decrease in RD. Only one small cluster was found to have significant MI values for all three diffusion parameters in the far superior portion of the right premotor tract. While this may be a reasonable site for such a process, rates of change of both AD and RD were negative, a finding not likely in the event of increasing fiber coherence. Furthermore, the majority of axonal organization is thought to be largely concluding in the human fetus during the late preterm phase of development (Kostović and Jovanov-Milošević, 2006).

While we believe the observed MI patterns are reflective of the myelination process, it is worth considering non-myelin-specific contributions to the diffusion measurements used here. Spatial resolution is limited in the growing brain and because the brain is rapidly increasing in size, partial voluming of the fiber tracts may cause brain size dependent variation (Yoshida et al., 2013). To help account for this, intracranial volume was used in both model 1 and model 2. Similarly, the DTI acquisition methods employed in this work are susceptible to ambiguity caused by crossing fibers. While these voxels may obfuscate developmental changes, causing false negatives, it is unlikely that they would induce false positives, as the measures used here are relative, requiring the nature of the fiber crossings themselves to change as a result of birth. In addition, reductions in FA (Dubois et al., 2014) are expected when the amount, diameter or integrity of crossing fibers is increased, and such values were not observed in this study. Finally, it should be stated that the interpretation of observed effects made here is predicated on the DTI model of maturation provided by Dubois et al. (2008), and is therefore not an unequivocal observation of pre- or true-myelination patterns in the perinatal period.

While the aim of this study was to apply the MI method to perinatal diffusion data, this framework may extend to other dynamic processes with temporally well-defined events including maturation during pubertal onset, and neurodegeneration surrounding the onset of Alzheimer's disease. The MI can be generalized as the change in slope after a well-defined “event” (i.e., birth). A known “initiation” and measurement at an “observation” time point following the “event” are also required. The event, initiation and observation in the current context are birth, conception and postnatal age at MRI, respectively. The changes used in the calculation of MI are always considered using the event (birth) as the frame of reference. The variation in time separating initiation (conception) and observation (scan age) ought to be comparable in order to give equal weighting in explanatory power between the relative exposure times. While the resultant change in slope at the time of the event (birth) implies causation driven by the event, in the context of this work, the knee of an exponentially increasing or decreasing maturation curve such as those found in logistic function models of growth (Dean et al., 2014) would also drive similar results as they have a non-zero first derivative. As such, this work does not directly confirm the physiological changes occurring at birth as a mechanism for change in white matter maturation. Logistic growth has also been previously modeled as being either biphasic or monophasic linear growth and would be consistent with significant MI in this study (Ball et.al., 2013). It seems plausible from a developmental perspective that the inflection point in maturation curves be in sync with birth given the abrupt transition to the extrauterine environment. In this study, this was interpreted as rapid premyelination (large RD and FA change) before birth across large regions of the brain and rapid true myelination (large RD and AD change) in areas known to have trace amounts of myelin at birth followed by mature myelin within 28 weeks after birth (Deoni et al., 2011).

Because the developmental trajectories suggested by the MI are in concordance with our understanding of perinatal maturation of white matter fiber tracts based on histological postmortem studies, the novel MI approach used here seems to be informative about prenatal relative to postnatal maturational change using a cross-sectional design of healthy late preterm and full-term newborns. By considering three diffusion parameters and their role in different stages of white matter development, we have constructed a plausible model of the ontogeny of early life white matter. While the MI described here has been shown to be useful for characterizing average group patterns, it is not designed to probabilistically identify differences in individuals or between groups. Future efforts will focus on developing between-group tests to identify deviations from normal brain development and to better understand environmental conditions that are associated with such deviations that may be amenable to intervention.

Highlights.

• DTI data were examined for dependence on gestational (GA) and postnatal age (SA).

• The Maturation Index (MI) captures the dependence of DTI data on GA relative to SA.

• Tract-based analysis demonstrates negative MI in regions known to myelinate early.

• Positive MI was also observed and may be reflective of in-utero pre-myelination.

• MI maps are presented, postulated to be indicative of perinatal brain maturation.