Pancreatic Tumor Growth Prediction with Elastic-Growth Decomposition, Image-Derived Motion, and FDM-FEM Coupling

Abstract

Pancreatic neuroendocrine tumors are abnormal growths of hormone-producing cells in the pancreas. Unlike the brain which is protected by the skull, the pancreas can be significantly deformed by its surrounding organs. Consequently, the tumor shape differences observable from images at different time points arise from both tumor growth and pancreatic motion, and tumor growth model personalization may be compromised if such motion is ignored. Therefore, we incorporate pancreatic motion information derived from deformable image registration in model personalization. For more accurate mechanical interactions between tumor growth and pancreatic motion, elastic-growth decomposition is used with a hyperelastic constitutive law to model the mass effect, which allows growth modeling while conserving the mechanical properties. Furthermore, a way of coupling the finite difference method and the finite element method is proposed to greatly reduce the computation time. With both 2-[¹⁸F]-fluoro-2-deoxy-D-glucose positron emission tomographic and contrast-enhanced computed tomographic images, functional, structural, and motion data are combined for a patient-specific model. Experiments on synthetic and clinical data show the importance of image-derived motion on estimating pathophysiologically plausible mechanical properties and the promising performance of our framework. From seven patient data sets, the recall, precision, Dice coefficient, relative volume difference, and average surface distance between the personalized tumor growth simulations and the measurements were 83.2±8.8%, 86.9±8.3%, 84.4±4.0%, 13.9±9.8%, and 0.6±0.1 mm, respectively.

I. Introduction

Pancreatic neuroendocrine tumors are abnormal growths of hormone-producing cells in the pancreas [1], [2]. These are rare tumors with only about 1000 new cases in the United States per year. They are slow growing with tumor doubling times more than 500 days, and are usually not treated until reaching a certain size such as 3 cm in diameter. If patient-specific tumor growth can be accurately predicted, treatment or surgical planning can be improved, so that the risk of metastatic disease, operative resection, and unnecessary testing can be better managed. For example, accurate prediction of tumor doubling time can help decide between nonoperative or surgical treatments for these tumors [1].

Tumor growth prediction can be achieved by pathophysiological modeling and model personalization from clinical measurements. As tumor growth modeling is particularly applicable for tumors that are unresectable or not removed until reaching a certain size [3], [2], image-based personalization has been actively researched [4], [5], [6], [7], [8], [9], [10]. An image-based tumor growth prediction framework typically requires several key components, including pathophysiological models, image-derived measurements, and model-measurement coupling. Models provide the pathophysiology and thus the prediction capability of tumor growth. Image-derived measurements provide patient-specific information for model personalization. Model-measurement coupling describes how models are personalized using measurements.

Unlike the brain which is protected by the skull, the pancreas can be significantly deformed by its surrounding organs. Consequently, the tumor shape differences observable from images at different time points arise from both tumor growth and pancreatic motion, and model personalization may be compromised if such motion is ignored. As existing frameworks do not account for such motion, this paper investigates how pancreatic motion can be incorporated for more pathophysiologically plausible model personalization. This involves extracting motion information from images, and adopting an appropriate biomechanical model for more accurate interactions between tumor growth and pancreatic motion.

A. Macroscopic Tumor Growth Model

Tumor growth is associated with cell invasion and mass effect [11]. For cell invasion, tumor cells migrate as a cohesive group and penetrate the surrounding tissues. Mass effect is the outward pushing of the growing tumor mass which displaces the tumor cells and the surrounding tissues. Cell invasion and mass effect are mutually reinforcing [11]. Because of the computational complexity of model personalization and the macroscopic nature of imaging data, macroscopic models are mostly used for image-based personalization. Most macroscopic tumor growth models account for cell invasion [4], [5], [6], [7], [8], [9], [10]. Some models, including ours in this paper, also account for mass effect [4], [5], [8], [9], [10]. Cell invasion is mostly modeled by reaction-diffusion equations [4], [5], [6], [7], [8], [9], [10]. The differences among models are usually the choices between isotropic and anisotropic diffusion, Gompertz and logistic cell proliferation, or with and without treatment effects. Because of the highly deformable nature of the pancreas, we focus on the mass effect in this paper. We also study the numerical approach for more efficient simulation and thus model personalization.

B. Mass Effect Modeling

Mass effect modeling includes active growth and passive material properties. Active growth properties provide the stress or strain boundary conditions to simulate tumor growth. Passive material properties govern mechanical behaviors such as deformation when active growth properties are applied. For passive material properties, because of simplicity or limitation of imaging data, almost all image-based frameworks use isotropic materials which give identical properties in all directions [4], [12], [5], [8], [9], [10]. For stress-strain relations, most models use simpler linear elastic models [4], [5], [8], [9] and some use more realistic but complicated hyperelastic models [12], [10]. For active growth properties, most frameworks model mass effect by explicitly enforcing tumor size change or by exerting tumor-density-induced forces to an elastic mechanical model. In [4], the volume change of the bulk tumor of a brain glioma was modeled as an exponential function, which was imposed by a penalty method via homogeneous pressure. For the edema, tumor-density-induced forces proportional to the negative gradients of the local tumor densities were introduced to displace the tumor and its surrounding structures. In [12], the expansive force of the bulk tumor was approximated by constant outward pressure acting on the tumor boundary, and the growth of the edema was modeled by a constant isotropic expansive strain. In [5], the tumor-density-induced forces were applied to the entire brain glioma. The forces were converted to velocities by a linear mechanical model, which displace the tumor cell densities in a reaction-advection-diffusion equation. The tumor-density-induced forces were also used in [9] for breast cancer response prediction, and in [8], [10] for pancreatic tumor growth prediction.

Despite the promising results, there are several limitations of the above frameworks. As discussed, the pancreas can be greatly deformed by its surrounding abdominal organs [13]. Nevertheless, no frameworks have considered such motion. Furthermore, for the approaches using only the tumor-density-induced forces [5], [8], [9], [10], the tumor volume change could not be explicitly modeled. These approaches, together with those converting the volume change into pressure [4], [12], modeled the tumor growth by stress-strain relations in continuum mechanics. Firstly, this contradicts the nearly incompressible nature of most soft tissues [14], and thus the tissue incompressibility of the model has to be compromised. Secondly, for the mechanical models with nonlinear constitutive laws, the elastic volume change of the tumor increases its stiffness regardless of the underlying pathophysiology, and this reduces the model accuracy especially when pancreatic motion is considered. Therefore, we adopt a more appropriate model for mass effect modeling with pancreatic motion incorporated.

C. Numerical Approach

Because of the complicated model formulations, numerical approaches of temporal and spatial integrations are necessary for tumor growth simulation. In [8], the reaction-advection-diffusion equation was used to account for both the cell invasion and mass effect, and the system equation was solved by the finite difference method (FDM) with explicit time integration. In [6], as only the evolution of the tumor delineation was considered, the reaction-diffusion equation was approximated by a modified anisotropic Eikonal model and was solved by a modified fast marching method. For the frameworks using more sophisticated biomechanical models [4], [12], [10], the finite element method (FEM) has been used to handle more complicated boundary conditions and provide more accurate results with implicit time integration [15].

Nevertheless, using FEM for both the reaction-diffusion and biomechanical models may not be optimal. Firstly, FEM is computationally more expensive than other simpler methods, such as FDM which can properly handle the reaction-diffusion equation [16]. Secondly, the requirements of the mesh resolution of the models are different. The reaction-diffusion model usually requires a denser mesh for higher resolution front propagation, while mechanical deformation is usually smooth and requires fewer elements [15]. Thus, using the same mesh may reduce the accuracy and/or increase the computation time. Therefore, we propose a way of coupling the FDM and FEM simulations for more efficient model personalization.

D. Contributions

To properly incorporate pancreatic motion for tumor growth prediction, we propose a framework comprising the multiplicative elastic-growth decomposition for the mass effect and FDM-FEM coupling for the numerical approach (Fig. 1). The pancreatic motion information is extracted from contrast-enhanced computed tomographic (CT) images at different time points using nonrigid image registration to provide the image-derived motion. The elastic-growth decomposition was initially introduced to study residual stresses in soft tissues, which decomposes the continuous deformation field of a body after growth into its elastic and growth parts [17] (Fig. 2). With this decomposition, tumor growth can be modeled separately from elasticity. This preserves the accuracy of the elastic response and thus the accuracy of incorporating the pancreatic motion. For the FDM-FEM coupling, we use FDM for the reaction-diffusion model and FEM for the biomechanical model, which can be combined for the tumor growth simulation by our proposed information exchange method.

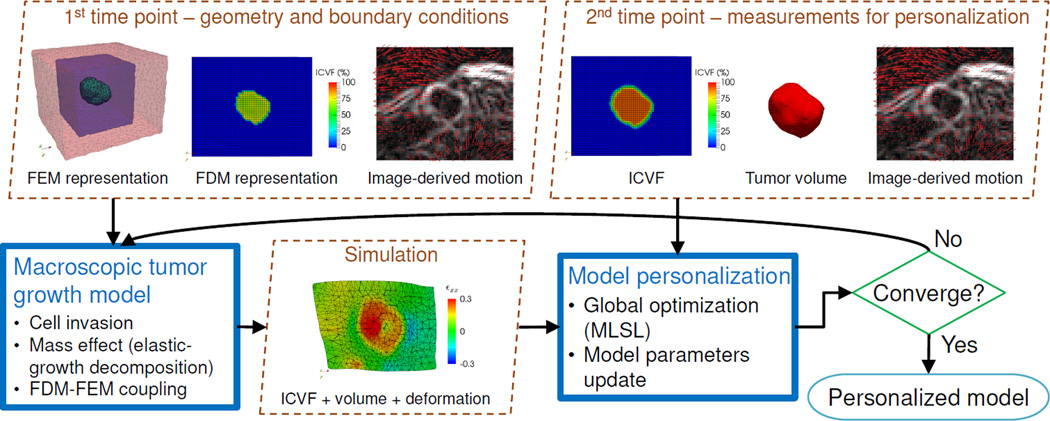
Fig. 1.

Flow diagram of the proposed framework. Measurements at the first time point provide the tumor geometry and boundary conditions for the growth simulation. Measurements at the second time point are compared with the simulation to personalize the model parameters through global optimization.

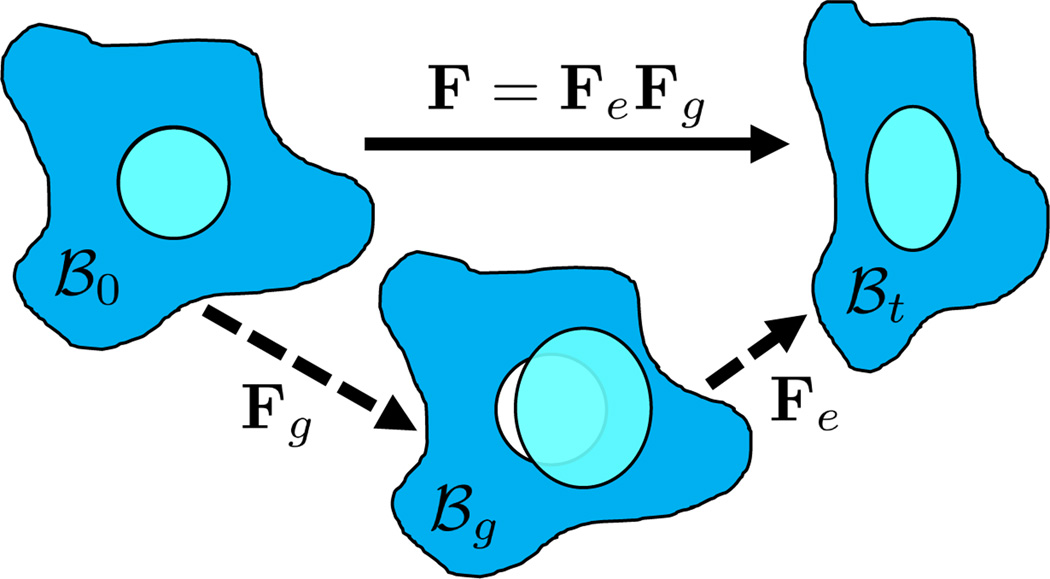
Fig. 2.

Elastic-growth decomposition. The original configuration ℬ₀ comprises the tumor (cyan) and its surroundings (blue). The growth deformation gradient F_g leads to an intermediate incompatible configuration ℬ_g. The elastic deformation gradient F_e is then applied for the compatible configuration ℬ_t.

In this paper, the tumor growth model is personalized using longitudinal imaging data. The mass effect is modeled by the elastic-growth decomposition, with the elastic part modeled by a hyperelastic constitutive law, and the growth part modeled as logistic growth. The cell invasion is modeled by a reaction-diffusion equation. The tumor growth personalization is achieved by model parameter estimation with derivative-free global optimization. Following [10], 2-[¹⁸F]-fluoro-2-deoxy-D-glucose positron emission tomographic (FDG-PET) images are used to provide the proliferation rates, and contrast-enhanced CT images are used to provide the local tumor cell densities. Different from [10], the CT images are also used to provide image-derived pancreatic motion. Experiments were performed on synthetic and clinical data to evaluate the performance.

Therefore, assuming the shape differences of a tumor among different time points are solely caused by tumor invasion, mass effect, and motion exerted by its surrounding organs, our overall goal is to obtain a personalized model using image information to accurately predict the tumor growth. This goal is mainly achieved by incorporating the elastic-growth decomposition which eliminates the contradiction between tumor size change and tissue incompressibility for the mass effect. The use of image-derived pancreatic motion enables more accurate comparisons of tumor shapes between simulations and measurements during model personalization [13].

This manuscript is substantially different from our previous publications in [10] and [18] as follows:

1. Unlike [10] which used tumor-density-induced forces for the mass effect, here we use elastic-growth decomposition. Preliminary results were published in [18].

2. For image measurements, pancreatic motion was not considered in [10]. In [18], such motion was only applied as the boundary conditions of the biomechanical model, and the model personalization was sensitive to the ranges and initial values of the model parameters. In this paper, the motion information is also used in the objective function. This provides more precise and pathophysiologically plausible mechanical parameter estimation.

3. Unlike [10] and [18], here we present a new FDM-FEM coupling method which reduces hours of computation especially when intratumor heterogeneity is considered.

4. As the framework of this manuscript is substantially different from [18], all experiments were redone. More experiments were also added to illustrate the properties and performance of the framework.

II. Macroscopic Tumor Growth Model

The macroscopic tumor growth model is used as the central link to combine several imaging data. It also provides the prediction capability when personalized. We emphasize the modeling of mass effect as it is our main contribution.

A. Mass Effect

Mass effect comprises the tumor mass growth and its mechanical interactions with the surrounding tissues [11]. In most image-based tumor growth personalization [12], [5], [8], [9], [10], the active growth has been modeled by stress-strain relations in continuum mechanics. This contradicts the tissue incompressibility of most tumors, and is undesirable when passive tumor deformation exerted by the surrounding tissues needs to be considered. Furthermore, the effects of mass growth on the passive mechanical properties of the tumor have not been considered.

In the biomechanics community, a well-known approach for growth and remodeling is the multiplicative elastic-growth decomposition, which has been applied to model the growth of cardiac muscle, skin, and tumor [19], [20], [21], [22]. By adopting this decomposition, the deformation of a tumor can be decomposed into its elastic and growth parts which can be modeled separately. This allows the tumor growth to be modeled independently from the elastic response, and thus the tissue incompressibility can be preserved. This also systematically handles the effects of the tumor growth on the stress-strain relations. The decomposition, passive mechanical model, and tumor growth model are presented next.

1) Hyperelastic Biomechanical Model with Elastic-Growth Decomposition

Let X and x be the coordinates in the original configuration (ℬ₀) and the final (deformed) configuration (ℬ_t), respectively (Fig. 2). In solid mechanics, the deformation gradient F = ∂x/∂X maps the original configuration to the final configuration as dx = FdX [15]. F can be decomposed multiplicatively into its elastic (F_e) and growth (F_g) parts as F = F_eF_g [17]. Inhomogeneous growth, such as the growth of a tumor but not its surrounding tissues, can result in gaps or overlaps in the intermediate configuration (ℬ_g). This configuration is physically impossible and the system equation cannot be solved therein. Therefore, although the elastic response is from ℬ_g to ℬ_t, we need to reformulate the quantities in ℬ_g in terms of those in the compatible configuration ℬ₀ for the total-Lagrangian formulation [15].

In the decomposition, the elastic part is governed by a strain energy function. The Green-Lagrange strain tensor $\mathit{\epsilon }=\frac{1}{2}({\mathbf{F}}^{\mathrm{T}}\mathbf{F}-\mathbf{I})$ and its elastic part ${\mathit{\epsilon }}_e=\frac{1}{2}({\mathbf{F}}_e^{\mathrm{T}}{\mathbf{F}}_e-\mathbf{I})$ and growth part ${\mathit{\epsilon }}_g=\frac{1}{2}({\mathbf{F}}_g^{\mathrm{T}}{\mathbf{F}}_g-\mathbf{I})$ are related as [17]:

$${\mathit{\epsilon }}_e={\mathbf{F}}_g^{-\mathrm{T}}(\mathit{\epsilon }-{\mathit{\epsilon }}_g){\mathbf{F}}_g^{-1}$$ (1)

With tissue growth, the change of mass needs to be considered for accurate stress-strain relations. Let ^tm be the grown mass, and ⁰V and ^gV be the volumes in ℬ₀ and ℬ_g, respectively. The densities of the grown mass with respect to different configurations are given as ${}_0{}^t\rho =\mathrm{d}{}^{t}m/\mathrm{d}{}^{0}V$ and ${}_g{}^t\rho =\mathrm{d}{}^{t}m/\mathrm{d}{}^{g}V$, with relation ${}_0{}^t\rho ={}_g{}^t\rho J_g(J_g=\text{det }{\mathbf{F}}_g=\mathrm{d}{}^{g}V/\mathrm{d}{}^{0}V$ indicates the volume ratio). Therefore, the second Piola-Kirchhoff (PKII) stress tensor in ℬ_g is:

$${\mathbf{S}}_e=\frac{\partial ({}_g{}^t\rho \psi )}{\partial {\mathit{\epsilon }}_e}=\frac{1}{J_g}\frac{\partial ({}_0{}^t\rho \psi )}{\partial {\mathit{\epsilon }}_e}$$ (2)

where ψ is the strain energy per unit grown mass, and thus ${}_g{}^t\rho \psi$ and ${}_0{}^t\rho \psi$ are the strain energy per unit intermediate and original volume, respectively. As we model F_g independently of F (Section II-A2), the PKII stress tensor in ℬ₀ is:

$$\mathbf{S}=\frac{\partial ({}_0{}^t\rho \psi )}{\partial {\mathit{\epsilon }}_e}:\frac{\partial {\mathit{\epsilon }}_e}{\partial \mathit{\epsilon }}={\mathbf{F}}_g^{-1}\frac{\partial ({}_0{}^t\rho \psi )}{\partial {\mathit{\epsilon }}_e}{\mathbf{F}}_g^{-\mathrm{T}}=J_g{\mathbf{F}}_g^{-1}{\mathbf{S}}_e{\mathbf{F}}_g^{-\mathrm{T}}$$ (3)

and the corresponding fourth-order elasticity tensor is:

$$ℂ=\frac{\partial \mathbf{S}}{\partial \mathit{\epsilon }}=J_g({\mathbf{F}}_g^{-1}\overline{\otimes }{\mathbf{F}}_g^{-1}):{ℂ}_e:({\mathbf{F}}_g^{-\mathrm{T}}\overline{\otimes }{\mathbf{F}}_g^{-\mathrm{T}})$$ (4)

with non-standard dyadic product [A⊗̄B]_ijkl = [A]_ik [B]_jl and ℂ_e = ∂S_e/∂ε_e. If no growth, S = S_e and ℂ = ℂ_e.

Modeling the highly deformable pancreas requires finite strains and incompressibility under large deformation. Furthermore, an isotropic material model is used as tissue structure is unavailable in our data. Therefore, the modified Saint-Venant-Kirchhoff (hyperelastic) constitutive law is adopted [23]:

$${}_g{}^t\rho \psi ({\mathit{\epsilon }}_e)=\frac{1}{2}\lambda {(J_e-1)}^2+\mu \text{Tr}({\overline{\mathit{\epsilon }}}_e^2)$$ (5)

where J_e = det F_e. The tensor ${\overline{\mathit{\epsilon }}}_e=\frac{1}{2}({\overline{\mathbf{F}}}_e^{\mathrm{T}}{\overline{\mathbf{F}}}_e-\mathbf{I})$ is the isovolumetric part of ε_e, with ${\overline{\mathbf{F}}}_e=J_e^{-\frac{1}{3}}{\mathbf{F}}_e$ and det F̄_e ≡ 1. Therefore, the first and second term of (5) account for the volumetric and isochoric elastic response, respectively, and λ is the bulk modulus and μ is the shear modulus. The larger the value of λ, the more incompressible the tissue.

Given F_g from a growth model, and F the existing deformation, ε_e can be computed by (1). S_e and ℂ_e can then be computed using (5) and converted to S and ℂ by (3) and (4) for the total-Lagrangian formulation [15].

2) Tumor Volumetric Growth Model

The growth deformation F_g can be modeled as the general form [17], [22]:

$${\mathbf{F}}_g={\vartheta }_1{\mathbf{v}}_1\otimes {\mathbf{v}}_1+{\vartheta }_2{\mathbf{v}}_2\otimes {\mathbf{v}}_2+{\vartheta }_3{\mathbf{v}}_3\otimes {\mathbf{v}}_3$$ (6)

with ϑ₁, ϑ₂, and ϑ₃ the stretch ratios along the orthonormal vectors v₁, v₂, and v₃, respectively. All ϑ_i > 0.

There are different ways to model the stretch ratios. Stress-induced growth was used to model arterial wall thickness in response to stenting [19], and stretch-induced growth was used to model skin expansion in reconstructive surgery [21]. In our case, pancreatic tumor growth is neither stress- nor stretch-induced. Furthermore, the initially fast tumor growth slows down when reaching a certain size as nutrients are limited. Therefore, we model the stretch ratios as logistic functions:

$${\vartheta }_i(t)=\frac{{\overline{\vartheta }}_i}{1+(-1+\frac{{\overline{\vartheta }}_i}{{\vartheta }_i(t_0)})e^{-{\varrho }_i(t-t_0)}},i=1,2,3$$ (7)

with ϱ_i the proliferation rate, ϑ_i(t₀) the initial stretch ratio, and ϑ̄_i the maximum stretch ratio. As ϑ_i(t₀) is relative and cannot be measured from a single image, we assume ϑ_i(t₀ = 0) = 1 at the first measurement time point. The maximum stretch ratio is computed as the maximum allowable tumor size to the initial tumor size. In [24], the largest pancreatic neuroendocrine tumor size without metastasis is about 5 cm.

As tissue structure is unavailable, the isotropic version of (6) is used. By using ϑ = ϑ₁ = ϑ₂ = ϑ₃ and the standard basis as the orthonormal vectors, we have F_g = ϑI. This reduces the number of parameters to be estimated.

In the experiments, we set λ = 5 kPa empirically for tissue incompressibility. Therefore, μ and ϱ are the parameters to be estimated for the biomechanical model.

B. Tumor Cell Invasion by Reaction-Diffusion Equation

To facilitate the complicated inverse problem, the macroscopic reaction-diffusion equation is usually used for image-based model personalization [5], [6], [25], [8]:

$$\frac{\partial N}{\partial t}=\text{div}(\mathbf{D}\nabla N)+R(N)$$ (8)

with N the number of tumor cells, D the diffusion tensor characterizing the invasive property, and R the reaction term accounting for cell proliferation. As the pancreatic tumor grows slowly, we use the logistic growth as the reaction term:

$$\frac{\partial c}{\partial t}=\text{div}(\mathbf{D}\nabla c)+\rho c(1-c)$$ (9)

where c = (N/K) ∈ [0, 1] represents the normalized tumor cell ratio, with K the carrying capacity. ρ is the proliferation rate which can be computed from FDG-PET images for better subject-specificity (Section III-C). As the number of cells is proportional to the space they occupy, we represent c by the intracellular volume fraction (ICVF), which is the local ratio of the intracellular space to the tissue volume. ICVF can be computed from contrast-enhanced CT images to provide the initial conditions of (9) (Section III-B), and can be used as the measurements for model personalization. D can be a diagonal matrix with components D_x, D_y, D_z, but we use D = DI as the tissue structure is unavailable.

III. Image-Derived Information

Image information is necessary for patient-specific tumor growth prediction. As tumor growth involves morphological and physiological functions [11], both structural, functional, and motion data are used to improve the patient-specificity.

A. Image-Derived Pancreatic Motion

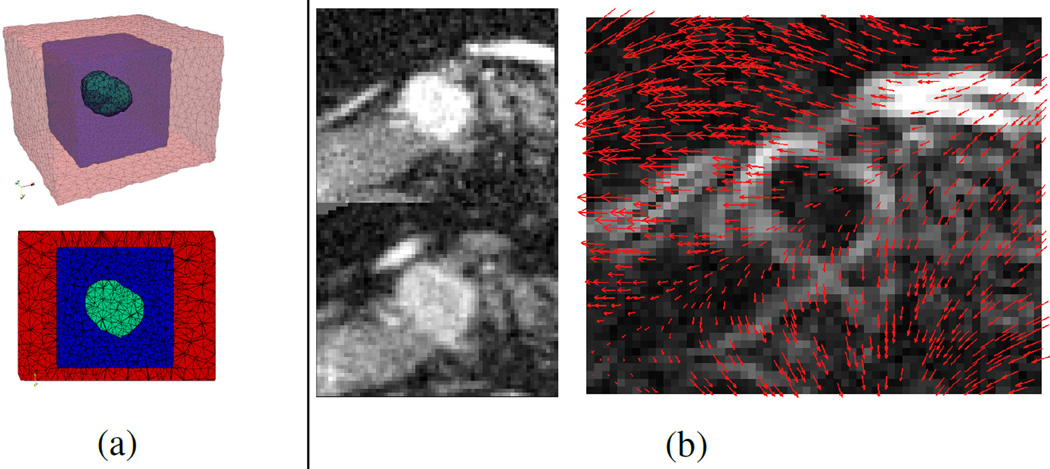
The tumor shape change observable from images is caused by both the tumor growth and the deformation of the pancreas. To incorporate such deformation for more realistic model personalization, the region of interest (ROI) around the tumor covering the boundaries of the pancreas is extracted from each post-contrast CT image. ROIs of consecutive time points are registered using deformable image registration with mutual information to provide the displacements of the salient features [26] (Fig. 3(b)). B-spline transform is used with linear interpolation, and the L-BFGS optimizer is adopted. The Insight Segmentation and Registration Toolkit (ITK) is utilized. The displacements are enforced as boundary conditions to deform the grown tumor through the biomechanical model in Section II-A1, and this allows more accurate comparison with the measurements during model personalization. To avoid interfering with the tumor growth, a 3D FEM mesh is constructed from the ROI with three zones: the tumor, its surroundings for growth, and the outer zone for enforcing the image-derived pancreatic motion (Fig. 3(a)). The surrounding (blue) zone is defined so that it can contain the tumor after growth. The outer (red) zone contains the pancreatic boundaries around the tumor so that the pancreatic motion can be captured. As image registration relies mostly on salient features such as the boundaries of the pancreas, only the displacements of pixels with large enough gradient magnitudes are used.

Fig. 3.

(a) A FEM mesh and its middle slice. The green zone is the tumor, which can grow into the blue zone. The red zone is for enforcing image-derived motion. (b) Image-derived motion. Left: ROIs of the post-contrast CT images at the earlier (top) and later (bottom) time points. Right: deformation field from the earlier to the later time point overlapping with the gradient magnitude at the earlier time point.

B. ICVF from Contrast-Enhanced CT Images

ICVF is the local ratio of the intracellular volume to the tissue volume, which can be computed using contrast-enhanced CT images [10](Fig. 4). Contrast enhancement is achieved by intravenous administration of an iodine-based contrast agent. The enhancement level is proportional to the extracellular space of a given type of tissue at a given phase, and is related to the delivery, retention, and elimination of the contrast agent, as well as the timing of image acquisition [27]. To compute the ICVF of the tumor, the pre- and post-contrast CT images are first registered using deformable image registration [26], and the difference image is computed to provide the enhancement in Hounsfield units. A known reference of contrast enhancement per extracellular space is required. The reference we use is the hematocrit (Hct), which is the ratio of the volume of red blood cells to the volume of blood. Hematocrit is measurable from a patient’s blood samples. However, as such records are not always available, the Hct value of 0.45 is used [28]. By using also the contrast enhancement at blood pools such as the aorta, the ICVF (c ∈ [0, 1]) of the tumor can be computed as [10]:

$$c=1-\frac{H{U}_{\text{post}\_\text{tumor}}-H{U}_{\text{pre}\_\text{tumor}}}{\mathrm{E}[H{U}_{\text{post}\_\text{blood}}-H{U}_{\text{pre}\_\text{blood}}]}(1-Hct)$$ (10)

where HU_{post_tumor}, HU_{pre_tumor}, HU_{post_blood}, and HU_{pre_blood} are the Hounsfield units of the post- and pre-contrast CT images at the segmented tumor and blood pool (aorta), respectively. E[•] represents the mean value. Therefore, the ICVF of the tumor is computed using the ICVF of the blood (Hct) as a reference. The computed ICVF can be used as the initial conditions in simulation, or as the measurements in personalization.

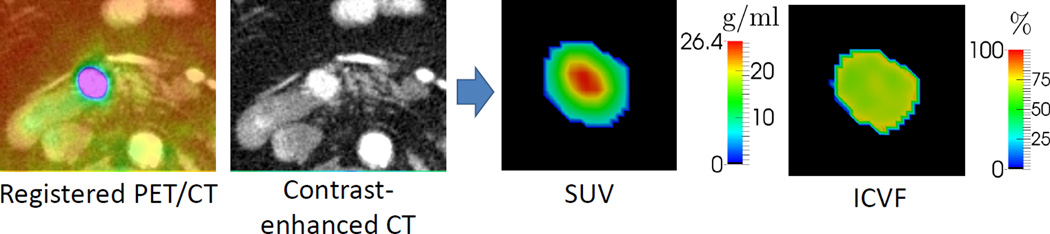
Fig. 4.

SUV and ICVF computed from FDG-PET and contrast-enhanced CT images. ICVF represents the normalized tumor cell ratio which provides the initial conditions for simulation or the measurements for model personalization. The proliferation rate in the reaction-diffusion equation can be computed by combining SUV and ICVF.

C. Proliferation Rates from FDG-PET Images

FDG-PET images provide functional information of increased glucose uptake and glycolysis of cancer cells for metabolic abnormalities [29]. Thus they can be used to infer the proliferation rate (ρ) in (9). To compensate for the variation of injected FDG dose and the patient’s weight, the standardized uptake value (SUV) is usually used (Fig. 4):

$$\mathrm{S}\mathrm{U}\mathrm{V}=\frac{\mathrm{P}\mathrm{E}\mathrm{T}\text{ image intensity}}{\text{injected dose}/\text{body weight}}$$ (11)

The SUV can be related to the proliferation rate through a quantitative model of metabolic energy allocation [30]. Some energy maintains existing cells and some creates new cells. Thus the rate of energy flow (B) can be modeled as:

$$B=B_{c}Kc+E_{c}K\frac{\partial c}{\partial t}$$ (12)

where B_c is the metabolic rate of a single cell and E_c is the metabolic energy to create a cell. With the assumption of logistic proliferation, the second term of (9), $\frac{\partial c}{\partial t}=\rho c(1-c)$, can be substituted into (12), and the equation becomes:

$$\rho =\frac{B-B_{c}Kc}{E_{c}Kc(1-c)}$$ (13)

As SUV is directly proportional to glucose metabolism [29], B can be inferred from SUV, and we can rewrite (13) as:

$$\rho =\frac{\alpha \mathrm{S}\mathrm{U}\mathrm{V}-\beta c}{c(1-c)};\text{ with }\alpha \mathrm{S}\mathrm{U}\mathrm{V}=\frac{B}{E_{c}K}\text{ and }\beta =\frac{B_c}{E_c}$$ (14)

where α > 0 and β > 0 are unknown scalars to be estimated. B = αE_cKSUV indicates that the overall metabolic rate is proportional to SUV. Given SUV and c from PET and CT images, (14) is a linear function of α and β. Therefore, α and β cannot be uniquely identified, and we set β = 0.02 day⁻¹ according to [30]. Hence, the proliferation rate (ρ) can be approximated from PET and CT images with the estimation of α using the patient’s longitudinal data.

IV. Model Personalization

The prediction capability of the model is achieved by the personalization of the model parameters. The objective function and optimization algorithm need to be properly considered for more subject-specific and accurate personalization.

A. Objective Function

Complementary data improve the subject-specificity of the personalized model [31]. Therefore, our objective function accounts for the ICVF, volume, and deformation differences. The simulated ICVF and displacements with model parameters θ are rasterized into images by referencing the CT image at the same time point, and the following objective function is computed:

$$f(\mathit{\theta })=w_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}\sqrt{\mathrm{E}\left[{(\overline{c}-c(\mathit{\theta }))}^2\right]}+w_{\text{Dice}}[1-\frac{2\times \mathrm{T}\mathrm{P}\mathrm{V}}{V_{\mathrm{m}}+V_{\mathrm{s}}}]+w_{\text{disp}}\mathrm{E}[|\mathbf{ū}-\mathbf{u}(\mathit{\theta })|]$$ (15)

where TPV is the true positive volume, the overlapping volume between the simulated tumor volume (V_s) and the measured (segmented) tumor volume (V_m). In the rasterized ICVF image, we define the tumor voxels as those with ICVF larger than 50% as almost all image-derived ICVF are larger than this value (Table I). c̄ and c(θ) are the respective measured and simulated ICVF within TPV. ū and u(θ) are the respective measured and simulated displacement vectors outside of the displacement-enforcing zone, the measured tumor, and the simulated tumor, i.e. within a subset of the blue region in Fig. 3(a). u(θ) is obtained by mechanical simulation, and ū is obtained by the procedure described in Section III-A. Therefore, the objective function accounts for both the ICVF root-mean-squared error (RMSE), Dice coefficient (Dice), and mean displacement difference (disp), and w_RMSE, w_Dice, and w_disp control their respective contributions. In our experiments, we set w_RMSE = w_Dice = w_disp = 1. The maximum values of the RMSE and the Dice terms are 1, so the same weight can be used. The displacement term does not have a theoretical bounding value, however, it is mostly smaller than 5 mm in the clinical data, and the parameters can be accurately estimated in the synthetic data with w_disp = 1.

TABLE I.

Tumor information at the 1st, 2nd, and 3rd measurement time points of seven patients.

	1st–2nd		2nd–3rd
Patient ID	Days	Growth (%)	Days	Growth (%)	Size (cm3, 3rd)	ICVF range (%, 3rd)	SUV max (g/ml, 1st)
1	384	34.6	804	33.4	2.3	[63.2, 84.1]	4.8
2	363	15.3	363	10.7	1.4	[64.5, 85.4]	6.2
3	378	18.9	372	7.5	0.4	[62.3, 83.8]	5.1
4	426	41.5	420	68.6	3.8	[63.4, 91.8]	26.9
5	372	7.4	360	12.5	6.3	[44.6, 83.8]	12.0
6	168	18.7	552	18.7	3.2	[56.0, 91.5]	7.8
7	363	16.9	525	34.7	0.3	[67.7, 88.2]	3.2

B. Derivative-Free Global Optimization

The analytical gradient of the objective function (15) is difficult to derive. We also found that local optimization may converge to local minima and could not accurately identify the parameters in most synthetic data. Therefore, a derivative-free global optimization method is required.

In our previous work [10], the global optimization algorithm DIRECT (DIviding RECTangles) was used [32]. DIRECT is a deterministic sampling algorithm which systematically divides the search domain into smaller hyperrectangles, and is designed to explore the variable space for the global minimum. Nevertheless, DIRECT could not accurately estimate the model parameters of the synthetic data in our current framework. Therefore, we use the multilevel single linkage (MLSL) global optimization instead [33], which provides satisfactory results on the synthetic data. MLSL is a multistart algorithm which performs local optimizations from random or low-discrepancy sampling points. Using the idea of single-linkage clustering, MLSL reduces the number of local searches and avoids repeated searches of the same local optima.

MLSL requires a local search method. As the shape of the objective function is unknown, methods based on quadratic shape assumption should not be used. In this work, we have adopted the subplex method (SUBPLEX) as it is derivative-free and has no shape assumption [34]. SUBPLEX is a generalization of the Nelder-Mead simplex method (NMS) [35]. A simplex in n-dimensional space is a convex hull of n + 1 points, such as a triangle in 2D. In NMS, a simplex moves through the objective function space, changing size and shape, and shrinking near the minimum. SUBPLEX improves NMS by decomposing the searching space into subspaces for better computational efficiency. We found that using MLSL with SUBPLEX can give satisfactory results on synthetic data.

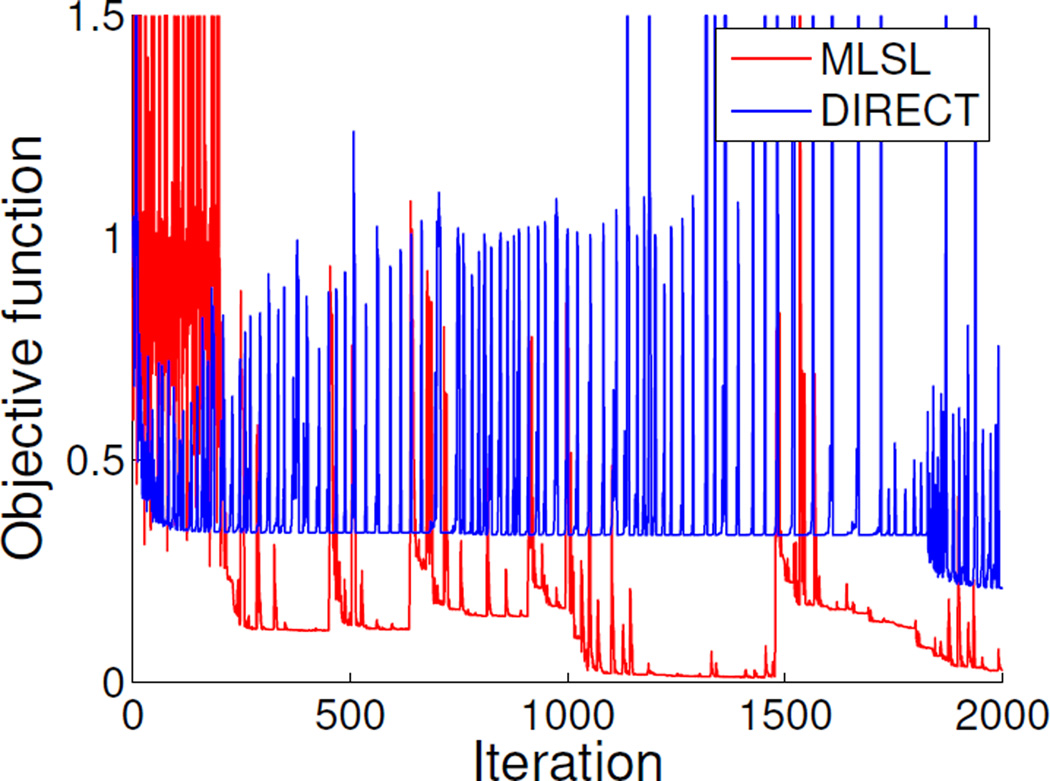
Fig. 5 shows an example of objective function evolution on synthetic data (Section VI-C). For DIRECT, the large fluctuation of the objective function value indicates its global search pattern. Although it had a trend to approach the optimal objective function value of zero, it failed with the given number of iterations (2000). For MLSL, the large fluctuation at the beginning indicates the evaluations of the sampling points, followed by the local search patterns. The best result was achieved in the fourth local search.

Fig. 5.

An example of objective function evolution. For DIRECT, the large fluctuation indicates its global search pattern. It failed to converge to the minimal objective function value with the given number of iterations (2000). For MLSL, the large fluctuation at the beginning indicates the evaluations of the sampling points, followed by the local search patterns. The best result was achieved in the fourth local search.

V. Numerical Approach

As analytical solutions are unavailable for sophisticated models, numerical methods are necessary. Reaction-diffusion models are usually solved by FDM [16], while mechanical models are mostly solved by FEM [15]. FDM is computationally efficient if explicit time integration is used, but it cannot handle complicated geometry and boundary conditions. In contrast, FEM is computationally more expensive, but it can better handle complicated geometries and boundary conditions. Therefore, frameworks with biomechanical models usually use FEM regardless of the reaction-diffusion models [4], [12], [25], [10]. Nevertheless, using FEM to solve the reaction-diffusion equation may unnecessarily increase the computational complexity, especially with model personalization that requires thousands of simulations. Hence, we use FDM for the reaction-diffusion model and FEM for the biomechanical model, and propose a way to combine their results for model personalization.

A. FDM-FEM Coupling

For the FDM implementation of the reaction-diffusion equation, we use the image pixels, which are resampled to be isotropic, as the FDM grid. Explicit time integration is used with central difference, and the Von Neumann stability analysis is used to ensure the appropriate time step size [16]. For the FEM implementation of the biomechanical model, the linear tetrahedral elements are used to solve the total Lagrangian formulation with Newton-Raphson iterations [15]. As the tumor growth is slow [1], quasi-static assumption is used and thus time integration is unnecessary.

The reaction-diffusion equation (9) governs the propagation of ICVF. ICVF is required by the mechanical model to define the current tumor geometry caused by tumor invasion, so that F_g in Section II-A2 can be properly defined. To achieve this purpose, the Visualization Toolkit (VTK) is used to interpolate the ICVF from the FDM grid to the FEM nodes [36]. With the ICVF available, the tumor region can be defined and the corresponding F_g can be computed.

The biomechanical model in Section II-A1 provides the deformation of the tumor and the surrounding tissues. To compute the objective function (15), the simulated ICVF from FDM needs to be transformed by the deformation to account for the mass effect. The idea of nonrigid image deformation is used to achieve this purpose. The deformation field of the FEM simulation is interpolated to the FDM grid using VTK. With this deformation field image available, the simulated ICVF can be deformed using a similar approach for nonrigid image registration.

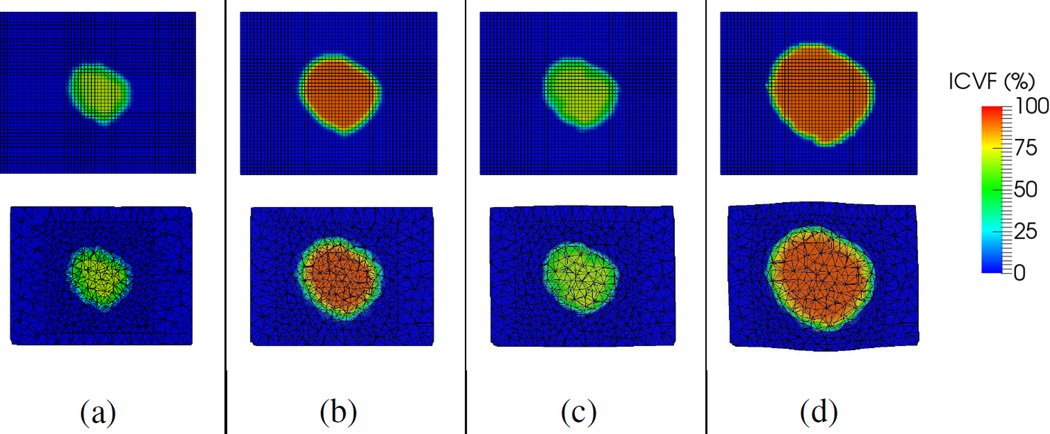
By iterating FDM and FEM with this coupling method, the resulted ICVF image comprises information from both the reaction-diffusion and biomechanical models. Illustrated in Fig. 6, the FDM-FEM coupling has the largest tumor growth as it comprises both tumor invasion and mass effect from the individual simulations.

Fig. 6.

FDM-FEM coupling. Top and bottom: FDM and FEM representations. (a) ICVF and geometry before simulation. (b) FDM simulation of tumor invasion without mass effect (top), and the interpolated FEM representation (bottom). (c) FEM simulation of mass effect without tumor invasion (bottom), and the transformed FDM representation (top). (d) The FDM-FEM coupling with the combined simulations of (b) and (c), which had the largest tumor growth as invasion and mass effect are mutually reinforcing.

VI. Experiments and Results

Different frameworks were tested on synthetic and clinical data to study the importance of including image-derived motion, and of the choice of using either elastic-growth decomposition or tumor-density-induced forces:

• EG-IM: the proposed framework with elastic-growth decomposition (EG) and image-derived motion (IM).

• EG: EG-IM framework without image-derived motion.

• F-IM: using tumor-density-induced forces (F), f_b = −γ∇c, for the mass effect, with γ a scalar to be estimated [10]. Image-derived motion was used.

• F: F-IM framework without image-derived motion.

• RD: using the reaction-diffusion (RD) model alone without mass effect.

• EG-IM-FEM: EG-IM framework using FEM for both the reaction-diffusion and biomechanical models. Tested on clinical data only.

w_disp in (15) was set to zero for non-IM frameworks. The tumor growth models in the F-IM and F frameworks are the same as that in [10]. The tumor growth model in the RD framework is similar to the ones in [6], [7].

Each experiment used measurements at three time points. The first time point provided the initial tumor geometry from the post-contrast CT image, the initial conditions of ICVF in (9), and also the proliferation rate from SUV. The second time point was used to provide measurements for model personalization. Deformation between the first and second time point was computed for the pancreatic motion, which was used for both the simulation and objective function. Prediction was performed by simulation using the personalized model, with the measurements at the second time point as inputs, and the prediction performance was evaluated using the measurements at the third time point. For a more meaningful comparison with the measurements, the deformation between the second and third time point was enforced to the prediction to account for the pancreatic motion. The prediction performance was represented by recall, precision, Dice coefficient, relative volume difference (RVD), average surface distance (ASD), and ICVF root-mean-squared error (RMSE). RMSE and Dice coefficient are defined in (15). For ASD, the absolute distance between each node on the simulated tumor surface and its nearest node on the measured tumor surface is computed, and ASD is the average of them. Recall, precision, and RVD are defined as:

$$\text{recall}=\frac{\mathrm{T}\mathrm{P}\mathrm{V}}{V_m};\text{precision}=\frac{\mathrm{T}\mathrm{P}\mathrm{V}}{V_s};\mathrm{R}\mathrm{V}\mathrm{D}=\frac{|V_s-V_m|}{V_m}$$ (16)

Not all parameters were estimated. Given SUV and c, (14) is a linear function of α and β, and thus α and β cannot be uniquely identified. In consequence, we set β = 0.02 day⁻¹ according to [30]. For λ in (5), we set its value to 5 kPa empirically for tissue incompressibility. Therefore, the parameters to be estimated were θ = {D, α, μ_normal, μ_tumor, ϱ} (Table II). For the F-IM and F frameworks, the force scaling parameter γ was estimated instead of ϱ.

TABLE II.

The preset parameters and their values, and the parameters to be estimated.

Preset parameters	β = 0.02 day−1, λ = 5 kPa
Parameters to be estimated	D, α, µnormal, µtumor, ϱ

A. FDM and FEM Representations

As uniform grids are required by FDM, we used the ICVF images for the FDM representations. The pixel size was resampled to 1.0×1.0×1.0 mm³, and the numbers of pixels ranged from 114 to 493×10³. For the FEM representations, the tumors were segmented from the post-contrast CT images by a semiautomatic level set algorithm [37]. Linear tetrahedral FEM meshes (23 to 36×10³ elements) were constructed.

B. Computation Time Comparison

Experiments were performed to compare the computation times between using FDM and FEM. Simulations were performed on seven patient geometries from the second to the third time point (Table I), with the time step size as one day using the reaction-diffusion model alone. For the FEM simulations of the reaction-diffusion equation, implicit time integration was used [15]. Two settings were tested. For the homogeneous setting, the entire geometry was one zone, and the FEM system matrices did not need to be updated for each time step. For the heterogeneous setting, the tumor and its surroundings were different zones. As the zones changed during tumor growth, the FEM system matrices were updated. For the FDM simulations, explicit time integration was used and no system matrices were formed. A computer with a 2.4-GHz Intel Xeon processor was used with a single core.

For FDM, the average times for the heterogeneous and homogeneous settings were almost the same (21.3 ± 11.1 s vs. 21.5 ± 11.2 s, p = 0.037) as the processes were identical (Table III). For FEM, the average time for the heterogeneous setting was almost double that of the homogeneous setting (52.8 ± 19.2 s vs. 28.8 ± 9.4 s, p = 0.002) because of the recomputations of the system matrices. Comparing FDM and FEM, the average time difference for the homogeneous setting was about seven seconds (p = 0.022), which means a four-hour difference for a model personalization with 2000 iterations. For the heterogeneous setting, the difference can reach 17 hours (p = 0.003). In our experiments on clinical data (Section VI-D), the average personalization time for 2000 iterations with the homogeneous setting and the FDM-FEM coupling was about 24 hours. Thus, the reduction in computation time was significant.

TABLE III.

Computation time comparison between FDM and FEM. Average computation times (seconds) of tumor rowth simulations using the reaction-diffusion model alone on seven patient data. Format: mean±std [min,max].

	FDM	FEM
Heterogeneous	21.3±11.1 [10.0, 40.5]	52.8±19.2 [24.3, 79.8]
Homogeneous	21.5±11.2 [10.1, 40.9]	28.8±9.4 [13.7, 42.3]

C. Synthetic Data

1) Experimental Setups

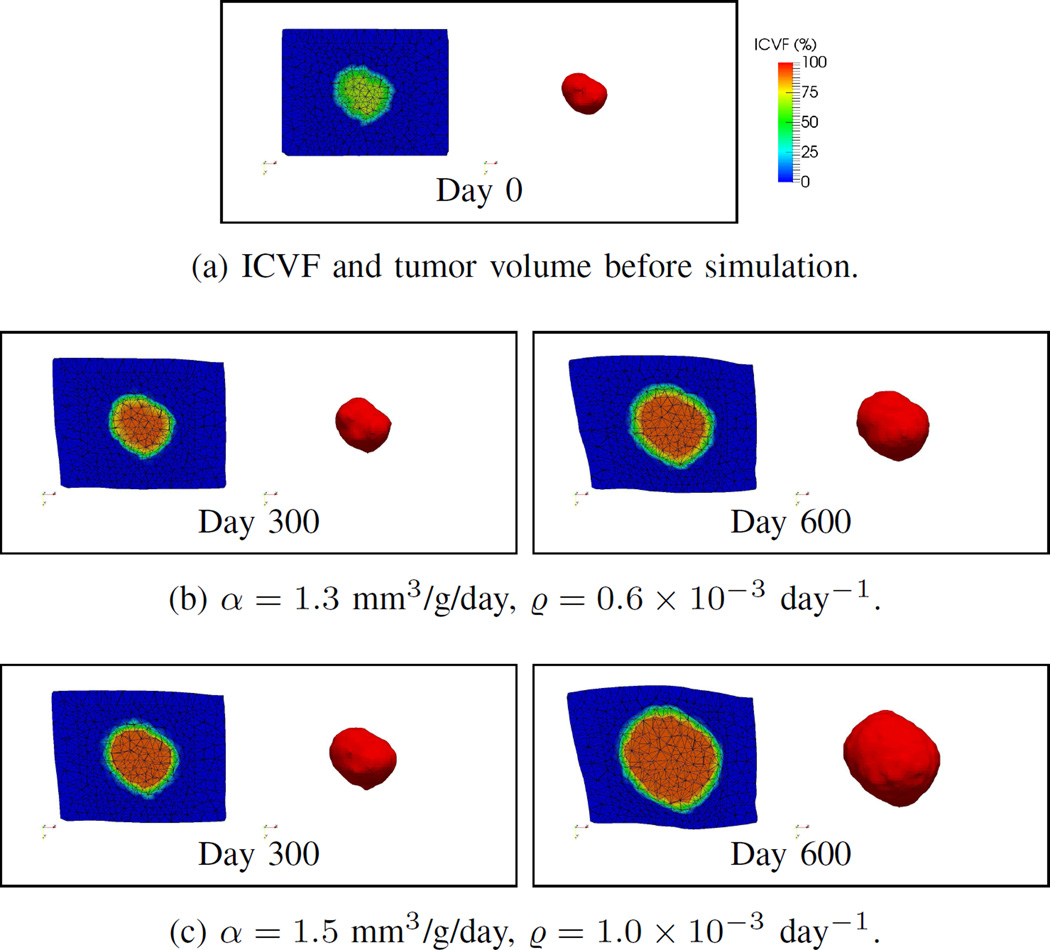
Using the FDM and FEM representations, SUV, and ICVF images of Patient 4 (Table I) at the first time point (Day 0, Fig. 7(a)), the second time point (Day 300) was simulated with the ground-truth model parameters (Table IV) to provide the measurements for model personalization (Fig. 7). The estimated parameters were then used to predict the tumor at the third time point (Day 600) and compared with the simulated ground truth.

Fig. 7.

Synthetic data. Tumor growth simulations with different model parameters. Left to right in each box: the simulated ICVF and tumor volume. (a) Before simulation. (b)–(c) Simulations with different values of α and ϱ. The tumor growth increased with α and ϱ.

TABLE IV.

Synthetic data. Results statistics of all cases. Estimated parameters, and the recall, precision, Dice coefficient, relative volume difference (RVD), average surface distance (ASD), and ICVF root-mean-squared error (RMSE). Format: mean±std [min,max]. The definitions of the frameworks can be found in Section VI.

(a) Estimated parameters corresponding to different ground-truth values of the SUV scaling parameter (α).
	D (mm2/day, 10−3)	α (mm3/g/day)			µnormal (kPa)	µtumor (kPa)	ϱ (day−1, 10−3)			γ (kPa)
Ground	0.5	1.1	1.3	1.5	1.0	5.0	1.0			-
EG-IM	0.7±0.3 [0.5, 1.0]	1.1	1.3	1.5	0.9±0.3 [0.6, 1.0]	4.4±1.2 [3.0, 5.2]	0.9±0.1 [0.7, 1.0]			-
EG	0.5±0.1 [0.4, 0.6]	1.1	1.3	1.5	7.2±2.6 [4.3, 8.9]	2.1±1.8 [0.5, 4.1]	3.5±1.8 [1.6, 5.0]			-
F-IM	0.4±0.1 [0.3, 0.5]	0.1	1.3	1.5	1.5±0.3 [1.2, 1.7]	15.3±2.7 [13.0, 18.2]	-			4.8±0.2 [4.7, 5.0]
F	0.5±0.1 [0.4, 0.6]	1.1	1.3	1.5	9.5±7.7 [4.2, 18.4]	19.6±0.3 [19.2, 19.9]	-			8.9±3.1 [7.0, 12.6]
RD	2.5±2.1 [1.2, 4.9]	1.2	1.4	1.6	-	-	-			-
(b) Estimated parameters corresponding to different ground-truth values of the mass effect proliferation rate (ϱ).
	D (mm2/day, 10−3)	α (mm3/g/day)			µnormal (kPa)	µtumor (kPa)	ϱ (day−1, 10−3)			γ (kPa)
Ground	0.5	1.3			1.0	5.0	0.6	0.8	1.0	-
EG-IM	0.6±0.1 [0.5, 0.7]	1.3±0.0 [1.3, 1.3]			1.0±0.0 [1.0, 1.0]	5.0±0.2 [4.8, 5.2]	0.6	0.8	1.0	-
EG	0.8±0.4 [0.4, 1.2]	1.3±0.1 [1.3, 1.4]			7.3±3.1 [3.7, 9.3]	7.2±2.8 [4.1, 9.4]	0.2	4.8	3.9	-
F-IM	0.3±0.0 [0.3, 0.3]	1.3±0.0 [1.3, 1.3]			1.4±0.1 [1.3, 1.6]	18.3±1.4 [16.9, 19.7]	-			3.6±1.0 [2.6, 4.7]
F	1.0±0.5 [0.6, 1.5]	1.3±0.0 [1.3, 1.4]			13.7±6.6 [6.1, 18.1]	15.0±6.9 [7.1, 19.2]	-			6.5±5.0 [1.1, 11.2]
RD	0.9±0.4 [0.6, 1.3]	1.4±0.0 [1.4, 1.5]			-	-	-			-
(c) Overall performance.
	Recall (%)	Precision (%)			Dice (%)	RVD (%)	ASD (mm)			RMSE (%)
EG-IM	99.0±2.2 [95.1, 100.0]	97.6±1.8 [95.2, 99.6]			98.2±1.6 [95.9, 99.8]	2.1±1.8 [0.3, 4.9]	0.1±0.1 [0.0, 0.2]			2.8±2.1 [0.8, 6.2]
EG	88.8±10.1 [75.6, 98.4]	90.2±9.7 [77.4, 99.1]			88.6±2.5 [85.8, 91.9]	18.2±8.8 [4.3, 27.2]	0.6±0.2 [0.4, 1.0]			7.0±0.8 [5.8, 7.7]
F-IM	70.8±4.1 [66.9, 76.0]	100.0±0.0 [100.0, 100.0]			82.9±2.8 [80.2, 86.4]	29.2±4.1 [24.0, 33.1]	0.9±0.2 [0.7, 1.1]			8.6±1.3 [7.0, 10.6]
F	80.2±11.1 [70.4, 98.5]	96.1±6.0 [85.4, 99.5]			86.8±3.6 [82.5, 91.5]	21.8±6.0 [15.4, 29.2]	0.7±0.2 [0.5, 0.9]			8.0±1.6 [6.0, 9.8]
RD	94.4±4.0 [90.2, 100.0]	86.8±13.1 [63.5, 94.7]			89.7±6.7 [77.7, 93.2]	15.0±23.7 [3.5, 57.4]	0.5±0.3 [0.3, 1.1]			7.7±2.4 [6.3, 12.0]

Simulations with different parameters (ground-truth parameters) were used to study the parameter estimation capability. The baseline parameters were D = 0.5×10⁻³ mm²/day, α = 1.3 mm³/g/day, μ_normal = 1.0 kPa, μ_tumor = 5.0 kPa, and ϱ = 1.0×10⁻³ day⁻¹. As α and ϱ are the respective sources of cell proliferation and mass effect, we simulated ground truths with α = {1.1, 1.3, 1.5} mm³/g/day and ϱ = {0.6, 0.8, 1.0}×10⁻³ day⁻¹ (Table IV).

For the model personalization, MLSL requires a bounded parameter space (Section IV-B). We used D ∈ [0.0, 5.0]×10⁻³ mm²/day, α ∈ [0.0, 5.0] mm³/g/day, μ_normal ∈ [0.5, 20.0] kPa, μ_tumor ∈ [0.5, 20.0] kPa, ϱ ∈ [0.0, 5.0]×10⁻³ day⁻¹, and γ ∈ [0.0, 20.0] kPa. For the local optimization SUBPLEX, the convergence criterion was that every parameter change in an iteration is less than 0.01. The maximum number of function evaluations was 2000 for each personalization.

2) Results

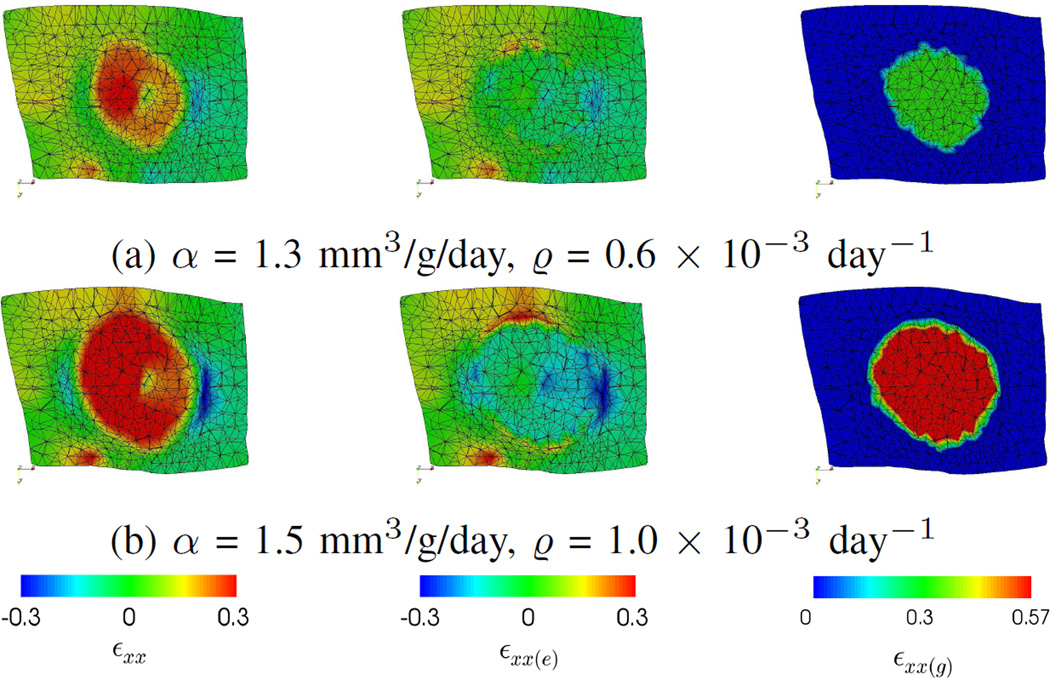
Fig. 7 shows the simulations with different ground-truth parameters, and Fig. 8 shows the corresponding strain components at day 600. ε_xx and its elastic (ε_xx(e)) and growth (ε_xx(g)) parts are shown for illustration. Fig. 7 shows that the tumor growth increased with α and ϱ. Fig. 8 shows that ε_xx(g) was positive and homogeneous inside the tumor because of the growth model (Section II-A2). As μ_tumor was five times of μ_normal, there was relatively small elastic deformation (ε_xx(e)) within the tumor, while deformation was more significant at the boundary between the tumor and the normal tissues. ε_xx indicates the actual deformation by combining ε_xx(e) and ε_xx(g). These show that the tumor size changes were mainly caused by the growth part of the elastic-growth decomposition, and the tumor elastic incompressibility was preserved.

Fig. 8.

Synthetic data. The ground-truth strains along the x-axis (ε_xx) and their elastic (ε_xx(e)) and growth (ε_xx(g)) parts at Day 600. Negative and positive values correspond to compression and expansion, respectively. (a) and (b) correspond to simulations with different parameters. The small magnitudes of ε_xx(e) inside the tumors indicate the tumor size changes were mainly caused by the growth part, and the tumor elastic incompressibility was preserved.

Table IV shows the estimated parameters and the prediction performances. α was well estimated by different frameworks except the RD framework. Comparing between the EG-IM and EG frameworks, without using the image-derived motion, the EG framework overestimated μ_normal and underestimated μ_tumor. Furthermore, the EG framework also overestimated the mass effect proliferation rate ϱ. Similar patterns can be observed between the F-IM and F frameworks. For example, the F-IM framework estimated μ_normal to be less than μ_tumor for all cases, while the F framework overestimated μ_normal. The F framework also found a larger force scaling parameter γ than the F-IM framework. For the RD framework, both D and α were larger than the ground-truth values and those estimated by the other frameworks in general.

For the overall performance, the EG-IM framework, which incorporated both the ground-truth model and the image-derived motion, had the best results. The F-IM and F frameworks performed worse than the EG framework. These two frameworks, especially the F-IM framework, underpredicted the tumor size as indicated by the small recalls and large precisions. For the RD framework, although it had the second-best overall performance, it also had the largest variance and contributed to the worst performance (e.g. maximum RVD = 57.4%).

D. Clinical Data

1) Experimental Setups

Seven diagnosed pancreatic neuroendocrine tumors from seven patients (five males and two females) were studied. In this IRB approved protocol for investigation of disease nature, there were no treatments to the tumors until they reached 3 cm in diameter. The average age and weight of the patients at the first time point were 48.6 ± 13.9 years and 88.1 ± 16.7 kg, respectively. Each set of data had three time points of contrast-enhanced CT and FDG-PET images, and the pixel sizes were less than 0.94 × 0.94 × 1.00 mm³ and 4.25 × 4.25 × 3.27 mm³, respectively. The tumor information is shown in Table I.

The ranges of some model parameters were larger than those of the synthetic data because of the larger variation in reality. with D ∈ [0.0, 5.0] × 10⁻³ mm²/day, α ∈ [0.0, 5.0] mm³/g/day, μ_normal ∈ [0.1, 50.0] kPa, μ_tumor ∈ [0.1, 50.0] kPa, ϱ ∈ [0.0, 5.0] × 10⁻³ day⁻¹, and γ ∈ [0.0, 50.0] kPa. Other settings were the same as those of the synthetic data.

2) Results

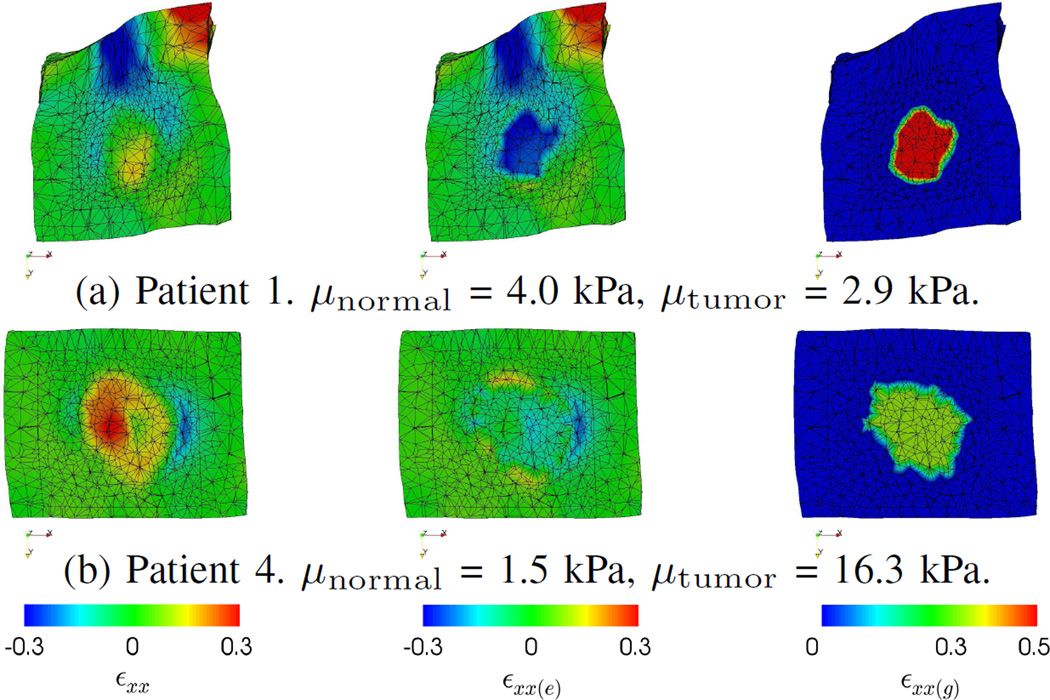
Fig. 9 shows the predicted strains of Patient 1 and 4. The overall deformation of Patient 1 was larger because of the larger deformation of the pancreas. Although Patient 1 had larger growth strain (ε_xx(g)), as the estimated μ_tumor was smaller than μ_normal, the tumor was compressed in the prediction as indicated by the negative values of (ε_xx(e)). Therefore, the combined strain (ε_xx) was smaller than the growth strain. In contrast, as the tumor of Patient 4 was stiffer than its surroundings, it was not compressed much. Thus, the combined strain was larger than that of Patient 1. These show how the mechanical parameters interact in our model.

Fig. 9.

Clinical data. EG-IM framework. Comparisons of the predicted strains along the x-axis (ε_xx) between Patient 1 and Patient 4, and their elastic (ε_xx(e)) and growth (ε_xx(g)) parts. The negative values of ε_xx(e) inside the tumor of Patient 1 indicate elastic contraction, thus the resulted tumor size change was small even ε_xx(g) was large.

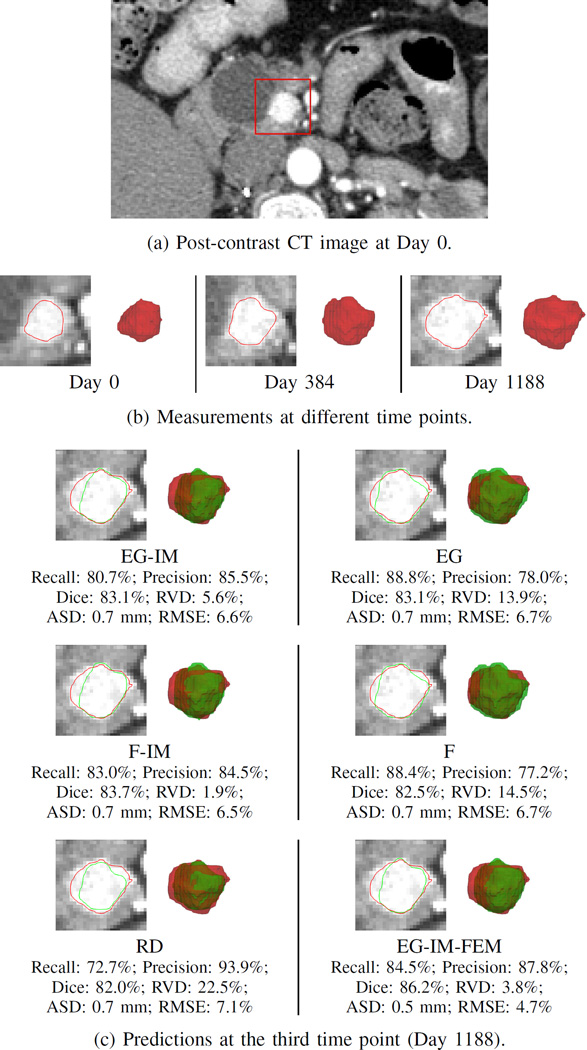
Fig. 10 shows the prediction results of Patient 1. In this example, the RVD of the EG-IM, EG-IM-FEM, and F-IM frameworks were small and much better than those of the EG and F frameworks. Although the Dice coefficients of all frameworks were similar, the EG and F frameworks had recalls larger than the precisions, which indicates the tumor was overpredicted. The RD framework underestimated the tumor volume and had the worst RVD value.

Fig. 10.

Clinical data. Patient 1. (a) The post-contrast CT image at Day 0 with the tumor highlighted. (b) The segmented tumor volumes at different time points, and the corresponding contours overlapping with the post-contrast CT images. (c) The prediction results at the third time point, with red and green represent measurements and predictions, respectively. The definitions of the frameworks can be found in Section VI.

Table V shows the overall estimated parameters and the prediction performances. Although the ground-truth parameters are unavailable, some characteristics similar to those of the synthetic data can be found. For the EG-IM and F-IM frameworks, the tumors were stiffer than the normal tissues on average. In contrast, the EG framework had similar stiffness for the normal tissues and tumors, and the F framework even had the normal tissues stiffer than the tumors. Tumors are known to be stiffer than their surroundings in general [38]. For the RD framework, similar to the synthetic data, the estimated values of diffusion parameter D were larger than those of the other frameworks. For the prediction performances, Table V shows that the EG-IM and EG frameworks outperformed the F-IM and F frameworks. Comparing predictions with and without using image-derived motion, the performances were similar. The RD framework had the worst RVD values. The EG-IM-FEM framework had the overall best performance, and the tumors were also stiffer than the normal tissues. Nevertheless, the values of parameter D were zeros.

TABLE V.

Clinical data. Results statistics of all patients. Estimated parameters, and the recall, precision, Dice coefficient, relative volume difference (RVD), average surface distance (ASD), and ICVF root-mean-squared error (RMSE). Format: mean±std [min,max]. The definitions of the frameworks can be found in Section VI.

	D (mm2/day, 10−3)	α (mm3/g/day)	µnormal (kPa)	µtumor (kPa)	ϱ (day−1, 10−3)	γ (kPa)
EG-IM	0.1±0.1 [0.0, 0.2]	2.2±1.0 [1.0, 3.6]	11.2±16.1 [1.5, 46.7]	26.9±18.0 [2.9, 50.0]	3.4±1.3 [1.1, 5.0]	-
EG	0.1±0.0 [0.0, 0.1]	1.7±0.7 [0.8, 2.5]	15.1±13.0 [3.9, 38.0]	17.8±14.8 [3.2, 45.3]	3.4±1.1 [1.3, 4.6]	-
F-IM	0.1±0.2 [0.0, 0.6]	1.9±1.1 [0.0, 3.6]	6.6±6.9 [0.1, 18.5]	38.0±12.2 [13.9, 50.0]	-	9.1±9.2 [0.0, 24.0]
F	0.0±0.0 [0.0, 0.1]	2.2±0.7 [1.0, 3.0]	36.1±11.3 [19.6, 49.1]	16.5±19.9 [0.1, 48.4]	-	17.3±16.8 [0.9, 50.0]
RD	0.8±1.9 [0.0, 5.0]	1.9±0.7 [0.7, 2.6]	-	-	-	-
EG-IM-FEM	0.0±0.0 [0.0, 0.0]	1.9±1.0 [0.2, 3.4]	13.8±11.9 [1.6, 36.3]	30.1±13.5 [8.7, 49.5]	3.4±1.3 [1.2, 5.0]	-
	Recall (%)	Precision (%)	Dice (%)	RVD (%)	ASD (mm)	RMSE (%)
EG-IM	83.2±8.8 [69.4, 91.1]	86.9±8.3 [74.0, 97.8]	84.4±4.0 [79.5, 92.0]	13.9±9.8 [3.6, 25.2]	0.6±0.1 [0.3, 0.7]	11.3±4.0 [6.6, 18.2]
EG	83.4±6.9 [68.8, 88.8]	90.4±7.9 [78.0, 97.6]	86.3±3.8 [80.7, 91.3]	13.3±7.8 [4.9, 29.6]	0.5±0.1 [0.4, 0.7]	10.1±4.5 [5.2, 18.6]
F-IM	81.5±12.9 [57.8, 95.5]	87.5±9.7 [68.1, 98.0]	83.3±6.6 [71.5, 91.8]	17.1±17.3 [1.9, 40.2]	0.6±0.1 [0.3, 0.7]	11.2±4.9 [4.9, 18.1]
F	80.1±11.0 [62.3, 89.7]	90.3±9.6 [77.2, 99.9]	83.9±4.3 [76.8, 90.0]	19.0±11.0 [7.9, 37.6]	0.6±0.2 [0.4, 1.1]	9.7±4.6 [4.8, 18.4]
RD	81.9±11.7 [68.8, 104.8]	89.4±12.2 [63.1, 97.6]	84.1±3.9 [78.8, 90.0]	23.6±20.6 [4.9, 66.2]	0.7±0.4 [0.3, 1.5]	11.0±4.1 [7.1, 18.6]
EG-IM-FEM	86.8±5.8 [77.6, 96.1]	86.3±8.2 [72.7, 96.5]	86.1±3.2 [82.8, 91.7]	10.8±11.2 [2.3, 32.3]	0.4±0.2 [0.2, 0.8]	9.1±4.8 [4.1, 18.1]

VII. Discussion

As mentioned in the introduction, pancreatic neuroendocrine tumors are rare with only about 1000 new cases in the United States per year [2]. Furthermore, the proposed framework requires FDG-PET and contrast-enhanced CT images at multiple time points. Therefore, there were only seven patient data sets available. Although the results may not be statistically sound, they proved the concept of incorporating image-derived pancreatic motion for more pathophysiologically plausible biomechanical parameter estimation. Nevertheless, the pathophysiologically plausible model may under-perform due to the limited data. For example, if a larger and more diverse data set is available, parameters such as the ICVF threshold can be refined. Therefore, we expect better performance given a larger data set.

For the model personalization, because of the complexity of the overall framework, the optimal weights of different measurements in (15) were not systematically studied. As the weights are provided to increase the flexibility and potentially the accuracy through parameter optimization, the prediction performances could be improved with a systematic exploration such as sensitivity analysis.

For the synthetic data, the EG-IM framework had the best performance. This is because it had the same model as the ground truth, and the most complete set of measurements including ICVF, tumor volume, and image-derived motion. Nevertheless, having these does not necessarily provide accurate parameter estimation, and experiments were performed on synthetic data for the framework development. During the initial development, local optimization methods were studied and they did not usually provide accurate results. Image-derived motion was only used for the FEM simulation but not the objective function, and this led to suboptimal mechanical parameter estimation. Therefore, the use of synthetic data is important for framework development and for demonstrating the parameter estimation capability of the framework under ideal situations. On the other hand, the lower performances of the other frameworks were expected. The experiments on these frameworks were to study the effects of different model components and measurements on the parameter estimation.

The results show the importance of incorporating image-derived motion. For the synthetic data, the EG-IM framework had more accurate mechanical parameter estimations than the EG framework. For the clinical data, the frameworks with image-derived motion had the tumors stiffer than the normal tissues, which is consistent with the literature [38]. This is reasonable as motion is directly related to the biomechanical properties. Therefore, although the prediction performances of the EG and EG-IM frameworks were similar on the clinical data (e.g. 13.3% vs. 13.9% on RVD), the EG-IM model can provide a more pathophysiologically plausible mechanical model.

Comparing elastic-growth decomposition and tumor-density-induced forces, the latter tended to underpredict the tumor sizes especially for the synthetic data which had larger growths. A possible explanation of the underprediction is the use of a pure elastic model. When a tumor volume increased elastically, its volumetric stiffness in (5) also increased. As γ was constant during prediction, the forces could not catch up with the logistic growth. In contrast, with the elastic-growth decomposition, the tumor growth did not affect its volumetric stiffness, and logistic growth could be explicitly modeled. These show the potential advantages of using the elastic-growth decomposition.

For the RD framework, it had the largest estimated values of D and α for both synthetic and clinical data in general to compensate for the missing mass effect. For the synthetic data, the RD framework had the second-best overall performance. This means that the simulated mass effect can be partially accounted by adjusting D and α, though this may also lead to the worst prediction of the tumor size (see Table IV). For the clinical data, the RD framework had the worst RVD and ASD values. This means that using the reaction-diffusion model alone may be less capable to capture the underlying pathophysiology of the actual tumor growths.

The EG-IM-FEM framework had the best performance on clinical data. Similar to the EG-IM framework, the estimated mechanical parameters were pathophysiologically plausible. Nevertheless, the estimated diffusion parameters were zeros, which means that the tumor growths were completely driven by the mass effect and this may be pathophysiologically less plausible. As the diffusion parameters characterize the invasiveness and thus the malignancy of the tumors [11], more accurate estimation could aid better surgical or treatment planning [1]. A probable reason for the zero diffusion is the relatively low resolution of the FEM meshes. Reaction-diffusion equations usually require high spatial resolutions. The spatial resolutions for FDM were 114 to 493×10³ pixels, while for FEM were 23 to 36×10³ elements (Section VI-A). Therefore, the reaction-diffusion simulations were less accurate with FEM. Increasing the FEM mesh resolutions can improve the accuracy, but the computation time will also increase. Therefore, as stated in Section I-C, using FEM for both reaction-diffusion and biomechanical models may not be optimal.

The computation of ICVF uses the ratio between the contrast enhancements of the tumor and the blood pools. Thus, the effects of injection doses and X-ray energy levels can be alleviated. Nevertheless, since the ratio depends on the time between injection and imaging [27], CT images acquired at the same phase should be used for consistent ICVF interpretation at different time points.

For simplicity, nonrigid image registration is used to compute the image-derived motion, and the gradient magnitude is used as an indicator of salient features. For more accurate enforcement of image-derived motion, segmentation of the pancreas is required. As manual segmentation is tedious, this approach will not be considered until automatic segmentation of tumorous pancreas is available.

With FDM, the simulation time of the reaction-diffusion model can be greatly reduced. Nevertheless, FEM with implicit time integration is required for accurate mass effect simulation. This becomes the bottleneck of the computational efficiency and thus the average time for model personalization on clinical data was about 24 hours. To further reduce the computation time, less computationally expensive numerical approaches or better optimization methods will be investigated.

The numerical accuracy of the FDM-FEM coupling is not evaluated in this paper. For a proper evaluation, an analytical solution of a problem is required, and the accuracy is evaluated as the difference between the analytical and numerical solutions [39]. Nevertheless, such analytical solutions are only available for very simple geometries, models, and problems. As our model is complicated and comprising both reaction-diffusion equation and biomechanical model, this approach is very difficult if not impossible. Other possible ways of evaluation are under investigation.

VIII. CONCLUSION

We have proposed a pancreatic tumor growth prediction framework with elastic-growth decomposition, image-derived motion, and FDM-FEM coupling. With the elastic-growth decomposition, the growth and elastic parts can be modeled separately. This avoids compromising the realism of the models. Using the FDM-FEM coupling, the simulation and thus personalization time can be greatly reduced. Experiments on synthetic and clinical data showed that, with the use of image-derived motion, more pathophysiologically plausible biomechanical parameters can be estimated. Experiments on synthetic data showed that the optimization framework can properly identify the model parameters, and the experiments on clinical data showed that the proposed framework can achieve promising prediction performance.