Deterministic Absolute Negative Mobility for Micro- and Submicrometer Particles Induced in a Microfluidic Device

Abstract

Efficient separations of particles with micron and submicron dimensions are extremely useful in preparation and analysis of materials for nanotechnological and biological applications. Here, we demonstrate a nonintuitive, yet efficient, separation mechanism for µm and subµm colloidal particles and organelles, taking advantage of particle transport in a nonlinear post array in a microfluidic device under the periodic action of electrokinetic and dielectrophoretic forces. We reveal regimes in which deterministic particle migration opposite to the average applied force occurs for a larger particle, a typical signature of deterministic absolute negative mobility (dANM), whereas normal response is obtained for smaller particles. The coexistence of dANM and normal migration was characterized and optimized in numerical modeling and subsequently implemented in a microfluidic device demonstrating at least 2 orders of magnitude higher migration speeds as compared to previous ANM systems. We also induce dANM for mouse liver mitochondria and envision that the separation mechanisms described here provide size selectivity required in future separations of organelles, nanoparticles, and protein nanocrystals.

Graphical abstract

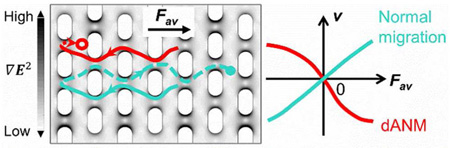
Separation and fractionation of micron- and submicron-sized particles is important for the development of nanoparticle-based applications, but also in biology, since effective isolation methods are required to study biological particles such as cells, organelles, or large DNA complexes. In addition, revealing size heterogeneity of biological particles might allow novel insights into the roles of subpopulations in malfunction and disease. For instance, the appearance of giant mitochondria¹ in multiple diseases including neurodegeneration,^2,3 metabolic disorders,^4–6 and myopathies^7,8 suggests that such size heterogeneity may be an important factor associated with disease initiation and progression. Reliable and effective techniques allowing subpopulation analysis and fractionation of organelles by size are therefore needed.

Traditional fractionation or isolation methods for organelles are typically based on centrifugation methods relating to sample density or size such as differential centrifugation^9,10 and density gradient centrifugation.^10–13 Other techniques have been successfully used for organelle analysis,^14,15 including electromigration methods such as free flow electrophoresis (FFE),^16–18 micro-FFE,¹⁹ isoelectric focusing,²⁰ and capillary electrophoresis²¹ or dielectrophoresis (DEP).^22,23 A recent approach additionally suggests localized trapping of mitochondria by nanohole arrays on a metal-coated film for assessing individual mitochondria.²⁴ However, these techniques are not easily adapted for subpopulation fractionation. In addition, flow field-flow fractionation²⁵ has been applied for the size-based separation of mitochondria,²⁶ however, with only moderate size selectivity.

Here we describe a nonintuitive and novel migration mechanism to allow for size-based subpopulation analysis. Micro- and nanofluidic devices in combination with the tailored integration of structured elements, fluid and force fields (thermal, electric, dielectrophoretic, magnetic) have been shown to evoke novel migration mechanisms, which cannot occur on the macroscale. Prominent examples are ratchets and Brownian motors capable of directed transport of nanoparticles or even molecules.^27,28 Another recent demonstration is the phenomenon absolute negative mobility (ANM), in which particles can be transported in directions opposite to an average force.^29–32 The ANM phenomenon seems counterintuitive, however, it obeys the laws of physics and results from nonequilibrium conditions created by a periodic driving force and nonlinear elements (created through obstacles in a microfluidic structure). The coexistence of “normal” migration and migration in the direction opposite to an average force for differently sized particles can be exploited for separation.

Most ratchets or ANM systems require a source of randomness, which is commonly Brownian motion of biomolecules or nanoparticles. For separation purposes, such methods are poorly suited because the Brownian diffusion of particles in the target size range is intrinsically slow. Moreover, ANM systems use geometrical traps defined by system features similar in size to the particles of interest. Hence, designing ANM systems for nm-sized particles is technically challenging.

Here, we describe a novel method of inducing ANM, not requiring Brownian motion of analytes, termed deterministic ANM (dANM). In order to induce size selectivity and the characteristic migration of ANM we combine insulator-based DEP (iDEP) in a nonlinear, symmetric microfluidic structure with electrokinetically induced transport. The system to induce dANM is based on a simple photolithographic device fabrication strategy without the need of nanofabrication techniques. The numerical simulations and experiments of dANM for binary mixtures of µm- and subµm-sized polystyrene particles are in excellent agreement. Moreover, we demonstrate that, with adequate selection of the applied electrical potentials, dANM is applicable to migration of mouse liver mitochondria.

EXPERIMENTAL SECTION

Numerical Modeling

The simulations were performed using COMSOL Multiphysics 5.1 in a nonlinear spatially periodic structure (Figure 1b). Since the particles are treated as point-like particles in the simulation, virtual walls were additionally constructed with a distance equal to the particle radius to account for specific particle sizes. The parameters used in the preliminary and the refined simulations are listed in Table 1. The DEP mobilities (μ_dep) were calculated with eq S-5 (see Supporting Information) for the respective particle sizes. For the refined model, post geometries were matched to those in the actual experimental device and a parameter sweep was additionally performed for the DEP mobility parameter to find matching velocities in accordance with the experimental velocities. This is shown in Figure 4 and discussed in detail in the Results and Discussion section.

Figure 1.

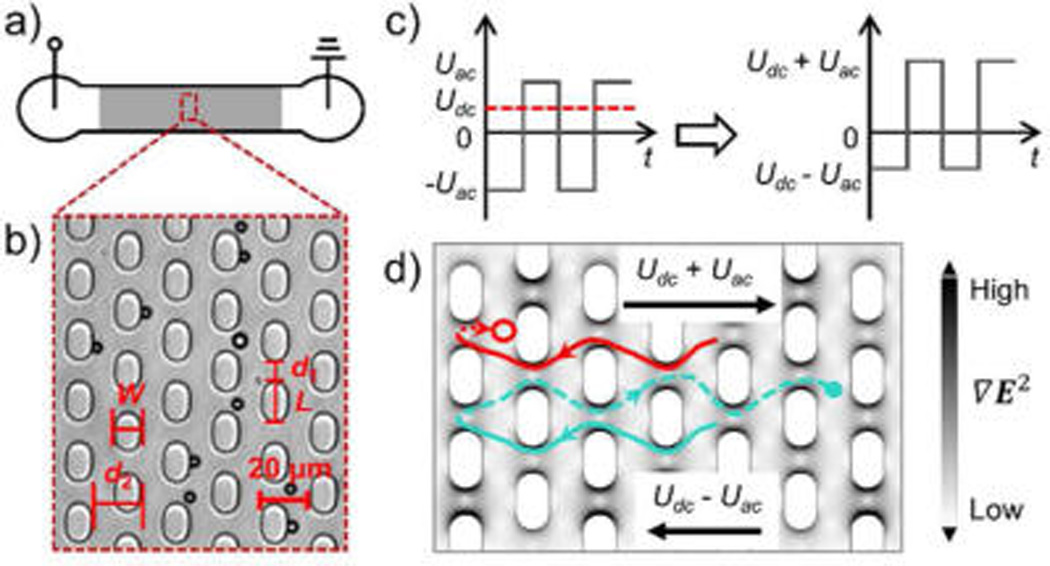
(a) Top view of the 1 cm long channel (not to scale). The shaded area refers to the post array section in the channel. (b) Bright field microscopy image of a section of the post array region. W, L, d₁, and d₂ refer to post width, length, gap distance, and row distance, respectively, and are defined in the Numerical Modeling section. The dark circles correspond to 4.4 µm polystyrene beads. (c) The combination of an AC amplitude U_ac and a DC offset U_dc results in a waveform used in both simulation and bead experiments. (d) The dANM behavior (red trace) and the normal migration (turquoise trace) in one driving period are shown. Particles are assumed to exhibit negative DEP (nDEP, particles move away from high electric field gradient) and are also subject to electrokinetic migration. In the first half period at the applied potential U_dc − U_ac, particles are transported to the left and the trajectories are depicted by solid lines. When particles migrate to the right in the second half period at U_dc + U_ac, two situations occur: (1) For large DEP forces, particles are trapped near a post as indicated by the red dashed line and circle (end position of particle after one period). This situation relates to dANM, as the particle migrates opposite to the average force (F_av). (2) For small DEP forces, particles migrate through the gaps, as indicated by the turquoise dashed line and dot (end position of particle). This relates to normal migration behavior following F_av. The surface plot shows the gradient of the electric field (see grayscale).

Table 1.

Parameters Used in the Preliminary and the Refined Simulations

	preliminary simulation			refined simulation
post size L × W (µm)	13.2 × 2			17 × 10
gap size d1 (µm)	11.8			8
row spacing d2 (µm)	20			20
particle diameter (µm)	3.5	4.5	5.0	4.4
μek (×10−9 m2·V−1·s−1)	15	15	15	2.2
μdep (×10−19 m4·V−2·s−1)	−4.1	−6.7	−8.3	−6.4

Figure 4.

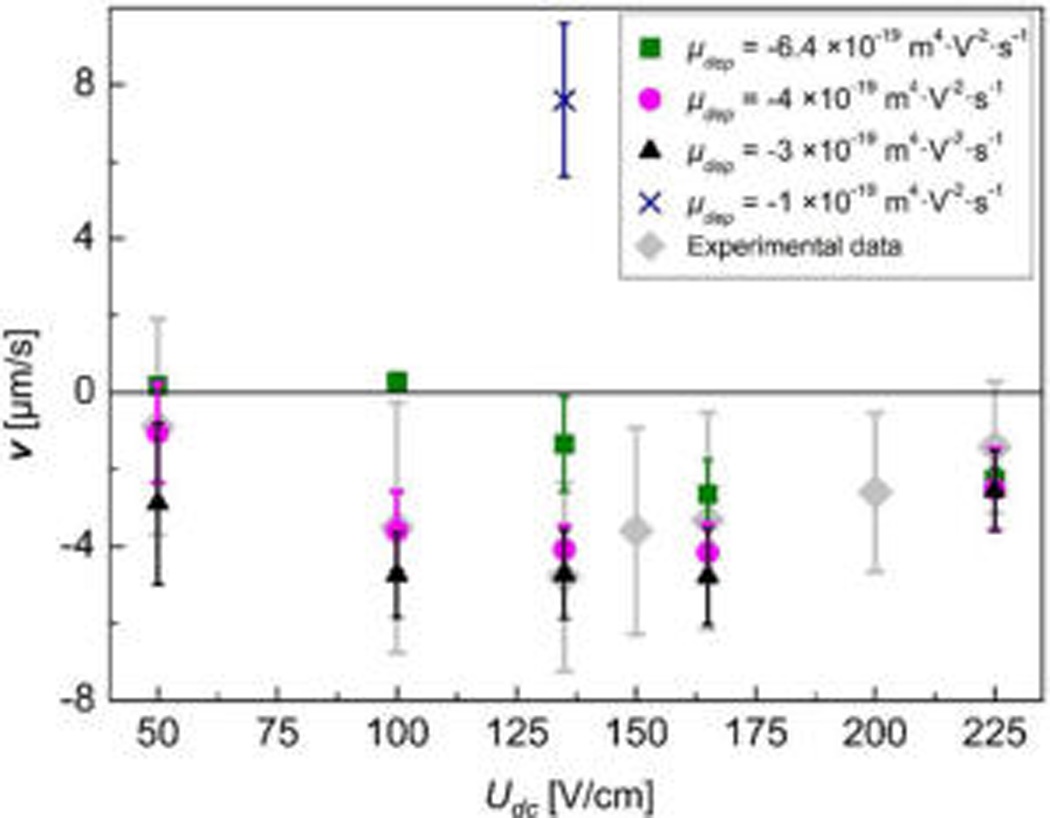
Migration velocity vs DC offset obtained from the refined simulation for 4.4 µm particles at U_ac = 275 V/cm and U_dc < U_ac. μ_dep of −6.4 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ (solid square) resulted in much slower velocities than the experimental data (solid diamond) at U_dc ≤ 135 V/ cm, while μ_dep of −1 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ (cross symbol) even showed normal behavior. The best match of the parameter sweep of μ_dep with the experimental data was found at μ_dep between −3 (solid triangle) and −4 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ (solid circle).

Three relevant physics were considered to model particle migration: electrokinetic (EK) force, DEP, and Brownian force. First, by combining the static study result of the Electric Currents module with a rectangle and an analytic function, a tunable alternating electric field with square waveform (Figure 1c) was realized representing the combination of U_ac and U_dc. This was then coupled with the time-dependent study using the Creeping Flow module providing an alternating flow profile in which the electrokinetic components were considered. Based on eq S-1 (see Supporting Information), the flow profile was obtained by the apparent velocity u. Electrophoresis of particles was neglected for the preliminary simulations (results shown in Figure 2) and the electrokinetic component was considered through the electroosmotic mobility (μ_eo) for F108-coated PDMS.³³ In the refined simulations (Figure 4), experimentally determined electrokinetic mobility (μ_ek) for 4.4 µm polystyrene beads (see Supporting Information for details) was used. Finally, the electric field and the flow profile were additionally integrated with the DEP force (F_dep) and the Brownian force (F_B) to perform the time-dependent study with the Particle Tracing for Fluid Flow module. The particle trajectory was then visualized by solving the instant velocity of a particle (v) time-dependently (see eqs S-6 and S-7 in the Supporting Information):

$${\mathit{F}}_{{\mathrm{d}}_{(t)}}=6\pi \eta R({\mathit{u}}_{(t)}-{\mathit{v}}_{(t-1)})$$ (1)

and

$$\frac{m_{\mathrm{P}}({\mathit{v}}_{(t)}-{\mathit{v}}_{(t-1)})}{\mathrm{\Delta }t}={\mathit{F}}_{{\mathrm{d}}_{(t)}}+{\mathit{F}}_{{\text{dep}}_{(t)}}+{\mathit{F}}_{{\mathrm{B}}_{(t)}}$$ (2)

where F_d is the drag force, η is the viscosity of the medium, R is the particle radius, and m_p is the particle mass. Δt is the time step as defined through the simulation. F_dep(t) was calculated by eq S-2 (see Supporting Information) with ∇E² at the current particle position.

Figure 2.

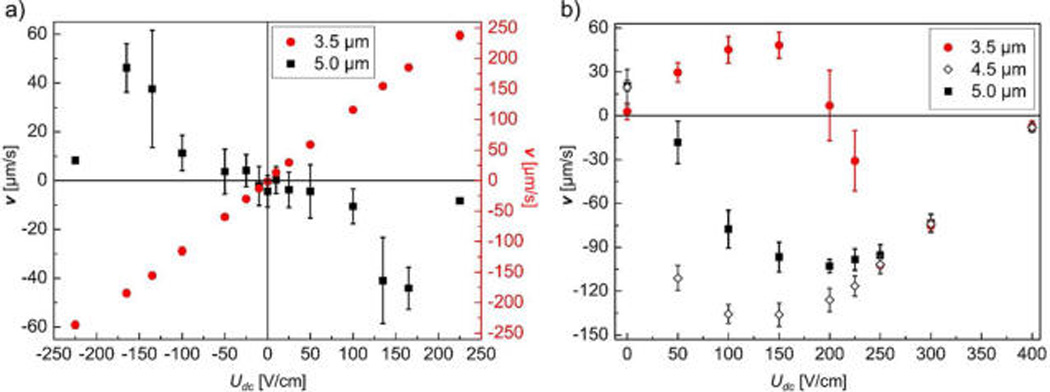
Numerical modeling results revealing regimes of dANM. Particle diameters of 3.5, 4.5, and 5.0 µm are represented by solid circles, hollow diamonds, and solid squares, respectively. The error bars represent the standard deviations of the velocities as obtained at each applied potential averaged for 10 to 20 beads. (a) For U_ac = 275 V/cm and |U_dc| < U_ac, 5.0 µm particles exhibited dANM, while 3.5 µm particles showed normal migration due to the weak DEP trapping force. (b) For U_ac = 450 V/cm and |U_dc| < U_ac, 5.0 and 4.5 µm particles showed dANM. 3.5 µm particles had normal behavior at U_dc < 200 V, whereas dANM was induced when larger DEP trapping forces acted for U_dc > 200 V. For small DC offsets, 4.5 µm particles migrated faster than 5.0 µm particles because smaller sizes experience less strong DEP force in the first half of the driving period (U_dc − U_ac).

For the particle sizes used in this study, the Brownian force F_B was negligible and had no influence on dANM, as expected for this deterministic migration effect. For comparison, numerical modeling was performed with the same model but no Brownian motion contribution and resulted in similar results (data not shown). However, it was found that particles may disappear at the borders of the structures due to zero velocity during modeling without Brownian motion contribution. Therefore, the Brownian force was still included in the modeling to decrease the events of particle vanishing.

For each simulation case, the resultant particle trajectories were used for calculating the average migration velocities. In all simulations, particle–particle interactions (i.e., particle collision and solvent-mediated hydrodynamic interactions) were not considered because the particle concentration was low. Also, the particle gravity was not considered because polystyrene beads sediment very slowly so that they can be considered as suspended. The time step and the period were chosen carefully to ensure each particle traveled at least one spatial period in the considered time period.

Chemicals

4.4 µm diameter (FP-3065-2. Supplier info: 2.5–4.5 µm, mean = 4.41 µm) and 0.9 µm diameter (FP-0852-2. Supplier info: mean = 0.87 µm, std dev = 0.02 µm) polystyrene beads that were made using persulfate as the initiator and thus preserving negative surface charges were purchased from Spherotech (Lake Forest, IL, U.S.A.). SYLGARD 184 silicone elastomer kit for polydimethylsiloxane (PDMS) was obtained from Dow Corning Corporation (Midland, MI, U.S.A.). 4-(2-Hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES), poly(ethylene glycol)-block-poly-(propylene glycol)-block-poly(ethylene glycol) (brand name Pluronic F108), potassium hydroxide (KOH), potassium chloride (KCl), potassium phosphate dibasic anhydrous (K₂HPO₄), magnesium chloride (MgCl₂), ethylene glycol tetraacetic acid (EGTA), dimethyl sulfoxide (DMSO), and sucrose were purchased from Sigma-Aldrich (St. Louis, MO, U.S.A.). Deionized water was from a Synergy purification system (Millipore, U.S.A.). Tris(hydroxymethyl)aminomethane (Tris), 3-(N-morpholino)propanesulfonic acid (MOPS), and Fisherbrand Plain Microscope glass slides (75 × 50 × 1.0 mm; U.S.A.) were purchased from Thermo Fisher Scientific Inc. (Waltham, MA, U.S.A.). Gold-Seal coverslips were purchased from Electron Microscopy Sciences (48 × 60 mm, No. 1; Hatfield, PA, U.S.A.). Platinum wire was purchased from Alfa Aesar (Ward Hill, MA, U.S.A.).

Microchip Fabrication

A silicon master wafer patterned with the microfluidic structures was fabricated by standard photolithography as reported previously,³⁴ followed by elastomer molding via soft lithography. Briefly, the PDMS silicon elastomer base and curing agent were mixed at a 10:1 ratio (w/w), poured onto the master wafer, degassed under vacuum, and cured in an oven for at least 4 h at 80 °C. The PDMS mold was then peeled off the master wafer, resulting in channels with a depth of 10 µm. Then, 2 mm diameter reservoirs were manually punched at the channel ends. The PDMS slab was cleaned in isopropanol and distilled water and a glass slide was cleaned in acetone, isopropanol, and distilled water in an ultrasonic bath and dried in a stream of nitrogen. The slide and PDMS slab were subsequently treated in an oxygen plasma (PDC-001; Harrick Plasma, Ithaca, New York, U.S.A.) at high RF for 1 min. After treatment, the PDMS mold was irreversibly bonded to the glass slide to form a sealed microchannel system.

Fluidic Operations

The experiments were performed using the microfluidic device as schematically shown in Figure 1. A 0.5 cm thick PDMS holder was employed to increase reservoir volume and provide stability for the electrodes. Solution A (0.5 mM F108 for bead studies and 1 mM F108 for mitochondrial studies, 10 mM HEPES, pH adjusted to 7.4 by KOH, sterile-filtered to 0.2 µm) was used to coat the channel surface with F108. Briefly, each channel was filled with solution A by capillarity, and the chip was placed in a humid environment overnight (16–24 h). Solution B (250 mM sucrose in solution A, pH 7.4, 0.03 S/m, sterile-filtered to 0.2 µm) was used to rinse the channel and to prepare the polystyrene bead or the mitochondrial suspension. The prepared bead or mitochondrial suspension was added to an inlet reservoir and solution B to another reservoir. Mineral oil was added on top of the liquid layer in both reservoirs to prevent evaporation. Platinum electrodes attached to the reservoirs were connected via microclamps (LabSmith, Livermore, CA, U.S.A.) to an AC power supply from a high voltage amplifier (AMT-3B20, Matsusada Precision Inc.) driven through a Multifunction DAQ card (USB X Series, National Instruments, TX, U.S.A.) programmed by LabVIEW 2014 (version 14.0, National Instruments).

Preparation of Bead and Mitochondria Suspensions

The bead suspension was prepared by diluting 1 µL of original bead suspension from the manufacturer in 100 µL of solution B. Then, the beads were rinsed three times by repeating a procedure of 1 min vortex, centrifugation at 10000g for 5 min, removing of the supernatant, and resuspension of the pellet in 100 µL of solution B. After rinsing, the bead suspension was sonicated for 1 h.

Mitochondrial particles, referred here after as mitochondria, were prepared from the liver of a four week old male C57BL/6 mouse as previously described.³⁵ All mice were housed in a designated clean facility and treated in accordance with protocols approved by the Institutional Animal Care and Use Committee at the University of Minnesota. The mouse was euthanized and the liver was excised and placed in 10 mL of ice-cold isolation buffer (10 mM Tris, 1 mM EGTA, 10 mM MOPS, 200 mM sucrose). All subsequent isolation steps were performed on ice or at 4 °C as appropriate. The liver was transferred to a Petri dish, rinsed with isolation buffer and minced into small (~1 mm) pieces using a razor blade. The liver pieces were again rinsed with isolation buffer and resuspended in 4 mL of isolation buffer and transferred to a 15 mL glass Potter-Elvehjem homogenizer tube (Wheaton, Millville, NJ). The liver was homogenized by 4 strokes of a tight-fitting motor driven Teflon pestle (Wheaton) operated at 1600 rpm. The homogenate was transferred to a 15 mL conical tube and centrifuged at 600g for 10 min. The supernatant was removed, divided into four 1.5 mL Eppendorf tubes, and centrifuged at 7000g for 10 min. Each pellet was washed in 1 mL of isolation buffer and centrifuged at 7000g for 10 min. Each pellet was resuspended in 900 µL of isolation buffer, transferred to cryotubes containing 100 µL of DMSO, and snap frozen in liquid nitrogen. Then the mitochondria samples were shipped from the University of Minnesota to Arizona State University on dry ice and stored in a nitrogen dewer when received. Sample was transferred to a −80 °C freezer 1 day prior to the experiment. The 1 mM MitoTracker Green (Life Technologies, U.S.A.) stock solution in DMSO was thawed to room temperature, diluted by solution C (100 mM sucrose, 125 mM KCl, 10 mM HEPES, 2 mM K₂HPO₄, 5 mM MgCl₂, pH adjusted to 7.4 by KOH, sterile-filtered to 0.2 µm), and added to the mitochondria sample to reach a final concentration of 800 nM MitoTracker Green. The mitochondria suspension was incubated at 37 °C with gentle shaking (160 rpm) for 15 min and then centrifuged (10000g) for 10 min. After removal of the supernatant, the pellet was resuspended gently in solution B, followed by a 5 min centrifugation (10000g) step. After removing the supernatant, the resulting mitochondria pellet was resuspended in solution B.

Detection and Data Analysis

Fluorescence images were acquired with an inverted microscope (IX71, Olympus, Center Valley, PA, U.S.A.) equipped with a 100 W mercury burner (U-RFL-T, Olympus, Center Valley, PA, U.S.A.) and fluorescence filter set (for 0.9 µm beads and mitochondria: exciter ET470/ 40, dichroic T495LP, emitter ET525/50, Semrock, U.S.A.; for 4.4 µm beads: exciter 607/36, emitter 670/39). A 20× (LUCPlanFLN, NA = 0.45) or a 40× (LUCPlanFLN, NA = 0.60) objective was used to visualize bead migration and a 60× (UPLSAPO60×W, water immersion, NA = 1.20) objective was used to visualize mitochondria migration in the microchannel. Images were captured by a CCD camera (QuantEM:512SC, Photometrics, Tucson, AZ, U.S.A.) and Micro-Manager software (version 1.4.16, Vale Lab, UCSF, CA, U.S.A.).

The obtained videos were then processed by ImageJ software (version 1.47d, NIH). For 4.4 µm beads at each applied potential, over 230 individual trajectories were analyzed using the MTrack2 plugin.³⁶ Depending on when the particle moved out/in the focus region, 1–9 complete periods were considered per particle. For the studies with 0.9 µm beads, 40 trajectories of 1–2 complete periods for each applied potential were analyzed using the Manual Tracking plugin.³⁷ For mitochondria, the trajectories of 20 individual mitochondria in a complete period at the specific driving conditions were evaluated using the Manual Tracking plugin.³⁷ Stroboscopic images were manually generated by overlaying either bead or mitochondria images at corresponding locations for each image frame which originated from Video S-3 for Figure 3 and Video S-4 for Figure 5.

Figure 3.

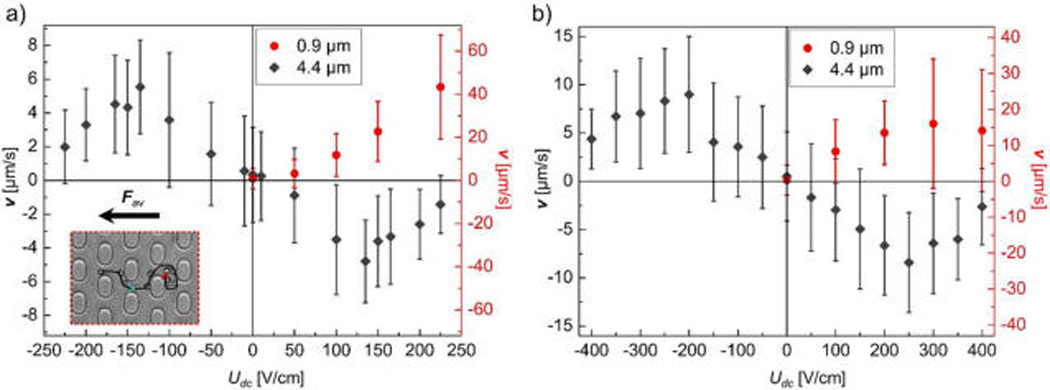
Experimental results of migration velocity vs DC offset. Diameters of 0.9 and 4.4 µm are represented by solid circle and solid diamond, respectively. The error bars represent the standard deviations of the velocities as obtained at each applied potential from tracking over 230 particle trajectories for 4.4 µm beads and 40 trajectories for 0.9 µm beads. (a) U_ac = 275 V/cm and |U_dc| < U_ac. (b) U_ac = 450 V/cm and |U_dc| < U_ac. The 4.4 µm beads had dANM behavior in both (a) and (b), while 0.9 µm beads migrated “normally” following F_av. The inserted stroboscopic image in (a) shows the trajectory of a 4.4 µm bead in a complete driving period at U_dc = −135 V/cm (see Video S-3). At −U_dc + U_ac, the bead moved along the depicted trajectory following the turquoise arrowhead. At −U_dc − U_ac, it was trapped at the position marked by the red arrowhead. This resulted in the dANM migration of the bead since its net migration was to the right while F_av pointed to the left.

Figure 5.

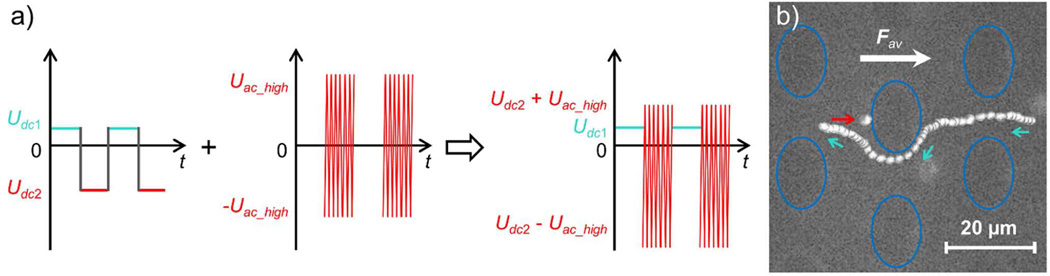
(a) Waveform applied for dANM studies with mitochondria: The typical dANM U_ac driving (here indicated through U_dc1 and U_dc2 on the left) was combined with a high-frequency AC component U_{ac_high} to obtain the waveform shown on the right. To distinguish the two half driving periods, the potential applied in the first half period is displayed turquoise and that applied in the second half period is red. (b) The stroboscopic image shows the trajectory of a fluorescently labeled mitochondrion in a complete driving period. During the application of U_dc1, the mitochondrion moved in the direction indicated by the turquoise arrows. In the second half period, when U_dc2 + U_{ac_high} was applied, the mitochondrion was trapped at the position pointed at by the red arrow. This resulted in dANM behavior of the mitochondrion since its net migration was to the left, while the average driving force F_av dominated by its electrophoretic mobility pointed to the right. The blue ovals indicate the insulating posts in the channel.

RESULTS AND DISCUSSION

dANM Mechanism and Numerical Modeling

First, we studied dANM of polystyrene particles in an elastomer microchannel in which an array of posts was integrated, as shown schematically in Figure 1a,b. The directed motion of different particle sizes was induced due to the interplay of electrokinetic driving and dielectrophoretic trapping. Due to the symmetry in the system, particles are on average not displaced if a periodic potential U_ac below the iDEP trapping threshold is applied; the average force (F_av) acting on the particles is zero. If this periodic potential is however combined with a static offset component U_dc (F_av ≠ 0) as exemplarily shown in Figure 1c, dielectrophoretic trapping may be induced and directed particle migration occurs. Particles of different sizes migrate with different velocities and in different directions. This is schematically depicted in Figure 1d, displaying the migration trajectories for two particle sizes. Both particles migrate according to their electrokinetic properties in the first half of the driving period (solid lines). The conditions are set such that DEP cannot trap the particles. In the second half driving period (dashed lines), the applied potential is stronger, inducing DEP trapping, but only for the larger particle (red trace, Figure 1d). Hence, the larger particle will be trapped, whereas the smaller particle can still migrate (turquoise trace, Figure 1d). Repeating this process periodically leads to the average transport of larger particles against F_av, whereas smaller particles respond in the direction of F_av.

To characterize the conditions where dANM occurs, we first employed numerical modeling. The contributing factors giving rise to particle migration under dANM regimes are electrokinesis (bulk electroosmotic flow and particle electrophoresis) as well as DEP. Various combinations of U_ac and U_dc were tested as well as post array geometries in order to find the threshold parameters under which normal and dANM particle responses exist. Initially, we investigated this regime with 3.5 and 5 µm particle sizes. Figure 2a shows the characteristic signature of dANM for the 5 µm particles as apparent in a negative velocity for positive U_dc offset (see Video S-1). In other words, the 5 µm particles were transported against F_av in a regime of ±225 V/cm U_dc offset, an AC amplitude of 275 V/ cm and 0.625 Hz. In contrast, 3.5 µm beads showed “normal” behavior (see Video S-2) as they migrated in the direction of F_av.

Interestingly, we observe dANM for the larger particles (5 µm) under the coexistence of normal migration for the smaller particles (3.5 µm). This is contrary to what was previously reported in the literature³⁰ since, in the Brownian motion based mechanism, smaller particles show ANM, while larger sizes migrate in a normal manner. This results from the difference in the trapping mechanism. Previously, ANM was induced by utilizing geometric traps that particles need to avoid due to random Brownian motion during the periodic driving. The smaller the particles, the more readily they avoid a trap and thus show ANM in contrast to larger particles, for which the Brownian motion is not sufficient to induce migration around a geometric trap. In dANM, trapping occurs when the dielectrophoretic force is large enough to trap a particle, while smaller particles are not affected. Note that the dielectrophoretic force scales with the cube of the particle radius. As a consequence, the size-ANM relationship is reversed in dANM as compared to ANM.

The second important result is that a maximum dANM velocity of ~50 µm/s was observed (Figure 2a). This average velocity is 3 orders of magnitude larger as compared to ANM velocities for comparable µm-sized particles.³⁸ This is advantageous for further separation and fractionation applications exploiting this counterintuitive migration phenomenon. We point out that particles suspended in a 100 µm × 100 µm section could be effectively transported and collected at the extreme ends of this section in an overall time of ~2 s. Additionally, the dielectrophoretic force scales with the cube of the particle radius, which provides enhanced size selectivity and can be exploited in future devices for separation and fractionation of particles. Moreover, the combination with iDEP allows the tuning of dANM driving parameters to subµm particles sizes without the need of nanofabrication technology as we will demonstrate below.

We further investigated the dependency of the amplitude of U_ac as well as the selectivity for a third particle size. Figure 2b shows the velocity versus U_dc response for U_ac of 450 V/cm for 3.5, 4.5, and 5 µm particles. Two major observations can be made: First, due to the augmented amplitude, larger DEP forces were induced thus causing dANM for 3.5 µm particles for U_dc > 200 V/cm. Second, in the range of 50 V/cm < U_dc < 200 V/cm, all three particles showed differing average velocities indicating the potential to exploit this regime for separations. The two larger particles showed negative (but distinct) while the 3.5 µm particles showed positive velocities. In addition to these major observations we note that 4.5 µm particles migrated faster than 5 µm particles for U_dc < 200 V/cm, suggesting that a maximum difference in velocity occurs for particles with sizes intermediate between 3.5 and 5 µm. From a detailed analysis of the simulated trajectories, the second half of the driving period (U_dc + U_ac; Figure 1c) affected the migration of both particles equally due to sufficiently large trapping forces for both. However, the main difference resulted from the first half of the periodic driving, when U_dc − U_ac (Figure 1c). In this phase, DEP slowed down the overall migration due to slightly larger DEP forces acting on the larger particles. Indeed, this reversal in size dependence of dANM only occurs, when DEP forces influence the first half driving period as observed for U_ac = 450 V/cm.

Proof-of-Principle Experiments

Next, we investigated the occurrence and regimes of dANM in experiments to proof the migration behavior predicted in the numerical model. A microchannel exhibiting a post array as featured in Figure 1 was fabricated with PDMS and the migration of 0.9 and 4.4 µm diameter polystyrene beads in aqueous solution buffered at pH 7.4 was observed. Similar periodic driving parameters as in the simulations were employed and the average velocity of particles was evaluated by individual particle tracking. Figure 3 shows the obtained average migration velocities for both particle sizes. Note that only for the larger particles negative U_dc offset values were tested for consistency with the numerical modeling since the physical principles contributing to dANM are not dependent on the sign of U_dc (see Figure 2a). As shown in Figure 3a, a dANM signature is apparent for the 4.4 µm beads in a range of 50 V/cm < U_dc < 225 V/cm, whereas 0.9 µm particles show normal behavior. The stroboscopic image inserted in Figure 3a is an example of the dANM migration of the 4.4 µm bead in a complete driving period during which F_av points to the left, while the net migration of the bead is to the right. Figure 3b indicates the corresponding experimental studies with U_ac of 450 V/cm, similarly showing dANM. Both studies (Figure 3a,b) clearly indicate the occurrence of dANM similarly to what was predicted in the model.

Several factors, however, differ from the numerical model. First, the maximum dANM velocity was ~5 µm/s for the 4.4 µm beads, which is 2 orders of magnitude larger than previously reported for ANM with similar bead sizes.³⁸ However, this velocity is slower than that predicted with the numerical model (Figure 2). We attribute this to an overestimation of the dielectrophoretic trapping component and an underestimation of the electrophoretic component of the beads in the model (which we will further discuss below). Second, the experimentally measured velocities exhibit increased error compared to the simulations, even though a larger amount of beads has been analyzed with particle tracking (over 230 particle trajectories) than was released in the numerical simulation (20 particles per offset). To some extent, we attribute this to the heterogeneity in size and potentially surface charge of the employed beads, which are intrinsic parameters of the commercially obtained polystyrene beads. In addition, the error in the velocity measurement is influenced by the bead migration path through the post array, resulting in trapping areas that can spread out over a few rows of posts. We believe this to be the major contributing factor, since the experimentally observed velocity variations surmount the errors expected from particle size variations only. Another factor influencing the particle velocity is viscosity due to temperature increase in the channel. However, due to the low buffer conductivity (0.03 S/m) and applied potentials not exceeding 950 V over periods of 60 s, the temperature change in the channel was estimated to be within 2 °C.³⁹ The resultant viscosity change amounts less than 5%,⁴⁰ not significantly contributing to the experimental error.

Since the experimentally observed maximum dANM velocities were smaller than obtained with the numerical model, we revisited the parameters employed in the numerical model. The major driving force leading to transport of the particles through the post array is related to the electokinetic migration in the respective phases of the periodic driving. We thus experimentally determined the apparent electrokinetic mobility of 4.4 µm beads via particle tracking (see Supporting Information) and then employed this value for a refined simulation. The resulting μ_ek value is tabulated in Table 1. Since we have no experimental method at hand determining the dielectrophoretic mobility μ_dep of polystyrene beads, we varied the values for the 4.4 µm beads in the model calculations until the results were consistent with the experimental studies.

Figure 4 and Figure S-1 (see Supporting Information) represent an overview of this parameter sweep. Represented in Figure 4 are velocities at five U_dc offsets for μ_dep of −3, −4, and −6.4 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ corresponding to variations in the Clausius-Mossoti factor f_CM (see eq S-5 in the Supporting Information). At U_dc = 135 V/cm, where the maximum dANM velocity was found experimentally, the corresponding velocity for μ_dep of −1 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ is also shown, and those for μ_dep of −2 and −5 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ are additionally shown in Figure S-1 (see Supporting Information). Furthermore, the experimentally observed dANM velocities are overlaid in Figure 4 (solid diamond). This parameter sweep indicates that the model coincides excellently with the observed velocities at μ_dep between −3 and −4 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹. Second, for μ_dep < −4 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹ or μ_dep > −3 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹, the maximum velocities were reduced and the dANM effect was less prominent. Moreover, for μ_dep of −1 × 10⁻¹⁹ m⁴·V⁻²·s⁻¹, normal behavior was observed, that is, a positive velocity. The latter observation clearly supports the characteristic selectivity mechanism in our dANM approach: If the DEP forces are too weak and can no longer trap a particle (in the driving phase where U_dc + U_ac act), the dANM effect vanishes.

Demonstration of dANM for Mitochondria

To further exploit the size selectivity of dANM and to extend its application on biological samples, we designed driving forces suitable to induce dANM for mouse liver mitochondria. Since iDEP forces in DC mode were too weak to induce large enough trapping forces for the much smaller mitochondria (~400 nm in diameter), we induced iDEP trapping through the overlay with an AC component in the kHz range as we have previously investigated for iDEP trapping.²³ The modified waveform is represented in Figure 5a. Briefly, a low DC potential (U_dc1) was employed in the first half period, which provided the driving force for all mitochondria, while the DC-induced DEP trapping force was negligible. In the second half period, a high-frequency AC component (U^ac_high) was utilized and overlaid with a DC component (U_dc2). The frequency and amplitude of U_{ac_high} can be adjusted to suit the need for trapping a target particle size, here mitochondria. This combination of the potentials in the two half driving periods essentially represents a dANM case with a low frequency U_ac driving force and U_dc offset similar to the bead studies. The only difference results in the trapping force induced through U_{ac_high}.

Based on the previous DEP study of mitochondria²³ and the current microfluidic structure (Figure 1b), U_{ac_high} was chosen with an amplitude of 700 V/cm and a frequency of 30 kHz to induce trapping in the second half driving period. Potentials of U_dc1 = 20 V/cm and U_dc2 = −30 V/cm were chosen, with each half period lasting 10 s. The resultant migration of mitochondria resulted in negative mobilities, as shown in Video S-4 (see Supporting Information for details). Figure 5b depicts a trajectory of a mitochondrion in a complete driving period in form of a stroboscopic image, showing the induced migration. Under these conditions, the velocity was evaluated to be −2.90 ± 0.90 µm/s for mitochondria in the same order of magnitude as obtained with µm-sized microparticles as demonstrated above. In addition, some mitochondria were observed to show normal migration as observed in Video S-4 indicating that the DEP force induced by U_{ac_high} overlaid with U_dc2 was not strong enough for trapping in the second half driving period. Interestingly, these mitochondria appeared smaller in size, indicating that smaller mitochondria show a normal migration behavior, whereas larger species exhibit negative mobilities. This example demonstrates the potential of dANM for size-based separation of organelles, which is critical for organelle subpopulation analysis and isolation.

Note that the dANM device reported here was designed to separate a binary mixture of beads or organelles. We based the development on the separation of mitochondria into subpopulations, aiming at separating subµm particles from µm-sized particles. The goals of separating binary mixtures was demonstrated with modeling (Figure 2) and experimentally (Figure 3). With suitable microfluidic injectors, the observed particle migration direction and velocity indicate baseline separation within only one U_ac driving period. For future tuning of the size selectivity, the electric field gradient induced around the insulating posts is the most important factor. This is because the DEP force determines whether a particle can be trapped, slows down, or just migrates ahead with negligible deceleration effect. The magnitude of the DEP force is influenced by the particle size and the electric field gradient (see eq S-2 in the Supporting Information). Therefore, to induce dielectrophoresis for even smaller species, larger electric field gradients need to be evoked. This can be accomplished by reducing the constriction size, that is, the dimension of the insulating posts and the gap between the posts, as well as modifying the shape of the posts. Instead of the round shape of posts used in this work, adding sharper features or tips could evoke higher electric field gradients while the other conditions are maintained.⁴¹

CONCLUSION

We demonstrated the first design study for dANM and the experimental realization of this deterministic counterintuitive migration phenomenon with µm and subµm colloidal particles and mouse liver mitochondria. We were motivated by the size selectivity of this novel migration technique, which is ideally suited for separation and fractionation, since it allows steering of analyte particles into opposite directions and at different rates. We have successfully developed a microfluidic post array in which dANM can be evoked, demonstrated suitable parameter selection of the driving forces through numerical modeling, and confirmed this principle experimentally. Employing µm- and subµm-sized polystyrene microbeads we were able to prove the occurrence of dANM, in excellent agreement with the numerical model. An intrinsic advantage of dANM lies in the 2 orders of magnitude improved average migration velocities of polystyrene beads observed experimentally as compared to the existing ANM approaches³⁸ and up to four times larger magnitude to ratchet approaches,⁴² which is favorable for future separation or fractionation applications. In addition, the dANM system described here can be readily implemented with standard photolithographic and soft lithographic techniques and allows dANM for subµm species via the adjustment of the DEP trapping forces through variation of the externally applied potentials. As proof-of-principle we demonstrated the dANM behavior of mouse liver mitochondria, which represents the first experimental application of an ANM migration mechanism to a bioparticle. We envision this novel migration mechanism to be applicable to a large range of separation problems in which size selectivity is required, such as in the fractionation of disease-related abnormal organelles, in nanotechnological applications or as fractionation method for nanocrystals.