Fibrin mechanical properties and their structural origins

Abstract

Fibrin is a protein polymer that is essential for hemostasis and thrombosis, wound healing, and several other biological functions and pathological conditions that involve extracellular matrix. In addition to molecular and cellular interactions, fibrin mechanics has been recently shown to underlie clot behavior in the highly dynamic intra- and extravascular environment. Fibrin has both elastic and viscous properties. Perhaps the most remarkable rheological feature of the fibrin network is an extremely high elasticity and stability despite very low protein content. Another important mechanical property that is common to many filamentous protein polymers but not other polymers is stiffening occurring in response to shear, tension, or compression. New data has begun to provide a structural basis for the unique mechanical behavior of fibrin that originates from its complex multi-scale hierarchical structure. The mechanical behavior of the whole fibrin gel is governed largely by the properties of single fibers and their ensembles, including changes in fiber orientation, stretching, bending, and buckling. The properties of individual fibrin fibers are determined by the number and packing arrangements of double-stranded half-staggered protofibrils, which still remain poorly understood. It has also been proposed that forced unfolding of sub-molecular structures, including elongation of flexible and relatively unstructured portions of fibrin molecules, can contribute to fibrin deformations. In spite of a great increase in our knowledge of the structural mechanics of fibrin, much about the mechanisms of fibrin's biological functions remains unknown. Fibrin deformability is not only an essential part of the biomechanics of hemostasis and thrombosis, but also a rapidly developing field of bioengineering that uses fibrin as a versatile biomaterial with exceptional and tunable biochemical and mechanical properties.

Fibrin is a major component of intra- or extravascular blood clots that form at the sites of vessel wall damage and also of the extracellular matrix. Fibrin provides clots and thrombi with elasticity that is important for their hemostatic function, obstructiveness and stability; it also determines the functionality of various cellular processes, including adhesion, migration, proliferation and differentiation, wound healing, angiogenesis, inflammation, etc.

Since pioneering systematic studies of the structural biomechanics of fibrin performed by John Ferry [1-4], this problem has evolved into a rapidly developing area of interdisciplinary research. First of all, fibrin mechanics is an important part of the field of hemostasis and thrombosis because blood clots and thrombi that contain the fibrin scaffold undergo dramatic deformations under (patho)physiological conditions such as hydrodynamic blood shear [5-7], contraction of platelets [8, 9], and aortic aneurisms [10-13]. Therefore, the outcomes of many bleeding and thrombotic disorders, including thromboembolisms, are largely determined by mechanical behavior of the fibrin network [14]. At the same time, fibrin mechanics has become increasingly important in view of extensive new applications of fibrin as a biomaterial, e.g., in tissue engineering, cell culturing, drug delivery, wound sealing, etc., where the mechanical support provided by a fibrin network, in combination with other properties, makes it a unique, versatile, and quite useful hydrogel [15].

Viscoelastic properties of fibrin (fibrin rheology)

Fibrin is a viscoelastic polymer, which means that it has both elastic and viscous properties. The elasticity (or stiffness) is characterized by reversible mechanical deformation, while viscosity (or plasticity) is characterized by irreversible deformation induced by force. Viscoelastic biomaterials differ in the relative degrees of both elastic and viscous properties, which are quantified by measuring the responses to deformation, referred to as rheometry. For fibrin clots, the elastic component is generally about an order of magnitude higher than the viscous component, although the viscous component increases rapidly at higher rates of deformation. Remarkably, during creep experiments, in which continued changes in strain are measured over time after application of stress, some clots do not change in stiffness [16], which means that fibrin is a “self-repairing” structure, most likely because the knob-hole bonds holding the structure together are reversible [17].

Devices used to measure viscoelasticity (rheometers), vary by geometry and protocol of the induced deformation. The most commonly used are shear rheometers that impose a controlled shear strain (or a controlled shear force) on the fibrin clot sample placed between two surfaces, one of them being moved in an oscillatory manner to deform fibrin in the plane of shear. A sinusoidal oscillation has the form of γ = γ_0*sin(ωt), where ω is the frequency and γ₀ is the strain amplitude, and the shear stress σ required to impose such a deformation is measured. For a linear viscoelastic material, shear stress is a sinusoidal function with some phase shift δ, i.e. σ = σ_0*sin(ωt+δ), where σ₀ is the shear stress amplitude. The elastic response of the fibrin clot is characterized by the shear storage modulus, G′, corresponding to the part of shear stress that is in phase with strain and is calculated as G′ = (σ₀/γ₀)*cos(δ). The viscous response of the clot to applied shear is measured by the shear loss modulus, G″, calculated as the out-of-phase part of the stress as G″= (σ₀/γ₀)*sin(δ). The terms “storage” and “loss” refer to the energy stored or lost during the deformation, respectively. The storage and loss moduli determine how the clot responds to the forces to which it is subjected. For example, a stiffer clot (higher G′) will not deform as much as a less stiff one with the same applied stress.

In a tensile rheometer, the elastic properties are measured by applying a longitudinal or stretching stress (i.e., force per unit area) to a cylindrical or bar-like sample and determining the resulting strain (S), which is the stretching or distortion of the polymer normalized with respect to total length (S = L/L₀ - 1, where L is the stretched length and L₀ is the initial length). The resulting stress-strain curve is used to determine its slope or the ratio of the stress required to produce a certain strain (tensile elastic modulus). If a large stress is necessary to produce displacement, then that object is stiff, while a small modulus means that less stress is required, so this other object is less stiff. Similarly, compressive properties can be measured by applying a pressure on the sample with the degree of compression defined as a negative strain and the (compressive) elastic modulus determined by the slope of a stress-strain curve obtained in response to strain- or force-controlled compression. The rheometry-based quantification of fibrin viscoelasticity is described in detail elsewhere [18]. Table 1 compares the elasticity of some proteinaceous filaments.

Table 1.

Comparative stiffness and mechanical stability of various proteinaceous filaments^*

Protein	Young's modulus (MPa)	Fracture strain (%)
Fibrin fiber, uncrosslinked	1.7±1.3**	226
Fibrin fiber, crosslinked	14.5±3.5**	332
Elastin	1	150
Myofibrils	1	200
Resilin	1-2	190, 313
Fibronectin#	0.1-3.5	700
Spider silk (Araneus Flag)	3	270
Fibrillin	0.2-100	>185
Intermediate filament	6-300	160-220
Mussel byssus	10-500	109
Collagen, tendon	160-7,500	12
Microtubules	1,000-1,500	≤ 20
α-Keratin wet	2,000	45
Actin	1,800-2,500	≤ 15
Collagen, crosslinked	5,000-7,000	12-16
Spider silk (Araneus Ma)	10,000	27

^*Based on [43]

^**[49]

^#[133]

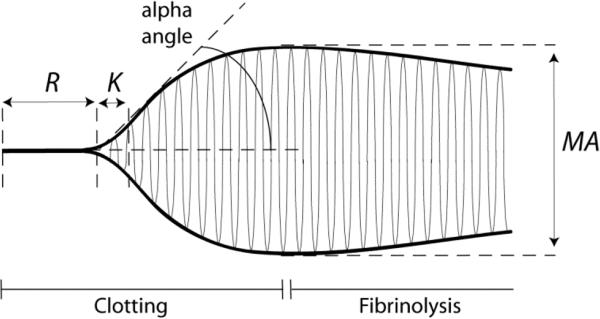
Simplified systems that are not rheometers yet record changes in clot stiffness over time, named thromboelastography (or thromboelastometry), have been widely used in clinical medicine to monitor the formation of whole blood or plasma clots based on their elasticity [19-22]. In thromboelastography a small cylindrical anchor (pin) is immersed into the activated blood or plasma sample placed inside a round cuvette, which is slowly rotated at a small angle around its initial position. In the absence of a clot, the rotation of the cuvette is not transmitted to the anchor, while after the beginning of clot formation the anchor becomes tethered to the walls of the cuvette and starts to rotate synchronously with the cuvette. The circular amplitude of the anchor increases as the clot is getting stiffer. A curve that circumscribes the amplitudes of the anchor over time shows the time course of clotting based on the increasing stiffness of the clot (Fig. 1). The width of this curve after stabilization characterizes the stiffness of the clot in arbitrary units. This method can be also used to follow dissolution of the clot due to fibrinolytic activity that results in decrease of clot stiffness during enzymatic cleavage of fibrin until complete clot dissolution. Thromboelastometry is similar but different from thromboelastography in that the pin immersed into the blood sample oscillates, not the cuvette, and when fibrin strands are formed between the pin and the wall of the cuvette an increasing force is exerted on the pin, which is recorded. The output of thromboelastography and thromboelastometry is basically the same and visualized as a curve that provides information on the clotting lag time, rate of clot growth or dissolution, and clot stiffness.

Figure 1.

Thromboelastography and thromboelastometry are commonly used in clinical medicine to characterize clotting. A typical thromboelastogram comprises a symmetrical curve that circumscribes the rotational amplitude of the anchor immersed in the clotting blood or plasma. The anchor starts oscillating when fibrin forms and connects the anchor to the walls of the oscillating cuvette. The main parameters of the curve are: R (minutes) – reaction time or time from initiation of clotting to the first signs of clot formation; K (minutes) – time until clot reaches about 20 mm; MA – maximal amplitude or the maximum strength of the clot; alpha angle (degrees) – the angle that reflects with K the rate of fibrin formation or clotting; MA (mm) – maximal amplitude or stiffness of the clot. Fibrinolysis can be measured as the eventual decrease of stiffness of the clot as it is digested.

Based on the same physical principles, novel tests for viscoelasticity of a clot have also been developed [23]. One of them is based on free oscillation rheometry, in which the cup containing the blood sample is set into free oscillation by a torsion wire device and the damping and frequency of the change in the oscillating movement is recorded and translated by the system into viscous and elastic parameters, respectively [24]. Atomic force microscopy-based micro- and nanorheology allows for precise measurements of the clot viscoelastic properties using a very small sample volume in the 3-50 nN force range [25, 26]. Another method named resonant acoustic spectroscopy with optical vibrometry measures the clot elastic modulus from the intrinsic resonant frequency of a clot [27]. Fibrin stiffness can be also measured using magnetic tweezers based on mechanical manipulation of magnetic beads embedded into the network [28-30].

Although the extensive biological and clinical relevance of fibrin viscoelastic properties is beyond the scope of this review, here are some examples. Based on viscoelastic properties of incipient blood clots, a new biomarker of healthy, bleeding or prothrombotic clot microstructure was proposed, named the fractal dimension, which has been shown to have clinically important correlations [31-33]. Clots derived from the blood of subjects with pulmonary embolism showed accelerated establishment of viscoelastic properties compared to healthy donors [34]. Studies have shown that the stiffness of clots formed from the blood of patients who have had heart attacks at an early age is 50% greater than that of controls, indicating that these clots are abnormal [35]. It was recently shown that platelets sense the stiffness of the underlying fibrin/fibrinogen substrate so that higher substrate stiffness leads to increased platelet activation, adhesion and spreading [36]. Lastly, the stiffness of the fibrin scaffold of occlusive thrombi is a major determinant for effectiveness of their mechanical damage and removal to restore the impaired blood flow [37].

Non-linear elasticity and high deformability of fibrin

Irrespective of the type of rheometer used, elasticity of fibrin clots can be characterized by a stress-strain curve, in which an applied stress is plotted against the degree of induced deformation (strain). At low strains or deformations, stress is directly proportional to strain and the slope of the curve (the elastic modulus) is constant. At larger strains, the linearity is broken and the slope of the curve increases dramatically, so that the elastic modulus or stiffness of the clot increases up to an order of magnitude [38]. This non-linearity is called strain hardening or strain stiffening and is a fundamental property of biological gel-like structures [39].

Fibrin is a highly extensible polymer, which means that under stress blood clots will tend to stretch rather than break. Plasma clots stabilized with factor XIIIa could be stretched to over three times their relaxed length before breaking with an average stretch of 2.7-fold [40]. Using hydraulic tension, plasma clots were elongated more than 2-fold until the moment of rupture that happened at an average rupture stress of 550 mN/mm² [41]. The fracture strain of a clot has been shown to depend strongly on the volume fraction of red blood cells, which may be important for embolization [42].

The extraordinary extensibility, viscoelasticity, including strain stiffening, has been demonstrated and quantified not only for the whole fibrin clots but also at the level of individual fibers. This can be observed when a fibrin fiber is laterally stretched with a tip of an atomic force microscope, so that crosslinked and uncrosslinked fibrin fibers are stretched to about 2.5 and 3.3 times their original length before rupturing [43-45]. The elasticity of individual fibers depends strongly on their diameter such that thin fibers can be 100 times stiffer than thick fibers [46]. Propagation of strain-stiffening throughout the entire fibrin gel is largely determined by the fine structure and non-linear elastic properties of individual fibrin fibers [47, 48]. As fibers are stretched, they become stiffer than any surrounding fibers at lower strains; this allows the more strained, stiffer fibers, to distribute the strain load to the less strained fibers and reduce strain concentrations [47]. The stiffening of single fibers was observed at strains >110% with an increase of the elastic modulus by a factor of 1.9 for crosslinked and 3.0 for uncrosslinked fibers, respectively [44]. Individual fibrin fibers are much stiffer for stretching than for flexion as would be expected from their diameter and length [49].

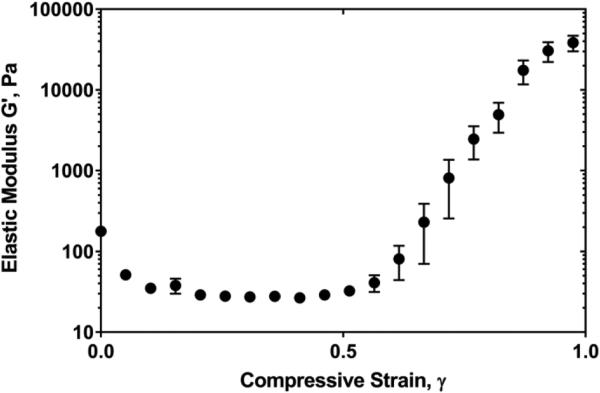
In addition to shear and tension, the non-linear elasticity of fibrin has been observed also in response to compressive deformations [50]. When a fibrin network is exposed to an external compressive load, the viscoelastic properties of the network exhibit a complex non-uniform behavior reflected by gradual softening followed by dramatic stiffening (Fig. 2). The compressive normal force increases non-linearly, also revealing a stress-softening-stiffening transition [50]. The compressive stiffening, i.e., an increase in the elastic modulus and normal force at higher degrees of compression, correlates with an increase in fibrin network density and crisscrossing of fibrin fibers observed by confocal microscopy of hydrated fibrin clots. These rheological measurements, in combination with structural studies, reveal a complex interplay between entropic and enthalpic fibrin fiber elasticity playing an important role in determining fibrin network mechanical response to compression.

Figure 2.

Non-linear elasticity of fibrin. In response to compression, the shear elastic modulus (G′) of a fibrin network first decreases, followed by a dramatic increase of the stiffness at compressive strains γ>0.8. At the maximal compressions (γ>0.9), fibrin networks display more than a 100-fold increase in the shear elastic modulus compared to their uncompressed states. The degree of compression (compressive strain, γ) is defined as the absolute fractional decrease in fibrin clot thickness, $\gamma =\mid \frac{\Delta L}{L_0}\mid$, where ΔL = L – L₀, and L₀ and L are the initial and reduced thickness dimensions of the uncompressed and compressed clots, respectively. (Adapted from Kim, et al. [50])

There are a number of environmental factors that modulate fibrin stiffness both in vitro and in vivo. One of the main physiological modulators of fibrin mechanics is factor XIIIa, which increases the elastic modulus of fibrin several-fold by catalyzing fibrin covalent crosslinking and compacting fibers [51]. Clot rigidity correlates strongly with the structure of fibrin networks, namely with fiber size and branching that varied upon conditions of clotting [52]. Based on the in vitro effects of zinc that reduces fibrin clot stiffness, it was suggested that zinc released from activated platelets may modulate clot strength and stability in cooperation with factor XIIIa [53]. Fibrin polymerized under continuous mechanical perturbation was shown to form a rigid clot with dramatically altered viscoelastic properties [54]. Cells embedded into extracellular matrix can induce stiffening of fibrin gels via myosin-driven cell contraction, which may be important for a number of patho(physiological) conditions, such as wound healing and cancer genesis [55]. Fibrin elasticity can be modulated by other physical [56-58] or biochemical [59, 60] modifications as well as by blood components incorporated into the fibrin network [60-62].

The tunable non-linear elasticity of fibrin may be important biologically because it allows fibrin clots to be compliant at smaller strains and then become stiffer at larger deformations that could otherwise threaten clot integrity and make them prone to embolization. In addition, the complex mechanical behavior of filamentous biopolymers, such as fibrin, is important for the interaction between cells and extracellular matrix [63]. Since mechanical stress makes fibrin more resistant to fibrinolysis [64, 65], fibrin elasticity may be a significant determinant of susceptibility of clots and thrombi to endogenous or exogenous thrombolytics. For example, fibrin formed in the presence of the vessel wall components displayed a reduced stiffness associated with increased susceptibility to enzymatic lysis [66]. On the contrary, the addition of histone-DNA complexes to fibrin (mimicking their interaction in the neutrophil extracellular traps at the site of inflammation/thrombosis) results in an increased fibrin rigidity and slower fibrinolysis [67].

Multiscale structural basis for fibrin mechanics

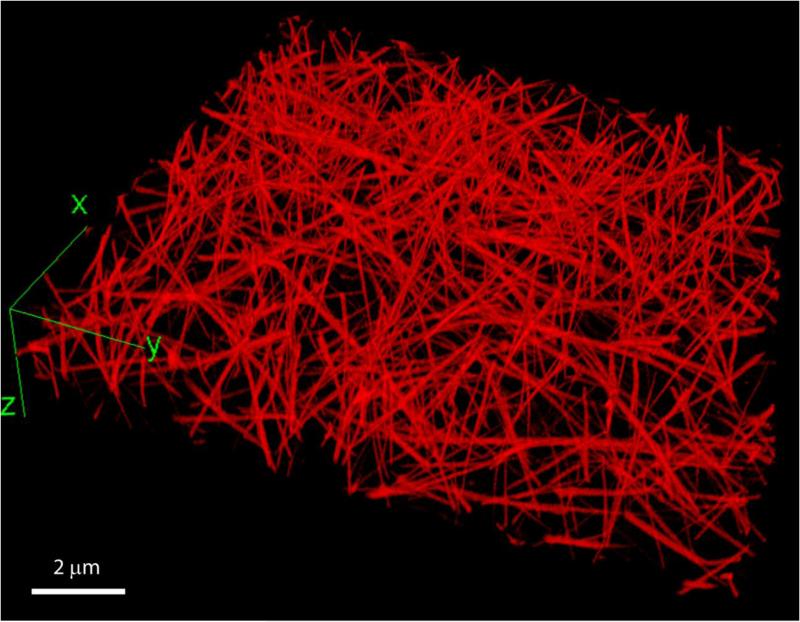
Plasma fibrin clots have a remarkably porous structure with the mass fraction of protein of only about 0.3% (Fig. 3). Some of the relationships between clot structure and mechanical properties have been investigated with respect to concentrations of fibrinogen and calcium ions as well as the activity of thrombin and factor XIIIa [18]. The fibrin network densities resulting from low and high fibrinogen concentration were shown to be a major determinant of clot elasticity [52, 68]. Additional clues to the origins of fibrin elasticity have come from examination of the structural changes accompanying controlled deformations of fibrin clots. Structural changes underlying the elastic properties of fibrin occur at different, yet interconnected, spatial levels, namely the molecular level, individual fibers, fiber network, and the whole clot.

Figure 3.

A three-dimensional reconstruction of a hydrated fibrin network. The clot was formed in human citrated platelet-poor plasma at room temperature for 30 minutes after addition of calcium chloride (20 mM) and thrombin (0.5 U/ml). To visualize fibrin network structure using fluorescent confocal microscopy, Alexa-Fluor 488-labeled human fibrinogen was added to the plasma sample before clotting at a final concentration of 0.04 mg/ml. The network was imaged using a Zeiss LSM710 laser scanning confocal microscope to generate z-stack images spanning 100 μm of sample thickness, with a distance of 0.5 μm between slices and 1024×1024 pixel resolution for each slice.

At the macroscopic scale (10⁻² m), in addition to their large extensibility, fibrin clots also display a dramatic decrease in volume when they are stretched [40]. The shrinkage of the stretched clot is due to water expulsion and network densification, as confirmed by an approximately 10-fold increase in the protein content in clots stretched 3-fold. This observation might be related to the phenomenon of negative normal stress observed for networks of semiflexible polymers, because even though fibrin fibers are relatively stiff, it is still possible that they buckle more easily than they stretch, thus leading to an effective inward force [69]. An alternative or additional explanation, which has been confirmed experimentally, is that the volume change is associated with a molecular structural transition that occurs in stretched fibrin fibers [40, 70].

At the network scale (10⁻⁵ m) non-deformed clots, imaged using scanning electron microscopy, have well separated fibers with an essentially random orientation, building an isotropic filamentous web (Fig. 4A). When tensile strain is applied, the fibers begin to align along the direction of strain (Fig. 4B) [40, 70, 71]. In addition to the alignment of fibers, transmission electron microscopy of transverse sections through fibrin clots at increasing strain showed that the fibers become thinner, closer together, and bundle [40, 72]. Using scanning electron microscopy (Fig. 4C) and confocal microscopy [50], a dramatic rearrangement of the fibrin network is also observed in response to compressive deformation. As compression proceeds, the fibrin network density increases, fibers reorient in the compression plane and shorter fiber segments are formed as a result of fiber crisscrossing. At higher degrees of compression, the number of crisscrossed fibers dramatically increases. In addition, fibers undergo re-orientation, transforming the whole network architecture to a planar-like structure aligned in a plane perpendicular to the compression direction. This newly formed network composed of shorter fiber segments and aligned in a plane of shear has higher shear elasticity, because average strain of individual plane-oriented fiber segments is larger compared to the strain imposed on randomly oriented fibers in an uncompressed network.

Figure 4.

Scanning electron microscopy images of unperturbed (A), 4-fold stretched (B), and strongly compressed (C) fibrin clots. Note fiber bundling both in the stretched and compressed fibrin clots. To form fibrin clots, 9 volumes of human citrated platelet-poor plasma were mixed with 1 volume of 0.025M CaCl₂ and allowed to clot for 2 hours at 37°C. The conditions of clot stretching and compression as well as preparation of the clots for scanning electron microscopy are described in detail elsewhere [71].

At the fiber scale (10⁻⁶ m), in response to compression or shear individual fibrin fibers in the network begin to buckle and bend in the direction of deformation [50, 73]. As compression proceeds over small and intermediate compressive strains, more fibers of the network buckle and bend, thus reducing the amount of load-sustaining network elements. Because buckling and subsequent bending make fibers more compliant, the stiffness of the network in the transverse shear direction gradually decreases with compression.

The stress-strain curves of fibrin networks display remarkable changes in response to repeated large strain loading [74]. These changes look much like weakening because with every new step of deformation the same strain is reached at a smaller stress. However, when the repeated stress-strain cycles are corrected for a shift of the onset of strain-hardening, the superimposed curves have the same slopes, indicating the same stiffness of the networks, so the loadings do not weaken the networks. What actually changes after repeated increasing deformations is only the absolute strain at which the strain-hardening begins. This delay is attributed to the interplay between persistent lengthening and buckling of individual fibers as a result of each stretching event, so that every new deformation starts only after the buckled filaments are stretched again to higher strain. A clue to the mechanism of adaptation of individual fibrin fibers to loading conditions was found when fibrin was covalently crosslinked. The crosslinking completely abrogated the changes in stress-strain response to subsequent deformations. Because the covalent crosslinking precludes slippage of protofibrils within a fibrin fiber, this slippage has been proposed to be the main molecular mechanism for the plasticity observed in bulk and single-fiber experiments with repeated deformation of fibrin [75].

The molecular scale (10⁻⁸ m) of fibrin elasticity comprises a new and remarkable field of protein nanomechanics and is described in a separate subsequent section.

Molecular structural origins of fibrin mechanical properties

The cutting edge of fibrin mechanics is identifying parts of fibrin fibers, protofibrils, and monomers that undergo structural transitions in response to deformations of clots. It has been shown by us [40, 70] as well as others [48, 76] that fibrin mechanics is governed by a structural hierarchy, implying that fibrin deformation is accompanied by multiple structural rearrangements at different scales (Fig. 5). At the molecular level, it has been shown that the most important structural changes during fibrin deformations include unfolding of coiled-coils [77], the γ-nodules [78, 79], and the αC regions converted to αC polymers [80]. The role of the αC polymers, which seems to have been underestimated in the past, has been studied intensively more recently [81-86]. In addition, other studies point to a role of network branch points [87] and the γA/γ′ splice variants [29, 88]. Based on the known crystal structure of a folded fibrin(ogen) molecule, it could be predicted that full hypothetical unfolding of compact structures would results in a ~4.7-fold elongation (Fig. 6), which characterizes a large potential contribution of molecular unfolding in overall extensional deformations of fibrin [89, 90].

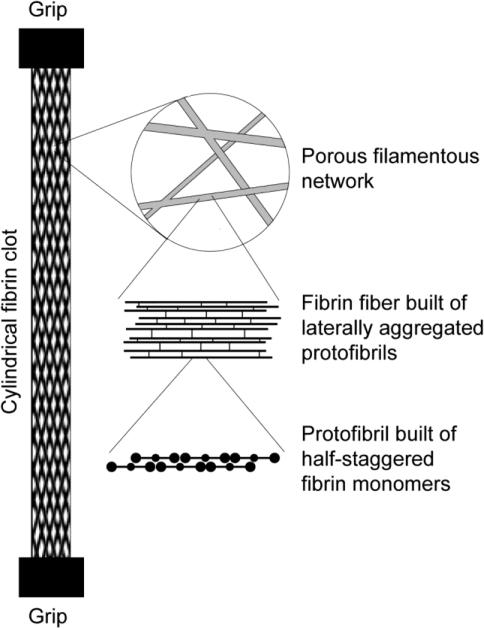
Figure 5.

Diagram of the structure of the fibrin clot at different spatial scales, including macroscopic whole clot, network arrangement, single fiber composition, and molecular packing within a protofibril.

Figure 6.

Schematic representation of the fibrin(ogen) molecule in the naturally folded and fully unfolded states. The mechanical unfolding force is applied to the C-terminal parts of the γ chains. Structural details show the unfolding transitions of the γ-nodules, the coiled coil regions, and the central nodule. Dimensions are shown for the compact crystal structure (PDB Entry: 3GHG), and the contour lengths of various structural elements are shown in the fully unfolded state, assuming a contour length per residue of 0.38 nm.

Based on the existence of two relatively long and co-axially aligned coiled-coils in rod-like fibrin(ogen), it has been hypothesized that an α-helix to β-strand conversion of the coiled-coils accompanies molecular extension of fibrin [43, 91]. The first direct experimental observation for an α-β transformation in fibrin was the low-resolution wide-angle X-ray scattering of squeezed fibrin films published back in 1943 [91], providing preliminary evidence for the transition from α-helix to β-sheet upon fibrin stretching. Much later, in 2011, by means of Congo red staining to detect the β-structures, which is commonly used to identify stacks of β-sheets in amyloid proteins, the formation of congophilic material, presumably new β-sheets, in stretched fibrin fibers was revealed [70], but the specificity of this method is not fully justified. Recently, the secondary structure changes during deformations of fibrin polymers studied using Fourier Transform infrared spectroscopy showed that both extension and compression of a hydrated fibrin clots are accompanied by a transition of α-helix to β-sheet [71]. This structural transition has been confirmed and analyzed in detail using full-atom Molecular Dynamics simulations of extensional mechanical unfolding of a fibrin(ogen) molecule resolved crystallographically [92]. The unfolding transition from coiled-coil α-helices to β-sheets is a common feature of elastomeric proteinaceous fibers and networks [93].

Based on the paracrystalline molecular packing within a fibrin fiber, which results in a 22.5-nm repeat from half-staggering of 45 nm molecules, it has been hypothesized that forced unfolding of fibrin molecules during fiber elongation must result in an increase of this periodicity. Using small angle X-ray scattering as readout of the molecular length, it was shown that the position of the peak corresponding to the 22.5-nm spacing does not change significantly as the clot is stretched. Instead, an increase in sample disorder was reveled consistent with an increasing number of molecules unfolding non-uniformly in response to the large strain [40]. This behavior is expected for two-state-like extension in which some molecules extend completely while others remain folded. These molecular structural transitions begin at strains of about 1.2, at which point some compact structures become unfolded and the clots begin to strain-harden as the unfolded domains are stretched.

The mechanically unfolded sub-molecular structures in fibrin other than the α-helical coiled-coils have been identified in single-molecule forced unfolding experiments. Unfolding experiments on single fibrinogen molecules and naturally occurring fibrin polymers yield results that are nearly impossible to interpret, because the structures are so complex and irregular that many unfolding events are possible. To get around these problems, single-stranded fibrinogen oligomers (tandems) have been prepared and the unfolding of fibrinogen domains has been measured by single-molecule atomic force microscopy [90, 94]. In addition, computer-based modeling of the experimental data enabled the visualization of the various structural transitions and to relate them to the force signals observed in the experimental or simulated force-extension curves. It turned out that molecular elongation of fibrin(ogen) (without considering the αC regions) is largely determined by the combined sequential unfolding transitions in the C-terminal γ chain nodules and limited reversible extension-contraction of the α-helical coiled-coil connectors. The enthalpy of mechanical unfolding of the full-length fibrin(ogen) monomer is ΔH_Fg= 1520 kcal/mol.

In addition to the coiled-coil connectors and the γ nodules, fibrin mechanics is significantly affected by the relatively unstructured αC regions arranged into the factor XIIIa-cross-linked αC polymers during formation and maturation of a fibrin clot [51, 81]. It has been shown that the transglutaminase-catalyzed covalent cross-linking of the α-chains contributes substantially to the fibrin clot stiffness and elasticity in addition to the γ-γ-crosslinking [48, 81, 84, 95], including the fast elastic recoil of stretched fibrin fibers [89]. Based on the exceptional role of the αC regions in fibrin mechanics, a structural model of fibrinogen has been proposed that captures the stress-strain behavior of individual fibrin fibers [82].

Modeling fibrin mechanical properties

To describe, explain, and predict the behavior of fibrin networks upon mechanical deformations, a number of models (all incomplete) have been proposed based on various experimental data and/or theoretical arguments. It is noteworthy that modeling fibrin structure and mechanics is a particular case of modeling filamentous networks, which has a long history presented in Purohit et al. [70]. Here we provide examples of theoretical approaches to fibrin mechanics.

A fundamental model proposed by Qi et al. [96] for random networks of folded proteins uses a system of connected fibers. Although this model is not explicitly based on the microscopic structure of the network, it has been shown to accurately describe other random networks and serves to connect the microscopic and macroscopic mechanical properties. Classical thermodynamic arguments from continuum mechanics are used to obtain an expression for the force-extension (or stress-strain) relation of the network in terms of the force-extension relation of a single fiber. This force-extension relation models the molecules making up the fiber as two-state systems that can be either folded, in which case the fiber is modeled as a linear spring, or unfolded, in which case it is modeled as a worm-like chain [97]. The original model of Qi et al. does not include any volume change, so it was modified by associating a volume decrease with the structural transition at the molecular level [70]. By fitting the high-strain portion of the curve, the fractional volume change per domain can be determined. Then, with no further fitting, the observed volume drop in the earlier part of the curve is captured using the same parameters as those used to fit the force-extension curve. This increases confidence in the model and also suggests a connection between clot shrinkage and a molecular structural transition, perhaps as a result of protein aggregation to bury hydrophobic residues that were exposed during forced protein unfolding [70].

An alternative model of filamentous gels starts from the assumption that the homogeneous, isotropic networks are built of semiflexible fibers that experience thermal fluctuations. This model predicts that in response to a stretching force the fluctuations are reduced which leads to an increase of the stress. The mechanical behavior of the network is determined by extension of the individual fiber and that is why stiffness increases with strain. With these assumptions, the model can be used to compute the mechanical properties of the fibrin network after choosing a fiber force-extension curve [39]. A similar model was later extended to explain negative normal stress in semiflexible polymers as a consequence of fiber buckling of a significant fraction of the polymer. In addition to elastic nonlinearities of the filaments, geometric nonlinearities of the network as a whole also give rise to negative normal stresses [98].

The model of wormlike semiflexible polymers was used with respect to the fine structure of a fibrin fiber [48]. The phenomenon of strain-stiffening in fibrin networks has been analyzed experimentally and modeled with emphasis on formation of a bundle-like structure within fibrin fibers comprising either protofibrils or the αC regions. Notably, this model does not include molecular unfolding and suggests that fibrin clots break before the monomers are fully unfolded, which, at least in part, may be because of low strains applied and the inherent differences between shear- and tension-induced fibrin deformations. This model of the elasticity of fibrin based on the extension of bundled protofibrils within the fibers has been extended recently with the focus on the tightness of coupling between protofibrils that can be modulated by factor XIIIa-mediated crosslinking [99]. Based on stretching experiments with non-linear mechanical behavior of individual fibrin fibers, Hudson et al. [47] used a worm-like chain model of a single fiber to describe the high strain behavior of the entire network.

Fibrin mechanics was studied and modeled under simultaneous uniaxial compression or extension combined with shear deformations that better mimic multidirectional strains occurring in vivo [100]. A complex interplay between shear and Young's moduli in response to these complex deformations was modeled based on undulations, bending, and buckling of individual fibers. Changes in shear elasticity after stepwise extension or compression of a fibrin network have been modeled at the network level also with bendable and stretchable fibers, which explained the softening/stiffening behavior for fixed lateral boundaries in 2D and 3D networks [101]. Analysis of the non-uniformity of fibrin network structure with synchronous measurement of the fibrin storage and loss moduli at increasing degrees of compression enabled the modeling of the compressive behavior of fibrin networks using the theory of cellular solids or foams [102].

A number of models for fibrin mechanics have been proposed that take into account nonaffine network rearrangements, including fiber bending, stretching and alignment [69, 103, 104]. A constitutive model has been proposed to describe the time-dependent, nonlinear viscoelastic behavior of fibrin networks in large amplitude oscillatory shear deformation. The model describes the softening, strain stiffening, and increasing viscous dissipation that occur during multiple deformation cycles [105, 106]. The mechanical properties of fibrin gels under uniaxial strains have been analyzed at low fibrin concentrations, which revealed the strain-hardening properties of fibrin gels for strain amplitude below 5%. This nonlinear viscoelastic behavior of the gels has been precisely analyzed through numerical simulations of the overall gel response to the strain step sequences [107].

Fibrin as a biomaterial

An additional impetus to study fibrin mechanics came from biomedical engineering [108-111], since fibrin turns out to be very promising for many applications, such as a delivery vehicle for cells, drugs, growth factors, and genes, tissue engineering, and stiffness-controlled cell behavior on fibrin matrices. Mechanical properties of fibrin clots are extremely important for their clinical use as tissue sealants.

Tissue engineering is aimed at regeneration of damaged organs and their parts via the use of functionally active cells embedded in a biocompatible scaffold, most often based on filamentous proteins comprising extracellular matrix. Fibrin has been extensively used as a biopolymer scaffold in tissue engineering for a number of unique biological and physical characteristics, including its deformability and elasticity [112]. Fibrin alone or in combination with other materials has been used as a biological scaffold for stem or primary cells to regenerate adipose tissue, bone, cardiac tissue, cartilage, liver, nervous tissue, ocular tissue, skin, tendons, and ligaments. Thus, fibrin is a versatile biopolymer, which shows a great potential in tissue regeneration and wound healing. Some examples of the use of fibrin for tissue engineering include fibrin-alginate matrices for in vitro ovarian follicle development [113], collagen-fibrin matrices polymerized using ancrod snake venom enzyme [114], the use of fibrin polymerization holes for the delivery of therapeutic proteins functionalized with knobs [115], building of cardiac tissue on a fibrin scaffold [116], regeneration of the nucleus pulposus using silk-fibrin/hyaluronic acid composite gels [117], stimulation of angiogenesis [118], etc. Although fibrin can be used as the only biomaterial, it has been shown that addition of collagen to fibrin hydrogel can provide extra stiffness and durability of the forming biomaterial [119]. Composite fibrin-collagen matrices were shown to be permissive to endothelial network formation in vitro [120] and in vivo [121]. Mixing of atelocollagen with fibrin glue more effectively sealed pulmonary air leakage due to the increased elasticity of the glue while its adhesion strength decreased [122].

Gels based on fibrin, alone or in combination with gelatin, collagen, or elastin, have been used to optimize cellular activities, including differentiation, proliferation, and changes in morphology [123-126]. The ability of cells to modify their phenotype and behavior in response to variations in the stiffness of a fibrin-containing substrate (mechanosensing) has been used, e.g., in regulation of neurite outgrowth in fibrin gels [127] and modulation of the secretory activity of endothelial cells and mesenchymal stem cells [120].

Fibrin sealants are usually formed by mixing thrombin and concentrated (up to 60 mg/ml) pathogen-free fibrinogen followed by application to a bleeding wound to achieve hemostasis (comprehensive information on fibrin glues and their applications [128]). In some fibrin sealants, other components are added, such as factor XIII or tranexamic acid (an inhibitor of fibrinolysis) to improve mechanical and chemical stability of the glue. Hemostatic efficacy of these glues has been demonstrated in cardiovascular and thoracic, plastic and reconstructive surgeries, neurosurgery, ophthalmology, oral and maxillofacial surgery, etc. [21, 129]. Various commercially available fibrin sealants have diverse mechanical properties [130] and glues with distinct structure and stiffness had different clinical outcomes [131]. Although the overall beneficial effects of fibrin glues has been demonstrated in clinical trials and numerous studies, the comparison between properties of different fibrin sealants remains difficult because of the lack of standardization, quite variable formulations and testing conditions.

Concluding remarks

Although the mechanical properties of fibrin have been studied systematically since fibrinogen was first purified on a large scale more than 70 years ago, most of what we now know of the molecular origins of fibrin's mechanical properties has been discovered in the past 10 years. More recently, it was proposed that these studies are helping to define a new and highly promising field called biomechanics in hemostasis and thrombosis [132]. At the same time that the biophysical and computational approaches used for these studies are pushing current technology, it has become all the more evident that the clinical implications of the biomechanics of fibrin are vitally important. The youth of this field and the incompleteness of our understanding are reflected in the large gaps in our knowledge that are apparent in what is described in this review, but the vibrancy and promise of this field are evident in the recent discoveries, including some published in other articles that are part of this issue.