A Loudness Model for Time-Varying Sounds Incorporating Binaural Inhibition

Abstract

This article describes a model of loudness for time-varying sounds that incorporates the concept of binaural inhibition, namely, that the signal applied to one ear can reduce the internal response to a signal at the other ear. For each ear, the model includes the following: a filter to allow for the effects of transfer of sound through the outer and middle ear; a short-term spectral analysis with greater frequency resolution at low than at high frequencies; calculation of an excitation pattern, representing the magnitudes of the outputs of the auditory filters as a function of center frequency; application of a compressive nonlinearity to the output of each auditory filter; and smoothing over time of the resulting instantaneous specific loudness pattern using an averaging process resembling an automatic gain control. The resulting short-term specific loudness patterns are used to calculate broadly tuned binaural inhibition functions, the amount of inhibition depending on the relative short-term specific loudness at the two ears. The inhibited specific loudness patterns are summed across frequency to give an estimate of the short-term loudness for each ear. The overall short-term loudness is calculated as the sum of the short-term loudness values for the two ears. The long-term loudness for each ear is calculated by smoothing the short-term loudness for that ear, again by a process resembling automatic gain control, and the overall loudness impression is obtained by summing the long-term loudness across ears. The predictions of the model are more accurate than those of an earlier model that did not incorporate binaural inhibition.

Introduction

This article describes a new model of loudness for time-varying sounds, including sounds that differ at the two ears, a situation that is common in everyday life. An earlier model for predicting the loudness of time-varying sounds (Glasberg & Moore, 2002) was based on the assumption that loudness is simply summed across ears. Under this assumption, a diotic sound should be twice as loud as that same sound presented monaurally, and the level difference required for equal loudness (the BLDEL) of a monaural and diotic sound should be about 10 dB (since, for sound levels above about 40 dB SPL, a 10-dB increase in level leads roughly to a doubling of loudness). While some early data were consistent with this assumption (Algom, Ben-Aharon, & Cohen-Raz, 1989; Fletcher & Munson, 1933, 1937; Hellman & Zwislocki, 1963; Levelt, Riemersma, & Bunt, 1972; Marks, 1978), other data, including more recent data, suggest less than perfect loudness summation across ears (Algom, Rubin, & Cohen-Raz, 1989; Gigerenzer & Strube, 1983; Irwin, 1965; Scharf, 1969; Scharf & Fishken, 1970; Zwicker & Zwicker, 1991). In particular, the BLDEL at medium sound levels appears to be 5 to 6 dB, rather than 10 dB (Edmonds & Culling, 2009; Moore, Gibbs, Onions, & Glasberg, 2014; Scharf, 1969; Schlittenlacher, Ellermeier, & Arseneau, 2014; Whilby, Florentine, Wagner, & Marozeau, 2006). For reviews, see Moore and Glasberg (2007) and Sivonen and Ellermeier (2011).

To account for less than perfect loudness summation across ears, Moore and Glasberg (2007) proposed the concept of binaural inhibition, namely, that a signal applied to one ear can reduce the internal response to a signal applied to the other ear (Glasberg & Moore, 2010; Moore & Glasberg, 2007). This concept had previously been used in some models of sound localization and binaural unmasking (Breebaart, van de Par, & Kohlrausch, 2001; Lindemann, 1986). The concept is supported by data on the loudness of dichotic sounds (Gigerenzer & Strube, 1983; Glasberg & Moore, 2010; Scharf, 1969). In particular, Scharf (1969) showed that the loudness of a tone presented to one ear could be reduced by presenting a tone with a different frequency to the other ear. When implementing the model, it was assumed that the binaural inhibitory interactions are relatively broadly tuned, consistent with the data of Scharf (1969).

Previously, the concept of binaural inhibition was used to modify a model for stationary sounds (Moore, Glasberg, & Baer, 1997), so as to give more accurate predictions of binaural loudness summation (Moore & Glasberg, 2007). This model has recently been approved as an ISO standard (ISO 532-2, 2016), and it is referred to hereafter as ISO532-2. The ISO532-2 model predicts that a diotic sound should be 1.5 times as loud as that same sound presented monaurally, and that the BLDEL should be 5 to 6 dB for sounds at moderate levels. Here, the concept of binaural inhibition is applied to a modified version of the model of loudness for time-varying sounds described by Glasberg and Moore (2002).

The perception of loudness depends on summation or integration of neural activity over times longer than 1 ms (Scharf, 1978). This summation process in the model of Glasberg and Moore (2002) is simulated by two forms of temporal averaging, giving estimates of the short-term and long-term loudness. The short-term loudness is meant to represent the loudness of a short segment of sound, such as a syllable in speech or a single note in a piece of music. It could be used to predict, for example, how loudness changes with increasing duration. The long-term loudness is meant to represent the overall loudness of a longer segment of sound, such as a phrase or sentence in speech or a musical phrase.

For a review of these earlier models of loudness, see Moore (2014). The model described in this article is referred as the binaural TVL model. Note that the structure of the model described here differs from that of the binaural TVL model described by Moore (2014), for reasons that are explained later.

Stages of the Model

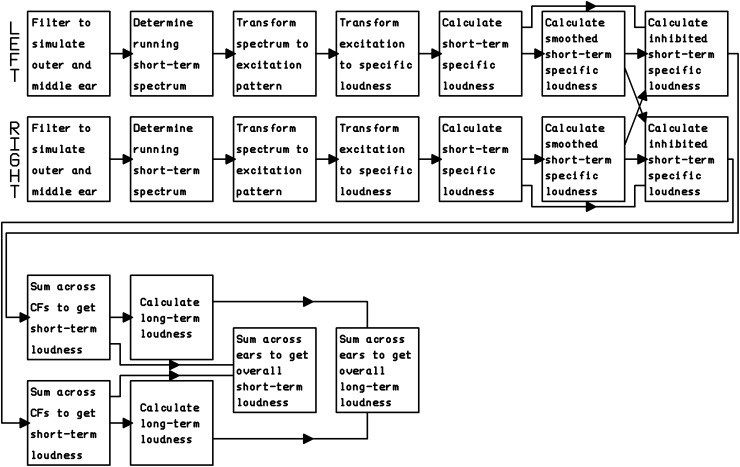
A block diagram of the binaural TVL model is shown in Figure 1. Each stage of the model is described later. The model uses a sample rate of 32 kHz, meaning that the highest allowable frequency in the input is a little below 16 kHz.

Figure 1.

Block diagram of the binaural TVL model.

Transmission Through the Outer and Middle Ear

The transfer of sound through the outer and middle ear is modeled using one of three finite impulse response filters with 4,097 coefficients. Different filters are used for different sound presentation methods. Each filter represents the combined effect of the outer ear and the middle ear.

There are three “standard” options, which differ in the way that the sound is affected by the outer ear in its transmission to the eardrum. For sounds presented in a free field from a frontal direction, it is assumed that the transformation from free-field sound pressure (measured in the absence of the listener at the position corresponding to the center of the listener’s head) to eardrum sound pressure is as specified in Shaw (1974). Another option is diffuse-field presentation, the transfer function for which is derived by averaging the sound-field-to-eardrum transfer function over many directions of incidence. The values used are based on the average of measurements given in Killion, Berger, and Nuss (1987), Kuhn (1979), and Shaw (1980). The free-field and diffuse-field options would often be used for sound picked up by a single microphone placed at the center of the position of the listener’s head, after the listener has been removed from the sound field. In this case, the sound would be diotic (the same at the two ears). However, the free-field option can be used when the waveforms of sounds are preprocessed using a free-field equalizer prior to delivery to the earphones (Fastl & Zwicker, 1983). Similarly, the diffuse-field option can be used when sounds are delivered via earphones that are designed to have a diffuse-field response (e.g., Etymotic Research ER4, Sennheiser HD580 or Sennheiser HD650). With such earphone presentation, the waveforms may differ at the two ears.

A third option is applicable when the waveform at each eardrum is specified. Such waveforms might be recorded using small probe microphones placed in the ear canal close to the eardrum, or they might be recorded using a dummy head that mimics the acoustic properties of the torso, head, and pinna (e.g., Burkhard & Sachs, 1975). This option can also be used when sounds are delivered via earphones with a “flat” response at the eardrum (e.g., Etymotic Research ER2), or when the electrical signal delivered to the earphones is digitally filtered to simulate the response of the earphone at the eardrum prior to being used as input to the model.

The assumed transmission characteristic of the middle ear is broadly based on data obtained from human cadavers (Aibara, Welsh, Puria, & Goode, 2001; Puria, Rosowski, & Peake, 1997; Rosowski, 1991), but the exact form was chosen so that the model accurately predicted the absolute thresholds published in ISO 226 (2003), as described by Glasberg and Moore (2006). The transfer functions for the three options are illustrated in Figure 2.

Figure 2.

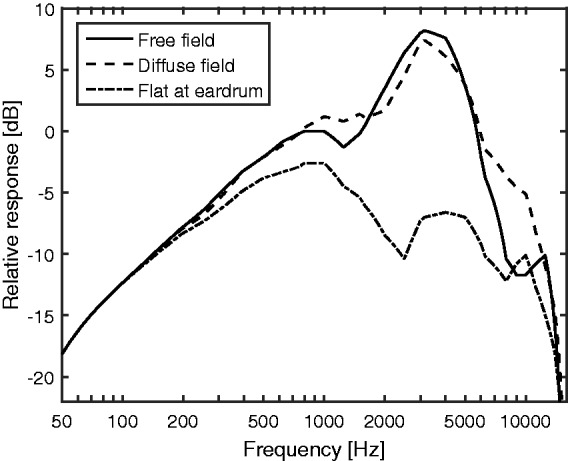
Transfer functions representing the combined effect of the outer and middle ear. The solid curve is for free-field presentation with frontal incidence. The dashed curve is for diffuse field presentation. The dashed-dotted curve shows the transfer function when the waveform is recorded close to each eardrum; in this case, the curve represents the transfer function of the middle ear.

Calculation of the Running Short-Term Spectrum

A running estimate of the spectrum of the sound at the output of the finite impulse response filter for each ear is obtained by calculating six Fast Fourier Transforms (FFTs) in parallel, using signal segment durations that decrease with increasing center frequency (CF). This is done to give sufficient spectral resolution at low frequencies and sufficient temporal resolution at high frequencies. The six FFTs are based on Hann-windowed segments with durations of 2, 4, 8, 16, 32, and 64 ms, all aligned at their temporal centers. The windowed segments are zero padded, and all FFTs are based on 2,048 sample points. All FFTs are updated every 1 ms. For further details, see Glasberg and Moore (2002).

Each FFT is used to calculate spectral magnitudes over a specific frequency range; values outside that range are discarded. These ranges are 20 to 80 Hz, 80 to 500 Hz, 500 to 1,250 Hz, 1,250 to 2,540 Hz, 2,540 to 4,050 Hz, and 4,050 to 15,000 Hz, for segment durations of 64, 32, 16, 8, 4, and 2 ms, respectively.

Calculation of the Short-Term Excitation Pattern

An excitation pattern is calculated from the short-term spectrum at 1-ms intervals, using the same method as described by Moore et al. (1997). The excitation pattern is defined as the output of the auditory filters, plotted as a function of CF (Moore & Glasberg, 1983). The outputs of the auditory filters are calculated for CFs spaced at 0.25-Cam intervals on the ERB_N-number scale (Glasberg & Moore, 1990; Moore, 2012).

Transformation of Excitation to Specific Loudness

The short-term excitation at each CF is transformed to specific loudness, which is a kind of loudness density; it represents the loudness evoked over a 1-Cam wide range of CFs. The conversion involves a compressive nonlinearity, intended roughly to represent the compression that occurs in the cochlea (Robles & Ruggero, 2001). The conversion is performed in the same way as described by Moore et al. (1997), with one exception. In the loudness model of Moore et al. (1997), the equations relating specific loudness to excitation include a constant C, with value equal to 0.047. Its value was chosen so that the loudness of a 1-kHz sinusoid presented binaurally in a free field with frontal incidence at 40 dB SPL was exactly one sone. With the modifications to include binaural inhibition, as described later, the loudness of a binaural sound is reduced by a factor of 0.75 relative to that calculated using the original model. To restore the loudness of a 1-kHz binaural 40-dB SPL tone to one sone, the value of C in the modified model is increased by a factor of 1/0.75 to 0.063.

The specific loudness pattern for a given ear at this stage is what would occur if there were no input to the other ear. In other words, the effects of binaural inhibition are not yet taken into account.

Calculation of Short-Term Specific Loudness

The specific loudness as a function of CF is called the specific loudness pattern. The pattern calculated from a single short-term spectral estimate is called the instantaneous specific loudness pattern. This is smoothed over time to give the short-term specific loudness pattern. The short-term specific loudness is calculated from a running average of the instantaneous specific loudness, separately for each CF, using a process resembling the way that a control signal is generated in an automatic gain control circuit, with an attack time, T_a, and a release time, T_r. This was implemented in the following way. S′_n is defined as the running short-term estimate of specific loudness at the time corresponding to the nth frame, S_n as the instantaneous specific loudness at the nth frame, and S′_n−1 as the short-term specific loudness at the time corresponding to frame n−1.

If S_n > S′_n−1 (corresponding to an attack, as the instantaneous specific loudness at frame n is greater than the short-term loudness at the previous frame), then

$$S{\text{'}}_n={\alpha }_a{S}_n+(1-a)S{\text{'}}_{n-1}$$ (1)

where α_a is a constant that is related to T_a:

$${\alpha }_a=1-\exp (-T_i/T_a)$$ (2)

where T_i is the time interval (1 ms) between successive values of the instantaneous specific loudness.

If $S_n\le S{\text{'}}_{n-1}$ (corresponding to a release, as the instantaneous specific loudness at frame n is less than the short-term loudness), then

$$S{\text{'}}_n={\alpha }_r{S}_n+(1-{\alpha }_r)S{\text{'}}_{n-1}$$ (3)

where α_r is a constant that is related to T_r:

$${\alpha }_r=1-\exp (-T_i/T_r)$$ (4)

The values of α_a and α_r were set to 0.045 and 0.02, respectively. The value of α_a was chosen to give reasonable predictions of the variation of loudness with duration. The value of α_r was chosen to give reasonable predictions of the long-term loudness of amplitude-modulated sounds. The fact that α_a is greater than α_r means that the short-term specific loudness can increase relatively quickly when a sound is turned on, but it takes somewhat longer to decay when the sound is turned off; the decay may correspond to persistence of neural activity at some level in the auditory system.

Calculation of Smoothed Short-term Specific Loudness

The calculation of binaural inhibition is described in some detail here, since this stage is critical for the model, and because some details were omitted in the earlier description of binaural inhibition (Moore & Glasberg, 2007). Let N′_L(i) and N′_R(i) denote the short-term specific loudness values evoked at the left and right ears, respectively, at a given CF. The CF is expressed in terms of ERB_N-number i in Cams. To implement the assumed broad tuning of the binaural inhibition, the short-term specific loudness pattern at each ear is initially smeared or smoothed by a process resembling convolution with a Gaussian-shaped weighting function. The smoothed result at i Cam for the left ear is calculated as:

$$N{\text{'}}_{\text{L}}(i{)}_{\mathrm{smoothed}}=\sum _{D_i=-18}^{D_i=+18}N{\text{'}}_{\text{L}}(i-D_i)\exp [-({\mathrm{BD}}_i{)}^2]$$ (5)

where D_i is the deviation from the given i and B is a parameter determining the degree of spread of inhibition along the ERB_N-number scale. The value of B is set to 0.08. This value was chosen to give a good fit to the data of Scharf (1969), which are described in detail later in this article. D_i is changed in steps of 0.25. Equation (5) results in an increase in overall magnitude after smoothing, but this is irrelevant because only ratios of the smoothed specific loudness patterns for the two ears are used subsequently. When i + D_i is less than 1.75 Cam (corresponding to a CF of 48 Hz) or greater than 39 Cam (corresponding to a CF of about 15,100 Hz, N_L′ is set to 0, since it is assumed that there are no auditory filters centered below 48 Hz (Jurado & Moore, 2010; Jurado, Pedersen, & Moore, 2011) or above about 15,100 Hz (Yasin & Plack, 2005). The smoothed short-term specific loudness for the right ear is calculated in a similar way. The values of the smoothed short-term specific loudness are determined for i = 1.75 to 39 at intervals of 0.25.

Calculation of Inhibited Short-term Specific Loudness

Let INH_IPSI(i) denote the factor by which the short-term specific loudness evoked by the signal at one ear is reduced after inhibition produced by the signal at the contralateral ear. The inhibition is modeled by

$${\mathrm{INH}}_{\mathrm{IPSI}}(i)=2/[1+\{\text{sech}(N{\text{'}}_{\text{CONTRA}}(i{)}_{\text{smoothed}}/N{\text{'}}_{\mathrm{IPSI}}(i{)}_{\text{smoothed}}){\}}^{\theta }]$$ (6)

where N′_CONTRA and N′_IPSI represent the smoothed short-term specific loudness values for the contralateral and ipsilateral ears, respectively, sech represents the mathematical function hyperbolic secant, and θ = 1.598. To prevent problems associated with dividing by zero when N′_IPSI(i)_smoothed or N′_IPSI(i)_smoothed are zero, a small number (10⁻¹³) is added to the values of N′_IPSI(i)_smoothed and N′_IPSI(i)_smoothed prior to entering them into Equation (6). The sech function was chosen since it gave a good fit to data on how loudness changes when the relative level at the two ears is changed (Keen, 1972; Shao, Mo, & Mao, 2015; Zwicker & Zwicker, 1991).

The factors calculated using Equation (6) are applied to the original short-term specific loudness values for each ear to give inhibited short-term specific loudness values. Specifically, the value of N′_L(i) is divided by INH_L(i) and the value of N′_R(i) is divided by INH_R(i). When a sound is diotic, so that the smoothed short-term specific loudness is the same for each ear, the value of [sech(1)]^1.598= 0.5. As a result, a diotic sound is predicted to be 1.5 times as loud as that same sound presented monaurally.

Calculation of Short-term Loudness

The short-term loudness for each ear is calculated by summing the inhibited short-term specific loudness values over Cam values on the ERB_N-number scale from 1.75 to 39. The overall binaural short-term loudness is obtained by summing the short-term loudness values across the two ears.

Calculation of Long-Term Loudness

The long-term loudness for each ear is calculated from the short-term loudness for that ear, again using a form of averaging resembling the operation of an automatic gain control circuit. The long-term loudness for a given ear at the time corresponding to frame n is denoted $S{″}_n$. If $S{\text{'}}_n>S{″}_{n-1}$, then

$$S{″}_n={\alpha }_{\mathrm{al}}S{\text{'}}_n+(1-{\alpha }_{\mathrm{al}})S{″}_{n-1}$$ (7)

where ${\alpha }_{\mathrm{al}}$ is a constant related to the attack time of the averager (as described in Equation (6)).

If $S{\text{'}}_n\le S{″}_{n-1}$, then

$$S{″}_n={\alpha }_{\mathrm{rl}}S{\text{'}}_n+(1-{\alpha }_{\mathrm{rl}})S{″}_{n-1}$$ (8)

where ${\alpha }_{\mathrm{rl}}$ is a constant related to the release time of the averager.

The values of ${\alpha }_{\mathrm{al}}$ and ${\alpha }_{\mathrm{rl}}$ were set to 0.01 and 0.0005, respectively. The values of ${\alpha }_{\mathrm{al}}$ and ${\alpha }_{\mathrm{rl}}$ were chosen to give reasonably accurate predictions of the overall loudness of sounds that are amplitude modulated (AM) at low rates (Moore, Vickers, Baer, & Launer, 1999). Also, the fact that ${\alpha }_{\mathrm{al}}$ is greater than ${\alpha }_{\mathrm{rl}}$ means that the long-term loudness can increase relatively quickly when a sound is turned on, but it takes a long time to decay when the sound is turned off. The overall long-term loudness is calculated by summing the long-term loudness values for each ear.

For sounds like speech and music, the calculated long-term loudness fluctuates slightly even when the sound lasts several seconds. The overall perceived loudness can be predicted either from the average of the long-term loudness value (excluding roughly the first 1 sec of the sound) or from the maximum value of the long-term loudness. We have found that the rank-ordering of the predictions for different sounds is similar for these two methods of prediction. However, the maximum value of the long-term loudness has been shown to give slightly more accurate predictions of judged overall loudness than the mean long-term loudness for a variety of transient sounds (Marshall & Davies, 2007) and for unprocessed speech and speech that has been processed to increase or decrease its fluctuations in amplitude (Zorila, Stylianou, Flanagan, & Moore, 2016). Hence, in what follows, predictions of overall loudness are based on the maximum value of the long-term loudness.

Both C and Matlab software implementing the binaural TVL model can be downloaded free of charge from http://hearing.psychol.cam.ac.uk

Predictions of the Model

For stationary sounds like sinusoidal tone bursts, the predictions of the binaural TVL model are very similar to the predictions of the model for stationary sounds described by Moore and Glasberg (2007). The model gives accurate predictions of absolute thresholds for pure tones and equal-loudness contours. We give a single example of predictions for stationary sounds, based on the data of Scharf (1969). These data were chosen since the binaural inhibition in the model was chosen to fit these data. For diotic steady and time-varying sounds, the predictions of the binaural TVL model are very similar to (within 0.5 phon) the predictions of the model of Glasberg and Moore (2002). Here, the focus is on predictions for sounds that are not the same at the two ears. When the stimuli in a given experiment were bands of noise, which have inherent random amplitude fluctuations, all predictions were based on the average results obtained using 100 randomly and independently generated samples for each bandwidth and CF used. We also describe data from a new experiment using amplitude-modulated tones whose phase of modulation differed at the two ears.

Data of Scharf (1969)

Scharf (1969) asked subjects to make loudness matches between two successive sounds: (a) a single sinusoid presented to one ear with frequency f₁; (b) a sinusoid with frequency f₁, presented to the same ear as in (a), together with an equally loud sinusoid with frequency f₂, presented to the opposite ear. The separation between f₁ and f₂ was varied. For small separations, subjects reported hearing the dichotic sound (stimulus 2) as a single sound image, but for larger separations, subjects reported hearing two separate tones, one at each ear. On trials where two separate tones were heard, subjects were asked to match the loudness of the two successive tones that were heard in the same ear. For example, if f₁ was 1,720 Hz and was presented to the left ear, and f₂ was 2,320 Hz and was presented to the right ear, then subjects would be asked to match the loudness of the single 1,720-Hz tone in stimulus (a) with that of the 1,720-Hz tone heard in the left ear in stimulus (b). The match was made either by adjusting the level of the single tone in Stimulus (a), or by adjusting the level of both tones together in Stimulus (b).

Scharf (1969) used center frequencies of 500, 1,000, and 2,000 Hz. In a preliminary experiment, the tones that were used for each CF were adjusted to have the same loudness as a tone at that CF with a level of either 20, 50, or 80 dB SL. The values of the absolute thresholds of the subjects were not specified, so, for simplicity, we assumed that the component tones had loudness levels of 20, 50, or 80 phons. Initially, we used the loudness model to calculate the level of each monaural component tone required to give a loudness level of 20, 50, or 80 phons. Then, the conditions of Scharf’s experiment were simulated. The long-term loudness was calculated separately for each ear.

For one type of match, the level of a monaural tone, for example, at 1,720 Hz, was adjusted until its calculated loudness level equaled the loudness level calculated for the same tone when presented in the presence of a tone in the opposite ear, for example, at 2,320 Hz; the calculated loudness here is for the ear receiving the 1,720-Hz tone alone. The amount of adjustment is denoted ΔL1. For the other type of match, the two tones in the dichotic stimulus were adjusted in level by the same amount until the calculated loudness level of the 1,720-Hz component was equal to that for the 1,720-Hz tone presented alone. The amount of this adjustment is denoted ΔL2. The predicted level difference required for equal loudness of the 1,720-Hz tone when presented alone and when presented together with the 2,320-Hz tone in the opposite ear was taken as the mean of the values of ΔL1 and ΔL2. This whole calculation was then repeated with the role of the two tones swapped, that is, the single tone was at 2,320 Hz rather than 1,720 Hz. The mean of two resulting level adjustments, ΔL3 and ΔL4, was taken as the predicted level difference required for equal loudness of the 2,320-Hz tone when presented alone and when presented together with the 1,720-Hz tone in the opposite ear. The mean of ΔL1, ΔL2, ΔL3, and ΔL4, denoted ΔL_mean, was taken as the value to be compared with Scharf’s data.

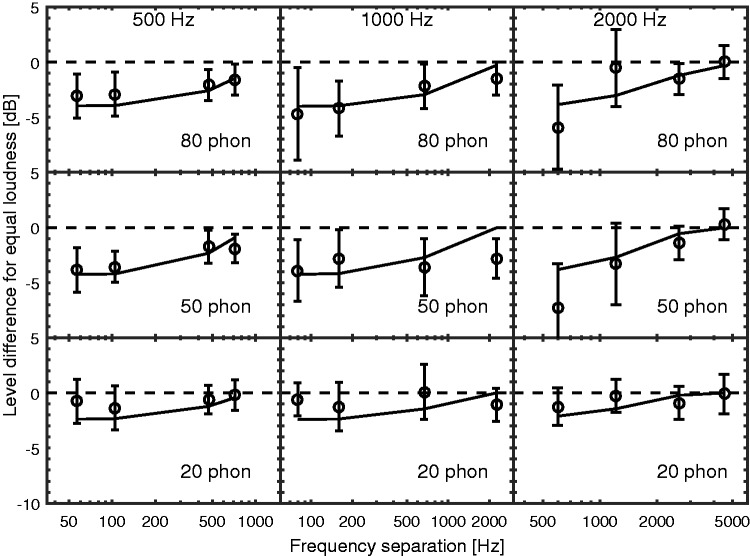
Figure 3 compares the predicted and obtained values of ΔL_mean. There is a good correspondence between the obtained and predicted values, including the decrease in the values of ΔL_mean with increasing frequency separation of the two tones and the decrease in the values of ΔL_mean at the lowest loudness level. As expected, the predictions are similar to those of the model of Moore and Glasberg (2007) for stationary sounds. Almost all of the predicted values lie within the range of the error bars (interquartile ranges). Note that the model of Glasberg and Moore (2002) predicts that a tone presented to one ear should not affect the loudness of a tone of a different frequency presented to the other ear, so that model cannot account for the data of Scharf (1969).

Figure 3.

Comparison of the data of Scharf (1969) (circles) and predictions of the binaural TVL model (black continuous lines). The figure shows values of ΔL_mean, representing the level difference required for equal loudness of a tone presented alone to one ear (whose frequency is indicated at the top of each column) and that same tone presented together with a tone of different frequency in the opposite ear. The frequency separation of the two tones is plotted on the abscissa. Each row is for one reference loudness level of the tone presented alone.

Data of Edmonds and Culling (2009)

Edmonds and Culling (2009) estimated the BLDEL between monaural bands of noise (denoted M) and binaural bands of noise with the same CF and bandwidth. The binaural noise bands had the same level at each ear and were either diotic (perfectly correlated at the two ears, denoted here C), anticorrelated (interaural correlation –1, denoted here A) or uncorrelated at the two ears (denoted here U). An adaptive two-interval two-alternative paradigm was used. In each trial, the subject was asked to indicate the interval containing the louder stimulus. The adaptive procedure tracked the 50% point on the psychometric function, that is, the level of the variable-level (adapted) stimulus at which its loudness matched that of the fixed (reference) stimulus. The order of the reference stimulus and the adapted stimulus was varied randomly. Several bandwidths and center frequencies were used.

The stimuli were generated in the same way as described by Edmonds and Culling (2009). The reader is referred to their article for details. To predict the results, we used each of the stimuli (conditions M, C, A, and U) as a reference with a fixed level of 70 dB SPL, as was done in the experiment of Edmonds and Culling (2009). The model was used to calculate the loudness level of each reference stimulus (in phons). One hundred randomly generated noise samples were used, each with a duration of 500 ms (since noise bands are stochastic, the exact calculated loudness level varied from one sample to the next, with a standard deviation of about 0.6 phons for stimuli M, C, and A and 0.4 phons for stimulus U). For each reference stimulus, the calculated loudness level was averaged over the 100 samples. We then used an iterative procedure to estimate the input level of each stimulus type required to match the mean loudness level of the reference stimulus within ± 0.1 phon. The difference between this estimated level and 70 dB SPL is the predicted BLDEL. Of course, when the adapted stimulus was the same as the reference stimulus, the predicted BLDEL was 0 dB. This was not always exactly the case for the measured data, but the deviations from 0 were small.

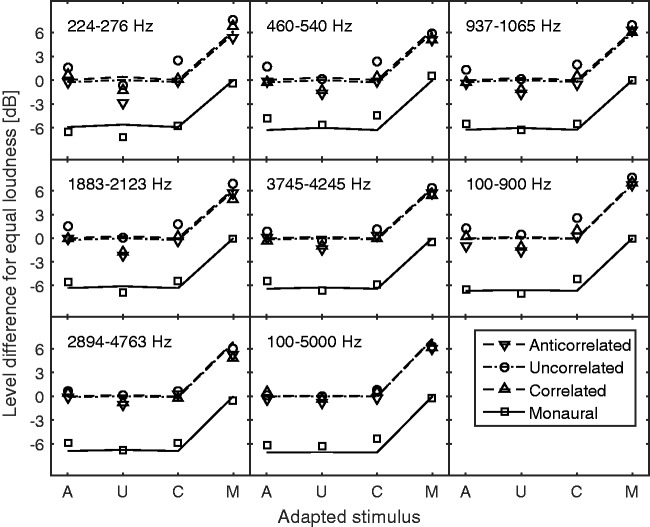
The symbols in Figure 4 show the measured BLDEL values of Edmonds and Culling (2009), as presented in their Figure 1. The BLDEL is shown on the ordinate, and the adapted stimulus is shown on the abscissa. The parameter is the reference stimulus. The lines show the predictions of the model. Generally, the predictions match the data well. The model correctly predicted that when stimulus M was the reference (squares, continuous lines), the BLDEL for the C, A, and U adapted stimuli was about −6 dB (the level of the C, A, and U stimuli was about 6 dB lower than for the M stimulus at equal loudness). Similarly, when the M stimulus was the adapted stimulus, the BLDEL for the C, A, and U reference stimuli was about 6 dB. Note that the model of Moore and Glasberg (2007) for stationary sounds would make similar predictions. However, the model of Glasberg and Moore (2002) for time-varying sounds predicts BLDEL values close to ±10 dB, which are very different from the measured values.

Figure 4.

Comparison of the data of Edmonds and Culling (2009; symbols) and predictions of the binaural TVL model (lines). Each panel is for a specific noise band, whose lower and upper cutoff frequencies are indicated. The BLDEL is shown on the ordinate, and the adapted stimulus is shown on the abscissa. The parameter is the reference stimulus. The stimuli were monaural (M, squares, continuous lines), correlated at the two ears (C, triangles, dashed lines), anticorrelated at the two ears (A, inverted triangles, dashed lines), or uncorrelated at the two ears (U, circles, dashed-dotted lines). Error bars are not shown since in most cases they were similar in size to the symbols used to represent the data.

Since the A stimulus was created by inverting the phase of the noise at one ear relative to the other ear, the short-term fluctuations in level were the same at each ear, and the model predicted the same loudness for the A stimuli as for the C stimuli (dashed lines). Consistent with this, the measured BLDEL values with A as the reference and C as the adapted stimulus or vice versa were close to 0 dB.

When stimulus U was the reference (circles), the measured BLDEL values were slightly (about 1–2 dB) positive for the A and C adapted stimuli for the narrow bands of noise centered at or below 1,000 Hz, indicating that at equal level the U stimulus would be slightly louder than the A and C stimuli. Similarly, when stimulus U was adapted, the BLDEL values were slightly negative for the A and C reference stimuli for the narrow bands of noise centered at or below 1,000 Hz. The model did not capture this effect. Edmonds and Culling (2009) suggested that the greater loudness of the U stimuli than of the C stimuli was consistent with theories of binaural unmasking. They argued that for the N₀S_π configuration, the interaural correlation progressively reduces as the level of the signal tone (S) increases, and that the resulting increase in loudness of the tone might be coded by the decrease in interaural correlation. However, one might argue that in the N_πS₀ configuration, the interaural correlation increases as the level of the tone increases, but an increase in loudness of the tone is still heard. Edmonds and Culling also suggested that the greater loudness of the U stimulus might be connected with the perceived width of the sound image. Consistent with this, the perceived width of a U stimulus is greater than that of a C stimulus (Blauert & Lindemann, 1986). However, an A stimulus is usually perceived as having a greater width than a C stimulus, while both measured and predicted BLDEL values between A and C stimuli were close to zero. This suggests that perceived image width does not provide a complete explanation of the data. Whatever the origin of the greater loudness of the U than of the A or C stimuli, the effect is not predicted by the binaural TVL model. Further research is needed to clarify the origins of the effect to guide possible modifications of the model that might improve the predictions.

In summary, the binaural TVL model predicted the major features of the data, particularly the approximately 6 dB BLDEL between the M stimulus and the other stimuli. The pattern of results generated by the model was similar across the different center frequencies and bandwidths used, suggesting that the prominent amplitude fluctuations that occur for narrow bands of noise did not influence the predictions, probably because of the temporal smoothing involved in the calculation of long-term loudness. The model also correctly predicted that the C and A stimuli would have equal loudness. However, the model failed to predict the slightly greater loudness of the U stimuli relative to the C or A stimuli for narrowband stimuli with center frequencies below 1,000 Hz.

Data of Sivonen and Ellermeir (2006)

Sivonen and Ellermeier (2006) obtained loudness matches between sounds presented from 0° azimuth and elevation and the same sounds presented from various locations within an anechoic chamber. The sounds were 1/3-octave wide bands of noise with various center frequencies. The interaural level difference (ILD) varied with the position of the sound source over a wide range, especially for the highest CF (5 kHz). The level of the sound from the non-frontal direction was adjusted to achieve a loudness match using a two-interval adaptive procedure tracking the point of subjective equality. To predict the data, the signals reaching each ear for the fixed sound from the frontal direction were specified as input to the model, and the binaural loudness level was calculated. The value obtained in this way is denoted Phon_BIN. Then, the input to the model was specified as corresponding to one of the sounds from a non-frontal direction. This signal had a relative level at the two ears as specified in Figure 8 of Sivonen and Ellermeier (2006), and its overall level was adjusted until the model predicted a loudness equal to Phon_BIN, within ±0.1 phon. This input level was taken as the predicted matching level. Note that the predictions of the model were not affected by whether or not the noise bands at the two ears had an ITD appropriate for the azimuth in question. The results were expressed as the difference in level between the fixed and adjustable sound at the point of equal loudness, where level is measured in the absence of a listener at the center position of the listener’s head. Sivonen and Ellermeier called this difference “directional loudness sensitivity” (DLS).

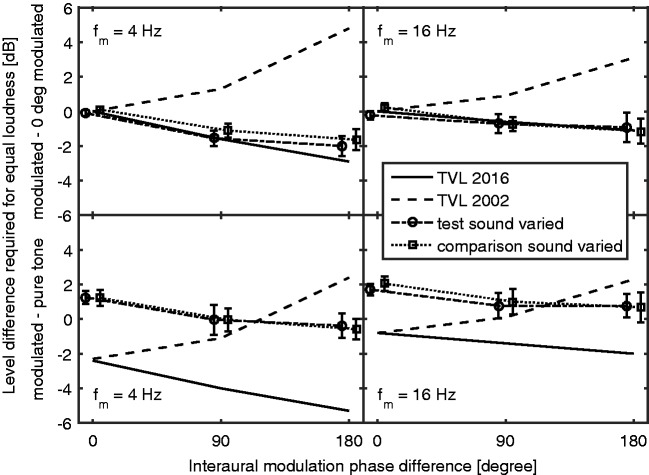
Figure 8.

Values of the level difference required for equal loudness (LDEL) of a comparison sound (either a 100% AM tone with 0° IMPD, top, or a pure tone, bottom) and a test sound that was 100% AM and had an IMPD of 0°, 90°, or 180°. The modulation rate was 4 Hz (left) or 16 Hz (right). Points are slightly laterally offset from their correct positions on the x-axis to avoid overlap of symbols. Error bars show ± 1 SE. Predictions of the binaural TVL model are shown by solid lines. Predictions of the model of Glasberg and Moore (2002) are shown by long-dashed lines. See text for details.

Figure 5 compares the obtained (solid line) and predicted (dashed line) DLS values for the stimuli centered at 5 kHz, for the higher level used. There is a reasonably good correspondence between the obtained and predicted DLS values, although the predicted values are slightly below the obtained values for both positive and negative DLS values. The largest discrepancy is 1.7 dB. For comparison, the dashed-dotted line shows predictions of the ISO 532-2 model. The models for time-varying and for stationary sounds give almost identical predictions, indicating that the short-term level fluctuations in the noise bands used as input to the binaural TVL model had little influence on the predictions.

Figure 5.

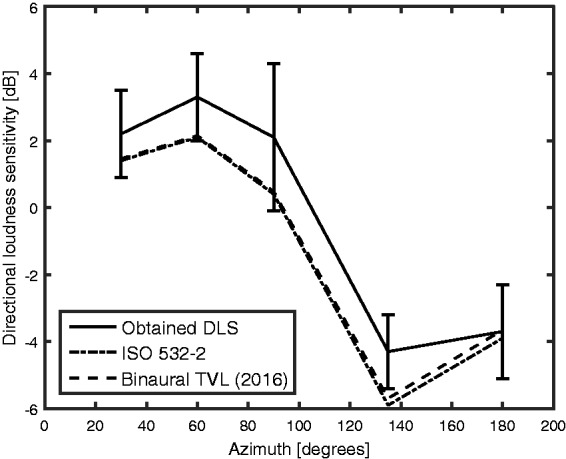
Comparison of “directional loudness sensitivity” (DLS) values obtained by Sivonen and Ellermeier (2006) (solid lines) with DLS values predicted by the binaural TVL model (long-dashed lines) for the stimuli centered at 5,000 Hz. The DLS values are plotted as a function of the azimuth of the stimulus. For comparison, the dashed-dotted curve shows predictions of the ISO 532-2 model. Error bars indicate 95% confidence intervals of the DLS values.

Data of Shao et al. (2015)

Shao et al. (2015) obtained loudness matches between fixed-level diotic stimuli presented via headphones and dichotic stimuli in which the level was increased at one ear and decreased at the other ear by the same amount in dB, such that the ILD varied from 2 to 12 dB. The stimuli were noise bands of various widths from 1/12 to 1/1 octaves with seven center frequencies ranging from 0.125 to 8 kHz. The results were presented as the difference between the level of the diotic stimulus, and the mean level across ears of the dichotic stimulus that matched the diotic stimulus in loudness. The results were similar for the different center frequencies, and to reduce the inherent variability in the results, they were averaged across CF.

To generate predictions, the stimuli were generated as described by Shao et al. (2015). The sound levels (in SPL) of the diotic reference stimuli were taken from Table 1 in Shao et al. (2015). The loudness level of the diotic stimulus was calculated for each CF. The level of each dichotic stimulus was then iteratively adjusted so that it matched the loudness level of the diotic stimulus at the same CF within ±0.1 phon. The resulting level was taken as the matching level. The level differences required for a loudness match were averaged across the seven center frequencies.

Figure 6 shows the obtained data (symbols) and the predictions of the binaural TVL model. The level difference required for a loudness match is plotted as a function of the ILD. The predictions for the smallest bandwidth (1/12 octave, circles and dotted line) match the data almost perfectly. The data show a small decrease in the level difference as the bandwidth increases up to 1/1 octave (diamonds). The predictions show a very small trend in the same direction, but it is smaller than the decrease in the data. However, the deviations of the data from the predicted values are always less than 0.5 dB.

Figure 6.

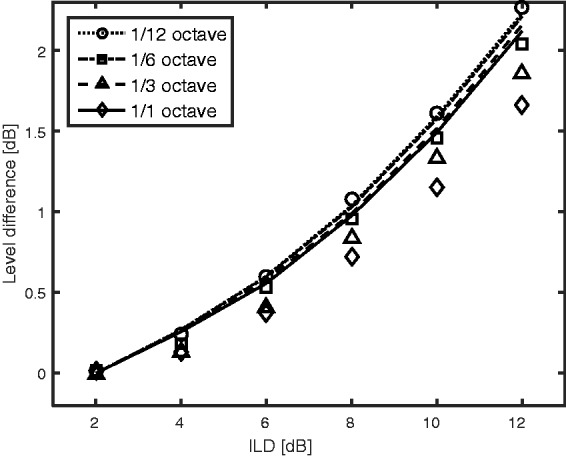
Comparison of the data of Shao et al. (2015) (symbols) with predictions of the binaural TVL model (lines). The level difference required for equal loudness of diotic and dichotic stimuli is plotted as a function of the interaural level difference (ILD) of the dichotic stimuli. The parameter is stimulus bandwidth: 1/12 octave, circles, and dotted line; 1/6 octave, squares, and dashed-dotted line; 1/3 octave, triangles, and dashed line; 1/1 octave, diamonds, and continuous line. No error bars were provided by the authors.

Data of Zwicker and Zwicker (1991)

Zwicker and Zwicker (1991) obtained estimates of loudness by asking subjects to rate the loudness of test signals relative to a reference signal, which was assigned a loudness of 100 units. In their Experiment 3, the reference signal was a uniformly exciting noise (Zwicker & Fastl, 1999) with an overall level of 70 dB SPL, presented either monaurally or diotically. The test sound consisted of uniformly exciting noise that was presented as rectangular bursts that alternated between the two ears. The repetition rate was 1, 7, 49, and 343 Hz, corresponding to durations in each ear of 500, 71, 10.2, and 1.4 ms. A test sound was included for which there was no temporal switching, and the test sound was identical at the two ears (diotic). The results are shown by the symbols in Figure 7. For both the monaural reference (open circles) and diotic reference (filled circles), the loudness increased when the switching rate increased from 1 to 7 Hz, and then stayed roughly constant. The loudness was slightly greater for the diotic test sound (right-most points) than for the sounds with dynamic switching.

Figure 7.

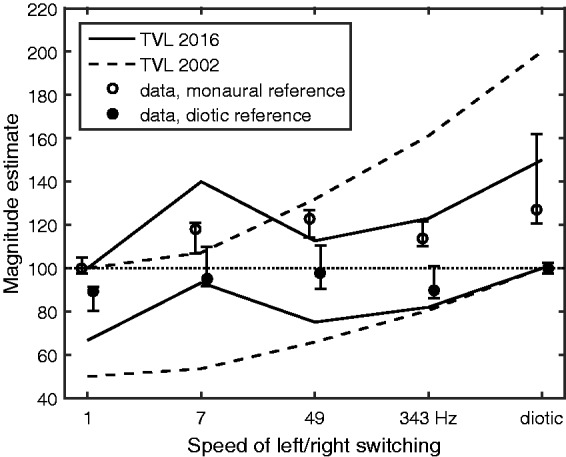
Comparison of the data of Zwicker and Zwicker (1991; symbols) with predictions of the binaural TVL model (solid lines) and the model of Glasberg and Moore (2002)(dashed lines). Magnitude estimates of loudness were obtained relative to a reference sound whose loudness was predefined as 100 units. The reference sound was either monaural (open circles) or diotic (filled circles). See text for details. Error bars indicate inter-quartile ranges of the data.

To generate predictions, it was assumed that the magnitude estimates would be directly proportional to the loudness in sones, so the magnitude estimate of a given test sound and a given anchor was predicted as (calculated loudness for test)/(calculated loudness for reference) × 100. The predictions of the binaural TVL model are shown as the solid lines in Figure 7. The model predicted an increase in loudness when the switching rate was increased from 1 to 7 Hz, then a decrease when the switching rate was increased to 49 Hz, and then a small increase when the rate was increased further to 343 Hz. The loudness was predicted to be greatest for the diotic test sound. The model captured the general trends in the data but with some deviations. These deviations, typically amounting to 25 units or less, correspond to about 2 to 3 phons.

The dashed lines in Figure 7 show the predictions of the model of Glasberg and Moore (2002). The predicted loudness increased monotonically with increasing switching rate. The deviations between the data and predictions exceeded 40 units for several points and exceeded 70 units for the diotic stimulus with monaural reference. Overall, the fit of the model of Glasberg and Moore (2002) was clearly poorer than that of the binaural TVL model.

It should be noted that the data in this experiment differ somewhat from those reported in other experiments from the same article. Across several experiments, Zwicker and Zwicker (1991) reported that a diotic sound was about 1.5 times as loud as that same sound presented monaurally, whereas the data in Figure 7 show a diotic to monaural loudness ratio of about 1.25 for the monaural reference and 1.12 for the diotic reference. Thus, the inherent variability in the data is comparable to the deviations between the data and the predictions of the binaural TVL model. Overall, it seems that the binaural TVL model gives reasonable predictions of the data, but more precise loudness estimates are needed with such stimuli, perhaps using loudness matches rather than magnitude estimation, to provide a more rigorous test of the model.

The model of loudness for stationary sounds incorporating binaural inhibition (Moore & Glasberg, 2007) uses as input the long-term average spectra of the stimuli. For the stimuli used by Zwicker and Zwicker (1991), the long-term average spectra were the same at the two ears, regardless of switching rate. Therefore, the model for stationary sounds does not predict the effects of switching rate that are apparent in the data of Zwicker and Zwicker (1991).

New Data on the Loudness of Dichotic Amplitude-Modulated Sounds

The structure of the model described here, as illustrated by the block diagram in Figure 1, differs from that described by Moore (2014) and illustrated in Figure 15 of that article. In the version described by Moore (2014), binaural inhibition was applied to the instantaneous specific loudness, before short-term loudness was calculated, and both short-term and long-term loudness were calculated after summation across ears. The change in the structure of the model was inspired by new data that are presented next.

To provide a test of the model using time-varying sounds that differed strongly across the two ears, we used a 70 dB SPL 1,000-Hz sinusoidal carrier that was 100% sinusoidally amplitude modulated (AM) at 4 or 16 Hz. The relative phase of the modulator at the two ears was either 0° (in-phase modulation), 90°, or 180° (out-of-phase modulation). The model described by Moore (2014) predicted that the loudness level should decrease by about 3 phons as the interaural phase of the modulator was increased from 0 to 180°. In fact, the data showed that the loudness increased slightly. The modified model presented in this article gives predictions in the correct direction, as is shown later.

Subjects

A total of 13 subjects (five female) with ages ranging from 20 to 30 years (mean = 23). were tested. All had audiometric thresholds ≤15 dB hearing level for frequencies from 125 to 8,000 Hz.

Stimuli and Method

The loudness of a 100% AM sinusoid with an interaural modulation phase difference (IMPD) of 0°, 90°, or 180° (test sounds) was compared with the loudness of either a steady tone or an AM tone with IMPD = 0° (comparison sounds). The carrier frequency was 1,000 Hz, and the carrier was in phase at the two ears. The starting phase of the modulator in one ear was randomly chosen (uniform distribution over the range 0°–360°), preserving the IMPD. The AM rate, f_m, was either 4 or 16 Hz. The duration was 1 sec, including raised-cosine rise and fall times of 5 ms.

These conditions were presented in 12 blocks; 2 values of f_m × 2 types of comparison sound × 3 IMPDs. The order of the blocks was pseudo-random and balanced as well as possible across subjects. A two-interval, two-alternative forced-choice paradigm with a one-up/one-down rule was used to estimate the level difference between the test sound and the comparison sound at the point of equal loudness (the LDEL). The interval between the two sounds was 500 ms, and the test and comparison sounds were equally often first and second (selected at random for each trial). The task of the subject was to indicate whether the first sound or the second sound in each trial was louder. The nominal root-mean-square (RMS) level of the fixed sound was 70 dB SPL. Within each block, there were four interleaved adaptive tracks: (a) with the level of the comparison sound fixed and the level of the test sound varied, the latter starting 10 dB above the former; (b) with the level of the comparison sound fixed and the level of the test sound varied, the latter starting 10 dB below the former; (c) with the level of the comparison sound varied and the level of the test sound fixed, the latter starting 10 dB above the former; (d) with the level of the comparison sound varied and the level of the test sound fixed, the latter starting 10 dB below the former. To encourage the subject to compare the two stimuli within a trial rather than making comparisons to a long-term memory estimate of loudness, the levels of both sounds within a trial were changed by an equal amount, drawn from a uniform distribution between −5 and +5 dB.

The order of the four interleaved tracks was random with the constraint that a reversal had to occur for all of them before moving on to the next step in the track. For each track, the initial step size of 5 dB was reduced to 3 dB after one reversal and to 1 dB after one more reversal. Six reversals were obtained using the 1-dB step size. The mean level over the last four reversals for each track was taken as the LDEL of the test and comparison sounds. The LDEL values were averaged across the two tracks with starting level differences of ±10 dB, separately for the two tracks with the comparison sound varied and the two tracks with the test sound varied.

Before testing proper commenced, each subject completed one practice block, with either the AM sound or the steady sound as the comparison, depending on which of them occurred in the first test block. The block was shorter than in the main experiment, with only four reversals for each track.

Stimuli were generated digitally at a sample rate of 44.1 kHz. The signal was D/A-converted by a M-Audio Delta 44 audio interface (Cumberland, RI) and passed through manual attenuators (Hatfield, 2125, Hatfield, UK) to a Sennheiser HD580 headset (Wedemark, Germany).

Results

The results obtained using the AM comparison sound are shown in the top two panels of Figure 8 by dotted lines (comparison sound varied) and dot-dashed lines (test sound varied). When the 0°-AM tone was compared with itself (left-most points in each panel), the LDEL values were close to 0 dB, indicating that biases were small. The LDEL values became negative with increasing modulator interaural phase, indicating that out-of-phase modulation led to an increase in loudness. An ANOVA with factors modulation rate, IMPD, and variable sound (test sound varied or comparison sound varied) was conducted. There was a significant effect of modulation rate, F(1, 12) = 5.69, p < .05, the LDEL being slightly smaller for the 16-Hz rate. There was a significant effect of IMPD, F(2, 24) = 4.85, p < .05. There was no significant effect of variable sound and no significant interactions. The predictions of the binaural TVL model are shown by the solid lines. They fit the data well: the root-mean square deviation between the data and predictions was 0.49 dB. The largest difference occurred for the 4-Hz modulation rate and the 180° IMPD, where the predicted LDEL was about 1 dB too negative. The predictions of the model of Glasberg and Moore (2002) are shown as long-dashed lines. The predicted LDEL increases with increasing IMPD, which is opposite to the trend in the data.

The results obtained using the steady comparison sound are shown in the bottom two panels of Figure 8 by dotted lines (comparison sound varied) and dashed lines (test sound varied). The LDEL values for the IMPD of 0° are slightly positive, by 1 to 2 dB. This means that at equal RMS level, the AM sound would have been perceived as slightly softer than the steady sound. At equal peak level, the AM sound would have been even softer than the steady sound. This result is counter-intuitive and is not predicted by the binaural TVL model (or any other model that we know of). The predictions of the binaural TVL model are shown by the solid lines in the lower panels of Figure 8. The model predicts that the LDEL values for IMPD = 0 should be somewhat negative, especially for the 4-Hz AM rate.

Previous comparisons of the loudness of AM tones and steady tones have given mixed results, especially for low AM rates, some showing slightly negative LDEL values (Bauch, 1956; Zhang & Zeng, 1997) and some showing slightly positive LDEL values or values very close to 0 (Moore, Launer, Vickers, & Baer, 1998; Moore, Vickers, Baer, et al., 1999). The differences across studies may reflect subjective reports of subjects that it is difficult to compare the overall loudness of a sound that is steady and a sound that has distinct fluctuations in loudness. This difficulty is reflected in the fact that the standard error (SE) of the measurements, as indicated by the error bars in Figure 8, was generally larger when the comparison sound was a steady tone (mean SE = 0.62) than when the comparison sound was an AM tone (mean SE = 0.45). Based on a t test, this difference was significant, t(11) = 3.81, p < .01. The predictions of the model are consistent with the idea that, for AM tones with low modulation rates, the loudness corresponds to a level between the RMS level and the peak level (Bauch, 1956; Zhang & Zeng, 1997), although the present data do not fit this pattern.

The obtained LDEL values decreased with increasing IMPD. An ANOVA with factors modulation rate, IMPD, and variable sound was conducted. There was a significant effect of modulation rate, F(1, 12) = 15.3, p < .01, the LDEL being slightly larger for the 16-Hz rate. There was a significant effect of IMPD, F(2, 24) = 6.11, p < .01. There was no significant effect of variable sound and no significant interactions. The binaural TVL model correctly predicted the decrease in LDEL with increasing IMPD (solid lines). In contrast, the model of Glasberg and Moore (2002) predicted an increase in LDEL with increasing IMPD (dashed lines).

In summary, the binaural TVL model correctly predicted that the loudness of the AM sounds increased slightly as the IMPD was increased from 0° to 180°, whereas the model of Glasberg and Moore (2002) did not. The binaural TVL model did not predict the slightly positive LDEL for the pure-tone comparison sound when the IMPD was 0°, but this may partly reflect the difficulties in loudness matching that occur when one of the sounds is steady and the other has distinct fluctuations in loudness. As noted above, the model of loudness for stationary sounds incorporating binaural inhibition (Moore & Glasberg, 2007) uses as input the long-term average spectra of the stimuli. Since these spectra were the same at the two ears regardless of the IMPD, the model for stationary sounds cannot account for the effects of IMPD that are apparent in the data.

Unresolved Issues and Limitations

The model presented here shares some limitations with other loudness models. Loudness perception can be influenced by a variety of factors that are not taken into account in the model, or in any other models to our knowledge (Moore, 2014). These factors may be important in everyday listening situations, where our sensory systems seem designed to estimate the properties of “auditory objects” or “sound sources,” rather than to estimate the properties of the signals reaching the ears or the eyes. For example, the perceived distance of a sound source can influence its loudness (Mershon, Desaulniers, Kiefer, Amerson, & Mills, 1981; Zahorik & Wightman, 2001).

Another limitation is that there can be significant individual variability in almost all of the factors that are included in the model, for example, the free field to eardrum transformation (Shaw, 1974), the middle-ear transfer function (Puria et al., 1997), the bandwidths of the auditory filters (Moore, 1987), and the amount of compression in the cochlea (Moore, Vickers, Plack & Oxenham, 1999). Hence, the predictions of the model are not likely to be accurate for individual listeners or even small groups of listeners. The model is intended to predict the mean results of large groups of listeners under conditions where biases are minimized.

Finally, a version of the model using a realistic time-domain auditory filter bank has not yet been developed. Although Chalupper and Fastl (2002) have described a loudness model for time-varying sounds based on an auditory filter bank, they derived their filter bank using a Fourier-t transform analysis (Terhardt, 1985). The resulting filter bank did not have a realistic phase response (Kohlrausch, 1988; Oxenham & Dau, 2001), and the filters did not vary with level in the way that the auditory filters do (Moore & Glasberg, 1987). Transmission-line models of the cochlea have been used as the basis for loudness models by Pieper, Mauermann, Kollmeier, and Ewert (2016), but their models required somewhat arbitrary correction filters to give accurate predictions of equal-loudness contours. A model using filters with more realistic level- and frequency-dependent gains and phase responses may be required to account for the effects of component phase on the loudness of complex sounds (Gockel, Moore, & Patterson, 2002).

Conclusions

We have described a model of loudness for time-varying sounds incorporating the concept of binaural inhibition. The model can be used in practical applications for situations where the sounds at the two ears are different. The model gives reasonably accurate predictions of the loudness of a tone in one ear in the presence of a tone of different frequency in the other ear, the loudness of noise bands presented at different azimuths, BLDEL values for monaural and diotic sounds and sounds that differ in interaural level, and the loudness of sounds whose amplitude patterns and spectra differ across ears. However, the model fails to predict the small effect of interaural correlation on the loudness of low-frequency narrow bands of noise (Edmonds & Culling, 2009).

Declaration of Conflicting Interests

The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the Engineering and Physical Sciences Research Council (UK, grant number RG78536).