Higher Quality and Lower Cost from Improving Hospital Discharge Decision Making

Abstract

This paper reports research on improving decisions about hospital discharges – decisions that are now made by physicians based on mainly subjective evaluations of patients’ discharge status. We report an experiment on uptake of our clinical decision support software (CDSS) which presents physicians with evidence-based discharge criteria that can be effectively utilized at the point of care where the discharge decision is made. One experimental treatment we report prompts physician attentiveness to the CDSS by replacing the default option of universal “opt in” to patient discharge with the alternative default option of “opt out” from the CDSS recommendations to discharge or not to discharge the patient on each day of hospital stay. We also report results from experimental treatments that implement the CDSS under varying conditions of time pressure on the subjects. The experiment was conducted using resident physicians and fourth-year medical students at a university medical school as subjects.

1. Introduction

In 2010 Americans spent 17.6 percent of GDP on healthcare, which was eight percentage points above the OECD average (Organization for Economic Cooperation and Development, 2012).¹ The objective of decreasing medical costs, or at least reducing their outsized rate of increase, would seem to be well served by reducing hospital length of stay (LOS). But discharging patients earlier can increase the rate of unplanned readmissions, an indicator of low quality and a cost inflator. In 2010, 19.2 percent of Medicare patients were readmitted within 30 days of discharge, resulting in additional hospital charges totaling $17.5 billion (Office of Information Products and Data Analytics, 2012).²

Hospitals and physicians are encountering increasing pressure both to reduce costs of hospital stay and to reduce unplanned readmissions. The research question we take up is how to assist physicians in making discharge decisions that decrease LOS as well as the likelihood of unplanned readmissions. Physicians have rapidly increasing access to large amounts of raw data on each patient they treat through electronic medical record systems. The problem for improving discharge decision making is not shortage of data on the patient but, rather, absence of evidence-based discharge criteria that can be effectively applied at the point of care.

Our central activity is a collaboration between physicians who make discharge decisions and economists – with expertise in research on decisions under risk and mechanism design – aimed at improving hospital discharge decision making. The objectives are to design, experimentally test, and disseminate a clinical decision support system (CDSS) that can be used to lower medical costs – by reducing average length of hospital stay – while increasing quality of medical care by decreasing the likelihood of unplanned readmissions.

An outline of current practice sheds light on the nature of the problem and a possible solution. Prior to deciding whether to discharge a patient, a physician examines the patient and reviews his or her electronic medical records. Criteria applied to making a discharge decision are derived from the physician’s medical training and own previous practice and, perhaps, recommendations of one or more colleagues. The evidence base of these typical discharge criteria is extremely limited in comparison to the voluminous information that could be derived from the electronic medical records of a hospital. A typical hospital will serve many thousands of patients per year. Each surviving patient will be discharged from the hospital and it will subsequently be revealed, in most cases, whether the discharge was successful or unsuccessful (i.e., led to unplanned readmission within 30 days). The central question addressed in our research is an operational use of this mass of data – from current and former patients’ electronic medical records and outcomes from previous discharges of patients – by developing evidence-based discharge criteria that can be effectively applied at the point of care where the discharge decision is made.

Our collaborative research began by analyzing a large sample of (de-identified) patient data to identify risk factors for unplanned hospital readmissions at a large southeastern teaching hospital (Kassin, et al. 2012). We subsequently elicited the hospital discharge criteria reported by physicians (Leeds, et al. 2013) and compared these self-reported criteria to (a) discharge criteria that can statistically explain actual discharges and (b) patient clinical and demographic data that predict successful or unsuccessful discharges (Leeds, et al. 2015). Although many self-reported criteria coincide with (statistically-explanatory) actual criteria, and many significant predictors of actual discharges coincide with significant predictors of successful discharges, various inconsistencies were identified which suggested the importance of research on creating and experimentally testing CDSS for improving discharge decision making.

In building the CDSS, we start with estimation of a probit model of determinants of unplanned readmission (i.e. unsuccessful discharge) probability. The probit model is estimated with data for about 3,200 patients from the electronic medical records of a large southeastern hospital. The estimated probit model provides the empirical foundation for a decision support model that is instantiated in the CDSS. The CDSS is designed to present the discharge decision implications of the underlying probit model to physicians in a user friendly way that can be applied at the point of care. The central research question for assessing the value of the CDSS is whether it is efficacious in improving discharge decision making. There are two ways in which the CDSS can fail to be efficacious: (1) the probit model underlying the CDSS may not be a good model and hence fail to provide the empirical foundation for good discharge decisions; or (2) the implementation of CDSS may fail to support uptake by physicians of the information in the underlying probit model. The laboratory experiment reported herein provides a test for uptake. Such a test is a practical and ethical requirement before application of the CDSS on patient wards in hospitals.³ If the CDSS is effective in supporting uptake then the planned next phase in our research program is a field experiment in the form of an intervention on patient wards. Such intervention will provide a joint test of items (1) and (2) above.

The organization of the rest of the paper is as follows. The next section discusses related literature, section 3 describes the CDSS, and sections 4 and 5 report on the design and results from an experimental test of uptake of the CDSS. A summary of the main findings and conclusions in section 6 completes the paper.

2. Related Economic and Medical Journal Literature

The use of advanced information technology has been advocated as a method to increase healthcare quality and reduce costs (Cebul et al. 2008). Our research is part of a larger program in economics that aims at the creation of information technology for medical decision making and its application in clinical environments intended to improve quality and lower costs of healthcare. A seminal contribution by economists to improving healthcare is the mechanism design incorporated into information technology for kidney exchange by Roth, Sönmez, and Ünver (2004, 2007). Their work provided a foundation for the New England Program for Kidney Exchange, and subsequent kidney exchange programs, which have led to increases in quality and length of life by matching patients with donors for transplant surgery while lowering the informational costs associated with organ matches. Support for improving medical decision making is needed in many additional areas. The present paper reports one such project. Our research targets improving hospital discharge decision making through development of CDSS.

One of the earliest investigations of the determinants of hospital readmission in the medical literature was conducted by Anderson and Steinberg (1985) who found that a patient’s disease history and diagnosis were important determinants of a patient’s probability of readmission. More recent research has further illustrated the role that these patient-specific factors have on the probability of readmission (Demir 2014) and that the use of electronic medical record (EMR) data on a patient’s vital signs and laboratory test results can be used to explain likelihood of readmissions (Amarasingham, et al. 2010). The Amarasignham, et al. reported results are relevant to our research because: (1) they validate the use of electronic medical records data in recovering readmission probabilities; and (2) they highlight a fundamental flaw with the current Medicare regulations that generate expectations for readmission rates with models that do not contain clinical information. The importance of using clinical information to inform estimates of readmission rates is also supported by Lee, et al. (2012), who study return visits to a pediatric emergency room within 72-hours. Both Amarasignham, et al. and Lee, et al. conclude that their research supports the importance of future development of CDSS to improve discharge decision making.

In a recent review of 148 studies, Bright, et al. (2012), conclude that the current CDSSs (mostly not for discharge decisions) are effective at improving healthcare when assisting with physician decision making at the point of care. None of these studies, however, reports CDSS that (a) can be applied at the point of care and (b) encourages physician attentiveness by replacing the default option of universal “opt in” to patient discharge with the alternative default option of “opt out” from the CDSS recommendations. We develop and test CDSS that applies at the point of care and includes a version which requires justification for opting out of default decisions provided by the software’s recommendation.

Previous research has reported that choice of default option can have important effects on outcomes in some contexts. For example, Madrian and Shea (2003) reports that change from opt in to opt out of 401K participation at a large U.S. corporation had a large effect on participation. In addition, a substantial fraction of employees hired under the opt out policy subsequently stayed with both the default contribution rate and the default mutual fund allocation. Cappelletti, et al. (2014) reports significant effect of default option in public goods provision. Haggag, et al. (2014) report that default tip suggestions have a large impact on tip amounts for taxi rides. Grossman (2014) reports that opt in or opt out default option has a significant effect on selection of the moral wriggle room provided by ignorance of other’s payoff in dictator games. Kressel, et al. (2007) reports that default options have significant effects on expressed preferences for end-of-life medical treatments. Other researchers have reported no significant effect of default options on outcomes. For example, Bronchetti, et al. (2013) report an experiment that compares effects of opt in with opt out of allocation of a portion of income tax refunds to U.S. savings bonds. They report no significant effect of changing the default option on savings behavior of low income tax filers. Löfgren, et al. (2012) report no significant effect of default option on choices of carbon offsets by experienced decision makers.

Effects of switching from opt in to opt out in some contexts appears to result from transaction costs from overturning the default option (for example, 401(k) participation). In other contexts, the effect of default option appears to result from suggesting a normative focal point (for example, public goods provision or taxi tips). In our context, we conjecture that making the CDSS discharge recommendation the default option might have an effect by focusing decision makers’ attention on the information provided by the CDSS. Having to enter reasons for overriding a recommendation can prompt one’s attention to the available information on which the recommendation is based.

3. Development of the CDSS

The research method for creating the CDSS proceeded as follows. We began with the following question: Do the data profiles for patients who are successfully discharged differ in identifiable ways from the data profiles for patients who are unsuccessfully discharged? The answer to this question was “yes” and that opened the possibility of building a decision support model that could inform discharge decisions for individual patients with the accumulated experience from discharging thousands of other patients. We proceeded as follows. We extracted a large sample of de-identified data from the “data warehouse” of patient electronic medical records of a large southeastern teaching hospital. The data were used to build an econometric model, which provided the foundation for a decision support model that could be instantiated in software (i.e., the CDSS) and applied at the point of care. The CDSS presents the physician with a recommended discharge decision and with estimated daily readmission probabilities (and 80% confidence intervals); in addition, it provides information on dynamically-selected key clinical variables for the individual patient in a user friendly format.

The CDSS was developed from an econometric model that used data from (de-identified) electronic medical records for 3,202 surgery patients who had been discharged from a large southeastern hospital and subsequently readmitted or not readmitted with the same diagnosis code within 30 days. We used probit regression to estimate probabilities of readmission with data that included the average values of clinical variables during a patient’s stay, the duration of time spent outside and within the normal range of values expected for a particular clinical variable, counts of medications, images and transfusions, as well as a full set of interaction terms between the laboratory test and vital sign variables. We also used census track data that could be linked to the patient charts in a procedure that conformed with HIPAA privacy rules.⁴

The electronic medical record and census track information were used to construct a data set that contained 48,889 unique patient-day observations that corresponded to the observed value of each patient’s data for each day during the hospital stay. This data set was used with the estimated probit model to construct the CDSS that reports probability of readmission for each individual patient in a representative sample if the patient were to be discharged from the hospital on that day. Time-varying point estimates of readmission probabilities and 80% confidence intervals were obtained from the probit-estimated parameter distributions and displayed by the CDSS (see Figures 2, 4 and Figure 5 below for examples). An 80% confidence interval was selected because it captures a 10% one-sided error on the decision criterion to discharge a patient on a given day. These daily readmission probabilities are used with targeted readmission rates that vary with patient diagnosis codes to determine the CDSS patient-specific daily discharge recommendations. The CDSS uses target readmission rates that are 10% reductions from historical readmission rates and are based on the targets stated by the Center for Medicare and Medicaid Services in 2010. A central objective for specification of our CDSS is the efficacy of inducing these new target readmission rates, rather than the historically higher figures, without increasing length of stay.

Figure 2.

Default Treatment Decision Screen with Negative Recommendation

Figure 4.

Default Treatment Decision Screen with Physician Judgment “Recommendation”

Figure 5.

Default Treatment Decision Screen with Positive Recommendation

In addition to readmission probabilities and discharge recommendations, the CDSS dynamically displays six clinical variables that the probit model indicates are most significant for the discharge status of the individual patient on that day of the hospital stay. The clinical variables displayed in the six charts for a patient can change from one day to another day, reflecting the model’s updated implications with daily varying data on patient status (see Figure 2, Figure 4 and Figure 5 below for examples).

4. Experimental Design and Protocol

The experiment is a 2 × 3 design that “crosses” the presence or absence of a 45 day constraint on the number of “experimental days” with three information and default conditions. The Baseline and the two CDSS treatments (Information and Default conditions) are explained at length in following subsections. The six treatments in the 2 × 3 design were conducted between subjects. Inclusion of the 45 day constraint increases the opportunity cost of keeping a patient longer in the hospital; this feature of the experiment is a stylized way of capturing the effect of a hospital’s “capacity” on discharge decision making. Fifty-four out of the total 125 subjects were recruited to participate in the design with the 45 experimental day constraint and 71 subjects for the design with no constraint on the number of experimental days.

Twenty of the total 125 subjects were resident physicians and the rest were fourth-year medical students. Subjects were distributed almost equally across the Baseline (43 subjects), Information (42 subjects), and Default (40 subjects) treatment cells. The overall number (64) of female participants was similar to the number (61) of male subjects, as was the gender composition across Baseline, Information, and Default treatment cells ((21F, 22M), (20F, 22M) and (23F, 17M); Pearson chi2(2)=0.95, p-value=0.62). Academic performance of subjects who participated in different treatments was at comparable levels.⁵

In addition to making discharge decisions, subjects were asked to complete an online questionnaire that was embedded in the experiment software. The questionnaire elicited demographic information and also included hypothetical response questions about risk attitudes.⁶ After completing the questionnaire, subjects would exit the lab one at a time to be paid in cash in private.

In order to conduct our experiment we selected 30 (de-identified) patient charts from the sample of 3,202 patient electronic medical records in our sample. The entire sample was first partitioned into low, medium and high readmission risk categories.⁷ We subsequently selected 10, patient charts from each of the three risk categories to provide a clear test of the efficacy of the software.

The alternative information and default conditions will be explained below. We first explain features of the experiment that are present in all treatment cells.

4.a Common Features of the Baseline, Information, and Default Treatments

The information provided to subjects in all treatment cells includes clinical variables that are the same as they would get from a hospital’s electronic medical records (EMR). Not only is the same information provided as in the hospital’s EMR, we also use a graphical interface that is a facsimile of the EMR computer display screens.

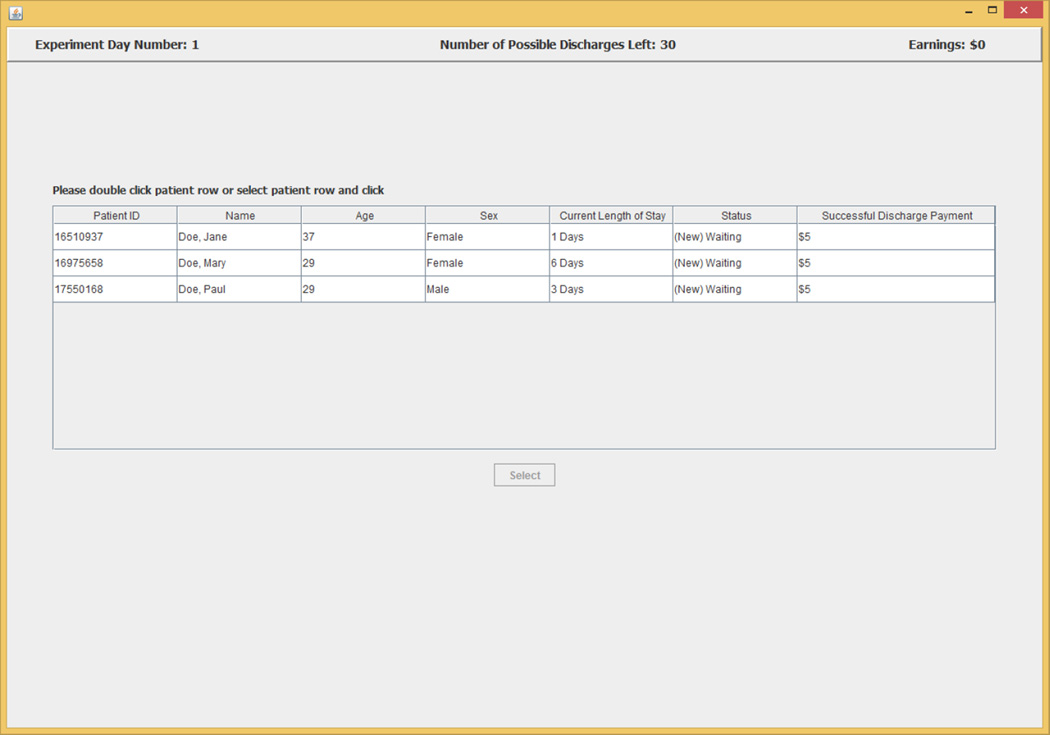
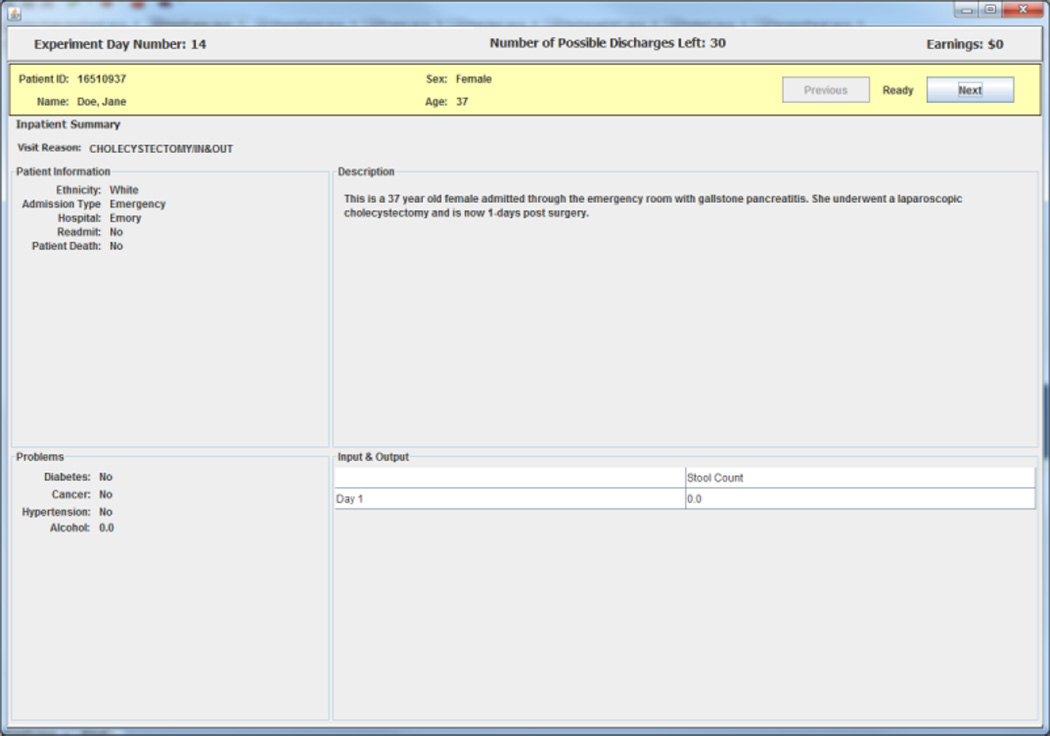
A subject begins each experimental day by selecting patients from a list on a screen that displays summary information from each of three randomly selected charts for patients who the subject has not previously discharged successfully.⁸ The information screen contains information on each patient’s age, sex, and length of stay in the hospital up to the current experimental day. An example of a three patient list is shown in Figure 1. After selecting a patient from the list, a subject in the experiment gets access to a facsimile of that patient’s de-identified electronic medical records (EMR) including all information for the patient up to the current experimental day. The information presented includes EMR facsimile screens that report an inpatient summary, laboratory tests data, physician orders, and vital signs. An example of the EMR facsimile chart information is presented in the figures in Appendix 1.

Figure 1.

Patient Selection

A subject in the experiment did not always have to review a patient’s chart for the first few calendar days they were in the hospital if there was no realistic prospect for considering discharge during those days. This procedure was adopted to avoid possible tedium for subjects. The first “experiment day” on which a subject was asked to review a chart was randomly selected to be between one and four days before the discharge model would first recommend that the patient be discharged; this one to four day period was independently selected for each of the 30 patient charts. This procedure was used to ensure that naïve decision rules such as “always discharge after X days” would not produce good outcomes. During an experimental session, the 30 patient charts were presented in a random order that was independently drawn for each subject. A subject would be able to access EMR information and serve only three patients at a time (that is, in one experimental day), from this set of 30 randomly ordered patients, by selection from an experiment software page like that shown in Figure 1.

In order to avoid leading the subjects towards making particular decisions, the dates of actual discharge of the patients were removed from the patient charts. Within the experiment it was, of course, possible that a patient could be retained longer than the observed length of stay in the EMR. Therefore, we constructed continuation charts for all 30 patients that imputed an extra five days of possible stay.⁹ In all treatments, the subjects were informed that they should assume that a patient was being managed at the appropriate standard of care while in the hospital and that the subjects were not being asked to speculate about additional tests or procedures that they might want to order. Instead, they were asked to make the hospital discharge decision on the basis of the clinical information contained in a patient’s EMR and (in all except the Baseline condition) the information presented by the CDSS.

Subjects could make at most a total of 30 choices of the Discharge Patient option. An unsuccessfully discharged patient “used up” one of these 30 feasible choices. This feature of the experimental design incorporates a cost to the subject of a decision that produces the bad outcome of a readmission: each readmission incurs a reduction of $5 in maximum attainable payoff in the experiment. Each experiment session could last no more than two hours. The two-hour time limit, however, was not a binding constraint for any subject. In three treatment cells there was an additional constraint that the subject could not participate in more than 45 experiment days. In contrast, there was no limit on the number of experiment days that a subject could use to make up to 30 discharge decisions in the other three treatment cells. The purpose of the 45 experiment day constraint was to simulate conditions in a crowded hospital that is running up against constraint on available hospital beds.¹⁰ This day constraint was set at 45 (rather than, say, 30 or 60) days because of the design feature, explained above, that subjects first saw a patient chart on an “experiment day” that was randomly selected to be between one and four days before the discharge model would first recommend that the patient be discharged. The 45 day constraint would allow, for example, 15 patients to be discharged on day 4 and 15 on day 5, hence would be expected to be binding for some subjects.¹¹ In contrast, a subject would only have been able to discharge all 30 patients in 30 experiment days by discharging all of them by the third day; thus an alternative 30 day constraint would have been severely restrictive. A subject could have satisfied a 60 day constraint by, for example, discharging 10 patients on day 5, 10 on day 6, and 10 on day 7; thus an alternative 60 day constraint would not have been expected to be binding on most subjects.

At the beginning of an experiment session, the subjects were welcomed to the decision laboratory by one of the researchers who self-identified as a medical doctor and explained that the research was supported by an NIH grant. The subjects subsequently read and signed the IRB-approved consent form and began reading the subject instructions on their computer monitors.¹² The instructions informed subjects that they would make a series of choices between the two options, “Discharge Patient” and “Do NOT Discharge Patient.” Any patient not discharged would return for consideration on the next experiment day with updated chart information. Any patient who was discharged could turn out to be successfully discharged or, alternatively, could be readmitted.¹³ Any patient readmitted in the experiment remained in the hospital for at least two experimental days during which the subject continued to view the updated chart.

4.b Idiosyncratic Features of the Baseline, Information, and Default Treatments

In Baseline treatment cells, a subject makes the discharge decisions using only the information in the EMR, as shown in the charts in Appendix 1. The default option in the Baseline treatment is the same as in current medical practice: the patient remains in the hospital unless the physician with authority initiates entry of “discharge orders” in the EMR. The Information treatment cells present all of the EMR-facsimile screens used in the Baseline treatment plus additional CDSS screens with selected patient information and a recommendation about the discharge decision. The default option in the Information treatment is the same as in the Baseline treatment. The Default treatment presents all of the same information as in the Information treatment, including a discharge recommendation, but uses a different default option. In the Default treatment, the CDSS initiates discharge orders in EMR when it makes a positive discharge recommendation; an attending physician who did not accept the recommendation would have to enter reasons in the EMR for overriding the recommended decision. When the CDSS makes a negative recommendation, a physician would have to enter reasons for overriding the recommendation before entering discharge orders in EMR.¹⁴

The subjects enter their decisions on screens that differ across the Baseline and CDSS treatments as follows. The decision screen for the Baseline treatment includes only the patient’s ID number, fictitious name, age, and sex and two decision buttons. These decision buttons are labeled “Discharge Patient” and “Do NOT Discharge Patient.” If the subject clicks on the Do NOT Discharge Patient button, the patient remains “in the hospital” and reappears in the subject’s list of patients on the following experiment day. If the subject clicks on the Discharge Patient button, the patient is discharged. In the event of a successful discharge, the subject is paid five dollars. In the event of an unsuccessful discharge, the subject receives no payment and the patient is readmitted and reappears in the subject’s list of patients.

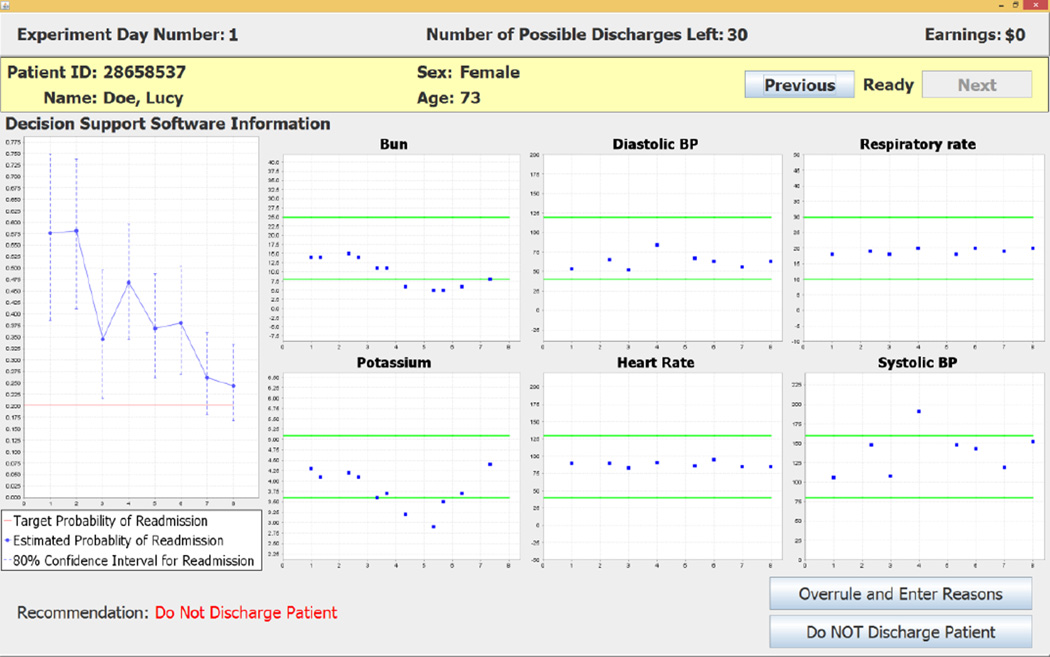
There are three decision screens for the Default treatment that will be described here (and three slightly different screens for the Information Treatment that will be described in footnotes). Which decision screen a subject encounters in the Default treatment depends on the recommendation of the decision support software for the patient on that day. In case of a negative recommendation the decision maker encounters a decision screen like the one shown in Figure 2 that reports the recommendation “Do Not Discharge Patient” at the bottom left of the screen. The left side of the decision screen shows probabilities of readmission if the patient were to be discharged on any experiment day up to the present decision day (which is day 8, as shown on the horizontal axis). The dots at kinks in the piecewise linear graph show point estimates of the probabilities of readmission on days 1–8. The vertical dashed lines that pass through the dots (at kinks) correspond to the 80% confidence intervals of the readmission probability. The horizontal line shows the target readmission probability for patients with the diagnosis code of this patient. For the selected patient (Lucy Doe), the left part of the figure shows point estimates that lie entirely above the horizontal line showing the target readmission rate; that is why the decision support software makes the negative recommendation. The six charts on the right two-thirds of the screen show the day 1–8 values of clinical variables that are probabilistically most important for the discharge decision for this specific patient on the present experiment day (which is day 8, in this case).

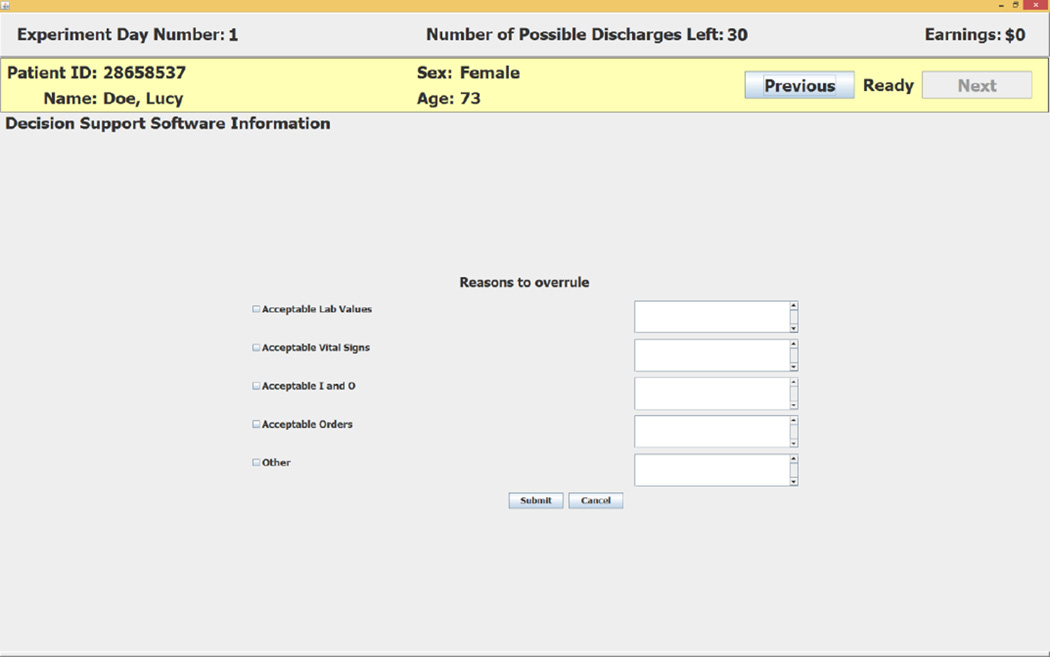
The subject enters her decision by clicking on one of the two buttons at the lower right of the screen. If the subject accepts the recommendation she clicks on the Do NOT Discharge Patient button. If the subject does not accept the negative recommendation she clicks on the Overrule and Enter Reasons button.¹⁵ This choice causes the decision support software to open the screen shown in Figure 3 that requires the subject to enter her reasons for overruling the CDSS recommendation.¹⁶ The reasons for overruling the recommendation can be recorded by clicking on (square) radio buttons on the left side of the screen and entering text on the right side of the screen.

Figure 3.

Reasons to Overrule a Negative Recommendation

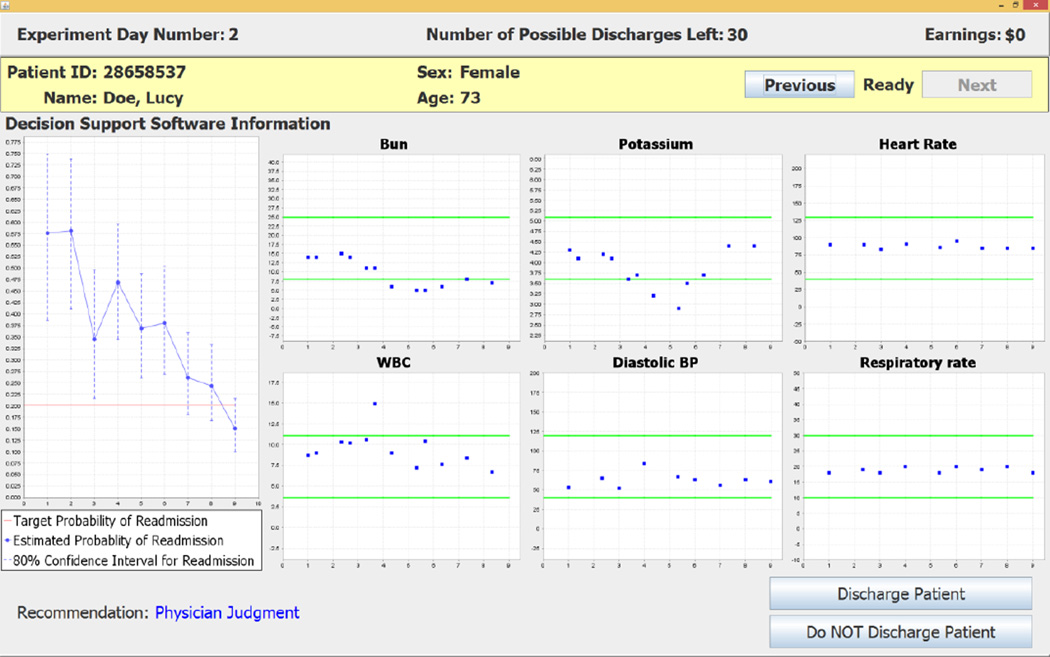
Figure 4 shows data for a day on which the decision support software does not make a recommendation whether to discharge or not to discharge Lucy Doe; instead, it exhibits the “recommendation” for day 9 as Physician Judgment. A Physician Judgment “recommendation” occurs when the target readmission rate falls between the point estimate and the upper bound on the 80% confidence interval for the readmission probability. Although there is no recommended decision in this case, the software does provide decision support with the information in the readmission probabilities on the left side of the screen and the six dynamically-selected clinical variables on the right side of the screen.¹⁷ The subject enters a decision on this screen by clicking on one of the two buttons in the bottom right corner of the screen shown in Figure 3.¹⁸

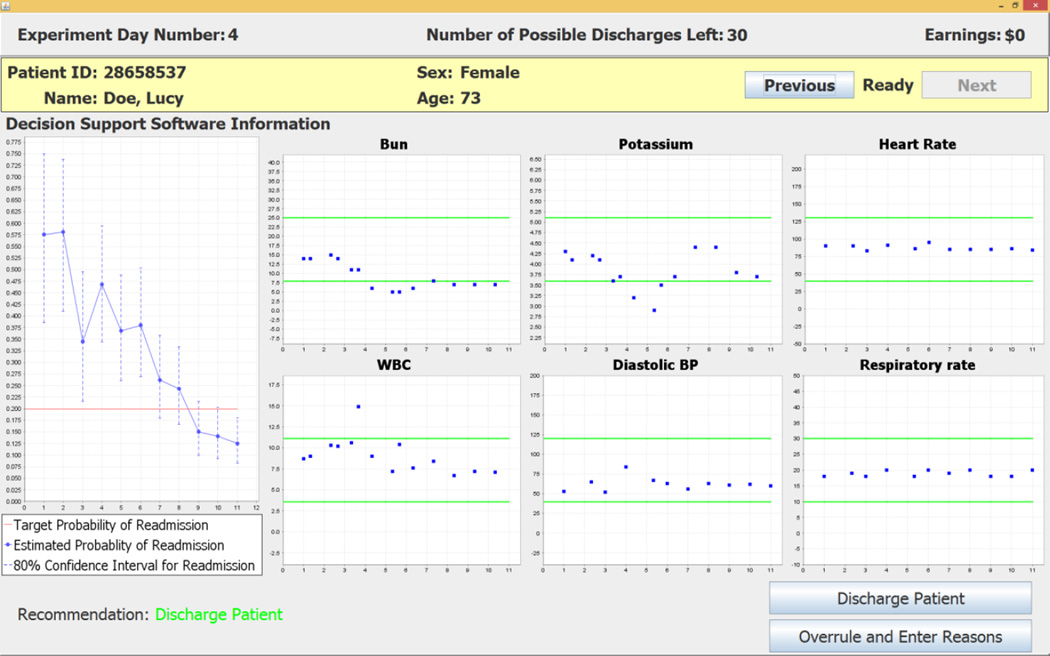
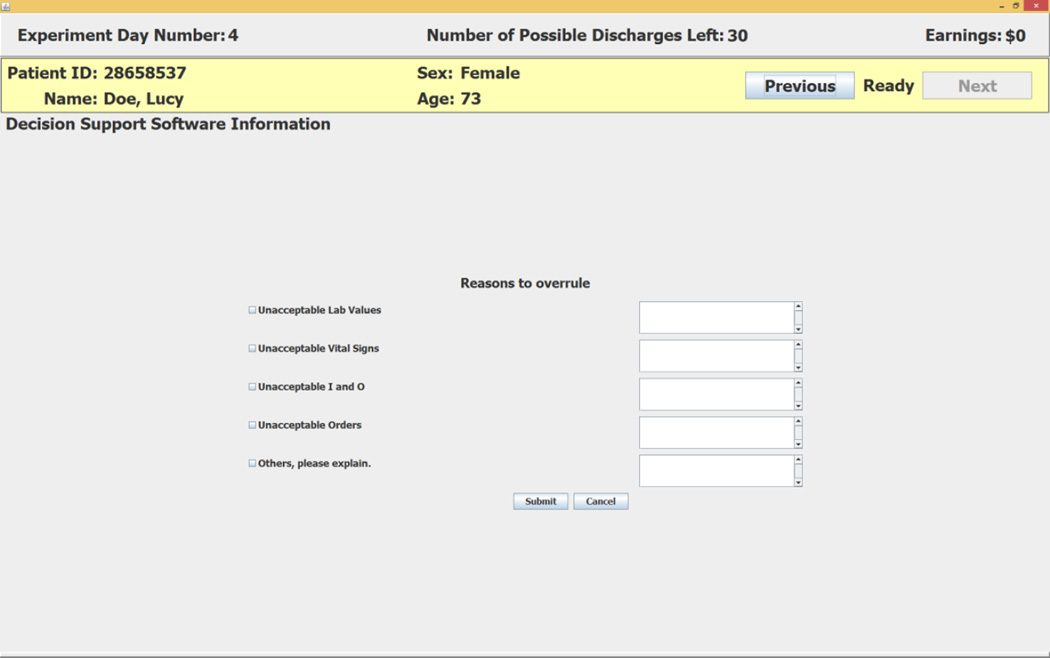
The CDSS first recommends that Lucy Doe be discharged on the experiment day in which the top of the 80% error bar dips below the target readmission rate. This conservative criterion reflects choice of an estimated 10% error for the positive recommendation. In the example shown in Figure 5, the first day on which the top of the error bar drops below the target readmission rate is experiment day 11. The software’s recommendation on that day is Discharge Patient. The subject enters her decision by clicking on one of the two buttons at the lower right of the screen.¹⁹ If the subject accepts the recommendation she clicks on the Discharge Patient button. If the subject does not accept the negative recommendation she clicks on the Overrule and Enter Reasons button. This choice opens the screen shown in Figure 6 that requires the subject to enter her reasons for overruling the software’s positive recommendation.²⁰

Figure 6.

Reasons to Overrule a Positive Recommendation

5. Results from the Experiment

Average subject payoff was $130 for participation lasting, on average, 90 minutes. Data from our experiment provide support for uptake of the CDSS, as evidenced by four measures of performance: subject earnings, readmission rate, hospital length of stay, and time efficiency (number of experimental days utilized to make a certain number of discharges). We report several ways of describing the data and statistical analysis for significance of treatment effects.

5.a Value of Decision Support Information

After completing all discharge decisions, subjects who participated in the Default and Information Treatments were asked (by the experiment software) to report their ranking on a five-point Likert scale (where higher is better) of the usefulness of being provided information on the estimated readmission probabilities and the 80% confidence intervals. Forty out of a total of 82 subjects who participated in the treatments with CDSS reported a score 3 or higher for both the point estimate and the 80% confidence interval; we call this group of subjects H and use L for the other group.

The difference between average daily earnings of subjects in the H and L groups provides an economic measure of the value of uptake of CDSS information. The mean daily earnings are $3.25 and $3.51 for groups L and H; the median figures are $2.89 and $3.43 for groups L and H. The Kolmogorov-Smirnov test rejects at 1% significance level (p-value is 0.004) the null hypothesis of daily earnings of the two groups being drawn from the same distribution. Similarly, the difference between mean number of experimental days under the subjects’ care for non-readmitted patients provides a measure of the healthcare cost implications of uptake of the CDSS information. The means are 3.29 (95% C.I. = [3.14, 3.43]) and 2.78 (95% C.I. = [2.65, 2.91]) experimental days for groups L and H.²¹ Note that the 95% C.I. are disjoint. Hence, in our experiment, a result from subjects’ recognizing the value of the information is a reduction of length of stay (in the experiment) of 0.46 days per patient, a decrease of 14%. We conclude that:

Result 1. Subjects who report they place relatively high value on usefulness of reported readmission probabilities: (a) keep their patients significantly fewer days in the hospital; and (b) earn significantly higher payoffs per experimental day

An interesting question is whether there are identifiable characteristics of subjects that make them more or less likely to highly value the information on daily probabilities of readmissions provided by CDSS (that is, to be in group H). We do not find (statistically significant) differences in the distribution of residents (46.15% (H) and 53.85% (L)) and fourth-year medical students (49.28% (H) and 50.72%(L)) between the H and L groups (Pearson chi2(1)=0.043, p-value=0.836). Data however reveal differences in the reported value of the information among subjects with high academic scores (GPA at least 3.7 as undergraduate and at least 3.5 in medical school) and the remaining subjects (with GPA either less than 3.7 as undergraduate or less than 3.5 in the medical school). The percentages in the H groups, 60.47 (26 out of a total of 43 high GPA subjects) and 35.90 (14 out of a total of 39 lower GPA) are significantly different at conventional levels (Pearson chi2(1)=4.94, p-value=0.026). These findings are also supported by probit regression with the dependent variable the dummy for being in group H and the list of regressors including subject demographics and dummy variables for the Default and 45-day Constraint treatments. Being in the high GPA group increases the likelihood of placing high value on the information by 27% (p-value=0.019). The estimates on the treatment dummies are not significant nor is the estimate on the dummy for being a resident (rather than a student).²²

We conclude that information provided by the CDSS can improve discharge decision making as subjects who report that they place relatively high value on usefulness of the CDSS readmission probability estimates perform better: they keep their patients fewer days in the hospital and earn more money per experimental day.

So far we have analyzed only data from the CDSS treatments. We now turn our attention to the degree of uptake of the information provided by the CDSS by comparing the performance metrics (time efficiency, daily earnings, readmission rates and hospital length of stay) in the CDSS treatments to the ones observed in the Baseline.

5.b Decision Time Efficiency and Daily Experiment Earnings

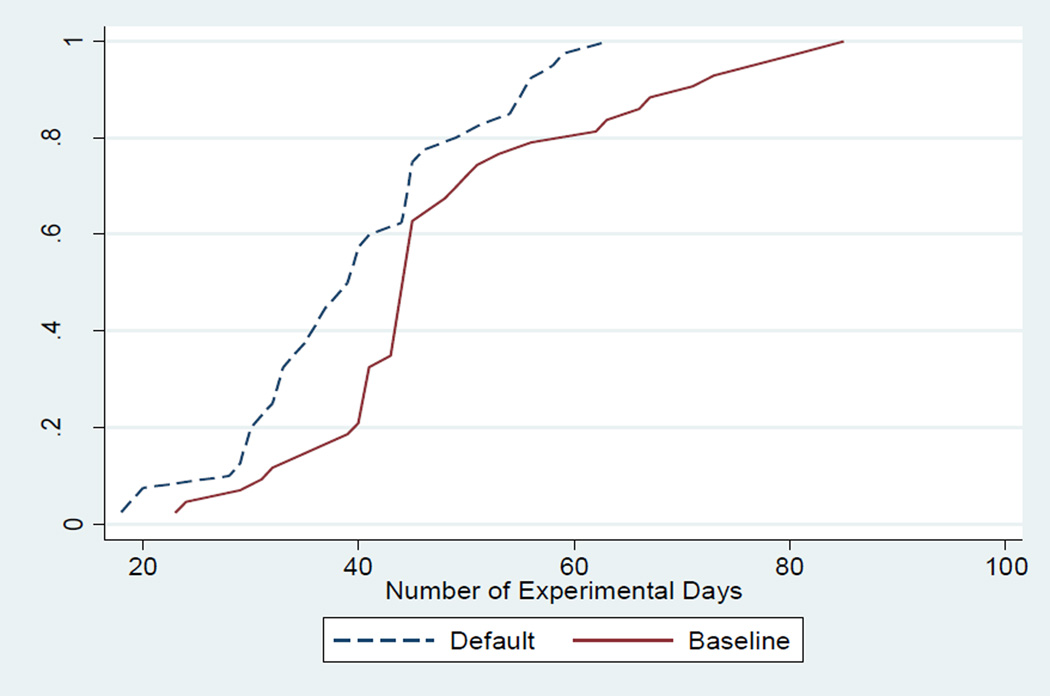
In the treatment cells without the 45 day constraint, subjects took on average 54 experimental days to finish the experiment (i.e. to make 30 discharges) in the Baseline treatment but in the Information and Default treatments they were able to complete the task of making 30 discharges within 47 and 42 experimental days, respectively, an improvement in time efficiency of 7 and 12 experimental days. The null hypothesis of equal time efficiency across treatments is rejected (chi2=6.42; p-value=0.04 according to Kruskal-Wallis test).²³ Data from treatments in which the discharge decision support software is used are significantly more efficient than the Baseline but the effect is stronger in the Default treatment (p-values for comparisons between groups as reported by Kruskal-Wallis test are 0.087 or 0.006, respectively, when the Baseline is compared with the Information or Default treatment). Figure 7 shows cumulative distributions of experimental days in the Baseline and Default treatments.

Figure 7.

Cumulative Distributions of Observed Experimental Days

Average subject earnings per experimental day were $2.83, $3.15 and $3.62 in the Baseline, Information and Default treatments, as reported in the top panel of Table 1 (with standard deviations in braces).²⁴ Subjects’ daily earnings are highest in the Default treatment and lowest in the Baseline treatment. We ran one-way analysis of variance by ranks (Kruskal-Wallis tests) to ascertain whether daily earnings across different treatments come from the same distribution. The null hypothesis (of the same earnings) is rejected by this test (chi-squared statistic is 12.33, two-sided p-value is 0.002).

Table 1.

Comparisons of Daily Earnings across Treatments

	Baseline	Information	Default
Number of Subjects	43	42	40
Mean {st. dev.}	$2.83 {0.94}	$3.15 {0.94}	$3.62 {1.16}
Kruskal-Wallis Test
RankMean	49.22	63.64	77.14
Information	0.033	--
Default	0.0002***	0.046	--

Next, we ask which treatments are responsible for this rejection. The means of the ranks of daily earnings of three treatments are shown in the lower panel of Table 1. P-values for each pairwise comparison are shown in the bottom two rows for the Kruskal-Wallis test. Without adjustment for multiple comparisons, both Information and Default treatment data are significantly different from Baseline data. However, using (Bonferroni) adjusted p-values for multiple comparisons, we conclude that Baseline and Default data on earnings per day are significantly different at 1% whereas Baseline and Information data are not significantly different. Subjects in the Default treatment are earning more per experimental day than subjects in the Baseline treatment.²⁵

There might be some interest in other features of the experimental design and individuals’ characteristics that are correlated with higher daily earnings. So we ran linear regressions (with robust standard errors) of daily earnings as a dependent variable and Information and Default treatment dummies, a dummy for the 45-day constraint, and subject demographic variables as right-hand variables.

Daily earnings are lower for residents (by 67 cents, p=0.003) and female physicians (by 46 cents, p=0.014). As the interest in behavior across gender is the topic of a large number of studies, to shed some light on the cause of this difference in earnings we looked at the number of days our female and male subjects kept their patients in the hospital. We find that averages of total hospital length of stay (LOS) per patient are 6.896 (st. dev.=3.303) and 7.510 (st. dev=3.489) for male and female groups respectively. As readmissions across the two groups are similar²⁶ (0.110 (M) and 0.093(F)), implications of this behavior are: (i) in the experiment with no constraint on experimental days total earnings are expected to be similar across the two groups but daily earnings cannot be larger for females; (ii) in the experiment with 45-experimental days constraint both total (as well as daily) earnings are expected to be lower for females as female subjects are making fewer discharges than male subjects. In the 45-day constraint treatment cells we see statistically fewer discharges for females (29 discharges (male) and 25 discharges (female); p-value=0.001). In the treatment cells without the 45-day constraint we see fewer experimental days for making 30 discharges for males (46 days; 95% CI is [41, 51])) than for females (49 days; 95% CI is [44, 54]) but the two distributions are not statistically different (t=−0.727, p=0.470).

We also find that daily earnings are higher in both CDSS treatments but statistically significantly higher only in the Default treatment: estimates for the Default and Information treatments are, respectively, 0.660 (p=0.010) and 0.288 (p=0.176). We conclude that:

Result 2. Use of the CDSS, with making the CDSS’s recommendation the default option, increases: (a) decision time efficiency; and (b) daily earnings

One may wonder whether the increased decision time efficiency that we observe in the treatments has a negative effect on the quality of care. Given the design of our experiment, lower quality would be manifested in higher readmissions. Readmission rate is one of the factors that affect the ranking of a hospital and it is also one that has attracted increasing attention from Medicare, including fines for excess readmissions beginning in October 2012. In the following section we look closely at the interaction between different treatments and readmission rates in our experiment.

5.c Readmissions as an indicator of the quality of care

An earlier discharge is not an indicator of better discharge decision making if it decreases the quality of care. An indicator of the quality of care is the readmission rate since a premature discharge increases the likelihood of an unplanned but necessary readmission. Averages of readmission rates of all non-readmitted patients observed across treatments are 10.21%, 10.40% and 9.84%, respectively, for the Baseline, Information and Default treatments. For non-readmitted patients with high levels of targeted readmission probabilities (at least 17%) the mean readmission rates are 13.49%, 12.70% and 10.80% for the Baseline, Information and Default treatments.²⁷ We ran probit regressions, reported in Table 2, with binary dependent variable that takes value 1 if a patient (who was not previously readmitted) is readmitted. Covariates include subjects’ demographics, a risk aversion index,²⁸ patients’ targeted readmission probabilities, whether the patient was discharged before the first recommended discharge day (Understay = 1) or after that day (Overstay = 1), and the recommended length of stay until first discharge recommendation (Rec. LOS). Table 2 reports the estimated marginal effects (and p-values) with clustered standard errors at the subject level using data for the high risk patients and all patients.

Table 2.

Regressions for Non-readmitted Patients (errors are clustered at subject level)

		Readmissions (Probit Model)		Total LOS (Censored Regressions)
		High Risk Patients	All Patients	High Risk Patients	All Patients
Rec. LOS		0.005 (0.185)	−0.009*** (0.000)	0.504*** (0.000)	0.602*** (0.000)
Understay		0.000 (0.976)	0.025*** (0.000)
Overstay		−0.003 (0.660)	−0.004 (0.252)
Target Probability		4.480*** (0.000)	0.954*** (0.000)	15.593*** (0.009)	2.923*** (0.000)
Treatment Effects
Information		−0.019 (0.397)	0.001 (0.958)	−0.471 (0.165)	−0.444 (0.152)
Default		−0.045** (0.027)	−0.015 (0.190)	−1.109*** (0.006)	−0.883** (0.012)
45 Day Constraint		0.050** (0.031)	0.043*** (0.001)	−0.004 (0.990)	−0.302 (0.289)
Demographics
Female		−0.015 (0.439)	−0.004 (0.723)	0.803*** (0.006)	0.807*** (0.001)
Athlete		0.019 (0.396)	0.007 (0.563)	0.023 (0.950)	−0.083 (0.796)
Musical		−0.035* (0.066)	−0.021** (0.040)	0.577** (0.041)	0.513** (0.041)
Medical GPA		0.013 (0.314)	0.007 (0.508)	−0.127 (0.390)	−0.151 (0.305)
Undergrad GPA		0.004 (0.929)	−0.021 (0.431)	−0.319 (0.626)	−0.411 (0.486)
Risk Avers. Index		−0.017*** (0.002)	−0.003 (0.262)	0.083 (0.353)	0.103 (0.231)
Resident		−0.016 (0.563)	0.014 (0.446)	0.876** (0.015)	0.950*** (0.005)
constant				0.910 (0.751)	3.164 (0.151)
Nobs		1,063	3,197	1,063	3,197
(left-censored, uncensored, right-censored) Nobs				(222, 841, 0)	(393, 2804, 0)

Results reported in Table 2 show treatment effects that are consistent with the aggregated data figures reported above; the Default treatment induces a significant reduction in the readmissions of high-risk patients. Probabilities of readmission in the Default treatment (holding all other covariates at their means) are 4.5 percentage points lower than in the Baseline for the high-risk patients. We conclude that:

Result 3. Use of the CDSS with making the CDSS’s recommendation the default option reduces readmissions of high risk patients

Referring to the estimates of Understay and Overstay in Table 2, we find that for data from all patients the patient Understay variable has a positive effect on readmission while the estimate of the Overstay variable is insignificant. Neither Understay nor Overstay has a significant effect for high risk patients: the risk of readmission for such patients remains high but that risk was not significantly changed by the observed Overstay or Understay. We conclude that:

Result 4. Discharging a low or medium risk patient earlier than recommended by the CDSS significantly increases the likelihood of unplanned readmission while later-than-recommended discharge does not significantly decrease it

Readmissions are significantly higher in the design with a constraint (of 45 days) on the maximum number of experimental days. Subjects with musical training have lower readmissions for all patients and high risk patients while those with a higher risk aversion index have lower readmissions with high risk patients. The recommended hospital length of stay (Rec. LOS) also has a significantly negative effect on readmissions but the effect disappears when only the high risk patients are considered. We next turn our attention to hospital length of stay (LOS) across treatments.

5.d Hospital Length of Stay

The average figures for observed LOS prior to any readmissions are 7.766, 7.160 and 6.677 for the Baseline, Information and Default treatments.²⁹ The censored regression estimates (and robust standard errors in parentheses) of the hospital length of stay prior to any readmissions for high risk patients and all patients are reported in Table 2. LOS is significantly lower (by about one day) in the Default treatment and insignificantly lower in the Information treatment compared to the Baseline treatment. LOS is significantly higher for residents and female subjects compared, respectively, to fourth year medical students and male subjects.

Using results reported in Table 2, we conclude female subjects and resident physicians kept their patients in the hospital longer but their readmissions were not lower than others. The hospital length of stay of regular patients is lower in both the Information (by a half day, though not statistically significant) and Default (by almost one day) treatments while there are no higher readmission rates in these treatments. We conclude that:

Result 5. Use of the CDSS, with making the CDSS’s recommendation the default option, reduces hospital length of stay without increasing readmissions

5.e Effects of Capacity Constraint

The probit regressions in Table 2 show higher readmission rates in the presence of the 45-day constraint. The censored regression shows, however, that LOS was not significantly affected by the 45-day constraint. Taken together, these results indicate that the time constraint decreases quality of decision making.

This suggests the question of why subjects did not keep patients much longer in treatments without the 45 day constraint where readmission risk could be lowered through higher LOS without encountering a constraint on number of experiment days. Observation of subjects’ behavior during the experiment sessions suggests a time-cost explanation. Subjects in the experiment were resident physicians and fourth year medical students with very busy schedules. They behaved in the experiment as though they were marginally trading off time cost, from longer participation, with possibly increased earnings from lower readmissions. This is the type of decision making one would expect, a priori, on a hospital ward with time-constrained attending physicians.

Censored regression estimates reported in Table 2 reflect differences in numbers of patients discharged between the no-constraint and 45-day constraint treatments. We seek to isolate the effects on readmissions per patient discharged. For each subject we constructed a new variable, ReadmitRate, which is the number of patients readmitted divided by the total number of discharges. Figure 8 shows kernel densities of this variable for both designs, with and without the 45-day constraint. It can be easily seen that the readmission rates are higher for subjects who were making discharge decisions under the 45-day constraint. ¹ We find that the mean readmission rates are 7.8% and 11.9% respectively in the no-constraint and 45-day constraint treatments. The t-test rejects the null hypothesis in favor of the alternative hypothesis of higher readmissions in the presence of the 45-day constraint at 1% (p-value is .0001). Numbers of observations are 71 and 54 in the no-constraint and 45-day constraint treatments.³⁰

Figure 8.

Kernel Densities for Readmissions/Discharges

5.f Reduction in Length of Stay

According to their electronic medical records, the 30 patients whose de-identified charts are used in our experiment were kept in the hospital an average of 10 days. In our Baseline treatment, the average total length of stay was 7.77 days. This reduction may have resulted from the exclusive focus on the discharge decision created by the experimental environment. The average total LOS in the Default treatment was 6.68, which is 14% lower than the Baseline number of 7.77 days. This reduction in LOS did not produce higher readmission rates since the rates for the Baseline and Default treatments were, respectively, 10.2% and 9.8%.

5.g Further Exploration of CDSS Effects

The reported results suggest questions concerning the reasons why the CDSS leads to better discharge decisions in the experiment, especially in the Default treatment. Does this occur only because a high proportion of subjects are reluctant to overrule CDSS recommendations, most especially when they have to enter reasons for doing so? Or does the Default treatment produce some of its effectiveness by prompting subjects to pay closer attention to the seven charts of detailed information presented by the CDSS even in the absence of an explicit discharge recommendation?

Some insight into these questions is provided by analyzing only that subset of the data in which the CDSS does not provide a recommendation to discharge or not to discharge the patient; these are the experimental days in which the CDSS’s “recommendation” is Physician Judgment. Subjects’ earnings during only the Physician Judgment experimental days are $35.82, $36.31 and $46.13 for the Baseline, Information and Default treatments. Compared with the Baseline, earnings are higher in the Default (D=0.298, two-sided p=0.051) but not in the Information treatment (D=0.079, p=0.999). Readmission rates for patients discharged during the Physician Judgment experimental days do not significantly differ across treatments. Average LOS for patients discharged during Physician Judgment experimental days are 7.70, 7.51, and 6.96 in the Baseline, Information and Default treatments. Censored regression estimates (with the same list of regressors as the ones reported in Table 2) are −0.473 (p=0.003) for the Default treatment and −0.056 (p=0.703) for the Information treatment. These results suggest that the Default treatment implementation of the CDSS elicits better uptake of the new information provided by the CDSS even in those instances when it does not report a recommended decision.

6. Summary and Concluding Remarks

The hospital discharge decision plays a central role in the increasingly important interplay between the quality of healthcare delivery and medical costs. Premature discharge can lead to unplanned readmission with higher costs and questionable quality of care. Needlessly delayed discharge wastes increasingly expensive healthcare resources.

Our research program has analyzed patient data to identify risk factors for unplanned hospital readmissions (Kassin, et al. 2012), elicited physicians’ stated criteria for discharge decisions (Leeds, et al 2013), estimated predictors of physicians’ actual discharge decisions (Leeds, et al. 2015), and estimated clinical and demographic patient variables that predict successful vs. unsuccessful discharges (Leeds, et al. 2015). Inconsistencies between stated criteria, statistically-explanatory actual criteria, and predictors of successful discharge suggest that discharge decision making might be improved by application of large-sample, evidence-based discharge criteria at the point of care where the discharge decision is made. Our approach to providing a tool for improving discharge decision making is to develop and test a Clinical Decision Support System (CDSS) for hospital discharges.

The laboratory experiment reported herein explores whether the CDSS is effective in eliciting uptake of the information derived from probit estimation of determinants of unplanned readmission (i.e. unsuccessful discharge) probabilities with electronic medical records data. The experiment produces data for treatment cells in a 2 by 3 design that crosses presence or absence of a 45 experimental day constraint with Baseline, Information, and Default treatments. The Baseline treatment presents subjects only with the kind of information that they receive from currently-used electronic medical records (EMR); indeed, the subject screens used in the Baseline treatment are facsimiles of EMR screens. The Information and Default treatments use these same EMR-facsimile screens plus new screens that report information provided by the CDSS. The information screens show point estimates of marginal readmission probabilities and their 80 percent error bounds for experimental days prior to and including the relevant experimental decision day. The information screens display six charts of dynamically-selected clinical variables that the probit regression model indicates have the highest marginal effects for predicting outcomes from discharge of that patient on that day during their hospital stay. Finally, the information screens show one of three recommendations (discharge, physician judgment, or do not discharge) that are based on the relationship between Medicare’s target readmission probability for patients with the relevant diagnosis code and the readmission probability point estimate and 80 percent confidence interval for the patient whose data are under consideration. The Default treatment differs from the Information treatment by changing the default option for patient discharge. In the Information treatment, the default option is that the patient remains in the hospital unless the responsible decision maker initiates an affirmative discharge order. In contrast, in the Default treatment the patient is discharged or not discharged according to the recommendation of the decision support software unless the decision maker overrides that recommendation and provides reasons for rejecting it.

Data from our experiment provide support for effectiveness of the CDSS, with using the CDSS recommendation as the default option, in eliciting uptake of the information in the estimated probit model. This is demonstrated for the two central performance measures for hospital discharge decision making, lower readmission rate and shorter length of stay. The data also provide support for effectiveness of the CDSS in promoting time efficiency in making discharge decisions and for the traditional experimental economics performance measure of subject earnings in the experiment. The CDSS is more effective in the Default treatment than in the Information treatment; in other words, combining the information provided by the CDSS with making the software’s recommendation the default option is more effective in promoting better discharge decisions than simply providing the information. Superior outcomes with the Default treatment occur even for the subset of experimental days in which the CDSS does not offer a recommended decision; hence it is not solely subjects’ conformance to recommendations that accounts for the treatment effect. Subjects perform generally better in the absence than presence of a (“45 experimental day”) constraint that puts them under time pressure. Subjects who report they place relatively high value on information provided by the CDSS make better discharge decisions.

Highlights.

• We conduct an experiment to test uptake of our clinical decision support system (CDSS) for hospital discharge decision making.

• The CDSS provides dynamically-updated information on the likelihood of readmission if the patient is discharged on any day while in the hospital.

• We find that the CDSS with opt out default option supports uptake and improved discharge decision making.

• We also investigate the cross-effects of time constraint and the uptake of the CDSS.

• We use a specialized subject pool of resident physicians and fourth year medical students.

Appendix 1: EMR Facsimile Patient Charts

Figure A.1. Inpatient Summary

Figure A.2. Laboratory Data

Figure A.3. Orders

Figure A.4. Vital Signs