PROSNET: INTEGRATING HOMOLOGY WITH MOLECULAR NETWORKS FOR PROTEIN FUNCTION PREDICTION

Abstract

Automated annotation of protein function has become a critical task in the post-genomic era. Network-based approaches and homology-based approaches have been widely used and recently tested in large-scale community-wide assessment experiments. It is natural to integrate network data with homology information to further improve the predictive performance. However, integrating these two heterogeneous, high-dimensional and noisy datasets is non-trivial. In this work, we introduce a novel protein function prediction algorithm ProSNet. An integrated heterogeneous network is first built to include molecular networks of multiple species and link together homologous proteins across multiple species. Based on this integrated network, a dimensionality reduction algorithm is introduced to obtain compact low-dimensional vectors to encode proteins in the network. Finally, we develop machine learning classification algorithms that take the vectors as input and make predictions by transferring annotations both within each species and across different species. Extensive experiments on five major species demonstrate that our integration of homology with molecular networks substantially improves the predictive performance over existing approaches.

1. Introduction

Comprehensively annotating protein function is crucial in illustrating activities of millions of proteins at molecular level, which can further advance basic biological research and biomedical sciences.¹ Although massive annotations have been curated, such as popular Gene Ontology (GO) annotations,² current experimental approaches are infeasible to fully exploring protein function annotations. As a result, computational approaches have become a more accessible way to annotate protein function^3,4 and help biologists prioritize their experiments.

Computational prediction of protein function has been extensively studied in the context of molecular evolution. Homologous proteins have most likely evolved from a common ancestor. They often carry out similar protein functions, because functions are generally conserved during molecular evolution. Consequently, computational approaches can predict the function of query proteins by transferring those of their annotated homologs. In addition to automatic annotations based on orthology or domain information or pre-existing cross-references and keywords,⁵ a variety of machine learning algorithms^6–12 have been proposed to extract annotations based on sequence similarity-detection tools such as BLAST, PSI-BLAST,¹³ and phylogenetic analysis.^14,15 Despite the success of homology-based approaches, their major constraint arises from a lack of annotated sequences.¹⁶ In fact, among over 65 million protein sequences in publicly accessible databases,¹⁷ only 2 million of them are manually curated.¹⁸ Consequently, the predictive power of homology-based methods has been limited due to the scarcity of annotations. Furthermore, reliable homology relationships are sparse between distantly related species, thus posing computational and statistical challenges when making faithful predictions.

Fortunately, the rapidly growing interactome data from high-throughput experimental techniques allows us to extract patterns from neighbors in molecular networks^19–21 in addition to homologous proteins. This idea is supported by the established “guilt-by-association” principle, which states that proteins that are associated or interacting in the network are more likely to be functionally related.²² Recently, this “guilt-by-association” principle has become the foundation of many network-based function prediction algorithms.^23–30 Among them, Gen-eMANIA³¹ and clusDCA³² are state-of-the-art network-based function prediction approaches. In addition to incorporating network topology, clusDCA also leverages the similarity between GO labels and obtains substantial improvement on sparsely annotated functions. GeneMA-NIA uses a label propagation algorithm on an integrated network specifically constructed for each functional label, and is currently available as a state-of-the-art web interface for gene function prediction for many organisms.

Intuitively, integrating homology data with molecular networks can synergistically improve function prediction results. On one hand, it enables us to transfer annotations from functionally well-characterized neighbors in the molecular network as well as from homologous proteins with conserved similar functions. On the other hand, homology data can further mitigate the incomplete and noisy nature of molecular networks through interologs,³³ which states that a conserved interaction occurs between a pair of proteins that have interacting homologs in another organism.³⁴

Nevertheless, integrating homology data with molecular networks is both computationally and statistically challenging. Since they are heterogeneous data sources, it is likely sub-optimal to integrate them in an additive way which simply averages the prediction results of either of these two data sources. Moreover, we also need an efficient algorithm that scales to hundreds of thousands of proteins from multiple species. One way to integrate these two heterogeneous data sources seamlessly is to construct a multiple species heterogeneous network in which both nodes and edges are associated with different types. With this network, we can predict functions for query proteins based on annotations extracted from both their homologs and their neighbors in molecular networks. Furthermore, information can also be transferred between two proteins that are neither homologs nor neighbors in molecular networks. Notably, the only previous attempt to integrate these two heterogeneous data sources is using multi-view learning.³⁵ However, it does not scale to multiple species. In addition, they formulated protein function prediction as a structured-output hierarchical classification problem whose performance for sparsely annotated functional labels is far from satisfactory.³²

In this work, we introduce ProSNet, a novel Protein function prediction algorithm which efficiently integrates Sequence data with molecular Network data across multiple species. Specifically, an integrated heterogeneous network is first constructed to include all molecular networks of multiple species, in which homologous proteins across multiple species are also linked together. Based on this integrated network, a novel dimensionality reduction algorithm is applied to obtain compact low-dimensional vectors for proteins in the network. Proteins that are topologically close in the molecular networks and/or have similar sequences are co-localized in this low-dimensional space based on their vectors. These low-dimensional vectors are then used as input features to two classifiers which utilize annotations from molecular networks and homologous proteins, respectively. In addition, ProSNet is inherently parallelized, which further promises scalability. When compared to the state-of-the-art methods that only use homology data or molecular networks, ProSNet substantially improves the function prediction performance on five major species.

2. Methods

As an overview, ProSNet first constructs a heterogeneous biological network by integrating homology data with molecular network data of multiple species. It then performs a novel dimensionality reduction algorithm on this heterogeneous network to optimize a low-dimensional vector representation for each protein. The vectors of two proteins will be co-localized in the low-dimensional space if the proteins are close to each other in the heterogeneous biological network. A key computational contribution is that ProSNet obtains low-dimensional vectors through a fast online learning algorithm instead of the batch learning algorithm used by previous work.^23,32 In each iteration, ProSNet samples a path from the heterogeneous network and optimizes low-dimensional vectors based on this path instead of all pairs of nodes. Therefore, it can easily scale to large networks containing hundreds of thousands or even millions of edges and nodes. After finding low-dimensional vector representation for each node, ProSNet calculates an intra-species affinity score and an inter-species affinity score by transfering annotations within the same species and across different species, respectively. Finally, ProSNet predicts functions for a query protein by averaging these scores and picking the function(s) with the highest score(s).

2.1. Heterogeneous biological network

Definition 1

Heterogeneous Biological Networks (HBNs) are biological networks where both nodes and edges are associated with different types. In an HBN G = (V, E, R), V is the set of typed nodes (i.e., each node has its own type), R is the set of edge types in the network, and E is the set of typed edges. An edge e ∈ E in a heterogeneous biological network is an ordered triplet e = 〈u, υ, r〉, where u ∈ V and υ ∈ V are two typed nodes associated with this edge and r ∈ R is the edge type.

Definition 2

In an HBN G = (V, E, R), a heterogeneous path is a sequence of compatible edge types ℳ = 〈r₁, r₂, …, r_L〉, ∀i, r_i ∈ R. The outgoing node type of r_i should match the incoming node type of r_i+1. Any path 𝒫_{e1⇝ eL} = 〈e₁, e₂, …, e_L〉 connecting node u₁ and u_L+1 is a heterogeneous path instance following ℳ, iff ∀i, e_i is of type r_i.

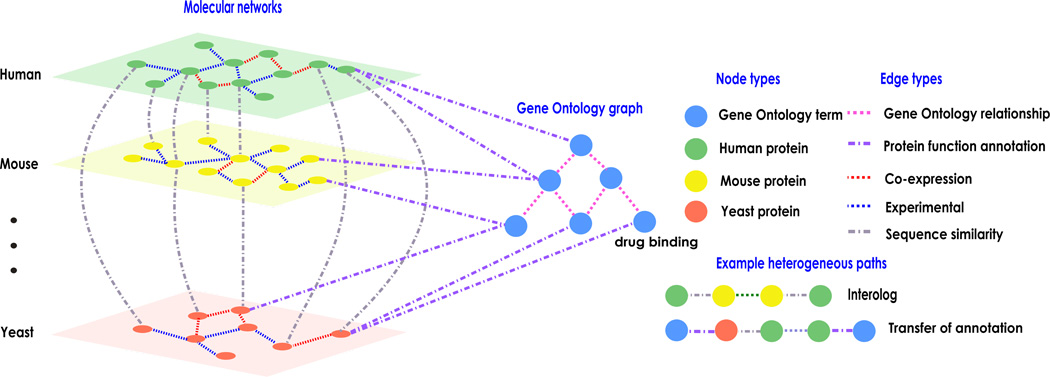
In particular, any edge type r is a length-1 heterogeneous path ℳ = 〈r〉. We show a toy example of an HBN under our function prediction framework in Fig. 1.

Fig. 1.

An example of the heterogeneous biological network under our function prediction framework. The node set V consists of four types, {“Human protein”, “Yeast protein”, “Mouse protein”, and “Gene Ontology term”}. The edge type set R consists of five types, {“Sequence similarity”, “Protein function annotation”,“Gene Ontology relationship”,“Experimental”, and “Co-expression”}. This HBN explicitly captures interolog and transfer of annotation through heterogeneous paths across different species.

2.2. Low-dimensional vector learning in the heterogeneous biological network

ProSNet finds the low-dimensional vector for each node through first sampling a large number of heterogeneous path instances according to the HBN. It then finds the optimal low-dimensional vector so that nodes that appear together in many instances turn to have similar vector representations. We first define the conditional probability of node υ connected to node u by a heterogeneous path ℳ as:

$$\mathit{\text{Pr}}(\upsilon |u,ℳ)=\frac{\text{exp}(f(u,\upsilon ,ℳ))}{{\sum }_{\upsilon \prime \in V}\text{ exp}(f(u,\upsilon \prime ,ℳ))},$$ (1)

where f is a scoring function modeling the relevance between u and υ conditioned on ℳ. Inspired from the previous work,³⁶ we define the following scoring function:

$$f(u,\upsilon ,ℳ)={\mu }_{ℳ}+{{\mathbf{p}}_{ℳ}}^T{\mathbf{x}}_{\mathbf{u}}+{{\mathbf{q}}_{ℳ}}^T{\mathbf{x}}_{\mathbf{v}}+{{\mathbf{x}}_{\mathbf{u}}}^T{\mathbf{x}}_{\mathbf{v}}.$$ (2)

Here, μ_ℳ ∈ ℝ is the global bias of the heterogeneous path ℳ. p_ℳ and q_ℳ ∈ ℝ^d are local bias d dimensional vectors of the heterogeneous path ℳ. x_u and x_v ∈ ℝ^d are low-dimensional vectors for nodes u and υ respectively. Our framework models different heterogeneous paths differently by using p_ℳ and q_ℳ to weight different dimensions of node vectors according to the heterogeneous path ℳ.

For a heterogeneous path instance 𝒫_{e1⇝ eL} = 〈e₁ = 〈u₁, υ₁, r₁〉, …, e_L = 〈u_L, υ_L, r_L〉〉 following ℳ= 〈r₁, r₂, …, r_L〉, we propose the following approximation.

$$\mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|ℳ)\propto C{(u_1,1|ℳ)}^{\gamma }\times \mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|u_1,ℳ),$$ (3)

where C(u, i|ℳ) represents the count of path instances following ℳ with the i^th node being u. C(u, i|ℳ) can be efficiently computed through a dynamic programming algorithm. γ is a widely used parameter to control the effect of overly-popular nodes, which is set to 0.75 in previous work.³⁷ We assume that each node on the path only depends on its previous node. Then we have

$$\mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|u_1,ℳ)=\prod _{i=1}^L\mathit{\text{Pr}}({\upsilon }_i|u_i,r_i).$$ (4)

Given the conditional distribution defined in Eq. (1) and (3), the maximum likelihood training is tractable but expensive because computing the gradient of the log-likelihood takes time linear in the number of nodes. Following the noise-contrastive estimation (NCE),³⁸ we reduce the problem of density estimation to a binary classification, discriminating between samples from path instances following the heterogeneous path and samples from a known noise distribution. In particular, we assume these samples come from the following mixture.

$$\frac{1}{\theta +1}{\mathit{\text{Pr}}}^{+}({𝒫}_{e_1⇝e_L}|ℳ)+\frac{\theta }{\theta +1}{\mathit{\text{Pr}}}^{-}(P_{e_1⇝e_L}|ℳ),$$ (5)

where θ is the negative sampling weight and Pr⁺(𝒫_{e1⇝ eL}|ℳ) denotes the distribution of path instances in the HBN following the heterogeneous path ℳ. Pr⁻(𝒫_{e1⇝ eL}|ℳ) is a noise distribution, and for simplicity we set

$${\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ)\propto \prod _{i=1}^{L+1}C{(u_i,i|ℳ)}^{\gamma }.$$ (6)

We further assume noise samples are θ times more frequent than positive path instance samples. The posterior probability that a given sample D came from positive path instance samples following the given heterogeneous path is

$$\mathit{\text{Pr}}(D=1|{𝒫}_{e_1⇝e_L},ℳ)=\frac{{\mathit{\text{Pr}}}^{+}({𝒫}_{e_1⇝e_L}|ℳ)}{{\mathit{\text{Pr}}}^{+}({𝒫}_{e_1⇝e_L}|ℳ)+\theta ·{\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ)},$$ (7)

where D ∈ {0, 1} is the label of the binary classification. Since we would like to fit Pr(𝒫_{e1⇝ eL}|ℳ) to Pr⁺(𝒫_{e1⇝ eL}|ℳ), we simply maximize the following expectation.

$${ℒ}_{ℳ}={𝔼}_{{\mathit{\text{Pr}}}^{+}}\left[\text{log}\frac{\mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|ℳ)}{\mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|ℳ)+\theta ·{\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ)}\right]+\theta ·{𝔼}_{{\mathit{\text{Pr}}}^{-}}\left[\text{log}\frac{\theta ·{\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ)}{\mathit{\text{Pr}}({𝒫}_{e_1⇝e_L}|ℳ)+\theta ·{\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ)}\right].$$ (8)

The loss function can be derived as

$${ℒ}_{ℳ}\approx \sum _{{𝒫}_{e_1⇝e_L}\text{ following }ℳ}\text{log }\sigma (\sum _{i=1}^{L}f(u_i,{\upsilon }_i,r_i))+{\sum }_{j=1}^{\theta }{𝔼}_{{𝒫}_{e_1⇝e_L}^j~{\mathit{\text{Pr}}}^{-}|u_1,ℳ}\left[\text{log }\right(1-\sigma ({\sum }_{i=1}^{L}f(u_i^j,{\upsilon }_i^j,r_i))\left)\right],$$ (9)

where σ(·) is the sigmoid function. Note that when deriving the above equation we used exp(f(u, υ, ℳ)) in place of Pr(υ|u, ℳ), ignoring the normalization term in Eq. (1). We can do this because the NCE objective encourages the model to be approximately normalized and recovers a perfectly normalized model if the model class contains the data distribution.³⁸ Following the idea of negative sampling,³⁷ we also replaced ${\sum }_{i=1}^{L}f(u_i,{\upsilon }_i,r_i)-\text{log }(\theta ·{\mathit{\text{Pr}}}^{-}({𝒫}_{e_1⇝e_L}|ℳ))$ with ${\sum }_{i=1}^{L}f(u_i,{\upsilon }_i,r_i)$ for ease of computation. We optimize parameters x_u, x_v, p_r, q_r, and μ_r based on Eq. (9).

2.3. Runtime improvements through online learning

Like diffusion component analysis,²³ the number of pairs of nodes 〈u, υ〉 that are connected by some path instances following at least one of the paths is O(|V|²) in the worst case. This is too large for storage or processing when |V| is at the order of hundreds of thousands. Therefore, sampling a subset of path instances according to their distribution is the most feasible choice when optimizing, instead of going through every path instance per iteration. Thus, our method is still very efficient for networks containing large numbers of edges. Based on Eq. (3), we can sample a path instance by sampling the nodes on the heterogeneous path one by one. Once a path instance has been sampled, we use gradient descent to update the parameters x_u, x_v, p_r, q_r, and μ_r based on Eq. (9). As a result, our sampling-based framework becomes a stochastic gradient descent framework. The derivations of these gradients are trivial and thus are omitted. Moreover, since stochastic gradient descent can generally be parallelized without locks, we can further optimize via multi-threading. Decomposing a heterogeneous network with more than sixty thousand nodes and ten million edges into a 500-dimensional vector space takes less than 30 minutes on a 12-core 3.07GZ Intel Xeon CPU through this online learning framework.

2.4. Function prediction

After using the above framework to find the low-dimensional vector for each protein in the HBN, ProSNet transfers annotations both within the same species and across different species to predict for a query protein.

To transfer annotations within the same species, ProSNet first uses diffusion component analysis²³ on the Gene Ontology graph² to find low-dimensional vector y_i for each functional label i. It then uses a transformation matrix W to project proteins from the protein vector space to the function vector space, which allows us to match proteins to functions based on geometric proximity. Let ${\mathbf{y}}_{\mathbf{i}}^{\prime }$ be the projection of the protein vector x_i:

$${\mathbf{y}}_{\mathbf{i}}^{\prime }={\mathbf{x}}_{\mathbf{i}}\mathbf{W}.$$ (10)

We define the intra-species affinity score z_ij between gene i and function j to be used for function prediction as:

$$z_{ij}={\mathbf{x}}_{\mathbf{i}}\mathbf{W}{\mathbf{y}}_{\mathbf{j}}^{\mathbf{T}}.$$ (11)

A larger z_ij indicates that gene i is more likely to be annotated with function j. We follow clusDCA³² to find the optimal W.

Since proteins from different species are located in the same low-dimensional vector space, ProSNet is able to use the annotations across different species as well. Instead of using the annotations from all the other proteins, ProSNet only considers the k most similar proteins based on the cosine similarity between their low-dimensional vectors. It then calculates the inter-species affinity score s_ij between gene i and function j as:

$$s_{ij}=\sum _{g_{\in }{B}_i}\text{cos}({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{g}})·\mathrm{𝟙}(g\in T_j),$$ (12)

where B_i is the set of k most similar proteins of i and T_j is the set of genes that are annotated to function j in the training data.

After obtaining the intra-species affinity score z and inter-species affinity score s, ProSNet normalizes them by z-scores. It predicts functions for a query protein by averaging these two normalized affinity scores and picking the function(s) with the highest score(s)

3. Experimental results

3.1. Construction of heterogeneous biological network for function prediction

To construct the heterogeneous biological network (HBN), we obtained six molecular networks for each of five species, including human (Homo sapiens), mouse (Mus musculus), yeast (Saccharomyces cerevisiae), fruit fly (Drosophila melanogaster), and worm (Caenorhabditis elegans) from the STRING database v10.²⁰ These six molecular networks are built from heterogeneous data sources, including high-throughput interaction assays, curated protein-protein interaction databases, and conserved co-expression data. We excluded text mining-based networks to avoid potential confounding. Each edge in the molecular networks has been associated with a weight between 0 and 1 representing the confidence of interaction. Next, we obtained protein-function annotations and the ontology of functional labels from the GO Consortium.² We only used annotations that have experimental evidence codes including EXP, IDA, IPI, IMP, IGI, and IEP. As a result, annotations that are based on an in silico analysis of the gene sequence and/or other data are removed to avoid potential leakage of labels. We built a directed acyclic graph of GO labels from all three categories [biological process (BP), molecular function (MF) and cellular component (CC)] based on “is a” and “part of” relationships. This graph has 13,708 functions and 19,206 edges. We set all edge weights of protein-function links to 1 and all edge weights between GO labels to 1. Finally, we extracted amino acid sequences of all proteins in our five-species network from the STRING database and the Universal Protein Resource (Uniprot).¹⁷ To construct homology edges, we performed all-vs-all BLAST¹³ and excluded edges with E-value larger than 1e-8. We then used the negative logarithm of the E-values as the edge weights and rescaled them into [0, 1]. We showed the statistics of our HBN in Tab. 1. For simplicity, all edges are undirected. Note that we excluded the protein-function annotation edges that are in the hold-out test set in the following experiments for rigorous comparisons. Our heterogeneous network is similar to the example network in Fig. 1, except that our network has five species and six different types of molecular networks.

Table 1.

Statistics of our heterogeneous network

	Human	Mouse	Yeast	Fruit fly	Worm
#proteins	16,544	16,649	6,307	11,261	13,469
#co-expression edges	1,319,562	1,406,572	628,014	2,466,234	2,774,840
#co-occurrence edges	28,334	29,472	5,328	17,962	14,678
#database edges	275,860	347,406	66,972	116,748	69,948
#experimental edges	492,548	672,326	439,956	380,046	298,684
#fusion edges	2,678	3,994	2,722	4,026	4,336
#neighborhood edges	78,440	77,962	91,220	69,934	49,890
#human homology edges	0	525,221	55,884	202,993	159,481
#mouse homology edges	525,221	0	52,916	188,729	151,408
#yeast homology edges	55,884	52,916	0	26,950	28,269
#fruit fly homology edges	202,993	188,729	26,950	0	75,831
#worm homology edges	159,481	151,408	28,269	75,831	0
#annotations	77,950	66,238	28,668	32,259	21,655

3.2. Experimental setting

We used 3-fold cross-validation to evaluate the methods of interest. For a given species for evaluation, we randomly split proteins of the species into three equal-size subsets. Each time, the GO annotations of proteins in one subset were held out for testing, and the annotations of the other two subsets were used for intra-species classification training. For inter-species training, we used all experimental GO annotations from the other four species, ensuring no leakage of label information in the training data. To evaluate the predictive performance, we measured the extent to which the predicted ranked list was consistent with the ground truth ranked list by computing the receiver operating characteristic curve (AUROC). We used the macro-AUROC as the evaluation metric following previous work.^31,32 The macro-AUROC is calculated by separately averaging the area under the curves for each label. We set the vector dimension d = 500, the number of nearest neighbors k = 2000, and the negative sampling weight θ = 5 in our experiment. We observed that the performance of our algorithm is quite stable with different d, k, and θ values. We included all edge types in the predefined heterogeneous path set. Additionally, we added “transfer of annotation” to the predefined heterogeneous path set (Fig. 1).

To show the improvement from integrating homology data with molecular networks of multiple species, we compared our method with three existing state-of-the-art function prediction methods: GeneMANIA,³¹ clusDCA,³² and BLAST.¹³ GeneMANIA and clusDCA integrate protein molecular networks within a given species. Neither of them is able to integrate information across different species. We used the latest released code and the suggested parameter settings for these two methods. BLAST uses bit score to rank annotations from significant hits by BLAST. We used the same datasets (i.e. annotations, proteins, and networks) and the same evaluation scheme for every method we tested.

3.3. Molecular network data and homology data are complementary in function prediction

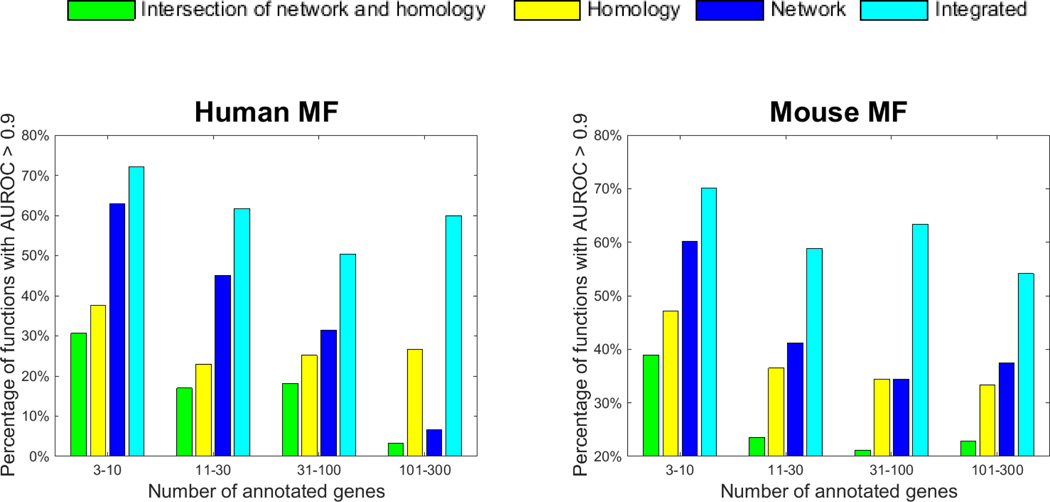
We first studied whether information extracted from homology and from molecular networks are complementary. We compared the predictive performance of three different data sources: 1) molecular networks, 2) homology, 3) both molecular network and homology (integrated). We used clusDCA to predict function annotations based on molecular networks. We used BLAST to make predictions of function annotation based on homology. We summarized how many functions can be accurately annotated (AUROC>0.9) by each data source (Fig. 2). We notice that there are many functions that can only be accurately predicted by homology or network. For example, on mouse MF with 3–10 labels, 9% of functions (difference between yellow bar and green bar) can be accurately predicted only by homology but not by network. In the same category, another 21% of functions (difference between blue bar and green bar) can be accurately predicted only by network but not by homology. This suggests that these two data sources are complementary, and integrating them can synergistically improve the function prediction results. To this end, we integrated homology and network data by simply taking average of the z-scores of predicted annotations from these two data sources. We found that the predictive performance using both molecular network data and homology data is significantly better than only using one in all categories on both human and mouse. For example, on human MF with 101–300 labels, using both network data and homology data accurately annotates 60% of functions, which is much higher than 4% of only using network data and 26% of only using homology data. Notably, we only use the homology data from five species here. When including homology data from more species in the future, homology data may further boost the function prediction performance.

Fig. 2.

Comparison of using different data sources for function prediction

3.4. ProSNet substantially improves function prediction performance

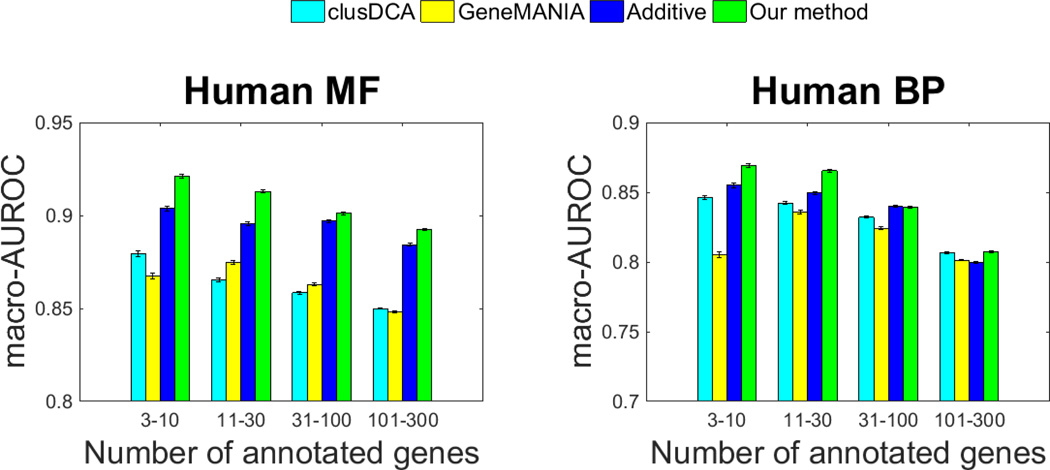
We performed large-scale function prediction on all five species to compare our method to other state-of-the-art function prediction approaches. The results are summarized in Fig. 3 and Supplementary Fig. 1 (Supplementary Data). It is clear that our approach achieved the best overall results in all five species. When comparing with homology-based methods, we found that ProSNet significantly outperforms BLAST on both sparsely annotated and densely annotated labels (data not shown). For example, ProSNet achieves 0.8690 AUROC on human BP labels with 3–10 annotations, which is much higher than the 0.6326 AUROC by BLAST.

Fig. 3.

Comparison of different methods

Furthermore, we compared ProSNet to existing state-of-the-art network-based methods, including clusDCA and GeneMANIA, which only integrate molecular networks of single species. We found that the overall performance of our approach is substantially higher than that of both of these methods. For instance, in human, our method achieved 0.9211 AUROC on MF labels with 3–10 annotations, which is much higher than 0.8673 by GeneMANIA and 0.8794 by clusDCA. In mouse, our method achieved 0.8523 AUROC on BP labels with 31–100 annotations, which is much higher than 0.8078 AUROC by GeneMANIA and 0.8299 AUROC by clusDCA.

To evaluate the integration of homology and network data, we developed a baseline approach that simply merges predictions made from homology data and sequence data, separately. This additive approach takes the average z-scores of the annotation score of clusDCA and BLAST to rank functional labels for each protein. We note that this baseline approach outperformes both GeneMANIA and clusDCA, indicating that integrating homology with molecular networks can substantially improve the function prediction performance. We then compared this additive approach to our method. We found that ProSNet also outperforms the additive approach. For instance, in human, our method achieves 0.9129 AUROC on MF labels with 11–30 labels, which is higher than 0.8956 AUROC by the additive approach. The improvement of our method in comparison to the additive approach demonstrates a better data integration by constructing a heterogeneous network and finding low-dimensional vector representations for each node in this network.

The improvement of ProSNet over existing network-based approaches is more pronounced on sparsely annotated functions. Since very few proteins are annotated to these functions, it is very easy to overfit any classification algorithm if we only use the data from a single species. With the integrated heterogeneous biological network, ProSNet successfully transfers annotations from other species to have a more robust and improved predictive performance on sparsely annotated functions.

4. Conclusion

In this paper, we have presented ProSNet, a novel protein function prediction method which seamlessly integrates homology data and molecular network data. ProSNet constructs a heterogeneous network to include molecular networks from all species and homology links across different species. We have designed an efficient dimensionality reduction approach which only takes 30 minutes to decompose a heterogeneous network containing hundreds of thousands of proteins. We have demonstrated that ProSNet outperforms state-of-the-art network-based approaches and homology-based approaches on five major species. Furthermore, ProSNet has achieved improved performance over an additive integration approach that simply adds predictions from network and homology data. This result supports our hypothesis that constructing a heterogeneous network and then finding low-dimensional vector representations for each node in this network is a better data integration approach. In the future, we plan to study how to annotate proteins of species that have very sparse molecular networks or even no molecular network. In addition, we plan to pursue further improvement by integrating networks and homology data from a complete spectrum of reference species.