Efficient computation of the joint sample frequency spectra for multiple populations

Abstract

A wide range of studies in population genetics have employed the sample frequency spectrum (SFS), a summary statistic which describes the distribution of mutant alleles at a polymorphic site in a sample of DNA sequences and provides a highly efficient dimensional reduction of large-scale population genomic variation data. Recently, there has been much interest in analyzing the joint SFS data from multiple populations to infer parameters of complex demographic histories, including variable population sizes, population split times, migration rates, admixture proportions, and so on. SFS-based inference methods require accurate computation of the expected SFS under a given demographic model. Although much methodological progress has been made, existing methods suffer from numerical instability and high computational complexity when multiple populations are involved and the sample size is large. In this paper, we present new analytic formulas and algorithms that enable accurate, efficient computation of the expected joint SFS for thousands of individuals sampled from hundreds of populations related by a complex demographic model with arbitrary population size histories (including piecewise-exponential growth). Our results are implemented in a new software package called momi (MOran Models for Inference). Through an empirical study we demonstrate our improvements to numerical stability and computational complexity.

1 Introduction

Massive increases in the availability of DNA sequence data are creating exciting new opportunities for discovery in evolutionary genetics. With those opportunities come new challenges, as algorithms and statistical models originally designed to analyze small amounts of DNA from a limited number of individuals are now called on to study thousands to tens of thousands of individuals at a time. As in other branches of statistics, the arrival of “big data” has led to a new focus on scalability, accuracy, speed, and related computational issues within statistical genetics.

In this paper, we tackle this challenge by presenting a new method for computing the expected joint sample frequency spectrum (SFS), a summary statistic on DNA sequences which lies at the core of a large number of empirical investigations and inference procedures in population genetics (Bhaskar et al., 2015; Coventry et al., 2010; Excoffier et al., 2013; Gazave et al., 2014; Gravel et al., 2011; Griffths and Tavaré, 1998; Gutenkunst et al., 2009; Jenkins et al., 2014; Nelson et al., 2012; Nielsen, 2000; Wakeley and Hey, 1997). As we discuss in greater technical detail below, the joint SFS is of interest because it maps complex demographic models involving population size changes, population splits, migration, and admixture to a low-dimensional vector. This dimensionality reduction is useful for performing inference using sampled DNA sequences. Inferring population demographic histories is not only innately interesting, for example in dating events such as the out-of-Africa migration of modern humans (Gutenkunst et al., 2009; Schaffner et al., 2005), but is also important for biological applications, such as distinguishing between the effects of natural selection and demography (Beaumont and Nichols, 1996; Boyko et al., 2008).

We argue both theoretically and by simulation that existing methods in population genetics cannot scale to the problem sizes encountered in modern genetic analyses. Our primary contribution is a novel algorithm (and accompanying open-source software package) which is several orders of magnitude faster (in the number of sampled individuals n) than existing approaches. Moreover, by careful algorithmic design we are able to mitigate certain numerical issues (e.g., underow and catastrophic cancellation) that often arise when applying these models to data. The combined effect of these innovations is to permit the analysis of much larger data sets, which will lead to improved inference in population genetics.

The rest of the paper is organized as follows: In Section 2, we describe the problem more precisely, survey related work, and summarize our main results. Section 3 presents the theoretical results that lead to the improved algorithm described in Section 4. Runtime and numerical accuracy results are discussed in Section 5. Mathematical proofs of our theoretical results are deferred to Section 6.

Software availability

The algorithms presented in this paper are implemented in a new software package called momi (MOran Models for Inference), which is freely available at https://github.com/popgenmethods/momi.

2 Background and summary

In this section, we briefly review some terminology and concepts from population genetics that are relevant to our problem. We then discuss existing work and summarize our main results.

2.1 Motivation

To simplify the exposition, suppose that the genomes of n individuals have been randomly sampled from a single population. (We will shortly consider the general case where genomes are sampled from multiple related populations, which is substantially more challenging to analyze and is the main focus of this paper.) The positions in the genome where at least one, but fewer than all, of the sampled individuals bears a mutant allele (or genetic type) are called segregating sites. Assume that all such sites are dimorphic, meaning that we can label each sampled individual at each segregating site as either “ancestral” or “derived”. The sample frequency spectrum is defined to be the count vector $\hat{\mathit{\xi }}\in {\mathbb{Z}}_{+}^{n-1}$, of which the ith entry ξ̂_i records the number of segregating sites that have exactly i copies of the mutant allele in the sample. (Thus, ‖ξ̂‖₁ equals the total number of segregating sites found in the sampled genomes.)

The SFS is of interest because its distribution encodes past demographic events experienced by the population(s) from which the samples were obtained. In particular, suppose we are analyzing a single population and let α⁻¹(t) : ℝ_≥0 → ℝ_>0 be a strictly positive function such that α⁻¹(t) equals the effective size (Ewens, 2004) of the population at t time units back in the past. (The inverse exponent is included because the function α(t) is used below to describe the rate at which a pair of individuals in the population find a common ancestor or coalesce; intuitively, this is more probable when the population is small.) There is a well-defined map

$${\alpha }^{-1}\mapsto \mathit{\xi }({\alpha }^{-1})={𝔼}_{{\alpha }^{-1}}\hat{\mathit{\xi }}$$ (1)

which takes population size histories to their expected frequency spectra. Here, the notation 𝔼_α⁻¹ denotes expectation with respect to the distribution on genomes induced by α⁻¹. (For illustrative purposes we prefer to define this map abstractly for now; a concrete instantiation is given in Section 3.3).

Although the above map is not injective for an arbitrary function (Myers et al., 2008), a general sufficient condition for injectivity has been found recently (Bhaskar and Song, 2014). For most classes of size functions of interest to population geneticists (for example, piecewise-exponential), the map is injective provided that the sample size n is sufficiently large. Hence, this leads to the inverse problem of estimating a size function α̂⁻¹(·) given the sample statistic ξ̂. This machinery may be generalized to more complex demographic scenarios involving multiple populations which split or merged from one another, migration between populations, and other features, although we note that identifiability for these more general models has yet to be established.

The map (1) cannot in general be analytically inverted, so numerical methods are required to recover α⁻¹. In order to numerically solve this inverse problem, it is necessary to be able evaluate (1) rapidly and accurately.

2.2 Existing work

Two approaches exist for computing the forward mapping (1). One is based on the so-called Wright-Fisher diffusion (Ewens, 2004), a stochastic process which describes the frequency trajectory of a mutant allele segregating in a population as time moves forward. The diffusion framework has the advantage of being applicable to arbitrary demographic models, but its computational complexity grows exponentially with the number of populations. Also, it requires numerically solving a system of partial differential equations, which can be difficult in practice. For these reasons, current implementations (Gravel et al., 2011; Gutenkunst et al., 2009; Lukić and Hey, 2012) of the diffusion approach are limited to analyzing no more than four populations at once.

An alternative class of methods, which includes ours, relies on a backward-in-time stochastic process called the coalescent (Kingman, 1982a,b,c), which is dual to the Wright-Fisher diffusion. Intuitively, the coalescent describes the genealogical structure of a sample of chromosomes; below we provide a more detailed description of the coalescent since it is an integral part of our method. Using the coalescent, one computes the expected SFS by integrating over all genealogies underlying the sample. This can be done either via Monte Carlo or analytically. Monte Carlo integration (Nielsen, 2000) can effectively handle arbitrary demographic histories with a large number of populations, and Excoffier et al. (2013) have recently developed a useful implementation. However, when the number 𝒟 of populations (or demes) is moderate to large, most of the O(n^𝒟) SFS entries will be unobserved in simulations, and thus the Monte Carlo integral may naively assign a probability of 0 to observed SNPs. Monte Carlo computation of the expected SFS thus requires careful regularization techniques to avoid degeneracy.

An alternative to the Monte Carlo approach is to compute the expected SFS exactly via analytic integration over coalescent genealogies (Griffiths and Tavaré, 1998; Wakeley and Hey, 1997). For a demography involving multiple populations, this can be done by a dynamic program (Chen, 2012, 2013). This algorithm is more complicated and less general than both the Monte Carlo and diffusion approaches: while it can handle population splits, merges, size changes, and instantaneous gene flow, it is difficult to include continuous gene flow between populations. However, it scales well to a large number 𝒟 of populations, since it only computes entries of the SFS that are observed in the data, and ignores the O(n^𝒟) SFS entries that are not observed.

2.3 Summary of our main results

Unfortunately, existing coalescent-based algorithms (Chen, 2012, 2013; Wakeley and Hey, 1997) do not scale well to large sample size n, either in terms of running time or numerical stability. These algorithms rely on large alternating sums that explode with n and exhibit catastrophic cancellation. To circumvent these problems, we obtain new results for computing the truncated SFS, a key quantity needed to compute the joint SFS for multiple populations. For a fixed time τ, the truncated SFS gives the expected number of mutations arising in the time interval [0, τ) that are found in k = 1, 2, …, n individuals sampled at time 0. We provide an algorithm for computing this quantity efficiently and in a numerically stable manner.

For general demographic histories, the complexity of the dynamic program devised by Chen (2012, 2013) is O(n⁵V + WL), where V is the number of populations (vertices) throughout the history, L is the number of distinct SFS entries to be computed, and W is a term that depends on n and the graph structure of the demography; in this paper, we improve this to O(n²V + WL). For the special case of a tree-shaped demography without migration or admixture, Chen’s algorithm gives W = O(n⁴V), for a total cost of O(n⁵V + n⁴VL). In this special case (without admixture), we introduce an additional speedup that improves the runtime to O(n³V + n²VL). (See Section 4.2.2). We show through an empirical study that our algorithm is not only orders of magnitude faster, but also more numerically stable.

Lastly, we note that our algorithm relies on ideas similar to those found in Bryant et al. (2012) and De Maio et al. (2013), but with a different focus. Those methods aim to compute a “phylogenetic SFS”, in which mutations are allowed to be recurrent and time scales are sufficiently long that population size can be assumed to be constant. In contrast, our method considers an infinite sites model (Kimura, 1969) without recurrent mutation, and can handle arbitrary population size change functions. These features make it more appropriate for use in population genetics.

3 Theoretical results on the truncated SFS

In this section we study the truncated sample frequency spectrum, which is the key object needed to compute the joint SFS in our algorithm. For readers who are unfamiliar with this area, we first give a brief introduction to the key concepts in order to make our results more understandable.

3.1 Background on the coalescent and the SFS

Kingman’s coalescent (Kingman, 1982a,b,c) is a partition-valued stochastic process which describes shared ancestry of a group of individuals sampled randomly from a population. More precisely, the coalescent ${\{{𝒞}_t^n\}}_{t\ge 0}$ on n leaves is the backward-in-time Markov jump process whose value at time t is a partition of {1, …, n}, and at time t, each pairs of blocks in ${𝒞}_t^n$ merge with rate α(t). We also call $\frac{1}{\alpha (t)}$ the population size history function. We often drop the dependence on n, and write ${𝒞}_t={𝒞}_t^n$. We prefer to denote a dependence on n through the probability ℙ_n and the expectation 𝔼_n. So if X(𝒞ⁿ) denotes a random variable of the process 𝒞ⁿ, we usually write 𝔼_n[X] instead of 𝔼[X(𝒞ⁿ)]

A sample path of ${\{{𝒞}_t^n\}}_{t\ge 0}$ can be viewed as a rooted ultrametric binary tree with n leaves, labeled 1, …, n, corresponding to sampled individuals. The tree extends backwards in time and each branch represents a partition block of the process such that ${𝒞}_t^n$ corresponds to the partition induced on {1, …, n} by cutting the tree at height t. Merging a pair of blocks after a random amount of time results in a corresponding merger of tree lineages. This process repeats until all individuals have “coalesced” into a single common ancestor.

The coalescent may be used to model the mutation patterns arising in sampled DNA. The basic idea is as follows: each branch in the coalescent tree represents a succession of individuals who are ancestral to the present-day individuals (leaves) they subtend. Now suppose one of those ancestral individuals experiences a mutation at a certain position in her genome. Then, barring mutations at that position in all other parts of the tree, all of her present-day descendants will bear the mutant allele at that position, while all other members of the sample will not. If we suppose that the probability of a mutation occurring on a particular branch of a coalescent tree is proportional to the length of that branch, then this creates a link between observed mutation data and the distribution of the coalescent tree, and hence between the observed data and α(t).

It turns out that this assumption is accurate for selectively neutral mutations: conditional on the underlying coalescent tree, they are distributed roughly as a Poisson point process occurring at some rate θ/2 ≪ 1 on the tree. (The scaling factor 1/2 is a convention in the literature.) This implies that, given that a mutation is segregating within the sample, it falls uniformly with respect to branch lengths on the coalescent tree of the sampled individuals. Now let ℳ ⊊ {1, …, n} be the set of leaves carrying the mutant allele (we only consider mutations beneath the root, so by assumption ℳ ≠ {1, …, n}. Then we define the sample frequency spectrum f_n(k), for 0 < k < n, as the first order Taylor series coefficient of ℙ_n(|ℳ| = k) in the mutation rate,

$${\mathbb{P}}_n(|ℳ|=k)=\frac{\theta }{2}{f}_n(k)+o(\theta ).$$

We will generally refer to f_n(k) as the sample frequency spectrum (SFS). We also note two alternative definitions of the SFS. First, f_n(k) is the expected number of mutations with k descendants when $\frac{\theta }{2}=1$. Second, $\frac{1}{(\begin{array}{c}\hfill n\hfill \\ \hfill |K|\hfill \end{array})}{f}_n(|K|)$ is the expected length of the branch whose leaf set is K ⊂ {1, …, n}. More specifically, let 𝕀 denote the indicator function, and define ${ℒ}_K≔{\int }_0^{\infty }{𝕀}_{K\in {𝒞}_t}dt$. Then

$$\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill |K|\hfill \end{array}\right)}{f}_n(|K|)={𝔼}_n[{ℒ}_K].$$

The equivalence of these alternate definitions follows from previous results in Bhaskar et al. (2012); Griffiths and Tavaré (1998); Jenkins and Song (2011).

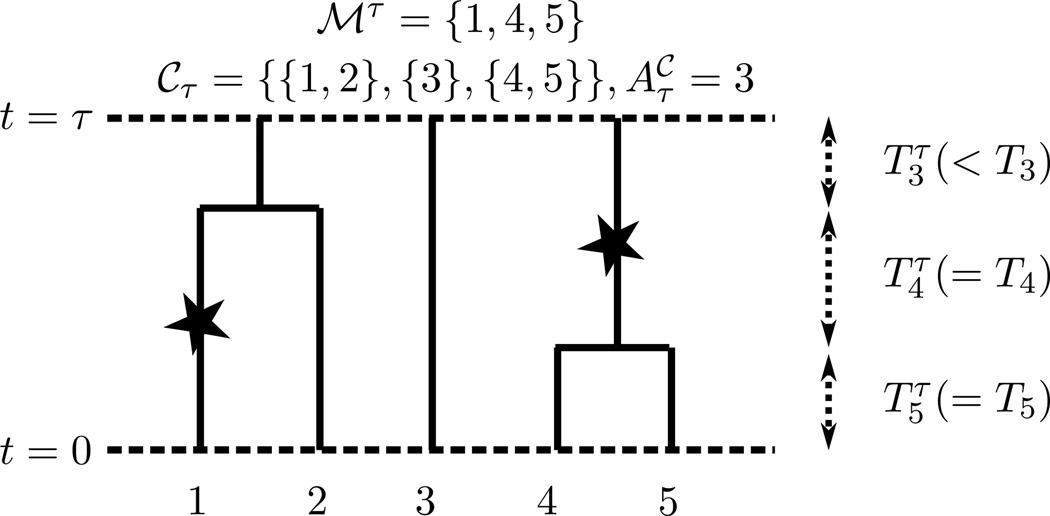
We now consider truncating the coalescent with mutation at time τ, as illustrated in Figure 1. Let ℳ^τ denote the set of leaves under mutations occurring in the time interval [0, τ). We define the truncated SFS $f_n^{\tau }(k)$ according to

$${\mathbb{P}}_n(|{ℳ}^{\tau }|=k)=\frac{\theta }{2}{f}_n^{\tau }(k)+o(\theta ),$$

where $f_n^{\tau }(k)$ corresponds to the total expected length of all branches in the time interval [0, τ) each of which subtends k leaves. Using the truncated SFS $f_n^{\tau }(k)$ for each population appearing in a demographic history, where τ denotes the length of time a particular population exists, it is possible to compute the joint SFS for multiple related populations (Chen, 2012). In Section 4.1, we describe a dynamic program algorithm for computing the joint SFS for multiple populations related by a complex demography, and the way in which this algorithm uses the truncated SFS $f_n^{\tau }(k)$.

Figure 1.

A sample path of the coalescent truncated at time τ. Star symbols denote mutations, while ℳ^τ denotes the set of leaves under those mutations. $T_k^{\tau }$ denotes the waiting time in the interval [0, τ) while there are k lineages.

3.2 Previous work on the truncated SFS

The key challenge is to compute the truncated SFS $f_n^{\tau }(k)$. Let $A_t^{𝒞}$ be the random variable which equals the number of coalescent lineages at time t ancestral to the sample. This is a pure death process which decreases by one each time a coalescence event occurs, until finally reaching the absorbing state 1 when all individuals have found a common ancestor. More precisely, $A_t^{𝒞}=|{𝒞}_t|$ and the rate of transition from m to m − 1 is given by ${\lambda }_{m,m-1}^{𝒞}(t)=\left(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array}\right)\alpha (t)$. We define a conditional version of the SFS via $f_n^{\tau }(k|A_{\tau }^{𝒞}=m)$ according to

$${\mathbb{P}}_n(|{ℳ}^{\tau }|=k|A_{\tau }^{𝒞}=m)=\frac{\theta }{2}{f}_n^{\tau }(k|A_{\tau }^{𝒞}=m)+o(\theta ).$$ (2)

Here, $f_n^{\tau }(k|A_{\tau }^{𝒞}=m)$ is the total expected length of all branches each subtending k leaves given that there are m ancestors at time τ.

In what follows we will introduce a recursive method for calculating the truncated SFS. The recursion is in terms of the sample size n so we let m ≤ ν ≤ n denote a generic sample size from this point forward. The method of Chen (2012, eq. 5) computes the truncated SFS by summing over the number m of ancestors remaining at time τ:

$$f_{\nu }^{\tau }(k)=\sum _{m=1}^{n-k+1}{\mathbb{P}}_{\nu }(A_{\nu }^{𝒞}=m)f_{\nu }^{\tau }(k|A_{\tau }^{𝒞}=m).$$ (3)

The first term in the summand, ${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)$, can be computed in at least three ways: by numerically exponentiating the rate matrix of A^𝒞, by computing an alternating sum with O(ν) terms (Tavaré, 1984), or by solving a recursion described in Section 6.1. We note that the recursion described in Section 6.1 has the advantage of computing all values of ${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)$, m ≤ ν ≤ n, in O(n²) time.

The second term $f_{\nu }^{\tau }(k|A_{\tau }^{𝒞}=m)$ in the summand of (3) is computed in Chen (2012, eq. 4) as

$$f_{\nu }^{\tau }(k|A_{\tau }^{𝒞}=m)=\sum _{i=m}^{\nu }i{p}_{\nu ,i}^{k,1}{𝔼}_{\nu }[T_i^{\tau }|A_{\tau }^{𝒞}=m],$$ (4)

where

$$p_{\nu ,i}^{k,j}≔\{\begin{array}{cc}\frac{\left(\begin{array}{c}k-1\hfill \\ j-1\hfill \end{array}\right)\left(\begin{array}{c}\nu -k-1\hfill \\ i-j-1\hfill \end{array}\right)}{\left(\begin{array}{c}\nu -1\hfill \\ i-1\hfill \end{array}\right)},\hfill & \text{if }k\ge j>0\text{ and }\nu -k\ge -i-j>0,\hfill \\ 1,\hfill & \text{if }j=k=0\text{ or }i-j=\nu -k=0,\hfill \\ 0,\hfill & \text{else},\hfill \end{array}$$

is the transition probability of the Pólya urn model, starting with i − j white balls and j black balls, and ending with ν − k white balls and k black balls (Johnson and Kotz, 1977), and

$$T_i^{\tau }≔{\int }_0^{\tau }{𝕀}_{A_t^{𝒞}=i}dt$$

is the length of time in [0, τ) where there are i ancestral lineages to the sample, as illustrated in Figure 1. Chen (2012, eq. 3) provides a formula for the conditional expectation ${𝔼}_{\nu }[T_i^{\tau }|A_{\tau }^{𝒞}=m]$ for the case of constant population size, which he later extends (Chen, 2013) to the case of an exponentially growing population. However, these formulas involve an alternating sum with O(ν²) terms. Thus, computing ${𝔼}_{\nu }[T_i^{\tau }|A_{\tau }^{𝒞}=m]$ for every value of i, m, ν, as required to compute ${\{f_{\nu }^{\tau }(k)\}}_{k\le \nu \le n}$ with (3) and (4), takes O(n⁵) time with these formulas. In addition, large alternating sums are numerically unstable due to catastrophic cancellation (Higham, 2002), and so these formulas require the use of high-precision numerical libraries, further increasing runtime.

3.3 A fast, stable algorithm for computing the truncated SFS

Here, we present a numerically stable algorithm to compute $\{f_{\nu }^{\tau }(k)|1\le k\le \nu \le n\}$ in O(n²) time instead of O(n⁵) time. Our approach utilizes the following two lemmas:

Lemma 1

The entry $f_n^{\tau }(n)$ of the truncated SFS is given by

$$f_n^{\tau }(n)=\tau -\sum _{k=1}^{n-1}\frac{k}{n}{f}_n^{\tau }(k).$$ (5)

Lemma 2

For all 1 ≤ k ≤ ν, the truncated SFS $f_{\nu }^{\tau }(k)$ satisfies the linear recurrence

$$f_{\nu }^{\tau }(k)=\frac{\nu -k+1}{\nu +1}{f}_{\nu +1}^{\tau }(k)+\frac{k+1}{\nu +1}{f}_{\nu +1}^{\tau }(k+1).$$ (6)

We prove Lemma 1 in Section 6.2. We note here that our proof also yields the identity $𝔼[T_{\mathrm{M}\mathrm{R}\mathrm{C}\mathrm{A}}]={\sum }_{k=1}^{n-1}\frac{k}{n}{f}_n(k)$, where T_MRCA denotes the time to the most recent common ancestor of the sample; to our knowledge, this formula is new. A proof of Lemma 2 is provided in Section 6.3.

We now sketch our algorithm. For a given n, we show below that all values of $f_n^{\tau }(k)$, for 1 ≤ k < n, can be computed in O(n²) time. We then compute $f_n^{\tau }(n)$ using Lemma 1 in O(n) time. Finally, using $f_n^{\tau }(k)$ for 1 ≤ k ≤ n as boundary conditions, Lemma 2 allows us to compute all $f_{\nu }^{\tau }(k)$, for ν = n − 1, n − 2, …, 2 and k = 1, …, ν, in O(n²) time.

We now describe how to compute the aforementioned terms $f_n^{\tau }(k)$, for all k < n, in O(n²) time. We first recall the result of Polanski and Kimmel (2003) which represents the untruncated SFS f_n(k), for 1 ≤ k ≤ n − 1, as

$$f_n(k)=\sum _{m=2}^n{W}_{n,k,m}{c}_m,$$ (7)

where

$$c_m≔{𝔼}_m[T_m]={\int }_0^{\infty }t\left(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array}\right)\alpha (t)\text{ exp }[-(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array}){\int }_0^t\alpha (x)\mathrm{d}x]\mathrm{d}t={\int }_0^{\infty }\text{ exp }[-(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array}){\int }_0^t\alpha (x)\mathrm{d}x]\mathrm{d}t$$ (8)

denotes the waiting time to the first coalescence for a sample of size m, and W_n,k,m are universal constants that are efficiently computable using the following recursions (Polanski and Kimmel, 2003):

$$W_{n,k,2}=\frac{6}{n+1},$$

$$W_{n,k,3}=30\frac{(n-2k)}{(n+1)(n+2)},$$

$$W_{n,k,m+2}=-\frac{(1+m)(3+2m)(n-m)}{m(2m-1)(n+m+1)}{W}_{n,k,m}+\frac{(3+2m)(n-2k)}{m(n+m+1)}{W}_{n,k,m+1},$$ (9)

for 2 ≤ m ≤ n − 2. The key observation is to note that, in a similar vein as (7), we have:

Lemma 3

The truncated SFS $f_n^{\tau }(k)$, for 1 ≤ k ≤ n − 1, can be written as

$$f_n^{\tau }(k)=\sum _{m=2}^n{W}_{n,k,m}{c}_m^{\tau },$$ (10)

where $c_m^{\tau }$ is a truncated version of (8):

$$c_m^{\tau }≔{𝔼}_m[T_m^{\tau }]={\int }_0^{\tau }\text{ exp }[-(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array}){\int }_0^t\alpha (x)\mathrm{d}x]\mathrm{d}t.$$ (11)

We prove Lemma 3 in Section 6.4. For piecewise-exponential α(t), $c_m^{\tau }$ can be computed explicitly using formulas from Bhaskar et al. (2015). Using (9), we can compute all values of W_n,k,m, for 1 ≤ k ≤ n and 2 ≤ m ≤ n, in O(n²) time. Then, using (10), all values of $f_n^{\tau }(k)$, for 1 ≤ k ≤ n − 1 can be computed in O(n²) time.

Note that the above algorithm not only significantly improves computational complexity, but also resolves numerical issues, since it allows us to avoid computing the expected times ${𝔼}_{\nu }[T_i^{\tau }|A_{\tau }^{𝒞}=m]$, which are alternating sums of O(n²) terms and are numerically unstable to evaluate for large values of n (say, n > 100).

3.4 An alternative formula for piecewise-constant subpopulation sizes

For demographic scenarios with piecewise-constant subpopulation sizes, we present an alternative formula for computing the truncated SFS within a constant piece. This formula has the same sample computational complexity as that described in the previous section.

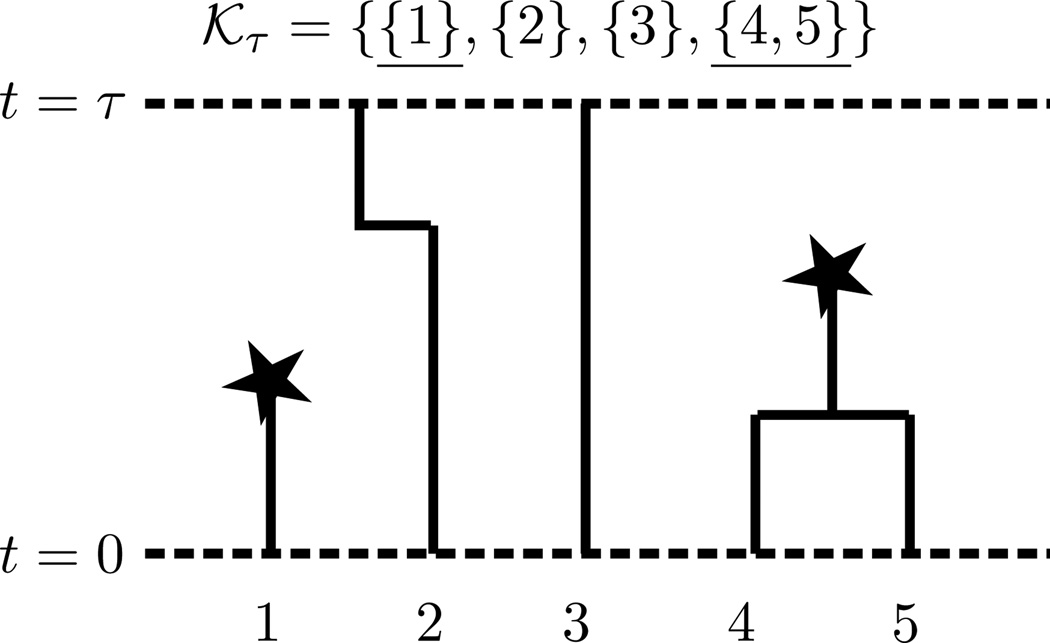
Let 𝒦_t denote the coalescent with killing, a stochastic process that is closely related to the Chinese restaurant process, Hoppe’s urn, and Ewens’ sampling formula (Aldous, 1985; Hoppe, 1984). In particular, the coalescent with killing {𝒦_t}_t≥0 is a stochastic process whose value at time t is a marked partition of {1, …, n}, where each partition block is marked as “killed” or “unkilled”. We obtain the partition for 𝒦_t by dropping mutations onto the coalescent tree as a Poisson point process with rate $\frac{\theta }{2}$, and then defining an equivalence relation on {1, …, n}, where i ~ j if and only if i, j have coalesced by time t and there are no mutations on the branches between i and j (i.e., i and j are identical by descent). We furthermore mark the equivalence classes (i.e. partition blocks) of 𝒦_t that are descended from a mutation in [0, t) as “killed”. See Figure 2 for an illustration. The process 𝒦_τ can also be obtained by running Hoppe’s urn, or equivalently the Chinese restaurant process, forward in time (Durrett, 2008, Theorem 1.9).

Figure 2.

The coalescent with killing for the genealogy in Figure 1. Note that 𝒦_τ is a marked partition, with the blocks killed by mutations in [0, τ) being specially marked.

Let $A_{\tau }^{𝒦}$ be the number of unkilled blocks in 𝒦_t, so that $A_{\tau }^{𝒦}$ is a pure death process with transition rate ${\lambda }_{i,i-1}^{𝒦}(t)=\left(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array}\right)\alpha (t)+\frac{i\theta }{2}$ (the rate of coalescence is the number of unkilled pairs $\left(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array}\right)\alpha (t)$, and the rate of killing due to mutation is $\frac{i\theta }{2}$). Our next proposition gives a formula for the truncated conditional sample frequency spectrum given $A_{\tau }^{𝒦}$, i.e., $f_n^{\tau }(k|A_{\tau }^{𝒦}=m)$.

Proposition 1

Consider the constant population size history $\frac{1}{\alpha (t)}=\frac{1}{\alpha }$ for t ∈ [0, τ), and let m > 0 and 0 < k ≤ n − m. The joint probability that the number of derived mutants is k and the number of unkilled ancestral lineages is m, when truncating at time τ, is given by

$${\mathbb{P}}_n(|{ℳ}^{\tau }|=k,A_{\tau }^{𝒦}=m)=\frac{\theta }{2}{f}_n^{\tau }(k|A_{\tau }^{𝒦}=m)\mathbb{P}(A_{\tau }^{𝒞}=m)+o(\theta ),$$

where

$$f_n^{\tau }(k|A_{\tau }^{𝒦}=m)=\frac{2}{\alpha k}\frac{\left(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill k\hfill \end{array}\right)}.$$ (12)

We prove Proposition 1 in Section 6.5. Note that this equation does not hold for the case k = n, m = 0, but fortunately we do not need to consider that case in what follows below.

We can use Proposition 1 to stably and efficiently compute the terms $f_{\nu }^{\tau }(k)$, for k ≤ ν ≤ n, as follows. We first compute the case k < ν = n. Note that ${\mathbb{P}}_n(|{ℳ}^{\tau }|=K)={\sum }_m{\mathbb{P}}_n(|{ℳ}^{\tau }|=K,A_{\tau }^{𝒦}=m)$. So for k < n, by Proposition 1

$$f_n^{\tau }(k)=\sum _{m=1}^n{f}_n^{\tau }(k|A_{\tau }^{𝒦}=m){\mathbb{P}}_n(A_{\tau }^{𝒞}=m)=\sum _{m=1}^n\frac{2}{\alpha k}\frac{\left(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill k\hfill \end{array}\right)}{\mathbb{P}}_n(A_{\tau }^{𝒞}=m).$$ (13)

The sum in (13) contains O(n) terms, so it costs O(n²) to compute $f_n^{\tau }(k)$ for all k < n. After this, we use Lemma 1 to compute $f_n^{\tau }(n)$, and then use Lemma 2 to compute $f_{\nu }^{\tau }(k)$ for all 1 ≤ k ≤ ν < n. Since there are O(n²) such terms, this also takes O(n²) time.

4 The joint SFS for multiple populations

In this section we discuss an algorithm for computing the multi-population SFS (Chen, 2012, 2013; Wakeley and Hey, 1997). We describe the algorithm in Section 4.1, and note how the results from Section 3 improve the time complexity of this algorithm. In Section 4.2, we focus on the special case of tree-shaped demographies, and introduce a further algorithmic speedup by replacing the coalescent with a Moran model.

Let V be the number of subpopulations in the demographic history, n the total sample size, and L the number of SFS entries to compute. Then the results from Section 3 improve the computational complexity of the SFS from O(n⁵V + WL) to O(n²V + WL), where W is a term that depends on n and the structure of the demographic history. In the special case of tree-shaped demographies, the algorithm from Chen (2012) gives WL = O(n⁴VL). The Moran-based speedup introduced in Section 4.2 improves the runtime of tree-shaped demographies from O(n⁴VL) to O(n³V + n²VL).

The Moran-based speedup can be generalized to non-tree demographies, but the notation, implementation, and analysis of computational complexity becomes substantially more complicated. We thus leave its generalization to future work.

4.1 A coalescent-based dynamic program

Suppose at the present we have 𝒟 populations, and in the ith population we observe n_i alleles. For a single point mutation, let x = (x₁, …, x_𝒟) denote the number of alleles that are derived in each population. We wish to compute f(x), where $\frac{\theta }{2}f(\mathbf{x})$ is the expected number of point mutations with derived counts x.

For demographic histories consisting of population size changes, population splits, population mergers, and pulse admixture events, Chen (2012) gave an algorithm to compute f(x) using the truncated SFS $f_n^{\tau }(k)$ that we defined in Section 3.

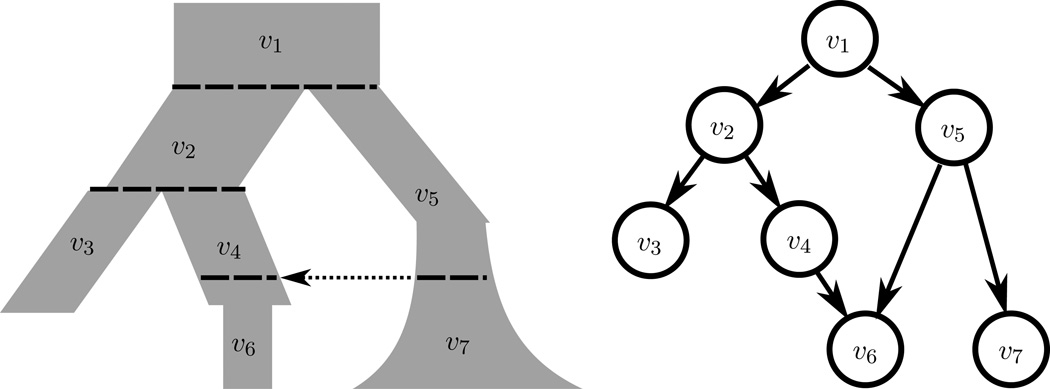
We describe this algorithm to compute f(x). We start by representing the population history as a directed acyclic graph (DAG), where each vertex υ represents a subpopulation (Figure 3). We draw a directed edge from υ to υ′ if there is gene flow from the bottom-most part of υ to the top-most part of υ′, where “down” is the present and “up” is the ancient past. Thus, the leaf vertices correspond to the subpopulations at the present. For a vertex υ in the population history graph, let τ_υ ∈ (0, ∞) denote the length of time the corresponding population persists, and let α_υ : [0, τ_υ) → ℝ⁺ denote the inverse population size history of υ So going backwards in time from the present, α_υ(t) gives the instantaneous rate at which two particular lineages in υ coalesce, after υ has existed for time t. We use $f_n^{\upsilon }(k)$ to denote the truncated SFS for the coalescent embedded in υ, i.e., $f_n^{\upsilon }(k)=f_n^{{\tau }_{\upsilon }}(k)$ for a coalescent with coalescence rate α_υ(t). Then we have

$$f(\mathbf{x})=\sum _{\upsilon }\sum _{m_0^{\upsilon },k_0^{\upsilon }}{f}_{m_0^{\upsilon }}^{\upsilon }(k_0^{\upsilon })\mathbb{P}(\mathbf{x}|k_0^{\upsilon },m_0^{\upsilon })\mathbb{P}(m_0^{\upsilon })$$ (14)

where $m_0^{\upsilon }$ denotes the number of lineages at the bottom of υ that are ancestral to the initial sample, and $k_0^{\upsilon }$ denotes the number of these lineages with a derived allele.

Figure 3.

A demographic history with a pulse migration event (left), and its corresponding directed graph (right).

In order to use (14), we must compute $f_{m_0^{\upsilon }}^{\upsilon }(k_0^{\upsilon })$ for every population υ, and every value of $m_0^{\upsilon }$ and $k_0^{\upsilon }$. If n is the total sample size and V the total number of vertices, then this takes O(n⁵V) time using the formulas of Chen (2012). Our results from Section 3 improve this to O(n²V).

To use (14), we must also compute the terms $\mathbb{P}(\mathbf{x}|k_0^{\upsilon },m_0^{\upsilon })\mathbb{P}(m_0^{\upsilon })$, for which Chen (2012) constructs a dynamic program, starting at the leaf vertices and moving up the graph. This dynamic program essentially consists of setting up a Bayesian graphical model with random variables $m_0^{\upsilon },k_0^{\upsilon }$ and performing belief propagation, which can be done via the sum-product algorithm (“tree-peeling”) if the population graph is a tree (Felsenstein, 1981; Pearl, 1982), or via a junction tree algorithm if not (Lauritzen and Spiegelhalter, 1988).

The time complexity of the algorithm thus depends on the topological structure of the population graph. In the special case where the demographic history is a binary tree, the tree-peeling algorithm computes the values $\mathbb{P}(\mathbf{x}|k_0^{\upsilon },m_0^{\upsilon })\mathbb{P}(m_0^{\upsilon })$ in O(n⁴V) time, since the vertex υ has O(n²) possible states $(k_0^{\upsilon },m_0^{\upsilon })$, so summing over the transitions between every pair of states costs O(n⁴). Note that Chen (2012) mistakenly states that the computation takes O(n³V) time.

To summarize, let W be the time it takes to compute (14) after the terms $f_m^{\upsilon }(k)$ have been precomputed, and let L be the number of distinct entries x for which we wish to compute f(x). Then our results from Section 3 improve the computational complexity from O(n⁵V + WL) to O(n²V + WL). In the case of a binary tree the original algorithm of Chen (2012) gives WL = O(n⁴VL). In the following section, we improve this to O(n³V + n²VL).

4.2 A Moran-based dynamic program

Here, we describe a new dynamic program that improves the computational complexity of computing f(x) for tree-shaped demographies. The main idea is to replace the backwards-in-time coalescent with a forwards-in-time Moran model.

4.2.1 Algorithm description

We assume the 𝒟 populations at the present are related by a binary rooted tree with 𝒟 leaves, where each leaf represents a population at the present, and at each internal vertex, a parent population splits into two child populations. (Note that a non-binary tree can be represented as a binary tree, with additional vertices of height 0).

Instead of working with the multi-population coalescent directly, we will consider a multi-population Moran model, in which the coalescent is embedded (Moran, 1958). In particular, let 𝔏(υ) denote the leaf populations descended from the population υ, and let n_υ = ∑_i∈𝔏(υ) n_i be the number of present-day alleles with ancestry in υ. For each population υ (except the root), we construct a Moran model going forward in time, i.e. starting at τ_υ and ending at 0. The Moran model consists of n_υ lineages, each with either an ancestral or derived allele. Going forward in time, every lineage copies itself onto every other lineage at rate $\frac{1}{2}{\alpha }_{\upsilon }(t)$. Thus, the total rate of copying events is $\left(\begin{array}{c}\hfill n_{\upsilon }\hfill \\ \hfill 2\hfill \end{array}\right){\alpha }_{\upsilon }(t)$. Let ${\mu }_t^{\upsilon }$ denote the number of derived alleles at time t in population υ. Then the transition rate of ${\mu }_t^{\upsilon }$ when ${\mu }_t^{\upsilon }=x$, is ${\lambda }_{x\to x+1}(t)={\lambda }_{x\to x-1}(t)=\frac{x(n_{\upsilon }-x)}{2}{\alpha }_{\upsilon }(t)$ since there are x(n_υ − x) pairs of lineages with different alleles.

The coalescent is embedded within the Moran model, because if we trace the ancestry of genetic material backwards in time in the Moran model, we obtain a genealogy with the same distribution as under the coalescent (Durrett, 2008, Theorem 1.30). Thus, we can obtain the expected number of mutations with derived counts x, by summing over the population υ in which the mutation occurred:

$$f(\mathbf{x})=\sum _{\upsilon }\sum _{k=1}^{n_{\upsilon }}{f}_{n_{\upsilon }}^{\upsilon }(k)\mathbb{P}(\mathbf{x}|{\mu }_0^{\upsilon }=k,{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=0).$$ (15)

Let x_υ = {x_i : i ∈ 𝔏(υ)} denote the subsample of derived allele counts in the populations descended from υ. Similarly, let ${\mathbf{x}}_{\upsilon }^c=\{x_i:i\notin 𝔏(\upsilon )\}$. Then for k ≥ 1,

$$\mathbb{P}(\mathbf{x}|{\mu }_0^{\upsilon }=k,{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=0)=\{\begin{array}{cc}\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=k),\hfill & \text{if }{\mathbf{x}}_{\upsilon }^c=\mathbf{0},\hfill \\ 0,\hfill & \text{if }{\mathbf{x}}_{\upsilon }^c\ne \mathbf{0}.\hfill \end{array}$$ (16)

So it suffices to compute $\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=k)$ for all υ and k. If υ is the ith leaf population, then $\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=k)={𝕀}_{k=x_i}$. On the other hand, if υ is an interior vertex with children υ₁ and υ₂, then

$$\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=k)=\sum _{k_1=0}^{n_{{\upsilon }_1}}\frac{\left(\begin{array}{c}\hfill n_{{\upsilon }_1}\hfill \\ \hfill k_1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_{{\upsilon }_2}\hfill \\ \hfill k-k_1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n_{\upsilon }\hfill \\ \hfill k\hfill \end{array}\right)}\mathbb{P}({\mathbf{x}}_{{\upsilon }_1}|{\mu }_{{\tau }_{{\upsilon }_1}}^{{\upsilon }_1}=k_1)\mathbb{P}({\mathbf{x}}_{{\upsilon }_2}|{\mu }_{{\tau }_{{\upsilon }_2}}^{{\upsilon }_2}=k-k_1),$$ (17)

where $\mathbb{P}({\mathbf{x}}_{{\upsilon }_i}|{\mu }_{{\tau }_{{\upsilon }_i}}^{{\upsilon }_i})$ can be computed from

$$\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=k)=\sum _{j=0}^{n_{\upsilon }}\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=j)\mathbb{P}({\mu }_0^{\upsilon }=j|{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=k).$$ (18)

To compute the transition probability $\mathbb{P}({\mu }_0^{\upsilon }=j|{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=k)$, note that the transition rate matrix of ${\mu }_t^{\upsilon }$ can be written as Q^(n_υ)α(t), where $Q^{(n_{\upsilon })}={\left(q_{ij}^{(n_{\upsilon })}\right)}_{0\le i,j\le n_{\upsilon }}$ is a (n_υ + 1) × (n_υ + 1) matrix with

$$q_{ij}^{(n_{\upsilon })}=\{\begin{array}{cc}-i(n_{\upsilon }-i),\hfill & \text{if }i=j,\hfill \\ \frac{1}{2}i(n_{\upsilon }-i),\hfill & \text{if }|j-i|=1,\hfill \\ 0,\hfill & \text{else},\hfill \end{array}$$

so then the transition probability is given by the matrix exponential

$$\mathbb{P}({\mu }_0^{\upsilon }=j|{\mu }_{{\tau }_{\upsilon }}^{\upsilon }=k)={[e^{Q^{(n_{\upsilon })}{\int }_0^{{\tau }_{\upsilon }}{\alpha }_{\upsilon }(t)dt}]}_{k,j}.$$ (19)

Thus, the joint SFS f(x) can be computed using (15) and (16), with $\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_0^{\upsilon }=k)$ given by recursively computing (17), (18), and (19), in a depth-first search on the population tree (i.e., Felsenstein’s tree-peeling algorithm, or the sum-product algorithm for belief propagation).

4.2.2 Computational complexity of Moran approach

We now consider the computational complexity associated with (17), (18), and (19) for each vertex υ. For fixed configuration x, (17) and (18) must be computed for O(n_υ) values, and are each sums with O(n_υ) terms; they thus contribute $O(n_{\upsilon }^{2}L)$ to the total runtime, where L is the number of distinct values of x. The matrix exponential $e^{(Q^{(n_{\upsilon })}{\int }_0^{{\tau }_{\upsilon }}{\alpha }_{\upsilon }(t)dt)}$ in (19) can be computed in several ways, including spectral decomposition or scaling-and-squaring, and costs $O\left(n_{\upsilon }^3\right)$ time (Moler and Van Loan, 2003). The computational complexity associated with a single vertex υ is thus $O(n_{\upsilon }^3+n_{\upsilon }^{2}L)$. Therefore, for a binary population tree with V nodes, arbitrary population size functions, and no migration, the total cost of computing the observed SFS entries is O(n³V + n²VL).

The time complexity can be further improved with techniques applied by Bryant et al. (2012), but in practice we found that the decreased running time was offset by other problems such as numerical instability or large hidden time costs. In particular, let ${\ell }_t^{\upsilon }(k)=\mathbb{P}({\mathbf{x}}_{\upsilon }|{\mu }_t^{\upsilon }=k)$, and ${\tilde{\ell }}_t^{\upsilon }(k)=\left(\begin{array}{c}\hfill n_{\upsilon }\hfill \\ \hfill k\hfill \end{array}\right){\ell }_t^{\upsilon }(k)$. Then (17) can be written as a convolution

$${\tilde{\ell }}_0^{\upsilon }={\tilde{\ell }}_{{\tau }_{{\upsilon }_1}}^{{\upsilon }_1}*{\tilde{\ell }}_{{\tau }_{{\upsilon }_2}}^{{\upsilon }_2},$$ (20)

which can be computed via the FFT (Cooley and Tukey, 1965), reducing the complexity of (17) from $O\left(n_{\upsilon }^{2}L\right)$ to O(n_υ log(n_υ)L). Another potential speedup is to rewrite (18) as

$${\ell }_{{\tau }_{\upsilon }}^{\upsilon }=e^{(Q^{(n_{\upsilon })}{\int }_0^{{\tau }_{\upsilon }}{\alpha }_{\upsilon }(t)dt)}{\ell }_0^{\upsilon }$$ (21)

and utilize the sparsity of Q^(n_υ) (Al-Mohy and Higham, 2011). In particular, (21) can be computed by 𝒯 sparse matrix-vector products, where 𝒯 depends on Q^(n_υ) and the desired level of precision. This reduces the cost of (18) and (19) from $O(n_{\upsilon }^3+n_{\upsilon }^{2}L)$ to O(n_υ𝒯L).

These two speedups were applied by Bryant et al. (2012) to reduce the complexity of their coalescent-based approach from $O(n_{\upsilon }^6+n_{\upsilon }^{4}L)$ to $O(n_{\upsilon }^{2}L(\text{log}(n_{\upsilon })+𝒯))$. When applied in our Moran-based approach, they reduce the complexity of (17), (18), and (19) from $O(n_{\upsilon }^3+n_{\upsilon }^{2}L)$ to O(n_υL(log(n_υ) + 𝒯)). In practice, however, we found 𝒯 to be quite large, and it was faster to use the naive approach to compute and multiply $e^{(Q^{(n\upsilon )}{\int }_0^{{\tau }_{\upsilon }}{\alpha }_{\upsilon }(t)dt)}$. Furthermore, computing (20) via the FFT can be very numerically unstable. Taking the Fourier transform introduces cancellation errors, due to multiplying and adding terms like e^−ix, and we found that converting from ${\tilde{\ell }}_0^{\upsilon }$ back to ${\ell }_0^{\upsilon }$ can cause these errors to blow up, due to the combinatorial factors.

5 Runtime and accuracy results

5.1 Comparison with Chen (2012)

We implemented our formulas and algorithm in Python, using the Python packages numpy and scipy. We also implemented the formulas from Chen (2012), and compared the performance of the two algorithms on simulated data.

We simulated datasets with n ∈ {2, 4, 8, …, 256} lineages and 𝒟 ∈ {2, 4, 8, …, n} populations at present, each containing $\frac{n}{𝒟}$ lineages. For each value of n, 𝒟, we used the program scrm (Staab et al., 2015) to generate 20 random datasets, each with a demographic history that is a random binary tree.

In Figure 4, we compare the running time of the original algorithm of Chen (2012) against our new algorithm that utilizes the formulas for $f_n^{\tau }(k)$ presented in Section 3 and our new Moran-based approach described in Section 4.2. We find our algorithm to be orders of magnitude faster; the difference is especially pronounced as the number n of lineages grows. Note that, due to the increased running time of Chen’s algorithm, we did not finish running his method for n = 256 and 𝒟 ≥ 32.

Figure 4.

Average computation time of the joint SFS. For each combination of the sample size n and the number 𝒟 of populations (with $\frac{n}{𝒟}$ samples per population), we generated 20 random datasets, each under a demographic history that is a random binary tree. The expected joint SFS for the resulting segregating sites were then computed using our method (momi) and that of Chen (2012). In the top row, we plot the average runtime per joint SFS entry, and in the bottom row, the average amount of time needed to precompute the truncated SFS for every subpopulation within each demographic history. (a) Runtime results plotted separately for each method in a linear scale. Note the y-axis is on a different scale for each row. (b) Runtime results with the axes on a log-log scale, so that shorter runtimes are visible.

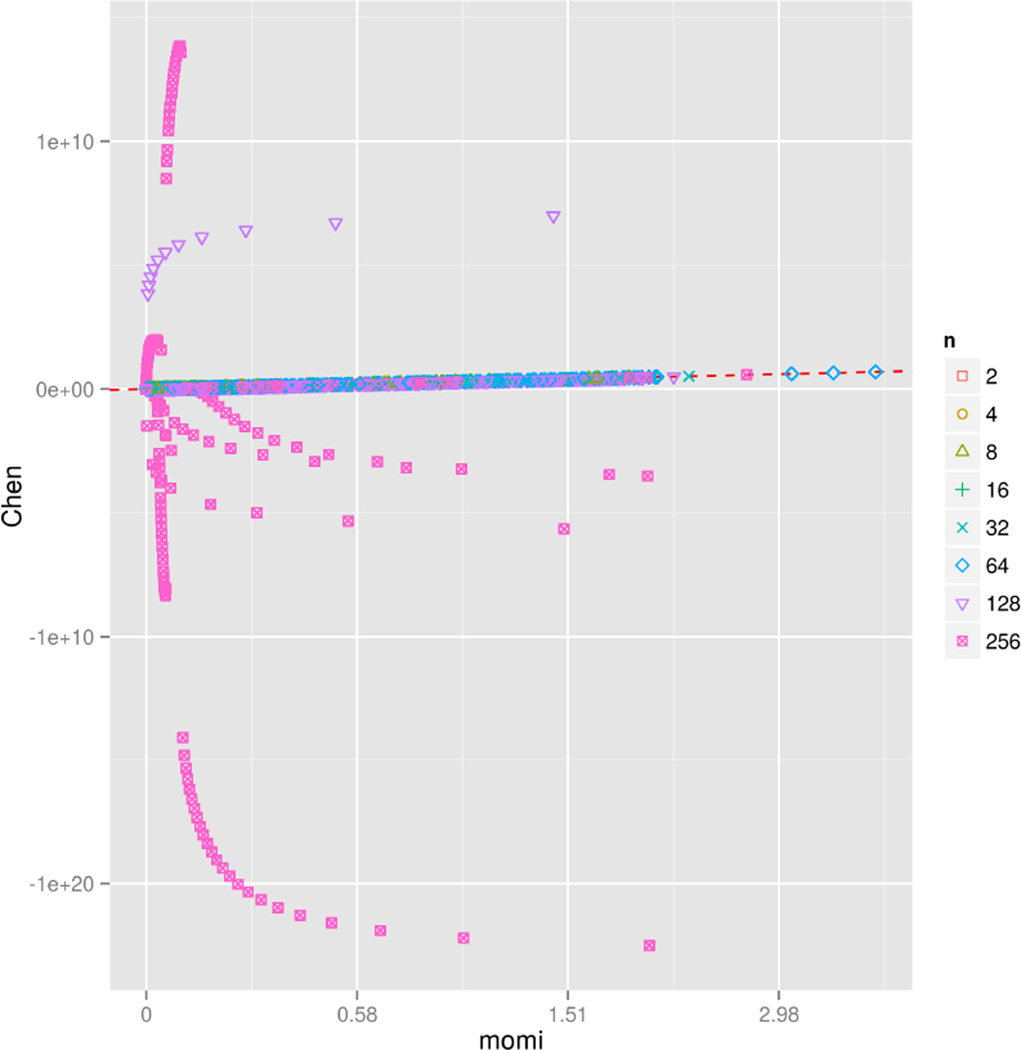
In Figure 5, we compare the accuracy of the two algorithms. The figure compares the SFS entries returned by the two methods across a subset of the simulations depicted in Figure 4. The line y = x is also plotted; points falling on the line depict the SFS entries where both methods agreed. All negative return values represent numerical errors. For n ≤ 64 the two methods generally agree, but for larger n Chen’s algorithm displays considerable numerical instability, returning extremely large positive and negative numbers.

Figure 5.

Numerical stability of the two algorithms. The plot compares the numerical values returned by our method (momi) and Chen’s method, for the simulations described in Figure 4. The dashed red line represents the identity y = x. To adequately illustrate the full numerical range (both positive and negative) of values encountered in the simulations, we applied the transformation z ↦ sign(z) log(1 + |z|) to the values of each method in order to produce the scatter plot. The two methods agree for n ≤ 64, while Chen’s method is extremely unstable for larger n.

5.2 Comparison with ∂a∂i

We also compared our method with the popular program ∂a∂i (Gutenkunst et al., 2009). We note that our method has several key differences from ∂a∂i, and the two methods have strengths in distinct use cases. ∂a∂i computes the joint SFS by numerically integrating a PDE. This PDE can be easily modified to include effects such as natural selection and continuous migration, which gives ∂a∂i more flexibility than the coalescent or Moran-based approaches discussed in this paper. However, numerical integration of multidimensional PDEs is a challenging problem; thus ∂a∂i can handle only a small number of populations (up to 3), and may occasionally encounter numerical instability.

We compared our method (momi) with ∂a∂i on a modified version of the three-population out-of-Africa demography inferred by Gutenkunst et al. (2009). In this history, the Eurasian population initially splits off from the African population, and then splits into separate European and Asian populations. The populations experience several piecewise constant size changes, and the European and Asia populations experience exponential growth in the recent past. The original, unmodified history also contains continuous migration between the separated populations; since our implementation does not currently support migration, we modified the demographic history to have no migration. (Support for migration will be added to our method in the future.)

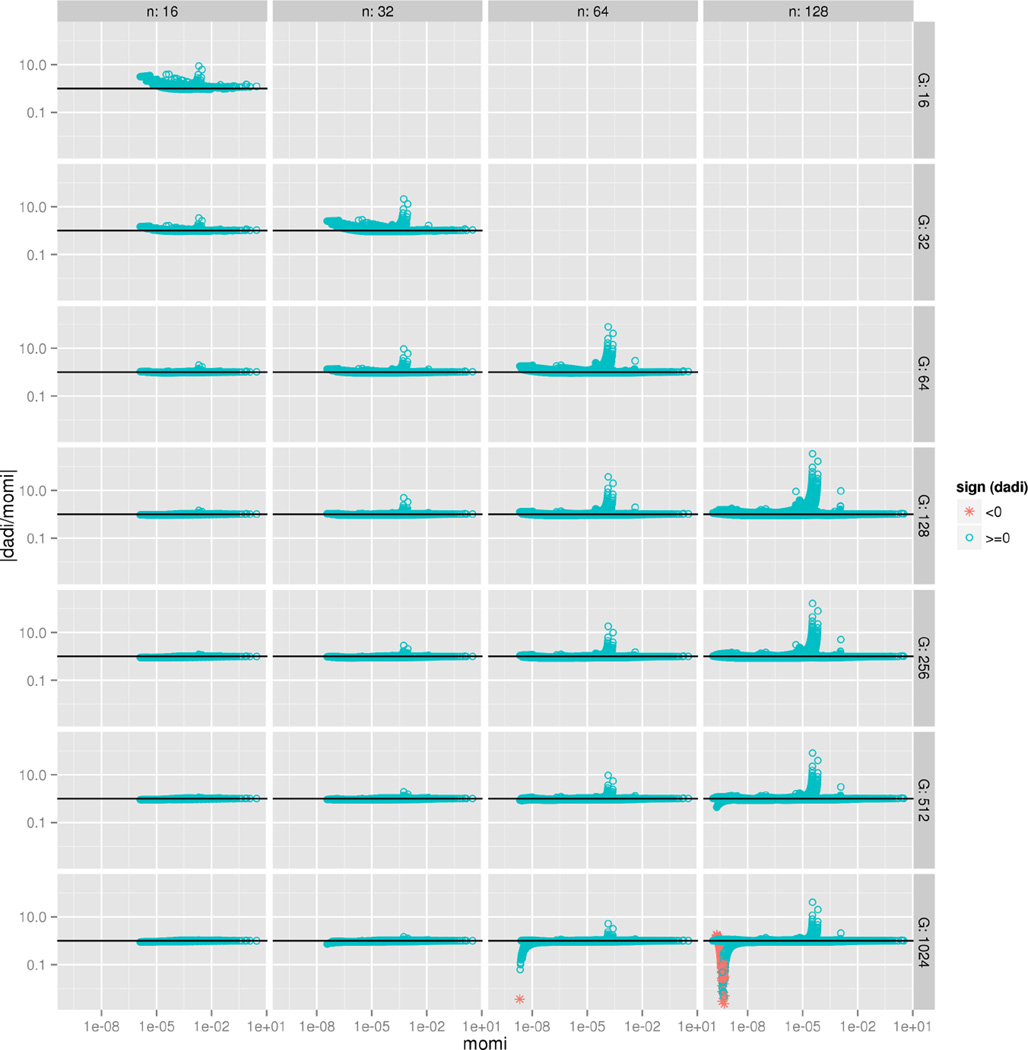
We consider sample sizes of n = 16, 32, 64, 128 per population; for ∂a∂i, we consider discretization grid sizes of G = 16, 32, …, 512, 1024 points per population, with G ≥ n. We compare the values returned by momi and ∂a∂i in Figure 6. momi and ∂a∂i mostly agree, but some entries of ∂a∂i are off by a factor of 10 or 100, especially when $\frac{G}{n}$ is small. In general the value computed by ∂a∂i converges to that of momi as G increases. However, for G = 1024 and n = 64, 128, ∂a∂i appears to have some numerical instability. In particular, ∂a∂i diverges in some of the smaller entries, and returns some negative numbers.

Figure 6.

Comparison of SFS values computed by ∂a∂i and momi, varying the sample size n per population and the number G of grid points per population in ∂a∂i. We used the 3-population out-of-Africa demography inferred in Gutenkunst et al. (2009), but modified to have no gene flow (migration). The x-axis is f_momi(x) the value computed by momi, the y-axis is the absolute value of the ratio $\left|\frac{f_{\partial a\partial i}(\mathbf{x})}{f_{\mathit{\text{momi}}}(\mathbf{x})}\right|$, and the color gives the sign of f_∂a∂i(x) (all values returned by momi were positive). f_∂a∂i generally converges to f_momi(x) as G increases, but for large values of n and G, ∂a∂i appears to diverge, and returns some negative values.

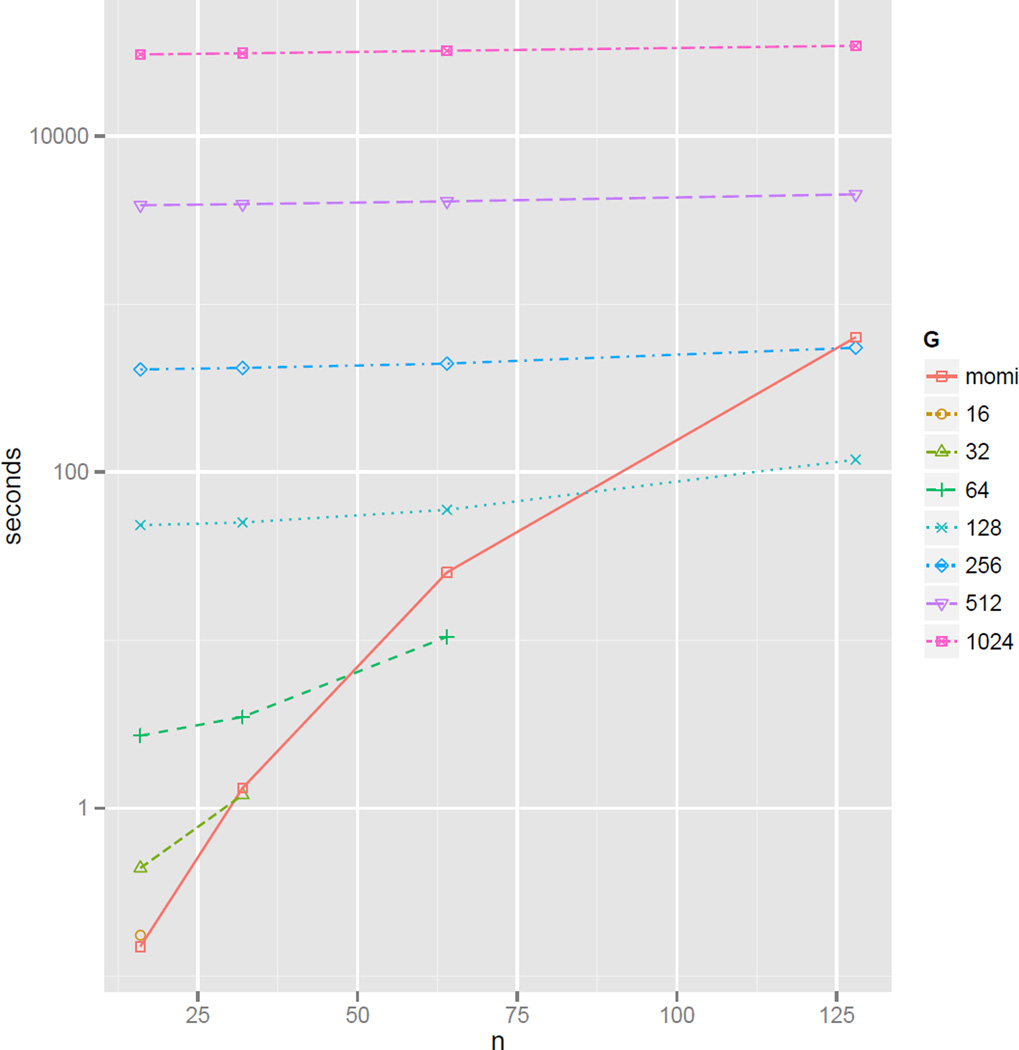
We compare the runtime of momi and ∂a∂i in Figure 7, which shows the time to compute all entries of the SFS. The two methods are roughly comparable, depending on the number G of grid points in ∂a∂i. We note that ∂a∂i computes all entries of the SFS together, whereas momi and the method of Chen (2012, 2013) can easily compute a subset of the SFS. This is a key advantage for the latter methods when the number of populations 𝒟 is large, as the size of the SFS grows exponentially with 𝒟.

Figure 7.

Runtime of momi and ∂a∂i to compute the results in Figure 6.

6 Proofs

In this section, we provide proofs of the mathematical results presented in earlier sections.

6.1 A recursion for efficiently computing ${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)$

We describe how to compute ${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)$, for all values of m ≤ ν ≤ n, in O(n²) time. First, note that

$${\mathbb{P}}_{\nu -1}(A_{\tau }^{𝒞}=m)={\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m+1,\{\nu \}\in {𝒞}_{\tau })+{\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m,\{\nu \}\notin {𝒞}_{\tau })=\frac{(m+1)p_{\nu ,m+1}^{1,1}}{(\begin{array}{c}\hfill \nu \hfill \\ \hfill 1\hfill \end{array})}{\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m+1)+(1-\frac{m{p}_{\nu ,m}^{1,1}}{(\begin{array}{c}\hfill \nu \hfill \\ \hfill 1\hfill \end{array})}){\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)=\frac{(m+1)(m)}{\nu (\nu -1)}{\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m+1)+(1-\frac{m(m-1)}{\nu (\nu -1)}){\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m).$$

Rearranging, we get the recursion

$${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)=\frac{1}{1-\frac{m(m-1)}{\nu (\nu -1)}}[{\mathbb{P}}_{\nu -1}(A_{\tau }^{𝒞}=m)-\frac{(m+1)(m)}{\nu (\nu -1)}{\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m+1)]$$ (22)

with base cases

$${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=\nu )=e^{-(\begin{array}{c}\hfill \nu \hfill \\ \hfill 2\hfill \end{array}){\int }_0^{\tau }\alpha (t)dt}.$$

So after solving ${\int }_0^{\tau }\alpha (t)dt$, we can use the recursion and memoization to solve for all of the O(n²) terms ${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=m)$ in O(n²) time. In particular, in the case of constant population size, α(t) = α, the base case is given by

$${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=\nu )=e^{-(\begin{array}{c}\hfill \nu \hfill \\ \hfill 2\hfill \end{array})\alpha \tau },$$

and in the case of an exponentially growing population size, α (t) = α (τ)e^β(τ−t), the base case is given by

$${\mathbb{P}}_{\nu }(A_{\tau }^{𝒞}=\nu )=e^{-(\begin{array}{c}\hfill \nu \hfill \\ \hfill 2\hfill \end{array})\alpha (\tau )(e^{\beta \tau }-\frac{1}{\beta })}.$$

6.2 Proof of Lemma 1

Let T_MRCA denote the time to the most recent common ancestor of the sample. We first note that

$$f_n^{\tau }(n)=\tau -{𝔼}_n[T_{\mathrm{M}\mathrm{R}\mathrm{C}\mathrm{A}}\wedge \tau ],$$

since the branch length subtending the whole sample is the time between τ and T_MRCA.

Next, note that $\frac{\theta }{2}{𝔼}_n[T_{\mathrm{M}\mathrm{R}\mathrm{C}\mathrm{A}}\wedge \tau ]$ is equal to the number of polymorphic mutations in [0, τ) where the individual “1” is derived. This is because, as we trace the ancestry of “1” backwards in time, all mutations hitting the lineage below T_MRCA are polymorphic, while all mutations hitting above T_MRCA are monomorphic.

The expected number of polymorphic mutations with “1” derived is also equal to $\frac{\theta }{2}{\sum }_{k=1}^{n-1}\frac{k}{n}{f}_n^{\tau }(k)$, since if a mutation has k derived leaves, the chance that “1” is in the derived set is $\frac{k}{n}$. Thus

$${𝔼}_n[T_{\mathrm{M}\mathrm{R}\mathrm{C}\mathrm{A}}\wedge \tau ]=\sum _{k=1}^{n-1}\frac{k}{n}{f}_n^{\tau }(k),$$

which completes the proof.

6.3 Proof of Lemma 2

We first note that

$${\mathbb{P}}_n({ℳ}^{\tau }=\{1,\dots ,k\})={\mathbb{P}}_{n+1}({ℳ}^{\tau }=\{1,\dots ,k\})+{\mathbb{P}}_{n+1}({ℳ}^{\tau }=\{1,\dots ,k,n+1\}).$$

By exchangeability, we have ${\mathbb{P}}_n({ℳ}^{\tau }=K)=\frac{\theta }{2}\frac{f_n^{\tau }(|K|)}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill |K|\hfill \end{array}\right)}+o(\theta )$ for all K ⊆ {1, …, n}, so

$$\frac{1}{(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array})}{f}_n^{\tau }(k)=\frac{1}{(\begin{array}{c}\hfill n+1\hfill \\ \hfill k\hfill \end{array})}{f}_{n+1}^{\tau }(k)+\frac{1}{(\begin{array}{c}\hfill n+1\hfill \\ \hfill k+1\hfill \end{array})}{f}_{n+1}^{\tau }(k+1).$$

Multiplying both sides by $(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array})$ gives

$$f_n^{\tau }(k)=\frac{n-k+1}{n+1}{f}_{n+1}^{\tau }(k)+\frac{k+1}{n+1}{f}_{n+1}^{\tau }(k+1).$$

6.4 Proof of Lemma 3

Let α*(t) denote the inverse population size history given by

$${\alpha }^{*}(t)=\{\begin{array}{cc}\alpha (t)\hfill & \text{if }t<\tau \hfill \\ \infty \hfill & \text{if }t\ge \tau .\hfill \end{array}$$

So the demographic history with population size $\frac{1}{{\alpha }^{*}(t)}$ agrees with the original history up to time τ, at which point the population size drops to 0, and all lineages instantly coalesce into a single lineage with probability 1.

Let T_{m, *} denote the amount of time there are m ancestral lineages for the coalescent with size history $\frac{1}{{\alpha }^{*}(t)}$. Similarly, let f_n,*(k) denote the SFS under the size history $\frac{1}{{\alpha }^{*}(t)}$. Then from the result of Polanski and Kimmel (2003),

$$f_{n,*}(k)=\sum _{m=2}^n{W}_{n,k,m}{𝔼}_m[T_{m,*}].$$

Note that for m > 1, we almost surely have $T_{m,*}=T_{m,*}^{\tau }$, i.e. the intercoalescence time equals its truncated version, since all lineages coalesce instantly at τ with probability 1. Thus, ${𝔼}_m[T_{m,*}]={𝔼}_m[T_{m,*}^{\tau }]$. Similarly, for k < n, $f_{n,*}(k)=f_{n,*}^{\tau }(k)$, i.e. the SFS equals the truncated SFS, because the probability of a polymorphic mutation occurring in [τ, ∞) is 0.

Finally, note that ${𝔼}_m[T_{m,*}^{\tau }]={𝔼}_m[T_m^{\tau }]$ and $f_{n,*}^{\tau }(k)=f_n^{\tau }(k)$, because α(t) and α*(t) are identical on [0, τ).

6.5 Proof of Proposition 1

We start by showing that ${\mathbb{P}}_n(A_{\tau }^{𝒦}=m)={\mathbb{P}}_n(A_{\tau }^{𝒞}=m)+O(\theta )$. Let $T_i^{\tau }(𝒦)={\int }_0^{\tau }{𝕀}_{A_t^{𝒦}=i}dt$ denote the amount of time where 𝒦 has i unkilled lineages. Let p denote the probability density function. For (t_n, …, t_m) with ∑ t_i = τ, we have

$$p(T_n^{\tau }(𝒦)=t_n,\dots ,T_m^{\tau }(𝒦)=t_m)=e^{-{\lambda }_{m,m-1}^{𝒦}{t}_m}\prod _{i=m+1}^n{\lambda }_{i,i-1}^{𝒦}{e}^{-{\lambda }_{i,i-1}^{𝒦}{t}_i}=e^{-((\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array})\alpha +\frac{m\theta }{2})t_m}\prod _{i=m+1}^n\left(\right(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array})\alpha +\frac{i\theta }{2})e^{-((\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array})\alpha +\frac{i\theta }{2})t_i}=e^{-(\begin{array}{c}\hfill m\hfill \\ \hfill 2\hfill \end{array})\alpha t_m}\prod _{i=m+1}^n\left(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array}\right)\alpha e^{-(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array})\alpha t_i}+O(\theta )=p(T_n^{\tau }=t_n,\dots ,T_m^{\tau }=t_m)+O(\theta ),$$

and so

$$\underset{\theta \to 0}{\text{lim}}{\mathbb{P}}_n(A_{\tau }^{𝒦}=m)=\underset{\theta \to 0}{\text{lim}}{\int }_{\sum t_i=\tau }p(T_n^{\tau }(𝒦)=t_n,\dots ,T_m^{\tau }(𝒦)=t_m)d\mathbf{t}={\int }_{\sum t_i=\tau }p(T_n^{\tau }=t_n,\dots ,T_m^{\tau }=t_m)d\mathbf{t}={\mathbb{P}}_n(A_{\tau }^{𝒞}=m).$$

where we can exchange the limit and the integral by the Bounded Convergence Theorem, because $p(T_n^{\tau }(𝒦)=t_n,\dots ,T_m^{\tau }(𝒦)=t_m)\le {\prod }_{i=m+1}^n\left(\right(\begin{array}{c}\hfill i\hfill \\ \hfill 2\hfill \end{array})\alpha +\frac{i}{2})$

Thus we have

$${\mathbb{P}}_n(|{ℳ}^{\tau }|=k,A_{\tau }^{𝒦}=m)={\mathbb{P}}_n(|{ℳ}^{\tau }|=k|A_{\tau }^{𝒦}=m){\mathbb{P}}_n(A_{\tau }^{𝒦}=m)=(\frac{\theta }{2}{f}_n^{\tau }(k|A_{\tau }^{𝒦}=m)o(\theta ))({\mathbb{P}}_n(A_{\tau }^{𝒞}=m)+O(\theta ))=\frac{\theta }{2}{f}_n^{\tau }(k|A_{\tau }^{𝒦}=m){\mathbb{P}}_n(A_{\tau }^{𝒞}=m)+o(\theta ),$$

which proves the first part of the proposition.

We next solve for $f_n^{\tau }(k|A_{\tau }^{𝒦}=m)$, the first order Taylor series coefficient for ${\mathbb{P}}_n(|{ℳ}^{\tau }|=k|A_{\tau }^{𝒦}=m)$ in the mutation rate $\frac{\theta }{2}$.

When there are i unkilled lineages, the probability that the next event is a killing event is $\frac{\theta }{\alpha (i-1)+\theta }=\frac{\theta }{\alpha (i-1)}+O(\theta )$. Given that the event is a killing, the chance that the killed lineage has k leaf descendants is $p_{n,i}^{k,1}$. So summing over i, and dividing out the mutation rate $\frac{\theta }{2}$, we get

$$f_n^{\tau }(k|A_{\tau }^{𝒦}=m)=\frac{2}{\alpha }\sum _{i=m+1}^{n-k+1}\frac{1}{i-1}{p}_{n,i}^{k,1}=\frac{2}{\alpha }\sum _{i=m+1}^{n-k+1}\frac{1}{i-1}\frac{\left(\begin{array}{c}\hfill n-k-1\hfill \\ \hfill i-2\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill i-1\hfill \end{array}\right)}=\frac{2}{\alpha }\sum _{i=m+1}^{n-k+1}\frac{1}{i-1}\frac{(n-k-1)!(i-1)!(n-i)!}{(i-2)!(n-k-i+1)!(n-1)!}=\frac{2(n-k-1)!}{\alpha (n-1)!}\sum _{i=m+1}^{n-k+1}\frac{(n-i)!}{(n-k-i+1)!}=\frac{2(n-k-1)!}{\alpha (n-1)!}\sum _{j=0}^{n-k-m}\frac{(j+k-1)!}{j!}=\frac{2}{\alpha k(\begin{array}{c}\hfill n-1\hfill \\ \hfill k\hfill \end{array})}\sum _{j=0}^{n-k-m}(\begin{array}{c}\hfill j+k-1\hfill \\ \hfill j\hfill \end{array})=\frac{2}{\alpha k}\frac{(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array})}{(\begin{array}{c}\hfill n-1\hfill \\ \hfill k\hfill \end{array})},$$

where we made the change of variables j = n − k − i + 1, and where the final line follows from repeated application of the combinatorial identity $\left(\begin{array}{c}\hfill a\hfill \\ \hfill b\hfill \end{array}\right)=\left(\begin{array}{c}\hfill a-1\hfill \\ \hfill b\hfill \end{array}\right)+\left(\begin{array}{c}\hfill a-1\hfill \\ \hfill b-1\hfill \end{array}\right)$.

6.5.1 Alternative proof for $f_n^{\tau }(k|A_{\tau }^{𝒦}=m)$ via the Chinese Restaurant Process

We sketch an alternative proof of the expression for $f_n^{\tau }(k|A_{\tau }^{𝒦}=m)$, using the Chinese Restaurant Process.

Consider the coalescent with killing going forward in time (towards the present), and only looking at it when the number of individuals increases. Then when there are i lineages, a new mutation occurs with probability $\frac{\theta }{\alpha i+\theta }=\frac{\theta /\alpha }{i+\theta /\alpha }$, and each lineage branches with probability $\frac{\alpha }{\alpha i+\theta }=\frac{1}{i+\theta /\alpha }$. Thus, conditional on $A_{\tau }^{𝒦}=m$, the distribution on 𝒦_τ is given by a Chinese Restaurant Process (Aldous, 1985), starting with m tables each with 1 person, and with new tables founded with parameter θ/α.

Let (x)_i↑ = x(x + 1) ⋯ (x + i − 1) denote the rising factorial. If there is a single mutation with k descendants, then there are $(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array})$ ways to pick which of the n − m events involve mutant lineages. The probability of a particular such ordering is

$$\frac{\theta }{\alpha }\frac{{(1)}_{k\uparrow }{(m)}_{n-k-m\uparrow }}{{(m+\theta /\alpha )}_{n-m\uparrow }}=\frac{\theta }{\alpha }\frac{(k-1)!(n-k-1)!/m!}{(n-1)!/m!}+o(\theta ).$$

Summing over all $(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array})$ orderings, and dividing by $\frac{\theta }{2}$, yields

$$f_n^{\tau }(k|A_{\tau }^{𝒦}=m)=\frac{2}{\alpha }(\begin{array}{c}\hfill n-m\hfill \\ \hfill k\hfill \end{array})\frac{(k-1)!(n-k-1)!/m!}{(n-1)!/m!}.$$