Linear Regression with a Randomly Censored Covariate: Application to an Alzheimer’s Study

Summary

The association between maternal age of onset of dementia and amyloid deposition (measured by in vivo positron emission tomography (PET) imaging) in cognitively normal older offspring is of interest. In a regression model for amyloid, special methods are required due to the random right censoring of the covariate of maternal age of onset of dementia. Prior literature has proposed methods to address the problem of censoring due to assay limit of detection, but not random censoring. We propose imputation methods and a survival regression method that do not require parametric assumptions about the distribution of the censored covariate. Existing imputation methods address missing covariates, but not right censored covariates. In simulation studies, we compare these methods to the simple, but inefficient complete case analysis, and to thresholding approaches. We apply the methods to the Alzheimer’s study.

1. Introduction

The risk of Alzheimer’s disease (AD) increases with age (Austin and Hoch, 2004) and with family history (FH), and in particular, younger parental age of onset (Jarvik et al., 2005, 2008; Silverman et al., 2003, 2005). The e4 allele of the apolipoprotein E (APOE) genotype is a known component of the FH risk (Mayeux, 2010) and an interaction of APOEe4 effects and gender has been recognized (Miech et al., 2002). Some evidence for a maternal transmission factor for AD has been reported (Duara et al., 1993; Edland et al., 1996); however, this is not consistent after controlling for age and female longevity (Heggeli et al., 2012; Ehrenkrantz et al., 1999). To explore the biological basis of these risk factors, investigators have evaluated AD imaging endophenotypes in relation to maternal FH. AD-like patterns of regional brain volume (Honea et al., 2010; Berti et al., 2011), F-fluorodeoxyglucose (FDG) metabolism (Mosconi et al., 2007), and amyloid deposition, as imaged in vivo with Pittsburgh Compound B (PiB) (Mosconi et al., 2010), have been reported more frequently in non-demented subjects with maternal FH than in those with no FH or in those with paternal FH. Importantly, these features have been detected even after controlling for APOE e4 carrier status. To further investigate this observation, a study was conducted at Massachusetts General Hospital and Brigham and Women’s Hospital that investigated the relationship between maternal history of dementia and amyloid burden in offspring (Maye et al., 2016) over age 60.

Participants in this study completed parental history questionnaires that ascertained information about parental ages of dementia onset, other illnesses, and death. The primary statistical framework to be used to address the scientific question of interest is a linear regression model of expected amyloid in the offspring as a function of maternal age of dementia onset, offspring age, gender, education, and Clinical Dementia Rating (CDR) global score. However, as not all mothers experienced onset of dementia at the time of the offspring’s interview, their ages at onset are right censored by their ages at the offspring interview, or their ages at death, if this occurred prior to the interview. This introduces the analytical challenge of how to handle right censored covariates in a regression model.

While there is a large literature on the treatment of missing covariates in regression models, there is a more limited literature on the treatment of censored covariates, which present a structured form of missingness. Use of the censored covariates without any adjustment for the censoring is well known to lead to bias in the coefficients of interest (Rigobon and Stoker, 2009) and inflated type I error (Austin and Brunner, 2003). A simple approach is that of complete case analysis (Little and Rubin, 2002). This approach discards all subjects who have a censored covariate and fits the regression model using only those subjects whose covariate is uncensored. This is valid in our study as long as offspring amyloid is independent of age at censoring given age at maternal dementia and other covariates. It is potentially highly inefficient in the presence of even moderate censoring. The majority of the literature addresses the simple case of type I censoring, in which the covariate is censored by a fixed limit of detection such as might arise from an assay measurement. Early papers simply replaced the censored covariate with the limit of detection or some function of it (Moulton and Halsey, 1995; Liang et al., 2004; Lynn, 2001). While this may be reasonable when there is a natural limit (such as zero) and when the limit of detection is close to the natural limit, it may otherwise lead to substantial bias (Nie et al., 2010). Other approaches assumed parametric distributions for the censored covariate and replaced censored observations with the expectation of the covariate given that it lies below the limit of detection (Lynn, 2001; Richardson and Ciampi, 2003) or applied maximum likelihood estimation that accounts for the censoring (Lynn, 2001; Austin and Hoch, 2004; May et al., 2011; Rigobon and Stoker, 2007), or multiple imputation (Lynn, 2001). The first of these approaches leads to underestimation of the standard error, and all of them require correct specification of the distribution of the covariate. A recent paper (Kong and Nan, 2016) proposed a likelihood-based approach for limit of detection censoring. They employed a semi-parametric accelerated failure time model for the censored covariate, which may be extended to the case of random censoring. It is a two-stage approach, which may suffer from some loss of efficiency. Alternative, distribution-free approaches for the case of type I censoring employ multiple imputation based on M-regression models that replaces censored observations with conditional quantiles given the observed data (Wang and Feng, 2012) or single imputation with the expected value of the covariate of interest among subjects for whom it was observed (Schisterman et al., 2006). The latter approach yields an unbiased estimator for the coefficient of interest, but can lead to slight overestimation of standard errors. A different approach is that of dichotomizing the potentially censored covariate to a binary covariate (Austin and Hoch, 2004; Rigobon and Stoker, 2009). This approach yields substantial bias in the coefficient of interest (Austin and Hoch, 2004; Rigobon and Stoker, 2009). Other papers have treated the problem of censored covariates in the context of a censored outcome as a bivariate estimation problem (D’Angelo et al., 2008; Clayton, 1978).

In this paper, we consider the problem of randomly censored covariates in regression models, such as arise in our study with maternal age at onset of dementia. To our knowledge, there are no publications that treat randomly censored covariates (versus type I censored covariates), other than the inefficient complete case analysis and the inadequate substitution method (Nie et al., 2010). We consider two innovative approaches to this problem. First, we extend the single imputation methods (Lynn, 2001; Richardson and Ciampi, 2003) to the semi-parametric setting and do not make distributional assumptions about the covariate of interest. Second, we develop a proper multiple imputation approach that also does not impose distributional assumptions on the covariate of interest, but rather uses a Cox proportional hazards model for the distribution of the censored covariate given other covariates in the model. While multiple imputation methods and software exist for the problem of missing covariates, they do not handle the structured, partial missingness introduced by right censoring of covariates. We evaluate our approaches in simulation studies and in application to the Alzheimer’s disease study of the association between amyloid in offspring and maternal history of dementia.

2. Notation, model and current approaches

We consider the linear model,

$$Y={\alpha }_0+{\alpha }_{1}X+{\alpha }_{2}Z+\epsilon ,$$ (1)

where X is the covariate of interest (e.g., maternal age at onset of dementia), Z is a vector of other covariates, and ε is the random error. Additionally, X is observed only if X < C, where C is the censoring variable, which we assume is independent of X. In our example, C is maternal age last known by the offspring to be dementia-free. We additionally assume that ε is independent of (C,X,Z). While we consider right censoring, all of our developments apply as well to the case of a left censored covariate. The observed data are {Y_i, T_i, Z_i, D_i}, i = 1, …, n, where n is the number of subjects in the sample, T_i = min(X_i,C_i) and D_i = 1 if X_i ≤ C_i and D_i = 0 if X_i > C_i. Motivated by the Alzheimer’s study, our primary goal is to make valid inference about α₁. However, there are situations in which inference for α₂ is of interest, as well.

2.1. Complete case analysis

The complete case analysis discards all subjects with D = 0 and fits the linear regression model to the subjects with D = 1. This restricted regression satisfies the linear regression model based on the entire sample and thus yields unbiased estimators as long as Y is independent of C, conditional on (X,Z) (Little and Rubin, 2002), i.e.,

$$E(Y|X=x,Z=z,D=1)=E(Y|X=x,Z=z,C\ge x)=E(Y|X=x,Z=z)={\alpha }_0+{\alpha }_{1}x+{\alpha }_{2}z.$$

The obvious drawback of the complete case analysis is that it potentially sacrifices information by discarding subjects. The resulting impact depends on the amount of censoring present in the sample.

2.2. Substitution methods

The simplest version of the substitution approach replaces censored values with a function of the limit of detection, C, e.g., C, $\sqrt{2}C$, 2C. Clearly this approach leads to biased estimation of α₁; the extent of the bias depends on the extent of censoring and the severity of censoring (i.e., the distance between the limit of detection or random censoring value and the natural limit for X).

An alternative version in the context of right censoring replaces censored values with E(X|X > C), where this expectation is calculated assuming a parametric distribution for X (Lynn, 2001; Richardson and Ciampi, 2003). The parameters of the distribution are estimated using the observed data in the presence of the right censoring. If the distribution of X is correctly specified, and for the simple linear regression model with no covariates other than X, this yields an unbiased estimator for α₁, though its standard error is underestimated (Richardson and Ciampi, 2003). This could be applied to limit of detection censoring or to random censoring.

Yet another version (Schisterman et al., 2006), restricted to the case of limit of detection censoring and simple linear regression with no covariates other than X, replaces censored values with E(X|X < C), where this expectation is calculated empirically from the observed data as

$$E(X|X<C)={\left(\sum _{i=1}^n{D}_i\right)}^{-1}\sum _{i=1}^n{D}_i{T}_i.$$

It is somewhat non-intuitive that this approach produces an unbiased estimator for α₁ (though with biased standard error estimation); it does, however, yield biased estimation for α₀.

2.3. Threshold methods

A different approach is that of dichotomizing the potentially censored covariate to a binary covariate (Austin and Hoch, 2004; Rigobon and Stoker, 2009) that indicates presence of absence of the event. Two authors evaluated the considerable bias in estimation of α₁ that arises from use of the estimate of the coefficient of a binary version of the censored covariate (Austin and Hoch, 2004; Rigobon and Stoker, 2009). However, they did not derive a bias correction and they did not investigate the properties of associated hypothesis tests. Qian et al. (2016) proposed two methods for estimation and inference after dichotomizing the time to event covariate relative to a threshold. The idea of this approach is to deal with the censoring by extracting information about the event time relative to the fixed threshold when it is available, and excluding observations for whom this is not possible. In the deletion threshold regression approach, subjects are coded as events if their events definitely occurred prior to the threshold and as non-events otherwise. Specifically, a threshold t* is selected and a derived binary covariate is constructed that indicates whether X ≤ t*, i.e., whether X is uncensored and observed to be less than t*, or whether X > t*, i.e., whether T = min(X,C) > t*. If C < X and C < t*, then the observation is deleted, as the relationship between X and t* is indeterminate. In the complete threshold regression approach, subjects are coded as events if their observation time preceded the threshold and as non-events otherwise. Specifically, a derived binary covariate is constructed that indicates whether T ≤ t* or T > t*. This binary covariate is less informative about X than the derived binary covariate of the first approach, but has the advantage of not deleting any observations. After the regression coefficient of the derived binary covariate is estimated through a linear regression model, a bias correction is used to estimate the regression coefficient of the original censored covariate.

3. Proposed Approaches

We propose a nonparametric and semi-parametric approach that apply to the setting of random censoring. The first approach modifies that of Richardson and Ciampi (2003) to be based on the Kaplan-Meier or Cox model estimator of the distribution of the censored covariate, rather than an assumed parametric distribution. The second approach employs proper multiple imputation, again based on the Kaplan-Meier or Cox model estimator for the censored covariates. We also present a “reverse survival regression” approach that reverses the roles of Y and X and fits a Cox model for the hazard for X given Y and Z.

3.1. Single Imputation

We consider a nonparametric version of the single imputation method proposed by Richardson and Ciampi (2003) and briefly described by Little (1992). In particular, in the case of simple linear regression with a right-censored covariate we impute the conditional expectation $E(X_j|X_j>C_j)=S^{-1}(C_j){\int }_{C_j}^{\tau }S(u)du+C_j$, which can be approximated using the trapezoidal rule as

$$\frac{{\sum }_{i=1}^{n}I\{T_{(i)}>C_j\}[S\{T_{(i)}\}+S\{T_{(i+1)}\}]\{T_{(i+1)}-T_{(i)}\}}{2S(C_j)}+C_j,$$

where S(.) is the survival function of X, τ is the upper limit of the support of X, and T₍₁₎ < T₍₂₎ < … < T_(n) are the ordered, observed values of the covariate of interest (i.e., T = min(X,C)). In practice, we estimate S(·) with the Kaplan-Meier estimator of X, Ŝ(·), and we linearly interpolate Ŝ between observed event times to approximate the values of S at censored observations. For improved approximation of the integral of the Kaplan-Meier estimate, we treat the largest observation as uncensored even if it is censored (Datta, 2005). In some cases, this may provide a close approximation to the true survivor function, but in others, such as when the largest observed age is censored at an age well below the upper limit of the support of the age of interest, it will not. In effect, this amounts to a hybrid approach between subject specific conditional expectation single imputation, and a limit of detection substitution approach. Beyond our ability to estimate the conditional expectation from the data, we resort to a simple substitution.

For the case of multiple regression with additional covariates, Z, we use a Cox model based estimator of the adjusted survivor distribution in our approximation of the conditional expectation, E(X|X > C,Z) for imputation. In particular, we assume that h(x|z) = h₀(x) exp(βz), where h(x|z) is the hazard function for X given Z = z evaluated at x, h₀(x) is the baseline hazard function for X at Z = 0 and S₀(·) is the baseline survivor function for X, and approximate E(X_j|X_j > C_j,Z_j) as

$$\frac{{\sum }_{i=1}^{n}I\{T_{(i)}>C_j\}{[S_0\{T_{(i)}\}+S_0\{T_{(i+1)}\}]}^{\text{exp}(\beta Z_j)}\{T_{(i+1)}-T_{(i)}\}}{2S_0{(C_j)}^{\text{exp}(\beta Z_j)}}+C_j.$$

In practice, we estimate the baseline survivor function using the method of Breslow (1972). This approach requires that X and C be independent conditional on Z. An alternative approach is based on a Cox model that conditions on Y, as well as Z; this is advisable if there is high partial correlation between Y and X given the observed portion of X (Little, 1992).

3.2. Multiple Imputation

Multiple imputation was originally developed for the purpose of accounting for variability in imputed estimates of missing data (Rubin, 1987). Theoretical justification of multiple imputation has been established from both Bayesian and frequentist perspectives (Rubin, 1987; Schafer, 1999). Under certain assumptions, multiple imputation mimics maximum likelihood estimation and thus yields consistent estimators (Kenward and Carpenter, 2007; Wang and Robins, 1998). These assumptions include correct full likelihood specification, which includes correct specification of the regression model for Y given (X,Z) and of the model for X given Z. Our semi-parametric model for X given Z should provide some robustness to our procedure (Lazzeroni et al., 1990). In our context of a censored covariate, the consistency of the estimates also depends on independence of C and Y given (X,Z), as required for the complete case analysis, and of C and X given Z. Our simulation results (Section 4) demonstrate this with small bias when these assumptions are met (Tables 1 and 2) and increased bias under dependence of C and Y (Tables 3 and 4). We note that the problem of a censored covariate is a highly structured imputation setting, which is not accommodated by generic software procedures that handle multiple imputation. Those procedures do not accommodate the special missing data structure of right censoring.

Table 1.

Estimation and testing of α₁ (truth is 0.5): light censoring independent of Y.

	Method	Bias	SD	SE	MSE	Type 1 error	Power
n = 100	No Censoring	0.0078	0.2685	0.2634	0.0697	0.048	0.517
	Complete Case	0.0102	0.3664	0.3529	0.1246	0.051	0.340
	Single Imputation1	0.0083	0.4046	0.2940
	Multiple Imputation	0.0233	0.3331	0.3315	0.1104	0.045	0.345
	Deletion Thresholding	−0.0351	0.2313	0.2284	0.0534	0.049	0.135
	Complete Thresholding	0.0188	0.2057	0.2100	0.0445	0.047	0.123
	Reverse survival2					0.052	0.411
n = 250	No Censoring	0.0057	0.1614	0.1604	0.0258	0.048	0.880
	Complete Case	0.0059	0.2177	0.2175	0.0474	0.050	0.656
	Single Imputation1	0.0018	0.1844	0.1763
	Multiple Imputation	−0.0129	0.1988	0.1844	0.0342	0.046	0.721
	Deletion Thresholding	−0.0179	0.1430	0.1443	0.0207	0.052	0.388
	Complete Thresholding	0.0143	0.1402	0.1324	0.0177	0.049	0.307
	Reverse survival2					0.053	0.797

¹: MSE, type I error and power not reported due to invalid SE for single imputation

²: bias, SD and SE not reported due to non-interpretability of estimate from reverse survival regression

Table 2.

Estimation and testing of α₁ (truth is 0.5): heavy censoring independent of Y.

	Method	Bias	SD	SE	MSE	Type 1 error	Power
n = 100	No Censoring	0.0078	0.2685	0.2634	0.0697	0.048	0.517
	Complete Case	0.0610	0.7576	0.7458	0.5600	0.053	0.126
	Single Imputation1	0.0815	0.5125	0.4331
	Multiple Imputation	0.0514	0.4158	0.5068	0.2594	0.051	0.132
	Deletion Thresholding	0.0509	0.2323	0.2372	0.0589	0.052	0.141
	Complete Thresholding	0.0372	0.2229	0.2219	0.0506	0.044	0.111
	Reverse Survival2					0.054	0.277
n = 250	No Censoring	0.0057	0.1614	0.1604	0.0258	0.048	0.880
	Complete Case	0.0646	0.4738	0.4746	0.2294	0.049	0.228
	Single Imputation1	0.0567	0.2997	0.2541
	Multiple Imputation	0.0442	0.2911	0.3200	0.1044	0.048	0.360
	Deletion Thresholding	0.0481	0.1457	0.1493	0.0246	0.046	0.249
	Complete Thresholding	0.0643	0.1267	0.1403	0.0238	0.053	0.186
	Reverse Survival2					0.048	0.580

¹: MSE, type I error and power not reported due to invalid SE for single imputation

²: bias, SD and SE not reported due to non-interpretability of estimate from reverse survival regression

Table 3.

Estimation and testing of α₁ (truth is 0.5): light censoring dependent on Y.

	Method	Bias	SD	SE	MSE	Type 1 error	Power
n = 100	No Censoring	0.0060	0.2709	0.2624	0.0689	0.052	0.524
	Complete Case	0.0484	0.3702	0.3619	0.1333	0.050	0.348
	Single Imputation1	−0.0104	0.3199	0.3016
	Multiple Imputation	0.0087	0.3003	0.3199	0.0709	0.048	0.366
	Deletion Thresholding	−0.0375	0.2306	0.2342	0.0563	0.055	0.119
	Complete Thresholding	−0.0343	0.2117	0.2151	0.0474	0.052	0.102
	Reverse Survival2					0.048	0.416
n = 250	No Censoring	0.0001	0.1605	0.1605	0.0258	0.047	0.872
	Complete Case	0.0368	0.2278	0.2222	0.0507	0.051	0.690
	Single Imputation1	−0.0174	0.3301	0.1819
	Multiple Imputation	0.0222	0.2144	0.2103	0.0447	0.046	0.722
	Deletion Thresholding	0.1278	0.1544	0.1539	0.0400	0.048	0.377
	Complete Thresholding	1.2149	0.1335	0.1352	1.4938	0.046	0.251
	Reverse Survival2					0.049	0.754

¹: MSE, type I error and power not reported due to invalid SE for single imputation

²: bias, SD and SE not reported due to non-interpretability of estimate from reverse survival regression

Table 4.

Estimation and testing of α₁ (truth is 0.5): heavy censoring dependent on Y.

	Method	Bias	SD	SE	MSE	Type 1 error	Power
n = 100	No Censoring	0.0060	0.2709	0.2624	0.06892	0.052	0.524
	Complete Case	−0.3810	0.8527	0.8286	0.8317	0.091	0.098
	Single Imputation1	0.1001	0.5021	0.4891
	Multiple Imputation	0.1011	0.5216	0.5314	0.2926	0.055	0.152
	Deletion Thresholding	0.0300	0.2476	0.2515	0.0641	0.059	0.129
	Complete Thresholding	−0.1049	0.2059	0.2045	0.0528	0.060	0.094
	Reverse Survival2					0.062	0.227
n = 250	No Censoring	0.0001	0.1605	0.1605	0.0258	0.047	0.872
	Complete Case	−0.3256	0.5357	0.5186	0.3750	0.110	0.157
	Single Imputation1	0.0732	0.3896	0.2837
	Multiple Imputation	0.0999	0.3659	0.3319	0.1201	0.090	0.240
	Deletion Thresholding	0.1399	0.1777	0.1868	0.0545	0.055	0.247
	Complete Thresholding	1.3124	0.1643	0.1633	1.7491	0.054	0.151
	Reverse Survival2					0.051	0.548

¹: MSE, type I error and power not reported due to invalid SE for single imputation

²: bias, SD and SE not reported due to non-interpretability of estimate from reverse survival regression

The general multiple imputation scheme consists of three steps: imputation, completed data analysis, and pooling. The imputation step involves first drawing the parameters of the posterior distribution of X given the observed data from their distribution (D’Angelo et al., 2008), and then drawing M sets of imputed values for the missing data from their posterior distribution given the observed data. The first part of this imputation step is necessary to account for the fact that the parameters are unknown and their estimates have inherent variability. The completed data analysis involves performing the desired analysis on the M completed data sets. The pooling step involves combining the estimates from the M analyses into a single multiple imputation estimate and likewise combining the estimates of variability from the M analyses, along with the between imputation variability, into a single multiple imputation variance estimate.

In particular, our multiple imputation algorithm proceeds in the following steps:

1. Sample with replacement from the original data.

2. Apply the complete case analysis. This involves fitting model (1) using the uncensored observations to sample from the distribution of the coefficients (α₀, α₁, α₂) and obtain estimates $({\hat{\alpha }}_0^c,{\hat{\alpha }}_1^c,{\hat{\alpha }}_2^c)$.

3. Fit a model to the sampled data for X given Z to estimate β and f_β(x|z), the model-based estimate of the density of X given Z, with corresponding survivor function, S_β(x|z). Standard model fitting strategies should be employed to ascertain the best fitting model for X given Z. A proportional hazards model can be assessed through examination of Schoenfeld residuals (Schoenfeld, 1982) and through inclusion of interactions of covariates with time, and through use of other graphical and numerical methods (Lin et al., 1993). To protect against multiple testing, we favor a global interaction test. These methods suggest adjustments to covariate forms used in the model for improved fit of the data. Alternative models, such as the accelerated failure time model, could be used. If the covariates X and Z are independent, or only weakly correlated, then model choice is not critical, as any model will be fit under an approximate null and will reduce to a Kaplan Meier based estimator for f(x). As we noted for single imputation (Section 3.1), we require a full estimate of the predictive density for X, f_β(x|z), which may not be available if there are censoring times that exceed the observed failure times. As we noted in Section 3.1, in this case we resort to a hybrid approach that utilizes substitution for event time generation that exceed our estimate of its distribution.

4. Generate X from its predictive distribution, P(X = x|C = c,X > c, Y = y,Z = z). This is given by:

   $$\frac{\text{Pr}(Y=y|X=x,C=c,X>c,Z=z)\text{Pr}(X=x|C=c,X>c,Z=z)\text{Pr}(C=c,X>c,Z=z)}{\text{Pr}(C=c,X>c,Y=y,Z=z)},$$

   which, under the various independence assumptions, is equal to

   $$\frac{P(Y=y|X=x,Z=z)\text{Pr}(X=x|X>c,Z=z)\text{Pr}(C=c,X>c,Z=z)}{{\int }_c\text{Pr}(Y=y|X=\upsilon ,Z=z)\text{Pr}(X=\upsilon |X>c,Z=z)\text{Pr}(C=c,X>c,Z=z)\mathrm{d}\upsilon }=\frac{\text{Pr}(Y=y|X=x,Z=z)\text{Pr}(X=x|X>c,Z=z)}{{\int }_c\text{Pr}(Y=y|X=\upsilon ,Z=z)\text{Pr}(X=\upsilon |X>c,Z=z)\mathrm{d}\upsilon }.$$

   We estimate this using the sampled coefficients from Steps 2 and 3 and the assumed linear and Cox models using:

   $$\frac{\frac{1}{\sqrt{2\pi }\hat{\sigma }}\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^{c}x-{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(x|z)/S_{\hat{\beta }}(c|z)}{{\int }_c\frac{1}{\sqrt{2\pi }\hat{\sigma }}\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^c\upsilon -{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(\upsilon |z)/S_{\hat{\beta }}(c|z)\mathrm{d}\upsilon }=\frac{\frac{1}{\sqrt{2\pi }\hat{\sigma }}\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^{c}x-{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(x|z)}{{\int }_c\frac{1}{\sqrt{2\pi }\hat{\sigma }}\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^c\upsilon -{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(\upsilon |z)\mathrm{d}\upsilon }.$$

   Thus, we impute values for X by equating a Uniform(0,1) random variable to the conditional survivor distribution for X, which is given by

   $$\widehat{\text{Pr}}(X>x|C=c,X>c,Z=z,Y=y)=\frac{{\int }_x\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^c\upsilon -{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(\upsilon |z)\mathrm{d}\upsilon }{{\int }_c\text{exp }[-{(y-{\hat{\alpha }}_0^c-{\hat{\alpha }}_1^c\upsilon -{\hat{\alpha }}_2^{c}z)}^2/2{\hat{\sigma }}^2]f_{\hat{\beta }}(\upsilon |z)\mathrm{d}\upsilon .}$$

   In practice, we use integration by parts to avoid direct estimation of the density function and the trapezoidal rule for estimation of integrals.

5. Fit a linear regression model of Y on the completed data (X,Z) and estimate the parameters of the model, $({\hat{\alpha }}_0^m,{\hat{\alpha }}_1^m,{\hat{\alpha }}_2^m)$, where the superscript m labels the estimates from the mth imputation.

6. Repeat Steps 1–5 M times.

7. Obtain multiple imputation estimates and variances, e.g., α̂₁ = ∑ α̂_1m/M and

   $$\text{Var}({\hat{\alpha }}_1)=\sum _{m=1}^M\text{Var}({\hat{\alpha }}_{1m})/M+(1+1/M)\sum _{m=1}^M{({\hat{\alpha }}_{1m}-{\hat{\alpha }}_1)}^2/(M-1),$$

   where Var(α̂_1m) is the model-based analytical variance from the fit of the linear regression model to the mth imputed data set.

We note that this multiple imputation algorithm could not be used in the case of limit of detection censoring, as there would be no observed data with which to semi-parametrically estimate the density of X|Z for X > C. In this case, a fully parametric model would be required.

3.3. Reverse survival regression

As an alternative approach to the test for association between Y and X, controlling for Z, we use the Cox proportional hazards model, h(x|y, z) = h₀(x) exp(α̃₁y + α̃₂z), where h(x|y, z) is the hazard function for X given Y and Z and h₀(x) is the baseline hazard function for X. This has the advantage of automatically and naturally handling the censored X, as it is the outcome, rather than covariate in the Cox model framework. Under the assumptions of model (1), and independence of C and X given Y and Z, we will justify that the test of H₀ : α̃₁ = 0 based on this model that reverses the natural roles of Y and X yields a valid test for H₀ : α₁ = 0, where α₁ is the effect of covariate X in model (1). However, the parameter from the Cox model, α̃₁, does not have a meaningful interpretation, as it reverses the natural chronological ordering.

First we show that α₁ = 0 implies that α̃₁ = 0. This is seen by expressing the conditional density of X given Y and Z in terms of the conditional density of Y given X and Z using Bayes’ theorem. When α₁ = 0, this leads to h(x|y, z) = k(x, z), for some function k(·), which implies that α̃₁ = 0. In particular,

$$h(x|y,z)=\frac{f_{X|Y}(x|y,z)}{{\int }_x^{\infty }{f}_{X|Y}(\upsilon |y,z)\mathrm{d}\upsilon }=\frac{\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp }\{-\frac{{(y-{\alpha }_0-{\alpha }_{1}x-{\alpha }_{2}z)}^2}{2{\sigma }^2}\}{f}_{X|Y}(x)}{{\int }_x^{\infty }\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp }\{-\frac{{(y-{\alpha }_0-{\alpha }_1\upsilon -{\alpha }_{2}z)}^2}{2{\sigma }^2}\}{f}_{X|Y}(\upsilon )\mathrm{d}\upsilon },$$

which equals $f_{X|Z}(x){\{{\int }_x^{\infty }{f}_{X|Z}(\upsilon )\mathrm{d}\upsilon \}}^{-1}=k(x,z)$ when α₁ = 0, which implies that α̃₁ = 0.

Second we show that α̃₁ = 0 implies that α₁ = 0. If α̃₁ = 0, then h(x|y, z) = h₀(x) exp(α̃₂z), which implies that for all x in the support of X,

$${\int }_x^{\infty }\text{exp }\{-{(y-{\alpha }_0-{\alpha }_{1}x-{\alpha }_2^{T}z)}^2\}g(u)\mathrm{d}u={\int }_x^{\infty }\text{exp }\{-{(y-{\alpha }_0-{\alpha }_{1}u-{\alpha }_2^{T}z)}^2\}g(u)\mathrm{d}u.$$

Taking partial derivatives with respect to x of both sides of this equation yields that α₁ = 0.

Since we use this approach only for the purpose of testing, the actual model used is less important, and must be valid only under the null hypothesis. In fact, even when proportional hazards holds for X|Z, as we assume for multiple imputation, it does not hold for X|(Y,Z). Nonetheless, as we have shown above, this provides a valid test of the null hypothesis regardless of likely violation of this proportional hazards assumption.

4. Simulations

We conducted several simulations to evaluate and compare the performances of the standard analysis when there is no censoring with the complete case analysis, threshold regression, single imputation, multiple imputation and reverse survival regression under a range of sample sizes and degree of censoring, as well as under independent versus dependent censoring. We also investigated the performance under a scenario in which the requisite assumption (for multiple imputation) of proportional hazards for X|Z was violated. We did not compare to substitution methods as they are known to be biased and suboptimal, and in some cases, intended for limit of detection and not random censoring (Schisterman et al., 2006). We used a fixed threshold of 0.056 for the threshold methods under light censoring and a threshold of 0.054 under heavy censoring, and M = 20 imputations for the multiple imputation. We assumed the true linear regression model to be given by model (1), with (α₀, α₁, α₂) = (1, 0.5, 0.25). We generated X ~ Weibull(3/4, 1/4), C₁ ~ Weibull(1/2, q), C₂ ~ Weibull(1, q), ε ~ 𝒩(0, 0.99), and Z ~ Bernoulli(0.5), with q = 2 and q = 0.35 to obtain light censoring (10–20%) and heavy censoring (40%), respectively. For our independent censoring scenarios, we set C = C₂. For our dependent censoring scenarios, we set C = C₁ if Y > 1.1 and C = C₂ if Y ≤ 1.1 and we set q = 2 for light censoring and q = 0.3 for heavy censoring. Under this dependent censoring scenario, the complete case analysis is not valid, as C is not independent of Y given (X,Z). Likewise, the multiple imputation approach is not valid as it relies on the complete case analysis as well as on the assumption of independence of X and C given Z, which does not hold under this censoring model. The single imputation and threshold approaches are likewise not valid. The reverse survival regression method is valid, as it requires only independence of X and C given (Y,Z), which is satisfied by this model. We note also that the proportional hazards model for X|(Y,Z) assumed by the reverse survival regression is not satisfied. As we noted in Section 3.3, and as we validate in our simulations, this does not matter for the purpose of hypothesis testing.

We generated 5000 replications to assess type I error and 1000 replications for power, bias, and standard error estimation. We report the simulation estimate of the bias of α̂₁ (Bias), the simulation based standard deviation (SD), the average of the standard error based on the completed data set (SE), the averaged mean squared error (MSE), the estimated type I error rate based on the Wald test and the estimated power based on the Wald test. We do not report MSE, type I error or power for the single imputation method, as the standard error for this method is underestimated. We do not report bias or standard errors or MSE for the reverse survival regression method, as this method does not provide an estimate of α₁.

Table 1 lists the simulation results for the independent, light censoring scenario, under which all methods are valid and are expected to display reasonable performance. The bias is small for all methods, and decreases with increased sample size. The standard deviations of the threshold method estimators are smaller than those from other methods, with the complete case standard deviation being the largest for n = 250 and the second largest for n = 100, at which the single imputation standard deviation is largest. The simulation standard deviations are comparable to the average of the analytical standard errors, except for the single imputation method, for which the within sample standard errors are biased downward. The type I error rates are all close to the nominal level of 0.05. The no-censoring entries in the tables provide the benchmark for power. The multiple imputation approach achieves higher power than the complete case approach, but is surpassed by the reverse survival approach.

Table 2 lists the simulation results for the independent, heavy censoring scenario. As expected, the biases are larger than seen in Table 1, under light censoring. The multiple imputation approach achieves lower bias than the complete case analysis. The multiple imputation standard errors are considerably lower than those of the complete case analysis, though the threshold method standard errors are the lowest among all methods. As for the case of light censoring, the type I error is close to the nominal 0.05 for all methods and the power of the multiple imputation method beats that of the complete case, but is surpassed by that of the reverse survival regression method.

Tables 3 and 4 list the simulation results for the dependent censoring scenario, under which only the reverse survival regression method is valid. The inappropriateness of the complete case, imputation and thresholding methods are especially apparent in the presence of the heavy censoring of Table 4. In that scenario, inflated type I errors and large biases are evident. The reverse survival regression method maintains the nominal 0.05 level of significance for n = 250 and has reasonable power.

To evaluate the robustness of the multiple imputation procedure under violation of proportional hazards of X|Z, we simulated data as for the analyses reported in Tables 1 and 2, with the exception of X, which we simulated from a Weibull distribution with shape equal to 0.6+0.9Z and scale equal to 1/4. This induces a log hazard for X of

$$\text{log}(0.6+0.9Z)+(0.6+0.9Z-1)\text{ log }x-(0.6+0.9Z)\text{ log}(1/4),$$

which clearly is not a proportional hazards model for binary Z. In a separate simulation of 5000 observations of (X,Z) we verified that under this model, the proportional hazards assumption is strongly violated using martingale residuals (p < 0.0001). In Supplementary Table S.1 it is seen that under light censoring, the multiple imputation estimate under the misspecified proportional hazards model results in a 25% increase in bias relative to the complete case estimate and slightly lower power. In Supplementary Table S.2 under heavy censoring, the bias of the multiple imputation estimate is increased by 50% relative to the complete case bias for n = 250, though no difference is seen for n = 100. The power for n = 250 is about twice that of the complete case analysis due to a decreased standard error. The type I error in all cases is just slightly above the nominal level of 0.05. This example reinforces the importance of fitting an appropriate model for X|Z within the multiple imputation procedure, but also suggests that incorrect use of a proportional hazards model still may produce a valid test that preserves the type I error.

5. Association between myloid in offspring and maternal history of dementia

In an Alzheimer’s disease study conducted at Massachusetts General Hospital and Brigham and Women’s Hospital, the association between amyloid deposition, as measured through in vivo imaging with Pittsburgh Compound B (PiB), and maternal age of onset of dementia, was of interest (Maye et al., 2016). However, as not all mothers were known to have had onset of dementia at the time of the offspring interview, their ages at onset were right censored by their ages at the last time they were known by their offspring to be dementia-free. One hundred and forty seven participants were enrolled in the study, which was approved by the Partners Human Research Committee. All participants were evaluated with interviews, cognitive testing and informant interviews, and judged to be either cognitively normal with Clinical Dementia Rating [CDR] 0 (Morris, 1993) (N=104) or mildly impaired (N = 43; CDR 0.5). None of the participants had any neurological or medical illness or any history of alcoholism, drug abuse, or head trauma. All scored 11 or lower on the Geriatric Depression Scale [GDS] (Yesavage et al., 1982), 22 or higher on the Mini Mental State Examination [MMSE] (Folstein et al., 1975) and 93 or higher on the American National Adult Reading Test [AMNART] (Ryan and Paolo, 1992).

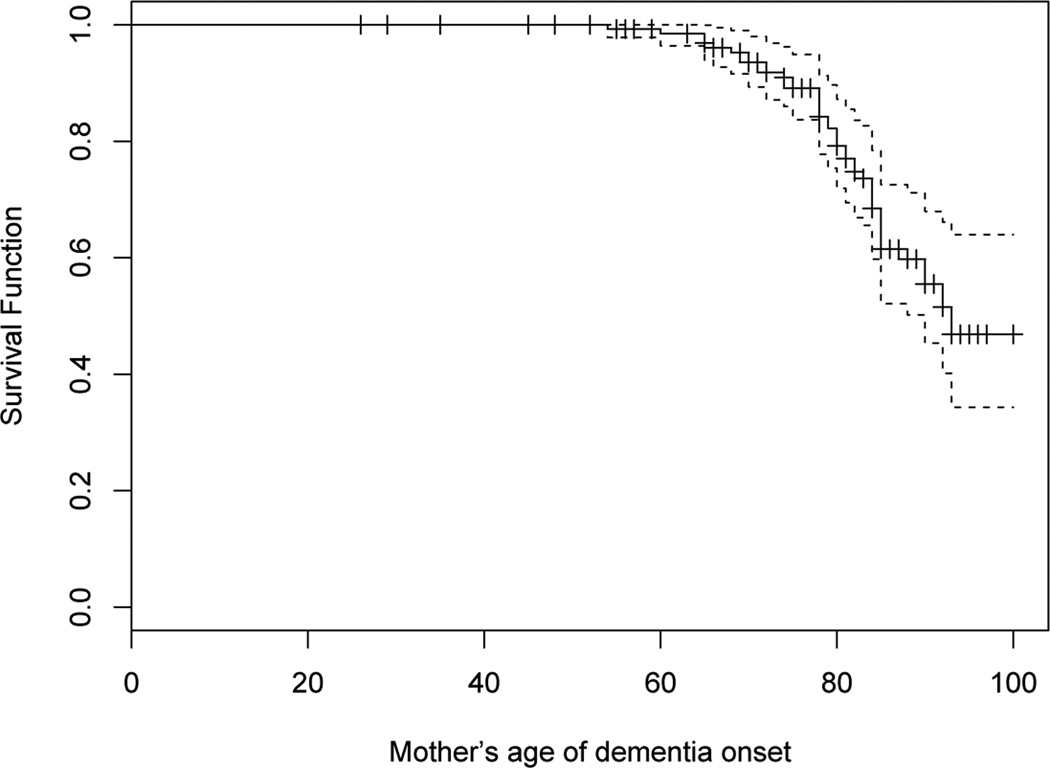
A parental history questionnaire yielded information about 141 mothers of participants. Age of dementia onset was reported for 42 of these mothers and it was right censored for 99 (70%) of them. The median age of follow up without dementia for these 99 mothers was 83 (with 25th percentile of 71.5 and 75th percentile of 89). The median age of onset of dementia was 92 (see Figure 1). Thus, these mothers are likely to contribute important information to the estimate of association due to their advanced ages without dementia. Using complete case analysis, multiple imputation (M = 20), and the two threshold regression approaches (using an age threshold of 75), we fitted a linear regression model to the continuous outcome measure of amyloid, as a function of maternal age of onset of dementia, with adjustment for offspring age, gender, CDR and education. We obtained similar results with a threshold of 70 (not shown), and did not obtain stable results for smaller thresholds. We confirmed that the data did not reject proportional hazards for age of onset given the covariates through a global test of interaction between the covariates in the model and log age of onset, which supported our multiple imputation modeling (Step 3 in Section 3.2). We also applied the reverse survival regression approach and fit a Cox proportional hazards model with maternal age at dementia as the possibly right censored outcome, and amyloid as the primary covariate, along with adjustment for age of offspring (thresholded at 81, the third quartile of the distribution), gender, CDR and education. Readers may contact Dr. Folefac Atem (Folefac.D.Atem@uth.tmc.edu) for software assistance.

Fig. 1.

Kaplan-Meier Estimator of the distribution of mother’s age of dementia onset.

The results of these analyses are presented in Table 5. The estimates from the different methods are reasonably close and qualitatively similar; they all suggest a decrease in amyloid of about 0.05–0.1 units for every increase of 10 years in maternal onset. The actual difference between the complete case estimate (−0.0098) and the multiple imputation estimate (−0.0049) could be due to imperfect estimation of the density of X|Z due to incomplete estimation of the survivor function for age at onset (Figure 1) or to violation of the independent censoring assumption, both of which are required for the multiple imputation. Although the Kaplan Meier estimate in Figure 1 does not drop below about 50%, it does extend to about age 100. As our imputation procedure treats the largest censored age as a dementia onset age, and since this largest age is extremely old, this “fix” should not be problematic. However, it is possible that it is contributing to a bias in the estimate of α₁. Although the actual reverse survival regression log hazard ratio estimate is not meaningful, its sign is informative about the direction of the association; it is positive, which is consistent with an association between higher amyloid in offspring and earlier onset of dementia in mothers. Consistent with the results from the simulations, the reverse survival regression approach yielded the most significant association between offspring amyloid and maternal age of onset of dementia (p=0.001). The multiple imputation p-value is 0.01, similar to that of the deletion threshold method, while the complete case p-value is 0.05. The multiple imputation standard error is less than half that of the complete case standard error, which suffers from deletion of 70% of subjects. While we cannot test for independent censoring, we might be concerned that death prior to onset of dementia would not qualify as an independent censoring event. In this case, we need to view our Cox models as models for the cause specific hazard for dementia that are conditional on being alive. We discuss alternative approaches in the Discussion.

Table 5.

Application to study of amyloid and maternal age of onset of dementia.

Method	Estimate (α̂1)	SE	p-value	% deleted
Complete Case	−0.0098	0.0050	0.057	70.2%
Multiple Imputation	−0.0049	0.0019	0.010
Deletion Thresholding	−0.0085	0.0034	0.012	24.8%
Complete Thresholding	−0.0082	0.0049	0.094
Reverse Survival1			0.001

¹: estimate and SE not reported by reverse survival regression due to non-interpretability of the estimate

6. Discussion

We have developed a multiple imputation method to accommodate randomly censored covariates in a regression model. Our method is semi-parametric, in that it uses the parametric assumptions on the linear regression model of interest in conjunction with the semi-parametric Cox model for the censored covariate. It performs well in simulations, exhibiting superior performance to the complete case analysis. However, it has lower power for testing for association between the outcome and the censored covariate than the reverse survival regression approach, while requiring stronger assumptions for validity. Nonetheless, it has the important advantage of providing a consistent estimator for the association parameter, α₁. The reverse survival regression approach does not yield a meaningful estimator. Multiple imputation is not uniformly better than the threshold methods, though it has the important advantage of not requiring selection of the threshold, t*.

Motivated by the Alzheimer’s study, we have focused exclusively on estimation and testing of α₁, which measures the association between maternal age of onset and amyloid in the offspring. In other settings, the coefficients for all covariates in the linear model may be of scientific interest. Under correct model specification and the assumptions of independence of censoring, we expect these estimators following multiple imputation of the censored covariate to have good properties, as well.

One extension of our method is to allow for a mixture model for maternal onset of dementia, to accommodate the possibility that some individuals will never experience onset of dementia. Currently, we treat all mothers who were not observed with dementia as right censored. Another consideration is a more complex treatment of some censoring events as competing risks for the event of dementia onset through use of the cumulative incidence function and subdistribution hazard regression (Fine and Gray, 1999). Another extension of potential interest is to multiple censored covariates. This situation would arise if the covariates included ages of onset of multiple conditions for a single individual, for example. This could also be handled by an expanded multiple imputation algorithm or threshold methods. A simple test based on reverse survival regression would require estimation of a more complicated frailty model. Another important extension is to alternative regression models, such as logistic regression and Cox regression. In these nonlinear regression settings the threshold method will not be applicable, but the multiple imputation and the reverse survival regression will be.