Abstract
The density bias, documented within the foraging domain for some monkey species and for human infants, emerges when perceived numerosity is affected by inter-stimulus distance such that densely arranged food items appear more numerous relative to the same amount of food sparsely arranged. In this study, capuchin monkeys and rhesus monkeys were presented with a computerized relative discrimination task that allowed for the control of stimulus size, inter-elemental distance, and overall array pattern. The main objective was to determine whether the density bias was a more widespread and general perceptual phenomenon that extends beyond the foraging domain, similar to other numerosity illusions and biases. Furthermore, we compared the current results to these same monkeys’ data from a previous study on the Solitaire numerosity illusion to investigate a potential link between a density bias and this related numerical illusion. Capuchin monkeys showed a density bias in their perceptual discrimination of dense versus sparse stimuli; however, rhesus monkeys perceived this bias to a lesser degree. Individual differences were evident, as with the Solitaire illusion. However, there was not a relation between susceptibility to a density bias and susceptibility to the Solitaire illusion within these same monkeys.
Keywords: Quantity discrimination, Density bias, Rhesus monkeys, Capuchin monkeys, Solitaire illusion
The ability to discriminate based on relative quantity, or to discern more from less, is an evolutionarily ancient and phylogenetically widespread cognitive ability that extends from distantly-related species to our closest-living relatives, the primates (see Beran, Parrish, & Evans, 2014, and Brannon & Merritt, 2011, for reviews). Such a capacity for representing quantitative information is presumably adaptive in the sense that discriminating stimuli based on relative quantity (e.g., discerning more food from less, avoiding larger numbers of predators, joining larger social groups for protection, and attracting a greater number of potential mates) directly translates into greater survival and higher reproductive success (Hamilton, 1971; Kitchen, 2004; Lyon, 2003). Many species show evidence of a shared system for the approximate representation of quantitative information (see Beran & Parrish, 2016; Brannon, 2006, for reviews). This shared system, often referred to as the approximate number system, represents quantities inexactly with decreasing accuracy in discriminating and estimating set size as true set size increases (e.g., Brannon & Roitman, 2003; Cantlon, Platt, & Brannon, 2009; Gallistel & Gelman, 2000).
Further evidence for continuity in quantity processing stems from work on numerosity illusions, which emerge when stimuli are under- or overestimated in terms of number or amount as a function of the spatial arrangement of individual items within a set. There is evidence for shared processing of a variety of visual illusions across human and nonhuman primate species. For example, human adults (Chesney & Gelman, 2012) and rhesus macaques (Macaca mulatta; Beran & Parrish, 2013) underestimate sets of individual circles if one set contains circles that overlap or are contained wholly within other circles (i.e., nested sets). Humans (Ginsburg, 1976, 1980) and rhesus macaques (Beran, 2006) overestimate sets of regularly arranged items (e.g., straight rows and columns) relative to the same number of items that are randomly arranged (e.g., scattered placement). Importantly, this continuity in the perceptual processing of numerosity illusions across primates provides support for the idea of similarity in the underlying perceptual and numerical systems responsible for perceiving, assessing, and estimating quantitative information.
A specific quantity bias that may have broader implications for other perceptual illusions is the density bias, in which perceived numerosity is affected by inter-stimulus distance. Decreased density of sets leads to perceptions of increased numerosity for human adults such that sets of dots are overestimated as items become more sparsely arranged (Allik & Tuulmets, 1991, 1993; Krueger, 1972, 1984). As proposed within Allik and Tuulmets’ (1991) occupancy model of perceived numerosity, these results suggest that the set with the overall larger surface area occupied by all dots will be chosen as more numerous. Contrary to these results, a developmental study reported an opposite bias among 10-month old infants presented with two sets of edible items (cookies), one densely arranged and the other sparsely arranged (Uller, Urquhart, Lewis, & Berntsen, 2013). The infants demonstrated a density bias, preferentially reaching for densely arranged food sets more often than they did for sparse arrangements of the same number of food items across two experiments, although there were individual differences among infants. Comparative work with cotton-top tamarins (Saguinus oedipus) and marmosets (Callithrix jacchus) also provided evidence of a density bias among New World monkeys, whose data indicated a significant preference for densely arranged food items relative to the same amount of food sparsely arranged (Stevens, Wood, & Hauser, 2007).
A possible explanation for this difference comes from foraging theory, which predicts that organisms should maximize caloric intake while reducing energy expenditure (Stephens & Krebs, 1986). In some cases, this could occur if an animal attends to non-numerical quantitative variables such as volume and surface area to discriminate the largest food patch available (Davis & Pérusse, 1988). Experimental evidence suggests that a diverse set of species display denseness-sensitivity in foraging scenarios, with a preference for more densely baited food sites among primates (e.g., orangutans (Pongo pygmaeus abelii): MacDonald & Agnes, 1999) and several species of birds (e.g., pigeons (Columba livia): Mitchell, Calton, Threlkeld, & Schachtman, 1996; turnstones (Arenaria interpres): Vahl, Lok, van der Meer, Piersma, & Weissing, 2005). For example, turnstones experienced increased foraging success (measured as food intake rate) in response to clumped food sources as compared to dispersed sources (Vahl et al., 2005). Food from a more densely arranged patch has a lower energetic cost than a more sparsely arranged food patch, because less energy would be expended to collect the food in the former case during foraging. A density bias would therefore maximize the benefit-to-cost ratio of animals’ foraging efforts (see Uller et al., 2013, for a full discussion).
A food set’s distribution relative to other sets within a foraging situation also impacts search efficiency, such that densely arranged food clusters are preferred by some species. In an experimental foraging task, capuchin monkeys’ search behavior was affected by the spatial distribution of baited containers such that monkeys exhausted each container in a clustered location before moving to the next food patch (De Lillo, Visalberghi, & Aversano, 1997). By exhausting a cluster of food containers (i.e., a food patch), errors in re-searching a depleted food site were decreased. Attending to the distribution among food patches as well as within-set item distribution may attenuate memory load during an exhaustive search, such that organisms have to remember fewer clustered sets, rather than many individual locations (see De Lillo et al., 1997).
From a food competition standpoint, densely arranged food sets (clumped resources) lead to a decrease in cooperative behavior in some experimental settings testing cooperation in capuchin monkeys (de Waal & Davis, 2003). Similarly, dense food patches lead to subsequent reductions in foraging success for subordinate birds that were in the presence of more dominant birds (Vahl et al., 2005). Dispersed food sets are preferred in cooperative scenarios to clumped resources, reducing the potential likelihood for competition over food with conspecifics and the monopolization of food sources by dominant foragers. Thus, sensitivity to the spatial arrangement of edible items in a foraging context can lead to higher rates of return and reduced competition, placing a premium on attention to not only a set’s quantity, but also to set distribution. Taken together, these results suggest that density is a particularly salient cue for nonhuman primates within the foraging domain when judging the relative quantity of multiple food sets or individual food items within a set.
In the current study, we investigated the extent to which density impacts perceptual quantity discrimination in a non-foraging domain. Our prediction was that if density is a salient cue regarding quantitative processing, we should expect this bias to emerge when judging inedible sets of stimuli. If this prediction held, the density bias would be considered a prevalent and domain-general cue for assessing stimulus quantity among primates. Thus, we investigated whether density influenced quantity discriminations in rhesus macaques and capuchin monkeys to the extent reported for human infants and other monkey species (Stevens et al., 2007; Uller et al., 2013). The current work differed from the previous tests of the density bias with infants and callitrichids that presented a foraging paradigm to its participants. Instead, we presented monkeys with a computerized relative quantity discrimination task and systematically varied the density of items within virtual sets. We predicted that monkeys would overestimate dense quantities relative to sparse quantities, in line with evidence of the density bias in previous work.
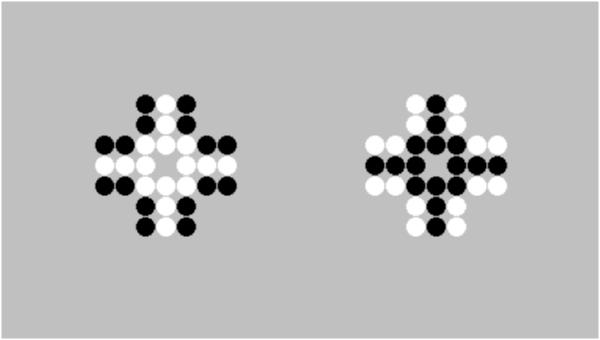
Our secondary interest in the density bias stems from its possible explanatory value regarding a different numerosity illusion that is prevalent in humans but thus far has been observed inconsistently in nonhuman primates. The Solitaire numerosity illusion (Figure 1) causes adult humans to misperceive the relative quantities of two different colored (but otherwise identical) items in intermingled sets (Frith & Frith, 1972). The number of same-color items is overestimated when clustered in the center of an array and underestimated when arranged along the perimeter of the same array (i.e., people overestimate the centrally-located black dots in the image at right, despite both images having equal numbers of both colors of dots). One hypothesis is that this illusion occurs because the peripheral dots lack a clustered appearance, consistent with Gestalt theory that states that items forming a better Gestalt, or overall shape or pattern, appear more numerous (Frith & Frith, 1972; Wertheimer, 1938). Chimpanzees (Pan troglodytes) do not fall prey to this illusion, showing no bias towards perceiving internally clustered patterns as more numerous, while rhesus macaques and capuchin monkeys sometimes demonstrated this bias, with their overall group performances providing evidence of a potential Solitaire illusion effect (Agrillo, Parrish, & Beran, 2014). However, large individual differences were reported in these primate species.
Figure 1.
The Solitaire illusion. Each array contains an equal number of black and white dots, but human adults typically overestimate the centrally-located black dots in the image at right relative to the peripherally-located black dots in the image at left.
Young children also demonstrated an overall less frequent perception of the illusion relative to older children who were more consistent in their illusory perception (Parrish, Agrillo, Perdue, & Beran, 2016). We documented a significant positive correlation of age in months (from 29 to 66 months) and the percentage of choices of the Solitaire array as more numerous, suggesting that human-unique experiences (e.g., emerging counting principles) may lead to stronger illusion susceptibility rather than this illusion being more deeply grounded in perceptual processing. Consistent with this reported age effect, other research suggests that children develop a more adult-like global processing bias around 6 years of age (as compared to 4 years of age), which impacts the perceptual grouping of individual items comprising a figure into a cohesive array (Dukette & Stiles, 1996). Global-to-local processing of multi-element figures is a hallmark characteristic of human adult perceptual processing (e.g., Navon, 1977, 1981), and also may support the emergence of the Solitaire illusion in older children and adults.
In the current study, we compared these individual monkeys’ performance in the quantity discrimination task in the current study to their individual performances with the Solitaire illusion from previous testing (Agrillo et al., 2014). We predicted that monkeys would show a correlation between the extent of their perception of the Solitaire illusion and the extent to which they showed a density bias in the current study. This correlation could provide evidence of a potential mechanism underlying the individual differences in nonhuman primates’ perception of the Solitaire illusion.
Methods
Participants
We tested 15 adult capuchin monkeys, seven males and eight females, and seven adult male rhesus monkeys (see Table 1). All monkeys previously had been trained to use the computerized apparatus (Evans, Beran, Chan, Klein, & Menzel, 2008; Richardson, Washburn, Hopkins, Savage-Rumbaugh, & Rumbaugh, 1990). Monkeys worked in test sessions typically between 2 and 4 hours, and they worked or rested at their own choosing throughout these sessions. Monkeys always had access to water, and were given a daily meal each afternoon independent of how much they worked on the computer task. All testing protocols complied with guidelines for working with nonhuman primates as established by protocols approved by the Georgia State University Institutional Animal Care and Use Committee. GSU is accredited by the Association for Assessment and Accreditation of Laboratory Animal Care.
Table 1.
Demographic information and number of test sessions completed for monkeys.
| Name | Gender | Age | # of Sessions |
|---|---|---|---|
| Capuchin Monkeys | |||
| Bailey | Female | 16 | 5 |
| Benny | Male | 12 | 5 |
| Gabe | Male | 17 | 6 |
| Gambit | Female | 19 | 6 |
| Gonzo | Female | 9 | 7 |
| Gretel | Female | 12 | 4 |
| Griffin | Male | 18 | 5 |
| Liam | Male | 12 | 5 |
| Lily | Female | 18 | 10 |
| Logan | Male | 10 | 3 |
| Mason | Male | 17 | 3 |
| Nala | Female | 13 | 9 |
| Nkima | Male | 8 | 6 |
| Widget | Female | 7 | 6 |
| Wren | Female | 13 | 4 |
| Rhesus monkeys | |||
| Chewie | Male | 16 | 5 |
| Han | Male | 13 | 4 |
| Hank | Male | 33 | 9 |
| Lou | Male | 23 | 4 |
| Luke | Male | 16 | 6 |
| Murph | Male | 23 | 13 |
| Obi | Male | 12 | 4 |
Apparatus
The monkeys were tested using the Language Research Center’s Computerized Test System. This system consisted of a personal computer, digital joystick, color monitor, and pellet dispenser (Evans et al., 2008; Richardson et al., 1990). Monkeys manipulated the joystick with their hands to control a small cursor somewhere on the computer screen. Contacting stimuli with the cursor sometimes resulted in the delivery of 94-mg (rhesus monkeys) or 45-mg (capuchin monkeys) banana-flavored chow pellets (Bio-Serv, Frenchtown, NJ) via a pellet dispenser that was connected to the computer. The task program was written in Visual Basic 6.0.
Design and procedure
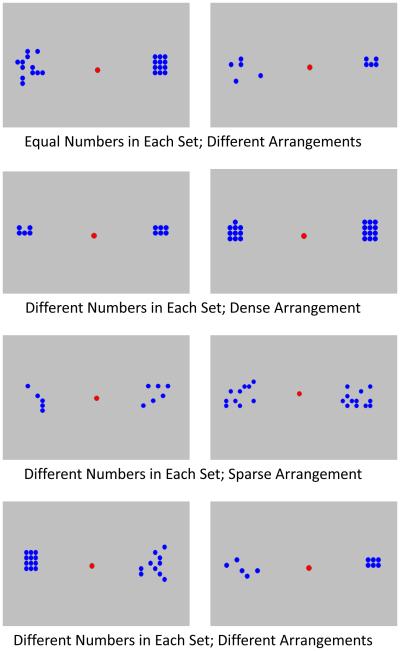
Each trial presented a monkey with two stimulus arrays, on the left center and right center of the screen. Those arrays consisted of blue dots on a grey background, and the goal was to select the array with the larger number of dots. The dots were positioned within a 7 by 7 array grid on each side of the screen, and the diameter of each dot was 17 pixels. Figure 2 presents all of the trial presentation types.
Figure 2.
Examples of the various trial types.
Some trials had unequal numbers of dots, and on those trials, choosing the larger array led to a melodic tone and the delivery of a single food pellet. Incorrect selections led to a buzz tone, and a 20 second timeout period during which the screen remained blank. Then, the next trial was presented. Other trials presented equal numbers of dots. Any selection on those trials led to a .50 probability of food reward and tone and a .50 probability of simply advancing to the next trial without any timeout or other feedback. We presented two different quantity comparisons: 5 versus 6 items and 10 versus 12 items.
For trials with unequal numbers of dots, both arrays could be densely arranged, sparsely arranged, or one could be densely arranged and one sparsely arranged. This created a number of conditions. The Sparse Control and Dense Control conditions included all trials where the arrangement (sparse or dense) was the same for both arrays. The Dense More condition included trials in which the larger array was densely arranged and the smaller array was sparsely arranged. If the density bias emerged, this trial type should lead to performance levels greater than baseline (control trials) because the truly larger number of items was densely arranged, leading to a greater likelihood of selecting this array. The Dense Less condition included trials in which the smaller array was densely arranged and the larger array was sparsely arranged. If the density bias were to emerge, this trial type should disrupt performance, as the monkeys should overestimate the denser but smaller array relative to the sparser but larger array.
In Equal trials, an equal number of dots were presented in each array. One array was presented in a dense arrangement where all dots touched each other and were tightly clustered and one array was sparsely arranged so that none of the dots touched each other (see Figure 2). If the density bias emerged, monkeys should select the densely arranged array at levels greater than chance.
All trial possibilities are outlined in Table 2. Each monkey completed 2,400 trials in the experiment. Monkeys worked for as many trials as they chose in daily sessions and so the number of sessions varied across monkeys (see Table 1).
Table 2.
Description of trial types.
| Comparison of Equal Sets | Comparison of Unequal Sets | ||
|---|---|---|---|
|
| |||
| Set 1 | Set 2 | Set 1 | Set 2 |
| 5 Sparse | 5 Dense | 5 Sparse | 6 Sparse |
| 6 Sparse | 6 Dense | 5 Sparse | 6 Dense |
| 10 Sparse | 10 Dense | 5 Dense | 6 Sparse |
| 12 Sparse | 12 Dense | 5 Dense | 6 Dense |
| 10 Sparse | 12 Sparse | ||
| 10 Sparse | 12 Dense | ||
| 10 Dense | 12 Sparse | ||
| 10 Dense | 12 Dense | ||
Note. For all trial types, the left-right presentation of these sets was randomized across trials.
Results
Capuchin monkeys
The capuchin monkeys performed statistically better than chance at selecting the larger array when there was a true numerical difference (M = 62.76, SEM = 1.59, t(14) = 8.05, p < .001, Cohen’s d = 2.08; one-sample t-test comparing performance to 50% chance level). This also was true examining only the small comparison (5 versus 6; M = 65.29, SEM = 1.70, t(14) = 9.00, p < .001, Cohen’s d = 2.32) and the large comparison (10 versus 12; M = 59.96, SEM = 1.72, t(14) = 5.80, p < .001, Cohen’s d = 1.50). Interestingly, capuchin monkeys performed significantly better on the small comparison than on the large comparison, despite both having the same ratio, t(14) = 4.81, p < .001, Cohen’s d = 0.84. These data confirm that even with this difficult comparison ratio, monkeys chose the larger array.
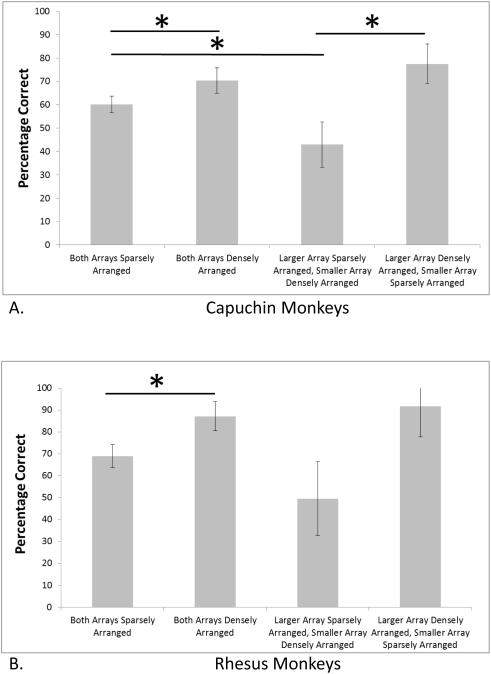
We next conducted a within-subjects ANOVA with trial type as the independent variable. There were four trials types (Figure 3a – capuchin monkeys; Figure 3b – rhesus monkeys): Sparse Control, Dense Control, Dense More, and Dense Less. Because of a violation of the assumption of sphericity, we used the Greenhouse-Geisser correction (epsilon = .389) for this ANOVA. This analysis revealed a significant difference among these trials types for capuchin monkeys, F(1.17, 16.36) = 12.57, p = .001, partial η2 = .52. To examine this effect more closely, we compared performance for select comparisons to evaluate the role of stimulus density, and because we performed multiple tests, we applied the Bonferroni correction and set alpha at .0125. Performance was significantly better for Dense Control trials than Sparse Control trials, t(14) = 4.46, p = .001, Cohen’s d = 1.16. Performance was significantly better for Dense More trials than Dense Less trials, t(14) = 3.92, p = .002, Cohen’s d = 1.99. Performance was significantly better for Sparse Control trials than Dense Less trials, t(14) = 3.58, p = .003, Cohen’s d = 1.24. The difference between Dense Control trials and Dense More trials approached but did not exceed conventional levels of statistical significance, t(14) = 2.14, p = .051, Cohen’s d = 0.53. These significant effects all are reflective of a bias to perceive dense arrays as being more numerous than sparse arrays.
Figure 3.
The percentage of trials correct for capuchin monkeys (A) and rhesus monkeys (B) for the four trial types in which array sizes differed in number of items and stimulus organization. Asterisks indicate significant differences in performance between two trial types. The error bars indicate 95% confidence intervals.
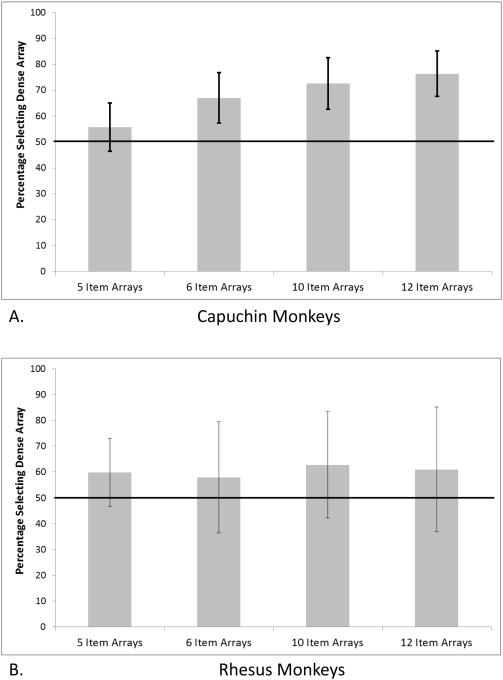
For Equal trials, Figure 4a presents the percentage of trials the capuchin monkeys selected the more densely arranged array for trials in which both sets contained the same number of items. The monkeys showed a significant bias for the densely arranged array for the comparisons with six items in each set, t(14) = 3.46, p = .004, Cohen’s d = 0.89, 10 items in each set, t(14) = 4.45, p = .001, Cohen’s d = 1.15, and 12 items in each set, t(14) = 5.92, p < .001, Cohen’s d = 1.53. There was no preference for 5 items, t(13) = 1.23, p = .24, Cohen’s d = 0.32.
Figure 4.
The percentage of trials for capuchin monkeys (A) and rhesus monkeys (B) in which the dense set of stimuli was selected for each of the set sizes for Equal trials. The long horizontal line indicates the chance level, and the errors bars indicate 95% confidence intervals.
Rhesus monkeys
The rhesus monkeys performed statistically better than chance at selecting the larger array when there was a numerical difference (M = 65.01, SEM = 1.32, t(6) = 11.34, p < .001, Cohen’s d = 4.29; one-sample t-test comparing performance to 50% chance level). This also was true when examining only the small comparison (5 versus 6; M = 65.53, SEM = 1.76, t(6) = 8.80, p < .001, Cohen’s d = 3.33) and the large comparison (10 versus 12; M = 64.50, SEM = 1.59, t(6) = 9.11, p < .001, Cohen’s d = 3.44). Unlike for the capuchin monkeys, the rhesus monkeys showed no difference in performance on the large comparison than on the small comparison, t(6) = 0.50, p = .63, Cohen’s d = 0.24. These data confirm that even with this difficult comparison ratio, monkeys chose the larger array.
We conducted the same within-subjects ANOVA as with the capuchins with the same four trials types (Figure 3b). Because of a violation of the assumption of sphericity, we used the Greenhouse-Geisser correction (epsilon = .40) for this ANOVA. This analysis revealed a significant difference among these trials types for rhesus monkeys, F(1.2, 7.2) = 5.76, p = .04, partial η2 = .49. To examine this effect more closely, we compared performance for select comparisons to evaluate the role of stimulus density, and because we performed multiple tests, we applied the Bonferroni correction and set alpha at .0125. Performance was significantly better for Dense Control trials than Sparse Control trials, t(6) = 2.58, p = .04, Cohen’s d = 1.85. Performance approached but did not exceed statistically significant levels of difference for Dense More trials in comparison to Dense Less trials, t(6) = 2.32, p = .06, Cohen’s d = 2.00. Performance approached but did not exceed statistically significant levels of difference for Sparse Control trials versus Dense Less trials, t(6) = 2.34, p = .058, Cohen’s d = 1.05. There was no difference for Dense Control trials compared to Dense More trials, t(6) = 0.61, p = .57, Cohen’s d = 0.27.
For Equal trials, Figure 4b presents the percentage of trials the rhesus monkeys selected the more densely arranged array for trials in which both sets contained the same number of items. The monkeys showed no significant bias for the densely arranged array or the sparsely arranged array for any of the comparisons, all t(6) < 1.45, p > .19, all Cohen’s d < 0.55.
Performance Compared to Solitaire Illusion Perception
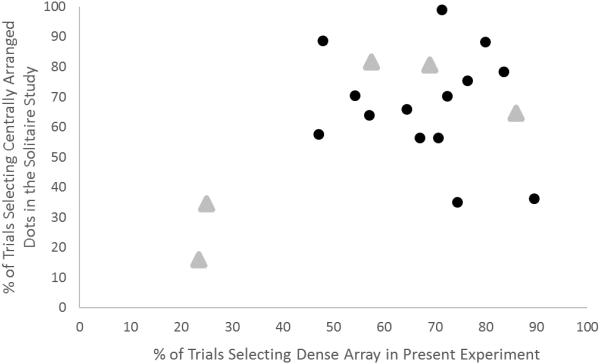
Figure 5 presents for each individual within each species the proportion of trials in which the Solitaire illusion was selected in Agrillo et al. (2014) and Parrish et al. (2016) and the proportion of trials in which the more densely arranged set was selected over the sparsely arranged set when both sets had equal numbers of items in the present experiment. The figure illustrates that most monkeys showed a bias in both tasks to choose the centrally arranged stimuli when Solitaire arrangements were presented and the densely arranged arrays in the present study. However, although the rhesus monkeys showed a high correlation between these two proportions, it was not statistically significant, r(3) = .80, p = .10, 95% CI [−.27, .98]. The capuchin monkeys showed a non-significant negative correlation, r(12) = −0.17, p = .57, 95% CI [−.63, .40].
Figure 5.
The percentage of trials in which each monkey selected the centrally arranged dots in the Solitaire illusion studies (Agrillo et al., 2014; Parrish et al., 2016) and the percentage of trials in which the densely arranged array was selected in the present experiment in which both sets had equal numbers of items. Black circles indicate individual capuchin monkeys and grey triangles indicate rhesus monkeys.
Discussion
This experiment extended the study of the density bias to novel primate species (capuchin monkeys and rhesus monkeys) in a non-foraging domain using a computerized relative quantity judgment task. Monkeys were trained to select the larger of two dot sets that varied in terms of stimulus density. Both species performed statistically better than chance at selecting the larger of two dot arrays when there was a true numerical difference, even in the presence of rather difficult discrimination ratios (5 items vs. 6 items and 10 items vs. 12 items). Furthermore, both species performed better in the dense control trials (both arrays were dense) relative to the sparse control trials (both arrays were sparse). This result indicated elevated discrimination performance when comparing dense versus sparse sets, but this result alone does not support a density bias.
In the truest test of the density bias, the capuchin monkeys showed a significant bias for three of the four array sizes (6, 10, and 12, but not 5) in choosing the densely arranged array over the sparsely arranged array when the arrays were equal in number. This is a clear indication of the bias among capuchin monkeys, but the same pattern of results was not documented for rhesus macaques. When the two arrays to be compared differed in dot quantity, capuchin monkeys performed better when the larger array was more densely arranged than when it was sparsely arranged. Rhesus performance approached but did not exceed statistically significant levels of difference for these same comparisons. Furthermore, there was variability between individual monkeys for both species. Thus, there appears to be a species difference in terms of sensitivity to the density bias when presented in a non-foraging domain, with more robust effects seen in the capuchin monkey.
These results are interesting in light of the Stevens et al. (2007) study with marmosets and tamarins and the Uller et al. (2013) study with human infants using a food-choice discrimination paradigm. Uller and colleagues predicted that the density bias emerges within animals (and infants) as a predisposition to forage for clumped food resources as a means to reduce energy expenditure and maximize caloric intake as predicted by foraging theory (see also Stephens & Krebs, 1986). Our results suggest that this bias may also emerge to a degree among some nonhuman primate species using quantity discrimination paradigms with inedible stimuli in which inter-stimulus distance can be varied. Thus, perhaps an active foraging mode is not necessary to elicit the density bias, but rather it is a more general hallmark of quantitative processing. Future studies that vary the item type (edible versus inedible) and the spatial location of stimuli (so as to mimic natural foraging situations with a time cost to searching and obtaining foods at different locations) would shed light on the extent to which this bias emerges more readily across species within natural foraging scenarios.
There also was an interesting pattern of results for both species of monkeys in which higher performance levels occurred for control trials with a true difference in set size when both sets were densely arranged (Dense Control) than when both sets were sparsely arranged (Sparse Control). This result alone does not indicate a density bias, but it may complement the bias seen amongst other trial types such as the Equal condition. Here, monkeys were presented with two equal sets, one sparsely arranged and the other densely arranged. For capuchin monkeys, there was a preference for dense arrays in three of the four quantity discriminations (6, 10, and 12). It is possible that the elevated performance levels in Dense Control trials indicated a greater overall proficiency in apprehending denser arrays than sparser arrays, which may have led to a preference (but not necessarily a perceptual bias) for dense sets in capuchin monkeys when quantity was equal. There were limits in the possible presentation formats for dense versus sparse sets, such that sparse arrays were arranged in a larger possible number of random arrangements than dense arrays, for which there was only one canonical presentation format (e.g., a dense six-item array was always two rows of three dots). This consistent presentation style for dense sets but not sparse sets was a design feature of the computerized presentation format, but it may have led to the elevated performance levels seen amongst Dense Control trials for both monkey species. Further research controlling for the presentation style between these sparse and dense arrays and the proficiency by animals across these trial types is necessary for ruling out any confounding variables.
It was interesting to find a more robust effect of the density bias among capuchin monkeys as compared to rhesus monkeys. Both species performed significantly better for Dense Control trials than Sparse Control trials as discussed above, but capuchins demonstrated the strongest evidence of the bias with a significant preference for dense sets to sparse sets when set quantity was equal. One possibility is that a more robust density bias can be linked to ecological or biological differences between the two species; however, we feel that these differences are unlikely to explain the present results. Capuchin monkeys, an arboreal New World primate species, forage on a range of diverse foods with a preference for readily accessible fruits. They also are known to eat a large variety of plant foods including hard nuts, bark, palm fronds, and saplings as well as insects and small vertebrates (see Fragaszy, Visalberghi, & Fedigan, 2004 for a review). Rhesus macaques, an Old World monkey species, are considered one of the most adaptable primate species, living in a large variety of diverse habitats with flexible foraging patterns ranging from largely folivorous diets in deciduous forests to largely frugivorous diets in other habitats (see Thierry, 2007, for a review). Furthermore, all primate species to some degree are faced with patchy, clumped food resources as determined by the seasonality of available foods (see Strier, 2007). Capuchin monkeys and rhesus monkeys are impacted similarly by low food availability and clumped resources, increasing within-group competition for both species (e.g., rhesus: Deutsch, & Lee, 1991; capuchins: Janson, 1985). Thus, the stronger density bias among capuchin monkeys does not seem easily tied to differences in foraging. The present results would be enhanced by future studies presenting the density bias within an active foraging domain to these two species, or using a two-choice discrimination task with edible food items, to determine the extent to which the current species differences hold within a more natural foraging environment.
Another possibility is that capuchin monkeys are unique in the perceptual processing of multi-element arrays; however, we do not believe this to be the underlying cause of the current species differences either. There is extensive evidence for a shared local advantage in perceptual processing mode across these two species. When perceiving complex arrays that are comprised of multiple smaller features, several species of monkey perceive the individual items (i.e., the local features) prior to and sometimes more accurately than the global configuration (cotton-top tamarins: Neiworth, Gleichman, Olinick, & Lamp, 2006; capuchin monkeys: De Lillo, Spinozzi, Truppa, & Naylor, 2005; Spinozzi, De Lillo, & Truppa, 2003; Spinozzi, De Lillo, Truppa, & Castorina, 2009; rhesus monkeys: Hopkins & Washburn, 2002; baboons: Deruelle & Fagot, 1998; Fagot & Deruelle, 1997). This local advantage stands in contrast to a robust global advantage documented in humans (e.g., Broadbent, 1977; Lamb & Robertson, 1988; Navon, 1977, 1981).
Relevant to the current work, density impacts the grouping of local features into a cohesive figure, such that increased item density eliminates the local advantage for capuchins (De Lillo et al., 2005; Spinozzi et al., 2003), baboons (Deruelle & Fagot, 1998; Fagot & Deruelle, 1997), and chimpanzees (Fagot & Tomonaga, 1999), and even reverses it to a global advantage for cottontop tamarins (Neiworth et al., 2006). Relatedly, capuchin monkeys rely on density (i.e., the spatial proximity of items within an array) more so than other grouping cues such as orientation to guide perceptual matching (Spinozzi et al., 2009). These results suggest that density, like other non-numerical dimensions including area and volume, is a particularly salient cue for nonhuman primates whether one is in a foraging context judging the relative quantity of multiple food sets or discriminating complex visual stimuli in a perceptual discrimination task. Notably, the majority of the work on variables influencing processing mode in monkeys has been concentrated to capuchin monkeys, with comparably fewer studies among rhesus macaques. Further, the density bias has been studied in relatively few primate species and, thus far, has been documented only among New World monkey species (capuchin monkeys, cotton-top tamarins, and marmosets), all of which are known to display a local-to-global processing bias. Future studies with other Old World primates and specifically with species with alternative perceptual processing styles may shed light on species differences in sensitivity to perceptual grouping cues, including density.
For our secondary objective to the study, we predicted that perception of the Solitaire illusion and the density bias may be positively correlated as they appear to tap into similar grouping mechanisms, in which patterns forming a better Gestalt (as seen for the Solitaire illusion) and clumped patterns may be similarly over-estimated. However, this relation was not present, particularly for the capuchin monkeys. The rhesus monkeys showed a trend for such a relation, but they also were the species that showed overall lower evidence of a density bias in their behavioral responses in the present experiment. Thus, despite our prediction, there did not appear to be a clear relation between susceptibility to the Solitaire illusion and perception of the density bias. Despite both biases being at least somewhat present in these species, they may not be as related to each other as suggested by their shared perceptual and spatial features in terms of stimulus presentation and organization.
Although we originally predicted a significant correlation between the density bias and the Solitaire illusion, there is a fundamental difference between the two tasks that may account for the non-significant correlation that was found. The density bias presents one dot color in each array, which then differs as a function of inter-stimulus distance. Contrary to this, the Solitaire illusion presents two dot colors presented in intermingled sets with a consistent inter-stimulus distance (black and white dots are intermixed equidistant from one another in each array). The Solitaire illusion may emerge as a function of the relative difference in the perceived numerosity of the different colored dots within each array (i.e., there may appear to be more black dots than white dots in the illusory array with central black dots). Thus, black dots are perceived as more numerous in the illusory array versus the non-illusory array. However, the density bias appears to emerge strictly as a function of inter-stimulus distance, rather than a contrast seen between different element types as in the Solitaire illusion, which leads to overestimations of numerosity. Future studies presenting the density bias using intermixed arrays (with more than one item type present in each array, even if only a single color is the relevant cue to use) are necessary to assess the possibility that the Solitaire illusion specifically emerges due to better relative Gestalts in two separate arrays, and not as a function of density or a greater number of clumped items within the single illusory array.
The degree to which different individuals, age groups, and species perceive and misperceive their worlds reveals important differences in the mechanisms underlying the perceptual and numerical systems responsible for assessing and estimating quantitative information and the role that experience plays in shaping these processes. Nonhuman primates share many of the hallmark characteristics for encoding and representing numerical cognition with humans. Thus, understanding the extent to which they also misperceive numerical information is crucial in disentangling shared processes across species and the role of human-unique experiences.
Acknowledgments
The authors thank the animal care and enrichment staff for maintaining the health and wellbeing of the monkeys, making this research possible. Support for this research was provided by the National Institutes of Health (grant HD060563). We also appreciate the comments by two anonymous reviews on earlier drafts of the manuscript.
References
- Agrillo C, Parrish AE, Beran MJ. Do primates see the solitaire illusion differently? A comparative assessment of humans (Homo sapiens), chimpanzees (Pan troglodytes), rhesus monkeys (Macaca mulatta), and capuchin monkeys (Cebus apella) Journal of Comparative Psychology. 2014;128:402–413. doi: 10.1037/a0037499. [DOI] [PubMed] [Google Scholar]
- Allik J, Tuulmets T. Occupancy model of perceived numerosity. Perception & Psychophysics. 1991;49:303–314. doi: 10.3758/bf03205986. [DOI] [PubMed] [Google Scholar]
- Allik J, Tuulmets T. Perceived numerosity of spatiotemporal events. Perception & Psychophysics. 1993;53:450–459. doi: 10.3758/bf03206789. [DOI] [PubMed] [Google Scholar]
- Beran MJ. Quantity perception by adult humans (Homo sapiens), chimpanzees (Pan troglodytes), and rhesus macaques (Macaca mulatta) as a function of stimulus organization. International Journal of Comparative Psychology. 2006;19:386–397. [Google Scholar]
- Beran MJ, Parrish AE. Visual nesting of stimuli affects rhesus monkeys’ (Macaca mulatta) quantity judgments in a bisection task. Attention, Perception and Psychophysics. 2013;75:1243–1251. doi: 10.3758/s13414-013-0474-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beran MJ, Parrish AE. Going for more: Discrete and continuous quantity judgments by nonhuman animals. In: Henik A, editor. Continuous issues in numerical cognition: How many or how much. Academic Press; San Diego: 2016. pp. 175–192. [Google Scholar]
- Beran MJ, Parrish AE, Evans TA. Numerical cognition and quantitative abilities in nonhuman primates. In: Geary D, Berch D, Mann Koepke K, editors. Evolutionary origins and early development of basic number processing. Vol. 1. Elsevier; New York: 2014. pp. 91–112. [Google Scholar]
- Brannon EM. The representation of numerical magnitude. Current Opinion in Neurobiology. 2006;16:222–229. doi: 10.1016/j.conb.2006.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Merritt D. Evolutionary foundations of the pproximate Number System. In: Dehaene S, Brannon EM, editors. Space, time, and number in the brain: Searching for the foundations of mathematical thought. Elsevier; New York, NY: 2011. pp. 207–224. [Google Scholar]
- Brannon EM, Roitman JD. Nonverbal representations of time and number in animals and human infants. In: Meck WH, editor. Functional and neural mechanisms of interval timing. CRC Press; Boca Raton, FL: 2003. pp. 143–182. [Google Scholar]
- Broadbent DE. The hidden preattentive processes. American Psychologist. 1977;32:109–118. doi: 10.1037//0003-066x.32.2.109. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Platt ML, Brannon EM. Beyond the number domain. Trends in Cognitive Sciences. 2009;13:83–91. doi: 10.1016/j.tics.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chesney DL, Gelman R. Visual nesting impacts approximate number system estimation. Attention, Perception and Psychophysics. 2012;74:1104–1113. doi: 10.3758/s13414-012-0349-1. [DOI] [PubMed] [Google Scholar]
- Davis H, Pérusse R. Numerical competence: from backwater to mainstream of comparative psychology. Behavioral and Brain Sciences. 1988;11:602–615. [Google Scholar]
- De Lillo C, Spinozzi G, Truppa V, Naylor DM. A comparative analysis of global and local processing of hierarchical visual stimuli in young children (Homo sapiens) and monkeys (Cebus apella) Journal of Comparative Psychology. 2005;119:155–165. doi: 10.1037/0735-7036.119.2.155. [DOI] [PubMed] [Google Scholar]
- De Lillo C, Visalberghi E, Aversano M. The organization of exhaustive searches in a patchy space by capuchin monkeys (Cebus apella) Journal of Comparative Psychology. 1997;111:82–90. [Google Scholar]
- De Waal FB, Davis JM. Capuchin cognitive ecology: cooperation based on projected returns. Neuropsychologia. 2003;41:221–228. doi: 10.1016/s0028-3932(02)00152-5. [DOI] [PubMed] [Google Scholar]
- Deruelle C, Fagot J. Visual search for global/local stimulus features in humans and baboons. Psychonomic Bulletin & Review. 1998;5:476–481. [Google Scholar]
- Deutsch JC, Lee PC. Dominance and feeding competition in captive rhesus monkeys. International journal of primatology. 1991;12:615–628. [Google Scholar]
- Dukette D, Stiles J. Children's analysis of hierarchical patterns: Evidence from a similarity judgment task. Journal of Experimental Child Psychology. 1996;63:103–140. doi: 10.1006/jecp.1996.0044. [DOI] [PubMed] [Google Scholar]
- Evans TA, Beran MJ, Chan B, Klein ED, Menzel CR. An efficient computerized testing method for the capuchin monkey (Cebus apella): Adaptation of the LRC-CTS to a socially housed nonhuman primate species. Behavior Research Methods. 2008;40:590–596. doi: 10.3758/brm.40.2.590. [DOI] [PubMed] [Google Scholar]
- Fagot J, Deruelle C. Processing of global and local visual information and hemispheric specialization in humans (Homo sapiens) and baboons (Papio papio) Journal of Experimental Psychology: Human Perception and Performance. 1997;23:429–442. doi: 10.1037//0096-1523.23.2.429. [DOI] [PubMed] [Google Scholar]
- Fagot J, Tomonaga M. Global and local processing in humans (Homo sapiens) and chimpanzees (Pan troglodytes): Use of a visual search task with compound stimuli. Journal of Comparative Psychology. 1999;113:3–12. [Google Scholar]
- Fragaszy DM, Visalberghi E, Fedigan LM. The complete capuchin: The biology of the genus Cebus. Cambridge University Press; Cambridge: 2004. [Google Scholar]
- Frith CD, Frith U. The solitaire illusion: An illusion of numerosity. Perception and Psychophysics. 1972;11:409–410. [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: From reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Ginsburg N. Effect of item arrangement on perceived numerosity: Randomness vs regularity. Perceptual and Motor Skills. 1976;43:663–668. doi: 10.2466/pms.1976.43.2.663. [DOI] [PubMed] [Google Scholar]
- Ginsburg N. The regular-random numerosity illusion: Rectangular patterns. Journal of General Psychology. 1980;103:211–216. doi: 10.1080/00221309.1980.9921000. [DOI] [PubMed] [Google Scholar]
- Hamilton WD. Geometry for the selfish herd. Journal of Theoretical Biology. 1971;31:295–311. doi: 10.1016/0022-5193(71)90189-5. [DOI] [PubMed] [Google Scholar]
- Hopkins WD, Washburn DA. Matching visual stimuli on the basis of global and local features by chimpanzees (Pan troglodytes) and rhesus monkeys (Macaca mulatta) Animal Cognition. 2002;5:27–31. doi: 10.1007/s10071-001-0121-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janson C. Aggresive competition and individual food consumption in wild brown capuchin monkeys (Cebus apella) Behavioral Ecology and Sociobiology. 1985;18:125–138. [Google Scholar]
- Kitchen DM. Alpha male black howler monkey responses to loud calls: Effect of numeric odds, male companion behaviour and reproductive investment. Animal Behaviour. 2004;67:125–139. [Google Scholar]
- Krueger LE. Perceived numerosity. Perception & Psychophysics. 1972;11:5–9. doi: 10.3758/bf03205949. [DOI] [PubMed] [Google Scholar]
- Krueger LE. Perceived numerosity: a comparison of magnitude production, magnitude estimation, and discrimination judgments. Perception & Psychophysics. 1984;35:536–542. doi: 10.3758/bf03205949. [DOI] [PubMed] [Google Scholar]
- Lamb MR, Robertson LC. The effect of visual angle on global and local reaction times depends on the set of visual angles presented. Perception & Psychophysics. 1990;47:489–496. doi: 10.3758/bf03208182. [DOI] [PubMed] [Google Scholar]
- Lyon BE. Egg recognition and counting reduce costs of avian conspecific brood parasitism. Nature. 2003;422:495–499. doi: 10.1038/nature01505. [DOI] [PubMed] [Google Scholar]
- MacDonald SE, Agnes MM. Orangutan (Pongo pygmaeus abelii) spatial memory and behavior in a foraging task. Journal of Comparative Psychology. 1999;113:213–217. [Google Scholar]
- Mitchell KG, Calton JL, Threlkeld RC, Schachtman TR. Attenuation and reacquisition of foraging behavior in a patchy environment. Behavioural Processes. 1996;36:239–252. doi: 10.1016/0376-6357(95)00034-8. [DOI] [PubMed] [Google Scholar]
- Navon D. Forest before trees: The precedence of global features in visual perception. Cognitive Psychology. 1977;9:353–383. [Google Scholar]
- Navon D. The forest revisited: More on global precedence. Psychological Research. 1981;43:1–32. [Google Scholar]
- Neiworth JJ, Gleichman AJ, Olinick AS, Lamp KE. Global and local processing in adult humans (Homo sapiens), 5-year-old children (Homo sapiens), and adult cotton-top tamarins (Saguinus oedipus) Journal of Comparative Psychology. 2006;120:323–330. doi: 10.1037/0735-7036.120.4.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrish AE, Agrillo C, Perdue BM, Beran MJ. The elusive illusion: Do children (Homo sapiens) and capuchin monkeys (Cebus apella) see the Solitaire illusion? Journal of Experimental Child Psychology. 2016;142:83–95. doi: 10.1016/j.jecp.2015.09.021. [DOI] [PubMed] [Google Scholar]
- Richardson WK, Washburn DA, Hopkins WD, Savage-Rumbaugh ES, Rumbaugh DM. The NASA/LRC Computerized Test System. Behavior Research Methods, Instruments, and Computers. 1990;22:127–131. doi: 10.3758/bf03203132. [DOI] [PubMed] [Google Scholar]
- Spinozzi G, De Lillo C, Truppa V, Castorina G. The relative use of proximity, shape similarity, and orientation as visual perceptual grouping cues in tufted capuchin monkeys (Cebus apella) and humans (Homo sapiens) Journal of Comparative Psychology. 2009;123:56–68. doi: 10.1037/a0012674. [DOI] [PubMed] [Google Scholar]
- Spinozzi G, De Lillo C, Truppa V. Global and local processing of hierarchical visual stimuli in tufted capuchin monkeys (Cebus apella) Journal of Comparative Psychology. 2003;117:15–23. doi: 10.1037/0735-7036.117.1.15. [DOI] [PubMed] [Google Scholar]
- Stephens DW, Krebs JR. Foraging theory. Princeton University Press; 1986. [Google Scholar]
- Stevens JR, Wood JN, Hauser MD. When quantity trumps number: Discrimination experiments in cotton-top tamarins (Saguinus oedipus) and common marmosets (Callithrix jacchus) Animal cognition. 2007;10:429–437. doi: 10.1007/s10071-007-0081-8. [DOI] [PubMed] [Google Scholar]
- Strier KB. Primate behavioral ecology. Allyn & Bacon; Needham Heights, MA: 1999. [Google Scholar]
- Thierry B. Unity in diversity: Lessons from macaque societies. Evolutionary Anthropology: Issues, News, and Reviews. 2007;16:224–238. [Google Scholar]
- Uller C, Urquhart C, Lewis J, Berntsen M. Ten-month-old infants’ reaching choices for “more”: The relationship between inter-stimulus distance and number. Frontiers in Psychology. 2013;4:84. doi: 10.3389/fpsyg.2013.00084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vahl WK, Lok T, van der Meer J, Piersma T, Weissing FJ. Spatial clumping of food and social dominance affect interference competition among ruddy turnstones. Behavioral Ecology. 2005;16:834–844. [Google Scholar]
- Wertheimer M. Laws of organization in perceptual forms. In: Ellis WB, editor. A sourcebook of Gestalt psychology. Harcourt, Brace and Company; San Diego (USA): 1938. pp. 71–88. [Google Scholar]