View-tolerant face recognition and Hebbian learning imply mirror-symmetric neural tuning to head orientation

SUMMARY

The primate brain contains a hierarchy of visual areas, dubbed the ventral stream, which rapidly computes object representations that are both specific for object identity and robust against identity-preserving transformations like depth-rotations [1, 2]. Current computational models of object recognition, including recent deep learning networks, generate these properties through a hierarchy of alternating selectivity-increasing filtering and tolerance-increasing pooling operations, similar to simple-complex cells operations [3, 4, 5, 6]. Here we prove that a class of hierarchical architectures and a broad set of biologically plausible learning rules generate approximate invariance to identity-preserving transformations at the top level of the processing hierarchy. However, all past models tested failed to reproduce the most salient property of an intermediate representation of a three-level face-processing hierarchy in the brain: mirror-symmetric tuning to head orientation [7]. Here we demonstrate that one specific biologically-plausible Hebb-type learning rule generates mirror-symmetric tuning to bilaterally symmetric stimuli like faces at intermediate levels of the architecture and show why it does so. Thus the tuning properties of individual cells inside the visual stream appear to result from group properties of the stimuli they encode and to reflect the learning rules that sculpted the information-processing system within which they reside.

RESULTS

The ventral stream rapidly computes image representations that are simultaneously tolerant of identity-preserving transformations and discriminative enough to support robust recognition. The ventral stream of the macaque brain contains discrete patches of cortex that support the processing of images of faces [8, 9, 10, 11]. The face patches are arranged along an occipito-temporal axis (from the middle lateral (ML) and middle fundus (MF) patches, through the antero-lateral (AL) to the antero-medial (AM) patch (Figure 1A) [13]. Along this axis response latencies increase systematically, suggesting sequential forward-processing [7]. Selectivity to spatial position, size, and head orientation decrease from ML/MF to AM [7], replicating the general trend of the ventral stream [14, 1]. In accord with these properties, many hierarchical models of object recognition [15, 14, 16] and face recognition [4, 17, 18] feature a progression from view-specific early processing stages to view-invariant later processing stages. They do so by successive pooling over view-tuned units.

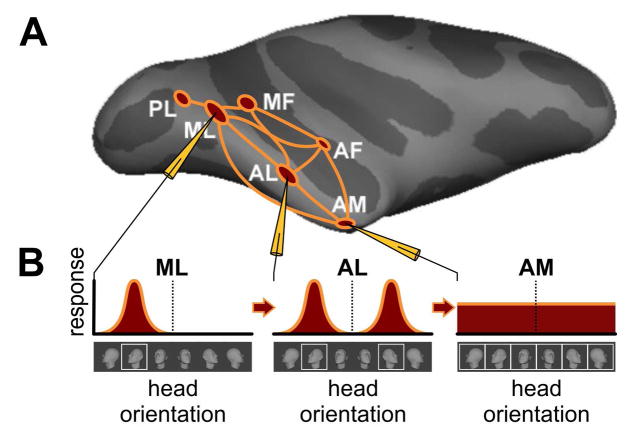
Figure 1. Schematic of the macaque face-patch system[12, 13, 7].

(A) Side view of computer-inflated macaque cortex with six areas of face-selective cortex (red) in the temporal lobe together with connectivity graph (orange). Face areas are named based on their anatomical location: PL, posterior lateral; ML; middle lateral; MF, middle fundus; AL, anterior lateral; AF, anterior fundus ; AM, anterior medial (3), and have been found to be directly connected to each other to form a face-processing network [12]. Recordings from three face areas, ML, AL, AM, during presentations of faces at different head orientations revealed qualitatively different tuning properties, schematized in B. (B) Prototypical ML neurons are tuned to head orientation, e.g., as shown, a left profile. A prototypical neuron in AL, when tuned to one profile view, is tuned to the mirror-symmetric profile view as well. And a typical neuron in AM is only weakly tuned to head orientation. Because of this increasing invariance to in-depth rotation, increasing to invariance to size and position (not shown) and increased average response latencies from ML to AL to AM, it is thought that the main AL properties, including mirror-symmetry, have to be understood as transformations of ML representations, and the main AM properties as transformations of AL representations [7].

Neurons in the intermediate face area AL, but not in preceding areas ML/MF, exhibit mirror-symmetric head orientation tuning [7]: an AL neuron tuned to one profile view of the head typically responds similarly to the opposite profile, but not to the front view (Figure 1B). This phenomenon is not predicted by classical and current hierarchical view-based models of the ventral stream, thus calling into question the idea that such models replicate the operations of the ventral stream.

Model Assumptions

Invariant information can be decoded from inferotemporal cortex, and the face areas within it, roughly 100ms after stimulus presentation [19, 20]. This, it has been argued, is too fast of a timescale for feedback to play a large role [21, 19, 22]. Thus while the actual face processing system might operate in other modes as well, fundamental properties of shape-selectivity and invariance need to be explained as a property of feedforward processing. We thus consider here a feed-forward face-processing model.

The population of neurons in ML/MF is highly face selective [9]. Thus, as in earlier computational models of face perception [23, 24, 18], we assume the existence of a functional gate that routes only images of face-like objects at the input of the face system.

We make the standard assumption that a neuron’s basic operation is a pooled dot product between inputs x and synaptic weight vectors { $w_i^k$}, which, in our settings, correspond to rotation in depth, g_i ∈ G, of template w^k. This yields a complex-like cell computing

$${\mu }^k(x)=\sum _{i=1}^{\mid G\mid }\eta \left(\langle x,g_i{w}^k\rangle \right),k=1,\dots ,K$$ (1)

where η:ℝ → ℝ is a nonlinear function e.g., squaring [25], (Supplemental Mathematical Appendix Section 1.1). We call μ⃑(x) ∈ ℝ^K the signature of image x.

Approximate View Invariance

The model described so far encodes a given image of a face x by its similarity to a set of stored images of rotated in depth familiar faces (called templates) acquired during the algorithm’s (unsupervised) training. The key observation to understand why the computation in eq. (1) gives a view-tolerant representation is that the similarity function of two faces has a sharp peak when they are at the same orientation. That is, 〈x, g_iw^k〉 is maximal when x and g_iw^k depict faces at the same orientation, even when they depict different identities. Thus since eq. (1) sums over all template orientations it is always dominated by the contribution from the templates at orientations matching x. In other words, it is approximatively unchanged by rotation. (We prove this in Supplemental Mathematical Appendix Section 1).

Since this model is based on stored associations of frames, (see Figure 2) it can be interpreted as taking advantage of temporal continuity to learn the simple-to-complex wiring from their view-specific to view-tolerant layers. They associate temporally adjacent frames from the video of visual experience as in, e.g., [26]. This yields a view-tolerant signature because, in natural video, adjacent frames almost always depict the same object [27, 28, 29, 30, 26]. Short videos containing a face almost always contain multiple views of the same face. There is considerable evidence from physiology and psychophysics that the brain employs a learning rule taking advantage of this temporal continuity [31, 32, 33, 34].

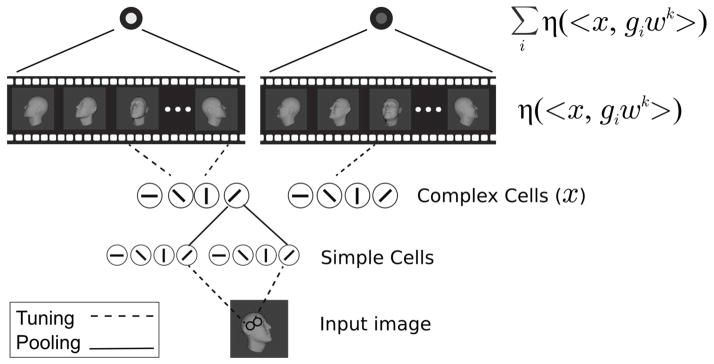
Figure 2. Illustration of the model.

Inputs are first encoded in a V1-like model. Its first layer (simple cells) corresponds to the S1 layer of the HMAX model. Its second layer (complex cells) corresponds to the C1 layer of HMAX [14]. In the view-based model, the V1-like encoding is then projected onto stored frames g_iw^k at orientation i, from videos of transforming faces k = 1,…,K. Finally, the last layer is computed as μ^k = Σ_iη(〈x, g_iw^k〉). That is, the kth element of the output is computed by summing over all responses to cells tuned to views of the kth template face. In the PCA-model, the V1-like encoding is instead projected onto templates $w_i^k$ describing the ith PC of the kth template face’s transformation video. The pooling in the final layer is then over all the PCs derived from the same identity. That is, it is computed as ${\mu }^k={\mathrm{\sum }}_i\eta (\langle x,w_i^k\rangle )$. In both the view-based and PCA models, units in the output layer pool over all the units in the previous layer corresponding to projections onto the same template individual’s views (view-based model) or PCs (PCA-model).

Thus, our assumption here is that in order to get invariance to non-affine transformations (like rotation in depth), it is necessary to have a learning rule that takes advantage of the temporal coherence of object identity. More formally, this procedure achieves tolerance to rotation in depth because the set of rotations in depth approximates the group structure of affine transformations in the plane (see Supplemental Mathematical Appendix Section 1). For the latter case, there are theorems guaranteeing invariance without loss of selectivity [35, 2].

Biologically Plausible Learning

The algorithm described so far can provide an invariant representation but is potentially biologically implausible: it requires the storing of discrete views observed during development. Instead we propose a more biologically plausible Hebb-like mechanism. Instead of storing separate frames, cortical neurons update their synaptic weights according to a Hebb-like rule. Over time, they become tuned to basis functions encoding different combinations of the set of views. Different Hebb-like rules lead to different sets of basis functions such as Independent Components (IC) or Principal Components (PC) [36]. Since each of the neurons becomes tuned to one of these basis functions instead of one of the views, a set of basis functions replaces the g_iw^k in the pooling equation. The question then is whether invariance is still present.

The surprising answer is that supervised backpropagation learning and most unsupervised learning rules will learn approximate invariance to viewpoint for an appropriate training set (see Supplemental Mathematical Appendix Section 2 for proof). This is the case for unsupervised Hebb-like plasticity rules such as Oja’s, Foldiak’s trace rule, and ICA, all of which provide bases over which the pooling equation provides invariance. One such Hebbian learning scheme is Oja’s rule [37, 38]. It can be derived as the first order expansion of a normalized Hebb rule. The assumption of this normalization is plausible, because homeostatic plasticity mechanisms are widespread in cortex [39].

For learning rate α, input x, weight vector w, and output y = 〈x,w〉, Oja’s rule is

$$\mathit{\Delta }w=\alpha (xy-y^{2}w)=\alpha (x{x}^{T}w-(w^{T}x{x}^{T}w)w)$$ (2)

The weights of a neuron updated according to this rule will converge to the top principal component (PC) of the neuron’s past inputs, that is to an eigenvector of the input’s covariance C [37]. Thus the synaptic weights correspond to the solution of the eigenvector-eigenvalue equation Cw = λw. Plausible modifications of the rule -- involving added noise or inhibitory connections with similar neurons -- yield additional eigenvectors [40, 38]. This generalized Oja rule works as an online algorithm that computes the principal components of an incoming stream of images.

The outcome of learning is dictated by the underlying covariance of the inputs. Thus, in order for familiar faces to be stored so that the neural response modeled by Eq. 1 tolerates rotations in depth of novel faces, we propose that Oja-type plasticity leads to representations for which the synaptic templates are given by principal components (PCs) of an image sequence depicting the depth-rotation of face k. Consider an immature functional unit exposed, while in a plastic state, to all depth-rotations of a face. Learning will converge to the eigenvectors corresponding to the top r eigenvalues and thus to the subspace spanned by them. Supplemental Mathematical Appendix Section 2 eq. 8 shows that for each template face k, the signature ${\mu }^k(x)={\mathrm{\sum }}_{i=1}^r\eta \left(\langle x,w_i^k\rangle \right)$ obtained by pooling over all PCs represented by different $w_i^k$ is an invariant. This is analogous to Eq. 1 with g_iw^k replaced by the i-th PC. Supplemental Mathematical Appendix Section 2 also shows that other learning rules for which the solutions are not PCs but a different set of basis functions, generate invariance as well---for instance, independent components. Figure 3B verifies that the signatures obtained by pooling over PCs are view-tolerant through a simulation of the task of matching unfamiliar faces despite depth-rotations.

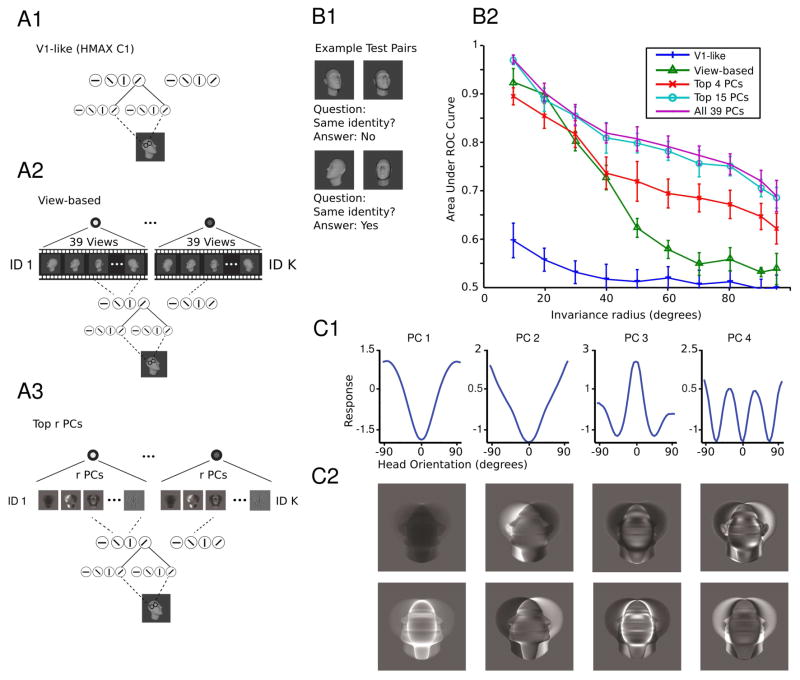
Figure 3. Model performance on the task of same-different face pair matching.

(A1–3) The structure of the models tested in B. (A1) The V1-like model encodes an input image in the C1 layer of HMAX which models complex cells in V1 [14]. (A2) The view-based model encodes an input image as ${\mu }^k(x)={\mathrm{\sum }}_{i=1}^{\mid G\mid }{\langle x,g_i{w}^k\rangle }^2$ where x is the V1-like encoding. (A3) The Top r PCs model encodes an input image as ${\mu }^k(x)={\mathrm{\sum }}_{i=1}^r{\langle x,w_i^k\rangle }^2$ where x is the V1-like encoding. (B1–2) The test of depth-rotation invariance required discriminating unfamiliar faces. That is, the template faces did not appear in the test set so this is a test of depth-rotation invariance from a single example view. (B1) In each trial, two face images appear and the task is to indicate whether they depict the same or different faces. They may appear at different orientations from each other. To classify an image pair (a,b) as depicting the same or a different individual, the cosine similarity of the two representations was compared to a threshold. The threshold was varied systematically in order to compute the area under the ROC curve (AUC). (B2) In each test, 600 pairs of face images were sampled from the set of faces with orientations in the current testing interval. 300 pairs depicted the same individual and 300 pairs depicted different individuals. Testing intervals were ordered by inclusion and were always symmetric about 0° the set of frontal faces; i.e., they were [−x, x] for x = 5°,…, 95°. The radius of the testing interval x, dubbed the invariance radius, is the abscissa. AUC declines as the range of testing orientations is widened. As long as enough PCs are used, the proposed model performs on par with the view-based model. It even exceeds its performance if the complete set of PCs is used. Both models outperform the baseline HMAX C1 representation. The error bars were computed over repetitions of the experiment with different template and test sets, see Supplemental Methods. (C1–2) Mirror symmetric orientation tuning of the raw pixels-based model. 〈x_θ, w_i〉² is shown as a function of the orientation of x_θ. Here each curve represents a different PC. Below are shown the PCs $w_i^k$ visualized as images. They are either symmetric (even) or antisymmetric (odd) about the vertical midline. See also Figure S1.

Mirror Symmetry

Consider the case where, for each of the templates w^k, the developing organism has been exposed to a sequence of images showing a single face rotating from a left profile to a right profile. Faces are approximately bilaterally symmetric. Thus, for each face view g_iw^k, its reflection over the vertical midline g_−iw^k will also be in the training set. It turns out that this property---along with the assumption of Oja plasticity, but not other kinds of plasticity---is sufficient to explain mirror symmetric tuning curves. The argument is as follows.

Consider a face, x and a set of its rotations in 3D

$$O_x=\left(r_{{\theta }_{-N}}x,\dots ,r_{0}x,r_{0}x,\dots r_{{\theta }_N}x\right).$$

where r_θi is a rotation matrix in 3D of angle θ_i, w.r.t., e.g., the z axis.

Projecting onto 2D we have

$$P(O_x)=\left(P(r_{{\theta }_{-N}}x),\dots ,P(r_{0}x),P(r_{0}x),\dots ,P(r_{{\theta }_N}x)\right).$$

Note now that, due to the bilateral symmetry, r_θ−nx = RP(r_θnx), n = 0,…,N where R is the reflection operator around the z axis. Thus the above set can be written as

$$P(O_x)=(x_0,\dots ,x_N,R{x}_0,\dots ,R{x}_N).$$

where x_n = P(r_θnx), n = 0, …, N. Thus the set consists of a collection of orbits w.r.t. the group G = {e, R} of the templates {x₀, …, x_N}.

This property of the training set is needed in order to show that the signature μ(x) computed by pooling over the solutions to any equivariant learning rule, e.g., Hebb, Oja, Foldiak, ICA, or supervised backpropagation learning, is approximately invariant to depth-rotation (Supplemental Mathematical Appendix Sections 1–2).

The same property of the training set, in the specific case of the Oja learning rule, is used to prove that the solutions for the weights (i.e., the PCs) are either even or odd (Supplemental Mathematical Appendix Section 3). This in turn implies that the penultimate stage of the signature computation: the stage where η(〈x,w〉) is computed, will have orientation tuning curves that are either even or odd functions of the view angle.

Finally, to get mirror symmetric tuning curves like those in AL, we need one final assumption: the nonlinearity before pooling at the level of the “simple” cells in AL must be an even nonlinearity such as η(z) = z². This is the same assumption as in the energy model of [25]. This assumption is needed in order to predict mirror symmetric tuning curves for the neurons corresponding to odd solutions to the Oja equation. The neurons corresponding to even solutions have mirror symmetric tuning curves regardless of whether η is even or odd.

An orientation tuning curve is obtained by varying the orientation of the test image θ. Figure 3C shows example orientation tuning curves for the model based on a raw pixel representation. It plots 〈x_θ,w_i〉² as a function of the test face’s orientation for five example units tuned to features with different corresponding eigenvalues. All of these tuning curves are symmetric about 0° -- i.e., the frontal face orientation. Figure 4A shows how the three model layers represent face view and identity and Figure 4B shows the same for populations of neurons recorded in ML/MF, AL, and AM. The model is the same one as in Figure 3B/C.

Figure 4. Population representations of face view and identity.

(A) Model population similarity matrices corresponding to the simulation of Figure 3B were obtained by computing Pearson’s linear correlation coefficient between each test sample pair. (Left) The similarity matrix for the V1-like representation, the C1 layer of HMAX [14]. (Middle) The similarity matrix for the penultimate layer of the PCA-model of Figure 3B. It models AL. (Right) The similarity matrix for the final layer of the PCA-model of Figure 3B. It models AM. (B) Compare the results in (A) to the corresponding neuronal similarity matrices from [7]. See also Figure S1.

These results imply that if neurons in AL learn according to a broad class of Hebb-like rules, then there will be invariance to viewpoint. Different AM cells would come to represent components of a view-invariant signature---one per neuron. Additionally, if the learning rule is of the Oja-type and the output nonlinearity is, at least roughly, squaring, then the model predicts that on the way to view invariance, mirror-symmetric tuning emerges, as a necessary consequence of the intrinsic bilateral symmetry of faces. In contrast to the Oja/PCA case, we show through a simulation analogous to Figure 3 that ICA does not generally yield mirror symmetric tuning curves (Supplemental Figure S1).

DISCUSSION

Neurons in the face network’s penultimate processing stage (AL) are tuned symmetrically to head orientation [7]. In the model proposed here, AL’s mirror symmetric tuning is explained as a necessary step along the way to computing a view-tolerant representation in the final face patch: AM. The argument begins with a theoretical characterization of how an idealized temporal association learning scheme could learn view-tolerant face representations like those in AM. It then proceeds by considering which of the various biologically-plausible learning rules satisfy requirements coming from the theory while also predicting mirror symmetric representation in the computation’s penultimate stage. It turns out that the Oja-like plasticity is the only biologically-plausible rule that fits.

This argument suggests that Oja-like plasticity may indeed be driving learning in AL. We now discuss potential implications of this hypothesis. While Oja’s learning rule was originally motivated on computational grounds [37], it is now believed to be a widespread mechanism in cortex because it describes the interaction of LTP, LTD, and synaptic scaling (a form of homeostatic plasticity) [39]. Biophysical mechanisms underlying homeostatic plasticity include activity-dependent scaling of AMPA receptor recycling rates [39]. It has been observed in mouse visual cortex in vivo under bi/monocular deprivation paradigms [41, 42] and is believed to be particularly important in developmental critical periods [43]. Such synaptic scaling has not yet been described in the face patch network, however, the present work can be seen as lending support to the hypothesis that it may act there. Just as monocular deprivation paradigms are used to study homeostatic plasticity in visual cortex, analogous “face deprivation” paradigms may reveal homeostatic plasticity in the developing face patch network.

In particular, to the best of our knowledge, this is the first account that explains why cells in the face network’s penultimate processing stage, AL, are tuned symmetrically to head orientation. This shows that feed-forward processing hierarchies can capture the main progression of face representations observed in the macaque brain. The mirror symmetry result is especially significant because it shows how a time-contiguous learning rule operating within this architecture can give rise to a counter-intuitive property that is not intrinsic to the temporal sequence of the stream of visual images impinging on the eyes. Rather, it arises as an interaction between an intrinsic property of the geometry of an object, here bilateral symmetry, and the computational strategy of the information-processing hierarchy, that is view-invariance.

Our model is designed to account only for the feed-forward processing in the face patch network (≤ 80ms from image onset). The representations computed in the first feedforward sweep are likely used to provide information about a few basic questions such as the identity or pose of a face. Feedback processing is likely more important at longer timescales. What computations might be implemented by the feedback processing occurring on longer timescales? One hypothesis addressed by the recent work of [44] combines a feedforward network like ours---also showing mirror-symmetric tuning of cell populations---with a probabilistic generative model. Thus our feedforward model may serve as a building block for future object-recognition models addressing brain areas such as prefrontal cortex, hippocampus and superior colliculus, integrating feed-forward processing with subsequent computational steps that involve eye-movements and their planning, together with task dependency and interactions with memory.