The Role Actin Filaments Play in Providing the Characteristic Curved Form of Drosophila Bristles

Abstract

Drosophila bristles display a precise orientation and curvature. An asymmetric extension of the socket cell overlies the newly emerging bristle rudiment to provide direction for bristle elongation, a process thought to be orchestrated by the nerve dendrite lying between these cells. Scanning electron microscopic analysis of individual bristles showed that curvature is planar and far greater near the bristle base. Correlated with this, as development proceeds the pupa gradually recedes from the inner pupal case (an extracellular layer that encloses the pupa) leading to less bristle curvature along the shaft. We propose that the inner pupal case induces elongating bristles to bend when they contact this barrier. During elongation the actin cytoskeleton locks in this curvature by grafting together the overlapping modules that comprise the long filament bundles. Because the bristle is curved, the actin bundles on the superior side must be longer than those on the inferior side. This is accomplished during grafting by greater elongation of superior side modules. Poor actin cross-bridging in mutant bristles results in altered curvature. Thus, the pattern of bristle curvature is a product of both extrinsic factors—the socket cell and the inner pupal case—and intrinsic factors—actin cytoskeleton assembly.

INTRODUCTION

Localized actin filament assembly not only accounts for the elaboration of cell surface processes, such as the acrosomal process of invertebrate sperm, the stereocilia of hair cells, or the microvilli of intestinal epithelial cells, but also provides a framework for motility seen in amoebae, keratocytes, and pathogens such as Listeria. Actin-dependent processes require actin filament nucleation, membrane attachment, filament-to-filament cross-linking, and capping of filament ends after localization of the assembly sites. We now recognize that all of these events are regulated by a large number of actin associated proteins.

In some cell types, the shape-defining cytoskeletal structure is nearly identical from cell to cell. Thus, filament length, number, and cross-bridging are regulated with precision. If we can understand how this occurs, we may better understand the generation of more complex cytoskeletons especially in cells with less stereotyped cell shapes. In short, we want a model system featuring precise cytoskeletal characteristics.

We chose Drosophila bristle cells because the length and width of these single cells are prescribed and mutant flies with bristle defects were identified and collected beginning in 1916 (Morgan and Bridges, 1916) and continuing until the present time; most are still available (FlyBase Consortium, 2003). Extending posteriorly from the dorsal surface of the adult thorax are ∼200 microchaete bristles with an average length of 65–70 μm (Supplemental Figure s1). In addition there are 22 macrochaetes, the longest measuring up to 400 μm. These cells sprout during pupal development and elongate over the course of 16 h. Growth takes place at the bristle tip (Lees and Picken, 1944) and is driven by actin filament polymerization (Tilney et al., 2000a). The polarized filaments are nucleated and cross-bridged into bundles referred to as modules, which are 1–5 μm in length (Tilney et al., 1996, 2000b). At least two cross-linking proteins are involved— forked and fascin. These modules are grafted together into seven to 11 stiff bundles, which run longitudinally along the bristle shaft (Guild et al., 2003). The bundles are attached to the plasma membrane and support the growing cell (Appel et al., 1993). After elongation is complete and after the deposition of a thickened cuticle layer, which hardens and ultimately supports the cell from the outside (Tilney et al., 1996), the actin bundles begin to breakdown (Overton, 1967; Guild et al., 2002). We and others have examined the construction of the actin cytoskeleton in wild-type Drosophila and in animals lacking individual actin binding proteins (Overton, 1967; Cant et al., 1994; Petersen et al., 1994; Tilney et al., 1998, 2000a; Wulfkuhle et al., 1998; Fei et al., 2002). This has allowed us to begin to understand what each protein contributes to the cytoskeleton and how this translates into the determination of cell shape.

In contrast to the relatively straight microvilli, stereocilia, and acrosomal processes, the bristle cell has a characteristic curve. This article is concerned with how the actin cytoskeleton contributes to a curved cell shape that is reproducible from cell to cell. When we began this project, we hypothesized that the longitudinal actin bundles by being composed of modules grafted together would cause the curvature. This was based upon the simple notion that bundles along the superior edge of a bristle must be longer than those running along the inferior edge, a situation that might be orchestrated by controlling module length. Although modular length is indeed different along these edges, we show here that this difference does not seem to induce curvature but instead occurs during module to module grafting. In short, bundles maintain the resultant curved shape of these long cell extensions but do not generate shape directly.

MATERIALS AND METHODS

Drosophila Stocks, Developmental Staging, and Dissection of Pupae

The Drosophila stocks used in these studies and their developmental staging were described recently (Guild et al., 2003 and Tilney et al., 2003). Times given are hours after white puparium formation at 25°C. After removing the outer pupal case, we filleted the pupae as outlined in detail previously (Tilney et al., 1998). The bristles were then examined by light and electron microscopy (see below).

Dissection of Pupae and Isolation of Mature Bristles

To examine the curvature of individual mature bristles we fixed flies in 70% ethanol and then gradually dehydrated them in increasing concentrations of ethanol. Once in 100% ethanol, we air dried the flies for 24 h and removed their wings. We then blotted them by touching the thorax of the fly to the surface of double-stick scotch tape. The fly was removed, and a coverslip was placed over the blotted region. Photographs of individual bristles were made using a compound microscope.

Light Microscopy

The procedures for fixation of the isolated thoraces, staining with rhodamine- or Texas Red-conjugated phalloidin, and confocal microscopy were described previously (Guild et al., 2002).

To examine the relationship between the inner pupal case and the pupa, we fixed pupae after removal of the outer pupal case by immersion in 2% glutaraldehyde in 0.05 M phosphate buffer at pH 6.8 for 20 h at 4°C. Further fixation was carried out after making a small cut in both ends of the pupa as well as removal of several legs. The pupae were then immersed in 1.5% OsO₄ in 0.05 M phosphate buffer at pH 6.2 for 1 h at 4°C. After washing, the pupae were slowly dehydrated in acetone then embedded in Epon. Thick (∼1-μm) sections were cut and dried down onto slides on top of a hotplate. While hot, they were stained with 0.5% toluidine blue in 1% sodium borate and washed with water. When dry, the sections were covered with a drop of immersion oil and a coverslip. The sections were viewed and photographed on an Olympus BH2-RFCA microscope.

Electron Microscopy

Methods for fixation and processing of tissues for transmission electron microscopy have been described previously (Tilney et al., 1998). For scanning electron microscopy, adult Drosophila were fixed for several hours by immersion in 70% ethanol. They were then dehydrated completely, air dried, placed on stubs, sputter coated with tungsten-platinum, and then examined with an AMR1000 scanning electron microscope (Amray, Bedford, MA).

To determine whether the bristle curvature was three dimensional or planar, we cut the fixed dried flies longitudinally (from the head to the abdomen) into two nearly equal pieces. These half-flies were mounted on stubs and sputter coated. The microchaetes along the cut edge of the thorax were first photographed from above, and then the stub was tilted by 90° and the same microchaetes were photographed a second time. The “top” view of the same microchaete enabled us to determine whether curvature was planar or three dimensional, a determination that would be impossible by our blotting technique. From the “side” or 90° view, we were able to measure the curvature as a function of their length.

Pupae 32–36 h of age were removed from their outer pupal cases, fixed, and dehydrated as mentioned above and critical point dried before being mounted, sputter coated, and examined in the scanning microscope.

Measurements of Bristle Curvature

Given a curve described by the x(s), y(s), where x and y are points along a curve and s is the arc length, we can determine the curvature, c(s) (Mathews and Walker, 1970):

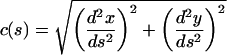1

To measure the curvature, we took 17 approximately equally spaced points along the superior edge of the bristle as seen in micrographs. From the x,y coordinates of these points, we determined the arc length as simply the distance between pairs of points. We then had a set of points x(s) and y(s). To smooth these points and to reduce them to an analytic function, we used the image analysis package, SPIDER (Frank, 1996; Frank et al., 1996, 1981; Penczek et al., 1992) to fit the points with a fourth order polynomial. By experimenting with different orders, we found that a third order polynomial generated a curve with systematic differences from the measured points (e.g., the calculated points were too high in the middle and too low at the ends), whereas a fifth order polynomial did not seem to do a much better job than the fourth order one (i.e., the calculated points seemed to fit the data by eye as well as the points chosen by eye). Thus, we had two analytic functions:

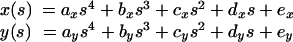2

Combining Eqs. 1 and 2, we can determine the curvature:

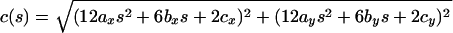3

RESULTS

Microchaete Curvature Is Planar

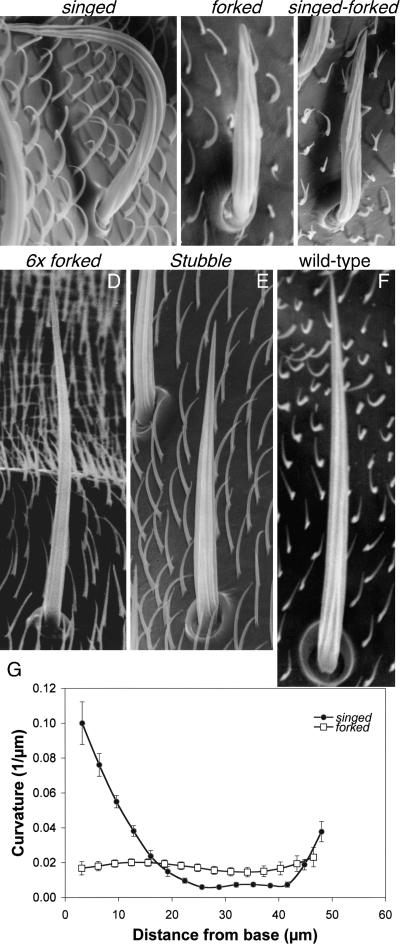
Before accurately measuring bristle curvature it is important to determine whether the curvature is planar or whether it is more complex (curving in three dimensions). Because of the limited depth of focus afforded by light microscopy, it is not possible to rigorously establish whether the curvature is planar with this technique, particularly if the curvature is complex. To circumvent this problem, we used scanning electron microscopy. We cut fixed adult flies longitudinally and mounted them on stubs so that we could look directly down on individual microchaetes adjacent to the cut surface and then tilt the half-fly by 90° and examine the same microchaete from the side. Specifically, we positioned the half-fly so we first looked along the superior surface of a microchaete; if the curvature is planar, the microchaete should look like a straight line. If the microchaete tilted by 90° (i.e., we look down on the plane containing the microchaete), the lateral view should look like a curved structure that is in sharp focus from the socket to the tip. We examined 35 microchaetes from 10 different wild-type half-flies and in all cases the curvature was planar (Figure 1A) and exhibited no complex three dimensional curvature (Figure 1B).

Figure 1.

Microchaete curvature is planar. (A and B) Adult Drosophila were sliced longitudinally and individual microchaetes were examined along the cut surface by SEM as one looks down on the thorax (A); the half-fly was then tilted by 90° (B) and the same microchaete (arrows) photographed. The sliced surface of the thorax is indicated by the white arrowhead in B. Bristles are fluted and what is apparent in this figure is that the flutes run linearly along the length of the bristle. They do not spiral around the bristle. Bars, 10 μm. (C) The curvature of wild-type microchaetes (n = 13) was measured and plotted as a function of bristle length. The greatest curvature is at the base and decreases as one moves up the bristle only to increase again near the tip. Bars indicate the SE of the mean.

The fluting along the length of these microchaetes is also planar. No twisting of the flutes around the surface of the microchaetes occurs, rather they run longitudinally along the length of the microchaete irrespective of the view of the microchaete studied (Figure 1, A and B).

The Curvature of the Microchaete Is Greatest Near the Bristle Base

We followed a standard definition of curvature as found in any physics textbook (Mathews and Walker, 1970; p. 409). The curvature of a circle of radius r is just 1/r; a straight line is a circle of infinite radius and has a curvature of zero. To measure the curvature of a bristle, we took points along the outermost part of the bristle; that is, along the part of the bristle that is farthest from the center of curvature. The choice was arbitrary and was done because it was part of the bristle that was easiest to measure because it was furthest away from the body of the fly. We examined bristles on flies with the least amount of debris that clung to the bristle. We fit the measured points with a fourth order polynomial a+b^*t+c^*t²+d^*t³+e^*t⁴, which smoothed out the errors in our measured points and gave us an easy way to determine the curvature by using derivatives of the polynomial. If we used too low an order polynomial, the curve clearly deviated from the bristle shape. When we used too high an order polynomial, the points were of course better fit, but the curvature became unreliable because the polynomial curve was more tightly bent this way and that to go through the measured points. We found that the result was about the same when either a fourth or fifth order polynomial was used.

We examined the curvature of microchaetes in situ from our scanning electron micrographs (SEMs) or along the cut surface such as illustrated in Figure 1. What is clear from our measurements is that the curvature is greatest within 15 μm of the base (Figure 1C). From there, the curvature flattens only to rise again near the tip. We also examined bristle curvature by light microscopic analysis of bristles from the dorsal thorax of the fly by “blotting,” a procedure in which the fly is touched to the surface of double-stick tape. Again, we observed the greatest curvature occurred within 15 μm of the base (Supplemental Figure s2).

Bristle Curvature Is Altered in Mutants with Cytoskeletal Defects

Examination of microchaetes by SEM reveals that mutants lacking one or both cross-bridging proteins have altered bristles. For example, bristles are 40% shorter in mutants lacking the forked proteins (forked mutant) or the forked proteins and fascin (forked-singed double mutant). These bristles are less rigid because they lie flat over the surface of the thorax (Figure 2, A–C), a fact consistent with previous results showing that the actin bundle size is markedly reduced in cross-bridging mutants (Tilney et al., 1995). If only fascin (the singed mutant) is eliminated the bristles are singed or twisted (Figure 2A). Some twist to the right, others twist to the left, and some twist first in one direction and then in the other. Careful examination of the fluting, which is related to the distribution of actin bundles (Overton, 1967; Tilney et al., 1996) shows that the flutes are not regularly spaced, but large gaps are seen between adjacent flutes (Figure 2A). This fact is consistent with our thin sections where gaps of varying size between actin bundles occur (Tilney et al., 1995, 2000a,b).

Figure 2.

Representative microchaetes from wild-type and mutant flies. (A–F) All micrographs were all printed at the same magnification. Notice that bristle length and width varies with the genotype of the fly. Furthermore, although all the bristles are fluted, the linearity of the fluting and their spacing is altered in the singed and singed-forked mutants. Bar, 10 μm. (G) Curvature measurements of wild-type and mutant bristles. The curvature for forked (n = 6) and singed (n = 13) microchaetes was measured from half-fly SEMs and plotted as a function of bristle length. For comparison, wild-type curvature measurements are shown in Figure 1C. Bars indicate the SE of the mean.

When we measured the curvature of these mutant bristles from light micrographs (Supplemental Figure s2) or from SEMs (Figure 2G), we find that just like the wild-type (Figure 1C) bristle curvature is maximal within 15 μm of the base with little curvature beyond except for the twisting of the singed mutants due presumably to improperly spaced actin bundles.

Short Modules of Equal Length Are Formed at the Bristle Tip; As They Become Grafted Together into Bundles, the Modules Forming Bundles That Lie Along the Superior Edge Elongate More Than Those Forming Bundles Along the Inferior Edge

Gaps between sequential modules in the actin bundles are present during bundle assembly near the elongating bristle tip (Figure 3, inset). What is significant is that the length of all the modules at the elongating tip is similar and short, often <1 μm in length. As the bristles elongate, the gaps between adjacent modules fill in by grafting, and the filaments of one module overlap the next module located immediately above it (Guild et al., 2003). Thus, as one moves basally down the bristle module gaps can no longer be found. When the bristle reaches its mature length, the gaps between modules reappear as actin filament disassembly proceeds (Guild et al., 2002).

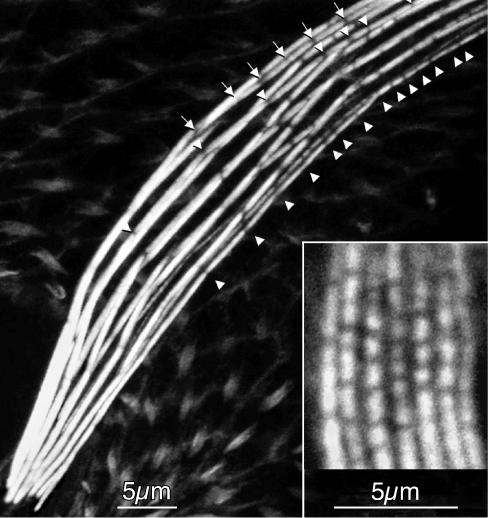
Figure 3.

Confocal image of a portion of a macrochaete from a 44-h pupa exhibiting curvature stained with fluorescent phalloidin. The arrows and arrowheads indicate positions of spaces between modules on the superior and inferior surfaces, respectively. What is apparent is that the modules making up the actin cables on the superior surface of the bristle are longer on average than those along the inferior surface of the bristle. Insert, confocal image near the elongating tip of a macrochaete from a 34-h pupa stained with fluorescent phalloidin. Notice that the length of the modules along the superior and inferior surfaces is approximately the same. These modules are all <0.5 μm in length and tend to be in transverse register. Bars, 5 μm.

The first evidence that we had that modules in bundles located near the superior margin were longer than those on the inferior margin came when we examined fully elongated bristles (Figure 3)—when the bundles begin to disassemble (Guild et al., 2002). Lateral views of the curved regions revealed that the gaps between modules in all the actin bundles occurred in approximately transverse register (Tilney et al., 1996; Guild et al., 2002). For this to occur, the modules located near the superior margin must be longer than those near the inferior margin.

Although successive modules located in superior side are on average larger than those on the inferior margin, module length does not seem to be precisely determined on any of the longitudinally oriented bundles; some long modules are being grafted to short modules as well as intermediate-sized modules. However, on average, the length of the modules that are grafted together end to end to form bundles situated along the superior margin are longer than those being grafted together to form the bundles along the inferior margin (Figure 3). This difference in average module length also was seen while examining fully elongated bristles where after the exoskeleton is deposited that actin bundle breakdown (Tilney et al., 1996).

The Dendrite That Innervates the Bristle Shaft Always Grows Over and Attaches to the Superior Margin of the Bristle

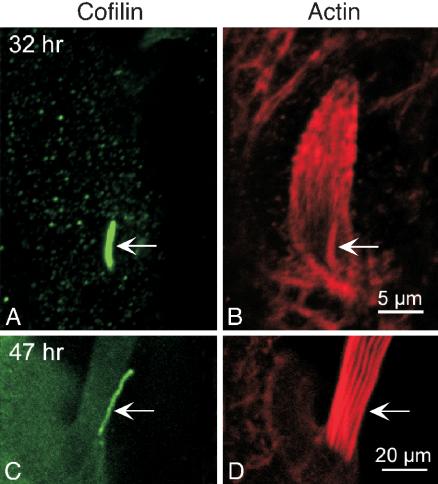
When we examined our thin sections cut through the basal end of bristles that have elongated to one-third or more of their length, it became obvious that the dendrite of the nerve was always located along the superior margin of the bristle, never along its lateral or inferior surfaces (Tilney et al., 1998). This phenomenon can best be seen by light microscopy when the dendrite could be stained selectively with antibodies directed against cofilin (Figure 4, A and C), but the bristle shaft is relatively unstained. These data are consistent with additional thin sections, showing that the dendrite is invariably attached to the superior surface of the bristle shaft (see below).

Figure 4.

Confocal view of the basal ends of two bristles illustrating the location of the dendrite. Both sprouting (A) and mature (C) bristles are stained by an antibody to cofilin, which avidly stains the dendrite of the nerve. In B and D, the bristles are stained with fluorescent phalloidin, illustrating the actin bundles of these bristles. The arrows indicate the dendrite. Bars, 5 μm (A and B); 20 μm (C and D).

We find that although the actin bundles are spaced approximately equally around the circumference of the wild-type bristle, the size of the bundles along the plasma membrane facing the underlying thorax (inferior surface of the bristle) are much larger than those on the membrane furthest from the thorax (superior surface) (Tilney et al., 1998; see below). We conclude that superior surface bundles contain fewer filaments than inferior surface bundles.

These two observations— bundle asymmetry and the invariant position of the nerve—suggested to us that the nerve might account for the asymmetry in the distribution and size of the actin bundles, an asymmetry that in turn influences bristle curvature. Evidence in support of a relationship between bristle asymmetry and the dendrite comes from studying bristles on the head, where the bristles can extend at predictable yet different angles relative to the center of the head. Figure 5 shows transverse sections through two head bristles that differ in orientation by 180°. In both bristles, the dendrite of the nerve runs along the superior edge of each bristle, and bundle asymmetry is exactly correlated with the position of the nerve, even though one bristle extends anteriorly toward the mouthparts, the other posteriorly toward the abdomen.

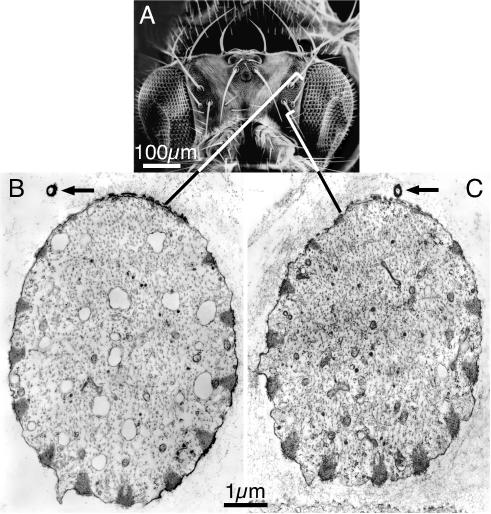
Figure 5.

The dendrite is attached to the superior surface of the bristle irrespective of bristle orientation. (A) SEM of the head of a Drosophila. Notice that 14 macrochaetes extend at predictable angles. Bar, 100 μm. (B and C) We cut thin sections through two pupal microchaetes corresponding to those indicated on the adult micrograph. Of interest is that the superior edge of each of these bristles have missing or tiny actin bundles; in each case the dendrite of the nerve (arrow) is located near this edge, even though one of the bristles extends anteriorly (B) and the other posteriorly (C). Bar, 1 μm.

The Direction of Curvature Is Established during Bristle Sprouting

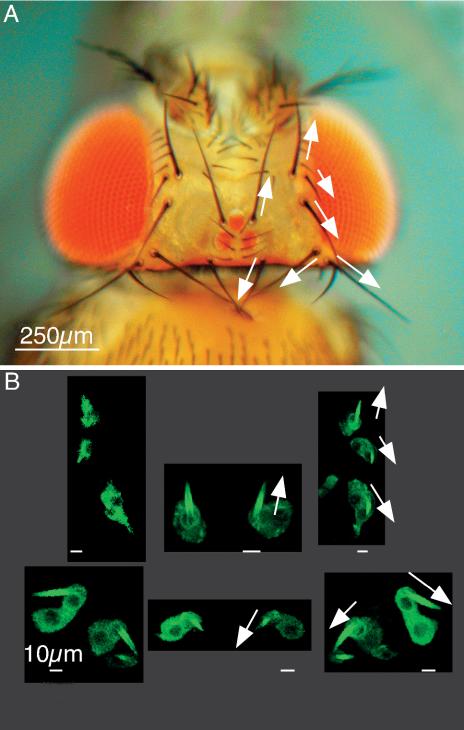
When is bristle orientation established during bristle morphogenesis? This question is best answered by examination of the bristles on the surface of the head where seven pairs of macrochaetes extend at different yet prescribed directions (Figure 6A). We examined sprouting bristles in 32-h pupae that were labeled with green fluorescent protein (GFP)-actin and found that the orientation of each of these 14 macrochaetes is identical to that of the corresponding fully elongated bristle (compare Figure 6, A and B). Thus, bristle orientation is established at the onset of bristle elongation, even before significant actin bundling takes place.

Figure 6.

Bristle orientation on the adult head is established at the onset of bristle elongation. (A) Light micrograph of the head of an adult fly. The arrows indicate the orientation of selected macrochaetes. Bar, 250 μm. (B) The same macrochaetes indicated by the arrows in A are visualized in a 32-h pupae expressing GFP-actin. These macrochaetes have just begun to elongate. Notice that the orientation of these tiny macrochaetes (arrows) is identical to that of the adult fly. Bars, 10 μm.

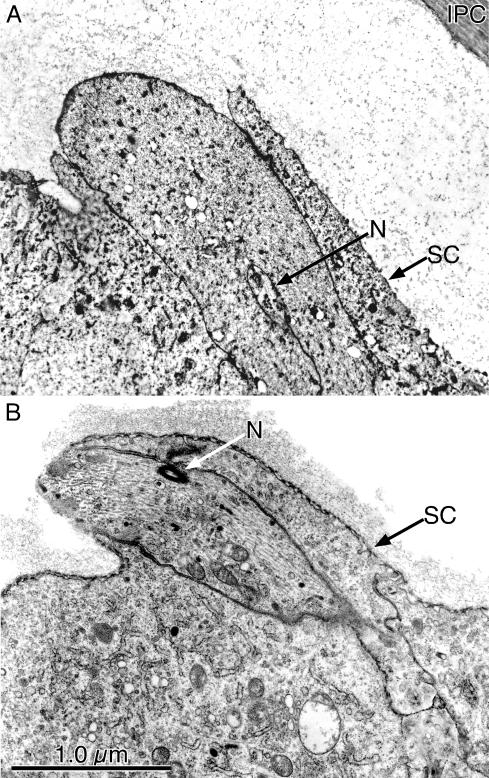
Clues as to how sprouting bristles are programmed to express their defined orientation come from thin sections through these sprouting bristles. We find that the anterior surface of the socket cell extends over these bristle rudiments as if directing bristle orientation. This asymmetric extension (Figure 7A) of the socket cell is even more pronounced in the leg bristles that are elongating during the same period (Figure 7B). Of significance is the fact that located within an indentation of the bristle rudiment shaft is the dendrite of the nerve (Figure 7B) that innervates the bristle. This dendrite elongates at the same time as the elongation of the newly emerging bristle shaft. This dendrite is always located on the side of the rudiment immediately adjacent to the extension of the socket cell. Because the dendrite is always positioned at or near the interface of the bristle shaft and the socket cell extension, it may be applying positional information to the socket cell and to the bristle shaft, information that plays a role in the orientation of the newly emerging bristle shaft.

Figure 7.

(A) Socket cell extension during the emergence (32-h pupa) of a microchaete from the surface of the thorax. Of interest is that the anterior surface of the socket cell (SC) extends outwards over what will be the superior surface of the microchaete. Within an infolding in the microchaete is the nerve (N). (B) Thin section cut through a newly emerging bristle from the leg of a 32-h pupa. As in A, the SC extends over what will be the superior surface of the bristle. Just beneath this expanding portion of the socket is the dendrite of N that will innervate the bristle. Bar, 1 μm.

Two additional facts can be gleaned from Figure 7. First, these early bristle rudiments extend from the thorax at an oblique angle and not perpendicular to it as one might expect if the socket cell lacked an asymmetric extension. Second, at these early stages in bristle growth, the actin bundles have not yet formed. What is present at this stage are tiny clusters of filaments attached to the plasma membrane and/or individual filaments aligned parallel to the elongating axis of the rudiment (our unpublished data).

External Forces May Influence Bristle Curvature

It is hard to see how module assembly would determine curvature, particularly because the curvature is not constant and the inferior and superior modules are the same length initially. Thus, at this point, we have eliminated many of the obvious ways curvature could be generated by the actin cytoskeleton and wondered whether there are any other possible mechanisms that could account for curvature.

One possibility is for an external force that when applied to the elongating bristle could influence curvature. Such a possibility is the constraint on bristle elongation imposed by the inner pupal case. This extracellular layer represents the entirety of the pupal cuticle that forms at the end of puparium development (∼12 h after white puparium formation) and surrounds the pupa (Figures 8 and 9A) (Fristrom and Fristrom, 1993). It is a tough extracellular covering consisting of multiple layers of fibers oriented in orthogonal planes like the layers in fish scales (Figure 8). The pupa is tightly associated with the inner pupal case in pupae younger than 36 h.

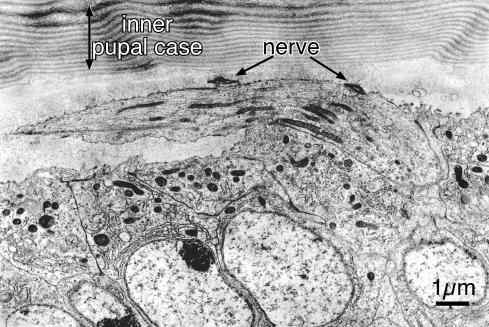
Figure 8.

The relationship between a newly emerging bristle and the inner pupal case. Extending from the thorax is a short bristle in this section through a portion of the thorax of a 32-h pupa. It curves over the surface of the thorax, apparently being compressed by the inner pupal case. Of particular interest in this section is the dendrite of the nerve that is cut in two places. Notice that the dendrite is found attached to the superior surface of the elongating bristle. Bar, 1 μm.

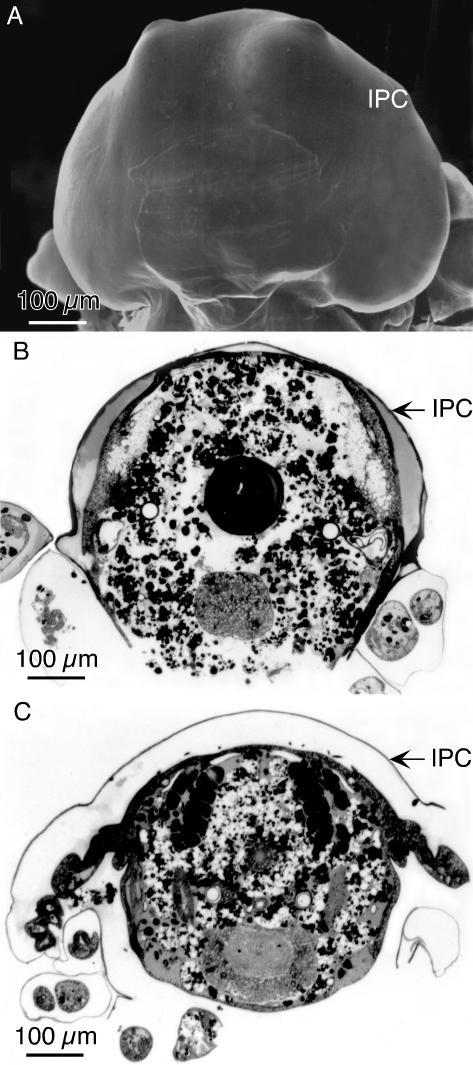
Figure 9.

The relationship of the inner pupal case to the thorax of pupae. (A) SEM of the head of a 32-h pupa. The outer pupal case has been removed. As seen here the inner pupal case (IPC) follows closely the contours of the pupal head. (B) Transverse Epon section through the thorax of a 32-h pupa stained with toluidine blue. Note that the IPC tightly encloses the dorsal surface of the thorax. (C) Transverse Epon section through the thorax of a 36-h pupae. Note that this pupa has shrunk leaving considerable space between the IPC and the pupa. Bars, 100 μm.

To see whether the inner pupal case might act as a “straightjacket” and thus influence bristle curvature as the bristles elongate, we examined micrographs of thin sections that were cut through bristles that included the overlying inner pupal case. We find that elongating bristles are sometimes found directly beneath the inner pupal case, whereas at other times they are located many microns away from this barrier. We wondered whether this discrepancy in spacing reflected different times in development. SEM micrographs in which portions of the inner pupal case were removed reveal that associated with the inner pupal case is a large amount of extracellular material that extends from the inner pupal case to the elongating bristles (our unpublished data). This material is easily seen in thin sections (e.g., Figures 7 and 8).

Accordingly, we carefully removed pupae of increasing ages from their outer pupal shell, an extracellular layer formed from the third instar cuticle. We put these pupae in fixative and carefully cut off the tips of the head and abdomen and removed legs so that the fixative could enter the inner pupal case, which is a barrier to fixation. After fixation and embedding in plastic, we cut 1-μm transverse Epon sections of the pupae and examined them after toluidine blue staining. What is interesting is that the inner pupal case tightly surrounds the pupae and lies directly over the dorsal surface of the thorax in 32-h-old pupae (Figure 9B), but by 36 h there is considerable space between the inner pupal case and the dorsal thorax (Figure 9C). Thus, shortly after bristles begin to sprout, which is at 32 h, the inner pupal case acts as a corset to force bristles to bend as they elongate obliquely from the surface of the pupae and thus follow the inside of the inner pupal case because they elongate primarily by tip growth (Lees and Picken, 1944; Tilney et al., 1996). In short, this corset would induce maximum bristle curvature at the base of the bristle (i.e., the portion made first). As development proceeds, the pupa must shrink because the space between the thorax and the inner pupal case expands. This in turn would induce less compression on the bristles, which as they elongate further by tip growth, would show progressively less curvature, a fact consistent with our curvature measurements (Figure 1C). Thus, our data are consistent with the hypothesis that the inner pupal case could induce the appropriate curvature.

If the pupal case generates curvature, the curvature of the bristles in forked and singed mutants, which have smaller actin bundles than the wild type, should behave like the wild type and show the greatest curvature at the base of the bristle. Thereafter, because the actin bundles are so small, they may be of insufficient size to adequately support elongating bristle so that the bristle would seem to lie flat on the surface of the thorax. This behavior was observed in our scanning micrographs (Figure 2) and in light micrographs of isolated bristles, which in turn show the greatest curvature near the base (Supplemental Figure s3). Thus, our data on mutants are consistent with our hypothesis that the developing cytoskeleton responds to compression induced by the inner pupal case as it did for the wild type.

Bristles That Exhibit Less Curvature Are Not Compressed by the Inner Pupal Case

Lees and Picken (1944) studied the Stubble mutant whose moniker indicates the bristles are short, straight, and stiff like an early stage in beard growth. They also noted that because Stubble and wild-type bristles contain similar volumes, Stubble bristles seem fatter (Figure 10). In addition, Stubble bristles contain more bundles than the wild type. In this example, there are 19 cortical bundles and an internal bundle, twice the number as the wild type. Furthermore, bundle size also has dramatically increased in this mutant (Figure 10C), and each bundle is maximally cross-bridged (Tilney et al., 2003). What is particularly relevant is that these bristles elongate more slowly than the wild type (Lees and Picken, 1944), so that the Stubble bristles will be less constrained by the inner pupal case during the early phases of bristle elongation, the result being a reduction in curvature at their base, a fact that can be confirmed by our blots (Figure 10B). Thus, Stubble represents a natural experiment where the contribution of the inner pupal case is removed and bristle curvature is reduced to negligible amounts.

Figure 10.

Stubble microchaetes. (A) Light micrograph of wild-type microchaetes. (B) Light micrograph of Stubble microchaetes that are short (>50 μm), fat, and straight. (C) Thin section through a Stubble microchaete. The superior surface can be identified by the dendrite of the nerve (N). The arrowhead indicates an internal bundle of actin filaments. In addition to this bundle, there are 19 large cortical bundles and one internal bundle (arrowhead). Thus, not only are the Stubble bristles shorter than the wild type but also the actin bundles are more numerous and larger than the wild type. Bar, 1 μm.

Similarly, we would expect that increasing bundle size and number by using other mutants also would lead to straighter and stiffer bristles. This is born out for the 6 × forked animals (Figure 2D), a mutant that contains additional forked genes, thus more forked cross-bridges that in turn result in a huge increase in the size and number of actin bundles (Tilney et al., 1998; Figure 9). Interestingly, the 6 × forked bristle also tends to be shorter than the wild type and straighter with little curvature at its base, although the tips of the bristles curve dramatically.

DISCUSSION

How Might the Direction of Bristle Curvature Be Established?

As soon as tiny bristle rudiments appear, they are already programmed as to the direction of elongation and the angle of elongation relative to the pupal surface whether on the head, thorax, or leg. This asymmetry arises before the generation of the actin cables. Because the pupal case covers the cellular surfaces, it seems as likely to deflect an extension in one direction as another. Asymmetries in the socket cell and the bristle cell, on the other hand, are correlated with the direction of curvature. Thus, the direction of curvature seems to be determined initially by an extension of the socket cell, a cell that surrounds the bristle shaft.

Is Curvature Programmed Directly by Actin Assembly?

The curved bristle then has both a direction of curvature and a variation of the amount of curvature along its length. The steps in development suggest three possible ways in which a curved bristle might be generated. First, curvature might be a direct result of actin polymerization. Second, the dendrite might provide a signal that generates curvature at the base of the bristle. Third, the pupal case might generate curvature by influencing the elongation of the bristle cell.

Could the actin cytoskeleton directly account for curvature? Four possible mechanisms could be imagined. First, we know that bends can be built into the actin bundles in Limulus polyphemus sperm. The bend, which corresponds to an obtuse angle of ∼155°, is specified by the interfilament spacing in a bundle of hexagonally packed actin filaments (DeRosier and Tilney, 1984). The bend could be spread out over an extended length in a bristle to generate the desired degree of curvature. The total angle, however, would be directly proportional to the interfilament spacing and would require “crystalline” regularity of actin packing. Because the angle varies considerably among various mutants and the wild type (Figure 2), yet the interfilament spacing (which is fixed by the cross-linking proteins) must be relatively constant, this mechanism does not fit our observations.

A second possibility is that the superior to inferior variation in the bundle diameter might cause the curvature. Suppose a constant slug of actin is polymerized in each bundle. The narrower (superior) bundle would elongate more than the wider (inferior) one so that the total amount F-actin, which would be related to the length of the module times its area, in each module is a constant. Thus, the cables on the superior surface would grow longer than those on the inferior surface, thereby generating curvature. The geometry of the cables does not support this mechanism. The ratio of the area of the superior over the inferior bundle would be (r – d)/r, where r is the curvature of the bristle and d is its diameter (see Materials and Methods). Given a curvature of 0.05 μm^-1, which corresponds to a radius of 20 μm, and a bristle diameter of ∼2 μm, the ratio of areas would be 0.9, whereas the real variation is a factor of at least 2. In addition, the variation in curvature along length is not reflected in the variation of bundle areas along the length (Tilney et al., 2000b). Thus, the actin cytoskeleton in and of itself does not vary in a correlated way with the curvature and seems unlikely to generate the curvature, but more likely, locks in the curvature generated by other means.

A third possibility is it that the control of module length might induce curvature.

For a curved object like a bristle, the actin bundles along the upper or superior surface must be longer than those along the inferior surface. Because the bundles are composed of repetitive units or modules (Tilney et al., 1996), an excellent way to achieve different bundle lengths is to construct modules on the superior surface longer than those on the inferior surface. What we find is that the first few modules that form at the tip of an elongating bristle are all short and approximately the same length (Guild et al., 2003; Tilney et al., 2004; this report). Farther down from the tip of an elongating bristle, the modules all increase in length but those on the superior surface seem to be, on average, longer than those on the inferior surface. When the modules finally become grafted together even further down the bristle, this would lead to longer bundles on the superior surface than on the inferior. However, there are three observations that are inconsistent with module length determining curvature. First, the size of adjacent modules on each cable is not rigorously controlled but the length, on average, is longer for superior cables versus inferior cables. Second, because curvature varies along the length of the bristle, the average length of superior modules must change and be cognizant of position. Third, module lengths in bundles located on the lateral margins must be different from those along the superior and inferior surfaces and in fact each cable must be different from others. In short, although module length varies, it seems unlikely that it is the causative agent in determining bundle curvature.

A final possibility is one that involves treadmilling in actin bundles and how this might generate curvature. Recent evidence shows that treadmilling goes on in the stereocilia (Rzadzinska et al., 2004) and in other bundles like microvilli (Tyska and Mooseker, 2002; Loomis et al., 2003). How is length so precisely maintained? The idea is akin to saying that the building blocks are taken off at the bottom and then motored up to the top and added back. Of course, that cannot be right as stated, but suppose that the disassembly at the bottom is “handshaking” with the motors to the top so that subunits are only trucked when others are removed. Under such conditions, the bundle length would be stable in the face of turnover. To make the rate vary with bundle length, one might use age (for example, perhaps determined by protein modification like methylation). We have shown that initially modules are only ∼1 μm in length when made but elongate and fill in to generate a curved bundle. Using treadmilling, the possibility exists that motors truck subunits to the end of the bundle for elongation. The bigger the circumference of the bundle, the more tracks to deliver the actin subunits. The more area of the bundle, the more subunits needed to lengthen the bundle. This would mean that the amount of lengthening would vary inversely with radius instead of the square of the radius as expected if a constant slug of actin subunits were polymerized. To check to see whether this possibility fits the existing data, we modeled this process by using the equations shown in the supplemental material. Using reasonable estimates for actin bundle parameters and actin monomer transport, we found that treadmilling could not account for curvature.

Although actin bundle size and distribution does not seem to program bristle curvature, these attributes can affect bristle curvature. For example, in mutants that lack one or more cross-bridges between the actin filaments, the bundle size is reduced (Tilney et al., 1995) and at the same time the curvature changes (Figure 2G). These changes in turn also relate to the stiffness of the bristle. For example, singed-forked double-mutant bristles seem flaccid and lie on the thoracic surface. Furthermore, bristles that lack fascin are no longer planar because the bundles are not evenly spaced around the circumference of the bristles. These differences in the separation of adjacent bundles combined with the fact that the actin bundles in singed bristles are small and flat permits twisting to occur.

Could the Dendrite Determine Bristle Curvature?

Because the dendrite overlies the superior surface of the bristle, it is possible that the dendrite could generate a signal that determines curvature. For example, we know that as the dendrite is extending its surface must be moving tipward. If the bristle cell is growing in contact with it and its surface is attached to the dendrite, it will be dragged along. Now suppose that the bristle cell is also extending. The rate of increase along the superior surface will then be the sum of the dendrite rate plus the bristle cell rate, whereas the rate of extension of the inferior surface, which is not attached to a moving surface, will be slower (i.e., just equal to the rate of bristle cell extension). Such a mechanism could generate curvature at its base as the dendrite only extends part way up the bristle. This assumes that bristle cell extension (at least the membrane portion) is carried out at the base and that it drags the cytoskeleton along with it. Although this mechanism could account for curvature at the base, it could not account for the decreasing curvature along the bristle length and its increase again at the tip because the dendrite only grows out over the basal fifth of the bristle. It further could not account for the lack of curvature in bristle mutants such as Stubble.

Could External Forces Influence or Determine Curvature?

Because neither actin assembly nor the position of the dendrite seems to be solely responsible to account for bristle curvature, for the lack of alternatives we have considered that the inner pupal case, an extracellular layer, may play a role in curvature development. In fact, we present supporting evidence for such a hypothesis. What we have shown is that in early (32-h) pupae the inner pupal case tightly encloses the pupa like a corset. However, as development proceeds (36 h), the space between the pupa and the inner pupal case increases, presumably because of a reduction in volume of the developing pupae. Thus, in early pupae, the elongating bristles will come in contact with the inner pupal case, which should influence the bristle curvature by deflecting the growing tips (Figure 11A). This also would predict that the curvature would be planar, not three dimensional. As the pupal case recedes, bristle tips will curve progressively less and less, a fact we established by measuring the curvature of mature bristles of the wild-type as well as bristles from mutants that contain smaller actin bundles. Thus, this corset that encloses the pupa, provides an external constraint so that the bristle curvature, at least for the first 20 μm, will depend upon the rate of elongation and the rate at which the pupal case recedes. Furthermore, because the inner pupal case surrounds the entire pupa it will affect the curvature of not only the thoracic bristles but also head and leg bristles. Also in keeping with this conclusion is the fact that hairs, or trichomes, projections of thoracic epithelial cells that are not innervated, also are curved in the same direction as the bristles. We presume that the curved behavior of the hairs could be accounted for by the influence of the inner pupal case and its associated material (Figures 7 and 8) and/or compression by the inner pupal case (see below).

Figure 11.

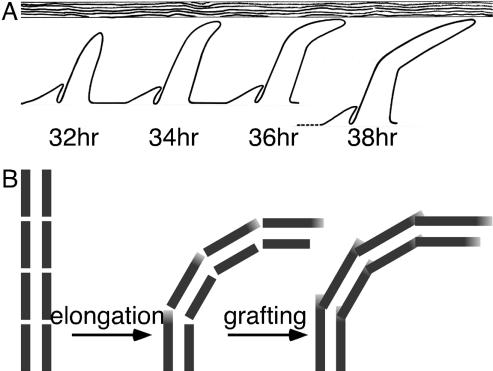
Models for bristle curvature. (A) Deflection model. Elongating bristle shafts of increasing developmental age are shown from left to right. Sprouting direction (posterior, to the right) has already been established by the socket cell. By 34 h the elongating bristle has been deflected by the inner pupal case (horizontal barrier). By 38 h, the distance between the inner pupal case and the pupa has widened resulting in less bristle curvature. (B) Model for locking-in bristle curvature with modular actin filament bundles. Left, all modules forming at the growing tip of the bristle are similar in length. Middle, as the bristle curves the superior-side modules elongate (gray regions) to provide the increased length required for superior-side bundles. Right, both superior- and inferior-side modules elongate in order to graft with adjacent modules forming continuous bundles.

Steps in bristle emergence and elongation provide clues to a mechanism of curvature generation. Bristle rudiments begin to emerge in 32-h pupae. These rudiments extend at an oblique angle relative to the surface of the thorax or the head and grow with the same orientation displayed by the mature bristle. As the bristle elongates primarily by tip growth, new modules composed of cross-linked actin filament bundles occur, elongate, and are grafted together end to end to form continuous actin cables that act as ribs running down the bristle shaft just beneath the plasma membrane. Thus, the modules forming the cables located along the superior surface elongate on average more during grafting than the modules making up the cables found on the inferior surface (Figure 11B).

What Role Could the Actin Cytoskeleton Play in Determining Bristle Curvature?

As has been mentioned repeatedly in the literature, actin filament assembly is key in extending the cell surface into a microvillus, a stereocilium, a microspike, and a bristle. Once this has occurred, the actin filaments are stabilized by being cross-bridged together into bundles. Could it be that although actin assembly is essential for bristle elongation, the main function of the actin cytoskeleton in bristles is not for orchestrating curvature or bristle orientation but rather to “lock in” curvature and orientation once it is generated by other factors and external stimuli?

This idea that the actin cytoskeleton is there to maintain cell asymmetry but not necessarily induce cell shape directly is not new. For example, actin assembly is responsible for the elongation of the acrosomal process in certain invertebrate sperm and for inducing the motion of Listeria in cells. Currently, most investigators agree that actin assembly induces these motions by biasing filament assembly. In short, actin filaments “push” by adding subunits to the ends of existing filaments that are separated from the distending membrane surface by Brownian motion (Mogilner and Oster, 1996, 2003) have termed this the “elastic Brownian ratchet.” Thus, bending actin filaments induce motion by biasing Brownian motion.

In a similar way, we imagine that the actin filaments in elongating bristle tips induce elongation. For the determination of curvature, we envision at least two external influences. The first is the influence of the dendrite in giving orientation to the bristle rudiment via the socket cell extension and in regulating bundle size on the inferior and superior surfaces of the bristle. The second is the restraint of the inner pupal case on the elongating bristle tip. The actin bundles that assemble then would follow the shape of the shaft cytoplasm. Then as the modules elongate and become grafted together the curvature is “locked in” (Figure 11B). A simple analogy may be helpful here. It is well known that the keratin fibrils in hair are cross-linked by disulfide links. One can produce curly hair as done routinely in beauty salons, simply by reducing all the disulfide bonds and after curling the hair over a curler, reoxidize them. When the curler is removed the hair remains curled. By this procedure each hair is effectively locked into curls, orchestrated by a flaccid hair binding to a round surface before it is reoxidized. In a similar way, the actin bundles lock in curvature but do not create it directly themselves.

Pattern Development: Bristle Curvature Is Programmed by Both Extrinsic and Intrinsic Factors

There are two clear examples of extrinsic factors that seem to determine the characteristic curvature of the bristle. The socket cell has an asymmetry that acts to determine the angle of bristle elongation, whereas the inner pupal case acts to confine bristle extension. One immediately wonders how the socket cell “knows” what part of the surface to extend. Because the dendrite of the nerve also is found between the socket extension and the bristle shaft, we suspect that the dendrite might be supplying this positional information, particularly because the dendrite is also circumstantially in a position to regulate actin bundle size and thus bristle flattening and curvature (Lees and Picken, 1944).

Assuming this speculation is reasonable, then one wonders how the dendrite is programmed to attach preferentially to the superior margin of the bristle. There have been extensive studies reported in the literature indicating that the position of the dendrite seems to be the result of a decision made earlier in development and involves the pattern of cell division of the sensory organ precursor cell (SOP) of a bristle (Hartenstein and Posakony, 1989; Gho and Schweisguth, 1998). The SOP divides sequentially to produce the bristle cell, the socket cell, the neuron, and the sheath cell. The first division of the SOP produces an anterior cell (pIIb), which subsequently divides to form the neuron, the sheath cell (that surrounds the axon of the neuron like the vertebrate schwann cell) and another cell, the glial cell, that migrates away. The second or more posterior cell (pIIa) divides transversely to form the socket and bristle cell. When we look at differentiating cells (∼10 h after the SOP division), we note that the developing neuron is always located anterior to the bristle and socket cells. Accordingly, if a dendrite elongates from the neuron it will invariably elongate over the superior margin of the bristle, which in fact we show to be the case.

Intrinsic factors also affect the bristle curvature. First, we know that actin assembly is essential for bundle elongation (Tilney et al., 1996). Second, mutants that affect the expression of actin filament cross-bridging influence bristle length, bristle rigidity, and bristle twistedness. Thus, if the bundles are small, rigidity and length are affected; and if the bundles are not equally spaced, the bristles are twisted. Furthermore, if bundle number and size are increased, the bristles are straighter and stiffer, e.g., in Stubble and 6 × forked. And third, because the fluting of the bristles is related to the position of the actin bundles (Overton, 1967; Tilney et al., 1995), which in turn orchestrates the deposition of the exoskeleton to produce the flutes (Tilney et al., 1996), actin bundle assembly clearly influences cell form.

In short, pattern development is accomplished by both extrinsic factors, e.g., the inner pupal case and the dendrite, and intrinsic factors such as actin assembly, actin cross-bridging, and actin bundle positioning.