GMDR: Versatile Software for Detecting Gene-Gene and Gene-Environ- ment Interactions Underlying Complex Traits

Abstract

Identification of multifactor gene-gene (G×G) and gene-environment (G×E) interactions underlying complex traits poses one of the great challenges to today’s genetic study. Development of the generalized multifactor dimensionality reduction (GMDR) method provides a practicable solution to problems in detection of interactions. To exploit the opportunities brought by the availability of diverse data, it is in high demand to develop the corresponding GMDR software that can handle a breadth of phenotypes, such as continuous, count, dichotomous, polytomous nominal, ordinal, survival and multivariate, and various kinds of study designs, such as unrelated case-control, family-based and pooled unrelated and family samples, and also allows adjustment for covariates. We developed a versatile GMDR package to implement this serial of GMDR analyses for various scenarios (e.g., unified analysis of unrelated and family samples) and large-scale (e.g., genome-wide) data. This package includes other desirable features such as data management and preprocessing. Permutation testing strategies are also built in to evaluate the threshold or empirical p values. In addition, its performance is scalable to the computational resources. The software is available at http://www.soph.uab.edu/ssg/software or http://ibi.zju.edu.cn/software.

1. INTRODUCTION

Statistical genetics has been attempting to understand the genetic architecture underlying complex traits. Although recent practice of genome-wide association studies (GWASs) have revealed many new loci that contribute to phenotypic variation, probably enlightening a way to decipher the genetic basis, a substantial proportion of undercounted phenotypic variation, the so-called “missing heritability” [1], is still waiting for further investigation. Ubiquitous gene-gene (G×G) and gene-environment (G×E) interactions are considered as one of the primary culprits for missing heritability [2-4], and thus identification of G×G and G×E interactions will help elucidate the missing heritability to a better extent.

Methods in which association is tested by incorporating multiple genes have been proposed for detection of interactions [5]. In general, those methods fall into two categories: regression methods and machine learning approaches. Regression methods are subject to several problems associated with the “the curse of dimensionality”: heavy computational burden (usually computationally intractable), increased Type I and II errors, and reduced robustness and potential bias as a result of highly sparse data in a multifactorial model [6]. Machine learning methods may circumvent the problems of sparse data, of which multifactor dimensionality reduction (MDR) method has sustained its popularity since its appearance [7]. Rather than exacting the interaction term per se as in the regression methods, MDR seeks for a combination of factors in question that maximizes the phenotypic variation it explains. It treats the main and the interaction effects as a whole, coinciding with the concept of the very original epistasis described by Bateson [8], and offering a solution to avoid decomposition as employed in the regression methods. MDR is still limited in practical use because of a few weaknesses until the generalized multifactor dimensionality reduction method (GMDR) was proposed [9].

GMDR has been further extended for tackling diverse phenotypes and samples [10-14], including analyzing a breadth of traits such as ordinal or polytomous nominal data, survival data and multivariate phenotypes, correcting for cryptic population structure in unrelated subjects to avoid inflated false positive and false negative rates, entertaining family structure by use of within-family association information, and unifying both unrelated and family samples into a joint analysis for improved power and prediction accuracy. Further, given the availability of genome-wide data, the features to manage and process large scale data are also desirable. To achieve these goals, in the present study, a versatile GMDR package is developed for GMDR analyses.

2. METHODS IMPLEMENTED IN GMDR SOFTWARE

The GMDR approach is a comprehensive framework for identification of interactions [14]. The workflow of GMDR involves three components: residual computation, membership calculation and constructive induction for data reduction Fig. (1). Phenotypes and covariates are used to compute the residuals under the null hypothesis based on an appropriate statistical model corresponding to the data type and the plausible data generation mechanism. The pedigree structure and attributes (e.g., gene/genetic markers and discrete environmental factors) are used to compute the membership coefficients that characterize to which cell(s) a subject can be allocated in a contingency table spanned by a set of target factors. The product of the residual and the membership coefficient offers a flexible metric to measure the association between the factors under consideration and the phenotype of interest, and serves as the input to the constructive induction for data reduction. We concisely recapitulate here the relevant methods as follows.

Fig. (1).

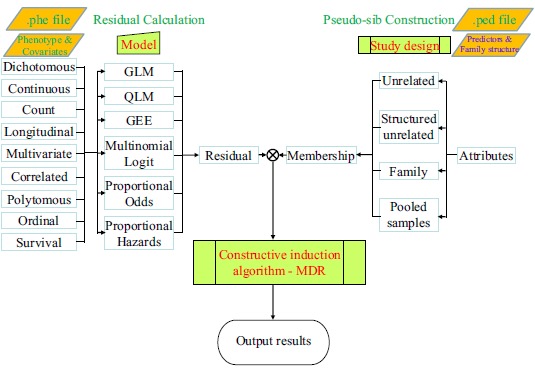
Schematic flowchart of data processing in the GMDR software. Data analysis in GMDR is divided into three components: residual calculation, membership coefficient calculation and MDR analysis. Phenotypes and covariates are used to compute the residuals under a null model. Attributes such as genetic loci and environmental factors are used to determine membership coefficients according to the study design. The metrics that are computed as the product of the residuals and the membership coefficients, respectively, are used for the dimensionality reduction. GLM, QLM and GEE represent generalized linear, quasi-likelihood and generalized estimating equations models, respectively.

2.1. Constructive Induction (Multifactor Dimensionality Reduction)

The GMDR approach employs the same data reduction strategy as that of the MDR. Briefly, MDR is a variable construction algorithm that creates a new dichotomous variable by pooling the cells in a space spanned by a set of discrete attributes into two contrasting groups and thus changes the representation space of the data from higher dimensions to one dimension [15]. First, each sample can be allocated to a cell in a -dimensional space that is spanned by a set of factors. Next, each nonempty cell is labeled as high-valued if the metric, which is calculated from the phenotypes of all the samples in the cell, is not less than a pre-set threshold, or low-valued otherwise; in the original MDR, the metric is the ratio of cases to controls in the cell and the threshold is one. Then, a multifactor model is formed by pooling high- and low-valued cells into two respective groups, i.e., high-valued and low-valued groups, and a new binary attribute is constructed. The new attribute is evaluated for its ability to classify or predict the phenotypes; accuracy (the proportion of the correct classifications, i.e., high-valued individuals in the high-valued group and low-valued individuals in the low-valued group) is a commonly used measure. When the set of discrete factors are a subset chosen from all factors of either genetic and/or environmental sources, the model with the highest classification ability among a total of $\left(\begin{array}{c}\mathrm{\omega }\\ \mathrm{\gamma }\end{array}\right)$ factor combinations is identified as the best model which best accounts for the phenotypic variation in a -dimensional space. Cross-validation and/or permutation testing can be used to empirically assess the significance of the identified model.

As a flexible generalization, GMDR uses more general metrics, in the place of ratio of cases to controls in MDR, in classifying nonempty cells into two contrasting groups; the MDR is therefore a special case of GMDR where covariates are not present and the trait of study is binary [9]. The metric of an individual corresponding to a certain cell in a given contingency table can be expressed as the product of the membership coefficient belonging to this cell and the residual under the null hypothesis:

$$S_{\mathit{ik}}=r_i{\pi }_{\mathit{ik}},$$ (1)

where S_ik is the metric of individual i with respect to cell k in a given contingency table, r_i is the residual, and π_ik is the membership coefficient. The residuals and the membership coefficients can be computed from the input data based on the statistical model and the study design, respectively.

2.2. Residuals in a Null Model

Multitudinous statistical models are available to characterize the diverse phenotypes. They include, but are not limited to: generalized linear models [16] such as logistic regression, Poisson and normal linear models, and quasi-likelihood (a generalization of generalized linear models) [17] for dichotomous, count and continuous phenotypes, respectively, generalized estimating equations (GEE) model for correlated observations and multiple complex traits [18], multinomial logistic model for polytomous data [19], proportional odds model for ordinal data [20], and proportional hazards model for survival data [21]. Although having various distribution properties, these models share the same form of linear predictor, η, to describe the influence of a set of explanatory variables on the outcome that can be expressed as,

$$\mathrm{\eta }=l\left(\mathrm{\mu }\right)=I{\mathrm{\beta }}_0+{\mathrm{X}}_t{\mathrm{\beta }}_t+{\mathrm{X}}_c{\mathrm{\beta }}_c=\mathrm{X}\mathrm{\beta },$$ (2)

where μ is the expectation of observation Y, l(.) is an invertible link function that relates the mean μ to the linear predictor η, β is the effect vector probably consisting of β ₀, β _t and β _c for the intercept(s), the target effects of interest and the effects of covariates (a type of variables related to the dependent variable that typically has a minimal relation to the other independent variable), respectively, X and I is the corresponding design matrix consisting of block matrices I, X_t, X_c is a unit matrix. The target effects vector β_t may consist of the genetic effects of genes tested and their interaction effects with some environmental factors and other predictor variables of interest, known as confounders (a type of variables that change the relation between an independent and the dependent variable because it is related to both the independent and the dependent variables) or mediators (a type of variables that are intermediate in the causal path from an independent variable to a dependent variable).

Under the null hypothesis of no target effects (i.e., β _t = 0), fit $\stackrel{\wedge }{{\mathrm{\beta }}_0}$ and $\stackrel{\wedge }{{\mathrm{\beta }}_{\mathrm{c}}}$ as well as other parameters to data implemented with maximum likelihood, quasi-likelihood or GEE methods. Then, the residuals can be computed under the fitting null model for forming the metric. As the null hypothesis assumes no target effects, the residuals need not re-compute for different combinations of target factors.

Many phenotypes can be modeled by the above-mentioned models with a proper link function, enabling GMDR to be applicable to various phenotypes such as real number-valued, count-valued, dichotomous, polytomous nominal, ordinal, time to event and multivariate as well as a combination of them, and also to allow for inclusion of covariate(s).

2.3. Membership Coefficients

Membership coefficient specifies the probabilities of an individual pertaining to a given cell in a contingency table and is an element of the incidence matrix, X_t , for the target effects in the statistical model, Equation (2). Membership coefficients are determined according to the study design and the sample structure. Family-based and unrelated subject-based designs are commonly used in genetic studies. The former is robust against population stratification and admixture that may inflate false positive and false negative rates if it is not properly corrected, while the latter is more economical and less laborious to collect samples and thus can be more efficient in the absence of population structure. GMDR can handle various sample scenarios, such as unrelated individuals from a homogeneous population, unrelated participants from an admixed population or heterogeneous populations, family samples and mixtures of them. The samples in a study may be divided into two subsets: unrelated individuals including singletons whose ancestors and descendants are not included in the study and founders in families or pedigrees, and nonfounders in families.

In the absence of population stratification, as in the MDR [7] and the original GMDR [9], the membership coefficient of an unrelated subject, π_ik , is an indicator variable, taking 1 if subject i is allocated to cell k and 0 otherwise. In the presence of population stratification, the principal components analysis (PCA) technique is integrated into GMDR for correction of population structure in the founders and singletons. Two adjustment strategies can be used: adjustment only on phenotypes [12], and adjustment both on phenotypes and on genetic factors [14]. The resulting GMDR of either strategy can well control population stratification and is valid in the sense of giving correct type I error rates; the latter is, in theory, more powerful [14], but more computationally intensive, because it needs to adjust each combination of genetic factors of interest one by one.

To handle family-based designs, GMDR uses the principle of transmission equilibrium that is intellectually indebted from the family-based association test method through the concept of within-family association between genotype and phenotype [22]. Each nonfounder in a pedigree has a corresponding nontransmitted sib that can serve as an internal control to test the null hypothesis. The genotype of the non-transmitted sib at each locus can be inferred from the genetic information on the pedigree member(s) [10]. The membership coefficient of a nonfounder, π_ik, can be defined as 0.5 if subject i is allocated to but his/her nontransmitted sib is not allocated to cell k, 0 if neither or both of subject i and his/her nontransmitted sib are allocated to cell k, and -0.5 otherwise. Such a coding is algebraically equivalent to contrasting the observed genotype with the control being from a population with equal numbers of transmitted and nontransmitted genotypes [23]. As in family-based association test, GMDR is therefore robust to population stratification and population admixture. When only nonfounders are considered, it is also equivalent to that in the pedigree-based GMDR [10].

When both unrelated individuals and nonfounders are available, two subsets of samples can be pooled into a unified framework. For unrelated individuals, founders in pedigrees or singletons, either PCA-adjusted or unadjusted membership coefficients can be used and their nontransmitted sibs are considered as being missing. For nonfounders, the membership coefficients from the principle of transmission can be used. Usually, a unified analysis can boost statistical power substantially as compared with the individual analysis of either unrelated or family samples, because the principle of transmission equilibrium makes only use of within-family association but ignores between-family information that can be potentially confounded with population structure, while the analysis of unrelated subjects excludes the within-family signal.

GMDR takes advantage of two flexible coding schemes, one related to the attributes of interest and the other related to the phenotypic outcome. The former takes care of the issues on the study design and sample structure while the latter accounts for different types and multiplicity of phenotypes. Thus, GMDR not only allows for covariate adjustment, is suitable for the analysis of almost any type of phenotypic data, but also is applicable to various study designs. Different combinations of coding schemes can well serve for a wide range of scenarios in genetic studies.

3. FEATURES OF GMDR SOFTWARE

3.1. General Overview

The GMDR software package was developed in Java, making it compatible with various platforms such as MS Windows, Linux and Mac. The software has two kinds of user-friendly interfaces: Graphical User Interface (GUI) and Command Line Interface (CLI). GUI can run in majority of desktop systems, and CLI can run in all the popular shell systems. GUI offers an integrated environment with a series of self-explanatory and easy-to-follow options. All of the options and the running parameters can be set in the GUI mode through typing directly, mouse clicking and drag-and-drop actions, as well as the identified interaction models can be also visualized and saved in various image file formats (e.g., JPG, PNG, BMP and EPS). GUI can create and export the current configuration file automatically and thereby reduce the complexity associated with learning the syntax of GMDR, and is particularly beneficial to novice users. CLI provides an alternative means to execute GMDR analysis. CLI can import the configurations that are generated from GUI or edited by users directly. It is more efficient for users to tune up the arguments according to their need and develop their own scripts to perform batch processing, particularly for experienced and secondary development users to run large-scale data analysis and integrate this software into their analysis protocol. As both GUI and CLI share the configuration resources and are capable of importing and exporting the configurations, users can switch freely between the two interfaces [24].

3.2. Graphic User Interface

Fig. (2) shows the GUI main interface of GMDR. It contains several main menus labeled as “Project”, “Data”, “Tools”, “Analysis”, “Advanced” and “Help”, and each will offer some submenus for implementing the specific functions by clicking. The “Data” menu is designed to load, convert and output data files. The “Tools” menu can be used to view data, produce summary statistics and filter data according to the criteria the users specify. The “Analysis” menu is the domain of function to execute the GMDR analysis with the imported data or the filtered data. The “Project” menu is for managing the project file. The “Advanced” menu is to import and export the configuration files including running parameters and arguments for facilitating the exchange of configurations between the analytical sessions. The “Help” menu provides the basic guidance for usage of GMDR package and the version information.

Fig. (2).

Main interface of the GMDR software.

This software can accept a variety of data formats. Both text and binary file formats are allowed as in PLINK [24]. When loading data, it can automatically detect and parse data formats. The fileset can be converted between text and binary formats. By clicking “Load Data” under the “Data” menu, an interface will appear to import data Fig. (3A). The input data are required to contain the fields corresponding to three pieces of information: pedigree structure, attributes, and phenotypes and covariates. (A singleton is treated as a special family that is composed of only one member whose ancestors and descendants are missing.) The former two are organized into one or several pedigree file(s) in the text format where the extension name of “.ped” is suggested to use, while they are organized into a family structure file and one or several attribute files, respectively, in the binary format where the extension names of “.fam” and “.bed” are suggested to use, respectively. Several pedigree files or attribute files can be merged into a single file for the subsequent analysis or outputting. The phenotypes and covariates are organized into a phenotype file where an extension name of “.phe” is usually used. Additionally, it is also required to provide a map file (“.map” in the text format and “.bim” in the binary format) that contains the information of genetic markers/genes such as name, chromosome number, physical and genetic positions.

Fig. (3).

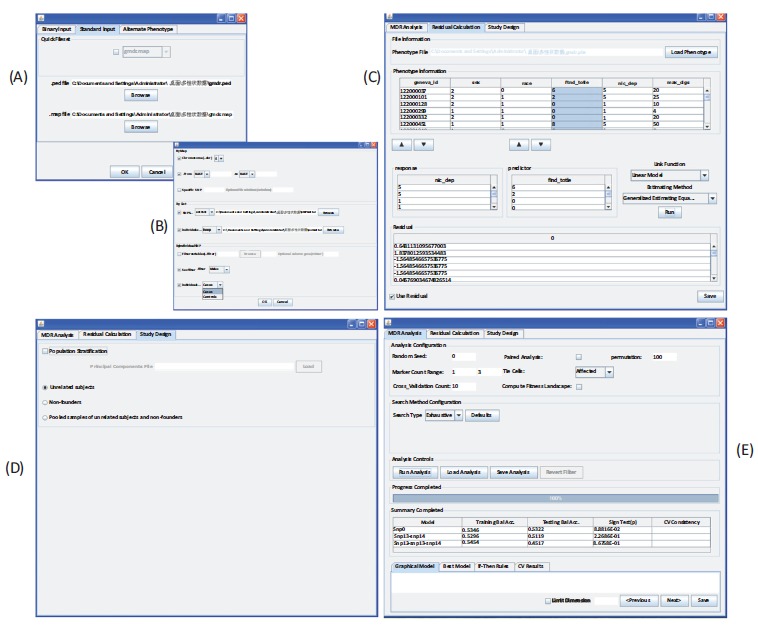
Illustration of features in the GMDR package. (A) Data Input interface. (B) Data Filtering interface. (C) Residual Calculation interface to compute residuals for diverse phenotypes with the appropriate null models including linear model, logistic model, Poisson model, generalized estimating equations model, multinomial logit model, proportional odds models, and Cox’s proportional hazards model. (D) Study Design interface to define the configuration for determination of membership coefficients including unrelated-subjects, non-founders and pooled unrelated subjects and non-founders as well as absence or presence of population stratification. (E) MDR Analysis interface to implement the data reduction algorithm.

This software has a data preprocessing module within the “Tools” menu to support basic management operations. Fig. (3B) shows an interface to select a desirable subset from the raw data by setting a set of inclusion or exclusion criteria. The filtered data can be used for the subsequent GMDR analysis and/or exporting into new data file(s). Data can be visually viewed by clicking the “View Data” button and the scroll bars. The summary statistics of data can be computed by clicking the “Summary Statistics” button. The “Tools” menu substantially facilitates to manage data.

Both the “Data” and the “Tools” menus are designed to accommodate large-scale (e.g., genome-wide) data. GMDR uses efficient data structure and optimal data management algorithm, greatly enhancing the computing speed. Once reading in, it stores the genotype data in a standardized data compression format, e.g., each biallelic genotype is converted and occupies 2 bits only. And this software adopts appropriate data media for different data order of magnitude: for a low level of dataset, the data media is primary files; for a middle level of dataset, the data media is built-in database; and for a high level of dataset, the data media is external database. Benefited from these, it is capable of handling GWAS data quickly and efficiently.

The “Analysis” menu is provided with the main analytic engine to run GMDR analysis. By clicking the “Analysis” menu, an interface will pop out that contains the tabs labeled as “MDR Analysis”, “Residual Calculation” and “Study Design” that implements or sets up the running parameters for the corresponding three components in the GMDR approach. Fig. (3C) shows the interface for residual calculation. The users can define a set of phenotypes of interest and a set of covariates from the input phenotype file. The choice of statistical model can be made by checking the appropriate link function such as identity and logit and the estimation method such as maximum likelihood, quasi-likelihood and GEE. The residuals will be computed with the specified null model by clicking the “Run” button and will appear in the “Residual” column(s) once completing calculation. The interface of “Study Design” Fig. (3D) is to define the desirable scenario for computing membership coefficients: unrelated samples, non-founders, and pooled unrelated samples and non-founders with or without population stratification. The products of the residuals and the membership coefficients are automatically loaded to the “MDR Analysis” module and then the data reduction analysis can be implemented therein. As shown in Fig. (3E), users can change the analytical configuration. After completion of analysis, it can export the output data in several popular formats as users need.

3.3. Command Line Interface

Alternatively to GUI, GMDR can also be run in the CLI mode. The syntax for running the GMDR by command line directives is:

java -jar gmdr.jar [options]

GMDR consists of two kinds of options: one requires argument and the other does not. Please refer to the online manual for a list of options. CLI can implement diverse analyses such as unrelated-subjects only (i.e., the original GMDR), non-founders only and the unified analysis of unrelated and family samples, as well as the data preprocessing, for various phenotypes with and without covariate adjustment through an appropriate combination of options. In addition, a set of options that facilitate the analysis of interactions have also been built into GMDR. Detection of interactions between/among SNP to SNP, SNP to region, SNP to chromosome, region to region, and region to chromosome are also supported. Heuristic searching by including or excluding certain patterns of interactions is also embedded in GMDR. The computational loading can be distributed to multiple computation units, and thus the performance of GMDR is scalable to computation resources. For example, given the availability of 100 nodes in a cluster, GMDR

allows dividing the task into 100 slices, each of which can be submitted to a node independently. The details of the options realized could be found in the user manual online.

4. DISCUSSION

GMDR package offers a powerful, user-friendly tool for performing GMDR analyses for detection of multifactor interactions with large-scale data. Compared with other software [25, 26] implementing MDR-type methods, the proposed GMDR is a more versatile and comprehensive in terms of algorithms realized and options provided. It implements a set of methods on the analysis of interactions with diverse study designs such as case-control design, family-based design or a combination of both. As detection of G×G interactions is plausibly a task which integrates endeavors of multiple stages, GMDR helps reveal genetic architecture in terms of gene-gene interactions underlying complex traits.

GMDR software is flexible for further development. In addition to the existing modules for analysis of multiple phenotypes, longitudinal data, ordinal phenotype and survival data (time to event), other link functions and statistical models can be easily added into the current framework. GMDR is developed in Java and its source code has been made available to the community. It is our hope that this tool helps deepen our understanding of genetic architecture underlying complex traits.

Currently, GMDR, like the other MDR-type methods, can only handle the discrete target factors. If a target factor is a continuous variable, it is suggested to discretize the variable in order to use the existing strategy. A potential solution to extend the GMDR for handling continuous target factor is to integrate the support vector machine or polynomial regression into the GMDR [27].

CONCLUSION

The versatile GMDR package can implement GMDR analyses to identify multifactor interactions for various scenarios. This package also includes other desirable features such as large-scale data management and preprocessing.

AVAILABILITY

The GMDR package is freely available from the Website: http://www.soph.uab.edu/ssg/software or http://ibi.zju.edu.cn/software.

SUPPLEMENTARY MATERIAL

All supplementary information including user manuals and example data can be found at the Website: http://www.soph.uab.edu/ssg/software or http://ibi.zju.edu.cn/software.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.