Trial-by-Trial Motor Cortical Correlates of a Rapidly Adapting Visuomotor Internal Model

Abstract

Accurate motor control is mediated by internal models of how neural activity generates movement. We examined neural correlates of an adapting internal model of visuomotor gain in motor cortex while two macaques performed a reaching task in which the gain scaling between the hand and a presented cursor was varied. Previous studies of cortical changes during visuomotor adaptation focused on preparatory and perimovement epochs and analyzed trial-averaged neural data. Here, we recorded simultaneous neural population activity using multielectrode arrays and focused our analysis on neural differences in the period before the target appeared. We found that we could estimate the monkey's internal model of the gain using the neural population state during this pretarget epoch. This neural correlate depended on the gain experienced during recent trials and it predicted the speed of the subsequent reach. To explore the utility of this internal model estimate for brain–machine interfaces, we performed an offline analysis showing that it can be used to compensate for upcoming reach extent errors. Together, these results demonstrate that pretarget neural activity in motor cortex reflects the monkey's internal model of visuomotor gain on single trials and can potentially be used to improve neural prostheses.

SIGNIFICANCE STATEMENT When generating movement commands, the brain is believed to use internal models of the relationship between neural activity and the body's movement. Visuomotor adaptation tasks have revealed neural correlates of these computations in multiple brain areas during movement preparation and execution. Here, we describe motor cortical changes in a visuomotor gain change task even before a specific movement is cued. We were able to estimate the gain internal model from these pretarget neural correlates and relate it to single-trial behavior. This is an important step toward understanding the sensorimotor system's algorithms for updating its internal models after specific movements and errors. Furthermore, the ability to estimate the internal model before movement could improve motor neural prostheses being developed for people with paralysis.

Introduction

It is believed that our nervous system uses computational processes called “internal models” to make accurate movements. These are defined as capabilities for predicting the motor and sensory consequences of efferent output and computing the correct command for generating a desired movement (Shadmehr et al., 2010). Neural correlates of internal models have been reported throughout the sensorimotor system, including in cerebellum (Shadmehr and Holcomb, 1997; Imamizu et al., 2000; Smith and Shadmehr, 2005; Krakauer and Shadmehr, 2006; Miall et al., 2007; Lisberger, 2009; Bhanpuri et al., 2013), parietal cortex (Shadmehr and Holcomb, 1997; Mulliken et al., 2008), supplementary motor area (Padoa-Schioppa et al., 2002), basal ganglia (Krakauer et al., 2004), brainstem (Ghasia et al., 2008; Green and Angelaki, 2010), spinal cord (Azim et al., 2014), and dorsal raphe nucleus (Kawashima et al., 2016). In motor cortex, neural differences consistent with internal model changes have been reported during the preparation (Wise et al., 1998; Paz et al., 2003; Xiao et al., 2006; Mandelblat-Cerf et al., 2011) and generation of arm movements (Gandolfo et al., 2000; Li et al., 2001; Arce et al., 2010; Mandelblat-Cerf et al., 2011), as well as during brain–machine interface (BMI) use (Jarosiewicz et al., 2008; Ganguly and Carmena, 2009; Chase et al., 2012; Golub et al., 2015).

These past studies examined time epochs after target presentation. They therefore measured neural changes corresponding to the internal model being used to prepare or generate a specific movement. But what about before the target is presented? Are there correlates of changes in the internal model “loaded” in motor cortex reflecting motor adaptation due to recent experience and predicting subsequent kinematics? In this study, we looked for neural correlates of the internal model of visuomotor gain when an animal is engaged in a task but not yet preparing or generating a specific reach; that is, during the so-called “baseline” period of each trial. Furthermore, we tested whether this more general signature of the internal model could be detected and related to behavior on single trials. Because the term “internal model” can mean different things within various motor control subcommunities, we wish to clarify that, here, we use the term broadly. We mean the information, which is likely widely distributed in the nervous system, that movement-related areas use to generate motor commands appropriate to the current physical relationship between the nervous system and the effector being monitored by the sensory system (Green and Kalaska, 2011). In this study, we did not differentiate between, for example, forward and inverse models (Sabes, 2000) and our definition includes neural changes due to trial history effects insofar as these influence subsequent motor behavior (i.e., visuomotor adaptation).

We looked for neural correlates of an internal model by training two monkeys to perform a reaching task with varying visuomotor gain, which has been shown to induce rapid adaptation that generalizes across the reaching workspace (Krakauer et al., 2000; Vindras and Viviani, 2002). As the animals performed the task, we recorded from motor cortex using chronic multielectrode arrays and examined gain-related neural differences preceding the target presentation. We show that there are indeed motor cortical correlates of a visuomotor gain internal model during the pretarget period. This neural activity reflects the monkeys' recent visuomotor gain experience and predicts how fast they will reach on the subsequent trial. This suggests that, in addition to previously known factors such as target direction, extent, or speed (Churchland et al., 2006b; Cisek and Kalaska, 2010), internal model parameters are additional factors that influence the motor cortical network state during reach preparation. We also demonstrate that simultaneous recording from a neural population enables exploring the interaction of past experience, internal model update, and subsequent behavior at a single-trial resolution. In addition to the scientific utility of observing these phenomena on single trials, we provide an offline demonstration of how estimating the internal model could be used to improve motor BMI performance.

Materials and Methods

Procedures and experiments.

All procedures and experiments were approved by the Stanford University Institutional Animal Care and Use Committee. Experiments were performed using two male rhesus macaques, monkeys J and R, which were chronically implanted with multielectrode arrays in motor cortex. Details of the experimental setup, monkeys J and R, array implantation, and neural spiking signal processing are the same as in Stavisky et al. (2015). Here, we provide essential information about the present study.

Neural recordings.

We recorded from motor cortical regions contralateral to the reaching arm using chronically implanted BlackRock Microsystems multielectrode arrays. Monkey J had two arrays: one in dorsal premotor cortex (PMd) and one in primary motor cortex (M1), for a total of 192 recording electrodes. For this study, we did not distinguish between M1 and PMd activity. In monkey R, we only had quality signals from a PMd array (95 recording electrodes). Most of the neural analyses in this study examined all spike events from a given electrode that crossed below −4.5 times the electrode's root mean square voltage (Chestek et al., 2011). These “threshold-crossing” spikes can include both single- and multi-unit activity and allowed us to extract useful neural activity information even from array electrodes that did not record well-isolated single unit activity (SUA). We believe that this approach is justified because we are making claims about information present in the population activity, rather than specific responses of individual neurons. Therefore, the summed activity of what may be several neurons still provides information about the motor cortical neural state. However, we recognize the value in examining how individual neurons respond during the behavioral task being studied, so we manually spike sorted each monkey's largest dataset using Plexon Offline Sorter version 3. Unit names are of the format <monkey initial> <electrode#> <unit>, where unit “a” is the first sorted neuron on a given electrode. Electrodes numbered 1–96 are in M1 and 97–192 are in PMd.

Varying visuomotor gain task.

We used a variant of the commonly used Radial 8 Target task in which a monkey viewed a cursor and target rendered in a virtual reality environment. The monkey was trained to bring the cursor, which was controlled by his hand velocity, to the target in a vertical 2D plane. The key manipulation was that we varied the gain scaling between the monkey's hand velocity and the cursor's velocity (Fig. 1A), as will be described in more detail below. The Wheatstone stereograph used to display the task prevented the monkey from seeing his arms and the nonreaching arm was gently restrained. The cursor's velocity followed that of a reflective bead taped to the middle and third fingers of the reaching arm, which was tracked at 60 Hz using a Polaris infrared tracking system (Northern Digital), and was scaled by the visuomotor gain. A trial began with the center target appearing, which instructed the monkey to bring the cursor within a 4 × 4 cm acquisition box centered on the target for a continuous 1 s. At the end of this hold period, the monkey received a small liquid reward. Leaving and reentering the acquisition area restarted the 1 s timer. After 212 ms into the 1 s center hold period, plus or minus some modest temporal jitter due to the 120 Hz monitor refresh rate, the cursor “locked” its position to the workspace center. If the monkey moved his hand outside the 4 × 4 cm area centered on the center of the workspace, the cursor “unlocked” and, if the cursor left the target area, the hold was interrupted. We only analyzed trials in which the cursor was locked for at least the last 500 ms (monkey J) or 400 ms (monkey R) of the hold period. These restrictions ensured that every trial to a radial target started from the same on-screen location and prevented the animal from seeing any velocity gain during this hold period due to small movements of the hand.

Figure 1.

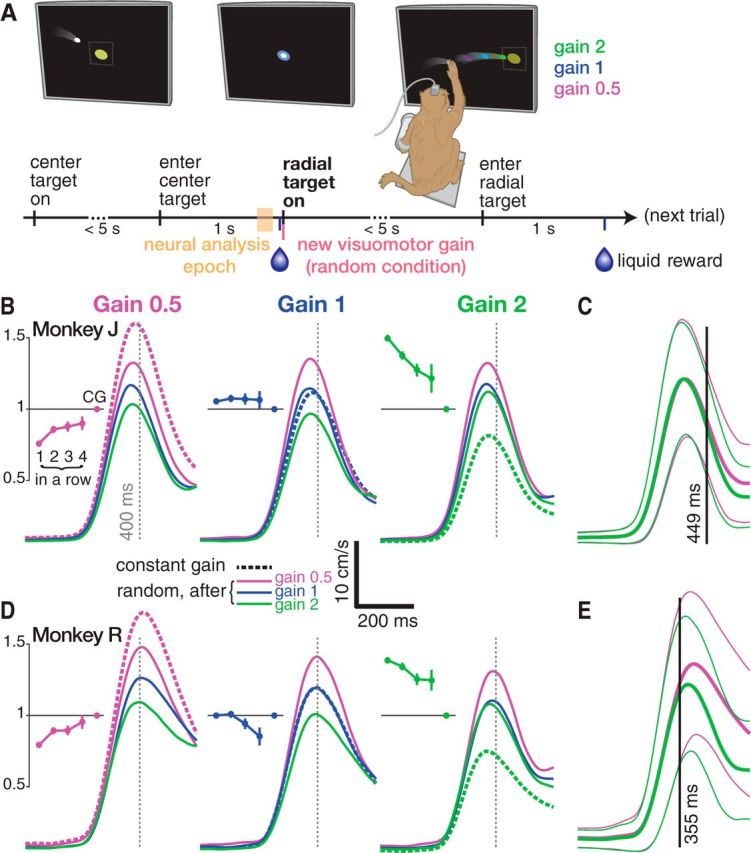
Monkey reaching behavior adapts rapidly during a varying visuomotor gain task. A, Task timeline. The monkey acquires yellow targets with the white cursor, which follows his hand velocity in the vertical plane with a variable visuomotor gain scaling factor. Unlike in this illustration, he cannot see his hand. A trial begins when he brings the cursor to the center target. He must hold it there for 1 s to receive a reward. This leads to 1 of 8 possible radial targets appearing 6 cm from the center. He must then reach to and hold this radial target for 1 s to obtain a second reward. An experimental session consisted of a series of interleaved RG and CG blocks. In RG blocks, the gain was randomly selected from {0.5, 1, 2} when the radial target appeared. It was held constant throughout CG blocks. In subsequent figures, we relate the monkey's reaching behavior to neural data from a 100 ms analysis epoch (yellow shading) before target on. During this time, the upcoming visuomotor gain is predictable in CG blocks but unpredictable during RG blocks. B, Monkey J's hand speed as a function of time after radial target on. Traces show mean speed averaged across trials from five datasets, divided by the current trial's gain (left, middle, right). Dashed traces show CG condition hand speed. Solid traces show RG condition speeds broken out by the previous trial's gain (violet if previous trial's gain was 0.5, blue if previous gain was 1, green if previous gain was 2). Behavior was affected by the previous trial, with faster reaches after the monkey having just experienced low gain and slower reaches following high gain. RG 0.5 reaches were too slow compared with the adapted CG 0.5 speed profile and RG 2 reaches were too fast. Insets show adaptation effects during RG blocks when there was a “streak” of 1, 2, 3, or 4 trials of the same gain in a row. Mean ± SEM speeds are shown for one to four repetitions of the same gain. Speed was averaged from 0 to 400 ms after target on and normalized to this gain's mean CG speed. C, Comparing RG 0.5 and RG 2 reach speeds reveals that they differ after 449 ms, reflecting the monkey's vision-mediated closed-loop correction. Traces show mean ± SD of RG 0.5 (violet) and RG 2 (green) hand speed. Axes are same as in B. D, Same as B for monkey R. E, Same as C for monkey R.

Twenty milliseconds after the center target was held successfully, the cursor was unlocked and a randomly chosen radial target (1 of 8 possible targets equally spaced along a circle of radius 6 cm from the workspace center) was presented. To acquire this radial target, the monkey had to bring the cursor inside its 4 × 4 cm acquisition area for a continuous 1 s. During random gain (RG) condition blocks, the visuomotor gain was randomly chosen on each trial from {0.5, 1, 2} at the time of the radial target appearing. During constant gain (CG) condition blocks, the gain was held constant throughout the entire block. To simplify our prose, we will also refer to gain 0.5 and gain 2 as “low gain” and “high gain,” respectively. Because the hand position could vary slightly during the center hold cursor lock, the cursor-hand offset was set at the time of the cursor unlocking. This offset was reset at the end of the trial (after the radial target was acquired or a failure happened), causing a small jump in the cursor position and preventing an accumulating hand-cursor bias. This ensured that the hand's location during the center target hold (i.e., the principal epoch that we analyzed) was within the same aforementioned center hold tolerances on all trials. Time limits were a generous 5 s for all targets, but both monkeys typically reached the target in <1 s.

We started a given day's experimental session (which generated one dataset) with ∼250 trials of the RG condition, followed by one block of ∼100 trials of each CG condition (i.e., a block of all gain 0.5, gain 1, or gain 2 trials). We then continued to repeat RG, CG block sets until the monkey was satiated and stopped working. The order of CG blocks was either {0.5, 2, 1} or {2, 0.5, 1}. We used a non-monotonic gain order to better differentiate possible fatigue effects from gain adaptation. This order was kept the same within a given session but varied across sessions. We did not analyze the day's final block if the monkey did not complete it with a high success rate, which would indicate waning motivation. We also did not analyze at least 10 “transition” trials at the start of any block to allow the monkey to adapt to the new task condition.

Behavioral analyses.

We collected and analyzed five datasets from each monkey. No datasets were excluded. To cull out data in which the monkey was likely disengaged from the task, we did not analyze failure trials (0.2% to 3.1% across datasets) or trials with time to target >3 SDs above the mean. The remaining trials we call “motivated.” For the same reason, we further excluded trials with movement start times (“RT,” conservatively defined as hand speed >20% for monkey J or >25% for monkey R of the trial's peak speed) longer than 400 ms (monkey J) or 450 ms (monkey R); this excluded 0.3–3.3% of motivated trials. We also excluded trials with RTs <100 ms (1.1–12.2% of motivated trials, 4.6% maximum not including monkey R's first dataset) because this indicated premature movement initiation before the end of the center hold. The aforementioned center hold cursor lock requirement excluded 8.4–17.3% of motivated trials (13.2% maximum not including monkey R's first dataset). After all trial exclusion criteria, we analyzed 6695 monkey J trials and 11,001 monkey R trials.

The principal kinematic metric that we analyzed was hand speed. Because biomechanical differences and gravity result in different speed statistics for reaches to the eight different targets, for all regressions involving hand speed, we z-scored the speed at each millisecond (aligned to target on) across all reaches to that target in a given dataset. We also used the metric of time to target to compare CG and RG performance. Time to target was defined for each successful trial as the time elapsed between radial target appearance and when the cursor entered the target acquisition area and then stayed within it for the required 1 s hold period; this 1 s was not included in time to target. When regressing hand-reaching speed against the hand's position before target presentation, we used the average (x, y, z) coordinate of the tracked bead in the 200 ms before the target appeared.

Neural analyses.

We analyzed firing rates of both SUA and unsorted threshold crossing spikes during the pretarget hold period and the subsequent perimovement epoch. When generating peristimulus time histograms (PSTHs) and calculating population firing rate differences, firing rates were computed using 25 ms bins slid in 1 ms steps, aligned to the time of target on, and averaged over trials of the condition of interest (e.g., mean firing rates across CG 0.5 trials). The timestamps for all presented data correspond to the last millisecond of the bin. We excluded a brief period of data to avoid occasional licking artifacts due to the monkey receiving a liquid reward after the center hold. These epochs were from 39 ms before to 25 ms after target on for monkey J and from 44 ms before to 25 ms after target on for monkey R.

Population-level neural differences between different visuomotor gain scaling conditions (see Fig. 2B) were quantified using a firing rate Euclidian distance measurement similar to that used in Ames et al. (2014). This method was used separately to quantify the time-varying firing rate difference between low and high CG trials and between RG trials after either low or high gain trials. First, threshold crossing firing rates on each electrode were trial averaged within the high gain and low gain conditions, yielding an E × T data matrix (where E is the number of electrodes and T is the number of time samples) for each condition. We then subtracted the high gain and low gain matrices element by element, resulting in a single E × T matrix of firing rate differences for each time point and electrode. To convert the E-dimensional population firing rate differences at any time t to a single neural population distance measure, we took the vector 2-norm of the t-th column of the firing rate difference matrix. This is equivalent to measuring the Euclidian distance between two points defined by the high gain and low gain neural population activities. This results in a time series that summarizes the firing rate distance between the high and low gain conditions. However, because a vector norm is by definition non-negative, there will be some firing rate distance between any two groups of distinct trials due to single-trial spiking variability even if there were no differences in the underlying firing rate distributions between the two groups. We therefore used a bootstrap procedure to subtract away an estimate of what this distance would be under the null hypothesis that the two groups of trials came from the same distribution. We generated 1001 shuffled datasets where trials' high and low gain labels were shuffled randomly while preserving the number of trials in each condition. The firing rate distance measurement was then computed between these faux-high and faux-low gain conditions, resulting in 1001 shuffled distance time series. For each time point, we subtracted away the mean distance across the corresponding 1001 shuffled distances from the true data's distance, such that distances >0 suggest population firing rate differences greater than what is expected by chance. These shuffled distances also allowed us to perform a nonparametric test for significance: a firing rate distance at a given time point was statistically significant at p < 0.001 if the true distance (before subtracting the mean shuffled distance) was greater than all of the shuffled distances at that time point. This shuffle-subtracted firing rate distance was divided by √E (E being the number of electrodes) to normalize it to the number of electrodes, which differed between the monkeys. The firing rate distances shown in Figure 2B are therefore in units of Hz/electrode.

Figure 2.

Motor cortical activity reflects recent visuomotor gain experience even before the target appears. A, Six example neurons' PSTHs during the center target hold and subsequent reaching movement. Mean firing rates during CG 0.5, 1, and 2 are shown in bright violet, blue, and green, respectively. RG trials were grouped by the visuomotor gain applied on the previous trial, which is shown with a darker shade of this gain's color. Horizontal black bars show the mean ±1 SD of reaction times across all analyzed trials. Datasets were J.2014.09.12 and R.2014.08.24. B, Trial-averaged population firing rate differences between trials after low and high gain trials for monkeys J (gray) and R (red). Lighter hues show the differences during CG conditions and darker hues show the differences between RG trials grouped based on the previous trial's gain. Differences were calculated as the vector norm of all electrodes' firing rate differences with chance-level differences subtracted and were normalized by the number of electrodes (see Materials and Methods). Traces are thickened when the firing rate difference is significantly larger than expected by chance (p < 0.001, shuffle test). Almost all RG and CG time points during the pretarget hold period show significant differences. The horizontal gray and red bars show each monkey's 100 ms pretarget time window chosen for more detailed subsequent analysis. Data are averaged across all five of each monkey's datasets. C, Histograms of electrodes' firing rate differences between CG 0.5 and CG 2 during the pretarget analysis windows shown in B. Each monkey's distribution median and mean are shown as dotted and solid vertical lines, respectively. Black shading within the histograms denotes the number of electrodes showing statistically significant differences (p < 0.01, rank-sum test). Data aggregated across all five of monkey J's (left) and monkey R's (right) datasets. D, Similar to C, but showing the pretarget firing rate differences between RG trials with a previous gain that was 0.5 versus 2.

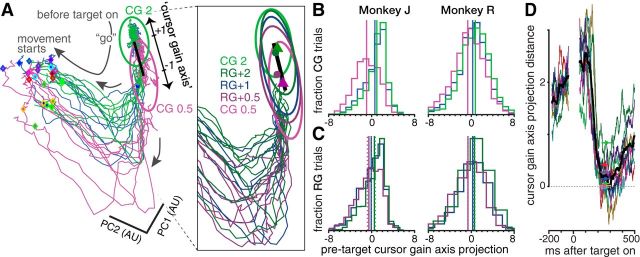
The principal neural analyses in this study more closely examined firing rates in a 100 ms epoch shortly before the radial target came on, relating it to the previous trial's gain (see Figs. 2C,D, 3B,C) and using it to predict subsequent behavior (see Figs. 4, 5). Monkey J's neural analysis epoch was 140–40 ms before target on and monkey R's was 145–45 ms before target on. We obtained qualitatively similar results with different analysis windows (data not shown), with a general (and unsurprising) trend of better behavioral prediction when using neural data later in the hold epoch. For several analyses, we projected firing rates during this analysis epoch onto a “cursor gain axis” defined by the vector connecting the CG 0.5 and CG 2 firing rate centroids; that is, the vector in which element i equals r_{i,CG 0.5} − r_{i,CG 2}, where r_i,cond is the firing rate from electrode i averaged over trials of a given condition “cond.” This vector was length 192 for monkey J and 95 for monkey R, corresponding to the number of electrodes. The gain axis was found separately in each dataset; single-trial projections onto each dataset's gain axis were then aggregated across datasets for each monkey. Gain axis projection scalars were normalized such that the centroids lay at −1 and +1. When computing gain axis projections for a CG 0.5 or CG 2 trial for the purpose of assessing whether the CG conditions' distributions differed (Fig. 3B,C), these projections were cross-validated by excluding that trial from the centroid calculations so as to not introduce a statistical bias favoring the hypothesis of differing distributions. It is worth emphasizing that we used the gain axis as an analytical tool to describe gain-related neural differences because it is conceptually simple (i.e., it is a vector between different gain conditions' trial-averaged centroids) and succinct (i.e., it allows single trial neural activity to be described with a single value). The method was not designed to separate single-trial projections maximally, which would be better achieved by alternative methods such as support vector machines, and we do not mean to suggest that all gain-related differences in our data lie along the gain axis neural dimension.

Figure 3.

Pretarget neural population state reflects recent visuomotor gain experience. A, Visualization of neural activity just before and at the start of reaches. The main panel shows 24 trial-averaged neural trajectories for the CG conditions, broken out by reach target (3 gains × 8 targets). Condition-averaged firing rates are projected onto the data's first two principal components (which capture 65% of the variance). Trajectories consist of one segment spanning 300–40 ms before target on (confined to the upper-right corner) and another segment 25–285 ms after target on (clockwise rotation). Mean reaction times for each condition are shown with diamonds with a unique border color for each of the eight targets. The bright violet and green ellipses show one SD of single-trial variance of the pretarget CG 0.5 and CG 2 neural state (combining across targets), respectively. We define a cursor gain axis (thick black line) connecting the centroids of these pretarget states. The inset shows an enlarged view of the neural state space close to the gain axis, now showing neural trajectories for RG conditions grouped by the previous trial's gain, denoted by a darker hue of the corresponding gain's color. The CG 0.5 and CG 2 variance ellipses and gain axis are replicated in the inset, along with 1 SD ellipses of RG conditions' pretarget state. Also shown are the RG+0.5 and RG+2 pretarget state centroids (violet and green circles), along with the centroids for trials preceded by two RG 0.5 trials in a row (violet triangle) and trials preceded by two RG 2 trials in a row (green triangle). Dataset was J.2014.09.12. The same color scheme is used to denote different gain conditions throughout A–C. B, Histograms of CG trials' pretarget neural states projected onto the gain axis. Each trial's projection were calculated based on within-dataset CG 0.5 and CG 2 centroids and then aggregated over all five of each monkey's datasets. Vertical lines show the corresponding distribution's mean. C, Similar to B, but now showing the distribution of RG trials' gain axis projections. Trials are grouped based on the visuomotor gain applied on the previous trial to determine whether experiencing a particular gain changes the subsequent center hold period's pretarget neural state. Solid vertical lines show the corresponding distribution means. Dashed vertical lines show the distribution means after two consecutive trials of the same gain (histograms for these distributions are not shown). D, Contrary to the impression given by the low-dimensional view in A, the separation between CG 0.5 and CG 2 neural trajectories along the gain axis did not persist as the reach progressed. Each colored trace corresponds to the difference between CG 0.5 and CG 2 trials' full-dimensional neural data projected onto the gain axis (data were averaged across trials to one of the eight targets). The black trace corresponds to the mean of these individual target traces. Mean ±1 SD of reaction times for each target are shown with colored horizontal bars. The pretarget gain axis separation of ∼2 is reduced to nearly 0 by the time movement starts. Dataset was J.2014.09.12.

Figure 4.

Pretarget neural state predicts upcoming reach speed. A, Pretarget firing rates' projection onto the gain axis explains a significant fraction of the variance in subsequent hand reach speed (linear regression). Each point corresponds to one CG trial, with colors denoting visuomotor gain. The fraction of speed variance explained by the gain axis projection for each condition is written above in the corresponding color. More positive gain axis projections (putatively signaling that the animal is expecting a higher gain) correlate with slower upcoming reaches and vice versa for more negative projections. Data are aggregated across all five monkey J datasets. Three data points are cut off on the left. B, To assess whether the gain axis generalizes across reach directions, we predicted hand speeds separately for CG reaches to each of the eight targets using a target-specific gain axis determined using reaches to a single (potentially different) target. Each element within the 8 × 8 data matrices shows how much of the variance in reach speeds to the target corresponding to the column number (test target) was explained by projecting that trial's pretarget firing rates onto a target-specific gain axis calculated using only trials immediately after reaches to the target corresponding to the row number (train target). Variance explained (r²) values within each column (i.e., when predicting hand speed for the same trials, using different train target-specific gain axes) were normalized to the maximum value within this test target. Each 8 × 8 matrix shows results for one gain condition, denoted by the border color. The best regression performances did not cluster along the (train target) = (test target) diagonal and a significant fraction of CG hand speed variance was explained by pretarget neural state for all 8 × 8 × 3 train–test pairs (p < 0.05). This indicates that the behavioral relevance of the gain axis generalizes across reach targets. C, Same as A, but for RG trials grouped by the upcoming trial's gain. Two and three data points are cut off from the top and left, respectively. D, Same as B, but for RG trials grouped by the upcoming trial's gain. A significant fraction of RG hand speed variance was explained by pretarget neural state for all 8 × 8 × 3 train–test pairs (p < 0.01).

Figure 5.

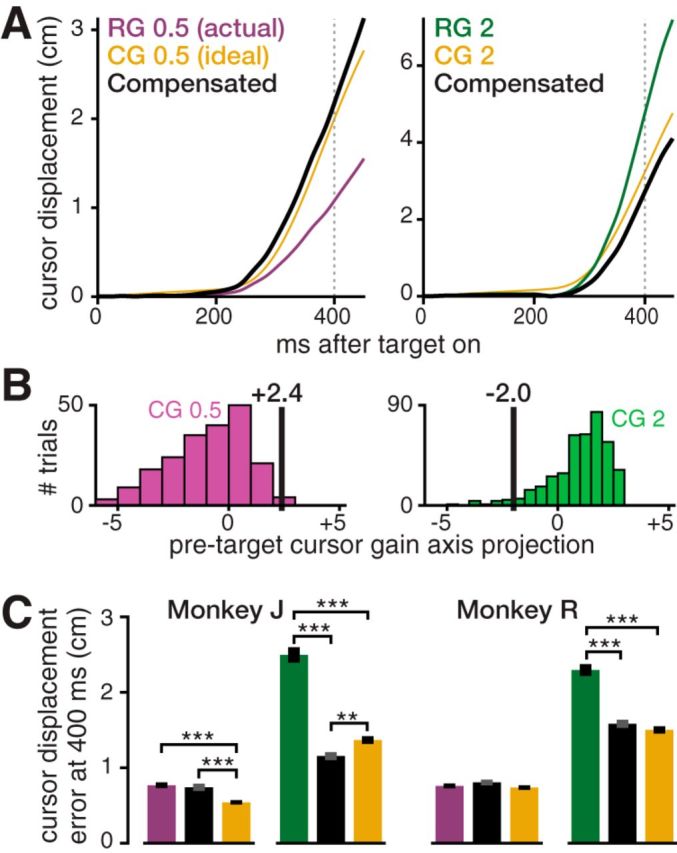
Offline proof-of-concept showing how an incorrect internal model could be detected and compensated for by a neural prosthesis. A, Two examples of monkey J trials' offline gain compensation. These trials' true cursor displacements toward the target are shown in violet (RG 0.5 trial, left) and green (RG 2 trial, right). The corresponding “ideal” cursor displacements (average of CG trials) are shown in gold. The monkey reached too slowly in the RG 0.5 trial and too quickly in the RG 2 trial. Our method predicted the monkey's hand displacement from neural activity preceding each reach and used it to calculate a compensatory hand-to-cursor gain. Black traces show the displacements that would have occurred had this gain actually been applied. The RG 0.5 trial exemplifies excellent compensation performance (90th percentile) for this gain. The RG 2 trial exemplifies typical (50th percentile) performance for this gain. B, Scalar visualizations of the high-dimensional pretarget neural activity (projection onto the gain axis) that the decoder uses to predict upcoming movement error. Black vertical lines show these same two example RG trials' gain axis projections. The histograms show projection distributions for all CG 0.5 (left) and CG 2 (right) trials, which were used to train the decoder. The RG 0.5 trial's positive projection correctly predicts an overly slow reach. The CG 2 trial's negative projection correctly predicts an overly fast reach. C, Mean ± SEM error compensation performance averaged across all trials in each monkey's dataset. RG 2 (green) cursor displacement error was significantly reduced using the gain compensation method (adjacent black bar). RG 0.5 (violet) error reduction was not significant. Gold bars show CG 0.5 and CG 2 errors indicating how precisely the monkey reaches when his internal model is nominally accurate. **p < 0.01, ***p < 0.001.

To summarize and visualize high-dimensional neural data (Fig. 3A), we used principal component analysis to reduce its dimensionality to two. Although this technique is useful for describing time-varying neural activity, a low-dimensional projection typically cannot adequately present all aspects of the data (for reviews, see Cowley et al., 2013; Cunningham and Yu, 2014). Intuitions provided by such a projection must be validated in the full-dimensional data. In particular, we performed an additional analysis, presented in Figure 3D, to show how the separation along the gain axis between high gain-adapted and low gain-adapted neural trajectories changes during the perimovement epoch. We calculated the difference vector between trial-averaged CG 0.5 and CG 2 firing rates at each time point (aligned to target on) and then projected this vector onto the gain axis. The resulting scalar was normalized to be consistent with the pretarget neural state projections described earlier; that is, the projection difference equals 2 before target on. Because neural trajectories differed between reaches to the eight different targets, this gain axis projection distance time series was calculated separately for reaches to each target.

Internal model error compensation analysis.

For the offline internal model error compensation analysis (Fig. 5), we used as our kinematic metric the cursor's displacement toward the target; that is, the integral of velocity projected onto the vector from the workspace center toward the target. We chose this metric because it is more closely (and more intuitively) related to progress toward the goal of reaching the target compared with, for example, speed averaged over a certain epoch. For simplicity, we chose a specific time (t = 400 ms after target on) at which to compare (and attempt to reduce) movement errors. Our strategy was to predict the upcoming RG trial's hand displacement toward the target by decoding its pretarget neural activity. We used this predicted displacement to calculate a different (post hoc, offline) gain that we expected to minimize the displacement error on this trial. In other words, we used the neural correlates of the visuomotor gain internal model, estimated before the target was cued or movement began, to predict the magnitude of the upcoming movement command (i.e., hand reach extent). Based on this prediction, we adjusted the gain up or down to compensate for the monkey reaching too slow or too fast. We focused our analyses on the RG 0.5 and RG 2 conditions, for which mismatches between the animal's internal model and the true visuomotor gain were prevalent.

We chose each monkey's largest dataset for this analysis because a neural prosthetic application would be contingent upon having good quality neural signals and ample training data. As our neural signal, we used firing rates in the same 100 ms epoch as in the previous analyses. We used the CG data, in which we assume neural activity accurately reflects the internal model, to train the algorithm. We also used the mean CG kinematics for each gain g to define the “ideal” cursor displacement ID_g for that particular gain. In other words, we assumed the CG condition represents how the monkey wants to move the cursor for a particular gain, as well as the natural variability around this ideal. A given trial's movement error was thus defined as |c − ID_g|, where c is the cursor's displacement on that trial and g is the trial's true applied gain. For each trial, we used the neural activity to predict hand displacement ĥ, an estimate of how far the monkey would move his hand toward the target by t = 400 ms. We then set our retrospective compensating gain to equal to ID_g/ĥ. With this problem formulation, if we were able to perfectly predict the upcoming trial's hand reach displacement, then the compensated cursor displacement error would be zero.

We used a standard machine learning approach to predict ĥ from the neural activity. Unlike for the main neural analyses, in which a simple and intuitive linear regression between cursor gain axis projection and hand speed addressed our scientific question, for this prosthetics-minded analysis, we sought to maximize predictive power. We first equalized the size of each gain's training data by restricting each CG condition's trial count to the minimum across the three gains. Outlier firing rates were reduced during preprocessing by setting them to a ceiling of 2 SDs above each electrode's mean firing rate (as calculated from the training data). To prevent decoder overfitting, we reduced the neural feature dimensionality from the number of electrodes (192 or 95) to the top 23 principal components of the training data. We then used least-squares quadratic regression to fit weights from the training data (i.e., we found coefficients for a squared, linear, and constant bias weight for each firing rate principal component). These weights were used to predict ĥ from test (RG) trials' neural data.

Results

Behavioral evidence of an adapting visuomotor gain internal model

Before relating monkeys' motor cortical activity changes during a varying visuomotor gain reaching task (Fig. 1A) to putative internal model changes, we first verified that this task elicited the expected adaptation behavior. Both monkeys altered their hand reaching speed depending on their recently experienced gain (Fig. 1B,D). If given time to adapt to each gain (CG condition), monkey J's reach speed (averaged from 0–400 ms after radial target on) was 10.9 ± 3.7 (mean ± SD) cm/s for CG 0.5 trials, 7.6 ± 3.2 cm/s for CG 1, and 5.6 ± 2.3 cm/s for CG 2 (95.6% faster reaches when adapted to the “low” CG 0.5 gain compared with the “high” CG 2 gain). Monkey R's speeds were 11.5 ± 5.3 cm/s for CG 0.5, 8.8 ± 4.1 cm/s for CG 1, and 6.2 ± 2.8 cm/s for CG 2 (85.6% faster during low gain than high gain). When the monkeys did not know the upcoming visuomotor gain (RG condition), they tended to reach slower during RG 0.5 and faster during RG 2: monkey J's RG 0.5 reach speeds were 8.3 ± 3.3 cm/s (23.9% slower than CG 0.5) and his RG 2 reaches were 8.4 ± 3.1 cm/s (50% faster than CG 2). Monkey R's RG 0.5 reaches were 9.1 ± 4.1 cm/s (20.9% slower than CG 0.5) and his RG 2 reaches were 8.6 ± 3.8 cm/s (38.7% faster than CG 2). The RG reaches were suboptimal in the sense that they led to longer times to target than during the CG condition. This was due primarily to moving too slowly during RG 0.5 trials and too quickly during RG 2, thereby overshooting the target. Monkey J's mean times to target were as follows: 866/644 ms (RG/CG 0.5), 600/544 ms (RG/CG 1), and 778/650 ms (RG/CG 2). Monkey R's mean times to target were 688/589 ms (RG/CG 0.5), 639/587 ms (RG/CG 1), and 816/649 ms (RG/CG 2).

Within an RG condition, we observed reach speed differences depending on the previous trial's gain, as evidenced by the consistent ordering of the solid traces in Figure 1, B and D. Monkey J reached 32.4%, 45.5%, and 26.0% faster when RG 0.5, RG 1, and RG 2 trials, respectively, followed a low gain trial compared with after a high gain trial. For Monkey R, these differences were 24.1%, 35.1%, and 14.5%, respectively. All of the aforementioned reach speed differences were significant at p < 0.001 (rank-sum test). During RG blocks, we also observed adaptation effects due to trial history going back multiple trials: there was further adaptation toward CG reach speeds when repeatedly encountering the same gain (Fig. 1B,D, insets).

Gain adaptation effects due to previous trials are visible from the start of the reach in the speed profiles shown in Figure 1, B and D, reflecting the open-loop consequences of differing visuomotor internal model. However, we note that reaches were also subject to closed-loop vision-guided corrections. In particular, later in an RG trial, the monkey could process visual information about how the cursor was moving and update his movement accordingly. To estimate when feedback affected the reach, we measured when RG 0.5 and RG 2 reach speed distributions diverged. These distributions differed significantly (p < 0.001, rank-sum test) 449 ms after target on for monkey J (Fig. 1C) and 355 ms after target on for monkey R (Fig. 1E). Therefore, particularly in monkey R, closed-loop feedback contributed to our primary kinematic feature of interest: speed averaged in the first 400 ms. This closed-loop contribution does not invalidate the significance of the relationship between pretarget neural activity and behavior described in the next section; if anything, one would expect closed-loop corrections to weaken this relationship. To summarize our behavioral analyses: overall, we observed behavioral effects consistent with previous reports of similar visuomotor gain tasks (Ojakangas and Ebner, 1991; Krakauer et al., 2000, 2004; Paz et al., 2005), providing us with the confidence to proceed with analyses of motor cortical correlates of this visuomotor gain adaptation.

Neural correlates of a changing internal model

Most of our neural analyses examined multiunit “threshold crossing” firing rates to increase the information yield of the electrode arrays for the purpose of estimating the motor cortical neural state. Before presenting the results, we first report a succinct summary of each monkey's multielectrode array(s) recording quality. We measured how electrodes' firing rates changed between a 100 ms “baseline” epoch before target appearance and a 100 ms “perimovement” epoch 300–400 ms after target on during all CG trials. This comparison was chosen to capture what fraction of electrodes were modulated in response to reaching movements. Across monkey J's five dual-array datasets, the activity of between 144 and 158 electrodes changed significantly between baseline and movement (p < 0.001, signed-rank test). These had a median change of between 10.4 and 18.7 Hz. Across monkey R's five single-array datasets, between 92 and 94 electrodes had a significant response, with median changes between 6.2 and 13.3 Hz.

We also recognize that the neural state ultimately reflects the activities of single neurons, and therefore we will present example PSTHs of sorted SUA and replicate the study's key analyses using ensemble SUA. To do so, we spike sorted each monkey's largest dataset. Sixty-nine sorted single units were identified across monkey J's two arrays, of which 52 were tuned for movement as defined above, with a median modulation of 3.7 Hz. Nine sorted single units were identified on monkey R's array, all of which were tuned for movement, and these units had a median modulation of 6.9 Hz. In addition to replicating key analyses with SUA, which will be presented below, we also verified that all of the other analyses had essentially the same results using spike-sorted data as when using threshold crossing data. However, we found that the additional information in threshold crossing data led to larger effect sizes, so for clarity of presentation, we primarily report threshing crossing results.

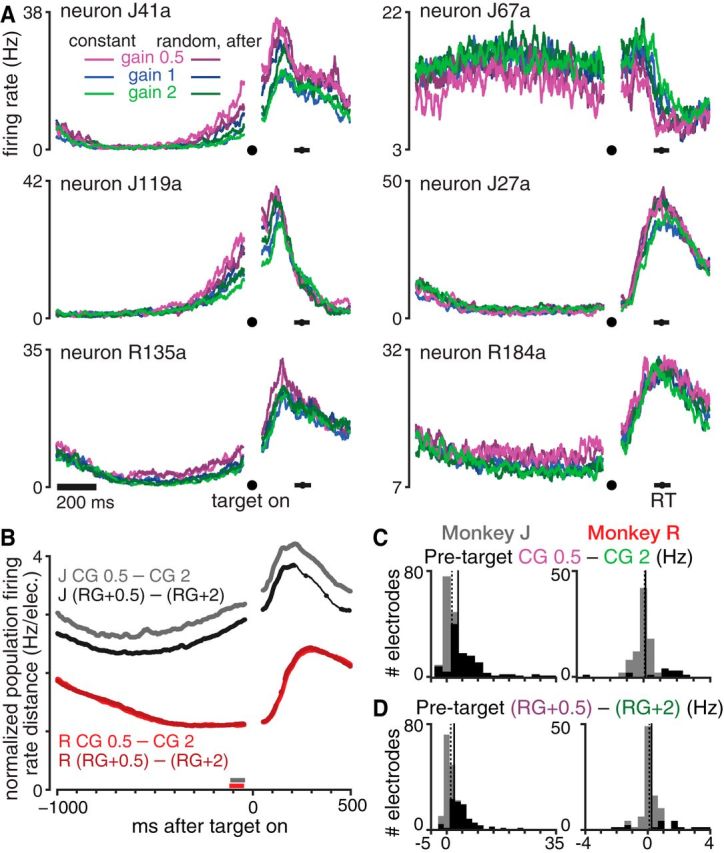
The behavioral differences between different visuomotor gain conditions described in the previous section were accompanied by differences in motor cortical activity. Figure 2A shows gain condition-averaged PSTHs of six example neurons and Figure 2B shows that ensemble threshold crossing firing rates differed significantly between high and low gain conditions over the course of a trial. Unsurprisingly, there were large differences in movement-epoch firing rates between the different gain conditions, consistent with their differing kinetics and kinematics. Perhaps more surprising, however, was that different gain conditions exhibited neural differences before the target appeared. The remainder of this report describes these differences, which we hypothesize reflect the animal's changing visuomotor gain internal model, and relates them to the upcoming trial's behavior.

Firing rate differences during the pretarget center hold period were greatest between CG 0.5 and CG 2, with CG 1 and the RG conditions tending to fall between the high and low CG firing rates. Figure 2A's neuron J41a illustrates an ordering of different conditions' firing rates, which we observed in many neurons/electrodes: CG 0.5 and CG 2 (when the animal is maximally adapted to low and high gain, respectively) form the two extremes; “RG+0.5” and “RG+2” trials, meaning that those after a low or high gain trial, respectively, are more moderate versions of the corresponding CG PSTHs; the “RG+1” and CG 1 conditions fall between the high and low gain extremes. This ordering appears to reflect the recent history of experienced visuomotor gain and is evocative of the reach speed ordering based on recent gain experience described in the previous section. Firing rate differences between gain conditions decreased during the beginning of the hold period and then increased leading up to the target presentation, the timing of which was fixed and thus predictable. Most SUA and threshold crossing firing rates were higher when the animal was putatively expecting a lower gain (e.g., neuron J119a), but some showed higher firing rates during high gain expectation conditions (illustrated by neuron J67a). Many other neurons and electrodes did not exhibit gain-related pretarget differences, as illustrated by neuron J27a.

Figure 2C shows histograms of the trial-averaged threshold crossing firing rate differences between CG 0.5 and CG 2, measured during a 100 ms window before target on. There were significant differences in firing rate on 110/192 of monkey J's electrodes (p < 0.01, rank-sum test comparing the two conditions' single-trial firing rate distributions), with ensemble-average differences of 4.0 ± 5.7 Hz (mean ± SD of the absolute values of individual electrode differences). Monkey R's firing rates differed by an average of 0.5 ± 0.7 Hz and were significantly different on 15/95 electrodes. In both monkeys, overall population firing rates were slightly higher for the CG 0.5 condition, but there were both rate increases and decreases across the ensemble. We note that the recording quality of monkey R's single electrode array was not as high as that of monkey J's two arrays, so the statistical strength of our neural analysis results in this second monkey is smaller. Figure 2D presents similar histograms summarizing the firing rate differences between RG+0.5 and RG+2 conditions. Monkey J's RG firing rates differed by 2.7 ± 3.4 Hz after high and low gain trials and were significantly different on 88/192 electrodes. Monkey R's RG+0.5 and RG+2 rates differed by 0.5 ± 0.8 Hz and were significantly different on 17/95 electrodes.

To better visualize population-wide neural differences related to recent cursor gain experience, we used principal components analysis to view “neural trajectories” showing how the two population activity patterns capturing the most variance among the electrodes' firing rates changed over time (Shenoy et al., 2013). Figure 3A shows one dataset's neural trajectories—trial-averaged within gain condition and reach target—leading up to target presentation, as well as during the subsequent reach initiation. As was the case for the PSTHs presented earlier, perimovement differences are readily apparent between gain conditions (and here also between reach targets). However, we once again focus our attention on pretarget differences. Figure 3A reveals substantial separation between the pretarget neural state during high and low CG trials, with CG 1 pretarget activity occupying a region of neural state space approximately midway between the CG 2 and CG 0.5 centroids. When RG trails were separated based on the previous trial(s)' gain (Fig. 3A, inset), their pretarget neural state distributions also differed systematically based on recent visuomotor gain history. Viewed along the line connecting the CG 2 to the CG 0.5 state space centroids, the RG distribution centroids were ordered as follows: CG 2, RG+2,2 (after two RG 2 trials in a row), RG+2, RG+1, RG+0.5, RG+0.5,0.5 (two in a row), and CG 0.5.

The approximately collinear arrangement of different gain conditions' pretarget neural state in the dimensionality-reduced view of the data suggested that we could summarize and quantify the neural activity's putative relationship to the animal's recently experienced visuomotor gain with a succinct scalar description: we defined a “cursor gain axis” as the vector connecting the CG 0.5 and CG 2 firing rate centroids in neural population state space. To quantify how neural activity differed along this gain axis on single trials, we linearly projected each trial's neural activity onto this axis and normalized this projection such that the CG 0.5 and CG 2 centroids were at −1 and +1, respectively. Figure 3B shows histograms of single-trial pretarget neural activity projected onto this gain axis. Monkey J's cross-validated projection means were −0.94 (CG 0.5), 0.61 (CG 1), and 0.97 (CG 2). Monkey R's cross-validated projection means were −0.65 (CG 0.5), 0.26 (CG 1), and 0.75 (CG 2). We then investigated whether RG trials' gain axis projections also differed depending on which gain was experienced previously (Fig. 3C). We divided the trials based on whether they followed a gain 0.5 trial, gain 1 trial, or gain 2 trial and found that monkey J's gain axis projection distribution means were −0.52 (RG+0.5), −0.08 (RG+1), and 0.50 (RG+2). Monkey's R's corresponding RG distribution means were −0.62, 0.26, and 0.59, respectively. All gain axis projection distribution means were significantly different from other gains' means (p < 0.001, rank-sum test) for both CG and RG conditions in both monkeys.

We next investigated whether neural activity differences along the gain axis neural dimension persisted throughout the beginning of the reach. This is the impression given by the neural trajectories shown in Figure 3A, but these could be a misleading consequence of that 2D projection of the high-dimensional neural data. Indeed, projecting the time-varying firing rate differences between CG 0.5 and CG 2 conditions onto the fixed gain axis revealed that differences along this neural dimension were markedly reduced by the time movement started (Fig. 3D). We observed similar results in the other monkey J datasets. Monkey R's results (data not shown) varied depending on the dataset and thus were difficult to interpret; this is consistent with his gain axis projections being more noisy due to his worse neural signal quality. Therefore, whereas changes along the gain axis neural dimension appear to reflect recent visuomotor gain experience before a reach target appears, this same neural dimension does not appear to capture major differences between perimovement activity during high gain versus low gain conditions.

Pretarget neural activity differences predict upcoming reach speed

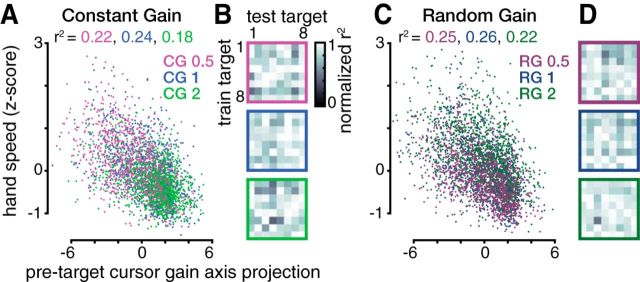
In the previous section, we showed trial-by-trial neural differences as a function of previous cursor gain experience. Our hypothesis that this neural activity reflects the animal's visuomotor gain internal model also predicts that it should correlate with upcoming reaching behavior. We therefore examined whether the pretarget neural state could predict the speed of the next reach. A simple linear regression between a trial's pretarget gain axis projection and z-scored hand speed explained 22.3%, 23.6%, and 18.1% of the variance within monkey J's CG 0.5, CG 1, and CG 2 conditions, respectively (Fig. 4A). For monkey R, the corresponding variances explained were 3.5%, 1.7%, and 3.5%, respectively. All of these regression r² values were significant (p < 0.001). The neural state in these analyses was estimated from threshold crossing spikes, but we also verified that qualitatively similar results were obtained using SUA. Predicting hand speeds from pretarget gain axis projections of the 69 neurons' firing rates in monkey J's spike-sorted dataset explained 18.5%, 14.3%, and 19.9% of the variance of CG 0.5, CG 1, and CG 2 conditions, respectively. The corresponding variances explained using the activity of the nine sorted neurons in monkey R's dataset were 10.0%, 2.2%, and 3.3%, respectively. All SUA regressions were also significant at p < 0.001. In both monkeys, the speed variance explained in the dataset that was spike sorted was higher using threshold crossings, which was to be expected given the large number of electrodes with modulating spiking activity that could not be unambiguously attributed to a single neuron. We attribute the difference between how much of each monkeys' behavioral variance could be explained by neural activity to monkey J's arrays having a greater number of sortable neurons, more electrodes able to record modulated threshold crossing spiking activity, as well as the greater gain-related neural modulation recorded on these electrodes. Monkey R's slightly smaller behavioral effects due to previous trials' visuomotor gains (Fig. 1) may also have partially contributed to the reduced predictive power of his pretarget neural activity.

We also regressed gain axis projections against RG trial reach speeds. This regression was performed separately for each RG condition to account for closed-loop speed adjustments within a particular gain (e.g., slowing down during a RG 2 trial) that would otherwise introduce a source of speed variance unrelated to the pretrial neural state. Monkey J's gain axis projections explained 25.0%, 25.7%, and 22.5% of RG 0.5, RG 1, and RG 2 reach speeds, respectively (Fig. 4C). For comparison, this pretarget neural data explained more variance than knowing each trial's previous RG: neural regression r² values were 2.91, 1.94, and 3.12 times that of the RG 0.5, RG 1, and RG 2 previous trial gain regression r² value, respectively. We also note that the predictive power of the gain axis projection in interleaved RG trials rules out the gain axis being an artifact of neural activity slowly drifting between the different CG blocks. For monkey R, the corresponding RG reach speed variances explained by gain axis projection were 4.5% for RG 0.5 (0.94 times that of the previous trial's gain regression r²), 3.8% for RG 1 (0.58 times that of previous gain regression), and 3.2% for RG 2 (1.32 times that of previous gain regression). The speed variances explained by SUA in each monkey's spike-sorted dataset were as follows: 19.6%, 24.8%, and 20.5% for monkey J's RG 0.5, RG 1, and RG 2 conditions, respectively, and 4.6%, 6.9%, and 7.0% for monkey R's corresponding conditions, respectively. All regressions were significant at p < 0.001.

Controls for interpretation

Because pretarget hand positions could slightly vary within the constraints of the center hold, we tested whether these differences could explain a similar amount of upcoming reach speed variance as gain axis projection differences. Such a result would raise the concern that the neural differences merely reflected hand position differences and only incidentally predicted reach speed. This was not the case. We found that gain axis projection explained much more reach speed variance than hand position. Multivariate linear regression against 3D hand position explained 2.0%, 1.0%, and 1.2% of RG 0.5, RG 1, and RG 2 monkey J hand speeds, respectively. Monkey R's corresponding values were 0.1%, 0.7%, and 1.4%, respectively.

Our hypothesis that the pretarget neural differences reported in the previous section reflect the animal's internal model of visuomotor gain—a mapping between motor command and cursor movement that holds true across the workspace—predicts that the relationship that we identified between gain axis projection and subsequent reach speed should generalize across reach directions. Specifically, we expected that if a “target-specific” gain axis were calculated from the neural activity after high and low CG reaches to one target, projections onto this target-specific gain axis would still exhibit the previously described inverse correlation with reach speeds to a different target. Figure 4, B and D, show the results of performing a regression between monkey J's pretarget neural state and subsequent reach speed, similar to that previously described for Figure 4, A and C. Now, however, the results for each gain were separated into 8 × 8 = 64 pairs of “train target” (i.e., the target reached to just before CG data used to calculate the target-specific gain axis) and “test target” (i.e., the target presented during the trials in which speed was being predicted). This analysis used the same neural and behavioral epochs as in Figure 4, A and C. These target-specific gain axis projections explained a significant fraction of speed variance for all 8 train targets × 8 test targets × 3 gains = 192 pairs of train and test targets, both during the CG condition (p < 0.05 for all target pairs) and the RG condition (p < 0.01 for all target pairs).

If the gain axis generalized poorly, then we would further expect that a given trial's neural activity would best predict hand speeds when the target-specific gain axis was computed from neural activity after reaches to this same target; that is, each test target's highest r² would be found along the train = test target matrix diagonal in Figure 4, B and D. Instead, we found that this identity pairing best predicted hand speeds in only 2/24 test targets (8 targets × 3 gains) during CG blocks and 3/24 test targets during RG blocks, which is no higher than chance. These results show that the behavioral relevance of the cursor gain axis holds for reaches in different directions, which is consistent with this being a neural read-out of the animal's visuomotor gain internal model. They also argue against the possibility that the gain axis projection regressions in our main analyses, which analyzed reaches to all targets together, were only significant because they accurately predicted the speeds of reaches toward a specific “default” target that the monkeys were preparing despite not actually knowing which target would be presented.

When we performed the same target-specific gain axis analysis on monkey R's data, we found that subdividing each experimental condition's data into eight groups reduced the fraction of speed variance that the neural data explained, which had already been small, below statistically significant levels. We therefore instead used a “leave-one-target-out” analysis variant that was less detailed but included more trials when determining the gain axes and within the regressions. Specifically, we projected each trial's pretarget neural activity onto a leave-one-target-out gain axis computed from CG 0.5 and CG 2 neural data after reaches to every target except for the target reached to during this trial. We then regressed these leave-one-target-out gain axis projections against normalized hand speeds. The percentage of speed variance explained using this method and its fraction of the variance explained using the standard gain axis reported in the previous section (where all targets' data were used to define the gain axis) were as follows: 3.3% for CG 0.5 (0.95 of main analysis), 1.4% for CG 1 (0.82), 3.4% for CG 2 (0.97), 4.2% for RG 0.5 (0.94), 3.7% for RG 1 (0.97), and 3.0% for RG 2 (0.96). All of these regressions, which tested that the cursor gain axis generalized across reach directions, were significant at p < 0.001.

Single-trial decoding of the gain internal model to predict movement errors

Finally, we performed an analysis to explore the utility of these putative single-trial visuomotor gain internal model neural correlates for motor neural prostheses, which are being developed to restore movement to people with paralysis (Green and Kalaska, 2011). A brain-controlled robotic arm user will need an accurate internal model of how her neural commands affect the arm. This is complicated by the arm's own physical dynamics (which could vary across, e.g., joint conformations) and its interaction with objects (e.g., when carrying a heavy versus a light object). Our RG 0.5 and RG 2 trials can be viewed as a (much simplified) example of a user underestimating and overestimating the gain between her neural command and the effector (Fig. 5A). We therefore investigated whether we could estimate the user's internal model from pretarget neural activity (Fig. 5B) and then use this estimate to adjust the gain to reduce cursor movement errors.

We tested this strategy post hoc using each monkey's largest dataset (Fig. 5C). In monkey J, we found that RG 2 trials' (offline) movement errors could be reduced to 46.3% of their original actual errors (p < 0.001, two-sample t test), and RG 0.5 trial error reduced to 96.5% (not significant). In monkey R, offline RG 2 movement errors were reduced to 68.9% of their original actual errors (p < 0.001) and RG 0.5 errors increased to 106.1% (not significant). The larger improvements in RG 2 trial errors can be attributed to RG 2 trials having much larger movement errors to begin with, as can be seen by comparing each gain's actual (uncompensated) RG errors with its “ideal” case CG errors in Figure 5C. Because overshooting when the cursor was faster than expected was more of a problem than undershooting when the cursor was slower than expected, this task provided greater opportunity for improving RG 2 reach overshoot using our decode-and-compensate strategy.

To revisit the motivating analogy, these offline results suggest that a neural prosthesis could detect an internal model mismatch in which users underestimate their “neural strength”; that is, the user expects that her movement intentions will cause prosthesis movements that are slower than what her decoded movement intentions would actually command. The BMI could then reduce the gain between decoded motor commands and prosthesis output preemptively to, for example, prevent the user from knocking over the glass that she is reaching for.

Discussion

The key new finding of this study is that the activity of motor cortical neurons correlates with an internal model of visuomotor gain during the pretarget delay; that is, before the exact movement goal is specified. These neural correlates became more pronounced leading up to the target appearance, which may reflect the visuomotor gain internal model being “readied” just before its expected use. This argues against two alternative hypotheses under which during this period the internal model is only reflected in other brain areas' activity, such as in cerebellum (Ramnani, 2006), or in purely subthreshold changes (Haider and McCormick, 2009). Rather, it suggests that network firing activity reflects an internal model even in the absence of the model being actively used, as has been shown for ferret visual processing (Berkes et al., 2011) and zebrafish locomotor gain (Kawashima et al., 2016). We therefore view these neural changes, which reflect prior information relevant to upcoming reaching movements, as expanding the scope of what factors influence motor preparatory activity. Motor cortical preparatory activity has been shown previously to reflect upcoming reach target (Riehle and Requin, 1989; Kurata, 1993; Messier and Kalaska, 2000), grasp type (Godschalk et al., 1985; Vargas-Irwin et al., 2015), accuracy (Gomez et al., 2000), curvature (Hocherman and Wise, 1991), force (Riehle et al., 1994), and feedback control policy (Gallivan et al., 2016). Of particular relevance is a previous experiment finding that motor cortical preparatory activity, measured after the target was cued, reflects instructed reach speed (Churchland et al., 2006a). Further analyses revealed that small variations in this preparatory neural state predict subsequent variations in reach speed even within a given instruction condition (Churchland et al., 2006b). Our results suggest that the visuomotor gain internal model, which informs how the visual target will be transformed into the appropriate motor output once it is presented, can be added to this list of what shapes a motor cortical “plan.” Much like the specific reach plan activity described by the two Churchland studies, the gain internal model component of preparatory activity reported here reflects differences between task conditions (i.e., different gain conditions) and predicts speed variations within a condition.

An important direction for future investigation is how the motor cortical activity corresponding to the current internal model is used mechanistically. More specifically, how does it shape the network's response to incoming reach target information to subsequently generate muscle outputs that are most appropriate for reaching to this particular target given the current relationship between motor cortex and movement of the final effector? A related, but distinct, open question is how neural correlates of the internal model, combined with knowledge of task constraints, influence the feedback control policy that shapes the neural and behavioral responses to sensory afferents signaling errors (Scott, 2004, 2012).

Interestingly, we found that the neural differences corresponding to expecting different gains were not along the same neural dimensions as (that is, not simply “smaller versions” of) movement epoch differences (Fig. 3D). This is consistent with previously described “tuning” differences between preparation and reaching, which we have used to argue for a time-varying population-level dynamical relationship between movement preparation and execution (Shenoy et al., 2013). That said, it remains to be seen whether the “gain plan” differences described in the present study bear an analogous lawful relationship to subsequent movement epoch differences (Churchland et al., 2012; Elsayed et al., 2016).

One might view these pretarget neural changes as less interesting if they were accompanied by changes in muscle tone, rather than reflecting a purely covert process. Although we cannot definitively rule out pretarget muscle differences because we did not record EMG in the present study, we believe them unlikely given that Churchland et al. (2006a) observed no EMG changes before target appearance when monkeys were expecting to make reaches of different speeds. Furthermore, multiple previous studies (Weinrich and Wise, 1982; Wise et al., 1998; Messier and Kalaska, 2000) found no EMG changes when monkeys prepared different types of reaches during an instructed delay period, even though this is when one might expect muscle tone differences to be most likely because the monkey has all of the information necessary to prepare his arm to make a specific reach.

Our findings differ from that of a human imaging study in which gain adaptation effects were not observed in motor cortex (Krakauer et al., 2004). This may be because the neural differences we described are small (in terms of firing rate changes) and involve both firing rate increases and decreases across the ensemble, which would be difficult to detect with PET. The ability to observe subtle internal model correlates during static hold periods between movements using intracortical recordings is noteworthy because it enables studying how these models change without the confound of ongoing movement generation. Motor neuroscience has exploited separating movement preparation and execution extensively to study how various movement parameters influence instructed delay activity (Shenoy et al., 2013). We suggest that a similar approach could be used to tease apart the neural correlates of learning various motor plant parameters, which could range from a simple gain (as in this study) or visuomotor rotation (Krakauer et al., 2000) to more complex parameters such as an arm's biomechanical dynamics (Todorov, 2000).

The second main finding of this study is that we could observe internal model neural correlates change with single-trial resolution. Our task design's RG condition, in which visuomotor gain changed unpredictably from trial to trial, allowed us to relate the monkey's experience on a given trial with subsequent neural state changes. These changes further predicted the following trial's reaching behavior. We believe this to be the first such report of motor cortical adaptation during arm reaching at the level of single trials. This result is evocative of behavioral and cerebellar changes that depend on the previous trial's error signals during oculomotor tasks (Medina and Lisberger, 2008; Yang and Lisberger, 2013; Kimpo et al., 2014) and, indeed, the cerebellum is a prime candidate for instructing these changes in motor cortex. The ability to observe internal model changes with single-trial resolution has utility for motor neural prostheses (Golub et al., 2015) and for studying the interaction of internal models, movements, and errors on the single-trial timescales at which these computations ultimately play out (Albert and Shadmehr, 2016).