Encoding of Both Reaching and Grasping Kinematics in Dorsal and Ventral Premotor Cortices

Abstract

Classically, it has been hypothesized that reach-to-grasp movements arise from two discrete parietofrontal cortical networks. As part of these networks, the dorsal premotor cortex (PMd) has been implicated in the control of reaching movements of the arm, whereas the ventral premotor cortex (PMv) has been associated with the control of grasping movements of the hand. Recent studies have shown that such a strict delineation of function along anatomical boundaries is unlikely, partly because reaching to different locations can alter distal hand kinematics and grasping different objects can affect kinematics of the proximal arm. Here, we used chronically implanted multielectrode arrays to record unit-spiking activity in both PMd and PMv simultaneously while rhesus macaques engaged in a reach-to-grasp task. Generalized linear models were used to predict the spiking activity of cells in both areas as a function of different kinematic parameters, as well as spike history. To account for the influence of reaching on hand kinematics and vice versa, we applied demixed principal components analysis to define kinematics synergies that maximized variance across either different object locations or grip types. We found that single cells in both PMd and PMv encode the kinematics of both reaching and grasping synergies, suggesting that this classical division of reach and grasp in PMd and PMv, respectively, does not accurately reflect the encoding preferences of cells in those areas.

SIGNIFICANCE STATEMENT For reach-to-grasp movements, the dorsal premotor cortex (PMd) has been implicated in the control of reaching movements of the arm, whereas the ventral premotor cortex (PMv) has been associated with the control of grasping movements of the hand. We recorded unit-spiking activity in PMd and PMv simultaneously while macaques performed a reach-to-grasp task. We modeled the spiking activity of neurons as a function of kinematic parameters and spike history. We applied demixed principal components analysis to define kinematics synergies. We found that single units in both PMd and PMv encode the kinematics of both reaching and grasping synergies, suggesting that the division of reach and grasp in PMd and PMv, respectively, cannot be made based on their encoding properties.

Introduction

Reaching to grasp is a fundamental, ethologically relevant primate behavior (Kaas et al., 2013). Several cortical and subcortical structures are involved in the generation of these movements (Fattori et al., 2004; Grafton, 2010; Kaas et al., 2013). Recently, much emphasis has been placed on understanding the behavior of single cells in primary motor cortex (MI), one of the main sources of cortical output to the spinal cord during reach-to-grasp movements (Saleh et al., 2010, 2012, Mollazadeh et al., 2011, 2014). The motor cortex, however, does not exhibit a clear hierarchical organization with MI as the sole source of corticospinal output (He et al., 1993; Dum and Strick, 2005). Rather, MI is part of a network of cortical areas involved in the production of reach-to-grasp movements. Two other cortical areas that are densely connected horizontally with MI are the dorsal and ventral premotor cortex (PMd and PMv, respectively), which provide a large proportion of cortical inputs to MI (Dum and Strick, 2005; Dea et al., 2016).

The dual-channels hypothesis has posited that reach-to-grasp movements arise from the temporal coordination of activity in independent reaching and grasping brain networks (Jeannerod, 1988; Karl and Whishaw, 2013) In this framework, PMd, which makes anatomical connections to superior parietal lobe, specifically area V6A (Fattori et al., 2010, 2012), has been considered part of a dorsomedial parietofrontal reaching network involving movements of the arm, whereas PMv, which makes anatomical connections to inferior parietal lobe, specifically AIP and VIP (Luppino et al., 1999; Borra et al., 2008), has been associated with a dorsolateral parietofrontal grasping network and concerned with distal aspects of the limb—namely, the hand (Dum and Strick, 2005; Hoshi and Tanji, 2007; Grafton, 2010; Dea et al., 2016). However, PM single unit spiking activities have been shown to encode both grip type and target position/reach direction during reach-to-grasp movements in both PMd and PMv (Stark et al., 2007; Lehmann and Scherberger, 2013). These previous studies considered grip type and target position/reach direction as categorical variables. What is unknown is whether the encoding of kinematic trajectories of reaching and grasping is spatially segregated across the premotor cortex.

Here, we tested directly whether representations of reaching and grasping kinematics were strictly segregated in PMd and PMv. However, to address this, we had to account for the fact that reaching for objects in different locations influenced, not only proximal limb kinematics of the arm, but also distal kinematics of the hand. Likewise, grasping different objects affected both hand and arm kinematics. Therefore, we applied a novel dimensionality reduction technique to dissociate anatomical representations (i.e., based on encoding specific joints) from functional representations (i.e., encoding reach-related or grasp-related kinematic synergies). We found no evidence of a strict segregation of reaching and grasping activity in PMd or PMv. Instead, we observed that both areas contained complete anatomical representations of the upper limb and functional representations of both reaching and grasping.

Materials and Methods

Neurophysiology

All surgical and experimental procedures were approved by the University of Chicago Animal Care and Use Committee and conformed to the principles outlined in the National Institutes of Health's Guide for the Care and Use of Laboratory Animals (NIH publication no 86–23 revised 1985). Two rhesus macaques (Macaca mulatta) were implanted with 96-electrode Utah arrays in the PMd and PMv contralateral to their working arm. Electrodes were 1.5 mm in length except for the array in PMd of animal J (1.0 mm). Neural spiking activity from the electrodes were amplified with a gain of 5000, band-pass filtered between 0.3 Hz and 7.5 kHz, and recorded digitally (14 bit resolution) using a Cerebus acquisition system (Blackrock Microsystems). A threshold was set above the noise floor on each channel (5.5 SDs) and, every time this threshold was crossed, a 1.6 ms sample (sampled at 30 kHz) was recorded as a putative spike waveform. These threshold crossings were subsequently sorted offline using a semimanual clustering procedure (Offline Sorter, RRID:SCR_000012; Plexon). Only sorted waveforms with a signal-to-noise ratio (SNR) >3 were used in subsequent analyses. Here, the SNR is defined as the peak minus the trough of the average waveform divided by the average SD of the waveform across time.

Behavioral task

Two male rhesus macaques were trained to perform a reach to grasp task with their left hand while their heads were fixed. A robot (RV-1A-S11 6-axis robot; Rixan Associates) presented each animal with objects (Fig. 1A) to grasp at four different spatial locations (Fig. 1B) in its peripersonal space. The set of objects consisted of geometric shapes that were designed to evoke a variety of different hand conformations when grasped. Object and location pairings were varied randomly on a trial-by-trial basis to minimize the amount of motor planning. In addition, the animal's vision was occluded between trials with a pneumatically controlled screen. Once the vision screen was opened, the animal made a reach-to-grasp movement to the target and held his grip for at least 500 ms to receive a juice reward. During each movement, the animal was able to see his arm and hand. Each object was attached to a shaft, the end of which was attached to a cube with a magnet that allowed the experimenter to quickly affix a different object to the end-effector of the robot on each trial.

Figure 1.

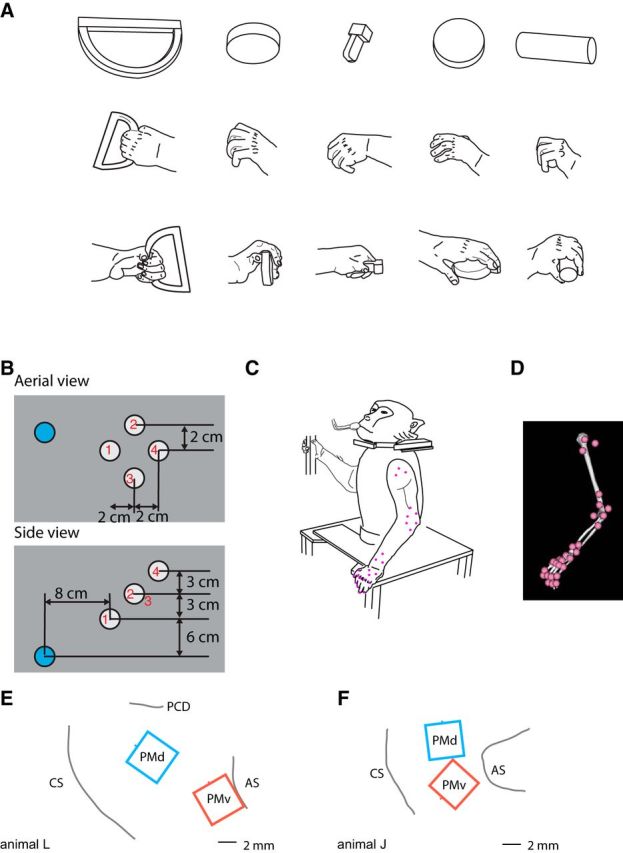
Methods. A, Animals were trained to grasp a variety of geometric shapes including (left to right) ring (vertical), small disc (out), key, small disc (horizontal), and cylinder (horizontal). These drawings depict static hand conformation during grasping of these objects. B, Target locations in relation to the starting position. Aerial view is shown at the top and side view at the bottom. Blue circle denotes the starting position and white circles denote target locations. Red numbers in or near the target circles indicate the location numbers 1–4. C, Drawing of animal J in rest position. Pink dots correspond to the approximate placement of the infrared markers. D, Depiction of the arm in the same position as in C in the Opensim software environment. E, F, Placement of electrode arrays in animals L and J, respectively. CS, Central sulcus; AS, Arcuate sulcus; PCD, Precentral dimple.

The precise set of objects that were presented to animal L consisted of five different objects (cylinder, small disc, key, large disc, and ring) in different orientations for a total of 11 different grasp conformations, or grips (cylinder horizontal, cylinder out, cylinder vertical, small disc horizontal, small disc out, small disc vertical, key, large disc horizontal, large disc vertical, ring horizontal, and ring vertical). On average, the animal completed 21 repetitions of each grip/location pairing, although some combinations were less frequent than others due to the random sampling of objects, with the minimum number of repetitions being five. Animal J was presented with three objects (cylinder, small disc, and ring) to evoke four different grips (cylinder out, small disc out, ring horizontal, and ring vertical). On average, animal J completed 36 repetitions of each grip/location pairing and all combinations were sampled at least 15 times. Data from each monkey were recorded from one session each.

Motion capture and inverse kinematics

A 10-camera motion capture system (Vicon Motion Tracking System) detected and recorded the 3D position of retroreflective markers glued to the animal. A total of 30 markers were placed on the animal's dorsal hand and dorsolateral arm, enabling the tracking of 21 degrees of freedom in the arm and hand (listed below). The motion capture system was also used to monitor the position of the object and vision block screen. The time series of 3D marker positions were low-pass filtered bidirectionally (fourth-order Butterworth filter 15 Hz cutoff). All filtering and calculations are done in MATLAB (The MathWorks, RRID:SCR_001622) unless otherwise noted. To measure grasp aperture, we computed the Euclidean distance between markers attached to the distal most aspects of the thumb and index finger (D1 and D2, respectively).

To compute wrist speed, we differentiated numerically the positional data of three markers on the animal's wrist. After numerical differentiation, wrist velocities were again low-pass filtered (using the same filter design as before). Wrist speed was defined as the average tangential velocity of the three wrist markers. Movement onset, derived from wrist speed, was defined as the first moment that wrist speed exceeded 10% of the maximum wrist speed. Reaction times were subsequently defined as the difference in time between movement onset and release of the vision block.

We used open-source software (Delp et al., 2007; Opensim, RRID:SCR_002683) to infer joint angles from marker positional data. We estimated joint angles for 21 degrees of freedom in the arm and hand including: humerus flexion/extension, humerus abduction/adduction, humerus rotation, elbow flexion/extension, wrist pronation/supination, wrist abduction/adduction, wrist flexion/extension, 1 carpal-metacarpal (CMC) flexion/extension, 1 CMC abduction/adduction, 1 metacarpal-phalangeal (MCP) flexion/extension, 1 MCP abduction/adduction, 2 MCP abduction/adduction, 2 MCP flexion/extension, 2 proximal interphalangeal (PIP) flexion/extension, 3 MCP flexion/extension, 3 MCP abduction/adduction, 4 MCP flexion/extension, 4 MCP abduction/adduction, 4 PIP flexion/extension, 5 MCP flexion/extension, 5 MCP abduction/adduction, and 5 CMC flexion/extension. Inverse kinematics were bidirectionally low-pass filtered with a 6 Hz cutoff.

Demixed principal components analysis

We used a novel dimensionality reduction technique, demixed principal components analysis (dPCA), to identify kinematic synergies associated with reaching, grasping, the interaction of reach and grasp, or synergies that were common across all experimental conditions (Brendel et al., 2011; Kobak et al., 2016). This analysis was motivated by two observations about the kinematics. First, on a given trial, there are often strong correlations between the kinematics of different joints, suggesting that most of the variance in the kinematics may be described by a few kinematic synergies, often estimated using PCA (Santello and Soechting, 1998; Mason et al., 2001). Second, the correlation patterns across joints during reach-to-grasp movements depend upon the exact nature of the movement; therefore, different experimental conditions may produce different correlation patterns (Todorov and Ghahramani, 2004). Briefly, the dPCA algorithm attempts to find linear combinations of kinematic variables that explain the most variance, yet also vary only with a given experimental condition.

We present a mathematical explanation of dPCA that closely mirrors the description in (Kobak et al., 2016). Suppose that every trial e (of E total trials) has an associated location l (of L possible locations) and grip o (of O possible grips). Also suppose that, on every trial, we have recorded the activity of J kinematic features at T different time points. We computed the trial-average kinematic trajectory of every kinematic feature j for each grip and location pairing denoted R_jlo(t). We then gathered all the trial-averaged kinematic trajectories into a single matrix, X of size J × LOT. We subsequently demeaned X such that the average of any kinematic feature over all locations, grips, and times was 0. It has been shown previously that matrix X can be decomposed into independent parts called marginalizations that satisfy the following:

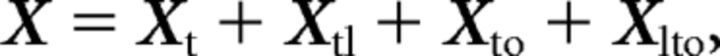where X_t denotes the time-varying, but location- and grip-invariant part of X, obtained by averaging X over all locations and grips as follows:

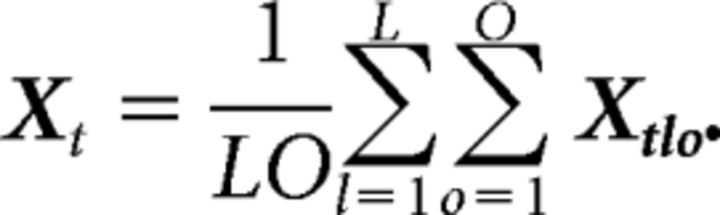The location-dependent term, X_tl, is obtained by averaging X − X_t over all grips and, similarly, the grip-dependent term, X_to, is obtained by averaging X − X_t over all locations. Finally, the location–grip interaction, X_lto, is obtained by computing X_lto = X − X_t − X_tl − X_to. It is important to note that every marginalization of X has the same dimension as X: J × LOT.

Using the decomposition of X into its marginalizations, dPCA aims to find directions in R^J that explain as much variance as possible, with the additional constraint that this variance should come from only one marginalization. Unlike standard PCA, dPCA relaxes the assumption that all the directions must be strictly orthogonal. Formulated as a constrained optimization problem, dPCA seeks to find a direction φ in R^J to minimize the following objective:

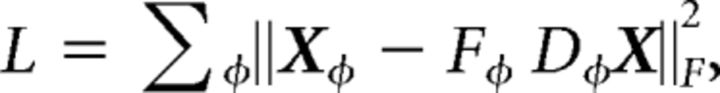where F_φ is an encoder matrix with q columns, D_φ is a decoder matrix with q rows, and ||•||²_F denotes the Frobenius norm of a matrix. An efficient algorithm was proposed recently to solve this objective function (Kobak et al., 2016).

To compute the cumulative variance explained by the first p dPCs, we cannot simply add variances because the dPCs are not strictly orthogonal. Instead, the cumulative variance explained by the first p dPCs is given by the following:

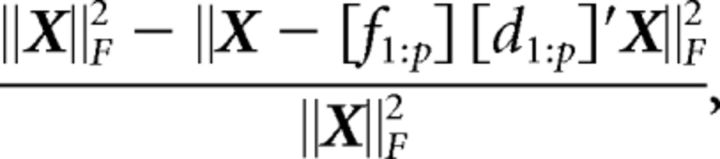where [f_1:p] is a matrix of the first p encoding vectors, [d_1:p] is a matrix of the first p decoding vectors, and [•]′ is a transpose of a matrix. We emphasize that the cumulative proportion of variance explained by each component is based off of the trial averaged data in the matrix, X.

Generalized linear model (GLM) analysis

Input features.

We attempted to predict the instantaneous probability of spiking in a given single unit from many different combinations of extrinsic covariates (i.e., kinematics and experimental factors) and intrinsic covariates (i.e., neural signals).

Extrinsic covariates.

We used the position and velocity of 21 joints in the arm and hand at various time lags as input features to our encoding model. We used eight different time lags from −156 ms (i.e., spikes lag kinematics by 156 ms) to 208 ms (i.e., spikes lead kinematics by 208 ms) in 52 ms steps. In total, there were 168 (21 joints × 8 lags) positions and velocities for a total of 336 kinematic features. Other extrinsic features included kinematic synergies identified via dPCA. Additional categorical variables indicating the reach location and grip on a given trial were defined; intertrial intervals were coded as one category in these variables.

Intrinsic covariates.

In addition to extrinsic features, intrinsic features such as a given neuron's own spike history and the spike history of other neurons may also contribute to a neuron's firing rate. To account for the fact that spike history may be relevant in different ways at different time scales, we filtered binary spike trains with raised cosine basis functions of the form:

for t such that a log(t + c) ∈ [φ − π, φ + π] and 0 elsewhere (Saleh et al., 2012). We specified three different values of ϕ, the temporal peak of the cosine curve, to account for short (16 ms), medium (44 ms), and long (108 ms) time scale spike history effects. Each basis vector was convolved with the binary spike train of a given neuron, thus giving rise to three spike history vectors for every neuron.

Logistic regression

We used logistic regression to predict the probability that a neuron fired a spike in a small time window (4 ms) based on previously described input features. Mathematically, this model may be expressed as follows:

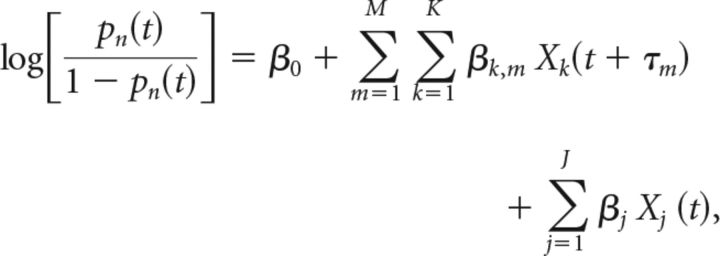where p_n(t) is the probability that neuron n fires a spike at time t, β₀ represents the baseline probability that the cell will spike, X_k(t − τ_i) is the value of the k^th (of K) extrinsic feature at time t − τ_m, where τ_m is the m^th (of M) lead or lag time (ranging from 52, 104, and 156 ms leading and 52, 104, 156, and 208 ms lagging) against the spike time at t and X_j(t) is the value of the j^th (of J) intrinsic feature at time t with corresponding weights β_k,m and β_j, respectively.

Data segmentation and assessing goodness of fit

Model goodness of fit (GoF) was quantified using the area under the receiver operating characteristic curve (AUROC) (Hatsopoulos et al., 2007; Saleh et al., 2010, 2012; Truccolo et al., 2010). We assessed GoF using 10 folds of cross-validated test data and, unless otherwise noted, all reported AUROC values are taken to be the median across cross-validation folds. Each training fold was composed of at least 329 experimental trials and intertrial activity between those trials. Because the folds were based on experimental trials rather than data points, the number of test and training data points varied across folds; however, at least 531,747 and 1,541,496 data points were in every fold in animals J and L, respectively.

Results

Kinematics of unconstrained reaching to grasp

We used a marker-based infrared motion tracking system combined with an advanced biomechanical model of the primate upper limb (Delp et al., 2007) to infer the kinematics of 21 joints in the arm and hand as two rhesus macaques engaged in an unconstrained reach-to-grasp task. We presented multiple grips at different locations in the animal's workspace designed to elicit a diversity of prehensile movements that included both precision and power grips (Fig. 1).

Differences in kinematics across experimental conditions were evident at the level of individual joints (Fig. 2). From visual inspection of Figure 2A, it can be seen that the different object locations elicited different patterns of arm movement and the different grip types elicited different patterns of hand movement. Less obvious, however, is that the object to be grasped also influenced arm kinematics and, to a lesser extent, the position of the object in space influenced hand kinematics (Fig. 2B). These differences at the level of single joints were also manifested in multijoint features. The average temporal profiles of grasp apertures were qualitatively different across grips (Fig. 2C) and, quantitatively, the maximum grasp aperture over time was significantly different across the four grasping conditions (Kruskal–Wallis test, animal J: X² with 3 df = 330.84, p < 0.01; animal L: X² with 3 df = 199.91, p < 0.01). Similarly, we observed differences in the peak wrist speed across object locations (Kruskal–Wallis test, animal J: X² with 3 df = 87.16, p < 0.01; animal L: X² with 3 df = 272.19, p < 0.01).

Figure 2.

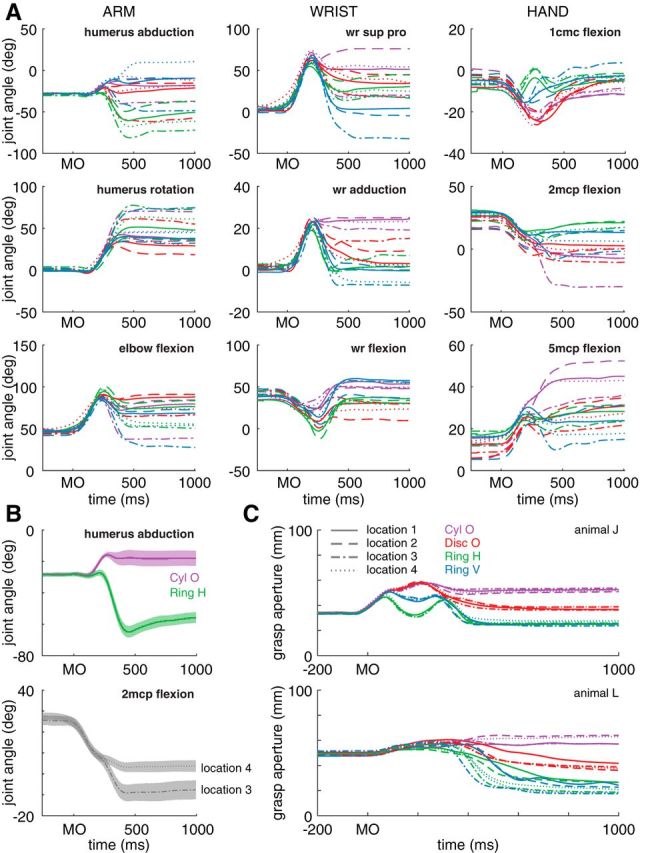
Trial-averaged kinematics of the arm, wrist, and hand relative to movement onset (MO). A, Within-condition trial-averaged kinematics for three degrees of freedom in the arm (left column), wrist (center column), and hand (right column) of animal J. Line style indicates object location and color indicates grip type. B, We found that the object can affect arm kinematics significantly (top). Here, we computed the average humerus abduction over all object locations when grasping Cyl o (purple trace) and Ring h (green trace). Shaded area indicates ±2 SEM. Similarly, reach location can affect hand kinematics (bottom). Flexion in the metacarpophalangeal joint of the second digit (2 mcp flexion) was averaged over all objects and is shown for two object locations. C, We computed the grasp aperture, defined as the distance between the distal-most thumb and index finger markers and plotted it relative to movement onset in both animals.

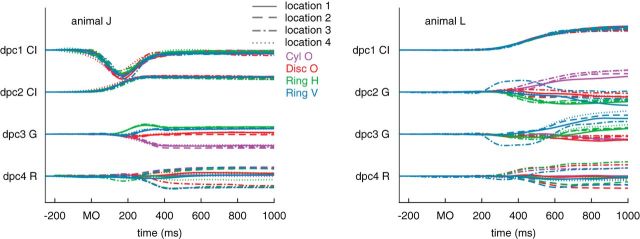
To control for the fact that both reaching and grasping affect kinematics in the entirety of the upper limb, we used a novel dimensionality reduction technique, dPCA, to identify functionally defined kinematic synergies. Each kinematic synergy (i.e., each dPC) could be reach related, grasp related, condition independent (i.e., common to all experimental conditions), or an interaction between reach and grasp (i.e., specific to a particular experimental condition). As with other studies that have applied dimensionality reduction techniques to kinematic data (Mason et al., 2001; Mollazadeh et al., 2014; Schaffelhofer et al., 2015), we found that a few functional kinematic synergies described the majority of the variability in the kinematics. In both animals, we found the eight components were sufficient to explain 90% of the variance in joint angles (Fig. 3A), whereas 10 and nine components were needed to explain 90% of the variance in joint angular velocities in animals J and L, respectively (result not shown). In both animals, we observed that a substantial proportion of the kinematic variance was common across all experimental conditions and that grasping components explained more variance than reaching components (Fig. 3B). Examples of the kinematic synergies in animal L are shown in Figure 3C. The temporal evolution of a subset of these kinematic synergies as a function of time relative to the movement onset is shown in Figure 4 for both animals. Although the convexity for animal J is flipped, dPC1s for both animals are condition independent, appear to resemble aperture trajectories, and clearly indicate behavioral differences between the two animals: animal J made much faster reaching than animal L. Other grasp- or reach-specific dPCs show object- and location-specific components such that trajectories associated with different locations formed clustered bundles that were distinct for different objects (dPC3 G for animal J and dPC2 G and dPC3 G for animal L) and trajectories associated with different objects formed bundles that were distinct for different locations (dPC4 R for animal J and dPC4 R for animal L).

Figure 3.

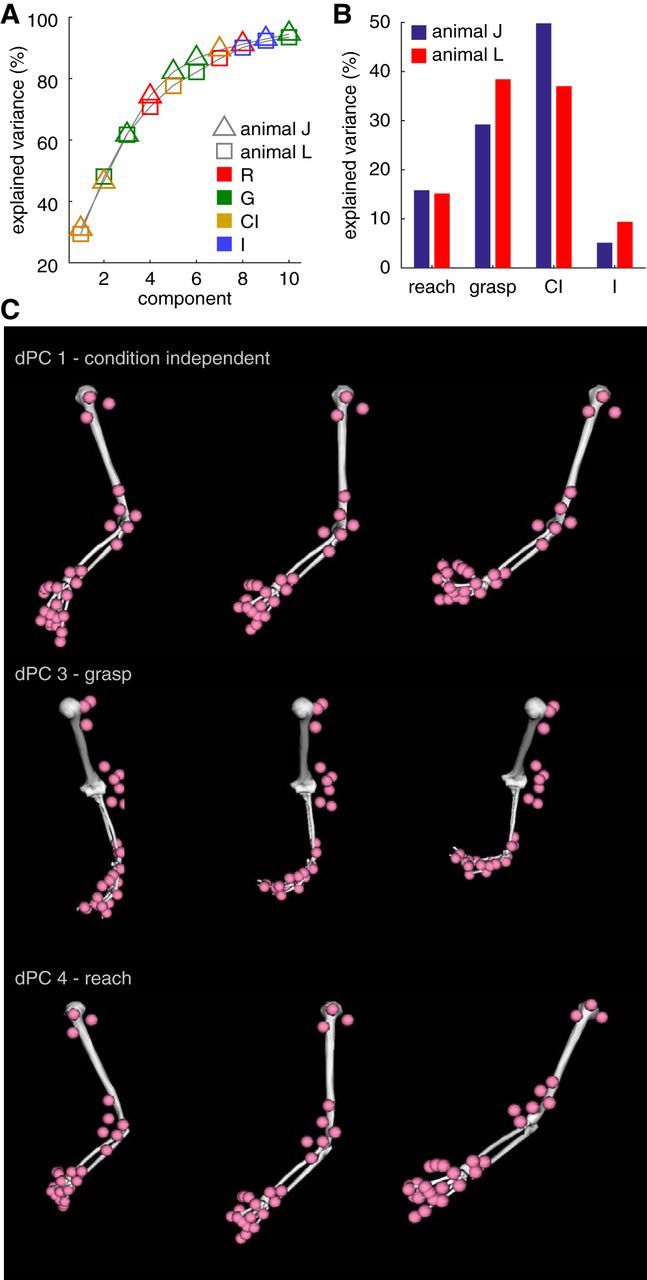
dPCA. A, Scree plot of dPCA. The cumulative percentage of explained variance for a given number of dPCs is shown for joint angles. Each individual component varies only along one task parameter. It can be reach related (R, red points), grasp related (G, green points), condition independent (CI, gold points), or an interaction between reach and grasp condition (I, blue points). Marker shape (either square or triangle) indicates animal. Note that the scree plots are highly similar across animals. B, Percentage of variance explained by the different task conditions in joint angle data. C, Visualization of kinematic synergies revealed by the dPCA. The posture of the upper limb is shown at various projections along the largest condition independent synergy (top row), the largest grasp synergy (middle row), and the largest reach synergy (bottom row). Data are from animal J.

Figure 4.

Trial-averaged dPCA trajectories relative to movement onset. The temporal profile of the first four dPCs is shown for the various object locations and grips. Conventions are the same as Figure 2. To the left of each dPC is an indication of whether it is a CI, grasp (G), or reach (R). The components are ordered from top to bottom in terms of variance explained; that is, dPC1 explained more variance than all others.

Encoding of extrinsic features in premotor cortex

One session for each monkey was performed to collect single unit-spiking activity from PMd and PMv arrays. We obtained populations of task-related units: 51 and 34 units from PMd and PMv, respectively, for monkey J and 29 and 22, respectively, for monkey L. Figure 5 illustrates one example each for PMd and PMv single unit activities across different objects and different locations.

Figure 5.

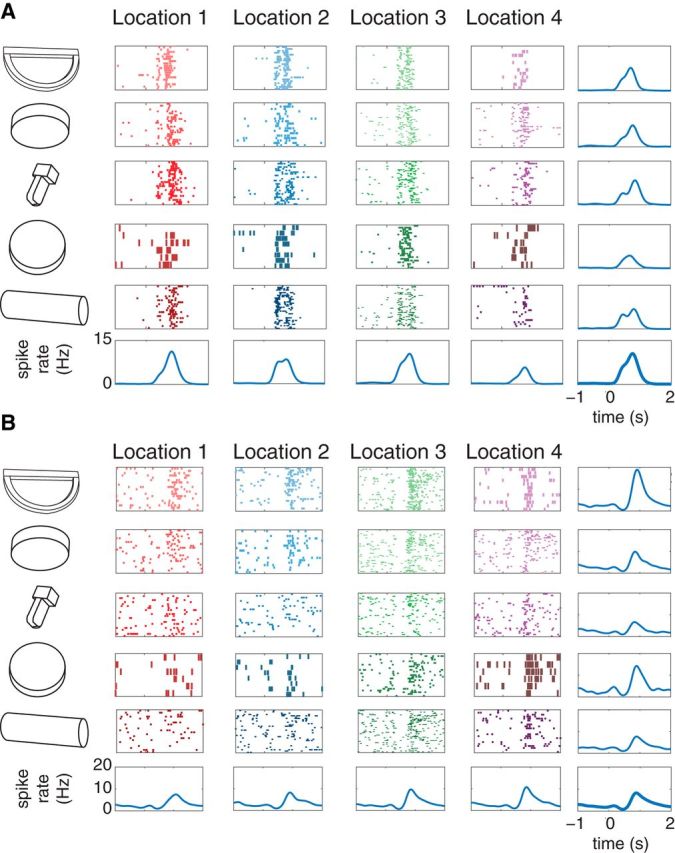
Exemplary single unit spiking activities of neurons in PMd (A) and PMv (B) for monkey L reaching to grasp different objects at different locations. Each raster plot corresponds to a particular object and location combination and each peristimulus time histogram was computed for either one object over all locations or one location over all objects. Time 0 corresponds to movement onset.

We used GLMs to develop encoding models of premotor cortical single unit activity and compared the performance of these models that explicitly accounted for the moment-by-moment kinematic features against a more abstract, set-related representation of behavior. In this first class of model, we used the detailed kinematics of 21 joints in the arm and hand at a variety of different time lags to predict spiking activity (see Materials and Methods for details). In contrast, the second class of model, the set-related model, assumed a single, constant firing rate for each experimental condition. To assess model performance, the AUROC was computed for each model.

Across all animals, brain areas, and types of model, we found that the median AUROC values across cells were significantly greater than the chance level of the AUROC, 0.5 (Fig. 6A; Wilcoxon signed-rank test, all p < 0.01). In both animals, we observed that kinematics better predicted activity in PMd compared with PMv (Fig. 6A; Mann–Whitney U test, animal J: Z = 2.85, p < 0.004; animal L: Z = 4.12, p < 0.01). The set-related models also predicted activity in PMd better than PMv in animal L (Fig. 6A; Z = 4.75, p < 0.01), but not in animal J (Z = 1.59, p > 0.05). In both animals and brain areas, we found that encoding models based on kinematics better predicted spiking activity than the set-related models (Fig. 6B; Wilcoxon signed-rank test, animal J PMd: Z = 5.74, p < 0.01; PMv: Z = 4.98, p < 0.01; animal L PMd: Z = 3.45, p < 0.01; PMv: Z = 4.11, p < 0.01). We computed AUROC for each kinematic lead/lag, but there was no clear indication of an optimal lead/lag time for either of the two cortical areas (results not shown).

Figure 6.

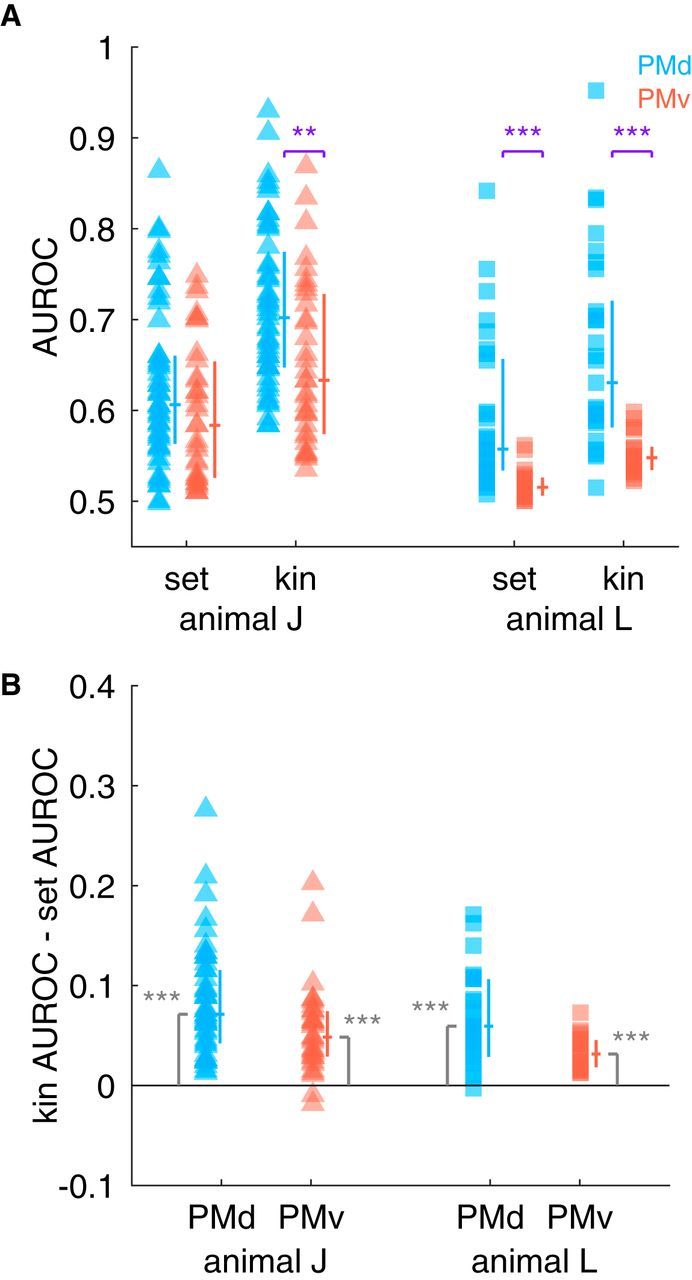
Encoding models that include kinematics predict spiking activity better than set-related models. A, We fit encoding models using either set-related activity or kinematics to each neuron in our sample and measured the AUROC across 10 folds of cross-validated data. Here, each point corresponds to the median AUROC across folds as a function of animal (triangles or squares) and model type. Cells in PMd are blue and cells in PMv are red. The vertical line next to each point set indicates the interquartile range; the median is indicated with the horizontal line. B, Distribution of differences between kinematic and set-related models. The lines to the immediate right of each point set follow the same conventions as in A. Kinematic models predicted spiking activity better than set-related activity models in PMd and PMv in both animals (significance codes: ***p < 0.0005, see main text for additional statistics).

Having established that whole arm kinematics were predictive of spiking activity in PMd and PMv, we subsequently considered which aspects of the kinematics were important. The dual-channels hypothesis posits that PMd is concerned with the proximal aspect of the limb, whereas PMv is related to the distal aspect. We tested the extent to which anatomical segments of the limb were represented in both areas. Encoding models were fit using only arm kinematics (i.e., shoulder and elbow kinematics) or only hand kinematics (i.e., wrist and fingers). We found evidence that both arm and hand kinematics were predictive of spiking in each area because the median AUROC across neurons was significantly >0.5 (Fig. 7A; Wilcoxon signed-rank test, all p < 0.01). However, in isolation, this finding does not provide strong evidence against the dual-channels hypothesis. For example, a cell that truly encodes only arm kinematics may appear to also encode hand kinematics simply because of correlations between arm and hand kinematics.

Figure 7.

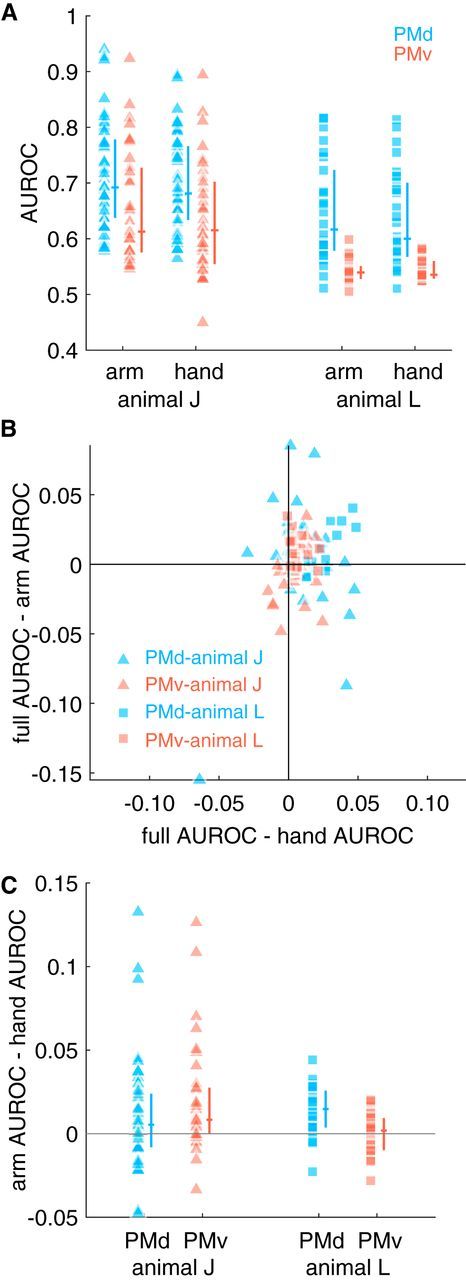
Comparing encoding performance of models based on an anatomical division of the upper limb. A, We fit GLMs using either arm or hand (including wrist) kinematics. For each model type and animal, the distribution of median AUROCs across folds is shown as raw data (left column; each point corresponds to a cell) and interquartile range + median (vertical and horizontal lines, respectively). B, Median AUROCs were compared between the full model that included all kinematic terms and reduced models that contained only arm or only hand kinematics. C, Distribution of differences in arm and hand AUROCs. We found that arm kinematics were encoded preferentially by PMd in both animals and also in PMv in animal J because a significant proportion of cells preferred arm kinematics in those two areas (significance codes: *p < 0.05, **p < 0.005; see main text for additional statistics).

We performed a control analysis to ensure that any putative encoding relationship was not a product of kinematic correlations. In this analysis, we subtracted off either arm or hand AUROC from the AUROC of the full model containing both arm and hand kinematics (Fig. 7B). Returning to the previous example, if a cell encodes only arm kinematics, then the difference between the full model AUROC and the arm AUROC should be 0. However, the difference between the full model AUROC and the hand AUROC should be positive because this example cell truly encodes arm kinematics, which the full model contains. In real data, cells that had a positive difference between full model AUROC and hand model AUROC were classified as encoding arm kinematics. Similarly, cells with positive differences between full model AUROC and arm model AUROC were classified as encoding hand kinematics. These classifications were not mutually exclusive. We found that both arm and hand kinematics were effective predictors of single premotor cortical neuron activity. We observed (Table 1) that 82% of PMd and 79% of PMv cells for monkey J and 100% of PMd and 95% of PMv cells for monkey L encoded arm kinematics, 56% of PMd and 53% of PMv cells for monkey J and 75% of PMd and 76% of PMv cells for monkey L encoded hand kinematics, whereas 42% of PMd and 41% of PMv cells for monkey J and 75% of PMd and 71% of PMv cells for monkey L encoded both arm and hand kinematics, respectively. The dual-channels hypothesis would predict that cells encode either arm kinematics or hand kinematics; that is, that they were anticorrelated. However, the proportion of cells that encoded both arm and hand kinematics simultaneously was not significantly different from what would be expected if both arm and hand kinematics were encoded statistically independently (binomial test, B_0.497,121 = 62, p > 0.05); that is, the presence of encoded arm kinematics does not affect the encoding of hand kinematics and vice versa.

Table 1.

Percentage (number of neurons/total number) of neurons encoding arm, hand, or both arm and hand kinematics by area and animal

	PMd		PMv
	Animal J	Animal L	Animal J	Animal L
Arm	82% (41/50)	100% (16/16)	79% (27/34)	95% (20/21)
Hand	56% (28/50)	75% (12/16)	53% (18/34)	76% (16/21)
Arm + hand	42% (21/50)	75% (12/16)	41% (14/34)	71% (15/21)

We subsequently tested whether the arm and hand were represented preferentially in PMd and PMv, respectively, by subtracting the AUROC of the hand-only from the arm-only models. We found that arm kinematics were represented preferentially in the PMd of both animals because the median AUROC differences were significantly >0 (Fig. 7C; Wilcoxon signed-rank test, animal J: Z = 2.51, p < 0.02; animal L: Z = 3.35, p < 0.01). Arm kinematics was also represented preferentially in the PMv of animal J (Z = 2.57, p < 0.01), but not in animal L (Z = −0.41, p > 0.05).

In the previous analysis, we showed that both PMd and PMv encode both arm and hand kinematics. Although this finding is seemingly in contradiction to the dual-channels hypothesis, one possibility is that the hand representation in PMd is in the service of reaching and the arm representation in PMv is in the service of grasping. Therefore, we tested explicitly whether there is any preferential encoding of single unit activities of PMd and PMv neurons using functional representations of prehensile movements revealed by dPCA. Specifically, we fit encoding models using only reaching components or only grasping components of the dPCA analysis. We found that both reach and grasp kinematic synergies predicted spiking activity in both PMd and PMv (Fig. 8A; Wilcoxon signed-rank test, all p < 0.01).

Figure 8.

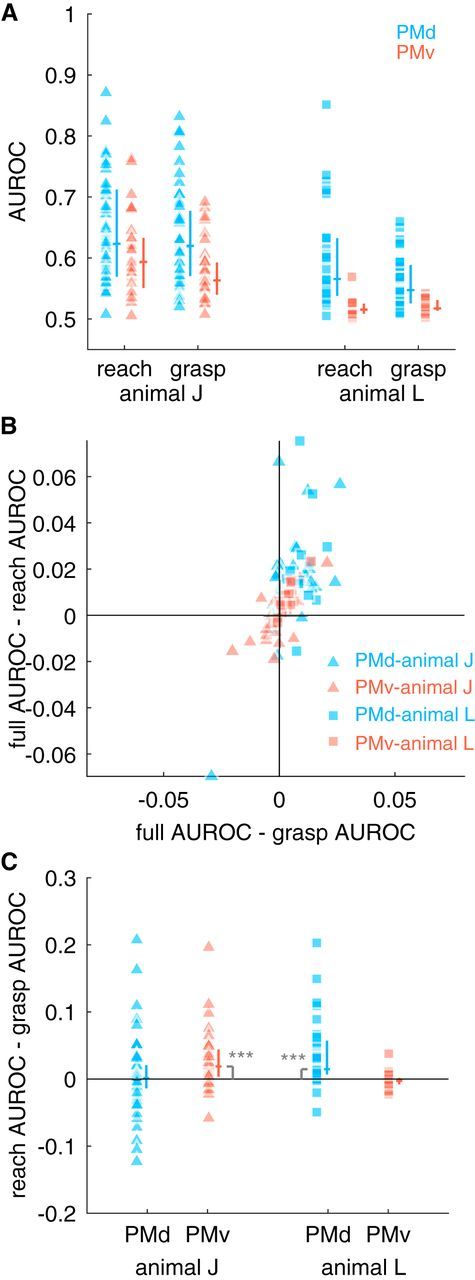
Comparing encoding performance of models based on a functional division of the upper limb. A, We fit GLMs using either reach or grasp kinematic synergies. For each model type and animal, the distribution of median AUROCs across folds is shown as raw data (left column) and interquartile range + median (vertical and horizontal lines, respectively). B, Median AUROCs were compared between the full model that included both reach and grasp synergies and reduced models that contained only reach or only grasp synergies. C, Distribution of differences in reach and grasp AUROCs. We found that reach kinematic synergies were encoded preferentially by PMv in animal J and by PMd in animal L (significance codes: ***p < 0.0005 see text for additional statistics).

Again, we performed a control analysis to verify that both reaching and grasping kinematic synergies were encoded in the spiking activity of premotor cortical cells. We assessed the extent to which a full model containing both reach and grasp synergies outperformed a model containing only reach or only grasp (Fig. 8B). Here, we found (Table 2) that 69% of PMd and 56% of PMv cells for monkey J and 93% of PMd and 91% of PMv cells for monkey L encoded reaching kinematics, whereas 88% of PMd and 65% of PMv cells for monkey J and 97% of PMd and 91% of PMv cells for monkey L encoded grasping. The proportion of cells that simultaneously encoded both reach and grasp (monkey J: 67% of PMd and 53% of PMv cells and monkey L: PMd 90% of PMd and 91% of PMv cells, respectively) was significantly more frequent than would be expected under chance if reach and grasp were independent (binomial test, B_{0.628, 136} = 98, p < 0.01). Although many cells encoded both reach and grasp simultaneously, subtracting the AUROC of the reach and grasp models revealed there was a preferential representation of reaching in the PMv of animal J and PMd of animal L because, as a population, the difference in AUROC between the reach-only and grasp-only models was significantly different from 0 (Fig. 8C, Wilcoxon signed-rank test, animal J: Z = 3.58, p < 0.01; animal L: Z = 3.75, p < 0.01).

Table 2.

Percentage (number of neurons/total number) of neurons encoding reaching, grasping, or both reaching and grasping kinematics by area and animal

	PMd		PMv
	Animal J	Animal L	Animal J	Animal L
Reaching	69% (35/51)	93% (27/29)	56% (19/34)	91% (20/22)
Grasping	88% (45/51)	97% (28/29)	65% (22/34)	91% (20/22)
Reaching + grasping	67% (34/51)	90% (26/29)	53% (18/34)	91% (20/22)

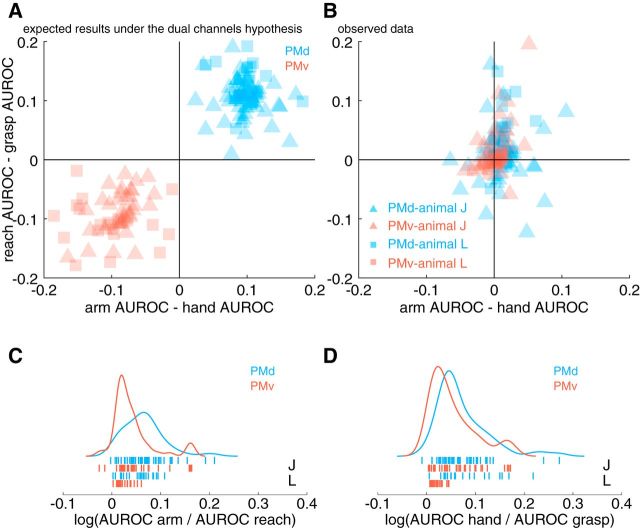
Finally, we considered the relationship between the anatomical and functional kinematic features encoded by each cell. To this end, we compared the difference of arm and hand model AUROCs to the difference of reach and grasp model AUROCs. Under the classical model, we might assume that PMd cells encode the kinematics of the arm preferentially and prefer the kinematics of reaching and, correspondingly, that PMv cells prefer the hand and grasping (Fig. 9A). Such a simplistic relationship, however, does not appear to capture the patterns that we observed in our data because we observed several cells that preferred both hand and reach or arm and grasp in both PMd and PMv (Fig. 9B). These results indicate that anatomical encoding preferences are not clearly related to functional encoding preferences because we failed to reject the null hypothesis that functional and anatomical encoding preferences were statistically independent (χ² test of independence, X² with 1 df = 3.03, p > 0.05).

Figure 9.

Comparing anatomical and functional representations in premotor cortex. We compared the differences of arm and hand AUROCs with the differences of reach and grasp AUROCs to determine whether there was a systematic relationship such that cells that encoded arm kinematics preferentially likewise encoded reaching synergies and, similarly, cells that encoded hand kinematics preferentially likewise encoded grasping synergies. A, Expected results based on the dual-channels hypothesis. PMd would be concerned exclusively with arm kinematics and reaching, whereas PMv would be concerned with hand kinematics and grasping. There would be a segregation of both function and anatomy between PMd and PMv. B, Actual results based on observed data. A χ² test of independence revealed no significant relationship between functional and anatomical encoding preferences. C, Comparing the relative encoding performance of anatomical and functional models. Here, we show the distribution of the logarithm of the ratio of arm and reach model AUROCs. If the log of this ratio is positive, then the arm model had a higher AUROC than the reach model and vice versa for negative values. We found that both PMd and PMv are better predicted by anatomical features rather than functional features, but this preference is stronger in PMd (see main text for additional statistics). D, Same conventions as C, but using hand and grasp models.

We additionally considered the strength of anatomical and functional representations in each area. Specifically, we sought to determine whether anatomical or functional relationships were more strongly encoded in a given area. We computed the logarithm of the ratio of the arm AUROC and reach AUROC (Fig. 9C) or the hand AUROC and the grasp AUROC (Fig. 9D). If this number is negative, then that would indicate that functional kinematic synergies predict spiking activity better than the anatomical features; however, if this number is positive, then the anatomical features predict spiking activity better than functional kinematic synergies. In both PMd and PMv, we found that anatomical features were more strongly encoded compared with functional synergies because the logs of AUROC ratios were positive (Wilcoxon signed-rank test, all p < 0.01). However, the degree to which anatomical features were preferred differed between areas. We found that anatomical features were significantly more strongly represented in the activity of PMd cells compared with PMv (Fig. 9C,D; Mann–Whitney U test, arm/reach: Z = 3.87, p < 0.01, hand/grasp: Z = 2.64, p < 0.01).

Encoding of intrinsic features in premotor cortex

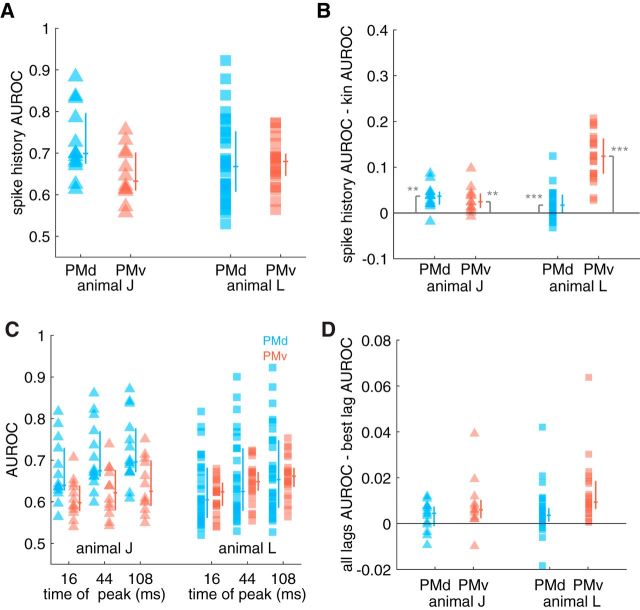
Since extrinsic features were not the sole predictors of spiking activity, we also explored how intrinsic features were encoded in premotor cortex. We compared the encoding performance of the full kinematic model to the full intrinsic; that is, the spike history model. The spike-history model contained information about the spike histories of all other simultaneously recorded neurons at a variety of temporal scales (Fig. 10; see Materials and Methods for details). We found that spike history was an effective predictor of spiking activity (Fig. 10A; Wilcoxon signed-rank test, animal J PMd: W = 91, p < 0.01; PMv: W = 78, p < 0.01; animal L PMd: Z = 4.7, p < 0.01 PMv: Z = 4.1, p < 0.01). In animal J, we found spike history predicted PMd activity significantly better than PMv (Mann–Whitney U test, Z = 2.20, p < 0.03), but there was no difference in animal L across areas (Z = −0.33, p > 0.05). In addition, spike history better predicted spiking activity than the kinematics in all areas (Fig. 10B, all Bonferroni corrected p < 0.011).

Figure 10.

Encoding properties of intrinsic features and comparing spike history with kinematics in premotor cortex. A, We found that spike history from all cells at multiple temporal scales effectively predicted spiking activity (see main text for statistics). Each point corresponds to a cell from a given animal (shape) and cortical area (color). Lines next to each column of data indicate interquartile range and median. B, We compared the performance of the spike history model to the full kinematic model and observed that, generally, spike history was a more effective predictor of spiking activity than kinematics. C, Median AUROC across cross-validation folds as a function of basis function, cortical area, and animal. In both areas, the longest spike history term had the best encoding performance. D, Distribution of the differences in AUROC between the full spike history model and a model based on the best single basis function (lag). To the right of each data column are the median and interquartile ranges of the data.

We wanted to identify which temporal scale of intrinsic activities led to the best encoding performance. We fit models using each of the three different temporal scales and found that the longest temporal scale (108 ms) led to the best encoding performance in both animals regardless of cortical area (Fig. 10C). We subsequently wondered if the information at each temporal scale was totally redundant or if using spike history at multiple temporal scales led to superior predictive ability. Accordingly, we compared the AUROC at the best temporal scale for each cell and compared it with the AUROC of the full spike history model including all temporal scales (Fig. 10D). In the PMd of animal J, we observed that there was no significant difference between the AUROC of the full spike history model and the model at the best lag (Wilcoxon rank-sum test, PMd: W = 69, p < 0.11). In contrast, spike history at multiple spatial scales better predicted spiking activity in the PMv of both animals (animal J: W = 69, p < 0.02, animal L: Z = 4.11, p < 0.01) and the PMd of animal L (Z = 3.30, p < 0.01).

Discussion

dPCA

We applied a novel dimensionality reduction technique, dPCA (Kobak et al., 2016), to identify kinematic synergies associated with either reaching or grasping during an unconstrained prehensile movement task. In both animals, we observed that a few functionally defined kinematic synergies accounted for most of the variance in the data. Moreover, reaching and grasping synergies each explained a large proportion of the kinematic variance. In contrast, comparatively little variance was due to interactions between reaching and grasping conditions, supporting the decomposition of kinematics into reaching and grasping submovements (Jeannerod, 1984; Haggard and Wing, 1995).

Although this method provides a promising avenue for gaining insight into prehensile movements, there are some limitations to the approach. Chiefly, the relationship between the demixed kinematic synergies and muscle synergies currently remains unknown. Using a similar approach to our current method, instantaneous lengths of 50 musculotendon units were estimated and it was found that eight PCA components were sufficient to explain >95% of variance, whereas at least 11 components were needed in the joint angle space to capture the same amount of variance for monkeys performing reach-to-grasp (Schaffelhofer et al., 2015). Recent work has argued that the encoding preferences of primary motor cortical neurons reflect muscle synergies evoked by intracortical microstimulation (ICMS) (Overduin et al., 2014). In complementary work, it was demonstrated that decoding joint kinematics from units on electrodes that evoked movements of that joint when stimulated led to better decoding performance compared with a simple random allocation (Best et al., 2014). The kinematic synergies identified by dPCA, however, arose from our experimental design. In future work, we address the similarity between kinematic synergies inferred using dPCA and kinematic or muscle synergies characterized via ICMS.

At a more technical level, dPCA is limited in that it is based on trial-averaged data and fails to account for trial-to-trial variation within an experimental condition. An additional limitation is that it does not support the use of continuous variables as conditions. That is, object locations were not treated as positions in Euclidean space, but rather as discrete covariates. Finally, on individual trials, the scores of the dPCs often exhibited strong moment-by-moment correlations, suggesting that, even though reach and grasp were decoupled across conditions, there may remain some strong correlation within a condition.

Implications for cortical control of reach to grasp

We used GLMs to develop encoding models of spiking activity in premotor cortex based on intrinsic and extrinsic features. We found evidence that challenged the dogmatic view of premotor cortical organization centered around discrete reaching (dorsomedial) and grasping (dorsolateral) pathways. In particular, we demonstrated that there was a complete anatomical representation of the upper limb in PMd. This finding is consistent with previous studies that used ICMS to study motoric representations in PMd and further work showing that firing rates of PMd neurons are modulated by changes in grasping condition (Raos et al., 2003, 2004; Fattori et al., 2010). Additional work has demonstrated that whole arm kinematics can be decoded from PMd ensemble activity (Bansal et al., 2012). Our work complements that study by showing that single cells encode complex, whole-arm kinematics. Furthermore, our finding is consistent with studies on single units from area V6A, which is a part of the dorsomedial reaching network, illustrating that the dorsomedial pathway is also involved in hand preshaping and grip formation and may play a central role for all phases of reach-to-grasp movements (Fattori et al., 2010, 2012). Similarly, in PMv, we also found a complete representation of the upper limb, although, in absolute terms, it was weaker than in PMd. This result is consistent with previous reports that ICMS of PMv occasionally evoked arm movements (Godschalk et al., 1981, 1985; Hocherman and Wise, 1991; Stark et al., 2007).

Kinematically, we demonstrated that arm kinematics were affected by grasping condition and hand kinematics were affected by reaching condition, so whereas we demonstrated that whole arm representations were present in both PMd and PMv, that was insufficient to argue against our null hypothesis that reach and grasp were processed in independent pathways. We used a novel dimensionality reduction technique to dissociate reaching from grasping and found that single neurons in PMd and PMv encoded both reaching and grasping kinematic synergies. Moreover, across the entire population of recorded cells, we found no relationship between anatomical and functional representations. That is, the anatomical preferences of a cell (i.e., whether it was biased toward arm or hand kinematics) were not related to its functional preferences (i.e., whether it preferred reach or grasp synergies).

Differences between PMd and PMv

In this work, we compared the encoding properties of neurons simultaneously recorded in the PMd and PMv of two rhesus macaques. By using this simultaneous recording paradigm, our results were not confounded by potential behavioral differences across sessions.

In both animals, we observed that movement kinematics were more strongly represented in PMd compared with PMv. One potential explanation for this finding is that PMd is seemingly more directly related to motor output. Pyramidal cells in layer V of PMd comprise ∼10% of fibers from the frontal lobe in the corticospinal tract (Dum and Strick, 1991) and ICMS of PMd is known to elicit arm movements (Weinrich and Wise, 1982; Weinrich et al., 1984). Consistent with this interpretation, we found that spiking activity in PMd was generally better predicted by anatomical features rather than functional kinematic synergies. PMv, too, sends projections to spinal cord, but it largely projects to the upper cervical spinal segments (He et al., 1993). Recent work using ICMS has shown that PMv acts on spinal cord primarily through facilitation of MI (Cerri et al., 2003; Shimazu et al., 2004).

In both animals, we observed that, although single cells in PMd encode whole arm kinematics, they exhibit a preferential encoding of arm kinematics. This is consistent with the classical studies of PMd implicating it in the control of reaching movements (Weinrich and Wise, 1982; Weinrich et al., 1984; Kurata and Tanji, 1986; Riehle and Requin, 1989; Pesaran et al., 2006).

In PMv, however, we observed no consistent bias for either arm or hand kinematics or grasp or reach kinematics even though some previous studies illustrated a causal influence of PMv lesion to a grasp deficit (Fogassi et al., 2001). In addition, in PMv, we found that spike history at multiple time scales was a better predictor of spiking activity than a single timescale. This suggests that PMv may be more influenced by several internal processes operating at different timescales and may also explain why kinematics were not strongly represented in PMv. An alternative possibility is that these types of unconstrained movements are not the most effective drivers of activity in PMv, but rather a different class of movement altogether may be represented (Wise, 2006; Lehmann and Scherberger, 2013; Bonini et al., 2014). It should be noted that the PMv arrays were placed on or close to the convexity of the inferior arm of arcuate sulcus. Therefore, we were not sampling from neurons in the sulcus, particularly F5p, and were likely recording from neurons in F4 as well as F5 divisions of PMv (Matelli et al., 1985).

Interanimal differences

We observed some differences in behavior between the two animals. Animal J had faster reaction times than animal L and generally executed faster movements that were qualitatively more stereotyped. Although the movements were executed at different speeds and with different reaction times, we observed many similarities in the dPCA analysis across the two animals, suggesting that the kinematic synergies that we identified were robust across a naturalistic range of self-selected movement speeds. In future work, it could be investigated whether the same set of dPCA synergies predicts movement kinematics at a variety of speeds by having an animal engage in a reach-to-grasp task with an explicit speed cue.

An additional difference in the kinematics between the two animals was their resting posture. In animal L, resting grasp aperture was proportionately much larger than in animal J. Indeed, the grasp aperture was maximal at the rest position for some trials in animal L. In contrast, animal J maintained a more closed aperture during the rest epoch. This finding may explain why the temporal profiles of the largest dPC in each animal are different. The temporal profile of the largest CI dPC in animal J was a bell-shaped curve, reflecting that the hand opened and closed during the reach-to-grasp movement. In contrast, the temporal profile of the largest CI dPC in animal L was a sigmoidal curve, corresponding to the fact that his hand started opened and gradually conformed to the shape of the object to be grasped. Finally, the animals adopted qualitatively different strategies to grasp the ring object successfully. Grasp aperture of the ring object in animal J followed a biphasic profile that was absent in animal L.

At the neural level, there were also several differences between the two animals. We observed that arm (compared with hand) kinematics were represented preferentially in PMv of animal J, but not animal L. One potential explanation for this finding is based on array placement. Although an attempt was made to place the arrays in approximately the same location in both animals, a large blood vessel constrained our placement of the PMv array in animal J. In both animals, we saw a preferential representation of the arm in PMd. However, animal J's PMv array was inserted much closer to its PMd array because of the aforementioned blood vessel compared with animal L. Accordingly, the arm representation in the PMv of J may be stronger because it is closer to PMd.

In summary, we used GLM framework to characterize encoding properties of single neurons in PMd and PMv with kinematic inputs that were computed using a novel dPCA technique to dissociate anatomical representations of arm and hand from functional representations of reach and grasp. We showed that kinematics were more prominently encoded in PMd responses compared with PMv. More importantly, there was no consistent preference for arm versus hand or for reach versus grasp kinematics in either PMd or PMv. By considering the encoding of kinematic trajectories, our findings extend but are consistent with the results in a previous study (Stark et al., 2007), which demonstrated that the encoding properties of PMd and PMv neurons often show mixing between reach and grasp, suggesting that these two cortical areas may serve functionally as a neural substrate for coordination between reach and grasp during prehension.