Thermodynamics of manganese oxides: Sodium, potassium, and calcium birnessite and cryptomelane

Significance

Manganese oxides with layer and tunnel structures occur widely in the natural environment and inspire technological applications. In addition to having variable compositions, these structures often are found as small particles (nanophases). This study explores, using experimental thermochemistry, the role of composition, oxidation state, structure, and surface energy in the thermodynamic stability of synthetic birnessites and cryptomelane. These quantitative thermodynamic findings help explain and support qualitative observations of phase-transformation patterns gathered over the past five decades.

Abstract

Manganese oxides with layer and tunnel structures occur widely in nature and inspire technological applications. Having variable compositions, these structures often are found as small particles (nanophases). This study explores, using experimental thermochemistry, the role of composition, oxidation state, structure, and surface energy in the their thermodynamic stability. The measured surface energies of cryptomelane, sodium birnessite, potassium birnessite and calcium birnessite are all significantly lower than those of binary manganese oxides (Mn₃O₄, Mn₂O₃, and MnO₂), consistent with added stabilization of the layer and tunnel structures at the nanoscale. Surface energies generally decrease with decreasing average manganese oxidation state. A stabilizing enthalpy contribution arises from increasing counter-cation content. The formation of cryptomelane from birnessite in contact with aqueous solution is favored by the removal of ions from the layered phase. At large surface area, surface-energy differences make cryptomelane formation thermodynamically less favorable than birnessite formation. In contrast, at small to moderate surface areas, bulk thermodynamics and the energetics of the aqueous phase drive cryptomelane formation from birnessite, perhaps aided by oxidation-state differences. Transformation among birnessite phases of increasing surface area favors compositions with lower surface energy. These quantitative thermodynamic findings explain and support qualitative observations of phase-transformation patterns gathered from natural and synthetic manganese oxides.

Complex manganese oxides, highly reactive fine-grained materials ubiquitous in nature, have served in a number of important capacities to benefit both the Earth and human society (1). These oxides have profoundly affected Earth’s critical zone throughout geologic time, influencing the evolution of the atmosphere and the bioinorganic chemistry of organisms. They are effective in accumulation and recovery of economic ores and have recently inspired development of novel catalysts for green chemistry and energy sustainability technologies. Minerals based on MnO₂ include multiple classes, two of which are well known to geochemists: the 2 × 2 tunnel structure hollandite (the potassium - bearing variety is cryptomelane) and the layered structure phyllomanganates (e.g., birnessite) (2, 3). Layered Mn oxides, such as the mineral birnessite, derived from MnO₂ by inclusion of cations and water, with concomitant decrease in manganese average oxidation state (Mn AOS) from 4 to typical values between 3.5 and 3.9, with manganese in tetravalent, trivalent and sometimes divalent oxidation states, are among the most important Mn oxides in nature (4). These “nanosheet” Mn oxides readily transform among phases, influencing crucial environmental and technological processes, including biogeochemical cycles (1, 4, 5) water oxidation catalysis (6–8) and radionuclide confinement (9, 10). A recent thermochemical study of layered calcium manganese oxides (6) relevant to water oxidation catalysis (7, 8) suggests that low surface energy and energetically accessible changes in oxidation state are important for stabilizing these minerals and enhancing their functionality.

There have been a number of qualitative observations of poorly understood phenomena concerning phase formation and/or transformation among birnessite and cryptomelane. (i) All natural and synthetic birnessite and cryptomelane phases appear to have small particle size, less than 100 nm and often much smaller, at their initial formation. However, on the geologic time scale, these natural minerals are able to grow in size (coarsen) to form particles of larger dimensions, particularly within the layers. Such growth often involves complex chemical reactions with changes in cation content, hydration, and oxidation state. (ii) Mixed sodium–potassium birnessite often forms in synthesis from aqueous solution, even when one is trying to make the ion-exchanged potassium form. (iii) Synthesis of calcium birnessite most successfully begins with sodium birnessite as the starting phase followed by exchange of calcium for sodium under aqueous conditions. (iv) Cryptomelane exists initially only within a limited size range, with surface area ∼50–350 m²/g (2, 11), when synthesized in the laboratory under ambient conditions. Again, given enough time and thermodynamic driving forces, macroscale size may be achieved, especially in natural materials. (v) The synthesis of cryptomelane in an aqueous medium appears to begin with potassium birnessite formation and then requires leaching of potassium from the birnessite layers before spontaneous formation of the tunnel structure (11).

In addition to kinetic controls on reaction rates, these observations must have fundamental thermodynamic underpinning, and yet the thermodynamic properties of these phases as a function of composition and particle size are poorly known. Some calorimetric studies of enthalpies of formation of layer and tunnel manganese oxides have been reported (12), although their compositions in terms of AOS of manganese, and therefore oxygen content, were not measured and their particle sizes and surface areas were not characterized. These factors have recently been shown to be important in the thermodynamics of binary oxides in the Mn–O system (13) and probably play an equal or more important role in the complex layer and tunnel materials.

The present work concentrates on measurements of enthalpies of formation and surface energies of synthetic birnessite and cryptomelane phases to explain these frequently observed phase formation and transformation phenomena on the basis that they are thermodynamically driven. Because the initially formed materials are fine grained, indeed nanophase, surface energies play a large role in selective stabilization of different phases and are emphasized in this study.

Results

Table 1 summarizes the synthesis parameters of the samples. Table 2 summarizes the sample compositions, the manganese Mn AOS, and the surface areas. For each of the suites of nanophase samples, the compositions were controlled remarkably well, with cation content and Mn AOS virtually constant. The actual values of these two parameters reflected the synthesis conditions and could neither be predicted beforehand nor easily explained afterward. It is interesting that similar aqueous synthesis parameters (except for the type of cation present) at constant ionic strength produced similar cation content within the sodium and calcium birnessite sample suites, but exactly twice the cation content was taken up by potassium birnessites. The reasons for this effect are unclear. Of further note is that the AOS in the birnessites is always significantly lower (more reduction of Mn⁴⁺ to Mn³⁺ or possibly Mn²⁺) than simply required for charge balancing the alkali or alkaline earth ions. This observation implies the presence of other charge balance mechanisms, such as the incorporation of protons under the acidic conditions of synthesis. The observation also implies close coupling between the solution ion content, the solution acidity, and the oxygen fugacity to determine composition and thermodynamic properties of the solid materials formed. Thus, the present study covers only a small range of possible conditions and compositions.

Table 1.

Synthesis conditions for the samples

Reagent, (i)	[Ci]/M	di	z2	(z2) × (c)	γ, Debye–Hückel	Davies activity coefficient
Birnessite synthesis*
H+; HCl	1.0 × e−2	0.9	1	0.01	0.717	1.421
Cl−; HCl	1.0 × e−2	0.3	1	0.01	0.470	1.421
Na+; NaCl	3.015	0.4	1	3.015	0.536	1.421
K+; KCl	3.015	0.3	1	3.015	0.470	1.421
Cl−; KCl	3.015	0.3	1	3.015	0.470	1.421
Na+; NaMnO4	0.125	0.4	1	0.125	0.536	1.421
K+; KMnO4	0.125	0.3	1	0.125	0.470	1.421
MnO4−	0.125	0.35	1	0.125	0.505	1.421
Cryptomelane synthesis†
H+; H2SO4	1.0	0.9	1	1	0.707	3.105
HSO4−; H2SO4	1.0	0.4	4	4	0.067	3.105
K+; KCl	3.0	0.3	1	3	0.435	92.933
Cl−; KCl	3.0	0.3	1	3	0.435	3.105
K+; KMnO4	0.125	0.3	1	0.13	0.435	3.105
MnO4−; KMnO4	0.125	0.35	1	0.13	0.475	3.105

Reagent parameters to calculate total ionic strength include: concentration [C_i] in mol/L of the reagent ions (i) with size parameter (d_i) and ionic charge (z). Debye–Hückel activity coefficient (γ) is computed from the Debye–Hückel equation, and the Davies activity coefficient is computed from Davies equation.

^*Final ionic strength: 1/2 Σz2c = 3.150.

^†Final ionic strength: 1/2 Σz2c = 5.625.

Table 2.

Composition, surface area, Mn AOS, wt% water loss, drop solution enthalpy, water-corrected drop solution enthalpy, formation enthalpy from the oxides (without and with oxidation reaction, and from the elements), and standard entropy for the nanophase samples

Composition*	BET surface area,† m2/g (m2/mol)	Mn AOS	TGA weight loss,‡ [wt %]	ΔHds,§ kJ/mol	ΔHds,corr,¶ kJ/mol	ΔH°f-ox,# kJ/mol	ΔH°f-ox*,|| kJ/mol	ΔH°f,** kJ/mol	S°298,†† J/mol⋅K
Na0.09MnO1.815·0.64H2O	94.64 ± 0.69 (9,295.45)	3.54 ± 0.01	12.52	193.91 ± 2.01 (10)	149.68 ± 2.65	−56.01 ± 2.11	−79.08 ± 3.82	−703.29	102.82 ± 0.09
Na0.08MnO1.82·0.42H2O	58.72 ± 0.18 (5,526.83)	3.56 ± 0.01	8.59	179.79 ± 1.85 (8)	150.71 ± 2.51	−55.09 ± 1.96	−78.92 ± 3.64	−639.19	86.97 ± 0.08
Na0.08MnO1.825·0.54H2O	28.30 ± 0.20 (2,726.47)	3.57 ± 0.01	10.81	191.65 ± 1.66 (8)	154.53 ± 2.21	−58.19 ± 1.78	−82.66 ± 3.34	−673.10	95.33 ± 0.09
Na0.09MnO1.82·0.47H2O	18.52 ± 0.16 (1,768.78)	3.55 ± 0.01	9.69	187.09 ± 1.35 (8)	154.35 ± 1.13	−60.45 ± 1.49	−83.69 ± 2.40	−656.17	90.88 ± 0.08
K0.21MnO1.87·0.49H2O	34.63 ± 0.44 (3,595.24)	3.53 ± 0.01	11.35	154.25 ± 1.93 (10)	120.47 ± 2.73	−51.23 ± 2.05	−74.40 ± 3.88	−679.98	98.86 ± 0.08
K0.21MnO1.90·0.47H2O	28.74 ± 0.21 (2,991.87)	3.59 ± 0.01	11.55	154.06 ± 1.90 (8)	121.29 ± 2.69	−49.57 ± 2.03	−75.27 ± 3.84	−678.34	97.21 ± 0.08
K0.21MnO1.85·0.23H2O	18.50 ± 0.17 (1,823.77)	3.49 ± 0.01	6.25	137.18 ± 1.88 (8)	121.33 ± 2.66	−54.00 ± 1.99	−74.95 ± 3.81	−603.22	80.82 ± 0.07
K0.20MnO1.84·0.13H2O	15.41 ± 0.10 (1,493.37)	3.48 ± 0.01	4.42	130.86 ± 1.39 (8)	121.91 ± 1.97	−53.46 ± 1.53	−76.23 ± 3.11	−574.89	73.39 ± 0.07
Ca0.12MnO1.825·0.81H2O	97.76 ± 0.87 (10,383.96)	3.53 ± 0.01	15.62	181.29 ± 1.88 (10)	125.71 ± 2.66	−33.63 ± 1.99	−55.44 ± 3.81	−817.68	115.95 ± 0.11
Ca0.11MnO1.79·0.73H2O	55.42 ± 0.51 (5,653.72)	3.47 ± 0.01	11.92	177.40 ± 1.73 (8)	127.04 ± 2.45	−37.21 ± 1.83	−57.08 ± 3.58	−777.27	110.21 ± 0.11
Ca0.12MnO1.82·0.66H2O	34.63 ± 0.44 (3,552.24)	3.52 ± 0.01	12.10	174.49 ± 1.29 (8)	128.80 ± 1.83	−37.66 ± 1.44	−58.86 ± 2.98	−770.26	105.49 ± 0.10
Ca0.12MnO1.80·0.67H2O	18.50 ± 0.17 (1,877.27)	3.48 ± 0.01	11.10	175.30 ± 1.19 (8)	128.88 ± 1.69	−39.68 ± 1.33	−59.49 ± 2.85	−765.85	106.35 ± 0.10
K0.10MnO1.885·0.43H2O	234.02 ± 0.77(22,852.59)	3.67 ± 0.01	11.88	124.58 ± 1.88 (10)	94.77 ± 2.66	−1.56 ± 2.02	−29.78 ± 3.81	−648.54	88.91 ± 0.07
K0.11MnO1.955·0.41H2O	150.63 ± 0.16 (14,842.18)	3.80 ± 0.01	12.59	132.71 ± 1.75 (8)	104.38 ± 2.48	−6.49 ± 1.94	−39.39 ± 3.61	−648.44	87.45 ± 0.07
K0.11MnO1.96·0.36H2O	128.05 ± 0.14 (12,503.15)	3.81 ± 0.01	11.69	129.34 ± 1.17 (8)	104.68 ± 1.66	−6.09 ± 1.45	−39.69 ± 2.83	−633.54	83.90 ± 0.07
K0.10MnO1.965·0.28H2O	58.00 ± 0.25 (5,581.71)	3.83 ± 0.01	10.38	128.04 ± 1.01 (8)	109.02 ± 1.44	−7.77 ± 1.34	−43.50 ± 2.64	−610.76	77.75 ± 0.07

^*Sample compositions are normalized to 1 mol of Mn.

^†BET surface areas are from the average of two runs.

^‡TGA total weight loss at 973 K and O₂ corrected to obtain water content. The final oxidation state for the Mn oxides is Mn³⁺ in sodium molybdate at 973 K.

^§ΔH_ds is measured drop solution enthalpy in which the error is 2 SDs of the mean and the values in parentheses are the mean number of experiments.

^¶ΔH_ds,corr is drop solution enthalpy corrected for water content.

^#Formation enthalpy from the oxides (ΔH^o_f-ox), computed as mA^c+O, Mn₂O₃, H₂O, and MnO₂, is without redox enthalpy contributions.

^||ΔH^o_f-ox* (as mA^c+O, Mn₂O₃, H₂O, and O₂) includes the exothermic oxidation enthalpy.

^**Standard formation enthalpies from the elements (∆H^o_f) were computed from standard formation enthalpies of simple binary oxides (Mn₂O₃ = −959.0 ± 1.0 kJ/mol and MnO₂ = −520.0 ± 0.7 kJ/mol) (13), and the propagated error is ±2.22 kJ/mol. Auxiliary drop solution enthalpy data, ΔH_ds, used to compute formation enthalpies of the complex Mn oxides, includes ΔH_dsNa₂O = −207.56 ± 4.25 kJ/mol, ΔH_dsK₂O = −318.0 ± 3.1 kJ/mol, and ΔH_dsCa₂O = −90.3 ± 1.8 kJ/mol from (29); ΔH_dsMn₂O₃ = 154.87 ± 1.00 kJ/mol and ΔH_dsMnO₂ = 124.92 ± 1.03 kJ/mol from ref. 13. The heat content of molecular oxygen is 21.84 kJ/mol (29) and of water (starting with liquid) is 69.0 ± 0.1 kJ/mol (29). Standard formation enthalpy (∆H°_f) and standard entropy (S°₂₉₈) of liquid water is −285.8 ± 0.1 kJ/mol and 70.0 ± 0.1 J/mol⋅K (29).

^††Standard entropy (S°₂₉₈) of molecular oxygen is 205.15 ± 0.01 J/mol⋅K (29). The standard entropy and enthalpy of hydrogen ion in water, S°_(aq,298) = 0 J/mol⋅K (29).

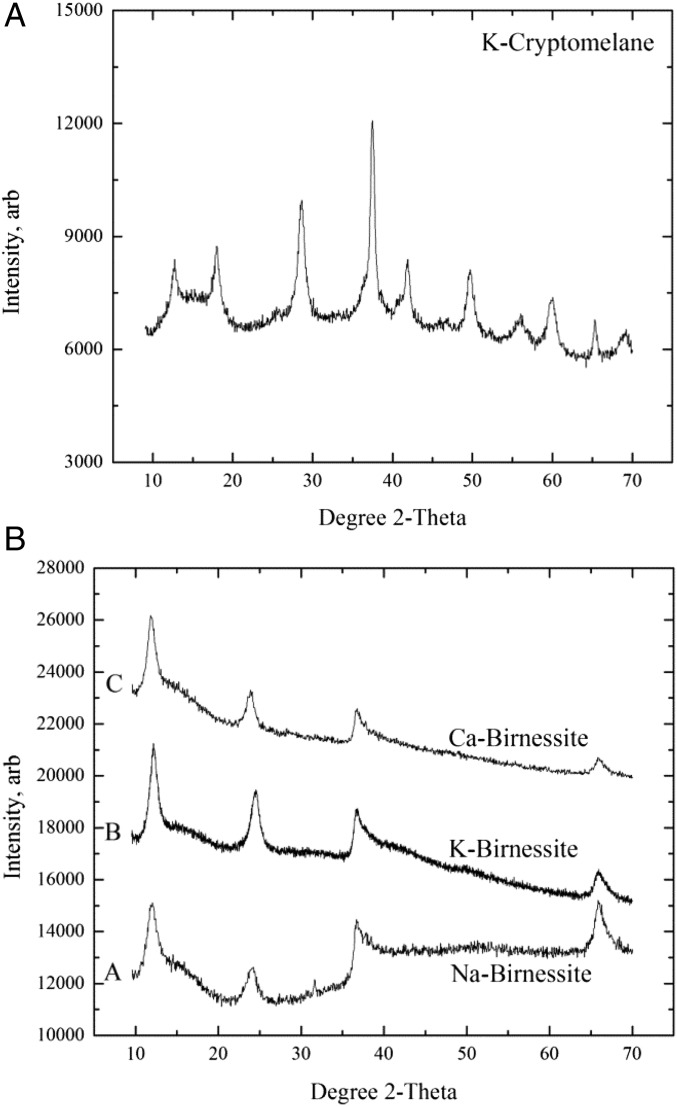
X-ray diffraction (XRD) patterns of cryptomelane samples (Fig. 1A) are consistent with previous reports for the potassium-bearing 2 × 2 tunnel structure hollandite (14, 15). XRD patterns of birnessite samples (Fig. 1B), similar to hexagonal acid birnessite, demonstrate common features of birnessite with a lack of long-range order between layers, peaks tailing toward higher angle two-theta, and asymmetric profiles (3, 16, 17). Because crystallography was not the focus of the present work, a further detailed structural study was not pursued.

Fig. 1.

XRD powder patterns of the tunnel structure phase, cryptomelane (K-cryptomelane) (A), and the birnessites (B), which are labeled as follows: A, sodium birnessite (Na-Birnessite); B, potassium birnessite (K-Birnessite); and C, calcium birnessite (Ca-Birnessite). The birnessite powder patterns are y-offset to improve readability. arb, arbitrary units.

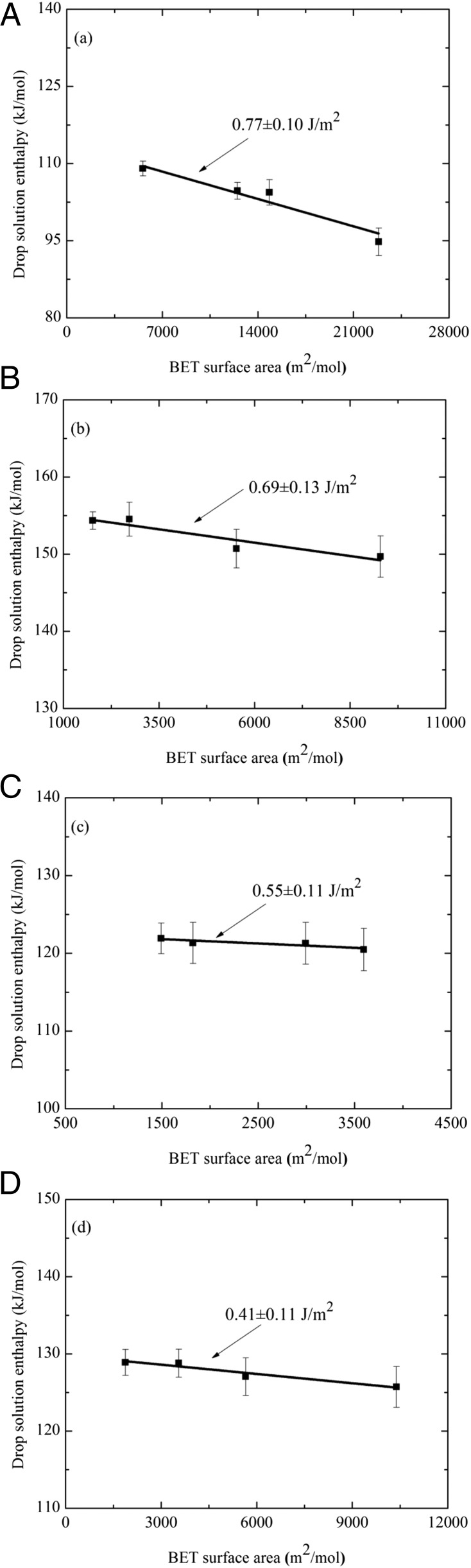
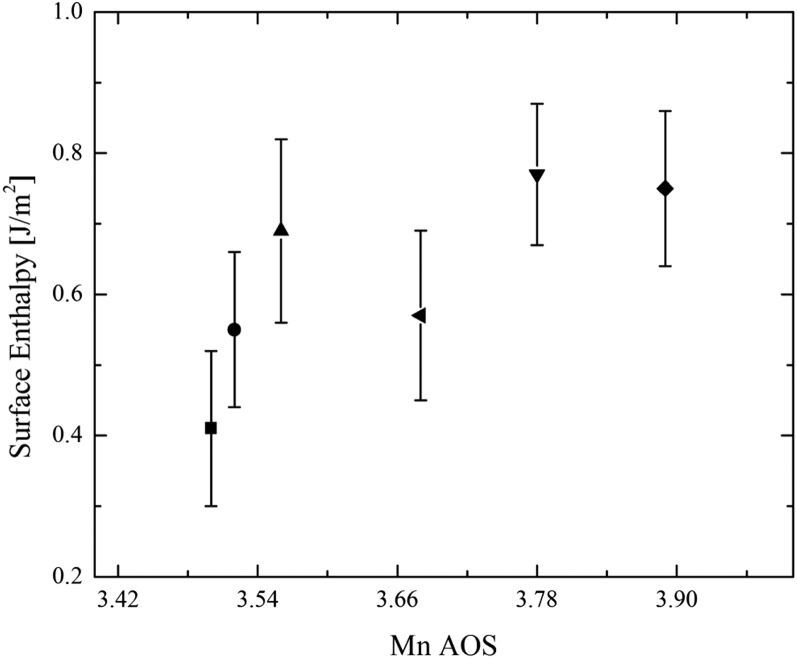
The measured enthalpy associated with dropping a sample from room temperature into molten oxide solvent at high temperature, where it dissolves, is called the enthalpy of drop solution, ΔH_ds. The difference between ΔH_ds of reactants and products (of the same composition) gives the enthalpy of reaction. Thus, the enthalpy associated with an increase in surface area can be obtained by comparing ΔH_ds for samples of different surface areas. Additionally, because the nanophase samples have different water contents, ΔH_ds is corrected to account for their surface-associated water, yielding a corrected drop solution enthalpy, ΔH_ds,corr. The correction subtracts the heat content of n moles of bulk H₂O (considered as physisorbed water) from the observed enthalpy of drop solution. Values of the directly measured enthalpy of drop solution, ΔH_ds, and the drop solution enthalpy values corrected for water content, ΔH_ds,corr, are listed in Table 2. As discussed previously (18–25), the slope of the line relating the water-corrected drop solution enthalpy, ΔH_ds,corr, (Table 2) and nanophase surface area (Table 2) yields the surface enthalpy (SE) (Table 3), which is essentially equivalent to surface energy (26, 27) for the hydrous surface (Fig. 2 A–D). Birnessite and cryptomelane have substantially lower SE (Fig. 2 A–D) than the binary Mn oxide phases previously studied (13), hausmannite, (Mn₃O₄, SE = 0.96 ± 0.08 J/m²), bixbyite (Mn₂O₃; SE = 1.29 ± 0.10 J/m2), and pyrolusite (MnO₂; SE = 1.64 ± 0.10 J/m2). The low SE values suggest that water is not strongly bound to the surfaces, interlayers, or tunnels, because water-adsorption enthalpy scales with the SE for many oxides (18–25, 28). There appears to be a small decrease in SE with decreasing Mn AOS (Fig. 3), that is, with an increase in mixed valence manganese (Mn^3+/4+).

Table 3.

Mean nanophase composition and corresponding proton balanced composition, mean Mn AOS for the sample suite, and surface enthalpy

Phases	Average composition	Average composition with proton balance	Mean Mn AOS	SE(hyd), J/m2*
CR2	K0.11·MnO1.94·0.37H2O	K0.11H0.12MnO2·0.37H2O	3.78 ± 0.01	0.77 ± 0.10
NaBi	Na0.09·MnO1.82·0.52H2O	Na0.09·H0.36MnO2·0.52H2O	3.56 ± 0.01	0.69 ± 0.13
KBi	K0.21·MnO1.87·0.33H2O	K0.21H0.27MnO2·0.33H2O	3.52 ± 0.01	0.55 ± 0.11
CaBi	Ca0.12·MnO1.81·0.72H2O	Ca0.12H0.38MnO2·0.72H2O	3.50 ± 0.01	0.41 ± 0.11
CaMnO†	Ca0.39MnO2.34·0.42H2O†	Ca0.05MnO2·0.42H2O†	3.89 ± 0.01	0.75 ± 0.11
CaMnO†	Ca0.43MnO2.27·0.31H2O†	Ca0.16MnO2·0.31H2O†	3.68 ± 0.01	0.57 ± 0.12

Cryptomelane: CR2, NaBi, KBi, and CaBi (Bi, birnessite) are from the present work.

^*Surface enthalpies are for the hydrous surfaces [SE(hyd)].

^†Samples of Ca–Mn–oxide nanosheets (6).

Fig. 2.

Water-corrected drop solution enthalpies versus molar surface area. Surface enthalpy of the hydrous surface is 0.77 ± 0.10 J/m² for cryptomelane (A), 0.69 ± 0.13 J/m² for sodium birnessite (B), 0.55 ± 0.11 J/m² for potassium birnessite (C), and 0.41 ± 0.11 J/m² for calcium birnessite (D).

Fig. 3.

Surface enthalpy (hydrous surface) versus Mn AOS. Values for sodium birnessite (Na_0.09·MnO_1.82·0.52H₂O) (■), potassium birnessite (K_0.21·MnO_1.87·0.33H₂O) (●), calcium birnessite (Ca_0.12·MnO_1.81·0.72H₂O) (▲), and cryptomelane (K_0.11·MnO_1.94·0.37H₂O) (◄) are from the present work. Samples of Ca–Mn–oxide nanosheets [Ca_0.39MnO_2.34·0.42H₂O (▼)] and [Ca_0.43MnO_2.27·0.31H₂O (♦)] are from N.B. et al. (6).

Enthalpies of formation (Table 2) were computed using thermochemical cycles and auxiliary data. For the nanophase complex Mn oxides, enthalpy of formation from the oxides can be calculated in two ways. The first (∆H^o_f-ox*) includes the enthalpy contribution from redox effects taking mA^c+O, Mn₂O₃, H₂O, and O₂ as reactants. This formation reaction is Eq. 1:

$$\begin{array}{l}{\left[{\text{mA}}^{\text{c}+}\text{O}+\left(0.5\right){\text{Mn}}_2{\text{O}}_3\right]}_{\left(\text{s},25°\text{C}\right)}+\left(0.25\right)\text{y}{\left({\text{O}}_2\right)}_{\left(\text{g},25°\text{C}\right)}+{\text{nH}}_2{\text{O}}_{\left(\mathrm{1,25}°\text{C}\right)}\\ ={\left[{\text{mA}}^{\text{c}+}\text{O}\mathrm{\cdot }\left(0.5\right){\text{Mn}}_2{\text{O}}_3\mathrm{\cdot }\left(0.25\right){\text{yO}}_2\mathrm{\cdot }{\text{nH}}_2\text{O}\right]}_{\left(\text{s},25°\text{C}\right)}.\end{array}$$ [1]

Coefficient “m,” defined as m = c⁺/2, where the cation charge, c⁺, accounts for moles of cation as well as the number of oxygen atoms entering into the reaction. Coefficient “n” corresponds to moles of water, and “y” corresponds to moles of molecular oxygen incorporating into the solid phase as a result of oxidation. The second method of calculation eliminates the redox effects (∆H^o_f-ox) by taking a mixture of Mn₂O₃ and MnO₂ (and no O₂) as reactants (e.g., mA^c+O, Mn₂O₃, MnO₂, and H₂O). This formation reaction is Eq. 2:

$$\begin{array}{l}{\left[{\text{mA}}^{\text{c}+}\text{O}+\left(0.5\right)\left(1-\text{y}\right){\text{Mn}}_2{\text{O}}_3+{\text{yMnO}}_2\right]}_{\left(\text{s},25°\text{C}\right)}+{\text{nH}}_2{\text{O}}_{\left(\mathrm{1,25}°\text{C}\right)}\\ ={\left[{\text{mA}}^{\text{c}+}\text{O}\mathrm{\cdot }\left(0.5\right)\left(1-\text{y}\right){\text{Mn}}_2{\text{O}}_3\mathrm{\cdot }{\text{yMnO}}_2·{\text{nH}}_2\text{O}\right]}_{\left(\text{s},25°\text{C}\right)}.\end{array}$$ [2]

Here, the coefficient y, normalized to one mole of manganese, accounts for the Mn(III) and Mn(IV) stoichiometry reflected in the Mn oxidation state speciation in the samples (e.g., coefficients, “1-y” and y). The enthalpies of formation from the oxides, ΔH_f-ox* and ΔH_f-ox, are strongly exothermic, which reflects the nature of strongly basic alkali and alkaline earth metal oxides combining with relatively acidic manganese (III,IV) oxide species. ΔH°_f-ox is less exothermic than ΔH°_f-ox* because the latter contains an intrinsically exothermic contribution from oxidation of Mn³⁺ to Mn⁴⁺.

Some birnessites also may contain divalent manganese (Mn²⁺). Because the AOS is between 3 and 4 in all of our samples, from a thermodynamic point of view, all reactions can be balanced using only Mn³⁺ and Mn⁴⁺ phases as written above. Although mass and charge balance are essential for proper thermodynamic analysis, further details of speciation and site occupancy are not necessary because a thermodynamic description can be fully defined in terms of the bulk composition of the system and intensive parameters such as temperature, pressure, and oxygen fugacity. Similarly, although knowing the exact water content is crucial for mass balance, its speciation (molecular H₂O, H⁺, and OH⁻) and location need not be considered for the present thermodynamic analysis. Thus, the solid phase is completely defined by four thermodynamic components thermodynamic components, which can be taken as alkali/alkaline earth oxide, Mn₂O₃, MnO₂, and H₂O or alkali/alkaline earth oxide, Mn₂O₃, O₂, and H₂O, although the number of distinct species present can be much greater.

Standard formation enthalpies from the elements (ΔH°_f) (Table 2) were calculated from values of formation enthalpy from the oxides by adding the standard formation enthalpies of binary (simple) oxides and water (29) in the appropriate reaction stoichiometry for each of the nanophase samples.

For a given cation, an increase in the cation content (with concomitant decrease in AOS) has a thermodynamically stabilizing influence on the enthalpy of formation. This influence is seen most clearly for the potassium birnessites, where the values of ΔH°_f-ox in kilojoules per formula containing 1 mol of manganese are −36.7 for x = 0.125 (12), −52.3 for x = 0.21 (this work), and −60.6 for x = 0.29 (12). The bulk sodium birnessite with x = 0.09 has more negative ΔH°_f-ox* and ΔH°_f-ox than the bulk potassium birnessite with x = 0.21 (Table 4). Both alkali birnessites are more energetically stable than the calcium birnessite with x = 0.12 (Table 4). The thermodynamic effect of the cation contribution is relatively small, as seen in relatively similar values of ΔH°_f-ox, where oxidation is not involved. In contrast, the ΔH°_f-ox* values are much more exothermic and vary somewhat more strongly with cation type and content, which reflects the contribution of the oxidation enthalpy. Thus, in considering formation and transformation reactions in both geological and technological settings, the redox energetics can easily compete with the energetic contribution made by the cations. Having more thermodynamically favorable standard formation enthalpies (Table 2), enthalpies of formation from the oxides (Table 2), and lower SE (Table 3), the birnessites (layer structure) are more stable relative to binary oxides than the cryptomelane (tunnel structure). Fritsch et al. (12) also observed that birnessites are more thermodynamically stable than tunnel structure Mn oxides.

Table 4.

Extrapolated drop solution enthalpies of bulk (zero surface area) materials, their enthalpies of formation from oxides and elements, their estimated standard entropies and estimated entropies of formation, and Gibbs free energies of formation from elements at 298 K

Phases	Average composition of the Phase	ΔHds,corr,bulk,* kJ/mol	ΔH°f-ox*, ΔH(with redox),† kJ/mol	ΔH°f-ox, ΔH(without redox),‡ (kJ/mol)	∆H°f(bulk),§ (kJ/mol)	So298 (standard entropy),¶ J/mol⋅K	ΔG°f(bulk),# kJ/mol
CR2	K0.11·MnO1.94	113.75 ± 3.00	−43.70 ± 3.16	−15.18 ± 3.42	−529.24 ± 0.94	58.32 ± 0.21	−540.31 ± 0.63
NaBi	Na0.09·MnO1.82	155.64 ± 3.47	−82.47 ± 3.67	−61.99 ± 4.49	−522.92 ± 0.71	64.13 ± 0.12	−556.00 ± 0.77
KBi	K0.21·MnO1.87	122.65 ± 3.58	−71.34 ± 3.78	−52.32 ± 3.42	−536.86 ± 1.14	58.28 ± 0.17	−580.64 ± 0.68
CaBi	Ca0.12·MnO1.81	129.80 ± 3.10	−58.22 ± 3.21	−33.86 ± 2.30	−563.26 ± 0.76	58.36 ± 0.11	−546.65 ± 0.80

Cryptomelane: CR2, NaBi, KBi, and CaBi (Bi, birnessite). *Extrapolated drop solution enthalpy for bulk scale samples (no surface hydration and x = 0 surface area). Estimated standard enthalpy of formation for bulk phases were computed from both oxides, including ^†redox enthalpy (ΔH°_f-ox*) and ^‡without redox energetics (ΔH°_f-ox), as well as from the ^§elements [∆H°_f(bulk)]. Estimated ^¶S^o₂₉₈ (standard entropy) for bulk phases. ^#Estimated bulk-scale reaction Gibbs free energy of formation was computed as G°_f(bulk) = ΔH°_f(bulk) – TΔS°₂₉₈ using the estimated standard entropies (S°₂₉₈).

The standard entropies (S°₂₉₈) of the complex manganese oxides are not generally available. As discussed previously (30), it is reasonable to approximate them as the weighted sum of standard entropies of binary oxides. Then the entropy change (ΔS°_f-ox) associated with a reaction involving only solid phases, such as the formation of the complex oxide from simple oxides without oxidation involved, can be approximated to be zero. This approximation enables an estimate of the standard entropy (S°₂₉₈) and the entropy and free energy of formation from the elements (ΔS°₂₉₈ and ΔG°₂₉₈) of the birnessites and cryptomelane (Table 2).

Transformation energetics at 298 K for reactions involving nanophases and bulk phases are presented in Table 5. For the phase-transformation reactions, the enthalpy terms, ΔH°_rxn-pt, are the dominant thermodynamic driving force with the TΔS°₂₉₈ terms contributing generally 10% or less to the reactions. Standard enthalpies, entropies, and free energies for nanophase and bulk transformations involving only solid oxides (i.e., without consideration of reactions from the aqueous phase) were computed using ΔH°_f-ox,pt, ΔS°_298(ox), and ΔG°_f-ox,pt, whereas transformations including aqueous components (e.g., ion-exchange reactions) were computed using ΔH°_f,pt, ΔS°_298(aq), and ΔG°_f,pt. These thermochemical data are discussed further below and provide explanations of the observations noted in the introduction.

Table 5.

Transformation thermodynamics at bulk and nanoscale at 298 K

Reactions	Surface area, m2/g (m2/mol)	ΔH°f-ox,nano-pt, kJ/mol	ΔS°298(ox), J/mol⋅K	ΔG°f-ox,nano-pt, kJ/mol	∆H°f-ox,bulk-pt, kJ/mol	∆G°f-ox,bulk-pt, kJ/mol
Phase-transformation (-pt) reactions
Na0.09·MnO1.815·0.64H2O = Ca0.12·MnO1.825·0.81H2O	95 (10,000)	−22.14 ± 2.96	6.72 ± 0.23	−20.14 ± 2.96	−21.86 ± 2.97	−23.86 ± 2.97
K0.21·MnO1.87·0.49H2O = Ca0.12·MnO1.82·0.66H2O	35 (3,600)	−13.33 ± 2.51	6.71 ± 0.22	−15.33 ± 2.51	−13.19 ± 2.52	−15.19 ± 2.52
Na0.08·MnO1.825·0.54H2O = K0.21·MnO1.90·0.47H2O	28 (3,000)	−7.78 ± 2.85	−1.12 ± 0.22	−7.45 ± 2.85	−7.36 ± 2.86	−7.03 ± 2.86
K0.21·MnO1.90·0.47H2O = K0.10·MnO1.965·0.28H2O	29 (3,000)	−31.71 ± 2.27	−13.29 ± 0.14	−27.75 ± 2.27	−32.37 ± 2.27	−28.41 ± 2.27
Nanophase transformation (nano,pt), charge-compensated formulas
Na0.09·H0.37MnO2·0.455H2O = Ca0.12H0.35MnO2·0.635H2O	95 (10,000)	−64.94 ± 3.17	32.73 ± 0.71	−74.69 ± 3.18	−64.66 ± 3.18	−74.41 ± 3.18
K0.21H0.26MnO2·0.36H2O = Ca0.12H0.36MnO2·0.48H2O	35 (3,600)	−25.21 ± 3.16	34.58 ± 0.21	−14.90 ± 3.16	−35.52 ± 3.17	−35.38 ± 3.17
Na0.08·H0.35MnO2·0.365H2O = K0.21H0.20MnO2·0.37H2O	28 (3,000)	−3.98 ± 3.14	−14.78 ± 0.20	0.43 ± 3.14	−3.56 ± 3.15	0.85 ± 3.15
K0.21H0.20MnO2·0.37H2O = K0.10H0.07MnO2·0.245H2O	29 (3,000)	−30.18 ± 3.14	−15.82 ± 0.15	−25.46 ± 3.14	−30.84 ± 3.16	−26.12 ± 3.16

Standard enthalpies, entropies, and free energies for nanophase and bulk transformations involving solid oxides are ∆H°_f-ox,pt, ΔS°_298(ox), and ∆G°_f-ox,pt, whereas those involving aqueous ion-exchange reactions are ∆H°_f,pt, ΔS°_298(aq), and ∆G°_f,pt.

Discussion

As observed for other layered Mn oxides (6), the very low SE values are not dramatically different between birnessite type phases, but these differences are enough to influence the overall phase-transformation energetics as the surface area dramatically increases or decreases. All synthetic birnessite and cryptomelane phases and natural forms that are present in reactive environments (e.g., soils and sediments) have small particle sizes (are not single crystals and may often be considered assemblages of nanoparticles). This finding is reflected in the current study in these oxides’ synthesis by precipitation in an aqueous environment near room temperature and by their rather small surface energies, which provide little thermodynamic driving force for coarsening. This result indicates that additional thermodynamic perturbations are needed for coarsening (crystal growth) to occur and that kinetics also plays a role in their growth. To be clear, however, initial formations and transformations of these phases are thermodynamically controlled and occur among phases of small particle size according to this study. Although the thermochemical data do not permit complete calculations of equilibria involving different cation content, Mn AOS, and particle size, a few illustrative examples using the current data are useful.

Synthesis of pure phase calcium birnessite (CaBi) successfully begins with sodium birnessite (NaBi) as the starting phase and then exchanging calcium for sodium by shaking (or stirring) NaBi in a concentrated solution of aqueous CaCl₂ (this work and refs. 14 and 31). This method reflects the lower stability of the calcium form, which may hinder its initial formation relative to other phases, but, once the structure forms, ion exchange is possible.

$$\begin{array}{l}\text{NaBi}=\text{CaBi}\left(\text{solid oxides}\right):{\text{Na}}_{0.09}\mathrm{\cdot }{\text{MnO}}_{1.815}\mathrm{\cdot }0.64{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.12\hspace{0.17em}{\text{CaO}}_{\left(\text{s}\right)}+0.17\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}=\\ {\text{Ca}}_{0.12}\mathrm{\cdot }{\text{MnO}}_{1.825}\mathrm{\cdot }0.81{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+\left(0.5\right)0.09\hspace{0.17em}{\text{Na}}_2{\text{O}}_{\left(\text{s}\right)}+0.0325\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}\end{array}$$

$$\begin{array}{l}\text{NaBi}=\text{CaBi}\left(\text{aqueous}\hspace{0.17em}\text{ion}\hspace{0.17em}\text{exchange}\right):{\text{Na}}_{0.09}\mathrm{\cdot }{\text{H}}_{0.37}{\text{MnO}}_2\mathrm{\cdot }0.455{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.12\hspace{0.17em}{\text{Ca}}_{\left(\text{aq}\right)}^{2+}+0.245\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}\\ ={\text{Ca}}_{0.12}{\text{H}}_{0.35}{\text{MnO}}_2\mathrm{\cdot }0.635{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.09\hspace{0.17em}{\text{Na}}_{\left(\text{aq}\right)}^{+}+0.15\hspace{0.17em}{\text{H}}_{\left(\text{aq}\right)}^{+}+0.065\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}.\end{array}$$

Because the cation content and Mn AOS both vary, it is premature to attempt a quantitative calculation that separates the energetics of ion exchange and oxidation-state change. As shown in Table 5, transformation from Na and K birnessite phases to Ca birnessite is favorable (much more so from Na birnessite than K birnessite) for both solid state (oxides only) and aqueous (ion-exchange) reactions, with the latter generally being more favorable. This result explains why one can use Na birnessite as the starting material for Ca birnessite.

$$\begin{array}{l}\text{KBi}=\text{CaBi}\left(\text{solid oxides}\right):{\text{K}}_{0.21}{\text{MnO}}_{1.87}\mathrm{\cdot }0.49{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.12\hspace{0.17em}{\text{CaO}}_{\left(\text{s}\right)}+0.17\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}=\\ {\text{Ca}}_{0.12}{\text{MnO}}_{1.82}\mathrm{\cdot }0.66{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+\left(0.5\right)0.21\hspace{0.17em}{\text{K}}_2{\text{O}}_{\left(\text{s}\right)}+0.0325\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}\end{array}$$

$$\begin{array}{l}\text{KBi}=\text{CaBi}\left(\text{aqueous}\hspace{0.17em}\text{ion}\hspace{0.17em}\text{exchange}\right):{\text{K}}_{0.21}{\text{H}}_{0.26}{\text{MnO}}_2\mathrm{\cdot }0.36{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.12\hspace{0.17em}{\text{Ca}}_{\left(\text{aq}\right)}^{+2}+0.185\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}=\\ {\text{Ca}}_{0.12}{\text{H}}_{0.36}{\text{MnO}}_2\mathrm{\cdot }0.48{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.21\hspace{0.17em}{\text{K}}_{\left(\text{aq}\right)}^{+}+0.03\hspace{0.17em}{\text{H}}_{\left(\text{aq}\right)}^{+}+0.065\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}.\end{array}$$

In contrast, the transformation between Na birnessite and K birnessite has less thermodynamic drive (nearly zero free energy change within the propagated error), as shown in Table 5. This result may account for the observed mixed Na- and K-birnessite solid solution phases when both of these cations are present in a birnessite synthesis in the laboratory as previously reported (32).

$$\begin{array}{l}\text{NaBi}=\text{KBi}\left(\text{solid oxides}\right):{\text{Na}}_{0.08}{\text{MnO}}_{1.825}\mathrm{\cdot }0.54{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+\left(0.5\right)0.21\hspace{0.17em}{\text{K}}_2{\text{O}}_{\left(\text{s}\right)}+0.005\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}=\\ {\text{K}}_{0.21}{\text{MnO}}_{1.90}\mathrm{\cdot }0.47{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+\left(0.5\right)0.08\hspace{0.17em}{\text{Na}}_2{\text{O}}_{\left(\text{s}\right)}+0.07\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}\end{array}$$

$$\begin{array}{l}\text{NaBi}=\text{KBi}\left(\text{aqueous}\hspace{0.17em}\text{ion}\hspace{0.17em}\text{exchange}\right):{\text{Na}}_{0.08}\mathrm{\cdot }{\text{H}}_{0.35}{\text{MnO}}_2\mathrm{\cdot }0.365{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.21\hspace{0.17em}{\text{K}}_{\left(\text{aq}\right)}^{+}+0.005\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}=\\ {\text{K}}_{0.21}{\text{H}}_{0.20}{\text{MnO}}_2\mathrm{\cdot }0.37{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.08\hspace{0.17em}{\text{Na}}_{\left(\text{aq}\right)}^{+}+0.13\hspace{0.17em}{\text{H}}_{\left(\text{aq}\right)}^{+}.\end{array}$$

Although the exact nature and content of the counter cations found in natural birnessites surely depend upon the types and amounts of cations present in the local environment, this work demonstrates the thermodynamic stability of pure phase Na-, K-, and Ca-birnessite to lend insight into observed trends found in the laboratory and the environment. Because we do not have complete thermochemical data for the Na and K birnessites as a function of alkali content, and because the Mn AOS also probably varies as a function of alkali content, we cannot completely quantify the thermodynamics of ion exchange or oxides reacting or separate ion exchange from redox reactions. The thermodynamic studies here however support observations that mixed cation (Na–K–Ca) birnessite [e.g., (Na_0.3Ca_0.1K_0.1)(Mn⁴⁺,Mn³⁺)₂O₄·1.5H₂O] is observable under laboratory synthesis conditions as well as in environmental conditions (33–35). These synthesis conditions reflect the mixed cation content of the aqueous solutions from which they form, but the thermodynamic factors discussed above, especially SE differences, also play a role in the thermodynamic equilibria. Specifically, although the ΔH°_f-ox values become less exothermic in the order Na, K, Ca, the surface energies also decrease in the same order. This finding suggests a competition between bulk thermodynamics and surface energy effects in determining the specific composition formed under a given set of external conditions. Transformation reaction enthalpy for the bulk phases is computed using the following equations and the results are shown in Table 5.

$$\mathrm{\Delta }{\text{H}}_{\text{bulk}-\text{pt}}^{°}=\left(\mathrm{\Delta }{\text{H}}_{f,\text{nano}-\text{pt}}^{°}-\mathrm{\Delta }\text{H}\left(\text{surface}\hspace{0.17em}\text{term}\right)\right)$$

$$\mathrm{\Delta }\text{H}\left(\text{surface}\hspace{0.17em}\text{term}\right)=\left(\text{SE}\hspace{0.17em}\text{product}-\text{SE}\hspace{0.17em}\text{reactant}\right)\times \text{SSA}\left({\text{m}}^2/\text{mol}\right)\mathrm{\times }1\hspace{0.17em}\text{kJ}/\mathrm{1,000}\hspace{0.17em}\text{J}$$

$$\mathrm{\Delta }{\text{G}}_{\text{bulk}-\text{pt}}^{°}=\left(\mathrm{\Delta }{\text{H}}_{\text{nano}-\text{pt}}^{°}-\mathrm{\Delta }\text{H}\left(\text{surface}\hspace{0.17em}\text{term}\right)\right)-\text{T}\mathrm{\Delta }{\text{S}}_{298}^{°}.$$

The phase-transformation enthalpies and free energies among nanophase birnessites appear to depend only weakly on Mn AOS and cation content. This result is similar to observations for layer structure Ca–Mn–oxide nanosheets which have a constant internal enthalpy of oxidation independent of Ca:Mn ratio and Mn AOS (6). A comparison of the enthalpies of birnessite transformation reactions from solid oxides and ion-exchange reactions indicates that the latter are more exothermic. Thus, it is likely that such transformations occur via the aqueous phase rather than by solid state reaction, being favored by both thermodynamic and probably kinetic factors. This conclusion, that aqueous ion exchange is the prevalent mechanism of transformation, is consistent with previous birnessite phase-transformation studies performed using synchrotron XRD studies (34).

Because all of the birnessites have roughly similar AOS, the thermodynamic contribution of changing Mn AOS is really only important for transformation of birnessites to cryptomelane with the higher AOS likely the major driving influence. Cryptomelane surface energy is relatively low, providing little driving force for coarsening, but it is higher than that of the corresponding K birnessite, favoring the latter at increasing surface area. These transformations are represented by the reactions below:

$$\begin{array}{l}\text{KBi}=\text{CR}2\left(\text{solid oxides}\right):{\text{K}}_{0.21}{\text{MnO}}_{1.90}\mathrm{\cdot }0.47{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.06-{\text{O}}_{2\left(\text{g}\right)}={\text{K}}_{0.10}{\text{MnO}}_{1.965}\mathrm{\cdot }0.28{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+\left(0.5\right)\\ 0.11\hspace{0.17em}{\text{K}}_2{\text{O}}_{\left(\text{s}\right)}+0.19\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}\end{array}$$

$$\begin{array}{l}\text{KBi}=\text{CR}2\left(\text{aqueous}\hspace{0.17em}\text{ion}\hspace{0.17em}\text{exchange}\right):{\text{K}}_{0.21}{\text{H}}_{0.20}{\text{MnO}}_2\mathrm{\cdot }0.37{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.11\hspace{0.17em}{\text{H}}_{\left(\text{aq}\right)}^{+}+0.12\hspace{0.17em}{\text{O}}_{2\left(\text{g}\right)}=\\ {\text{K}}_{0.10}{\text{H}}_{0.07}{\text{MnO}}_2\mathrm{\cdot }0.245{\text{H}}_2{\text{O}}_{\left(\text{s}\right)}+0.245\hspace{0.17em}{\text{H}}_2{\text{O}}_{\left(\text{liq}\right)}+0.11\hspace{0.17em}{\text{K}}_{\left(\text{aq}\right)}^{+}.\end{array}$$

Phase transformation of potassium birnessite to cryptomelane is slightly more favorable with the solid oxides reacting without aqueous ion exchange, although ion-exchange reaction is also quite favorable. Two factors may contribute to the energetics of this particular reaction. The first is that a main driving force for this transformation may be the push toward higher oxidation state (a thermodynamically favorable direction) despite the transformation to a higher surface energy phase (less thermodynamically favorable direction). An analogous argument was made in terms of the influence of hydration/dehydration on room temperature phase transformation (28) with thermodynamic competition between hydration (favoring the lower SE phase) and oxidation (pushing toward the formation of the higher SE but more oxidized phase because oxidation is strongly 10 exothermic). The second factor harkens back to observations made in a review by McKenzie (11) that significant acid leaching of potassium from between the layers of birnessite precedes phase transformation of birnessite to cryptomelane This finding was incidentally observed later by Villalobos et al. (17) while mimicking birnessite syntheses in natural aqueous environments.

In conclusion, the thermodynamic data obtained in this work offer explanations for many of the trends of phase formation and transformation among birnessite and cryptomelane phases in nature and in the laboratory. Specifically, this study shows strong competition between surface energy and oxidation effects in the transformation of K-birnessite to cryptomelane. Thus, cryptomelane formation is favored by more oxidizing conditions. In contrast, compositional differences in birnessites are driven by concentration effects in aqueous solution coupled with small differences in surface energies. Therefore, birnessites can be highly variable in composition, reflecting changes in aqueous solution chemistry with little thermodynamic constraint from the energetics of the solid phases. All of the phases studied have substantially lower surface energies than anhydrous manganese oxides, making the layer and tunnel phases thermodynamically favored at high surface areas. Thus, the initial formation of fine grained manganese oxide phases with layer and tunnel structures by relatively rapid precipitation from aqueous solution near room temperature in soils, sediments, or under laboratory conditions is thermodynamically driven.

Methods

The goal of synthesis was to make a series of birnessites and cryptomelane of constant cation composition but varying particle size for thermochemical measurements. McKenzie (11) and Bricker (36) reviewed several methods for producing various Mn oxides. The present work used a recent slight modification of these methods (32), but overall, the synthetic strategy was based on reduction of aqueous salts of permanganate by chloride at room temperature at low pH followed by warm (32 ± 5 °C), wet aging. At high enough salt concentration, with other variables held reasonably constant, we were able to produce samples of almost identical counter-cation concentration, similar AOS, but different particle size controlled by the aging time. Solid compositions were controlled using high concentrations of the desirable counter cation provided by alkali and alkaline earth chlorides. Total ionic strength was computed using concepts and values obtained from Tissue (37), Stumm and Morgan (38), and Kielland (39). Ion activities in solution were used to calculate the total activity for the concentrations of ionic reagents based on the Davies equation (40). For the reaction matrices for birnessite synthesis, the computed total ionic strength was 3.150 and for cryptomelane it was 5.625 (higher than for birnessite due to the presence of sulfate). Syntheses were carried out in covered glass reaction vessels, ionic strengths were held constant, and water volume monitored. Synthesis conditions are summarized in Table 1.

All phases were confirmed by powder XRD using a Bruker D8 Advance X-ray diffractometer (Cu Kα radiation; 45 kV and 40 mA) at 25 °C with step size 0.02 °2θ and 10-s dwell time. Comparison of reference powder patterns to profile fits of the samples was made using Jade software (version 6.11; 2002) and International Center for Diffraction Data.

Adsorption isotherms of nitrogen at −196 °C (liquid nitrogen temperature) were measured using a Micromeritics ASAP 2020 apparatus in the P/P₀ range of 0.05–0.3. Before measurements, the samples were outgassed at room temperature under turbo-molecular pump vacuum at room temperature for 24 h to remove most preadsorbed water without losing phase integrity or surface area. Specific surface area was calculated using the five-point Brunauer–Emmett–Teller (BET) method (41).

For proper interpretation of thermochemical data, one must know the complete composition of each sample, including the cation content, the Mn AOS (these two together then give the oxygen content), and the water content. A combination of techniques was used to obtain these parameters. Metal cation concentration of each sample was measured using inductively coupled mass spectrometry with a quadrupole mass spectrometer (7500a; Agilent Technologies). Cation contents were determined for 20- to 30-mg samples digested in 3 mL of 6 M HCl and then diluted with 18 mega-ohm water and HNO₃ to yield dissolved samples in a 3% (wt/vol) HNO₃ solution. The HCl and HNO₃ were trace-metal grade reagents.

Iodometric titration (42) was used to measure Mn AOS and speciation, by the reaction of iodide with dissolved manganese oxide samples at room temperature. Specific details of the titration of Mn(III and IV) oxidation state and calculations for complex Mn oxides are described elsewhere (6). Total oxidized equivalents, [Ox], of manganese may be expressed as the Mn AOS obtained from the titration: [Ox] = 2[Mn(IV)] + [Mn(III)]. Subsequently, the O/Mn ratio, as in MnO_x, is calculated as: x = 1 + 1/2[(total oxidized equivalents)/(total moles of Mn)], where “total moles of Mn” for a manganese oxide phase assemblage is taken to be “1.” The Murray titration is used to obtain “total oxidized equivalents.” In terms of x, 2 SDs of the mean can be very low (±0.002) with strict adherence to proper analytical methodology, although limitations in analytical glassware and propagation of errors increases the reported error to x ± 0.01.

The samples were heated to 973 K at 10 °C/min under a flow of argon (75 mL/min) in platinum crucibles using a Setaram Labsys Evo thermal analysis [thermogravimetric analysis (TGA)/differential scanning calorimetry] instrument and associated Calisto software. TGA data were corrected for buoyancy by running an empty crucible. H₂O content was determined from the weight difference (obtained on a microbalance) before and after annealing the samples overnight at 975 K. Part of the measured total weight loss was due to loss of oxygen as Mn⁴⁺ in the original sample was reduced on heating, and part was due to dehydration. The former was calculated from the difference in manganese oxidation state between the original and annealed sample measured by the Murray titration (42). This value was subtracted from the total weight loss to give the weight loss due to water. The details of this method are described elsewhere (6).

The custom built Calvet twin calorimeter and techniques for measurement of formation enthalpy by solution calorimetry in a molten salt solvent at high temperature have been described previously (24, 25). Before calorimetric measurements, samples were equilibrated with the controlled temperature and humidity conditions of the calorimetry suite. Sample pellets (∼5 mg) were dropped into molten sodium molybdate (3Na₂O–4MoO₃) (20 g) at 975 K, with oxygen flushing through the calorimeter at 30 mL/min and also bubbling through the solvent at 5 mL/min. Flushing and bubbling maintains oxidizing conditions, removes evolving water vapor, and aids dissolution. The methodology has been described in detail previously (18–25, 43, 44). To obtain the mean enthalpy of drop solution (ΔH_ds), experiments were replicated for a total of eight per sample. The difference between each replicate experiment value is within the 2-σ error.