Emergence of function from coordinated cells in a tissue

Significance

A basic problem in biology is understanding how information from a single genome gives rise to function in a mature multicellular tissue. Genome dynamics stabilize to give rise to a protein distribution in a given cell type, which in turn gives rise to the identity of a cell. We build a highly idealized mathematical foundation that combines the genome (within cell) and the diffusion (between cell) dynamical forces. The trade-off between these forces gives rise to the emergence of function. We define emergence as the coordinated effect of individual components that establishes an objective not possible for an individual component. Our setting of emergence may further our understanding of normal tissue function and dysfunctional states such as cancer.

Abstract

This work presents a mathematical study of tissue dynamics. We combine within-cell genome dynamics and diffusion between cells, so that the synthesis of the two gives rise to the emergence of function, akin to establishing “tissue homeostasis.” We introduce two concepts, monotonicity and a weak version of hardwiring. These together are sufficient for global convergence of the tissue dynamics.

Is there a basis for emergence of tissue-specific function? Emergence in this work is defined as the coordinated effect of individual components that establishes an objective not possible for an individual component. Our components are cells with their proteins, and the objective is the function of a tissue. Here tissue is a set of cells of the same cell type located together as exemplified by an organ in the body. In vertebrates, consider the liver, functioning to detoxify and ensure an appropriate composition of blood, and the skeletal muscle, functioning to contract and generate force. In each of these tissues millions of individual cells contribute to emergence of function according to their cell type. The main elements of emergence that we consider are first, the protein distribution in a given cell type and second, the cellular architecture of the tissue, a 3D structure with “diffusion” of molecules between cells. We build a mathematical model for emergence of function, from a large accumulation of data. We also use our previous work on cell dynamics (genome dynamics) and the work of Alan Turing on diffusion (1).

Underlying our setting are widely believed biological hypotheses: (i) Cells within a tissue (i.e., the same cell type) have the same dynamics and the same distribution of proteins at equilibrium and (ii) the function of a cell corresponds to the proteins of that cell. For reasons that will be discussed, we call the property in i “hardwiring” of the tissue (2, 3). Convergence of the tissue dynamics to such an equilibrium naturally takes on importance, for its role in maintenance of tissue function (4). Even a local stability of the (hardwiring) equilibrium, i.e., its robustness, gives some validity to our model in biology. Our main theorem (Theorem 5) establishes that monotonicity, a property that we introduce here, implies global convergence of the tissue dynamics to the equilibrium, where all cells have the same protein distribution. This gives a biological justification for our framework and a model for “emergence of function,” as well as suggestions for studying the passage from emergence to morphogenesis. On the other hand one could see the emergence described here as a final stage of morphogenesis, completing a cycle.

Our model could give some support to obtaining more insights. Further questions, where quantitative support is expected, are also suggested: (i) To what extent is there a common equilibrium of proteins in each cell in a tissue? (ii) How do cells in a tissue cooperate to give rise to function? And (iii) how do we measure the diffusion between the cells?

1. Simple Example

Here we model two cells, separated by a membrane, that each have a same single protein. Consider the following system,

$$\text{Cell}\hspace{0.17em}1:\hspace{1em}\frac{dx}{dt}=a\left(x-x_0\right)$$ [1a]

$$\text{Cell}\hspace{0.17em}2:\hspace{1em}\frac{dy}{dt}=b\left(y-y_0\right),\hspace{1em}a,b,<0,x_0,y_0>0,$$ [1b]

where $x$ and $y$ can be interpreted as protein concentration, $x$ in cell 1 and $y$ cell 2, both positive. Thus, $x,y\in 𝐗\times 𝐘=[0,c]\times [0,d]$, where $c$ and $d$ represent the maximum concentration of proteins $x$ and $y$, respectively. The equilibria are $x=x_0$ and $y=y_0.$ We introduce Turing-type (diffusion) coupling by adding a term with $\beta >0$ as follows:

$$\frac{dx}{dt}=a\left(x-x_0\right)+\beta (y-x)$$ [2]

$$\frac{dy}{dt}=b\left(y-y_0\right)+\beta (x-y),\hspace{1em}\beta >0.$$

The equilibrium for the above system is obtained by solving the system derived from Eq. 2 by setting the right-hand sides equal to zero. This is a linear system in two equations and two variables and we obtain

$$x=\frac{-ab{x}_0+a\beta x_0+b\beta y_0}{a\beta +b\beta -ab}$$ [3a]

$$y=\frac{-ab{y}_0+a\beta x_0+b\beta y_0}{a\beta +b\beta -ab}.$$ [3b]

It is not hard to see from Eqs. 3a and 3b that if $\beta \to \mathrm{\infty }$, $x$ and $y$ converge to the same value $\frac{a{x}_0+b{y}_0}{a+b}.$ Therefore, this system approaches a common protein concentration and the example exhibits the role of diffusion, even with different cell dynamics. We refer to this as an “emergent equilibrium.” Eigenvalues of the Jacobian matrix (see 2. The Genome Dynamics of One Cell and 5. Turing’s Paper on Morphogenesis) for the system in Eq. 2 at equilibrium and finite $\beta$ are expressed as

$$\frac{1}{2}(a+b)-\beta +\frac{1}{2}\sqrt{{(a-b)}^2+4{\beta }^2}$$

$$\frac{1}{2}(a+b)-\beta -\frac{1}{2}\sqrt{{(a-b)}^2+4{\beta }^2}.$$

Because the eigenvalues are real negative, this pair $(x,y)$ of Eq. 3 is a stable equilibrium.

Success of Emergence.

The magnitude of $(x-y)$ from Eq. 3 measures the departure from the “emergence” as

$$x-y=-\frac{ab\left(x_0-y_0\right)}{\beta (a+b)-ab}.$$ [4]

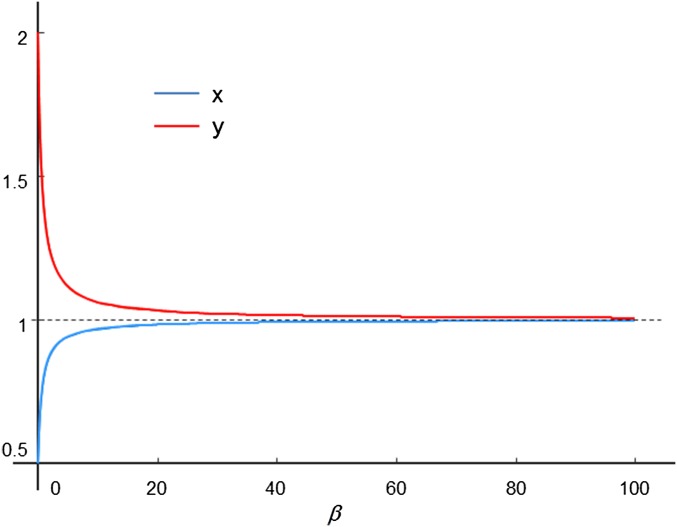
If $x_0-y_0$ is big and $\beta$ is small, there is ill-conditioning as follows. If $a=0$ in Eq. 3, the solution is $x=y_0$ and $y=y_0.$ If $a\ne 0$, no matter how small, and $\beta =0$, the solution is $x=x_0$ and $y=y_0$. Note from Eq. 4, for any finite $\beta$ the equilibrium for the pair $(x,y)$ has $x$ and not $y$ if $x_0\ne y_0$. We might say then that the system in Eq. 2 is not emergent (for any finite $\beta$). Fig. 1 shows a numerical example of this system.

Fig. 1.

Plot of Eqs. 3a and 3b for $a=-2$, $b=-1$, $c=-1$, $d=-2$ as $\beta$ changes. $x$ (red) and $y$ (blue) are the coordinates of the equilibrium of Eq. 2.

Remark 1: Here the $\beta$ anticipates the Fiedler number of a Laplacian defined by the cellular network of the tissue. We introduce the concept of a “hardwiring hypothesis,” which implies $x_0=y_0$. Diffusion is unnecessary in our example for emergence [and in fact it can defeat emergence (!) as we will see]. On the other hand diffusion can have a stabilizing effect.

This is an example of linear dynamics of one protein and one cell with stability. These dynamics although linear are also a good approximation of the general stable dynamics in a neighborhood of the equilibria. Moreover, the global dynamics of the basin of the stable equilibrium are qualitatively equivalent to the linear example.

2. The Genome Dynamics of One Cell

We use the setting of our paper on genome dynamics (2). For a single-cell state space $𝐗={\displaystyle \prod _{𝑗}^{𝑛}}$ $[0,c_j],$ where $c_j$ is the maximum concentration of protein $j.$ Sometimes we use $c_j=\mathrm{\infty }.$ The inner product is Cartesian. The genome dynamics are expressed as $\frac{d𝐱}{dt}=𝐅(𝐱),$ where $𝐅$ is a function from $𝐗\subset {ℝ}^n$ to ${ℝ}^n.$

Generally recall the notion of stable equilibrium ${𝐱}_0$ of $𝐗$ for $\frac{d𝐱}{dt}=𝐅(𝐱)$, as well as its basin. If every eigenvalue of the Jacobian matrix of first partial derivatives of $𝐅$ at ${𝐱}_0$ has negative real part, then all trajectories that start near ${𝐱}_0$ approach it as $t\to \mathrm{\infty }.$ The basin $𝐁\left({𝐱}_0\right)$ is the set of all points that tends to ${𝐱}_0$ when $t\to \mathrm{\infty }.$ Then ${𝐱}_0$ is a stable equilibrium.

The dynamics on the basin are “linear” provided that the $𝐅:𝐁\to {ℝ}^n$, $𝐁={ℝ}^n,$ has the form $𝐅\left(𝐱\right)={𝐅}_{lin}\left(𝐱-{𝐱}_0\right)$, where ${𝐅}_{lin}$ is a linear map, ${ℝ}^n\to {ℝ}^n$, $𝐱$ belongs to $𝐁$, and ${𝐱}_0$ is the equilibrium in $𝐁.$ Suppose that $𝐅$ is the dynamics, not necessarily linear, with stable equilibrium ${𝐱}_0$. Then $𝐅$ at ${𝐱}_0$ has the above form in a neighborhood of ${𝐱}_0$ (${𝐅}_{lin}$ is the derivative of $𝐅$ at ${𝐱}_0).$ Moreover, it can be shown that the dynamics on the basin are topologically equivalent to the linear dynamics as above. In fact, a main theorem about stable equilibria is that the linear dynamic in ${ℝ}^n$ is equivalent to the dynamics of $\frac{d𝐱}{dt}=𝐅\left(𝐱\right)$ in the basin $𝐁({𝐱}_0).$ This means there is a homeomorphism from ${ℝ}^n$ to the basin $𝐁\left({𝐱}_0\right)$ that preserves the solution curves. Then the dynamics of $𝐁\left({𝐱}_0\right)$ are the same topologically as the linear dynamics above. Browder (5) and Hirsch and Smith (6) have extensively studied the topic of monotonicity. Here we provide our version of monotonicity that has a common element with Hirsch (5) and Browder and Smith (6), but is quite different.

Definition 1: Monotonicity condition: Suppose we have dynamics $\frac{d𝐱}{dt}=𝐆(𝐱)$ on a domain $𝐗$ in a Euclidean space with its inner product. The monotonicity condition for $𝐆,$ and a point ${𝐱}_0\in 𝐗$, is then

$$⟨\mathrm{𝐆𝐱},\left(𝐱-{𝐱}_0\right)⟩<0\text{for all}𝐱\ne {𝐱}_0\text{in}𝐗.$$ [5]

Proposition 1. For any dynamics $\frac{d𝐱}{dt}=𝐆(𝐱)$ on $𝐗\subset$ ${ℝ}^k,$ ${𝐱}_0$ $\in$ $𝐗,$ the monotonicity condition for $𝐗,$ ${𝐱}_0,$ implies that $\parallel 𝐱\left(t\right)-{𝐱}_0\parallel$ is a decreasing function of $t$ for all nontrivial solutions $𝐱(t)$ in $𝐗,$ where $𝐱(t)$ is defined for all $t>0.$

Proof: Suppose Eq. 5 is true. Note that

$$\frac{d\left({\parallel 𝐱\left(t\right)-{𝐱}_0\parallel }^2\right)}{dt}=\frac{d⟨𝐱(t)-{𝐱}_0,𝐱(t)-{𝐱}_0⟩}{dt}=2⟨\frac{d\left(𝐱(t)\right)}{dt},𝐱(t)-{𝐱}_0⟩=2⟨\mathrm{𝐆𝐱}(t),\left(𝐱(t)-{𝐱}_0\right)⟩.$$

The quantity at the end is negative by Eq. 10, the monotonicity condition. QED.

One could call the $𝐗$ of Proposition 1 a “monotonic basin” for the dynamics. Under these conditions ${𝐱}_0$ is an equilibrium.

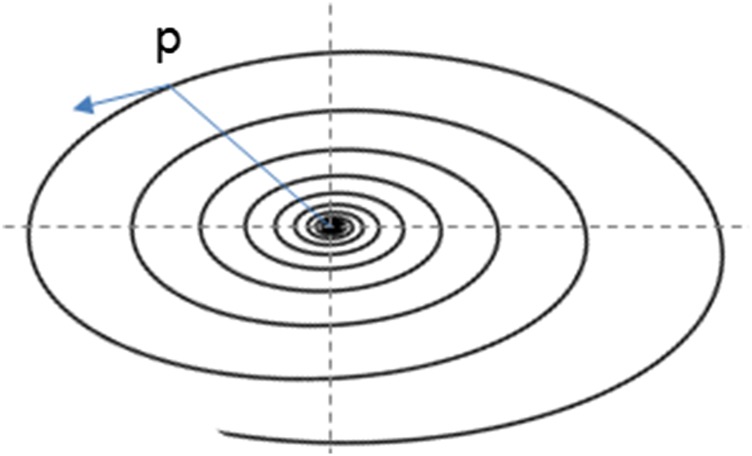
Thus, monotonicity on $𝐗,{𝐱}_0$ implies that $𝐱(t)$ is monotonically converging to ${𝐱}_0.$ This gives a stability of ${𝐱}_0$. The converse is not true not even in the linear case. One can take for an example a spiral sink where the axes are different (Fig. 2). When the solution is going in the direction of the long axis, then $𝐱(t)-{𝐱}_0$ is not decreasing, whereas ${𝐱}_0$ is a stable equilibrium. This example helps us understand the famous Turing phenomenon (5. Turing’s Paper on Morphogenesis).

Fig. 2.

$⟨𝐅p\mathit{\text{,}}\left(p-{𝐱}_0\right)⟩>0.$ This an example of a basin that is not a monotonic basin.

Example 1: Let $\mathrm{𝐅𝐱}=𝐀(𝐱-{𝐱}_0),$ where $𝐀$ is a linear map ${ℝ}^n\to {ℝ}^n,$ not necessarily symmetric. Then $𝐀$ is negative definite exactly when monotonicity holds.

Let us return to the biological setting. Single-cell dynamics are those of dynamics on a basin $𝐁\subset 𝐗$ as in our previous work on genome dynamics (2). We assume that the basin $𝐁$ is that of an equilibrium ${𝐱}_0$ and are excluding periodic attractors in the present paper. This means we are identifying a cell with its basin. The equilibrium of genome dynamics of a cell exhibits the distribution of proteins. That distribution can be identified with that cell.

We now examine explicitly the conditions for monotonicity in the linear case of one cell with two proteins. This case can be represented by the system

$$\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}=𝐀(𝐱-{𝐱}_0),\hspace{1em}𝐱=({𝐱}_1,{𝐱}_2),$$

where $𝐀=\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)$ and $\frac{d𝐱}{dt}=0$ when $𝐱={𝐱}_0.$ Then $𝐀$ (Jacobian matrix at ${𝐱}_0$) is stable and $𝐱\left(t\right)\to {𝐱}_0$ when all eigenvalues have negative real parts. The eigenvalues of $𝐀$ are given by the characteristic equation ${\lambda }^2-\tau \lambda +\mathrm{\Delta }=0,$ where

$$\tau =\text{trace}(𝐀)=a+d\hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{\Delta }=\text{det}(𝐀)=ad-bc.$$

Then ${\lambda }_1=\frac{\tau +\sqrt{{\tau }^2-4\mathrm{\Delta }}}{2},{\lambda }_2=\frac{\tau -\sqrt{{\tau }^2-4\mathrm{\Delta }}}{2}$ are the eigenvalues of $𝐀.$ For stability $𝐀$ must satisfy two criteria: (i) The trace, $a+d,$ must be negative, and (ii) the determinant, $ad-bc,$ must be positive (7, 8).

To derive the conditions for monotonicity, consider the quadratic form associated with $𝐀:$ $Q(u,v)=a{u}^2+d{v}^2-\left(\frac{b+c}{2}\right)uv,$ and suppose $a,d<0.$ Thus, $\frac{𝐀+{𝐀}^T}{2}=\left(\begin{array}{cc}\hfill a\hfill & \hfill \frac{b+c}{2}\hfill \\ \hfill \frac{b+c}{2}\hfill & \hfill d\hfill \end{array}\right)$, and $\frac{𝐀+{𝐀}^T}{2}$ is symmetric. The matrix of a quadratic form can always be forced to be symmetric in this way. The condition for monotonicity is $⟨\mathrm{𝐅𝐱},\left(𝐱-{𝐱}_0\right)⟩<0.$ This amounts to $⟨𝐀\left(𝐱-{𝐱}_0\right),\left(𝐱-{𝐱}_0\right)⟩<0$ or that the eigenvalues of $\left(\frac{𝐀+{𝐀}^T}{2}\right)$ are negative$,$ which is equivalent to $𝐀$ being negative definite. Because the determinant of $\frac{𝐀+{𝐀}^T}{2}$ is positive,

$$ad>{\left(\frac{b+c}{2}\right)}^2,\hspace{1em}a,d<0.$$ [6]

In summary the stability condition is $bc<ad$ and the monotonicity condition is ${\left(\frac{\left(b+c\right)}{2}\right)}^2<ad.$ Therefore, the excess of the left-hand sides of the previous inequalities is ${\left(\frac{\left(b+c\right)}{2}\right)}^2-bc.$ If the excess is positive or zero, monotonicity implies stability. The excess is never negative. More generally, as a consequence of Proposition 1 we can prove the following.

Proposition 2. For linear dynamics on ${ℝ}^n$ monotonicity implies stability.

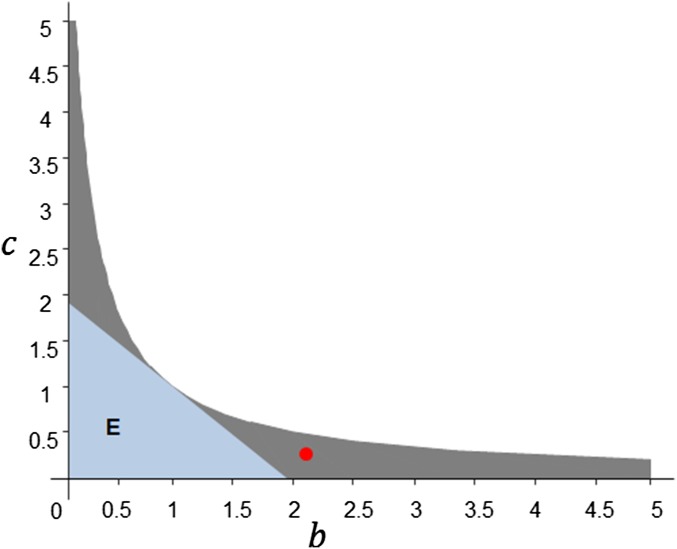
Fig. 3 shows an example of monotonicity and stability conditions in the $bc$ plane, where $a,d=-1$. $𝐄$ is the monotonic region and hence is part of the stable region. The red solid circle in Fig. 3 represents Turing’s two-cell example [Turing (1) and Chua (9)], discussed in 5. Turing’s Paper on Morphogenesis.

Fig. 3.

Monotonicity and stability conditions in the $bc$ plane for $a\text{,}d=-1$. The dark gray region together with the blue region (E) constitutes the stability region. E is the monotonic region. The red solid circle shows Turing’s two-cell example in the $bc$ plane.

Hardwiring.

The genes present in the human genome are the same in all cell types and all individuals. Now we describe a property of a family of cells, which we called hardwiring (2), motivated by the universality above. Our network in ref. 2 puts an oriented edge (between two nodes), between two genes, $i$ and $j$, if it is possible for the protein product of gene $i$ to bind to the promoter of gene $j$ and activate transcription. Gene $i$ will bind to this promoter only in some cell types, at certain stages of development. It can happen that gene $i$ as a transcription factor may be silenced. In that case gene $i$ can be removed from the network together with its edges. As an example, this phenomenon can occur through failure of chromatin accessibility (10). We say that a family of cells is hardwired provided that the genome dynamics are the same for every cell in the family. In the example of Turing [also Chua (9) and Smale (11)] below, hardwiring is assumed extensively.

Definition of Weak Hardwiring.

Thus, the family is hardwired provided that the dynamics of each cell in the family are the same; in particular, the equilibrium of each cell is the same. That is, the protein distribution at the equilibrium of each cell is the same. If the last property is true, then we say that the family satisfies “weak hardwiring.” The idea of the weak hardwiring concept is that in a single cell type all cells have the same equilibrium distribution of proteins (2). This helps justify the identification of a tissue with its protein distribution.

3. Cellular Dynamics and Their Architecture

We define a graph $𝚪$ as a mathematical model for the cellular structure for a single tissue. First, consider the $m$ cells of the single tissue and a single protein. The main biological object is the cellular architecture of a tissue that consists of $m$ cells in three dimensions. The graph $𝚪$ consists of nodes corresponding to the cells of the tissue. The weighted edges of the graph are associated with the membranes between two cells and define the notion of adjacency. This adjacency is represented by a number that represents the diffusion between two cells and it depends on the interactions at their cell membranes (12). This number could be interpreted as the product of the permeability and the area of the membrane between cell $i$ and cell $j$, a quantity represented by a matrix element $a_{ij}$. We write $𝐀=(a_{ij}).$ The matrix $𝐀$ is an $m\times m$ symmetric matrix, the adjacency matrix of the architecture. Note that $𝐀$ does not depend on the protein levels. Thus, $𝚪$ is a weighted graph whose nodes are $i=1,\mathrm{\dots },m$ and edges $a_{ij}$. We assume that the graph is connected. What we have discussed here is a network whose nodes are cells and it is not to be confused with the genome network in 3. Cellular Dynamics and Their Architecture. This model applies more literally to diffusion in the case of small molecules.

Definition of a State.

A state associated to the graph is a set of protein levels ${𝐱}_1,\mathrm{\dots },{𝐱}_m$, where ${𝐱}_i$ is the level of a single protein in the ith cell. Thus, a state $𝐱$ is a function of nodes $i$ and with value at node $i$ written as ${𝐱}_i$. The states form a linear space $𝐒$ and feasible states, the subspace of functions with nonnegative values ${𝐒}_{+}$. The function $𝐱\in 𝐒$ is harmonic provided that ${𝐱}_i$ is a constant function of $i.$ By our hypothesis that the graph $𝚪$ is connected, it follows that the space of harmonic functions is one dimensional. For $n$ proteins we generalize the notion of ${𝐱}_i$ and $𝐒.$ Now ${𝐱}_i$ is a distribution of proteins in the ith cell; i.e., ${𝐱}_i=({𝐱}_i^1,\mathrm{\dots },{𝐱}_i^n).$ Note that this expression can be thought of as a function of $i$. We assume that the membrane structure of the tissue affects all of the proteins equally [this is a strong idealization, but it can be relaxed easily as in Turing’s example (1) in 5. Turing’s Paper on Morphogenesis).

The Laplacian Matrix.

Let $𝐃$ be the diagonal matrix with the ith element of the diagonal defined by ${\displaystyle \sum _{𝑗}}{a}_{ij}.$ Then the Laplacian is given by

$$𝐋=𝐃-𝐀.$$

$𝐋$ is a $(m\times m)$ real symmetric matrix, and together with the nonnegativity of the weights, this implies that it is positive semidefinite (13). It is an operator on $𝐒$.

The diffusion dynamics defined by the cellular architecture may be written as follows:

$$\frac{d{𝐱}_i}{dt}=-{\displaystyle \sum _{j\in m_i}}{a}_{ij}({𝐱}_i-{𝐱}_j),\hspace{1em}i=1,\mathrm{\dots },m$$

or

$$\frac{d𝐱}{dt}=-\mathrm{𝐋𝐱}.$$ [7]

Note that Eq. 12 is a linear system of ordinary differential equations.

Remark 2: Harmonic functions are exactly a set of $𝐱$, such that $\mathrm{𝐋𝐱}$ = 0.

Note that our definition applies not just to a single protein, but also to an $n$-tuple ${𝐱}_i$ belonging to ${ℝ}^n$, and the feasible ones to ${\left({ℝ}_{+}\right)}^n.$

Proposition 3. The system is globally stable with equilibrium set, the harmonic functions.

Proof: $⟨-\mathrm{𝐋𝐱},𝐱⟩\le 0$ and $⟨-\mathrm{𝐋𝐱},𝐱⟩=0$ if and only if $𝐱$ = constant; i.e., ${𝐱}_1={𝐱}_2=\mathrm{\cdots }={𝐱}_m$. The solution to Eq. 7 is denoted by $𝐱(t)$ with initial conditions $𝐱(0)=𝐂,$ $𝐂\in {ℝ}^m$. Now the solution is

$$𝐱(t)=e^{-𝐋t}𝐂.$$

Then $\frac{d}{dt}⟨𝐱(t),𝐱(t)⟩=2⟨-\mathrm{𝐋𝐱}(t),𝐱(t)⟩<0,$ unless $𝐱(t)$ satisfies ${𝐱}_1(t)={𝐱}_2(t)=\mathrm{\cdots }={𝐱}_m(t)=$ constant. Therefore, the solution converges to a harmonic function. QED.

For the $n$-protein case, the harmonic functions form an $n$-dimensional space defined by ${𝐱}_1={𝐱}_2=\mathrm{\dots }={𝐱}_m$, where ${𝐱}_1$ is an arbitrary element of ${ℝ}^n$.

4. Dynamics of a Tissue

We use both the notations ${𝐗}_i={\displaystyle \prod _{𝑗}^{𝑛}}$ $[0,c_j]$ and the basin, ${𝐁}_i\subset {𝐗}_i$ with its equilibrium ${𝐱}_{0,i}$ for the domain of the genome dynamics, where $c_j$ is the maximum concentration of protein $j$ and $n$ is the number of proteins. ${𝐗}_i$ is important for the lapse of emergence and dealing with different cell types (different tissues) as in 6. Lapse of Emergence. ${𝐁}_i$ is suited for single-tissue theory as in the following.

Genome Dynamics for m Cells.

For a single cell say $i,$ ${𝐁}_i$ is the domain of the dynamics. For each cell $i$, ${𝐅}_i:{𝐁}_i\to {ℝ}^n$ represents the genome dynamics in cell $i$,

$$\frac{d{𝐱}_i}{dt}={𝐅}_i{𝐱}_i,\hspace{1em}{𝐱}_i\in {𝐁}_i,\hspace{1em}i=1,\mathrm{\dots }m.$$ [8]

For the case of cells of a tissue $𝐒=$ ${\displaystyle \prod _{𝑖}^{𝑚}}{𝐁}_i,i=1,\mathrm{\dots },m$ where $m$ is the number of cells in the tissue and $𝐒$ is the state space of 3. Cellular Dynamics and Their Architecture extended to $n$ proteins. We use an inner product on $𝐒$ derived from the inner products on ${𝐁}_i.$ Thus, ${𝐁}_i$ corresponds to cell $i$ with stable equilibrium ${𝐱}_{0,i}.$

Now we take the product of the dynamics over all of the cells at once to get $𝐅:𝐒\to {ℝ}^N(\text{or better}{\left({ℝ}^n\right)}^m),$ where $𝐅=({𝐅}_1,\mathrm{\cdots },{𝐅}_m),N=nm$ and

$$\frac{d𝐱}{dt}=\mathrm{𝐅𝐱},\hspace{1em}𝐱\in 𝐒.$$ [9]

Eq. 9 is rephrasing Eq. 8. This is the genome dynamics of the tissue. Thus, this tissue has genome dynamics and separates into individual cell dynamics ${𝐁}_i$ for cell $i.$ Let ${𝐱}_0$ be the point of $𝐒$ defined as ${𝐱}_0=({𝐱}_{\mathrm{0,1}},{𝐱}_{\mathrm{0,2}},\mathrm{\dots },{𝐱}_{0,m}),$ where ${𝐱}_{0,i}$ is the equilibrium in ${𝐁}_i.$ The weak-hardwiring hypothesis asserts that the ${𝐱}_{0,i}$ are all the same. Then ${𝐱}_0$ is the equilibrium for genome dynamics for the whole tissue. For the rest of this paper we assume the weak hardwiring for the cells in the tissue.

Extension of Monotonicity to the Genome Dynamics of the Tissue.

Extension of the definition of monotonicity to many cells is given by

$$⟨\mathrm{𝐅𝐱},\left(𝐱-{𝐱}_0\right)⟩<0,𝐅=\prod {𝐅}_i,\hspace{1em}𝐱\ne {𝐱}_0$$

$$𝐱=({𝐱}_1,{𝐱}_2,\mathrm{\dots },{𝐱}_m)\hspace{0.17em}\text{and}\hspace{0.17em}{𝐱}_1=({𝐱}_1^1,{𝐱}_1^2,\mathrm{\dots },{𝐱}_1^n)\in {𝐗}_1,\text{etc.}$$

Here ${𝐱}_i^j$ denotes the amount of the jth protein in the ith cell. $\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}$ is the dynamics on the basin $𝐁=\prod {𝐁}_i,{𝐱}_0=({𝐱}_{\mathrm{0,1}},{𝐱}_{\mathrm{0,2}},\mathrm{\dots },{𝐱}_{0,m})$ and ${𝐱}_0\in 𝐁.$ Observe from weak hardwiring ${𝐱}_{\mathrm{0,1}}={𝐱}_{\mathrm{0,2}}=\mathrm{\dots }={𝐱}_{0,m}.$

Example 2: $\mathrm{𝐅𝐱}=𝐀(𝐱-{𝐱}_0),$ where $𝐀=$ $\prod {𝐀}_i,$ so that $𝐀$ is a multilinear map and each ${𝐀}_i:{ℝ}^m\to {ℝ}^m$ is linear. Then ${𝐀}_i,$ for each $i$, is negative definite exactly when this monotonicity holds.

However, we are not assuming the linearity of the dynamics. We cannot get even a good model of robust stability of equilibria in the linear setting. We cannot model dynamics with two separate equilibria.

Diffusion Dynamics for n Proteins.

Recall in 3. Cellular Dynamics and Their Architecture, the diffusion dynamics between cells in a tissue for a protein distribution

$$\frac{d𝐱}{dt}=-\mathrm{𝐋𝐱}\hspace{0.17em}\text{or}\hspace{0.17em}\frac{d{𝐱}_i}{dt}=-{\mathrm{𝐋𝐱}}_i\hspace{0.17em}\text{for all}i=1,..,m.$$ [10]

Here $𝐱=({𝐱}_1,\mathrm{\dots },{𝐱}_m),{𝐱}_i\in {ℝ}^n$ is an $n$-tuple of proteins or “a distribution of proteins.”

The Basin Hypothesis.

Cells described by ${𝐅}_i:{𝐁}_i\to {ℝ}^m$ have the same basin ${𝐁}_i$ and the same equilibrium ${𝐱}_{0,i}$ (this is a consequence of the hardwiring hypothesis). We also suppose that the basins ${𝐁}_i$ are convex. These two hypotheses are made so that the diffusion terms in Eq. 11 below make sense and are called the basin hypothesis.

Following the spirit of Turing’s paper, we may combine two dynamics (genome dynamics within the cell and diffusion dynamics between cells) into a system (Eq. 11) that is the object of the study in this paper:

$$\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}-\mathrm{𝐋𝐱},\hspace{0.17em}𝐱\in 𝐁={\displaystyle \prod _{i=1}^{𝑚}}{𝐁}_i$$ [11]

We emphasize that differential Eq. 11 is not necessarily linear in contrast to Turing.

The main theorem of this paper is as follows.

Theorem 5. The dynamical system $\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}-\mathrm{𝐋𝐱}$ of a tissue (Eq. 11) is globally stable with equilibrium ${𝐱}_0$ provided the basin hypothesis is satisfied and $𝐅$ satisfies monotonicity.

Lemma 1. If $𝐅$ is monotone relative to $𝐁,{𝐱}_0$, then $\left(𝐅-𝐋\right)$ is monotone.

Proof of Lemma 1: Lemma 1 is true if $𝐅$ is monotone and if $-𝐋$ is monotone. First, $⟨-\mathrm{𝐋𝐱},\left(𝐱-{𝐱}_0\right)⟩\le 0$ is proved. From weak hardwiring ${𝐱}_{\mathrm{𝟎}}$ is harmonic and so ${\mathrm{𝐋𝐱}}_{\mathrm{𝟎}}=0.$ Moreover, $⟨-\mathrm{𝐋𝐱},𝐱⟩\le 0$ for any $𝐱\in 𝐒,$ because $-𝐋$ is negative semidefinite (4. Dynamics of a Tissue). Therefore, $⟨-\mathrm{𝐋𝐱},\left(𝐱-{𝐱}_0\right)⟩\le 0.$ Because ${\mathrm{𝐅𝐱}}_0=0,$ thus it remains only to prove $⟨\mathrm{𝐅𝐱},\left(𝐱-{𝐱}_0\right)⟩<0$ for $𝐱\ne {𝐱}_0.$ But $𝐅$ is monotone by hypothesis. QED.

By Proposition 1 applied to $𝐆=\left(𝐅-𝐋\right)$ and Lemma 1 we obtain the global stability of equilibrium ${𝐱}_0,$ thus proving Theorem 5.

We name the property of $\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}-\mathrm{𝐋𝐱}$ in Theorem 5 emergence. Theorem 5 establishes that monotonicity implies global convergence of the tissue dynamics to the equilibrium; that is, all cells have the same protein distribution, in a strong stable sense (“robustness”). This gives a biological justification for the concept of weak hardwiring in a tissue. Thus, we give a model for emergence of function.

Ours is not the first paper to address the issue of convergence after Turing’s paper. In particular, Wang and Slotine (14) have conditions designed to show convergence in systems resembling ours. Our work in Proposition 1 and Theorem 5 deals with a wider class of spaces as our basins and their products correspond to dynamics of protein levels. Also we do not use a derivative of $𝐆$ in our condition, and we do use a point ${𝐱}_0$ in ${ℝ}^n$, not the origin, as an equilibrium. Clearly the convergence results in ref. 14 do not imply ours. Our previous paper (15) follows our current perspective, with a passage from one basin to two basins. This is motivated by the biological example of Gardner et al. (16). Also Chua (9) has convergence results for systems related to ours. These two authors work in linear spaces with nonlinear equations, whereas we work in nonlinear spaces.

Remark 3: Recall the linear case $\frac{d𝐱}{dt}=𝐅\left(𝐱-{𝐱}_0\right)-\mathrm{𝐋𝐱},$ where $𝐱=({𝐱}_1,\mathrm{\dots },{𝐱}_m)$ and $\left(𝐅-𝐋\right)$ is not singular. This is in the form $\frac{d𝐱}{dt}=\mathrm{𝐏𝐱}-𝐐,$ where $𝐏=𝐅-𝐋$ and $𝐐={\mathrm{𝐅𝐱}}_0.$ The explicit solution (17) is $𝐱(t)=\exp (𝐏t)\left(𝐱\left(0\right)-{𝐏}^{-1}𝐐\right)+{𝐏}^{-1}𝐐.$

5. Turing’s Paper on Morphogenesis

The work of Alan Turing plays an important role in our paper. The main differential Eq. 11 owes much to ref. 1. There are some important differences. First, we use nonlinearity for the cell dynamics in contrast to the Turing linear setting. Nonlinearity allows us to address issues of stability, where the second derivative plays a crucial role and we are able to use associated domains of the cell dynamics more in accord with the biology. On the other hand, Turing developed his work in a partial differential equations framework, with reaction diffusion equations that reflect a continuum perspective of the nature of cells. That leads to some applications in morphogenesis, such as patterning in Zebra stripes (18, 19). Our own perspective differs. We feel that some of the basic features of morphogenesis must deal with few cells (embryogenesis, cell differentiation). The recent work of Chua (9) also develops Turing’s contributions in a different direction from our work.

Turing found an important example of the system of the same type we used in 4. Dynamics of a Tissue. The example shows how a system that is stable without diffusion becomes unstable in the presence of diffusion. Turing was motivated to understand morphogenesis with this example of instability. The example consists of two cells and two proteins. The variables $x_1,y_1$ represent concentrations of molecules (or proteins) for the first cell and $x_2,y_2$ represent those for the second cell. Turing’s two-cell reaction–diffusion example can be written as

$$\frac{d{x}_1}{dt}=\left(5x_1-6y_1+1\right)+0.5\left(x_2-x_1\right)$$ [12]

$$\begin{array}{c}\frac{d{y}_1}{dt}=\left(6x_1-7y_1+1\right)+4.5\left(y_2-y_1\right)\\ \frac{d{x}_2}{dt}=\left(5x_2-6y_2+1\right)+0.5\left(x_1-x_2\right)\\ \frac{d{y}_2}{dt}=\left(6x_2-7y_2+1\right)+4.5(y_1-y_2),\hspace{1em}{x}_1,y_1,x_2,y_2>0.\end{array}$$

The two cells are identical in this example and we can describe the cell dynamics as $\frac{d{x}_1}{dt}=\left(5x_1-6y_1+1\right)$, $\frac{d{y}_1}{dt}=\left(6x_1-7y_1+1\right)$. It is easy to transform the system in Eq. 12 into our form, $\frac{d𝐱}{dt}=\left(𝐅-𝐋\right)𝐱.$

Genome Dynamics of the Turing Example.

We now show that a key phenomenon of this example is the failure of the monotonicity condition. That is necessary to give rise to instability (morphogenesis).

Let us then study the monotonicity of 2. The Genome Dynamics of One Cell as well as perform a 2D analysis for the Turing example. First we construct matrix $𝐀$ for a single cell of the Turing example: $a=5,b=-7,c=6,d=7,$ and $𝐀=\left(\begin{array}{cc}\hfill 5\hfill & \hfill -6\hfill \\ \hfill 6\hfill & \hfill -7\hfill \end{array}\right)$. Here the Turing example assumes two identical cells and we can write the monotonicity condition as $⟨(5x-6y,6x-7y),(x,y)⟩<0$ for all $x,y>0.$ Thus, $5x^2-7y^2<0.$ If $x=2,y=1$, we can see that $5x^2-7y^2>0;$ therefore the Turing two-cell example fails the monotonicity condition (red solid circle in Fig. 3). Monotonicity is only a sufficient condition for stability. Now we check for stability.

The trace$\left(𝐀\right)=-2,$ and det$\left(𝐀\right)=1.$ Thus, the eigenvalues of $𝐀$ are given by ${\lambda }_i(𝐀)=-1,i=\mathrm{1,2}$ [and the eigenvectors are given by $v_i=\left(\mathrm{1,1}\right),i=\mathrm{1,2}$]. Therefore, the genome dynamics are stable for one cell and hence for two cells.

Diffusion Dynamics.

The diffusion dynamics in the system in Eq. 12 are expressed by the terms $0.5\left(x_2-x_1\right)$ and $4.5\left(y_2-y_1\right)$. Because the diffusion dynamics are represented by the negative Laplacian matrix as in 3. Cellular Dynamics and Their Architecture, their eigenvalues are nonpositive.

Full Dynamics.

Combining genome dynamics and diffusion dynamics gives the Turing example of the system in Eq. 19. The linear part of the system in Eq. 19 is

$$𝐌=\left(\begin{array}{cccc}\hfill 4.5\hfill & \hfill -6\hfill & \hfill 0.5\hfill & \hfill 0\hfill \\ \hfill 6\hfill & \hfill -11.5\hfill & \hfill 0\hfill & \hfill 4.5\hfill \\ \hfill 0.5\hfill & \hfill 0\hfill & \hfill 4.5\hfill & \hfill -6\hfill \\ \hfill 0\hfill & \hfill 4.5\hfill & \hfill 6\hfill & \hfill -11.5\hfill \end{array}\right).$$

The system in Eq. 19 has a unique equilibrium that is obtained by solving the right-hand side of the equation set equal to zero. Eigenvalues of $𝐌$ can be computed to be $2.0,-1,-1,-14.$ Because there is a positive eigenvalue, the system with diffusion is unstable. Therefore, the Turing system not only has a possibility of failure of stability but also in fact is unstable. Summarizing, the Jacobian at the equilibrium has four eigenvalues, one of which is positive. Thus, the full system with diffusion is not stable. In this way Turing showed that at equilibrium the two-cell example without diffusion is stable, but with diffusion has lost stability. We have remarked further on the role of monotonicity.

Wang and Slotine (20) examine a condition on the dynamics that depends on the diffusion coupling whereas our monotonicity depends only on the dynamics in each cell and not on the diffusion. But each condition plays a main role in the convergence.

Smale (11) examined similar equations with nonlinear cell dynamics. He considered each of two cells as having a global stable equilibrium, and therefore the cells were “dead” in an abstract mathematical sense. But upon coupling the two cells by diffusion, he proved that the resulting system has a global periodic attractor, and hence the cells become “alive.” Toward this end Smale’s work was a mathematical model similar to the Turing two-cell example but with dynamics of each cell not linear, leading to the model

$$\frac{d{x}^k}{dt}=R(x^k)+{\displaystyle \underset{i\in \text{set}\hspace{0.17em}\text{of}\hspace{0.17em}\text{cells}\hspace{0.17em}\text{neighboring}\hspace{0.17em}k\text{th}\hspace{0.17em}\text{cell}}{\sum {\mu }_{ik}(x^i-x^k)}},$$ [13]

where $k=1,\mathrm{\dots },N$ and $(x^i-x^k)\in {ℝ}^m.$ The first term above, $R\left(x^k\right)$ gives the dynamics for the kth cell and the second term describes the diffusion processes between cells. The principal case considered by Smale (11) is $m=4,$ $N=2,$ and shows for the appropriate choice of parameters $(R,{\mu }_k),$ the system has stable equilibria without diffusion and with diffusion has a global periodic attractor. Eq. 13 is precisely a form of our main equations. Again the phenomenon depends on the failure of monotonicity.

(Easy) Conjecture 1.

Generically monotonicity of a linear system in Euclidean space is equivalent to all eigenvalues negative (and real).

6. Lapse of Emergence

Here we discuss an avenue to study the departure from emergence, using our setting. Consider the Jacobian of $\frac{d𝐱}{dt}=\mathrm{𝐅𝐱}-𝐋$ (Eq. 11) at the equilibrium ${𝐱}_0$; that is,

$${\left(𝐃\left(𝐅-𝐋\right)\right)}_{{𝐱}_0},\hspace{1em}{𝐱}_0=({𝐱}_{\mathrm{0,1}},\mathrm{\dots },{𝐱}_{0,m}),$$

where ${𝐱}_{0,i}$ is the equilibrium of the dynamics of the ith cell and ${𝐱}_{0,i}$ are all equal. The main cause of lapse of emergence is the vanishing of the determinant of ${\left(𝐃\left(𝐅-𝐋\right)\right)}_{{𝐱}_0}$. As in our paper (15), the pitchfork bifurcation is signaled at a bifurcation parameter $\mu$, where the det${(𝐃\left(𝐅-𝐋\right))}_{{𝐱}_0}$ first becomes zero. Because ${𝐱}_{0,i}$ are equal, ${\mathrm{𝐋𝐱}}_0=0$ and ${𝐱}_0$ belongs to the $n$-dimensional harmonic space, kernel$\left(𝐋\right).$ Generically $-𝐋$ is contracting to kernel$\left(𝐋\right)$; that is, the eigenvalues of $-𝐋$ are ${\lambda }_k=0$ for $k\le n$, and for $k>n,{\lambda }_k<0.$

Now look at $𝐃{\left(𝐅\right)}_{{𝐱}_0}=(𝐃{\left({𝐅}_1\right)}_{{𝐱}_{\mathrm{0,1}}},\mathrm{\dots },𝐃{\left({𝐅}_m\right)}_{x_{0,m}})$ on the basin $𝐁$. Each $𝐃{\left({𝐅}_i\right)}_{{𝐱}_{0,i}}$ is contracting before the bifurcation, say for $\mu <0.$ At $\mu =0$, one can expect one of these contracting derivatives to become singular; for example, $𝐃{\left({𝐅}_1\right)}_{{𝐱}_{\mathrm{0,1}}}$ with one eigenvalue is equal to zero and the rest are negative. This is the beginning of the lapse of emergence in this scenario. Now restrict the dynamics to the protein space of the first cell to study the bifurcation. In this protein space we can expect the dynamics after the bifurcation to have two basins. This is the setting of the pitchfork bifurcation paper (15).

This paper can be used to examine the end of emergence in terms of cell division (symmetric or asymmetric or cancer) (21, 22).