Seafood prices reveal impacts of a major ecological disturbance

Significance

Coastal hypoxia is a growing problem worldwide, but economic consequences for fisheries are largely unknown. We provide evidence that hypoxia causes economic effects on a major fishery that was once the most valuable fishery in America. Our analysis is also a breakthrough in causal inference for coupled human-natural systems. Although establishing causality with observational data is always challenging, feedbacks across the human and natural systems amplify these challenges and explain why linking hypoxia to fishery losses has been elusive. We offer an alternative approach using a market counterfactual that is immune to contamination from feedbacks in the coupled system. Natural resource prices can thus be a means to assess the significance of an ecological disturbance.

Abstract

Coastal hypoxia (dissolved oxygen ≤ 2 mg/L) is a growing problem worldwide that threatens marine ecosystem services, but little is known about economic effects on fisheries. Here, we provide evidence that hypoxia causes economic impacts on a major fishery. Ecological studies of hypoxia and marine fauna suggest multiple mechanisms through which hypoxia can skew a population’s size distribution toward smaller individuals. These mechanisms produce sharp predictions about changes in seafood markets. Hypoxia is hypothesized to decrease the quantity of large shrimp relative to small shrimp and increase the price of large shrimp relative to small shrimp. We test these hypotheses using time series of size-based prices. Naive quantity-based models using treatment/control comparisons in hypoxic and nonhypoxic areas produce null results, but we find strong evidence of the hypothesized effects in the relative prices: Hypoxia increases the relative price of large shrimp compared with small shrimp. The effects of fuel prices provide supporting evidence. Empirical models of fishing effort and bioeconomic simulations explain why quantifying effects of hypoxia on fisheries using quantity data has been inconclusive. Specifically, spatial-dynamic feedbacks across the natural system (the fish stock) and human system (the mobile fishing fleet) confound “treated” and “control” areas. Consequently, analyses of price data, which rely on a market counterfactual, are able to reveal effects of the ecological disturbance that are obscured in quantity data. Our results are an important step toward quantifying the economic value of reduced upstream nutrient loading in the Mississippi Basin and are broadly applicable to other coupled human-natural systems.

Fertilizer use in coastal watersheds and agriculture intensification contribute to a growing incidence of coastal ecological disturbances (1–4). Of particular concern is coastal hypoxia [dissolved oxygen (DO) ≤ 2 mg/L] and potential impacts on marine fauna (1–4). The Western Hemisphere’s largest area of seasonal hypoxia is in the Gulf of Mexico (GoM; >20,000 km²) and overlaps with what was once the highest value fishery in the United States (brown shrimp) (www.st.nmfs.noaa.gov/commercial-fisheries/index) (5–7). Because controlling nutrient runoff upstream is costly, identifying and quantifying economic benefits downstream, including benefits to commercial fisheries, are essential for policy analysis (www.st.nmfs.noaa.gov/commercial-fisheries/index) (8–10). Although studies demonstrate ecological effects of hypoxia, economic consequences have not been established in this fishery.

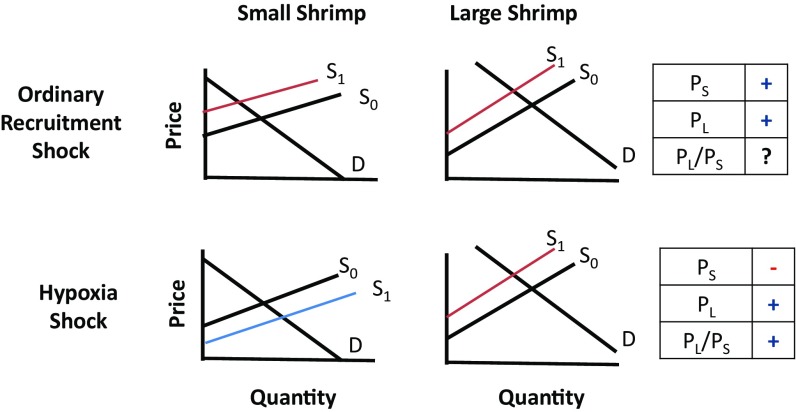
GoM brown shrimp (Farfantepenaeus aztecus) provide a unique opportunity to study the economic effects of hypoxia. First, the fishery is concentrated in regions of the GoM that become hypoxic seasonally (7) (SI Appendix, Figs. S1 and S2). Second, the temporal dynamics of brown shrimp and hypoxia match. Within season, harvest and hypoxic severity both peak in the summer, whereas across seasons, both the extent of hypoxia and shrimp populations exhibit substantial variation (5, 6, 7, 10, 11). This overlap highlights the potential significance of GoM hypoxia for the fishery but also the challenge of identifying its effects. Third, biological mechanisms that link hypoxia to shrimp abundance produce sharp predictions about the shrimp market. Bioenergetic consequences of hypoxia likely translate into impaired growth (12–16), reducing the average size of shrimp in the population. Shrimp also aggregate along the edges of the hypoxic area such that segments of the population are exposed to increased catchability early in the season when shrimp are small (12–14). Both mechanisms decrease the relative quantity of large shrimp, and thus increase the relative price of large shrimp (Fig. 1). In contrast, a positive recruitment shock increases (and a negative shock decreases) the number of shrimp that recruit into the fishery, and thus supply of both large and small shrimp, producing ambiguous predictions about relative quantity and price changes (Fig. 1). Recruitment shocks that alter the total number of individuals in the fishery could reflect changes in reproductive success, juvenile survival due to predation, or other environmental conditions in nursery grounds. Finally, the availability of fine-scale shrimp market data allows us to test the causal effects of hypoxia. Shrimp are sold in consistently used size-based categories defined by number of shrimp per pound, providing data on prices and quantities by size on a scale that is rarely available for other species (Fig. 2 and SI Appendix, Table S1 A and B).

Fig. 1.

Stylized model of the small and large shrimp markets. (Top) Short-run negative recruitment shock that decreases the abundance of new shrimp recruited into the fishery decreases the supply of both small and large shrimp (from S₀ to S₁). Holding demand (D) for each size class constant, both small and large shrimp prices (P_s and P_L) increase. Predictions about the relative price change (P_L/P_s) are ambiguous. (Bottom) Hypoxia shock increases the supply of small shrimp and decreases the supply of large shrimp due to aggregation (12) and bioenergetics effects on growth (13, 14). Holding D constant for each size class, P_s decreases and P_L increases. The relative price (P_L/P_s) increases unambiguously. The figure depicts the case of perfect market substitution between small and large shrimp, but the predictions hold for imperfect substitutes, P_L = α(P_s)^γ, where α > 0 is a constant and 0 ≤ γ ≤ 1 represents the degree of substitution, with γ = 1 being a perfect substitute (SI Appendix).

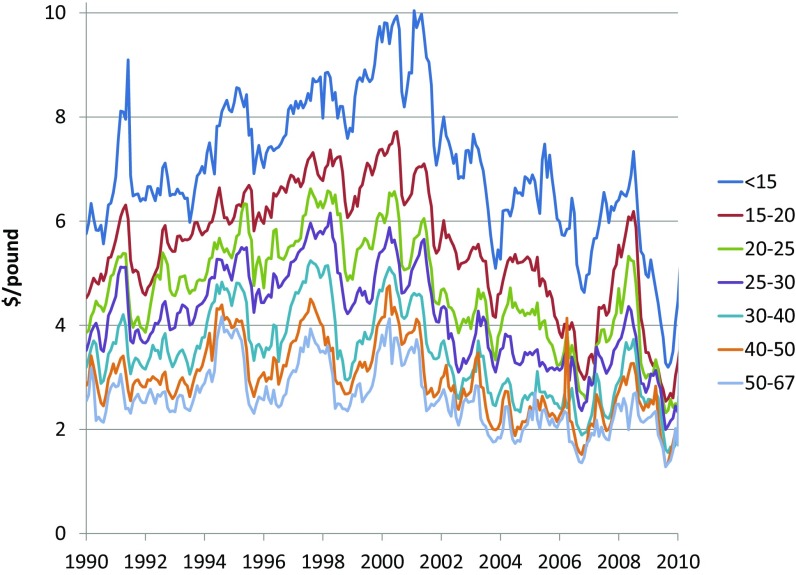
Fig. 2.

Monthly nominal brown shrimp prices by market size. GoM shrimp landings are sold in market categories based on number of shrimp per pound (Dataset S1). A smaller number of shrimp per pound indicates larger individual shrimp. The larger categories fetch higher prices (SI Appendix, Table S1B). Although price spreads fluctuate in the short run, price relationships across size categories are stable in the long run (23) (SI Appendix, Tables S14 and S15).

Although numerous effects of hypoxia on harvested marine species have been demonstrated, scientists have had difficulty linking large-scale, seasonal hypoxia to fishery losses (3). The areal extent of GoM hypoxia is negatively correlated with aggregate gulf-wide shrimp landings (7). Within the region most affected by hypoxia, these correlations are weaker and suggest negative effects on large shrimp and positive effects on small shrimp (SI Appendix, Table S2). Because establishing a causal effect of hypoxia requires a valid counterfactual, aggregate fishery landings are insufficient because so many environmental, economic, and institutional factors influence fishery outcomes (3, 10, 17, 18). Economic studies of other, smaller fisheries have found modest economic losses from hypoxia (17–20). For example, North Carolina brown shrimp experience low DO as juveniles and are caught as adults in oxygenated waters. The lagged response decreases catch by 13% (19), but economic value declines only 3.5% due to the mediating effect of human (fishing) behavioral responses to the natural system (17).

Data disaggregated by shrimp size, time within the season, and space provide new insights. All impact evaluations begin with a choice of which outcome or outcomes to measure. Moreover, which outcomes are relevant and feasible to track depend on feedbacks across the human and natural systems. Our theoretical model (Fig. 1) indicates that counterfactual outcomes (i.e., what would happen in the absence of hypoxia) could be defined in either terms of quantities landed or prices of small and large shrimp. A naive approach to analyze quantities would be to construct a quasi-experiment (a treatment effects model) based on spatial variation: Compare catches in a hypoxic location (treated) with catches in a nonhypoxic location (control) before and after the onset of hypoxia. We estimate this naive quantity-based model using difference-in-differences (DiD), which is a generalization of a before-after control impact (BACI) design. We then estimate models of fishing effort to evaluate the stable unit treatment value assumption (SUTVA) that is maintained in the naive model. The SUTVA requires that the treatment does not also affect control units. To contextualize the quantity-based results further, we run spatial-dynamic bioeconomic simulations in which, by construction, the counterfactual outcomes are known. We identify conditions under which SUTVA violations are consequential in coupled spatial-dynamic systems. Finally, we test the price-based implications of our theoretical model using time series analysis and a market-based counterfactual.

Results

The naive quantity-based analysis shows some evidence that contemporaneous hypoxia increases the catch of large shrimp but no evidence that contemporaneous hypoxia affects overall shrimp catch and no evidence of long-term impacts of hypoxia on shrimp catch (SI Appendix, Tables S3–S7). In summary, the treatment effects models produce null results. It is possible that the null results are valid and that hypoxia has no significant impact on the GoM shrimp fishery due to compensating responses by both the shrimp and the fishers. It is also possible that the SUTVA is violated in a way that significantly biases the results and leads to a null finding.

Analyses of fishing effort provide empirical evidence for violations of the SUTVA in the naive quantity-based analysis, which may account for null results. Effort response to profitability creates feedbacks between the human (fishing fleet) and natural (shrimp population) systems that undermine quasi-experimental approaches to observational data (10, 21). When an area becomes hypoxic, the increased catchability along the edge draws fishing effort into the area and away from nonhypoxic areas (12–14), changing the fishing effort in both places relative to the counterfactual. Dynamically, exposure to hypoxia impairs shrimp growth, changing the abundance and size structure of shrimp in the treated areas, thereby changing incentives and the resulting spatial behavior of fishermen. Because licensed commercial shrimp vessels can fish anywhere in the GoM brown shrimp fishery (i.e., off both the Louisiana and Texas coasts), fishing effort can substitute in or out of areas that we otherwise would expect to be unaffected by hypoxia. Estimates from panel data models of fishing effort as a function of contemporaneous and past hypoxia, as well as hypoxia in an adjacent area, show evidence of fleet-sorting behavior that would violate the SUTVA (SI Appendix, Tables S8–S13). Evidence for treatment/control contamination is strongest in models with the typical (<2.0 mg/L) hypoxia threshold. We also find empirical evidence for sorting behavior in the spatial discrete choice model of the GoM shrimp fleet behavior (SI Appendix, Table S3).

However, the SUTVA does not strictly hold in many treatment effects applications. Whether these models can be used to estimate reasonable causal relationships hinges on whether this contamination is small relative to the causal impact of treatment. We have shown that there is effort sorting based on hypoxia that could contaminate the control groups. Empirical evidence from a similar fishery (North Carolina brown shrimp) demonstrates that fishing behavior feeds back on the seasonal dynamics of the stock size and structure (22). We use a spatial-dynamic bioeconomic simulation to evaluate whether SUTVA violations are likely to be severe, thereby rendering estimates from quantity-based treatment effects models unreliable (10) (SI Appendix, Figs. S3 and S4).

The degree of treatment/control contamination depends on the extent of fishing responsiveness to expected revenues in the coupled system. The marginal rate of substitution (MRS) between the distance and expected revenue (the ratio of the distance and expected revenue coefficients) captures this responsiveness. When the fleet is highly responsive, it takes less expected revenue to move vessels (MRS = 4 km per dollar) and contamination is severe (SI Appendix, Fig. S3). With less responsiveness, more revenue is necessary to move vessels (MRS = 40 km per dollar), contamination is mild, and naive DiD on quantities will be nearly unbiased (SI Appendix, Fig. S4). The larger MRS is less responsive because, holding the distance coefficient fixed, the expected revenue coefficient is smaller. Empirical estimates are consistent with the high responsiveness. The mean MRS, which is vessel-specific, is 0.4 km per dollar, implying an order of magnitude more responsiveness than the severe contamination scenario in the simulation (SI Appendix, Fig. S3). Of the 3,576 vessels with at least two trip records during our sample period, 3,464 vessels (96.9%) appear more responsive to revenues than the cutoff for severe contamination (MRS = 4 km per dollar) and only seven vessels (0.2%) are less responsive than the mild contamination cutoff (MRS = 40 km per dollar). Simulation results combined with empirical evidence of sorting in panel data and discrete choice models imply that treatment effects from quantity-based models are highly unreliable in this setting.

In contrast to inferring causation from quantities landed, long-run shrimp price relationships provide a market-based counterfactual that does not require the SUTVA for validity (23) (Fig. 2). Rather, price-based tests rely on stable long-run relationships between shrimp prices in different size classes. To test for impacts of hypoxia, we analyze monthly brown shrimp prices in each of six size categories from January 1990 through March 2010 (SI Appendix, Table S1B). We first establish that long-run price relationships (Fig. 2) are stable according to bivariate cointegration tests (24) (SI Appendix, Tables S14 and S15). These tests imply that in the absence of any exogenous shocks to the fishery, short-run deviations from these relationships would be purely random.

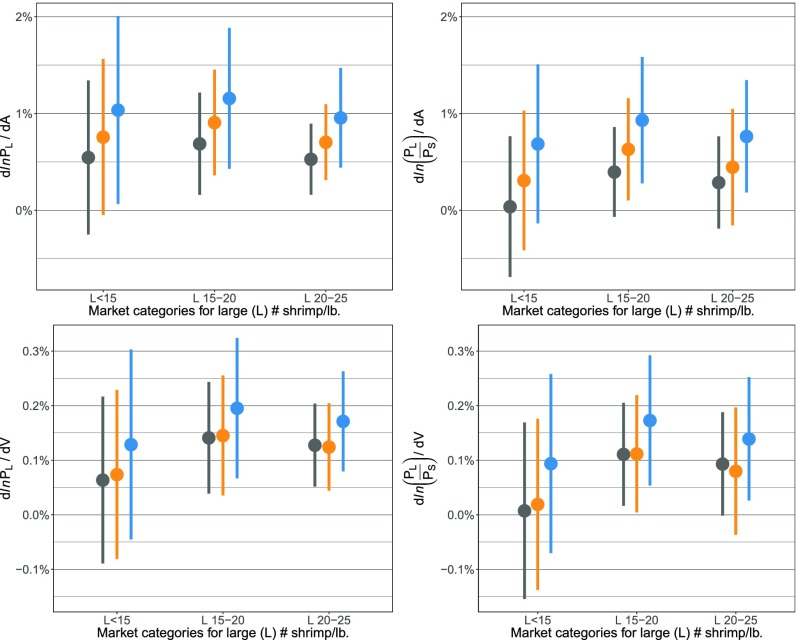
The test of impacts of hypoxia now centers on whether an exogenous shock from increasing or decreasing the areal extent of hypoxia affects the short-run relative prices of large and small shrimp. The results show that hypoxia explains short-run departures from long-run price relationships exactly as theory predicts (Fig. 1). Hypoxia unfolds continuously over time: Within each year, it builds up as summer approaches and dissipates in the winter months, and across years, its spatial extent varies. Results indicate that more severe hypoxia causes short-run increases in large shrimp prices compared with small shrimp prices (Fig. 3 and SI Appendix, Tables S16–S23). As markets adjust, short-run price deviations dissipate, presumably as fish buyers are able to secure more imports or shrimp from other US fisheries. Many of the coefficients are in the neighborhood of 0.01, which means that a 1,000-km² increase in the hypoxic area (a roughly 6% increase from the mean) triggers a 1% increase in the large shrimp price. Separate multivariate regressions for each large and small shrimp combination, two hypoxia measures, and two definitions of the dependent variable yield (3 × 3 × 2 × 2 = 36 regression results) (Fig. 3). In total, we run models for the nine pairwise size combinations: the two interpolation schemes, relative prices and prices in levels, two methods for calculating SEs (weighted least squares and Newey–West), and three different definitions of areal extent of hypoxia (1.5 mg/L, 2.0 mg/L, and 2.5 mg/L) plus a volumetric measure (2.0 mg/L) (9 × 2 × 2 × 2 × 4 = 288 regression results) (SI Appendix, Tables S16–S23). Our results are highly robust. Statistically significant hypoxia coefficients occur across a wide range of different pairwise price comparisons and model specifications.

Fig. 3.

Hypoxia increases large shrimp prices. Point estimates (circles) and 95% confidence intervals (lines) for the impact of hypoxia on large shrimp price in multivariate regressions using monthly data (SI Appendix, Tables S16 and S22) and weighted least squares are shown. Large (L) and small (S) shrimp are sold as the number of shrimp per pound. Small shrimp categories are 30–40 per pound (gray), 40–50 per pound (orange), and 50–67 per pound. (blue). (Left) Dependent variable is the natural logarithm of large brown shrimp price, and independent variables include the natural logarithm of small brown shrimp price, fuel price, sea surface temperature, hypoxia, and monthly fixed effects. (Right) Dependent variable is the natural logarithm of large-to-small relative brown shrimp price, and independent variables include fuel price, sea surface temperature, hypoxia, and monthly fixed effects. The horizontal axis in both panels labels the relevant large shrimp market category for regression, and each line result reflects a different combination of the small shrimp comparison group and the measure of hypoxia. The vertical axis reports the percentage of change in the large shrimp price [dln(P_L)] (Left) or large-to-small relative brown shrimp price [dln(P_L/P_S) (Right) associated with a 1,000-km² areal increase in the monthly hypoxia variable (dA) (Top) or a 1,000-km³ volume increase in the monthly hypoxia variable (dV) (Bottom). The monthly hypoxia measures are linearly interpolated annual snapshots of areal or volumetric extent of hypoxia (5) from July to the following July.

Furthermore, negative coefficients on fuel price indirectly support use of a market-based counterfactual (SI Appendix, Tables S16–S23). Exogenous increases in fuel prices reduce fishing effort, allowing more shrimp to escape capture and to reach larger sizes later in the season (10, 11, 22), increasing the catch of large shrimp and reducing the large shrimp price (Fig. 1).

Discussion

We analyze the impact of a large-scale environmental change (GoM hypoxia) on a natural resource sector (the GoM shrimp fishery). The singular challenge of conducting causal inference using observational data is to identify the counterfactual outcome: in our case, what would have happened in the absence of GoM hypoxia. We adopt a market counterfactual that theoretically combines ecological evidence about the effects of hypoxia with a multimarket model of size-based shrimp pricing. We find strong evidence in time series of prices that hypoxia causes economic effects. These effects could not be identified in a DiD model of quantities because feedbacks in the coupled human-natural system cause treated zones to contaminate control zones. The mechanism driving contamination is the fishing fleet’s dynamic response to profit opportunities over space. When some areas become hypoxic, the fishing fleet sorts into or out of other areas that are otherwise unaffected by hypoxia, rendering candidate control areas changed and thus contaminated. Whether contamination is severe enough to cause practical problems (large bias) for causal inference is an empirical question. We show that contamination is problematic in our setting by combining insights from a spatial-dynamic bioeconomic simulation, a panel model of fishing effort, and a discrete choice model of fishing location. Consistent with these findings, the naive DiD model produces null results. Time series analyses of prices, in contrast, are immune to this spatial contamination because the counterfactuals are based on the GoM-wide market, not on the stock of the resource in different locations over time.

Across time series models, hypoxia coefficients are consistently positive. Only 11 of 288 estimated hypoxia coefficients are negative, and of these coefficients, just one is statistically significant (at the 10% level). Although the results tend to be stronger when the dependent variable is the natural log of the large shrimp price (rather than the relative price of large shrimp to small shrimp) (SI Appendix, Tables S16–S23), the main conclusions hold for both definitions of the dependent variable. These conclusions are also invariant to the interpolation scheme, areal extent versus volumetric extent of hypoxia, DO cutoff for areal extent of hypoxia, and whether or not quantity weights are used in the models.

Although Fig. 1 does not predict specific magnitudes of hypoxic effects across size classes, effects appear less pronounced for the largest shrimp size class (0–15 shrimp per pound). A possible explanation is that 0–15 shrimp are substantially more expensive in absolute terms. So, a 1% change in price for the largest shrimp translates into a large absolute change compared with smaller size classes. Also, the markets for 0–15 shrimp are thin; that is, the trading volume for the largest shrimp is low, which could introduce more volatility and thus make it harder to resolve short-run disturbances attributable to hypoxia. The fact that the results are stronger for the weighted least squares regressions for 0–15 shrimp (and comparable for other size classes) provides some indirect support for this explanation. A related point is that the 0–15 shrimp are a unique product and, as a consequence, are potentially less integrated with other shrimp markets. We see some evidence of less integration in the low P value for the Law of One Price in the 0–15/30–40 comparison (SI Appendix, Table S15, column G).

Negative fuel price coefficients provide supporting evidence for the validity of using price-based models to infer the causal impact of hypoxia. People fish less with higher fuel prices; as a result, more small shrimp escape to larger size classes, putting downward pressure on the price of large shrimp. Fuel price coefficients are negative in all 144 models with the logarithm of large shrimp price as the dependent variable and statistically significant in 142 of those models. For the relative price models, the results are more mixed, although the only counterexamples (positive and significant fuel price coefficient) are for the 0–15/30–40 comparison, the same market that showed weaker results on the hypoxia coefficient.

There are limitations of the price analysis. First, use of an annual hypoxia measure potentially introduces errors-in-variables bias. In a univariate model, this effect would attenuate the hypoxia coefficient (decrease its magnitude) and reduce the likelihood that it is statistically significant. Under plausible conditions, this result generalizes to multivariate settings. Thus, the fact that we find strong statistical evidence for the effects of hypoxia on large shrimp prices suggests that the actual effects are quite pronounced and may be larger in magnitude than what we are able to quantify. Second, the global nature of the shrimp market implies that the price effects of hypoxia are transitory. Per capita consumption of shrimp in the United States is higher than any other seafood product, and roughly 80% of that consumption is imported (23). Short-run hypoxia-induced price changes do not last because buyers can source more product from imports. That process is not instantaneous, such that our models are able to reveal effects of hypoxia in monthly observations. Thus, economic data can indicate when a consequential ecological disturbance has occurred locally in the presence of a highly integrated global market for the affected resource, but a reasonably high level of temporal resolution is required. Third, the price analysis does not provide complete information for a policy analysis. An ideal claim for policy analysis would be something like “reducing nutrient runoff X% leads to economic benefits for shrimp (and other) fisheries of $Y.” The science of causal inference using observational data on spatial-dynamic systems is not sufficiently advanced to make such a claim at this point.

Our modeling demonstrates that the interaction between economic and ecological phenomena is more nuanced than a traditional approach to causal inference would imply. Because spatial sorting of the fishing fleet contaminates candidate control sites, we do not have estimates of quantity changes due to hypoxia. We also do not have enough spatiotemporal resolution in the environmental data to develop a structural empirical bioeconomic model of hypoxia and its effects on GoM fisheries. Nevertheless, we are able to show causal effects of hypoxia on shrimp markets, providing an important step toward quantifying the full economic consequences of nutrient pollution. This step significantly improves on simple correlation analysis that has neither theoretical nor empirical grounding in causation. A complete policy analysis of GoM hypoxia will require methodological developments in causal inference for coupled human-natural spatial-dynamic systems as well as increased efforts to measure and model DO over space and time in the GoM.

Departures from stable price relationships could reveal impacts of an ecological disturbance on other fisheries. Whether researchers can identify impacts from prices depends on the fisheries, the seafood markets, and data availability. Blue crabs (Callinectes sapidus) in North Carolina estuaries and in the Chesapeake Bay are exposed to varying levels of hypoxia (18). They are sold as hard, soft, and peeler (crabs in the process of molting). A substantial premium for soft and peeler crabs exists (the nominal 2014 Chesapeake Bay price for soft and peeler blue crabs was $3.63 per pound compared with $1.61 per pound for hard-shell crabs), but the markets are connected. Because laboratory studies demonstrate that hypoxia affects blue crab molting (25), prices could test for effects of hypoxia on blue crabs following the logic of our GoM shrimp analysis. A larger scale phenomenon is the effect of the El Nino-Southern Oscillation (ENSO) in the Pacific on the productivity of Peruvian anchoveta (Engraulis ringens), the world’s largest fishery by quantity. The anchoveta is a small, bony pelagic fish that is mostly reduced to fishmeal. Traditionally, fishmeal was a part of the larger market for vegetable meals that is dominated by soybean meal (26), and the price of fishmeal relative to soybean meal was constant in the long run. With increased demand for fishmeal from growth in aquaculture, this relationship changes during ENSO periods (27, 28). Another intriguing large-scale possibility is the use of market-based counterfactuals to analyze the effects of ocean acidification on capture fishery and aquaculture production of calcifying organisms. Nevertheless, not all disturbances will manifest in prices. A recent assessment of the impact of the Fukushima nuclear disaster on the Japanese markets for whitefish did not find price effects (29). In this case, there is a clear quantity effect (decreased purchases of locally caught Japanese fish) but no price change due to the highly integrated nature of the global whitefish market. Unlike our setting with shrimp markets differentiated by size, the commodity nature of whitefish allowed Japanese companies to replace domestic supplies with imports of other whitefish without bidding up the prices of individual products.

The problem of treatment/control contamination in coupled spatial-dynamic systems is generic and warrants further scientific attention. The sorting mechanism that poses identification problems in our quantity-based model applies to other spatially explicit shocks and interventions that influence human/environment interactions. Technological disasters, such as oil spills; policy interventions, such as forming a marine protected area; or a natural disaster, such as a major hurricane, could affect resource stocks in seemingly unaffected locations through human/natural feedbacks; that is, a disturbance occurring in a particular place at a particular time can induce sorting behavior of the fishing fleet. Other locations far from the oil spill, outside the marine reserve, or regions unaffected by the hurricane are problematic controls if sorting behavior reaches them. For oil spills and marine reserves, one might expect more fishing effort in the unaffected areas, whereas for hurricanes, one might expect less fishing effort. The economics literature on marine reserves explicitly raises concerns about this mechanism, but the marine conservation literature ignores it (10, 30, 31).

The logic extends to terrestrial systems. For example, if a researcher uses areas outside a protected area to identify effects of protection on deforestation, sorting effects on the timber industry or fuel-wood gathering could contaminate the control areas. Researchers have acknowledged this potential bias in evaluating the effects of terrestrial protected areas on deforestation (32). However, corrections for the bias assume that spillovers are local and not part of a spatial-dynamic system. As such, the SUTVA is invoked for nonlocal control sites without an explicit conceptual model of the coupled system. In all coupled spatial-dynamic systems, spatial identification in traditional DiD models may be possible if spatial sorting is minimal. However, when sorting (or spatial dispersal of the resource) is substantial, researchers should be skeptical of treatment effects or BACI-style estimates of impacts and explore alternative approaches to identification, including the use of market counterfactuals.

Materials and Methods

Naive Treatment Effects Models.

Hypoxia is first modeled as a natural experiment from which one might naively expect to identify causal effects of the ecological disturbance on shrimp quantities landed. “Treated” areas are ones that experience hypoxia, whereas “control” areas are ones that remain oxygenated. We use fine-resolution data both spatially (zones defined below) and temporally (daily).

The National Oceanic and Atmospheric Administration’s shrimp commercial landings (SHRCOM) database records, on a trip basis, landed weight and landed value for each shrimp species within each of 10 size classes that reflect standard market categories. Two size classes are not useful for most of our analysis (unclassified and pieces). The remaining classes correspond to the number of shrimp per pound: (i) <15, (ii) 15–20, (iii) 20–25, (iv) 25–30, (v) 30–40, (vi) 40–50, (vii) 50–67, and (viii) >67.

Landings in the SHRCOM data are assigned to National Marine Fisheries Statistics “subareas.” The SHRCOM database also contains the depth at which shrimp are caught. This information overestimates the amount of shrimping effort in the midshelf region (33), so we aggregate the depth indicator into three bins that redistribute some of the midshelf effort to near-shore and offshore bins. Combining depth information with statistical subareas yields depth-zone/subarea polygons (SI Appendix, Fig. S1).

We use two distinct sources of variation in hypoxia severity: seasonal variation within year and spatial variation across years (6, 13, 14). Hypoxia is defined by whether an observation in the polygon has DO < 2 mg/L during the summer or fall Southeast Area Monitoring and Assessment Program (SEAMAP) survey (34). We refer to this measure as a threshold measure. Because the SEAMAP survey provides data only twice during the year (summer: June–July, fall: October–November), we extrapolate hypoxia for the remaining months of the year. In effort models (below), we create alternative definitions based on polygon averages, as well as two different cutoff points (<1.5 mg/L and <2.5 mg/L). We use SEAMAP data for 1986 through 2009, noting that we truncated the sample in 2010 to avoid confounding effects of the Deepwater Horizon incident (SI Appendix, Fig. S2).

Catch (C) is conditional on whether zones are hypoxic (H) or nonhypoxic (N). With just two zones, the average effect of hypoxia on catch is:

$$\left\{E\left[C_1|H\right]-E\left[C_0|H\right]\right\}-\left\{E\left[C_1|N\right]-E\left[C_0|N\right]\right\},$$ [1]

where subscripts 1 and 0 indicate time with 1 = after hypoxia and 0 = before hypoxia. Nonhypoxic zones provide counterfactuals for hypoxic zones, differencing out seasonal variation in fishing outcomes shared across hypoxic and nonhypoxic zones. The treatment effect is identified using DiD (31, 35–38), and the estimating equation is:

$$ln{C}_{jmy}=\beta ln{E}_{jmy}+d_j+d_y+d_m+d_{jy}+d_{jm}+{\gamma }_0{H}_{jmy}+{\displaystyle \sum }_{\tau =1}^{{\tau }^{max}}{\gamma }_{\tau }{H}_{j\left(m-\tau \right)y}+{\epsilon }_{jmy}.$$ [2]

E is effort, j indexes the spatial location (combination of subarea and depth zone), m is month, y is year, d terms are fixed effects that capture different combinations of location and time, H is a binary variable to indicate whether the location is hypoxic in month m and year y, $\tau$ is the lag length, ${\tau }^{max}$ is the maximum lag length considered, and $\epsilon$ is a random shock. The dependent variable is defined in four different ways: aggregate catch, large shrimp catch, medium shrimp catch, and small shrimp catch (SI Appendix).

To address endogenous fishing effort, we use instrumental variables and construct an instrument for effort using a conditional logit model (39) with alternative specific constants (40, 41). The deterministic portion of the choice model (v) is defined for each individual vessel (i = 1, 2, … I), for each choice (j = 1, 2, … J), on each day (t = 1, 2, … T):

$$v_{ijt}={\delta }_j+{\mathit{X}}_{\mathit{t}}{\mathit{\theta }}_1+{\mathit{Y}}_{\mathit{ij}}{\mathit{\theta }}_2+{\mathit{Z}}_{\mathit{jt}}{\mathit{\theta }}_3.$$ [3]

There are alternative-specific constants (${\delta }_j$) and covariates that vary over just time X (shrimp price, fuel price), individual and location Y (travel distance), and location and time Z (expected revenue and catch, wave height). Results of the logit model generate predicted effort for each zone-time combination. Predictions use a daily time step in which all of the covariates are exogenous, and the predicted probabilities are aggregated across individual vessels and time to arrive at monthly predicted effort. The choice structure follows the naive treatment effects model with three depth bins and 10 statistical areas for a total of 30 discrete locations. We also include the choice of not fishing (42) for a total of 31 choices (j = 1, 2, …, 31). Following Smith et al. (40) and Zhang and Smith (43), we assume that daily choices are independent.

The treatment effects model spans January 1986–March 2010 for a total of 291 mo. The discrete choice model is daily, from January 1, 1986–April 19, 2010, so there are 8,875 days in our choice model (SI Appendix).

Diagnosing Treatment/Control Contamination.

A key assumption in treatment effects models is the SUTVA, which means that treatment does not affect the control. Sorting behavior in the discrete choice model calls into question the SUTVA. To examine this issue further, we estimate panel models of fishing effort with two-way fixed effects (zone-depth and year-month) that include hypoxia status as a covariate. Across models, we use average and threshold measures and three different cutoffs (DO < 1.5 mg/L, DO < 2.0 mg/L, and DO < 2.5 mg/L). Using nomenclature from Eq. 2, the estimating equation is:

$$E_{jmy}=d_j+d_y+d_m+d_{jy}+d_{jm}+{\gamma }_0{H}_{jmy}+{\displaystyle \sum }_{\tau =1}^{{\tau }^{max}}{\gamma }_{\tau }{H}_{j\left(m-\tau \right)y}+{\gamma }_{{\tau }^{max}+1}{H}_{(j-1)my}+{\epsilon }_{jmy}.$$ [4]

Hypoxia enters different models contemporaneously, lagged in time, and lagged in space. If the SUTVA holds, no hypoxia coefficient should be statistically different from zero.

A spatial-dynamic bioeconomic simulation of the GoM brown shrimp fishery illustrates the potential for treatment/control contamination by analyzing the effects of hypoxia on landings across space, time, and size classes. The model is an age- and size-structured bioeconomic model of brown shrimp (10). Each year, shrimp recruit exogenously to each of nine zones. They grow and experience natural and fishing mortality throughout the year. The nine zones reflect stylized, qualitative patterns in the spatial and temporal dynamics of hypoxia: One zone is seasonally hypoxic in every year, two zones are never hypoxic, and the remaining six zones are hypoxic in some years but not in others (based on random draws).

Three biological consequences of hypoxia are modeled in the stock dynamics: (i) Hypoxia increases mortality, (ii) hypoxia slows the growth of shrimp (flatter slope of the von Bertalanffy growth function), and (iii) hypoxia leads to aggregation of shrimp (increased catchability). Shrimp prices are exogenous but size-dependent, with larger shrimp fetching higher prices. Effort responds endogenously to distance to fishing grounds (the different zones) and to spatiotemporally explicit expected revenues, which are driven by size-specific abundance, catchability, and prices. Spatially explicit effort in each time period, in combination with the associated spatially explicit stock, produces spatially explicit fishing mortality, which feeds back into expected revenues in the next time period. Details on the analytical structure, parameterization, and model fit with observational data are provided in a study by Smith et al. (10). The model extension here distributes shrimp recruitment over 100 d and tracks individual daily shrimp cohorts as they grow and are differentially exposed to hypoxia over time and space.

Time Series Analysis of Prices.

In time series models, we aggregate all data spatially and focus on the entire GoM brown shrimp market. We use a continuous annual measure of areal extent of hypoxia (mean DO < 2.0 mg/L) (5) and then interpolate the annual measure to the monthly scale in two ways: a linearly interpolated annual snapshot of the areal extent of hypoxia in square kilometers (5) from July to the following July and a linearly interpolated annual snapshot of areal extent of hypoxia in square kilometers (5) from July down to zero in January and up to the next year’s annual snapshot in the following July. As robustness checks, we create three other hypoxia measures with the same two interpolation schemes (areal extent < 1.5 mg/L, areal extent < 2.5 mg/L, and volumetric extent < 2.0 mg/L). We use monthly prices of brown shrimp from the GoM fishery from January 1990 to March 2010. Although we have access to shrimp prices from earlier and later periods, we truncate the series in this manner for two reasons. First, the annual measure of hypoxia has a gap in 1989 because no data were collected in that year. This gap poses problems for time series models and would require interpolation across an entire year without any data. Second, the Deepwater Horizon incident and associated fishery closures occurred in April 2010.

The price data are aggregates from the SHRCOM database. Large shrimp prices are represented by the <15, 15–20, and 20–25 cohorts, where cohort refers to number of shrimp per pound as in previous sections. The small shrimp prices are represented by the 30–40, 40–50, and 50–67 cohorts. In the pairwise comparisons, we omit the size category 25–30. We include diesel price as a covariate due to its importance in influencing shrimping effort and sea surface temperature, which could influence abundance patterns and be correlated with hypoxia (SI Appendix, Table S1B).

We test that individual shrimp price series are nonstationary in levels but stationary in first differences (23, 44, 45). This test examines whether spurious correlations could be induced by regressing levels of shrimp prices on covariates such as hypoxia. We next test for whether pairwise small and large shrimp prices are cointegrated and that size-based prices are proportional to each other (24, 46). Cointegration implies that when regressing a large shrimp price on a small shrimp price, the residuals are stationary and spurious correlation is not an issue. These two steps provide justification for our analysis of the effects of hypoxia on shrimp prices because they establish stable long-run price relationships as a market counterfactual. Regressing large shrimp price on small shrimp price and hypoxia then becomes a test of whether hypoxia causes a departure from this stable long-run relationship. The regression models take one of the two following forms that capture different degrees of substitutability between large and small shrimp (Fig. 1):

$$ln{P}_{L,t}=\alpha +\beta H_{k,t}+\gamma ln{P}_{S,t}+{\mathit{X}}_{\mathit{t}}\mathit{\theta }+{\epsilon }_{L,t},$$ [5]

$$ln\left(P_{L,t}/P_{S,t}\right)=\alpha +\beta H_{k,t}+{\mathit{X}}_{\mathit{t}}\mathit{\theta }+{\epsilon }_{L,t}.$$ [6]

P is price per pound of brown shrimp, $\alpha$ is a constant, $\beta$ is the hypoxia parameter of interest, H is hypoxia (areal or volumetric extent and either of two temporal interpolations), k is the interpolation scheme used in the model, L is the large size category, S is the small size category, $\gamma$ is the parameter on small shrimp price, ${\mathit{X}}_{\mathit{t}}$ contains the other covariates with associated parameter vector $\mathit{\theta }$, and ${\epsilon }_{L,t}$ is a stationary error term (SI Appendix).

Our models control for other factors that influence either demand for or supply of domestic shrimp. Seasonal dummies account for seasonality of demand and seasonal pattern of the annual fishery. For the supply side, we include sea surface temperature, which could influence recruitment, and fuel prices, which are the major driver of variable costs and thus influence total fishing effort. All other demand and supply shocks (other than hypoxia) are captured in the random error term, which is assumed to be transitory.