How electron two-stream instability drives cyclic Langmuir collapse and continuous coherent emission

Significance

Electron two-stream instability (ETSI) is believed to be responsible for the radio bursts observed in both the solar corona and interplanetary medium. What nonlinear kinetic processes self-consistently reconcile the several orders of magnitude difference between the short linear saturation time scale of ETSI and the long duration of bursts is fundamental in plasma turbulence and has remained unsolved for nearly 50 y. Using massive particle-in-cell simulations, we find a self-consistent and complete nonlinear solution to this problem.

Abstract

Continuous plasma coherent emission is maintained by repetitive Langmuir collapse driven by the nonlinear evolution of a strong electron two-stream instability. The Langmuir waves are modulated by solitary waves in the linear stage and electrostatic whistler waves in the nonlinear stage. Modulational instability leads to Langmuir collapse and electron heating that fills in cavitons. The high pressure is released via excitation of a short-wavelength ion acoustic mode that is damped by electrons and reexcites small-scale Langmuir waves; this process closes a feedback loop that maintains the continuous coherent emission.

Electron beams accelerated by solar flares and nanoflares are believed to be responsible for several types of solar radio bursts observed in the corona and interplanetary medium, including flare-associated coronal type U and J and interplanetary type III radio bursts, and nanoflare-associated weak coronal type III bursts (1–4). In 1958, Ginzburg and Zhelezniakov first proposed a basic framework for such bursts, which was subsequently refined by others (refs. 5 and 6 and references therein). In essence, the scenario is one in which the electron two-stream instability (ETSI), driven by electron beams, generates Langmuir waves that are converted into plasma coherent emission via nonlinear three-wave coupling [e.g., two Langmuir waves and one ion acoustic wave (IAW)]. However, the mechanism whereby the nonlinear ETSI produces coherent emission with a duration of several orders of magnitude longer than the linear saturation time is not well understood (6–9). Nonlinear evolution of ETSI is a fundamental problem in nonlinear wave theory in which disparate three-wave couplings dominate the energy transport and dissipation (10). It has broad applications in plasma physics, planetary physics, and astrophysics, such as terahertz emission in laser beam experiments, radio bursts from Jupiter, pulsars, and the formation of exotic astrophysical objects.

In the classical Kolmogorov turbulence scenario, the balance between energy input and its final absorption is controlled by a nonlinear cascade from large spatial scales (the region of external forcing) to viscosity-dominated short wavelengths. In plasmas, the source of instability is often beams of charged particles that generate Langmuir waves. At shorter wavelengths, the natural candidate to provide the sink of wave energy is Landau damping. However, nonlinear disparate wave interactions, it follows from direct calculation of basic three-wave coupling, can only lead to inverse cascades (to longer wavelengths) through modulational instability (11), and away from the Landau damping region of the spectrum. The eventual nonlinear process capable of overriding this inverse cascade was suggested by Zakharov, namely Langmuir collapse (LC), which is analogous to a self-focusing of the Langmuir waves packets, or cavitons (12, 13). LC has been discovered in both experiments and space observations (14–16); in particular, LC has been observed in association with solar radio bursts (15–17).

There are several problems with the current models of type III radio bursts. The most important physics missed is the feedback of LC that, we will show, plays a critical role in maintaining continuous coherent emission. Second, the existing models (ref. 6 and references therein) use a common assumption that we call “weak turbulence condition,” specifically, the growth rate of Landau fluctuation driven by an electron beam is much smaller than that of the ETSI, or $v_{te,c}<v_b<<{(n_c/n_b)}^{2/3}{v}_{te,b}$, where $v_b$ is the electron beam drift, $v_{te,c}$ and $v_{te,b}$ are the thermal velocity of core background electrons and beams, respectively, and $n_c/n_b$ is the core-beam density ratio. However, recent observations suggest that the electron beam density near coronal source regions is comparable to the background density (18). Thus, the weak turbulence condition can be significantly violated. Third, the models assume that the emission is produced by coupling between Langmuir waves and IAWs, but IAWs are expected to be heavily damped in the nearly isothermal plasma of the corona.

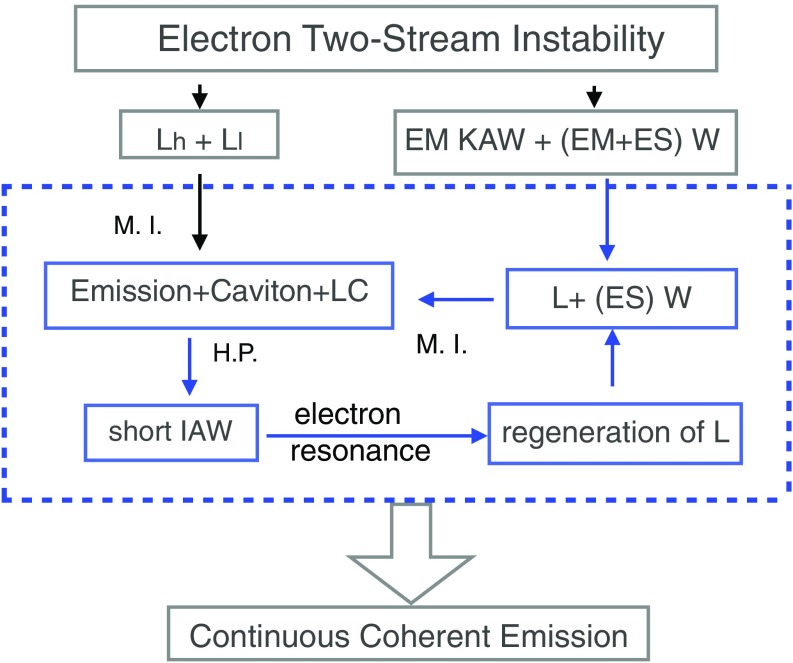
We here present a mechanism based on a model of cyclic LC and Langmuir wave regeneration. The results of massive particle-in-cell (PIC) simulations of the ETSI show how the nonlinear ETSI produces coherent emission that lasts five orders of magnitude longer than the linear saturation time. As shown in Fig. 1, the extended emission time is a consequence of repeated LC, which regenerates Langmuir waves through resonance with intermediary short-wavelength IAWs. The short-wavelength IAW is produced due to the release of the ions inside the caviton caused by LC. Near the linear saturation of the ETSI, LC is initiated by the interactions between the high-frequency Langmuir waves produced in the background and the low-frequency Langmuir waves in the solitary wave-trapped electrons. As the ETSI enters the nonlinear decay, LC regenerates Langmuir waves, interacts with electrostatic (ES) whistler waves, and reinitiates LC, thus forming a feedback loop. ES whistler waves are sustained by electromagnetic (EM) kinetic Alfvén waves (KAWs) and whistler waves that are produced simultaneously with the Langmuir waves. The structure of this paper is as follows: we first present the simulation results on the generation and regeneration of LC and emission during the nonlinear stage of ETSI. We then give the governing equations and condition for LC. Finally, we show how LC regenerates Langmuir waves.

Fig. 1.

Schematic diagram showing how LC, occurring during the nonlinear stage of the ETSI, forms a feedback loop (within the blue-dashed line box) that produces coherent emission continuously. H.P., high pressure; L, Langmuir wave; $L_h$, Langmuir wave with higher frequency produced by the background electrons; $L_l$, Langmuir wave with lower frequency produced by the trapped electrons in solitary waves; M.I., modulational instability; $W$, Whistler wave.

Simulation Results of Cyclic Emission

The initialization of 2.5D PIC simulation is described in the caption of Fig. 2. The ratio between the initial beam velocity and the thermal velocity $v_{bd,0}/v_{te,0}\approx 12>{(n_c/n_b)}^{2/3}\approx 5$, where $v_{te,0}$ is the initial thermal velocity of both core and beam electrons, guarantees a strong ETSI. The total simulation time is ${\omega }_{pe,0}t=\mathrm{14,400}$, during which ETSI experiences a linear and nonlinear stage, saturation, and nonlinear decay, and eventually reaches turbulent equilibrium, where the energy exchange between particles and waves reaches balance (19).

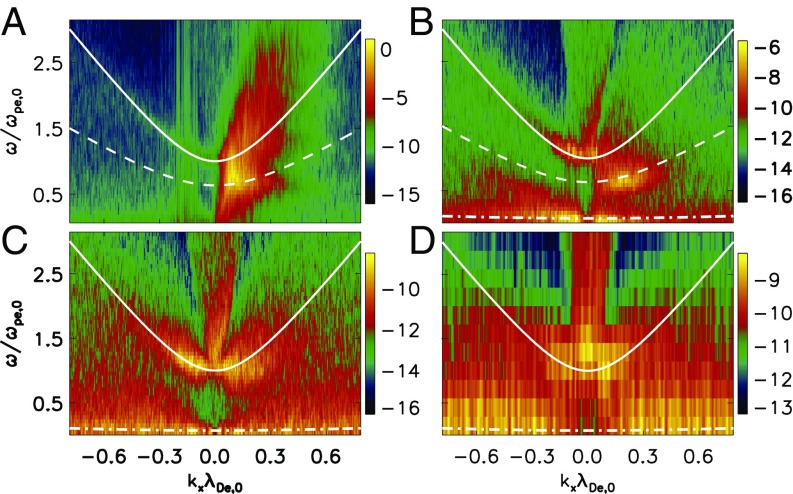
Fig. 2.

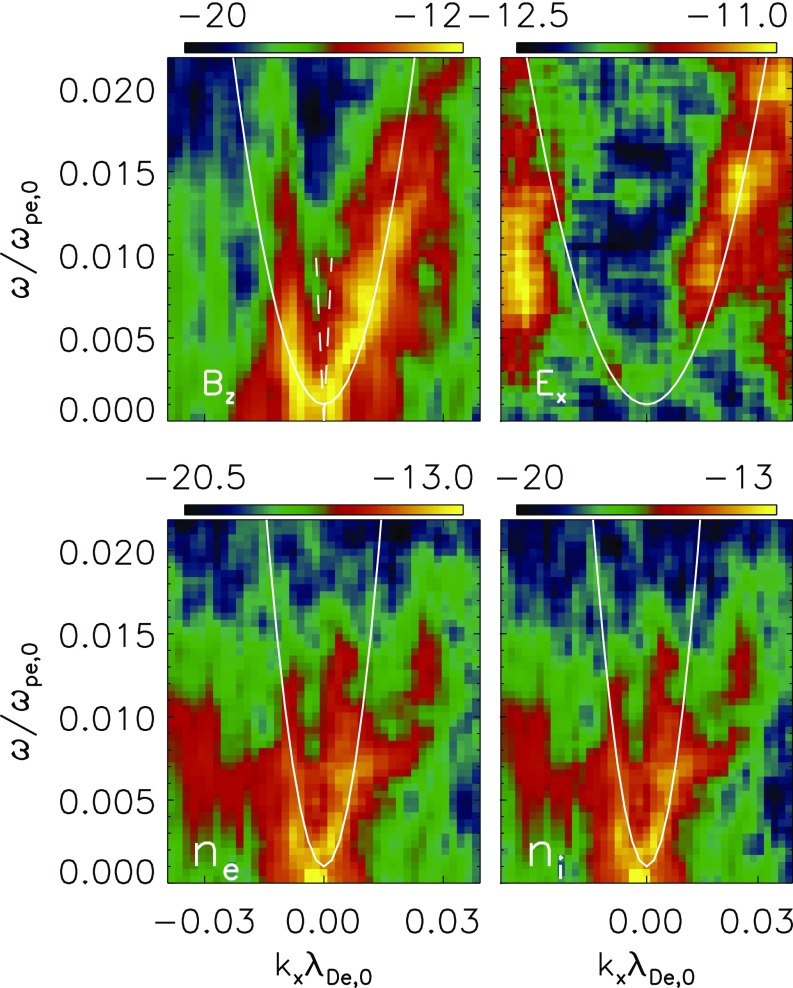
The $\omega /{\omega }_{pe,0}$–$k_x{\lambda }_{De,0}$ diagrams of the parallel propagating high-frequency electric field component $E_x$ at four time intervals: (A) ${\omega }_{pe,0}t=0–100$, (B) ${\omega }_{pe,0}t=320–420$, (C) ${\omega }_{pe,0}t=\mathrm{2,880}–\mathrm{2,980}$, and (D) ${\omega }_{pe,0}t=\mathrm{10,560}–\mathrm{10,580}$. Also shown are the dispersion relations (Eq. 1) of the background electrons (solid lines), trapped electrons (dashed lines), and the short-wavelength IAW (dash-dotted lines). For the waves in space, see Figs. S1–S3. The 2.5D PIC simulation is initialized with a homogeneous plasma and uniform magnetic field $𝐁=B_0\widehat{x}$. The initial ion velocity distribution function is a single Maxwellian and the electron velocity distribution function is core–beam bi-Maxwellian (19). The initial density ratio of the beam and core is $n_{b0}/n_{c0}=0.1$, and the core and beam temperatures $T_{b,0}=T_{c,0}$. The initial drifts of the core $v_{cd,0}$ and the beam $v_{bd,0}$ satisfy $(1-\delta )v_{cd,0}=-\delta v_{bd,0}$ to maintain null current; $v_{bd,0}=12v_{te,0}=60v_{A,0}$, where $v_{A0}$ is the initial Alfvén speed and $v_{te,0}={(k{T}_{c,0}/m_e)}^{1/2}$. The speed of light $c=100v_{A,0}$ and $m_i/m_e=100$. The ion temperature $T_{i,0}=T_{c,0}$. The boundaries are periodic, and the box size $L_x=L_y=\mathrm{3,200}{\lambda }_{De,0}$ (${\lambda }_{De,0}\equiv v_{te,0}/{\omega }_{pe,0}$), where ${\omega }_{pe,0}$ is the initial electron plasma frequency. The electric field is normalized by $E_0=v_{A,0}{B}_0/c$; $\beta =16\pi k{T}_{c,0}/B_0^2=0.25$.

The growth stage of ETSI includes the linear and nonlinear stage (${\omega }_{pe,0}t=0$ to 200). The saturation stage is from ${\omega }_{pe,0}t\approx 200$ to 1,000. The linear stage only lasts for ${\omega }_{pe,0}t=2$ as defined by the growth rate of the ETSI from quasi-linear theory [i.e., $\gamma =\sqrt{3}/2{(n_{b0}/n_{c0})}^{1/3}{\omega }_{pe,0}\approx 2{\omega }_{pe,0}$]. During the growth stage, the large beam drift suppresses the generation of Langmuir waves (20). The fastest-growing mode of the solitary wave has $k_x{\lambda }_{De,0}\approx v_{te,0}/v_{bd,0}\approx 0.1$ and $\omega /{\omega }_{pe,0}\approx {(n_{b0}/n_{c0})}^{1/3}{\omega }_{pe,0}\approx 0.5{\omega }_{pe,0}$ as shown in Figs. 2A and 3A. Quickly, the ETSI loses $\sim$85% of the kinetic energy of the beams and reaches saturation with the beam drift $v_{db}$ being about 2 times the core thermal velocity $\sim 2v_{te,c}\text{to}\sim 30v_{A,0}$. The thermal velocity of the electron beams $v_{te,b}$ increases to 40 $v_A$ and a bump forms at the tail of the core electron velocity distribution function (21). The core-beam density ratio changes to $n_b/n_c\approx 0.05$. The ratio $v_{bd}/v_{te,b}\approx 0.7<{(n_c/n_b)}^{2/3}\approx 3$ indicates that the ETSI becomes weak turbulence. The bump starts to excite Langmuir waves as well as coherent emission (Figs. 2B and 3B). The backward propagating Langmuir waves with frequency near ${\omega }_{pe,0}$ are excited in the background plasma while the propagating forward Langmuir waves with frequency near $0.6{\omega }_{pe,0}$ are excited by the trapped electrons due to the low density and high temperature in the electron potential well (22). These two Langmuir waves satisfy the following dispersion relation (normalized by the initial ${\omega }_{pe,0}$ and ${\lambda }_{De,0}$):

$$\frac{\omega }{{\omega }_{pe,0}}={\left(\frac{n_e^2}{n_0^2}+\frac{T_{ce}{n}_e}{T_{ce,0}{n}_0}\gamma k_x^2{\lambda }_{De,0}^2\right)}^{1/2},$$ [1]

where $\gamma =3$, as the electron heating caused by the solitary wave, is nearly adiabatic (23).

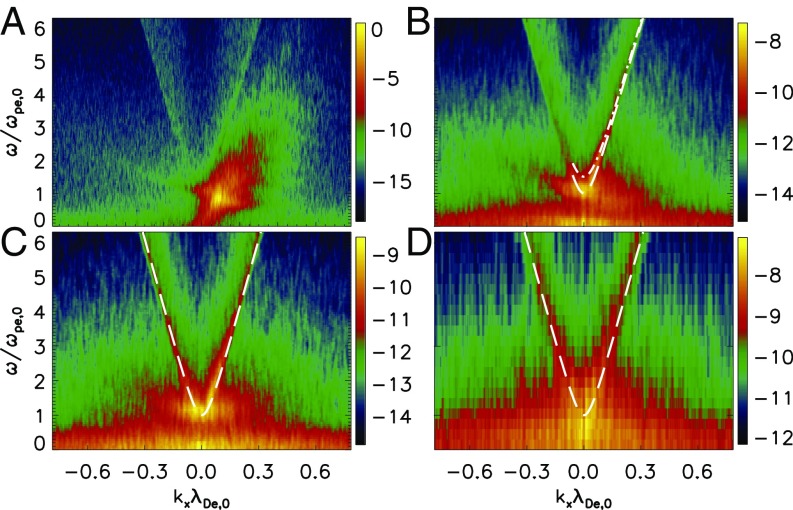
Fig. 3.

The $\omega /{\omega }_{pe,0}$–$k_x{\lambda }_{De,0}$ diagrams of parallel propagating high-frequency $E_y$ are shown for the same four time intervals as for Fig. 2. (A) ${\omega }_{pe,0}t=0$–100, (B) ${\omega }_{pe,0}t=320$–420, (C) ${\omega }_{pe,0}t=2\mathit{\text{,}}880$–2,980, and (D) ${\omega }_{pe,0}t=10\mathit{\text{,}}560$–10,580. Dashed lines denote dispersion relation of plasma emission with frequency $\approx {\omega }_{pe,0}$. Dash-dotted line in B is dispersion relation of plasma emission with frequency $\omega /{\omega }_{pe,0}=1.6$.

The coalescence of the two antiparallel Langmuir waves drives modulational instability and leads to LC (11, 12), accompanied by a harmonic emission with $\approx 1.6{\omega }_{pe,0}$ (Supporting Information). The emission is shown in Fig. 3B, propagating much more strongly forward than backward and satisfying the dispersion relation

$$\frac{\omega }{{\omega }_{pe,0}}={\left(\frac{n_e^2}{n_0^2}+\frac{c^2}{v_{te}^2}{k}_x^2{\lambda }_{De,0}^2\right)}^{1/2}.$$ [2]

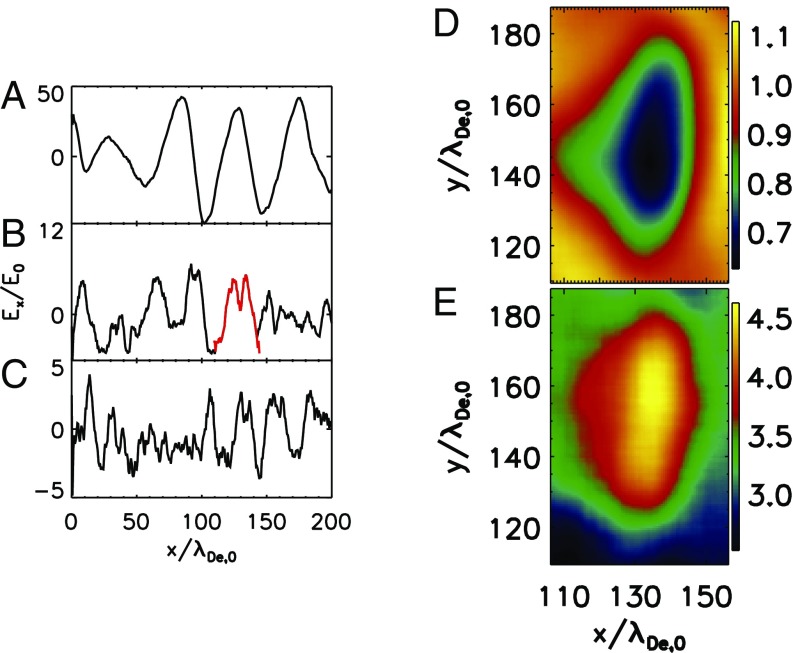
The LC leads to the contraction of the modulated Langmuir envelope and the formation of ion density cavitons (see Movie S1). We plot a sample of parallel electric field $E_x$ in Fig. 4 A–C at three moments: ${\omega }_{pe,0}t=72$, 320, and 680. At ${\omega }_{pe,0}t=72$, the solitary waves with wavelength near the fastest-growing mode reach the peak. The critical condition for LC $E^2/8\pi n_0{T}_e>\frac{1}{4}{k}_x^2{\lambda }_{De}^2$ is satisfied because ${(E^2/8\pi n_0{T}_e)}^{1/2}\approx 0.4$ with $E/E_0\approx 50$ is larger than the fastest-growing mode of the ETSI $k{\lambda }_{De}/2\approx v_{te,0}/2v_{db,0}\approx 0.05$. At ${\omega }_{pe,0}t=$ 320, the modulated wave envelopes decrease from 50 to 30 ${\lambda }_{De,0}$, and ion density cavitons form. In Fig. 4D, we show an example of caviton in the $xy$ plane for the Langmuir envelope plotted in red in Fig. 4B (see Movie S1). Contraction of the Langmuir wave envelopes efficiently dissipates the Langmuir wave energy into electron thermal energy because the rate of Landau damping is proportional to $n_b{\omega }_{pe}^3/n_0{v}_{te,b}^2{k}^2$ (20). The electron temperature along the magnetic field $T_{ex}$ inside the caviton is shown in Fig. 4E. The increased pressure inside the caviton releases the excess density and produces an intermediary short IAW with frequency ${\omega }_{pi}$ (dash-dotted line in Fig. 2B). The time scale for the growth of caviton is consistent with the modulation instability growth rate ${\omega }_{pi}{(⟨E^2⟩/8\pi n_0{T}_e)}^{1/2}\approx 0.01{\omega }_{pe}$. At ${\omega }_{pe,0}t=680$, some wave envelopes continue to contract to wavelengths about 10 ${\lambda }_{De,0}$, whereas some collapses lead to the vanishing of cavitons.

Fig. 4.

(A–C) The parallel electric field $E_x$ cuts for $x\in [\mathrm{0,200}]{\lambda }_{De,0}$ and $y=100{\lambda }_{De,0}$ at (A) ${\omega }_{pe,0}t=72$ when the ETSI nearly saturates and hot electrons excites Langmuir waves; (B) ${\omega }_{pe,0}t=320$ when the modulational instability grows, LCs start, and cavitons form; and (C) ${\omega }_{pe,0}t=648$ when LCs continue. (D) The ion density in $xy$ plane, i.e., the caviton, and (E) the electron temperature in x direction $T_{ex}$ inside the caviton corresponding to the Langmuir envelope in red in B (see Movie S1).

With the onset of LC, ETSI enters the nonlinear decay stage at ${\omega }_{pe,0}t\approx \mathrm{1,000}$. The LC in saturation stage causes the two antipropagating Langmuir waves to merge into a single Langmuir wave with frequency $\approx {\omega }_{pe,0}$ (Fig. 2C). Simultaneously, both whistler and kinetic KAW are generated, which were investigated in a previous study (19). The whistler wave dispersion relation $\omega =v_A^{2}k{k}_{\parallel }/{\mathrm{\Omega }}_{ci}+{\mathrm{\Omega }}_{ci}$ (24) indicates that the whistler wave has ES component with a frequency of $\sim 0.001{\omega }_{pe,0}$ and is strongly affected by density (Fig. 5 A and B). In Fig. 5 C and D, we show both the electron and ion density fluctuations in $(\omega ,k)$ phase space and find that both agree with the dispersion relation of ES whistler waves ($W_s$). Plasma fundamental emission (Fig. 3C) is produced through both coalescence $L+W_s\to T$ and decay $L\to T+W_s$, where $T$ is the transverse emission. A new Langmuir wave $L\prime$ is produced through $L+W_s\rightleftharpoons L\prime$. The coalescence $L+L\prime \rightleftharpoons T$ is much weaker because it is a second-order process. As a result, harmonic emission in this stage is not identifiable.

Fig. 5.

The $\omega /{\omega }_{pe,0}$–$k_x{\lambda }_{De,0}$ diagram of parallel propagating low-frequency fluctuations of $B_z$, $E_x$, density $n_e$, and density $n_i$. The data are from ${\omega }_{pe,0}t=$720 to 14,400. Solid line denotes the dispersion relation of whistler wave; Dashed line denotes the dispersion relation of parallel propagating KAW. The details on the generation of KAWs and whistler waves by the nonlinear ETSI can be found in ref. 19.

The ETSI reaches nonlinear saturation around ${\omega }_{pe,0}t\approx \mathrm{10,000}$. The wavelength of Langmuir wave and ion caviton becomes longer and EM emission is produced in a broad range of frequencies and wavenumbers (Figs. 2D and 3D), which is a consequence of repeating LC maintained by the feedback loop shown in Fig. 1 (see Movie S2). The turbulent fluctuations of density and electric field in phase space increase to levels comparable to that of the Langmuir waves and emissions. The emission reaches its balance between the plasmons of Langmuir waves and whistler waves—the Manley–Rowe relation—and the coupling becomes $L+W_s\rightleftharpoons T$ (25, 26). During this stage, electrons are strongly heated and scattered, and the initial anisotropic electron beams become an isotropic halo population superposed over the core electron distribution function (21).

L–W_s Coupling and LC

The ES component of whistler wave, that is, the ES whistler wave with frequency of several ${\mathrm{\Omega }}_{ci}$ and wavelength $k{\lambda }_{De}<<1$, defines a slow time scale and a large spatial scale, whereas the Langmuir wave defines a fast time scale and small spatial scale $k{\lambda }_{De}\approx 1$. The coupling between ES whistler waves and Langmuir waves drives modulational instability that leads to the formation of long-wavelength Langmuir envelopes ${𝐄}_L(𝐱,t)$ and cavitons. Langmuir waves exert a low-frequency ponderomotive force on the motion of electrons and ions and mediate their interaction with whistler waves in a manner similar to L–IAW coupling (11, 12). The difference here is that whistler waves are produced in magnetized plasmas whereas IAWs are less sensitive to magnetic fields. The ES whistler wave is associated with EM whistler wave and cannot independently exist. In the following, we show this difference and why it does not significantly affect the critical condition for LC. Assuming perturbations $𝐄={𝐄}_s+{𝐄}_L$, ${𝐯}_e={𝐯}_s+{𝐯}_L$, $n_e=n_0+\delta n_L+\delta n_s$ and $\delta n_i\approx \delta n_s$, where the subscripts $L$ and $s$ represent fast and slow time scales, respectively. Neglecting the high-frequency interactions, we have the same driven equation as for the L–IAW coupling (12),

$$\frac{i}{{\omega }_{pe,0}}\frac{\partial {𝐄}_L}{\partial t}+\frac{\gamma v_{te}^2}{4{\omega }_{pe,0}^2}{\mathrm{▽}}^2{𝐄}_L-\frac{\delta n_s}{2n_0}{𝐄}_L=0.$$ [3]

On the slow time scale, ions play the same role as electrons in maintaining the cavitons. In Fig. 5, both the ion and electron density fluctuations propagate at the phase speed of whistler waves $\sim 3v_A,\sim 6v_{ti}$, and $\sim 0.2v_{te}$. The slow component of electron and ion motions in a magnetized plasma can be described by the following equations:

$$\frac{\partial {𝐯}_s}{\partial t}+({𝐯}_s\cdot \nabla ){𝐯}_s+\frac{e}{m_e}{𝐄}_s+\frac{e}{m_{e}c}{𝐯}_s\times {𝐁}_0+\frac{{\gamma }_e{T}_e}{n_0{m}_e}\nabla \delta n_s+\frac{1}{m_e{n}_0}\nabla {\varphi }_{\mathrm{pm}}=0,$$ [4]

$$\frac{\partial {𝐯}_i}{\partial t}+({𝐯}_i\cdot \nabla ){𝐯}_i-\frac{e}{m_i}{𝐄}_s-\frac{e}{m_{i}c}{𝐯}_i\times {𝐁}_0+\frac{{\gamma }_e{T}_i}{n_0{m}_i}\nabla \delta n_s+\frac{m_e}{m_i^2{n}_0}\nabla {\varphi }_{\mathrm{pm}}=0,$$ [5]

where ${\varphi }_{\text{pm}}\equiv {|E_L|}^2/16\pi$, and $\nabla {\varphi }_{\text{pm}}$ is the ponderomotive force.

Eliminating ${𝐄}_s$ and using the approximation $m_e{𝐯}_s/m_i+{𝐯}_i\approx 𝐯$, together with the ion continuity equation, $\partial (m_e+m_i)\delta n_s/\partial t+n_0(m_e+m_i)\nabla \cdot 𝐯)=0$, we obtain

$$\frac{{\partial }^2}{\partial t^2}\frac{\delta n_s}{n_0}-c_s^2{\nabla }^2\frac{\delta n_s}{n_0}-M={\nabla }^2\frac{{\varphi }_{\mathrm{pm}}}{n_0{m}_i},$$ [6]

where $M={𝐁}_0\cdot \nabla \times 𝐣/(m_i{n}_{0}c)$ is the modulation of the magnetic field that excites the whistler wave, $𝐣=e{n}_0(v_i-v_s)$ is the current density, and $c_s^2\approx ({\gamma }_e{T}_e+{\gamma }_i{T}_i)/m_i$ is the phase speed of the IAW. In a homogeneous plasma, to first order, the current density is caused by the polarization drift, i.e., $𝐣\approx [(m_e+m_i)n_0/B_0^2]\partial {𝐄}_s/\partial t$. The curl in $M$ implies that ES whistler waves originate from the perpendicular EM components of whistler waves and KAWs (22). In other words, the density fluctuations on the slow time scale are mediated predominantly by the EM whistler and KAW waves, and the influence of $M$ is small. We will neglect $M$ when discussing the modulational instability and the critical condition of LC.

From Eqs. 3 and 6, the maximum growth rate for modulational instability is ${\gamma }_m={\omega }_{pi}{(⟨E_L^2⟩/8\pi n_0{T}_e)}^{1/2}$, and the critical condition for LC is (12)

$$\frac{E_L^2}{8\pi n_e{T}_e}>\frac{1}{4}{k}_x^2{\lambda }_{De}^2.$$ [7]

In the nonlinear stage, the time scale of the modulational instability becomes longer than it is in linear saturation, due to the decrease of the electric field, but ${(E^2/8\pi n_e{T}_e)}^{1/2}\approx 0.2$ is still larger than the typical Langmuir wavenumber $k{\lambda }_{De}/2\approx 0.05$ for the ES whistler waves, indicating LC can repeatedly occur.

Regeneration of Langmuir Waves

LC transfers energy from large to small scales, inverse to the modulational instability. Repeating LC requires regeneration of Langmuir waves so that $L–W_s$ coupling can continue to produce emission (Fig. 1).

In Eq. 6, ions fill the cavitons and excite short-wavelength IAWs (27) when the balance between the thermal pressure and radiation pressure is lost and Langmuir envelopes collapse. The dispersion relation of IAWs with thermal correction under the condition $v_{ti}<w/k<v_{te}$ is

$$1+\frac{1}{k^2{\lambda }_{De}^2}-\frac{{\omega }_{pi}^2}{{\omega }^2}\left(1+\frac{3k^2{v}_{ti}^2}{{\omega }^2}\right)=0,$$ [8]

where the term $3k^2{v}_{ti}^2/{\omega }^2$ in the bracket comes from the first-order expansion of the ion zeta function $Z(w/k/2v_{ti})$, a higher order correction for the case $w/k/v_{ti}>1$, but not $\gg 1$.

For short-wavelength IAWs with $k{\lambda }_{De}\approx 1$ in a plasma with $T_i\approx T_e$, the dispersion relation becomes

$${\omega }^2\approx {\omega }_{pi}^2\frac{1+\sqrt{3T_i/T_e}}{4}+\sqrt{\frac{3T_e}{T_i}}{k}^2{v}_{ti}^2,$$ [9]

and, for long-wavelength $k{\lambda }_{De}\ll 1$,

$$\omega =\pm \sqrt{\frac{T_e}{m_i}}k.$$ [10]

Eq. 9 shows that the phase speed of short-wavelength IAWs satisfies ${\omega }^2/k^2/v_{ti}^2\approx 1/k^2{\lambda }_{De}^2$, and thus, for the short-wavelength IAW with a few tenths $k{\lambda }_{De}$, the exponential ion damping rate is comparable to electrons, and the rate is ${\gamma }_{ia}\approx {(m_e/m_i)}^{1/2}{\omega }_{pi}/k^3{\lambda }_{De}^3$. The dissipation of the short-wavelength IAW is slower by a factor of ${\gamma }_{ia}/{\gamma }_m\approx {(m_e/m_i)}^{1/2}$ than the modulational instability, and thus this wave can be observed (Fig. 2 B–D). On the other hand, the damping rate of long-wavelength IAW is too strong to maintain L–IAW coupling and is suppressed by L–W_s coupling.

During LC, the wave energy is transferred from long-wavelength Langmuir waves to short-wavelength IAWs and then is returned to the newly generated short-wavelength Langmuir waves. Such energy transfer can be shown in the phase space $(\omega ,k)$ using quasi-particle (plasmon) description. The plasmon number is defined as $N=E_k/{\omega }_k$, where $E_k$ is the energy density of Langmuir envelope and $N(k,x,t)$ is the number of plasmons (26). The evolution of the mean plasmon number $⟨N(k,x,t)⟩$ in phase space during wave interactions is determined by the wave self-interactions and wave-wave interactions,

$$\frac{d⟨E_k⟩}{dt}=-{𝐯}_g\cdot 𝐃\cdot \frac{\partial ⟨N⟩}{\partial 𝐤},$$ [11]

where the group velocity ${𝐯}_g=\partial \omega /\partial 𝐤$, phase space diffusion coefficient $𝐃=\mathrm{𝐪𝐪}\int {\int }_{𝐪,\mathrm{\Omega }}i{\omega }_{pe,0}^2\delta n_s^2/(\mathrm{\Omega }-𝐪\cdot {𝐯}_g+i\widehat{\mathrm{\Gamma }})d𝐪d\mathrm{\Omega }$, $\mathrm{\Gamma }$ is the self-interaction of Langmuir wave, the primary part $⟨\mathrm{\Gamma }⟩$ is associated with the mean plasmon number $⟨N⟩$, and $\widehat{\mathrm{\Gamma }}$ is the first-order self-nonlinearity of Langmuir wave, such as linear growth or damping, where $𝐪$ and $\mathrm{\Omega }$ are the wave vector and frequency of IAWs, respectively.

In the case of linear growth $\widehat{\mathrm{\Gamma }}\approx 0$, a second instability can occur at $\mathrm{\Omega }\simeq 𝐪\cdot {𝐯}_g$. If ${𝐪\cdot \partial ⟨N⟩/\partial 𝐤|}_{\mathrm{\Omega }}>0$, we have $d{E}_k/dt<0$, indicating the energy transfers from the Langmuir wave to IAWs. The Langmuir wave is depleted by the Landau damping of caviton trapped wave-scattering, and the short-wavelength IAWs repopulate the energy of the short-wavelength part of the energy distribution. If ${𝐪\cdot \partial ⟨N⟩/\partial 𝐤|}_{\mathrm{\Omega }}<0$, we have $d{E}_k/dt>0$, indicating the regeneration of Langmuir waves. The short-wavelength IAW is damped by electrons, and the hot electrons reproduce the short-wavelength Langmuir waves.

The short-wavelength IAW acts as an intermediary wave in the regeneration of Langmuir waves. The Langmuir wave energy gain by modulational instability and loss by LC can reach a balance, i.e., ${\gamma }_{ia}{W}_{ia}={\gamma }_m{W}_L$, where the short-wavelength IAW wave energy density $W_{ia}=n_0{T}_e{\sum }_k\delta n_{s,k}^2/n_0$, the short-wavelength Langmuir wave energy density $W_L=⟨E_L^2⟩{(k_0/k)}^{3/2}/8\pi$, and $k_0=1/{\lambda }_{De}{(⟨E_L^2⟩/8\pi T_e)}^{1/2}$—the critical Langmuir wavenumber corresponding to LC at which the short-wavelength IAW energy is transferred into short-wavelength Langmuir waves (27).

The electron resonance with the short-wavelength IAWs reexcites Langmuir waves with a frequency shift, and Eq. 3, when modified to include the short-wavelength IAW excitation (27), becomes

$$\frac{i}{{\omega }_{pe,0}}\frac{\partial {𝐄}_L}{\partial t}+\frac{\gamma v_{te}^2}{4{\omega }_{pe,0}^2}{\mathrm{▽}}^2{𝐄}_{𝐋}-\frac{\delta n_s}{2n_0}{𝐄}_L=\frac{\delta n_{s,new}}{2n_0}{𝐄}_L=-\frac{{\omega }_{pe}}{12}\sum _k\frac{{|\delta n_s^k|}^2}{n_0^2{k}^2{\lambda }_{De}^2}\left(1+i\frac{2}{3}\frac{{\gamma }_k}{{\omega }_{pe}{k}^2{\lambda }_{De}^2}\right){𝐄}_L,$$ [12]

where ${\gamma }_k$ is the damping rate of short-wavelength Langmuir wave with wavenumber $k$. The first term on the right-hand side of Eq. 12 is the frequency shift of a plain Langmuir wave by the scattering of the ion density fluctuations driven by short-wavelength IAWs. The second term corresponds to the damping of long-wavelength Langmuir waves due to their conversion to short-wavelength IAWs. The frequency shift is

$$\delta \omega =-\frac{{\omega }_{pe}}{12}\sum _k\frac{{|\delta n_s^k|}^2}{n_0^2{k}^2{\lambda }_{De}^2}.$$ [13]

This shift is the same for the entire Langmuir wavepacket spectrum and has no influence on the modulational instability.

After each LC, the frequency of the new Langmuir wave will decrease by a shift $\approx {\omega }_{pe}{n}_s^2/n_0^2/12\approx 0.01{\omega }_{pe}$ assuming $k{\lambda }_{De}\approx 1$. We assume that the interval for LC is comparable to the time scale of modulational instability $100{\omega }_{pe}^{-1}$; the whole simulation is about 10,000 ${\omega }_{pe}^{-1}$. Thus, the total frequency shift is about ${\omega }_{pe}$. This agrees with what is shown in Fig. 2 in which Langmuir wave finally shifts to $k{\lambda }_{De}\ll 1$.

Concluding Remarks

PIC simulations were conducted to explore how the evolution of the strong ETSI produces Langmuir waves and plasma coherent emission. We found that LC plays a critical role in the process, which enables regeneration of Langmuir waves and maintains a feedback loop for emission beyond the linear ETSI saturation (Fig. 1). The onset of LC is introduced by the L–L wave coupling at the ETSI linear saturation stage and maintained by L–W_s coupling from the nonlinear decay stage to the nonlinear saturation. The low-frequency KAWs and whistler waves generated near the ETSI peak finally reach equilibrium with the non-Maxwellian electron velocity distribution function (e.g., core–halo structure), as found in previous studies (19, 21).

In our simulations, the ETSI nonlinear saturation time is $\sim 1.5\times {10}^4{\omega }_{pe}^{-1}$. Because the modulational instability nearly dominates the entire process, the nonlinear saturation time is approximately proportional to ${(m_i/m_e)}^{1/2}$, and, for the physical mass ratio, the ETSI nonlinear saturation time should be $\sim {10}^5{\omega }_{pe}^{-1}$, which is significantly longer than the ETSI linear saturation time ${(n_0/n_b)}^{1/3}{\omega }_{pe}^{-1}\approx 2{\omega }_{pe}^{-1}$. Note that our simulation assumes instantaneous injection of the electron beam, whereas, in the corona, the electron acceleration time is finite and the beam will propagate out of the region of initial generation. The acceleration time also affects the actual duration of the bursts (28, 29). The overall scenario is that coronal bursts produce nonthermal electrons that escape into space and produce interplanetary bursts (3) with accompanying waves. Our simulation assumes the beam energy is about 100 times that of the coronal thermal energy. For nanoflares, the beam energy is about a few kiloelectron volts if the corona temperature is $\sim 10$ eV. For flares, the electron beam energy can reach about a few megaelectron volts. The larger beam energy will change the results slightly because the ETSI growth rate does not rely on the velocity once the threshold is reached, but the turbulence becomes stronger and the decay lasts longer. On the other hand, we can estimate the emission power from Fig. 3 B–D, in which the intensity ratio of the $E_y$ of the radiation and the Langmuir wave is about 0.01 to 0.001, and thus the emission power is about a factor of ${10}^{-4}\hspace{0.17em}\text{to}\hspace{0.17em}{10}^{-6}$ of the Langmuir wave power. Such energy loss is negligible dynamically. Therefore, the mechanism we have explored can provide a complete and self-consistent solution to the long-standing puzzle of why the duration of solar radio bursts is much longer than the linear saturation time of the ETSI [“Sturrock’s dilemma”(30)].

The short-wavelength IAWs and ion cavitons are two characteristics of LC, and can be detected by in situ solar wind observations. In particular, the forthcoming Solar Probe Plus mission will be capable of in situ detection of such radiation at 10 $R_{\odot }$ from the Sun. The newly launched Magnetospheric Multiscale Mission is capable of in situ detections of Langmuir waves and cavitons in magnetosphere and solar wind at 1 AU.

We summarize some basic observations, which are consistent with our model predictions, in Table 1.

Table 1.

Model predictions and observational evidence

Model predictions	Observations	Refs.
In the solar corona, emission duration	Coronal type J and U radio bursts	(3, 4, 31)
$\approx {10}^5{\omega }_{pe}^{-1}\approx 1-10$ ms	Weak coronal type III radio bursts
Langmuir waves and whistler waves	Interplanetary type III radio bursts	(16, 32, 33)
Langmuire collapse and short wavelength IAW	Interplanetary type III radio bursts	(15, 34, 35)

L–L Coupling and Emission

The Langmuir waves generated in solitary wave-trapped electrons $L_l$ propagate forward while the Langmuir waves generated in background electrons $L_h$ propagate backward. In the following, we will clarify how the two Langmuir waves propagating in opposite direction produce emission through $L_h+L_l\to T$.

Langmuir wave and emission satisfy the following dispersion relations:

$${\omega }_L\approx {\omega }_{pe}+3k_L^2{v}_{te}^2/2{\omega }_{pe},$$ [S1]

$${\omega }_T\approx {({\omega }_{pe}^2+k_T^2{c}^2)}^{1/2},$$ [S2]

where the dispersion relation of Langmuir wave is approximated under the condition $k{\lambda }_{De,0}\ll 1$.

The coupling $L_h+L_l\to T$ satisfies the following selection rule:

$${\omega }_h\pm {\omega }_l={\omega }_T$$ [S3]

$${𝐤}_{𝐡}+{𝐤}_{𝐥}={𝐤}_{𝐓}.$$ [S4]

Fig. 3B shows that both the fundamental and harmonic emissions have $k_T{\lambda }_{De,0}<v_{te}/c\approx 0.1$; thus we approximate the dispersion relation of the emission as ${\omega }_T\approx {\omega }_{pe}+k_T^2{c}^2/2{\omega }_{pe}$. It is easy to show that the plus sign in the selection rule requires ${𝐤}_{𝐡}{𝐤}_{𝐥}<0$, i.e., the two Langmuir waves must be antiparallel. The resulting ${𝐤}_{𝐓}$ is more likely to be positive and the emission propagates forward with harmonic frequency $\omega /{\omega }_{pe}\approx 1.6$.

Waves in Real Space

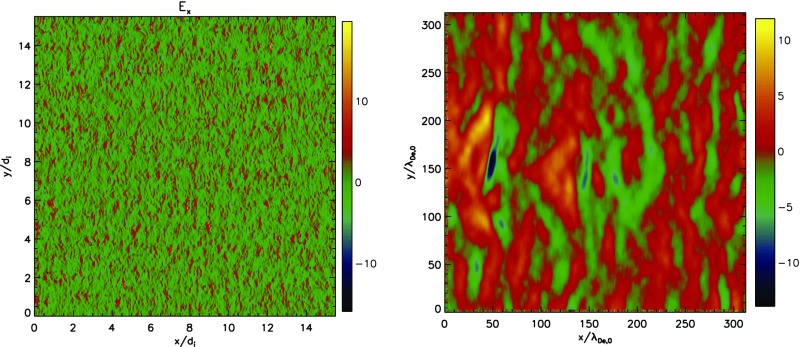
In the following, we show the ES waves presented in Fig. 2 B–D in real space.

In Fig. S1, we show $E_x$ in the $xy$ plane at ${\omega }_{pe\text{,}0}t=344$, when the forward propagating Langmuir wave is produced in the background plasma and the backward propagating Langmuir wave is produced in the trapped electrons by the solitary waves. The coupling of these two Langmuir waves produces emission and cavitons (Time Evolution of Ion Cavitons). The LC leads to the regeneration of Langmuir waves through the intermediate short IAWs. Fig. S1 (Left) shows the waves propagating along magnetic field ($x$ direction) in full simulation domain. Because the wavelengths of Langmuir waves and short IAWs are much smaller than the ion inertial length $d_i$, and to better visualize the waves, we also show a cutout of a small region with $x$, $y\in [\mathrm{0,1.5}]\times d_i$ in Fig. S1. Obviously, there are two kinds of waves: one with wavelengths of $\approx 10–20$ Debye length and the other $\approx 50$ Debye length; these are the Langmuir waves and the short IAWs, respectively.

Fig. S1.

(Left) $E_x$ in xy plane at ${\omega }_{pe\text{,}0}t=344$. (Right) A zoom in showing $E_x$ within spatial range $x$, $y\in [0,1.5]\times d_i$, and $d_i=200{\lambda }_{De\text{,}0}$.

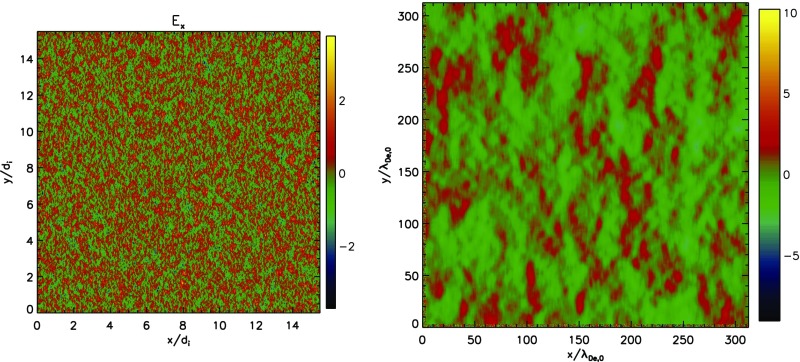
In Fig. S2, we show Langmuir waves, short IAW, and ES whistler waves in real space. The wavelength of ES whistler waves is of the same order as that of the ion inertial length $d_i$, but the amplitude of ES whistler waves is much smaller than those of Langmuir waves and short IAWs; thus it is difficult to see ES whistler waves while Langmuir waves and short IAWs are present. However, the components $B_z$ and $E_y$ of EM whistler waves are visible in real space, which we have studied in a previous paper (19) and the ES component is distinguishable in the phase space of frequency and wavevector as shown in Fig. 5.

Fig. S2.

(Left) $E_x$ in xy plane at ${\omega }_{pe\text{,}0}t=656$. (Right) $E_x$ cutout with $x$, $y\in [0,\hspace{0.17em}1.5]\times d_i$, where $d_i=200{\lambda }_{De\text{,}0}$.

Time Evolution of Ion Cavitons

We demonstrate the evolution of ion cavitons, i.e., the ion density in the $xy$ plane in Movies S1 and S2.

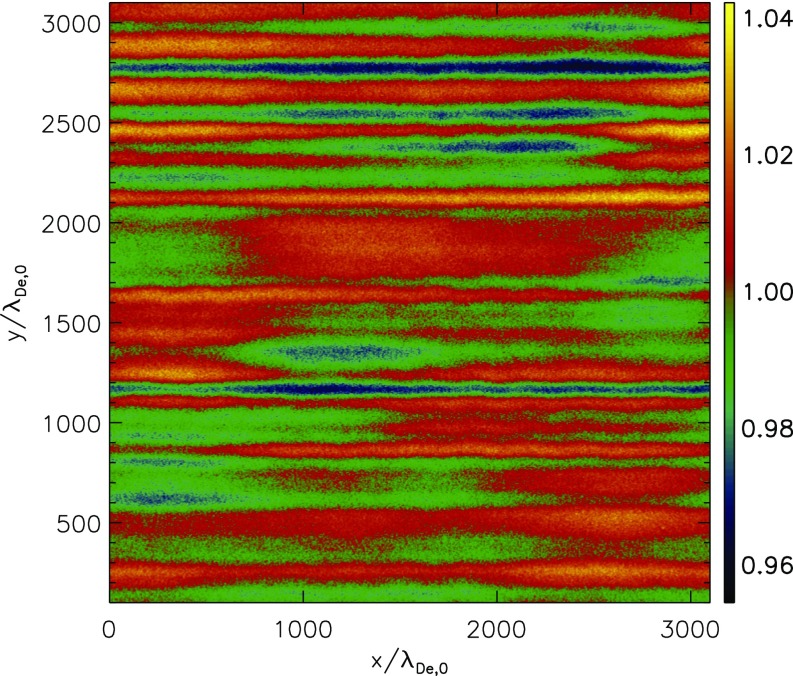
We show the ion caviton in Fig. S3 when the turbulence reaches its nonlinear equilibrium at ${\omega }_{pe,0}t=\mathrm{10,000}$. We can see that the width of ion density caviton becomes very large in x direction and the density depletion at the center of caviton is rather weak, which is consistent with the nonlinear effect caused by the feedback of LC, i.e., the frequency shift of Langmuir wave leads to the Langmuir wave to move to $k{\lambda }_{De,0}\ll 1$.

Fig. S3.

The ion density in space xy at ${\omega }_{pe\text{,}0}t=\mathrm{10,000}$.