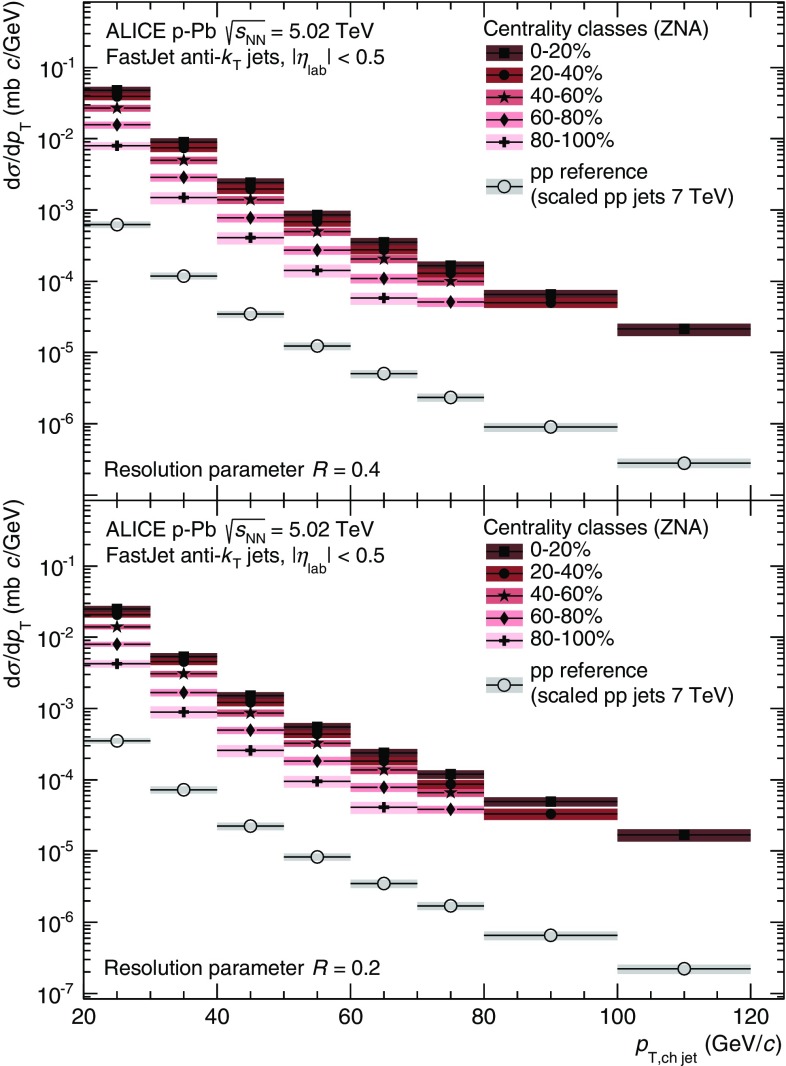
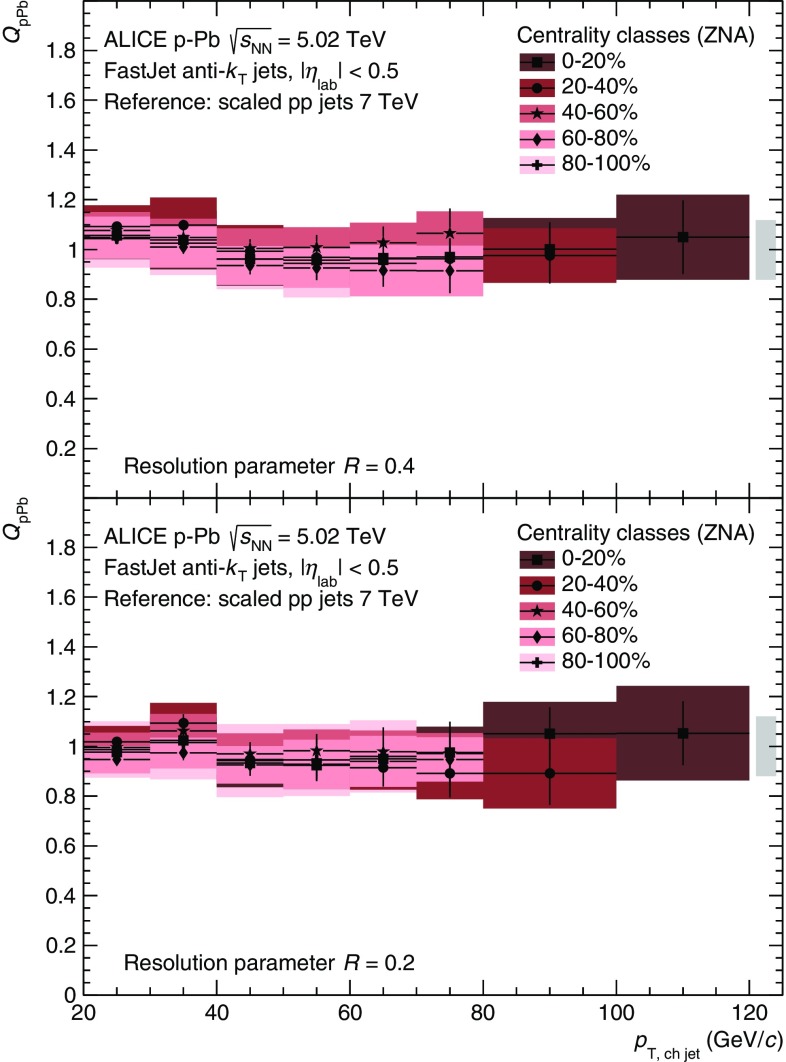
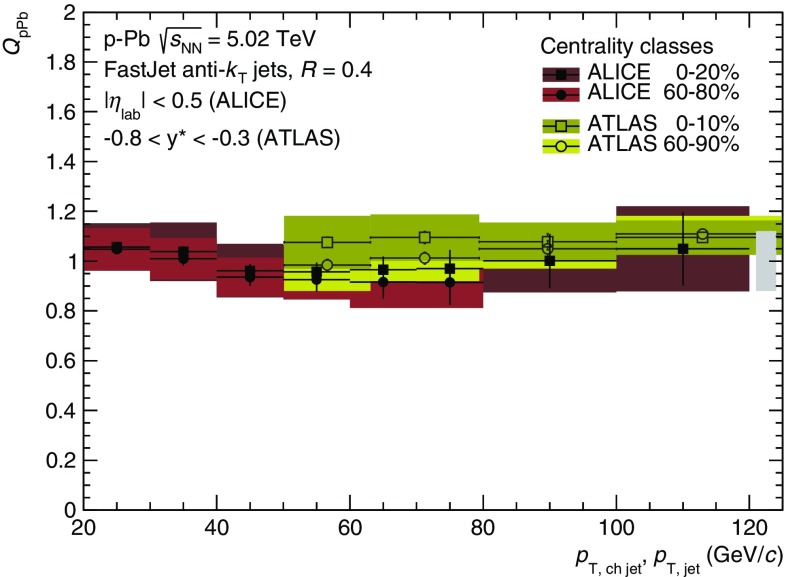
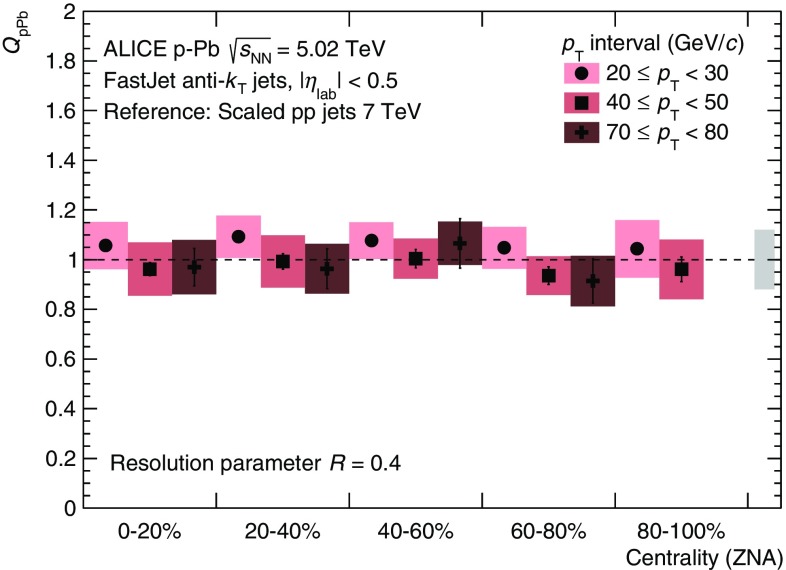
Alice Collaboration140,
J Adam
J Adam
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
D Adamová
D Adamová
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
M M Aggarwal
M M Aggarwal
88Physics Department, Panjab University, Chandigarh, India
88,
G Aglieri Rinella
G Aglieri Rinella
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M Agnello
M Agnello
110Sezione INFN, Turin, Italy
110,
N Agrawal
N Agrawal
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
Z Ahammed
Z Ahammed
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S Ahmad
S Ahmad
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
S U Ahn
S U Ahn
68Korea Institute of Science and Technology Information, Daejeon, South Korea
68,
S Aiola
S Aiola
137Yale University, New Haven, CT USA
137,
A Akindinov
A Akindinov
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
S N Alam
S N Alam
133Variable Energy Cyclotron Centre, Kolkata, India
133,
D S D Albuquerque
D S D Albuquerque
121Universidade Estadual de Campinas (UNICAMP), Campinas, Brazil
121,
D Aleksandrov
D Aleksandrov
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
B Alessandro
B Alessandro
110Sezione INFN, Turin, Italy
110,
D Alexandre
D Alexandre
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
R Alfaro Molina
R Alfaro Molina
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
A Alici
A Alici
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
104Sezione INFN, Bologna, Italy
12,104,
A Alkin
A Alkin
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
J R M Almaraz
J R M Almaraz
119Universidad Autónoma de Sinaloa, Culiacán, Mexico
119,
J Alme
J Alme
18Department of Physics and Technology, University of Bergen, Mons, Norway
37Faculty of Engineering, Bergen University College, Mons, Norway
18,37,
T Alt
T Alt
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
S Altinpinar
S Altinpinar
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
I Altsybeev
I Altsybeev
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
C Alves Garcia Prado
C Alves Garcia Prado
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
C Andrei
C Andrei
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
A Andronic
A Andronic
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
V Anguelov
V Anguelov
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
T Antičić
T Antičić
98Rudjer Bošković Institute, Zagreb, Croatia
98,
F Antinori
F Antinori
107Sezione INFN, Padua, Italy
107,
P Antonioli
P Antonioli
104Sezione INFN, Bologna, Italy
104,
L Aphecetche
L Aphecetche
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
H Appelshäuser
H Appelshäuser
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
S Arcelli
S Arcelli
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
R Arnaldi
R Arnaldi
110Sezione INFN, Turin, Italy
110,
O W Arnold
O W Arnold
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
I C Arsene
I C Arsene
22Department of Physics, University of Oslo, Oslo, Norway
22,
M Arslandok
M Arslandok
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
B Audurier
B Audurier
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
A Augustinus
A Augustinus
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
R Averbeck
R Averbeck
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M D Azmi
M D Azmi
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
A Badalà
A Badalà
106Sezione INFN, Catania, Italy
106,
Y W Baek
Y W Baek
67Konkuk University, Seoul, South Korea
67,
S Bagnasco
S Bagnasco
110Sezione INFN, Turin, Italy
110,
R Bailhache
R Bailhache
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
R Bala
R Bala
91Physics Department, University of Jammu, Jammu, India
91,
S Balasubramanian
S Balasubramanian
137Yale University, New Haven, CT USA
137,
A Baldisseri
A Baldisseri
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
R C Baral
R C Baral
61Institute of Physics, Bhubaneswar, India
61,
A M Barbano
A M Barbano
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
R Barbera
R Barbera
28Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Catania, Italy
28,
F Barile
F Barile
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
G G Barnaföldi
G G Barnaföldi
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
L S Barnby
L S Barnby
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
35,101,
V Barret
V Barret
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
P Bartalini
P Bartalini
7Central China Normal University, Wuhan, China
7,
K Barth
K Barth
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
J Bartke
J Bartke
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
E Bartsch
E Bartsch
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
M Basile
M Basile
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
N Bastid
N Bastid
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
S Basu
S Basu
133Variable Energy Cyclotron Centre, Kolkata, India
133,
B Bathen
B Bathen
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
G Batigne
G Batigne
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
A Batista Camejo
A Batista Camejo
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
B Batyunya
B Batyunya
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
P C Batzing
P C Batzing
22Department of Physics, University of Oslo, Oslo, Norway
22,
I G Bearden
I G Bearden
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
H Beck
H Beck
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
53,94,
C Bedda
C Bedda
110Sezione INFN, Turin, Italy
110,
N K Behera
N K Behera
48Indian Institute of Technology Indore (IITI), Indore, India
50Inha University, Inchon, South Korea
48,50,
I Belikov
I Belikov
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
F Bellini
F Bellini
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
H Bello Martinez
H Bello Martinez
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
R Bellwied
R Bellwied
122University of Houston, Houston, TX USA
122,
R Belmont
R Belmont
135Wayne State University, Detroit, MI USA
135,
E Belmont-Moreno
E Belmont-Moreno
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
V Belyaev
V Belyaev
75Moscow Engineering Physics Institute, Moscow, Russia
75,
G Bencedi
G Bencedi
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
S Beole
S Beole
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
I Berceanu
I Berceanu
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
A Bercuci
A Bercuci
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
Y Berdnikov
Y Berdnikov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
D Berenyi
D Berenyi
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
R A Bertens
R A Bertens
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
D Berzano
D Berzano
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
L Betev
L Betev
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
A Bhasin
A Bhasin
91Physics Department, University of Jammu, Jammu, India
91,
I R Bhat
I R Bhat
91Physics Department, University of Jammu, Jammu, India
91,
A K Bhati
A K Bhati
88Physics Department, Panjab University, Chandigarh, India
88,
B Bhattacharjee
B Bhattacharjee
44Department of Physics, Gauhati University, Guwahati, India
44,
J Bhom
J Bhom
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
128University of Tsukuba, Tsukuba, Japan
117,128,
L Bianchi
L Bianchi
122University of Houston, Houston, TX USA
122,
N Bianchi
N Bianchi
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
C Bianchin
C Bianchin
135Wayne State University, Detroit, MI USA
135,
J Bielčík
J Bielčík
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
J Bielčíková
J Bielčíková
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
A Bilandzic
A Bilandzic
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
93Physik Department, Technische Universität München, Munich, Germany
36,81,93,
G Biro
G Biro
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
R Biswas
R Biswas
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
4,
S Biswas
S Biswas
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
79National Institute of Science Education and Research, Bhubaneswar, India
4,79,
S Bjelogrlic
S Bjelogrlic
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
J T Blair
J T Blair
118Physics Department, The University of Texas at Austin, Austin, TX USA
118,
D Blau
D Blau
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
C Blume
C Blume
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
F Bock
F Bock
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
74,94,
A Bogdanov
A Bogdanov
75Moscow Engineering Physics Institute, Moscow, Russia
75,
H Bøggild
H Bøggild
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
L Boldizsár
L Boldizsár
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
M Bombara
M Bombara
40Faculty of Science, P.J. Šafárik University, Kosice, Slovakia
40,
J Book
J Book
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
H Borel
H Borel
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
A Borissov
A Borissov
96Pusan National University, Pusan, South Korea
96,
M Borri
M Borri
83Nuclear Physics Group, STFC Daresbury Laboratory, Daresbury, UK
124University of Liverpool, Liverpool, UK
83,124,
F Bossú
F Bossú
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
E Botta
E Botta
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
C Bourjau
C Bourjau
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
P Braun-Munzinger
P Braun-Munzinger
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M Bregant
M Bregant
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
T Breitner
T Breitner
52Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
52,
T A Broker
T A Broker
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
T A Browning
T A Browning
95Purdue University, West Lafayette, IN USA
95,
M Broz
M Broz
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
E J Brucken
E J Brucken
45Helsinki Institute of Physics (HIP), Helsinki, Finland
45,
E Bruna
E Bruna
110Sezione INFN, Turin, Italy
110,
G E Bruno
G E Bruno
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
D Budnikov
D Budnikov
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
H Buesching
H Buesching
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
S Bufalino
S Bufalino
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
26,35,
P Buncic
P Buncic
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
O Busch
O Busch
128University of Tsukuba, Tsukuba, Japan
128,
Z Buthelezi
Z Buthelezi
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
J B Butt
J B Butt
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
J T Buxton
J T Buxton
20Department of Physics, Ohio State University, Columbus, OH USA
20,
J Cabala
J Cabala
115Technical University of Košice, Kosice, Slovakia
115,
D Caffarri
D Caffarri
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
X Cai
X Cai
7Central China Normal University, Wuhan, China
7,
H Caines
H Caines
137Yale University, New Haven, CT USA
137,
L Calero Diaz
L Calero Diaz
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
A Caliva
A Caliva
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
E Calvo Villar
E Calvo Villar
102Sección Física, Departamento de Ciencias, Pontificia Universidad Católica del Perú, Lima, Peru
102,
P Camerini
P Camerini
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
F Carena
F Carena
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
W Carena
W Carena
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
F Carnesecchi
F Carnesecchi
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
J Castillo Castellanos
J Castillo Castellanos
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
A J Castro
A J Castro
125University of Tennessee, Knoxville, TN USA
125,
E A R Casula
E A R Casula
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
C Ceballos Sanchez
C Ceballos Sanchez
9Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN), Havana, Cuba
9,
J Cepila
J Cepila
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
P Cerello
P Cerello
110Sezione INFN, Turin, Italy
110,
J Cerkala
J Cerkala
115Technical University of Košice, Kosice, Slovakia
115,
B Chang
B Chang
123University of Jyväskylä, Jyväskylä, Finland
123,
S Chapeland
S Chapeland
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M Chartier
M Chartier
124University of Liverpool, Liverpool, UK
124,
J L Charvet
J L Charvet
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
S Chattopadhyay
S Chattopadhyay
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S Chattopadhyay
S Chattopadhyay
100Saha Institute of Nuclear Physics, Kolkata, India
100,
A Chauvin
A Chauvin
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
V Chelnokov
V Chelnokov
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
M Cherney
M Cherney
87Physics Department, Creighton University, Omaha, NE USA
87,
C Cheshkov
C Cheshkov
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
B Cheynis
B Cheynis
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
V Chibante Barroso
V Chibante Barroso
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
D D Chinellato
D D Chinellato
121Universidade Estadual de Campinas (UNICAMP), Campinas, Brazil
121,
S Cho
S Cho
50Inha University, Inchon, South Korea
50,
P Chochula
P Chochula
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
K Choi
K Choi
96Pusan National University, Pusan, South Korea
96,
M Chojnacki
M Chojnacki
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
S Choudhury
S Choudhury
133Variable Energy Cyclotron Centre, Kolkata, India
133,
P Christakoglou
P Christakoglou
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
82,
C H Christensen
C H Christensen
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
P Christiansen
P Christiansen
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
T Chujo
T Chujo
128University of Tsukuba, Tsukuba, Japan
128,
S U Chung
S U Chung
96Pusan National University, Pusan, South Korea
96,
C Cicalo
C Cicalo
105Sezione INFN, Cagliari, Italy
105,
L Cifarelli
L Cifarelli
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
12,27,
F Cindolo
F Cindolo
104Sezione INFN, Bologna, Italy
104,
J Cleymans
J Cleymans
90Physics Department, University of Cape Town, Cape Town, South Africa
90,
F Colamaria
F Colamaria
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
D Colella
D Colella
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
35,59,
A Collu
A Collu
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
M Colocci
M Colocci
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
G Conesa Balbastre
G Conesa Balbastre
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
Z Conesa del Valle
Z Conesa del Valle
51Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France
51,
M E Connors
M E Connors
137Yale University, New Haven, CT USA
137,
J G Contreras
J G Contreras
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
T M Cormier
T M Cormier
85Oak Ridge National Laboratory, Oak Ridge, TN USA
85,
Y Corrales Morales
Y Corrales Morales
110Sezione INFN, Turin, Italy
110,
I Cortés Maldonado
I Cortés Maldonado
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
P Cortese
P Cortese
31Dipartimento di Scienze e Innovazione Tecnologica dell’Università del Piemonte Orientale and Gruppo Collegato INFN, Alessandria, Italy
31,
M R Cosentino
M R Cosentino
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
F Costa
F Costa
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
P Crochet
P Crochet
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
R Cruz Albino
R Cruz Albino
11Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
11,
E Cuautle
E Cuautle
63Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
63,
L Cunqueiro
L Cunqueiro
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
35,54,
T Dahms
T Dahms
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
A Dainese
A Dainese
107Sezione INFN, Padua, Italy
107,
M C Danisch
M C Danisch
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
A Danu
A Danu
62Institute of Space Science (ISS), Bucharest, Romania
62,
D Das
D Das
100Saha Institute of Nuclear Physics, Kolkata, India
100,
I Das
I Das
100Saha Institute of Nuclear Physics, Kolkata, India
100,
S Das
S Das
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
4,
A Dash
A Dash
79National Institute of Science Education and Research, Bhubaneswar, India
79,
S Dash
S Dash
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
S De
S De
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
A De Caro
A De Caro
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
12,30,
G de Cataldo
G de Cataldo
103Sezione INFN, Bari, Italy
103,
C de Conti
C de Conti
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
J de Cuveland
J de Cuveland
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
A De Falco
A De Falco
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
D De Gruttola
D De Gruttola
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
12,30,
N De Marco
N De Marco
110Sezione INFN, Turin, Italy
110,
S De Pasquale
S De Pasquale
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
30,
A Deisting
A Deisting
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
94,97,
A Deloff
A Deloff
77National Centre for Nuclear Studies, Warsaw, Poland
77,
E Dénes
E Dénes
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
C Deplano
C Deplano
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
82,
P Dhankher
P Dhankher
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
D Di Bari
D Di Bari
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
A Di Mauro
A Di Mauro
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
P Di Nezza
P Di Nezza
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
M A Diaz Corchero
M A Diaz Corchero
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
10,
T Dietel
T Dietel
90Physics Department, University of Cape Town, Cape Town, South Africa
90,
P Dillenseger
P Dillenseger
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
R Divià
R Divià
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
Ø Djuvsland
Ø Djuvsland
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
A Dobrin
A Dobrin
62Institute of Space Science (ISS), Bucharest, Romania
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
62,82,
D Domenicis Gimenez
D Domenicis Gimenez
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
B Dönigus
B Dönigus
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
O Dordic
O Dordic
22Department of Physics, University of Oslo, Oslo, Norway
22,
T Drozhzhova
T Drozhzhova
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
A K Dubey
A K Dubey
133Variable Energy Cyclotron Centre, Kolkata, India
133,
A Dubla
A Dubla
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
L Ducroux
L Ducroux
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
P Dupieux
P Dupieux
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
R J Ehlers
R J Ehlers
137Yale University, New Haven, CT USA
137,
D Elia
D Elia
103Sezione INFN, Bari, Italy
103,
E Endress
E Endress
102Sección Física, Departamento de Ciencias, Pontificia Universidad Católica del Perú, Lima, Peru
102,
H Engel
H Engel
52Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
52,
E Epple
E Epple
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
137Yale University, New Haven, CT USA
36,93,137,
B Erazmus
B Erazmus
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
I Erdemir
I Erdemir
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
F Erhardt
F Erhardt
129University of Zagreb, Zagreb, Croatia
129,
B Espagnon
B Espagnon
51Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France
51,
M Estienne
M Estienne
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
S Esumi
S Esumi
128University of Tsukuba, Tsukuba, Japan
128,
J Eum
J Eum
96Pusan National University, Pusan, South Korea
96,
D Evans
D Evans
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
S Evdokimov
S Evdokimov
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
G Eyyubova
G Eyyubova
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
L Fabbietti
L Fabbietti
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
D Fabris
D Fabris
107Sezione INFN, Padua, Italy
107,
J Faivre
J Faivre
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
A Fantoni
A Fantoni
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
M Fasel
M Fasel
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
L Feldkamp
L Feldkamp
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
A Feliciello
A Feliciello
110Sezione INFN, Turin, Italy
110,
G Feofilov
G Feofilov
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
J Ferencei
J Ferencei
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
A Fernández Téllez
A Fernández Téllez
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
E G Ferreiro
E G Ferreiro
17Departamento de Física de Partículas and IGFAE, Universidad de Santiago de Compostela, Santiago de Compostela, Spain
17,
A Ferretti
A Ferretti
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
A Festanti
A Festanti
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
V J G Feuillard
V J G Feuillard
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
15,70,
J Figiel
J Figiel
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
M A S Figueredo
M A S Figueredo
120Universidade de São Paulo (USP), São Paulo, Brazil
124University of Liverpool, Liverpool, UK
120,124,
S Filchagin
S Filchagin
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
D Finogeev
D Finogeev
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
F M Fionda
F M Fionda
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
E M Fiore
E M Fiore
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
M G Fleck
M G Fleck
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
M Floris
M Floris
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
S Foertsch
S Foertsch
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
P Foka
P Foka
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
S Fokin
S Fokin
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
E Fragiacomo
E Fragiacomo
109Sezione INFN, Trieste, Italy
109,
A Francescon
A Francescon
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
29,35,
U Frankenfeld
U Frankenfeld
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
G G Fronze
G G Fronze
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
U Fuchs
U Fuchs
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
C Furget
C Furget
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
A Furs
A Furs
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
M Fusco Girard
M Fusco Girard
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
30,
J J Gaardhøje
J J Gaardhøje
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
M Gagliardi
M Gagliardi
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
A M Gago
A M Gago
102Sección Física, Departamento de Ciencias, Pontificia Universidad Católica del Perú, Lima, Peru
102,
M Gallio
M Gallio
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
D R Gangadharan
D R Gangadharan
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
P Ganoti
P Ganoti
89Physics Department, University of Athens, Athens, Greece
89,
C Gao
C Gao
7Central China Normal University, Wuhan, China
7,
C Garabatos
C Garabatos
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
E Garcia-Solis
E Garcia-Solis
13Chicago State University, Chicago, IL USA
13,
C Gargiulo
C Gargiulo
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
P Gasik
P Gasik
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
E F Gauger
E F Gauger
118Physics Department, The University of Texas at Austin, Austin, TX USA
118,
M Germain
M Germain
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
M Gheata
M Gheata
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
62Institute of Space Science (ISS), Bucharest, Romania
35,62,
P Ghosh
P Ghosh
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S K Ghosh
S K Ghosh
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
4,
P Gianotti
P Gianotti
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
P Giubellino
P Giubellino
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
110Sezione INFN, Turin, Italy
35,110,
P Giubilato
P Giubilato
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
E Gladysz-Dziadus
E Gladysz-Dziadus
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
P Glässel
P Glässel
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
D M Goméz Coral
D M Goméz Coral
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
A Gomez Ramirez
A Gomez Ramirez
52Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
52,
A S Gonzalez
A S Gonzalez
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
V Gonzalez
V Gonzalez
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
10,
P González-Zamora
P González-Zamora
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
10,
S Gorbunov
S Gorbunov
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
L Görlich
L Görlich
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
S Gotovac
S Gotovac
116Technical University of Split FESB, Split, Croatia
116,
V Grabski
V Grabski
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
O A Grachov
O A Grachov
137Yale University, New Haven, CT USA
137,
L K Graczykowski
L K Graczykowski
134Warsaw University of Technology, Warsaw, Poland
134,
K L Graham
K L Graham
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
A Grelli
A Grelli
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
A Grigoras
A Grigoras
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
C Grigoras
C Grigoras
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
V Grigoriev
V Grigoriev
75Moscow Engineering Physics Institute, Moscow, Russia
75,
A Grigoryan
A Grigoryan
1A.I. Alikhanyan National Science Laboratory (Yerevan Physics Institute) Foundation, Yerevan, Armenia
1,
S Grigoryan
S Grigoryan
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
B Grinyov
B Grinyov
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
N Grion
N Grion
109Sezione INFN, Trieste, Italy
109,
J M Gronefeld
J M Gronefeld
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
J F Grosse-Oetringhaus
J F Grosse-Oetringhaus
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
R Grosso
R Grosso
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
F Guber
F Guber
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
R Guernane
R Guernane
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
B Guerzoni
B Guerzoni
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
K Gulbrandsen
K Gulbrandsen
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
T Gunji
T Gunji
127University of Tokyo, Tokyo, Japan
127,
A Gupta
A Gupta
91Physics Department, University of Jammu, Jammu, India
91,
R Gupta
R Gupta
91Physics Department, University of Jammu, Jammu, India
91,
R Haake
R Haake
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
Ø Haaland
Ø Haaland
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
C Hadjidakis
C Hadjidakis
51Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France
51,
M Haiduc
M Haiduc
62Institute of Space Science (ISS), Bucharest, Romania
62,
H Hamagaki
H Hamagaki
127University of Tokyo, Tokyo, Japan
127,
G Hamar
G Hamar
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
J C Hamon
J C Hamon
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
J W Harris
J W Harris
137Yale University, New Haven, CT USA
137,
A Harton
A Harton
13Chicago State University, Chicago, IL USA
13,
D Hatzifotiadou
D Hatzifotiadou
104Sezione INFN, Bologna, Italy
104,
S Hayashi
S Hayashi
127University of Tokyo, Tokyo, Japan
127,
S T Heckel
S T Heckel
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
E Hellbär
E Hellbär
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
H Helstrup
H Helstrup
37Faculty of Engineering, Bergen University College, Mons, Norway
37,
A Herghelegiu
A Herghelegiu
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
G Herrera Corral
G Herrera Corral
11Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
11,
B A Hess
B A Hess
34Eberhard Karls Universität Tübingen, Tübingen, Germany
34,
K F Hetland
K F Hetland
37Faculty of Engineering, Bergen University College, Mons, Norway
37,
H Hillemanns
H Hillemanns
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
B Hippolyte
B Hippolyte
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
D Horak
D Horak
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
R Hosokawa
R Hosokawa
128University of Tsukuba, Tsukuba, Japan
128,
P Hristov
P Hristov
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
T J Humanic
T J Humanic
20Department of Physics, Ohio State University, Columbus, OH USA
20,
N Hussain
N Hussain
44Department of Physics, Gauhati University, Guwahati, India
44,
T Hussain
T Hussain
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
D Hutter
D Hutter
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
D S Hwang
D S Hwang
21Department of Physics, Sejong University, Seoul, South Korea
21,
R Ilkaev
R Ilkaev
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
M Inaba
M Inaba
128University of Tsukuba, Tsukuba, Japan
128,
E Incani
E Incani
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
M Ippolitov
M Ippolitov
75Moscow Engineering Physics Institute, Moscow, Russia
80National Research Centre Kurchatov Institute, Moscow, Russia
75,80,
M Irfan
M Irfan
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
M Ivanov
M Ivanov
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
V Ivanov
V Ivanov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
V Izucheev
V Izucheev
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
N Jacazio
N Jacazio
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
P M Jacobs
P M Jacobs
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
M B Jadhav
M B Jadhav
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
S Jadlovska
S Jadlovska
115Technical University of Košice, Kosice, Slovakia
115,
J Jadlovsky
J Jadlovsky
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
115Technical University of Košice, Kosice, Slovakia
59,115,
C Jahnke
C Jahnke
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
M J Jakubowska
M J Jakubowska
134Warsaw University of Technology, Warsaw, Poland
134,
H J Jang
H J Jang
68Korea Institute of Science and Technology Information, Daejeon, South Korea
68,
M A Janik
M A Janik
134Warsaw University of Technology, Warsaw, Poland
134,
P H S Y Jayarathna
P H S Y Jayarathna
122University of Houston, Houston, TX USA
122,
C Jena
C Jena
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
S Jena
S Jena
122University of Houston, Houston, TX USA
122,
R T Jimenez Bustamante
R T Jimenez Bustamante
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
P G Jones
P G Jones
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
A Jusko
A Jusko
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
P Kalinak
P Kalinak
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
59,
A Kalweit
A Kalweit
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
J Kamin
J Kamin
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
J H Kang
J H Kang
138Yonsei University, Seoul, South Korea
138,
V Kaplin
V Kaplin
75Moscow Engineering Physics Institute, Moscow, Russia
75,
S Kar
S Kar
133Variable Energy Cyclotron Centre, Kolkata, India
133,
A Karasu Uysal
A Karasu Uysal
69KTO Karatay University, Konya, Turkey
69,
O Karavichev
O Karavichev
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
T Karavicheva
T Karavicheva
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
L Karayan
L Karayan
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
94,97,
E Karpechev
E Karpechev
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
U Kebschull
U Kebschull
52Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
52,
R Keidel
R Keidel
139Zentrum für Technologietransfer und Telekommunikation (ZTT), Fachhochschule Worms, Worms, Germany
139,
D L D Keijdener
D L D Keijdener
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
M Keil
M Keil
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M Mohisin Khan
M Mohisin Khan
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
P Khan
P Khan
100Saha Institute of Nuclear Physics, Kolkata, India
100,
S A Khan
S A Khan
133Variable Energy Cyclotron Centre, Kolkata, India
133,
A Khanzadeev
A Khanzadeev
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
Y Kharlov
Y Kharlov
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
B Kileng
B Kileng
37Faculty of Engineering, Bergen University College, Mons, Norway
37,
D W Kim
D W Kim
43Gangneung-Wonju National University, Gangneung, South Korea
43,
D J Kim
D J Kim
123University of Jyväskylä, Jyväskylä, Finland
123,
D Kim
D Kim
138Yonsei University, Seoul, South Korea
138,
H Kim
H Kim
138Yonsei University, Seoul, South Korea
138,
J S Kim
J S Kim
43Gangneung-Wonju National University, Gangneung, South Korea
43,
M Kim
M Kim
138Yonsei University, Seoul, South Korea
138,
S Kim
S Kim
21Department of Physics, Sejong University, Seoul, South Korea
21,
T Kim
T Kim
138Yonsei University, Seoul, South Korea
138,
S Kirsch
S Kirsch
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
I Kisel
I Kisel
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
S Kiselev
S Kiselev
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
A Kisiel
A Kisiel
134Warsaw University of Technology, Warsaw, Poland
134,
G Kiss
G Kiss
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
J L Klay
J L Klay
6California Polytechnic State University, San Luis Obispo, CA USA
6,
C Klein
C Klein
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
J Klein
J Klein
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
C Klein-Bösing
C Klein-Bösing
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
S Klewin
S Klewin
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
A Kluge
A Kluge
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M L Knichel
M L Knichel
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
A G Knospe
A G Knospe
118Physics Department, The University of Texas at Austin, Austin, TX USA
122University of Houston, Houston, TX USA
118,122,
C Kobdaj
C Kobdaj
114Suranaree University of Technology, Nakhon Ratchasima, Thailand
114,
M Kofarago
M Kofarago
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
T Kollegger
T Kollegger
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
A Kolojvari
A Kolojvari
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
V Kondratiev
V Kondratiev
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
N Kondratyeva
N Kondratyeva
75Moscow Engineering Physics Institute, Moscow, Russia
75,
E Kondratyuk
E Kondratyuk
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
A Konevskikh
A Konevskikh
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
M Kopcik
M Kopcik
115Technical University of Košice, Kosice, Slovakia
115,
P Kostarakis
P Kostarakis
89Physics Department, University of Athens, Athens, Greece
89,
M Kour
M Kour
91Physics Department, University of Jammu, Jammu, India
91,
C Kouzinopoulos
C Kouzinopoulos
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
O Kovalenko
O Kovalenko
77National Centre for Nuclear Studies, Warsaw, Poland
77,
V Kovalenko
V Kovalenko
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
M Kowalski
M Kowalski
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
G Koyithatta Meethaleveedu
G Koyithatta Meethaleveedu
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
I Králik
I Králik
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
59,
A Kravčáková
A Kravčáková
40Faculty of Science, P.J. Šafárik University, Kosice, Slovakia
40,
M Krivda
M Krivda
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
59,101,
F Krizek
F Krizek
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
E Kryshen
E Kryshen
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
86Petersburg Nuclear Physics Institute, Gatchina, Russia
35,86,
M Krzewicki
M Krzewicki
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
A M Kubera
A M Kubera
20Department of Physics, Ohio State University, Columbus, OH USA
20,
V Kučera
V Kučera
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
C Kuhn
C Kuhn
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
P G Kuijer
P G Kuijer
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
82,
A Kumar
A Kumar
91Physics Department, University of Jammu, Jammu, India
91,
J Kumar
J Kumar
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
L Kumar
L Kumar
88Physics Department, Panjab University, Chandigarh, India
88,
S Kumar
S Kumar
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
P Kurashvili
P Kurashvili
77National Centre for Nuclear Studies, Warsaw, Poland
77,
A Kurepin
A Kurepin
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
A B Kurepin
A B Kurepin
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
A Kuryakin
A Kuryakin
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
M J Kweon
M J Kweon
50Inha University, Inchon, South Korea
50,
Y Kwon
Y Kwon
138Yonsei University, Seoul, South Korea
138,
S L La Pointe
S L La Pointe
110Sezione INFN, Turin, Italy
110,
P La Rocca
P La Rocca
28Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Catania, Italy
28,
P Ladron de Guevara
P Ladron de Guevara
11Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
11,
C Lagana Fernandes
C Lagana Fernandes
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
I Lakomov
I Lakomov
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
R Langoy
R Langoy
41Faculty of Technology, Buskerud and Vestfold University College, Vestfold, Norway
41,
K Lapidus
K Lapidus
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
C Lara
C Lara
52Institut für Informatik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
52,
A Lardeux
A Lardeux
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
A Lattuca
A Lattuca
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
E Laudi
E Laudi
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
R Lea
R Lea
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
L Leardini
L Leardini
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
G R Lee
G R Lee
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
S Lee
S Lee
138Yonsei University, Seoul, South Korea
138,
F Lehas
F Lehas
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
82,
S Lehner
S Lehner
112Stefan Meyer Institut für Subatomare Physik (SMI), Vienna, Austria
112,
R C Lemmon
R C Lemmon
83Nuclear Physics Group, STFC Daresbury Laboratory, Daresbury, UK
83,
V Lenti
V Lenti
103Sezione INFN, Bari, Italy
103,
E Leogrande
E Leogrande
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
I León Monzón
I León Monzón
119Universidad Autónoma de Sinaloa, Culiacán, Mexico
119,
H León Vargas
H León Vargas
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
M Leoncino
M Leoncino
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
P Lévai
P Lévai
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
S Li
S Li
7Central China Normal University, Wuhan, China
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
7,70,
X Li
X Li
14China Institute of Atomic Energy, Beijing, China
14,
J Lien
J Lien
41Faculty of Technology, Buskerud and Vestfold University College, Vestfold, Norway
41,
R Lietava
R Lietava
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
S Lindal
S Lindal
22Department of Physics, University of Oslo, Oslo, Norway
22,
V Lindenstruth
V Lindenstruth
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
C Lippmann
C Lippmann
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M A Lisa
M A Lisa
20Department of Physics, Ohio State University, Columbus, OH USA
20,
H M Ljunggren
H M Ljunggren
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
D F Lodato
D F Lodato
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
P I Loenne
P I Loenne
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
V Loginov
V Loginov
75Moscow Engineering Physics Institute, Moscow, Russia
75,
C Loizides
C Loizides
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
X Lopez
X Lopez
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
E López Torres
E López Torres
9Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN), Havana, Cuba
9,
A Lowe
A Lowe
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
P Luettig
P Luettig
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
M Lunardon
M Lunardon
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
G Luparello
G Luparello
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
T H Lutz
T H Lutz
137Yale University, New Haven, CT USA
137,
A Maevskaya
A Maevskaya
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
M Mager
M Mager
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
S Mahajan
S Mahajan
91Physics Department, University of Jammu, Jammu, India
91,
S M Mahmood
S M Mahmood
22Department of Physics, University of Oslo, Oslo, Norway
22,
A Maire
A Maire
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
R D Majka
R D Majka
137Yale University, New Haven, CT USA
137,
M Malaev
M Malaev
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
I Maldonado Cervantes
I Maldonado Cervantes
63Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
63,
L Malinina
L Malinina
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
D Mal’Kevich
D Mal’Kevich
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
P Malzacher
P Malzacher
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
A Mamonov
A Mamonov
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
V Manko
V Manko
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
F Manso
F Manso
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
V Manzari
V Manzari
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
103Sezione INFN, Bari, Italy
35,103,
M Marchisone
M Marchisone
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
65iThemba LABS, National Research Foundation, Somerset West, South Africa
126University of the Witwatersrand, Johannesburg, South Africa
26,65,126,
J Mareš
J Mareš
60Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
60,
G V Margagliotti
G V Margagliotti
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
A Margotti
A Margotti
104Sezione INFN, Bologna, Italy
104,
J Margutti
J Margutti
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
A Marín
A Marín
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
C Markert
C Markert
118Physics Department, The University of Texas at Austin, Austin, TX USA
118,
M Marquard
M Marquard
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
N A Martin
N A Martin
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
J Martin Blanco
J Martin Blanco
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
P Martinengo
P Martinengo
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M I Martínez
M I Martínez
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
G Martínez García
G Martínez García
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
M Martinez Pedreira
M Martinez Pedreira
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
A Mas
A Mas
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
S Masciocchi
S Masciocchi
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M Masera
M Masera
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
A Masoni
A Masoni
105Sezione INFN, Cagliari, Italy
105,
A Mastroserio
A Mastroserio
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
A Matyja
A Matyja
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
C Mayer
C Mayer
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
J Mazer
J Mazer
125University of Tennessee, Knoxville, TN USA
125,
M A Mazzoni
M A Mazzoni
108Sezione INFN, Rome, Italy
108,
D Mcdonald
D Mcdonald
122University of Houston, Houston, TX USA
122,
F Meddi
F Meddi
23Dipartimento di Fisica dell’Università ‘La Sapienza’ and Sezione INFN, Rome, Italy
23,
Y Melikyan
Y Melikyan
75Moscow Engineering Physics Institute, Moscow, Russia
75,
A Menchaca-Rocha
A Menchaca-Rocha
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
E Meninno
E Meninno
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
30,
J Mercado Pérez
J Mercado Pérez
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
M Meres
M Meres
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
Y Miake
Y Miake
128University of Tsukuba, Tsukuba, Japan
128,
M M Mieskolainen
M M Mieskolainen
45Helsinki Institute of Physics (HIP), Helsinki, Finland
45,
K Mikhaylov
K Mikhaylov
58Institute for Theoretical and Experimental Physics, Moscow, Russia
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
58,66,
L Milano
L Milano
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
35,74,
J Milosevic
J Milosevic
22Department of Physics, University of Oslo, Oslo, Norway
22,
A Mischke
A Mischke
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
A N Mishra
A N Mishra
48Indian Institute of Technology Indore (IITI), Indore, India
48,
D Miśkowiec
D Miśkowiec
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
J Mitra
J Mitra
133Variable Energy Cyclotron Centre, Kolkata, India
133,
C M Mitu
C M Mitu
62Institute of Space Science (ISS), Bucharest, Romania
62,
N Mohammadi
N Mohammadi
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
B Mohanty
B Mohanty
79National Institute of Science Education and Research, Bhubaneswar, India
79,
L Molnar
L Molnar
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
L Montaño Zetina
L Montaño Zetina
11Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
11,
E Montes
E Montes
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
10,
D A Moreira De Godoy
D A Moreira De Godoy
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
L A P Moreno
L A P Moreno
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
S Moretto
S Moretto
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
A Morreale
A Morreale
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
A Morsch
A Morsch
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
V Muccifora
V Muccifora
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
E Mudnic
E Mudnic
116Technical University of Split FESB, Split, Croatia
116,
D Mühlheim
D Mühlheim
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
S Muhuri
S Muhuri
133Variable Energy Cyclotron Centre, Kolkata, India
133,
M Mukherjee
M Mukherjee
133Variable Energy Cyclotron Centre, Kolkata, India
133,
J D Mulligan
J D Mulligan
137Yale University, New Haven, CT USA
137,
M G Munhoz
M G Munhoz
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
R H Munzer
R H Munzer
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,53,93,
H Murakami
H Murakami
127University of Tokyo, Tokyo, Japan
127,
S Murray
S Murray
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
L Musa
L Musa
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
J Musinsky
J Musinsky
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
59,
B Naik
B Naik
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
R Nair
R Nair
77National Centre for Nuclear Studies, Warsaw, Poland
77,
B K Nandi
B K Nandi
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
R Nania
R Nania
104Sezione INFN, Bologna, Italy
104,
E Nappi
E Nappi
103Sezione INFN, Bari, Italy
103,
M U Naru
M U Naru
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
H Natal da Luz
H Natal da Luz
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
C Nattrass
C Nattrass
125University of Tennessee, Knoxville, TN USA
125,
S R Navarro
S R Navarro
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
K Nayak
K Nayak
79National Institute of Science Education and Research, Bhubaneswar, India
79,
R Nayak
R Nayak
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
T K Nayak
T K Nayak
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S Nazarenko
S Nazarenko
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
A Nedosekin
A Nedosekin
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
L Nellen
L Nellen
63Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
63,
F Ng
F Ng
122University of Houston, Houston, TX USA
122,
M Nicassio
M Nicassio
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M Niculescu
M Niculescu
62Institute of Space Science (ISS), Bucharest, Romania
62,
J Niedziela
J Niedziela
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
B S Nielsen
B S Nielsen
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
S Nikolaev
S Nikolaev
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
S Nikulin
S Nikulin
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
V Nikulin
V Nikulin
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
F Noferini
F Noferini
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
104Sezione INFN, Bologna, Italy
12,104,
P Nomokonov
P Nomokonov
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
G Nooren
G Nooren
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
J C C Noris
J C C Noris
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
J Norman
J Norman
124University of Liverpool, Liverpool, UK
124,
A Nyanin
A Nyanin
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
J Nystrand
J Nystrand
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
H Oeschler
H Oeschler
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
S Oh
S Oh
137Yale University, New Haven, CT USA
137,
S K Oh
S K Oh
67Konkuk University, Seoul, South Korea
67,
A Ohlson
A Ohlson
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
A Okatan
A Okatan
69KTO Karatay University, Konya, Turkey
69,
T Okubo
T Okubo
46Hiroshima University, Hiroshima, Japan
46,
L Olah
L Olah
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
J Oleniacz
J Oleniacz
134Warsaw University of Technology, Warsaw, Poland
134,
A C Oliveira Da Silva
A C Oliveira Da Silva
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
M H Oliver
M H Oliver
137Yale University, New Haven, CT USA
137,
J Onderwaater
J Onderwaater
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
C Oppedisano
C Oppedisano
110Sezione INFN, Turin, Italy
110,
R Orava
R Orava
45Helsinki Institute of Physics (HIP), Helsinki, Finland
45,
M Oravec
M Oravec
115Technical University of Košice, Kosice, Slovakia
115,
A Ortiz Velasquez
A Ortiz Velasquez
63Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
63,
A Oskarsson
A Oskarsson
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
J Otwinowski
J Otwinowski
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
K Oyama
K Oyama
76Nagasaki Institute of Applied Science, Nagasaki, Japan
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
76,94,
M Ozdemir
M Ozdemir
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
Y Pachmayer
Y Pachmayer
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
D Pagano
D Pagano
131Università di Brescia, Brescia, Italy
131,
P Pagano
P Pagano
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
30,
G Paić
G Paić
63Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Mexico City, Mexico
63,
S K Pal
S K Pal
133Variable Energy Cyclotron Centre, Kolkata, India
133,
J Pan
J Pan
135Wayne State University, Detroit, MI USA
135,
A K Pandey
A K Pandey
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
V Papikyan
V Papikyan
1A.I. Alikhanyan National Science Laboratory (Yerevan Physics Institute) Foundation, Yerevan, Armenia
1,
G S Pappalardo
G S Pappalardo
106Sezione INFN, Catania, Italy
106,
P Pareek
P Pareek
48Indian Institute of Technology Indore (IITI), Indore, India
48,
W J Park
W J Park
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
S Parmar
S Parmar
88Physics Department, Panjab University, Chandigarh, India
88,
A Passfeld
A Passfeld
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
V Paticchio
V Paticchio
103Sezione INFN, Bari, Italy
103,
R N Patra
R N Patra
133Variable Energy Cyclotron Centre, Kolkata, India
133,
B Paul
B Paul
100Saha Institute of Nuclear Physics, Kolkata, India
110Sezione INFN, Turin, Italy
100,110,
H Pei
H Pei
7Central China Normal University, Wuhan, China
7,
T Peitzmann
T Peitzmann
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
H Pereira Da Costa
H Pereira Da Costa
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
D Peresunko
D Peresunko
75Moscow Engineering Physics Institute, Moscow, Russia
80National Research Centre Kurchatov Institute, Moscow, Russia
75,80,
E Perez Lezama
E Perez Lezama
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
V Peskov
V Peskov
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
Y Pestov
Y Pestov
5Budker Institute for Nuclear Physics, Novosibirsk, Russia
5,
V Petráček
V Petráček
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
V Petrov
V Petrov
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
M Petrovici
M Petrovici
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
C Petta
C Petta
28Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Catania, Italy
28,
S Piano
S Piano
109Sezione INFN, Trieste, Italy
109,
M Pikna
M Pikna
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
P Pillot
P Pillot
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
L O D L Pimentel
L O D L Pimentel
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
O Pinazza
O Pinazza
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
104Sezione INFN, Bologna, Italy
35,104,
L Pinsky
L Pinsky
122University of Houston, Houston, TX USA
122,
D B Piyarathna
D B Piyarathna
122University of Houston, Houston, TX USA
122,
M Płoskoń
M Płoskoń
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
M Planinic
M Planinic
129University of Zagreb, Zagreb, Croatia
129,
J Pluta
J Pluta
134Warsaw University of Technology, Warsaw, Poland
134,
S Pochybova
S Pochybova
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
P L M Podesta-Lerma
P L M Podesta-Lerma
119Universidad Autónoma de Sinaloa, Culiacán, Mexico
119,
M G Poghosyan
M G Poghosyan
85Oak Ridge National Laboratory, Oak Ridge, TN USA
87Physics Department, Creighton University, Omaha, NE USA
85,87,
B Polichtchouk
B Polichtchouk
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
N Poljak
N Poljak
129University of Zagreb, Zagreb, Croatia
129,
W Poonsawat
W Poonsawat
114Suranaree University of Technology, Nakhon Ratchasima, Thailand
114,
A Pop
A Pop
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
S Porteboeuf-Houssais
S Porteboeuf-Houssais
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
J Porter
J Porter
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
J Pospisil
J Pospisil
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
S K Prasad
S K Prasad
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
4,
R Preghenella
R Preghenella
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
104Sezione INFN, Bologna, Italy
35,104,
F Prino
F Prino
110Sezione INFN, Turin, Italy
110,
C A Pruneau
C A Pruneau
135Wayne State University, Detroit, MI USA
135,
I Pshenichnov
I Pshenichnov
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
M Puccio
M Puccio
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
G Puddu
G Puddu
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
P Pujahari
P Pujahari
135Wayne State University, Detroit, MI USA
135,
V Punin
V Punin
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
J Putschke
J Putschke
135Wayne State University, Detroit, MI USA
135,
H Qvigstad
H Qvigstad
22Department of Physics, University of Oslo, Oslo, Norway
22,
A Rachevski
A Rachevski
109Sezione INFN, Trieste, Italy
109,
S Raha
S Raha
4Department of Physics, Centre for Astroparticle Physics and Space Science (CAPSS), Bose Institute, Kolkata, India
4,
S Rajput
S Rajput
91Physics Department, University of Jammu, Jammu, India
91,
J Rak
J Rak
123University of Jyväskylä, Jyväskylä, Finland
123,
A Rakotozafindrabe
A Rakotozafindrabe
15Commissariat à l’Energie Atomique, IRFU, Saclay, France
15,
L Ramello
L Ramello
31Dipartimento di Scienze e Innovazione Tecnologica dell’Università del Piemonte Orientale and Gruppo Collegato INFN, Alessandria, Italy
31,
F Rami
F Rami
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
R Raniwala
R Raniwala
92Physics Department, University of Rajasthan, Jaipur, India
92,
S Raniwala
S Raniwala
92Physics Department, University of Rajasthan, Jaipur, India
92,
S S Räsänen
S S Räsänen
45Helsinki Institute of Physics (HIP), Helsinki, Finland
45,
B T Rascanu
B T Rascanu
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
D Rathee
D Rathee
88Physics Department, Panjab University, Chandigarh, India
88,
K F Read
K F Read
85Oak Ridge National Laboratory, Oak Ridge, TN USA
125University of Tennessee, Knoxville, TN USA
85,125,
K Redlich
K Redlich
77National Centre for Nuclear Studies, Warsaw, Poland
77,
R J Reed
R J Reed
135Wayne State University, Detroit, MI USA
135,
A Rehman
A Rehman
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
P Reichelt
P Reichelt
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
F Reidt
F Reidt
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
35,94,
X Ren
X Ren
7Central China Normal University, Wuhan, China
7,
R Renfordt
R Renfordt
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
A R Reolon
A R Reolon
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
A Reshetin
A Reshetin
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
K Reygers
K Reygers
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
V Riabov
V Riabov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
R A Ricci
R A Ricci
73Laboratori Nazionali di Legnaro, INFN, Legnaro, Italy
73,
T Richert
T Richert
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
M Richter
M Richter
22Department of Physics, University of Oslo, Oslo, Norway
22,
P Riedler
P Riedler
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
W Riegler
W Riegler
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
F Riggi
F Riggi
28Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Catania, Italy
28,
C Ristea
C Ristea
62Institute of Space Science (ISS), Bucharest, Romania
62,
E Rocco
E Rocco
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
M Rodríguez Cahuantzi
M Rodríguez Cahuantzi
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
11Centro de Investigación y de Estudios Avanzados (CINVESTAV), Mexico City and Mérida, Mexico
2,11,
A Rodriguez Manso
A Rodriguez Manso
82Nikhef, Nationaal instituut voor subatomaire fysica, Amsterdam, The Netherlands
82,
K Røed
K Røed
22Department of Physics, University of Oslo, Oslo, Norway
22,
E Rogochaya
E Rogochaya
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
D Rohr
D Rohr
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42,
D Röhrich
D Röhrich
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
F Ronchetti
F Ronchetti
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
35,72,
L Ronflette
L Ronflette
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
P Rosnet
P Rosnet
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
A Rossi
A Rossi
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
29,35,
F Roukoutakis
F Roukoutakis
89Physics Department, University of Athens, Athens, Greece
89,
A Roy
A Roy
48Indian Institute of Technology Indore (IITI), Indore, India
48,
C Roy
C Roy
55Institut Pluridisciplinaire Hubert Curien (IPHC), Université de Strasbourg, CNRS-IN2P3, Strasbourg, France
55,
P Roy
P Roy
100Saha Institute of Nuclear Physics, Kolkata, India
100,
A J Rubio Montero
A J Rubio Montero
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
10,
R Rui
R Rui
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
R Russo
R Russo
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
B D Ruzza
B D Ruzza
107Sezione INFN, Padua, Italy
107,
E Ryabinkin
E Ryabinkin
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
Y Ryabov
Y Ryabov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
A Rybicki
A Rybicki
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
S Saarinen
S Saarinen
45Helsinki Institute of Physics (HIP), Helsinki, Finland
45,
S Sadhu
S Sadhu
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S Sadovsky
S Sadovsky
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
K Šafařík
K Šafařík
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
B Sahlmuller
B Sahlmuller
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
P Sahoo
P Sahoo
48Indian Institute of Technology Indore (IITI), Indore, India
48,
R Sahoo
R Sahoo
48Indian Institute of Technology Indore (IITI), Indore, India
48,
S Sahoo
S Sahoo
61Institute of Physics, Bhubaneswar, India
61,
P K Sahu
P K Sahu
61Institute of Physics, Bhubaneswar, India
61,
J Saini
J Saini
133Variable Energy Cyclotron Centre, Kolkata, India
133,
S Sakai
S Sakai
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
M A Saleh
M A Saleh
135Wayne State University, Detroit, MI USA
135,
J Salzwedel
J Salzwedel
20Department of Physics, Ohio State University, Columbus, OH USA
20,
S Sambyal
S Sambyal
91Physics Department, University of Jammu, Jammu, India
91,
V Samsonov
V Samsonov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
L Šándor
L Šándor
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
59,
A Sandoval
A Sandoval
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
64,
M Sano
M Sano
128University of Tsukuba, Tsukuba, Japan
128,
D Sarkar
D Sarkar
133Variable Energy Cyclotron Centre, Kolkata, India
133,
N Sarkar
N Sarkar
133Variable Energy Cyclotron Centre, Kolkata, India
133,
P Sarma
P Sarma
44Department of Physics, Gauhati University, Guwahati, India
44,
E Scapparone
E Scapparone
104Sezione INFN, Bologna, Italy
104,
F Scarlassara
F Scarlassara
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
C Schiaua
C Schiaua
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
R Schicker
R Schicker
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
C Schmidt
C Schmidt
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
H R Schmidt
H R Schmidt
34Eberhard Karls Universität Tübingen, Tübingen, Germany
34,
M Schmidt
M Schmidt
34Eberhard Karls Universität Tübingen, Tübingen, Germany
34,
S Schuchmann
S Schuchmann
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
J Schukraft
J Schukraft
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M Schulc
M Schulc
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
Y Schutz
Y Schutz
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
35,113,
K Schwarz
K Schwarz
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
K Schweda
K Schweda
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
G Scioli
G Scioli
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
27,
E Scomparin
E Scomparin
110Sezione INFN, Turin, Italy
110,
R Scott
R Scott
125University of Tennessee, Knoxville, TN USA
125,
M Šefčík
M Šefčík
40Faculty of Science, P.J. Šafárik University, Kosice, Slovakia
40,
J E Seger
J E Seger
87Physics Department, Creighton University, Omaha, NE USA
87,
Y Sekiguchi
Y Sekiguchi
127University of Tokyo, Tokyo, Japan
127,
D Sekihata
D Sekihata
46Hiroshima University, Hiroshima, Japan
46,
I Selyuzhenkov
I Selyuzhenkov
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
K Senosi
K Senosi
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
S Senyukov
S Senyukov
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
3,35,
E Serradilla
E Serradilla
10Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
64Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
10,64,
A Sevcenco
A Sevcenco
62Institute of Space Science (ISS), Bucharest, Romania
62,
A Shabanov
A Shabanov
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
A Shabetai
A Shabetai
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
O Shadura
O Shadura
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
R Shahoyan
R Shahoyan
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M I Shahzad
M I Shahzad
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
A Shangaraev
A Shangaraev
111SSC IHEP of NRC Kurchatov institute, Protvino, Russia
111,
A Sharma
A Sharma
91Physics Department, University of Jammu, Jammu, India
91,
M Sharma
M Sharma
91Physics Department, University of Jammu, Jammu, India
91,
M Sharma
M Sharma
91Physics Department, University of Jammu, Jammu, India
91,
N Sharma
N Sharma
125University of Tennessee, Knoxville, TN USA
125,
A I Sheikh
A I Sheikh
133Variable Energy Cyclotron Centre, Kolkata, India
133,
K Shigaki
K Shigaki
46Hiroshima University, Hiroshima, Japan
46,
Q Shou
Q Shou
7Central China Normal University, Wuhan, China
7,
K Shtejer
K Shtejer
9Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN), Havana, Cuba
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
9,26,
Y Sibiriak
Y Sibiriak
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
S Siddhanta
S Siddhanta
105Sezione INFN, Cagliari, Italy
105,
K M Sielewicz
K M Sielewicz
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
T Siemiarczuk
T Siemiarczuk
77National Centre for Nuclear Studies, Warsaw, Poland
77,
D Silvermyr
D Silvermyr
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
C Silvestre
C Silvestre
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
G Simatovic
G Simatovic
129University of Zagreb, Zagreb, Croatia
129,
G Simonetti
G Simonetti
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
R Singaraju
R Singaraju
133Variable Energy Cyclotron Centre, Kolkata, India
133,
R Singh
R Singh
79National Institute of Science Education and Research, Bhubaneswar, India
79,
S Singha
S Singha
79National Institute of Science Education and Research, Bhubaneswar, India
133Variable Energy Cyclotron Centre, Kolkata, India
79,133,
V Singhal
V Singhal
133Variable Energy Cyclotron Centre, Kolkata, India
133,
B C Sinha
B C Sinha
133Variable Energy Cyclotron Centre, Kolkata, India
133,
T Sinha
T Sinha
100Saha Institute of Nuclear Physics, Kolkata, India
100,
B Sitar
B Sitar
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
M Sitta
M Sitta
31Dipartimento di Scienze e Innovazione Tecnologica dell’Università del Piemonte Orientale and Gruppo Collegato INFN, Alessandria, Italy
31,
T B Skaali
T B Skaali
22Department of Physics, University of Oslo, Oslo, Norway
22,
M Slupecki
M Slupecki
123University of Jyväskylä, Jyväskylä, Finland
123,
N Smirnov
N Smirnov
137Yale University, New Haven, CT USA
137,
R J M Snellings
R J M Snellings
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
T W Snellman
T W Snellman
123University of Jyväskylä, Jyväskylä, Finland
123,
J Song
J Song
96Pusan National University, Pusan, South Korea
96,
M Song
M Song
138Yonsei University, Seoul, South Korea
138,
Z Song
Z Song
7Central China Normal University, Wuhan, China
7,
F Soramel
F Soramel
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
S Sorensen
S Sorensen
125University of Tennessee, Knoxville, TN USA
125,
R D de Souza
R D de Souza
121Universidade Estadual de Campinas (UNICAMP), Campinas, Brazil
121,
F Sozzi
F Sozzi
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
M Spacek
M Spacek
39Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Prague, Czech Republic
39,
E Spiriti
E Spiriti
72Laboratori Nazionali di Frascati, INFN, Frascati, Italy
72,
I Sputowska
I Sputowska
117The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Cracow, Poland
117,
M Spyropoulou-Stassinaki
M Spyropoulou-Stassinaki
89Physics Department, University of Athens, Athens, Greece
89,
J Stachel
J Stachel
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
I Stan
I Stan
62Institute of Space Science (ISS), Bucharest, Romania
62,
P Stankus
P Stankus
85Oak Ridge National Laboratory, Oak Ridge, TN USA
85,
E Stenlund
E Stenlund
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
G Steyn
G Steyn
65iThemba LABS, National Research Foundation, Somerset West, South Africa
65,
J H Stiller
J H Stiller
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
D Stocco
D Stocco
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
113,
P Strmen
P Strmen
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
A A P Suaide
A A P Suaide
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
T Sugitate
T Sugitate
46Hiroshima University, Hiroshima, Japan
46,
C Suire
C Suire
51Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France
51,
M Suleymanov
M Suleymanov
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
M Suljic
M Suljic
25Dipartimento di Fisica dell’Università and Sezione INFN, Trieste, Italy
25,
R Sultanov
R Sultanov
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
M Šumbera
M Šumbera
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
S Sumowidagdo
S Sumowidagdo
49Indonesian Institute of Sciences, Jakarta, Indonesia
49,
A Szabo
A Szabo
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
I Szarka
I Szarka
38Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovakia
38,
A Szczepankiewicz
A Szczepankiewicz
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M Szymanski
M Szymanski
134Warsaw University of Technology, Warsaw, Poland
134,
U Tabassam
U Tabassam
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
J Takahashi
J Takahashi
121Universidade Estadual de Campinas (UNICAMP), Campinas, Brazil
121,
G J Tambave
G J Tambave
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
N Tanaka
N Tanaka
128University of Tsukuba, Tsukuba, Japan
128,
M Tarhini
M Tarhini
51Institut de Physique Nucléaire d’Orsay (IPNO), Université Paris-Sud, CNRS-IN2P3, Orsay, France
51,
M Tariq
M Tariq
19Department of Physics, Aligarh Muslim University, Aligarh, India
19,
M G Tarzila
M G Tarzila
78National Institute for Physics and Nuclear Engineering, Bucharest, Romania
78,
A Tauro
A Tauro
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
G Tejeda Muñoz
G Tejeda Muñoz
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
A Telesca
A Telesca
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
K Terasaki
K Terasaki
127University of Tokyo, Tokyo, Japan
127,
C Terrevoli
C Terrevoli
29Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Padua, Italy
29,
B Teyssier
B Teyssier
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
J Thäder
J Thäder
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
74,
D Thakur
D Thakur
48Indian Institute of Technology Indore (IITI), Indore, India
48,
D Thomas
D Thomas
118Physics Department, The University of Texas at Austin, Austin, TX USA
118,
R Tieulent
R Tieulent
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
A Tikhonov
A Tikhonov
56Institute for Nuclear Research, Academy of Sciences, Moscow, Russia
56,
A R Timmins
A R Timmins
122University of Houston, Houston, TX USA
122,
A Toia
A Toia
53Institut für Kernphysik, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
53,
S Trogolo
S Trogolo
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
G Trombetta
G Trombetta
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
32,
V Trubnikov
V Trubnikov
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
W H Trzaska
W H Trzaska
123University of Jyväskylä, Jyväskylä, Finland
123,
T Tsuji
T Tsuji
127University of Tokyo, Tokyo, Japan
127,
A Tumkin
A Tumkin
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
R Turrisi
R Turrisi
107Sezione INFN, Padua, Italy
107,
T S Tveter
T S Tveter
22Department of Physics, University of Oslo, Oslo, Norway
22,
K Ullaland
K Ullaland
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
A Uras
A Uras
130Université de Lyon, Université Lyon 1, CNRS/IN2P3, IPN-Lyon, Villeurbanne, France
130,
G L Usai
G L Usai
24Dipartimento di Fisica dell’Università and Sezione INFN, Cagliari, Italy
24,
A Utrobicic
A Utrobicic
129University of Zagreb, Zagreb, Croatia
129,
M Vala
M Vala
59Institute of Experimental Physics, Slovak Academy of Sciences, Kosice, Slovakia
59,
L Valencia Palomo
L Valencia Palomo
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
S Vallero
S Vallero
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
J Van Der Maarel
J Van Der Maarel
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
J W Van Hoorne
J W Van Hoorne
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
M van Leeuwen
M van Leeuwen
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
T Vanat
T Vanat
84Nuclear Physics Institute, Academy of Sciences of the Czech Republic, Řež u Prahy, Czech Republic
84,
P Vande Vyvre
P Vande Vyvre
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
D Varga
D Varga
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
136,
A Vargas
A Vargas
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
M Vargyas
M Vargyas
123University of Jyväskylä, Jyväskylä, Finland
123,
R Varma
R Varma
47Indian Institute of Technology Bombay (IIT), Mumbai, India
47,
M Vasileiou
M Vasileiou
89Physics Department, University of Athens, Athens, Greece
89,
A Vasiliev
A Vasiliev
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
A Vauthier
A Vauthier
71Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS-IN2P3, Grenoble, France
71,
O Vázquez Doce
O Vázquez Doce
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
V Vechernin
V Vechernin
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
A M Veen
A M Veen
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
M Veldhoen
M Veldhoen
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
A Velure
A Velure
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
E Vercellin
E Vercellin
26Dipartimento di Fisica dell’Università and Sezione INFN, Turin, Italy
26,
S Vergara Limón
S Vergara Limón
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
R Vernet
R Vernet
8Centre de Calcul de l’IN2P3, Villeurbanne, France
8,
M Verweij
M Verweij
135Wayne State University, Detroit, MI USA
135,
L Vickovic
L Vickovic
116Technical University of Split FESB, Split, Croatia
116,
J Viinikainen
J Viinikainen
123University of Jyväskylä, Jyväskylä, Finland
123,
Z Vilakazi
Z Vilakazi
126University of the Witwatersrand, Johannesburg, South Africa
126,
O Villalobos Baillie
O Villalobos Baillie
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
A Villatoro Tello
A Villatoro Tello
2Benemérita Universidad Autónoma de Puebla, Puebla, Mexico
2,
A Vinogradov
A Vinogradov
80National Research Centre Kurchatov Institute, Moscow, Russia
80,
L Vinogradov
L Vinogradov
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
Y Vinogradov
Y Vinogradov
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
T Virgili
T Virgili
30Dipartimento di Fisica ‘E.R. Caianiello’ dell’Università and Gruppo Collegato INFN, Salerno, Italy
30,
V Vislavicius
V Vislavicius
33Division of Experimental High Energy Physics, University of Lund, Lund, Sweden
33,
Y P Viyogi
Y P Viyogi
133Variable Energy Cyclotron Centre, Kolkata, India
133,
A Vodopyanov
A Vodopyanov
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
M A Völkl
M A Völkl
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
K Voloshin
K Voloshin
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
S A Voloshin
S A Voloshin
135Wayne State University, Detroit, MI USA
135,
G Volpe
G Volpe
32Dipartimento Interateneo di Fisica ‘M. Merlin’ and Sezione INFN, Bari, Italy
136Wigner Research Centre for Physics, Hungarian Academy of Sciences, Budapest, Hungary
32,136,
B von Haller
B von Haller
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
35,
I Vorobyev
I Vorobyev
36Excellence Cluster Universe, Technische Universität München, Munich, Germany
93Physik Department, Technische Universität München, Munich, Germany
36,93,
D Vranic
D Vranic
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
35,97,
J Vrláková
J Vrláková
40Faculty of Science, P.J. Šafárik University, Kosice, Slovakia
40,
B Vulpescu
B Vulpescu
70Laboratoire de Physique Corpusculaire (LPC), Clermont Université, Université Blaise Pascal, CNRS-IN2P3, Clermont-Ferrand, France
70,
B Wagner
B Wagner
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
J Wagner
J Wagner
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
H Wang
H Wang
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
M Wang
M Wang
7Central China Normal University, Wuhan, China
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
7,113,
D Watanabe
D Watanabe
128University of Tsukuba, Tsukuba, Japan
128,
Y Watanabe
Y Watanabe
127University of Tokyo, Tokyo, Japan
127,
M Weber
M Weber
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
112Stefan Meyer Institut für Subatomare Physik (SMI), Vienna, Austria
35,112,
S G Weber
S G Weber
97Research Division and ExtreMe Matter Institute EMMI, GSI Helmholtzzentrum für Schwerionenforschung, Darmstadt, Germany
97,
D F Weiser
D F Weiser
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
J P Wessels
J P Wessels
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
U Westerhoff
U Westerhoff
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
54,
A M Whitehead
A M Whitehead
90Physics Department, University of Cape Town, Cape Town, South Africa
90,
J Wiechula
J Wiechula
34Eberhard Karls Universität Tübingen, Tübingen, Germany
34,
J Wikne
J Wikne
22Department of Physics, University of Oslo, Oslo, Norway
22,
G Wilk
G Wilk
77National Centre for Nuclear Studies, Warsaw, Poland
77,
J Wilkinson
J Wilkinson
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
M C S Williams
M C S Williams
104Sezione INFN, Bologna, Italy
104,
B Windelband
B Windelband
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
M Winn
M Winn
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
P Yang
P Yang
7Central China Normal University, Wuhan, China
7,
S Yano
S Yano
46Hiroshima University, Hiroshima, Japan
46,
Z Yasin
Z Yasin
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
Z Yin
Z Yin
7Central China Normal University, Wuhan, China
7,
H Yokoyama
H Yokoyama
128University of Tsukuba, Tsukuba, Japan
128,
I-K Yoo
I-K Yoo
96Pusan National University, Pusan, South Korea
96,
J H Yoon
J H Yoon
50Inha University, Inchon, South Korea
50,
V Yurchenko
V Yurchenko
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
A Zaborowska
A Zaborowska
134Warsaw University of Technology, Warsaw, Poland
134,
V Zaccolo
V Zaccolo
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
A Zaman
A Zaman
16COMSATS Institute of Information Technology (CIIT), Islamabad, Pakistan
16,
C Zampolli
C Zampolli
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
104Sezione INFN, Bologna, Italy
35,104,
H J C Zanoli
H J C Zanoli
120Universidade de São Paulo (USP), São Paulo, Brazil
120,
S Zaporozhets
S Zaporozhets
66Joint Institute for Nuclear Research (JINR), Dubna, Russia
66,
N Zardoshti
N Zardoshti
101School of Physics and Astronomy, University of Birmingham, Birmingham, UK
101,
A Zarochentsev
A Zarochentsev
132V. Fock Institute for Physics, St. Petersburg State University, St. Petersburg, Russia
132,
P Závada
P Závada
60Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
60,
N Zaviyalov
N Zaviyalov
99Russian Federal Nuclear Center (VNIIEF), Sarov, Russia
99,
H Zbroszczyk
H Zbroszczyk
134Warsaw University of Technology, Warsaw, Poland
134,
I S Zgura
I S Zgura
62Institute of Space Science (ISS), Bucharest, Romania
62,
M Zhalov
M Zhalov
86Petersburg Nuclear Physics Institute, Gatchina, Russia
86,
H Zhang
H Zhang
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
X Zhang
X Zhang
7Central China Normal University, Wuhan, China
74Lawrence Berkeley National Laboratory, Berkeley, CA USA
7,74,
Y Zhang
Y Zhang
7Central China Normal University, Wuhan, China
7,
C Zhang
C Zhang
57Institute for Subatomic Physics of Utrecht University, Utrecht, The Netherlands
57,
Z Zhang
Z Zhang
7Central China Normal University, Wuhan, China
7,
C Zhao
C Zhao
22Department of Physics, University of Oslo, Oslo, Norway
22,
N Zhigareva
N Zhigareva
58Institute for Theoretical and Experimental Physics, Moscow, Russia
58,
D Zhou
D Zhou
7Central China Normal University, Wuhan, China
7,
Y Zhou
Y Zhou
81Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
81,
Z Zhou
Z Zhou
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
H Zhu
H Zhu
18Department of Physics and Technology, University of Bergen, Mons, Norway
18,
J Zhu
J Zhu
7Central China Normal University, Wuhan, China
113SUBATECH, Ecole des Mines de Nantes, Université de Nantes, CNRS-IN2P3, Nantes, France
7,113,
A Zichichi
A Zichichi
12Centro Fermi-Museo Storico della Fisica e Centro Studi e Ricerche “Enrico Fermi”, Rome, Italy
27Dipartimento di Fisica e Astronomia dell’Università and Sezione INFN, Bologna, Italy
12,27,
A Zimmermann
A Zimmermann
94Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
94,
M B Zimmermann
M B Zimmermann
35European Organization for Nuclear Research (CERN), Geneva, Switzerland
54Institut für Kernphysik, Westfälische Wilhelms-Universität Münster, Münster, Germany
35,54,
G Zinovjev
G Zinovjev
3Bogolyubov Institute for Theoretical Physics, Kiev, Ukraine
3,
M Zyzak
M Zyzak
42Frankfurt Institute for Advanced Studies, Johann Wolfgang Goethe-Universität Frankfurt, Frankfurt, Germany
42