Fechner’s law in metacognition: a quantitative model of visual working memory confidence

Abstract

Although visual working memory (VWM) has been studied extensively, it is unknown how people form confidence judgments about their memories. Peirce (1878) speculated that Fechner’s law – which states that sensation is proportional to the logarithm of stimulus intensity – might apply to confidence reports. Based on this idea, we hypothesize that humans map the precision of their VWM contents to a confidence rating through Fechner’s law. We incorporate this hypothesis into the best available model of VWM encoding and fit it to data from a delayed-estimation experiment. The model provides an excellent account of human confidence rating distributions as well as the relation between performance and confidence. Moreover, the best-fitting mapping in a model with a highly flexible mapping closely resembles the logarithmic mapping, suggesting that no alternative mapping exists that accounts better for the data than Fechner's law. We propose a neural implementation of the model and find that this model also fits the behavioral data well. Furthermore, we find that jointly fitting memory errors and confidence ratings boosts the power to distinguish previously proposed VWM encoding models by a factor of 5.99 compared to fitting only memory errors. Finally, we show that Fechner's law also accounts for metacognitive judgments in a word recognition memory task, which is a first indication that it may be a general law in metacognition. Our work presents the first model to jointly account for errors and confidence ratings in VWM and could lay the groundwork for understanding the computational mechanisms of metacognition.

INTRODUCTION

The contents of visual working memory (VWM) have been subject of much recent investigation, with a focus on explaining storage limitations (Luck & Vogel, 2013; Ma, Husain, & Bays, 2014). A range of competing models have been proposed. For example, some postulate that VWM resource consists of discrete quanta (W. Zhang & Luck, 2008), while others claim it to be continuous (Bays & Husain, 2008; Palmer, 1990; Wilken & Ma, 2004). What all models have in common, however, is that they conceptualize working memories as point estimates: the memory of a feature is represented by a single value. This view is inconsistent with the recently documented correlation between VWM confidence ratings and VWM performance (Bona, Cattaneo, Vecchi, Soto, & Silvanto, 2013; Bona & Silvanto, 2014; Rademaker, Tredway, & Tong, 2012): larger memory errors tend to be accompanied by lower confidence ratings (Fig. 1). This correlation – which is sometimes called metacognitive accuracy (Fleming & Dolan, 2012) – indicates that VWM contents are richer than assumed by current models: besides the memories themselves, VWM also contains representations of the precision of the memories. As of yet, no quantitative account exists for metacognition in any form of working memory. Here, we develop and test a generalizable model that jointly accounts for people’s VWM errors, their confidence ratings, and the relation between them.

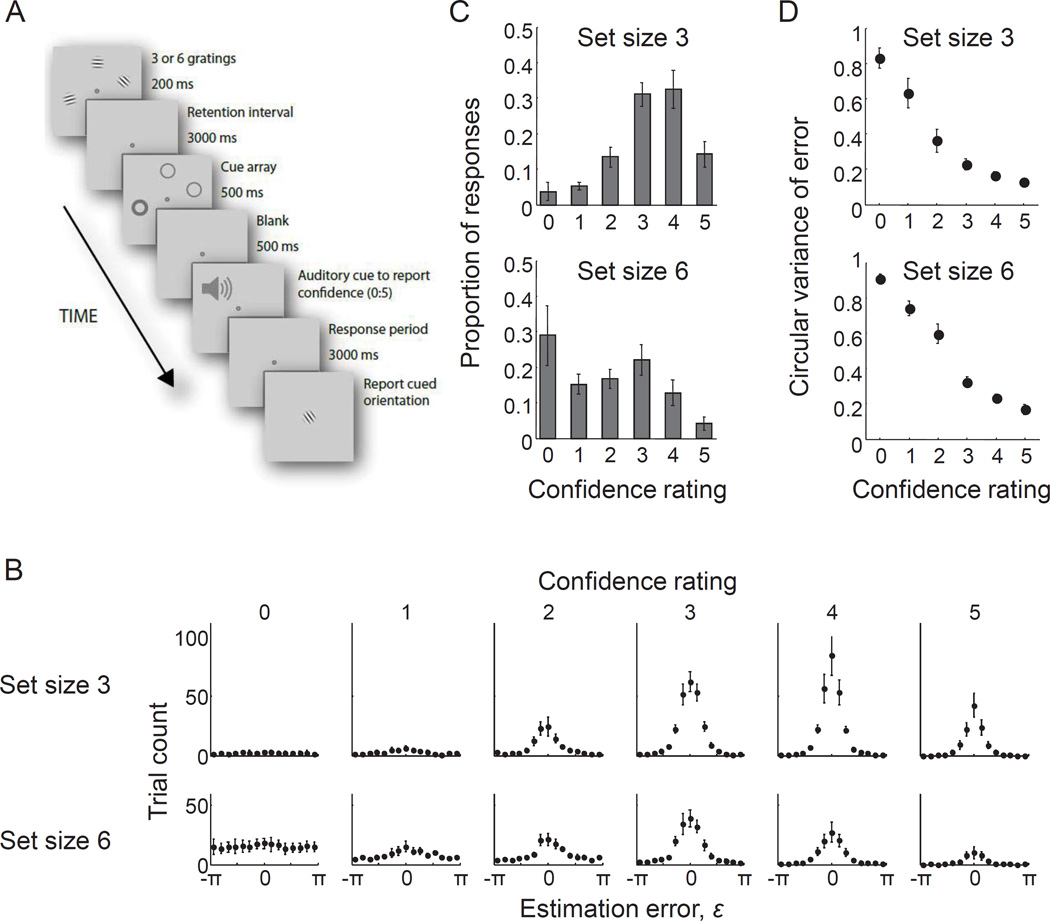
Figure 1. Previously reported evidence for metacognitive knowledge in visual working memory.

(A) Trial procedure of the delayed-estimation experiment performed by Rademaker, Tredway, and Tong (2012). On each trial, both a confidence rating and orientation estimate were obtained, allowing the experimenter to sample the joint probability distribution of these two behavioral measures. Reprinted with permission. (B) Raw data: histograms of estimation errors, split by confidence rating (columns) and set size (rows). (C) First summary statistic: histograms of reported confidence rating for set sizes 3 (top) and 6 (bottom). Each bar corresponds to the summed trial count of one of the histograms in panel B. (D) Second summary statistic: circular variance of the error distribution as a function of confidence rating for set sizes 3 (top) and 6 (bottom). Each point corresponds to the width of one of the histograms in panel B. The data shown in panels B–D were published in Rademaker, Tredway, and Tong (2012). All data points represent averages across subjects and error bars represent 1 s.e.m.

Generally stated, any model of confidence takes the form confidence=f(x), where “x” is the mental variable from which confidence ratings are derived and “f” is a function that maps this variable to a confidence rating. Since VWM confidence correlates with VWM precision (Bona et al., 2013; Bona & Silvanto, 2014; Rademaker et al., 2012), we postulate that precision is the variable from which confidence ratings are derived. For the mapping, f, we draw inspiration from Charles Peirce’s suggestion that “the feeling of belief” (i.e., confidence) is related to “the expression of the state of facts which produces the belief” through Fechner’s law, i.e., through a logarithmic mapping (Fechner, 1860; Peirce, 1878). Finally, because of the abundance of noise in the nervous system (Faisal, Selen, & Wolpert, 2008), and following previous literature on metacognition (De Martino, Fleming, Garrett, & Dolan, 2013; Harlow & Donaldson, 2013; Jang, Wallsten, & Huber, 2012; Maniscalco & Lau, 2012; Mueller & Weidemann, 2008), we postulate that confidence ratings may be corrupted by “metacognitive” noise.

Combining these three postulates, we hypothesize that VWM confidence is derived from VWM precision through a logarithmic mapping that is corrupted by noise. Below, we turn this hypothesis into a process model and combine it with the best available VWM encoding model. We fit the combined model to data from a delayed-estimation experiment, critically evaluate several of its assumptions, propose a neural implementation, consider alternative encoding models, and provide a preliminary assessment of the generality of Fechner’s law in metacognition.

MODEL CONSTRUCTION

VWM noise and precision

We develop our model in the context of the delayed-estimation experiment performed by Rademaker et al. (2012). In their experiment, human observers memorized a set of orientation stimuli on each trial. After a brief delay, they provided a near-continuous estimate of a randomly chosen target stimulus, together with a confidence report (Fig. 1A). Since the stimulus domain is circular, we make the common assumption that memory noise follows a Von Mises distribution (Bays & Husain, 2008; Wilken & Ma, 2004; W. Zhang & Luck, 2008), which can be interpreted as the circular equivalent of the normal distribution. Denoting the stimulus value by s and the stimulus memory by x, the memory distribution is formally written as

$$p(x|s,\kappa )=\frac{1}{2\pi I_0(\kappa )}{e}^{\kappa \text{cos}(x-s)},$$

where κ is the concentration parameter and I₀ is the modified Bessel function of the first kind of order 0. The width of the noise distribution is controlled by parameter κ: the larger its value, the narrower the distribution (κ=0 is the uniform distribution on [−π,π] and in the limit of large κ, the Von Mises distribution approximates a Gaussian distribution with σ² = 1/κ).

As in previous work (Keshvari, van den Berg, & Ma, 2012; van den Berg, Awh, & Ma, 2014; van den Berg, Shin, Chou, George, & Ma, 2012), we define memory precision as Fisher information, J, which provides a lower bound on the variance of any unbiased estimator of the stimulus and is a common tool in the study of theoretical limits on stimulus coding and discrimination precision (Abbott & Dayan, 1999; Cover & Thomas, 2005; Ly, A., Marsman, Verhagen, Grasman, & Wagenmakers, 2015; Paradiso, 1988). It is monotonically related to κ through the relation $J(\kappa )=\kappa \frac{I_1(\kappa )}{I_0(\kappa )}$ (Keshvari et al., 2012), where I₁ is the modified Bessel function of the first kind of order 1. Hence, a larger memory precision J means a narrower memory noise distribution and a smaller expected memory error (Fig. S1 in Online Supplemental Material). Of course, Fisher information is not the only possible definition of precision. Any quantity that is monotonically related to the expected memory error could be a suitable candidate, such as the concentration parameter of the memory noise distribution, κ, itself. While Fisher information will serve as our main definition of memory precision, we will later also evaluate our proposed model under two alternative definitions (see Model Evaluation).

Distribution of VWM errors for a given level of precision

We define estimation error, ε, as the circular distance between stimulus s and memory x. Under the above defined noise distribution, the distribution of estimation errors for a given precision J is formally written as

$$p(\epsilon |J)=\frac{1}{2\pi I_0(\kappa (J))}{e}^{\kappa (J)\text{cos }\epsilon },$$ (1)

where κ(J) maps Fisher information to a concentration parameter. This mapping is not analytic, but can easily be computed by numerical inversion of mapping J(κ) that was presented above (Fig. S1). Although there are many different models of VWM encoding – such as “slot” and “resource” models – there is nothing controversial about Eq. (1): it simply states that for a given level of precision, working memory errors for circular features follow a Von Mises distribution. What is not generally agreed upon is the distribution of precision with which memories are encoded. This distribution is formalized in an “encoding” model, which we will describe below.

Fechner model of VWM confidence

Following Peirce’s proposal that confidence obeys Fechner’s law, we postulate that VWM confidence, which we denote by γ, is derived from VWM precision, J, through a logarithmic mapping. Furthermore, we assume that confidence judgments are corrupted by “metacognitive noise” (De Martino et al., 2013; Harlow & Donaldson, 2013; Jang et al., 2012; Maniscalco & Lau, 2012; Mueller & Weidemann, 2008). This leads to a process model of the form

$$\gamma =a\text{ log}J+b+\eta ,$$ (2)

where parameters a and b establish the scaling and shifting that is required to transform the observer’s internal sense of confidence to the response range imposed by the experimenter – which is arbitrary and varies from experiment to experiment. These parameters also control an observer's mapping "strategy": the larger the value of a, the more sensitive the confidence ratings are to small changes in precision and the more of them will be “0” (lowest) or “5” (highest); the larger the value of b, the more the confidence rating histogram shifts to the right. Parameter η is the metacognitive noise term, which we assume to be normally distributed with standard deviation σ_mc. Thus, when a memory is encoded with precision J, the probability that it is accompanied by a confidence of magnitude γ takes the form

$$p(\gamma |J)=\frac{1}{\sqrt{2\pi {\sigma }_{\mathrm{m}\mathrm{c}}^2}}{e}^{-\frac{{(\gamma -(a\text{ log}J+b))}^2}{2{\sigma }_{\mathrm{m}\mathrm{c}}^2}}.$$ (3)

In equations (2) and (3), confidence is as a continuous variable. However, in many experiments, subjects report confidence on an integer scale. To model data from such experiments, we round γ to the nearest value included in the integer scale. For example, to model data from an experiment that measured confidence as integer ratings between 0 and 5, all ratings smaller than 0.5 are rounded to “0”, all ratings between 0.5 and 1.5 to “1”, etc.

How to evaluate this model of confidence? A common way to test whether a subjective variable – such as perceived weight or loudness – obeys Fechner’s law is to use the method of paired comparison (Thurstone, 1927). This method consists of measuring subjectively reported stimulus intensity differences for a range of known, objective intensity differences. In our case, this would amount to measuring confidence rating differences for a range of known memory precision differences. This is difficult, if not impossible, using behavioral measures alone, because precision is an internal variable that is unknown to the experimenter. However, we can instead evaluate our model of VWM confidence indirectly, by coupling it with a model of VWM errors and exploit the fact that the model predicts confidence and error to be correlated, as explained below.

Joint distribution of VWM errors and confidence ratings

Above, we separately specified a model for VWM errors, p(ε|J), and one for VWM confidence, p(γ|J). While we presented these models largely independently of each other, their predictions are coupled through a shared dependence on memory precision, J: precision affects the memory error, because it determines the width of the memory noise distribution (Eq. (1) and Fig. S1); and it affects confidence, because of the mapping between precision and confidence (Eq. (2) and Fig. 2A). Due to this coupling, we expect the model to predict a correlation between estimation errors and confidence ratings. Indeed, simulations show that on trials when precision J is high, the estimation error ε tends to be small and confidence γ tends to be high (Fig. 2B). Moreover, the model makes specific, quantitative predictions for the relation between estimation error and confidence rating, whose shape depends on properties of the assumed mapping between VWM precision and VWM confidence (Fig. 2C). The fact that error and confidence are correlated allows us to evaluate the validity of our proposed model of VWM confidence by fitting joint distributions of estimation errors and confidence ratings: if our hypothesis is correct, then a model that uses Fechner’s law to map precision to confidence, Eq. (2), should: i) provide accurate fits to subjects’ joint distributions of estimation errors and confidence ratings; ii) provide better fits than models that use an alternative kind of mapping.

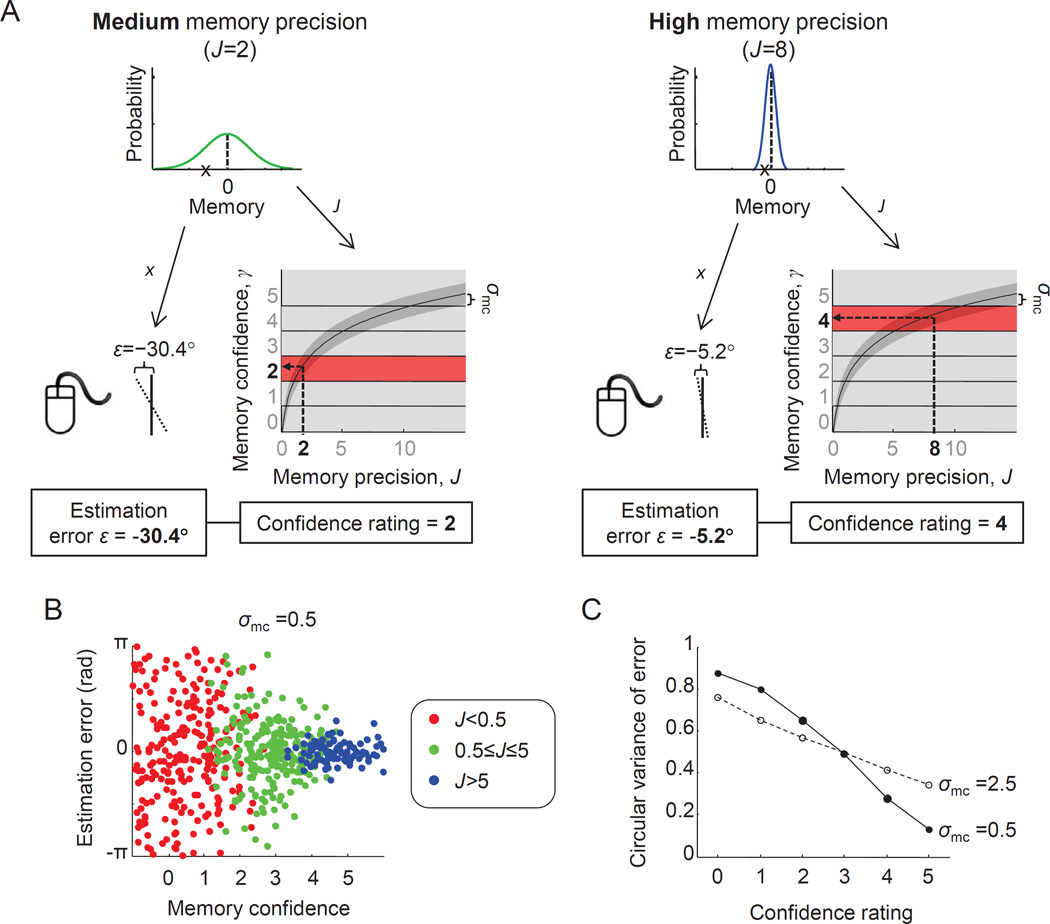
Figure 2. A Fechnerian model of working memory confidence.

(A) Illustration of how our proposed model jointly produces a near-continuous estimation error and a discrete confidence rating in a delayed-estimation experiment. The example on the left shows a trial in which a memory is encoded with medium precision (J=2) and the one on the right a trial in which it is encoded with high precision (J=8). Precision, J, determines the width of the noise distribution and is also the variable that is mapped – through Fechner's law – to a confidence rating. Hence, J affects both the subject's estimation error and her confidence. (B) Simulation results from 1000 trials, with J drawn on each trial from a gamma distribution with a mean of 1.5 and a scale parameter of 10. Each dot shows the estimation error (y-axis) and confidence (x-axis) of one trial. Trial-to-trial variability in J induces a negative correlation between estimation error and confidence: when precision is low (red), estimation errors tend to be larger and confidence tends to be lower than when precision is medium (green) or high (blue). (C) Circular variance of the error as a function of confidence rating in the same simulation, for two different values of σ_mc. The strength of the negative correlation depends on the amount of metacognitive noise.

Before we can test whether our model meets these two criteria, we need to make the joint distribution of VWM error and confidence mathematically precise. Since precision J is unknown to the experimenter, the predicted joint distribution of error ε and confidence γ is obtained by integrating over J. Assuming that ε and γ are conditionally independent, we obtain

$$p(\epsilon ,\gamma )=\int p(\epsilon |J)p(\gamma |J)p(J)dJ.$$

The first two distributions in the integral, p(ε|J) and p(γ|J), were described above – the only part that remains to be specified is the distribution of precision, p(J), which determines how many items are encoded on a trial and with what precision. We refer to this distribution as a “VWM encoding model”.

VWM encoding model

There is an ongoing debate about the question which of the many available VWM encoding models best describes human VWM limitations (Luck & Vogel, 2013; Ma et al., 2014). In a recent factorial comparison of 32 of such models (van den Berg et al., 2014), we found that the most successful model has the following three properties: 1) precision of remembered items is variable, following a Gamma distribution; 2) mean precision decreases with set size through a power law; 3) the number of remembered items varies across trials, following a Poisson distribution. We call this the “variable-precision model with a Poisson number of remembered items”. It has 4 free parameters: average memory precision at set size 1, denoted J̅₁; the shape parameter of the Gamma distribution, denoted τ, which controls the amount of variability; the power, α, of the power-law function that controls the relation between memory precision and set size, J̅ (N) = J̅₁N^α; the mean of the Poisson distribution, K_mean, which controls the variability in the number of remembered items. Mathematical details about this model can be found in Online Supplemental Material and our earlier work (van den Berg et al., 2014). We first evaluate our proposed Fechner model of VWM confidence in combination with this particular encoding model. Thereafter, we also consider alternative encoding models.

MODEL EVALUATION

Data

We evaluate the model by fitting it to data made available by Rademaker, Tredway and Tong (Rademaker et al., 2012). They performed a delayed-estimation experiment in which subjects reported on each trial the orientation of a randomly chosen stimulus out of a set of memorized stimuli (Fig. 1A). Subjects also rated their confidence as an integer between 0 (“no memory at all”) and 5 (“the best possible memory”). The raw data thus consist of a paired estimation error and confidence rating for each trial. Six subjects each performed 796 trials at set sizes 3 and 6, which were randomly intermixed. Confidence ratings varied greatly even within a given set size (Fig. 1C). Moreover, for a given set size, circular variance of the estimation error correlated negatively with confidence rating (Fig. 1D): subjects had wider error histograms when they reported lower confidence, which indicates that they possessed metacognitive knowledge of their VWM contents.

Model fits

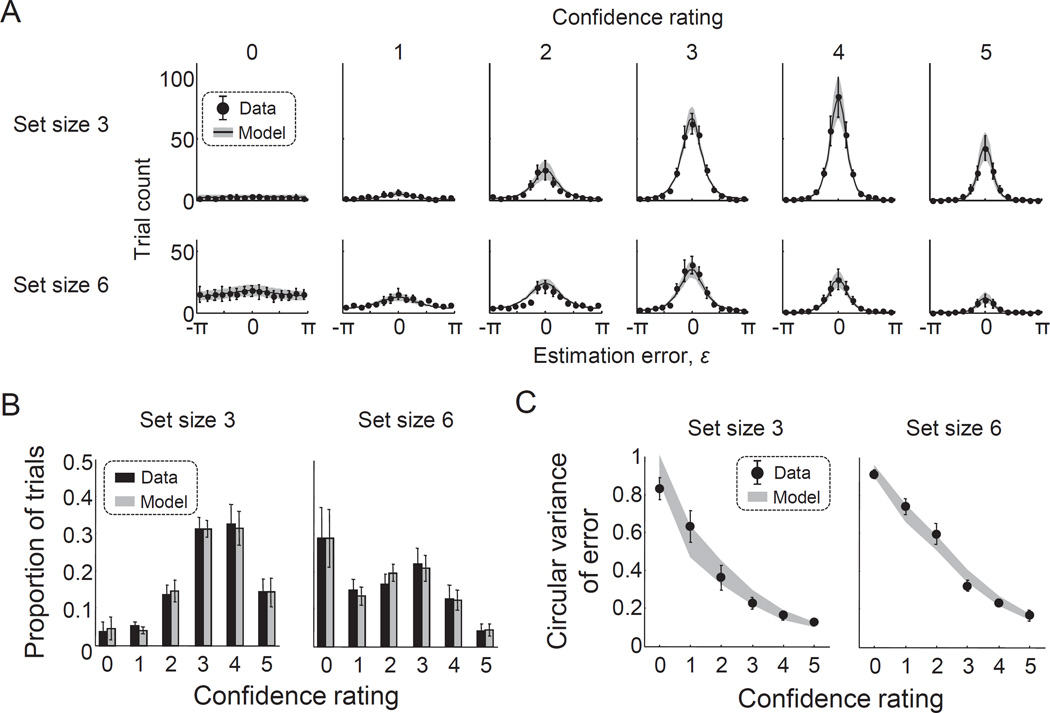
We use a genetic algorithm (see Online Supplemental Material) to estimate the maximum-likelihood parameter values, separately for each subject (Matlab code can be found at http://xxxxxx). We find that the model provides an excellent account of the raw data, both at the group level (Fig. 3A) and the level of individual subjects (Figs. S2–S7). It also accounts well for the two statistics that summarize the raw data: the marginal confidence rating histograms (Fig. 3B) and the circular variance of the error as a function of confidence (Fig. 3C).

Figure 3. The Fechnerian model of working memory confidence allows for excellent fits to people’s joint distributions of working memory errors and confidence ratings.

(A) Model fits to the histogram of estimation errors, split by confidence rating (columns) and set size (rows). (B) Model fits to the distribution of confidence ratings, split by set size. (C) Model fits to the circular variance of the estimation error as a function of confidence rating, split by set size. The presented data and model fits were averaged across subjects. Error bars and shaded areas indicate 1 s.e.m. Fits to individual subjects can be found in Supplementary Figures S1–S7.

Under the best-fitting parameter values (Table 1), the average confidence ratings produced by the model are close to the empirical averages: 3.22±0.22 versus 3.26±0.19 at set size 3 and 1.86±0.27 versus 1.87±0.27 at set size 6 (here and elsewhere, X±Y refers to the mean and s.e.m. across subjects). At both set sizes, a Bayesian paired samples t-test (JASP_Team, 2016) favors the null hypothesis that the mean of the empirical population is identical to the average rating produced by the model, with Bayes factors of 1.89 and 2.22, respectively. At the level of individuals, Bayesian one-sample t-tests support the null hypothesis in 11 out of 12 cases, with Bayes factors ranging from 5.7 to 25.7. The only exception is the case of set size 3 of subject S2, where the alternative hypothesis is supported - nevertheless, even for that case the deviation is small (2.51 vs 2.31).

Table 1.

Maximum likelihood parameter estimates of the Fechner model of VWM confidence combined with the variable-precision encoding model.

	a	b	σmc	J̅1	α	τ	Kmean
S1	0.982	3.627	0.515	19.9	−2.19	1.77	7.12
S2	1.255	2.487	0.073	6.17	−1.39	0.40	3.08
S3	0.788	2.624	0.469	36.5	−1.84	1.63	9.42
S4	0.408	3.146	1.043	30.9	−1.45	7.01	90.3
S5	0.429	3.144	0.707	17.5	−1.31	7.44	128.7
S6	0.83	1.963	0.870	49.0	−2.37	1.08	53.0
mean±sem	0.78±0.13	2.83±0.24	0.61±0.14	26.7±6.2	−1.76±0.18	3.2±1.3	6.5±1.9*

^*Subjects S4–S6 are excluded from the mean, because their estimates of K_mean are unreliable (see main text).

Finally, metacognitive accuracy – defined as the correlation coefficient between the absolute estimation error and confidence rating (Fleming & Dolan, 2012) – produced by the fitted model is −0.453±0.018, which closely matches the empirical value of −0.464±0.020. A Bayesian paired sample t-test favors the null hypothesis that the population averages are identical, with a Bayes factor of 1.81.

These results support the hypothesis that VWM confidence is a noisy, logarithmic function of VWM precision, Eq. (2). In the remainder of the paper, we critically evaluate our model, propose a neural implementation, examine the model fits under alternative VWM encoding models, and assess whether it generalizes to another task.

Evaluation of parameter estimates

The model has 7 free parameters, 4 of which are associated to the VWM encoding model and 3 to the mapping between VWM precision and VWM confidence. We next discuss the plausibility of the estimated values of these parameters (Table 1) and – where possible – compare them with findings from earlier studies.

For three of the six subjects (S4–S6), the estimated average number of remembered items on a trial, K_mean, is so high (>50) that essentially all items are remembered on every trial. For these subjects, the estimated value of K_mean has no sensible interpretation – experiments with larger set sizes would be required to obtain reliable estimates. For the remaining subjects, the estimated average number of remembered items is 6.5±1.9, which is consistent with the earlier reported median of 6.4 (van den Berg et al., 2014). Note that the estimate of K_mean is about a factor 2 larger than the typical "3±1" estimate from slot-based models. The explanation for this difference is that the variable-precision model treats some of the large estimation errors as low-precision estimates, while standard slot-based models can only account for them as random guesses.

The estimate of parameter J̅₁ – which represents encoding precision at set size 1, expressed as Fisher information – is 26.7±6.2. This corresponds to a circular standard deviation¹ of 12.9±2.2°, which seems plausible. The value is a bit higher than the 7.7±1.5° that we found in one of our own delayed-estimation experiments with orientation as the relevant feature (van den Berg et al., 2012). We suspect that this is due to the relatively long memory delay period in the study by Rademaker et al. (7 s between stimulus offset and estimation response onset, versus 1 s in our own study).

The estimated power of the power law that describes the relation between mean encoding precision and set size is −1.76±0.18. This means that mean precision is estimated to decrease with set size, which is what we would expect. The value is lower than the −1 that one would expect if the total amount of memory resource were constant (Palmer, 1990). This is consistent with our earlier findings (van den Berg et al., 2014) and may be explained as an inefficiency in distributing memory resources over multiple items.

The 3 parameters associated with the mapping between VWM confidence and VWM precision are a, b, and σ_mc in Eq. (2). The estimated value of σ_mc is 0.61±0.14. To assess the plausibility of the estimated values for the level of metacognitive noise, we compute through simulations how often it causes a confidence response to change – for example, when confidence on a particular trial is 3.2 before noise is added, then a noise value of 0.4 would change the confidence response from “3” to “4”. We find that the noise leaves the confidence rating unchanged in 61.7±8.5% of the trials and causes changes of magnitudes 1, 2, and 3 in 34.0±6.9%, 4.0±1.9%, and 0.24±0.17% of the trials, respectively. Hence, the estimated level of metacognitive noise causes a change in the confidence response on around 40% of the trials, but rarely of a magnitude larger than 1.

The remaining two parameters, a and b, determine the mapping between precision and confidence (visualized in Fig. 4C). It is difficult to define a psychologically plausible range for these parameters, because their values depend on both the estimated distribution of precision and the range of the confidence response scale imposed by the experimenter, which is arbitrary.

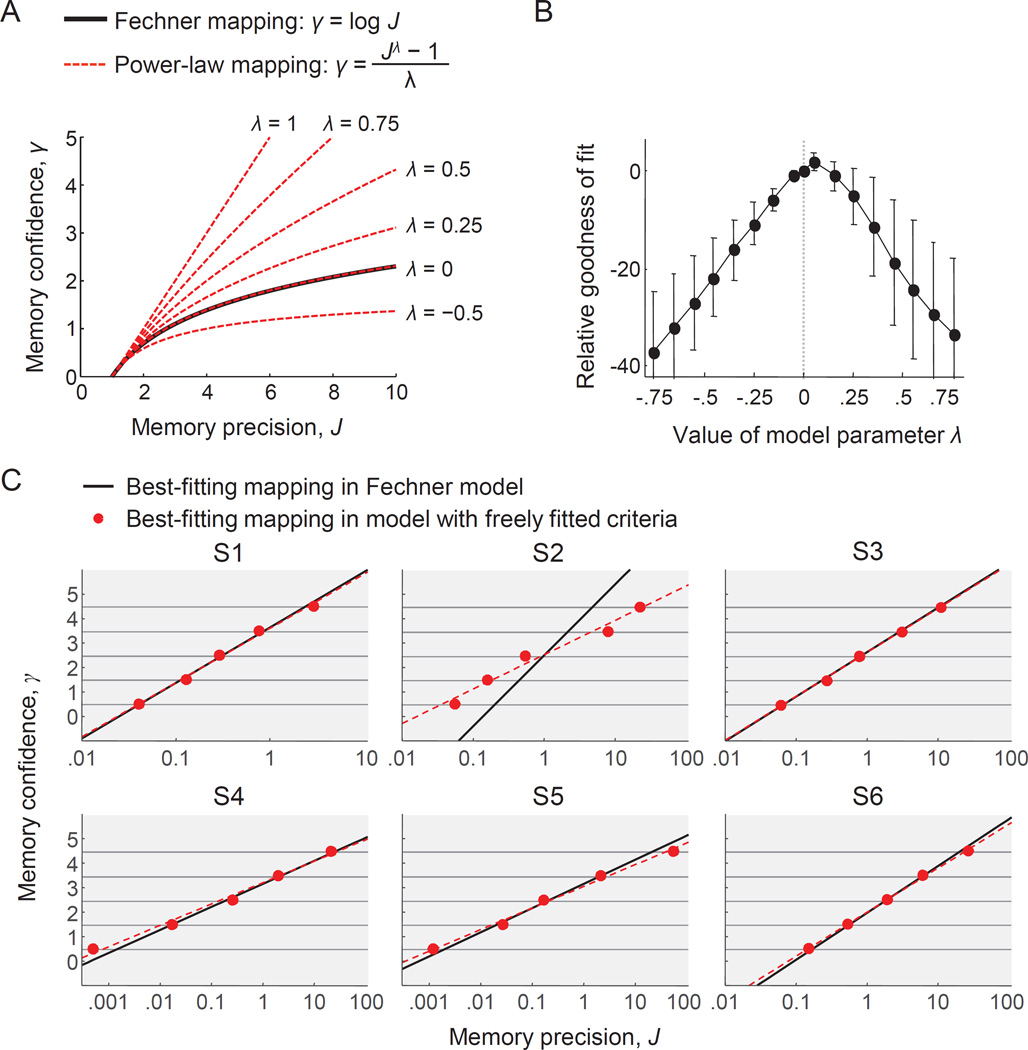
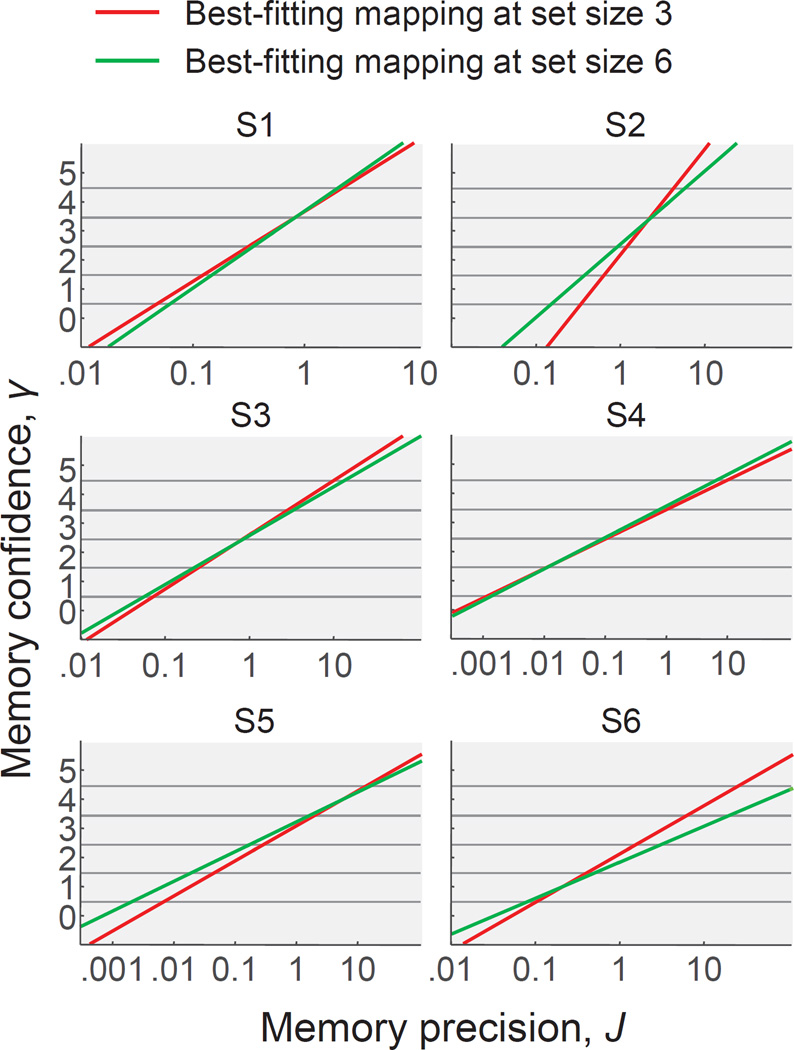
Figure 4. The best-fitting mapping between working memory precision and confidence is near-perfectly logarithmic.

(A) Examples of possible mappings between VWM precision and confidence in the power-law model. The logarithmic (Fechnerian) mapping is a special case of the power-law mapping, namely the case of λ=0. (B) Subject-averaged goodness of fit of the power-law model as a function of λ. Goodness of fit is expressed as the maximum log likelihood under a given value of λ, relative to the maximum log likelihood of the original model (λ=0). The goodness of fit is maximal when λ is close to 0. Error bars represent 1 s.e.m. (C) Maximum-likelihood estimates of the mapping in the Fechner model (black lines) compared with the maximum-likelihood estimates of the mapping in the model with freely fitted criteria (red dots). For visualization, the x-axis is logarithmically scaled, such that logartihmic mappings appear as linear. The dashed line shows the best linear fit to the flexible criteria. For five subjects, the best-fitting mapping in the flexible model is nearly identical to the logarithmic mapping in the Fechner model. For subject S2, the best-fitting mapping is slightly different in the flexible model, but still close to logarithmic.

Evaluation of the assumption that the mapping between precision and confidence is logarithmic

The excellent model fits support the hypothesis that VWM confidence is derived from VWM confidence through Fechner’s law. However, for a model to be convincing, it should not only fit well, it should also fit better than alternative models. In particular, it may be that there is an alternative, non-Fechnerian model that fits the data equally well or better, which would weaken and potentially falsify our model. We next try to find such an alternative, better-fitting model in two different analyses. In the first, we replace the logarithmic mapping in Eq. (2) by a highly flexible power-law mapping,

$$\gamma =a\left(\frac{J^{\lambda }-1}{\lambda }\right)+b+\eta .$$ (4)

In the limit of λ=0, this mapping reduces to our original model, Eq. (2), as can be verified by applying L'Hôpital's rule². However, when λ is a free parameter, this model variant allows for any possible power-law mapping between VWM precision and confidence (Fig. 4A)³. If our hypothesis that VWM confidence obeys Fechner’s logarithmic law is correct, then we should find that the best-fitting value of λ is close to 0. A systematic deviation from 0, on the other hand, would falsify our hypothesis and instead constitute support for Stevens’ power law (Stevens, 1957).

We estimate the best-fitting value of λ in two different ways. First, we fit the power-law model separately to each subject’s data set in the same way as we fitted the original model, but now with λ as an additional free parameter. We find that the average maximum-likelihood estimate of λ is −0.10±0.13 and that a Bayesian t-test favors the hypothesis that the population mean is equal to 0 over the hypothesis that it is not (Bayes factor: 2.08). In a second analysis, we fix λ to the same value for all subjects and then refit their data. We repeat this 16 times, with λ ranging from −0.75 to 0.75 in steps of 0.10. We find that the goodness of fit is maximal when λ is close to 0 (Fig. 4B). Both results indicate that the best-fitting mapping in this family of power-law functions closely resembles a logarithmic mapping.

In the second analysis, we make the mapping even more flexible: instead of imposing a functional form, we fit the five criteria that divide the VWM precision domain into six confidence bins as free parameters, which allows for any monotonic mapping between precision and confidence. For five of the subjects, the best-fitting mapping in this model is nearly identical to the best-fitting mapping in the logarithmic model (Fig. 4C; compare red dots with black lines). More importantly, however, for all six subjects, the mapping corresponding to the best-fitting criteria is close to logarithmic (Fig. 4C; compare red dots with dashed line). This indicates that there exists no monotonic mapping between VWM precision and VWM confidence that captures these data substantially better than the logarithmic one.

Evaluation of the assumption that confidence ratings are corrupted by additive metacognitive noise

We next perform two analyses to evaluate the assumption that confidence judgments are corrupted by “metacognitive noise”. First, we test a variant of the model without metacognitive noise, by setting σ_mc to 0. To compare the fit of this variant with that of the original model, we compute the Akaike Information Criterion (AIC), which is a measure of goodness of fit that takes into account differences in number of parameters between the models (Akaike, 1974). The AIC difference is 59±25 in favor of the original model, which means that there is a clear benefit to having this parameter in the model.

Second, we test whether multiplicative noise might have been a better assumption than additive noise. To this end, we fit a model variant in which we replace Eq. (2) with γ = (alogJ + b)·η, where η is a normal random variable with a mean of 1 and a standard deviation σ_mc. Since this model has the same number of parameters as the original one, we can compare their goodness of fit using the maximum log likelihood values. The model with additive noise outperforms the one with multiplicative noise, but the difference in maximum log likelihoods is small (4.2±2.9). Moreover, the results are mixed at the level of individuals: additive noise fits better than multiplicative noise for four, while for the other two subjects it is the other way around. Therefore, we conclude that although inclusion of metacognitive noise is important to account for the data, we cannot draw strong conclusions about the exact form of the noise.

Evaluation of the assumption that the mapping between VWM precision and VWM confidence is independent of set size

So far, we have assumed that the mapping between VWM precision and VWM confidence is independent of set size. We next evaluate this assumption by fitting a model variant in which parameters a and b – which control the mapping – are fitted separately for set sizes 3 and 6. The best-fitting mappings are very similar at both set sizes (Fig. 5). At the group level, the model with a set-size-dependent mapping marginally outperforms the original model, with an AIC difference of 4.2±3.7. At the level of individual subjects, the model variant is preferred for two of the six subjects (S2 and S6). Hence, for two subjects there is some evidence that the mapping between VWM precision and VWM confidence differs across set sizes, but the differences seem small.

Figure 5. The best-fitting mappings between VWM precision and VWM confidence are very similar at set sizes 3 and 6.

For all subjects, except S2 and S6, model comparison based on AIC favors the model with a single mapping for both set sizes. However, even for S2 and S6 the best-fitting mappings at set sizes 3 and 6 are quite similar.

Evaluation of the model using an alternative definition of VWM precision

Although we had good reasons to define VWM precision as Fisher information (see above), other choices would have been possible: any quantity that is inversely related to the expected memory error is, in principle, a sensible basis for confidence ratings. One such quantity is the concentration parameter of the memory noise distribution, κ. Since the relation between κ and J is nonlinear for low precision values (Fig. S1), and since most of the confidence ratings in the lower bins originate from low-precision trials (Fig. 4C), we may expect the model predictions to be different under these two definitions of precision. To examine how sensitive the goodness of fit of our model is to the chosen definition of memory precision, we refit the data with a variant in which we replace J in Eq. (2) with κ. We find that the maximum log likelihood differences between the original model and this variant is negligible (2.8±2.9, in favor of the original model), which suggests that both models account approximately equally well for the data. Hence, the model's ability to account for metacognitive judgments through Fechner's law generalizes to an alternative definition of VWM precision.

Evaluation of the model using probability correct as a basis for confidence

So far we have assumed that confidence reflects memory precision. While this may be a sensible assumption in the context of an estimation task, it does not readily generalize to tasks with discrete decisions, such as a binary choice between two alternatives. In such tasks, there is no straightforward notion of "precision" and confidence is instead typically assumed to reflect the probability that the choice is correct (e.g., (Kiani, Corthell, & Shadlen, 2014; Kiani & Shadlen, 2009; Pouget, Drugowitsch, & Kepecs, 2016; van den Berg et al., 2016)). While probability correct is perhaps a less intuitive basis for confidence in the context of the VWM estimation task, it has the appealing property that it could serve as a general (task-independent) basis of confidence. In the estimation task, a "correct" response, x, would be one that is identical to the true stimulus value, s. Conditioned on memory precision, J, we can quantify the probability of a correct response as p_correct=p(x=s|J)=e^κ/(2πI₀(κ)), where κ is the concentration parameter corresponding to J (see Model Construction). When we replace J in Eq. (2) by p_correct and refit the model, we find that the maximum log likelihood difference with the original model is small (6.5±6.7, in favor of the original model). We draw two conclusions from this finding: first, that p_correct may serve as a general basis for confidence, although it is a somewhat unintuitive measure in the context of estimation tasks; second, the model's ability to account for metacognitive judgments through Fechner's law generalizes to an alternative basis for confidence.

NEURAL IMPLEMENTATION

The model presented above provides an account of memory confidence at the “algorithmic” level of David Marr’s Tri-Level hypothesis, which addresses “the representation for the input and output of a system, and the algorithm used for the transformation” (Marr, 1982). A more complete theory should also account for confidence at what Marr called the implementational level, which addresses how the representation and algorithm be realized physically. Here, we offer such an account by extending an existing encoding model with our proposed model of confidence.

A neural model for VWM errors

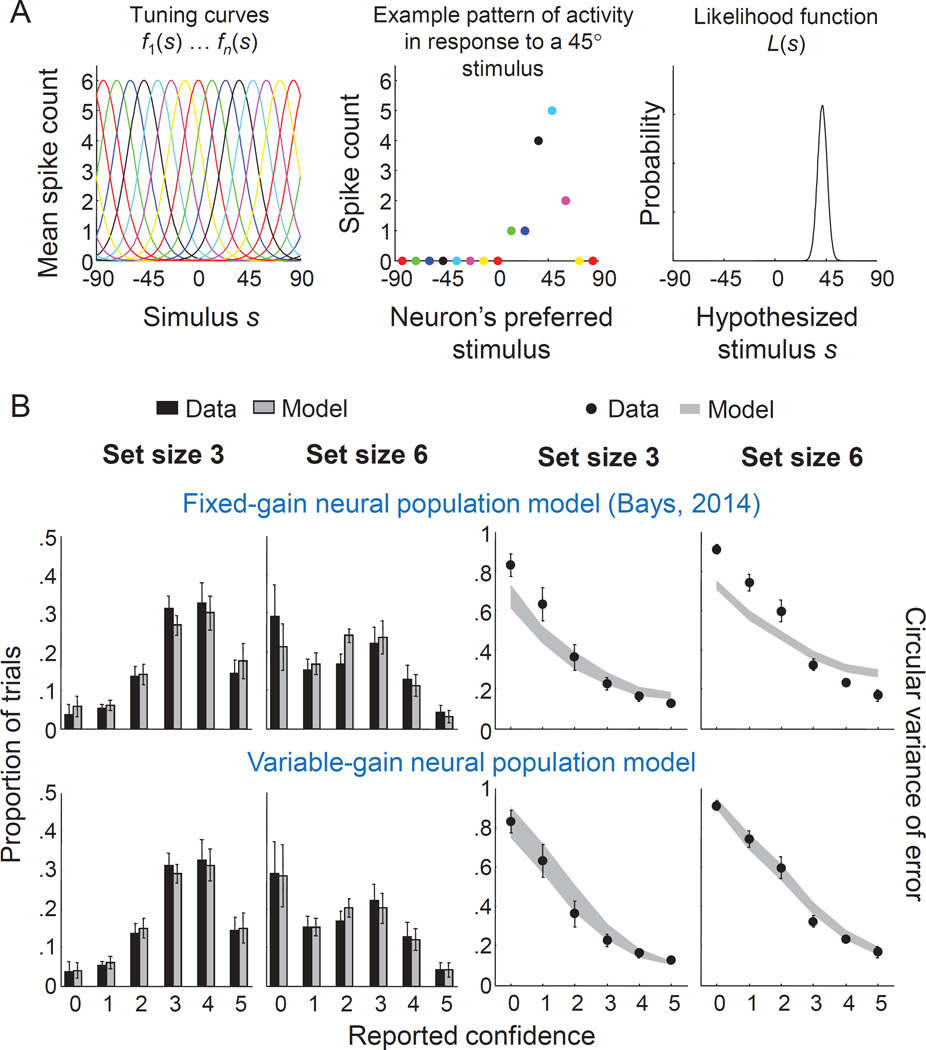
A recent paper introduced a neural model to account for VWM estimation errors in a delayed-estimation task (Bays, 2014), based on the framework of probabilistic population codes (Ma, Beck, Latham, & Pouget, 2006; Ma & Jazayeri, 2014; Pouget, Dayan, & Zemel, 2003). Memories are assumed to be encoded in the activity, r, of a population of neurons with Von Mises tuning curves of the form f_i (s) = g exp(κ_tc cos(θ_i − s)), where s is the stimulus value, θ_i is the preferred orientation of the i-th neuron, g is the neural gain, and κ_tc controls the width of the tuning curve (Fig. 6A). In addition, the model assumes independent Poisson noise on the spike counts. Hence, the number of spikes, r_i, elicited by the i-th neuron in response to a stimulus s is a Poisson random variable with mean f_i(s). The maximum-likelihood estimate of the stimulus value, extracted from the noisy population activity, is the equivalent of the scalar memory x in the algorithmic-level model discussed above (Ma, 2010). Bays (2014) showed that the model accounts well for human subjects’ error distributions in a delayed-estimation experiment. We extend this model with our proposed model of confidence and examine whether the combined model accounts for joint distributions of VWM errors and confidence ratings.

Figure 6. A neural model extended with the Fechner model of confidence accounts well for the data when the gain is assumed to be variable.

(A) Schematic of how a stimulus is represented in a population coding model. Each neuron in the population has a tuning curve, centered at the cell’s preferred stimulus (left). When a stimulus is presented, each cell generates a stochastic number of spikes (center). The pattern of activity encodes a (normalized) likelihood function over the stimulus (right). When the tuning curves are Von Mises functions, the shape of the likelihood function is also a Von Mises function. (B) Top: fits of the fixed-gain neural model to the distribution of confidence ratings (first two columns) and the circular variance of the error as a function of confidence rating (last two columns). Bottom: fits of the variable-gain neural model. Error bars indicate standard error of the mean. Both results are from the model variant with the J_neural1 measure of precision are shown; results look similar for J_neural2.

Neural representation of memory precision

As in our algorithmic-level model, we hypothesize that VWM confidence is derived through Fechner’s law from the subject’s internal representation of VWM precision. Any neural measure of VWM precision, which we denote J_neural, should have two properties: first, it should be a function of population activity r and, second, it should be inversely related to the expected memory error. We test our model under two such measures. The first one is a neural approximation of measure J in the algorithmic-level model. We derive this measure by first noting that population activity r encodes a Von Mises likelihood function over stimulus value s, with the following mean and concentration parameter (see Online Supplemental Material for a derivation):

$${\mu }_{1\mathrm{h}}=\mathrm{a}\text{tan}2(\sum _i{r}_i\text{ cos}({\theta }_i),\sum _i{r}_i\text{ sin}({\theta }_i))$$

$${\kappa }_{1\mathrm{h}}={\kappa }_{\mathrm{t}\mathrm{c}}\sqrt{{(\sum _i{r}_i\text{ cos}({\theta }_i))}^2+{(\sum _i{r}_i\text{ sin}({\theta }_i))}^2},$$

where r_i and θ_i are the spike count and preferred orientation, respectively, of the ith neuron. Quantity κ_lh is similar to quantity κ in the algorithmic-level model. For consistency, we apply the same Fisher Information transformation to κ_lh as we applied to κ, which gives us $J_{\text{neural},1}={\kappa }_{\mathrm{l}\mathrm{h}}\frac{I_1({\kappa }_{\mathrm{l}\mathrm{h}})}{I_0({\kappa }_{\mathrm{l}\mathrm{h}})}$. The second measure of precision that we test was proposed by Bays (Bays, 2016) and is simply the sum of the spiking activity in the population encoding of the stimulus, $J_{\text{neural},2}=\sum _i{r}_i$. While these two measures are highly correlated⁴, it is easy to see that there is no one-to-one mapping between them: the latter measure does not depend on how activity is distributed across cells, while the former clearly does. Therefore, the model predictions will be different under both measures.

Model fits

To obtain model predictions, we simulate a population with M=50 neurons with equally spaced preferred orientations that cover the full circular domain. We relate the gain, g, to set size, N, through a power-law function, g(N)=g_total·N^α, where g_total and α are free parameters. We thus give the model slightly more freedom than the original version (Bays, 2014), which assumed an inverse proportionality (i.e., α=−1)⁵. We fit both versions of the neural model to each subject’s data set using maximum-likelihood estimation and compared their fits to that of the algorithmic-level model. While the results are mixed at the level of individuals, overall the algorithmic-level model outperforms the neural models, both in terms of fit to summary statistics (Fig. 6B, top) and AIC values (Table 2).

Table 2.

AIC differences between the algorithmic-level model and the four variants of the neural model. A positive difference means that the neural model outperforms the algorithmic-level model.

	Fixed gain		Variable gain
	Jneural,1	Jneural,2	Jneural,1	Jneural,2
S1	−217	−457	13.6	20.7
S2	−548	−924	−286	−270
S3	17.8	−282	65.4	44.1
S4	−155	−295	−8.4	−16.1
S5	−136	−433	33.7	26.6
S6	95.1	−0.24	111	103.3
mean±s.e.m.	−157±91	−400±120	12±57	15±53

The misfit in the summary statistics suggests that the neural models perhaps have too little variability in memory precision, which means that the fixed-gain assumption may be wrong: while some variability in precision arises due to trial-to-trial fluctuations in spike counts even if the population gain is fixed, this might not be sufficient to explain the data. Indeed, there is physiological evidence suggesting that neural gain in the cortex is itself variable (Cohen & Kohn, 2011; Goris, Movshon, & Simoncelli, 2014).

To examine whether releasing the fixed-gain assumption improves the model fits, we next fit a variable-gain variant of each of the two neural models. As in the fixed-gain model, gain is related to set size through g(N)=g_total·N^α. However, we now treat g(N) as a mean and draw the actual gain on each trial from a gamma distribution with a shape parameter τ, analogous to how we drew J in the algorithmic-level model. These variable-gain variants perform much better: while there is again large spread at the level of individuals, at a group level the AIC differences with the algorithmic-level model are inconclusive (Table 2) and the subject-averaged fits to the summary statistics look as good as that of the algorithmic-level model (Fig. 6B, bottom; cf. Fig. 3B–C).

We draw two conclusions from this analysis. First, our proposed model of VWM confidence has a simple neural counterpart that fits the data overall as well as the algorithmic-level model, although there are large individual differences. Second, the variability in spike counts induced by Poisson spiking may not fully capture the variability in precision that is required to successfully fit behavioral data; gain fluctuations might be needed on top of that.

A RE-EVALUATION OF VWM ENCODING MODELS

In the Model Evaluation section, we tested our proposed model of confidence in combination with a particular model of VWM encoding, namely the “variable-precision model with a Poisson number of remembered items”. We next consider alternative encoding models. Earlier proposed encoding models differ from each other in essentially a single aspect, namely the postulated distribution of VWM precision, p(J|θ), where θ is a vector with model-specific parameters. For example, the oldest slot model (Luck & Vogel, 1997; Pashler, 1988) postulates that an item is encoded either with near-infinite precision (J≈∞) or, when memory is full, not at all (J=0); the oldest “resource model” of working memory (Palmer, 1990; Wilken & Ma, 2004) postulates that all items are stored in memory, with equal precision; the variable-precision model (Fougnie, Suchow, & Alvarez, 2012; van den Berg et al., 2012) postulates that memory precision varies across items and follows a continuous distribution. In an earlier paper (van den Berg et al., 2014), we organized these models in a factorial space – that also contained a large number of hybrid models – and ranked them by using formal model comparison. We expect that inclusion of confidence data will yield a stronger comparison, because models with little or no variability in precision should predict little spread in confidence ratings and may therefore not be able to account for the inverse relation between the averaged VWM error and confidence (Fig. 1D).

Factorial model design

We organize the encoding models in a factorial design with three factors (Table 3): number of encoded items, quantization of memory precision, and presence of variability in precision. These factors have 3, 3, and 2 levels, respectively, thus defining a set of 18 models. This set of models is the same as in our previous work (van den Berg et al., 2014), except for three small differences: we do not consider models with non-target responses, we dissociate quantized precision from slots, and we do not consider response noise (see Discussion for motivation).

• First factor: maximum number of remembered items. The three levels in this factor differ in the assumption about the maximum number of encoded items, K. One possibility is that subjects always remember all items, K=N; we denote this level choice by ‘A-’ (all). Another possibility is that K is a fixed integer, in which case we label the level ‘F-’ (fixed). The third possibility is that K varies from trial to trial (Dyrholm, Kyllingsbæk, Espeseth, & Bundesen, 2011; Sims, Jacobs, & Knill, 2012) according to a Poisson distribution with rate parameter K_mean. We denote this level by ‘P-’ (Poisson).

• Second factor: quantization of memory precision. This factor also has three levels: memory is a continuous quantity (‘-C-’), a quantized quantity that is evenly distributed across items (‘-Qe-’), or a quantized quantity that is unevenly distributed across items (‘-Qu-’). In -C-models, the mean precision with which an item is remembered, denoted J̅, is related to the number of remembered items in a power-law fashion, J̅ = J̅₁N^α, as in previous work (Keshvari et al., 2012; Keshvari, van den Berg, & Ma, 2013; van den Berg et al., 2014, 2012). In the -Qe- and -Qu- models, memory resource comes in Q discrete quanta, each providing a certain level of precision J̅₁. In the -Qe- models, the quanta are distributed as evenly as possible. For example, if four items are remembered and five quanta are available, then three of them are remembered with precision J̅ = J̅₁ and one of them with precision J̅ = 2J̅₁. In the -Qu- models, the quanta are distributed randomly across items, in which case the number of quanta with which an item is remembered follows a binomial distribution. When an item is assigned zero quanta of resource (J̅ = 0), the estimate distribution is uniform.

• Third factor: variability in precision. This model factor has two levels. In the equal-precision (‘-EP’) models, the precision J with which each item is remembered is equal to J̅, as determined by the second model factor. In the variable-precision (‘-VP’) models, precision follows a gamma distribution with mean J̅ and scale parameter τ.

This model space contains four prominent models from previous literature: A-C-EP is similar to the sample-size model (Palmer, 1990), F-Qe-EP and F-Qu-EP are similar to the “slots-plus-averaging” model (W. Zhang & Luck, 2008)⁶, F-C-EP is similar to the “slots-plus-resources” model (W. Zhang & Luck, 2008), and A-C-VP is the “variable-precision” model (van den Berg et al., 2012). P-C-VP is the model that we used in the Model Evaluation section. Details about the implementation of these models can be found in Online Supplemental Material.

Table 3.

Overview of abbreviations used to label the VWM model factor levels.

Factor	Level abbreviations			Meaning
Number of encoded items	A-			All items are remembered
	F-			A fixed number of items is remembered
	P-			A variable number of items is remembered (Poisson distribution)
Quantization of precision		-C-		Memory precision is continuous
		-Qe-		Memory precision is quantized and evenly distributed across items
		-Qu-		Memory precision is quantized and unevenly distributed across items
Variability of precision			-EP	There is no random variability in memory precision
			-VP	There is random variability in memory precision

Factorial model comparison results

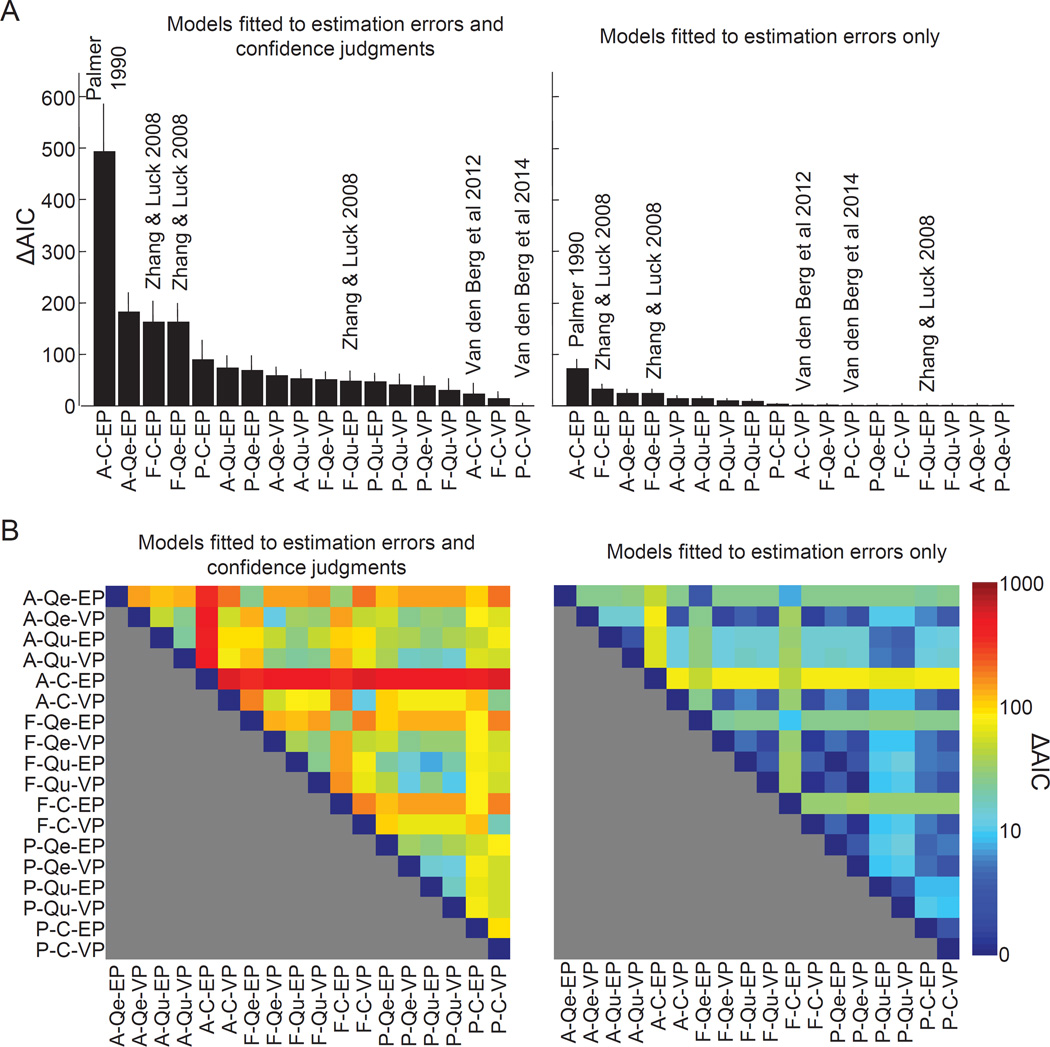
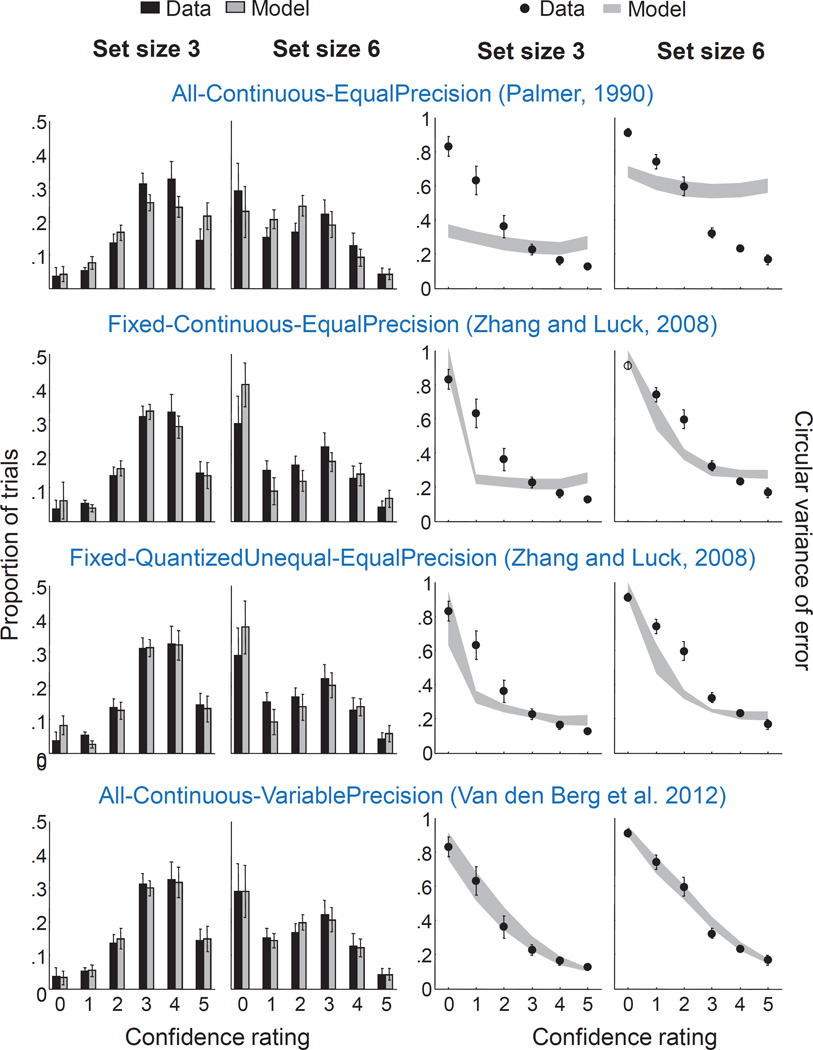
We fit all 18 models to all 6 subject data sets. When ranked by AIC score (Fig. 7A, left), the P-C-VP model comes out as best, followed by F-C-VP and A-C-VP. Hence, all encoding models in which memory precision is continuous and variable fit well, which is consistent with the main findings of our earlier meta-analysis of VWM encoding models (van den Berg et al., 2014). Moreover, all previously proposed models except A-C-VP perform poorly in the model comparison. This is reflected in the fits to the summary statistics (Fig. 8): only A-C-VP accounts well for the relation between confidence rating and performance. The problem of the other three models seems to be that they predict too little spread in encoding precision.

Figure 7. Including confidence ratings in model comparison greatly improves the distinguishability of working memory encoding models.

Subject-averaged AIC scores relative to the AIC of the P-C-VP model, obtained from fitting the models with (left) and without (right) inclusion of confidence judgment data. The models are sorted from worst to best. The citations to papers correspond to previously proposed models (see text). Error bars indicate 1 s.e.m. (B) Subject-averaged absolute AIC score for each pair of models, obtained from fitting the models with (left) and without (right) inclusion of confidence judgment data. The absolute AIC difference between any pair of models increases by a factor 5.99 when including confidence ratings in the model comparison (median factor across all 918 comparisons).

Figure 8. Most previously proposed working memory encoding models account poorly for the relationship between confidence ratings and estimation error.

Left: fits to the distribution of confidence ratings. Right: fits to the circular variance of the estimation error as a function of confidence rating. Error bars indicate standard error of the mean. From top to bottom: Palmer’s sample size model, Zhang and Luck’s slots-plus-resources model, the best-fitting version of Zhang and Luck’s slots-plus-averaging model, and Van den Berg et al.’s variable-precision model. The only old model that describes the data reasonably well is the variable-precision model.

Is there a benefit to using confidence data when comparing VWM encoding models? When comparing models, we want the AIC differences between models to be large. Therefore, one way to answer this question is by examining by how much the AIC differences change when we exclude the confidence data and fit the models to estimation errors only. We find that the AIC differences reduce greatly (Fig. 7A, right), which indicates that inclusion of confidence data is indeed beneficial for model comparison. To quantify this benefit, we compute the AIC difference between any possible pair of models under both ways of fitting (Fig. 7B). We find that the AIC difference increases on average by a factor 5.99 when including confidence ratings (median; mean±s.e.m: 128±4). Hence, one experiment that includes confidence ratings is as informative about the VWM encoding process as six experiments that only measure estimation errors.

GENERALIZATION TO A WORD RECOGNITION MEMORY TASK

The results so far support the hypothesis we started with: VWM confidence is derived from VWM precision through Fechner's law and corrupted by metacognitive noise. We next address the generality of the hypothesis, by testing whether Fechner’s law can also account for confidence ratings in a qualitatively different task, namely the word recognition memory task by Mickes et al. (Mickes, Wixted, & Wais, 2007).

Experiment

The experiment by Mickes et al. consisted of two phases. In the study phase, 14 subjects memorized a list of 150 words. In the subsequent test phase, they were sequentially presented with the same set of target words along with a set of 150 randomly interspersed lure words that were not part of the study list. On each trial, subjects first made a binary choice by indicating whether the test word was on the study list and then rated their “memory strength” on a 1–20 Likert scale (Likert, 1932), with 1 meaning that the test word was “definitely not on the list” and 20 meaning that it was “definitely on the list.” The data were made available to us by the authors.

Model

A model widely used for word recognition memory is the Unequal-Variance Signal-Detection (UVSD) model (e.g., Ratcliff, Sheu, & Gronlund, 1992; Wixted, 2007). In this model, each test word produces a “memory strength” or “familiarity” value x, which is assumed to be drawn from a Gaussian distribution with parameters μ_lure and σ_lure for lures and μ_target and σ_target for targets (Fig. 9A, top left)⁷. It is common to use the variable x as the decision variable and impose confidence criteria such that the observer’s confidence rating that the test word is a target increases monotonically with x. This practice is somewhat questionable in view of the unequal variances, which cause the distributions of x for targets and lures to have two intersection points rather than one. For example, if σ_target > σ_lure, both the lowest (most negative) and highest values of x are more likely to be caused by a target than by a lure. This means that the strength of the evidence that x carries about the test word being a target does not monotonically increase with x. To solve this inconsistency, we instead compute the optimal decision variable based on x, which is the log posterior ratio of “target” versus “lure” (Glanzer, Hilford, & Maloney, 2009): $d=\text{log}\frac{p(\text{target}|x)}{p(\text{lure}|x)}$, which evaluates to a quadratic relationship between d and x, $d=\text{log}\frac{{\sigma }_{\mathit{\text{lure}}}}{{\sigma }_{t\text{arg}et}}-\frac{1}{2}[\frac{{(x-{\mu }_{\text{target}})}^2}{{\sigma }_{\text{target}}^2}-\frac{{(x-{\mu }_{\text{lure}})}^2}{{\sigma }_{\text{lure}}^2}]$ (Fig. 9A, top right).

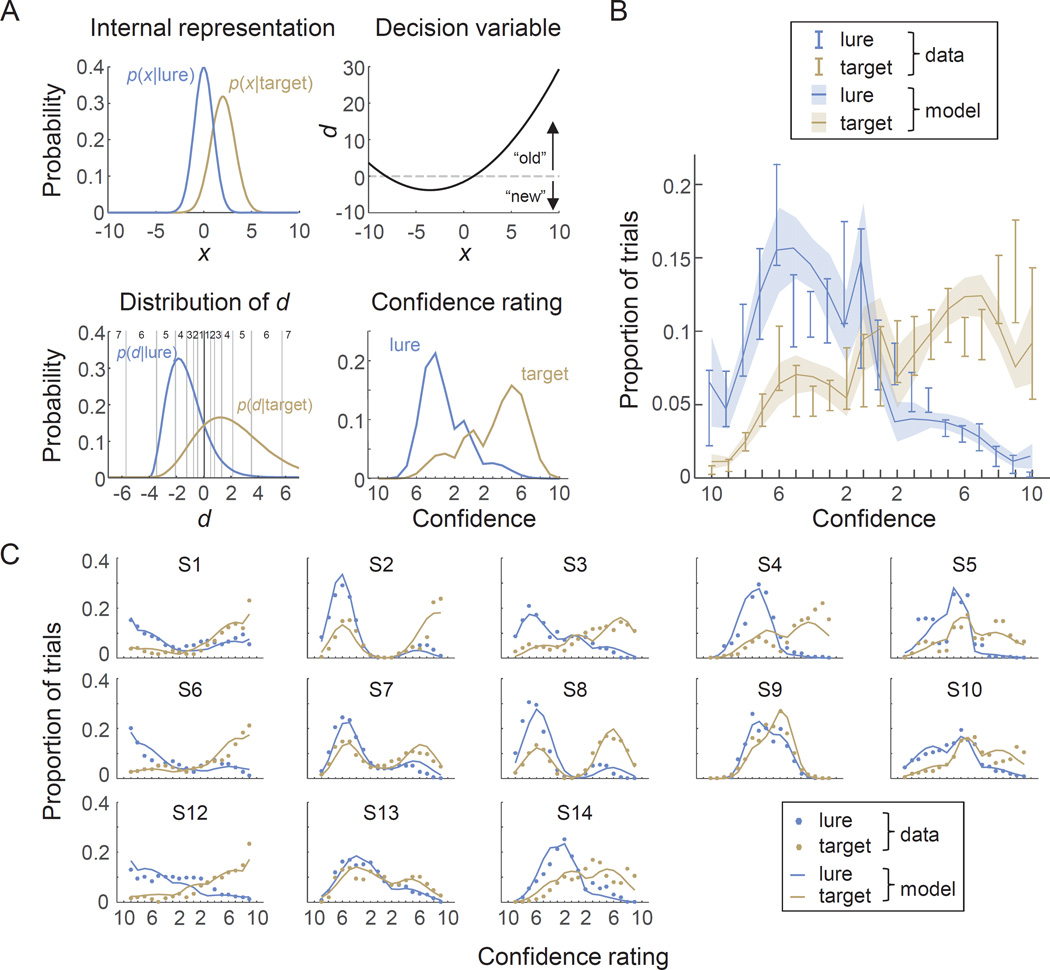
Figure 9. A variant of the UVSD model extended with a logarithmic model of confidence accounts for memory strength ratings in a word memory recognition experiment.

(A) Illustration of the model (parameter values: μ_target=2.00, σ_target=1.25, a=2.00, b=3.00 σ_mc=1.00). Each test word produces an internal representation, x, that is drawn from a Gaussian distribution whose parameters depend on whether the word is a target or a lure (top left). The observer’s choice (“old” or “new”) is based on the log posterior ratio of evidence, d, contained in x (top right). The distribution of d is different for targets and lures. A confidence rating is obtained by applying Fechner’s law to the absolute value of d, which is equivalent to placing exponentially spaced confidence criteria on d (bottom left). This results in a predicted confidence distribution for targets and lures (bottom right; note that these distributions are broader than in the bottom left panel, due to addition of metacognitive noise). (B) Subject-averaged rating histograms from the experiment by Mickes et al. (2007). (D) Subject-level fits. For visualization, we smoothed the subject-level histograms (which are quite noisy) using a moving averaging window with a width of 3 bins. The same smoothing was applied to data and model fit.

The distributions of d for targets and lures are inherited from the distributions of x for targets and lures, respectively; however, the distributions of d are guaranteed to have only a single intersection point, with stronger evidence for the test word being a target lying above the separating criterion (Fig. 9A, bottom left). Thus, the observer reports “old” if d(x) > 0 and “new” otherwise.

We next assume that the subject's confidence in their choice derives from the absolute value of d via Fechner’s law, in the same way as in the working memory task, i.e., γ = alog(|d|)+b+η, where η is metacognitive noise with mean 0 and standard deviation σ_mc. We turn γ into a discrete rating by rounding it to the nearest integer in the range 1–10, which in the absence of metacognitive noise would be equivalent to imposing exponentially spaced confidence criteria on |d| (Fig. 9A, bottom right). Finally, we interpret the 1–20 scale as two concatenated confidence scales, in which the first half is confidence about choosing “lure” and the second half is confidence about choosing “target”. Therefore, the last step consists of mapping the confidence rating to the second half of the scale if the observer believes that the test word is a target (by adding 10) and to the first half otherwise (by subtracting the confidence rating from 11).

Model fit

We estimate the maximum-likelihood values of the five free model parameters (μ_target, σ_target, a, b, and σ_mc) separately for each subject (Table 4)⁸. The model accounts well for the data, both at the level of the group (Fig. 9B) and that of single subjects (Fig. 9C). This result suggests that our proposed logarithmic model of confidence is not limited to working memory but may generalize to metacognition in other domains.

Table 4.

Maximum-likelihood parameter estimates of the model fits to the word recognition memory task.

	μtarget	σtarget	a	b	σmc
S1	0.93	0.79	1.09	7.59	2.99
S2	1.06	3.22	1.14	6.33	1.14
S3	1.31	1.04	3.32	5.26	0.19
S4	2.53	2.20	2.12	2.54	1.60
S5	0.00	2.99	1.38	3.11	2.77
S6	1.35	0.89	2.16	6.79	2.21
S7	0.67	1.18	1.71	6.80	1.20
S8	1.60	1.93	0.00	5.79	1.61
S9	0.61	0.95	0.43	2.82	1.11
S10	0.99	1.04	3.48	5.10	1.74
S12	1.77	1.05	2.17	5.70	3.02
S13	0.00	1.44	0.89	5.26	2.23
S14	1.56	1.56	1.96	3.60	1.75
M±s.e.m.	1.14±0.18	1.53±0.21	1.81±0.29	5.18±0.42	1.93±0.24

An interesting secondary observation is that the model accounts well for the rather large variability in rating “strategies” between subjects: some subjects primarily used the center of the scale (e.g., S9), while others primarily used the ratings at the edges (e.g., S1, S6, S12), and yet others seemed to avoid both the center and the very edges of the scale (e.g., S2, S7, S8). At first sight, this variability in the data could suggest that there must be large variability in how subjects place their criteria to map evidence to confidence, which makes it unexpected that a model based on Fechner’s law accounts so well for the data. The variance in rating patterns is partly captured by differences in scaling and offset parameters (a and b) of the confidence mapping. However, we believe that the variability is also in part caused by between-subject differences in the distribution of the decision variable (Fig. 9, bottom left).

DISCUSSION

In this paper, we introduced a quantitative process model for visual working memory (VWM) metacognition that uses Fechner’s law to map VWM precision to VWM confidence. The model predicts the often reported correlation between confidence and performance and provides an excellent quantitative account of joint distributions of estimation error and confidence in human VWM. We critically evaluated several important assumptions of our model, but none of these evaluations resulted in a falsification. We proposed a neural counterpart of the model and showed that it accounts for the data as well as the best algorithmic-level model, but only when neural gain is allowed to vary across items. Moreover, we re-evaluated previously proposed VWM encoding models and found that inclusion of confidence data boosts the model differences on average by a factor of 5.99. Finally, we showed that a model based on Fechner's law is also able to account for confidence ratings in a word recognition memory experiment, which provides preliminary evidence that Fechner's law may be a general law in metacognition.

Generality of Fechner’s law

Fechner's law has traditionally been used to describe how the intensity of a physical stimulus maps to a subjective sensation. Our results suggest that the same law may underlie sensations of metacognitive information, such as the quality of a working memory or the posterior probability that a choice was correct. The parallel applicability of Fechner’s law in basic perception metacognition might be a coincidence, but could also reflect something deeper about how the brain represents information. The traditional Fechner law has been motivated normatively by arguing that logarithmic coding of perceptual quantities has information-theoretical advantages (Sun, Wang, Goyal, & Varshney, 2012). Moreover, empirical findings – both behavioral and physiological – have suggested that logarithmic coding is indeed widespread in the brain (Gold & Shadlen, 2001, 2002; Juslin, Nilsson, Winman, & Lindskog, 2011; Maloney & Dal Martello, 2006; Phillips & Edwards, 1966; H. Zhang & Maloney, 2012). In light of this, it may seem less surprising – and perhaps even expected – that we find evidence for Fechner's law in metacognition. While we believe that our results are promising, the generality of a phenomenon can obviously not be established in a single paper – future studies will have to test the law in a larger variety of tasks.

Metacognitive noise

Removing the metacognitive noise parameter from our model substantially worsened the fit for 5 out of 6 subjects. This suggests that there are imperfections in the quality of a subject’s knowledge about the precision of their own memory contents, which is consistent with previous literature on metacognition (De Martino et al., 2013; Harlow & Donaldson, 2013; Jang et al., 2012; Maniscalco & Lau, 2012; Mueller & Weidemann, 2008). However, our results do not explain the cause of these imperfections: the metacognitive noise parameter serves as an umbrella term for all stochastic processes between the implicit representation of memory uncertainty, possibly in early sensory cortex (Harrison & Tong, 2009), and the brain’s confidence reporting system. We chose to add the metacognitive noise to the confidence variable, γ, which is obtained through a log transformation of memory precision, J. However, it could just as well be that metacognitive noise is already present in the representation of memory precision. We cannot distinguish these two types of noise, because the effect of adding normal noise after a log transformation is mathematically equivalent to that of adding lognormal noise before the transformation. A third – and perhaps the most likely – possibility is that both variables are subject to noise. Future work will need to break down the processes that contribute to noise in metacognition.

One may wonder whether the presence of metacognitive noise makes metacognition non-Bayesian or suboptimal. We believe that these two questions have to be treated separately, because Bayesian computation and optimality are distinct notions (Ma 2012). A Bayesian decision maker uses the posterior over the world state of interest to make decisions. Since confidence ratings in our model are derived from the posterior distribution, our model of confidence is in this sense Bayesian, despite the presence of metacognitive noise. An optimal decision maker maximizes performance with respect to a reward function. In the tasks that we modelled, confidence ratings did not affect the reward feedback that subjects perceived. Therefore, there was no obvious reward function for the confidence rating in these tasks and we cannot make any statements about optimality of the confidence ratings. However, if the observer had to make a post-decisional wager (Fleming & Dolan, 2010; Persaud, McLeod, & Cowey, 2007; Seth, 2008), and if that wager were based on the subject’s noise-corrupted measure of confidence, then this noise would make the observer suboptimal in an absolute sense, but not necessarily in a relative sense (Ma 2012).

The nature of VWM precision

Rademaker et al. (2012) speculated that only a model with random variability in precision would probably be able to account for their finding that confidence varied strongly even within a set size. Here, we formally tested this speculation by performing a factorial comparison of encoding models and found that their speculation was correct: the only models that account well for their data are variable-precision models; the best-fitting equal-precision model is ranked 7^th and is outperformed by the best-fitting variable-precision model with an AIC difference of 46.4±18.8 (Fig. 6A). Moreover, we found that successful models had another property in common: none of these models assumed that memory precision is a discretized quantity (the best-fitting model with discretized precision is ranked 4^th and is outperformed by the best-fitting continuous-precision model with an AIC difference of 30.6±23.7). Hence, our results show that metacognition data pose a serious challenge to not only equal-precision models, but also to the idea of quantized precision, which is still actively advocated to date (Cappiello & Zhang, 2016; Luck & Vogel, 2013).

Sources of variability in precision

We treated variability in precision as random, but many of its components can probably be characterized more deterministically once the sources of variability in precision have been identified. Such sources may include heteroskedasticity (Bae, Allred, Wilson, & Flombaum, 2014; Girshick, Landy, & Simoncelli, 2011), configuration and context effects (Brady & Alvarez, 2011; Brady & Tenenbaum, 2010), variability in memory decay (Fougnie et al., 2012), attentional fluctuations, attentional shifts, and competition between memories. It has also been suggested that random variability in neural spike counts – that exists even when neural gain is fixed – may be a major source of the variability in precision observed at the behavioral level. However, we found that a neural model with fixed gain (Bays, 2014) does not account well for the correlation between performance and confidence. This mismatch disappeared when we introduced variability in the gain of the neural population that encodes an item, which is consistent with recent physiological findings that suggested the existence of such variability (Cohen & Kohn, 2011; Goris et al., 2014). However, since we did not explore the neural model as extensively as the algorithmic-level model, we currently cannot exclude the possibility that there are other possible modifications to the fixed-gain model (e.g., a different definition of J_neural) that improve the fit without the need of a variable gain.

Limitations and future work

Our study has several limitations in addition to the ones already discussed above. One is that we treated confidence as a variable that can take arbitrarily large or small values. However, we cannot rule out that confidence has a floor and/or ceiling, in other words, that Eq. (2) only applies in a limited range of J and saturates outside of it. One could test for such saturation effects by using a continuous or near-continuous confidence scale and examining the distribution of responses at the ends of the scale. If saturation effects exist, the model could possibly account for them by extending it with a sigmoid transformation on γ in Eq. (2).

Another limitation of our study is that we did not address possible effects of response noise. Subjects in the experiment by Rademaker et al. (2012) provided their stimulus estimates by rotating a test grating through button presses, which will likely have involved some degree of response noise. However, the fits of our model seem to leave little room for improvement (Figs. 3 and S2–S7), which suggests that effects of response noise must have been negligible. An interesting question that the current study cannot answer is whether response noise is taken into account in confidence judgments when this noise is substantial, i.e., whether confidence judgments reflect the precision of the memory or the precision of the response. To test this, a more suitable experiment would be one in which the level of response noise is manipulated experimentally (e.g. through the sensitivity of the response buttons) and confidence is rated after the stimulus estimate is given.

A final limitation of our study is that we could not evaluate the postulated Fechner law between VWM precision and VWM confidence directly, because precision is an internal variable, inaccessible to the experimenter. Instead, we evaluated it indirectly, by fitting joint distributions of VWM confidence ratings and VWM errors. A weakness of this approach – which we think cannot be avoided – is that the evidence that it presents for Fechner’s law in metacognition depends on how one defines VWM precision. As in our previous work (Keshvari et al., 2012, 2013, van den Berg et al., 2014, 2012), we defined it here as Fisher information. However, had we defined precision differently, we might have found a different mapping between VWM precision and confidence. While this concern was partly alleviated by our finding that the Fechnerian mapping also successfully accounts for the data when defining precision as the concentration parameter of the noise distribution or when deriving confidence from the probability that the response was correct, there may be other, just as defensible definitions of VWM precision that account for the data using a non-logarithmic mapping. Even so, the flexible version of our model, Eq. (4), would in such a case probably still be able to account for the joint distribution of VWM errors and confidence. Therefore, hesitations about labeling our model as “Fechnerian” do not have to stand in the way of appreciating its quantitative success in accounting for VWM metacognition.