Identifying subgroups of enhanced predictive accuracy from longitudinal biomarker data using tree-based approaches: applications to fetal growth

Summary

Longitudinal monitoring of biomarkers is often helpful for predicting disease or a poor clinical outcome. In this paper, We consider the prediction of both large and small-for-gestational-age births using longitudinal ultrasound measurements, and attempt to identify subgroups of women for whom prediction is more (or less) accurate, should they exist. We propose a tree-based approach to identifying such subgroups, and a pruning algorithm which explicitly incorporates a desired type-I error rate, allowing us to control the risk of false discovery of subgroups. The proposed methods are applied to data from the Scandinavian Fetal Growth Study, and are evaluated via simulations.

1. Introduction

In obstetrics, it is common to monitor fetal development by collecting repeated ultrasound measurements, which may be useful for predicting a variety of poor pregnancy outcomes (Albert, 2012). For example, estimated fetal weight (EFW), a derived summary of multiple anthropometric ultrasound measurements (Hadlock et al., 1991), is often measured repeatedly in high risk pregnancies. The use of longitudinal ultrasound measurements to predict a binary outcome at birth has been considered by a number of authors, including Albert (2012); Zhang et al. (2012) and Liu and Albert (2014). Much of this research has been on how to best use these longitudinal measurements to predict a given outcome (i.e. selecting the best modeling framework) and, more generally, on whether or not the longitudinal measurements are actually useful in predicting that outcome. In this context, the longitudinal biomarker measurements are considered to be “useful” when they improve prediction of the binary outcome over standard covariates for the entire population; however, it is also possible that good predictive accuracy is only seen in a subgroup of the population. If such subgroups exist, it is desirable that they be identified in order to guide the design of follow-up schemes in future studies.

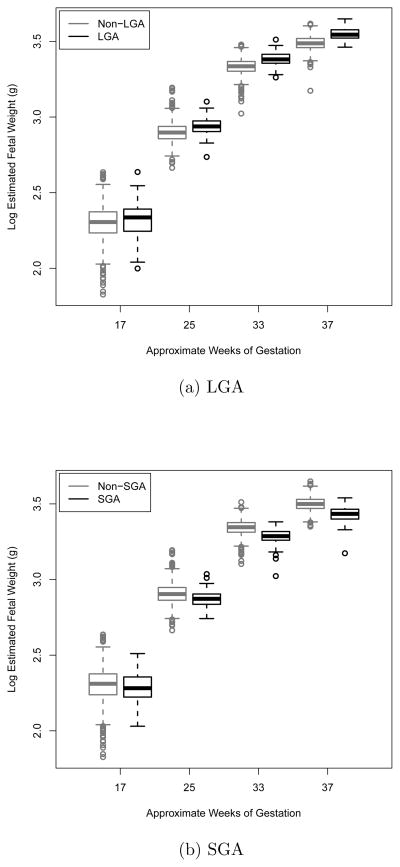
This work was motivated by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) study of successive small-for-gestational-age births in Scandinavia, a prospective study designed to investigate the etiology and consequences of intrauterine growth retardation (Bakketeig et al., 1993). The study population consisted of multiparous women of Caucasian origin who spoke one of the Scandanavian languages and had a singleton pregnancy, and each woman was scheduled to receive an ultrasound at approximately 17, 25, 33 and 37 weeks of gestation. Zhang et al. (2012) showed that longitudinal measurements taken at approximately 17 to 25 weeks of gestation were not predictive of large-for-gestational-age (LGA) birth, while measurements taken closer to full term (37 weeks) were highly predictive of LGA. This is illustrated in figure 1(a), where we can see that separation in the distribution of EFW between LGA and non-LGA at approximately 17 weeks of gestation is minimal, but gets progressively larger until, at approximately 37 weeks of gestation, the groups are quite distinct. Looking at figure 1(b), a similar trend can be seen for small-for-gestational-age (SGA) birth. While important clinically, these results suggest that early monitoring of a pregnancy for LGA and SGA may not be useful. Given these results, two natural clinical questions are: (1) are there subgroups of women for whom early monitoring for LGA or SGA may be effective and (2) are there some women for whom prediction is more or less accurate if all available measurements are used? The focus of this paper will be on the development of statistical methods which can be used to identify such subgroups.

Fig. 1.

Log estimated fetal weight at nominal observation times

One common way to identify subgroups is to use tree-based methods (Negassa et al., 2005; Hothorn et al., 2006; Su et al., 2008, 2009; Foster et al., 2011; Lipkovich et al., 2011; Loh et al., 2015). Recently, a number of authors have also proposed Bayesian trees-based methods, such as Bayesian additive regression trees (BART) (Chipman et al., 2010; Bleich et al., 2014). Tree-based methods work by partitioning the data into subgroups defined by the covariates, within which a simple model is fit to predict the outcome (Hastie et al., 2009). Tree-based methods make only mild model assumptions, and are capable of handing large numbers of covariates with complicated interactions. Moreover, their simple structure makes them easy to interpret. Though much consideration has been given to the use of tree-based approaches for identifying treatment-by-covariate interactions, we are unaware of any previous work on methods designed to identify subgroups of enhanced predictive accuracy, tree-based or otherwise. The latter will be the focus of this paper. Specifically, we propose a tree-based approach to identifying subgroups, within which longitudinal biomarker measurements may be especially useful in predicting a subsequent binary outcome.

A well-known problem in subgroup analysis is that of false positive findings (Yusuf et al., 1991; Peto et al., 1995; Assmann et al., 2000; Brookes et al., 2001; Berger et al., 2014). Tree-based methods recursively choose the “best” partition of the remaining data until some pre-defined “stopping” conditions are met, often leading to very large initial trees. These initial trees are then “pruned,” i.e. weak partitions are collapsed using some pruning function, reducing the initial tree to a less complex subtree. This pruning can help to remove spurious partitions, but often will still result in overfitting, i.e. partitioning of the data, even when no true subgroups exist. We consider this type of false positive finding to be a type-I error. In the case of our example, this means partitioning the data when the truth is that the longitudinal biomarker measurements are equally useful in predicting the binary outcome across the population. In this paper, we propose a parametric bootstrap-based procedure to explicitly incorporate the desired type-I error rate into our pruning algorithm. Though not considered in this paper, an alternative approach is to take a Bayesian perspective and control for multiplicity by assigning prior probabilities to possible subgroup effects (Berger et al., 2014).

The remainder of this paper is organized as follows. In Section 2, we introduce methods for prediction of a binary outcome using longitudinal measurements, and propose a tree-based approach to identifying subgroups in which this prediction is especially good (or bad). In Section 3, the proposed methods are applied to data from the Scandinavian Fetal Growth Study (Bakketeig et al., 1993) and in Section 4 we present simulation studies to examine the performance of the proposed methodology. A discussion is given in Section 5.

2. General Methods and Extension to Subgroup Identification

Let D_i, i = 1, . . . , N be the binary outcome indicator of interest for subject i, where D_i = 1 if the subject experienced the outcome and D_i = 0 otherwise, and let Y_i = (Y_i1, . . . , Y_ini)^T be the vector of longitudinal biomarker measurements for subject i, taken at times t_i1, . . . , t_ini. Additionally, let Z be an N × p baseline covariate matrix with columns Z₁, . . . , Z_p and rows z₁, . . . , z_N.

2.1. The Shared Random Effects Model

To predict the binary outcome using the longitudinal biomarker, we employ the shared random effects (SRE) model (Albert, 2012). This method is designed to jointly model the longitudinal biomarker process and the binary outcome, conditional on some random effects. These random effects are shared by both models, which introduces a correlation between the biomarker and binary outcome. Because our ultimate interest is in predicting LGA and SGA births using longitudinal fetal growth measurements, we consider a specific version of the SRE model which has been shown to be appropriate in this case. Specifically, we assume that the longitudinal measurements follow a linear mixed model:

$${\mathbf{Y}}_i={\mathbf{X}}_i^T\beta +{\mathbf{W}}_i^T{\mathbf{b}}_i+{\epsilon }_i,$$ (1)

where β are fixed effect parameters, b_i are random effects, and errors ε_ij follow independent normal distributions with mean 0 and variance ${\sigma }_{\epsilon }^2$. We use the general notation X_i and W_i to represent the fixed and random effect design matrices, respectively, for subject i. In this paper, we will consider the special case where

$${\mathbf{X}}_i={\mathbf{W}}_i=\left(\begin{array}{ccc}1& t_{i1}& t_{i1}^2\\ 1& t_{i2}& t_{i2}^2\\ ⋮& ⋮& ⋮\\ 1& t_{{in}_i}& t_{{in}_i}^2\end{array}\right);$$

however, we have kept these matrices distinct in (1) because in practice, these two matrices need not be the same. We limited ourselves to quadratic time effects, as this model performed very well for the Scandinavian Fetal Growth data, but if desired, higher order terms could easily be added. It is worth noting that the variance of the estimated fetal weight changes with time. Though not obvious from the statement of the model, we have found that the random effects in (1) are able to effectively capture this heteroskedasticity, giving estimated variances which are very similar to the observed variances at each time point. In addition, though we have not included main effects for z_i in (1), such terms could certainly be added. We chose to exclude these terms because our interest is in the prediction of D_i using Y_i, and adding these baseline covariates to (1) did not have a noticeable impact on this prediction. Intuitively, we think this happens because, if such terms are left out, they are essentially absorbed by the random intercept, and are thus still “accounted for” in (1).

We introduce the association between D_i and the longitudinal marker through the shared random effects, b_i. That is, we link the binary outcome D_i to the longitudinal marker:

$$P(D_i=1\mid {\mathbf{b}}_i,{\mathbf{z}}_i)=\mathrm{\Phi }\{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+\alpha c_i(t_{\ast })\},$$ (2)

where, Φ is the probit link function, $c_i(t_{\ast })=b_{i0}+b_{i1}{t}_{\ast }+b_{i2}{t}_{\ast }^2$ and t_* is a time point near the time at which the binary outcome is generally observed (e.g. 39 weeks, a time point near the time of birth). Thus, the longitudinal measurements are related to the probability of experiencing the outcome D_i = 1 through an individual’s predicted measurement at time t_*. For simplicity, we use the same t_* value for all subjects. Note that the strength of the association between the binary outcome and the longitudinal marker measurements is controlled by α in (2), i.e. if α = 0, P(D_i = 1|Y_i, z_i) = P (D_i = 1|z_i), meaning D_i and Y_i are independent given z_i. To simplify parameter estimation, the random effects are assumed to follow a multivariate normal distribution with mean 0 and variance V.

As discussed by Albert (2012), when the random effects are assumed to follow a normal distribution, parameter estimates can be obtained using a two-stage pseudo-likelihood approach. In stage 1, we fit the linear mixed model (1) using standard software, and obtain the posterior mean of the random effects for subject i, b̂_i, i.e. the empirical Bayes estimator. In stage 2, the conditional likelihood of D given Y and Z is maximized given the parameter estimates from stage 1. This conditional likelihood can be obtained following arguments similar to Albert (2012). In particular, note that $E[\mathrm{\Phi }(X+W)]=\mathrm{\Phi }[(\mu +W)/\sqrt{1+{\sigma }^2}]$ when X ~ N(μ, σ²). Thus, P(D_i = 1|Y_i, z_i) can be expressed as follows:

$$\begin{array}{l}P(D_i=1\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)\\ =\int P(D_i=1\mid {\mathbf{b}}_i,{\mathbf{z}}_i)f({\mathbf{b}}_i\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)d\mathbf{b}=E_{\mathbf{b}\mid {\mathbf{Y}}_i,{\mathbf{z}}_i}\mathrm{\Phi }\{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+\alpha c_i(t_{\ast })\}\\ =E_{\mathbf{b}\mid {\mathbf{Y}}_i,{\mathbf{z}}_i}\mathrm{\Phi }\{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+\alpha E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)-\alpha [E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)-c_i(t_{\ast })]\}\\ =\mathrm{\Phi }\left\{\frac{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+\alpha E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)}{{(1+{\alpha }^2\text{var}[E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)-c_i(t_{\ast }))])}^{\frac{1}{2}}}\right\}.\end{array}$$

In the next section, covariate-by-c_i(t_*) interaction terms will also be included in Model (2) in order to construct a regression tree; however, the conditional likelihood-based estimation procedure described above still holds in principle. More details will be given below.

2.2. Subgroup Identification

To identify subgroups, we follow the general CART framework. That is, we begin by splitting the data into two subgroups, or nodes, {i : z_ik > ω_k} and {i : z_ik ≤ ω_k}, by finding the covariate z_k, k ∈ [1, 2, . . . , p] and corresponding cutpoint ω_k which maximize the splitting criterion of interest. Note that for each k ∈ [1, 2, . . . , p], ω_k could potentially be any one of the unique values of covariate z_k observed in the data. This process is then repeated within each of these “child” nodes. We continue in this fashion until the data can no longer be subdivided, based on some pre-defined rules which govern the size of the tree. For instance, one may wish to limit the depth of the tree (i.e. how many times the above process is repeated), or set a minimum number of subjects that must be present in order to further subdivide a particular node in the tree. This procedure generally results in a large initial tree. Once this initial tree is obtained, a pruning algorithm is used to collapse “weak” splits, thereby reducing the large initial tree to the optimal subtree (given a specific pruning function). Details of our specific splitting criteria and pruning algorithm are given below. For the remainder of the paper, ξ will denote indices of subjects in the child node within which additional splits are currently being evaluated. When we are choosing the first split, ξ includes all subjects, but for subsequent splits, ξ will only contain a subgroup of the subjects.

2.2.1. Choosing Splits

Identifying subgroups of the population within which prediction based on joint models (1) and (2) is especially accurate amounts to identifying subgroups within which c_i(t_*) is especially useful in classifying D_i. In other words, we would like to identify covariate-by-c(t_*) interactions. To achieve this, we will choose splits using a statistic which is analogous to that of Su et al. (2009). Let ψ_k be the one-dimensional partition of ξ defined by covariate z_k and cutpoint ω_k. Our splitting criterion, s_P (ψ_k) (or more generally s_P (ψ)), will be the squared statistic which would be used to test H₀ : α₂ = 0 in the model

$$P(D_i=1\mid c_i(t_{\ast }),{\mathbf{z}}_i)=\mathrm{\Phi }\{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+{\alpha }_{0}I(z_{ik}>{\omega }_k)+{\alpha }_1{c}_i(t_{\ast })+{\alpha }_2{c}_i(t_{\ast })I(z_{ik}>{\omega }_k)\},$$ (3)

i.e. s_P (ψ_k) = [α̂₂/SE(α̂₂)]², where SE(α̂₂) is a standard error estimate for α̂₂. Note that, in (3), the level of enhancement in the region z_k > ω_k is controlled by the magnitude of α₂, i.e. if α₂ = 0, this region is not enhanced. Thus, when evaluating splits, we will choose the z_k/ω_k pair which maximizes s_P (ψ_k), as this suggests the highest degree of enhancement. Under Model (3), and following arguments similar to those used in Section 2.1 for Model (2), we have

$$P(D_i=1\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)=\mathrm{\Phi }\left\{\frac{{\eta }_0+{\eta }_1^T{\mathbf{z}}_i+{\alpha }_{0}I(z_{ik}>{\omega }_k)+{\alpha }_{1}E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)+{\alpha }_{2}E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)I(z_{ik}>{\omega }_k)}{{(1+var[E(c_i(t_{\ast })\mid {\mathbf{Y}}_i,{\mathbf{z}}_i)-c_i(t_{\ast })]{({\alpha }_1+{\alpha }_{2}I(z_{ik}>{\omega }_k))}^2)}^{\frac{1}{2}}}\right\}.$$ (4)

We obtain s_P(ψ) by maximizing the conditional log-likelihood of D given Z, Y:

$$l(\mathbf{D}\mid \mathbf{Z},\mathbf{Y})=-\sum _{i\in \xi }(ln({\mathrm{\Phi }}_{(4)})D_i+ln(1-{\mathrm{\Phi }}_{(4)})(1-D_i))$$ (5)

with respect to η₀, η₁, α₀, α₁ and α₂, where Ψ₍₄₎ denotes the conditional probability defined by equation (4). In practice, when maximizing (5), b_i is replaced by the empirical Bayes estimator, b̂_i, i.e. E(c_i(t_*)|Y_i, z_i) is replaced by ${\widehat{c}}_i(t_{\ast })={\widehat{b}}_{i0}+{\widehat{b}}_{i1}{t}_{\ast }+{\widehat{b}}_{i2}{t}_{\ast }^2$, and we replace var[E(c_i(t_*)|Y_i, z_i) − c_i(t_*)] with an estimate of var[ĉ_i(t_*)−c_i(t_*)] (see Albert (2012) for additional details). As noted by Albert (2012), equation (4) allows for the estimation of η₀, η₁, α₀, α₁ and α₂ accounting for the calibration error in using a plug-in estimator for b_i. Occasionally, when analyzing real data, the hessian matrix for η₀, η₁, α₀, α₁ and α₂ can be “nearly singular,” causing numerical problems. To combat this, we include a very small ridge penalty on η₀, η₁, α₀, α₁ and α₂ (specifically, ${10}^{-6}[{\eta }_0+{\sum }_{j=1}^p{\eta }_{1j}+{\sum }_{j=1}^3{\alpha }_j]$) in (5) when analyzing real data. This does not noticeably impact the parameter estimates, but dramatically improves numerical stability.

It is worth noting that, in order to identify the optimal split in practice, all possible cutpoints for each of the p covariates must be considered every time we partition the data, which means s_P(ψ_k) is generally computed a very large number of times when constructing a tree. Thus, constructing a tree using s_P (ψ) can be computationally expensive, particularly when some or all of the covariates are continuous. For this reason, we also consider a splitting criterion based on a linear model, which is more computationally efficient than s_P (ψ). In particular, we consider the square of the statistic that would be used to test H₀ : γ₃ = 0 in the model

$$c_i(t_{\ast })={\gamma }_0+{\theta }^T{\mathbf{z}}_i+{\gamma }_1{D}_i+{\gamma }_{2}I(z_{ik}>{\omega }_k)+{\gamma }_{3}I(z_{ik}>{\omega }_k)D_i+{\epsilon }_i.$$ (6)

This criterion will be referred to as s_L(ψ), and can be obtained using standard software. In practice, c_i(t_*) is replaced by ĉ_i(t_*) to obtain s_L(ψ). It should be noted that when fitting model (6), we assume ĉ_i(t_*), i = 1, …, n are iid normal random variables. Though ĉ_i(t_*), i = 1, …, n are not independent in the finite sample because of the plug-in estimator β̂, they are asymptotically independent following the results of Jiang (1998), and thus we feel that our assumptions of independence and normality are reasonable.

Following the brief arguments outlined below, (6) can be viewed as an approximation to (3). Note that $\mathit{logit}(x)\approx {\mathrm{\Phi }}^{-1}(x)/\sqrt{\pi /8}$, so (3) can be approximately rewritten as

$$ln\left[\frac{P(D_i=1\mid c_i(t_{\ast }),{\mathbf{z}}_i)}{P(D_i=0\mid c_i(t_{\ast }),{\mathbf{z}}_i)}\right]={\eta }_0^{\ast }+{{\eta }_1^{\ast }}^T{\mathbf{z}}_i+{\alpha }_0^{\ast }I(z_{ik}>{\omega }_k)+{\alpha }_1^{\ast }{c}_i(t_{\ast })+{\alpha }_2^{\ast }{c}_i(t_{\ast })I(z_{ik}>{\omega }_k).$$

Furthermore, note that if (6) is assumed to hold, so that $(c_i(t_{\ast })\mid {\mathbf{z}}_i,D_i=j)~N({\mu }_j,{\sigma }_{c(t_{\ast })}^2)$, and in addition, we assume that P(D_i = 1|z_i) follows a logistic model:

$$ln\left[\frac{P(D_i=1\mid {\mathbf{z}}_i)}{P(D_i=0\mid {\mathbf{z}}_i)}\right]={\nu }_0+{\nu }_1^T{\mathbf{z}}_i+{\nu }_{2}I(z_{ik}>{\omega }_k),$$ (7)

then we have

$$\begin{array}{c}ln\left[\frac{f(c_i(t_{\ast })\mid D_i=1,{\mathbf{z}}_i)}{f(c_i(t_{\ast })\mid D_i=0,{\mathbf{z}}_i)}\right]+ln\left[\frac{P(D_i=1\mid {\mathbf{z}}_i)}{P(D_i=0\mid {\mathbf{z}}_i)}\right]=\\ -\frac{{(c_i(t_{\ast })-{\mu }_1)}^2}{2{\sigma }_{c(t_{\ast })}^2}+\frac{{(c_i(t_{\ast })-{\mu }_0)}^2}{2{\sigma }_{c(t_{\ast })}^2}+{\nu }_0+{\nu }_1^T{\mathbf{z}}_i+{\nu }_{2}I(z_{ik}>{\omega }_k)=\\ {\gamma }_0^{\ast }+{\gamma }_1^{\ast }{c}_i(t_{\ast })+{\gamma }_3^{\ast }{c}_i(t_I)I(z_{ik}>{\omega }_k)+{\nu }_0+{\nu }_1^T{\mathbf{z}}_i+{\nu }_{2}I(z_{ik}>{\omega }_k).\end{array}$$

Thus, the linear model (6) is compatible with the probit model (3).

2.2.2. Pruning and Controlling Type-I Error

To select the “optimal” subtree, we employ the interaction-complexity measure proposed by Su et al. (2009):

$$G_{\lambda }(T)=\sum _{h\in T-\stackrel{\sim }{T}}G(h)-\lambda \Vert T-\stackrel{\sim }{T}\Vert ,$$ (8)

where T is some tree, T − T̃ is the set of internal nodes of T, ||T − T̃ is the number of internal nodes of T, i.e. its complexity, G(h) is the splitting criterion value (s_P or s_L) corresponding to node h, and λ ≥ 0 is a complexity parameter. Choosing λ = 0 returns the initial tree (i.e. no pruning), and increasing λ produces a nested sequence of subtrees, eventually leading to a “null” tree, containing no splits (if true, this means that predictive accuracy is the same for all subjects).

As previously mentioned, in order to control the risk of false positives, we explicitly incorporate the desired type-I error rate into the selection of λ. To do this, we employ a parametric bootstrap based on the joint models (1) and (2). Model (2) can be viewed as a “null” model, as it assumes a fixed α for the entire population. Thus, we can use the resulting estimated conditional probabilities to perform a parametric bootstrap. Suppose we have fit the joint models (1) and (2), giving estimates of P(D_i = 1|Y_i, z_i) for each subject, as well as random effect estimates, b̂₁, …, b̂_N. In addition, suppose we have obtained a tree, T₀, using the above algorithm with one of the proposed splitting criteria. We now select λ as follows:

1. Using the estimated probabilities, generate new binary outcome indicators, $D_1^{(1)\ast },\dots ,D_N^{(1)\ast }$, where $D_i^{(1)\ast }~\text{Bernoulli}(\widehat{P}(D_i=1\mid {\mathbf{Y}}_i,{\mathbf{z}}_i))$.

2. Using data $(D_1^{(1)\ast },{\mathbf{z}}_1),\dots ,(D_N^{(1)\ast },{\mathbf{z}}_N)$, obtain a tree, T⁽¹⁾.

3. Using (8), obtain the sequence of λ values which correspond to each subtree, and select the smallest value of λ which returns the null tree, say λ⁽¹⁾.

4. Repeat steps 2 and 3 M − 1 times, giving M “null” complexity parameter values, λ⁽¹⁾, …, λ^(M).

5. Choose the “final” λ value, λ_δ, to be the 1 − δ^th percentile of λ⁽¹⁾, …, λ^(M), where δ is the desired type-I error rate. The “final” tree, T_δ, is then found by using (8) to obtain the subtree for T₀ which corresponds to λ_δ.

Because the bootstrap data is generated under a null model, using λ_δ to select the final tree should lead to the desired type-I error. Note that, though we use (8), we select the tuning parameter value which corresponds to a desired type-I error rate, rather than that which minimizes (8) (or a cross-validated estimate of (8)). For the remainder of this paper, λ_δP and λ_δL will denote the λ_δ values for trees constructed using s_P(ψ) and s_L(ψ) respectively.

2.2.3. Evaluation of Identified Subgroups

The selection of a non-null tree suggests that one or more subgroups exist; however, once a tree is selected, one will generally wish to assess the degree of enhancement within each of the identified subgroups, which in our case means assessing the strength of the relationship between c_i(t_*) and D_i within each subgroup. To do this for a given subgroup, say A, we simply obtain the within-A test statistic for α, i.e. α̂_A/SE(α̂_A), by re-fitting (2) using only subjects in A. We then compare â_A/SE(α̂_A) to the complete-data statistic, α̂/SE(α̂). Note that, because trees may vary widely in complexity, A could be one-dimensional or multi-dimensional. It is desirable that we remain consistent with the form of the model used to choose splits, so when choosing splits with s_L(ψ), we assess enhancement of identified subgroups using the linear analog of (2). That is, the enhancement of A is assessed using γ̂_1A/SE(γ̂_1A) based on c_i(t_*) = γ₀ + θ^Tz_i + γ₁D_i + ε_i. These statistics may be positive or negative, and any value which is larger than the complete data value in magnitude suggests potential enhancement. Rather than suggesting a ‘hard’ rule for determining enhancement, we recommend that the practitioner compute these statistics and use them as a guide to describe the characteristics of the identified subgroups. If preferred, one could instead directly compare the within-A estimate and the complete data estimates (i.e. without rescaling by the standard errors).

2.2.4. Evaluating Early Prediction

Recall that one of our goals is to identify subjects for whom accurate prediction can be achieved using only early measurements, i.e. those taken at or before some pre-specified time t̃. To address this issue, we will consider the use of reduced-data random effect estimates to compute our splitting criteria.

When considering all biomarker measurements, splits are chosen using the best linear unbiased prediction (BLUP) of b_i, which for subject i is

$${\widehat{\mathbf{b}}}_i=\widehat{\mathbf{V}}{\mathbf{W}}_i^T{\left\{{\mathbf{W}}_i\widehat{\mathbf{V}}{\mathbf{W}}_i^T+{\widehat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n_i}\right\}}^{-1}\left({\mathbf{Y}}_i-{\mathbf{X}}_i\widehat{\beta }\right),$$ (9)

where V̂ is the estimated random effect variance, σ̂_ε is the estimated error standard deviation, β̂ is the fixed effect parameter estimate, and I_ni is the n_i × n_i identity matrix. Thus, to assess early prediction, we simply compute (9) using only those observations which were taken at or before time t̃. That is, we select splits using the reduced data BLUP of b_i:

$${\widehat{\mathbf{b}}}_i^{{\mathbf{\Omega }}_i(\widehat{t})}=\widehat{\mathbf{V}}{\mathbf{W}}_i^{{\mathbf{\Omega }}_i{(\stackrel{\sim }{t})}^T}{\left\{{\mathbf{W}}_i^{{\mathbf{\Omega }}_i(\stackrel{\sim }{t})}\widehat{\mathbf{V}}{\mathbf{W}}_i^{{\mathbf{\Omega }}_i{(\stackrel{\sim }{t})}^T}+{\widehat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n_i}^{{\mathbf{\Omega }}_i(\stackrel{\sim }{t})}\right\}}^{-1}\left({\mathbf{Y}}_i^{{\mathbf{\Omega }}_i(\stackrel{\sim }{t})}-{\mathbf{X}}_i^{{\mathbf{\Omega }}_i(\stackrel{\sim }{t})}\widehat{\beta }\right),$$ (10)

where the superscript Ω_i(t̃) indicates that only the rows which correspond to observations taken at or before time t̃ are used. It should be noted that V̂, σ̂_ε and β̂ in (10) are exactly the same as in (9), i.e. they are calculated using data from all time points. The proposed methods are designed to use data from all time points in order to determine if prediction based on a subgroup of biomarker measurements is more accurate in certain subgroups, so it is sensible to use all data to obtain these estimates, as the true underlying values of these parameters are fixed with respect to the number of biomarker observations.

3. Application to Fetal Growth Data

We are interested in identifying subgroups of women for whom prediction of LGA or SGA based on some or all of the available ultrasound measurements is more (or less) accurate, should they exist. This is an important problem, as early prediction could have implications for intervention. A SGA birth might indicate growth restriction, while a LGA birth could be associated with an increased likelihood of being overweight in adulthood. If such a subgroup is identified, it could also have implications for the number and timing of ultrasound measurements in pregnancy. For instance, should everybody receive multiple ultrasounds throughout pregnancy, or should some women only receive them earlier or later in pregnancy? In addition, the identification of subgroups may suggest that risk stratification should be done separately within these subgroups.

To this end, the proposed methods were applied to data from the NICHD study of successive small-for-gestational-age births in Scandinavia. The study included 1945 multiparous women of Caucasian origin who spoke one of the Scandanavian languages, had a singleton pregnancy, and were registered by the study center before 20 weeks of gestation (Zhang et al., 2012). About 30% of these women were a random reference sample from a Nordic population of Caucasians, and the rest were considered to be at high risk for a SGA birth, meaning they had previously delivered a low-birthweight (< 2750 g) infant, experienced a stillborn pregnancy or neonatal death, experienced two or more spontaneous miscarriages, had a history of phlebitis, had initial systolic blood pressure above 140 mmHg, had a previous preterm birth, had a prepregnancy weight at first clinic visit of less than 50 kg, currently smoked or smoked at conception, or currently used alcohol (Zhang et al., 2012). Each woman was scheduled to receive an ultrasound at approximately 17, 25, 33 and 37 weeks of gestation. In order to compare subgroup identification when predicting with only early measurements versus using complete longitudinal data, we limit ourselves to the observations with complete baseline covariate data, resulting in an analysis sample of 1699 subjects.

We considered estimated fetal weight on the log scale, which was measured at approximately 17, 25, 33 and 37 weeks of gestation. Using this biomarker, we separately considered, the prediction of LGA and SGA births. The baseline covariates considered as candidates to potentially define subgroups in this analysis were the mother’s age (continuous), smoking behavior (average number of cigarettes smoked per day - essentially continuous), body mass index (BMI) (continuous) and history of previous SGA birth (binary – yes or no). To obtain estimates of the fixed effect parameters, and the error and random effect variances, (1) was fit using the ‘complete’ data, i.e. all available observations on all 1699 subjects. For both LGA and SGA, we constructed trees using the complete data BLUPs, as well as those based only on measurements taken at or before 35, 27 and 19 weeks of gestation. That is, we considered t̃= 41 weeks (the maximum observed gestational age), 35 weeks, 27 weeks and 19 weeks. This was done twice for each outcome; once using s_L(ψ) and once using s_P (ψ). Thus, in total, 16 trees were constructed. To help ensure numerical stability, each initial tree was required to have at least 20 observations in each node, at least five cases and controls in each node, and was grown to a maximum depth of five. We also include a small ridge penalty (10⁻⁶) when maximizing (5), as noted in Section 2.2.1. All initial trees were pruned using (8) by selecting the complexity parameter value corresponding to a type-I error level of 0.05 based on 1000 bootstrap data sets, i.e. λ_0.05P for s_P (ψ) and λ_0.05L for s_L(ψ).

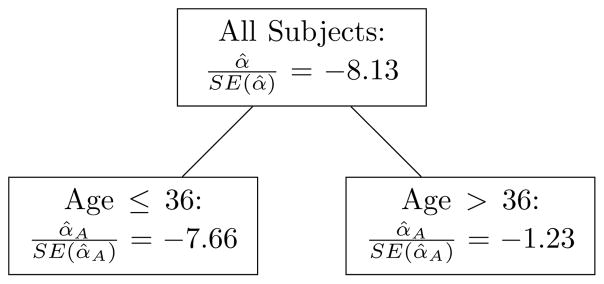
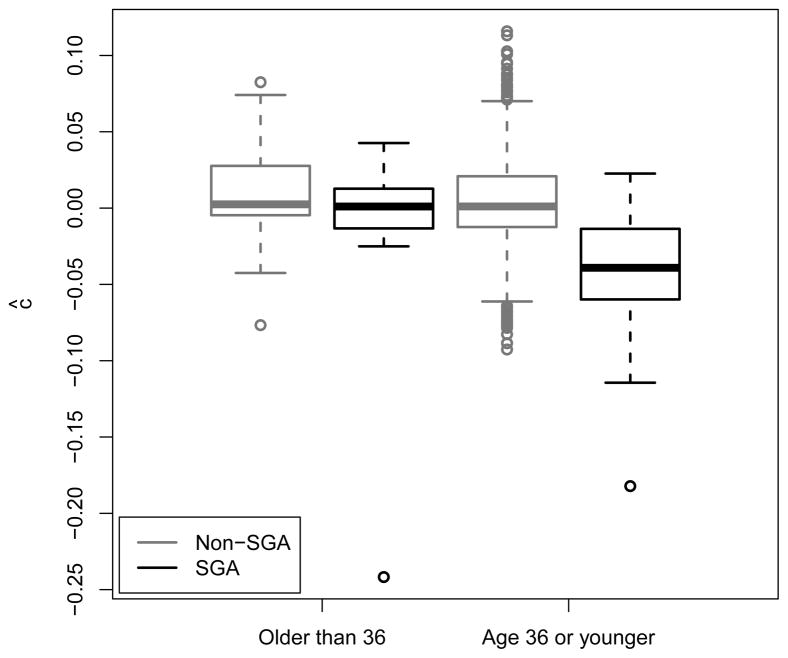
Among the 16 trees we considered, only the SGA tree constructed using the complete data BLUPs and Probit splitting criterion (s_P (ψ)) was found to be non-null at the 0.05 level. In fact, the largest complexity parameter value which corresponds to this tree is larger than all but five of the 1000 boostrap λ_P values, meaning that this tree is actually non-null at the 0.005 level. Thus, this tree would still have been identified with a Bonferroni correction within each outcome (i.e. set the type-I error level at $\frac{0.05}{8}=0.0063$). As shown in Figure 2, the identified tree suggests that prediction of SGA birth based on measurements taken at or before 41 weeks of gestation is quite good for women who are 36 years of age or younger (n = 1629), but is relatively poor for women over the age of 36 (n = 70). This potential interaction is illustrated in figure 3, where we can see considerable separation between SGA and non-SGA births in the younger group, but only minimal separation in the older group.

Fig. 2.

SGA tree for t̃= 41 weeks, identified using s_P (ψ).

Fig. 3.

SGA interaction box plot for t̃= 41

4. Simulations

To assess the performance of the proposed methods, a simulation study was performed. For six of our scenarios, 1000 data sets of size 1000 were generated from the joint models:

$$\begin{array}{c}{Y}_{ij}=0+3t_{ij}-0.4t_{ij}^2+b_{i0}+b_{i1}{t}_{ij}+b_{i2}{t}_{ij}^2+{\epsilon }_{ij};\\ P(D_i=1\mid {\mathbf{b}}_i)=\mathrm{\Phi }\{-1.3+0.5z_{i3}+0.5z_{i5}+[{\alpha }_0+{\alpha }_1({\mathbf{z}}_i)I({\mathbf{z}}_i\in A)]c_i(4.5)\},\end{array}$$

where c_i(4.5) = b_i0 +4.5b_i1 +4.5²b_i2, A = {z : z₁ = 1, z₂ = 1}, ε’s were iid N (0, 0.5), Z’s were iid Bernoulli(0.5), observation times were t = 1, 2, 3, and 4, b_i ~ N (0, V), with

$$\mathbf{V}=\left(\begin{array}{ccc}0.200& 0.040& 0.020\\ 0.040& 0.050& 0.010\\ 0.020& 0.010& 0.012\end{array}\right),$$

and the correlation among the random effects was 0.4. The choice of t^* was motivated by our interest in fetal growth, with 4.5 being analogous to a gestational age of approximately 39 weeks. The probit model intercept of −1.3 was chosen to give a prevalence of approximately 20%.

Scenario 1 is a null case in which, for all subjects, the longitudinal measurements are useless for predicting the binary outcome. Scenario 2 is also null, i.e. no true subgroup exists, but in this case, prediction is very good for all subjects. In Scenario 3, prediction is moderately good for subjects with z_i1 = 1 and z_i2 = 1, but for all others, Y_i is useless for predicting D_i. In Scenario 4, prediction is at least moderately good for all subjects, and slightly enhanced for those with z_i1 = 1 and z_i2 = 1. In Scenario 5, prediction is again at least moderately good for all subjects, but in this case, subjects with z_i1 = 1 and z_i2 = 1 are very strongly enhanced. Scenarios 1–5 were chosen to assess the performance of the proposed methods when all longitudinal measurements are used (i.e. t̃= 4); however, Scenario 6 is an “early prediction” case, with α₀ = 0.1 and α₁ = 2 being selected so that prediction using only observations taken at time t̃ = 1 was poor overall, but good for subjects with z_i1 = 1 and z_i2 = 1. Thus, in Scenario 6, only the first biomarker measurement will be used to select splits.

We also considered a scenario based on the Scandinavian Fetal Growth data, which we refer to as Scenario 7. To obtain all parameter values for this scenario, the Scandinavian data were modeled using binary versions of the three continuous baseline covariates to allow for computational efficiency in the simulations. In particular, mother’s age was defined to be 1 if it was greater than 36 and 0 otherwise (the subgroup identified in our real data analysis - about 5% of values are 1s), and mother’s BMI and average cigarettes smoked per day were defined to be 1 for values larger than the median and 0 otherwise. History of SGA birth was not changed, as it was already binary (approximately 25% 1s). Once the parameter estimates were obtained, we generated 1000 data sets of size 1700 (the number of subjects in the Scandinavian data set) from the models:

$$\begin{array}{c}{Y}_{ij}=1.50+0.88t_{ij}-0.09t_{ij}^2+b_{i0}+b_{i1}{t}_{ij}+b_{i2}{t}_{ij}^2+{\epsilon }_{ij};\\ P(D_i=1\mid {\mathbf{b}}_i)=\mathrm{\Phi }\{-2.98+1.06z_{i1}^{\ast }+0.16z_{i2}^{\ast }+0.78z_{i3}^{\ast }+0.43z_{i4}^{\ast }+[-36.52+31.12z_{i1}^{\ast }]c_i(4.5)\},\end{array}$$

where ε’s were iid N(0, 0.023). Covariates $z_{i1}^{\ast },z_{i2}^{\ast },z_{i3}^{\ast }$, and $z_{i4}^{\ast }$ were analogous to the binary age, binary BMI, history of SGA birth, and binary cigarettes smoked covariates mentioned above, and were thus generated as iid Bernoulli random variables with “success” probabilities of 0.05, 0.5, 0.25 and 0.5, respectively. Observation times were t = 1, 2, 3, and 4, and b_i was multivariate normal with covariance and correlation matrices (respectively)

$$\left(\begin{array}{ccc}0.0044& -0.0040& 0.0007\\ -0.0040& 0.0045& -0.0009\\ 0.0007& -0.0009& 0.0002\end{array}\right);\left(\begin{array}{ccc}1.00& -85& 0.73\\ -0.85& 1.00& -0.97\\ 0.73& -0.97& 1.00\end{array}\right).$$

For each simulated data set, we constructed initial trees using s_P (ψ) and s_L(ψ). To help ensure numerical stability, these trees were required to have at least 20 observations in each node, at least five cases and controls in each node, and were grown to a maximum depth of five. These initial trees were pruned using (8) based on a desired type-I error rate of 0.05 obtained from 1000 bootstrap samples. In order to evaluate the ability of our procedure to identify “truly” enhanced individuals, we consider an “automated” version of the enhancement classification step. In particular, if a non-null tree was selected, terminal nodes for which α̂_A > α̂ were classified as “enhanced.” The final identified subgroup consisted of all terminal nodes which were classified as enhanced, and whenever a subgroup was identified, we computed the sensitivity, specificity, positive predictive value, negative predictive value and the number of subjects it contained.

Looking at Table 1, we can see that, for non-null cases, i.e. Scenarios 3–5, trees constructed using s_P (ψ) have higher power to detect a tree than those constructed using s_L(ψ). As might be expected, when a clearly enhanced subgroup exists, as in Scenarios 3 and 5, both criteria have very good power, and in Scenario 4, where everyone has at least moderately good prediction, and the true subgroup is only mildly enhanced, both methods appear to lose power. This is especially true for s_L(ψ), which only identified a non-null tree 35 % of the time in Scenario 4. In the null Scenarios (1 and 2), both criteria led to approximately the correct type-I error rate, suggesting that, in this case, the parametric bootstrap may be incorporated into the pruning process to effectively control type-I error.

Table 1.

Simulation results

Splitting Criterion	Sens.	Spec.	PPV	NPV	Subgroup Size		Prop. Tree non-null
					Est.	True
Scenario 1
sP (ψ)1	-	0.97	-	1.00	33.10	0	0.062
sL(ψ)1	-	0.97	-	1.00	30.67	0	0.060
Scenario 2
sP (ψ)1	-	0.98	-	1.00	22.69	0	0.046
sL(ψ)2	-	0.98	-	1.00	20.38	0	0.043
Scenario 3
sP (ψ)1	0.97	0.95	0.92	0.99	278.58	250.76	0.972
sL(ψ)3	0.93	0.94	0.91	0.98	276.98	250.75	0.941
Scenario 4
sP (ψ)3	0.68	0.89	0.77	0.92	252.55	250.75	0.692
sL(ψ)4	0.34	0.91	0.63	0.83	152.16	250.73	0.354
Scenario 5
sP (ψ)5	1.00	0.96	0.93	1.00	283.22	250.77	1.00
sL(ψ)3	0.89	0.91	0.85	0.97	288.41	250.78	0.891
Scenario 66
sP (ψ)4	0.87	0.92	0.86	0.97	279.69	250.8	0.877
sL(ψ)1	0.72	0.90	0.80	0.93	253.71	250.76	0.729
Scenario 7
sP (ψ)7	0.83	1.00	1.00	0.99	72.83	85.10	0.833
sL(ψ)7	0.53	0.99	0.95	0.98	63.79	85.10	0.538

^1,2,3,4,5,7Due to numerical issues, results are based on 996, 994, 995, 992, 976 and 974 data sets, respectively.

⁶Splits were chosen using only the first longitudinal measurement, i.e. t̃= 1.

Sens., Spec., PPV and NPV denote the average (of the non-null values among the 1000 simulated data sets) sensitivity, specificity, positive predictive value and negative predictive value, respectively. To calculate these, subjects in terminal nodes classified as “enhanced” were considered to be “called enhanced” and those in the true subgroups (i.e. those with z₁ = z₂ = 1 for Scenarios 3–6; those with $z_1^{\ast }=1$ for Scenario 7) were considered to be “truly enhanced.”

Looking now at sensitivity, specificity, and positive and negative predictive values, we can see that, in Scenarios 3–5, s_P (ψ) trees tend to outperform those based on s_L(ψ), though in Scenarios 3 and 5, both methods do an excellent job of identifying truly enhanced individuals, while also avoiding falsely classifying non-enhanced individuals as “enhanced.” In Scenario 4, both methods have good specificity and negative predictive values, but seem to have more difficulty identifying truly enhanced subjects, especially when splits are chosen using s_L(ψ). Trees based on s_P (ψ) still perform relatively well in this scenario

Looking at the results for Scenario 6, we can see that the proposed methods were very successful at identifying those subjects for whom accurate prediction based on only the first longitudinal marker measurement was possible, particularly when splits were chosen using s_P (ψ). Again we see relatively good sensitivity, specificity, and positive and negative predictive values for both splitting criteria, suggesting that both methods can effectively identify the truly enhanced individuals, without falsely classifying too many non-enhanced individuals as “enhanced.”

In the “fetal growth” scenario (Scenario 7), trees constructed using s_P (ψ) again had good power and sensitivity, and excellent specificity, positive and negative predictive values. Trees constructed using s_L(ψ) also had excellent specificity, positive and negative predictive values, but were null nearly half of the time, and thus lacked sensitivity. This may be due to the fact that the true subgroup was quite small, consisting of only about 5% of the population. Overall, the proposed methods are very promising for identifying the correct subgroup. In practice, we recommend constructing trees using s_P (ψ) unless the computational burden is unreasonable, as this approach can be much more powerful, particularly when only modest subgroups exist. When very strong subgroups exist, either method should work well.

5. Discussion

We considered a tree-based approach to identifying subgroups for which longitudinal biomarker measurements are useful in predicting a subsequent binary outcome, and proposed the use of the parametric bootstrap to explicitly incorporate the desired type-I error rate into our pruning algorithm. A simulation study was undertaken, and the proposed methods were found to effectively identify truly enhanced individuals in a number of different scenarios, while also effectively controlling the type-I error.

In this paper, our goal was to identify subgroups within which prediction based on a specific, pre-defined model is especially good (or bad). That is, we focused on using the subgroup analysis with the hopes of improving our understanding of the predictive accuracy of the chosen model. Alternatively, one could consider first implementing a subgroup identification procedure in order to help determine which prediction model should be used for a particular application. It may be interesting to consider this further.

In the context of prediction, Hothorn et al. (2006) considered the use of model-based splitting criteria, and proposed a conditional inference framework, which allowed them to overcome the issues of overfitting and variable selection bias brought on by recursive partitioning procedures. An area of future research could be to consider a similar conditional framework in the context of subgroup identification. In addition to helping with overfitting and variable selection bias, this could help us to reduce the computational burden of our procedure, as the framework of Hothorn et al. (2006) does not require the evaluation of all possible splits for nominal covariates.

We propose a splitting criterion, s_P (ψ), based on our posited model, as well as s_L(ψ), a criterion based on a linear approximation. We favor s_P (ψ), as it is consistent with the proposed modeling framework; however, we realize the immense computational burden for this approach. For example, using the Biowulf Linux cluster at the NIH (http://biowulf.nih.gov), implementing our entire procedure for a single data set from simulation Scenario 7 took approximately 15 hours using s_P (ψ), whereas when s_L(ψ) was used, implementing the entire procedure on a single data set took approximately 7 minutes on average. Thus, though it suffers from some loss of power in a few scenarios, s_L(ψ) is an attractive alternative to s_P (ψ).

The proposed methods were motivated by and applied to data from the NICHD study of successive small-for-gestational- age births in Scandinavia. Though further validation is needed, the results of this analysis suggest that, for women over the age of 36, prediction (using joint models (1) and (2)) of SGA birth from estimated fetal weights taken at or before 41 weeks of gestation may be considerably less accurate than that for women who are 36 years of age or younger.