Abstract
This article represents the first in a series of tutorials on model evaluation in nonlinear mixed effect models (NLMEMs), from the International Society of Pharmacometrics (ISoP) Model Evaluation Group. Numerous tools are available for evaluation of NLMEM, with a particular emphasis on visual assessment. This first basic tutorial focuses on presenting graphical evaluation tools of NLMEM for continuous data. It illustrates graphs for correct or misspecified models, discusses their pros and cons, and recalls the definition of metrics used.
Nonlinear mixed effects models (NLMEMs) have been established as the state of the art methodology in pharmacometrics for analysis of longitudinal pharmacokinetic (PK) and pharmacodynamic (PD) measurements collected in preclinical and clinical studies, especially in drug development.1, 2, 3 NLMEM for continuous PK/PD data use nonlinear dynamic models that draw on physiological or pharmacological principles to provide a reasonable approximation of the dynamics of the drug in the body and of their effects. They describe both population and subject‐specific characteristics, represented as fixed parameters for population characteristics and random parameters for subjects. NLMEMs are widely applied because of their ability to quantify several levels of variability, to handle unbalanced data, and to identify individual specific covariates.
In any regression modeling, after fitting a model to a dataset, it is essential to assess the goodness‐of‐fit between the model and the dataset and to determine whether the underlying model assumptions seem appropriate. In this tutorial, we refer to this procedure as “model evaluation,” although, in literature, it has been described under several more or less equivalent terms, such as “model diagnostics,” “model adequacy,” “model assessment,” “model checking,” “model appropriateness,” and “model validation.” Model evaluation has to be clearly distinguished from “model building” and “model qualification” processes, which are two steps of model development that require model evaluation but imply different concepts. “Model building” is the process of developing a model on a given dataset to achieve clearly defined analysis objectives. “Model qualification” is the assessment of the performance of a model in fulfilling the analysis objectives. “Model evaluation” is required for both processes to diagnose one or several intermediary or key models in a model‐building step or evaluate a selected model with respect to the modeling objectives. In this tutorial, we will only focus on the model evaluation step and describe various tools for evaluation of a NLMEM, regardless of whether it is an intermediary model, a key model in the model‐building step, or a best model that can be used for further inferences.
Although there are many statistical tools for model evaluation, the primary tool for most biomedical science and engineering modeling applications is graphical analysis. Graphical methods have an advantage over numeric methods for model evaluation because they readily shed light on a broad range of complex aspects of the relationship between the model and the data. Different types of graphical analyses evaluating a fitted model provide information on the adequacy of different aspects of the model. NLMEM methodology is naturally linked with many assumptions related to executed design (e.g., unbalance design), data collection, form of structural model, multiple levels of variability to be quantified, residual model, and covariate model. Interactions between model components such that misspecification of one component may have consequences for the apparent appropriateness of other components in the fitted NLMEM adds to the challenge of model evaluation, therefore, a large set of tools is required.
In recent years, many new methods for graphical model evaluation have been developed. For example, new residual‐based model diagnostics have been developed (e.g., conditional weighted residuals (CWRES), normalized prediction distribution errors (NPDE), etc.),4, 5, 6 new models for the study of variance have been proposed, shortcomings of commonly used empirical Bayes estimates (EBEs) have been underlined7 and methods for using visual predictive checks (VPCs) have been developed and described.8, 9
To provide a compass and fit‐for‐purpose direction in the emerging and very active field of model‐based drug development, the International Society of Pharmacometrics (ISoP) Best Practice Committee has initiated a “Model Evaluation Group” to provide detailed guidance for model evaluation of NLMEM. This basic tutorial represents the first in a series of tutorials on model evaluation. It describes a core set of graphical tools for evaluation of NLMEM for continuous data and provides guidance, especially to beginner modelers, on how they are meant to be used. It includes a description of the different metrics, an illustration about their graphical use on “true” and “misspecified” models, and a discussion of their pros and cons. Each metric is first described by equations and then by a less technical explanation in order to make the definition of each tool easier to understand for readers with statistical or pharmacometric backgrounds. The graphs are broadly separated into two categories: prediction‐based (basic) and simulation‐based tools (Table 1). The use of each graph is illustrated via two case examples, which were chosen to show the properties and behaviors of different evaluation tools in different situations. This is not necessarily to mimic what should be done in real‐world modeling. Therefore, in these two examples, we used only simulated data and ignored important steps, such as exploring data, researching literature to understand the data, and to propose a set of plausible models, etc. The first example is a contrived example, in which we used a very simple PK model. The designs (dose, distribution of covariates, and allocation of sampling times) were selected to easily show the properties of various evaluation tools, although they may not resemble real data conditions. In the second part of the tutorial, we applied the presented graphical tools to evaluate a more complex example that is based on a real study. This is a PK/PD model describing the total warfarin concentration and its effect on prothrombin complex activity. For each example, we simulated data from a “true” model and fitted different models, including the “true” and various “misspecified” models to highlight some types of model deficiency. To show the availability of several software tools developed for NLMEM estimation and simulation, the steps of simulating data, estimating parameters, and computing evaluation metrics were performed using a variety of software, including R (https://cran.r-project.org/), NONMEM (http://www.iconplc.com/innovation/solutions/nonmem/), MONOLIX (http://lixoft.com/products/monolix/), and PHOENIX (https://www.certara.com/software/pkpd-modeling-and-simulation/phoenix-nlme/). The graphical displays presented in the tutorial are a suggestion using R scripts but it is not a recommendation from the ISoP Model Evaluation group.
Table 1.
Various evaluation graphs in nonlinear mixed effect model a and proposal for a core set of evaluation graphs
| Graphs | In core set | What to expect if the model is correct? | What to do if the graph does not fulfill the requirements? |
|---|---|---|---|
| Basic (prediction‐based) evaluation | |||
| Population‐based graphs | |||
| OBS vs. xPRED (x= ∅, C, and P b ) |
Yes NB: CPRED or PPRED c |
Data points are scattered around the identity line (but not necessarily evenly) | Trends may suggest a modification of structural model, residual error model or interindividual variability model. NB: Trends can also appear in absence of model misspecifications for models highly nonlinear with respect to random effects and large interindividual variability, especially when using PRED. |
| xWRES (x= ∅, C, and P b ) vs. time or xPRED |
Yes NB: CWRES or PWRES c |
Data points are scattered around the horizontal zero‐line (more or less evenly) | Trends may suggest a modification of structural model, residual error model, or interindividual variability model. Trends by conditioning on covariates suggest including covariates. NB: Trends can also appear in absence of model misspecifications for models highly nonlinear with respect to random effects and large interindividual variability, especially when using WRES. |
| xWRES (x= ∅, C, and P b ) vs. covariates | Yes if covariates are considered | No substantial correlation appears | Trends suggest including covariates or changing the covariate model. |
| Individual‐based graphs d | |||
| Individual fits |
Yes NB: at least for some representative individuals |
Observations are distributed evenly around the individual predicted curve | A substantial discordance between observations and predictions suggests a modification of the structural model, parameter variability model, or the residual error model. NB: This diagnostic is not useful for sparse data. |
| OBS vs. IPRED | Yes | Data points are scattered evenly around the identity line. Points cluster closer to the line than with observations vs. PRED, especially when interindividual variability is large | Trends may suggest a modification of the structural model or the residual error model. A lack of trend may not necessarily be associated with absence of model misspecification if data are sparse. |
| IWRES vs. time or IPRED |
Yes NB: Graphs of absolute IWRES vs. IPRED are also informative |
Data points are scattered evenly around the horizontal zero‐line. Most of the points lie within (−1.96 to 1.96) | Trends suggest a modification of structural model or residual error model. A cone‐shaped graph of IWRES vs. IPRED suggests a change in the error model. A lack of trend may not be necessarily be associated with absence of model misspecification if data are sparse. |
| Correlation between EBEs | Yes | No trend is expected in model without correlation between random effects if data are rich (i.e., low eta‐shrinkage) | Correlation between EBE suggests including correlation between random effects unless data are sparse. |
| EBEs vs. covariates | Yes if covariates are considered | No substantial correlation appears between EBE and covariates | Trends between EBE and covariates suggest, including covariates or changing the covariate model. |
| Simulation‐based graphs | |||
| VPC or pcVPC |
Yes NB: The choice between the two depends on the importance of covariates and use of adaptive designs |
Observed percentiles are not systematically different from the corresponding predicted percentiles and are within the corresponding confidence interval | Trends may suggest a modification of the structural model, the residual error model, or the parameter variability model. Trends when conditioning on covariates suggest including covariates or changing the covariate model. |
| NPC coverage | Observed percentiles are within the confidence interval of the corresponding predicted percentiles | Trends may suggest a modification of the structural model, the residual error model, or the interindividual variability model. Trends when conditioning on covariates suggest including covariates. | |
| npd (NPDE) vs. time or PPRED e | Yes | Data points are scattered evenly around the horizontal zero‐line. Most of the points lie within (−1.96 to 1.96). For graphs with observed and predicted percentiles and the confidence intervals: observed percentiles are not systematically different from the corresponding predicted percentiles and are within the corresponding confidence interval | Trends may suggest a modification of structural model, residual error model, or interindividual variability models. A cone‐shaped graph if npd vs. PPRED suggest a change in the residual error model. Trends when conditioning on covariates suggest including covariates. |
| npd (NPDE) vs. covariates | Yes if covariates are considered | No substantial correlation appears | Trends suggest including covariates or changing the covariate model |
CPRED, conditional population predictions; EBE, empirical Bayes estimate; FO, first order; IPRED, individual prediction; IWRES, individual weighted residuals; NB, nota bene; NPC, numerical predictive check; npd, normalized prediction distribution; NPDE, normalized prediction distribution error; OBS, observations; pcVPC, prediction‐corrected visual predictive check; PPRED, simulation‐based population predictions; PRED, FO population predictions; VPC, visual predictive check; WRES, weighted residuals.
aSee text or Supplementary Table S3 for definition of terms. bPPRED and PWRES are denoted EPRED and expectation weighted residuals in NONMEM, respectively. cDepending on the method used for parameter estimation (see text). dCaution in interpretation in case of high shrinkage. enpd is preferred over NPDE for graphical use.
PHARMACOKINETIC CASE EXAMPLE
Structural model
A simple PK model for a hypothetical drug was utilized throughout the next two sections (Basic evaluation tools & Simulation‐based evaluation tools) to illustrate different evaluation tools for detecting various types of model misspecification. The PK model is a two‐compartment model with first‐order elimination following a single i.v. bolus administration. Time course of drug concentration is described by Eq. (1):
| (1) |
The model has four parameters CL, V1, Q, and V2 representing clearance, volume of distribution for the central compartment, intercompartmental clearance, and volume of distribution for the peripheral compartment, respectively. We evaluated a binary covariate effect of concomitant treatment (without = 0, with = 1) on clearance and a linear effect of body weight on the central volume of distribution. Half of the hypothetical patients received a concomitant treatment in addition to the drug. Body weight is assumed to be distributed normally across the population, with a mean value of 70 kg and SD of 15 kg.
Statistical model
The central compartment drug concentration yij for individual i, observed at time tij is given by:
| (2) |
where f is the PK function, which is identical for all the individuals; θi is a vector of p individual parameters for the individual i, and εij is the residual error. Let yi denote the vector of ni observations yij, ti the vector of ni sampling times tij, εi the vector of ni residual errors εij with j=1…ni. εi is assumed to follow a normal distribution with mean 0 and variance Σ(θi,ti) as follows:
| (3) |
For this example, we assumed a combined error model with σadd, σprop ≠ 0.
The vector of individual parameters θi can be characterized by a function h of the fixed effects, representing the typical population values of the parameters and random effects ηi specific for each individual. The random effects are assumed to follow a multinormal distribution with mean 0 and variance Ω, N(0, Ω). Here, we assumed that each PK parameter follows a log‐normal distribution, therefore, h has an exponential form. For instance, for the kth parameter, h is given by:
| (4) |
The variance‐covariance matrix Ω of the random effects is assumed in this PK model to have all diagonal elements equal to ω2, where ω is the SD of the individual random effects for each PK parameter. Of course, this is not a common situation because the variability of parameter usually differs from each other. We also assumed a correlation between the random effects of CL and V1 (i.e., a non‐null covariance term between CL and V1 in the matrix Ω). A part of the interindividual variability may be explained by including covariates. In the presence of covariates, the individual parameters θik are described by:
| (5) |
where zi is the vector of covariates for individual i, which can be a binary (or categorical) covariate (e.g., concomitant treatment in this example), or a continuous covariate (e.g., body weight in this example), and β is the vector of covariate effect. Of note, a transformation was made for the body weight so that the reference profile corresponds to that of a patient with a weight of 70 kg.
| (6) |
We call Ψ the vector of population parameters, where Ψ = {µ, Ω, β, σadd, σprop}.
Study design and data simulation
We considered a balanced design, with five sampling times per patient (t = 0.5, 1, 4, 12, 24 hours after treatment), which we call the standard design. Two other designs, referred to as the sparse and very sparse designs, with two or one sampling times per patient, respectively, were also used to illustrate the influence of shrinkage on some of the evaluation graphs. In these sparse sampling designs, samples were randomly selected from the five sampling times above. A dataset of 180 patients with three treatment groups each receiving one of the three different doses of 10, 100, and 1,000 mg, was simulated using the model with the sampling designs described above and parameters provided in Supplementary Table S1.
Evaluated scenarios
To illustrate the properties of various evaluation graphs in different situations in which the model may or may not be appropriate for describing the data, we fitted several models to the simulated data: i) the true model that was used for data simulation; ii) a misspecified structural model, in which the structural model was changed into a one‐compartment model; iii) a model without covariates, in which no covariate effect was considered; iv) a misspecified correlation model, in which we neglected the correlation between the random effects of clearance and distribution volume; and v) two misspecified residual error models, in which we considered only a constant (σadd ≠ 0, σprop = 0) or proportional error model (σadd = 0, σprop ≠ 0). Note that we modified only one property of the true model at the same time to obtain these different types of model misspecifications.
Parameter estimation, computation of evaluation metrics, and software
Population parameters were estimated using the default option of the Stochastic Approximation Expectation Maximization algorithm implemented in MONOLIX version 4.3.3 (http://lixoft.com/products/monolix/). The simulated data and medians of predictions for different models are shown in Supplementary Figure S1.
Individual parameters were then estimated as EBEs which are the mode of the conditional posterior distribution, given the observed data and the population model. Let the conditional distribution of ηI. The EBE estimate of ηi is given by:
| (7) |
At this stage, μ has been estimated. Therefore, once is estimated, can be easily calculated.
Once the model parameters were estimated, evaluation metrics were computed using additional software. In this paper, all the goodness‐of‐fit graphs were generated using R and several R packages for which scripts are available in Supplementary R Codes. The full process for generating evaluation graphs for the different models is summarized in Supplementary Figure S2.
BASIC EVALUATION TOOLS
Evaluation based on population predictions
Population predictions
By definition, population predictions (xPRED, with x = ∅, C, or P) are the expectation of the model, E(yi), given the individual designs and covariates. There are several methods for computing xPRED. The simplest way is model linearization using the First‐Order (FO) linearization (Eq. (8)) (i.e., the prediction assuming all random effects equal 0; denoted PRED). The corresponding predicted profile, given design and covariates, is often called the prediction for typical individual or typical profile.
| (8) |
An alternative method is to use first order conditional expectation (FOCE) approximation giving predictions denoted conditional population predictions (CPRED) (Eq. (9)):
| (9) |
Another method for computing xPRED is to use the Monte Carlo simulation, in which population predictions (denoted PPRED) are defined as the mean of the model predictions (Eq. (10)). By definition, PPRED is the “average” prediction (response) of the population.
| (10) |
where is the vector of data obtained at the kth simulation using the model and the design of the individual i (ti). As in NLMEM, E(f(h(μ,ηi),ti) ≠ f(μ,ti), the “average prediction” for the population (PPRED) in general differs from PRED, the prediction for a “typical” patient, especially for models with high interindividual variability and high nonlinearity.
Observations can be plotted vs. population predictions to evaluate the population model (the first and second rows of Figure 1 a). The line of identity (and sometimes a local regression line) is added to the graph. Even if the model is correctly specified, the data points are not necessarily scattered around the line of identity but the regression line will be more or less close to the identity line. This can be seen in the first column of the first and second rows of Figure 1 a, in which the data were fitted to the true model. A systematic departure of the data points or the trend line from the identity line (as seen in the second column of the first and second rows of Figure 1 a) could indicate a misspecification in the structural model. On the other hand, misspecification in the residual error model is difficult to detect using these graphs (i.e., the third and second column of the two first rows of Figure 1 a) because the residual error model is not considered in the computation of xPRED. Deviations between the local regression and identity lines could appear independently of model misspecification because, in NLMEM, the observations are not symmetrically distributed around the mean. This can occur especially for models with high nonlinearity and large interindividual variability, regardless of the method of xPRED computations. Trends can also appear by using linearization to compute xPRED, by neglecting the intra‐individual correlation, the heterogeneity of residual errors, or the presence of data below the quantification limits when calculating the local regression line.7 It is also useful to examine the graph of observations vs. population predictions in both normal and log‐scale in order to better evaluate the quality of fit, especially when the data cover several orders of magnitude.
Figure 1.
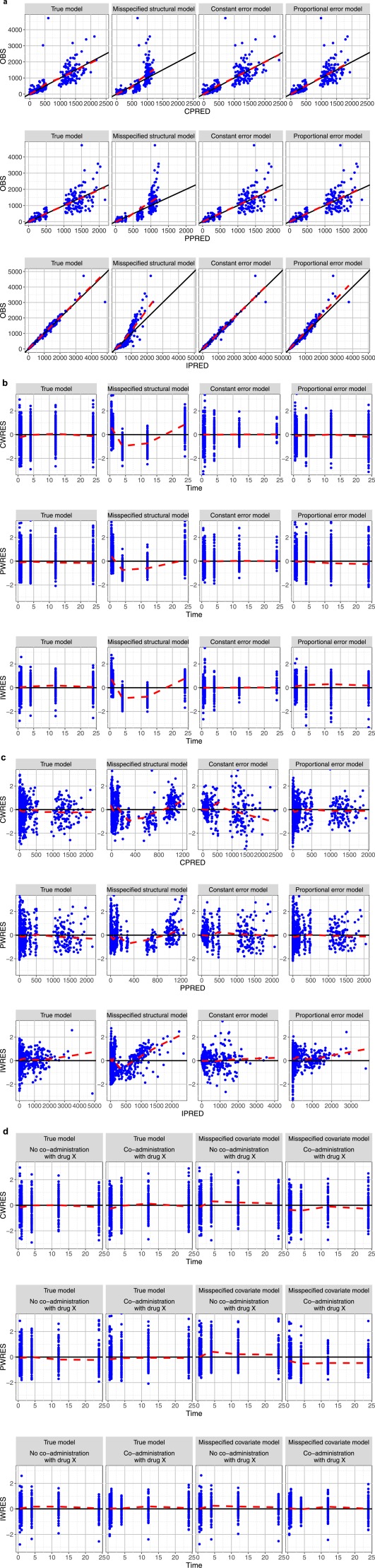
Basic goodness‐of‐fit plots for different models (a) Observation vs. population predictions calculated using the first order conditional estimation (FOCE) method (conditional population predictions (CPRED), first row), Monte Carlo simulation (simulation‐based population predictions (PPRED), second row), or individual predictions (IPRED, third row) for true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). Identity and local regression lines are presented in black and red, respectively. This graph clearly points out that the wrong structural model underpredicted high concentrations, whereas misspecification of the residual error model is more difficult to be detected using this type of goodness‐of‐fit plots. (b) Weighted residuals (conditional weighted residual (CWRES), population weighted residual (PWRES), and individual weighted residuals (IWRES) from the first row to third row, respectively) vs. time plots for true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). The xWRES are shown as blue points, spline lines are also added in these graphs as the red curves. A systematic trend indicates a misspecification in the structural model (second column). A cone‐shape of residuals indicates a problem of residual errors (third and last columns). (c) Weighted residuals (CWRES, PWRES, and IWRES from the first row to third row, respectively) vs. population predictions plots for true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). (d) Weighted residuals (CWRES, PWRES, and IWRES from the first row to third row, respectively) vs. time, stratifying on binary covariate (concomitant treatment yes/no) for the true model and the model lacking covariate effects. Systemic biases in the PWRES vs. time plots when conditioning on covariate indicates the need to include the covariate in the model (third and second lines). Unlike PWRES, no visually significant trend can be found in the plots of IWRES vs. time of the model lacking covariates. This emphasizes once again that IWRES‐based graphs cannot be used to evaluate a covariate model.
Population residuals
The population residuals (– xRES with x = ∅, C, or P) are defined as the difference between the observations and population predictions (xRESi = yi – xPREDi). These residuals are correlated within each individual and their magnitude may depend on that of observations if the residual error model is not homogeneous (i.e., an additive error model), which we call heteroscedastic. Population weighted residuals (xWRES) standardize and decorrelate the population residuals using the model‐predicted variance‐covariance matrix of observations, Var(yi):
| (11) |
Depending on the methods used to compute population xPRED and model‐predicted Var(yi), there are various types of population weighted residuals (PWRES). The classical PWRES, termed WRES, are calculated from PRED and Var(yi) obtained with the FO approximation (Eqs. (8) and (12)).
| (12) |
Another type of PWRES, termed CWRES, is obtained from CPRED and Var(yi) computed by FOCE (Eqs. (9) and (13)).
| (13) |
Weighted residuals can also be obtained using PPRED and Var(yi) calculated from Monte Carlo simulation (Eqs. (10) and (14)). These residuals are called PWRES or expectation weighted residuals in MONOLIX and NONMEM, respectively.
| (14) |
Among these three types of population weighted residuals, WRES was shown to result in misleading diagnoses in some instances, especially when the model becomes highly nonlinear, which causes the FO approximation to be poor.5, 7 CWRES obtained by FOCE and PWRES obtained by Monte Carlo simulation have been shown to have better performance in evaluation of NLMEM5, 7 and we present graphs for these types of weighted residuals for the PK example. By definition, if the model is true, xWRES should have zero mean and unit variance. However, unlike weighted residuals of linear mixed models, which should follow a normal distribution if the model is correct, the xWRES of NLMEM have an unknown distribution because the marginal distribution of observations is not normal.
Various graphs based on PWRES have been proposed to evaluate NLMEM, such as the scatterplots of PWRES vs. time (first and second rows of Figure 1 b) or vs. population predictions (first and second rows of Figure 1 c). If the model is true, the PWRES should be randomly scattered around the horizontal zero‐line, as shown in the first row of Figure 1 b and 1 c), in which the true model was fitted to the data. A systematic bias from the zero‐line may imply deficiencies in the structural model (second row of Figure 1 b and 1 c) but can also be a consequence of informative censoring or adaptive designs. A misclassified error model can be identified from the amplitude of the residual distribution along the x‐axis (e.g., a cone‐shape pattern of residuals would suggest a heteroscedastic error model; third and last rows of Figure 1 b and 1 c). Trends that appear when conditioning on covariates (first and second rows of Figure 1 d) or when plotting PWRES vs. covariates may suggest a problem in the covariate model or of the need to include covariates in the model. Of note, as in NLMEM, observations may not be distributed symmetrically around the mean, the xWRES, regardless of how they are computed, are not necessarily distributed evenly around the horizontal zero line even in absence of misspecification, especially for models with high nonlinearity with respect to random effects and large interindividual variability. Another point to bear in mind when examining these weighted residuals is that decorrelation using the full variance‐covariance matrix may cause some modifications in the trend lines, for instance, the position where the trend appears in the plots vs. time or predictions may be different from where it is when examining graphs of normal residuals vs. time or vs. predictions.
Evaluation based on individual predictions and individual random effects
Individual predictions and individual residuals
Individual estimated vector of random effect ( (i.e., evaluation based on effects (EBEs)) can be used to calculate other individual‐based evaluation metrics, such as individual predictions (IPRED) and individual weighted residuals (IWRES).
| (15) |
| (16) |
Several types of graphs based on these individual metrics can be used for model evaluation. First of all, the graph of IPRED vs. observations offers a global assessment of the individual fit for all patients, mainly to identify a misspecification in structural model (last row of Figure 1 a). The considerations provided for the observations vs. population predictions graph are also applicable here. Deficiencies in structural and residual error models can be detected using the scatterplot of IWRES vs. time (last row of Figure 1 b) or IPREDs (last row of Figure 1 c). The graphs based on IPREDs or residuals are similar to those based on population predictions but with less variability because interindividual variability was taken into account in their computation. Therefore, in some cases, model misspecification can be detected more easily with individual‐based metrics. However, unlike population‐based metrics, IPRED and residuals do not allow for evaluation of covariate models (last row of Figure 1 d) as the variability that results from any existing covariate that is not taken into account will be considered to be part of interindividual variability and, therefore, is included in the estimated individual random effect, .
Finally, the individual fit, obtained by superposing the individual observations and the IPRED over the independent variable in the same graph, is one of the most frequently presented evaluation graphs. It provides a simple way to visualize whether the model is able to describe individual data profiles. A substantial discordance between predictions and observations could indicate a problem in the population model, either in the structural model or in the variability model. However, it would be difficult to determine the primary cause based solely on this graph (Supplementary Figure S3). This graph is also useful for identifying practical problems in the data, such as sample switching, bioanalysis errors, etc. However, with a large number of patients, it will be challenging to examine all the individual fitted graphs. Population predictions can be added to the individual fits to provide more information, for instance, about shrinkage (see below) or how an individual response differs from that of the population. This is a helpful way of seeing the IPRED appear to be randomly scattered around the population prediction.
Evaluation based on empirical Bayes estimates
The estimated EBEs can also be used as an evaluation metric. They can be used to evaluate the interindividual variability model. For each component of the vector of EBEs (or of the vector individual parameter estimates), graphs, such as a histogram or a boxplot, could be drawn and compared to their estimated predicted population distribution. A substantial discordance between an EBE distribution and a population distribution may imply misspecification of the random effect models. For instance, a multimodal distribution of an EBE would suggest the need to include covariates or use a parameter distribution other than the assumed distribution (e.g., log‐normal distribution) for the corresponding random effect; a high kurtosis in an EBE distribution may indicate poor individual information or an incorrect underlying distribution assumption and suggest that variability of this random effect may be poorly estimated. EBEs can also be plotted vs. each other to identify correlation between random effects (Supplementary Figure S4a). High correlation between EBEs of several parameters may also indicate a problem in model parameterization (overparameterization or nonidentifiability of model parameters). If the model correctly handles random effect correlation, one expects to see almost no trend in the graphs with decorrelated EBEs, (Supplementary Figure S4b), obtained by standardizing the EBEs using the estimated variance‐covariance matrix of random effects (Eq. (17)).
| (17) |
EBE‐based evaluation graphs can also be used to detect deficiencies in the structural model. For instance, the graph of each EBE component vs. doses is one of the simplest methods to detect model deficiencies for drugs with nonlinear PK. Another important and frequent use of EBE‐based evaluation graphs is to screen covariate effect and evaluate a covariate model. This can be done by examining the correlation between EBE component and a continuous covariate or a boxplot stratified by different classes of a categorical covariate. If the model correctly takes into account the covariate effect, a correlation would be expected between the covariate and the corresponding individual parameter estimates (Supplementary Figure S5a), but no correlation should remain between the corresponding EBE and the covariate (Supplementary Figure S5b). With rich individual information, the square value of the coefficient of correlation between the covariate and the individual parameter estimates represents the fraction of interindividual variability that is explained by the covariate.
Influence of shrinkage on individual‐based evaluation tools
The estimation of EBE and IPREDs is susceptible to a phenomenon called shrinkage that occurs when the individual data are not sufficiently informative with respect to one or more parameters.10 Under these conditions, the EBE and individual parameter estimates would shrink close to the population mean. This phenomenon can be quantified by η‐shrinkage, estimated by 1‐ SD(EBE)/ω or 1‐ var(EBE)/ω2, where ω is the interindividual SD estimated in the population model.10 The fact that IPREDs may tend to the individual observations for more or less sparse designs can be quantified by ε‐shrinkage, defined as 1‐SD(IWRES) or 1‐var(IWRES), where IWRES are the individual weighted residuals.10 Of note, there are two definitions of shrinkage in literature, one based on the ratio of variances, and one based on the ratio of SDs.
With high shrinkage, the individual‐based evaluation tools become less informative and do not allow for a correct evaluation of a model. For instance, a high η‐shrinkage may hide or falsely induce the true relationships or distort the shape of the EBE distribution, of the correlation between EBEs (Supplementary Figure S6a) or of the correlation between EBEs and covariates (Supplementary Figure S6b).7, 10 If overfitting occurs, IWRES will shrink toward 0, which makes model evaluation based on this metric less effective or informative.7 Supplementary Figure S7a provides IPRED vs. observations plots, at different levels of ε‐shrinkage, of the misspecified structural model. Supplementary Figure S7b shows the same graphs of population predictions in which we can also see the influence of limited information.
SIMULATION‐BASED EVALUATION TOOLS
Simulation‐based evaluation tools were first developed by Bayesian statisticians and are now increasingly used to evaluate NLMEM. They rely on the concept of the posterior predictive check,11 whose principle is that if a model correctly describes a dataset, the data simulated under that model would be similar to the observations. Hence, to evaluate a model with these methods, one needs to simulate a large number (K) of Monte Carlo samples under the tested model, using the design of the observed dataset then compare a statistic computed from the observed data with that computed from the simulated data. The chosen statistic can be a PK parameter calculated from noncompartmental analysis, for instance, area under the curve, half‐life, steady‐state concentration, maximum or minimum concentration,12, 13 or other statistical inferences, such as mean prediction errors (residuals), root mean square prediction errors,11, 13 or objective function value.14
Instead of using a statistic that condenses all the information of the observations into a single value, one can also evaluate a model using all the observations by comparing the observations with their predicted distribution. These observation‐based posterior predictive checks, such as the VPC,8 prediction discrepancies (pd), and normalized prediction distribution errors (NPDE)4, 6 are among the most frequently used simulation‐based evaluation tools. We may compare the observed statistics or observations with their distribution via graphical assessment or statistical tests. The use of statistical tests is not considered in this tutorial but is discussed in several papers.6, 11, 15, 16, 17
Visual and numeric predictive check
The VPC offers a graphical comparison of the distribution of observations and the distribution of predictions vs. an independent variable, such as time, dose, or other covariates.8 It comprises in comparing the distribution of the observations with that of the predictions using different percentiles of the distributions. A classical presentation of VPC, originally termed “scatter VPC,” is obtained by plotting the observations together with the predicted percentiles of the simulated data (usually 2.5, 50, and 97.5th, or 5, 50, and 95th, or 10, 50, and 90th percentiles) over the independent variable.8, 9 The area defined by the lowest and highest percentiles is usually called the prediction interval (PI) of the data, for instance, 10th and 90th percentile define a 80% PI (Supplementary Figure S8a). The “scatter VPC” characterizes model appropriateness by comparing the number of observations included within or outside a selected PI of data with a theoretical value. For instance, in a VPC with an 80% PI, we expect to have 80% of the observations within the 80% PI, 50% above and 50% below the median, 10% above the 90th percentile and 10% below the 10th percentile.
A more visually intuitive representation of VPC has been proposed and has rapidly gained popularity within the last few years.9 In this new version of VPC, termed “confidence interval (CI) VPC,” the percentiles of the observations, the predicted percentiles, and their 95% CIs are plotted (Supplementary Figure S8b).9 For this type of VPC, data binning, in which an independent variable (usually time) has to be split into several bins, each containing an approximately equal number of observations, is necessary to calculate the percentiles of observed and predicted data.9 The CIs of the predicted percentiles are obtained using the K Monte Carlo samples: the same selected percentiles (e.g., 2.5, 50, and 97.5th percentiles), are calculated for each of the K simulated datasets. The 95% CI for each of the selected percentiles is then easily obtained from the distribution of the K percentiles computed for the K simulated datasets. If the model is correct, the observed percentiles should be close to the predicted percentiles and remain within the corresponding CI. However, an appropriate VPC may still result from models in which individual unexplained variability is misspecified, either because it is absorbed by other model components (interoccasional variability by residual variability, for instance) or because it is contributing little to the overall variability (e.g., residual variability in the presence of large interindividual variability).
An important property of VPC is that it conserves the original units (e.g., time, concentration, etc.) of the model, therefore, appears familiar. However, VPC also has some drawbacks. First of all, data binning (frequently necessary to construct a “CI VPC”) is challenging for unbalanced designs with differing numbers of observations at each time point and may influence the interpretation of VPC.18, 19 Second, heterogeneity in design, such as differing doses, dosing regimen, route of administration, or covariates, may render the VPC for the whole data noninformative.20 For instance, in Supplementary Figures S8a,b, the upper, median, and lower predicted percentiles or CIs correspond to the observations following the highest, median, and lowest dose, respectively. In such cases, data stratification by dose and/or by important covariates or dose normalization may mitigate these problems. However, data stratification often leads to a loss of power and dose normalization may not be appropriate for nonlinear pharmacokinetics (i.e., the model is nonlinear with respect to dose). Prediction‐corrected VPC (pcVPC) offers a solution to these problems while retaining the visual presentation of the VPC (Supplementary Figure S8c,d).20 In a pcVPC, the variability in each bin is removed by normalizing the observed and simulated dependent variables based on the typical population prediction for the median independent variables.20 The observation yij and the corresponding simulated data are corrected by the given formulae:
| (18) |
| (19) |
where is the population prediction for the median independent variables in a specific bin and is the population prediction for individual i at time j. In the seminal paper, Bergstrand et al.20 proposed to use PRED for population predictions, whereas in the PK example, we calculated the pcVPC using PPRED. Of note, for continuous covariates, a VPC may be constructed using a covariate, such as body weight, age, or model predictions, as the independent variable. This does not lose power like data stratification methods and can provide useful confirmation of the appropriateness of a covariate model.9, 21
Despite these limitations, the VPC offers a very intuitive assessment of misspecification in structural, variability, and covariate models, therefore, has now become a widely used evaluation tool for evaluating NLMEM. Figure 2 a,b shows the VPC plots of different models. We can clearly see that observed percentiles remain within the corresponding intervals for the true model (first column) whereas clear departure from the CI is evident for misspecified structural, residual error (Figure 2 a) and covariate models (Figure 2 b).
Figure 2.
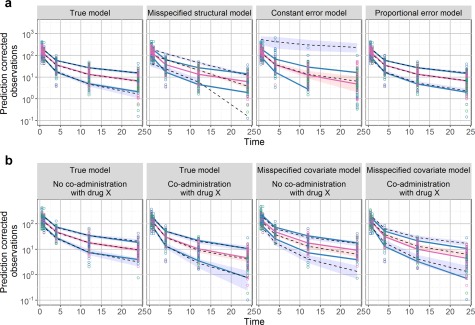
The prediction‐corrected visual predictive checks (pcVPCs) plots of different models. The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Observations corresponding to the lowest, median, and highest doses are shown in blue, pink, and green, respectively. (a) pcVPC for different models: true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). A systemic departure of the observed percentiles from the prediction intervals could indicate a misspecification in structural or residual error model. (b) pcVPC stratified by covariate for true model (first two columns) and misspecified covariate model (last two columns) Trends observed when stratifying on covariates helps to evaluate the covariate model.
The numeric version of VPC, known as the numeric predictive check (NPC), is also used in model evaluation.9, 22 It summarizes the information of several “scatter VPCs” evaluated at different selected PIs, for instance, the 0, 20, 40, 50, 60, 80, 90, and 95% PI.9, 22 NPC calculates the percentages of outliers for each selected PI, which are the observed data above and below different PIs. By providing the same calculation for each of the K simulated datasets, we can obtain a CI for the percentages of outliers. The observed percentages can be compared with the empirical CI using a coverage plot. Just as in a VPC plot, a trend in the NPC coverage plot would indicate a misspecification of the structural, interindividual variability, or residual error model (Supplementary Figure S9). As NPC evaluates model misspecification on several PIs, it may provide additional information compared to the VPC, which only presents one selected PI. In addition, it compares each observation with its own simulated distribution, so normalization and stratification to handle the binning, as in the VPC, is not necessary. However, unlike VPC, which is a representation of observations and predictions vs. time, NPC loses the time dimension; therefore, it would not be able to point out at which time points the model overpredicted or underpredicted the data.
Prediction discrepancies and normalized prediction distribution errors
Prediction discrepancies are a form of observation‐based posterior predictive checks, developed for NLMEM by Mentré and Escolano.4 Let Fij denote the cumulative distribution function of the observation yij for the individual i. The prediction discrepancy of this observation is defined as its percentile in the predictive distribution, given by:
| (20) |
Using the predictive distribution approximated by the K Monte Carlo simulation samples, the prediction discrepancy is then calculated by:
| (21) |
The computation of the pd uses the same simulations as the VPC. The pd of an observation yij are indeed computed as the number of times that the simulations are under the observation in a VPC.
A decorrelated version of pd, the prediction distribution error, has been proposed in order to enable the use of statistical tests.6 The prediction distribution errors are computed in the same way of pd but from decorrelated (observed and simulated) data, obtained using Eq. (11) with PPRED and Var (yi) calculated by a Monte Carlo method (Eqs. (10) and (14)):
| (22) |
where and are decorrelated observed and simulated data, respectively. By construction, pd and prediction distribution error are expected to follow a uniform distribution, U[0,1] if the model describes the data adequately. The normalized pd and prediction distribution error, denoted npd and NPDE, calculated by Eq. (23), follow a normal distribution with zero‐mean and unit variance, N(0,1):
| (23) |
where Φ is the inverse function of the cumulative distribution function of N(0,1).
As the npd and NPDE naturally account for the heterogeneity in study design by comparing the observations with their own distribution, no data stratification or dose normalization are required for a global evaluation using these metrics (Supplementary Figure S10a), although covariate model exploration can benefit from stratifying the NPDE plots vs. covariate values or categories. This is an advantage of npd or NPDE compared to the traditional VPC. The assessment of npd and NPDE could be done using several types of graphs, such as scatterplots vs. time or predictions, quantile‐quantile (q‐q) plots or histograms, scatterplots or boxplots vs. continuous or categorical covariates or doses. For those who prefer the presentation of a VPC, in which the original units of the model and data are conserved, a transformed version of the npd and NPDE has been proposed to take into account the shape of data evolution over time (Supplementary Figure S10b).23 As in a VPC, the observed percentiles and CIs of predicted percentiles can also be added into the evaluation graphs of npd and NPDE, which requires binning the data. Like graphs based on population residuals, scatterplots of npd or NPDE vs. time or predictions are helpful to detect and distinguish different types of model misspecification (e.g., structural, residuals, or covariates). Figure 3 a–c shows the graphs of npd vs. time and predictions for different models. We can see that misspecification in the structural model, the error model, and the covariate model can be detected by the departure of the observed percentiles from their prediction intervals. For graphical evaluation, it may sometimes be better to use npd instead of NPDE because decorrelation can induce artifacts (i.e., create trends or make trends less apparent in the scatterplots of NPDE vs. time or predictions),17 as we can see in Figure 3 d,e.
Figure 3.
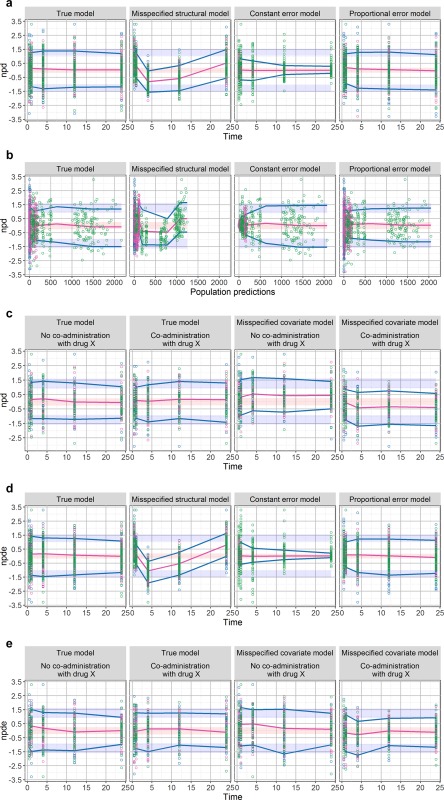
Scatterplots of normalized prediction distribution (npd) or normalized prediction distribution error (NPDE) vs. time or population predictions (PPREDs) for different models. The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Observations corresponding to the lowest, median, and highest doses are shown in blue, pink, and green, respectively. (a) The npd vs. time (first row) for the true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). A systematic trend indicates a misspecification in the structural model. A cone‐shape of residuals indicates a problem of residual errors. (b) The npd vs. PPRED (second row) for the true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). (c) The npd vs. time stratified by binary covariate for the true (first and second columns) and misspecified covariate model (third and last columns). Systemic biases when conditioning on covariate reveal a deficiency in the covariate model. (d) NPDE vs. time for the true model (first column), misspecified structural model (second column), misspecified constant error model (third column), and misspecified proportional error model (last column). In this case, decorrelation makes the trends become less apparent, especially for the misspecified proportional error model. (e) NPDE vs. time for the true (first and second columns) and misspecified covariate model (third and last columns), stratified by the binary covariate (concomitant treatment). In this case, decorrelation makes the trends to detect a lack of covariate effect become less apparent.
CORE SET OF COMMON GRAPHS FOR MODEL EVALUATION
Because NLMEM relies on several assumptions and that no evaluation tool can address all the components of a model, a comprehensive evaluation of a pharmacometric model would usually require examination of several diagnostic graphs, as described in detail in the previous section. A brief description of each evaluation tool and which model component it addresses is summarized in Table 1 and Supplementary Table S3.
In this tutorial, we recommend a core set of common graphs that are useful in most situations for comprehensive evaluation of a pharmacometric model (column “In core set” in Table 1). This core set of evaluation graphs includes basic prediction‐based graphs, such as population or IPREDs vs. observations, individual fits, EBE correlation graphs, and simulation‐based graphs (VPC and npd). However, any diagnostic based on EBEs (i.e., EBE, IPRED, and IWRES), may be misleading in the presence of substantial shrinkage. For population predictions and residuals, we recommend to use CPRED (and CWRES) or PPRED (and PWRES), depending on the estimation method. More specifically CPRED and CWRES could be used for FOCE estimation, and PPRED and PWRES when the estimation methods do not involve linearization.
For VPC, we recommend to use VPC showing observed and predicted percentiles, such as the “CI” VPC or the “percentile” VPC.9 The scatter VPC is discouraged because it is hard to compare the observation distribution with the predictions, especially when there are many data points. The pcVPC is recommended if there are important covariate effects, or different dose groups, or an adaptive trial design has been used.
For EBE correlation graphs, scatterplots of decorrelated EBEs can also be examined if the variance‐covariance matrix of random effects was not diagonal.
To evaluate a covariate model, some additional graphs are required according to the column “In core set” in Table 1.
PHARMACOKINETIC PHARMACODYNAMIC CASE EXAMPLE
In this section, we illustrate the use of the core set of evaluation graphs on a PK/PD example that is more realistic for modeling practice. In this example, we only evaluate the PD model and, as there is no covariate effect in the PD model, no graphs for evaluating covariate model are displayed.
Structural and statistical models
The exemplary PK/PD model for warfarin is based on data reported by O'Reilly et al.24 and O'Reilly and Aggeler.25 The PK model, describing total warfarin concentration following a single dose administration, is a one‐compartment model with first‐order absorption, a lag‐time, and first‐order elimination. A turnover PD model with an inhibitory maximum effect (Emax) function on the rate of prothrombin complex activity (PCA) production describes the effect of warfarin on PCA. The structural model for the PK/PD of warfarin is described by the following set of differential equations:
| (24) |
where A1(t) and A2(t) are the warfarin amounts at the site of absorption and in the central compartment, respectively. C(t) is the total warfarin concentration, CL, V, Tabs, and Tlag represent clearance, central volume of distribution, absorption half‐life, and lag time, respectively. CL and V were allometrically scaled by body weight using 70 kg as the reference value with the allometric exponent β fixed at 3/4 and 1, respectively (Eq. (25)). This is an equivalent expression of Eq. (5) with the transformation described in Eqs. (5) and (6). There are no covariate effects on the PD parameters. PCA(t) denotes the activity of prothrombin complex. PCA is produced with a zero‐order rate Rin and eliminated with first‐order rate constant kout, equal to ln(2)/Teq, where Teq is the half‐life of PCA elimination. PCA was assumed to be at steady state before administration of warfarin with the baseline PCA0 = Rin/kout. The models were parameterized using PCA0 instead of Rin. Emax is a parameter denoting the maximum possible effect of warfarin and C50 denotes the concentration of warfarin that results in half‐maximal inhibition.
| (25) |
We assumed log‐normal distribution for CL, V, Tabs Tlag, Emax, C50, PCA0, and Teq (Eq. (4)). A combined additive and proportional residual error model was used for the PK predictions and an additive residual error model for the PD predictions. Model parameters are provided in Supplementary Table S2.
Study design and data simulation
We considered the same design as the one used in the original study.24 There were 27 male and 5 female patients (N = 32). Body weight ranged from 40–102 kg. The administered doses were calculated on a 1.5 mg per kg basis. Central compartment drug concentrations (mg/L) and PCA (PCA unit) were measured as described in the original report. A dataset was simulated using the design and models described above.
Evaluated scenarios
To mimic different types of model misspecification, we fitted several models to the simulated data: a) a misspecified structural PD model with effect immediately related to concentration (misspecified delay, immediate effect); b) a misspecified structural PD model with an effect compartment (misspecified delay, effect compartment); c) a misspecified structural PD model and variability model, in which an effect compartment was used for the PD part and covariance between all PK parameters in one block and all PD parameters in another block was considered (misspecified delay and correlation, effect compartment, and full omega); and d) the true model that was used for data simulation (true model, turnover PD).
Parameter estimation, computation of evaluation metrics, and software
Data simulation was performed using NONMEM version 7.3 (http://www.iconplc.com/innovation/solutions/nonmem/). For parameter estimation, the PK model was first fitted to the simulated concentrations. The population PK parameters were then fixed at their estimated values to perform data fitting for the PCA observations. Thus, only the PD model was misspecified in this example. Parameter estimation was performed using the Quasi‐random Parametric Expectation Maximization algorithm26 in Phoenix NLME 7.0 (https://www.certara.com/software/pkpd-modeling-and-simulation/phoenix-nlme/) keeping all default settings. For simulation‐based evaluation graphs, a thousand replicates were performed.
Core set of graphs for model evaluation
In this section, we go through a core set of model evaluation graphs for each PK/PD model (Figure 4 for the misspecified delay, immediate effect model; Figure 5 for the misspecified delay, effect compartment model; Figure 6 for the misspecified delay and correlation model; and Figure 7 for the true turn‐over model) and provide our assessment in a more general sense to illustrate how these evaluation graphs may be interpreted if the true model is not known. Here, as our model does not contain covariates, we did not present the specific graphs that can be used to evaluate the covariate model. For the basic prediction‐based graphs, we presented PPRED and PWRES graphs because we estimated parameters using the Expectation‐Maximization algorithm.
Figure 4.
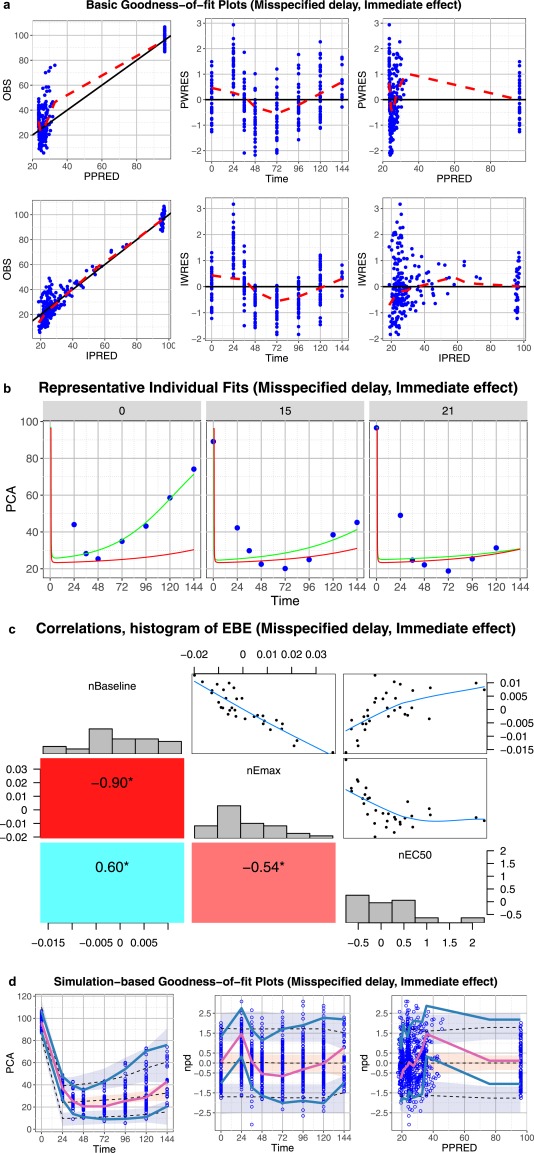
Core set of diagnostic graphs for misspecified delay, immediate effect model. (a) Basic goodness‐of‐fit plots. Blue points denote individual data points. Lowess lines are in red. Interpretation should focus on areas where the data are available with little attention to gaps. (b) Representative randomly selected individual fits. Blue points denote individual observed data points, the green curve is the individual predicted (IPRED), and the red curve is the population predicted (PRED). (c) Correlations and histogram of empirical Bayes estimates. (d) Simulation‐based diagnostic plots (visual predictive check (VPC), normalized prediction distribution (npd)). The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Blue circles are individual observations. Several graphs are pointing to a potential model deficiency. Residuals, individual fits, VPCs, and npd vs. time show an obvious problem with the ability to fit the time course of the data. The model predicts a fast and sharp decline from time 0 to 24 hours, whereas the data show a gradual delayed decrease.
Figure 5.
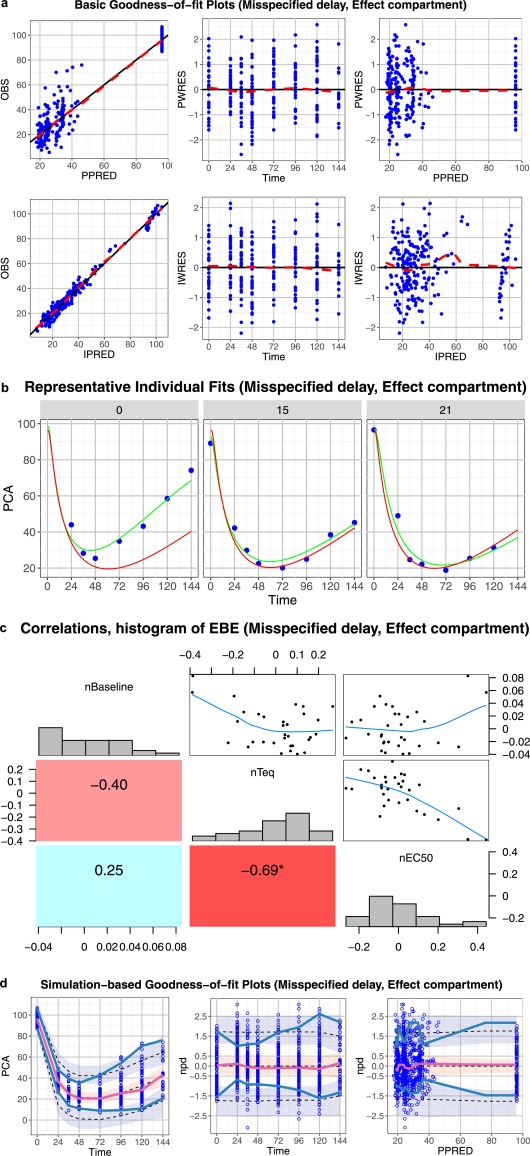
Core set of diagnostic graphs for misspecified delay, effect compartment model. (a) Basic goodness‐of‐fit plots. Blue points denote individual data points. Lowess lines are in red. Interpretation should focus on areas where the data are available with little attention to gaps. (b) Representative randomly selected individual fits. Blue points denote individual observed data points, green curve is the individual prediction (IPRED), red curve is the population predicted (PRED). (c) Correlations, distribution, and histogram of empirical Bayes estimates (EBEs). (d) Simulation‐based diagnostic plots (visual predictive check (VPC), normalized prediction distribution (npd)). The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Blue circles are individual observations. Basic goodness‐of‐fit plots and individual fits provide no hint for model and data disagreement. Simulation‐based graphs clearly show that the model can only describe the median and fails to characterize the upper and lower percentiles. The EBE correlation graphs show high correlations between all pharmacodynamic (PD) parameters and this could be an indication of model misspecification.
Figure 6.
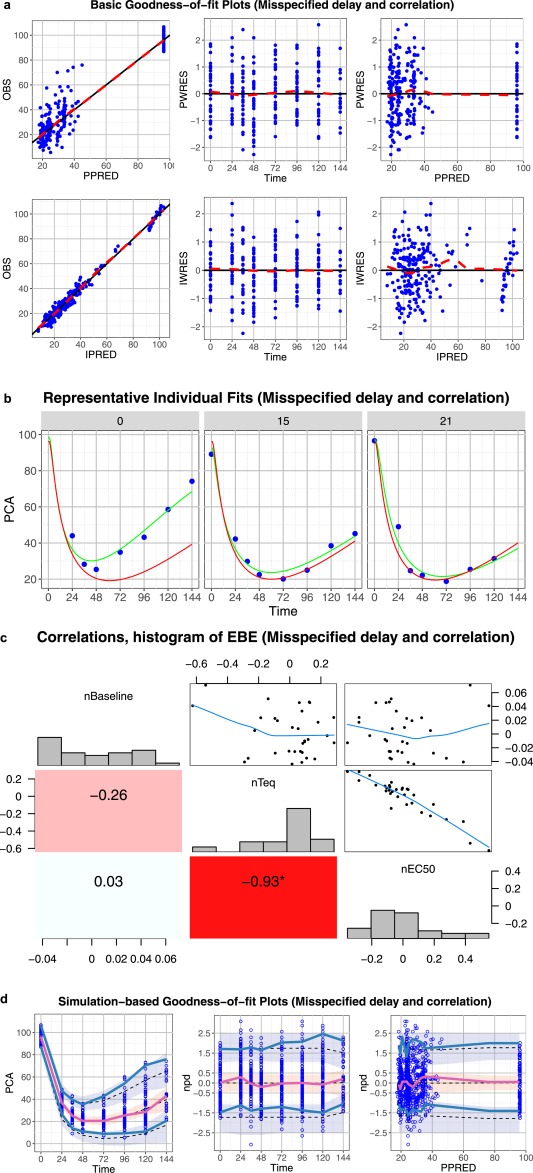
Core set of diagnostic graphs for misspecified delay and correlation model (effect compartment, full omega). (a) Basic goodness‐of‐fit plots. Blue points denote individual data points. Lowess lines are in red. Interpretation should focus on areas where the data are available with little attention to gaps. (b) Representative randomly selected individual fits. Blue points denote individual observed data points, green curve is the individual prediction (IPRED), red curve is the population predicted (PRED). (c) Correlations, distribution, and histogram of empirical Bayes estimates. (d) Simulation‐based diagnostic plots (visual predictive check (VPC), normalized prediction distribution (npd)). The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Blue circles are individual observations. The discordance between the 10th and 90th observed percentiles and the corresponding predicted percentiles show that the model may not be able to characterize the data. High correlation between two parameters may indicate a problem in model parameterization.
Figure 7.
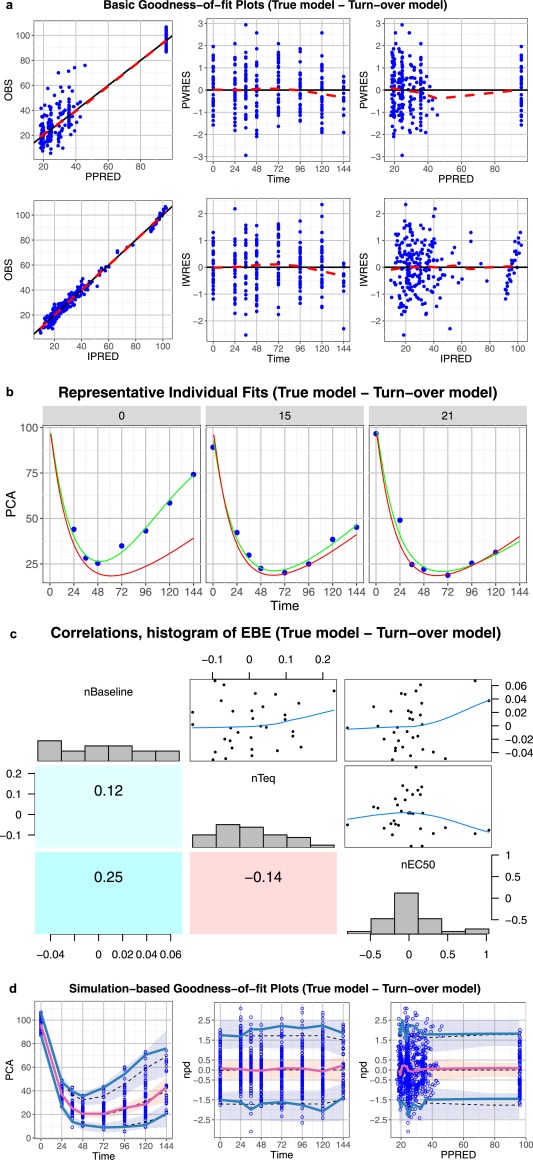
Core set of diagnostic graphs for true model – turnover model. (a) Basic goodness‐of‐fit plots for the true turnover pharmacodynamic (PD) model. Blue points denote individual data points. Lowess lines are in red. Interpretation should focus on areas where the data are available with little attention to the gaps. (b) Representative randomly selected individual fits from the true turnover PD model. Blue points denote individual observed data points, green curve is the individual prediction (IPRED), red curve is the population predicted (PRED). (c) Correlations, distribution histogram, and scatterplots of empirical Bayes estimates. (d) Simulation‐based diagnostic plots (visual predictive check (VPC), normalized prediction distribution (npd)). The blue and red lines are the observed percentiles (10, 50, and 90th percentiles), the blue and red ribbons are the corresponding 95% confidence intervals. The dashed black lines are predicted percentiles. Blue circles are individual observations. In general all graphs point to a good model with the exception of the VPC and npd vs. time graphs that are pointing to a potential underestimation of the data 90th percentiles and to a lower extent to an underestimation of the 10th percentiles.
Misspecified delay, immediate effect model
Because the data covers a large range, although the scatterplots of observations vs. PPRED or IPRED or the graphs of PWRES or IWRES vs. predictions are not very informative as there is a big gap in the data, the trends in those graphs can still show that there is a discordance between the data and model (Figure 4 a, first and last columns). Splitting those graphs into several graphs with different scales may allow for easier interpretation. Clear trends can be observed in the graphs of PWRES or IWRES vs. time, showing that the structural model is not sufficient to describe the observations (Figure 4 a, second column). The discordance between the model and observations can also be seen in the individual fit graphs of three randomly selected individuals (Figure 4 b) as well as in the simulation‐based graphs (Figure 4 d). Very high correlations between all PD parameters may be a result of misspecification of the structural model (Figure 4 c).
Misspecified delay, effect compartment model
The basic (prediction‐based) goodness‐of‐fit plots (Figure 5 a), as well as the individual fits (Figure 5 b) do not show any important disagreement between the data and model predictions. However, the simulation‐based graphs with CIs added show that the chosen structural model can describe the median but not sufficiently characterize the upper and lower percentiles (Figure 5 d). High correlations between all PD parameters may indicate that the model is misspecified (Figure 5 c).
Misspecified delay and correlation model
Similar to the previous model, the basic goodness‐of‐fit plots (Figure 6 a) as well as the individual fit plots (Figure 6 b) do not allow seeing an important discordance between the data and model. The simulation‐based diagnostics show that the model describes well the median but seems to fail to capture the 90th percentile and the 10th percentile.
True model – turnover model
All the evaluation graphs of the turnover model show that the model seems to be adequate to describe the data (Figure 7) and reveal no problem with the parametrization of the model (Figure 7 c). Some potential underestimation of the upper 90th percentile can be observed in the VPC and npd vs. time plots and this could indicate that the model may still have some problems in describing the variability. However, in this case, it results from the limited number of observations or patients included in the analysis (Figure 7 d) because the model is known to be correctly specified. This illustrates why the percentiles and CIs should not be used too rigorously to either accept a model or identify problems.
For completeness, Supplementary Figure S12 presents the NPC coverage for different models. The immediate effect model had some observed/expected ratios outside of the CI. Even the observed/expected ratios of the two effect compartment models that remained within the CI show a systemic departure from the expected ratio of 1, indicating that the models may not be appropriate. Finally, an NPC coverage plot of the turnover model with the lower and upper ratio close to 1 confirms that this model seems sufficient to describe the observed data.
DISCUSSION
Numerous model evaluation metrics have been developed to evaluate NLMEM and their underlying assumptions. As mentioned earlier, we focus here only on graphical tools used in model evaluation and not in model building nor in model qualification, even though model evaluation is involved in the two latter steps of modeling. A brief description of each evaluation tool and which model components it addresses are provided in Table 1 and Supplementary Table S3.
Besides the graphical tools presented in this paper, numeric tools and methods, such as model identifiability assessment,27 parameter estimation SEs,2, 12 resampling‐based methods, such as the bootstrap28 or model selection criteria (−2 log likelihood or objective function, Akaike information criterion, and Bayesian information criteria),2, 12, 29, 30 are always used in parallel to provide additional information for the reliability of a model or for model comparison. However, in this first tutorial about model evaluation, we chose to focus only on graphical tools for several reasons. First, graphical tools are commonly used and reported tools for model evaluation. Second, unlike numerical tools that compact all the information of model misspecification in a single statistic, such as a P value, graphical tools can show how much the model is able to characterize the data, where it fails to do so, and, therefore, provide hints for model misspecification. Finally, many numerical tools (e.g., objective function, Akaike information criterion, and Bayesian information criterion) are only useful for comparison between models (in model building or qualification) and do not allow the evaluation of a single model for its adequacy. Of course, we cannot neglect their role in model development.
The evaluation metrics and their visualization discussed in this paper can be classified in two categories: prediction‐based and simulation‐based metrics. Prediction‐based metrics, except for PPRED and PWRES, two metrics that are computed by Monte Carlo simulation, can be provided with little computational burden and, therefore, can be used to assess model appropriateness in every step of model building. However, population prediction‐based metrics computed using FO or FOCE linearization may result in misleading evaluation when the linearization used is inappropriate. Individual prediction‐based metrics may not be sufficiently reliable at high levels of shrinkage (see specific section for more details). For this reason, shrinkage should be evaluated and reported to provide information about relevance of the IPRED‐based evaluation tools. Currently, there is no consensus on the level of shrinkage that renders these individual metrics no longer reliable. A shrinkage value of 30% or 50%, if calculated from SD or variance, respectively, has been suggested as a threshold for high shrinkage,7, 10 but whether this threshold should be applied for all models and population parameter values remains to be evaluated.
As indicated by their name, simulation‐based metrics requires data simulation. However, many design and data features, such as adaptive design, response‐guided treatment, changes in dosing regimen to limit adverse effect or to maintain drug concentrations within the therapeutic window (therapeutic drug monitoring), missing data, or dropout, etc., may be difficult to reproduce through simulation. If these features are neglected, simulation‐based graphs may show significant trends, even though the underlying model is adequate to describe the data.20, 31, 32 One solution is to develop joint models that describe the longitudinal data and the features in question, for instance a time‐to‐event coupled with longitudinal data to handle dropouts, so that the link between the two processes may be correctly taken into account during simulation.31, 32, 33As a large number of simulations is required (usually ≥1,000 simulations),34 the computation of these metrics can be a time‐consuming process, especially with complex models and large datasets, and, therefore, may not always be feasible for evaluating models when the timelines for decision‐making are tight, especially in an industrial setting. However, the resource limitations related to time may become less severe with the widespread availability of high performance computing and better project management.
In general, the uncertainty in model parameters is not always accounted for when computing simulation‐based evaluation metrics. Using a simple PK/PD example, Yano et al.11 found that using point estimates provided similar results to other approaches, which consider not only the point estimates but also parameter uncertainty. Nevertheless, they did mention that this conclusion may depend on study designs and the extent of interindividual variability. Samtani et al.35 suggested that parameter uncertainty could be ignored in data simulation if it is negligible with respect to the between and within subject variability and the sample size available. Otherwise, the computation of simulation‐based metrics should account for uncertainty in the model parameter.35 Even though simulation‐based evaluation tools now have become standard evaluation graphs, which are reported in most population analysis, they may still remain less familiar than classical evaluation tools, such as predictions or weighted residuals to audiences composed of nonmodelers.
Throughout the two examples, we show the properties of several evaluation tools in various situations in which we have different types of model misspecification. Of note, in this tutorial, we used many instances of the terms “model misspecification” or “model deficiency,” as in both examples, we used simulated data and fitted them to different models, which were already known to be true or false. In our opinion, these two terms should not be used in real‐world data‐driven analysis as there is no “true” model and other terms, such as “goodness‐of‐fit” or “agreement with data” are more appropriate.
Various tools have been developed and are required to evaluate NLMEM because no single evaluation tools or planar graphs can effectively address all aspects of the model components. To detect a specific misspecification or to identify a problem, one diagnostic graph may be sufficient (Table 1 and Supplementary Table S3). However, a model may present deficiencies in various components and a misspecification of one component may conceal misspecification in other components. Therefore, in our opinion, in order to comprehensively evaluate a model, the core set of graphs proposed in this paper should be examined.
In summary, we presented in this tutorial different evaluation tools and illustrated their graphical use to evaluate simple pharmacometric models that may arise during all the processes of model development. We also defined a core set of common graphs that may be shown and examined during model evaluation. As the target audience of this tutorial is beginner modelers with statistical or pharmacometric backgrounds, we did not attempt to provide an exhaustive list of all the existing evaluation tools and methods for NLMEM but restricted ourselves to some of the most frequently used tools in pharmacometrics. Although some methods have been proposed to account for several factors that can influence model evaluation, as mentioned in the previous paragraph such as adaptive design,20 data below the limit of quantification36 or dropout,32, 33 we avoided describing these more advanced methods and chose to keep this subject for a future tutorial of the ISoP Model Evaluation group. We also focused only on model evaluation for continuous longitudinal data, which represents a significant portion of population modeling. Model evaluation for other types of data and models, such as discrete data, categorical data, time‐to‐event data, etc., requires additional evaluation tools and would merit additional tutorials.
Supporting information
Supplementary information accompanies this paper on the CPT: Pharmacometrics & Systems Pharmacology website (http://www.wileyonlinelibrary.com/psp4)
Supporting Information S1
Supporting Information S2
Supporting Information S3
Acknowledgments
This work was performed by members of the Model Evaluation (MoEv) Group of the “ISoP Best Practice Committee.” The authors would like to thank other members of the group who participated in the outline of this first tutorial: Malidi Ahamadi, Brian Corrigan, Kevin Dykstra, Marc Lavielle, Robert Leary, Don Mager, Peter Milligan, Flora Musuamba Tshinanu, Rune Overgaard, Marc Pfister, Richard Upton, and Byon Wonkyung. The authors would like also to thank René Bruno, chair of the ISoP Best Practice Committee, for his involvement in the preparation of the tutorial.
References
- 1. Mould, D.R. & Upton, R.N. Basic concepts in population modeling, simulation, and model‐based drug development. CPT Pharmacometrics Syst. Pharmacol. 1, e6 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Mould, D.R. & Upton, R.N. Basic concepts in population modeling, simulation, and model‐based drug development – part 2: introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst. Pharmacol. 2, e38 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Upton, R.N. & Mould, D.R. Basic concepts in population modeling, simulation, and model‐based drug development: part 3 – introduction to pharmacodynamic modeling methods. CPT Pharmacometrics Syst. Pharmacol. 3, e88 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Mentré, F. & Escolano, S. Prediction discrepancies for the evaluation of nonlinear mixed‐effects models. J. Pharmacokinet. Pharmacodyn. 33, 345–367 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Hooker, A.C. , Staatz, C.E. & Karlsson, M.O. Conditional weighted residuals (CWRES): a model diagnostic for the FOCE method. Pharm. Res. 24, 2187–2197 (2007). [DOI] [PubMed] [Google Scholar]
- 6. Brendel, K. , Comets, E. , Laffont, C. , Laveille, C. & Mentré, F. Metrics for external model evaluation with an application to the population pharmacokinetics of gliclazide. Pharm. Res. 23, 2036–2049 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Karlsson, M.O. & Savic, R.M. Diagnosing model diagnostics. Clin. Pharmacol. Ther. 82, 17–20 (2007). [DOI] [PubMed] [Google Scholar]
- 8. Holford, N. VPC: the visual predictive check superiority to standard diagnostic (Rorschach) plots. 14, Abstract 738. <www.page-meeting.org/?abstract=738> (2005).
- 9. Ma, G. , Olsson, B.L. , Rosenborg, J. & Karlsson, M.O. Quantifying lung function progression in asthma. 18, Abstract 1562. <www.page-meeting.org/?abstract=1562> (2009).
- 10. Savic, R.M. & Karlsson, M.O. Importance of shrinkage in empirical Bayes estimates for diagnostics: problems and solutions. AAPS J. 11, 558–569 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Yano, Y. , Beal, S.L. & Sheiner, L.B. Evaluating pharmacokinetic/pharmacodynamic models using the posterior predictive check. J. Pharmacokinet. Pharmacodyn. 28, 171–192 (2001). [DOI] [PubMed] [Google Scholar]
- 12. Bonate, P.L. Pharmacokinetic‐Pharmacodynamic Modeling and Simulation (Springer, New York, NY, 2006). [Google Scholar]
- 13. Acharya, C. , Hooker, A.C. , Jönsson, S. & Karlsson, M.O. A diagnostic tool for population models using non‐compartmental analysis: nca_ppc functionality for R. 23, Abstract 3103. <www.page-meeting.org/?abstract=3103> (2014). [DOI] [PubMed]
- 14. Largajolli, A. , Jönsson, S. & Karlsson, M.O. The OFVPPC: A simulation objective function based diagnostic. 23, Abstract 3208. <www.page-meeting.org/?abstract=3208> (2014).
- 15. Jadhav, P.R. & Gobburu, J.V. A new equivalence based metric for predictive check to qualify mixed‐effects models. AAPS J. 7, E523–E531 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Laffont, C.M. & Concordet, D. A new exact test for the evaluation of population pharmacokinetic and/or pharmacodynamic models using random projections. Pharm. Res. 28, 1948–1962 (2011). [DOI] [PubMed] [Google Scholar]
- 17. Comets, E. , Brendel, K. & Mentré F. Model evaluation in nonlinear mixed effect models, with applications to pharmacokinetics. J. Société Fr. Stat. 151, 106–128 (2010). [Google Scholar]
- 18. Lavielle, M. & Bleakley, K. Automatic data binning for improved visual diagnosis of pharmacometric models. J. Pharmacokinet. Pharmacodyn. 38, 861–871 (2011). [DOI] [PubMed] [Google Scholar]
- 19. Sonehag, C. , Olofsson, N. , Simander, R. , Nordgren, R. & Harling, K. Automatic binning for visual predictive checks. 23, Abstract 3085. <www.page-meeting.org/?abstract=3085> (2014).
- 20. Bergstrand, M. , Hooker, A.C. , Wallin, J.E. & Karlsson, M.O. Prediction‐corrected visual predictive checks for diagnosing nonlinear mixed‐effects models. AAPS J. 13, 143–151 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. McCune, J.S. , Bemer, M.J. , Barrett, J.S. , Scott Baker, K. , Gamis, A.S. & Holford, N.H. Busulfan in infant to adult hematopoietic cell transplant recipients: a population pharmacokinetic model for initial and Bayesian dose personalization. Clin. Cancer Res. 20, 754–763 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Wilkins, J. , Karlsson, M. & Jonsson, E. Patterns and power for the visual predictive check. 15‐2006. 15, Abstract 1029. <www.page-meeting.org/?abstract=1029> (2006).
- 23. Comets, E. , Nguyen, T.H.T. & Mentré, F. Additional features and graphs in the new NPDE library for R. 22, Abstract 2775. <http://www.page-meeting.org/default.asp?abstract=2775> (2013).
- 24. O'Reilly, R.A. , Aggeler, P.M. & Leong, L.S. Studies on the coumarin anticoagulant drugs: the pharmacodynamics of warfarin in man. J. Clin. Invest. 42, 1542–1551 (1963). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. O'Reilly, R.A. & Aggeler, P.M. Studies on coumarin anticoagulant drugs. Initiation of warfarin therapy without a loading dose. Circulation 38, 169–177 (1968). [DOI] [PubMed] [Google Scholar]
- 26. Leary, R. , Dunlavey, M. , Chittenden, J. , Matzuka, B. & Guzy, S. QRPEM—a new standard of accuracy, precision, and efficiency in NLME population PK/PD methods. Pharsight Certara Co <https://www.certara.com/wp-content/uploads/Resources/Brochures/BR_Top10ReasonsWhyPhoenixNLME.pdf> (2011).
- 27. Hengl, S. , Kreutz, C. , Timmer, J. & Maiwald, T. Data‐based identifiability analysis of non‐linear dynamical models. Bioinformatics 23, 2612–2618 (2007). [DOI] [PubMed] [Google Scholar]
- 28. Thai, H.T. , Mentré, F. , Holford, N.H. , Veyrat‐Follet, C. & Comets, E. Evaluation of bootstrap methods for estimating uncertainty of parameters in nonlinear mixed‐effects models: a simulation study in population pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 41, 15–33 (2014). [DOI] [PubMed] [Google Scholar]
- 29. Chen, J. & Chen, Z. Extended Bayesian information criteria for model selection with large model spaces. Biometrika 95, 759–771 (2008). [Google Scholar]
- 30. Delattre, M. , Lavielle, M. & Poursat, M.A. A note on BIC in mixed‐effects models. Electron. J. Stat. 8, 456–475 (2014). [Google Scholar]
- 31. Mould, D.R. & Frame, B. Population pharmacokinetic‐pharmacodynamic modeling of biological agents: when modeling meets reality. J. Clin. Pharmacol. 50(9 suppl), 91S–100S (2010). [DOI] [PubMed] [Google Scholar]
- 32. Friberg, L.E. , de Greef, R. , Kerbusch, T. & Karlsson, M.O. Modeling and simulation of the time course of asenapine exposure response and dropout patterns in acute schizophrenia. Clin. Pharmacol. Ther. 86, 84–91 (2009). [DOI] [PubMed] [Google Scholar]
- 33. Björnsson, M.A. & Simonsson, U.S. Modelling of pain intensity and informative dropout in a dental pain model after naproxcinod, naproxen and placebo administration. Br. J. Clin. Pharmacol. 71, 899–906 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Comets, E. , Brendel, K. & Mentré, F. Computing normalised prediction distribution errors to evaluate nonlinear mixed‐effect models: the NPDE add‐on package for R. Comput . Methods Programs Biomed. 90, 154–166 (2008). [DOI] [PubMed] [Google Scholar]
- 35. Samtani, M.N. , Perez‐Ruixo, J.J. , Brown, K.H. , Cerneus, D. & Molloy, C.J. Pharmacokinetic and pharmacodynamic modeling of pegylated thrombopoietin mimetic peptide (PEG‐TPOm) after single intravenous dose administration in healthy subjects. J. Clin. Pharmacol. 49, 336–350 (2009). [DOI] [PubMed] [Google Scholar]
- 36. Nguyen, T.H. , Comets, E. & Mentré, F. Extension of NPDE for evaluation of nonlinear mixed effect models in presence of data below the quantification limit with applications to HIV dynamic model. J. Pharmacokinet. Pharmacodyn. 39, 499–518 (2012). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary information accompanies this paper on the CPT: Pharmacometrics & Systems Pharmacology website (http://www.wileyonlinelibrary.com/psp4)
Supporting Information S1
Supporting Information S2
Supporting Information S3


